Abstract
The objective of this study was to characterise the behaviour of cross laminated timber (CLT) panels and the influence of the panel lay-up on the failure strength. Three different panel configurations of thickness, 60 mm, 100 mm, and 120 mm, were loaded in the out-of-plane direction. The 60 mm and 120 mm panel configuration comprised three layers of equal thickness, and the intermediate 100 mm thick panel comprised five layers of equal thickness. The mean and characteristic bending and rolling shear strength of the panels were examined. The results show that the mean bending and rolling shear strength decrease with the panel thickness. The characteristic results have shown that there is an influence because of the number of boards within the panel. The characteristic bending strength values for the five-layer 100 mm thick panel were found to be higher than that of the three-layer 60 mm panel. The characteristic rolling shear values decreased in the five-layer panels, however, the increased number of layers subjected to the rolling shear results in a reduced variability in the rolling shear strength.
1. Introduction
The construction industry has seen an increased movement towards more sustainable solutions, leading to a requirement for more environmentally friendly, low carbon, thermally insulating, and less labour-intensive materials in the construction of buildings. Cross laminated timber (CLT) is one of the most promising materials meeting these requirements. CLT is a multi-layer engineered wood panel product, manufactured from at least three layers of boards by glueing their surfaces together with an adhesive under pressure. At present, the mechanical properties of CLT are regulated in industry-produced technical approvals and there are currently steps being taken to collate these technical approvals into the harmonized standard. CLT technology was developed in Europe approximately 20 years ago, and is largely responsible for the increase in timber construction throughout the world. CLT buildings are typically erected using platform or balloon construction methods, connecting the walls and floors with angular metal brackets in combination with screws or nails.
The first activities to standardise CLT in Europe began in 2008 and the first European product standard for CLT, EN 16351 [1], is currently in effect. This product standard details the requirements for CLT production, relating to the material and geometric constraints, manufacturing procedures, and tolerances, in addition to test protocols. EN 16351 [1] defines the board width and thickness. The board width and thickness should be between 40–300 mm and 12–45 mm, respectively. The boards used for the manufacture of CLT are generally conditioned to a moisture content (u) of 12 ± 2% and are visually or mechanically strength graded. The common strength classes according to EN 338 [2] are C24 for a homogeneous layup, C24 for longitudinal layers, and C16/C18 for the transverse layers in a combined layup. In general, the guidelines and requirements of the adhesive manufacturers must be followed in the manufacture of CLT panels. It must be stated that some parameters, such as the bonding pressure, the quantity of applied adhesive, and the moisture content of adherends, are based on experience with glulam production [3,4,5,6,7].
Many studies have examined CLT and its uses in the timber construction industry. Its excellent in-plane and out-of-plane strength, rigidity, and stability have allowed larger and taller buildings to be built [3,8,9,10,11,12]. In Europe, spruce is largely used when manufacturing CLT, however, many other timber species have been investigated worldwide. Fortune and Quenneville [11] aimed to establish the use of CLT in New Zealand using locally-grown Radiata pine, bonded using resorcinol adhesive. In Japan, Sugi timber CLT panels were manufactured by Okabe et al. [13]. In the United States, Hindman and Bouldin [14] produced CLT using Southern pine, which was tested to establish the bending strength, bending stiffness, and shear strength. The CLT panels made from Scottish Sitka spruce was investigated by Crawford et al. [15]. Four CLT panels for each panel configuration (three- and five-layers) were prefabricated using Sitka spruce boards, graded to C16, and bonded with polyurethane (PUR) adhesive. Established bending strengths and stiffnesses in- and out-of-plane were not dissimilar to commercially available CLT panels, manufactured in Central Europe. Similarly, a sample of the CLT panels were manufactured from Irish Sitka spruce by Sikora et al. [9]. Sikora et al. [9] tested six panels in-plane and 12 panels out-of-plane, to investigate the effect of the thickness of CLT panels on the bending stiffness and strength. The tests performed on three-layer and five-layer panels showed a general tendency that the bending strength decreased with panel thickness, but it was stated that further tests are required to determine the characteristic strength values and confirm the observed trend. In all of the cases, the importance of proper quality control, especially for the bonding process, was stated to be significant in ensuring adequate bonding. Manufacturing defects have been shown to result in delamination failure rather than bending or shear failure in isolated cases [9,13,15].
The shear behaviour of the CLT panels is often deemed as one of the most significant factors leading to the failure of the panel, because of the reduced strength in the transverse layers orientated perpendicular to the major axis of the panel. The reason for this is the increased tension perpendicular to the grain stresses in the transverse layers, which, together with rolling shear stresses, lead to a remarkable decrease in resistance [3,16,17]. The comprehensive knowledge of the rolling shear modulus and strength is therefore of the utmost importance in the design of CLT structures. Ehrhart et al. [17] investigated the effect of the sawing pattern and board geometry on the rolling shear behaviour for different timber species. Tests were performed on individual boards and the results showed that the shear modulus and strength were generally underestimated in the product approvals [18,19]. They stated that the higher rolling shear modulus results from current CLT practices, at least in Europe, of using an increasing amount of boards taken closer to the pith than CLT products in the past, which primarily used side-boards [17]. They observed a significant relationship between the rolling shear modulus and the annual ring pattern. Many researchers have performed experimental tests on large scale CLT panels in accordance with EN 16351 [1,8,9,11,15,17,20,21,22]. Blaß and Görlacher [23] established a characteristic value of 1.0 N/mm2 for the rolling shear strength of European spruce, independent of the strength class. The shear tests performed by Sikora et al. [9] on three-layer and five-layer panels, have shown that rolling shear values decrease with the panel thickness, with the mean reported values ranging between 1.0 N/mm2 to 2.0 N/mm2. The geometric properties of the individual boards have also been shown to influence the rolling shear behaviour [3,16,17]. As a result, for the rolling shear stresses in the layers of the CLT loaded out-of-plane, a minimum board width-to-thickness ratio of four is proposed; otherwise, a reduced rolling shear resistance has to be considered [1]. Brandner et al. [3] state that, in accordance with practical applications, the characteristic rolling strength values, ƒr,CLT,k, of 1.40 N/mm2 and 0.80 N/mm2 should be assumed for width-to-thickness ratios greater than or equal to four and width-to-thickness ratios less than four, respectively. According to EN 16351 [1], if the boards are edge glued, a characteristic rolling shear strength of 1.10 N/mm2 may be applied. If edge glueing is not used, and a minimum board width-to-thickness ratio is not achieved, a characteristic rolling shear value of 0.70 N/mm2 is recommended. The typical mean values of rolling shear strength from the experimental results range from 1.0 N/mm2 to 2.0 N/mm2, and while there are characteristic design values proposed dependent on the ratio of the board width-to-thickness, there is no information on the influence of the number of layers and the position of the transverse layer relative to the neutral axis of the CLT panel.
This study examines the bending and rolling shear strength behaviour of CLT panels and the influence of the panel lay-up on the failure behaviour. Three panel configurations are manufactured and tested in accordance with EN 16351 [1]. These comprise two three-layer panel configurations (60 mm and 120 mm thick) and one five-layer panel configuration of thickness 100 mm. A reduced mean bending strength and mean rolling shear strength with an increased panel thickness has been reported [9], with no consideration for the influence of the number of layers on the characteristic failure behaviour. As characteristic strength values are used in the design of structural CLT panels, the influence of the panel thickness and panel lay-up on the characteristic behaviour is investigated here.
2. Materials and Specimen Manufacture
The manufacture of the CLT panels was carried out in accordance with EN 16351 [1]. Three different sizes and test configurations of CLT panels were manufactured in order to determine the bending and rolling shear properties. Boards of C16 Irish Sitka spruce (Picea sitchensis) with nominal cross-sectional dimensions of 100 mm × 35 mm (for panels comprising 20 mm thick layers), and 150 mm × 44 mm (for panels comprising 40 mm thick layers), were used to manufacture the CLT panels. The boards were initially stored in a conditioning chamber at a relative humidity of 65 ± 5% and at a temperature of 20 ± 2 °C, for a period of two months prior to specimen preparation. Prior to fabrication, all of the sides of the boards were planed to the desired board thickness (20 mm and 40 mm) and width (75 mm and 150 mm). The natural frequency of each board was recorded using the MTG acoustic grader in order to determine the modulus of elasticity parallel to grain. A mean value of 8098 N/mm2 was observed. All of the panels were manufactured using a one-component PUR adhesive (PURBOND HB S309), with a spreading rate of 160 g/m2, and a pressure (face bonding only, no edge bonding) of 0.6 N/mm2. These manufacturing parameters are based on the adhesive qualification testing undertaken by Sikora et al. [4]. The pressure was applied using steel plates, tightened with M20 steel bolts to provide the required compressive force, and maintained for a period of 120 min. The manufactured panels were then stored in a conditioning chamber for a period of one month, prior to experimental testing.
3. Experimental Programme
3.1. Introduction
The test panel configurations are presented in Table 1, which gives the number of layers, layer thickness, panel thickness, panel width, and the test span of the panel. The span of the panel was determined from the geometrical constraints outlined in EN 16351 [1]. These geometrical constraints result in different failure modes, namely bending and shear failure modes, allowing the bending and shear strengths to be determined, respectively. For each test configuration, shown in Table 1, eight replicates were tested, giving a total of 48 CLT panels.

Table 1.
Test panel configuration and determined properties.
3.2. Bending Test and Rolling Shear Test
The experimental testing of the strength and stiffness properties of the CLT panels was in accordance with EN 16351 [1]. This standard specifies four-point bending tests over spans of 24–30 times the thickness for the bending strength and stiffness determination, and 12 times the thickness for the (rolling) shear strength determination perpendicular to the plane. The distance between the load points was equal to six times the panel thickness for all of the test configurations. The CLT panels were simply supported, as seen in Figure 1. A load was applied across the whole width of the CLT specimens using steel spreader beams and plates of a width, not greater than half of the panel thickness. The load was applied at a constant rate of displacement, adjusted so that the maximum load was reached within 300 ± 120 s. The bending test set-up for one five-layer panel over a test span of 2400 mm can be seen in Figure 1.

Figure 1.
Four-point bending test set-up on a five-layer cross laminated timber (CLT) panel (B-5-20-7) over a span of 2400 mm.
Initially, each specimen was loaded up to 40% of the estimated maximum load, in order to determine the global and local bending stiffness. The local displacement was measured by linear variable differential transformers (LVDTs) over a central gauge length of five times the panel thickness, in accordance with EN 16351 [1]. The global displacement was measured using two LVDTs at the mid-span on either side of the test specimen. The mean value of these two values was used to calculate the global deflection. The specimen was then loaded to failure at a constant rate of displacement, and the maximum load and vertical global displacement of the test were recorded. The recorded local and global deflection measurements allowed the local and global elastic moduli (EL and EG, respectively), and the local and global stiffnesses (ELI and EGI, respectively) of each panel to be calculated.
The theoretical maximum bending stress (σmax) and rolling shear stress (τrmax) in the specimens loaded perpendicular to the plane were calculated using the maximum test values of the bending moment and the shear force, respectively. The following theoretical methods were applied to evaluate the stresses in the timber: layered beam theory, Gamma beam theory, and shear analogy theory. A comparison of these approximate verification procedures for CLT has been comprehensively investigated by Bogensperger et al. [24] and Li [25]. For the stress calculations in this study, the mean value used for the modulus of elasticity parallel to the grain was 8098 N/mm2, in line with the test results on the modulus of the elasticity of the Sitka spruce boards. The normal and shear stress distributions in a five-layer panel are illustrated in Figure 2a,b, respectively. As the modulus of elasticity perpendicular to the grain (E90) is very low for timber, the contribution of the transverse layers to the bending performance was excluded from the calculations. For the Gamma beam theory calculations, a constant value of 50 N/mm2 was used for the rolling shear modulus, GR, in accordance with Bogensperger et al. [20]. In Figure 2b, the distinction between the maximum shear (τmax) and maximum rolling shear (τrmax) strengths can be seen.
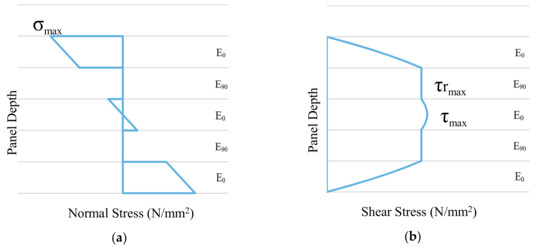
Figure 2.
CLT element loaded out of plane. (a) Normal stress distribution through a five-layer panel assuming E90 = 0 N/mm2; (b) shear stress distribution assuming E90 = 0 N/mm2.
In a five-layer panel, the maximum shear stress occurs in the middle layer, which is orientated similarly to the outermost layers (E0). The maximum rolling shear stress is the greatest in the transverse layers (E90) either side of the middle layer (E0). In a three-layer panel, the maximum shear stress and maximum rolling shear stress both occur in the central transverse layer of the CLT panel.
The theoretical panel bending stiffness (EICLT) based on composite theory is used for comparison with the experimental results. This is calculated using Equation (1).
where:
- E0 = mean MOE of the batch of timber boards used to manufacture the CLT panels.
- Ii = second moment of area of the board, i.
- Ai = area of the board, i.
- yi = distant from the neutral axis of the panel to the centroid of the board, i.
- n = total number of boards, orientated parallel to the span.
Statistical methods have been implemented to examine the distribution of the experimental bending and the shear test results. This has been applied to examine the differences in the panel configuration (Table 1). The characteristic or fifth percentile bending and shear values were determined in accordance with EN 14358 [26], taking into account the adjustment factor, ks, to account for the sample size.
4. Experimental Results
4.1. Introduction
This section details the experimental test results for the CLT panels subjected to four-point flexural tests in accordance with EN 16351 [1]. The bending and shear test configurations have allowed for the respective strength and stiffness values to be determined. The statistical methods have been utilised to establish the characteristic bending strength, and shear and rolling shear values. The influence of the number of layers in each panel configuration has been examined.
4.2. Bending Test Results
The bending test results for all of the panel configurations are presented. All of the specimens failed in tension in the bottom lamination, because of bending as expected. The bending failure of a five-layer panel can be seen in Figure 3 after testing to destruction.

Figure 3.
Bending failure on the bottom tensile face of the panel (B-5-20-7).
The total deflection to the failure of each panel was recorded using the mean measurement from two LVDT’s located at the mid-span on each side of the panel. The deflection to failure from the bending tests on the five-layer panels (configuration B-5-20) can be seen in Figure 4. The maximum moment has been calculated for each test and the analytical models previously mentioned have been used to determine the theoretical maximum bending strength.
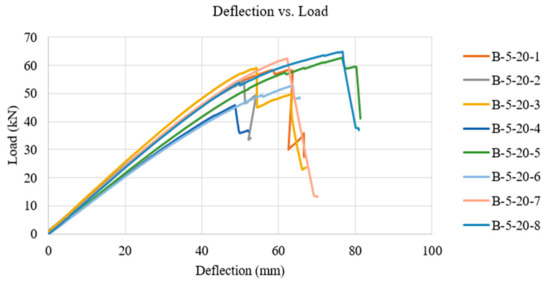
Figure 4.
Panel configuration B-5-20: deflection to failure load behaviour.
Table 2, Table 3 and Table 4 present the individual global and local modulus of elasticity (EG and EL, respectively) and bending stiffness (EGI and ELI, respectively) results of each panel of the three-layer B-3-20, five-layer B-5-20, and three-layer B-3-40 configurations, respectively. The maximum theoretical bending strengths calculated using the layered beam theory, gamma method, and shear analogy method are also presented in addition to the failure mode. The average, standard deviation, and fifth percentile values are also tabulated.

Table 2.
Bending test results for three-layer B-3-20 configuration. EG—global elastic moduli; EGI—global elastic moduli; EL—local stiffness; ELI—global stiffness.

Table 3.
Bending test results for five-layer B-5-20 configuration.

Table 4.
Bending test results for three-layer B-3-40 configuration.
When examining the maximum bending strength, the behaviour of each panel configuration is relatively consistent with the exception of panel B-3-20-5. Panel B-3-20-5 failed in the tension as expected, but failed at a relatively low load of 29.52 kN, due to a series of large knots in adjacent boards on the bottom tension face of the panel.
The mean bending strength results of the 60 mm B-3-20 panel configuration from the layered beam theory, gamma method, and shear analogy method are 35.98 N/mm2, 35.71 N/mm2, and 35.93 N/mm2, respectively. These values are similar to one another with the almost identical results from the layered beam theory and the shear analogy method, and a slightly reduced value for the gamma method. The comparative values for the 100 mm B-5-20 configuration are slightly reduced with bending strength values of 34.43 N/mm2, 34.35 N/mm2, and 34.08 N/mm2, respectively, and the 120 mm B-3-40 panel configuration values are further reduced with bending strength values of 29.47 N/mm2, 29.25 N/mm2, and 29.43 N/mm2, respectively, from the layered beam theory, gamma method, and shear analogy method.
The mean characteristic bending strength results for the 60 mm B-3-20 panel configuration were found to be quite high for the C16 timber, with values from the layered beam theory, gamma method, and shear analogy method of 24.11 N/mm2, 23.98 N/mm2, and 24.08 N/mm2, respectively. The characteristic bending strength for the 100 mm B-5-20 panel configuration were found to be greater than that of the 60 mm B-3-20 panel configuration, with comparative characteristic values of 26.38 N/mm2, 26.34 N/mm2, and 26.13 N/mm2 for the layered beam theory, gamma method, and shear analogy method, respectively. While the mean maximum bending strength results are lower than that observed in the panel configuration B-3-20, the characteristic strength values are higher. This indicates less scatter in the experimental results and more predictable failure behaviour from the five-layer configuration. The characteristic bending strength for the 120 mm B-3-40 panel configuration from the layered beam theory, gamma method, and shear analogy method were 19.52 N/mm2, 19.38 N/mm2, and 19.49 N/mm2, respectively. This is a low result when compared to the three-layer configuration B-3-20 with a reduced board thickness of 20 mm, but the values are still relatively high considering the raw material used to manufacture the panels was C16 grade.
The theoretical panel stiffness has been calculated using Equation (1). The mean flexural stiffness results for different the CLT panel configurations using global and local deformations are presented and compared to the theoretical values in Figure 5. The stiffness results obtained from testing are adjusted to the per meter width of panel values for comparison with the theoretical results. The highest stiffness of 1.03 × 1012 Nmm2 and 1.27 × 1012 Nmm2 using global and local deformations, respectively, was recorded for the thickest three-layer panels of the 40 mm layers (B-3-40) as expected. The corresponding values for the five-layer panels (B-5-20) were 5.19 × 1011 Nmm2 and 6.63 × 1011 Nmm2, and for the thinner three-layer panels (B-3-20), the values were 1.28 × 1011 Nmm2 and 1.67 × 1011 Nmm2. As seen in Figure 5, the global stiffness results are in good agreement with the theoretical stiffness results. The same cannot be said for the local stiffness results, but it should be noted that the values calculated using the local deformation measurements presented greater scatter than those from the global deformations. This is thought to be a consequence of local variabilities within test specimens that influences the local deformations to a greater extent than measured globally. This phenomenon is in agreement with the finding made by Ridley-Ellis et al. [27], who suggested that the primary reason the for observed differences between the global and local deformations in timber is not necessarily attributed to the shear deformations, but to the variation of modulus of elasticity within a specimen.
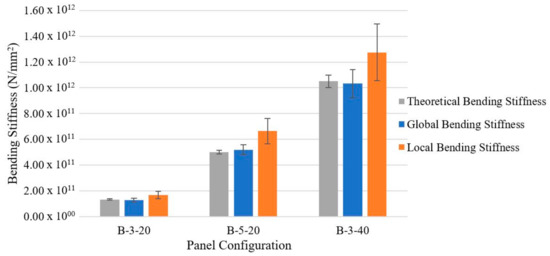
Figure 5.
Mean bending stiffness results per meter width and the influence of panel configuration and depth.
The mean maximum bending strength results and the influence of the panel configuration can be seen in Figure 6. The analytical models examined in this study have been shown to give reliable results for individual panel configurations. The analytically determined bending strength values, calculated using the layered beam theory and shear analogy theory, were found to be very similar for all of the specimens. For the five-layer panels, the Gamma beam theory produced similar results to the layered beam theory and the shear analogy theory, but the values were lower by 0.5–3.5% for the three-layer panel configurations. This is thought to be associated with the conservative value of 50 N/mm2, assumed for the rolling shear modulus, GR [9]. When comparing the different panel configurations, the highest mean values of approximately 36 N/mm2 were obtained for the thinnest samples (B-3-20), and the lowest of approximately 29 N/mm2 for the thickest (B-3-40). Based on these results, there is a general tendency that the thicker the CLT panel, the lower the bending strength.
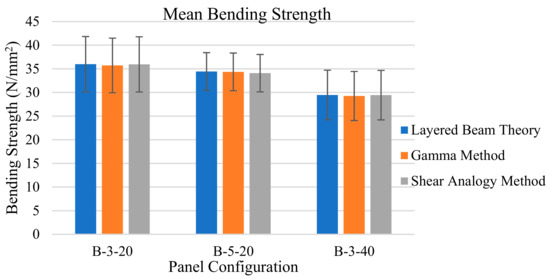
Figure 6.
Mean maximum bending strength results and the influence of panel configuration.
The influence of the number of layers can also be seen to have an effect when examining the mean and standard deviation associated with the five-layer panels (B-5-20). There is a reduced scatter of the results associated with this panel configuration, when compared to the three-layer panels. This is due to the increased number of layers and the homogenising effect or laminating effect, whereby defects such as knots, seasoning checks, reaction wood, and sloping grain, which may be crucial in the performance of a solid timber piece, are generally limited to one board in a CLT panel, greatly reducing the effect on the structural integrity of the panel. The statistical distribution of the bending strength results (layered beam theory) for each panel configuration are presented in Figure 7, and the influence of panel thickness can be seen. The lines representing the mean and characteristic fifth percentile values are also presented, in order to examine the differences due to the panel configurations.
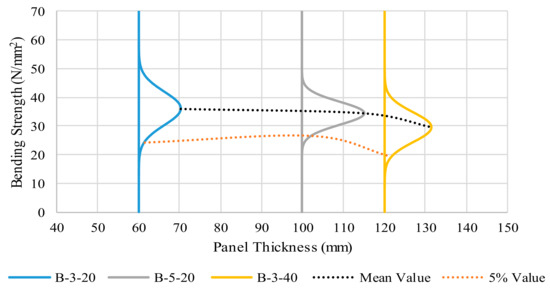
Figure 7.
Bending strength distribution and influence of panel thickness and number of layers.
The variability and the shape of the distribution decreases in the five-layer panel with a thickness of 100 mm. There is an increase in the characteristic bending strength in the five-layer panel to a level higher than that of the three-layer panel of a 60 mm thickness. A small upward trend in the characteristic bending strength is observed as the panel thickness increases from 60 mm to 100 mm, indicating the positive effect of an increased number of boards in the panel configuration. The observations of a reduced bending strength with an increased panel thickness are not valid when examining the characteristic bending strength behaviour of the CLT panels.
4.3. Rolling Shear Test Results
The shear test results for all of the panel configurations are presented. Each panel failed in the rolling shear as expected, with the exception of panel S-5-20-1, which delaminated prior to shear failure. The shear and rolling shear test failure behaviour in a five-layer panel (S-5-20-5) and a three-layer panel (S-3-40-7) can be seen Figure 8a,b, respectively. The failure mechanism can be seen in the transverse layers of both of the panel types. The load-deflection response of the three-layer panels (configuration S-3-40) can be seen in Figure 9. The maximum moment has been calculated for each test specimen and the analytical models have been used to determine the theoretical maximum shear and maximum rolling shear stress.

Figure 8.
Rolling shear failure: (a) five-layer panel (S-5-20-5) and (b) three-layer panel (S-3-40-7).
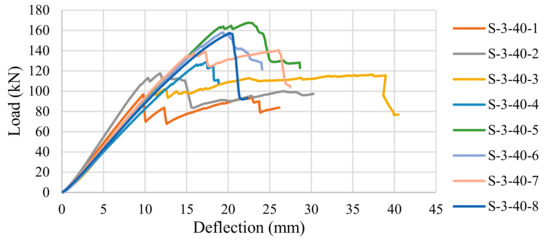
Figure 9.
Panel configuration S-3-40: deflection to failure load behaviour.
Table 5, Table 6 and Table 7 present the maximum rolling shear strength results of each panel of the three-layer S-3-20, five-layer S-5-20, and three-layer S-3-40 panel configurations. All of the panels failed in rolling shear in the transverse cross layers, with the exception of panel S-5-20-1. Panel S-5-20-1 had minor manufacturing defects, which resulted in delamination failure rather than shear failure, therefore, this result was excluded from the average, standard deviations, and fifth percentile calculations of shear and rolling shear strength. There is no distinction made between the maximum shear and maximum rolling shear strength in the three-layer panels, as they both occur at the same place (transverse layer) and have the same value. There is a distinction made between the maximum shear strength (τmax) and the maximum rolling shear strength (τrmax) in the five-layer panels (Figure 2b). This is due to the maximum shear stress occurring in a board at the neutral axis, which is orientated in the longitudinal direction (E0). The maximum rolling shear stress occurs in the adjacent transverse layers (E90) and is accounted for and presented by analysing the entire cross section.

Table 5.
Shear/rolling shear test results for three-layer S-3-20 configuration.

Table 6.
Rolling shear test results for five-layer S-5-20 configuration.

Table 7.
Shear/Rolling shear test results for three-layer S-3-40 configuration.
The mean shear/rolling shear strength from the layered beam theory, gamma method, and shear analogy method for the 60 mm S-3-20 panel configuration are 2.19 N/mm2, 2.14 N/mm2, and 2.22 N/mm2, respectively. The reduced mean rolling shear strength values were observed for the 100 mm S-5-20 panel configuration, where the mean rolling shear strength from the layered beam theory, gamma method, and shear analogy method were 1.40 N/mm2, 1.39 N/mm2, and 1.39 N/mm2, respectively. By comparison, the mean rolling shear strength for the thickest 120 mm S-3-40 panel configuration was further reduced with the rolling shear values from the layered beam theory, gamma method, and shear analogy method of 1.33 N/mm2, 1.30 N/mm2, and 1.35 N/mm2, respectively. The results indicated similar trends observed for the bending strength specimens, the thicker the CLT panel, the lower its rolling shear strength.
The characteristic rolling shear strength values were found to follow the same trend as the mean rolling shear strength values, with reduced mean/characteristic rolling shear strength values with increased panel thickness. The maximum characteristic values were achieved by the 60 mm S-3-20 panel configuration with values of 1.67 N/mm2, 1.63 N/mm2, and 1.69 N/mm2, respectively from the layered beam theory, the gamma method, and the shear analogy method, calculated in accordance to EN 14358 [26]. The characteristic rolling shear strength values for the 100 mm S-5-20 panel configuration from the layered beam theory, gamma method, and shear analogy method were 1.07 N/mm2, 1.06 N/mm2, and 1.06 N/mm2, respectively, and the characteristic rolling shear strength for the 120 mm S-3-40 panel configuration from the layered beam theory, gamma method, and shear analogy method are 0.90 N/mm2, 0.88 N/mm2, and 0.91 N/mm2, respectively.
The established mean values of rolling shear strength are in agreement with the study by Blaß and Görlacher [23], where rolling shear results ranged from 1.2 N/mm2 to 2.1 N/mm2, and a characteristic value of 1.0 N/mm2 for the rolling shear strength of European spruce was proposed. The mean characteristic rolling shear values of the tests were found to range from 0.88 N/mm2 to 1.69 N/mm2. The lowest values were observed in the thickest panel configuration, S-3-40. The boards used in this panel configuration had board width-to-thickness ratios less than four. The two most common design recommended values for such layers are 0.7 N/mm2, prescribed by EN 16351 [1], and 0.8 N/mm2, prescribed by Brandner et al. [3]. In Figure 10, the influence of the panel thickness and number of layers on the rolling shear strength distribution can be seen. When examining the rolling shear strength distribution, there is a decrease in the mean and characteristic shear strength with the increasing panel thickness. The variability in the distribution of the rolling shear strength for the five-layer configuration is seen to be less than either of the three-layer configurations.
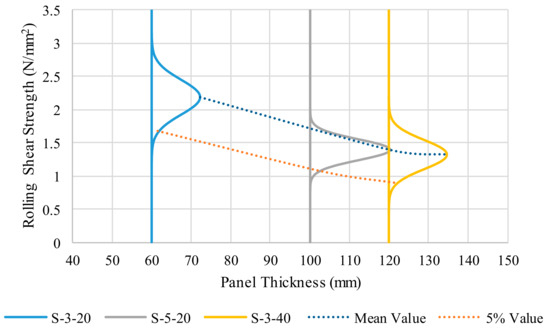
Figure 10.
Rolling shear strength distribution and influence of panel thickness and number of layers.
5. Conclusions
The following conclusions can be formulated based on the investigations presented on the bending and shear performance of the CLT panels manufactured from C16 timber.
- -
- The findings of this research project suggest that C16 timber is suitable for the manufacture of CLT products.
- -
- The global bending stiffness results are in good agreement with the theoretical bending stiffness results, regardless of the panel thickness or lay-up studied.
- -
- The mean and characteristic bending strength was higher than expected for the CLT panels manufactured from C16 grade timber.
- -
- The test results generally indicated a decreasing bending strength with an increasing panel thickness. The highest mean bending strength value, of approximately 36 N/mm2, was obtained for the thinnest panels (B-3-20), and the lowest, of approximately 29 N/mm2, for the thickest (B-3-40).
- -
- The characteristic bending strength was found to be influenced by the number of layers, with the highest characteristic bending strength values being achieved by the intermediate 100 mm five-layer panel configuration. The homogenising or laminating effect resulting from the increased number of layers in a CLT panel may be utilised to achieve an additional capacity in the structural design of the CLT structures.
- -
- The mean rolling shear strength was found to reduce with the increasing panel thickness. The mean values ranged between 1.30 N/mm2 and 2.22 N/mm2, which is in line with the rolling shear values presented by Blaß and Görlacher [23] of between 1.2 N/mm2 and 2.1 N/mm2, for European spruce.
- -
- The characteristic rolling shear strength of the panels was found to range from 0.88 N/mm2 to 1.69 N/mm2. Given that the board width-to-thickness ratio in this study was less than four, the experimental results are greater than the characteristic rolling shear values of 0.7 N/mm2, prescribed by EN 16351 [1], and 0.8 N/mm2, prescribed by Brandner et al. [3].
- -
- The results show that the mean bending and rolling shear strength decrease with the increasing panel thickness, irrespective of the number of layers. The characteristic bending strength is also influenced by the panel thickness, but the number of layers is found to have a significant impact.
- -
- To further examine these initial findings, tests are required on the panels of equal thickness comprising a different number of layers to allow the influence of the layer thickness on the bending and rolling shear strength to be assessed.
Author Contributions
C.O.C. contributed to the conceptualization, experimental investigation and analysis of the project in addition to writing, reviewing and editing of the final article. K.S. was involved in the acquisition of funding for this project in addition to experimental activities and writing, reviewing and editing of the final article. A.M.H. was involved in the acquisition of funding for this project, supervison of all experimental activities and writing, reviewing and editing of the final article.
Funding
This work has been carried out as a part of the project entitled ‘Commercialisation of Irish Cross Laminated Timber’ (project ref. 15/C/694), funded by the Department of Agriculture, Food, and the Marine of the Republic of Ireland.
Acknowledgments
The contribution of the technical staff of the College of Engineering and Informatics, National University of Ireland Galway, in particular, Peter Fahy, Colm Walsh, and Gerard Hynes, is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Timber Structures—Cross Laminated Timber—Requirements; CEN EN 16351:2015; Comité Européen de Normalisation: Brussels, Belgium, 2015.
- Structural Timber—Strength Classes; CEN EN 338:2016; Comité Européen de Normalisation: Brussels, Belgium, 2016.
- Brandner, R.; Flatscher, G.; Ringhofer, A.; Schickhofer, G.; Thiel, A. Cross laminated timber (CLT): Overview and development. Eur. J. Wood Wood Prod. 2016, 74, 331–351. [Google Scholar] [CrossRef]
- Sikora, K.S.; McPolin, D.O.; Harte, A.M. Shear Strength and Durability Testing of Adhesive Bonds in Cross-Laminated Timber. J. Adhes. 2016, 92, 758–777. [Google Scholar] [CrossRef]
- Vallée, T.; Tannert, T.; Fecht, S. Adhesively bonded connections in the context of timber engineering—A Review. J. Adhes. 2017, 93, 257–287. [Google Scholar] [CrossRef]
- Raftery, G.; Harte, A.; Rodd, P. Qualification of wood adhesives for structural softwood glulam with large juvenile wood content. J. Inst. Wood Sci. 2008, 18, 24–34. [Google Scholar] [CrossRef]
- Betti, M.; Brunetti, M.; Lauriola, M.P.; Nocetti, M.; Ravalli, F.; Pizzo, B. Comparison of newly proposed test methods to evaluate the bonding quality of Cross-Laminated Timber (CLT) panels by means of experimental data and finite element (FE) analysis. Constr. Build. Mater. 2016, 125, 952–963. [Google Scholar] [CrossRef]
- Brandner, R.; Bogensperger, T.; Schickhofer, G. In Plane Shear Strength of Cross Laminated Timber (CLT): Test Configuration, Quantification and Influencing Parameters. In Proceedings of the CIB-W18-Meeting 46, Vancouver, BC, Canada, 26–29 August 2013; pp. 227–242. [Google Scholar]
- Sikora, K.S.; McPolin, D.O.; Harte, A.M. Effects of the thickness of cross-laminated timber (CLT) panels made from Irish Sitka spruce on mechanical performance in bending and shear. Constr. Build. Mater. 2016, 116, 141–150. [Google Scholar] [CrossRef]
- Shahnewaz, M.; Tannert, T.; Alam, M.S.; Popovski, M. In-Plane Stiffness of Cross-Laminated Timber Panels with Openings. Struct. Eng. Int. 2017, 27, 217–223. [Google Scholar] [CrossRef]
- Fortune, A.; Quenneville, P. Feasibility Study of New Zealand Radiata Pine Cross-Laminated Timber. N. Z. Timber Des. J. 2011, 19, 3–7. [Google Scholar]
- Harte, A.M. Mass timber—The emergence of a modern construction material. J. Struct. Integr. Maint. 2017, 2, 121–132. [Google Scholar] [CrossRef]
- Okabe, M.; Yasumura, M.; Kobayashi, K.; Fujita, K. Prediction of bending stiffness and moment carrying capacity of sugi cross-laminated timber. J. Wood Sci. 2014, 60, 49–58. [Google Scholar] [CrossRef]
- Hindman, D.P.; Bouldin, J.C. Mechanical Properties of Southern Pine Cross-Laminated Timber. J. Mater. Civ. Eng. 2015, 27, 04014251. [Google Scholar] [CrossRef]
- Crawford, D.; Hairstans, R.; Smith, R.E. Feasibility of Cross-Laminated Timber Production from UK Sitka Spruce. In Proceedings of the Focus Solid Timber Solutions—European Conference on Cross Laminated Timber (CLT), Graz, Austria, 21–22 May 2013. [Google Scholar]
- Kreuzinger, H.; Scholz, S. Schubtragverhalten von Brettsperrholz (Shear Behaviour in Cross Laminated Timber); Research Report; Technische Universitat München: München, Germany, 2001. (In German) [Google Scholar]
- Ehrhart, T.; Brandner, R.; Schickhofer, G.; Frangi, A. Rolling Shear Properties of some European Timber Species with Focus on Cross Laminated Timber (CLT): Test Configuration and Parameter Study. In Proceedings of the 48th Meeting of the International Network on Timber Engineering Research (INTER 2015), Šibenik, Croatia, 24–27 August 2015; pp. 61–76. [Google Scholar]
- Solid Wood Slab Element to be Used as Structural Elements in Buildings; ETA-06/0138; KLH Massivholz GmbH: Teufenbach-Katsch, Austria, 2011.
- Multilayered Timber Elements for Walls, Ceilings, Roofs and Special Construction Components; ETA-06/0009; Binderholz Bausysteme GmbH: Unternberg, Austria, 2013.
- Blaß, H.J.; Fellmoser, D.P. Design of solid wood panels with cross layers. In Proceedings of the 8th World Conference on Timber Engineering, Lahti, Finland, 14–17 June 2004. [Google Scholar]
- Bogensperger, T.; Augustin, M.; Schickhofer, G. Properties of CLT-Panels Exposed to Compression Perpendicular to their Plane. In Proceedings of the International Council for Research and Innovation in Building and Construction, Working Commission W18—Timber Structures Meeting, Alghero, Italy, 28 August–1 September 2011; pp. 1–15. [Google Scholar]
- Follesa, M.; Fragiacomo, M.; Vassallo, D.; Piazza, M.; Tomasi, R.; Rossi, S.; Casagrande, D. A proposal for a new Background Document of Chapter 8 of Eurocode 8. In Proceedings of the 48th Meeting of the International Network on Timber Engineering Research (INTER 2015), Šibenik, Croatia, 24–27 August 2015; pp. 369–387. [Google Scholar]
- Blaß, H.J.; Görlacher, R. Rolling shear in structural bonded timber elements. In Proceedings of the International Conference on Wood and Wood Fibre Composites, Stuttgart, Germany, 13–15 April 2000; pp. 327–337. [Google Scholar]
- Bogensperger, T.; Silly, G.; Schickhofer, G. Comparison of Methods of Approximate Verification Procedures for Cross Laminated Timber; Research Report; Institute for Timber Engineering and Wood Technology Management, Holzbau Forschungs Gmbh: Graz, Austria, 2012. [Google Scholar]
- Li, Y. Duration-of-Load and Size Effects on the Rolling Shear Strength of Cross Laminated Timber. PhD Thesis, University of British Columbia, Vancouver, BC, Canada, 2015. [Google Scholar]
- Timber Structures—Calculation of Characteristic 5-Percentile Values and Acceptance Criteria for a Sample; CEN EN 14358; Comité Européen de Normalisation: Brussels, Belgium, 2006.
- Ridley-Ellis, D.; Moore, J.; Khokhar, A. Random acts of elasticity: MoE, G and EN408. In Proceedings of the Wood EDG Conference, Bled, Slovenia, 23 April 2009. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).