Abstract
The construction industry faces increasing pressure to reduce energy consumption and carbon emissions. Promoting sustainable practices, such as using hot-rolled H-shapes and minimizing welding, can address these challenges. This study introduces low-carbon H-shape bolted composite beams (HBCBs) as a sustainable alternative. Experimental and numerical investigations into the lateral-torsional buckling behavior of HBCBs demonstrated that high-strength bolts significantly enhance structural stability and capacity. A reliable simulation method was developed and validated based on experimental results. The study reveals that bolt spacing exceeding 1/15 of the beam span has negligible effects on load-bearing capacity, and HBCB performance reaches approximately 95% of plug-welded counterparts. Despite this, longitudinal slip reduction remains challenging, warranting further research to optimize performance.
1. Introduction
The traditional construction sector faces unprecedented challenges in energy saving and carbon emission reduction (CEs). The construction industry significantly impacts the environment, accounting for about 30% of global CEs, 40% of world energy consumption [,], and 51.3% of total CEs in China [,]. Consequently, it must play a crucial role in reducing emissions. Most embodied CEs occur before the operation phase [], making material selection, efficient building processes, design for disassembly, and optimized logistics essential [].
Choosing low-carbon materials can notably reduce a building’s initial carbon footprint. Low-carbon materials refer to materials that minimize carbon emissions throughout their entire life cycle, including raw material extraction, production, transportation, construction, usage, and disposal. The carbon footprint of a material is typically assessed based on its embodied carbon (kgC/kg). According to the data from Hammond and Jones [], the embodied carbon of steel, concrete, and timber are 0.482, 0.035, and 0.125 kgC/kg, respectively. Timber generally has a lower carbon footprint, and some types of timber can absorb CO2 during their growth. Therefore, timber generally has lower CEs than concrete and steel [], but poor design can result in higher emissions []. Prefabricated steel structures, on the other hand, often conserve energy and reduce CEs more effectively than concrete [], making them a promising long-term solution for the construction industry. During construction, carbon emissions for a steel frame are 10.1 tCO2, whereas for reinforced concrete (RC), they are 45.5 tCO2 [], further highlighting the advantages of steel structures in reducing environmental impact, especially by replacing the traditional RC shear wall structure with a new steel plate shear wall system [,] and other new technologies [,]. Therefore, in this study, the concept of low carbon specifically refers to reducing carbon emissions during construction.
Studies have shown that the component production phase is the primary source of carbon emissions (CEs) in steel structures, accounting for 60–73% of total lifecycle emissions []. Within this phase, welding-related CEs are particularly significant, comprising 57.2% of emissions in the prefabrication process []. Therefore, reducing welding can significantly lower overall carbon emissions. Hence, steel components should utilize hot-rolled shapes (HRSs) or cold-formed shapes (CFSs) to minimize welding. Although CFSs with fasteners have the lowest carbon emissions [], their application is limited. Conversely, the utilization rate of HRSs remains low. For example, in China, the world’s largest steel producer, the engineering utilization rate of HRSs is only 15–20%, with no significant changes in recent years []. Developing high-performance HRS built-up components is crucial. Lu et al. [,] introduced innovative designs such as flanged cruciform H-shape columns (FCHCs) and T-shaped built-up columns (NTBCs). Also, bolts should replace welding where possible, exemplified by developing weld-free columns [].
Beams, which use more steel than columns in steel buildings, face limitations due to insufficient manufacturing and market standards for hot-rolled H-shapes. To address this, the authors propose H-shape bolted composite beams (HBCBs), similar to using high-strength bolts to connect steel plate girders’ two sub-beams to solve issues of shipping and field lifting []. HHLBs can be used for new construction and can also strengthen existing H-beams. Zhu et al. [] investigated the bearing capacity of composite and I-section plate beams of the same height and flange plates through experimental comparison. Although all specimens exhibited lateral-torsional buckling with slight web yielding near loading points, the composite plate beam’s bearing capacity was 6.1% higher than the I-section one. However, they did not thoroughly address composite plate beams’ lateral-torsional buckling or overall stability.
Xu et al. [,,] used a similar strategy connecting two cold-formed channels in modular light steel buildings. Their findings revealed that laminated equal channel beams had greater loading capacity and bending stiffness than independent bending double beams []. Increasing the number of bolt connections constrained slipping behavior, suggesting that an appropriate number of bolts should be used in engineering practice for optimal efficiency []. The results [] showed that the influence of design factors on EIe (bending stiffness) and Pu (ultimate capacity) were ranked as follows: n > β > f > b > p for EIe and p > b > β > f > n for Pu. Here, n represents the number of bolts, f interfacial friction, β layer height ratio, p load type, and b boundary condition. However, Xu et al.’s [,,] study did not focus on hot-rolled H-shapes.
In summary, several research gaps remain in studying low-carbon H-shape bolted composite beams (HBCBs). Systematic experimental and numerical investigations into their lateral-torsional buckling behavior are lacking, and the main influencing factors are still unclear. Therefore, this paper explores the lateral-torsional buckling behavior of HBCBs and the effects of different factors through experimental and numerical studies. The main contributions are as follows: first, lateral-torsional buckling tests were conducted on an HBCB specimen and a bolted-free comparison specimen; second, a complete ABAQUS analysis methodology was proposed and validated through experiments; and finally, numerical investigations were carried out on the influence of high-strength bolt pre-loadings and the influence of high-strength bolt spacings. These studies lay the foundation for future research on the mechanical performance analysis and design methods of HBCBs.
2. Experimental Investigations
2.1. Specimens Design and Original Data
The cross-section and geometric symbols of an HBCB specimen are shown in Figure 1. Two extension lengths were arranged outside of two supports to fix the beam and the supports, making the specimen length L, where L = Le + 2 × 150 mm. Thus, the geometric length L of all test beams was 3000 mm, with an effective length Le of 2700 mm.
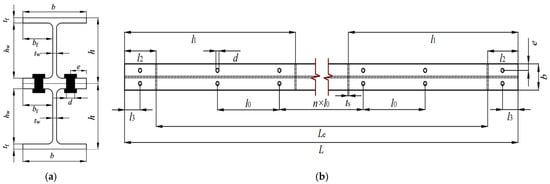
Figure 1.
Cross-sectional configurations and dimensional symbols of the HBCB specimen. (a) Cross-section; (b) top view.
In this study, an HBCB used two Q235B HW100 × 100 × 6 × 8 H-shapes combined with 8.8-grade M12 high-strength bolts. A corresponding no-connection laminated beam (NCLB) specimen was also created to study the effect of bolts. According to GB50017-2017 [], beams met the S1 cross-section requirements, which allows for the entire section’s plasticity. A pair of 6 mm thick transverse stiffeners were placed at the supports, quarter points, and mid-span of the beam’s effective length.
The bolts were spaced at 300 mm spacings equal to 1/9 Le. At the supports, two bolts were positioned 75 mm apart. According to GB50017-2017 [], a pre-tensioned force of 38.5 kN was given to a high-strength bolt of the HHLB, and the bolts’ center spacing l0, end spacing l3, and edge margin spacing e complied with the requirements.
The actual geometric dimensions of the specimens were measured before and after assembly, as detailed in Table 1 and Table 2. Figure 2 presents the simplified engineering stress–strain curve, and the data from the coupon tensile test are listed in Table 3.

Table 1.
Dimensions of cross-sections (Unit: mm).

Table 2.
Dimensions of specimens (Unit: mm).
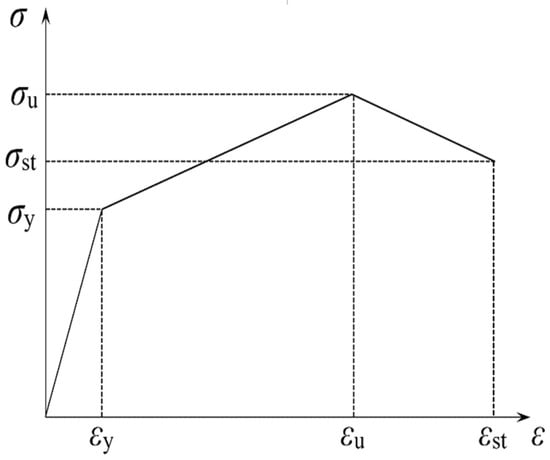
Figure 2.
Three-line stress–strain relationship curve.

Table 3.
Mechanical properties of steel and bolts.
2.2. Test Setup
Figure 3a shows the loading system and on-site photos of the specimen. An actuator, a rigid extension rod, a load distribution beam, and two loading point solid round steel bars were used in the loading system to apply two-point concentrated loads at the four quarter points of the upper flange of the specimen, causing the beam to form a pure bending between the two loading points. Two particular beam end supports, including a simple-supported support and splint support at each beam end, were designed, as shown in Figure 3b. At the supporting end, the beam cannot freely warp and can rotate around the major and minor axes without lateral displacement and rotate around its longitudinal axis.

Figure 3.
Photo of the test setup on site. (a) Test setup; (b) Beam end support.
Before testing loading, all specimens were pre-loaded with 5 mm and held for 10 min to check the loading equipment and data collection system and eliminate the gaps between the specimen parts and test setup. After pre-loading, they were unloaded to zero. A displacement loading controlled the formal testing loading; the speed was 1 mm/min. The displacement increment of each step was 1 mm, held for 2 min to check and judge whether there were any abnormalities in the specimen. After the overall instability of a specimen, we continued loading until the load dropped to 80% of the peak load or the maximum elongation capacity of the actuator was reached, and at this time, we finished the test.
2.3. Arrangement of Displacement Meters and Strain Gauges
Figure 4a shows the specimen’s displacement meters arrangement. Because the beam moved downward during the test, a smooth glass piece was pasted outside the mid-span stiffener of the specimen to ensure that the displacement meters D1, D2, and D3 measuring the lateral displacement of the beam could slip up and down freely without changing its horizontal direction. Among them, D2 was located at the superimposed flange of the upper and lower beams. The displacement meter D4 measured the vertical displacement of the beam at mid-span. Displacement meters D5 and D6 measured the longitudinal relative slip of the upper and lower steel beams. Displacement meters D7 and D8 measured the vertical displacement at the support. With the displacement meter D4, the actual deflection at the mid-span of the beam was calculated. Because the pure bending section of the beam should be the first to undergo overall instability failure, strain gauges were only arranged on the mid-span area of the specimen, as shown in Figure 4b. A data acquisition system hooked up to the loading system automatically recorded loads, displacements, and strains.
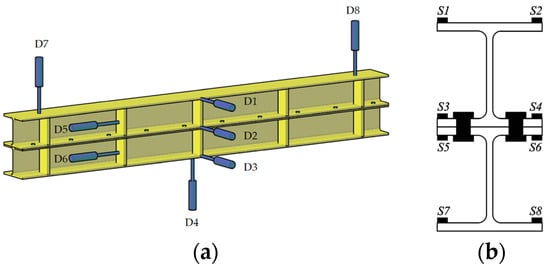
Figure 4.
Displacement meters and strain gauges of specimens. (a) Arrangement of displacement meters; (b) arrangement of strain gauges.
3. Test Results and Discussion
3.1. Test Observations
3.1.1. HBCB Specimen
In the initial loading stage, the HBCB remained in the elastic phase. A clear and loud sound was heard when the loading displacement reached 14 mm (approximately 92 kN), indicating a longitudinal relative slip between the upper and lower flanges connected by bolts. Real-time data from displacement meters D1, D2, and D3 showed that the mid-span section of the specimen tilted. After that, the load continued to increase, the mid-span deflection grew significantly, and the load increment rate began to slow.
At the loading displacement of 22 mm (approximately 104 kN), another sudden sound occurred, and the load dropped to about 93 kN. Real-time monitoring with displacement meters D5 and D6 revealed longitudinal relative slip along the beam’s length. As loading progressed, the load data continued to rise, and at a displacement of 124 mm (approximately 127 kN), the actuator reached its maximum range due to equipment limitations, resulting in a mid-span deflection of 117 mm, at which point the test was terminated.
The HBCB specimen did not exhibit significant mid-span section torsion or lateral shifting. Minor displacements were noted at the stiffeners of the upper and lower beams, and the connecting bolts of the composite beam were tilted, indicating longitudinal relative slip. At the end of the test, the mid-span failure mode of the HBCB specimen is shown in Figure 5a, while the overall lateral deformation and deflection after unloading are presented in Figure 5b,c.

Figure 5.
The failure modes of the HBCB specimen. (a) Lateral-torsional buckling and longitudinal slippage; (b) residual plastic deformation out of the plane; (c) residual plastic deformation in the plane.
The results suggest that lateral-torsional buckling of the specimens occurred, in which the upper and lower beams worked together (see Figure 5). No local buckling was found in the test.
3.1.2. NCLB Specimen
In the initial loading phase, the specimen remained in the elastic stage. As loading continued, when the displacement reached 20 mm (load of 84 kN), the rate of increase in bearing capacity began to slow. Real-time data from displacement meters D1, D2, and D3 showed that the mid-span section of the specimen tilted. When the displacement increased to 25 mm (load of 89 kN), a clear and loud sound was heard, and real-time data monitoring from displacement meters D5 and D6 revealed a longitudinal relative slip at the stiffeners of the upper and lower beams of the specimen. At this point, the specimen’s bearing capacity suddenly dropped to 86 kN. When the displacement loading was up to 31 mm (load of 93 kN), a second distinct sound occurred, and real-time data from displacement meters D1, D2, and D3 showed that the mid-span section of the specimen tilted strongly, and the bearing capacity dropped to 90 kN. The bearing capacity data continued to rise as loading progressed. The specimen reached its maximum bearing capacity when the displacement reached 47 mm (load of 95 kN). During this phase, the specimen emitted continuous sounds, and data from the displacement meters revealed that with each sound, lateral shifting and longitudinal relative slip occurred at both the upper and lower parts of the composite beam. The displacement was further increased to 110 mm, at which point the bearing capacity was 82 kN, approximately 80% of the peak load. Due to actuator range limitations, the test was terminated, and the mid-span deflection was 106 mm.
During the test, it was observed that a lack of bolt constraints exhibited poorer overall performance. Consequently, significant torsion and lateral shifting occurred at the mid-span section of the upper and lower beams, and substantial longitudinal relative slip was also observed. The final failure mode was independent lateral-torsional buckling for upper and lower beams. The failure mode and local phenomena are shown in Figure 6a, and the overall lateral deformation and deflection after unloading are shown in Figure 6b,c.

Figure 6.
The failure modes of the NCLB specimen. (a) Lateral-torsional buckling and longitudinal slippage; (b) residual plastic deformation out of the plane; (c) residual plastic deformation in the plane.
In addition to longitudinal relative slip, the two beams (upper and lower beams) underwent a relative transverse slip, as shown in Figure 6, which revealed that the lateral movement and torsion of the upper and lower beams are not synchronized. It implied that the lateral-torsional buckling of the upper and lower beams does not develop simultaneously. No local buckling was also found.
3.2. Specimens’ Load and Displacement Curves
3.2.1. Load vs. Mid-Span Deflection
Consider the self-weight of the specimen, and the load vs. mid-span deflection is given based on the test data, where the displacement is the average of the differences between the measurement data of displacement meters D4, D7, and D8. Due to insufficient estimation of specimen deflection, the HBCB specimen failed to be loaded to the predetermined end load because the loading actuator reached its limit. Therefore, it has no declining section after the peak value. Figure 7a shows that the HBCB specimen experienced noticeable elastic and elastoplastic stages, and the NCLB specimen underwent three stages from the start of loading to the end of the test: elastic, elastoplastic, and failure.
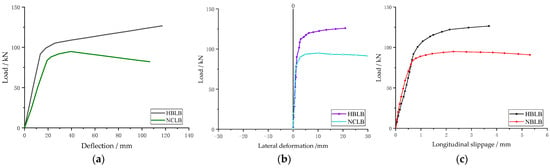
Figure 7.
Specimens’ load and displacement curves. (a) Curves of load–deflection; (b) curves of load–lateral deformation; (c) Curves of load–longitudinal slippage.
The critical load (Pcr), maximum load (Pmax), and final load (Pend) corresponding to the three stages of the specimen are shown in Table 4. The data indicate that with the addition of bolt connections, the critical load and maximum load of the HBCB specimen increased by 9.31% and 33.38%, respectively, compared with the NCLB specimen. The bolt assembly effect is significant.

Table 4.
The bearing capacity of the test and ABAQUS (Unit: kN).
3.2.2. Load vs. Mid-Span Lateral Deformation
The calculation formula for the mid-span lateral deformation at the centroid of the HBCB is Equation (1).
Because there was relative lateral slippage between the upper and lower beams of the NCLB specimen and because the real-time data of the relative lateral slippage of the upper and lower beams could not be measured during the test, the accurate lateral displacement of the specimen cannot be calculated. Because the lateral deformation value is an auxiliary index, this study still uses Equation (1) for approximate calculation.
Figure 7b shows the load vs. mid-span lateral deformation of specimens. At lower loads, both specimens exhibited almost no lateral displacement at the mid-span cross-section. However, once the load increased to the critical load (Pcr), lateral displacement at the mid-span cross-section began to occur and gradually increased until lateral-torsional buckling occurred. After buckling, the lateral displacement of the mid-span cross-section grew rapidly while the load-carrying capacity decreased sharply, consistent with the typical characteristics of global instability in flexural members. Due to the limitations of the loading device, the HBCB specimen could not be loaded to its ultimate load capacity, resulting in the absence of a descending curve for lateral displacement at the mid-span. However, this does not affect the identification of its lateral-torsional buckling behavior.
3.2.3. Load vs. Relative Longitudinal Slippage
The calculation formula for the relative longitudinal slippage is Equation (2).
Figure 7c shows that the longitudinal relative slip between the upper and lower beams of the specimen gradually increased with the load. When the load-carrying capacity reached the critical load of the HBCB specimen, the longitudinal relative slip between the upper and lower beams accelerated until the specimen eventually failed due to instability.
In addition, although the longitudinal relative slip of the HBCB specimen was smaller than that of the NCLB specimen, the collaborative performance between the upper and lower beams of the structure was still far from perfect. This indicates that the number of high-strength bolts used in the specimen might be insufficient to effectively restrict the development of longitudinal relative slip between the upper and lower beams, necessitating further research in the future.
3.3. Specimens’ Load and Strain Curve
Figure 8 illustrates the load–strain curves for eight strain gauge measurement points located at the mid-span cross-section of the two specimens, with the strain gauge arrangement shown in Figure 4a. The figure shows that at lower load levels, the measured strain data from strain gauges S1, S2, S7, and S8 are symmetric about the neutral axis, and their curves exhibit a linear growth trend. This indicates that the specimens primarily experienced in-plane bending during the initial loading phase.
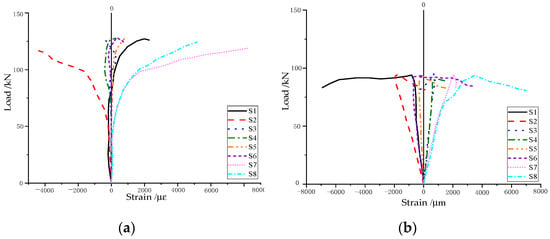
Figure 8.
Specimens’ load and strain curves. (a) HBCB specimen; (b) NCLB specimen.
As the load increased, the curves displayed clear inflection points and deviations, with their symmetry disrupted, indicating that lateral deformation and torsion occurred in the mid-span cross-section alongside bending, both of which intensified with further loading. Furthermore, Figure 8 shows that the compressive strain in the flanges of the specimens exceeded the average yield strain of the steel flanges obtained from material testing (see Table 3), confirming that the specimens had elastoplastic deformation consistent with observed experimental phenomena.
Comparing the load–strain curves at the mid-span for the specimens, it was found that strain gauges S5 and S6 of the HBCB specimen remained in a state of low strain (close to the neutral axis) until the final load was reached, whereas S5 and S6 of the NCLB specimen were consistently under compression. This phenomenon demonstrates that the high-strength bolted HBCB specimen behaved as an integrated beam, working as a single unit under load, whereas the non-bolted laminated NCLB specimen functioned with the upper and lower beams independently bearing the load.
4. ABAQUS Analysis Methodology and Validation
The two-point loading tests on the HBCB and NCLB specimens effectively demonstrated the beams’ lateral-torsional buckling failure mode, indicating the tests’ success. The high-strength bolt-connected hot-rolled H-shape composite beams can be considered as a unified beam working together under load, while the upper and lower beams independently load the unbolted pure laminated beam specimens. However, the HBCB specimen still exhibited longitudinal relative slip between the upper and lower beams, indicating that the number of high-strength bolts used in the test was insufficient. Numerical investigations are essential to investigate bolts’ influence on the lateral-torsional buckling, load-bearing capacity, deformation, and relative slip of the HBCB. Therefore, this study proposes a reliable numerical analysis method that can be utilized for future investigations involving various parameter variations. The detailed ABAQUS 6.1.4 numerical analysis methodology for model development and verification is outlined below.
4.1. Finite Element Model
4.1.1. Model Component Dimensions
In ABAQUS, the dimensions of the modeled specimens are identical to the actual measured dimensions of the two composite beam specimens used in the experiment. The measured geometric data are shown in Table 1 and Table 2. The specimen uses high-strength bolts with diameters corresponding to their nominal diameters (e.g., M12 uses 12 mm). The bolt holes in the experimental specimen are based on actual measured values (Table 2), while the bolt hole diameters in the numerical model are set as the nominal bolt diameter plus 2 mm.
4.1.2. True Stress–Strain Relationship of Steel and Bolts
The ABAQUS analysis accounts for material nonlinearity. According to the stress–strain model of steel and bolts shown in Figure 2, the engineering stress and strain listed in Table 3 must be converted into true stress and strain before inputting the material constitutive model into ABAQUS. The conversion method can be found in Reference [].
4.1.3. Contact Settings
In ABAQUS, contact settings typically involve defining contact surfaces, the type of contact, and the contact properties.
The contact relationships in the HBCB specimen primarily exist between the lower surface of the upper flange of the upper beam and the upper surface of the lower flange of the lower beam, the bolt cap and the flange surface, the bolt shank and the flange hole wall, and the lower surface of the lower flange of the lower beam and the upper surface of the support base plate. The complex contact relationships can lead to difficulties in model convergence and excessively long computation times during analysis. Therefore, to reduce the convergence difficulty and time in finite element analysis, the high-strength bolt model is simplified by replacing the hexagonal bolt cap with a circular bolt cap, and the influence of the bolt threads is ignored. “Surface-to-Surface Contact” is applied between the flange overlap faces, between the bolt cap and the flange surface, and between the lower surface of the lower flange of the lower beam and the upper surface of the support base plate, with interaction properties defined.
For normal behavior, “Hard Contact” is selected in the pressure-overclosure option, with the “Allow Separation” option being enabled to prevent penetration between model components. For tangential behavior, Coulomb friction is used to describe the sliding behavior between contact surfaces, with the friction coefficient being set to 0.3 according to GB 50017-2017 [] for “Q235 steel with wire-brushed surfaces to remove rust or untreated clean rolled surfaces”. The stiffeners are connected to the flanges and webs of the hot-rolled H-shaped steel beams using fillet welds, with “Tie” constraints being applied in the interaction settings.
The bolt contact settings were removed for the specimen NCLB, while other contact settings remained consistent with those of the HBCB specimen.
4.1.4. Boundary Conditions and Load Application
Appropriate boundary conditions and load applications were defined in the numerical model as follows to simulate the experimental setup accurately.
The experiment utilized simple and splint supports (Figure 3), with line-point contact between the angle knife edge and the side of the beam. At the support locations, the specimen ends were allowed to undergo minor rotations around the X-axis (strong axis) and Y-axis (weak axis), as well as longitudinal sliding along the Z-axis (specimen’s longitudinal axis) and free warping. However, lateral and vertical displacements along the X-axis and Y-axis were restricted.
In the numerical analysis, these boundary conditions needed to be implemented in the finite element model by applying displacement and rotational degree-of-freedom constraints and support boundary conditions to ensure consistency with the actual experimental setup. The simple support at one end is the hinge, and the boundary condition of the left end reference point is set as U1 = U2 = U3 = UR2 = UR3 = 0; the simple support at the other end needs to release the degree of freedom in the Z-axis, and the boundary condition of the right end reference point is set as U1 = U2 = UR2 = UR3 = 0; we set the boundary conditions at the stiffeners, flanges, and support pads at both ends of the model as U1 = 0.
When applying concentrated loads, reference points RP-1 and RP-2 should be created at the loading points. A “Coupling” constraint should be established within a 3 mm range on either side of the loading points, and the concentrated load should be applied along the Y-axis direction.
During the BUCKLE analysis phase, it is necessary to determine the most unfavorable model of the component, i.e., the first-order buckling mode. Therefore, a unit concentrated force is applied, and the resulting eigenvalue represents the buckling load of the component.
In the nonlinear analysis phase, loading is performed by applying displacement to the component.
An example of an HBCB specimen is shown in Figure 9a.
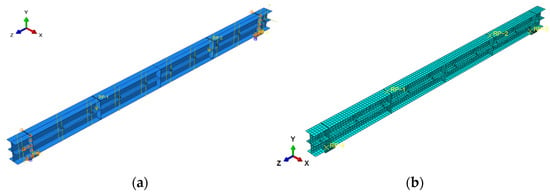
Figure 9.
Finite element model of the HBCB specimen. (a) Boundary condition; (b) element and mesh.
4.1.5. Element and Mesh
For nonlinear buckling analysis, shell elements provide better analysis accuracy compared with solid elements. Therefore, except for the bolts, which are modeled using solid element C3D8R, all other components are modeled using shell element S4R in the ABAQUS model.
Through extensive modeling and analysis, the final mesh sizes selected were 25 mm for the H-beam model, 10 mm for the stiffener model, and 2 mm for the high-strength bolt model. Additionally, sections with bolt holes were subdivided, and mesh refinement was applied to these areas to achieve optimal mesh quality. The overall model mesh division is shown in Figure 9b.
4.1.6. Bolt Pre-Tension Force
The bolt pre-load is simulated by defining the bolt load before applying the displacement load. Figure 10 shows the location and direction of the applied bolt pre-load. In the finite element simulation, the middle face of the bolt shank was cut, and the bolt load was applied to this middle face in the axial direction of the bolt shank.
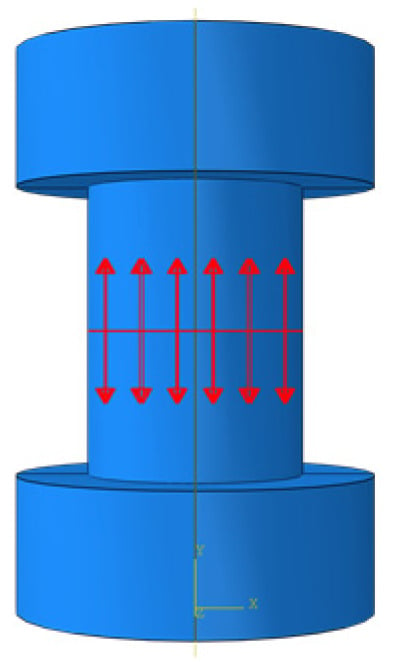
Figure 10.
Addition of bolt pre-load in finite element modeling.
4.1.7. Initial Geometric Imperfections
The initial geometric imperfections (initial bending) were introduced using the “consistent defect mode method”. This method utilizes the first-order buckling mode obtained from the BUCKLE analysis as the most critical mode. The node coordinates were adjusted according to this mode and scaled by a specified defect coefficient. According to GB 50017-2017 [], the initial bending was set to one-thousandth of the component’s span. In ABAQUS, these imperfections were incorporated using the “*IMPERFECTION” command.
4.1.8. Residual Stress
The residual stress distribution for hot-rolled H-shapes was given by ECCS [], as shown in Figure 11a. Here, σrc represents residual compressive stress, and σrt represents residual tensile stress, with σrc = −σrt = 0.3fy; fy is the steel’s yield strength, using σy in Table 3. It was assumed that the local bolt holes do not alter the distribution of residual stresses. These residual stresses were combined to obtain the residual stress distribution for the HBCB, shown in Figure 11b. In ABAQUS, a predefined field was created in the load module, selecting “stress” and the field area according to the residual stress distribution and introducing the residual stress as the initial stress in the model.
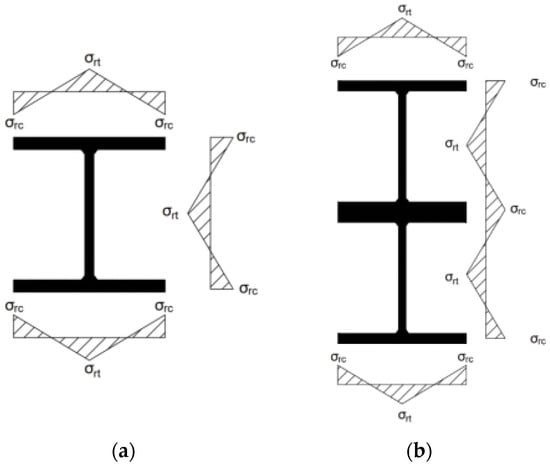
Figure 11.
Residual stress distribution. (a) Residual stress distribution of an H-beam; (b) residual stress distribution of the HBCB and NCLB.
4.2. Finite Element Verification
4.2.1. Comparison of Failure Modes
The modeling and analysis of the HBCB and NCLB specimens were performed following the method in Section 4.1. The finite element simulation failure modes obtained are shown in Figure 12a and Figure 13a. When compared with the experimental failure modes shown in Figure 12b and Figure 13b, it is observed that the FE failure modes are highly similar to the experiments.
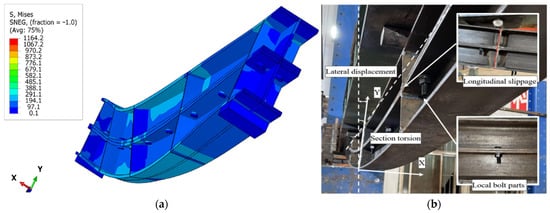
Figure 12.
Comparison of failure modes of the HBCB specimen. (a) ABAQUS analysis; (b) experiment.
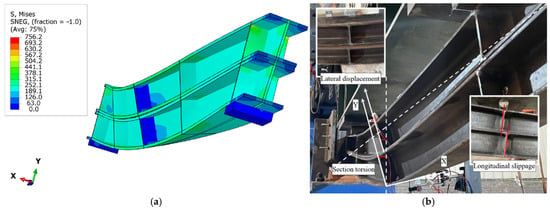
Figure 13.
Comparison of failure modes of the NCLB specimen. (a) ABAQUS analysis; (b) experiment.
4.2.2. Comparison of Load–Deformation Curves
Figure 14 and Figure 15 show the load–deformation curves, load–mid-span deflection curves, load–mid-span lateral displacement curves, and load–longitudinal slip curves for the HBCB and NCLB specimens.
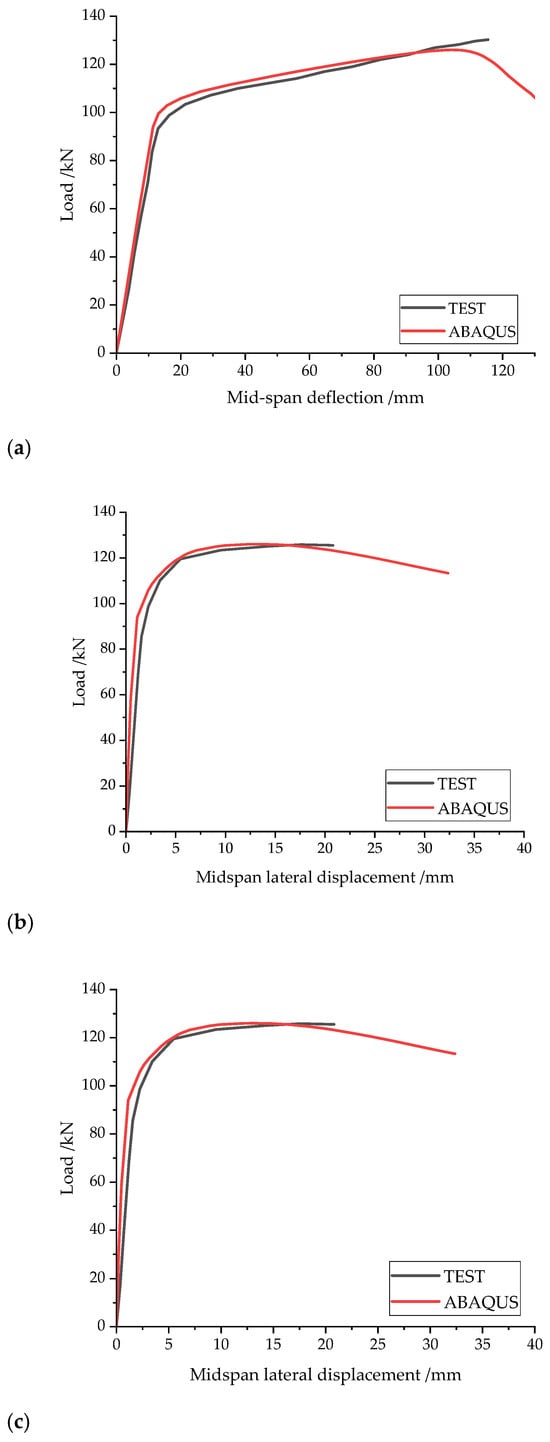
Figure 14.
Comparison of load–deformation curves of the HBCB specimen. (a) Load–Mid-span deflection; (b) load–mid-span lateral displacement; (c) load–longitudinal slip.
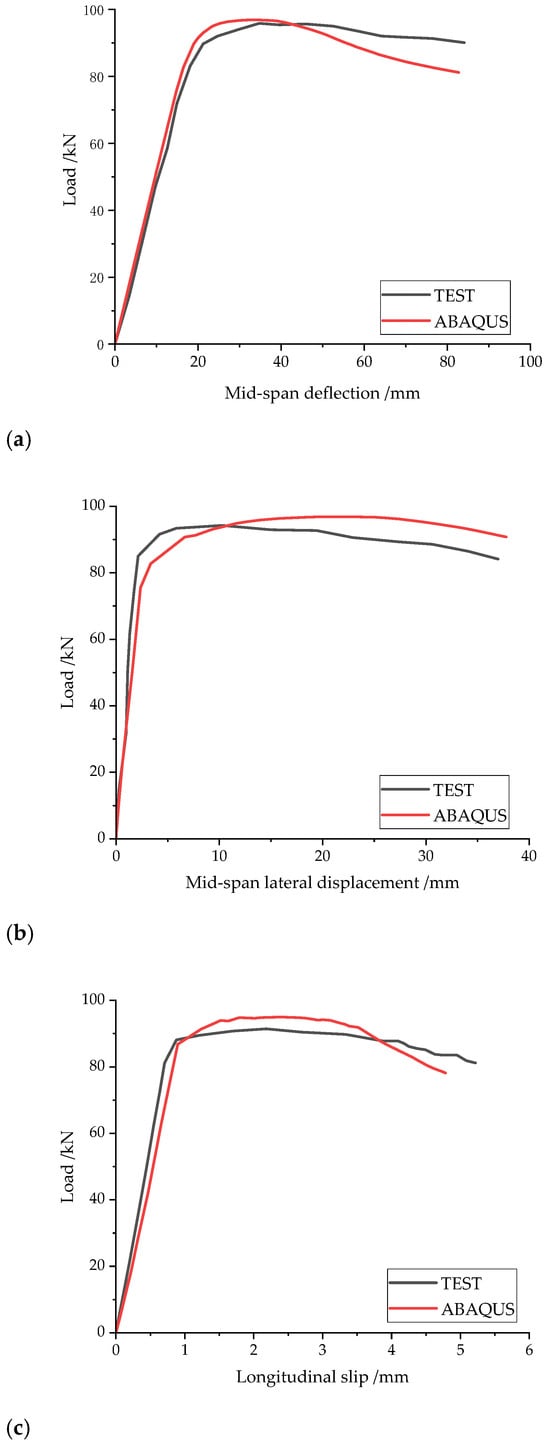
Figure 15.
Comparison of load–deformation curves of the NCLB specimen. (a) Load–Mid-span deflection; (b) load–mid-span lateral displacement; (c) load–longitudinal slip.
By comparing Figure 14 and Figure 15, it can be observed that the ABAQUS simulation analysis performs well for the bolted HBCB specimens, with the curve trends closely matching the experimental results. The simulation aligns well with the experiments before lateral-torsional buckling occurs for the boltless NCLB specimens but shows larger deviations in the post-buckling (elastic-plastic) stage. The specimens’ critical load (corresponding to elastic lateral-torsional buckling), peak load, and ultimate load (corresponding to the test end) are extracted and listed in Table 4. The error between the critical loads obtained from the ABAQUS analysis and the experimental values is less than 9%, with the error for the peak loads being less than 3%. For the relatively complex composite beams with high-strength bolts discussed in this paper, focusing on the lateral-torsional buckling of the beam, both experimental and numerical simulation approaches are highly challenging. However, the current error magnitude is within an acceptable range. The FE model cannot fully capture material nonlinearity, contact behavior, and bolt slip (NCLB). Test specimens have manufacturing errors, residual stresses, and boundary condition differences. Discrepancies mainly appear in the post-buckling (elastic-plastic) stage, but the overall error is within 9%, ensuring reliability. The current differences mostly reflect the simulation of NCLB, while the accuracy for HBCB is good. Therefore, the gap in NCLB simulation does not affect future research.
These results demonstrate the reliability and validity of the ABAQUS simulation method used in this study, making it a suitable tool for further research on HBCB specimens.
5. Analysis of the Influence of High-Strength Bolts
The influence of bolts on the structural performance of specimens is a critical aspect of this study. For bolted HBCB specimens, the bolts significantly enhance the stability and overall behavior under load, as evidenced by the closer agreement between ABAQUS simulation results and experimental data. The presence of bolts delays lateral-torsional buckling, resulting in higher critical and peak loads compared with boltless NCLB specimens.
All specimens are modeled based on the experimental HBCB specimen as the prototype, with the same Q235 steel and M12 8.8-grade high-strength bolt specifications remaining unchanged, while only pre-tension forces and bolt spacings are varied.
5.1. The Influence of High-Strength Bolt Pre-Loadings
Due to potential improper operations during the actual assembly of composite beams, the pre-tension force applied to high-strength bolts may deviate from the values specified in the standards. To investigate the effect of bolt pre-tension on the load-bearing capacity of H-shaped steel composite beams, the degree of pre-tension force is described as cd = Nr/Ns, representing the deviation between the actual pre-tension force and the standard requirement. Nr is the actual applied pre-loading (kN), and Ns is the required pre-loading (kN) according to GB50017-2017 [].
High-strength bolts of M12 8.8 grade were selected, with a bolt spacing of L/10. A finite element model was established with designed pre-loading application degrees of 0.6, 1.0, and 1.4, corresponding to cases of insufficient, standard, and excessive pre-tension, respectively, in practical engineering. Figure 16a shows the load–mid-span deflection curves of the composite beams, while Figure 16b illustrates the load–longitudinal relative slip curves.
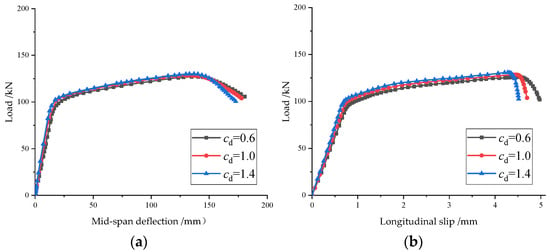
Figure 16.
Effect of bolt pre-loadings vs. deformation. (a) Mid-span deflection curves; (b) Longitudinal slip curves.
Figure 16 shows that the slope of the curves in the elastic stage and the elastic-plastic ultimate load increase with the degree of bolt pre-tension force. However, during the failure stage, the overall deformation of the composite beam decreases as the bolt pre-tension force increases. This indicates that higher bolt pre-tension force improves the composite beam’s overall stiffness and load-bearing capacity. In the deflection curve (Figure 16a), higher pre-tension increases stiffness and ultimate load while reducing final deformation. In the slip curve (Figure 16b), higher pre-tension reduces longitudinal slip, enhancing overall stability, but the effect is limited.
According to Table 5, when the actual pre-tension force of M12 8.8-grade high-strength bolts decreases from 38.5 kN to 23.1 kN, the maximum load-bearing capacity of the composite beam reduces by 1.50%, and the maximum longitudinal slip (udmax) increases by 5.96%. Conversely, when the pre-tension force increases from 38.5 kN to 53.9 kN, the maximum load-bearing capacity rises by 3.20%, and the maximum longitudinal relative slip (udmax) decreases by 4.04%.

Table 5.
The ultimate bearing capacity and the maximum longitudinal slip value of composite beams under different degrees of pre-tension application (Unit: kN).
The comparison indicates that the degree of pre-tension force can enhance the composite beam’s ultimate load-bearing capacity and longitudinal slip resistance, though the influence is not significant.
5.2. The Influence of High-Strength Bolt Spacings
In order to further investigate the influence of high-strength bolt spacings, this paper analyzes the different bolt spacings carried out to establish eight bolt spacings of L, L/2, L/4, L/5, L/8, L/10, L/15, L/16, and T, where L represents the length of the member and T represents the connections to the spliced upper and lower beams with plug welds at the bolt holes to replace the high-strength bolts. All specimens are modeled based on the experimental HBCB specimen as the prototype, with the same Q235 steel and M12 8.8-grade high-strength bolt specifications remaining unchanged, while only the bolt spacing arrangement is varied.
Figure 17 shows that as the bolt spacing decreases (equivalent to increasing the number of bolts), the load-bearing capacity of the specimen improves, and longitudinal relative slip is suppressed.
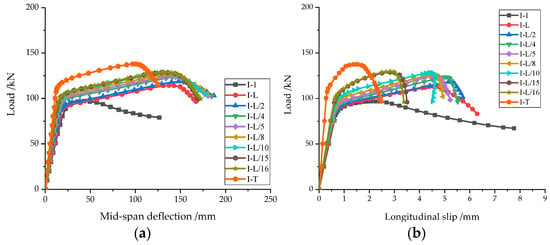
Figure 17.
Effect of different bolt spacing on load vs. deformation. (a) Mid-span deflection curves; (b) longitudinal slip curves.
The data in Table 6 show that when the bolt spacing is reduced from L/10 to L/15, the maximum load changes by only +0.37%. Similarly, reducing the spacing from L/10 to L/16 results in an increase of just +0.76% in maximum load. Moreover, the maximum load for a spacing of L/10 is 93% of the corresponding welded connection, and for L/16, it is 93.7%. This indicates that when the bolt spacing is reduced to 1/10 of the span, a further reduction in spacing has a negligible effect on improving the load-bearing capacity. However, the data in Table 6 also show that when the bolt spacing is reduced from L/10 to L/15, the maximum longitudinal slip decreases by 21.5%. When the spacing is further reduced from L/15 to L/16, the reduction in maximum longitudinal slip is only 3.4%. Balancing load-bearing capacity and reducing longitudinal slip, the current data suggest that the optimal bolt spacing is L/15. While this spacing reduces the relative longitudinal slip between the upper and lower beams, it does not achieve the same performance as welding. Further research is needed to explore ways to minimize longitudinal slip and enhance the load-bearing capacity of HBCBs.

Table 6.
The ultimate load-bearing capacity of high-strength bolt connected composite beams under varying bolt spacings.
6. Conclusions
This study aims to reduce CO2 emissions during the manufacturing phase of steel components and proposes a novel “low-carbon H-shape bolted composite beam (HBCB)”. Experimental investigations were conducted on its lateral-torsional buckling behavior, and a comprehensive numerical analysis method was developed. After validating the feasibility of the numerical method, further investigations were carried out on the influence of high-strength bolts. Based on the findings from experimental and numerical analyses, the following conclusions can be drawn:
- The proposed low-carbon H-shape bolted composite beams (HBCBs) demonstrated reliable lateral-torsional buckling behavior, validated through experimental and numerical investigations.
- High-strength bolt connections significantly enhanced the stability and load-bearing capacity of the beams compared with boltless laminated counterparts.
- Bolt spacing critically influences performance when the bolt spacing exceeds 1/15 of the beam span. At a spacing of L/15, the load-bearing capacity of HBCBs reached approximately 93.3% of that of beams with plug-weld connections.
- High-strength bolts reduced longitudinal slip effectively, but they did not fully replicate the performance of welded connections. Further research is necessary to optimize bolt arrangements and reduce longitudinal slips to enhance the overall mechanical performance of HBCBs.
7. Limitations, Advantages, and Future Perspectives
7.1. Limitations
Despite the significant contributions of this study, several limitations should be acknowledged:
- Simplifications in finite element modeling: The numerical model simplifies the bolt geometry by replacing the hexagonal bolt cap with a circular cap and ignoring bolt threads to improve convergence and computational efficiency. While this simplification does not affect overall trends, minor discrepancies may exist compared with actual behavior.
- Longitudinal slip effects: The study found that high-strength bolted composite beams (HBCBs) exhibited longitudinal relative slip between the upper and lower beams. Although increasing bolt spacing beyond L/15 had negligible effects on load-bearing capacity, slip control remains a challenge and requires further optimization.
- Limited parameter investigation: The current study primarily focuses on bolt pre-loadings and bolt spacing, while other influential factors, such as material properties, flange–web interaction, and residual stresses, were not extensively investigated.
- Lack of cyclic loading tests: This research focuses on monotonic loading conditions, whereas real-world structures often experience cyclic loading. The performance of HBCBs under repeated loads needs further exploration.
7.2. Advantages
- Low-carbon strategy: This study emphasizes reducing welding-related CO2 emissions, which constitute 57.2% of the prefabrication process emissions. By using hot-rolled H-shapes and bolted connections, this study presents an environmentally friendly alternative to traditional welded structures.
- Enhanced structural performance: Experimental and numerical results demonstrate that HBCBs achieve approximately 93.3% of the load-bearing capacity of plug-welded connections while significantly reducing construction emissions.
- Reliable numerical modeling: The proposed ABAQUS finite element model was validated against experimental data, with errors in critical and peak loads remaining within 9% and 3%, respectively, ensuring its applicability for further parametric studies.
- Engineering applicability: This study provides practical insights into optimizing bolt spacing (L/15 as the optimal threshold) and bolt pre-loading (increased pre-tension enhances stiffness and reduces slip), guiding real-world design and construction.
7.3. Future Perspectives
- Further optimization of bolt arrangements: While L/15 was identified as an effective bolt spacing, additional investigations into alternative patterns (e.g., staggered arrangements) could further enhance performance and slip resistance.
- Cyclic performance studies: Future research should explore the long-term durability of HBCBs under seismic loading to ensure their reliability in extreme conditions.
- Incorporation of residual stresses: More detailed modeling of residual stresses, particularly around bolt holes, could refine the accuracy of numerical predictions.
- Hybrid connection approaches: Investigating the combination of bolted and minimal welding techniques may help balance load-bearing capacity, slip control, and sustainability goals.
This study lays a solid foundation for developing low-carbon, high-strength bolted composite beams, and future research can build upon these findings to further enhance their mechanical performance and structural efficiency.
Author Contributions
Conceptualization, L.L.; investigation. K.K.D., B.L. and H.H.; validation, B.L., Z.H. and H.H.; resources, L.L.; writing—original draft preparation, K.K.D., L.L., B.L., Z.H. and H.H.; writing—review and editing, L.L., B.L. and Z.H.; project administration, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Gan, V.; Wong, C.; Tse, K.; Chen, J.; Lo, I.; Chan, C. Parametric modelling and evolutionary optimization for cost-optimal and low-carbon design of high-rise reinforced concrete buildings. Adv. Eng. Inform. 2019, 42, 100962. [Google Scholar] [CrossRef]
- Arogundade, S.; Dulaimi, M.; Ajayi, S. Holistic Review of Construction Process Carbon-Reduction Measures: A Systematic Literature Review Approach. Buildings 2023, 13, 1780. [Google Scholar] [CrossRef]
- You, J.; Xu, X.; Wang, Y.; Xiang, X.; Luo, Y. Life cycle carbon emission assessment of large-span steel structures: A case study. Structures 2023, 52, 842–853. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Chen, Y.; Wang, J.; Zhao, L.; Chen, M. Evaluation of Carbon Emission Efficiency in the Construction Industry Based on the Super-Efficient Slacks-Based Measure Model: A Case Study at the Provincial Level in China. Buildings 2023, 13, 2207. [Google Scholar] [CrossRef]
- BS EN 15978:2011; Sustainability of Construction Works-Assessment of Environmental Performance of Buildings-Calculation Method. British Standards Institute: London, UK, 2011.
- Li, Q.; Yue, Q.; Feng, P.; Xie, N.; Liu, Y. Development Status and Prospect of Steel Structure Industry Based on Carbon Peak and Carbon Neutrality Target. Prog. Steel Build. Struct. 2022, 24, 1–6. [Google Scholar]
- Hammond, G.; Jones, C. Embodied energy and carbon in construction materials. Proc. Inst. Civ. Eng. Energy 2008, 161, 87–98. [Google Scholar] [CrossRef]
- Dani, A.; Roy, K.; Masood, R.; Fang, Z.; Lim, J. A comparative study on the life cycle assessment of New Zealand residential buildings. Buildings 2022, 12, 50. [Google Scholar] [CrossRef]
- Hart, J.; D’Amico, B.; Pomponi, F. Whole-life embodied carbon in multistory buildings: Steel, concrete and timber structures. J. Ind. Ecol. 2021, 25, 403–418. [Google Scholar] [CrossRef]
- Mostafavi, F.; Tahsildoost, M.; Zomorodian, Z.S. Energy efficiency and carbon emission in high-rise buildings: A review (2005–2020). Build. Environ. 2021, 206, 108329. [Google Scholar] [CrossRef]
- Rousta, A.M.; Azandariani, M.G.; Ardakani, M.A.S.; Shoja, S. Cyclic behavior of an energy dissipation system with the vertical steel panel flexural-yielding dampers. Structures 2022, 45, 629–644. [Google Scholar] [CrossRef]
- Sadeghi, M.; Shoja, S.; Ardakani, M.A.S.; Jahangiri, M. Innovative improvement towards steel plate shear walls employing the grid stiffeners along with the metallic yielding dampers. J. Constr. Steel Res. 2024, 223, 109080. [Google Scholar] [CrossRef]
- Hu, S.; Liu, S.; Zeng, S.; Zhang, B.; Xu, Z. Investigating seismic performance of a novel self-centering shear link in EBF utilizing experimental and numerical simulation. J. Constr. Steel Res. 2025, 224, 109129. [Google Scholar] [CrossRef]
- Liu, S.; Chen, S.; Zeng, S.; Zhang, B.; Hu, S. Seismic performance analysis of K-shaped EBF with an innovative crack-resistant composition beam. J. Build. Eng. 2025, 101, 111818. [Google Scholar] [CrossRef]
- Huang, Z.; Zhou, H.; Tang, H.; Zhao, Y.; Lin, B. Carbon emissions of prefabricated steel structure components: A case study in China. J. Clean. Prod. 2023, 406, 137047. [Google Scholar] [CrossRef]
- Roy, K.; Dani, A.A.; Ichhpuni, H.; Fang, Z.; Lim, J.B.P. Improving sustainability of steel roofs: Life cycle assessment of a case study roof. Appl. Sci. 2022, 12, 5943. [Google Scholar] [CrossRef]
- Lu, L.; Wang, D.; Dai, Z.; Luo, T.; Ding, S.; Hao, H. Global Buckling Investigation of the Flanged Cruciform H-shapes Columns (FCHCs). Appl. Sci. 2021, 11, 11458. [Google Scholar] [CrossRef]
- Nie, W.; Lu, L.; Li, R.; Hao, H.; Luo, T. Global buckling investigation of T-shaped built-up columns composed of two hot-rolled H-shapes. Structures 2023, 58, 105485. [Google Scholar] [CrossRef]
- Lin, X.; Okazaki, T.; Chung, Y.L.; Nakashima, M. Flexural performance of bolted built-up columns constructed of H-SA700 steel. J. Constr. Steel Res. 2013, 82, 48–58. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, J. Experimental and analytical studies on bearing capacity of bolt connected composite plate girders. Int. J. Steel Struct. 2017, 17, 1317–1329. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. Flexural behaviour of pairs of laminated unequal channel beams with different interfacial connections in corner-supported modular steel buildings. Thin-Walled Struct. 2020, 154, 106792. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Ma, R.; Chang, H.; Yang, C.; Zhang, L. Investigation on interfacial slipping response of laminated channel beams with bolt connections in modular steel buildings. J. Build. Eng. 2023, 63, 105441. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Chen, X.; Yang, C.; Zhang, L. Numerical-analytical investigation on bending performance of laminated beams in modular steel buildings. J. Constr. Steel Res. 2024, 217, 108630. [Google Scholar] [CrossRef]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- Xin, H.; Veljkovic, M. Evaluation of high strength steels fracture based on uniaxial stress-strain curves. Eng. Fail. Anal. 2021, 120, 105025. [Google Scholar] [CrossRef]
- ECCS. Ultimate Limit State Calculation of Sway Framed with Rigid Joints; Technical Committee 8 (TC 8) of European Convention for Constructional Steelwork (ECCS): Brussels, Belgium, 1984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).