The Safe Load-Bearing Capacity of Railway Tunnel Linings under High-Pressure and Water-Rich Conditions

Abstract

High water pressure has been identified as the direct cause of water seepage problems in tunnels. Consequently, it is imperative to ascertain the safety load-bearing limits of tunnel linings in high-pressure, water-rich strata. In this study, FLAC3D (V5.0) numerical simulation software was employed to establish seepage models of tunnels under high-pressure, water-rich conditions, taking an actual engineering project as a reference. The hydrostatic pressure on tunnel linings under various conditions, including different permeability coefficients of the surrounding rock, grouting rings, levels of the water table, and coordinates of lining positions, was computed. By extracting the results of these simulations, correlations between lining water pressure and various parameters were analyzed, and preliminary hydrostatic pressure calculation formulas were deduced. Through regression analysis using SPSS (19.0) software, a general calculation formula for lining water pressure was derived. Given similar surrounding rock conditions, it was revealed that railway tunnel lining types adhere to a universal standard. The calculation formula for lining water pressure, when integrated with lithostatic pressure in the seepage model, facilitates the computation of the maximum pressure head that the tunnel lining can withstand under different conditions. A tabulation summarizing safe water head heights under various conditions is also presented, which enables rapid consultation of the safe load-bearing range of tunnel lining under corresponding conditions. This study provides a new calculation method for the lining water pressure of a water-rich railway tunnel, filling the literature gap. The safe tunnel head query table provides a new research approach for the design of water-rich tunnels. The research method in this article is rare in the literature, and the research approach has obvious innovations. The findings of this study have the potential to provide a theoretical foundation and data reference for the structural design of tunnel linings and the remediation of related issues.

1. Introduction

Currently, cracking and leakage in tunnel linings are recognized as the most formidable challenges faced in tunnels situated in high-pressure, water-rich zones. High water pressure endured by tunnel linings is attributed as the direct cause of this issue. Figure 1 presents a typical site of water damage in a tunnel, where it is demonstrated that water damage severely compromises the safety of both traffic and human lives, thereby posing substantial adverse social impacts. To reduce the volume of water influx and alleviate water pressure on tunnel linings, grouting is injected within a certain range behind the tunnel walls during construction, with this range designated as the grouting ring.

Figure 1. A typical site of water damage in a tunnel.

A large number of studies on the water pressure in tunnel linings in water-rich zones have been conducted by researchers [1,2]. The methodologies primarily encompass the seepage analytical method [3,4,5], numerical calculation method [6,7], field measurement method [8,9], and laboratory model testing method [10,11], although calculation formulas for lining water pressure are seldom furnished in the literature. Likewise, in regard to the safety load-bearing capacity of tunnel linings in water-rich zones, extensive efforts have been made by researchers, mainly focusing on theoretical analysis methods [12,13,14], similar model experiment methods [15], and numerical simulation methods [16,17,18]. However, the majority of the literature is geared towards qualitative evaluation of forces acting on tunnel linings, with scarce provision of numerical values or ranges for the safe load-bearing capacity of tunnel linings.

In this study, a numerical calculation model for tunnel seepage was established, taking an engineering example as the background. The correlations between the computation parameters of tunnel linings and lining water pressure were analyzed, and a calculation formula for lining water pressure in high-pressure, water-rich zones is provided. By applying the calculated values of lining water pressure and lithostatic pressure to the tunnel lining, the critical values of safety load-bearing capacity of tunnel linings under different computation parameters and lining types are determined. The methodology proposed in this study holds potential for furnishing a theoretical foundation and data reference for optimizing the cross-sectional design of tunnel linings.

2. Regression Analysis-Based Calculation Formula for Water Pressure in Railway Tunnels

2.1. Calculation Principles and Model Establishment

(1)

Calculation Principles

For double-line railway tunnels, standard cross-sectional forms are typically chosen based on the geological strata, and the design for water prevention and drainage generally adheres to universal standards. For instance, the “Railway Tunnel Design Code” [19] recommends the adoption of Type IVa composite lining for Class IV surrounding rock, and Type Va composite lining for Class V surrounding rock. Therefore, when the lining type is established, the principal factors influencing the water pressure on the lining encompass the permeability coefficients of the surrounding rock k_r, the permeability coefficient of the grouting ring k_g, the thickness of the grouting ring, tunnel water head height H, and positional coordinates.

In this study, four parameters, namely the lining positional coordinates (x, y), the permeability coefficient of the surrounding rock k_r, the permeability coefficient of the grouting ring k_g, and the height H from the crown center point to the free surface of groundwater, were considered. The anticipated lining water pressure formula is presented as $P=F\left(x,y,k_r,k_g,H\right)$, but due to the tunnel’s symmetry about the y-axis, the formula can be simplified to $P=F\left(y,k_r,k_g,H\right)$.

(2)

Numerical Calculation Model

To ascertain the tunnel lining water pressure formula, this section selects values for k_r, k_g, and H within a reasonable range, based on the surrounding rock and geological conditions of a water-rich tunnel, in conjunction with the “Engineering Geology Manual” [20]. The parameter values and working condition numbers are displayed in Table 1.

Table 1. Numerical calculation conditions.

Water Head Height/m	kg/kr	10−2 cm/s	10−3 cm/s	10−4 cm/s	10−5 cm/s
20	10−4 cm/s	Working conditions 1	Working conditions 2	Working conditions 3	Working conditions 4
	10−5 cm/s	Working conditions 5	Working conditions 6	Working conditions 7	Working conditions 8
	10−6 cm/s	Working conditions 9	Working conditions 10	Working conditions 11	Working conditions 12
50	10−4 cm/s	Working conditions 13	Working conditions 14	Working conditions 15	Working conditions 16
	10−5 cm/s	Working conditions 17	Working conditions 18	Working conditions 19	Working conditions 20
	10−6 cm/s	Working conditions 21	Working conditions 22	Working conditions 23	Working conditions 24
100	10−4 cm/s	Working conditions 25	Working conditions 26	Working conditions 27	Working conditions 28
	10−5 cm/s	Working conditions 29	Working conditions 30	Working conditions 31	Working conditions 32
	10−6 cm/s	Working conditions 33	Working conditions 34	Working conditions 35	Working conditions 36
150	10−4 cm/s	Working conditions 37	Working conditions 38	Working conditions 39	Working conditions 40
	10−5 cm/s	Working conditions 41	Working conditions 42	Working conditions 43	Working conditions 44
	10−6 cm/s	Working conditions 45	Working conditions 46	Working conditions 47	Working conditions 48
200	10−4 cm/s	Working conditions 49	Working conditions 50	Working conditions 51	Working conditions 52
	10−5 cm/s	Working conditions 53	Working conditions 54	Working conditions 55	Working conditions 56
	10−6 cm/s	Working conditions 57	Working conditions 58	Working conditions 59	Working conditions 60

In accordance with practical calculation principles, the following assumptions were made for the numerical calculations:

• The surrounding rock is isotropic, homogeneous, continuous, and a medium.
• Groundwater seepage complies with Darcy’s law.
• Groundwater replenishment is sufficient.

(3)

Boundary Conditions

• The seepage boundary conditions are as follows: the permeable boundary has a fixed pore pressure on both sides of the formation; a permeable boundary with fixed pore pressure is set at the top of the formation to ensure that the lining bears the corresponding head pressure; the bottom of the formation is impermeable.
• The mechanical boundary conditions are as follows: horizontal constraints are set on the left and right sides of the formation; vertical constraints are set at the bottom of the formation; mechanical boundary conditions are set at the top of the formation to ensure that the tunnel bears the corresponding buried depth pressure.

FLAC3D software was employed to calculate the water pressure on tunnel linings under 60 different conditions. The calculation model is illustrated in Figure 2. In the horizontal direction, three times the tunnel diameter is taken to the left and right from the tunnel body; three times the tunnel height is taken downwards from the tunnel body and upwards from the tunnel crown. Based on the Saint-Venant principle, it is assumed that the surrounding rock at the model’s periphery is unaffected by tunnel drainage, and the pore pressure at the model’s periphery is fixed. Solid elements are utilized for all calculation units, with the surrounding rock, circumferential blind tubes, and permeable blind tubes adopting the Mohr–Coulomb model, while lining, drainage ditches, and invert filling adopt the elastic model. Parameter selections are depicted in Table 2.

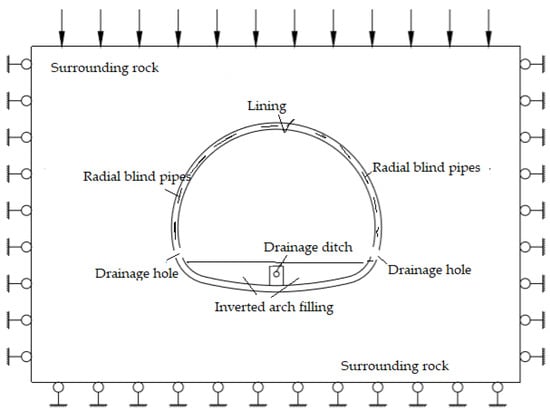
Figure 2. Schematic diagram of tunnel calculation model.

Table 2. Parameter values for numerical calculations.

Material	Density (kg/m3)	Density (kg/m3)	Poisson’s Ratio	Internal Friction Angle	Cohesion (GPa)	Porosity	Coefficient (cm/s)
Surrounding rock	2000	1.5	0.35	20	0.1	0.2
Lining	2500	35	0.2	-	-	0.1	1 × 10−6
Drainage hole	2500	35	0.2	-	-	0.5	7.85 × 10−3
Inverted arch filling	2300	28	0.2	-	-	0.15	2 × 10−6
Drainage ditch	2300	35	0.2	-	-	0.2	2 × 10−6
Radial blind pipes	2000	1.5	0.35	20	0.1	0.5	2.45 × 10−3

2.2. Derivation of Water Pressure on Tunnel Lining

Based on the water pressure formula p = ρgh, it is initially conceived that the water head height in the lining water pressure formula interacts with other parameters in a multiplicative fashion. The correlations between H, k_r, and k_g water pressure on the lining are subsequently analyzed.

2.2.1. Tunnel Lining Water Pressure and Water Head Height

The relationship between lining water pressure and water head height across various working conditions was analyzed. Figure 3 illustrates the maximum lining water pressure in tunnels at different H values, with $k_r=1\times 10^{-4}$ cm/s and $k_g=1\times 10^{-5}$ cm/s.

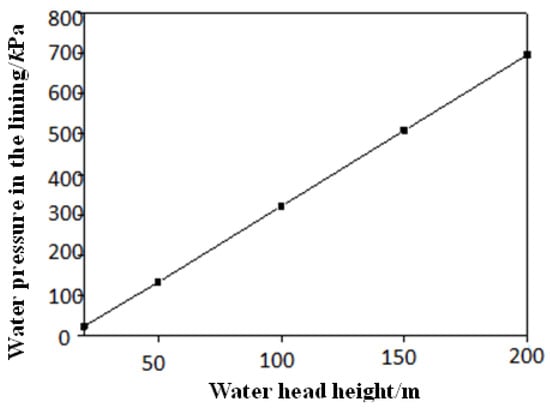
Figure 3. Curve of maximum lining water pressure vs. water head height (H).

As can be observed from Figure 3, the maximum lining water pressure and H approximate a linear relationship, which leads to the following formula:

$$\mathrm{P}=\mathrm{a}\mathrm{H}\left[f\left(k_r,k_g,\mathrm{y}\right)\right]+\mathrm{c}$$

(1)

The distance from the lining location point (x, y) to the free surface of the groundwater, h, is used as the fitting parameter, as depicted in Figure 4. The formula is consequently modified to:

$$\mathrm{P}=\mathrm{a}\mathrm{h}\left[f\left(k_r,k_g,\mathrm{y}\right)\right]+\mathrm{c}$$

(2)

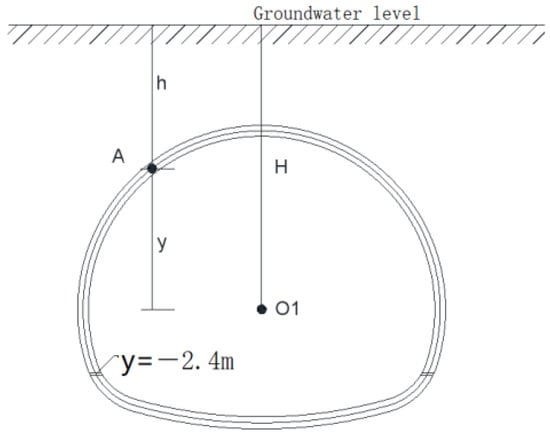
Figure 4. Schematic of calculation cross-section.

A coordinate system is established with the lining crown center O₁ as the origin; h denotes the distance from point A to the free surface of the groundwater, h = H − y; and y represent the distance from the lining (point in question) to the crown center, where a and c are constants.

2.2.2. Lining Water Pressure and Surrounding Rock Permeability Coefficient

The relationship between lining water pressure and surrounding rock permeability was analyzed for various working conditions. Figure 5 shows a linear graph of the maximum lining water pressure in tunnels for various working conditions with $H=100\mathrm{m}$ and $k_g=1\times 10^{-5}$ cm/s. Therefore, lnk_r is used as a substitute for k_r. After substitution, the relationship between lnk_r and the maximum lining water pressure is obtained, as depicted in Figure 6. Consequently, a tentative formula for lining water pressure is designed as:

$$\mathrm{P}=\mathrm{a}\left[\mathrm{b}\ln k_r+f\left(k_g\right)+f\left(\mathrm{y}\right)\right]\mathrm{h}+\mathrm{c}$$

(3)

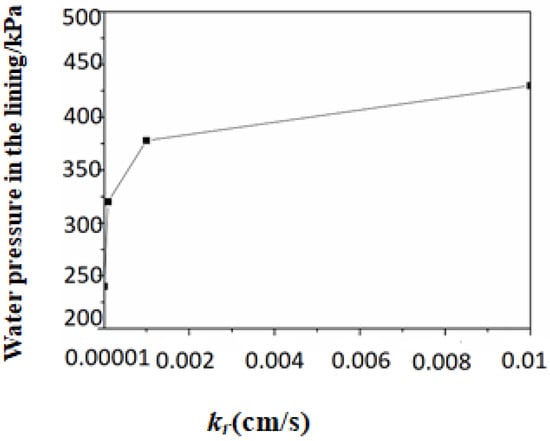
Figure 5. Relationship curve between maximum lining water pressure and k_r.

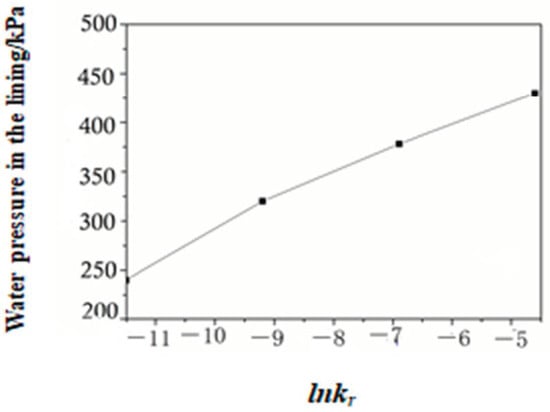
Figure 6. Relationship curve between maximum lining water pressure and lnk_r.

2.2.3. Grouting Ring Permeability Coefficient and Lining Water Pressure

The relationship between lining water pressure and the grouting ring permeability coefficient across various working conditions was analyzed. Figure 7 shows the water pressure at various points on the tunnel lining when H = 100 m and $k_r=1\times 10^{-4} \mathrm{c}\mathrm{m}/\mathrm{s}$. Similarly, lnk_g is used in place of k_g, as depicted in Figure 8.

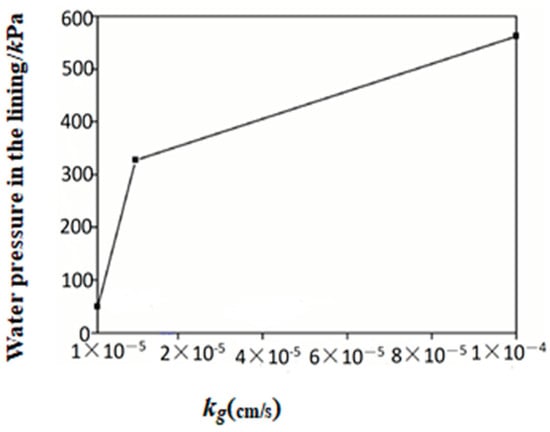
Figure 7. Relationship curve between maximum lining water pressure and k_g.

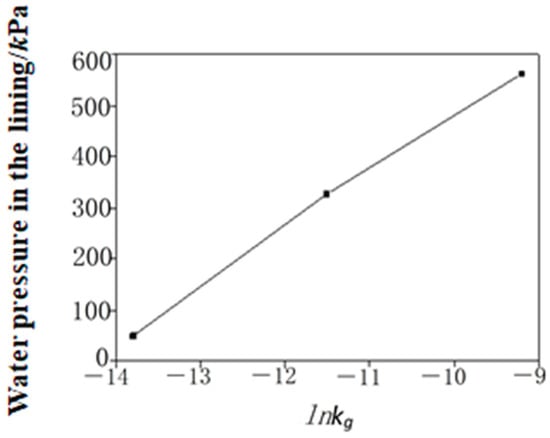
Figure 8. Relationship curve between maximum lining water pressure and lnk_r.

The tentative formula for lining water pressure is designed as:

$$\mathrm{P}=\mathrm{a}\left[\mathrm{b}\ln k_r+\mathrm{d}\ln k_g+f\left(\mathrm{y}\right)\right]\mathrm{h}+\mathrm{c}$$

(4)

2.2.4. Maximum Lining Water Pressure and Lining Coordinates

The relationship between lining water pressure and lining coordinates across various working conditions was analyzed. Figure 9 depicts the water pressure on the lining at various points (calculation model nodes) around the entire tunnel ring when H = 100 m, $k_r=1\times 10^{-4}$ cm/s, and $k_g=1\times 10^{-5}$ cm/s. Figure 9 shows that, when y > −2.4 and lining water pressure has a curve relationship, a quadratic curve function to determine the formula is considered; when y ≤ −2.4 and lining water pressure approximates a linear relationship, a linear function is considered. Hence, the tentative formulas for lining water pressure are designed as:

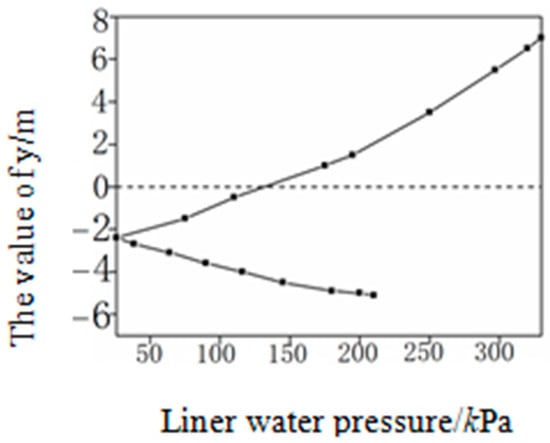
Figure 9. Curve of relationship between lining water pressure and lining coordinates.

For y > −2.4:

$$\mathrm{p}=\mathrm{a}\left[\mathrm{b}\ln k_r+\mathrm{d}\ln k_g+\mathrm{e}{y}^2+\mathrm{f}\mathrm{y}+\mathrm{g}\right]\mathrm{h}+\mathrm{c}$$

(5)

For y ≤ −2.4:

$$\mathrm{p}=\mathrm{a}\left[\mathrm{b}\ln k_r+\mathrm{d}\ln k_g+iy+j\right]\mathrm{h}+\mathrm{c}$$

(6)

For the convenience of calculation, Formulas (5) and (6) are simplified to:

For y > −2.4:

$$\mathrm{p}=\left(\mathrm{A}\ln k_r+\mathrm{B}\ln k_g+\mathrm{C}{y}^2+\mathrm{D}\mathrm{y}+\mathrm{E}\right)\mathrm{h}+\mathrm{F}$$

(7)

For y ≤ −2.4:

$$\mathrm{P}=\left(\mathrm{G}\ln k_r+\mathrm{H}\ln k_g+Iy+J\right)\mathrm{h}+\mathrm{K}$$

(8)

where, A, B, C, D, E, F, G, H, I, J, K are constants.

2.3. Final Determination of Formula

All parameters are extracted from each working condition. SPSS regression analysis software was used to perform fitting calculations and analysis of the data and preliminary water pressure formulas under various working conditions. Several constants are obtained in Formulas (7) and (8), and the goodness of fit of the formulas is assessed based on the coefficient of determination R² from multiple regression analysis.

The calculations reveal that when y > −2.4 and y ≤ −2.4, the coefficients of determination are $R^2=0.896$ and $R^2=0.858$, respectively, indicating a good fit of the formulas.

Ultimately, the formula for calculating the water pressure on the lining of railway tunnels in high-pressure, water-rich areas is:

y > −2.4,

$$\mathrm{p}=\left(320.5\ln k_r+1333.3\ln k_g-33.7y^2+572.5\mathrm{y}+27082.7\right)\mathrm{h}-10265$$

(9)

y ≤ −2.4,

$$\mathrm{p}=\left(362.8\ln k_r+963.9\ln k_g-1059.8+17164.3\right)\mathrm{h}+13798.2$$

(10)

3. Calculation of Stress on Lining Structure of Railway Tunnels in High-Pressure, Water-Rich Zones

The current “Railway Tunnel Design Code” [19] classifies the surrounding rock of tunnels into six grades, as shown in Table 3. Regarding the influence of groundwater, a modified form was adopted, and the state of groundwater is divided into three grades based on the seepage amount per unit of time, as shown in Table 4 and Table 5.

Table 3. Surrounding rock grading [19].

Rock Level	Qualitative Characteristics	Basic Quality Indicators of Rock Mass (BQ) (MPa)
I	Hard rock, complete rock mass	>550
II	Hard rock, sub-complete rock mass Sub-hard rock, complete rock mass	550~451
III	Hard rock, some broken Some Soft rock, complete rock mass	450~351
IV	Hard rock, broken rock mass Soft rock, complete rock mass	350~251
V	Soft rock, broken rock mass	<250

Table 4. Groundwater state grading [19].

Grade	State	Seepage Amount (L/(min·10 m))
I	Dry or Damp	<10
II	Occasional Seepage	10~25
III	Regular Seepage	25~125

Table 5. Groundwater impact correction [19].

Groundwater State Grade	Surrounding Rock Grade
	I	II	III	IV	V	VI
I	I	II	III	IV	V	-
II	I	II	IV	V	VI	-
III	II	III	IV	V	VI	-

BQ = 100 + 3 Rc + 250 Kv. Its unit is MPa. RC: uniaxial saturated compressive strength of rock. Its unit is MPa. Kv: integrity coefficient of rock mass. Its value range is 0 to 1.

In the quantitative description of water seepage, the statistics are generally based on the water seepage volume per minute for a 10 m tunnel length (L/(min·10 m)).

As can be seen from Table 4 and Table 5, the Railway Tunnel Design Code provides limited information on the influence of groundwater and is only applicable to geological formations with a seepage amount of less than 125 L/(min·10 m). The Railway Tunnel Design Code does not mention the correction of surrounding rock in high water head and water-rich zones. The combination of the surrounding rock pressure and water pressure in high water head strata is a complex issue, which is not fully considered in current railway tunnel design.

In this section, the calculation formulae for lining water pressure (Equations (9) and (10)) developed in this study are utilized to compute and analyze the safety stresses on the standard cross-section of railway tunnel linings under various combinations of strata and water pressures by integrating the developed formulae with the conventional load structure method. The calculation boundary conditions are the same as those in Section 2.1.

3.1. Computational Approach and Selection of Working Conditions

• Computational Approach

  (1)

  For deep-buried tunnels, a groundwater head height H is initially selected, and the surrounding rock is classified as grade II, with type IIb lining selected. The permeability coefficient of the surrounding rock is set at $1\times 10^{-2}$ cm/s and the grouting ring permeability coefficient at $1\times 10^{-4}$ cm/s. On the basis of the conventional load structure method, the water pressure load (Formulas (9) and (10)) developed in this study is applied to the tunnel lining, the internal forces in the lining are extracted, and the minimum safety factor of the lining is calculated for comparison with the code limits.

  (2)

  The water head height is varied, and the calculations are repeated to find the water head height at which the minimum safety factor of the lining just meets the code requirements, which is termed the “safe water head height” under the given working conditions.

  (3)

  The permeability coefficients of the surrounding rock and the grouting reinforcement ring are varied to find the “safe water head height” under type IIb lining and grade II surrounding rock at different permeability coefficients.

  (4)

  The surrounding rock grade is varied, selecting grades II–V, to find the “safe water head height” for type IIb, IIIa, IVa, and Va linings under different surrounding rock grades and permeability coefficients.

  (5)

  The results are summarized in a reference table.

• Selection of Working Conditions

In line with the actual conditions of tunnels in water-rich karst regions, the safe water head heights under 48 working conditions are calculated. The specific working conditions for the calculations are presented in Table 6.

Table 6. Safe water head height calculation working conditions.

Surrounding Rock and Lining	kg	kr
		10−2 cm/s	10−3 cm/s	10−4 cm/s	10−5 cm/s
Grade II Type IIb Lining	10−4 cm/s	Working conditions 1	Working conditions 2	Working conditions 3	Working conditions 4
	10−5 cm/s	5	6	7	8
	10−6 cm/s	9	10	11	12
Grade III Type IIIa Lining	10−4 cm/s	Working conditions 12	Working conditions 14	Working conditions 15	Working conditions 16
	10−5 cm/s	17	18	19	20
	10−6 cm/s	21	22	23	24
Grade IV Type IVa Lining	10−4 cm/s	Working conditions 25	Working conditions 26	Working conditions 27	Working conditions 28
	10−5 cm/s	29	30	31	32
	10−6 cm/s	33	34	35	36
Grade V Type Va Lining	10−4 cm/s	Working conditions 37	Working conditions 38	Working conditions 39	Working conditions 40
	10−5 cm/s	41	42	43	44
	10−6 cm/s	45	46	47	48

3.2. Computational Models and Parameter Selection

(1)

Computational Models

In the computations, type IIb plain concrete lining is selected for grade II surrounding rock; type IIIa plain concrete lining is employed for grade III surrounding rock; type IVa reinforced concrete lining is chosen for grade IV surrounding rock; and type Va reinforced concrete lining is used for grade V surrounding rock. The tunnel lining is subjected to strata pressures N₁, N₂, and N₃, as well as water pressure P (formula value), as depicted in Figure 10.

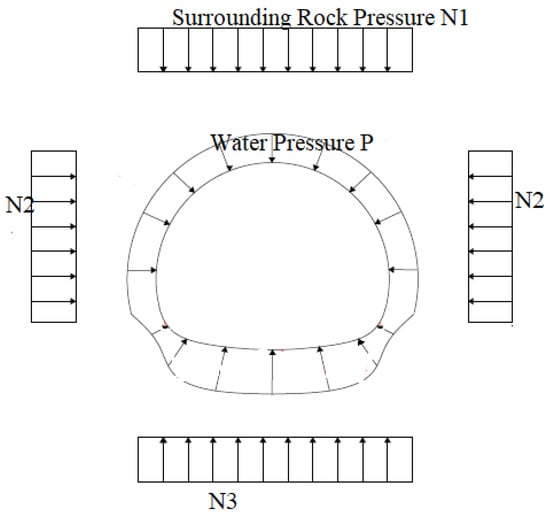
Figure 10. Schematic diagram of applied loads.

(2)

Computational Parameters

Two-dimensional beam elements are uniformly adopted in the computations. The physical and mechanical parameters of the surrounding rock refer to the “Railway Tunnel Design Code” [19]; the permeability coefficients of the surrounding rock are referenced from geotechnical data, the “Engineering Geology Manual” [20], and “Rock Hydraulics and Engineering” [20]. The tunnel lining parameters are shown in Table 7:

Table 7. Selection of computational parameters.

Surrounding Rock Grade	Unit Weight (kN/m3)	Elastic Reaction Coefficient (MPa/m)	Lining Selection	Lining Circumferential Reinforcement Configuration
II	26	1500	IIb	Plain Concrete
III	24	850	IIIa	Plain Concrete
IV	20	300	IVa	18@200
V	18	150	Va	20@200

3.3. Analysis of Lining Safe Water Head Calculation Results

The calculations for the height of the standard lining cross-section’s safety water head in a double-line railway tunnel are shown in Table 8. Taking into consideration that in practical engineering scenarios, the water head exceeding 200 m is rather rare, for workload reduction, water heads above 200 m in the calculations for the working conditions are denoted as greater than 200 m.

Table 8. Summary of tunnel safe water head heights.

Surrounding Rock and Lining	kg	kr
		10−2 cm/s	10−3 cm/s	10−4 cm/s	10−5 cm/s
Grade II Surrounding Rock Type IIb Lining	10−4 cm/s	20 m	24 m	29 m	35 m
	10−5 cm/s	40 m	45 m	60 m	80 m
	10−6 cm/s	120 m	150 m	>200 m	>200 m
Grade III Surrounding Rock Type IIIa Lining	10−4 cm/s	32 m	36 m	41 m	46 m
	10−5 cm/s	55 m	60 m	68 m	79 m
	10−6 cm/s	130 m	>200 m	>200 m	>200 m
Grade IV Surrounding Rock Type IVa Lining	10−4 cm/s	50 m	56 m	64 m	78 m
	10−5 cm/s	80 m	100 m	130 m	150 m
	10−6 cm/s	170 m	>200 m	>200 m	>200 m
Grade V Surrounding Rock Type Va Lining	10−4 cm/s	62 m	67 m	78 m	90 m
	10−5 cm/s	100 m	120 m	145 m	180 m
	10−6 cm/s	>200 m	>200 m	>200 m	>200 m

The following conclusions are drawn from Table 8:

• It can be observed from Table 8 that, when the lining types were the same, a smaller permeability coefficient of the grouting reinforcement ring resulted in a higher safe water head for the lining. When the permeability coefficient of the grouting ring reached 10⁻⁶ cm/s, the safe water head of the lining exceeded 200 m under almost all working conditions.
• With the lining types being the same, a smaller permeability coefficient of the surrounding rock led to a higher safety water head for the lining. Therefore, for surrounding rocks with strong permeability, it is recommended to use grouting reinforcement to reduce the permeability of the surrounding rocks, thereby enhancing the safety of the lining.

For a more intuitive observation, the data from Table 8 is presented using bar charts in Figure 11 and Figure 12.

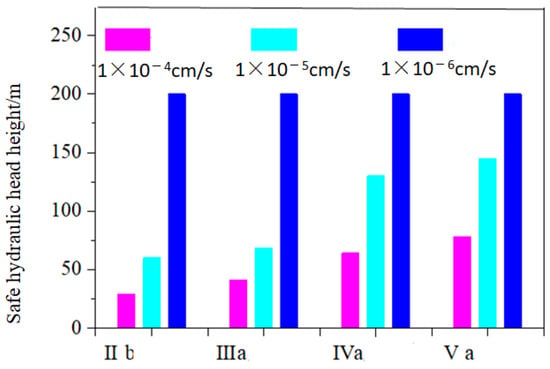
Figure 11. Relationship between grouting ring permeability coefficient and safe water head.

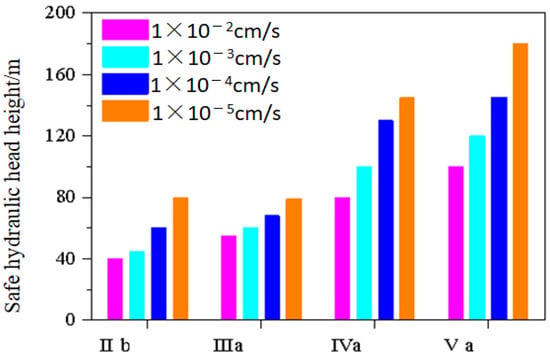
Figure 12. Relationship between surrounding rock permeability coefficient and safe water head height.

Figure 11 illustrates the relationship between the grouting ring’s permeability coefficient and the safe water head height when the surrounding rock’s permeability coefficient is $1\times 10^{-4}$ cm/s. It can be observed that when the lining types are the same, the lining’s safety water head height increases as the grouting ring’s permeability coefficient decreases. Similarly, the larger the lining type, the higher the lining’s safety water head when the grouting ring’s permeability coefficient is the same, indicating that in high-pressure, water-rich areas, the occurrence of water damage can be prevented by increasing the lining standards.

Figure 12 illustrates the relationship between the surrounding rock’s permeability coefficient and the safety water head height where the grouting ring’s permeability coefficient is in cm/s. It can be observed that when the lining types are the same, the lining’s safe water head height increased as the surrounding rock’s permeability coefficient decreased.

3.4. Application of Lining Structure Safety Water Head Summary Table

Table 8 displays the safe hydraulic head height of the lining under different tunnel lining types, grouting reinforcement ring permeability coefficients, and surrounding rock permeability coefficients. Table 8 enables the quick and convenient determination of the maximum water head height that a tunnel can withstand under certain working conditions (lining type, surrounding rock, grouting ring), providing valuable data for railway tunnel design in high-pressure, water-rich areas.

The use of this table is extremely convenient. For instance, if a section of a tunnel’s geological strata is identified as a water-rich area, encountering heavy rain during operation could potentially lead to the destruction of the tunnel lining. In this area, the surrounding rock is classified as Class IV, with dolomite being exposed on the tunnel face. The groundwater is karst water, which flows through karst channels and fissures in substantial amounts. According to the tunnel design documents, the tunnel lining is of type IVa. Based on the tunnel’s geological survey report and geological conditions, the permeability coefficient of the surrounding rock is taken as $1\times 10^{-4}$ cm/s. According to the on-site construction conditions, the permeability coefficient of the grouting ring is taken as $1\times 10^{-5}$ cm/s. By consulting Table 8, it is found that the safe water head height for a section of this tunnel is 130 m, meaning that if the actual water head experienced by the tunnel section exceeds 130 m, the tunnel lining may be compromised.

4. Conclusions

This study focused on the analysis of safety loading in high-pressure, water-rich railway tunnels, with the following key findings and conclusions:

(1)

A general calculation formula for water pressure on the lining of high-pressure, water-rich railway tunnels is provided, serving as a reference for tunnel lining design.

(2)

Calculations were performed to determine the safety water head heights for standard tunnel lining under various working conditions, which were then summarized in a table. This table enables the rapid querying of critical water head values for safety loading in tunnels under similar conditions.

(3)

A smaller permeability coefficient of the grouting ring results in a greater safety water head height and more secure lining load. Similarly, a smaller permeability coefficient of the surrounding rock results in greater water head pressure that the lining can withstand, thereby enhancing the safety of the lining.

(4)

This manuscript method can be used for railway tunnel design, taking into account the surrounding groundwater content, groundwater recharge, and adverse weather conditions to determine the type of tunnel lining.

(5)

The method in this manuscript only considers the influence of the permeability coefficient of the grouting reinforcement ring (kg) on the water pressure of the lining, without considering the influence of the thickness of the grouting ring. In numerical calculations, the thickness of the grouting ring is taken as 5 m.

(6)

The method used in this manuscript is based on numerical calculations. Next, the tunnel lining water pressure formula can be improved by comprehensively considering indoor experiments, on-site testing, and other data.