Numerical Evaluation of Transverse Steel Connector Strengthening Effect on the Behavior of Rubble Stone Masonry Walls under Compression Using a Particle Model
Abstract
1. Introduction
2. Modeling of the Masonry by a Particle Model
2.1. Particle Model Formulation
2.2. Contact Stiffness and Contact Strength
2.3. Particle Model Generation
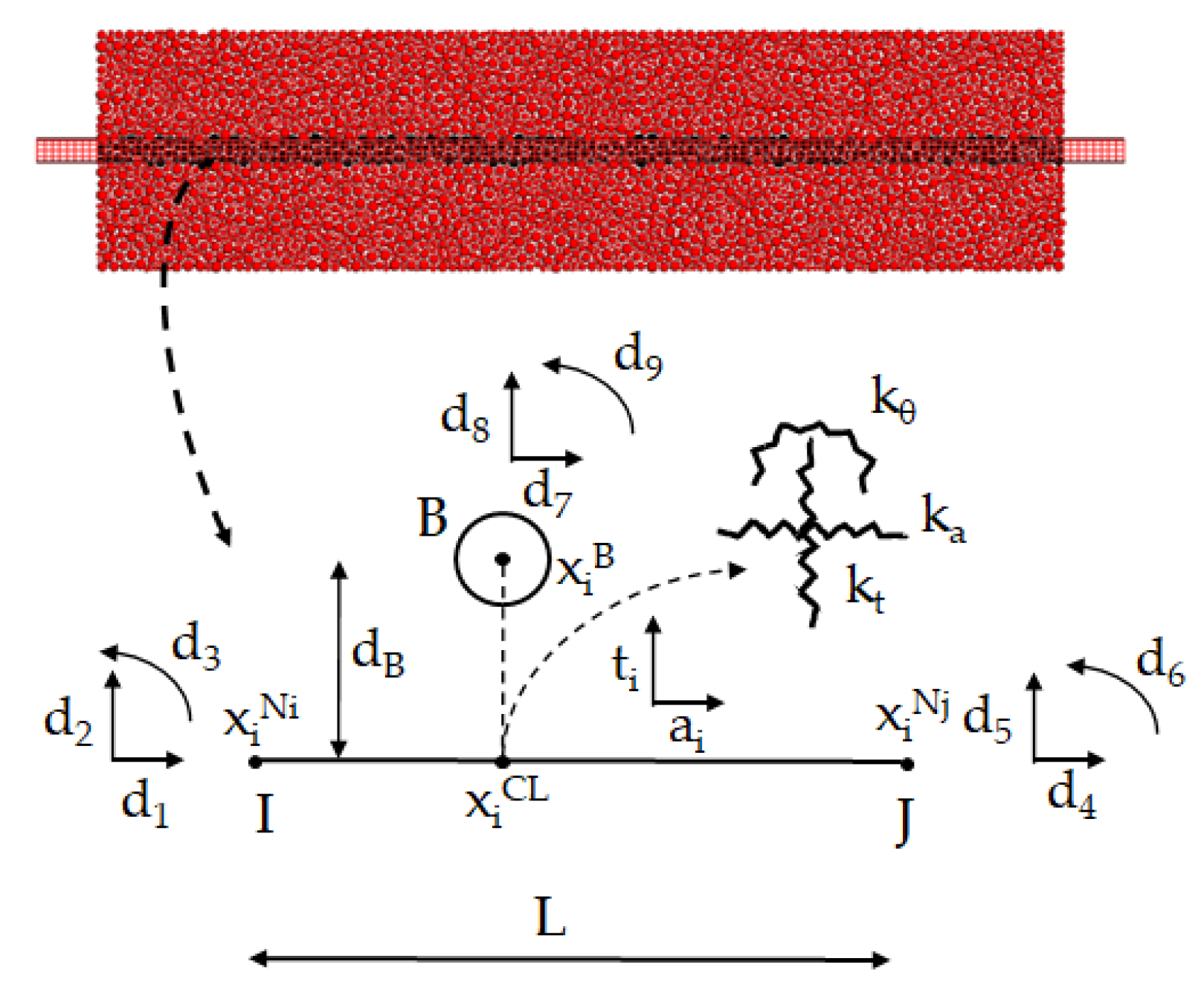
2.4. Steel Connectors and Steel Bar-Particle Interaction Model
2.5. PM Contact Model Parameters
3. Experimental Campaign
4. Numerical Modeling
4.1. 2D-PM Numerical Model Generation
4.2. Contact Parameter Calibration
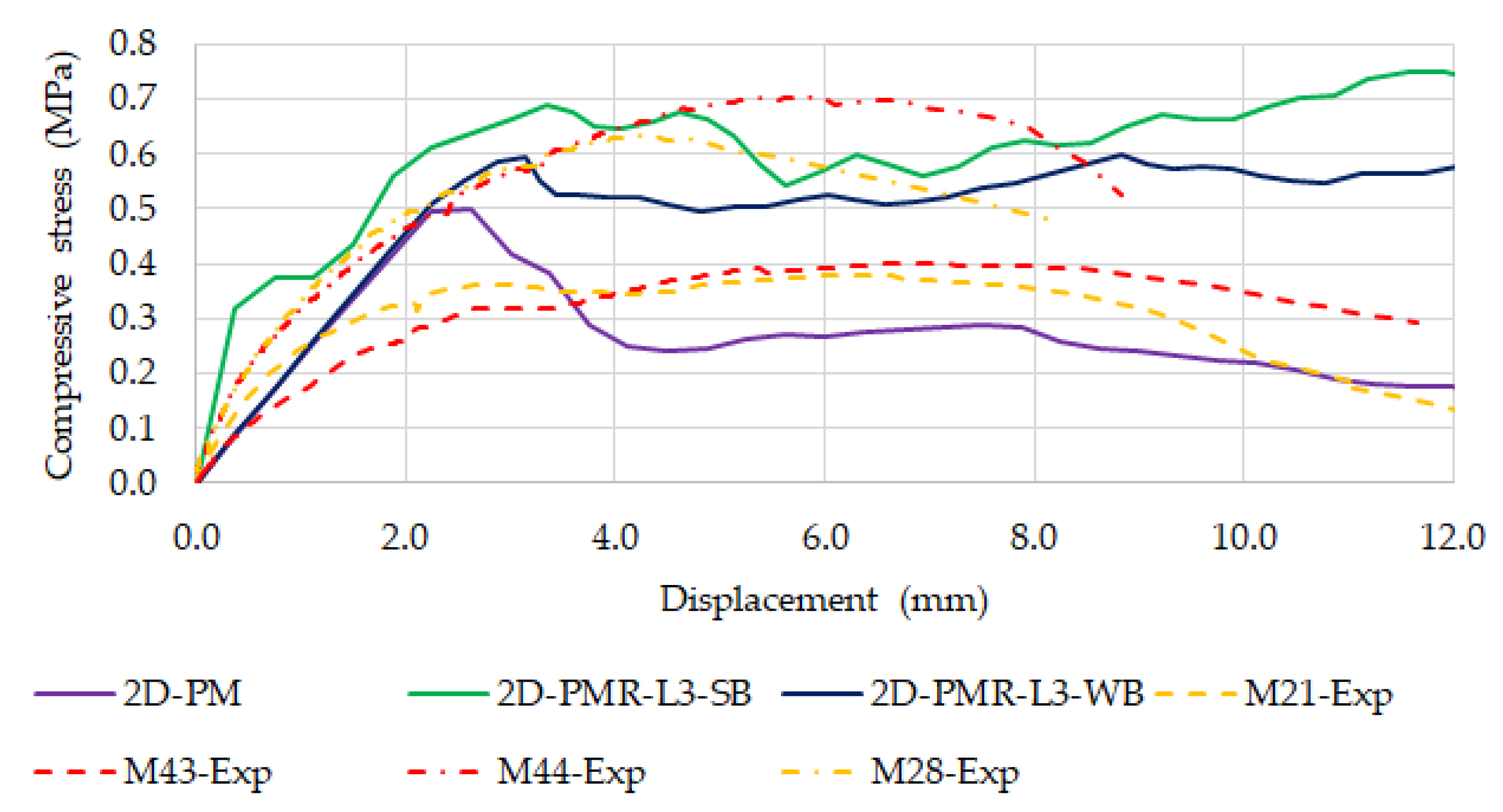
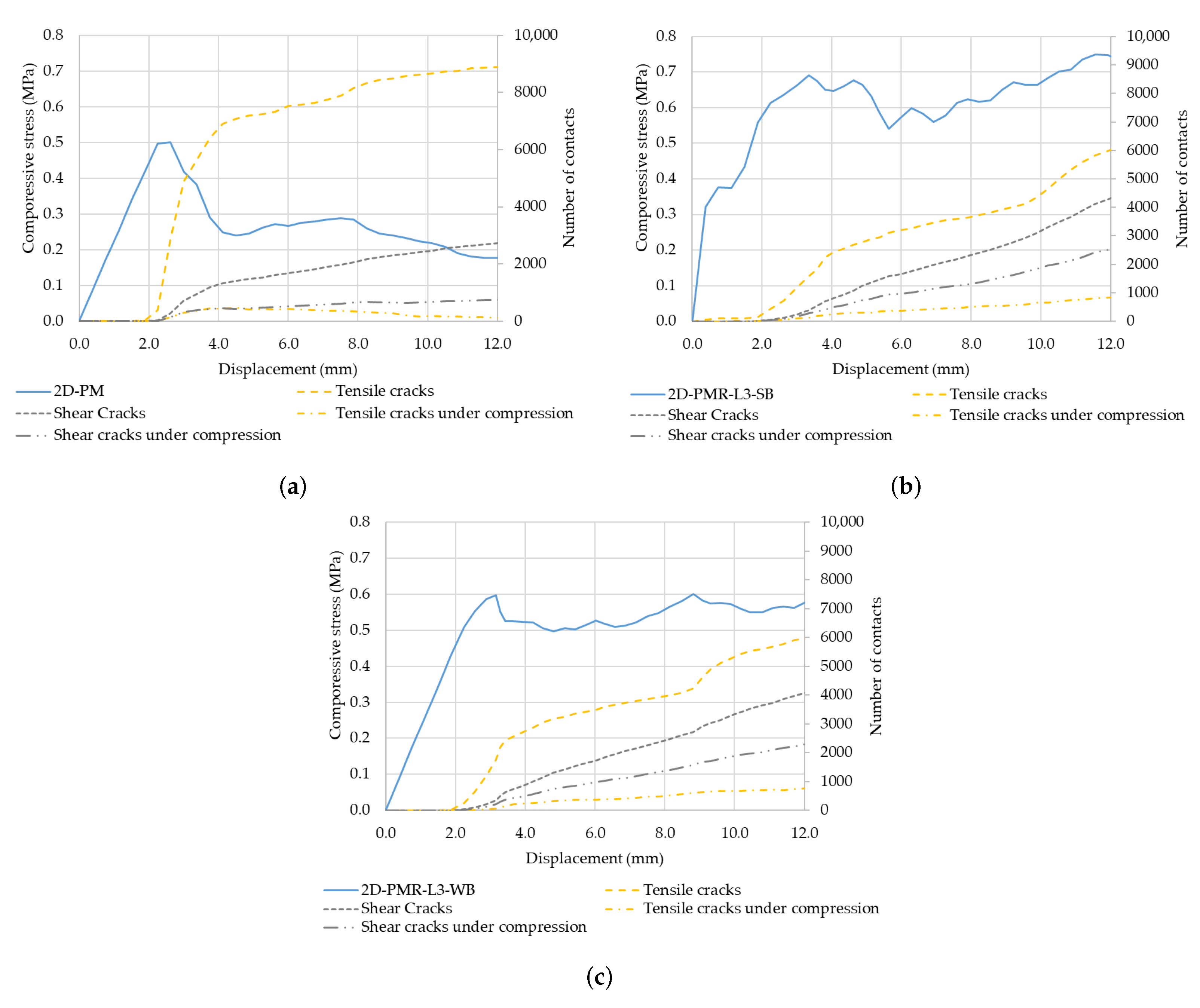
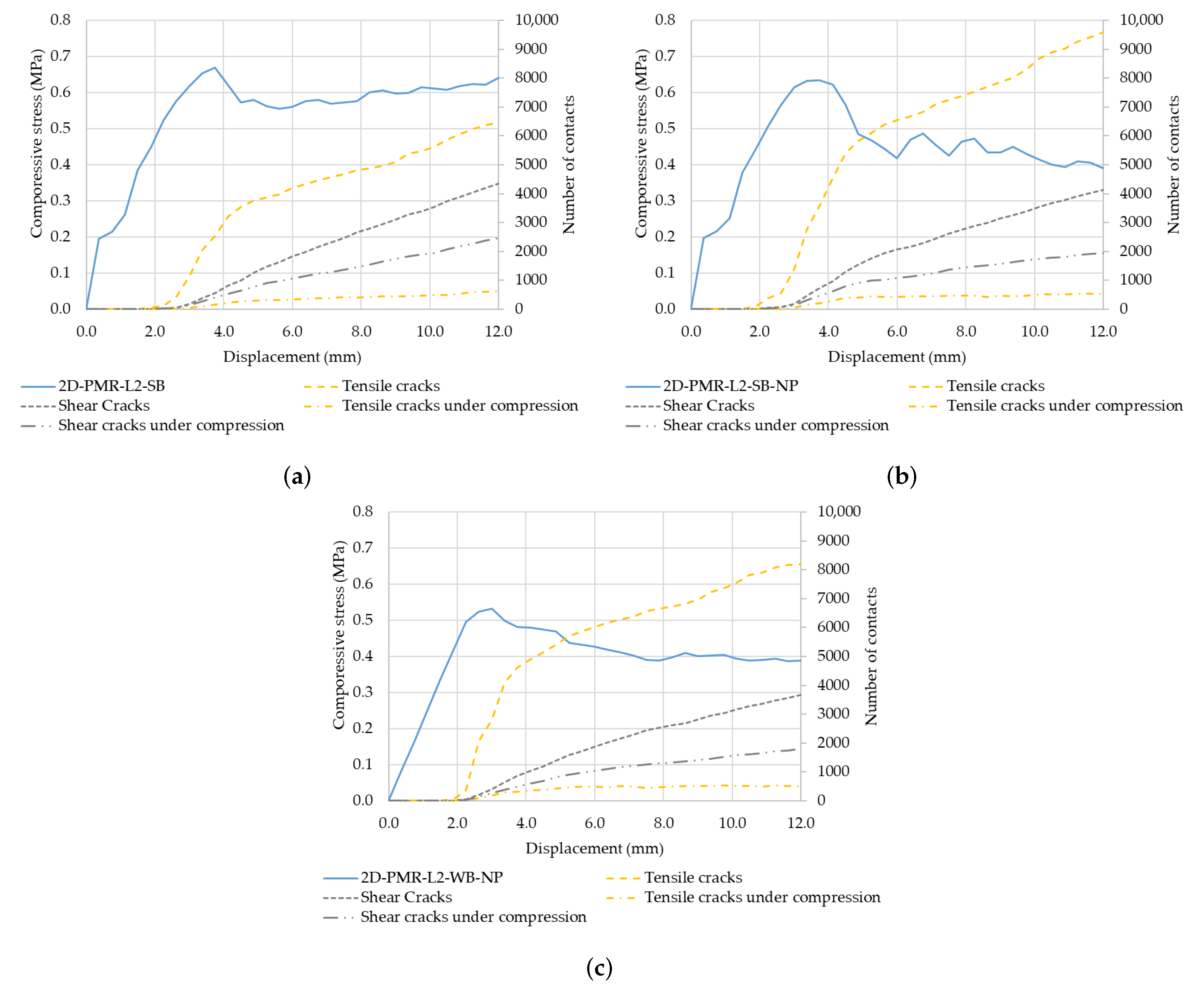
5. 2D-PM Reinforced Model Prediction
6. Parametric Studies
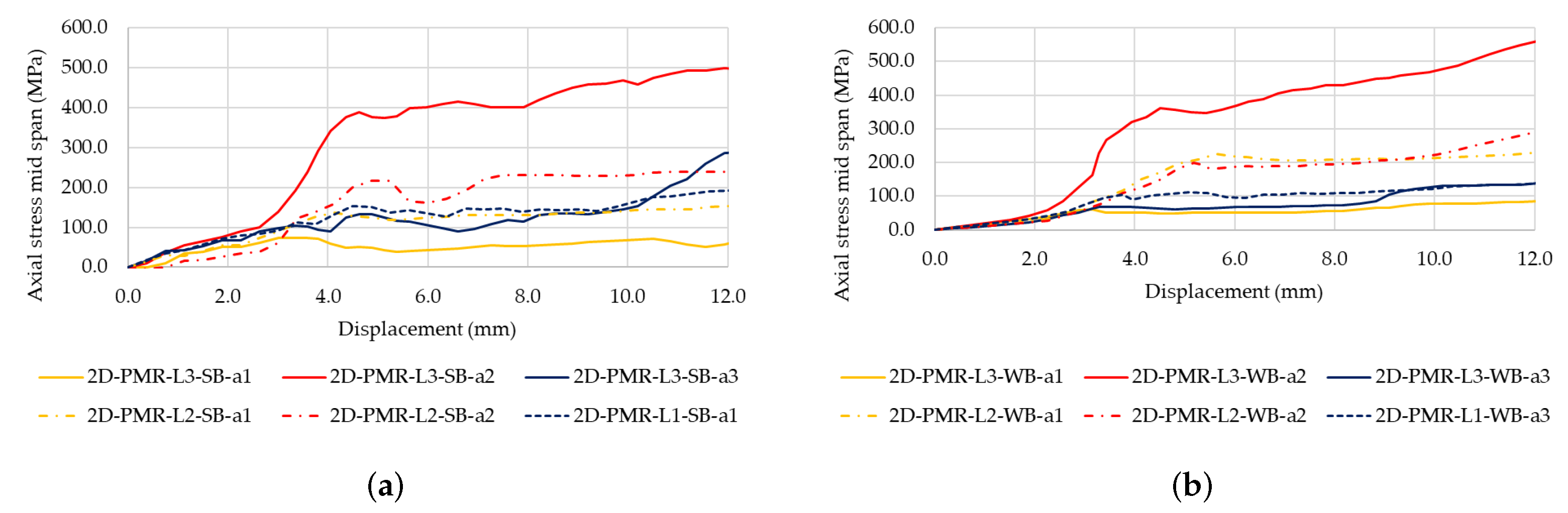
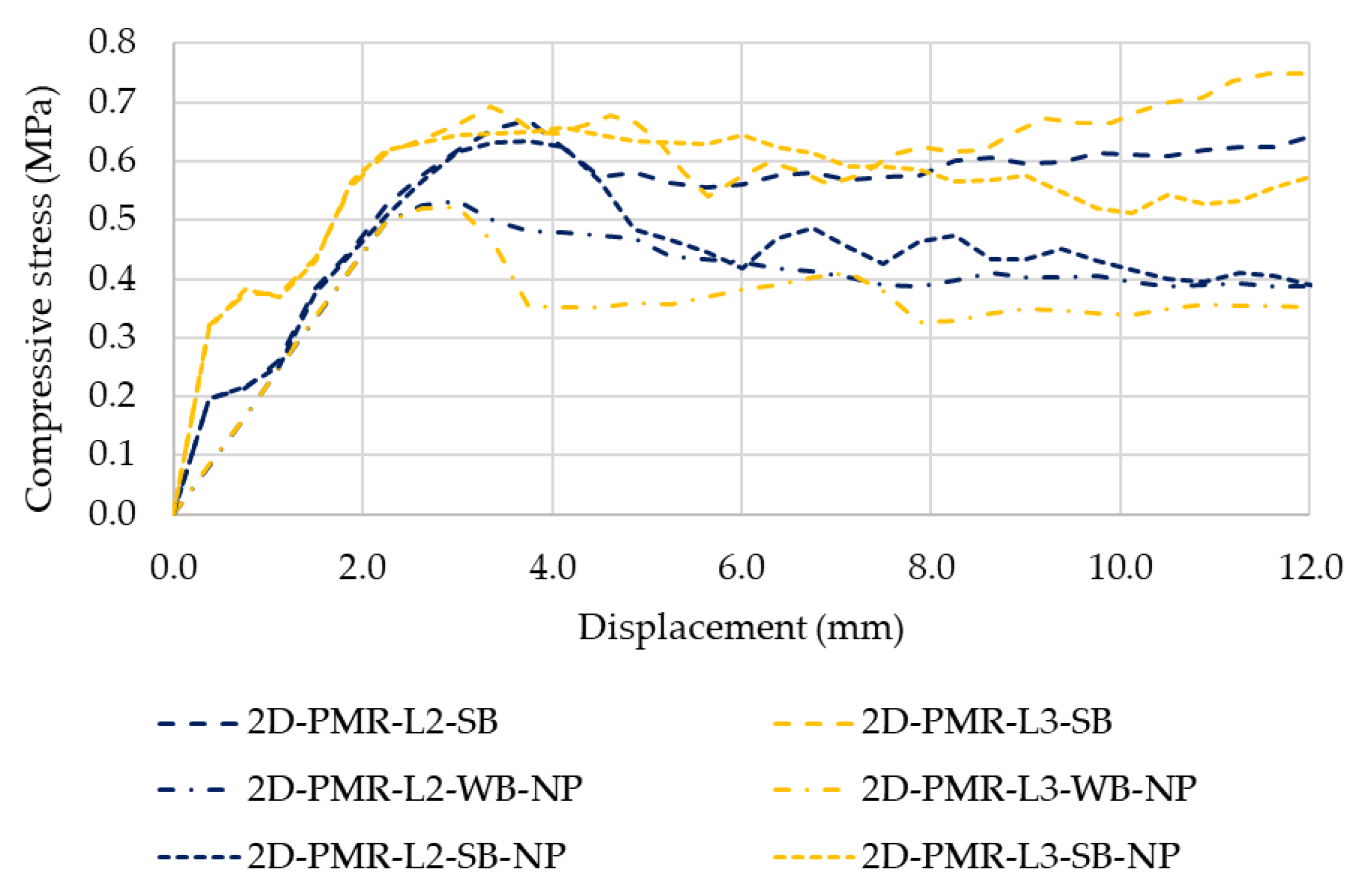
6.1. Reinforcement Scheme
6.2. Connector–Particle Bond
6.3. Lateral Plate Influence
6.4. Steel Bar Diameter
7. Conclusions
- The proposed 2D reinforced particle model formulation allows the 2D-PMR model to replicate the transverse confinement effect of steel-based reinforcement on rubble stone masonry walls. The formulation is straightforward and can be easily incorporated into similar models that use other commercial or open-source implementations.
- The 2D-PMR model can predict the improved strength and ductility, the crack growth process, and the reduction in horizontal detachments of the masonry observed in the experimental tests of strengthened rubble stone masonry walls. Numerical results indicate that a strong particle/bar bond approach (50%) predicts a higher peak strength increase than the average increase in strength (47%) observed experimentally for the reference specimen.
- The presented discussion, from a numerical modeling perspective, regarding the relevance of the bond between the steel bar connectors, the presence and importance of the end plates, and the connectors’ diameters, provides useful information for the consolidation and understanding of this reinforcing technique.
- The results and discussions presented underline the complexity of capturing the accurate behavior of the existing/real rubble stone masonry walls and the difficulty in numerically estimating the effect of this intervention technique.
- Overall, the proposed 2D-PMR model can be adopted in the design phase of reinforcement solutions involving simple transverse confinement, particularly in the definition of bar characteristics, positioning, quantification, and in the assessment of the relevance of the grout injection in the application process of the steel connectors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| URM | unreinforced masonry |
| RM | reinforced masonry |
| FEM | finite element method |
| DEM | discrete element method |
| DDA | discontinuous deformation analysis |
| 2D-PM | 2D particle model |
| 2D-PMR | 2D particle reinforced model |
| SB | strong bond approach |
| WB | weak bond approach |
References
- National Institute of Statistic. Census 2011. Definitive Results; INE: Lisbon, Portugal, 2012; ISBN 978-989-25-0181-9. (In Portuguese) [Google Scholar]
- Pinho, F.F.S. Ordinary Masonry Walls—Experimental Study with Unstrengthened and Strengthened Specimens. Ph.D. Thesis, Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa, Lisbon, Portugal, 2007. (In Portuguese). [Google Scholar]
- Pinho, F.F.S.; Lúcio, V.J.G.; Baião, M.F.C. Rubble stone masonry walls in Portugal strengthened with reinforced micro-concrete layers. Bull. Earthq. Eng. 2012, 10, 161–180. [Google Scholar] [CrossRef]
- Pinho, F.F.S.; Lúcio, V.J.G.; Baião, M.F.C. Rubble Stone Masonry Walls Strengthened by Three-Dimensional Steel Ties and Textile Reinforced Mortar Render, Under Compression. Int. J. Archit. Herit. 2014, 8, 670–689. [Google Scholar] [CrossRef]
- Pinho, F.F.S.; Lúcio, V.J.G.; Baião, M.F.C. Rubble Stone Masonry Walls Strengthened by Three-Dimensional Steel Ties and Textile-Reinforced Mortar Render, Under Compression and Shear Loads. Int. J. Archit. Herit. 2015, 9, 844–858. [Google Scholar] [CrossRef]
- Pinho, F.F.S.; Lúcio, V.J.G.; Baião, M.F.C. Experimental analysis of rubble stone masonry walls strengthened by transverse confinement under compression and compression-shear loadings. Int. J. Archit. Herit. 2018, 12, 91–113. [Google Scholar] [CrossRef]
- Gkournelos, P.; Triantafillou, T.; Bournas, D. Seismic upgrading of existing masonry structures: A state-of-the-art review. Soil Dyn. Earthq. Eng. 2022, 161, 107428. [Google Scholar] [CrossRef]
- Valluzzi, M.; Da Porto, F.; Modena, C. Behaviour of multi-leaf stone masonry walls strengthened by different intervention techniques. In Historical Constructions 2001; Universidade do Minho: Braga, Portugal, 2001; pp. 1023–1032. ISBN 972-8692-01-3. [Google Scholar]
- Pinho, F.F.S. Structural Rehabilitation of Traditional Stone Masonry Walls; Science, Engineering and Technology Collection, Nova.FCT Editorial: Lisbon, Portugal, 2021; ISBN 978-989-54493-5-4. (In Portuguese) [Google Scholar]
- Pinho, F.F.S.; Lúcio, V.J.G. Rubble Stone Masonry Walls in Portugal: Material Properties, Carbonation Depth and Mechanical Characterization. Int. J. Archit. Herit. 2017, 11, 685–702. [Google Scholar]
- Corradi, M.; Borri, A.; Poverello, E.; Castori, G. The use of transverse connectors as reinforcement of multi-leaf walls. Mater. Struct. 2016, 50, 114. [Google Scholar] [CrossRef]
- Rots, J.G. Numerical simulation of cracking in structural masonry. Heron 1991, 36, 49–63. [Google Scholar]
- Lourenço, P.B. Computations on historic masonry structures. Prog. Struct. Eng. Mater. 2002, 4, 301–319. [Google Scholar] [CrossRef]
- Lourenço, P.B.; Rots, J.G. Multisurface Interface Model for Analysis of Masonry Structures. J. Eng. Mech. 1997, 123, 660–668. [Google Scholar] [CrossRef]
- Lemos, J. Discrete element modelling of the seismic behaviour of stone masonry arches. In Computer Methods in Structural Masonry—4 Fourth International Symposium, 1st ed.; Pande, G., Middleton, J., Kralj, B., Eds.; CRC Press: London, UK, 1998; pp. 220–227. ISBN 9780419235408. [Google Scholar]
- Sarhosis, V.; Lemos, J. A detailed micro-modelling approach for the structural analysis of masonry assemblages. Comput. Struct. 2018, 206, 66–81. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J.V.; Rocha, J.d.A. Discrete Element Particle Modelling of Stone Masonry. In Computational Modeling of Masonry Structures Using the Discrete Element Method; IGI Global: Hershey, PA, USA, 2016; pp. 146–170. [Google Scholar] [CrossRef]
- Smoljanović, H.; Živaljić, N.; Željana, N. A combined finite-discrete element analysis of dry stone masonry structures. Eng. Struct. 2013, 52, 89–100. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J.V. A Hybrid Particle/Finite Element Model with Surface Roughness for Stone Masonry Analysis. Appl. Mech. 2022, 3, 608–627. [Google Scholar] [CrossRef]
- Thavalingam, A.; Bicanic, N.; Robinson, J.I.; Ponniah, D.A. Computational framework for discontinuous modelling of masonry arch bridges. Comput. Struct. 2001, 79, 1821–1830. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J.; Rocha, J.d. Influence of aggregate deformation and contact behaviour on discrete particle modelling of fracture of concrete. Eng. Fract. Mech. 2008, 75, 1569–1586. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Candeias, M.; Gouveia, F. A Rigid Particle Model for Rock Fracture Following the Voronoi Tessellation of the Grain Structure: Formulation and Validation. Rock Mech. Rock Eng. 2014, 48, 535–557. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Wang, H.; Agrawal, A.K.; Chan, A.H.; Cheng, Y. Simulating the failure of masonry walls subjected to support settlement with the combined finite-discrete element method. J. Build. Eng. 2021, 43, 102558. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Pinho, F.F.S.; Cismaşiu, I.; Souza, M. Prediction of Rubble-Stone Masonry Walls Response under Axial Compression Using 2D Particle Modelling. Buildings 2022, 12, 1283. [Google Scholar] [CrossRef]
- Azevedo, N.M. A Rigid Particle Discrete Element Model for the Fracture Analysis of Plain and Reinforced Concrete. Ph.D. Thesis, Herito-Watt University, Edinburgh, UK, 2003. [Google Scholar]
- Senthivel, R.; Lourenço, P.B. Finite element modelling of deformation characteristics of historical stone masonry shear walls. Eng. Struct. 2009, 31, 1930–1943. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Pinho, F.F.S.; Cismasiu, I.; Souza, M.B.d. Modeling traditional stone masonry walls with a particle model. In Proceedings of the Congresso Nacional Reabilitar & Betão Estrutural 2020, LNEC, Lisbon, Portugal, 3–5 November 2021; p. 10. (In Portuguese). [Google Scholar]
- CEB-FIP MODEL CODE 1990; Thomas Telford Publishing: London, UK, 1993. [CrossRef]
















| Strengthening Solution | Specimens | Age(★) [Days] |
[kN] |
[MPa] |
[mm] |
[] | E [GPa] |
|---|---|---|---|---|---|---|---|
| Transverse steel connectors | M41 | 925 | 168.5 | 0.53 | 4.0 | 3.3 | 0.477 |
| M44 | 927 | 226.0 | 0.71 | 5.8 | 4.8 | 0.485 | |
| M28 | 931 | 203.3 | 0.64 | 4.3 | 3.6 | 0.505 | |
| RM Average | – | 199.3 | 0.63 | 4.7 | 3.9 | 0.489 | |
| URM specimens | M43 | 618 | 134.2 | 0.42 | 6.8 | 5.7 | 0.239 |
| M21 | 626 | 127.7 | 0.40 | 6.4 | 5.3 | 0.409 | |
| M32 | 638 | 148.5 | 0.46 | 4.3 | 3.6 | 0.267 | |
| URM Average | – | 136.8 | 0.43 | 5.8 | 4.9 | 0.305 |
| Model | Particles | Contacts | |||
|---|---|---|---|---|---|
| Stone(s) | Mortar(m) | m–m | m–s | s–s | |
| Lateral | 7501 | 45,381 | 20,034 | 127,176 | 10,154 |
| Contacts |
[GPa] |
[–] |
[MPa] |
[MPa] |
[–] |
[N/m] |
[N/m] |
|---|---|---|---|---|---|---|---|
| s–s | 8.60 | 0.11 | 8.90 | 35.7 | 1.0 | 0.3838 | 56.1403 |
| m–m & m–s | 0.09 | 0.43 | 0.16 | 0.16 | 1.0 | 0.0013 | 0.0030 |
| (a) Experimental values [2] | ||||
| Material | [GPa] | [MPa] | [MPa] | |
| mortar | 0.075 | 0.16 | 0.65 | 0.3 |
| stone | 6.0 | 0.3 | 47.8 | – |
| (b) Numerical predictions after calibration [24] | ||||
| Material | [GPa] | [MPa] | [MPa] | |
| mortar | 0.075 | 0.16 | 0.66 | 0.16 |
| stone | 6.0 | 0.3 | 47.8 | – |
| Model | [MPa] | |
|---|---|---|
| Numerical | MP-2D | 0.50 |
| 2D-PM-L3-SB | 0.75 | |
| 2D-PM-L3-WB | 0.60 | |
| Experimental | Average URM [2] | 0.43 |
| Average RM [2] | 0.63 | |
| Bond Type | Model | |
|---|---|---|
| Strong Bond | 2D-PM-L1-SB | 23 |
| 2D-PM-L2-SB | 38 | |
| 2D-PM-L3-SB | 50 | |
| Weak Bond | 2D-PM-L1-WB | 21 |
| 2D-PM-L2-WB | 33 | |
| 2D-PM-L3-WB | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cismaşiu, I.; Azevedo, N.M.; Pinho, F.F.S. Numerical Evaluation of Transverse Steel Connector Strengthening Effect on the Behavior of Rubble Stone Masonry Walls under Compression Using a Particle Model. Buildings 2023, 13, 987. https://doi.org/10.3390/buildings13040987
Cismaşiu I, Azevedo NM, Pinho FFS. Numerical Evaluation of Transverse Steel Connector Strengthening Effect on the Behavior of Rubble Stone Masonry Walls under Compression Using a Particle Model. Buildings. 2023; 13(4):987. https://doi.org/10.3390/buildings13040987
Chicago/Turabian StyleCismaşiu, Ildi, Nuno Monteiro Azevedo, and Fernando F. S. Pinho. 2023. "Numerical Evaluation of Transverse Steel Connector Strengthening Effect on the Behavior of Rubble Stone Masonry Walls under Compression Using a Particle Model" Buildings 13, no. 4: 987. https://doi.org/10.3390/buildings13040987
APA StyleCismaşiu, I., Azevedo, N. M., & Pinho, F. F. S. (2023). Numerical Evaluation of Transverse Steel Connector Strengthening Effect on the Behavior of Rubble Stone Masonry Walls under Compression Using a Particle Model. Buildings, 13(4), 987. https://doi.org/10.3390/buildings13040987








