Experimental and Theoretical Investigation of Viscoelastic Damper by Applying Fractional Derivative Method and Internal Variable Theory

Abstract

Viscoelastic dampers are conventional passive vibration control devices with excellent energy dissipation performance. The fractional derivative has a simple form and high accuracy in the modelling of viscoelastic materials/dampers. The internal variables reflect the internal state evolution of materials, and are often used to analyze the deformation and thermal process of materials. In the present work, the mechanical properties of a plate-shear-type viscoelastic damper at room temperature are tested under sinusoidal displacement excitations. The impacts of frequency and displacement amplitude on the dynamic properties of the viscoelastic damper in a wide frequency domain (0.1–25 Hz) are investigated. The higher-order fractional derivative model and the temperature–frequency equivalent principle are employed to characterize the frequency and temperature influence, and the internal variable theory considering the internal/microscale structure evolutions is introduced to capture the displacement affection. The higher-order fractional derivative model modified with the internal variable theory and temperature–frequency equivalent principle (ITHF) is accurate enough in describing the dynamic behaviors of viscoelastic dampers with varying frequencies and displacement amplitudes.

1. Introduction

Viscoelastic dampers are perfect energy dissipation devices and have been widely used in seismic/wind vibration control, micro vibration suppression, and platform vibration isolation, etc. [1,2,3,4]. The damping performance and energy dissipation capacity of viscoelastic dampers mainly depend on the mechanical properties of viscoelastic materials [5]. Scholars have accomplished a lot of achievements in the research of viscoelastic materials and dampers [6,7,8,9].

In 1992, Zhang et al. [10] proposed a sequential design procedure for optimal placement of viscoelastic dampers in structures, and experimentally verified it with a five-story steel model structure. Aprile et al. [11] studied the influence of loading frequency and displacement amplitude on the dynamic modulus of viscoelastic dampers. Tsai et al. [12] investigated the temperature impacts on the seismic control effect of viscoelastically dampered building structures. Viscoelastic dampers can effectively reduce seismic responses of structures, and the damping effect decreases with the increment in temperature. Cazenove et al. [13] conducted numerical and theoretical observations on the self-heating effect of viscoelastic dampers. The results show that the self-heating phenomenon of viscoelastic dampers is very important and should not be neglected in vibration control analysis and structural design. Xu et al. studied the damping properties of viscoelastic dampers with different viscoelastic materials [5,14], and utilized the shaking table test to study the seismic response of structure models retrofitted with viscoelastic dampers [15,16,17,18]. Sato et al. [19] proposed an evaluation method for the practical application of viscoelastic dampers in wind vibration control by using equivalent sinusoidal waveforms of long-duration random excitations in along- and across-wind directions. Xu et al. [20] proposed a micro-vibration isolation and mitigation platform with four viscoelastic damper components to reduce disturbance generated by flywheels onboard spacecraft. He et al. [21] designed a new type of viscoelastic damper to control the translational vibration and the rotational vibration of offshore platforms simultaneously, and shaking table tests were conducted to verify the capability of dampers in mitigating the multi-dimensional seismic responses of platforms.

The dynamic characteristics and energy dissipation performance of viscoelastic dampers show a significantly nonlinear variation trend with varying temperatures, frequencies, and loading displacement amplitudes. The appropriate mathematical model is conducive to more efficient characterization of mechanical properties of dampers and response analysis of viscoelastic damper-retrofitted structures. Traditional constitutive models, the Kelvin model, Maxwell model, Zerner model, and fractional derivative models, etc. [22], of viscoelastic materials are mature in characterizing frequency dependence and rheological properties, but the temperature and frequency reliance of materials cannot be reflected well. Tsai [23] established a finite element model for viscoelastic dampers by using a fractional derivative operator and empirical formula to consider the dependence of temperature, frequency, and displacement amplitude at the same time. However, it is rarely utilized by researchers due to its complex form. Payne et al. [24] assumed that the displacement dependence of the material was mainly due to the influence of the micro filler network system, and used the Kraus model to explain the correlation characteristics between dynamic properties of the damper and displacement amplitudes. Liang et al. [25] built a constitutive model of viscoelastic materials based on a complex combination of multiple relaxation viscoelastic and viscoplastic models, which can predict the remarkable temperature- and rate-dependent deformation behaviors of materials well. Bagley et al. [26] and Lewandowski [27] investigated the mechanical behavior of viscoelastic materials and conducted a structural seismic analysis of damping structures based on fractional derivative theory, which has a more concise form and higher accuracy than integral derivative models. Xu et al. [28,29] formulated the temperature–frequency equivalent principle based on the W-L-F equation, and theoretically translated the effects of temperature into frequency impacts. Conti et al. [30] proposed a new mathematical model to describe the aging effects of viscoelastic materials. The convolution kernel of the integro-differential equation for describing the viscoelasticity was redefined as a function of time. Wang et al. [31] theoretically studied the macro properties of viscoelastic materials with the assumption that the multi-layer molecular networks interpenetrated together with different chain lengths. Lu et al. [32] investigated the constitutive relation of viscoelastic materials considering the friction effect of single molecular chains from surrounding environments at the microscale.

Most of the aforementioned research considers the constitutive relationship and mechanical properties of viscoelastic materials from the macroperspective, and there are few examples of literature from the microperspective. In traditional thermodynamic theories, the state of materials at an arbitrary moment determined by the macro variables, deformation, temperature, etc., and the internal variables, which could be one or a set of state variables, such as the damage accumulation, nonelastic deformation, phase transformation, free volume variation, and changes in material particle size, etc. [33,34]. The internal variables reflect the evolution process of the internal structure state of materials, and affect the macro mechanical properties and damping performance of viscoelastic materials significantly. The purpose of the present research is to study the dynamic performance of viscoelastic dampers with different frequencies and displacements at room temperature, and theoretically propose new mathematical models with fractional derivative and internal variable theory. The mechanical properties of a plate-shear type-viscoelastic damper at room temperature are tested under sinusoidal displacement excitations. The impacts of frequency and displacement amplitude on the dynamic properties of a viscoelastic damper in a wide frequency domain (0.1–25 Hz) are investigated. The higher-order fractional derivative model and the temperature–frequency equivalent principle are employed to predict the dynamic property variation of the damper with frequency and temperature changes, and the internal variable theory considering the internal/microscale structure evolutions is introduced to capture the displacement affection. The higher-order fractional derivative model modified with the internal variable theory and temperature–frequency equivalent principle (ITHF) is accurate enough and more appropriate than the higher-order fractional derivate model modified with the Kraus model and temperature–frequency equivalent principle (KTHF) in describing the dynamic performance of viscoelastic dampers with varying temperatures, frequencies, and displacement amplitudes.

2. Performance Test

To study the dynamic properties and vibration reduction efficiency of the viscoelastic damper with a wide frequency range (0.1~25 Hz), the hydraulic servo fatigue tests were conducted under external exactions with different loading frequencies and displacement amplitudes. The results show that the viscoelastic damper has great efficiency in energy dissipation. The properties parameters storage modulus, loss modulus, loss factor, energy dissipation, equivalent stiffness, and equivalent damping are importantly affected by the excitation frequency, and the impact of displacement amplitude on properties parameters of the viscoelastic damper is relatively slight.

2.1. Test Situation

The viscoelastic damper is fabricated based on the nitrile rubber matrix, and composed of three steel plates and two viscoelastic layers in parallel, as shown in Figure 1b. The dimensions of the viscoelastic layers are 60 mm × 50 mm × 10 mm. During the performance tests, the viscoelastic layers undergo simple shear deformation along the length direction of the damper and the external mechanical energy can be dissipated through the shear deformation. The dynamic performance tests of the damper are conducted with a 100 kN hydraulic servo fatigue test machine manufactured by w+b Company, Switzerland, as seen in Figure 1a. The viscoelastic damper is fixed tightly on the machine by steel joints and bolts (see Figure 1b). A temperature controlling box is utilized to adjust the environmental temperature to 18 °C, and the viscoelastic damper is put inside an incubator to make the temperature stable. The external displacement excitation $u_d=u_0\sin \left(\omega t\right)$ is applied to the viscoelastic damper, where $u_d$ is the displacement of the damper and $u_0$ denotes the displacement amplitude. $\omega$ is angular frequency and $\omega =2\pi f$, where $f$ denotes the loading frequency and $t$ is time. All the test conditions of the viscoelastic damper are given in Table 1, and the force and displacement at each test condition are recorded by the data record system.

Figure 1. Dynamic properties tests of the viscoelastic damper. (a) Schematic diagram of the dynamic test. (b) Viscoelastic damper inside the incubator.

Table 1. Conditions of the dynamic performance tests.

Frequencies f (Hz)	Amplitudes d (mm)	Temperature T (°C)	Cycle Number
0.1, 0.2, 0.3, 0.5, 1.0, 1.5, 2.0, 3.0, 4.0, 5.0, 7.0, 10.0, 15.0, 20.0, 25.0	0.5, 1.0, 1.5, 2.5	18	5

2.2. Results Analysis

To better analyze the mechanical properties and dynamic damping characteristics of the viscoelastic damper, the force–displacement hysteresis curves of the damper with changing external excitation frequencies and loading displacement amplitudes are shown in Figure 2 and Figure 3, respectively.

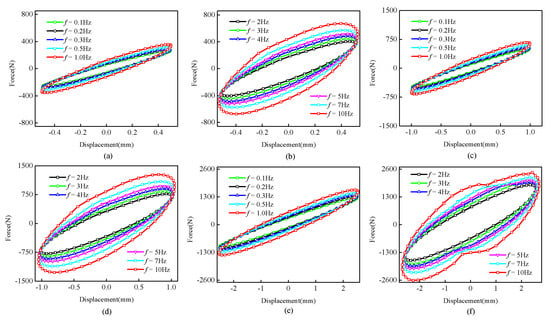
Figure 2. Hysteretic curves of the viscoelastic damper with changing frequencies. (a) d = 0.5 mm, f = 0.1~1 Hz. (b) d = 0.5 mm, f = 2~10 Hz. (c) d = 1 mm, f = 0.1~1 Hz. (d) d = 1 mm, f = 2~10 Hz. (e) d = 2.5 mm, f = 0.1~1 Hz. (f) d = 2.5 mm, f = 2~10 Hz.

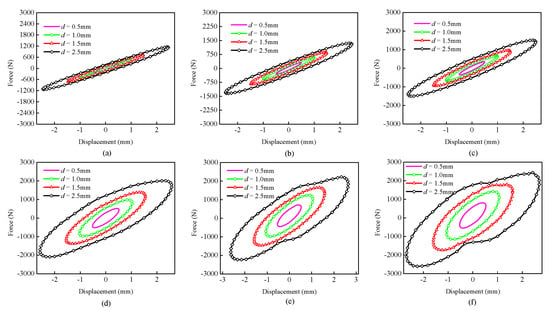
Figure 3. Hysteretic curves of the viscoelastic damper with changing displacement amplitudes. (a) f = 0.1 Hz. (b) f = 0.5 Hz. (c) f = 1 Hz. (d) f = 5 Hz. (e) f = 7 Hz. (f) f = 10 Hz.

The force–displacement curves of the viscoelastic damper with different loading frequencies are presented in Figure 2. It reveals that the viscoelastic damper has great energy dissipation properties, especially at high frequencies. The maximum damping force, major axis slope, smoothness, and plumpness of the hysteresis curve increase remarkably with increasing frequencies. Taking the maximum damping forces and areas at 0.1 Hz and 10 Hz as an example, the maximum damping forces and areas at frequency 10 Hz are almost twice of those at frequency 0.1 Hz.

The force–displacement curves of the viscoelastic damper with different displacement amplitudes are given in Figure 3. The damping performance of the viscoelastic damper are significantly influenced by the displacement amplitudes. The maximum damping force, smoothness, and plumpness of the force–displacement curves are increased rapidly with increasing displacement amplitudes. However, the impacts of the displacement amplitudes on the major axis slopes of the force–displacement curves are not obvious, as the equivalent stiffness changes slightly when the displacement amplitude varies from 0.5 mm to 2.5 mm.

To further analyze the mechanical properties and dynamic damping performance of the viscoelastic damper, the characteristic parameters of the viscoelastic damper storage modulus, loss modulus, loss factor, energy dissipation, equivalent stiffness, and equivalent damping at each test condition are calculated based on the force–displacement curves. According to the classical theories of viscoelastic dampers [35,36], the hysteresis curve of the viscoelastic damper can be considered as a standard ellipse as seen in Figure 4. The analytic equation of the ellipse has the form

$${\left(\frac{F_d-K_{\mathrm{e}}{u}_d}{\eta K_e{u}_0}\right)}^2+{\left(\frac{u_d}{u_0}\right)}^2=1$$

(1)

where $u_d$ is the displacement and has been given as $u_d=u_0\sin \left(\omega t\right)$ in the dynamic fatigue tests. $F_d$ is the corresponding damping force of the viscoelastic damper at $u_d$. $u_0$ represents the displacement amplitude of the damper, and $F_1$ is the corresponding damping force at $u_0$. $K_e$ means the equivalent stiffness, and $K_e=F_1/u_0$. $F_2$ denotes the damping force when $u_d=0$ and $\eta =F_2/F_1$. $F$ means the biggest damping force at each hysteresis curve.

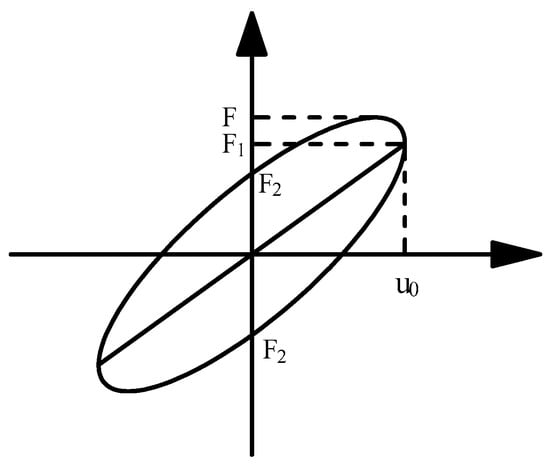
Figure 4. Force–displacement hysteresis curve.

The experimental results of the storage modulus, loss modulus, loss factor, energy dissipation, equivalent stiffness, and equivalent damping can be obtained with following equations:

$$G_1=\frac{F_1{h}_v}{n_v{A}_v{u}_0}$$

(2)

$$G_2=\frac{F_2{h}_v}{n_v{A}_v{u}_0}$$

(3)

$$\eta =\frac{F_2}{F_1}$$

(4)

$$E_d=\pi F_2{u}_0$$

(5)

$$K_e=\frac{F_1}{u_0}$$

(6)

$$C_e=\frac{F_2}{\omega u_0}$$

(7)

where $G_1$ denotes the storage modulus, $h_v$ denotes the thickness of the viscoelastic layers, $n_v$ represents the number of viscoelastic layers, and $A_v$ means the shear area of the viscoelastic layers. For the viscoelastic damper utilized in present work, $h_v$ = 10 mm, $n_v$ = 2, and $A_v$ = 60 mm × 50 mm = 3000 mm². $G_2$ means the loss modulus and $\eta$ is the loss factor. $E_d$ is the energy dissipation at each hysteresis curve, which is calculated as the area of the ellipse. $K_e$ is the equivalent stiffness and $C_e$ is the equivalent damping.

The characteristic parameters of the viscoelastic damper $G_1$, $G_2$, $\eta$, $E_d$, $K_e$, and $C_e$ with changing frequencies and different amplitudes have been obtained in Table 2 and Table 3, and vividly pictured in Figure 5 and Figure 6.

Table 2. Properties parameters G₁, G₂, and η of the viscoelastic damper under different conditions.

Frequency f (Hz)	Displacement Amplitude d (mm)	Storage Modulus G1 (MPa)	Loss Modulus G2 (MPa)	Loss Factor η
0.1	0.5	0.8774	0.1891	0.2155
	1.0	0.8309	0.168	0.2022
	1.5	0.8123	0.1627	0.2002
	2.5	0.758	0.1472	0.1941
0.5	0.5	1.0082	0.3025	0.3
	1.0	0.9582	0.2836	0.296
	1.5	0.936	0.2711	0.2896
	2.5	0.8934	0.2501	0.28
1.0	0.5	1.1385	0.4071	0.3576
	1.0	1.1018	0.4627	0.42
	1.5	0.9952	0.3648	0.3666
	2.5	0.9638	0.3379	0.3506
5.0	0.5	1.4372	0.9166	0.6378
	1.0	1.3529	0.8668	0.6407
	1.5	1.2226	0.8076	0.6605
	2.5	1.0845	0.741	0.6833
10.0	0.5	1.6264	1.4151	0.8701
	1.0	1.4936	1.328	0.8891
	1.5	1.3255	1.2319	0.9294
	2.5	1.1564	0.9978	0.8628
20.0	0.5	1.7128	2.1143	1.2344
	1.0	1.4687	1.8828	1.2819
	1.5	1.2394	1.5164	1.2235
	2.5	1.1948	1.0873	0.91

Table 3. Properties parameters E_d, K_e, and C_e of the viscoelastic damper under different conditions.

Frequency f (Hz)	Displacement Amplitude d (mm)	Energy Dissipation Ed (N·m)	Equivalent Stiffness Ke (KN/m)	Equivalent Damping Ce (KN·s/m)
0.1	0.5	0.0859	526.4681	180.5752
	1.0	0.3053	498.5189	160.4234
	1.5	0.664	487.4013	155.3158
	2.5	1.6705	454.776	140.5169
0.5	0.5	0.1385	604.9157	57.7726
	1.0	0.5195	574.9053	54.1656
	1.5	1.1186	561.5877	51.7731
	2.5	2.861	536.03	47.7705
1.0	0.5	0.1906	683.0747	38.8732
	1.0	0.8881	661.0809	44.1857
	1.5	1.5401	597.1266	34.8371
	2.5	3.9516	578.3022	32.2703
5.0	0.5	0.4665	862.3496	17.5064
	1.0	1.7457	811.7594	16.5545
	1.5	3.6414	733.5588	15.4236
	2.5	9.2452	650.7179	14.1523
10.0	0.5	0.7364	975.8111	13.5127
	1.0	2.7693	896.144	12.681
	1.5	5.7994	795.3137	11.7641
	2.5	13.1152	693.8486	9.5278
20.0	0.5	1.3034	1027.6901	10.0951
	1.0	4.7438	881.2364	8.9897
	1.5	8.7057	743.6433	7.2403
	2.5	18.4049	716.8831	5.1913

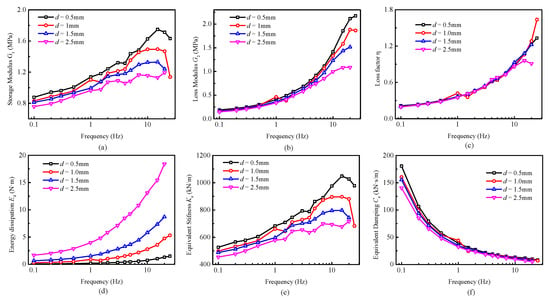
Figure 5. Dynamic properties parameters with varying frequencies. (a) Storage modulus. (b) Loss modulus. (c) Loss factor. (d) Energy dissipation. (e) Equivalent stiffness. (f) Equivalent damping.

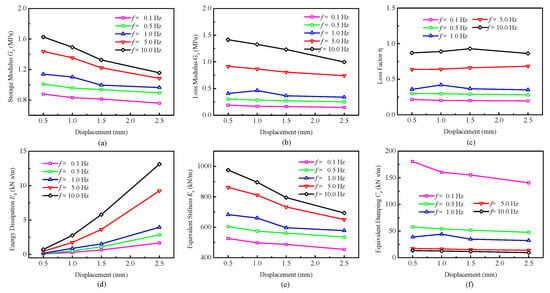
Figure 6. Dynamic properties parameters with varying displacement amplitudes. (a) Storage modulus. (b) Loss modulus. (c) Loss factor. (d) Energy dissipation. (e) Equivalent stiffness. (f) Equivalent damping.

The variations of the characteristic parameters $G_1$, $G_2$, $\eta$, $E_d$, $K_e$, and $C_e$ with increasing frequencies are shown in Figure 5. It is shown that all the dynamic parameters increase rapidly when the loading frequency increases except the equivalent damping $C_e$, which is reduced rapidly with frequency increment. The changing rates of the properties parameters at low frequencies (0.1~1 Hz) are much larger than those at high frequencies (1~25 Hz). Taking the test conditions with $d$ = 0.5 mm as an example, the characteristic parameters’ changing rates with increasing frequencies are given in Table 4. These phenomena can be explained together with the micro structures of viscoelastic materials. The macro mechanical properties and energy dissipation performance are closely related to the micro molecular chain structures. When the frequency initially increases, the excitation time of external loading is gradually shortened, becoming closer to the molecular chain relaxation time. Therefore, the dynamic modulus and stiffness increase with increasing frequencies in 0.1~1 Hz. The excitation time of external loading is further shortened, becoming far less than the relaxation time of the molecular chains when the frequency further increases in the range of 1~25 Hz. The molecular chains cannot keep up with the movement of external excitations, and the increasing rates of dynamic modulus and stiffness are gradually decreased.

Table 4. Parameters’ changing rate with different frequencies when d = 0.5 mm.

Frequency f (Hz)	0.1~0.5	0.5~1	1~5	5~10	10~20
Storage modulus $G_1$	+14.91%	+12.92%	+26.24%	+13.16%	+5.31%
Loss modulus $G_2$	+59.97%	+34.58%	+125.15%	+54.39%	+49.41%
Loss factor $\eta$	+39.21%	+19.2%	+78.36%	+36.42%	+41.87%
Energy dissipation $E_d$	+61.23%	+37.62%	+144.75%	+57.86%	+77%
Equivalent stiffness $K_e$	+14.9%	+12.92%	+26.25%	+13.16%	+5.32%
Equivalent damping $C_e$	−68.01%	−32.71%	−54.97%	−22.81%	−25.29%

The equivalent damping $C_e$ decreases with the increment of frequency, which can be explained by Equation (7). Furthermore, the characteristic parameters $G_1$ and $K_e$, and $G_2$ and $E_d$ have the same change ratio with increasing frequencies, because there is a positive correlation between $G_1$ and $K_e$, and $G_2$ and $E_d$, as formulated in Equations (2)–(6). In conclusion, the dynamic performance of the viscoelastic damper is significantly affected by the excitation frequency.

Figure 6 shows the dynamic parameters’ variation when displacement amplitude changes from 0.5 mm to 2.5 mm. The dynamic properties and damping parameters decrease slightly with displacement amplitude increment. This trend is more obvious at high frequencies (5 Hz and 10 Hz). The energy dissipation increases notably with the increment of excitation amplitudes. Taking the test conditions with $f$ = 5 Hz as an example, the characteristic parameters’ changing rates with varying displacement amplitudes are shown in Table 5.

Table 5. Parameters’ changing rate with varying displacement amplitudes when f = 5.0 Hz.

Displacement d (mm)	0.5~1.0	1.0~1.5	1.5~2.5
Storage modulus $G_1$	−5.87%	−9.63%	−11.3%
Loss modulus $G_2$	−5.43%	−6.83%	−8.25%
Loss factor η	+0.45%	+3.09%	+3.45%
Energy dissipation $E_d$	+274.21%	+108.59%	+153.89%
Equivalent stiffness $K_e$	−5.87%	−9.63%	−11.29%
Equivalent damping $C_e$	−5.44%	−6.83%	−8.24%

The intermolecular force, van der Waals force, between filler particles, carbon black, silicon, etc., and the micro molecular chains adsorption on filler particle surfaces significantly enhance the modulus and strength of viscoelastic materials. With the increment of displacement amplitudes, the van der Waals force between filler particles and the molecular chain adsorption will be gradually weakened, which leads to the reduction in characteristic parameters $G_1$, $G_2$, $\eta$, $K_e$, and $C_e$. The energy dissipation $E_d$ clearly increases when the displacement amplitude increases, which can be explained with the positive proportional relationship shown in Equation (5). The displacement amplitudes possess slight influence on mechanical behaviors but have great significance for the damping properties of viscoelastic dampers.

3. Theoretical Modeling

From the abovementioned experimental results, it can be seen that the dynamic loading frequency and displacement amplitude are two factors that significantly affect the mechanical and energy dissipation performance of viscoelastic dampers. Accurate and reasonable mathematical models are essential to describe the dynamic behaviors of viscoelastic dampers. In this part, the higher-order fractional derivative model is modified with the internal variable theory and temperature–frequency equivalent principle to characterize the performance of viscoelastic dampers with changing frequencies, displacement amplitudes, and temperatures.

3.1. Higher-Order Fractional Derivative Model

The higher-order fractional derivative model consists of a fractional Kelvin model and a fractional Maxwell model in parallel, as shown in Figure 7, which has three fractional derivative parameters and is more accurate in describing the static creep and dynamic damping characteristics of viscoelastic materials.

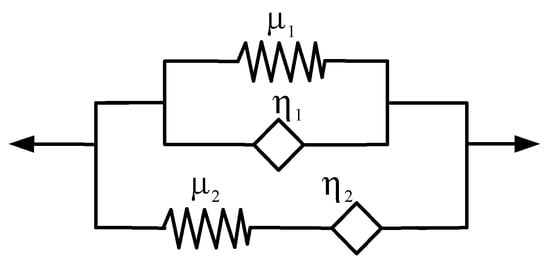
Figure 7. The higher-order fractional derivative model.

The stress–strain expressions of the higher-order fractional derivative model has the form

$$\frac{c_2}{{\eta }_1}\sigma \left(t\right)+\frac{1}{{\eta }_1}{D}^{\alpha }\sigma \left(t\right)=D^{\alpha +\gamma }\epsilon \left(t\right)+c_1{D}^{\alpha }\epsilon \left(t\right)+\frac{{\mu }_2}{{\eta }_1}{D}^{\beta }\epsilon \left(t\right)+c_2{D}^{\gamma }\epsilon \left(t\right)+c_1{c}_2\epsilon \left(t\right)$$

(8)

where ${\mu }_1$ and ${\mu }_2$ are elastic modules of the spring elements. ${\eta }_1$ and ${\eta }_2$ are viscous parameters of the fractional dashpots. $c_1={\mu }_1/{\eta }_1$ and $c_2={\mu }_2/{\eta }_2$. $\alpha$, $\beta$, and $\gamma$ are the $\alpha$-order, $\beta$-order, and $\gamma$-order fractional derivatives, respectively.

By applying the Fourier transform to Equation (8), the complex form modulus of the higher-order fractional derivative model can be obtained as

$$G^{*}\left(\omega \right)=\frac{{\sigma }^{*}\left(\omega \right)}{{\epsilon }^{*}\left(\omega \right)}={\mu }_1+{\eta }_1{\left(i\omega \right)}^{\gamma }+\frac{{\mu }_2{\left(i\omega \right)}^{\beta }}{c_2+{\left(i\omega \right)}^{\alpha }}$$

(9)

The dynamic modulus can be gained by decomposing Equation (9) into two parts; the real part is the storage modulus, the imaginary part is the loss modulus, and the loss factor is the ratio of the imaginary part to the real part:

$$G_1={\mu }_1+{\eta }_1{\omega }^{\gamma }\cos \left(\gamma \pi /2\right)+\frac{{\mu }_2{c}_2{\omega }^{\beta }\cos \left(\beta \pi /2\right)+{\mu }_2{\omega }^{\alpha +\beta }\cos \left[\left(\alpha -\beta \right)\pi /2\right]}{c_2^2+2c_2{\omega }^{\alpha }\cos \left(\beta \pi /2\right)+{\omega }^{2\alpha }}$$

(10)

$$G_2={\eta }_1{\omega }^{\gamma }\sin \left(\gamma \pi /2\right)+\frac{{\mu }_2{c}_2{\omega }^{\beta }\sin \left(\beta \pi /2\right)+{\mu }_2{\omega }^{\alpha +\beta }\sin \left[\left(\beta -\alpha \right)\pi /2\right]}{c_2^2+2c_2{\omega }^{\alpha }\cos \left(\beta \pi /2\right)+{\omega }^{2\alpha }}$$

(11)

$$\eta =\frac{G_2}{G_1}$$

(12)

3.2. Internal Variable Theory

The dynamic modulus of carbon black-filled viscoelastic materials not only has temperature and frequency dependence, but also has displacement/strain amplitude reliance. Therefore, it is of crucial significance to describe the temperature, frequency, and strain amplitude dependence of the dynamic modulus of carbon black-filled viscoelastic materials with an appropriate model. Payne et al. [24] believed that the dynamic modulus of materials decreased with increments of strain amplitudes, which was due to the destruction of the filler network structures. The energy dissipation is mainly caused by the destruction and rebuilding of the filler network structures, and the Kraus model is introduced to describe the strain amplitude influence.

Both classical irreversible thermodynamics and rational thermodynamics use internal variables to describe the thermomechanical state of materials. These internal variables are microscale state variables such as damage accumulation, phase transformation, free volume variation, grain size change, inelastic strain, stress, etc., which are impossible to be observed at the macroscale. Their changes reflect the internal state evolution of materials, and have an important impact on the deformation and thermal process of materials. The deformation history and strain amplitude have a critical influence on the viscosity of viscoelastic materials. Lion et al. [37] introduced the intrinsic time with internal variables to characterize this correlation and describe the evolution process of materials:

$$u\left(t\right)=\psi \left(\omega ,{\epsilon }_0\right)t$$

(13)

where $u\left(t\right)$ is the intrinsic time, and ${\epsilon }_0$ denotes the excitation strain amplitude. $\psi \left(\omega ,{\epsilon }_0\right)$ is the reduction factor, which has the form

$$\psi \left(\omega ,{\epsilon }_0\right)=1+\frac{2}{\pi }\chi {\omega }^{\zeta }{\epsilon }_0$$

(14)

where $\chi$ and $\zeta$ are material parameters, and $\omega =2\pi f$.

Based on the Riemann–Liouville-type definition, the $i$th order fractional derivative of stress has the form

$$D^i\left[\sigma \left(t\right)\right]=\frac{{\mathrm{d}}^i}{\mathrm{d}{t}^i}\sigma \left(t\right)=\frac{1}{\mathrm{\Gamma }\left(1-i\right)}{\displaystyle {\int }_0^t\frac{\dot{\sigma }\left(s\right)}{{\left(t-s\right)}^i}}\mathrm{d}s$$

(15)

According to Equation (13), by defining $z=\psi \left(\omega ,{\epsilon }_0\right)s$, the $i$th order fractional derivative of stress with intrinsic time has the form

$$D^i\left[\sigma \left(u\right)\right]=\frac{{\mathrm{d}}^i}{\mathrm{d}{t}^i}\sigma \left(u\right)=\frac{1}{\mathrm{\Gamma }\left(1-i\right)}{\displaystyle {\int }_0^u\frac{\dot{\sigma }\left(z\right)}{{\left(u-z\right)}^i}}\mathrm{d}z=\frac{1}{{\psi }^i\left(\omega ,{\epsilon }_0\right)\mathrm{\Gamma }\left(1-i\right)}{\displaystyle {\int }_0^t\frac{\dot{\sigma }\left(s\right)}{{\left(t-s\right)}^i}}\mathrm{ds}$$

(16)

Then, we obtain

$$D^i\left[\sigma \left(u\right)\right]=\frac{1}{{\psi }^i\left(\omega ,{\epsilon }_0\right)}{D}^i\left[\sigma \left(t\right)\right]$$

(17)

It also can be obtained that

$$D^i\left[\epsilon \left(u\right)\right]=\frac{1}{{\psi }^i\left(\omega ,{\epsilon }_0\right)}{D}^i\left[\epsilon \left(t\right)\right]$$

(18)

By replacing the physical time t in the constitutive equation of viscoelastic materials in Equation (8) with the intrinsic time $u\left(t\right)$, the viscoelastic constitutive equation based on the internal variable theory can be obtained as

$$\begin{array}{l}\frac{c_2}{{\eta }_1}\sigma \left(t\right)+\frac{1}{{\eta }_1{\psi }^{\alpha }}{D}^{\alpha }\sigma \left(t\right)\\ =\frac{1}{{\psi }^{\alpha +\gamma }}{D}^{\alpha +\gamma }\epsilon \left(t\right)+\frac{c_1}{{\psi }^{\alpha }}{D}^{\alpha }\epsilon \left(t\right)+\frac{{\mu }_2}{{\eta }_1{\psi }^{\beta }}{D}^{\beta }\epsilon \left(t\right)+\frac{c_2}{{\psi }^{\gamma }}{D}^{\gamma }\epsilon \left(t\right)+c_1{c}_2\epsilon \left(t\right)\end{array}$$

(19)

Then, Equations (10) and (11) can be rewritten as

$$\begin{array}{ll}{G}_1& ={\mu }_1+{\eta }_1{\left(\omega /\psi \right)}^{\gamma }\cos \left(\gamma \pi /2\right)\\ & +\frac{{\mu }_2{c}_2{\left(\omega /\psi \right)}^{\beta }\cos \left(\beta \pi /2\right)+{\mu }_2{\left(\omega /\psi \right)}^{\alpha +\beta }\cos \left[\left(\alpha -\beta \right)\pi /2\right]}{c_2^2+2c_2{\left(\omega /\psi \right)}^{\alpha }\cos \left(\alpha \pi /2\right)+{\left(\omega /\psi \right)}^{2\alpha }}\end{array}$$

(20)

$$\begin{array}{ll}{G}_2& ={\eta }_1{\left(\omega /\psi \right)}^{\gamma }\sin \left(\gamma \pi /2\right)\\ & +\frac{{\mu }_2{c}_2{\left(\omega /\psi \right)}^{\beta }\sin \left(\beta \pi /2\right)+{\mu }_2{\left(\omega /\psi \right)}^{\alpha +\beta }\sin \left[\left(\beta -\alpha \right)\pi /2\right]}{c_2^2+2c_2{\left(\omega /\psi \right)}^{\alpha }\cos \left(\alpha \pi /2\right)+{\left(\omega /\psi \right)}^{2\alpha }}\end{array}$$

(21)

The performance of viscoelastic dampers is significantly affected by ambient temperature and excitation frequency, and temperature and frequency impacts are closely related. Especially for the temperature regions of T_g to T_g +100 °C, the storage modulus and loss modulus at high frequency are equal to those at low temperature, and the dynamic modules at low frequency are also equivalent to those at high temperature, which has been defined as the temperature–frequency equivalent principle [38]:

$$\begin{array}{l}{G}_1\left(\omega ,T\right)=G_1\left(a_T\omega ,T_0\right)\\ \eta \left(\omega ,T\right)=\eta \left(a_T\omega ,T_0\right)\end{array}$$

(22)

where $T_g$ is the glass transaction temperature, $a_T$ is the shaft factor, and $a_T={10}^{-12\left(T-T_0\right)/\left[525+\left(T-T_0\right)\right]}$. $T$ represents the environmental temperature and $T_0$ is the reference temperature. By applying Equation (22) to Equations (20) and (21), we have

$$\begin{array}{ll}{G}_1& ={\mu }_1+{\eta }_1{\left({\alpha }_T\omega /\psi \right)}^{\gamma }\cos \left(\gamma \pi /2\right)\\ & +\frac{{\mu }_2{c}_2{\left({\alpha }_T\omega /\psi \right)}^{\beta }\cos \left(\beta \pi /2\right)+{\mu }_2{\left({\alpha }_T\omega /\psi \right)}^{\alpha +\beta }\cos \left[\left(\alpha -\beta \right)\pi /2\right]}{c_2^2+2c_2{\left({\alpha }_T\omega /\psi \right)}^{\alpha }\cos \left(\alpha \pi /2\right)+{\left({\alpha }_T\omega /\psi \right)}^{2\alpha }}\end{array}$$

(23)

$$\begin{array}{ll}{G}_2& ={\eta }_1{\left({\alpha }_T\omega /\psi \right)}^{\gamma }\sin \left(\gamma \pi /2\right)\\ & +\frac{{\mu }_2{c}_2{\left({\alpha }_T\omega /\psi \right)}^{\beta }\sin \left(\beta \pi /2\right)+{\mu }_2{\left({\alpha }_T\omega /\psi \right)}^{\alpha +\beta }\sin \left[\left(\beta -\alpha \right)\pi /2\right]}{c_2^2+2c_2{\left({\alpha }_T\omega /\psi \right)}^{\alpha }\cos \left(\alpha \pi /2\right)+{\left({\alpha }_T\omega /\psi \right)}^{2\alpha }}\end{array}$$

(24)

Equations (22)–(24) are the expressions of the higher-order fractional derivative model modified with the internal variable theory and temperature–frequency equivalent principle (ITHF), which can reflect the impacts of surrounding temperature, excitation frequency, and loading displacement/strain amplitude on the dynamic behaviors of viscoelastic dampers well.

4. Experiments Verification

To verify the effectiveness and progressiveness of the ITHF model in describing the dynamic behaviors of viscoelastic dampers with changing displacement amplitudes and frequencies, the Kraus model [24] is introduced to modify the higher-order fractional derivative model and the comparisons of the experimental and numerical results of the viscoelastic damper are conducted. According to the Kraus model, the storage modulus $G_1\left(\epsilon \right)$ is proportional to $\frac{1}{1+{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^{2m}}$, and the loss modulus $G_2\left(\epsilon \right)$ is proportional to $\frac{2{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^m}{1+{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^{2m}}$, as seen below.

$$\{\begin{array}{l}{G}_1\left(\epsilon \right)=G_1\left(0\right)-{\overline{G}}_1+\frac{{\overline{G}}_1}{1+{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^{2m}};\\ G_2\left(\epsilon \right)=G_2^{\infty }+\frac{2\left(G_2^{\max }-G_2^{\infty }\right){\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^m}{1+{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^{2m}}.\end{array}$$

(25)

where $G_1\left(0\right)$, ${\overline{G}}_1$, $G_2^{\infty }$, $G_2^{\max }$, ${\epsilon }_{\mathrm{c}}$, and $m$ are constants. By applying Equations (22) and (25) to Equations (10) and (11), the higher-order fractional derivative model modified with the Kraus model and temperature–frequency equivalent principle (KTHF) can be obtained as

$$G_1=k_1\left\{\begin{array}{l}{\mu }_1+{\eta }_1{\left({\alpha }_T\omega \right)}^{\gamma }\cos \left(\gamma \pi /2\right)\\ +\frac{{\mu }_2{c}_2{\left({\alpha }_T\omega \right)}^{\beta }\cos \left(\beta \pi /2\right)+{\mu }_2{\left({\alpha }_T\omega \right)}^{\alpha +\beta }\cos \left[\left(\alpha -\beta \right)\pi /2\right]}{c_2^2+2c_2{\left({\alpha }_T\omega \right)}^{\alpha }\cos \left(\alpha \pi /2\right)+{\left({\alpha }_T\omega \right)}^{2\alpha }}\end{array}\right\}\frac{1}{1+{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^{2m}}+b_1$$

(26)

$$G_2=k_2\left\{\begin{array}{l}{\eta }_1{\left({\alpha }_T\omega \right)}^{\gamma }\sin \left(\gamma \pi /2\right)\\ +\frac{{\mu }_2{c}_2{\left({\alpha }_T\omega \right)}^{\beta }\sin \left(\beta \pi /2\right)+{\mu }_2{\left({\alpha }_T\omega \right)}^{\alpha +\beta }\sin \left[\left(\beta -\alpha \right)\pi /2\right]}{c_2^2+2c_2{\left({\alpha }_T\omega \right)}^{\alpha }\cos \left(\alpha \pi /2\right)+{\left({\alpha }_T\omega \right)}^{2\alpha }}\end{array}\right\}\frac{2{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^m}{1+{\left(\epsilon /{\epsilon }_{\mathrm{c}}\right)}^{2m}}+b_2$$

(27)

where k₁, b₁, k₂, and b₂ are material parameters.

The least squares method is utilized for parameter identification of the models. By optimizing min $F\left(\omega ,\epsilon ,T\right)$ in Equation (28) with test data of the storage modulus G₁ and the loss factor η, the parameters of the ITHF model and KTHF models can be achieved.

$$\begin{array}{ll}F\left(\omega ,\epsilon ,T\right)& =p_1{\left\{\left[G_1\left(\omega ,\epsilon ,T\right)-G_{10}\left(\omega ,\epsilon ,T\right)\right]/G_{10}\left(\omega ,\epsilon ,T\right)\right\}}^2\\ & +p_2{\left\{\left[\eta \left(\omega ,\epsilon ,T\right)-{\eta }_0\left(\omega ,\epsilon ,T\right)\right]/{\eta }_0\left(\omega ,\epsilon ,T\right)\right\}}^2\end{array}$$

(28)

where $p_1$ and $p_2$ are weighting parameters, $p_1+p_2=1.0$, $G_1\left(\omega ,\epsilon ,T\right)$ and $\eta \left(\omega ,\epsilon ,T\right)$ are numerical results, and $G_{10}\left(\omega ,\epsilon ,T\right)$ and ${\eta }_0\left(\omega ,\epsilon ,T\right)$ are experimental results.

Some experimental data from the viscoelastic damper with randomly selected frequencies and displacement amplitudes are used for data fitting, and the parameters of the ITHF model are determined as ${\mu }_1$ = 3.695 × 10⁵, ${\eta }_1$ = 2.0993 × 10⁻⁹, ${\mu }_2$ = 6.3021 × 10⁵, $c_2$ = 1.2507 × 10³, $\chi$ = 0.6368, $\zeta$ = 0.7114, $\alpha$ = 0.0853, $\beta$ = 0.2187, $\gamma$ = 0.9654, and $T_0$ = 570.2816 K. Similarly, the parameters of the KTHF model are also determined as ${\mu }_1$ = 1.6086 × 10¹⁰, ${\eta }_1$ = 3.8768 × 10⁸, ${\mu }_2$ = 7.0468 × 10⁸, $c_2$ = 3.4705 × 10⁸, $\alpha$ = 0.1766, $\beta$ = 0.5678, $\gamma$ = 0.2032, $k_1$ = 2.2937 × 10⁻⁸, $b_1$ = 8.0575 × 10⁵, $k_2$ = 1.1537 × 10⁻⁸, $b_2$ = 5.2489 × 10⁴, ${\epsilon }_c$ = 0.0125, $m$ = 0.3685, and $T_0$ = 634.3185 K. The comparisons of the numerical results of the ITHF model, KTHF model, and experimental results with frequency 1.0 Hz and displacement 1.0 mm are presented in Figure 8a,b, respectively.

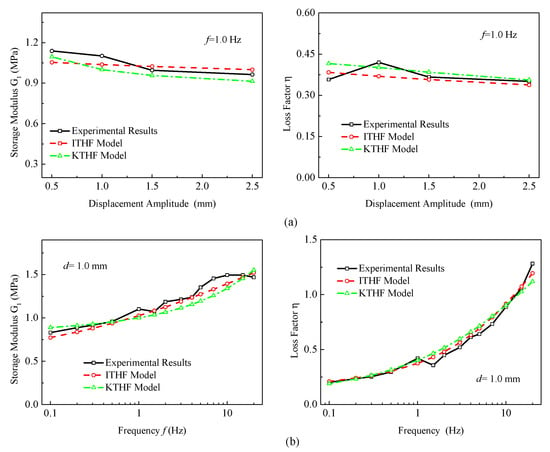
Figure 8. Comparisons of test data and numerical results for ITHF model and KTHF model. (a) f = 1.0 Hz. (b) d = 1.0 mm.

Figure 8a shows the experimental and numerical results of the storage modulus and loss factor with varying displacement amplitudes when f = 1.0 Hz. It reveals that the deviations of numerical results of both the ITHF model and the KTHF model from the experimental results are very small. The experimental and numerical results of the viscoelastic damper with changing displacement amplitudes are given in Table 6. For the storage modulus with frequency 1.0 Hz, the maximum error and root mean square error of the ITHF model in different displacement amplitudes are 7.44% and 5.28%, respectively, and the maximum error and root mean square error of the KTHF model in different displacement amplitudes are 8.59% and 6.03%, respectively. For the loss factor, the maximum error and root mean square error of the ITHF model with different displacement amplitudes are 12.04% and 7.38%, respectively, and the maximum error and root mean square error of the KTHF model in different displacement amplitudes are 16.25% and 8.78%, respectively. The ITHF model is more accurate in reflecting the dynamic behaviors of viscoelastic dampers with changing displacement amplitudes.

Table 6. The comparisons of the ITHF model and KTHF model when f = 1.0 Hz.

Displacement Amplitude d (mm)	Characteristic Parameters	Experimental Results	Numerical Results
			ITHF Model	Error	KTHF Model	Error
0.5	G1 (MPa)	1.1385	1.0538	7.44%	1.0953	3.94%
	$\eta$	0.3576	0.3836	7.23%	0.4157	16.25%
1	G1 (MPa)	1.1018	1.0379	5.8%	1	3.64%
	$\eta$	0.42	0.3694	12.04%	0.4015	4.41%
1.5	G1 (MPa)	0.9952	1.0238	2.87%	0.96	6.54%
	$\eta$	0.3666	0.3573	2.53%	0.3841	4.78%
2.5	G1 (MPa)	0.9638	1	3.76%	0.91	8.59%
	$\eta$	0.3506	0.3377	3.68%	0.3559	1.5%

The experimental and numerical result comparisons with varying frequencies at displacement amplitude 1 mm are shown in Figure 8b, and the test and numerical data with the ITHF model and KTHF model are listed in Table 7. The maximum error and root mean square error of the ITHF model for the storage modulus in different frequencies are 8.53% and 4.98%, respectively, and the maximum error and root mean square error of the KTHF model for the storage modulus in different frequencies are 15.08% and 6.34%, respectively. The maximum error and root mean square error of the ITHF model for the loss factor in different frequencies are 20.98% and 8.13%, respectively, and the maximum error and root mean square error of the KTHF model for the loss factor in different frequencies are 30.34% and 11.79%, respectively.

Table 7. The comparisons of the ITHF model and KTHF model when d = 1.0 mm.

Frequency f (Hz)	Characteristic Parameters	Experimental Results	Numerical Results
			ITHF Model	Error	KTHF Model	Error
0.1	G1 (MPa)	0.8309	0.7729	6.98%	0.8895	15.08%
	$\eta$	0.2022	0.2093	3.51%	0.1902	5.96%
0.2	G1 (MPa)	0.8874	0.8376	5.62%	0.9117	8.85%
	$\eta$	0.2342	0.2405	2.67%	0.233	0.51%
0.3	G1 (MPa)	0.9158	0.8798	3.93%	0.9282	5.5%
	$\eta$	0.2533	0.2641	4.25%	0.2651	4.65%
0.5	G1 (MPa)	0.9582	0.938	2.11%	0.9538	1.69%
	$\eta$	0.296	0.302	2.02%	0.3146	6.28%
1	G1 (MPa)	1.1018	1.0263	6.85%	1	2.56%
	$\eta$	0.42	0.3741	10.93%	0.4015	4.41%
1.5	G1 (MPa)	1.0734	1.0831	0.9%	1.0352	4.42%
	$\eta$	0.3565	0.4313	20.98%	0.4647	30.35%
2	G1 (MPa)	1.1868	1.1256	5.15%	1.0648	5.4%
	$\eta$	0.4482	0.4803	7.15%	0.5157	15.06%
3	G1 (MPa)	1.2141	1.1887	2.09%	1.1145	6.25%
	$\eta$	0.5197	0.5629	8.31%	0.597	14.86%
4	G1 (MPa)	1.2393	1.2356	0.3%	1.1565	6.4%
	$\eta$	0.614	0.6322	2.97%	0.6614	7.72%
5	G1 (MPa)	1.3529	1.273	5.91%	1.1935	6.24%
	$\eta$	0.6407	0.6925	8.08	0.7153	11.65%
7	G1 (MPa)	1.4552	1.3311	8.53%	1.2582	5.47%
	$\eta$	0.7325	0.7944	8.45%	0.803	9.62%
10	G1 (MPa)	1.4936	1.3945	6.64%	1.3404	3.87%
	$\eta$	0.8891	0.9171	3.14%	0.9038	1.66%
15	G1 (MPa)	1.4949	1.4684	1.78%	1.4547	0.93%
	$\eta$	1.0592	1.0739	1.38%	1.0272	3.02%
20	G1 (MPa)	1.4687	1.5217	3.61%	1.5521	2%
	$\eta$	1.2819	1.1954	6.75%	1.1194	12.67%

The ITHF model possesses enough precision in characterizing the dynamic and damping properties of the viscoelastic damper with changing displacement amplitudes and frequencies, and is more accurate than the KTHF model because it introduces the internal variable theory at the microscale to consider the displacement amplitude impacts. The ITHF model has fewer parameters than the KTHF model and is more appropriate to be utilized in describing the dynamic properties of viscoelastic dampers.

5. Conclusions

Viscoelastic dampers are well-known passive vibration control devices and have been widely used in seismic/wind vibration control, micro vibration suppression, and platform vibration isolation, etc. In the present work, the dynamic properties of a viscoelastic damper at room temperature (18 °C) are tested under sinusoidal displacement excitations with a wide frequency band (0.1–25 Hz). The impacts of frequency and displacement amplitude on the dynamic properties of the viscoelastic damper are discussed. The higher-order fractional derivate model and the temperature–frequency equivalent principle are employed to characterize the frequency and temperature influence, and the internal variable theory considering the microscale structure influence is introduced to reflect the displacement amplitude affection. The ITHF model is proposed and verified with experimental results. Some notable conclusions can be obtained, such as:

(1)

The viscoelastic damper has great energy dissipation properties at room temperature with frequencies 0.1 Hz~25 Hz, especially at high frequencies (1 Hz~25 Hz). The damping performance and stiffness of the damper are crucially affected by the excitation frequency, while the damping performance is greatly influenced by the displacement amplitude, and the stiffness is slightly affected.

(2)

The characteristic parameters of viscoelastic dampers are significantly dependent on the external excitation frequencies and loading amplitudes. The parameters $G_1$, $G_2$, $\eta$, $E_d$, and $K_e$ increase remarkably with increasing frequency, while $C_e$ decreases. The energy dissipation $E_d$ rises prominently with displacement amplitude, while and other parameters reduce mildly.

(3)

The ITHF model possesses enough precision in characterizing the dynamic and damping properties of viscoelastic dampers with changing displacement amplitudes and frequencies, and has higher accuracy and fewer parameters than the KTHF model.

(4)

The ITHF model introduces the internal variable theory to reflect the displacement amplitude impacts, which considers the internal structures’ evolution process at the microscale and is of great significance for material design and damping property improvement.