Abstract
The flanged, barbell, and rectangular squat reinforced concrete (RC) walls are broadly used in low-rise commercial and highway under and overpasses. The shear strength of squat walls is the major design consideration because of their smaller aspect ratio. Most of the current design codes or available published literature provide separate sets of shear capacity equations for flanged, barbell, and rectangular walls. Also, a substantial scatter exists in the predicted shear capacity due to a large discrepancy in the test data. Thus, this study aims to develop a single gene expression programming (GEP) expression that can be used for predicting the shear strength of these three cross-sectional shapes based on a dataset of 646 experiments. A total of thirteen influencing parameters are identified to contrive this efficient empirical compared to several shear capacity equations. Owing to the larger database, the proposed model shows better performance based on the database analysis results and compared with 9 available empirical models.
1. Introduction
Reinforced concrete squat walls are an efficient lateral force-resisting system situated in various low-rise buildings having a height-to-length aspect ratio of less than 2, such as commercial buildings and highways under and overpasses [1]. These walls are generally classified according to their cross-sectional shapes, out of which the rectangular and flanged walls are more commonly used. Because these walls are meant to resist the lateral force on buildings, several empirical models have been proposed for the prediction of shear strength [2,3,4,5,6,7]. Calculation guidelines for rectangular walls are widely available in the design codes [8,9,10], however, provisions for flanged walls are limited [11,12]. A review of the literature reveals a significant disparity in the available shear capacity equations of the flanged squat walls [1,13,14,15]. This discrepancy is attributed to the interaction of flanged and the web segment of these walls. Hence, it is justified to investigate the behavior of rectangular and flanged squat walls to formulate prescriptive guidelines.
Consequently, extensive study has been conducted [5,6,7,15] and several empirical formulas are proposed to predict the shear strength of squat flanged walls. These empirical models, however, have limitations that have to be recognized to obtain good estimation. For example, the model proposed by Gulec et al. [5] is restricted to squat flanged walls having an aspect ratio less than 1.0. Whereas Kassem’s analytical formula [6], derived based on strut-and-tie modeling, neglects the effect of the flange element, thus resulting in inconsistency between the experimental and predicted results. The underlying limitations of the empirical models proposed by Adorno et al. [7] and Ma et al. [15] are that the dataset comprises less than 140 experiments, and also the aspect ratio of the shear walls in the dataset is less than 1.20. Moreover, all of these previous investigations consider limited significant parameters because of which the prediction does not represent experiment outcomes well.
The existing inconsistencies in the findings of the available shear capacity models of the flanged shear walls, therefore, demand a robust solution in the light of careful research. Machine learning algorithms have emerged as a strong candidate capable of accurately predicting the uncertainties in material properties and configurations. Several evolutionary algorithms have been employed to develop shear equations of squat walls [16]. For instance, artificial neural network (ANNs) has been successfully applied by Ghaboussi et al. [17]. Many authors have used the artificial intelligence (AI) application to predict the shear strength of RC squat walls under cyclic or monotonic loading [18,19,20,21,22,23,24,25,26,27,28,29].
A similar machine learning ML algorithm approach has been applied successfully to predict the shear capacity of RC squat walls [30,31] and failure modes [32]. Chen et al. [30] have proposed a hybrid model, which is developed on a dataset of 139 experiments. Although the model accurately predicted the shear strength of RC rectangular walls, the formula suffered the drawback of being highly impractical, a very prevalent characteristic of hybrid models. Probably the most extensive database is constructed by Moradi and Hariri-Ardebili [31], which is categorized into slender and squat walls of both rectangular and flanged types of cross-sections. Similar to the hybrid modes, their ANN formula predicts the shear strength accurately, however, a practical tool for the design process is still lacking.
In summary, a reappraisal of the shear capacity model of the squat wall is essential to collecting the available experimental data. This consideration has given the current study impetus to developing a simplified regression-based model using a machine learning algorithm known as gene expression programming (GEP). The present investigation mainly focuses on the rectangular, flanged squat walls of H shape and barbell squat wall because they more efficiently resist seismic forces in both principal directions. Nevertheless, the derived model can also predict the shear capacity of rectangular squat walls with reasonable accuracy. An extensive experimental database of 646 tests is constructed to develop a GEP model, which is statistically evaluated and compared against existing models. Also carried out is the detailed assessment of various influencing parameters. Because of the improved capability, the current shear capacity model can be beneficially employed for structural analysis, design, and evaluation of flanged squat walls.
2. Research Significance
In a region of high seismic activity, low aspect ratio RC squat walls are key structural elements in many low-rise commercial buildings and highways under and overpasses. This has inspired many researchers to develop shear strength predictive models for rectangular and flanged squat walls. Despite the preferable effect of flanges or boundary elements in improving the strength of the flanged squat walls, the literature on the flanged and barbell walls is rather limited. Most of the studies have focused only on rectangular wall shapes. Few empirical studies have been carried out on wide-flanged squat walls, especially studies related to barbell walls are almost nonexistent. In this respect, the current study is concerned with deploying Gene Expression Programming (GEP) algorithm to develop a shear capacity model for rectangular, flanged, and barbell wall shapes. This equation gives a highly reliable estimate of the shear strength of flanged RC squat walls, thereby overcoming the failure of existing predictive models to reliably estimate the shear strength of flanged RC squat walls. A larger database and incorporation of all the influencing parameters in the GEP model play a key role in improving the performance and accuracy of the model.
3. Effect of Barbells and Flanges on the Ultimate Shear Strength
Barbells and flange boundary effects on the shear strength of squat reinforced concrete walls appear not to have been examined extensively, which leads to the expectation that their effect should be ignored. However, this expectation might not be realized because it is well established from tests that these boundary elements attain higher peak shear strength compared to rectangular walls. More specifically, it has been observed that more than 50% of the horizontal load is received by barbells or flanges of a squat wall on a stiff foundation. An analogous problem of steel W-shape beam to a column is studied by Lee and Stojadinovic [33] and Kim et al. [34]. These authors have shown that a higher percentage of shear force is transferred through the beam flanges.
The four predictive models proposed above have neglected the contribution of flanges or barbells, thus predicting identical shear strength for squat walls with boundary elements and rectangular walls. Therefore, these equations overestimate the shear capacity of rectangular walls, as the equations were calibrated using a dataset of walls having boundary elements.
To substantiate the contribution of boundary elements in transferring the lateral force to the foundation, the variation of normalized shear strength to moment-to-shear-arm ratio has been discussed by Gulec et al. [14]. This research concluded that the normalized shear capacity of walls with boundary elements is significantly higher than that of rectangular walls.
4. Factors Affecting Shear Strength
The selection of various influencing parameters is the essential step toward developing a robust predictive model. Therefore, the following variables have been identified after reviewing the literature pertaining to the factors affecting squat walls and the shear strength of squat walls.
4.1. Aspect Ratio
The wall height to length ratio, that is the aspect ratio, has significant relevance to the shear strength of squat walls subjected to lateral loading. One of the first studies in this context was provided by Barda et al. [2], in which eight flanged walls were investigated having aspect ratios of 0.25, 0.5, and 1.0. This study has shown that walls with a lower aspect ratio exhibit higher shear strength—for example, 20% higher shear strength was observed in the wall specimen with an aspect ratio of 0.5 than the walls having an aspect ratio of 1.0. The authors used the term lattice action, or arch action, to describe this increase in the shear strength. Lattice action involves transferring large shear force to the foundation from the top of the wall that consists of vertical wall reinforcement carrying the tie forces and the struts between the inclined cracks carrying the compressive forces. Remembering that the angle between the struts and ties should be large enough to avoid incompatibilities, it is principally because of the higher angle that the low aspect ratio walls demonstrate higher shear strength. A similar observation associated with higher shear strength resulting from a lower aspect ratio has been statistically validated by Gulec and Whitaker [35]. Several other researchers have also investigated the effect of aspect ratio on the shear strength of squat walls, some of these contributions are Hwang et al. [36], Gulec and Whittakaer [5], and Kassem [6].
On the other hand, it is shown that a lower aspect ratio can result in stiffer structures and be susceptible to shear sliding [37,38,39,40,41,42,43,44,45,46]. Thus, the lower aspect ratio walls have low energy dissipation levels than that of the higher aspect ratio.
4.2. Horizontal and Vertical Web Reinforcement
The study of horizontal and vertical web reinforcement has received considerable attention, and the literature devoted to this subject is vast. However, after decades of extensive research, there is a disagreement about this reinforcement’s underlying effect on the shear strength of squat walls. According to some researchers, the tensile strain of the squat walls can be controlled by the provision of appropriate horizontal web reinforcement [39,47,48,49,50,51,52]. Other researchers argue that the vertical web reinforcement contributes to resisting the tensile strains [3,44,53,54,55,56,57]. Nevertheless, all these investigations agree that the wall aspect ratio influences both the horizontal and vertical reinforcements. For instance, vertical web reinforcement becomes more effective than horizontal web reinforcement when the aspect ratio is more than 1, resulting in enhanced energy dissipation and improved deformational capacity.
Similarly, consideration of horizontal and vertical web reinforcement has been emphasized by various codes of practices. Codes such as ACI 318-14 [8] advocate vertical and horizontal web reinforcement for walls with an aspect ratio less than 1.0. In addition, both codes recommend minimum horizontal and vertical web reinforcement to control crack propagation.
4.3. Axial Load
Experimental investigation of axial load on the response of squat wall is somewhat limited [42,56,58,59]. Most of these studies are based on the axial load ratio to concrete compressive strength ranging from 0.0 to 40%. Studies show that the axial load can improve the lateral stiffness and shear resistance of the wall. The presence of axial load can also enhance the energy dissipation of the wall due to a substantial increase in the aggregate interlock. In contrast to energy dissipation, the wall deformability is adversely affected due to the presence of axial load.
However, the benefits of axial load on squat walls are overruled because these walls typically carry a small proportion of axial load [60,61,62]. The contribution of axial load is therefore ignored during the design of the squat walls.
5. Previously Proposed Models
Various researchers and codes of practice have proposed several empirical models that calculate the shear strength of squat flanged RC walls. Table 1 lists the selected equations and definitions of various parameters employed in these equations. These equations are derived from experimental investigations, and they lead to different answers to shear strength capacity. Therefore,

Table 1.
Previously proposed shear strength models of RC squat wall.
6. Experimental Database
For developing an empirical model, a dataset of 646 experiments of squat flanged and barbell RC walls is cataloged, out of which 60% of randomly selected experimental data is used to construct the model and the remaining portion is used for model validation. The database indicates thirteen variables that are candidates for inclusion in the functional relationship. Table 1 clearly shows the shear strength of squat flanged walls are varied according to height (hw), web length (lw), web thickness (tw), flange elements length (lf), flange thickness (tf), aspect ratio (hw/lw), compressive strength of concrete (), yield strength of the horizontal steel (fyh), and yield strength of vertical steel (fyv).
The histogram of Figure 1 provides the frequency distribution of thirteen variables selected from the dataset of 646 experiments. Conforming to the classification of squat walls, the aspect ratio (hw/lw) of all the selected walls is equal to or less than 2.0. The figure shows that concrete compressive strength () varies from 10 to 137 MPa, while the horizontal bars yield strength (fyh) and the vertical bars yield strength (fyv) ranges from 224 to 1420 MPa. Similarly, the horizontal bars reinforcement ratio (ρh) and the vertical bars reinforcement ratio (ρv) vary between 0.01% and 2.98%, while the flange element’s longitudinal reinforcement ratios (ρf) vary between 0.074% and 9.57%. Also considered in the database is the axial load (P) which varies from 0 to 2770 kN.


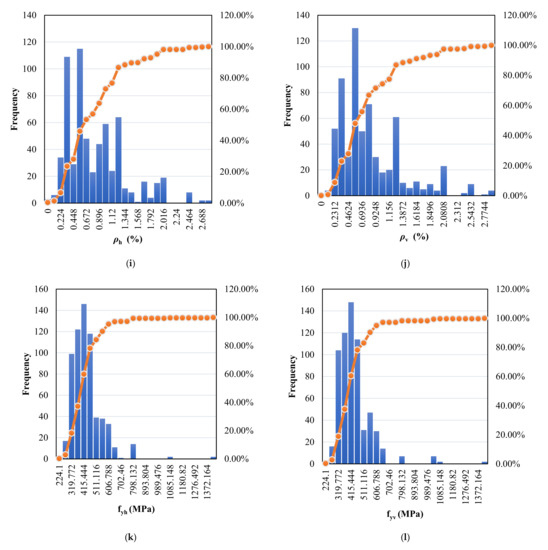
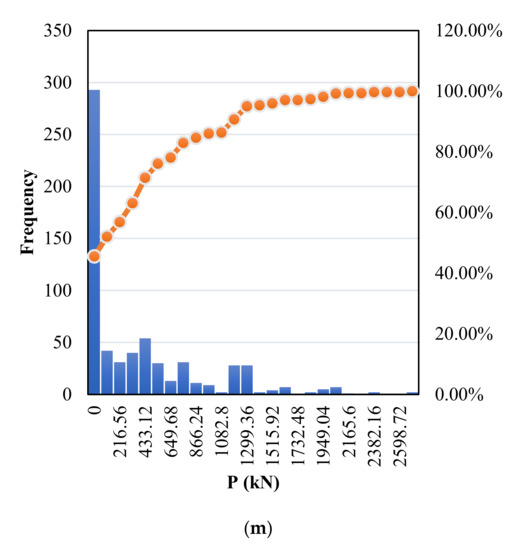
Figure 1.
Ranges of dataset parameters. (a) Height of wall (hw), (b) Web length (lw), (c)Web thickness (tw), (d) Flange thickness (tf), (e)Flange elements length (lf), (f) Compressive strength of concrete (fc′), (g) Longitudinal reinforcement ratios of the flanged element (ρf), (h) Yield strength of longitudinal reinforcement (fyf), (i) Reinforcement ratio of wall in the horizontal direction (ρh), (j) Reinforcement ratios of wall in vertical direction (ρv), (k) Yield strength of the horizontal bars (fyh), (l) Yield strength of vertical bars (fyv), (m) Axial load in wall (P).
7. Gene Expression Programming Algorithm
Gene expression programming (GEP) has been employed in this study to process the supplied data in a domain-independent mode [63]. GEP is different from other available artificial intelligence (AI) based algorithms as regards chromosome representation. The term chromosomes are linear strings of fixed length in GAs but are nonlinear entities of different sizes and shapes in GPs. GEP, on the other hand, encapsulates both the linear string of fixed length, as well as ramified structures of different sizes and shapes.
As with other genetic algorithms, for executing the evolutionary process, several trials are conducted by iteratively altering the number of chromosomes, the number of genes, head size, and linking functions. Thus, GEP optimizes solutions by selecting the best candidates among the supplied initial population based on their fitness. Notably, a complicated function can stem from increasing the number of genes and number of chromosomes, but the function can precisely fit the results. Therefore, several iterations are needed to simplify the model and attain reasonable accuracy.
A key step in the GEP algorithm is the convergence to the global optimal solution. It can sometimes happen that the algorithm is not able to select an optimal solution among several competing candidate solutions. In this state, the algorithm can lead to an indefinite sequence of steps resulting in either a non-terminating program or yielding an illogical expression. This predicament can be resolved by either varying the number of genes and chromosomes or adjusting the linking function. In this context, the role of an analyst comes into play for deciding if and what solution proposed by GEP should be further utilized for statistical analysis [64].
The benefits of GEP have attracted extensive applications in the field of structural engineering over the last decade [16]. Several authors have elegantly employed GEP to develop models for estimating the capacity of various structural components [65]. Recently, a regression-based model has been successfully used for predicting the behavior of RC corner joints, especially where the code formulations are not available [64]. A GEP-based model for corner joints is in progress and will be reported in due course.
The different steps of GEP optimization are illustrated in Figure 2. Prior to the execution of the evolutionary algorithm, the fitness function is prescribed, which leads to the creation of a random string of initial population, or in Genetic Programming parlance ‘Chromosomes’. These strings translate into an expression tree, whose results are compared with the fitness score of each chromosome. If the fitness criterion is not satisfied, roulette-wheel sampling is employed to select some chromosomes and then mutate them to get new generations. Whereas, if the variables are optimally tuned to the fitness function, the chromosomes are decoded following the best solution to the problem [63,65].
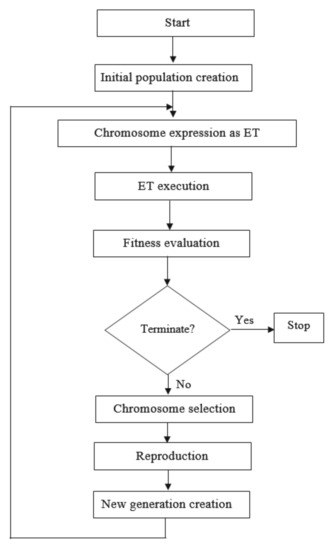
Figure 2.
Range of different parameters in the dataset.
Machine learning (ML) algorithms have been widely used to tackle real-world problems in the last ten years, particularly in civil engineering. ML algorithms have been successfully used in a variety of real situations, paving the way for several promising opportunities in civil engineering and other domains such as geotechnical, and structural engineering [65,66,67,68,69,70,71,72,73,74].
8. Proposed GEP Model for Estimating Joint Shear
The following simple GEP model is generated by employing the dataset of the flanged squat wall discussed in Section 6. Each Equation from (1) to (4) is extracted from relevant genes are shown in Figure 3a–d respectively. Finally, the four equations extracted from four genes are added in as shown in Equation (5). Moreover, the model construction parameter to run the gene expression programming is shown in Table 2.
where are the height, length, and thickness of the wall, respectively. represent the thickness and length of the flange and barbell define the steel yield strength of horizontal, and vertical reinforcement of wall and flange reinforcement respectively. Moreover, and represent the concrete compressive strength and axial load on the wall respectively. The term defines the reinforcement ratio of the flange. Finally, ρh and ρv represent the horizontal and vertical reinforcement ratios, respectively.

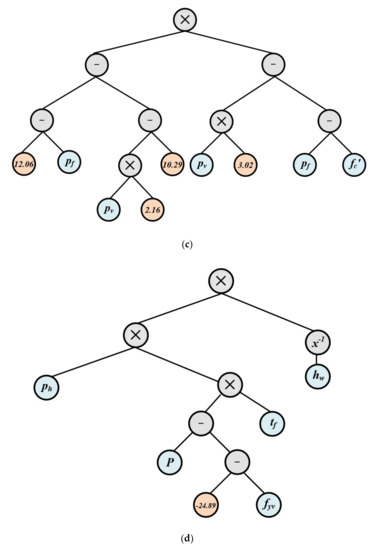
Figure 3.
Gene Expression Tress (a) Sub-ET 1 (b) Sub-ET 2 (c) Sub-ET 3 (d) Sub-ET 4.

Table 2.
Parameters setting for GEP model.
9. Statistical Performance Criteria
The performance of any empirical model is intimately related to the training and validation of these models using the available dataset. So, a random sample of 60% from the designated experiments of SFRC beams is used as training data (for model creation), while a randomly selected 40% of the sample is used as validation data. A variety of statistical approaches have been employed herein to gain quantitative insight into the proposed GEP model.
The coefficient of variation (CoV) is often used to measure data dispersion.
Average absolute error (AAE) is another statistical approach to measure the mean error in n test specimens.
The coefficient of determination () is one of the most popular statistical approaches to testing model reliability. The coefficient of determination equal to one is considered to provide the best fit.
It is worth noticing from Figure 4 that the coefficient of determination of 0.96, 0.94, and 0.95 for training, validation, and overall data, respectively. Thus, the GEP model of shear strength shows a strong relationship between the predicted and actual values.
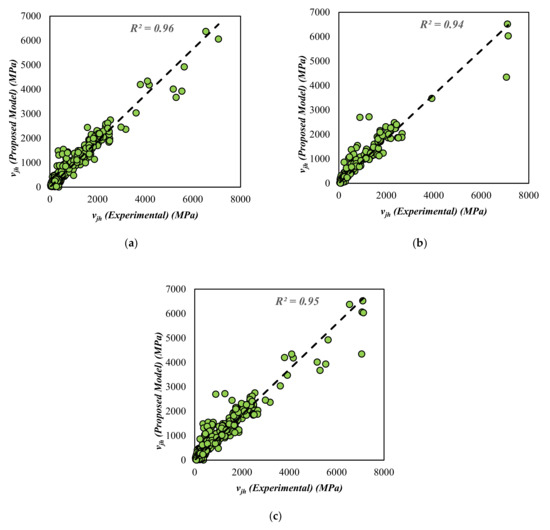
Figure 4.
Comparison of estimated and experimental shear strength of flanged and barbell squat wall (a) Training Data (b) Validation Data (c) All Data.
The reliability of the proposed GEP model can be further validated by performing a sensitivity analysis. Notably, Figure 1 shows that the key parameters influencing the shear strength of squat walls include geometric properties of walls and flanges, mechanical properties of concrete, and properties and quantity of reinforcement. Figure 5 and Figure 6 assess the relative contribution of key influencing parameters on the output results. From Figure 5a, the model accuracy of wall height shows the value of 1.00 denoting suitable performance of the proposed model in various levels of from 0.5–1.5. Similarly, the other influencing parameters in Figure 5b–m, i.e., all show an acceptable accuracy of 1.00. So, in the view of the experimental data, the predictive ability of the proposed model can be affirmed.
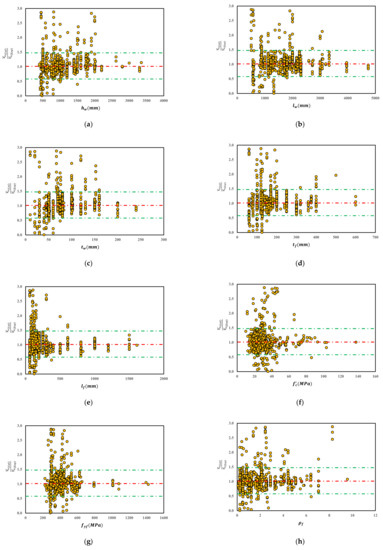
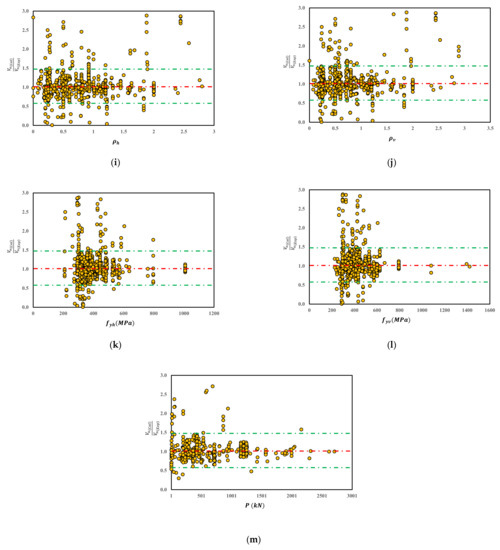
Figure 5.
The predictive performance of the proposed shear strength model based on the key parameters. (a) Height of wall hw, (b) Web length (lw), (c)Web thickness (tw), (d) Flange thickness (tf), (e) Flange elements length (lf), (f) Compressive strength of concrete (f′c), (g) Yield strength of flenged reinforcement (fyf), (h) Reinforcement ratios of flenge (ρf), (i) Reinforcement ratio of wall in the horizontal direction (ρh), (j) Reinforcement ratios of wall in vertical direction (ρv), (k) Yield strength of the horizontal bars (fyh), (l) Yield strength of vertical bars (fyv), (m) Axial load in wall (P).
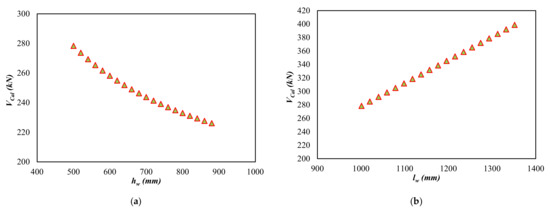
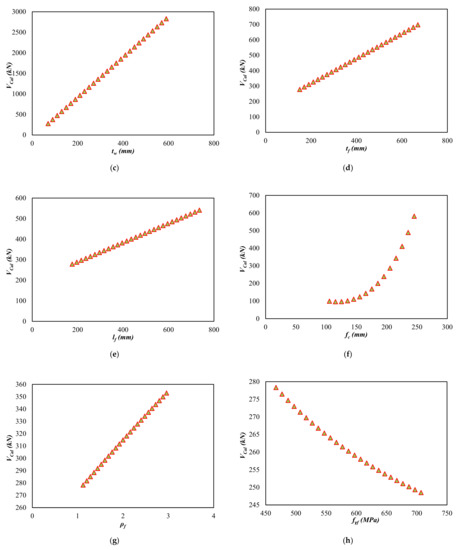
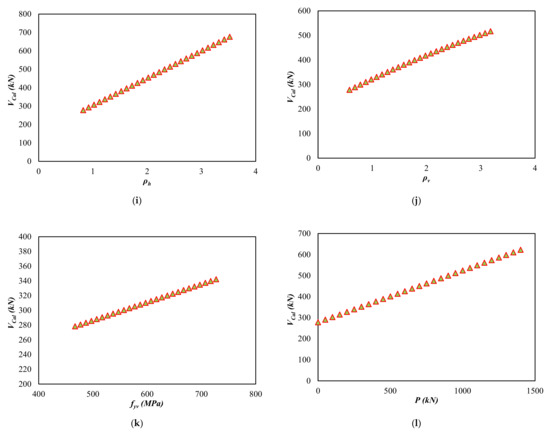
Figure 6.
Sensitivity of each influencing parameter on the shear strength of RC flanged and barbell squat wall. (a) Height of wall (hw), (b) Web length (lw), (c) Web thickness (tw), (d) Flange thickness (tf), (e) Flange elements length (lf), (f) Compressive strength of concrete (fc), (g) Reinforcement ratios of flenge (ρf), (h) Yield strength of flenged reinforcement (fyf), (i) Reinforcement ratio of wall in the horizontal direction (ρh), (j) Reinforcement ratios of wall in vertical direction (ρv), (k) Yield strength of vertical bars (fyv), (l) Axial load in wall (P).
10. Results and Discussion
10.1. Parametric Study
- This section describes the parametric study for identifying the influence of input variables on the shear strength capacity of squat walls. Therefore, a variable of interest is perturbed whilst other variables are locked at the mean values, considering the other variables are uncorrelated.
- If the wall height (i.e., hw) is incrementally increased, the shear strength of the squat flanged RC wall is expected to decrease, Figure 6a. This is because the lateral stiffness of the wall reduces with the increase in wall height.
- The web dimensions, including the length and thickness, are one of the significant parameters controlling the shear capacity of RC walls. As shown in Figure 6b,c, the trend for shear strength is upward which is associated with an increase in shear area.
- Similar to web dimensions, Figure 6c shows that the thickness and the length of flanges vary sharply with respect to the shear strength of the wall. So, it can be argued that an increase in flange dimensions significantly improves the shear capacity of the squat flanged RC wall.
- It can be seen from Figure 6d,e that the shear strength rises with the increase in flange element thickness (tf) and flange element length (lf).
- It can be observed in Figure 6g,i,j that the shear strength increases sharply with the increase in reinforcements.
- Figure 6h,k shows that the shear capacity slumps with the increase in the yield strength of web reinforcement and climbs gradually with the increase in the yield strength of flange reinforcement. These observations are consistent with the findings of Baek et al. [46].
- Figure 6f,l shows the compressive strength of concrete, and the axial load has a marginal influence on the shear capacity of the walls.
10.2. Performance of GEP Models
The main objective of this section is to show that the proposed regression model can defeat the existing models, as shown in Table 3. For instance, the proposed model has a coefficient of determination R2 = 0.95, which outclass all the models as shown in Figure 7. Moreover, the performance factor and the average absolute error of the proposed model are statistically better than the previously proposed model. Among the previously proposed model, the least predictive ability is obtained from the model proposed by Eurocode and Ma et al. [15]. The main reason for its low performance is that the Eurocodes [10] neglect the influence of flanges. Similarly, Figure 8 shows statistical performance checks of various models. A clear satistical excellence of the proposed model is observed having a performance factor of 0.9, coefficient of determination of 0.25, and average absolute error of 1.1.

Table 3.
Statistical analysis of shear strength prediction models of Squat wall.
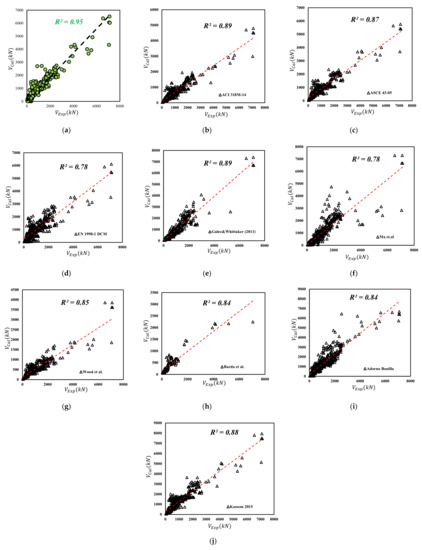
Figure 7.
Comparative results of test data and different available methods. (a) Proposed Model (b) ACI 318M-14 [8], (c) ASCE 43-05 [9], (d) EN 1998-1 [10], (e) Gulec &Whittaker [5], (f) Ma, et al. [15], (g) Wood, et al. [3], (h) Barda, et al. [2], (i) Adorno-Bonilla [7], (j) Kaseem [6].
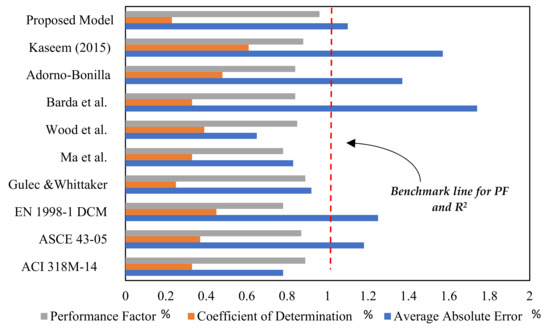
Figure 8.
Comparison of previously proposed models based on statistical investigations.
11. Conclusions
This study focuses on developing a single evolutionary genetic model to predict the shear capacity of barbell, flanged or rectangular squat RC walls. The test database comprises 646 experiments out of which 40% of data are used for the validation of the developed model. The model is also successfully calibrated against 9 existing empirical or semi-analytical models. The results show significant improvement in the estimate of shear resistance. The following conclusions are drawn:
- An increase in the wall web and flange dimensions, and the reinforcement ratio increase the shear capacity of the wall. Whereas, an increase in the wall height reduces the wall shear capacity. Parameters such as concrete compressive strength and axial load moderately influence the wall capacity.
- The developed model successfully incorporates all the aforementioned key parameters and, given the experimental data, these parameters show a high contribution to the development of the model.
- From statistical investigation, a high correlation (R2) of 0.96 is observed. Likewise, the performance factor of 1.1 and average absolute error of 23%, all substantiate the higher accuracy of the proposed.
- An important benefit of the proposed model is that a single model can effectively approximate the shear capacity of a barbell, flanged or rectangular wall.
- Finally, it is asserted that the proposed model offers a better prediction than the existing models of shear strength of flanged or barbed squat walls, leading toward the development of design guidelines for squat walls.
Author Contributions
Conceptualization, M.T. and K.R.K.; Methodology, M.T. and A.K.; Software, M.T.; Validation, M.T., A.K. and A.U.; Formal analysis, M.T. and M.A.; Investigation, M.T. and M.A.; Resources, M.T., A.K. and A.U.; Data curation, M.T. and A.U.; Writing—original draft preparation, M.T., A.K. and K.R.K.; Writing—review and editing, M.T., A.K. and M.A.; Visualization, B.Z. and K.R.K.; Supervision, M.T. and K.R.K.; Project administration, M.T., K.R.K. and M.A.; Funding acquisition, K.R.K. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by RUDN University Strategic Academic Leadership Program (recipient: Prof. Kazem Reza Kashyzadeh).
Data Availability Statement
Not applicable.
Acknowledgments
This paper has been supported by the RUDN University Strategic Academic Leadership Program.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gulec, C.K.; Whittaker, A.S.; Stojadinovic, B. Shear strength of squat rectangular reinforced concrete walls. ACI Struct. J. 2008, 105, 488–497. [Google Scholar] [CrossRef]
- Barda, F.; Hanson, J.M.; Corley, W.G. Shear strength of low-rise walls with boundary elements. Am. Concr. Inst. ACI Spec. Publ. 1977, SP-053, 149–202. [Google Scholar]
- Wood, S.L. Shear strength of low-rise reinforced concrete walls. ACI Struct. J. 1990, 87, 99–107. [Google Scholar] [CrossRef]
- Snchez-Alejandre, A.; Alcocer, S.M. Shear strength of squat reinforced concrete walls subjected to earthquake loading trends and models. Eng. Struct. 2010, 32, 2466–2476. [Google Scholar] [CrossRef]
- Gulec, C.K.; Whittaker, A.S. Empirical equations for peak shear strength of low aspect ratio reinforced concrete walls. ACI Struct. J. 2011, 108, 777. [Google Scholar]
- Kassem, W. Shear strength of squat walls: A strut-and-tie model and closed-form design formula. Eng. Struct. 2015, 84, 430–438. [Google Scholar] [CrossRef]
- Adorno-Bonilla, C.M. Shear Strength and Displacement Capacity of Squat Reinforced Concrete Shear Walls; University of Puerto Rico Mayagüez Campus: Mayagüez, Puerto Rico, 2016; p. 202. [Google Scholar]
- 318-14; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2014; p. 520. [CrossRef]
- ASCE/SEI 43-05; Seismic Design Criteria for Structures, Systems, and Components in Nuclear Facilities. American Society of Civil Engineers: Reston, VA, USA, 2005. [CrossRef]
- EN 1998-1; Eurocode 8—Design of Structures for Earthquake Resistance. CEN: Brussels, Belgium, 2004.
- Ma, J.; Li, B. Experimental and analytical studies on h-shaped reinforced concrete squat walls. ACI Struct. J. 2018, 115, 425–438. [Google Scholar] [CrossRef]
- Ma, J.; Li, B. Seismic Behavior of L-Shaped RC Squat Walls under Various Lateral Loading Directions. J. Earthq. Eng. 2019, 23, 422–443. [Google Scholar] [CrossRef]
- Del Carpio Ramos, M.; Whittaker, A.S.; Gulec, C.K. Predictive equations for the peak shear strength of low-aspect ratio reinforced concrete walls. J. Earthq. Eng. 2012, 16, 159–187. [Google Scholar] [CrossRef]
- Gulec, C.K.; Whittaker, A.S.; Stojadinovic, B. Peak shear strength of squat reinforced concrete walls with boundary barbells or flanges. ACI Struct. J. 2009, 106, 368–377. [Google Scholar] [CrossRef]
- Ma, J.; Ning, C.-L.; Li, B. Peak Shear Strength of Flanged Reinforced Concrete Squat Walls. J. Struct. Eng. 2020, 146, 04020037. [Google Scholar] [CrossRef]
- Gao, W.; Karbasi, M.; Derakhsh, A.M.; Jalili, A. Development of a novel soft-computing framework for the simulation aims: A case study. Eng. Comput. 2019, 35, 315–322. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.H.; Wu, X. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1992, 118, 1059. [Google Scholar] [CrossRef]
- Vanluchene, R.D.; Sun, R. Neural Networks in Structural Engineering. Comput. Civ. Infrastruct. Eng. 1990, 5, 207–215. [Google Scholar] [CrossRef]
- Flood, I.; Kartam, N. Artificial Neural Networks for Civil Engineers: Advanced Features and Applications; ASCE Publications: Reston, VA, USA, 1998; p. 300. [Google Scholar]
- Tran, V.L.; Kim, S.E. Efficiency of three advanced data-driven models for predicting axial compression capacity of CFDST columns. Thin-Walled Struct. 2020, 152, 106744. [Google Scholar] [CrossRef]
- Nguyen, M.S.T.; Thai, D.K.; Kim, S.E. Predicting the axial compressive capacity of circular concrete filled steel tube columns using an artificial neural network. Steel Compos. Struct. 2020, 35, 415–437. [Google Scholar] [CrossRef]
- Cao, X.; Sugiyama, Y.; Mitsui, Y. Application of artificial neural networks to load identification. Comput. Struct. 1998, 69, 63–78. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Pham, T.M.; Hadi, M.N.S. Predicting Stress and Strain of FRP-Confined Square/Rectangular Columns Using Artificial Neural Networks. J. Compos. Constr. 2014, 18, 04014019. [Google Scholar] [CrossRef] [Green Version]
- Chojaczyk, A.A.; Teixeira, A.P.; Neves, L.C.; Cardoso, J.B.; Guedes Soares, C. Review and application of Artificial Neural Networks models in reliability analysis of steel structures. Struct. Saf. 2015, 52, 78–89. [Google Scholar] [CrossRef]
- Salehi, H.; Burgueño, R. Emerging artificial intelligence methods in structural engineering. Eng. Struct. 2018, 171, 170–189. [Google Scholar] [CrossRef]
- Tran, V.L.; Thai, D.K.; Kim, S.E. Application of ANN in predicting ACC of SCFST column. Compos. Struct. 2019, 228, 111332. [Google Scholar] [CrossRef]
- Tran, V.L.; Thai, D.K.; Kim, S.E. A new empirical formula for prediction of the axial compression capacity of CCFT columns. Steel Compos. Struct. 2019, 33, 181–194. [Google Scholar] [CrossRef]
- Tran, V.L.; Kim, S.E. A practical ANN model for predicting the PSS of two-way reinforced concrete slabs. Eng. Comput. 2021, 37, 2303–2327. [Google Scholar] [CrossRef]
- Moradi, M.J.; Hariri-Ardebili, M.A. Developing a library of shear walls database and the neural network based predictive meta-model. Appl. Sci. 2019, 9, 2562. [Google Scholar] [CrossRef] [Green Version]
- Mangalathu, S.; Jang, H.; Hwang, S.H.; Jeon, J.S. Data-driven machine-learning-based seismic failure mode identification of reinforced concrete shear walls. Eng. Struct. 2020, 208, 110331. [Google Scholar] [CrossRef]
- Kabeyasawa, T.; Hiraishi, H. Tests and analyses of high-strength reinforced concrete shear walls in Japan. Am. Concr. Inst. ACI Spec. Publ. 1998, SP-176, 281–310. [Google Scholar]
- Lee, K.H.; Goel, S.C.; Stojadinovic, B. Boundary Effects in Welded Steel Moment Connections; University of Michigan: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Kim, T.; Whittaker, A.S.; Gilani, J.; Bertero, V.V.; Takhirov, S.M. Cover plate and flange plate steel moment resisting connections. J. Struct. Eng. 2002, 128, 474–482. [Google Scholar] [CrossRef]
- Gulec, C.K.; Whittaker, A.S. Performance-Based Assessment and Design of Squat Reinforced Concrete Shear Walls; State University of New York at Buffalo: Buffalo, NY, USA, 2009. [Google Scholar]
- Hwang, S.-J.; Fang, W.-H.; Lee, H.-J.; Yu, H.-W. Analytical Model for Predicting Shear Strengthof Squat Walls. J. Struct. Eng. 2001, 127, 43–50. [Google Scholar] [CrossRef]
- Wiradinata, S. Behavior of Squat Walls Subjected to Load Reversals; University of Toronto: Toronto, ON, Canada, 1985; p. 171. [Google Scholar]
- Mestyanek, J.M. The Earthquake Resistance of Reinforced Concrete Structural Walls of Limited Ductility; University of Canterbury: Christchurch, New Zealand, 1986. [Google Scholar]
- Hidalgo, P.A.; Ledezma, C.A.; Jordan, R.M. Seismic behavior of squat reinforced concrete shear walls. Earthq. Spectra 2002, 18, 287–308. [Google Scholar] [CrossRef]
- Bimschas, M. Displacement Based Seismic Assessment of Existing Bridges in Regions of Moderate Seismicity. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2010. [Google Scholar]
- Saatcioglu, M. Hysteretic Shear Response of Low-Rise Walls. In Proceedings of the Concrete Shear in Earthquake: International Workshop on Concrete Shear in Earthquake, Houston, TX, USA, 13–16 January 1991; pp. 105–114. [Google Scholar]
- Salonikios, T.N.; Kappos, A.J.; Tegos, I.A.; Penelis, G.G. Cyclic load behavior of low-slenderness reinforced concrete walls: Design basis and test results. ACI Struct. J. 1999, 96, 649–660. [Google Scholar] [CrossRef]
- Salonikios, T.N.; Kappos, A.J.; Tegos, I.A.; Penelis, G.G. Cyclic load behavior of low-slenderness reinforced concrete walls: Failure modes, strength and deformation analysis, and design implications. ACI Struct. J. 2000, 97, 132–141. [Google Scholar] [CrossRef]
- Luna, B.N.; Rivera, J.P.; Whittaker, A.S. Seismic behavior of low-aspect-ratio reinforced concrete shear walls. ACI Struct. J. 2015, 112, 593–603. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.Y.; Hung, S.C.; Lequesne, R.D.; Lepage, A. Earthquake-resistant squat walls reinforced with high-strength steel. ACI Struct. J. 2016, 113, 1065–1076. [Google Scholar] [CrossRef]
- Baek, J.-W.; Park, H.-G.; Shin, H.-M.; Yim, S.-J. Cyclic Loading Tests for Reinforced Concrete Walls (Aspect Ratio 2.0) with Grade 550 MPa (80 ksi) Shear Reinforcing Bars. ACI Struct. J. 2017, 114, 673–686. [Google Scholar] [CrossRef]
- Pilakoutas, K.; Elnashai, A. Cyclic Behavior of RC Cantilever Walls, Part I: Experimental Results. ACI Struct. J. 1995, 92, 271–281. [Google Scholar] [CrossRef]
- Paulay, T.; Priestley, M.J.N. Ductility in Earth-quake Resisting Squat Shearwalls. ACI J. Proc. 1982, 79, 257–269. [Google Scholar]
- Beekhuis, W.J. An Experimental Study of Squat Shear Walls; University of Canterbury. Engineering: Christchurch, New Zealand, 1971; Volume 1971. [Google Scholar]
- Lopes, M.S. Experimental shear-dominated response of RC walls Part I: Objectives, methodology and results. Eng. Struct. 2001, 23, 229–239. [Google Scholar] [CrossRef]
- Lopes, M.S. Experimental shear-dominated response of RC walls. Part II: Discussion of results and design implications. Eng. Struct. 2001, 23, 564–574. [Google Scholar] [CrossRef]
- Carrillo, J.; Alcocer, S.M. Shear strength of reinforced concrete walls for seismic design of low-rise housing. ACI Struct. J. 2013, 110, 415–425. [Google Scholar] [CrossRef]
- Peng, Y.; Wu, H.; Zhuge, Y. Strength and drift capacity of squat recycled concrete shear walls under cyclic loading. Eng. Struct. 2015, 100, 356–368. [Google Scholar] [CrossRef]
- Farvashany, F.E.; Foster, S.J.; Rangan, B.V. Strength and deformation of high-strength concrete shearwalls. ACI Struct. J. 2008, 105, 21–29. [Google Scholar] [CrossRef]
- Gupta, A.; Rangan, B.V. Studies on Reinforced Concrete Structural Walls; Res. Rep. No. 2/96; School of Civil Engineering, Curtin University of Technology: Perth, Australia, 1996. [Google Scholar]
- Lefas, I.D.; Kotsovos, M.D.; Ambraseys, N.N. Behavior of reinforced concrete structural walls. Strength, deformation characteristics, and failure mechanism. ACI Struct. J. 1990, 87, 23–31. [Google Scholar] [CrossRef]
- Maier, J.; Thürlimann, B. Bruchversuche an Stahlbeton-Scheiben; ETH Zurich: Zürich, Switzerland, 1985. [Google Scholar]
- Looi, D.T.W.; Su, R.K.L.; Cheng, B.; Tsang, H.H. Effects of axial load on seismic performance of reinforced concrete walls with short shear span. Eng. Struct. 2017, 151, 312–326. [Google Scholar] [CrossRef]
- Li, B.; Pan, Z.; Xiang, W. Experimental evaluation of seismic performance of squat RC structural walls with limited ductility reinforcing details. J. Earthq. Eng. 2015, 19, 313–331. [Google Scholar] [CrossRef]
- Whyte, C.A.; Stojadinovic, B. Effect of Ground Motion Sequence on Response of Squat Reinforced Concrete Shear Walls. J. Struct. Eng. 2014, 140, A4014004. [Google Scholar] [CrossRef]
- Xu, M.; Chen, Z.; Zhang, W. Experimental study on the seismic behavior of concrete composite bearing walls. Adv. Mater. Res. 2011, 163–167, 1090–1095. [Google Scholar] [CrossRef]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley and Sons: New York, NY, USA, 1975. [Google Scholar]
- Teodorescu, L.; Sherwood, D. High Energy Physics event selection with Gene Expression Programming. Comput. Phys. Commun. 2008, 178, 409–419. [Google Scholar] [CrossRef]
- Kose, M.M.; Kayadelen, C. Modeling of transfer length of prestressing strands using genetic programming and neuro-fuzzy. Adv. Eng. Softw. 2010, 41, 315–322. [Google Scholar] [CrossRef]
- Tariq, M.; Khan, A.; Shayanfar, J.; Hanif, M.U.; Ullah, A. A regression model for predicting the shear strength of RC knee joint subjected to opening and closing moment. J. Build. Eng. 2021, 41, 102727. [Google Scholar] [CrossRef]
- Tariq, M.; Khan, A.; Ullah, A.; Shayanfar, J.; Niaz, M. Improved Shear Strength Prediction Model of Steel Fiber Reinforced Concrete Beams by Adopting Gene Expression Programming. Materials 2022, 15, 3758. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Ahmad, F.; Wróblewski, P.; Al-Mansob, R.A.; Olczak, P.; Kamiński, P.; Safdar, M.; Rai, P. Prediction of ultimate bearing capacity of shallow foundations on cohesionless soils: A gaussian process regression approach. Appl. Sci. 2021, 11, 317. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.; Ahmad, F. Evaluation of Liquefaction-Induced Settlement Using Random Forest and REP Tree Models: Taking Pohang Earthquake as a Case of Illustration. In Natural Hazards—Impacts, Adjustments and Resilience; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Ahmad, M.; Tang, X.W.; Qiu, J.N.; Ahmad, F.; Gu, W.J. Application of machine learning algorithms for the evaluation of seismic soil liquefaction potential. Front. Struct. Civ. Eng. 2021, 15, 490–505. [Google Scholar] [CrossRef]
- Ahmad, M.; Hu, J.L.; Hadzima-Nyarko, M.; Ahmad, F.; Tang, X.W.; Rahman, Z.U.; Nawaz, A.; Abrar, M. Rockburst hazard prediction in underground projects using two intelligent classification techniques: A comparative study. Symmetry 2021, 13, 632. [Google Scholar] [CrossRef]
- Ahmad, F.; Tang, X.W.; Qiu, J.N.; Wróblewski, P.; Ahmad, M.; Jamil, I. Prediction of slope stability using Tree Augmented Naive-Bayes classifier: Modeling and performance evaluation. Math. Biosci. Eng. 2022, 19, 4526–4546. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Al-Mansob, R.A.; Jamil, I.; Al-Zubi, M.A.; Sabri, M.M.S.; Alguno, A.C. Prediction of Rockfill Materials’ Shear Strength Using Various Kernel Function-Based Regression Models—A Comparative Perspective. Materials 2022, 15, 1739. [Google Scholar] [CrossRef]
- Ahmad, M.; Hu, J.L.; Ahmad, F.; Tang, X.W.; Amjad, M.; Iqbal, M.J.; Asim, M.; Farooq, A. Supervised learning methods for modeling concrete compressive strength prediction at high temperature. Materials 2021, 14, 1983. [Google Scholar] [CrossRef]
- Ahmad, M.; Amjad, M.; Al-Mansob, R.A.; Kamiński, P.; Olczak, P.; Khan, B.J.; Alguno, A.C. Prediction of Liquefaction-Induced Lateral Displacements Using Gaussian Process Regression. Appl. Sci. 2022, 12, 1977. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).