1. Introduction
The development of mold and/or condensation on the surface of building barriers are physical phenomena that occur in various types of buildings, mainly on their internal surfaces. These phenomena are harmful to the functioning of building barriers, but also to residents or users due to mold fungi growing on their surface [
1]. They cause the formation of disease entities such as allergies and allergic reactions in humans and animals, and the occurrence of a specific smell.
These phenomena occurred very sporadically in the past; nowadays they are quite common in buildings for various reasons [
2,
3,
4]. In the current period, when buildings with a higher number of sealed off areas and thermal insulation of external barriers are erected (more comfortable barriers due to the higher temperature of their internal surfaces), these phenomena appear more often and are even more disturbing [
5].
The reasons for these phenomena have been described in the article on alternative methods of determining mold risk [
5]. These include: external climate [
6], construction [
7], geometry, technology, and quality of the barrier [
8,
9], and the internal microclimate [
10,
11]. In addition, the way the rooms are used, the arrangement of the furniture and their installation can affect surface condensation and mold growth on the interior surfaces of the walls. In the article [
12] an analysis of thermal conditions occurring around built-in furniture in living rooms was carried out. The analysis covered both the summer and winter periods, because during these periods there was a phenomenon of condensation and mold on the internal surfaces of the walls from the construction side. The results confirm that the impact of mold on the internal surface of the walls is influenced by the way the residents use the rooms, as well as the lack of adequate ventilation between the wall surface and furniture. Increasing the temperature of the inner wall surface above 16 °C would reduce the risk of condensation on this surface [
12]. In general terms, it comes down to the relationship that occurs between the parameters of the internal microclimate affecting the barrier and temperatures on the surface of the barrier. If mold growth occurs on the barrier surface and the standard parameters of the internal microclimate are maintained, the reason for this phenomenon is usually on the side of the building barrier. The opposite situation may occur when the barrier has standard parameter. The reason then is usually on the side of the internal microclimate. It is often difficult to indicate one cause, as the occurrence of mold growth can be caused by both the building barrier and the internal microclimate. In any case of mold, corrective actions must be taken to eliminate the cause. When the problem of condensation appears in the barrier, various solutions should be applied to repair or modify the structure of the barrier [
8,
13], at the same time stabilizing the temperature of the internal surface of the barrier, and additives may be applied to modify this barrier [
14,
15]. Such solutions will also improve the indoor climate, reducing room temperature fluctuations.
Over the past decades, the approach to the design of building barriers has changed in terms of avoiding surface condensation. The standard requirements are also changing, which, due to the need to reduce CO2 emissions to the atmosphere, require newly designed buildings to be more airtight and have better thermal insulation. At the same time, there are still older facilities that do not meet the requirements for new facilities. That is why (with a similar method of use) older buildings function differently due to the lower insulation of external barriers and windows which are not well sealed, as opposed to new buildings with high insulation of external barriers and very well-sealed windows.
In older buildings, a frequent cause of condensation was the thermal bridges at the junctions of the external walls with the horizontal structural elements of the building [
16,
17].
Currently, the problem is among others, the risk of condensation forming on the outer surface of the window. The authors in article [
18] linked the increase in condensation on the external surface to the increase in the insulation of these windows and climate change. To reduce the formation of condensation, additional shading elements on the windows directed towards the sky have been proposed, which would limit the condensation of water vapor on the external surface of the glazing in the morning. In the article [
19], the authors attempted to determine the rate of surface condensation on cold glazed surfaces of building elements. The tests were carried out in a full-sized test chamber, using imaging techniques to analyze the appearance and increase of surface condensation on glazed surfaces.
The type of window frame used has an additional effect on the formation of condensation and mold. Appropriate use of profile types will reduce the risk of the above problem. In the article [
20], the authors, using computer simulations, compared different types of window frames to assess the risk of surface condensation on the example of double-sliding double-glazed windows.
The thermoplastic spacer with its size optimization and the insulation cover inserted into the window frame and window frame size were evaluated. The biggest impact on reducing the risk of condensation is the introduction of a spacer with a smaller area with an enlarged air gap between the panes and an increase in the size of the window frame. Both of these elements favorably increase the temperature in the areas where the glazing joins the frame.
The problem of mold growth and surface condensation appears periodically, often in buildings after retrofitting of external barriers. This condition is worrying because these phenomena, instead of disappearing completely, actually get worse in some cases. The task to be considered is the adoption of such a method of checking the functioning of the heat and humidity processes of the barrier as to allow a reliable assessment of the possibility of surface condensation and mold growth on the surface of the building component under certain climatic conditions and of the internal microclimate.
To analyze the above problem, various methods can now be used, such as computational [
18], experimental [
8,
19], and computer simulations [
21,
22,
23].
Currently, according to PN-EN ISO 13788 [24], to check the development of mold on the surface of a building barrier, one method is defined and acceptable, while there are no other alternative methods in this area. The method given in the standard [
24] boils down to a comparison of two temperature factors: the temperature factor
fRsi resulting from the insulation of the barrier (its construction), and the factor
fRsi,max resulting from the humidity conditions prevailing in the room in the so-called critical month. In order to meet the design condition (to eliminate the risk of mold growth), the minimum thermal insulation of the barrier
RT,min or the maximum value of the heat transfer coefficient
Umax need to be calculated. In practice, this involves the need to modernize the barrier, which in turn leads to the generation of costs for the task.
Considering the above, an attempt was made to compare different conditions for mold development and surface condensation and to define when a given phenomenon occurs, when it starts and when it does not occur. Then, for each condition of the occurrence of the relevant phenomenon, what is to be done to eliminate it is given, and calculation algorithms for how to implement it are given. Presented, among others, is the applicable standard condition related to the fRsi parameter, the calculation of internal humidity φi, humidity of the beginning of condensation φi,con, the permissible humidity in the room φi,max, with observance of the standard condition to avoid mold growth, the external temperature eliminating condensation Θe,con, and the minimum thermal insulation of the barrier eliminating condensation Ucon.
3. Results and Discussion
For the verification of the presented calculation methods for mold development and surface condensation, the following data was adopted: outdoor air temperature,
Θe, and relative humidity of the outdoor air
φe, according to the Rzeszów-Jasionka meteorological station [
25], indoor air temperature
Θi = 20 °C, moisture increase in a room for the 4th class of internal humidity Δ
p = 10.8 hPa [
24], external wall (50 cm thick made of solid brick) with a heat transfer coefficient
U = 1.20 W/(m
2.K); heat transfer resistance on the internal surface of the barrier
Rsi = 0.25 (m
2K)/W [
24]. Data for calculations are presented in
Table 5.
To illustrate the boundary conditions of a given method for each of the two phenomena, all necessary parameters for the twelve consecutive months of the year were calculated and presented in
Table 6 and
Table 7, respectively.
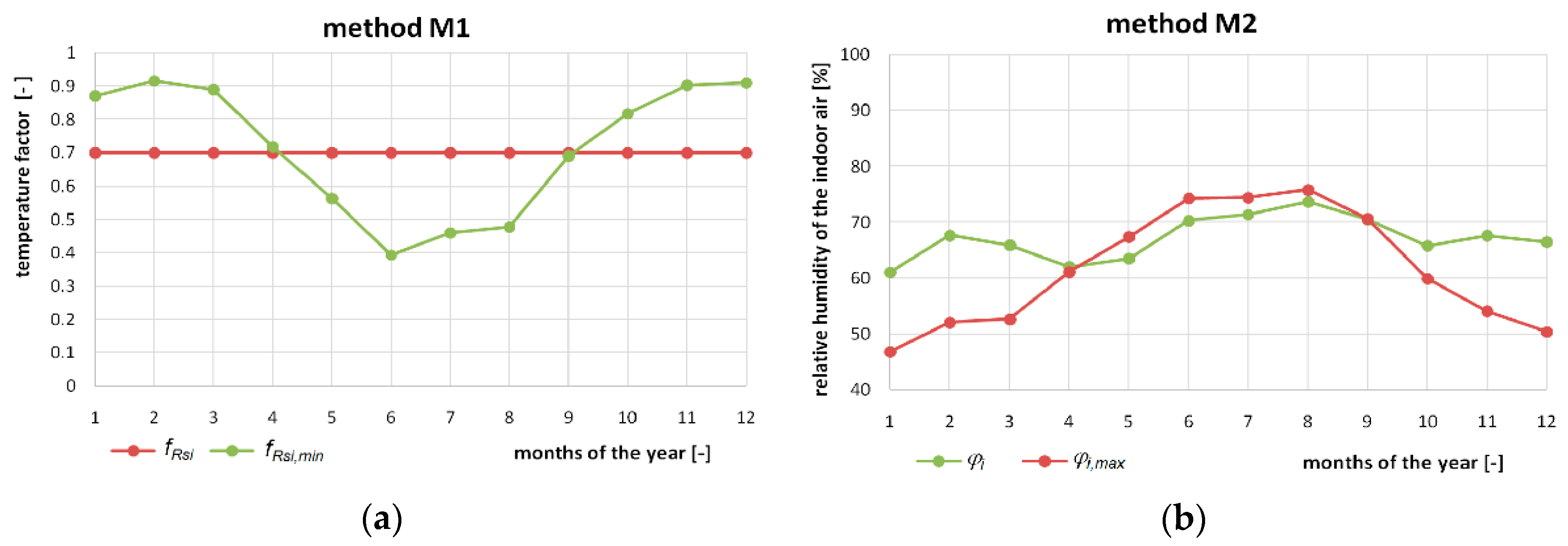
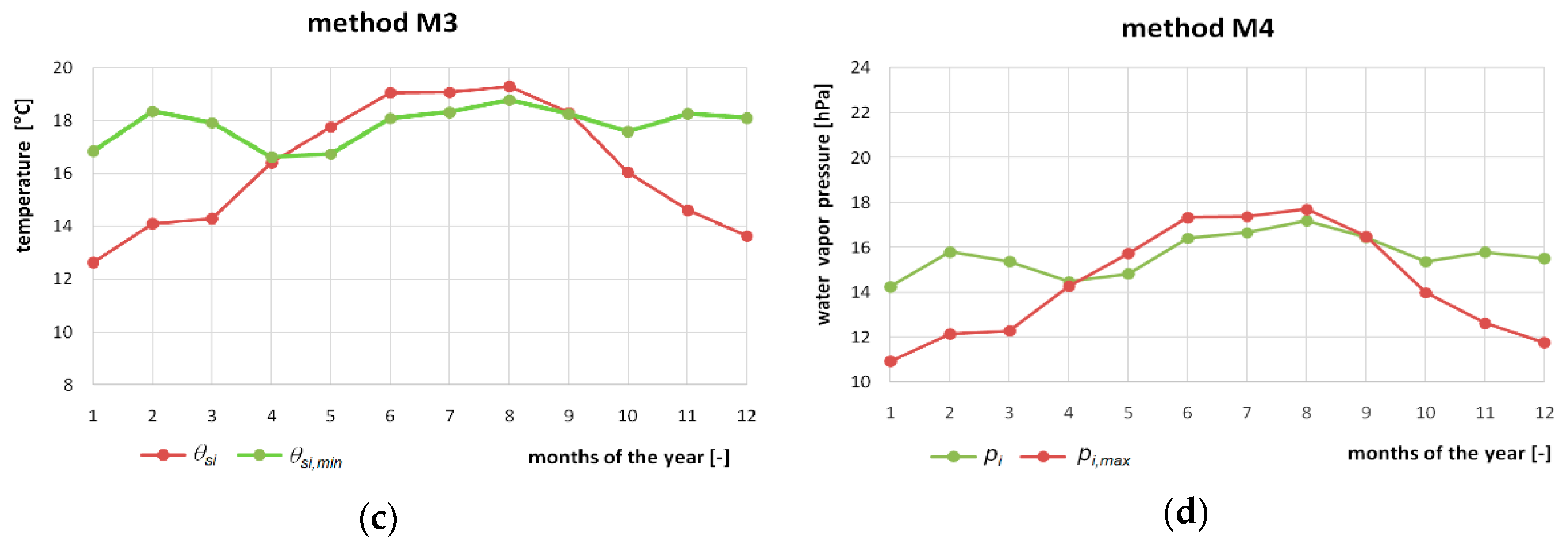
In the phenomenon of mold development, the characteristic parameters resulting from the insulation of the building barrier are: temperature factor of the barrier
fRsi; barrier temperature
Θsi; maximum water vapor pressure in the room
pi,max; maximum relative air humidity in the room
φi,max, while for the indoor microclimate it is: minimum permissible barrier temperature factor,
fRsi,min; minimum permissible barrier temperature
Θsi,min; water vapor pressure in the
pi room; relative air humidity in the room
φi, (
Table 6).
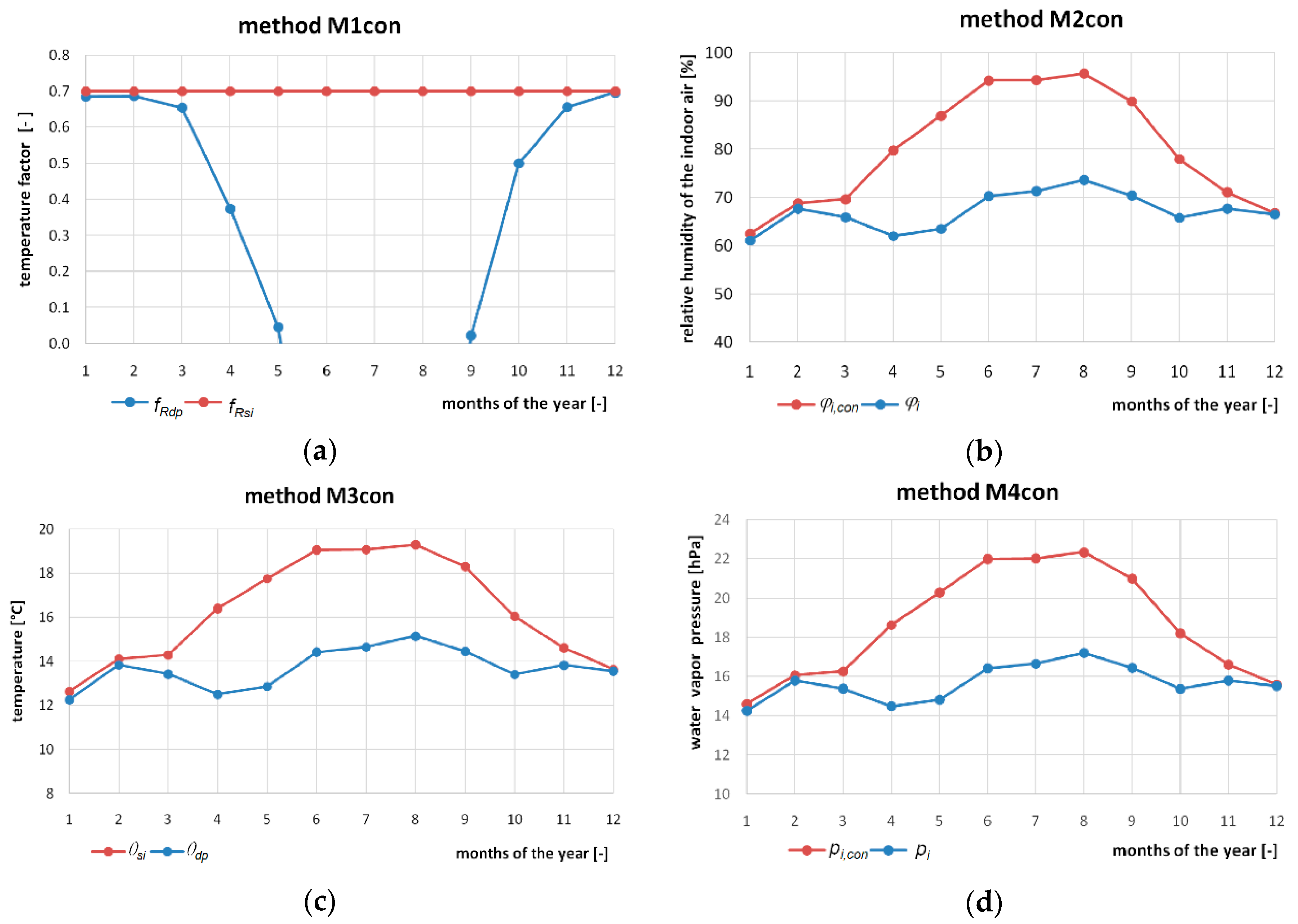
In the phenomenon of surface condensation, the characteristic parameters resulting from the insulation of a building barrier are: the temperature factor of the barrier
fRsi; barrier temperature,
Θsi; condensation pressure of water vapor
pi,con; condensation humidity in the room,
φi,con, while for the internal microclimate it is: barrier temperature factor
fRdp; dew point temperature
Θdp; water vapor pressure in the
pi room; relative air humidity in the room
φi, (
Table 7).
By comparing the relevant parameters characterizing the building barrier with the parameters characterizing the internal microclimate, all boundary conditions for mold development listed in
Table 1 and
Table 2 and for surface condensation given in
Table 3 and
Table 4 were checked. Thus, the state of the phenomenon (its occurrence or absence) was determined and the results were presented in
Table 7 and
Table 8 respectively.
3.1. Mold Growth on the Surface of the Barrier
Table 6 shows the calculated values of all necessary parameters to check mold growth for four methods in the twelve consecutive months of the year.
Table 9 presents the values of parameters necessary to check the boundary conditions of mold development for four methods in the twelve consecutive months of the year.
A graphic interpretation of the characteristic parameters for four methods in the phenomenon of mold development is shown in
Figure 1. The intersecting lines in the charts show the occurrence of the phenomenon of mold development.
3.2. Condensation on the Surface of the Barrier
Table 7 shows the calculated values of all necessary parameters needed to check surface condensation for four methods in the twelve consecutive months of the year.
Table 8 presents the necessary parameters to check the surface condensation boundary conditions for four methods in the twelve consecutive months of the year.
A graphic interpretation of the characteristic parameters for the four methods in the phenomenon of surface condensation is shown in
Figure 2. The non-intersecting lines in the charts show that there is no surface condensation.