Optimization of Hot Stamping Parameters for Aluminum Alloy Crash Beams Using Neural Networks and Genetic Algorithms
Abstract
1. Introduction
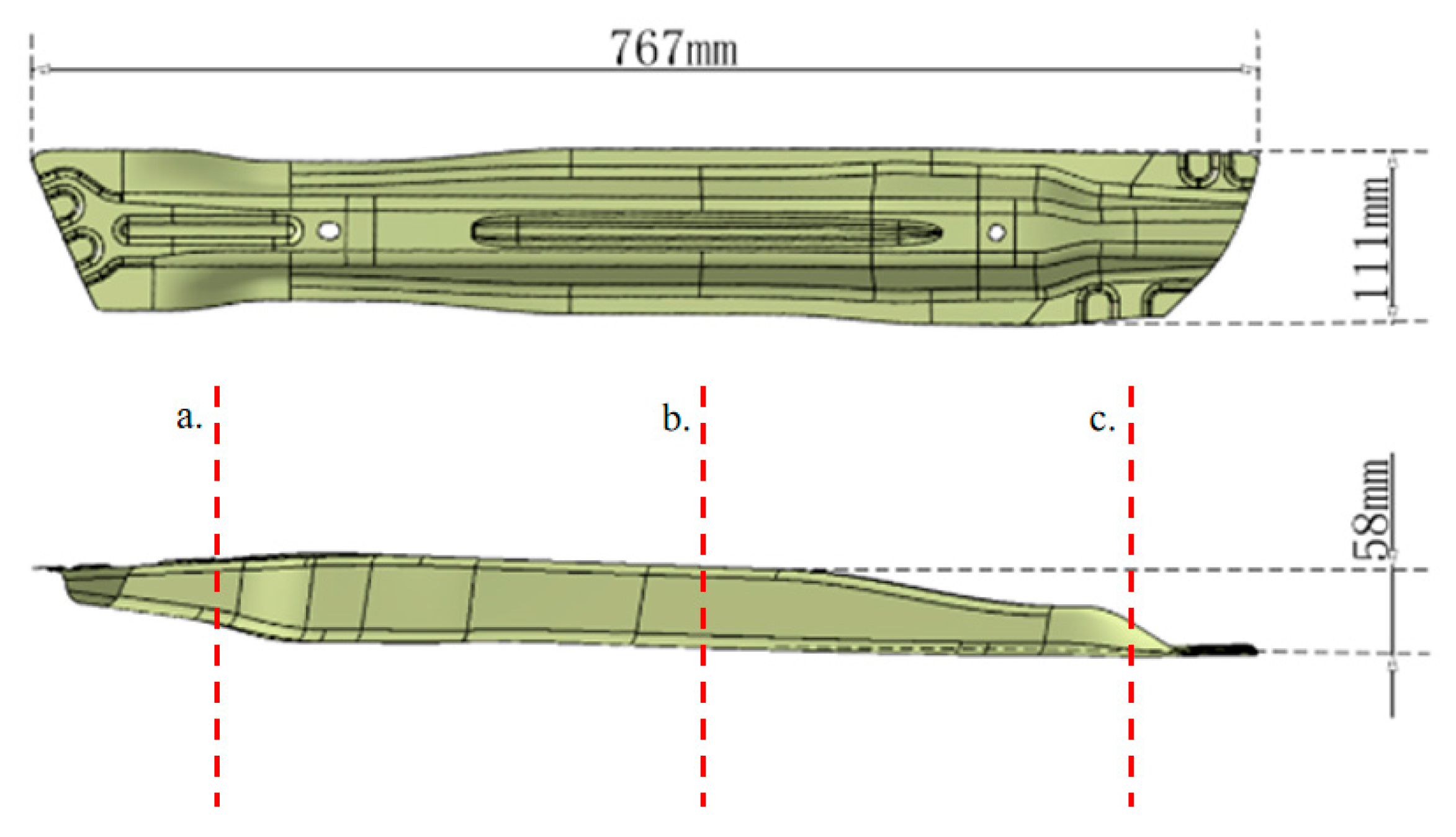
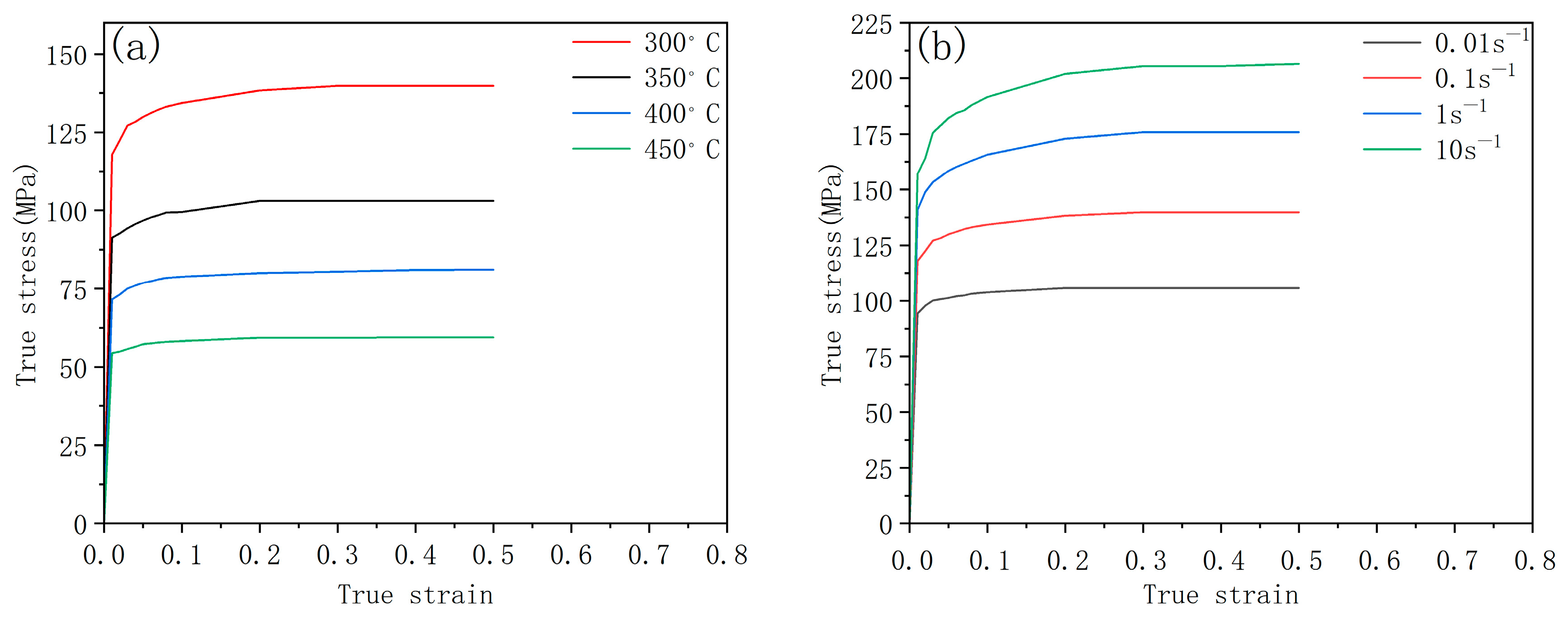
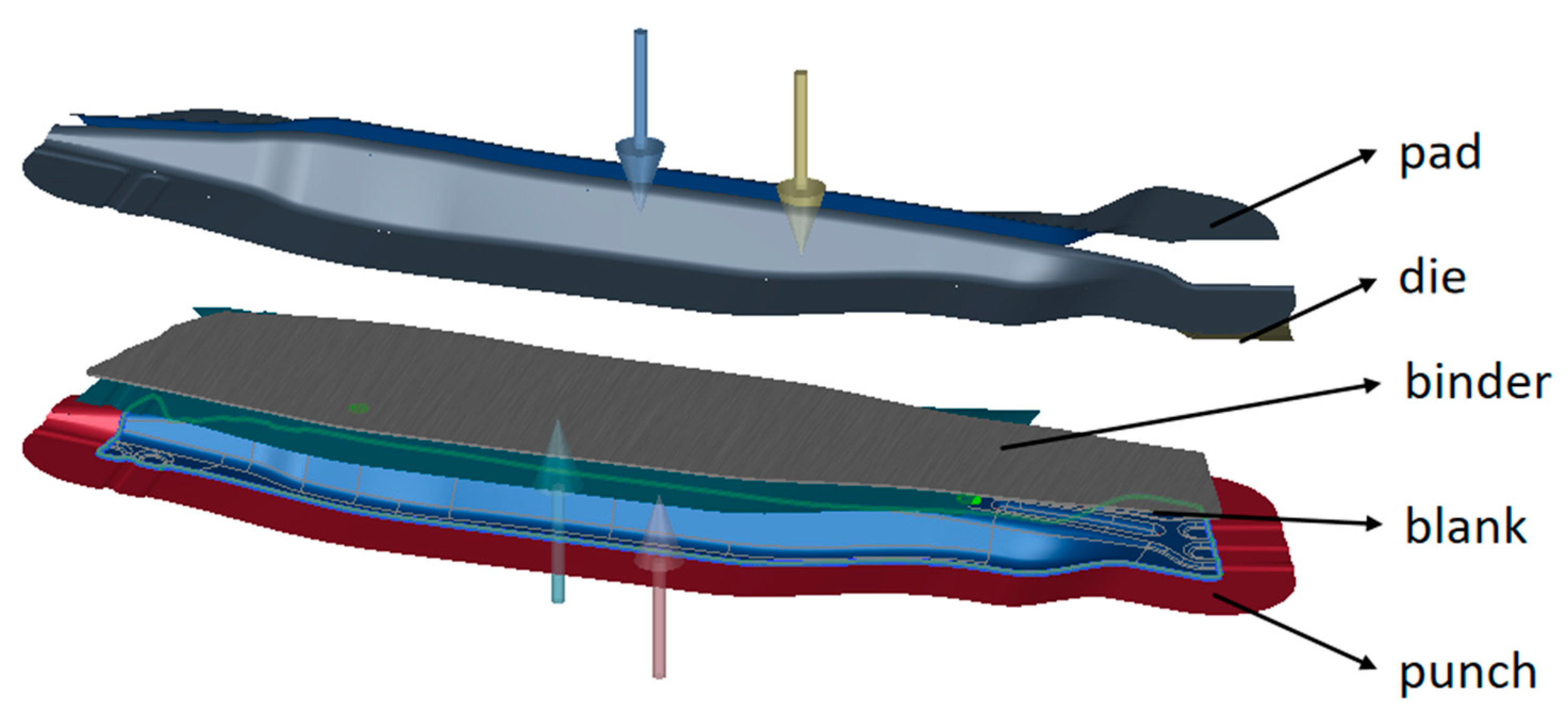
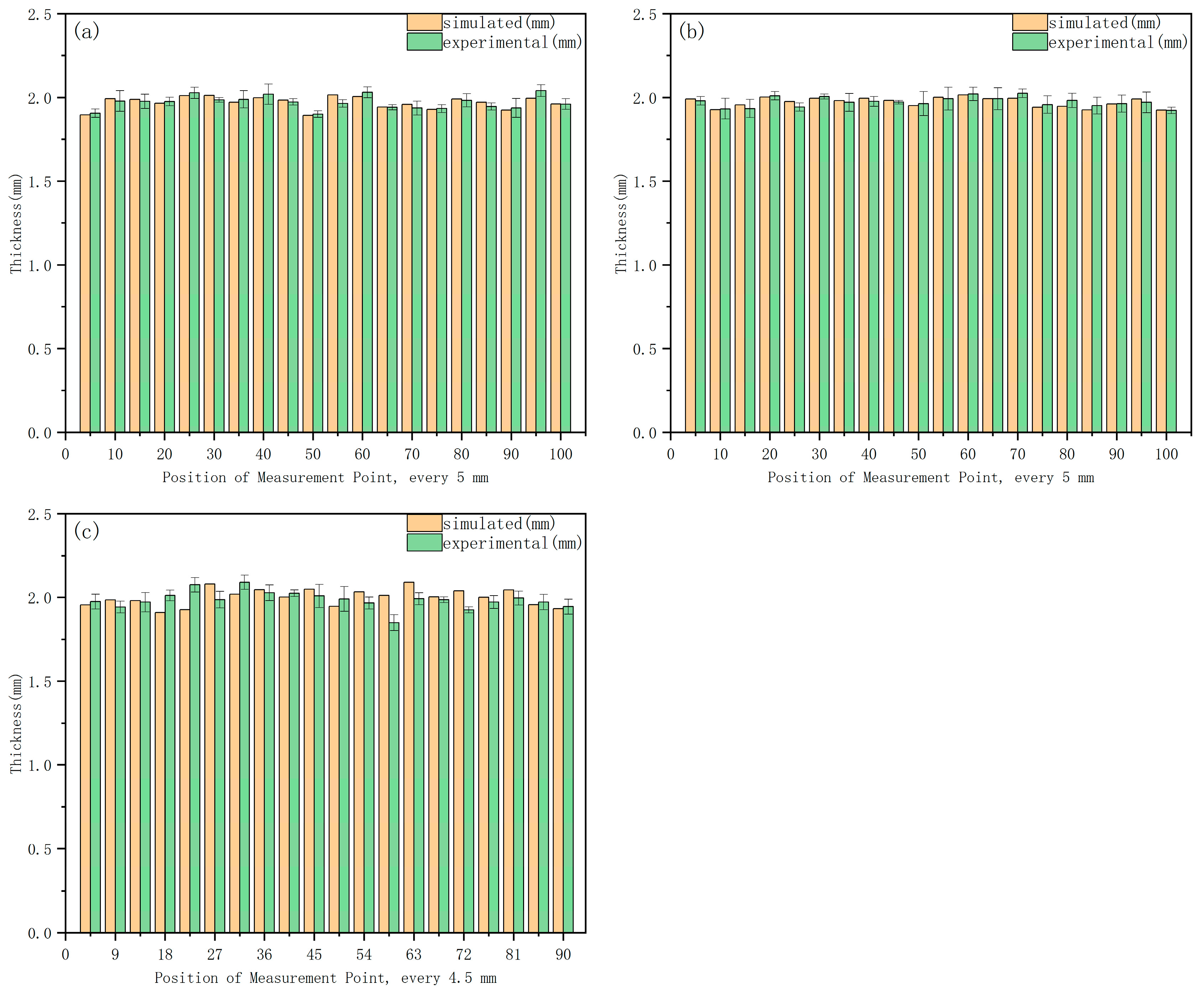
2. Finite Element Model of Crash Beam Hot Stamping
3. Development of BP Neural Network Prediction Model
3.1. Data Acquisition and Preprocessing
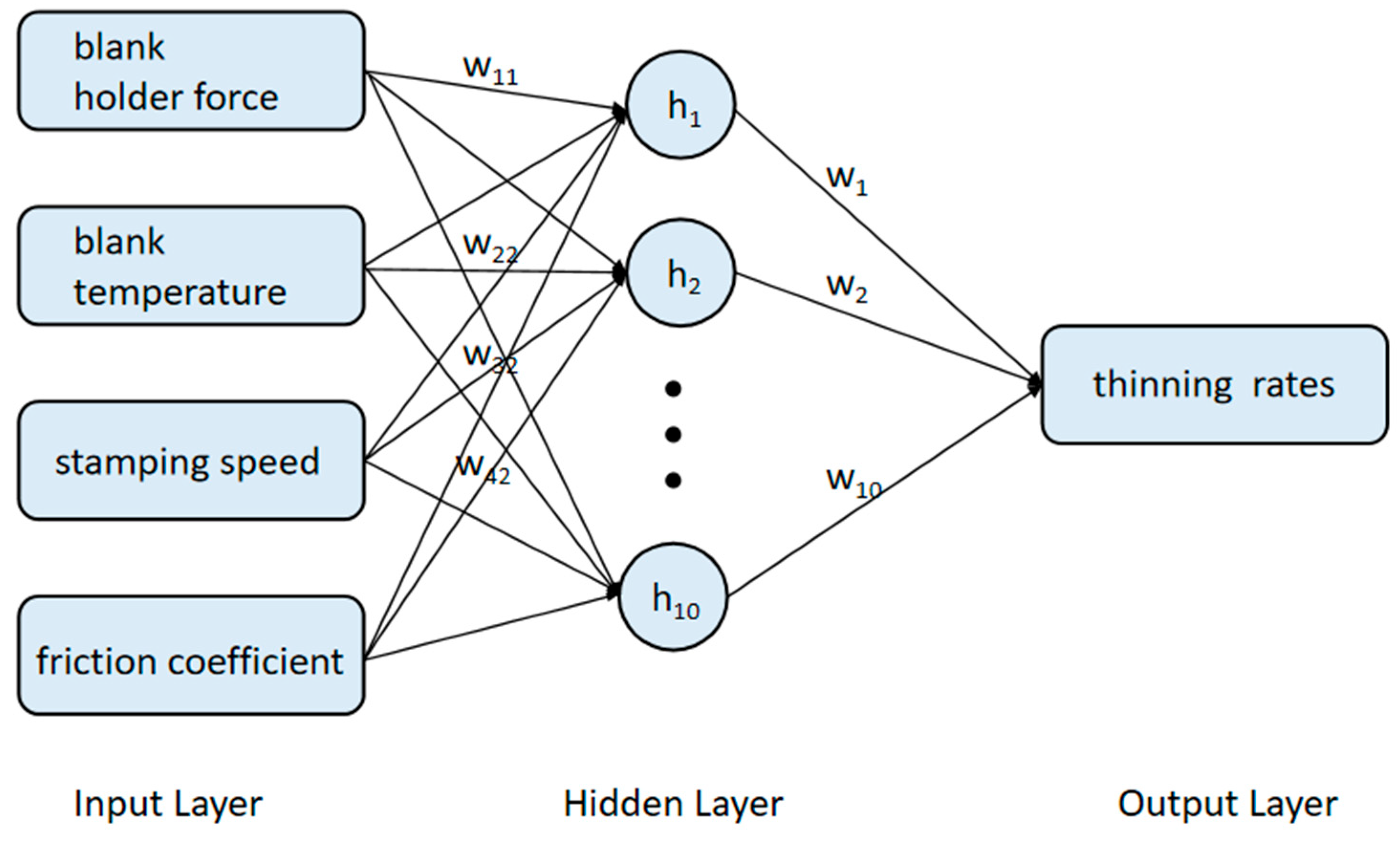
3.2. Development and Training of BP Prediction Model
3.3. Prediction and Evaluation
4. Model Optimization
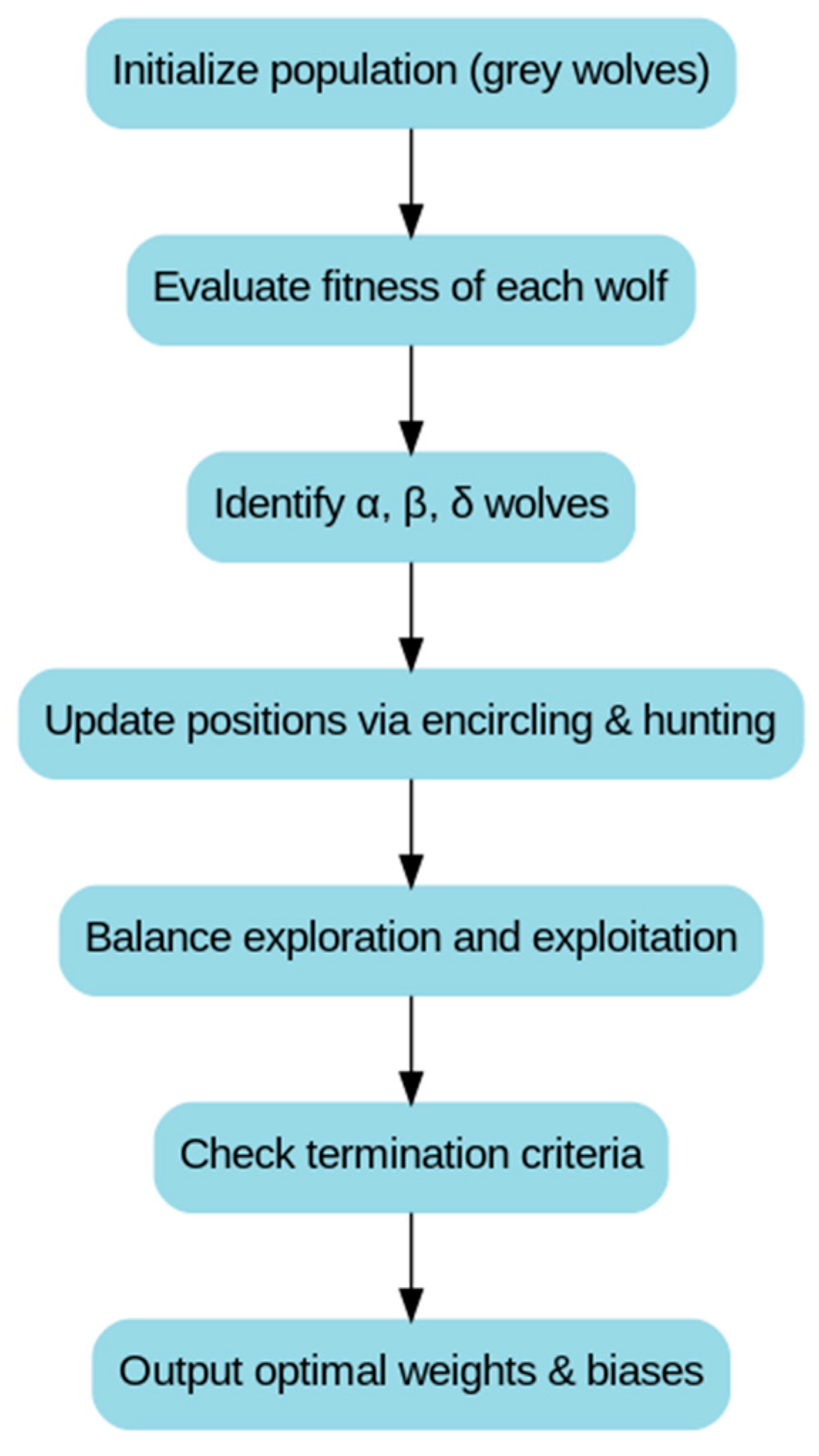
4.1. Grey Wolf Optimizer (GWO)
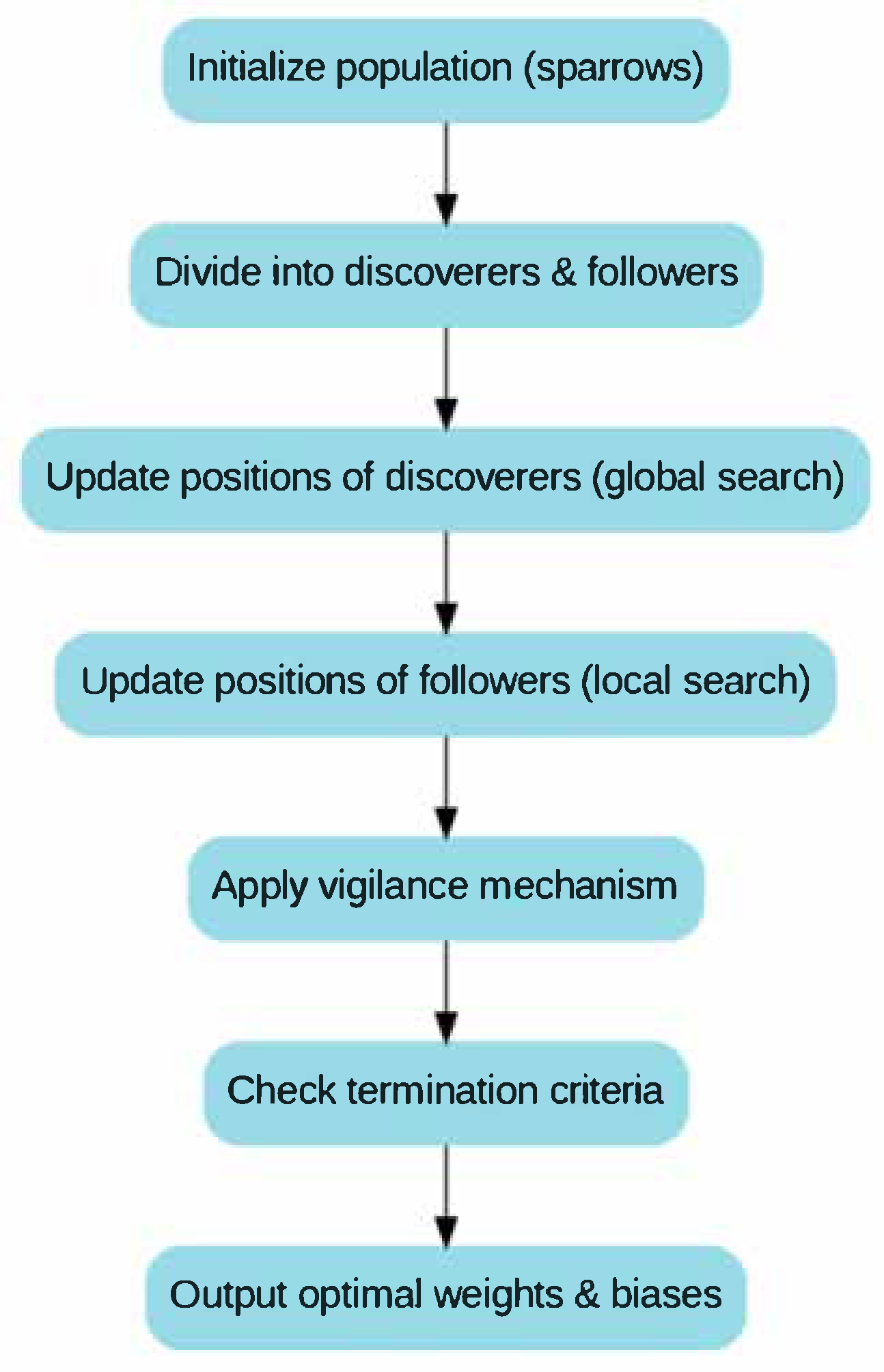
4.2. Sparrow Search Algorithm (SSA)
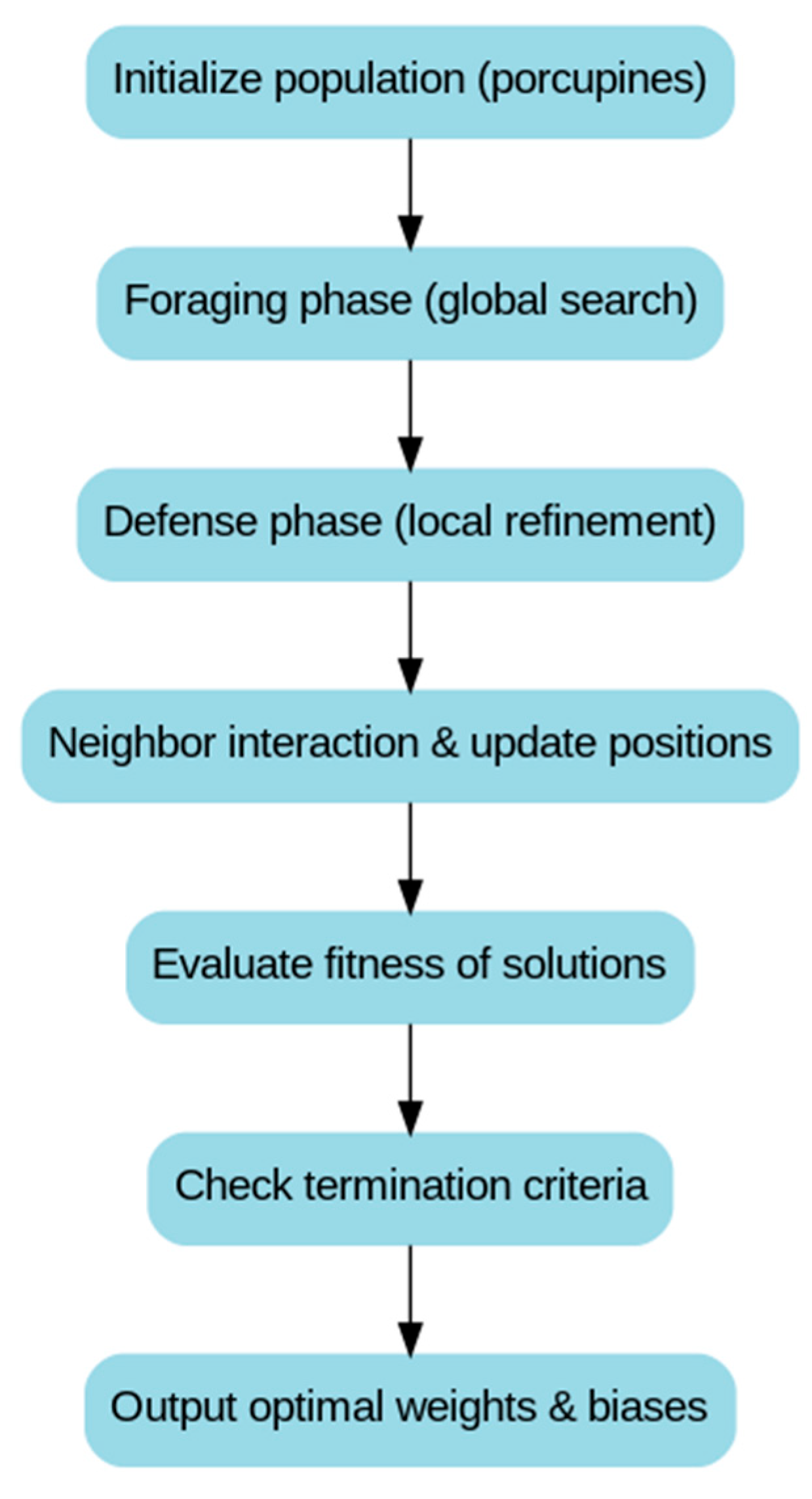
4.3. Crested Porcupine Optimization (CPO)
4.4. Goose Optimization Algorithm (GOOSE)
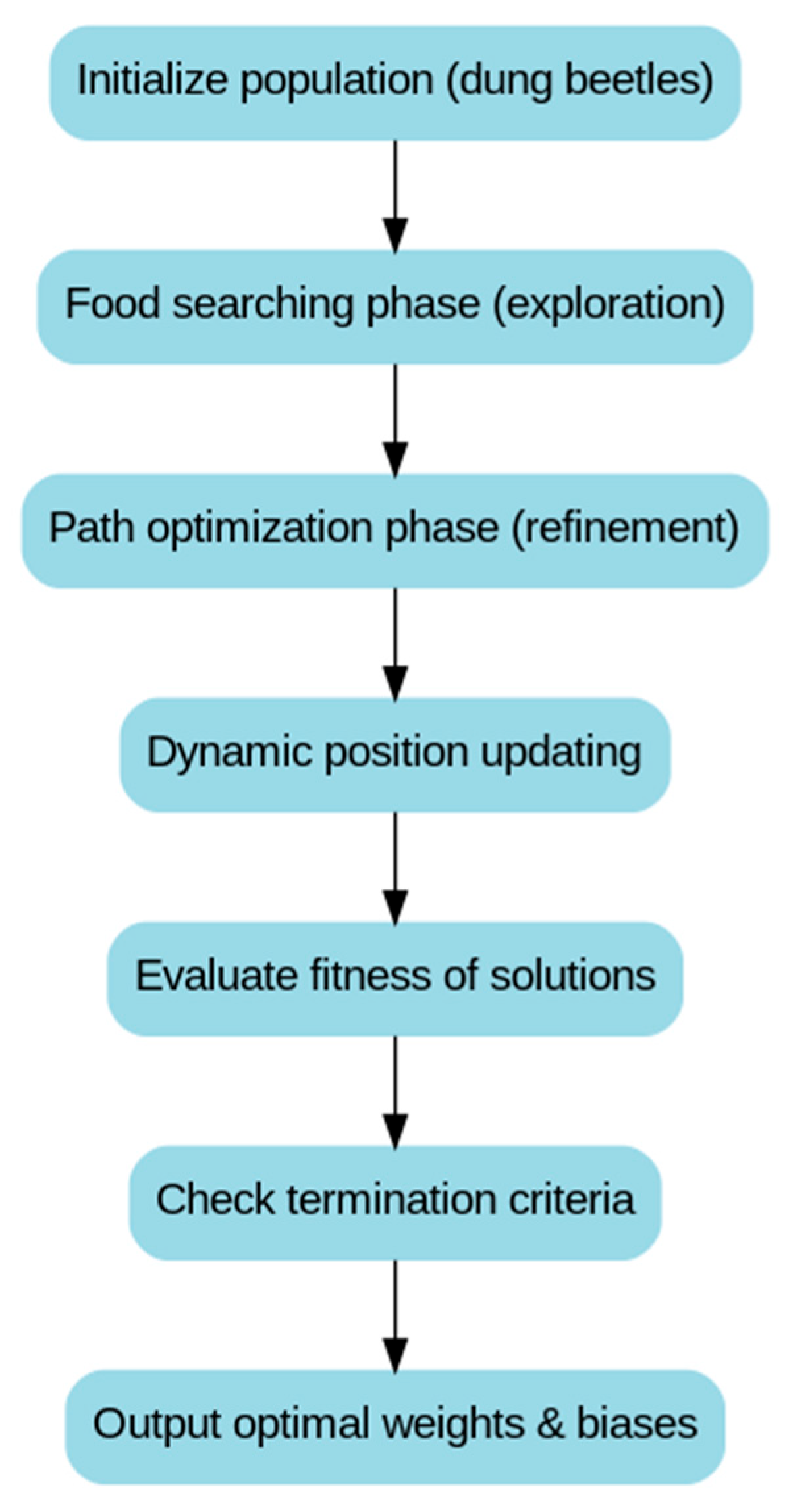
4.5. Dung Beetle Optimization (DBO)
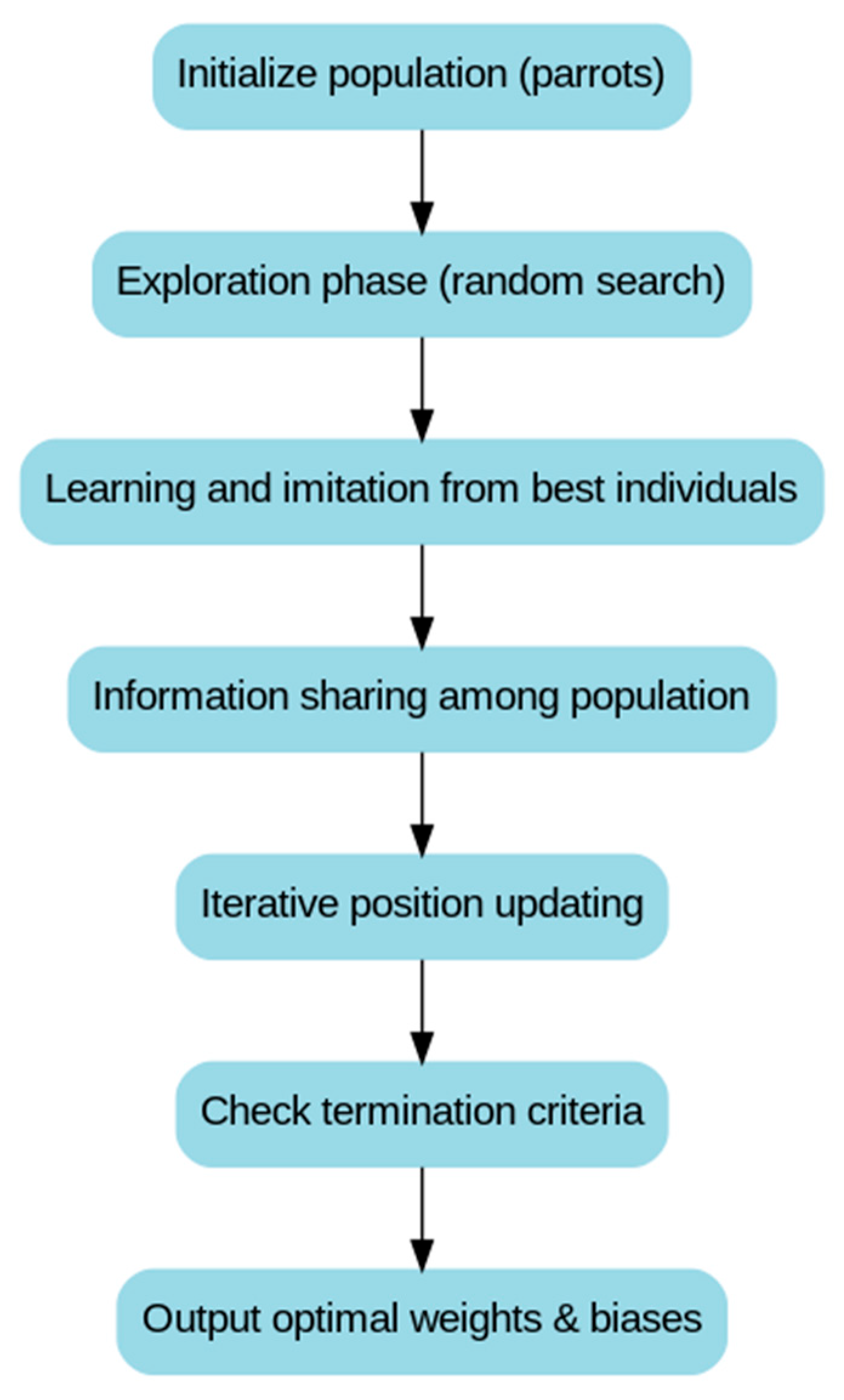
4.6. Parrot Optimization (PO)
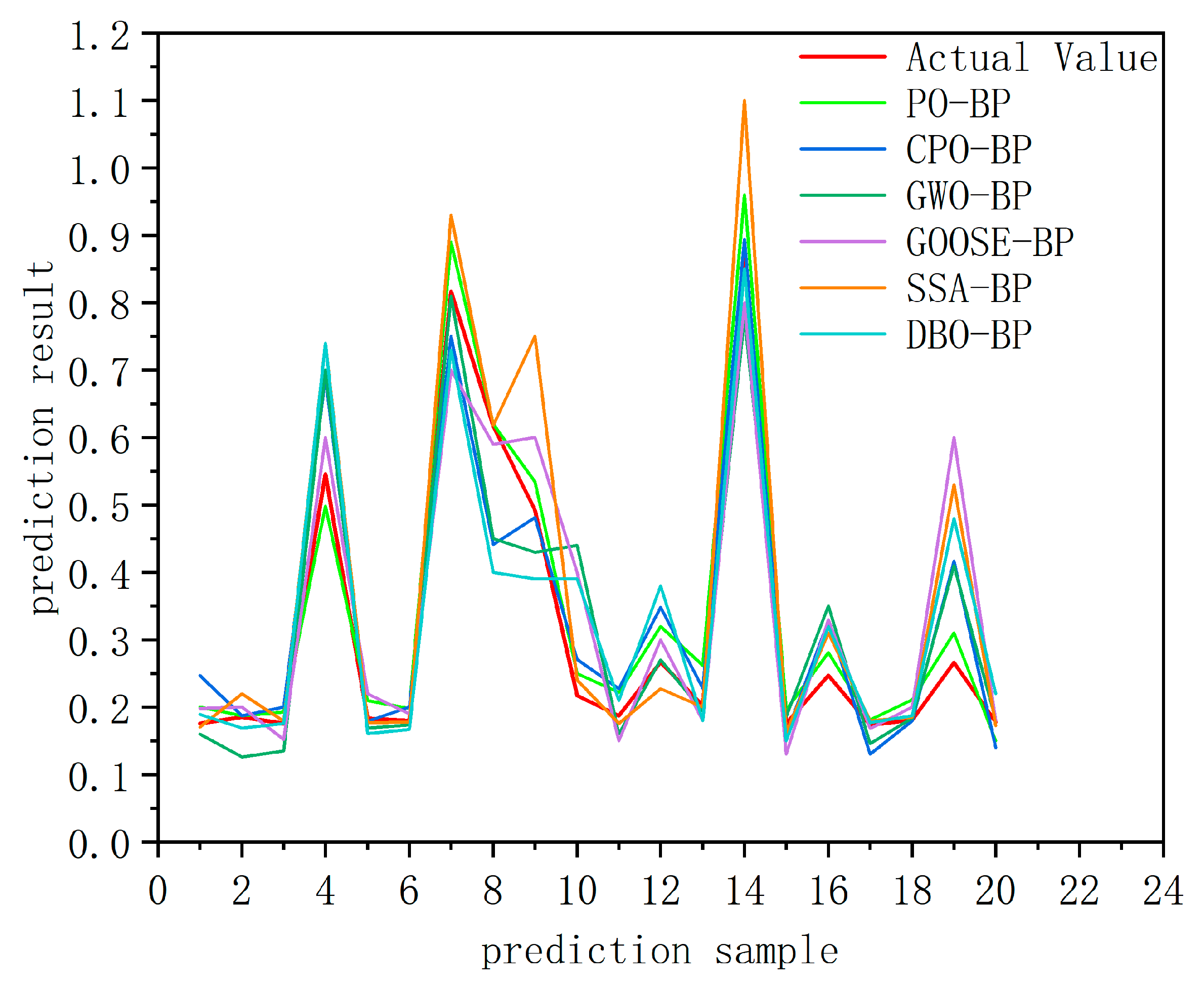
4.7. The Prediction Results of the Models
5. Genetic Algorithm of Process Parameters
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Z.; Jia, P.; Liu, W.; Yin, H. Car ownership and urban development in Chinese cities: A panel data analysis. J. Transp. Geogr. 2017, 58, 127–134. [Google Scholar] [CrossRef]
- Zhang, J.; Ning, Y.L.; Peng, B.D.; Wang, Z.H.; Bi, D.S. Numerical simulation of the stamping forming process of alloy automobile panel. In Proceedings of the 6th International Conference on Physical and Numerical Simulation of Materials Processing (ICPNS), Guilin, China, 16–19 November 2010. [Google Scholar]
- Al-Alimi, S.; Yusuf, N.K.; Ghaleb, A.M.; Lajis, M.A.; Shamsudin, S.; Zhou, W.; Altharan, Y.M.; Saif, Y.; Didane, D.H.; Adam, A.; et al. Recycling aluminium for sustainable development: A review of different processing technologies in green manufacturing. Results Eng. 2024, 23, 1–8. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, J. Advanced lightweight materials for automobiles: A review. Mater. Des. 2022, 221, 1–15. [Google Scholar] [CrossRef]
- Heggemann, T.; Homberg, W.; Sapli, H. Combined curing and forming of fiber metal laminates. In Proceedings of the 23rd International Conference on Material Forming (ESAFORM), Online, 4–8 May 2020. [Google Scholar]
- Huang, J.; Huang, B.; Qiao, X.B.; He, M.X.; Xie, L.Q.; Wang, X.S. Application and Challenge of Deformed Aluminum Alloys in Automotive Lightweight. Automob. Technol. Mater. 2022, 15–18. [Google Scholar]
- Li, S.S.; Yue, X.; Li, Q.Y.; Peng, H.L.; Dong, B.X.; Liu, T.S.; Yang, H.Y.; Fan, J.; Shu, L.S.; Jiang, Q.C.; et al. Development and applications of aluminum alloys for aerospace industry. J. Mater. Res. Technol. 2023, 27, 944–983. [Google Scholar] [CrossRef]
- Liu, Z.S.; Li, Y.D.; Zhao, J.W.; Fu, L.; Li, L.; Yu, K.; Mao, X.; Zhao, P. Study on Aluminum Alloy Materials and Application Technologies for Automotive Lightweighting. Chin. J. Mater. Sci. Prog. 2022, 41, 786–795+807. [Google Scholar]
- Liu, Y.; Geng, H.C.; Zhu, B.; Wang, Y.L.; Zhang, Y.S. Research Progress on High-Strength Aluminum Alloy Efficient Hot Stamping Process. Forg. Technol. 2020, 45, 1–12. [Google Scholar]
- Behrens, B.A.; Nürnberger, F.; Bonk, C.; Hübner, S.; Behrens, S.; Vogt, H. Influences on the formability and mechanical properties of 7000-aluminum alloys in hot and warm forming. In Proceedings of the 36th IDDRG Conference on Materials Modelling and Testing for Sheet Metal Forming, Munich, Germany, 2–6 July 2017. [Google Scholar]
- Li, H.H. Study on the Hot Stamping Deformation Behavior and Microstructure Evolution of 7075 Aluminum Alloy Body Components. Master’s Thesis, Jilin University, Changchun, China, 2020. [Google Scholar]
- Caudill, M. Neural networks primer, part I. AI Expert 1987, 2, 46–52. [Google Scholar]
- Attar, H.R.; Zhou, H.S.; Foster, A.; Li, N. Rapid feasibility assessment of components to be formed through hot stamping: A deep learning approach. J. Manuf. Process. 2021, 68, 1650–1671. [Google Scholar] [CrossRef]
- Quan, G.Z.; Wang, T.; Li, Y.L.; Zhan, Z.Y.; Xia, Y.F. Artificial Neural Network Modeling to Evaluate the Dynamic Flow Stress of 7050 Aluminum Alloy. J. Mater. Eng. Perform. 2016, 25, 553–564. [Google Scholar] [CrossRef]
- Pandya, K.S.; Roth, C.C.; Mohr, D. Strain Rate and Temperature Dependent Fracture of Aluminum Alloy 7075: Experiments and Neural Network Modeling. Int. J. Plast. 2020, 135, 1–15. [Google Scholar] [CrossRef]
- Zheng, G.; Ge, L.H.; Shi, Y.Q.; Li, Y.; Yang, Z. Dynamic Rolling Force Prediction of Reversible Cold Rolling Mill Based on BP Neural Network with Improved PSO. In Proceedings of the Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018. [Google Scholar]
- Xiao, W.; Wang, B.; Zhou, J.; Ma, W.; Yang, L. Optimization of aluminium sheet hot stamping process using a multi-objective stochastic approach. Eng. Optim. 2016, 48, 2173–2189. [Google Scholar] [CrossRef]
- Huanhuan, L.; Zhili, H.; Lin, H.; Yizhe, C. Optimization of Hot Forming-Quenching Integrated Process Parameters for Complex Aluminum Alloy Automotive Components. Rare Met. Mater. Eng. 2019, 48, 1029–1035. [Google Scholar]
- Fan, Y.T.; Yang, W.Y. A backpropagation learning algorithm with graph regularization for feedforward neural networks. Inf. Sci. 2022, 607, 263–277. [Google Scholar] [CrossRef]
- Singh, A.K.; Singhal, D.; Kumar, R. Machining of aluminum 7075 alloy using EDM process: An ANN validation. Mater. Today: Proc. 2020, 26, 2839–2844. [Google Scholar] [CrossRef]
- Liu, X.F.; Hu, Y.H.; Huang, W.J. Research on Simulation Technology for Auto Panel in Drawing Forming Based on Autoform. In Proceedings of the International Conference on Advanced Engineering Materials and Technology (AEMT2011), Sanya, China, 29–31 July 2011. [Google Scholar]
- Garg, V.V.; Stogner, R.H. Hierarchical Latin Hypercube Sampling. J. Am. Stat. Assoc. 2017, 112, 673–682. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Ramanuj Kumar, A.K.S.; Mishra, P.C.; Das, R.K. Comparative study on machinability improvement in hard turning using coated and uncoated carbide inserts: Part II modeling, multi-response optimization, tool life, and economic aspects. Adv. Manuf. 2018, 6, 155–175. [Google Scholar] [CrossRef]
- Singh, S.; Bansal, J.C. Mutation-Driven Grey Wolf Optimizer with Modified Search Mechanism. Expert Syst. Appl. 2022, 194, 1–10. [Google Scholar] [CrossRef]
- Xue, J.K.; Shen, B. A survey on sparrow search algorithms and their applications. Int. J. Syst. Sci. 2024, 55, 814–832. [Google Scholar] [CrossRef]
- Zang, J.J.; Cao, B.Y.; Hong, Y.M. Research on the Fiber-to-the-Room Network Traffic Prediction Method Based on Crested Porcupine Optimizer Optimization. Appl. Sci. 2024, 14, 4840. [Google Scholar] [CrossRef]
- El-Kenawy, E.S.M.; Khodadadi, N.; Mirjalili, S.; Abdelhamid, A.A.; Eid, M.M.; Ibrahim, A. Greylag Goose Optimization: Nature-Inspired Optimization Algorithm. Expert Syst. Appl. 2024, 238, 1–15. [Google Scholar] [CrossRef]
- Xu, D.M.; Li, Z.; Wang, W.C. An Ensemble Model for Monthly Runoff Prediction Using Least Squares Support Vector Machine Based on Variational Modal Decomposition with Dung Beetle Optimization Algorithm and Error Correction Strategy. J. Hydrol. 2024, 629, 1–10. [Google Scholar] [CrossRef]
- Saad, M.R.; Emam, M.M.; Houssein, E.H. An Efficient Multi-Objective Parrot Optimizer for Global and Engineering Optimization Problems. Sci. Rep. 2025, 15, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Li, F.C.; Zhang, T.Y. Study on Genetic Algorithm Based on Schema Mutation and Its Performance Analysis. In Proceedings of the 2nd International Symposium on Electronic Commerce and Security, Nanchang, China, 22–24 May 2009. [Google Scholar]



| Si | Fe | Cu | Mn | Mg | Cr | Zn | Al |
|---|---|---|---|---|---|---|---|
| ≤0.4 | ≤0.5 | 1.2–2.0 | ≤0.3 | 2.1–2.9 | 0.18–0.28 | 5.1–6.1 | Bal |
| No. | Temperature (°C) | Stamping Speed (mm·s−1) | Blank Holder Force (KN) | Friction Coefficient | Thinning Rate (%) |
|---|---|---|---|---|---|
| 1 | 371 | 384 | 233 | 0.36 | 0.443 |
| 2 | 363 | 230 | 198 | 0.32 | 0.286 |
| 3 | 355 | 101 | 242 | 0.38 | 0.790 |
| 4 | 322 | 108 | 43 | 0.36 | 0.176 |
| 5 | 334 | 74 | 27 | 0.14 | 0.181 |
| 6 | 415 | 246 | 221 | 0.27 | 0.291 |
| 7 | 300 | 299 | 87 | 0.21 | 0.174 |
| 8 | 326 | 218 | 259 | 0.21 | 0.210 |
| 9 | 356 | 63 | 228 | 0.12 | 0.172 |
| 10 | 338 | 34 | 248 | 0.30 | 0.379 |
| ...... | |||||
| 100 | 377 | 380 | 103 | 0.14 | 0.178 |
| MAE | MSE | RMSEP | MAPE | R2 |
|---|---|---|---|---|
| 0.0667 | 0.0113 | 0.106 | 0.208 | 0.702 |
| Bp | GWO | SSA | CPO | GOOSE | DBO | PO | |
|---|---|---|---|---|---|---|---|
| MAE | 0.0667 | 0.0543 | 0.0769 | 0.0532 | 0.0555 | 0.0777 | 0.0434 |
| MSE | 0.0113 | 0.0074 | 0.0121 | 0.0043 | 0.0051 | 0.0139 | 0.0035 |
| RMSEP | 0.106 | 0.086 | 0.110 | 0.065 | 0.071 | 0.118 | 0.058 |
| MAPE | 0.208 | 0.194 | 0.253 | 0.221 | 0.218 | 0.253 | 0.152 |
| R2 | 0.702 | 0.818 | 0.783 | 0.855 | 0.796 | 0.726 | 0.894 |
| run time/s | 7.39 | 9.27 | 21.69 | 12.97 | 11.67 | 10.73 | 16.68 |
| PO-BP Results (%) | Simulation Results (%) | Error Value (%) | Error Rate (%) |
|---|---|---|---|
| 17.0 | 17.2 | 0.2 | 1.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, R.; Zhang, Z.; Ren, M.; Jia, H.; Lv, T. Optimization of Hot Stamping Parameters for Aluminum Alloy Crash Beams Using Neural Networks and Genetic Algorithms. Metals 2025, 15, 1047. https://doi.org/10.3390/met15091047
Qu R, Zhang Z, Ren M, Jia H, Lv T. Optimization of Hot Stamping Parameters for Aluminum Alloy Crash Beams Using Neural Networks and Genetic Algorithms. Metals. 2025; 15(9):1047. https://doi.org/10.3390/met15091047
Chicago/Turabian StyleQu, Ruijia, Zhiqiang Zhang, Mingwen Ren, Hongjie Jia, and Tongxin Lv. 2025. "Optimization of Hot Stamping Parameters for Aluminum Alloy Crash Beams Using Neural Networks and Genetic Algorithms" Metals 15, no. 9: 1047. https://doi.org/10.3390/met15091047
APA StyleQu, R., Zhang, Z., Ren, M., Jia, H., & Lv, T. (2025). Optimization of Hot Stamping Parameters for Aluminum Alloy Crash Beams Using Neural Networks and Genetic Algorithms. Metals, 15(9), 1047. https://doi.org/10.3390/met15091047






