Multiscale Modeling and Analysis of Hydrogen-Enhanced Decohesion Across Block Boundaries in Low-Carbon Lath Martensite
Abstract
1. Introduction
2. Materials and Methods
2.1. Continuum Decohesion Model
2.2. Cohesive Zone Model
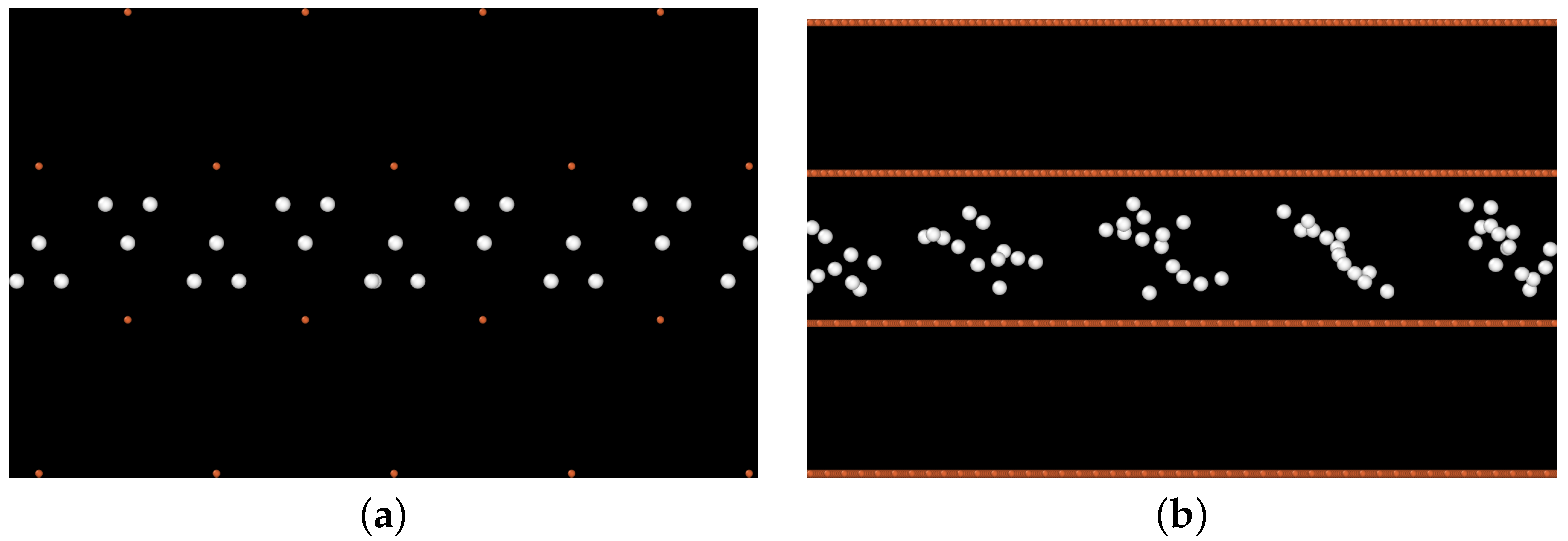
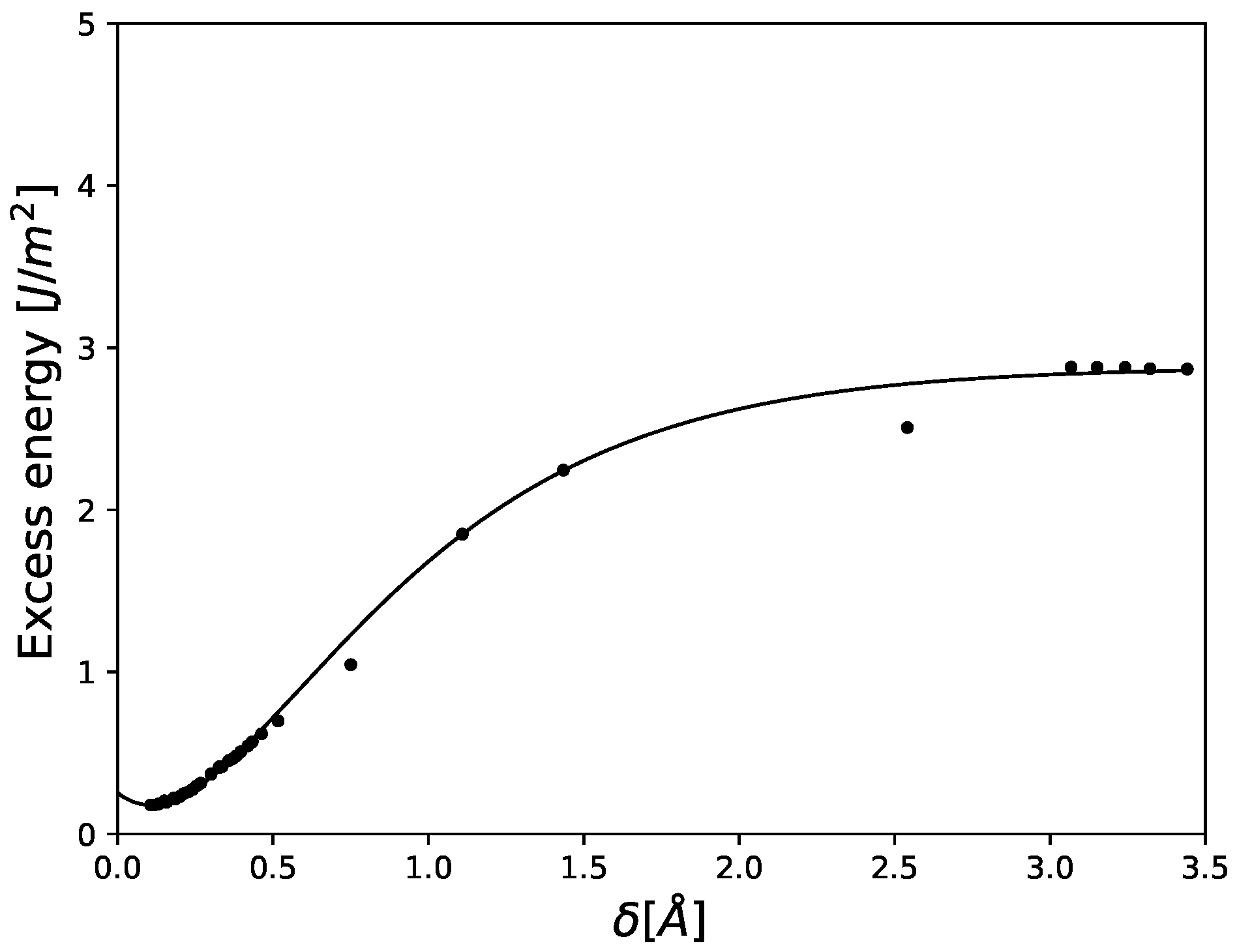
2.2.1. Cohesive Zone Model in a Pure Fe Bicrystal
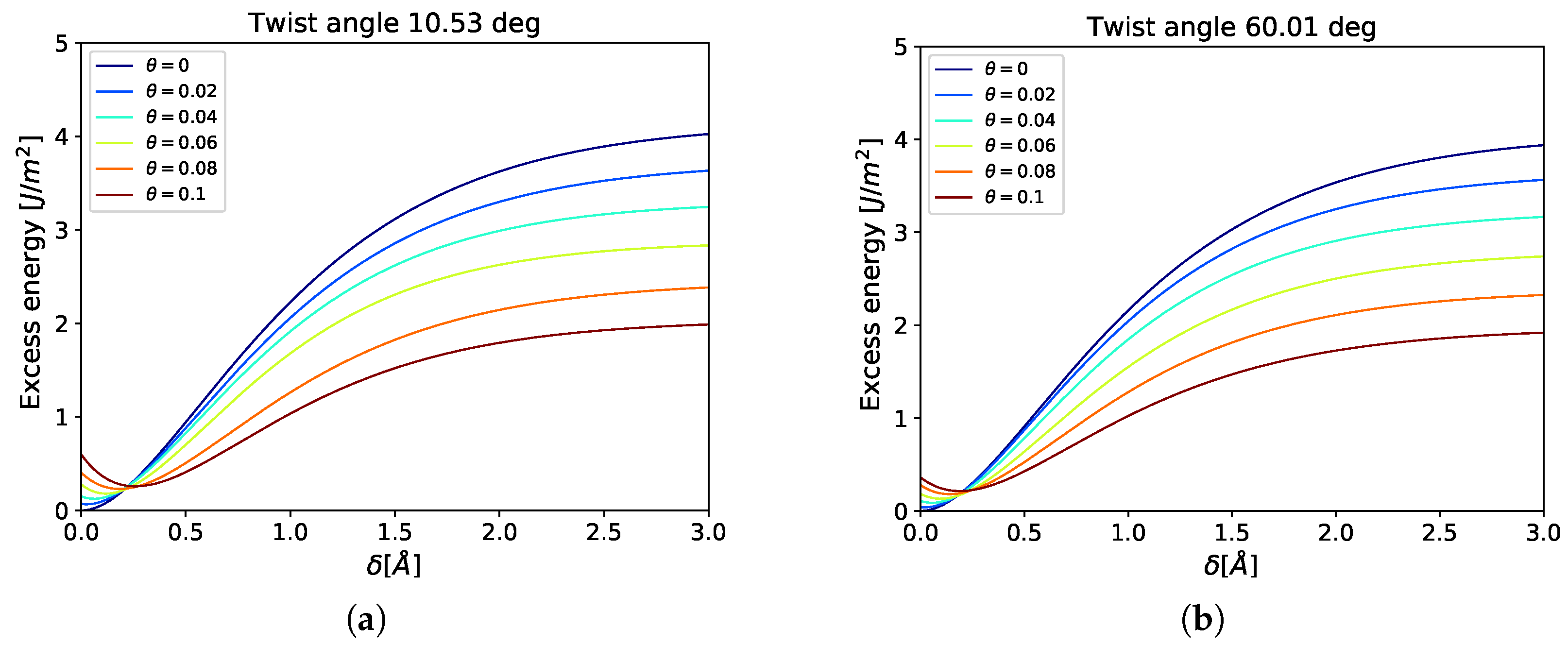
2.2.2. Cohesive Zone Model in the Presence of Hydrogen
3. Results
3.1. Cohesive Strength at Fixed Values of Hydrogen Occupancy
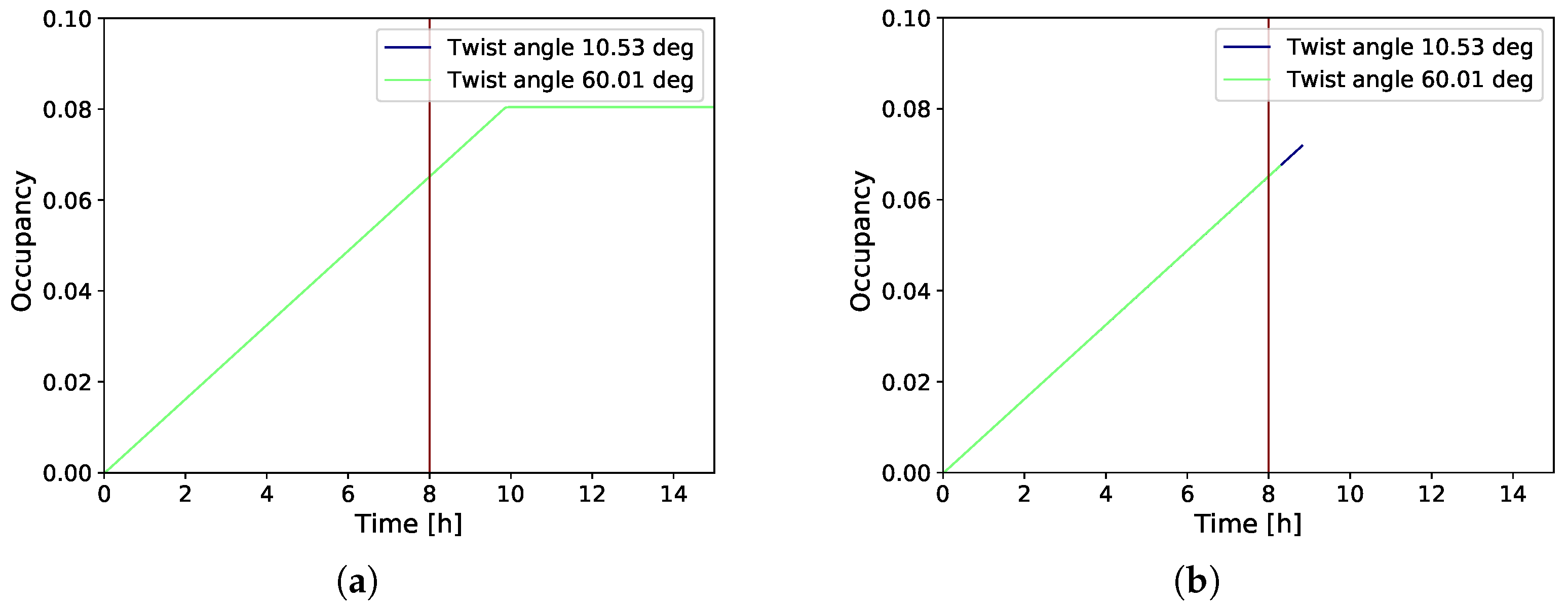
3.2. Gradual Decohesion Under Tensile Loading and a Fixed Hydrogen Flux
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lynch, S. Hydrogen embrittlement phenomena and mechanisms. Corros. Rev. 2012, 30, 105–123. [Google Scholar] [CrossRef]
- Chen, Y.S.; Huang, C.; Liu, P.-Y.; Yen, H.-W.; Niu, R.; Burr, P.; Moore, K.L.; Martínez-Pañeda, E.; Atrens, A.; Cairney, J.M. Hydrogen trapping and embrittlement in metals—A review. Int. J. Hydrogen Energy 2025, 136, 789–821. [Google Scholar] [CrossRef]
- Chang, Z.; Ruan, X.; Chen, Z.; Zhang, Y.; Li, L.; Lan, L. Comparative evaluation on hydrogen damage behavior of two martensitic high strength press hardening steels. Int. J. Hydrogen Energy 2024, 61, 1060–1070. [Google Scholar] [CrossRef]
- Birnbaum, H.K.; Sofronis, P. Hydrogen-enhanced localized plasticity—A mechanism for hydrogen-related fracture. Mater. Sci. Eng. A 1994, 176, 191–202. [Google Scholar] [CrossRef]
- Robertson, I.M. The effect of hydrogen on dislocation dynamics. Eng. Fract. Mech. 2001, 68, 671–692. [Google Scholar] [CrossRef]
- Ferreira, P.J.; Robertson, I.M.; Birnbaum, H.K. Hydrogen effects on the interaction between dislocations. Acta Mater. 1998, 46, 1749–1757. [Google Scholar] [CrossRef]
- Somerday, B.; Sofronis, P.; Jones, R. Effects of hydrogen on materials. In Proceedings of the 2008 International Hydrogen Conference, Jackson Lake Lodge, Grand Teton National Park, WY, USA, 7–10 September 2008. [Google Scholar]
- Abou Ali Modad, O.; Shehadeh, M.A. Modeling dislocation interactions with grain boundaries in lath martensitic steels. J. Mater. Sci. 2024, 59, 4829–4851. [Google Scholar] [CrossRef]
- Troiano, A.R. The Role of Hydrogen and Other Interstitials in the Mechanical Behavior of Metals. Trans. Am. Soc. Met. 1960, 52, 54–80. [Google Scholar] [CrossRef]
- Oriani, R.A.; Josephic, P.H. Equilibrium aspects of hydrogen-induced cracking of steels. Acta Metall. Mater. 1974, 22, 1065–1074. [Google Scholar] [CrossRef]
- Azócar Guzmán, A.; Janisch, R. Effects of mechanical stress, chemical potential, and coverage on hydrogen solubility during hydrogen-enhanced decohesion of ferritic steel grain boundaries: A first-principles study. Phys. Rev. Mater. 2024, 8, 073601. [Google Scholar] [CrossRef]
- Matsubara, K.; Takagi, S.; Meng, F.-S.; Ogata, S.; Ishikawa, N. Atomic-scale modelling of boundaries characterized lath martensite microstructure for hydrogen-induced crack initiation: A machine learning interatomic potentials study. In Proceedings of the 7th International Symposium on Steel Science, Kyoto, Japan, 11–14 November 2024; The Iron and Steel Institute of Japan: Tokyo, Japan, 2024. [Google Scholar]
- Beachem, C.D. Orientation of cleavage facets in tempered martensite (quasi-cleavage) by single surface trace analysis. Metall. Trans. 1973, 4, 1999–2000. [Google Scholar] [CrossRef]
- Boris, Y.; Yana, M.; Kateryna, V.; Vanya, D.; Krasimir, K.; Julieta, K.; Rumyana, L.; Ivaylo, K. Effect of Hydrogen Content on the Microstructure, Mechanical Properties, and Fracture Mechanism of Low-Carbon Lath Martensite Steel. Metals 2024, 14, 1340. [Google Scholar] [CrossRef]
- Cho, L.; Bradle, P.E.; Lauria, D.S.; Martin, M.L.; Connolly, M.J.; Benzing, J.T.; Seo, E.J.; Findley, K.O.; Speer, J.G.; Slifka, A.J. Characteristics and mechanisms of hydrogen-induced quasi-cleavage fracture of lath martensitic steel. Acta Mater. 2021, 206, 116635. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, S.; Zhou, L.; Tian, Z.; Shen, M.; Liu, X. Effect of Quenching Temperature on Microstructure and Hydrogen-Induced Cracking Susceptibility in S355 Steel. Materials 2025, 18, 1161. [Google Scholar] [CrossRef]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Tsuji, N.; Minamino, Y. Crystallographic features of lath martensite in low-carbon steel. Acta Mater. 2006, 54, 1279–1288. [Google Scholar] [CrossRef]
- Djukic, M.B.; Bakic, G.M.; Zeravcic, V.S.; Sedmak, A.; Rajicic, B. The synergistic action and interplay of hydrogen embrittlement mechanisms in steels and iron: Localized plasticity and decohesion. Eng. Fract. Mech. 2019, 216, 106528. [Google Scholar] [CrossRef]
- Nagao, A.; Smith, C.D.; Dadfarnia, M.; Sofronis, P.; Robertson, I.M. The role of hydrogen in hydrogen embrittlement fracture of lath martensitic steel. Acta Mater. 2012, 60, 5182–5189. [Google Scholar] [CrossRef]
- Kim, Y.H.; Morris, J.W. The nature of quasicleavage fracture in tempered 5.5Ni steel after hydrogen charging. Metall. Trans. A 1983, 14, 1883–1888. [Google Scholar] [CrossRef]
- Shibata, A.; Murata, T.; Takahashi, H.; Matsuoka, T.; Tsuji, N. Characterization of hydrogen-related fracture behavior in as-quenched low-carbon martensitic steel and tempered medium-carbon martensitic. Metall. Mater. Trans. A 2015, 46, 5685–5696. [Google Scholar] [CrossRef]
- Choo, W.; Lee, J.Y. Thermal analysis of trapped hydrogen in pure iron. Metall. Trans. A 1982, 13, 135–140. [Google Scholar] [CrossRef]
- Wei, F.-G.; Tsuzaki, K. Response of hydrogen trapping capability to microstructural change in tempered Fe–0.2C martensite. Scr. Mater. 2005, 52, 467–472. [Google Scholar] [CrossRef]
- Nagumo, M. Fundamentals of Hydrogen Embrittlement; Springer: New York, NY, USA, 2016. [Google Scholar]
- Zhong, L.; Wu, R.; Freeman, A.J.; Olson, G.B. Charge transfer mechanism of hydrogen-induced intergranular embrittlement of iron. Phys. Rev. B 2000, 62, 13938–13941. [Google Scholar] [CrossRef]
- Geng, W.-T.; Freeman, A.J.; Olson, G.B.; Tateyama, Y.; Ohno, T. Hydrogen-Promoted Grain Boundary Embrittlement and Vacancy Activity in Metals: Insights from Ab Initio Total Energy Calculatons. Mater. Trans. 2005, 46, 756–760. [Google Scholar] [CrossRef]
- Tian, Z.X.; Yan, W.; Hao, J.X.; Xiao, W. Effect of alloying additions on the hydrogen-induced grain boundary embrittlement in iron. J. Phys. Condens. Matt. 2011, 23, 015501. [Google Scholar] [CrossRef]
- Yamaguchi, M. First-Principles Calculations of Hydrogen Trapping Energy on Incoherent Interfaces of Aluminum Alloys. Metall. Mater. Trans. A 2011, 42, 319–329. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Ebihara, K.-I.; Itakura, M.; Kadoyoshi, T.; Suzudo, T.; Kaburaki, H. First-Principles Study on the Grain Boundary Embrittlement of Metals by Solute Segregation: Part II. Metal (Fe, Al, Cu)-Hydrogen (H) Systems. Metall. Mater. Trans. A 2011, 42, 330–339. [Google Scholar] [CrossRef]
- Rice, J.R. Hydrogen and Interfacial Cohesion. In Effect of Hydrogen on Behaviour of Materials; Thompson, A.M., Bernstein, I.M., Eds.; TMS-AIME: New York, NY, USA, 1976; pp. 455–466. [Google Scholar]
- Rice, J.R.; Wang, J.-S. Embrittlement of interfaces by solute segregation. Mater. Sci. Eng. A 1989, 107, 23–40. [Google Scholar] [CrossRef]
- Mishin, Y.; Sofronis, P.; Bassani, J.L. Thermodynamic and kinetic aspects of interfacial decohesion. Acta Mat. 2002, 50, 3609–3622. [Google Scholar] [CrossRef]
- Katzarov, I.H.; Paxton, A.T. Hydrogen embrittlement II. Analysis of hydrogen-enhanced decohesion across (111) planesin α-Fe. Phys. Rev. Mater. 2017, 1, 33603. [Google Scholar] [CrossRef]
- Hirth, J.P.; Rice, J.R. On the thermodynamics of adsorption at interfaces as it influences decohesion. Metall. Trans. A 1980, 11, 1501–1511. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Thermodynamics: An Advanced Treatment for Chemists and Physicists, 4th ed.; Elsevier Science: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Van der Ven, A.; Ceder, G. The thermodynamics of decohesion. Acta Mater. 2004, 52, 1223–1235. [Google Scholar] [CrossRef]
- Warrington, D. The coincidence site lattice (CSL) and grain boundary (DSC) dislocations for the hexagonal lattice. J. Phys. Colloq. 1975, 36, 87–95. [Google Scholar] [CrossRef]
- Zhou, X.; Foster, M.; Ronevich, J.; San Marchi, C. Review and construction of interatomic potentials for molecular dynamics studies of hydrogen embrittlement in Fe–C based steels. J. Comput. Chem. 2020, 41, 1299–1309. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In ‘t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Rose, J.H.; Ferrante, J.; Smith, J.R. Universal Binding Energy Relations in Metallic Adhesion. Phys. Rev. Lett. 1981, 47, 675. [Google Scholar] [CrossRef]
- Katzarov, I.; Ilieva, N.; Yanachkov, B. A molecular dynamics study of dislocation-interface boundary interactions in lath martensite. AIP Conf. Proc. 2022, 2522, 110007. [Google Scholar]
- Ramasubramaniam, A.; Itakura, M.; Carter, E.A. Interatomic potentials for hydrogen in α-iron based on density functional theory. Phys. Rev. B 2009, 79, 174101. [Google Scholar] [CrossRef]
- Paxton, A.T.; Elsässer, C. Electronic structure and total energy of interstitial hydrogen in iron: Tight-binding models. Phys. Rev. B 2010, 82, 235125. [Google Scholar] [CrossRef]
- Bombac, D.; Katzarov, I.H.; Pashov, D.L.; Paxton, A.T. Theoretical evaluation of the role of crystal defects on local equilibrium and effective diffusivity of hydrogen in iron. Mater. Sci. Technol. 2017, 33, 1505–1514. [Google Scholar] [CrossRef]
- Nagao, A.; Kuramoto, S.; Ichitani, K.; Kanno, M. Visualization of hydrogen transport in high strength steels affected by stress fields and hydrogen trapping. Scr. Mater. 2001, 45, 1227–1232. [Google Scholar] [CrossRef]
- Nagao, A.; Smith, C.D.; Dadfarnia, M.; Sofronis, P.; Robertson, I.M. Interpretation of hydrogen-induced fracture surface morphologies for lath martensitic steel. Procedia Mater. Sci. 2014, 3, 1700–1705. [Google Scholar] [CrossRef]



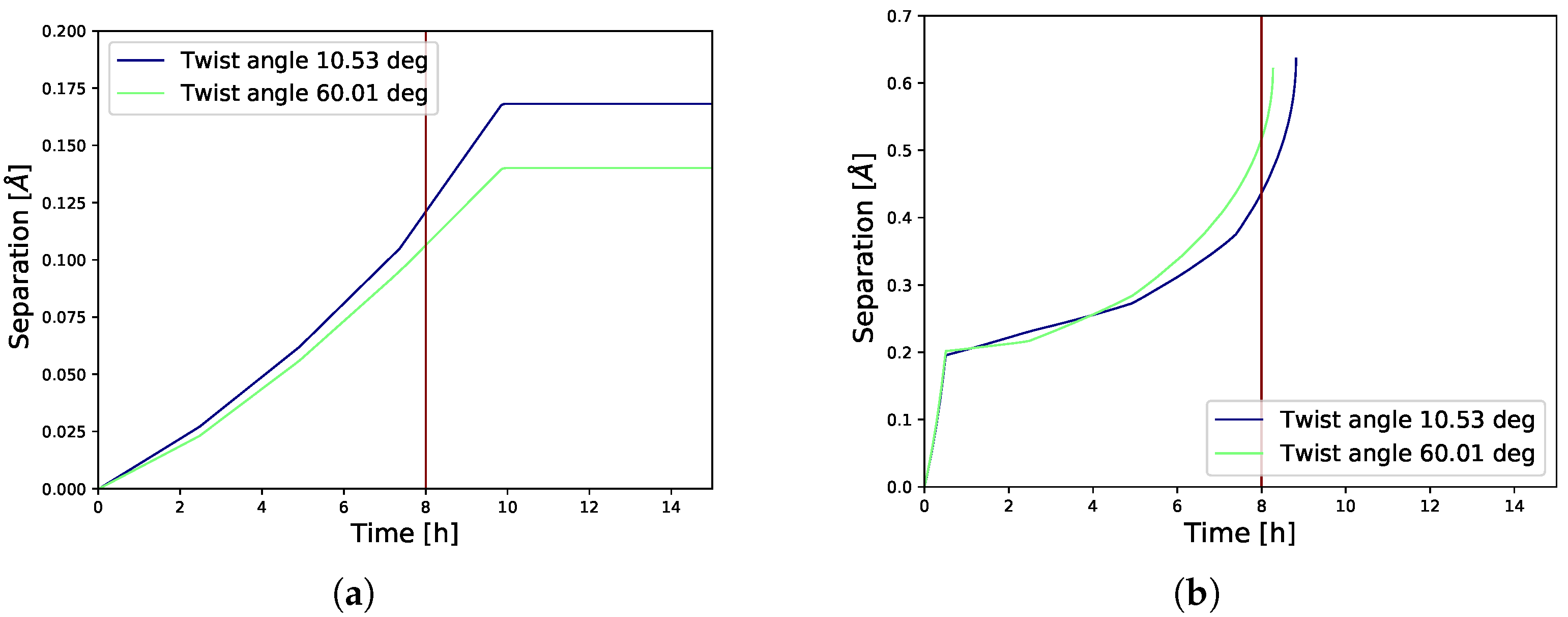
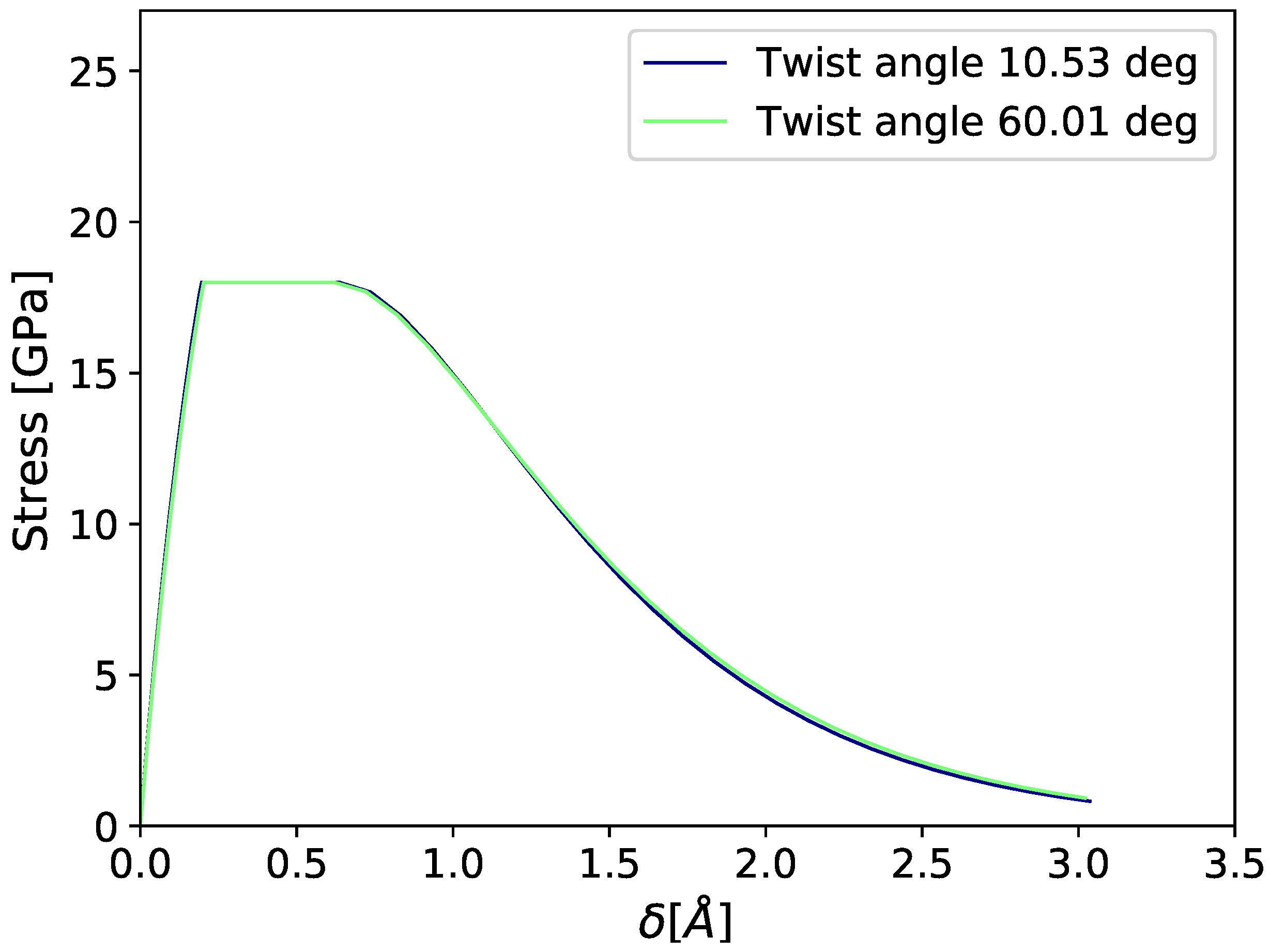
| Twist Angle | m | n | |
|---|---|---|---|
| 10.53 | 23 | 6 | 547 |
| 60.01 | 30 | 49 | 4201 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katzarov, I.H. Multiscale Modeling and Analysis of Hydrogen-Enhanced Decohesion Across Block Boundaries in Low-Carbon Lath Martensite. Metals 2025, 15, 660. https://doi.org/10.3390/met15060660
Katzarov IH. Multiscale Modeling and Analysis of Hydrogen-Enhanced Decohesion Across Block Boundaries in Low-Carbon Lath Martensite. Metals. 2025; 15(6):660. https://doi.org/10.3390/met15060660
Chicago/Turabian StyleKatzarov, Ivaylo H. 2025. "Multiscale Modeling and Analysis of Hydrogen-Enhanced Decohesion Across Block Boundaries in Low-Carbon Lath Martensite" Metals 15, no. 6: 660. https://doi.org/10.3390/met15060660
APA StyleKatzarov, I. H. (2025). Multiscale Modeling and Analysis of Hydrogen-Enhanced Decohesion Across Block Boundaries in Low-Carbon Lath Martensite. Metals, 15(6), 660. https://doi.org/10.3390/met15060660







