Abstract
This paper studies the plastic deformation of a rotating disk made of aluminum dispersion-hardened alloys using mechanical tensile tests and a structured study using optical microscopy methods. Alloys such as AA5056 and A356 with dispersed Al3Er and TiB2 particles are used as the initial materials. Tensile strength testing of the obtained alloys shows that the addition of Al3Er particles in the AA5056 alloy composition leads to an increase in its ultimate stress limit (USL) and plasticity from 170 to 204 MPa and from 14.7 to 21%, respectively, although the modifying effect is not observed during crystallization. The addition of TiB2 particles to the A356 alloy composition also leads to a simultaneous increase in the yield strength, USL, and plasticity from 102 to 145 MPa, from 204 to 263 MPa, and from 2.3 to 2.8%, respectively. The study of the stress-strain state of the disk was carried out in the framework of deformed solid mechanics. The equilibrium equations were integrated analytically, taking into account the hardening conditions obtained from the experimental investigations. This made it possible to write the analytical relations for the radial and circumferential stresses and to determine the conditions of plastic deformation and loss of strength. The plastic resistance of a disk depends on the ratio between its outer and inner radii. The plastic resistance decreases with increasing disk width at a constant inner radius, which is associated with a stronger effect from the centrifugal force field. At a higher rotational rate of narrow disks, the tangential stresses are high and can exceed the USL value. A356 and A356–TiB2 alloys are more brittle than the AA5056 and AA5056–Al3Er alloys. In the case of wide rotating disks, AA5056 and AA5056–Al3Er alloys are preferable.
1. Introduction
The improvement of process facility performance requires the creation of materials that provide the appropriate levels of reliability and life. Such materials must possess high strength and sufficient plastic potential. In order to achieve these goals, it is advisable to utilize composite materials consisting of high-strength fillers (dispersed phases) and plastic binders (matrices).
According to Matthews and Rawlings [1], dispersion-hardened materials with nanoparticles in their matrix are of particular interest. These alloys manifest unique properties compared to conventional alloys. Unlike reinforced and laminated materials, the main advantages of dispersion-hardened alloys are the isotropy of mechanical properties, high plasticity, and strength [2,3]. Compared to fibers, dispersion-hardened composite materials are characterized by a load-bearing matrix. An ensemble of dispersed particles strengthens the material due to its resistance to dislocation motion under loading [4]. This hinders plastic deformation and improves the strength and stress–strain properties of materials. Since the strength properties of dispersion-hardened materials depend on the particle shape and size, a variation in the matrix composition, particle size, and volume fraction makes it possible to create materials with the required properties. Kröpfl et al. [5] considered the deformation process in dispersion-hardened aluminum materials during uniaxial creep in a wide temperature range. It was found that the yield strength was significantly reduced at elevated temperatures. Stobrawa et al. [6] reported a considerable improvement in the properties of nanoparticle-strengthened composites.
The addition of strengthening particles greatly increases the mechanical properties (ultimate stress limit and hardness) and performance (wear resistance) of materials [7]. Dispersion-hardened metallic materials demonstrate an excellent strength/plasticity ratio. According to [8], a wide range of materials with the required property set can be obtained by changing the matrix, particle size, and volume fraction. The modification of these parameters provides a wide spectrum of materials with the required property set [9].
The use of nonmetallic particles is a promising technique to improve the structures of cast alloys. There are currently a number of experimental data on the use of metal oxides (Al2O3, TiO2), carbides, and borides for the grain structure modification of Al–Si alloys [10,11,12,13,14].
In our early research [15], we studied the microstructure and mechanical properties of the aluminum alloy A356 strengthened by the scandium trifluoride (ScF3) nanoparticles with a negative thermal expansion coefficient. The alloy demonstrated a highly efficient use of ScF3-based modifiers and additional ultrasonic treatment. The mechanical mixing and vibration treatment used in [16] affected the structure and mechanical properties of the aluminum alloy A356–C consisting of ≤1 wt.% nanodiamonds. It was shown that the yield strength and ultimate stress limit (USL) of the A356 alloy increased without changing its plasticity. In [17], we conducted an integrated study of the alloy production process and the treatment effect on its physical and mechanical properties. It was found that the grain structure of the alloys consisting of TiB2 particles was completely formed. The addition of TiB2 particles increased the yield strength, USL, and plasticity of the alloys. The highest effect from the ground structure of the cast alloys was achieved by using a master alloy consisting of 1 µm TiB2 particles.
As shown in [18], the strength properties of dispersion-hardened materials depend on the particle shape and size, strain temperature, and rate. Alloy strengthening depends on the particle type, volume fraction, and particle distribution in the matrix. Aluminum-based composites strengthened with particles are used in automobile construction, the construction industry, and aircraft engineering.
The plastic shear and strain hardening of heterophased alloys were studied by Orowan, Ashby, Hirsch [19,20,21,22,23,24,25,26,27,28,29], and others. It was found that the strain hardening of materials with nanoscale and nanodispersed strengthening phases independent of the matrix interface was more intensive than that of the materials with coarse particles at the same volume fraction of the strengthening phase.
The stress–strain state of copper pipe walls subjected to elastoplastic deformation was investigated in [30,31,32] by using the flow plasticity model combined with solid mechanics modeling.
Rotating disks are the most important elements in many mechanisms and devices [33,34,35,36]. Disk strength determines the high performance and lifetime of the mechanisms. Most of the up-to-date turbo-machines are provided with disks operating at higher loads, causing plastic deformation. These loads are mostly centrifugal forces induced by the rotation process. Due to the increased requirements for the safety and efficiency of up-to-date turbo-machines, it is necessary to develop new methods of investigating stress–strain states. In addition to solid disks, annular disks are used to study the stress–strain state of turbo-machine parts. This is also relevant for disks that are separately attached to a shaft.
The stress analysis of rotating disks and shafts is a classical problem in solid mechanics. Many studies are devoted to solving these problems using various methods [37,38,39]. Analytical solutions to the rotating disk problem are common in classical works devoted to theories of elasticity [40] and plasticity [41,42]. This problem is also discussed in many engineering studies. The simplest analytical modeling and preliminary design involve the use of a uniform solid or annular disk with a constant thickness subjected to one external centrifugal force. Most of the previous studies considered the Tresca–Saint Venant criterion and the material hardening conditions [43]. Another popular approach to this issue, proposed by Jahromi et al. [44], is the use of the von Mises yield criterion.
Apatay and Eraslan [45] suggested analytical solutions in terms of hypergeometric functions for the elastic deformation of rotating parabolic discs made of isotropic and homogeneous materials. Theoretical studies in [46] were used to investigate the stress–strain state of rotating hyperbolic disks fabricated from isotropic and homogeneous materials subjected to variable thermal loads. Using Tresca’s yield condition, Güven [47] investigated a linearly hardening rotating solid disk with variable thickness. A theoretical stress analysis was given in [48] for rotating hyperbolic disks made of isotropic and homogeneous materials. Using Tresca’s yield condition, Eraslan [49] suggested analytical solutions for stress distribution in rotating parabolic solid disks also made of an isotropic and homogeneous material with linear strain hardening. It was shown that the deformation behavior of a parabolic convex disk was similar to that of a uniform disk of the same thickness, but in the case of a parabolic concave disk, it was different. Based on Tresca’s yield condition, the associated plastic flow rule, and linear material hardening, Eraslan [50] suggested an analytical solution for the elastic–plastic deformation of rotating parabolic disks under pressurized and radially constrained boundary conditions.
Vebil Yildirim [51] conducted a parametric study on the centrifugal force-induced stress and displacements in power-law graded hyperbolic discs, depending on inhomogeneity, profile, and boundary conditions. The radial thickness of the discs was selected such that it was governed by the hyperbolic function determined by either the convergent or divergent function.
Seth’s transition theory was used in [52] to analyze elastoplastic stresses in a thin rotating disk with inclusion and edge loading. The obtained results could be used for both compressible and incompressible materials. It was found that at a high rotational rate of a loaded disk, it was necessary to account for material compressibility.
In terms of continuum mechanics, Aleksandrova et al. [53,54] considered the stress–strain state of a rotating disk with a constant thickness. The disk material was assumed to be homogeneous, elastic, and ideally plastic. A continuum-level solution was obtained for both the stresses and radial displacement using the von Mises yield criterion and the related plastic flow rule. In [55], a complete solution was suggested for practical engineering applications.
Afsar and Go [56] presented the finite element analysis of a thermoelastic field in a rotating thin circular disk with a concentric hole under a thermal load. The solution was obtained in [57] for a disk with a uniform thickness with regard to centrifugal forces and compressive stress.
The aim of this study is to determine the plastic deformation conditions for a rotating disk made of dispersion-hardened aluminum alloys, as illustrated in Figure 1.
Figure 1.
3D view of uniform disk profiles.
In order to calculate stresses in the disk material, we used the approach described in detail in [58,59,60,61]. Based on this approach, stresses in the disk material were calculated using solid mechanics equations [62,63,64,65].
2. Experimental Procedure and Results
2.1. AA5056–Al3Er Alloy
The aluminum alloy AA5056 (91.9–94.68% Al, 4.8–5.8% Mg) was used as the initial material. The Al–Al3Er master alloy was obtained by erbium (Er) hydrogenation in a chemical reactor with successive mixing with Al micropowder, compaction, and dehydrogenation in a vacuum furnace. A total of 1 kg of the AA5056 alloy was placed in a crucible and molted in a muffle furnace at 780 °C for 2 h. When the crucible was removed from the furnace, the Al–Al3Er master alloy was introduced into the melt via simultaneous ultrasonic treatment at a temperature of 730 °C. The ultrasonic treatment was performed using a magnetostriction water-cooling actuator at 4.1 kV voltage and 17.6 kHz frequency. After the complete dissolution of the master alloy, the melt was ultrasonically treated for 2 min. The melt was cast in a mold at 720 °C and underwent vibration treatment until complete crystallization. The initial AA5056 alloy was obtained under the same conditions but without the master alloy.
2.2. A356–TiB2 Alloy
The aluminum alloy A356 (Al base metal, 6.9% Si, 0.339% Mg, 0.136% Ti, 0.124% Fe, and <0.05% other elements) was used as the initial material. Titanium diboride (TiB2) particles were used to modify the alloy structure. The particle introduction and distribution in the A356 melt were performed by using master alloys with 60 wt.% Al and 40 wt.% TiB2 obtained by gas-free burning of a mixture of aluminum, titanium, and boron powders [66]. The alloy was fabricated by melting 1 kg of the A356 alloy in a crucible at 750 °C for at least 4 h in a closed furnace. Master alloys were incorporated at 730 °C and mixed in a mechanical mixer [67] for 1 min in an open furnace. In order to reduce the porosity, obtain a homogeneous structure, and improve the distribution of alloying elements in the melt, vibration treatment was applied during 700 °C casting into the crucible. Vibration was conducted at a frequency of 60 Hz and 0.5 mm amplitude. An alloy without TiB2 particles was created under the same conditions for comparison.
2.3. Methods
The metallographic analysis of the grain structure was conducted using an Olympus GX71 Inverted Microscope (Olympus, Tokyo, Japan). The alloy surface was then mechanically polished. Uniaxial tensile tests were carried out on an Instron 3369 Dual Column Tabletop Testing System (Instron, Norwood, MA, USA) at a 0.2 mm/min strain rate.
As can be seen in Figure 2a, the average grain size of the AA5056 alloy is 390 µm. The diffusion of Al3Er particles does not modify the alloy structure, and the average grain size is 410 µm, as shown in Figure 2b.

Figure 2.
Grain structure of different alloys. (a) AA5056; (b) AA5056–Al3Er; (c) A356; (d) A356–TiB2.
For the A356 alloy, the TiB2 particle diffusion decreases the average grain size from 180 to 140 µm due to the formation of new crystallization centers on the particle surface. Due to the structural proximity of TiB2 and Al crystals, titanium diboride is an effective nucleation center in the Al melt, which, in turn, leads to the formation of the fine structure of ingots. Based on the data obtained, it can be assumed that the modified aggregative state (crystallization) of the introduced (nano- or submicron-sized) particle surface has a significant effect on the grain size of the fabricated alloys. This is associated with the low-stability state of the melt–particle system, which provides a weak thermal effect from the inoculator microparticles on the final state of the alloy, namely, its structure and physical/mechanical properties. After the thermal interaction between the particles and the melt, the temperature of which approaches crystallization, the alloy crystallizes on the particle surface.
Tensile strength testing of the fabricated AA5056 alloy (see Figure 3, Table 1) shows that the introduction of Al3Er particles into the melt improves the USL and plasticity from 170 to 204 MPa and from 14.7 to 21%, respectively, despite the absence of the modifying effect during crystallization. This effect is achieved through the introduction of Al3Er particles, which contribute to the deflection of the potential crack from the grain boundaries into its volume, as well as increase the role of the aluminum matrix in the deformation and fracture processes. The TiB2 particle diffusion in the A356 alloy also leads to a simultaneous increase in the yield strength, USL, and plasticity from 102 to 145 MPa, from 204 to 263, and from 2.3 to 2.8%, respectively.

Figure 3.
Loading diagrams of AA5056, AA5056–Al3Er, A356, and A356–TiB2 alloys.

Table 1.
Parameters of initial and fabricated alloys.
The approximation of the experimental stress–strain curve allows us to obtain the function of with an error not exceeding 0.1%:
where is the effective modulus of plasticity and is the non-linearity parameter.
Parameters Γeff and n for different alloys are summarized in Table 2.

Table 2.
Material constants: and (1).
3. Mathematical Model
Let us consider the stress–strain state of the thin disk induced by its rotation at a constant rotational rate ω. The gravity force effect on the stress–strain state is neglected. The proposed mathematical model is based on balance equations, which take the following form in the cylindrical system of coordinates [80]:
The system of Equations (2)–(4) can be simplified using the following assumptions. Since this problem is axially symmetric (the symmetry relative to one and the same axis is a deformed solid contour and lading conditions), normal stresses do not depend on the angular coordinate φ, and circumferential displacement and tangential stress are zero, viz. , , . Therefore, (2) is identically satisfied.
We consider that the centrifugal force appearing during the disk rotation distributes symmetrically relative to the middle disk surface. If the disk base is free from external forces, the following conditions must be applied to it:
With respect to (4) and (5), we can conclude that at , not only σzz becomes zero but so does its derivative . On the strength of the symmetry conditions, in the center section, the axial shift and radial motion ur on the axial coordinate are both zero, i.e., and , respectively. Therefore, at rather low disk thickness, σzz and σrz stresses are small. Thus, it can be considered that these stresses are zero throughout the disk, whereas the radial motion depends on the radial coordinate only.
In the thin disk, the plane state is implemented approximately. It is enough to use (2) to describe the plane state, which takes the form as follows:
Next, we formulated the boundary conditions for (6). The pressure onto the inner and outer walls of the disk is suggested to be absent. Therefore, the boundary conditions are as follows:
Equation (6) contains two unknown values, namely, σrr and σφφ stress tensor components. The additional relation for elastic deformation can be obtained from the equation of strain compatibility, which in the plane state takes the form as follows:
During the plastic deformation of the hardening medium, an additional condition, which links the stress tensor components, is plastic strain hardening [80]:
The strength analysis of the disk is the most important task of calculating its stress–strain state. According to the maximum shear theory (Saint Venant’s theory), material disintegration occurs due to the shear that is induced by tangential stresses [81]. This theory is well-proven for plastic materials, which resist equally to tension and compression. It is assumed that the material fracture occurs when the highest tangential stress achieves the limit value. In this case, the strength condition takes the following form [82,83]:
Strain tensor components are determined by Cauchy relations and, in our case, they are determined as follows:
Thus, the complete mathematical arrangement of the problem includes the balance Equation (6) with the boundary conditions (7), closing relations (8) and (9), and physical (1) and geometrical (11) relationships.
The disk deformation is determined by the rotational rate ω. If the latter is low, the disk deformation is elastic. When the rotational rate grows, the inner disk surface undergoes plastic deformation [84]. The plastic zone occupies the ring domain with an increasing rotational rate, i.e., . The outer ring remains in the elastic state, i.e., . Thus, we can identify four situations for the deformation process of the rotating disk:
- The whole disk is in the elastic state ().
- The disk is in the elastic state, but its inner surface is in the plastic state ().
- Inner disk layers are in the plastic state, while outer layers are in the elastic state ().
- The disk material is in the plastic state throughout its width ().
Let us discuss the elastic deformation of the disk. In this case, stress and strain are both determined by Hooke’s law. Since σzz = 0, the following relations result from Hooke’s law:
where ν is the Poisson ratio, is the effective shear modulus.
Tangential stresses can be derived from (6) and applied to (12). We then use the equation of strain compatibility (8). The resulting differential second-order equation, which describes the radial stress σrr is as follows:
After integration of this equation with respect to the boundary conditions (7), we can determine the radial stress in the disk:
The tangential stress σφφ is derived from the balance equation (6):
Substitution of (14) into (15) yields
The stress in the disk grows with an increasing rotational rate. When the latter reaches a certain value ωel, plastic deformation occurs on the inner disk surface. The rotational rate describes the elastic limit of the disk. In order to determine the rotational rate, at which plastic deformation occurs on the inner surface, we use the tangential stress from (16) at . Note that the strain intensity relating to the elastic-plastic transition is . Thus, we obtain the following:
Let us now determine the conditions of the elastic–plastic transition for the whole disk material. It occurs when the rotational rate is .
The analysis of plastic deformation is based on the Tresca–Saint Venant criterion. Since the radial σrr and tangential σφφ stresses are tensile, they are positive, viz. σrr > 0, σφφ > 0. Moreover, we take into account that tangential stresses exceed radial (σφφ > σrr). Due to the plane state, the axial stress σzz is absent (σzz = 0). Hence, the conditions of the material hardening (9) and fracture (10) are calculated as follows:
According to multiple experiments, the volume does not change during plastic deformation, and the following condition is satisfied:
Taking the plane problem and (10) and (19) into consideration, it can be concluded that the axial strain εzz does not depend on the coordinate z and can be either the function of radial coordinate r or a constant. The absence of the shear stress () implies that the axial strain is a constant value.
Using (11), the condition of incompressibility (εV = 0) is written as follows:
The integration of (20) within the accuracy of integration constants allows us to determine the displacement field:
Considering Cauchy relations (11), the radial and tangential strains are written as follows:
In solid mechanics, an invariant variable is introduced to describe the deformation field called the shear strain intensity, which, according to Il’yushin [84,85], is determined by the following expression:
Substituting (22) into (23), we obtain the dependence between the shear strain intensity and radial coordinate:
In order to derive the axial strain εzz, let us use (12). It follows that the axial strain is as follows:
Since the axial strain εzz is constant, (25) holds for the whole disk. Considering the plastic state of the whole disk, the radial stress on its outer boundary equals the yield strength:
Now we can derive the integration constant C1 according to (24) and (26):
Let us consider the nonlinear hardening described by (18) to calculate the stress–strain state of the disk and the rotational rate limit at which the plastic zone covers the whole disk.
Using (18), (22), (24), we can find the tangential stress σφφ for the case of nonlinear hardening:
To simplify further integration, we write (28) in the form as follows:
where and .
The radial stress is derived from the balance Equation (6), which can be written as the following relation with regard to the nonlinear dependence between hardening and deformation:
The integration of (30) results in the dependence on the radial coordinate r:
In (31), C2 is the integration constant and is the hypergeometric Gaussian function determined by the Gaussian series sum:
At the disk boundary (r = Rout), radial stresses are assumed to be absent (). Hence, the integration constant C2 is as follows:
The rotational rate of the disk, at which its material transfers to the plastic state (), is obtained from the condition of the inner disk boundary, viz. , :
4. Mathematical Simulation
Plastic strain in the disk is conditioned by the centrifugal force field. The impact of these forces is evaluated by the resulting centrifugal bulk force:
Thus, the centrifugal force increases with increasing outer radius Rex at the constant inner radius Rin, i.e., h = Rex − Rin, and increasing inner radius at a constant outer radius, i.e., with decreasing disk width h.
Figure 4 presents plots of the rotational rate at which plastic strain ωel begins and the disk width h = Rex − Rin. As can be seen in Figure 4, the circular disk resistance to plastic strain depends on the Rin/Rex ratio. When the disk width expands at the constant Rin, the resistance reduces due to the increase in the centrifugal force field. On the contrary, when the disk width expands at the constant Rex, the centrifugal force reduces and the plastic transfer occurs at a higher rotation frequency. Note that the width effect on the plastic strain ωel is more significant for a small Rin/Rex ratio. The plastic strain slightly increases with the increasing Rin/Rex ratio. When the inner and outer radii increase at the same disk width, the centrifugal force applied to the disk increases. This results in a reduction in the plastic resistance, which occurs at a lower plastic strain.

Figure 4.
Dependences of disk width and rotational rate, at which plastic strain ωel begins in different alloys and different Rin: (a) A356; (b) A356–0.5TiB2; (c) AA5056; (d) AA5056–Al3Er; 1—15 mm, 2—30 mm, 3—45 mm, 4—60 mm, 5—75 mm, 6—90 mm, 7—105 mm, 8—120 mm, and 9—135 mm.
The plastic strain of the inner radius is also affected by the conventional yield strength σ0.2. Due to its growth, the plastic resistance increases, which requires a more intensive disk rotation. Thus, the plastic strain ωel becomes the highest for the A356–0.5%TiB2 alloy, whereas, for the AA5056 alloy, it is the lowest.
In Figure 5, one can see plots of the radial stress and coordinate. Since the outer and inner radii are not subjected to radial loads, at r = Rex and r = Rin, the radial stress is zero, viz. σrr = 0. The maximum radial stress occurs at the point, which is the geometric average of the inner and outer radii. The radial stress increases with an increasing disk width and rotational rate:
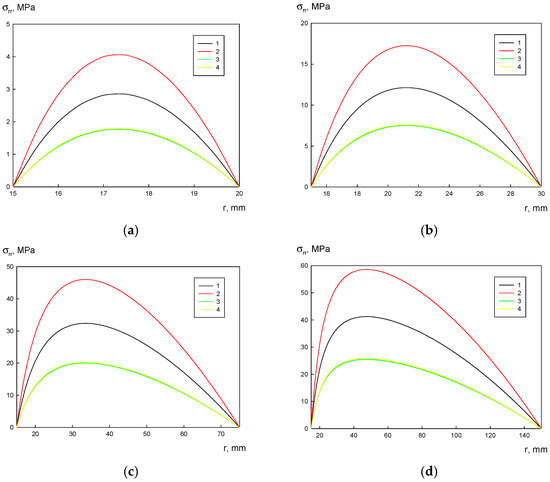
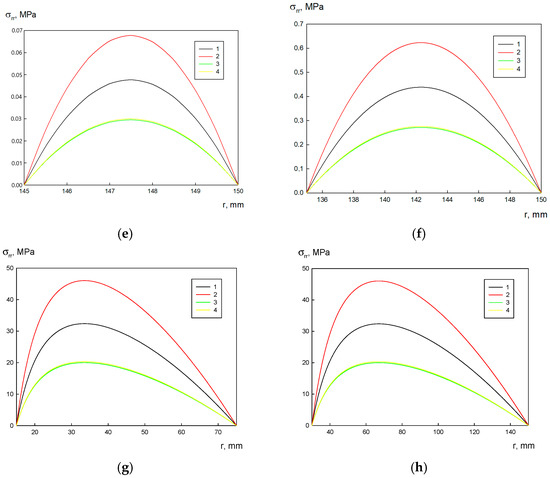
Figure 5.
Stress σrr distribution over the disk radii: (a) mm, Rex = 20 mm; (b) mm, Rex = 30 mm; (c) mm, Rex = 75 mm; (d) mm, Rex = 150 mm; (e) mm, Rex = 150 mm; (f) mm, Rex = 150 mm; (g) mm, Rex = 150 mm; (h) mm, Rex = 150 mm; 1—A356, 2—A356–0.5 TiB2, 3—AA5056, and 4—AA5056–Al3Er.
As mentioned above, the plastic state occurs on the inner disk surface at . In this case, the maximum radial stress is calculated as follows:
Equation (36) can be written as the following:
where ξ = Rin/Rex is the ratio between the inner and outer radii. The maximum radial stress monotonically decreases with increasing ξ. In the case of the solid disk (ξ = 0), this stress is 50% of the conventional yield strength, viz. .
The radial distribution of tangential stress σφφ is presented in Figure 6. The tangential stress σφφ is the highest on the inner disk radius and is calculated as follows:
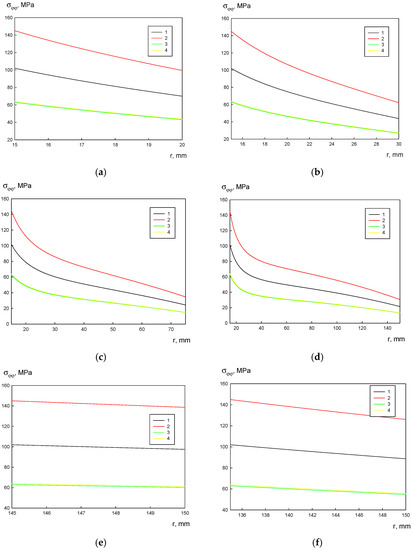
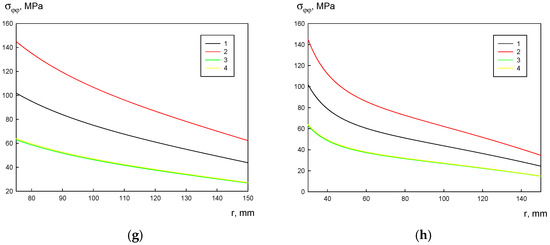
Figure 6.
Stress σφφ distribution over the disk radii: (a) mm, Rex = 20 mm; (b) mm, Rex = 30 mm; (c) mm, Rex = 75 mm; (d) mm, Rex = 150 mm; (e) mm, Rex = 150 mm; (f) mm, Rex = 150 mm; (g) mm, Rex = 150 mm; (h) mm, Rex = 150 mm; 1—A356, 2—A356–0.5 TiB2, 3—AA5056, and 4—AA5056–Al3Er.
The tangential stress monotonically decreases with the increasing radial coordinate r and its lowest value is observed at the outer disk radius:
Nonuniform tangential stress distribution in the disk material describes the ratio between the stresses on the outer and inner disk boundaries. This ratio θ is obtained from the following:
It is interesting to note that the ratio θ does not depend on the material and the rotational rate, and is rather determined by the disk geometry. At ξ = 0 (solid disk), this ratio is the lowest, i.e., , whereas at a higher ξ, .
When the inner disk surface is in the plastic state, which occurs at , the tangential stresses at the disk boundaries are as follows:
Now we consider the case when the rotational rate is and the whole disk is in the plastic state. The lowest tangential stress σφφ appears on the outer disk boundary (r = Rex) and equals σ0.2. The highest tangential stress is observed on the inner disk boundary (r = Rin) and is obtained from the following:
It follows from (43) that at low ξ values, tangential stresses are higher and can exceed the USL σB. At the disk rotational rate and with respect to (18) and (43), the condition of the disk strength retention can be defined as follows:
Equations (43) and (44) help to determine the geometrical parameter ξ, at which the disk fracture does not occur:

Table 3.
Parameter ξB values (45).
Note that the disk fracture may occur at , when the inner and outer disk boundaries are deformed plastically and elastically, respectively. The analysis of this case falls outside the scope of this work and will be addressed in our future works.
In Figure 7, the dependences of the limit frequency ωpl of rotation and the width h show the plastic zone, which occupies the whole disk with different radii Rin. At the constant value of the inner radius Rin, the centrifugal forces increase with an increasing width h. Therefore, the plastic strain of the disk occurs at a lower limit frequency ωpl. The plastic resistance increases with the decreasing inner radius , and total plastic deformation of the disk occurs at higher values of the limit frequency ωpl. In wide annular disks (), the strength loss occurs at the inner disk boundary at , and the disk fracture begins. In Figure 7, one can see two zones for different geometrical parameters: A denotes no fracture, and B denotes a fracture at the inner disk boundary.

Figure 7.
Dependences between the limit frequency ωpl of the rotation and disk width when the plastic zone occupies the whole disk made of different alloys: (a) A356; (b) A356–0.5TiB2; (c) AA5056; (d) AA5056–Al3Er; 1—Rin = 15 mm, 2—Rin = 30 mm, 3—Rin = 45 mm, 4—Rin = 60 mm, 5—Rin = 75 mm, 6—Rin = 90 mm, 7—Rin = 105 mm, 8—Rin = 120 mm, and 9—Rin = 135 mm. A—no fracture, B—fracture on the inner disk boundary.
The parameter can be used to describe the disk plastic properties. At low δ values, a slight increase in the rotational rate leads to the expansion of the plastic zone from the inner to the outer disk boundary. At a high δ parameter, the limit frequency ωpl must be significantly higher than the plastic strain ωel to gain total plastic deformation.
Figure 8 illustrates δ and width h dependence plots when the plastic zone occupies the whole disk with different inner radius Rin. In the narrow disks ( mm), the parameter δ contributes only a few percent. At the increased width h and fixed Rin, the δ parameter increases. This means that there is a wide range of rotational rates, which determines the transition of plastic strain on the inner boundary to the plastic strain of the whole disk. At a higher inner radius and constant width, the δ parameter decreases.

Figure 8.
Parameter δ/width dependence for different alloys and radii: (a) A356; (b) A356–0.5TiB2; (c) AA5056; (d) AA5056–Al3Er; 1—Rin = 30 mm, 2—Rin = 60 mm, and 3—Rin = 105 mm.
The distribution of the radial σrr and tangential σφφ stresses is presented in Figure 9 and Figure 10. These curves are similar to those given in Figure 4 and Figure 5. The radial stress σrr is characterized by the maximum, which increases with increasing Rin/Rex ratio. In our case, this stress is zero on the outer and inner radii as they are not loaded with radial forces.
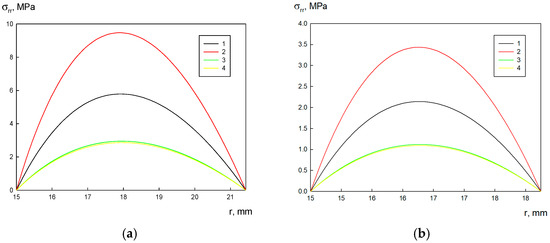
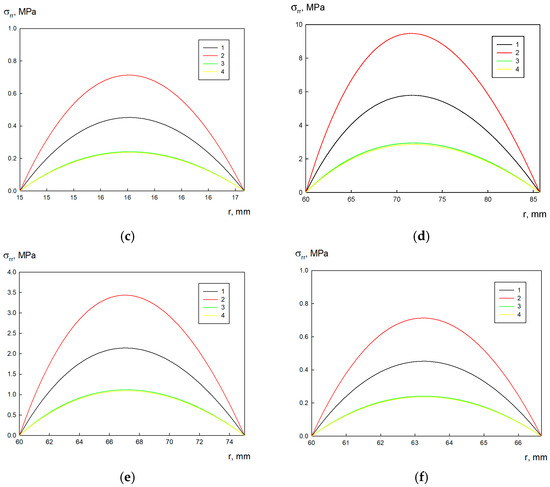
Figure 9.
Stress σrr distribution over the disk radii: (a) mm, ξ = 0.7; (b) mm, ξ = 0.8; (c) mm, ξ = 0.9; (d) Rin = 60 mm, ξ = 0.7; (e) Rin = 60 mm, ξ = 0.8; (f) Rin = 60 mm, ξ = 0.9; 1—A356, 2—A356–0.5TiB2, 3—AA5056, and 4—AA5056–Al3Er.
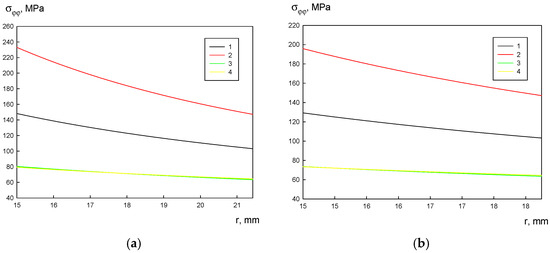

Figure 10.
Stress σrr distribution over the disk radii: (a) mm, ξ = 0.7; (b) mm, ξ = 0.8; (c) mm, ξ = 0.9; (d) Rin = 60 mm, ξ = 0.7; (e) Rin = 60 mm, ξ = 0.8; (f) Rin = 60 mm, ξ = 0.9; 1—A356, 2—A356–0.5TiB2, 3—AA5056, and 4—AA5056–Al3Er.
The tangential stress σφφ monotonically decreases with increasing radial coordinate r. The lowest tangential stress is observed on the outer disk boundary (r = Rex). At , the tangential stress on the outer disk boundary equals the yield strength. When approaching the inner diameter, the tangential stress increases. It is worth noting that at the disk geometrical parameters in Figure 8 and Figure 9, its fracture does not occur. Additionally, with increasing Rin/Rex ratio, the tangential stress decreases.
The inner radius values do not affect the distribution of radial σrr and tangential σφφ stresses in the disk material. The stress distribution over the disk width calculated for different inner radii is identical.
5. Conclusions
This paper investigated the stress–strain state, elastoplastic deformation, and disintegration conditions of the rotating circular disk made of the aluminum alloy strengthened with dispersed nanoparticles.
Aluminum alloys AA5056 and A356 with the use of master alloys AA5056–Al3Er and A356–TiB2 were employed as initial materials. According to tensile strength testing of the obtained alloys, the diffusion of Al3Er particles improved the USL and plasticity of the AA5056 alloy from 170 to 204 MPa and from 14.7 to 21%, respectively, although a modifying effect was not observed during crystallization. The addition of TiB2 particles to the A356 alloy composition also led to a simultaneous increase in its yield strength, USL, and plasticity from 102 to 145 MPa, from 204 to 263 MPa, and from 2.3 to 2.8%, respectively.
The annular disk’s ability to resist plastic depended on the ratio between its outer and inner radii. This plastic resistance decreased with increasing disk width at a constant inner radius, which was associated with a stronger effect from the centrifugal force field. On the contrary, when the disk width expanded at the constant Rex, the centrifugal force was reduced, and the plastic transfer occurred at a higher rotation frequency.
The radial stresses on the outer and inner disk radii were zero since the radii were not loaded with radial forces. The maximum radial stress was observed at the point inside the disk. The maximum radial stress increased with increasing Rin/Rex ratio and with increasing disk width and rotational rate. The tangential stress σφφ monotonically decreased with increasing radial coordinate r. The lowest tangential stress was achieved at the outer disk boundary (r = Rex), whereas the highest tangential stresses were observed at the inner disk boundary (r = Rin).
At and low values of ξ = Rin/Rex, the tangential stresses were high and could exceed the USL. The critical disk widths were and for A356 and A356–0.5TiB2 alloys, respectively. Additionally, for AA5056 and AA5056–Al3Er alloys, the values were and , respectively. Thus, A356 and A356–0.5TiB2 alloys were more brittle than AA5056 and AA5056–Al3Er alloys. It was found that at , the alloy sequence was A356–0.5TiB2, A356, AA5056, and AA5056–Al3Er for the disks to withstand the highest rotational rate without fracture. For wide disks (), AA5056 and AA5056–Al3Er alloys were preferable for fabrication.
Author Contributions
Conceptualization, O.M. and I.Z.; methodology, O.D.; software, O.M.; validation, O.D., O.M. and V.P.; formal analysis, V.P.; investigation, I.Z.; resources, A.V.; data curation, A.V.; writing—original draft preparation, O.D.; writing—review and editing, V.V.; visualization, V.V.; supervision, V.V.; project administration, A.V.; funding acquisition, I.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was carried out with financial support from the Ministry of Education and Science of the Russian Federation (State assignment No. FSWM-2020-0028).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The analyses were carried out with the equipment of the Tomsk Regional Core Shared Research Facilities Center of National Research Tomsk State University. The Center was supported by the Ministry of Science and Higher Education of the Russian Federation Grant No. 075-15-2021-693 (No. 13.RFC.21.0012).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Matthews, F.L.; Rawlings, R.D. Composite Materials: Engineering and Science; CRC Press: Boca Raton, FL, USA, 1999; p. 480. [Google Scholar]
- Arnhold, V.; Hummert, K. New Materials by Mechanical Alloying Techniques; DGM Informationsgeselischaft Verlag: Oberursel, Germany, 1989; p. 269. [Google Scholar]
- Weber, J.H.; Schelleng, R.D. Dispersion-Strengthened Aluminum Alloys; Marcel Dekker, Inc.: New York, NY, USA; Basel, Switzerland; Hong Kong, China, 1988; Part 1, Chapter 11; pp. 269–293. [Google Scholar]
- El-Labban, H.F.; Abdelaziz, M.; Mahmoud, E.R. Modification of carbon steel by laser surface melting: Part I: Effect of laser beam travelling speed on microstructural features and surface hardness. Am. J. Eng. Appl. Sci. 2013, 6, 352–359. [Google Scholar] [CrossRef]
- Kröpfl, O.; Vöhringer, E.; Macherauch, E. Creep Behavior of Dispersion-Hardened Aluminum Materials. Mech. Time-Depend. Mat. 1999, 3, 1–13. [Google Scholar] [CrossRef]
- Stobrawa, Z.M.; Rdzawski, W.; Głuchowski, W. Structure and properties of dispersion hardened submicron grained copper. J. Ach. Mat. Manuf. Eng. 2007, 20, 195–198. [Google Scholar]
- Berezovsky, V.V.; Shavnev, A.A.; Lomov, S.B.; Kurganova, Y.A. Obtaining and analysis of the structure of dispersion-strengthened composite materials of the Al-SiC system with different content of the reinforcing phase. Avia. Mat. Tech. 2014, 6, 17–23. [Google Scholar] [CrossRef]
- Boopathi, M.M.; Arulshri, K.P.; Iyandurai, N. Evaluation of Mechanical Properties of Aluminium Alloy 2024 Reinforced with Silicon Carbide and Fly Ash Hybrid Metal Matrix Composites. Am. J. Appl. Sci. 2013, 10, 219–229. [Google Scholar] [CrossRef]
- Lutz, A.R.; Galochkina, I.A. Aluminum Composite Alloys—Alloys of the Future: Educational Book; Samara State Technical University: Samara, Russia, 2013; p. 82. (In Russian) [Google Scholar]
- Kaldre, I.; Bojarevičs, A.; Grantsa, I.; Beinerts, T.; Kalvāns, M.; Milgrāvis, M.; Gerbeth, G. Nanoparticle dispersion in liquid metals by electromagnetically induced acoustic cavitation. Acta. Mater. 2016, 118, 253–259. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Q.; Easton, M.A.; Dargusch, M.S.; Qian, M.; Eskin, D.G.; StJohn, D.H. Role of ultrasonic treatment, inoculation and solute in the grain refnement of commercial purity aluminium. Sci. Rep. 2017, 7, 9729. [Google Scholar] [CrossRef] [PubMed]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zehetbauer, M.J.; Zhu, Y. Producing bulk ultrafine-grained materials by severe plastic deformation: Ten years later. JOM 2016, 68, 1216. [Google Scholar] [CrossRef]
- Zha, M.; Li, Y.; Mathiesen, R.H.; Bjørge, R.; Roven, H.J. Microstructure evolution and mechanical behavior of a binary Al–7Mg alloy processed by equal-channel angular pressing. Acta Mater. 2015, 84, 42–54. [Google Scholar] [CrossRef]
- Sunghak, L.; Dongil, K.; Dongwoo, S. Microstructure and fracture of SiC-particulate-reinforced cast A356 aluminum alloy composites. Metall. Mater. Trans. 1996, 27, 3893–3901. [Google Scholar] [CrossRef]
- Vorozhtsov, S.; Zhukov, I.; Promakhov, V.; Naydenkin, E.; Khrustalyov, A.; Vorozhtsov, A. The Influence of ScF3 Nanoparticles on the Physical and Mechanical Properties of New Metal Matrix Composites Based on A356 Aluminum Alloy. JOM 2016, 68, 3101–3106. [Google Scholar] [CrossRef]
- Khmeleva, M.; Khrustalev, A.; Vorozhtsov, A. Structure and mechanical properties of A356-C alloys. MATEC Web Conf. 2018, 243, 24. [Google Scholar] [CrossRef]
- Vorozhtsov, A.B.; Platov, V.V.; Kozulin, A.A.; Khrustalev, A.P.; Mishin, I.P.; Zhukov, I.A. Study of the effect of TiB2 particles on the structure, deformation behavior, and properties of the aluminum alloy 1550. Vestn. Tomsk. Gos. Univ. Mat. Mekh. 2020, 67, 102–116. [Google Scholar] [CrossRef]
- Stewart, A.T.; Martin, J.W. Dislocation-particle interactions in plastically deformed two-phase aluminium crystals. Acta Metall. 1975, 23, 1–7. [Google Scholar] [CrossRef]
- Hymphreys, F.J.; Hirsch, P.B. The deformation of single crystals of copper and copper-zinc alloys containing alumina particles—II. Microstructure and dislocation-particle interactions. Pros. Roy. Soc. Lond. 1970, A318, 73–92. [Google Scholar] [CrossRef]
- Orowan, E. Condition for dislocation passage of precipitations. Proc. Symp. Intern. Stress Met. Alloy. 1948, VIII, 451–454. [Google Scholar]
- Ashby, M.F. Work hardening of dispersion-hardened crystals. Phil. Mag. 1966, 14, 1157–1178. [Google Scholar] [CrossRef]
- Ebeling, R.; Ashby, M.F. Dispersion hardening of copper single crystals. Phil. Mag. 1966, 13, 805–834. [Google Scholar] [CrossRef]
- Hazzledine, P.M.; Hirsch, P.B. A coplanar Orowan loops model for dispersion hardening. Phil. Mag. 1974, 30, 1331–1351. [Google Scholar] [CrossRef]
- Hymphreys, F.J.; Martin, J.W. The effect of dispersed phases upon dislocation distributions in plastically deformed copper crystals. Phil. Mag. 1967, 16, 927–957. [Google Scholar] [CrossRef]
- Ashby, M.F.; Johnson, K. Materials and Design. In The Art and Science of Materials Selection in Product Design; Butterworth Heinemann: Oxford, UK, 2002; p. 336. [Google Scholar]
- Kovalevskaya, T.A.; Daneyko, O.I. Formation of maximum strength of disperse-strengthened aluminum-based crystalline alloys containing incoherent particles. Bullet. Rus. Acad. Scien. Phys. 2021, 85, 1002–1007. (In Russian) [Google Scholar] [CrossRef]
- Daneyko, O.I.; Kovalevskaya, T.A. Temperature Effect on Stress-Strain Properties of Dispersion-Hardened Crystalline Materials with Incoherent Nanoparticles. Russ. Phys. J. 2019, 61, 1687–1694. [Google Scholar] [CrossRef]
- Kovalevskaya, T.A.; Daneyko, O.I. The Influence of Scale Parameters of Strengthening Phase on Plastic Shear Zone in Heterophase Alloys with Incoherent Nanoparticles. Russ. Phys. J. 2020, 62, 2247–2254. [Google Scholar] [CrossRef]
- Daneyko, O.I.; Kovalevskaya, T.A.; Matvienko, O.V. The influence of incoherent nanoparticles on thermal stability of aluminum alloys. Russ. Phys. J. 2018, 61, 1229–1235. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Stress-Stain State of Pipe Made of Copper-Based Alloy Strengthened with Incoherent Nanoparticles. Russ. Phys. J. 2017, 60, 562–569. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Dislocation Structure of the Pipe Made of Alloy Reinforced with Incoherent Particles Under Uniform Internal Pressure. Russ. Phys. J. 2017, 60, 1233–1242. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T.; Khrus talyov, A.; Zhukov, I.; Vorozhtsov, A. Investigation of stresses induced due to the mismatch of the coefficients of thermal expansion of the matrix and the strengthening particle in aluminum-based composites. Metals 2021, 11, 279. [Google Scholar] [CrossRef]
- Birger, I.A.; Koterov, N.I. Strength Calculation of Aircraft Gas Turbine Engines; M: Mashinostroenie: Moscow, Russia, 1984; p. 208. (In Russian) [Google Scholar]
- Demyanushko, I.V.; Koroleva, E.F. Optimal design of turbomachinery disks. Izv. AN USSR 1972, 2, 176–180. (In Russian) [Google Scholar]
- Demyanushko, I.V.; Birger, I.A. Calculation of the Strength of Rotating Disks; M: Mashinostroenie: Moscow, Russia, 1978; p. 247. (In Russian) [Google Scholar]
- Malinin, N.N. Calculation of a rotating unevenly heated disc of variable thickness. Inz. Sb. 1953, 17, 151–163. [Google Scholar]
- Gamer, U. Tresca’s Yield Condition and the Rotating Disk. J. Appl. Mech. 1983, 50, 676–678. [Google Scholar] [CrossRef]
- Artemov, M.A.; Yakubenko, A.P. Rotating disc mechanical behaviour mathematical modelling. Proc. Voron. State Univ. Ser. Phys. Math. 2014, 1, 30–38. [Google Scholar]
- Lomakin, E.; Alexandrov, S.; Jeng, Y.R. Stress and strain fields in rotating elastic/plastic annular discs. Arch. Appl. Mech. 2016, 86, 235–244. [Google Scholar] [CrossRef]
- Timoshenko, S.; Goodier, J.; Abramson, H. Theory of Elasticity (3rd ed.). J. Appl. Mech. 1970, 37, 888. [Google Scholar] [CrossRef]
- Boresi, A.P.; Schmidt, R.J.; Sidebottom, O.M. Advanced Mechanics of Materials, 5th ed.; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Chakrabarty, J. Theory of Plasticity, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Gamer, U. Elastic-plastic deformation of the rotating solid disk. Ing. Arch. 1984, 54, 345–354. [Google Scholar] [CrossRef]
- Jahromi, B.H.; Nayeb-Hashemi, H.; Vaziri, A. Elasto-plastic stresses in a functionally graded rotating disk. J. Eng. Mat. Tech. 2012, 134, 021004. [Google Scholar] [CrossRef]
- Apatay, T.; Eraslan, A.N. Elastic deformation of rotating parabolic discs: Analytical solutions. J. Fac. Eng. Arch. Gazi Univ. 2003, 18, 115–135. [Google Scholar]
- Calderale, P.M.; Vivio, F.; Vullo, V. Thermal stresses of rotating hyperbolic disks as particular case of non-linearly variable thickness disks. J. Therm. Stress. 2012, 35, 877–891. [Google Scholar] [CrossRef]
- Güven, U. Tresca’s yield condition and the linear hardening rotating solid disk of variable thickness. J. Appl. Mat. Mech. 1995, 75, 805–807. [Google Scholar] [CrossRef]
- Vivio, F.; Vullo, V.; Cifani, P. Theoretical stress analysis of rotating hyperbolic disk without singularities subjected to thermal load. J. Therm. Stress. 2014, 37, 117–136. [Google Scholar] [CrossRef]
- Eraslan, A.N. Elastoplastic deformations of rotating parabolic solid disks using Tresca’s yield criterion. Eur. J. Mech. A/Solids 2003, 22, 861–874. [Google Scholar] [CrossRef]
- Eraslan, A.N. Elastic–plastic deformations of rotating variable thickness annular disks with free, pressurized and radially constrained boundary conditions. Int. J. Mech. Sci. 2003, 45, 643–667. [Google Scholar] [CrossRef]
- Yıldırım, V. A Parametric Study on the Centrifugal Force-Induced Stress and Displacements in Power-Law Graded Hyperbolic Discs. Lat. Am. J. Solids Struct. 2018, 15, e34. [Google Scholar] [CrossRef]
- Thakur, P. Analysis of stresses in a thin rotating disc with inclusion and edge loading. Sci. Technol. Rev. 2013, 63, 9–16. [Google Scholar]
- Aleksandrova, N.N.; Artemov, M.A.; Baranovskii, E.S.; Shashkin, A.I. On stress/strain state in a rotating disk. J. Phys. Conf. Ser. 2019, 1203, 012001. [Google Scholar] [CrossRef]
- Aleksandrova, N. Application of Mises yield criterion to rotating solid disk problem. Int. J. Eng. Sci. 2012, 51, 333–337. [Google Scholar] [CrossRef]
- Aleksandrova, N. Exact deformation analysis of a solid rotating elastic-perfectly plastic disk. Int. J. Mech. Sci. 2014, 88, 55–60. [Google Scholar] [CrossRef]
- Afsar, A.M.; Go, J. Finite element analysis of thermoelastic field in a rotating FGM circular disk. Appl. Math. Mod. 2010, 34, 3309–3320. [Google Scholar] [CrossRef]
- Lamb, H.; Southwell, R.V. The vibrations of a spinning disk. Proc. R. Soc. Ser. A 1921, 99, 272–280. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Residual Stresses Induced by Elastoplastic Unloading in a Tube Made of Dispersion-Hardened Alloy. Russ. Phys. J. 2018, 61, 730–742. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Strengthening Particle Size Effect on Residual Stresses in Dispersion-Hardened Alloy. Russ. Phys. J. 2018, 61, 962–973. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Elastoplastic Deformation of Dispersion-Hardened Aluminum Tube Under External Pressure. Russ. Phys. J. 2018, 61, 1520–1528. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Mathematical modeling of nanodispersed hardening of FCC materials. Acta Met. Sin. 2018, 31, 1297–1304. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Mathematical modeling of plastic deformation of a tube from dispersion-hardened aluminum alloy. MATEC Web Conf. 2018, 243, 8. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Mathematical modeling of plastic deformation of a tube from dispersion-hardened aluminum alloy in an inhomogeneous temperature field. Crystals 2020, 10, 1103. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T. Investigation of the influence of temperature distribution on the stress-strain state of the tube walls made from a disperse-hardened alloy. Bas. Prob. Mat. Sci. 2020, 17, 330–337. [Google Scholar] [CrossRef]
- Zhukov, I.A.; Promakhov, V.V.; Matveev, A.E.; Platov, V.V.; Khrustalev, A.P.; Dubkova, Y.A.; Vorozhtsov, S.A.; Potekaev, A.I. Principles of structure and phase composition formation in composite master alloys of the Al–Ti–B/B4c systems used for aluminum alloy modification. Russ. Phys. J. 2018, 60, 2025–2031. [Google Scholar] [CrossRef]
- Vorozhtsov, S.; Minkov, L.; Dammer, V.; Khrustalyov, A.; Zhukov, I.; Promakhov, V.; Vorozhtsov, A.; Khmeleva, M. Ex-situ introduction and distribution of nonmetallic particles in aluminum melt: Modeling and experiment. JOM 2017, 69, 2653–2657. [Google Scholar] [CrossRef]
- Vencl, A.; Bobić, I.; Stanković, M.; Hvizdoš, P.; Bobić, B.; Stojanović, B.; Franek, F. Influence of secondary phases in A356 MMCs on their mechanical properties at macro-and nanoscale. J. Brazil. Soc. Mech. Sci. Eng. 2020, 42, 1–12. [Google Scholar] [CrossRef]
- Wang, Q.G.; Caceres, C.H.; Griffiths, J.R. Damage by eutectic particle cracking in aluminum casting alloys A356/357. Met. Mater. Trans. A 2003, 34, 2901–2912. [Google Scholar] [CrossRef]
- Ma, S.; Wang, X. Mechanical properties and fracture of in-situ Al3Ti particulate reinforced A356 composites. Mat. Sci. Eng. A 2019, 754, 46–56. [Google Scholar] [CrossRef]
- Wang, M.; Chen, D.; Chen, Z.; Wu, Y.; Wang, F.; Ma, N.; Wang, H. Mechanical properties of in-situ TiB2/A356 composites. Mat. Sci. Eng. A 2014, 590, 246–254. [Google Scholar] [CrossRef]
- Königshofer, R.; Fürnsinn, S.; Steinkellner, P.; Lengauer, W.; Haas, R.; Rabitsch, K.; Scheerer, M. Solid-state properties of hot-pressed TiB2 ceramics. Int. J. Refr. Met. Hard Mat. 2005, 23, 350–357. [Google Scholar] [CrossRef]
- Wang, H.Y.; Xue, F.Y.; Zhao, N.H.; Li, D.J. First-principles calculation of elastic properties of TiB2 and ZrB2. Adv. Mat. Res. 2011, 150, 40–43. [Google Scholar] [CrossRef]
- Voitenko, A.F.; Skripnik, Y.D.; Solov’eva, N.G. Anisotropy of elasticity characteristics for a series of structural metals in the temperature from 4.2 to 300 °K. Strength Mat. 1987, 19, 89–92. [Google Scholar] [CrossRef]
- Khrustalyov, A.P.; Kakhize, N.I.; Platov, V.V.; Zhukov, I.A.; Vorozhtsov, A.B. Influence of Tungsten Nanoparticles on Microstructure and Mechanical Properties of an Al-5% Mg Alloy Produced by Casting. Metals 2022, 12, 989. [Google Scholar] [CrossRef]
- Aguiar, L.R.C.; Carneiro, S.H.S.; Paiano, S. Modal analysis of a satellite with different materials. Rev. Interdiscip. Pesqui. Eng. 2017, 2, 186–198. [Google Scholar]
- Zhang, X.; Jiang, W. First-principles investigation on vibrational, anisotropic elastic and thermodynamic properties for L12structure of Al3Er and Al3Yb under high pressure. Philos. Mag. 2016, 96, 320–348. [Google Scholar] [CrossRef]
- Tang, Z.; Cui, J.; Yu, M.; Zhu, W.; Xu, Z.; Zeng, J.; Xu, T.; Yang, H.; Tan, Y.; Yang, B. A new insight on the diffusion growth mechanism of intermetallic compounds in Al-Er system. Mat. Des. 2022, 224, 111341. [Google Scholar] [CrossRef]
- Ishlinskiy, A.Y.; Ivlev, D.D. Mathematical Theory of Plasticity; Fizmatlit: Moscow, Russia, 2003; p. 704. [Google Scholar]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Elastoplastic Deformation of Dispersion-Hardened Aluminum Tube Under External and Internal Pressure. Russ. Phys. J. 2019, 62, 720–728. [Google Scholar] [CrossRef]
- Yu, M.H. References and Bibliography. In Unified Strength Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2018; pp. 371–460. [Google Scholar] [CrossRef]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Stress-strain State of Dispersion-hardened Aluminum Tube Under External and Internal Pressure. Russ. Phys. J. 2020, 62, 1805–1812. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; Mcgraw Hill: New York, NY, USA, 2010. [Google Scholar]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. A Study of residual stress formation after elastoplastic deformation of pipe walls, made from disperse-hardened aluminum alloy, as a result of external pressure. Tomsk St. Univ. J. Math. Mech. 2021, 72, 102–117. [Google Scholar] [CrossRef]
- Gorhkov, A.G.; Starovoitov, E.I.; Tarlakovsky, D.V. Theory of Elasticity and Plasticity; Fizmatlit: Moscow, Russia, 2002; p. 416. (In Russian) [Google Scholar]
- Matvienko, O.V.; Daneyko, O.I.; Kovalevskaya, T.A. Stress-Strain State of Disperse-Hardened Aluminum Joint Tube Under Internal Pressure. Russ. Phys. J. 2020, 63, 779–790. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).