Critical Evaluation and Thermodynamic Modeling of the Li-Se and Na-Se Binary Systems Using Combined CALPHAD and First-Principles Calculations Method

Abstract

This work presents a complete review of the literature on and a critical evaluation and thermodynamic optimization of the Li-Se and Na-Se binary systems. The modified quasi-chemical model in the pair approximation (MQMPA) was employed to describe the liquid solution exhibiting a high degree of short-range ordering behavior of atoms. The thermodynamic properties of the compounds Li₂Se $\left(cF12\_Fm\overline{3}m\right)$, Na₂Se $\left(cF12\_Fm\overline{3}m\right)$, NaSe $\left(hP8\_P{6}_3/mmc\right),$ and NaSe₂ $\left(tI48\_I\overline{4}2d\right)$ were also calculated by using first-principles density functional theory (DFT) calculations to assist the thermodynamic description of these two binary systems. All the available and reliable experimental data are reproduced within experimental error limits. Moreover, the phase equilibria of these two systems at low total pressure were analyzed by using the developed thermodynamic model.

1. Introduction

Mg and its alloys have great potential as absorbable medical materials from the aspect of mechanical properties and biocompatibility [1]. The density and elastic modulus of Mg and its alloys are closer to human bones than stainless steels and titanium alloys, but the strength still needs to be improved [2]. The thermomechanical properties of Mg-based alloys can be enhanced by alloying elements such as Al, Zn, Ca, Sr, Li, Na, Se, etc. [3,4,5,6,7,8]. Among various alloying elements, Li, Na, and Se can influence the mechanical properties of Mg-based alloy and play certain essential roles in the human body system.

Liu et al. [9] reported that the ductility of Mg-3.3 wt.% Li alloy could be improved by using conventional extrusion and equal-channel angular pressing process. Furui et al. [10] reported that adding 8 wt.% Li to Mg-based alloys resulted in the alloys having excellent superplastic behavior (maximum elongation achieved ~970%) after extrusion with the ECAP process. Moreover, Li is an essential trace element of the human body that greatly impacts daily physiological functioning [11]. Li also has a regulating effect on central nervous activity [12]. In their study of precipitate hardening alloys, Mendis et al. [4,5] prepared Mg-Sn-based alloys with a significantly enhanced hardening effect, using Na as a micro-alloying element. Similar results also have been reported by Sasaki et al. [6] with Na and Zn additions. Gibson et al. [7] reported that Mg-Sn-Zn-Na alloys show excellent creep resistance compared with Mg-Sn binary alloys and Mg-Sn-Zn ternary alloys. On the other hand, Na affects neuromuscular function and plays an important role in neuromuscular junction conduction. It maintains the normal water electrolyte acid–base balance and stabilizes the internal environment of the human body [13]. Thus, Na can be a candidate-alloying element for biodegradable Mg-based alloys. Persaud-Sharma et al. [8] studied the addition of Se to Mg-Zn alloys for novel bio-absorbable cardiovascular stents. They showed that the as-cast Mg-Zn-Se alloy had a better elastic modulus compared with the commercial shape-memory alloys. Moreover, its better fracture elongation can adapt to the actual complex internal environment of the human body. Se participates in the synthesis of antioxidant selenium proteins in important organs, and this also has a potential role in resisting the damage of free radicals to tissues and organs [14,15]. A large number of studies had demonstrated that Se is an effective killer of cancer cells [16], as it forms an internal environment by inhibiting the division and proliferation of cancer cells in the body [17].

Although Li, Na, and Se have been gradually applied as alloying elements for Mg-based alloys to improve the mechanical and biomedical properties, there is still a lack of systematic study to optimize the properties to meet the requirement of body implants. The microstructure of alloys can directly influence the mechanical and biomedical properties. Therefore, the evaluation of the microstructure based on the phase diagram information is essential to develop the optimum Mg-based alloy containing Li, Na, and Se.

The most efficient method for simultaneously obtaining the phase diagrams and thermodynamic properties of alloys is the Calculation of Phase Diagrams (CALPHAD) method [18]. The thermodynamic modeling of Mg-Li [19] and Mg-Na [20] binary systems was already carried out by our group. In the present work, to complete our thermodynamic description of the Mg-Li-Se and Mg-Na-Se systems, the thermodynamic modeling of the Li-Se and Na-Se binary systems were performed based on the critical evaluation of all available experimental data in the literature. In order to assist the assessments, the thermodynamic properties of several intermetallic phases were obtained by using the first principles calculations (FPC) technique [21,22]. This is also part of a large thermodynamic database development of Mg-based alloy systems containing Ag, Ca, Cu, In, Li, Na, Se, Sr, and Zn for its application to Mg-based biomaterial design [23,24,25]. The present thermodynamic calculations were carried out by using the FactSage thermodynamic software [26].

2. Critical Literature Review

2.1. The Li-Se Binary System

The phase equilibria of Li-Se binary system were investigated by Cunningham et al. [27] by using differential thermal analysis (DTA), chemical analysis, optical microscopy, and X-ray diffraction (XRD) methods. The crystal structural information of all the solid phases in the Li-Se binary system is compiled in Table 1. The existence of the intermetallic compound Li₂Se with the antifluorite crystal structure ($cF12\_Fd\overline{3}m$) was confirmed in the referred works [27,28,29]. Moreover, the melting point of the Li₂Se compound was measured to be 1302 ± 2 °C, using DTA, and 1303 ± 5 °C by Cunningham et al. [27], using optical observation, respectively. Sangster and Pelton [30] pointed out that the vapor losses in the open crucibles at this high temperature may result in an error of ±25 °C for the results obtained by Cunningham et al. [27]. The lattice parameter measured by Cunningham [27] by using XRD indicates a narrow solid solubility range of Li₂Se with the excess Se when Se was added to Li containing ammonia. Bergstorm [31] reported the formation of a Li polyselenide with an average composition of Li₂Se_5.4 when Se was added to liquid ammonia containing Li. However, no evidence of a Li₂Se_5.4 compound in the Li-Se binary system was found by Cunningham et al. [27]. Only the Li₂Se compound was confirmed to be stable in the Li-Se binary system by Li et al. [32] through the FPC method. Therefore, it is concluded that Li₂Se is the only stable intermetallic phase, and Li₂Se_5.4 is unstable in the non-solvated state at ambient temperature. Moreover, in the present work, the first-principles density functional theory (DFT) method is introduced to calculate the lattice parameter of the intermetallic compound Li₂Se by using different van der Waal (vdW) methods (PBE, D3, D2, optB86b, optB88, DF, and DF2). It is seen that the vdW correction can greatly improve the descriptions of the lattice parameter of Se, as the vdW force dominates the interaction between Se atomic chains. In the following, we chose DFT-D2 methods as an example to represent the DFT evaluations.

Cunningham et al. [27] measured the liquid miscibility in the Se-rich region by chemical analysis of quenched molten samples. It should be noted that an analytical error for the liquidus composition is about ±5 wt.%, as mentioned by Cunningham et al. [27]. The critical temperature for liquid immiscibility was higher than 800 °C based on the optical analysis results of quenched samples. The liquidus in the composition range from 50 to 70 at.% Se was measured by using the microscopic analysis method. The samples were equilibrated in quartz crucibles at around liquidus temperatures, followed by quenching in liquid nitrogen. Its phase assemblage was analyzed by using an optical microscope. Sangster and Pelton [30] estimated that the error in liquidus measurements by Cunningham et al. [27] would be about ±5 °C at 350 °C and ±15 °C at 700 °C, respectively.

The eutectic reaction temperatures of bcc_A2 (Li) + Li₂Se ↔ liquid and hex_A8 (Se) + Li₂Se ↔ liquid were reported to be 180.5 ± 0.1 °C and 220 ± 0.4 °C, respectively [27]. The terminal solid solubility has not been reported by Cunningham et al. [27]. However, it can be estimated to be very small due to the large differences in chemical nature and crystal structure between Li and Se.

The activity of Li in Li-Se liquid was measured by Cairns et al. [33], using electromotive force (emf) measurements. It should be noted that the emf values were too complicated to be analyzed due to the reaction between the molten Li-Se and LiBr-RbBr or LiF-LiCl-LiI used as the electrolyte for the emf cell. However, the Gibbs energy of formation of Li₂Se compound at 360 °C was successfully derived to be −131.1 kJ/mol-atoms by Cairns et al. [33]. Later, the activity of Li in Li-Se liquid in the composition range of 0.2 to 15.9 at.% Li was measured by Chekova et al. [34], using emf technique. They employed a solid electrolyte membrane of Li₂O-B₂O₃-LiF to prevent the reaction between the Li-Se and salt electrolyte. A constant emf value of 2.085 ± 0.002 V at 420 °C, regardless of Li content, indicated the miscibility gap of the liquid phase in the Se-rich region. The Gibbs energy of mixing of Li-Se liquid at 420 °C in the composition range of 0.2 to 15.9 at.% Li was derived by Morachevskii [35], according to the emf results from Chekova et al. [34].

The enthalpy of formation of Li₂Se compound was first studied by Fabre [36], using aqueous solution calorimetry. A reassessed value of −147.4 ± 1.3 kJ/mol-atoms for the enthalpy of formation of Li₂Se compound at 25 °C was made by Olin et al. [37] based on the data from Fabre [36]. Later, the enthalpy of formation of Li₂Se compound at 25 °C was reported to be −141.97 ± 3 kJ/mol-atoms by Ader [38], using bomb calorimetry, which is less negative than the calculated one from Olin et al. [37]. The enthalpy of formation of the Li₂Se compound was derived to be −139.3 kJ/mol-atoms (at 150 °C) by Morachevskii. Later, the enthalpy of formation of the Li₂Se compound was calculated to be −120.3 kJ/mol-atoms by Li et al. [32], using the DFT method. As an inconsistency existed in the previous reported results [32,36,37,38], the DFT technique with different vdW methods (PBE, D3, D2, optB86b, optB88, DF, and DF2) was employed in the present work to verify the formation enthalpy of Li₂Se compound. The present calculated results are compiled in Table 1 and Table 2.

The entropy of the Li₂Se compound at 25 °C was estimated to be 32 ± 6.97 kJ/K·mol-atoms by Ader [38] based on the formula from Latimer’s method, and 23.3 ± 3.2 kJ/K·mol-atoms by Voronin [39], using a semi-empirical relationship involving vibrational contributions to the entropy. The Gibbs energy of formation of the Li₂Se compound was determined to be −134.97 kJ/mol-atoms (at 150 °C) by Morachevskii, using the Gibbs energy equation [35].

2.2. The Na-Se Binary System

Mathewson [40] investigated the phase diagram of the Na-Se binary system in the composition range of 10 to 98 at.% Se, using thermal analysis, chemical analysis, and optical microscopy methods for the first time. He followed meticulous experimental procedures, including preparing materials, choosing protection gas (dry H2), correcting melting loss, etc. Five intermetallic compounds, namely Na₂Se, NaSe, Na₂Se₃, NaSe₂, and NaSe₃, were reported. The eutectic reaction bcc_A2 (Na) + Li₂Se ↔ liquid occurs nearly at pure Na composition and 97 °C (which is 0.5 °C lower than the melting temperature of pure Na). Similar eutectic reactions were also reported in the Li-Se [27] and K-Se [41] binary systems. To explain the eutectic reaction, a very limited solid solubility of Se in bcc_A2 (Na) was assumed by Sangster and Pelton [42]. Mathewson [40] reported the melting point of compound Na₂Se, which had the same crystal structure as Li₂Se ($cF12\_Fd\overline{3}m$), to be higher than 875 °C. Sangster and Pelton [42] estimated it to be in the range of 900 to 1150 °C by considering the melting temperatures of Li₂Se, Rb₂Se, Li₂S, and Na₂S. Mathewson [40] reported the peritectic melting behavior of Na₂Se, NaSe, and NaSe₂ compounds. The lattice parameter of Na₂Se was measured by Zintl et al. [28], using the film stress determination method. Lattice parameters of Na₂Se and Na₂Se₄ were determined by Klemm et al. [43] by using the thermal analysis method. For the compound Na₂Se₂, Föppl et al. [44] measured its lattice parameter by using the X-ray diffraction method. Moreover, the lattice parameters of the intermetallic compounds Na₂Se, NaSe, and NaSe₂ were calculated by using DFT calculations similar to the Li-Se binary system in this work. The crystal structural information of all the solid phases in the Na-Se binary system is compiled in Table 1.

Table 1. Structural parameters of phases and thermodynamic models used in the present work.

Phase	Strukturb-ericht	Pearson Symbol	Space Group	Lattice Parameters, Å						Model
					References	vdW Method	a	b	c
Liquid	-	-	-	-	-	-	3.5093	-	-	MQMPA a
bcc_A2 (Li)	A2	cI2	$Im\overline{3}m$	Experimental data	[30]	-	3.4268	-	-	CEF b
				Calculated data	TW c	PBE	3.3721	-	-	-
					TW	D3	3.2674	-	-	-
					TW	D2	3.4569	-	-	-
					TW	optB86b	3.4741	-	-	-
					TW	optB88	3.4534	-	-	-
					TW	DF	3.3920	-	-	-
					TW	DF2	3.5093	-	-	-
hex_A8 (Se)	A8	hP3	$P{3}_{1}21$	Experimental data	[30]	-	4.3659	-	4.9537	CEF
				Calculated data	TW	PBE	4.6347	-	5.0300	-
					TW	D3	4.2577	-	5.0888	-
					TW	D2	4.3682	-	5.0609	-
					TW	optB86b	4.1722	-	5.1180	-
					TW	optB88	4.2898	-	5.0986	-
					TW	DF	4.7153	-	5.1036	-
					TW	DF2	4.5682	-	5.2096	-
bcc_A2 (Na)	A2	cI2	$Im\overline{3}m$	Experimental data	[42]	-	4.2906	-	-	CEF
				Calculated data	TW	PBE	4.1954	-	-	-
					TW	D3	4.1603	-	-	-
					TW	D2	3.9799	-	-	-
					TW	optB86b	4.1754	-	-	-
					TW	optB88	4.1841	-	-	-
					TW	DF	4.2130	-	-	-
					TW	DF2	4.1336	-	-	-
Li2Se	C1	cF12	$Fm\overline{3}m$	Experimental data	[27]	-	6.0014	-	-	ST d
					[27]	-	6.0001	-	-	-
					[28]	-	6.0170	-	-	-
					[29]	-	6.0020	-	-	-
				Calculated data	TW	PBE	6.0051	-	-	-
					TW	D3	5.8910	-	-	-
Li2Se	C1	cF12	$Fm\overline{3}m$	Calculated data	TW	D2	5.9999	-	-	-
					TW	optB86b	6.0012	-	-	-
					TW	optB88	6.0186	-	-	-
					TW	DF	6.0894	-	-	-
					TW	DF2	6.0890	-	-	-
Na2Se	C1	cF12	$Fm\overline{3}m$	Experimental data	[28]	-	6.8230	-	-	ST
					[43]	-	6.8130			-
				Calculated data	TW	PBE	6.8535	-	-	-
					TW	D3	6.7003	-	-	-
					TW	D2	6.7762	-	-	-
					TW	optB86b	6.7693	-	-	-
					TW	optB88	6.7761	-	-	-
					TW	DF	6.8792	-	-	-
					TW	DF2	6.8636	-	-	-
NaSe	-	hP8	$P{6}_3/mmc$	Experimental data	[44]	-	4.6850	-	10.5300	ST
				Calculated data	TW	PBE	4.7248	-	10.7860	-
					TW	D3	4.6303	-	10.5777	-
					TW	D2	4.6715	-	10.4226	-
					TW	optB86b	4.6352	-	10.6614	-
					TW	optB88	4.6392	-	10.7487	-
					TW	DF	4.7253	-	11.0405	-
					TW	DF2	4.7088	-	11.0724	-
Na2Se3	-	-	-	-	-	-	-	-	-	ST
NaSe2	-	tI48	$I\overline{4}2d$	Experimental data	[43]	-	10.1926	-	12.2177	ST
				Calculated data	TW	PBE	4.7248	-	10.7860	-
					TW	D3	10.0389	-	12.2162	-
					TW	D2	10.2005	-	11.7552	-
					TW	optB86b	10.1190	-	11.9942	-
					TW	optB88	10.2042	-	12.0233	-
					TW	DF	10.5358	-	12.2918	-
					TW	DF2	10.5920	-	12.1594	-
NaSe3	-	-	-	-	-	-	-	-	-	ST

^a MQMPA, modified quasi-chemical model in the pair approximation; ^b CEF, compound energy formalism; ^c TW, this work; ^d ST, stoichiometric compound.

Table 1. Structural parameters of phases and thermodynamic models used in the present work.

Phase	Strukturb-ericht	Pearson Symbol	Space Group	Lattice Parameters, Å						Model
					References	vdW Method	a	b	c
Liquid	-	-	-	-	-	-	3.5093	-	-	MQMPA a
bcc_A2 (Li)	A2	cI2	$Im\overline{3}m$	Experimental data	[30]	-	3.4268	-	-	CEF b
				Calculated data	TW c	PBE	3.3721	-	-	-
					TW	D3	3.2674	-	-	-
					TW	D2	3.4569	-	-	-
					TW	optB86b	3.4741	-	-	-
					TW	optB88	3.4534	-	-	-
					TW	DF	3.3920	-	-	-
					TW	DF2	3.5093	-	-	-
hex_A8 (Se)	A8	hP3	$P{3}_{1}21$	Experimental data	[30]	-	4.3659	-	4.9537	CEF
				Calculated data	TW	PBE	4.6347	-	5.0300	-
					TW	D3	4.2577	-	5.0888	-
					TW	D2	4.3682	-	5.0609	-
					TW	optB86b	4.1722	-	5.1180	-
					TW	optB88	4.2898	-	5.0986	-
					TW	DF	4.7153	-	5.1036	-
					TW	DF2	4.5682	-	5.2096	-
bcc_A2 (Na)	A2	cI2	$Im\overline{3}m$	Experimental data	[42]	-	4.2906	-	-	CEF
				Calculated data	TW	PBE	4.1954	-	-	-
					TW	D3	4.1603	-	-	-
					TW	D2	3.9799	-	-	-
					TW	optB86b	4.1754	-	-	-
					TW	optB88	4.1841	-	-	-
					TW	DF	4.2130	-	-	-
					TW	DF2	4.1336	-	-	-
Li2Se	C1	cF12	$Fm\overline{3}m$	Experimental data	[27]	-	6.0014	-	-	ST d
					[27]	-	6.0001	-	-	-
					[28]	-	6.0170	-	-	-
					[29]	-	6.0020	-	-	-
				Calculated data	TW	PBE	6.0051	-	-	-
					TW	D3	5.8910	-	-	-
Li2Se	C1	cF12	$Fm\overline{3}m$	Calculated data	TW	D2	5.9999	-	-	-
					TW	optB86b	6.0012	-	-	-
					TW	optB88	6.0186	-	-	-
					TW	DF	6.0894	-	-	-
					TW	DF2	6.0890	-	-	-
Na2Se	C1	cF12	$Fm\overline{3}m$	Experimental data	[28]	-	6.8230	-	-	ST
					[43]	-	6.8130			-
				Calculated data	TW	PBE	6.8535	-	-	-
					TW	D3	6.7003	-	-	-
					TW	D2	6.7762	-	-	-
					TW	optB86b	6.7693	-	-	-
					TW	optB88	6.7761	-	-	-
					TW	DF	6.8792	-	-	-
					TW	DF2	6.8636	-	-	-
NaSe	-	hP8	$P{6}_3/mmc$	Experimental data	[44]	-	4.6850	-	10.5300	ST
				Calculated data	TW	PBE	4.7248	-	10.7860	-
					TW	D3	4.6303	-	10.5777	-
					TW	D2	4.6715	-	10.4226	-
					TW	optB86b	4.6352	-	10.6614	-
					TW	optB88	4.6392	-	10.7487	-
					TW	DF	4.7253	-	11.0405	-
					TW	DF2	4.7088	-	11.0724	-
Na2Se3	-	-	-	-	-	-	-	-	-	ST
NaSe2	-	tI48	$I\overline{4}2d$	Experimental data	[43]	-	10.1926	-	12.2177	ST
				Calculated data	TW	PBE	4.7248	-	10.7860	-
					TW	D3	10.0389	-	12.2162	-
					TW	D2	10.2005	-	11.7552	-
					TW	optB86b	10.1190	-	11.9942	-
					TW	optB88	10.2042	-	12.0233	-
					TW	DF	10.5358	-	12.2918	-
					TW	DF2	10.5920	-	12.1594	-
NaSe3	-	-	-	-	-	-	-	-	-	ST

^a MQMPA, modified quasi-chemical model in the pair approximation; ^b CEF, compound energy formalism; ^c TW, this work; ^d ST, stoichiometric compound.

The existence of liquid immiscibility in the high Se-rich region has been demonstrated by several investigators using emf measurements [45,46,47,48] and electrical resistivity [49] method. However, the critical temperature for the liquid immiscibility has not been reported. Sangster and Pelton [42] compiled the experimental results and proposed a monotectic reaction Liquid#1↔ Liquid#2 + NaSe₃ at ~255 °C and the compositions of liquids at 78 and 99.95 at.% Se.

Table 2. The calculated enthalpies of formation of compounds in the Li-Se and Na-Se binary systems in this work compared with the experimental data from References [21,22,32,35,37,38,50,51].

Phase	Method	Enthalpy of Formation, (kJ/mol-atoms)	Reference
Li2Se	PBE	−120.3	[32]
	emf	−139.3	[35]
	calorimetry	−147.4 ± 1.3	[37]
	electrochemical and calorimetry	−141.97 ± 3	[38]
	PBE	−123.2	FTW a
	D3	−128.4	FTW
	D2	−134.4	FTW
	optB86b	−129.8	FTW
	optB88	−131.5	FTW
	DF	−130.7	FTW
	DF2	−136.1	FTW
	PBE	−142.1	[21,22]
	CALPHAD	−143.6	CTW b
Na2Se	PBE	−109.6	[32]
	electrochemical and calorimetry	−114.2	[38]
	emf	−131.9	[50]
	calorimetry	−114.3	[51]
	the NBS tables	−113.8	[52]
	PBE	−106.3	FTW
	D3	−108.5	FTW
	D2	−116.7	FTW
	optB86b	−108.5	FTW
	optB88	−114.1	FTW
	DF	−115.1	FTW
	DF2	−119.6	FTW
	PBE	−125.1	[21,22]
	CALPHAD	−121.8	CTW
NaSe	PBE	−84.5	[32]
	emf	−100.0	[50]
	calorimetry	−97.0	[51]
	PBE	−82.6	FTW
	D3	−87.5	FTW
	D2	−94.7	FTW
	optB86b	−85.5	FTW
NaSe	optB88	−89.8	FTW
	DF	−90.7	FTW
	DF2	−93.2	FTW
	PBE	−110.8	[21,22]
	CALPHAD	−106.0	CTW
Na2Se3	emf	−93.4	[50]
		−88.7	CTW
NaSe2	PBE	−58.3	[32]
	emf	−86.6	[50]
	PBE	−56.9	FTW
	D3	−62.1	FTW
	D2	−65.4	FTW
	optB86b	−58.3	FTW
	optB88	−61.0	FTW
	DF	−61.6	FTW
	DF2	−62.8	FTW
	PBE	−94.6	[21,22]
	CALPHAD	−74.5	CTW
NaSe3	CALPHAD	−56.3	CTW

^a FTW, calculated by DFT in this work; ^b CTW, calculated by CALPHAD in this work.

Table 2. The calculated enthalpies of formation of compounds in the Li-Se and Na-Se binary systems in this work compared with the experimental data from References [21,22,32,35,37,38,50,51].

Phase	Method	Enthalpy of Formation, (kJ/mol-atoms)	Reference
Li2Se	PBE	−120.3	[32]
	emf	−139.3	[35]
	calorimetry	−147.4 ± 1.3	[37]
	electrochemical and calorimetry	−141.97 ± 3	[38]
	PBE	−123.2	FTW a
	D3	−128.4	FTW
	D2	−134.4	FTW
	optB86b	−129.8	FTW
	optB88	−131.5	FTW
	DF	−130.7	FTW
	DF2	−136.1	FTW
	PBE	−142.1	[21,22]
	CALPHAD	−143.6	CTW b
Na2Se	PBE	−109.6	[32]
	electrochemical and calorimetry	−114.2	[38]
	emf	−131.9	[50]
	calorimetry	−114.3	[51]
	the NBS tables	−113.8	[52]
	PBE	−106.3	FTW
	D3	−108.5	FTW
	D2	−116.7	FTW
	optB86b	−108.5	FTW
	optB88	−114.1	FTW
	DF	−115.1	FTW
	DF2	−119.6	FTW
	PBE	−125.1	[21,22]
	CALPHAD	−121.8	CTW
NaSe	PBE	−84.5	[32]
	emf	−100.0	[50]
	calorimetry	−97.0	[51]
	PBE	−82.6	FTW
	D3	−87.5	FTW
	D2	−94.7	FTW
	optB86b	−85.5	FTW
NaSe	optB88	−89.8	FTW
	DF	−90.7	FTW
	DF2	−93.2	FTW
	PBE	−110.8	[21,22]
	CALPHAD	−106.0	CTW
Na2Se3	emf	−93.4	[50]
		−88.7	CTW
NaSe2	PBE	−58.3	[32]
	emf	−86.6	[50]
	PBE	−56.9	FTW
	D3	−62.1	FTW
	D2	−65.4	FTW
	optB86b	−58.3	FTW
	optB88	−61.0	FTW
	DF	−61.6	FTW
	DF2	−62.8	FTW
	PBE	−94.6	[21,22]
	CALPHAD	−74.5	CTW
NaSe3	CALPHAD	−56.3	CTW

^a FTW, calculated by DFT in this work; ^b CTW, calculated by CALPHAD in this work.

There are a few thermodynamic property data in the literature for the liquid and solid phases in the Na-Se binary system. The activities of Na in the liquid solution were measured over the composition range of 54 to 99.8 at.% Se at 348 °C and 75 to 97 at.% Se at 310 °C by Tumidajski and Toguri [47], using emf measurement. Later, Morachevskii et al. [50] reported the activities of Na in liquid alloys contains 50 to 98 at.% Se at 527 °C and derived the enthalpy of mixing of the liquid solution.

The standard enthalpy of formation of the Na₂Se compound was first measured to be −110.733 ± 1.967 kJ/mol-atoms by Fabre [36], using aqueous solution calorimetry. Mulder and Schmidt [51] determined the enthalpy of formation of Na₂Se and NaSe to be −114.367 and −104.6 kJ/mol-atoms, respectively, using a liquid ammonia calorimeter. The enthalpies of formation of the Na₂Se, NaSe, and NaSe₂ compounds were calculated to be −109.6, −84.5, and −58.3 kJ/mol-atoms by Li et al. [32], using the DFT technique. As listed in Table 2, a large deviations among these reported results of the compounds’ enthalpy of formation requires a further verification. Thus, the DFT technique with different vdW methods (PBE, D3, D2, optB86b, optB88, DF, and DF2) was employed in the present work. The present calculated enthalpy of formation in the Na-Se binary system was presented in Table 2, along with the previous data [21,22,32,35,37,38,50,51,52].

3. Thermodynamic Models

The stable phases in the Li-Se and Na-Se systems considered in the present work were listed in Table 1, along with the model used to describe their thermodynamic properties. The thermodynamic parameters of the pure elements were taken from the SGTE pure substance database [53].

3.1. Liquid Phase

The liquid phase was described by the MQMPA developed by Pelton et al. [54,55]. The important advantages of the MQMPA compared with the Bragg–Williams model (BWM) for modeling the thermodynamic properties of liquid solutions, particularly in high-order systems, have been well demonstrated. The MQMPA is designed to give a better entropy expression even for highly ordered systems in order to permit ordering about any desired composition to be treated by using coordination numbers. Moreover, the energy change for the reaction is introduced as a function of composition with adjustable parameters. Please note that it is not intended as a proper theory of liquid structure, but as a mathematical formalism which has the simplicity and generality and relatively reliable interpolations and extrapolations. Thus, the MQMPA will usually provide better extrapolations into dilute solutions and more realistic entropy-of-mixing curves for higher-order systems. There are significant differences in the predicted thermodynamic properties of ternary and higher-order systems when using the binary parameters based on the MQMPA or the BWM, even if the optimizations of the binary systems look quite similar. It was beneficial to use MQMPA for the liquid phase since it takes into account the short-range-ordering of first nearest neighbors and second nearest neighbors simultaneously. In general, the MQMPA for the liquid phase can be expected to provide more accurate extrapolations regarding multicomponent systems based on parameters in the binary systems. A detailed description of the MQMPA model and its associated notations can be found elsewhere [54,55]. The same notations are used in the present study, and a brief description of the MQMPA model is given below:

For the binary A-B system, the quasi-chemical pair exchange reaction can be considered:

$${(A-A)}_{pair}+{(B-B)}_{pair}=2{(A-B)}_{pair}{}_{,}\mathsf{\Delta }{g}_{AB}$$

(1)

where $i-j$ pair represents the first-nearest-neighbor pair of atoms. The Gibbs energy change for the formation of one mole of $\left(A-B\right)$ pairs with the broken of A-A and B-B pairs according to Reaction (1) is $\mathsf{\Delta }{g}_{AB}/2$. Let $n_A$ and $n_B$ be the number of moles of $A$ and $B$, $n_{AA}$, $n_{BB}$, and $n_{AB}$ be the number of moles of A-A, B-B and A-B pairs. Moreover, $Z_A$ and $Z_B$ are the coordination numbers of $A$ and $B$. Then the Gibbs energy of the solution is given by the following:

$$G=\left(n_A{G}_A^o+n_B{G}_B^o\right)-T\mathsf{\Delta }{S}^{config}+\left(n_{AB}/2\right)\mathsf{\Delta }{g}_{AB}$$

(2)

where $G_A^o$ and $G_B^o$ are respectively, the standard molar Gibbs energies of the pure component $A$ and $B$, and $\mathsf{\Delta }{S}^{config}$ is the configurational entropy of mixing given by randomly distributing the A-A, B-B and A-B pairs in the one-dimensional Ising approximation. The expression for $\mathsf{\Delta }{S}^{config}$ is as follows:

$$\mathsf{\Delta }{S}^{config}=-R\left(n_A\ln X_A+n_B\ln X_B\right)-R\left(n_{AA}\ln \frac{X_{AA}}{Y_A^2}+n_{BB}\ln \frac{X_{BB}}{Y_B^2}+n_{AB}\ln \frac{X_{AB}}{2Y_A{Y}_B}\right)$$

(3)

where $X_{AA}$, $X_{BB}$, and $X_{AB}$ are the mole fractions of the A-A, B-B and A-B pairs, respectively; and Y_A and Y_B are the coordination-equivalent fractions of $A$ and $B$:

$$X_{ij}=\frac{n_{ij}}{n_{AA}+n_{BB}+n_{AB}}\left(i,j=A\mathrm{or}B\right)$$

(4)

$$Y_i=\frac{Z_i{n}_i}{Z_A{n}_A+Z_B{n}_B}\left(i=A\mathrm{or}B\right)$$

(5)

where of Z_A and Z_B are the coordination number of A and B atoms in liquid solution that vary with composition, as follows:

$$Z_A{n}_A=2n_{AA}+n_{AB}$$

(6)

$$Z_B{n}_B=2n_{BB}+n_{AB}$$

(7)

It may be noted that there is no exact expression for the configurational entropy in three dimensions. Although Equation (3) is only an approximate expression in three dimensions, it is exact one-dimensionally (when Z = 2) [55]. As explained in Reference [55], one is forced by the approximate nature of Equation (3) to use non-exact values for the coordination numbers in order to yield good fits between the experimental data and calculated ones. The mathematical approximation of the one-dimensional Ising model of Equation (3) can be partially compensated by selecting values of Z_A and Z_B which are smaller than the experimental values [56]. As is known, the MQMPA model is sensitive to the ratio of coordination numbers, but less sensitive to their absolute values. From a practical standpoint for the development of large thermodynamic databases, values of Z_A and Z_B of the order of 6 were found to be necessary for the solutions with a small or medium degree of ordering (i.e., alloy solutions).

Furthermore, $\mathsf{\Delta }{g}_{AB}$ is the model parameter to reproduce the Gibbs energy of liquid phase of the A-B binary system, which is expanded as a polynomial in terms of the pair fractions, as follows:

$$\mathsf{\Delta }{g}_{AB}=\underset{ s, t\ge 0}{g_{AB}^{st}{X}_{AA}^s{X}_{BB}^t}$$

(8)

where $g_{AB}^{st}$ is the adjustable model parameters which can be a function of the temperature. The letters s and t stand for any real number greater than or equal to 0. The equilibrium state of the system is obtained by minimizing the total Gibbs energy at a constant overall elemental composition, temperature, and pressure. The equilibrium pair distribution is calculated by setting the following:

$${\left(\frac{\partial G}{\partial n_{AB}}\right)}_{n_A,n_B}=0$$

(9)

This gives the “equilibrium constant” for the “quasi-chemical pair reaction” of Equation (1):

$$\frac{X_{AB}^2}{X_{AA}{X}_{BB}}=4\times \exp \left(-\frac{\mathsf{\Delta }{g}_{AB}}{RT}\right)$$

(10)

Moreover, the model permits Z_A and Z_B to vary with composition as follows:

$$\frac{1}{Z_A}=\frac{1}{Z_{AA}^A}\left(\frac{2n_{AA}}{2n_{AA}+n_{AB}}\right)+\frac{1}{Z_{AB}^A}\left(\frac{n_{AB}}{2n_{AA}+n_{AB}}\right)$$

(11)

$$\frac{1}{Z_B}=\frac{1}{Z_{BB}^B}\left(\frac{2n_{BB}}{2n_{BB}+n_{AB}}\right)+\frac{1}{Z_{AB}^B}\left(\frac{n_{AB}}{2n_{BB}+n_{AB}}\right)$$

(12)

where $Z_{AA}^A$ and $Z_{AB}^A$ are the values of $Z_A$ when all nearest neighbors of an atom $A$ are $As$, and when all nearest neighbors of an atom $A$ are $Bs,$ respectively. $Z_{BB}^B$ and $Z_{AB}^B$ are defined similarly. The composition of maximum short-range-ordering is determined by the ratio of the coordination numbers $Z_{AB}^A/Z_{AB}^B$. In the present study, $Z_{AA}^A$ = $Z_{BB}^B$ = 6 to keep the consistency with the previous study, but $Z_{AB}^A$ and $Z_{AB}^B$ were determined in each binary system to reproduce the phase diagram and thermodynamic properties of liquid solution.

3.2. Solid Solutions

The compound energy formalism (CEF) was introduced by Hillert to describe the Gibbs energy of solid phases with sublattices, and ideal mixing of atoms on each sublattice is assumed [57]. In this work, the solid solutions bcc_A2 and hex_A8 (Se) in the Li-Se and Na-Se binary systems were modeled with the CEF, with their sublattice stoichiometry based on the reported crystal structures. Taking the bcc_A2 solution as an example, its Gibbs energy expression, based on the CEF, is obtained by mixing Li, Na, and Se atoms on one sublattice as (Li, Na, and Se). The Gibbs energy of the bcc_A2 solution can be expressed as follows:

$$\begin{gathered} G^{\mathrm{bcc}\_A2}=y_{\mathrm{Li}}{}_{ }{}^{0}G{}_{\mathrm{Li}}^{\mathrm{bcc}}+ y_{\mathrm{Na}}{}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}+y_{\mathrm{Se}}{}_{ }{}^{0}G{}_{\mathrm{Se}}^{\mathrm{bcc}}+RT\left(y_{\mathrm{Li}}\ln y_{\mathrm{Li}}+y_{\mathrm{Na}}\ln y_{\mathrm{Na}}+y_{\mathrm{Se}}\ln y_{\mathrm{Se}}\right)+y_i{y}_j{\left(y_i-y_j\right)}^n\times {}_{ }{}^{n}L{}_{i,j} \\ i,j=Li, \mathrm{Na}, or \mathrm{Se} and i\ne j, and n=0, 1, 2,\dots \end{gathered}$$

(13)

where $y_{\mathrm{Li}}$, $y_{\mathrm{Na}}$, and $y_{\mathrm{Se}}$ are the site fractions of elements Li, Na and Se on the sublattice. The values of ${}_{ }{}^{0}G{}_{\mathrm{Li}}^{\mathrm{bcc}}$, ${}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}$ and ${}_{ }{}^{0}G{}_{\mathrm{Se}}^{\mathrm{bcc}}$ represent the Gibbs free energies of the end members of the pure Li, Na and Se with bcc crystal structure. Moreover, ${}_{ }{}^{n}L{}_{i,j}$ represents the second-nearest-neighbor interaction parameters between Li↔Na, Li↔Se, or Na↔Se atoms in the sublattice, which can be expressed as follows:

$${}_{ }{}^{n}L{}_{i,j}=a_n+b_{n}T+c_{n}T\ln (T)+\cdot \cdot \cdot \cdot \cdot \cdot$$

(14)

The values of the ${}_{ }{}^{n}L{}_{i,j}$ temperature functions are the model parameters evaluated in the present work.

3.3. Stoichiometric Phases

The standard molar Gibbs energies of solid and liquid pure elements and all stoichiometric phases (Li₂Se, Na₂Se, NaSe, Na₂Se₃, NaSe₂, and NaSe₃) can be described by the following:

$$G_T^o=H_T^o-T{S}_T^o$$

(15)

$$H_T^o=\mathsf{\Delta }{H}_{298.15\mathrm{K}}^o+{{\displaystyle \int }}_{298.15\mathrm{K}}^T{C}_{p}dT$$

(16)

$$S_T^o=S_{298.15\mathrm{K}}^o+{{\displaystyle \int }}_{298.15\mathrm{K}}^T\left(C_p/T\right)dT$$

(17)

where $\mathsf{\Delta }{H}_{298.15\mathrm{K}}^o$ is the molar enthalpy of formation of a given species from pure elements ($\mathsf{\Delta }{H}_{298.15\mathrm{K}}^o$ of element stable at 298.15 K and 1 atm is assumed to be 0 J·mol⁻¹; reference state), $S_{298.15\mathrm{K}}^o$ is the molar entropy at 298.15 K, and $C_p$ is the molar heat capacity. As the experimental heat-capacity data for the intermetallics are unavailable, the heat capacities were evaluated by using the Neumann–Kopp rule [58] from its elements.

3.4. Gaseous Phase

Known gas species in this work are Li(g), Li2(g), Na(g), Na2(g), Se(g), and Se2(g) [59,60]. The standard Gibbs energy of each gas species can be expressed by Equations (15)–(17). They were taken from the FACT pure substances database, which utilized compiled values available in relevant compilations [59,60]. The ideal solution was assumed for the gaseous phase.

4. First-Principles Calculations

Due to Li, Na, and Se elements being relatively active, it is difficult to obtain accurate results, and one has to take extra precaution during an experimental procedure. Thus, it is necessary to test through the DFT technique. Based on DFT, all the first-principle calculations were performed with Vienna Ab initio Simulation Package (VASP) [61,62,63,64] and dealt with the ALKEMIE platform [65]. The Perdew–Burke–Ernzerhof functional (PBE) of generalized gradient approximation (GGA), using the projector augmented-wave (PAW) potential, was chosen to deal with the electron–ion interaction [66,67]. To provide an improved description of the van der Waals (vdW) interaction in Se, the advanced vdW corrected methods [68] and nonlocal van der Waals density functional (vdW-DF) [69] were introduced. Li (2s¹), Na (3s¹), and Se (4s²4p⁴) were employed as the valence-electron configurations. The cutoff energy of 700 eV was set for both the Li-Se and Na-Se alloys. The following $\mathrm{K}-\mathrm{points}$ based on the Monkhorst–Pack scheme [70] were adopted as Brillouin Zone sampling: 14 × 14 × 14 for Li and Se, 10 × 10 × 10 for Li₂Se, 8 × 8 × 8 Na₂Se, 8 × 8 × 3 for NaSe, and 4 × 4 × 5 for NaSe₂. The Gamma-centered MP grid was employed for some low-symmetric structures. The relaxation convergences for ions and electrons were 1 × 10⁻⁵ eV and 1 × 10⁻⁶ eV, respectively.

The formation energy, $E_{\mathrm{form}}$, of crystal $A_{\mathrm{x}}{B}_{\mathrm{y}}$ was obtained according to $E_{\mathrm{form}}=E_{total}^{A_{\mathrm{x}}{B}_{\mathrm{y}}}-x{E}^{\left(A\right)}-y{E}^{\left(B\right)}$, where $E_{total}^{A_{\mathrm{x}}{B}_{\mathrm{y}}}$, $E^{\left(A\right)}$, and $E^{\left(B\right)}$ were the total energy of $A_{\mathrm{x}}{B}_{\mathrm{y}}$ and chemical potentials of A and B atoms, respectively. The calculated lattice parameters and enthalpy of formation of the phases of Li₂Se, Na₂Se, NaSe, and NaSe₂ at 0 K, using standard PBE functional and different vdW corrections, are summarized in Table 1 and Table 2, respectively.

5. Results and Discussions

5.1. Thermodynamic Modeling and Evaluation of the Li-Se Binary System

The calculated enthalpy of formation of Li₂Se in the Li-Se binary system at 25 °C is shown in Figure 1 and compared with the previously reported results [32,35,37,38] and the present result with DFT. It is noted that, by including the vdW correction, the present DFT result can better reproduce the enthalpy of formation of Li₂Se than the standard PBE method in the Materials Project [21,22]. The present optimized result of enthalpy of formation of Li₂Se is −143.62 kJ/mol-atoms, which is in good agreement with the experimental data (−138.97 to −148.7 kJ/mol-atoms) and DFT result (−134.4 kJ/mol-atoms). The calculated entropy of formation of the Li₂Se phase at 25 °C is compared in Figure 2 with the estimated data by Morachevskii [35] and Ader [38]. The optimized entropy is within the error limit of the estimated values.

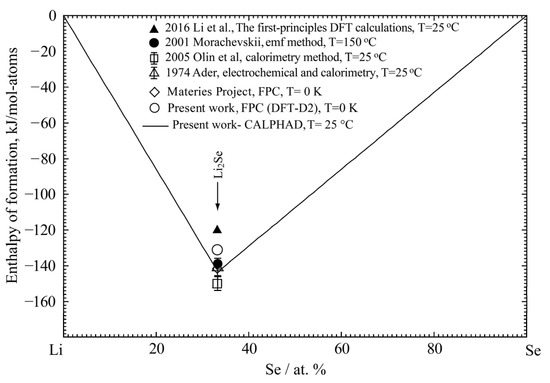
Figure 1. The calculated enthalpy of formation of the Li-Se binary system at 25 °C compared with the previously reported data [32,35,37,38] and the present results.

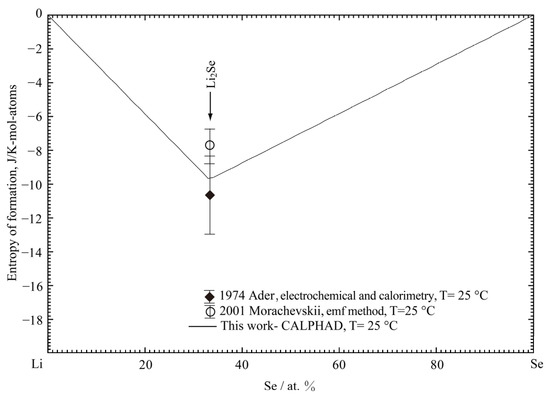
Figure 2. The calculated entropy of formation of the Li-Se binary system at 25 °C compared with the experimental data [35,38].

There is no information reported for the short-range-ordering behavior of Li and Se atoms in the liquid solution. The proposed composition with maximum short-range-ordering of liquid was estimated according to the composition with most negative of enthalpy of formation of solids, as shown in Figure 2. Thus, in order to reproduce such short-range ordering behavior, binary coordination numbers of $Z_{\mathrm{LiSe}}^{\mathrm{Li}}=3$ and $Z_{\mathrm{LiSe}}^{\mathrm{Se}}=6$ were set for the MQMPA in the present study, as listed in Table 3.

Table 3. Optimized model parameters of the liquid phase with MQMPA in the Li-Se and Na-Se binary systems.

Coordination Numbers a				Gibbs Energies of Pair Exchange Reactions (J/mol-atoms)
i	j	${\mathit{Z}}_{\mathit{i}\mathit{j}}^{\mathit{i}}$	${\mathit{Z}}_{\mathit{i}\mathit{j}}^{\mathit{j}}$
Li	Se	3	6	$\mathsf{\Delta }{g}_{\mathrm{Li},\mathrm{Se}}=-123200.0-2.101\times T-2599.7X_{\mathrm{Li}\mathrm{Li}}-\left(23000.0-3.381\times T\right)X_{\mathrm{Se}\mathrm{Se}}+28499.5X_{\mathrm{Se}\mathrm{Se}}^3$
Na	Se	3	6	$\mathsf{\Delta }{g}_{\mathrm{Na},\mathrm{Se}}=-100742.0-\left(9100.0+1.200\times T\right)X_{\mathrm{Na}\mathrm{Na}}-62800.0X_{\mathrm{Se}\mathrm{Se}}$$-27600.0X_{\mathrm{Se}\mathrm{Se}}^2+75700.0X_{\mathrm{Se}\mathrm{Se}}^3+\left(1000.0-8.900\times T\right)X_{\mathrm{Se}\mathrm{Se}}^5$

^a For all the pure elements (Li, Na, Se), $Z_{ij}^j=6$.

Very limited thermodynamic property data are available for the liquid Li-Se solution. Morachevskii [35] estimated the Gibbs energy of mixing in the Se-rich region from the emf data at 420 °C by Chekova et al. [34] in the composition range from 0.2 to 15.9 at.% Li. According to the phase diagram data, the composition range of the experiment by Chekova et al. [34] is in the liquid miscibility gap. Therefore, the partial Gibbs energy of Li in liquid solution should be constant. Based on this assumption and the experimental activity coefficient of Li in nearly pure Se [34], Morachevskii [35] estimated the integral Gibbs energy of liquid solution in the Se-rich region at 420 °C. The calculated Gibbs energy of mixing of the liquid phase of the Li-Se binary system at 420 °C is shown in Figure 3 in comparison with the estimated data by Morachevskii [35]. As shown in Figure 3, the present calculated results are in good agreement with the estimated values.

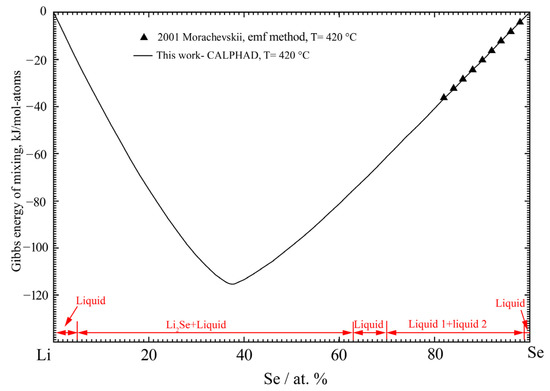
Figure 3. The calculated Gibbs energy of mixing for the liquid phase of the Li-Se binary system at 420 °C compared with the reported results by Morachevskii [35].

The model parameters for solid Li₂Se and liquid Li-Se solution were optimized to reproduce the phase diagram data in Figure 4 and all the available thermodynamic data in Figure 1, Figure 2 and Figure 3. Using the optimized model parameters, the thermodynamic properties and phase equilibria can be back calculated. Figure 5 shows the calculated entropy of mixing of liquid solution at 1400 °C in the present study. Extremely negative entropy of mixing of liquid solution (~−1.4 J/(K∙mol-atoms)) is calculated near 33.3 at.% Se. The entropy of mixing shows the typical M-shaped curve, which indicates that the liquid phase has the maximum short-range-order, with the composition being around 33.3 at.% Se.

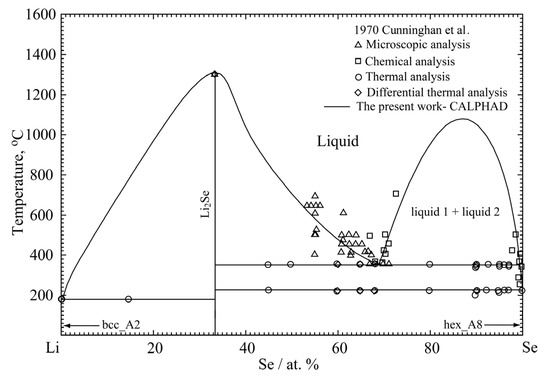
Figure 4. The calculated phase diagram of the Li-Se binary system compared with the experimental data [27].

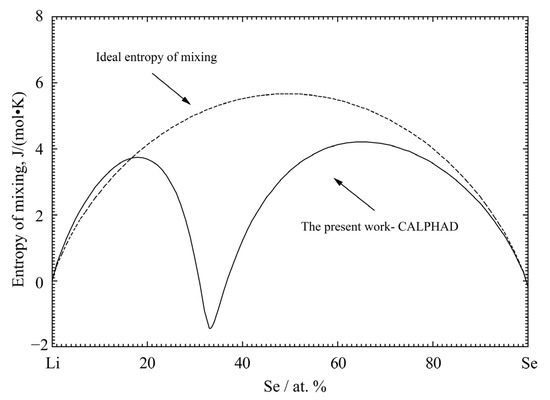
Figure 5. The calculated entropy of mixing for the liquid phase of the Li−Se binary system at 1400 °C.

The calculated phase diagram of the Li-Se binary system is shown in Figure 4, along with the experimental data from Cunningham et al. [27]. As can be seen, the phase equilibria of the Li-Se binary system are well reproduced. The melting point of the Li₂Se compound was calculated to be 1302 °C in the present optimization; thus, it is in good agreement with the experimental data [27]. According to the present optimization results, the critical temperature of liquid immiscibility in the Se-rich region was calculated to be 1068 °C with a liquid composition of 86.9 at.% Se. The optimized model parameters for the Li-Se binary system are listed in Table 3 and Table 4. The calculated invariant reactions and the experimental results from Cunningham et al. [27] are summarized in Table 5.

Table 4. Optimized thermodynamic parameters of solid solutions and compounds in the Li-Se and Na-Se binary systems.

Phase, Model, and Thermodynamic Parameters (J/mol or J/(mol·K))
hex_A8 phase, format (Li, Na, Se):
$G_{\mathrm{Li}}={}_{ }{}^{0}G{}_{\mathrm{Li}}^{\mathrm{bcc}}+20900.0$$;G_{\mathrm{Na}}={}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}+20900.0$$;G_{\mathrm{Se}}={}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}$;
bcc_A2 phase, format (Li, Na, Se):
$G_{\mathrm{Li}}={}_{ }{}^{0}G{}_{\mathrm{Li}}^{\mathrm{bcc}}$$;G_{\mathrm{Na}}={}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}$$;G_{\mathrm{Se}}={}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}+20900.0$;
Li2Se phase, format (Li)2(Se):
$G_{\mathrm{Li}:\mathrm{Se}}=2\times {}_{ }{}^{0}G{}_{\mathrm{Li}}^{\mathrm{bcc}}+{}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}-430855.8+29.288\times T$;
Na2Se phase, format (Na)2(Se):
$G_{\mathrm{Na}:\mathrm{Se}}=2\times {}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}+{}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}-345000.0+49.292\times T$;
NaSe phase, format (Na)(Se):
$G_{\mathrm{Na}:\mathrm{Se}}={}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}+{}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}-212015.5+24.895\times T$;
NaSe2 phase, format (Na)(Se)2:
$G_{\mathrm{Na}:\mathrm{Se}}={}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}+2\times {}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}-225650.0+30.585\times T$;
NaSe3 phase, format (Na)(Se)3:
$G_{\mathrm{Na}:\mathrm{Se}}={}_{ }{}^{0}G{}_{\mathrm{Na}}^{\mathrm{bcc}}+3\times {}_{ }{}^{0}G{}_{\mathrm{Se}}^{hex}-225000.0+28.028\times T$.

Table 5. Calculated invariant reactions in the Li-Se system compared with experimental data [27].

Reaction	Reaction Type	Temperature (°C)	Composition (Se at.%)			References
Liquid ↔ bcc_A2	Melting	180.6	-	0	-	[27]
		180.4	~0	0	-	This work
Liquid ↔ bcc_A2 +Li2Se	Eutectic	~180.6	~0	0	33.3	[27]
		180.4	~0	0	33.3	This work
Liquid ↔ Li2Se	Congruent	1302 ± 25	-	33.3	-	[27]
		1302	~0	33.3	-	This work
Liquid#1 ↔ Li2Se + Liquid#2	Monotectic	350±5	70 ± 2	33.3	99.5 ± 0.3	[27]
		353.8	69.1	33.3	99.6	This work
Liquid ↔ Li2Se + hex_A8	Eutectic	~221	100	33.3	100	[27]
		-	100	33.3	100	This work
Liquid ↔ hex_A8	Melting	221	-	100	-	[27]
		224.7	~0	100	-	This work

Although the Gibbs energies of liquid and solid phases in alloy systems are not very sensitive to the external pressure, the Gibbs energy of the gas phase depends highly upon the external pressure. The standard vapor pressure of Se is very high at high temperatures, so there is a high possibility of vaporization of alloy in the Se-rich region at high temperatures with decreasing total pressure of the system. The phase diagram of the Li-Se binary system under different pressures is calculated in Figure 6. In Figure 6, colored curves represent the isobars of Li-Se ideal mixed gas at different pressure. For example, the red curve represents the Li-Se ideal mixed gas isobar at the pressure of 10⁻³ atm. As can be seen from Figure 6, the evaporation temperature of the liquid phase decreases with decreasing pressure, meaning that the evaporation of liquid phase can be significantly influenced by the pressure. Moreover, the sublimation of intermediate compound can be expected with the decreasing of pressure. This high vapor pressure of the system can easily induce difficulty in the phase diagram measurement at high temperatures. For example, if experiments were carried out with an open crucible under gas-purging condition, the significant Se would be evaporated, and it would be hard to maintain the exact initial composition. Therefore, special care would be necessary to handle the materials and perform the experiments of this binary alloy system.

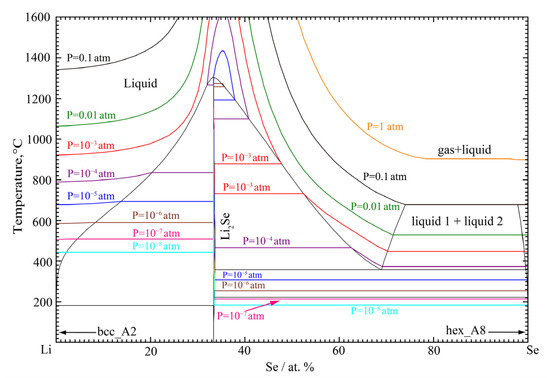
Figure 6. The calculated phase diagram of the Li-Se binary system under different pressures.

5.2. Thermodynamic Modeling and Evaluation of the Na-Se Binary System

Figure 7 shows the calculated enthalpies of formation of all solid phases at 25 °C compared with the experimental data from References [32,38,50,51,52] and the present DFT results. The results obtained with FPC are more negative than the experimental values. This is because the vdW correction can better reproduce the enthalpy of formation of compounds in the Na-Se binary system. As shown in Figure 7, a reasonable agreement was obtained in the present optimization.

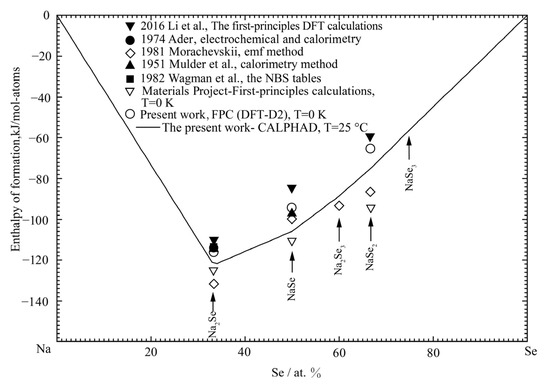
Figure 7. The calculated enthalpy of formation of the Na-Se binary system at 25 °C compared with the previously reported data [32,38,50,51,52] and the present DFT results.

Figure 8 presents the calculated entropies of formation of all solid phases at 25 °C compared with the experimental results [38,71]. The optimized entropies are within the error limit of the experimental value. It should be noted that the enthalpies of formation of solids are extremely negative, so its negative entropies of formation would be reasonable. It is similar to the Li-Se binary liquid solution, as discussed above. The proposed composition with maximum short-range-ordering of liquid was estimated according to the composition with the most negative of enthalpy of formation of solids. Thus, according to the enthalpy of formation of solids, as shown in Figure 7, the binary coordination numbers of $Z_{\mathrm{NaSe}}^{\mathrm{Na}}=3$ and $Z_{\mathrm{NaSe}}^{\mathrm{Se}}=6$ of the Na-Se binary system were set for the MQMPA in the present study, as listed in Table 3.

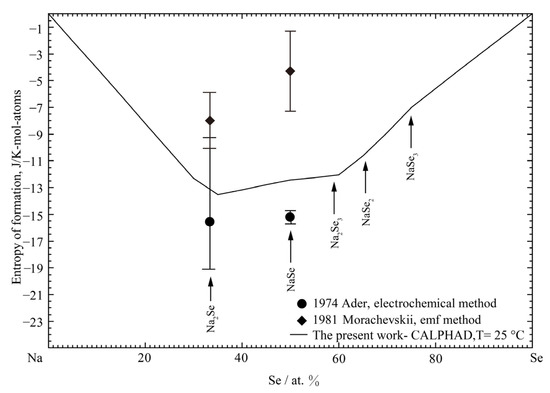
Figure 8. The calculated entropy of formation of the Na-Se binary system at 25 °C compared with the experimental data [38,71].

Only a few thermodynamic data of the liquid solution were available in the Na-Se binary system. Similar to the Li-Se system, Morachevskii [35] estimated the Gibbs energy of mixing in the Se-rich region from the emf data at 523 °C in the composition range from 20 to 50 at.% Se. According to the phase diagram data, the composition range of the experiment by Morachevskii [35] is in the liquid region. Therefore, the partial Gibbs energy of Na in liquid solution should be constant. The calculated Gibbs energy of the mixing of liquid phase at 523 °C compared with the experimental data from Morachevskii [35] is shown in Figure 9. As shown in Figure 9, the present calculated results are in good agreement with the estimated values. Figure 10 shows the calculated entropy of the liquid phase at 1400 °C.

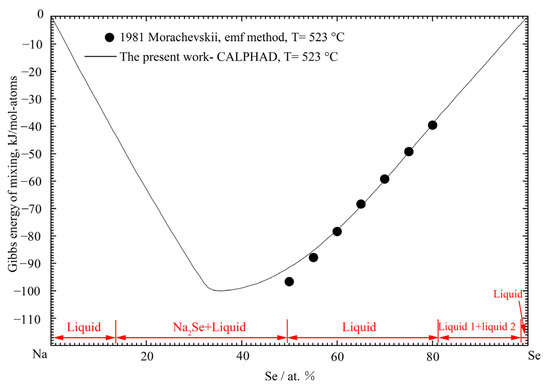
Figure 9. The calculated Gibbs energy of mixing for the liquid phase of the Na-Se binary system at 523 °C compared with the previously calculated result by Romanchenko [71].

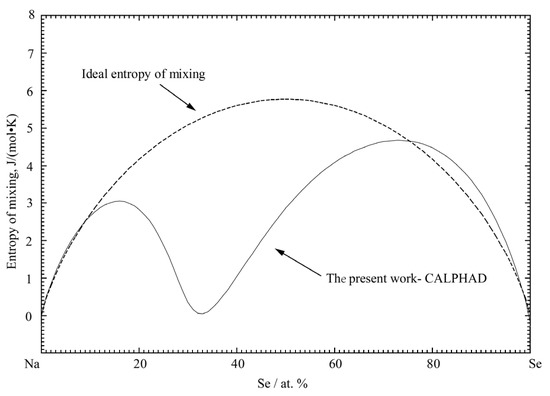
Figure 10. The calculated entropy of mixing for the liquid phase of the Na-Se binary system at 1400 °C.

The calculated phase diagram of the Na-Se binary system is shown in Figure 11, along with the experimental data from References [40,49,50]. The present calculated results are consistent with most of the experimental results shown in Figure 11. The Na-rich part of the calculated curve is slightly different from the experimental data measured by Mathewson [40]. As the high vapor pressure and oxidation of Na-Se alloys occur in the experimental processes, the accuracy of the experimental results is questionable. Therefore, the difference between the present calculated results and the experimental results is acceptable. The melting point of the Na₂Se compound was estimated to be in the range of 900 to 1150 °C by Sangster and Pelton [42], taking the melting temperatures of Li₂Se, Rb₂Se, Li₂S, and Na₂S as references. Therefore, according to the present optimization of the Na-Se system, the melting point of the Na₂Se compound was fixed to be 1087 °C. Moreover, the critical temperature of liquid immiscibility in the Se-rich region was calculated to be 752 °C with the liquid composition of 91.9 at.% Se. All the optimized parameters of the stable phases are listed in Table 3 and Table 4. The calculated invariant reactions and the experimental results from Sangster et al. [42] are all listed in Table 6.

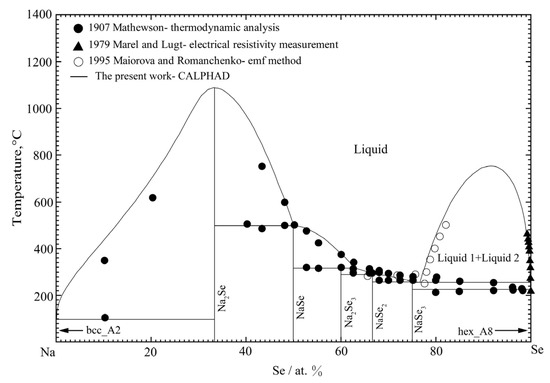
Figure 11. The calculated phase diagram of the Na-Se binary system compared with the experimental data [40,49,50].

Table 6. Calculated invariant reactions in the Na-Se system compared with the experimental data [42].

Reaction	Reaction Type	Temperature (°C)	Composition (Se at.%)			References
Liquid ↔ bcc_A2	Melting	97.8	-	0	-	[42]
		97.7	~0	0	-	This work
Liquid ↔ bcc_A2 + Na2Se	Eutectic	~97.8	~0	~0	33.3	[42]
		97.5	0	0	33.3	This work
Liquid ↔ Na2Se	Congruent	>875	-	33.3	-	[42]
		1087	~0	33.3	-	This work
Liquid+ Na2Se ↔ NaSe	Peritectic	~495	~52	33.3	50	[42]
		496.7	50.1	33.3	50	This work
Liquid+ NaSe ↔ Na2Se3	Peritectic	313	~64	50	60	[42]
		316.4	62.9	50	60	This work
Liquid+ Na2Se3 ↔ NaSe2	Peritectic	290	~69	60	66.7	[42]
		288.5	66.9	60	66.7	This work
Liquid+ NaSe2 ↔ NaSe3	Peritectic	258	~77	66.7	75	[42]
		255.9	75.6	66.7	75	This work
Liquid#1 ↔ Liquid#2 + NaSe3	Monotectic	~255	78	~99.95	75	[42]
		255.2	76.6	99.96	75	This work
Liquid ↔ hex_A8 + NaSe3	Eutectic	~221	99.98	~100	75	[42]
		224.7	99.95	100	75	This work
Liquid ↔ hex_A8	Melting	221	-	100	-	[42]
		224.8	~0	100	-	This work

The phase diagram of the Na-Se binary system under different pressures is calculated in Figure 12. In Figure 12, colored curves represent the isobars of Na-Se ideal mixed gas at different pressure. For example, the red curve represents the Na-Se ideal mixed gas isobar at the pressure of 10⁻³ atm. It can be seen that the evaporation temperature of the liquid phase decreases with the decreasing external pressure. This is similar to the Li-Se binary system in Figure 6. It also means that, as the external pressure decreases, the evaporation of the liquid phase can be significant, and even the sublimation of intermediate compounds can be expected. This high vapor pressure of the Na-Se system can easily induce difficulty in the phase diagram measurement at high temperatures. To sum up, the thermodynamic properties and phase equilibria of the Na-Se binary system were reproduced well in the present work.

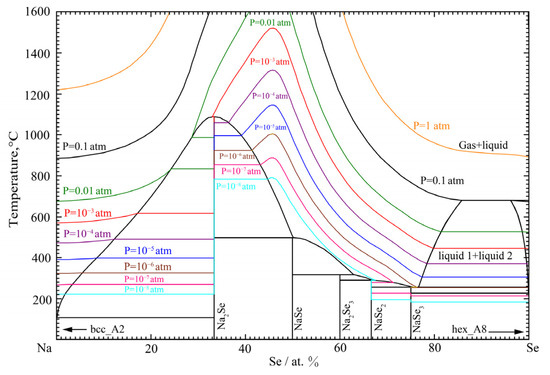
Figure 12. The calculated phase diagram of the Na-Se binary system under different pressures.

6. Conclusions

A critical evaluation and thermodynamic optimization of the Li-Se and Na-Se binary systems were presented in the present work. The MQMPA model was employed to describe the liquid solution exhibiting a high degree of short-range-ordering behavior. The thermodynamic properties of the compounds Li₂Se $\left(cF12\_Fm\overline{3}m\right)$, Na₂Se $\left(cF12\_Fm\overline{3}m\right)$, NaSe $\left(hP8\_P{6}_3/mmc\right)$, and NaSe₂ $\left(I\overline{4}2d\right)$ were calculated by using DFT to assist the thermodynamic medeling of these two binary systems. All the available and reliable experimental data were reproduced within experimental error limits. The phase equilibria of these two systems at low total pressure were analyzed by using the developed thermodynamic models. Finally, a self-consistent thermodynamic database of Li-Se and Na-Se binary systems was constructed as a part of the work of a comprehensive research program to develop the thermodynamic database of novel medical absorbable materials [72,73,74,75].