Abstract
Synovial joints are unique biological tribosystems that allow a person to perform a wide range of movements with minimal energy consumption. In recent years, they have been increasingly called “smart friction units” due to their ability to self-repair and adapt to changing operating conditions. However, in reality, the elements of the internal structure of the joints under the influence of many factors can degrade rather quickly, leading to serious disease such as osteoarthritis. According to the World Health Organization, osteoarthritis is already one of the 10 most disabling diseases in developed countries. In this regard, at present, fundamental research on synovial joints remains highly relevant. Despite the fact that the synovial joints have already been studied fully, many issues related to their operating, prevention, development of pathology, diagnosis and treatment require more detailed consideration. In this article, we discuss the urgent problems that need to be solved for the development of new pharmacological agents, biomaterials, scaffolds, implants and rehabilitation devices for the prevention, rehabilitation and improvement of the treatment effectiveness of synovial joints at various stages of osteoarthritis.
1. Introduction
Synovial joints are remarkable biotribosystems with unique properties, thanks to which a person is able to perform a huge range of motor actions with minimal energy losses due to friction. One of the factors contributing to this is that the basic elements of synovial joints, such as: articular surfaces, covered with articular cartilage; articular cavity; joint capsule; synovium; synovial fluid), are synergistically linked to each other and form an integral biomechanical system [1]. At the same time, a permanent change in the properties of at least one of the listed elements leads to a change in the properties of others and synovial joints in general.
Each of the many joints that form the human skeleton contributes to the preservation of posture and contributes to the realization of movements of the body and its individual parts in space, however, from a biomechanical point of view, large synovial joints of limbs (primarily the lower ones), among other things, perform bearing functions. It is in them that all the qualities that correspond to the so-called “smart friction units” are most clearly manifested [2,3], but at the same time they are also most often susceptible to diseases and injuries that limit the physical activity of people and in many cases lead to disability.
In fact, healthy synovial joint forms a semblance of a cybernetic system functioning on the basis of feedback with the sympathetic nerve center, which regulates the articular cartilage lubrication regime, the synovial fluid composition, and the removal of wear products from the joint capsule [4]. In a healthy body, this system works stably and provides a very low coefficient of friction of articular surfaces (~0.001), but in the course of aging of a person followed by development of diseases or injuries, it begins to malfunction due to the inability of one or several of its elements to perform their functions. As a result, synovial joints pathologies develop, the whole variety of which can be reduced to two forms: (a) arthritis—inflammatory lesion of the joint, regardless of the immediate cause (infections, autoimmune processes) (~20%) and (b) osteoarthritis—dystrophic-degenerative joint damage (~80%). It is osteoarthritis that is not only the most common synovial joints disease, but also the main cause of pain and disability.
The pain that patients with osteoarthritis usually experience is based on two mechanisms: nociceptive (performing a protective function and arising from tissue damage and/or inflammation, due to activation of nociceptors of peripheral or deep tissues) and dysfunctional (not accompanied by neurological deficits or tissue disorders, and arising with various neuro-biological changes in the central nervous system) [5,6]. Therefore, pain might be one of signs that pathological processes occur in the synovial joints: destruction of articular cartilage, structural changes in the subchondral bone, inflammatory processes in synovium, tissue repair, etc. However, the manifestation of pain and dysfunction do not always correlate with the severity of pathological changes in the synovial joints area [5]. Taking this fact into account, it is assumed that, in addition to the severity of the pathological process in synovial joints, other factors are involved in the formation of pain, such as age, gender, race, duration of the disease, body mass index, state of mental health, etc. [7]. Therefore, to assess the real state of synovial joints, only the objective characteristics of a particular patient should be used, established by various methods with a high degree of accuracy. In alternative approaches, big data and artificial intelligence technologies can be used, in which the real state of the synovial joints can be estimated with high reliability from a set of approximate data and the results of studying approximate mathematical models. However, in order to develop algorithms for such estimates, a more detailed study of the synovial joints of each type and the features of its functioning is required, considering the many factors noted above. In addition, these factors should be taken into account in synovial joints models, which is especially important for the development and practical use of technologies for tissue engineering, repair and regeneration of articular cartilage.
For example, the radiographs shown in Figure 1, Figure 2 and Figure 3 clearly show the differences in the developmental stages of the osteoarthritis of the ankle, knee and hip joints, respectively, which, in general, allow a fairly objective assessment of the current state of synovial joints even without taking into account some personalized patient data.
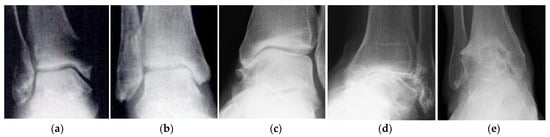
Figure 1.
Stages of development of ankle osteoarthritis: (a) zero (no changes); (b) the first; (c) the second; (d) third; (e) fourth (the complete obliteration of the joint). Adopted from [8].
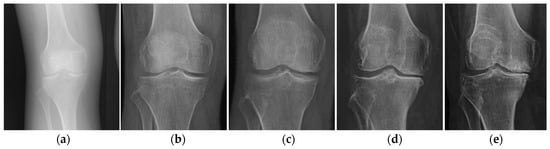
Figure 2.
Stages of development of osteoarthritis of the knee joint according to Kellgren and Lawrence: (a) zero (no changes); (b) the first; (c) the second; (d) third; (e) fourth (severe osteoarthritis). Adopted from [9].
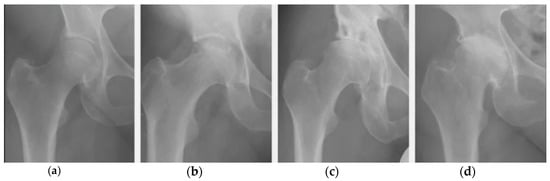
Figure 3.
Stages of development of osteoarthritis of the hip joint: (a) zero (no changes); (b) the first; (c) the second; (d) third (maximum disappearance of cartilaginous tissue from the joint surfaces). Adopted from [9].
There is also a lot of experimental data indicating that, depending on the stage of osteoarthritis, in the vast majority of patients, the synovial fluid indices change, which performs a number of important functions in the synovial joints: trophic (articular cartilage nutrition); metabolic (removal of cells in a state of decay); depreciation (damping the load on articular surfaces); tribological (low coefficient of friction of articular surfaces) and protective (delineation of articular surfaces) [10]. This allows, as shown in [11], informative indicators obtained as a result of cytological studies of synovial fluid to be used for an objective assessment of the stage of the pathological process in the synovial joints in some patients. For this, the authors propose using the value of the so-called “cell index”, defined as the ratio of cells of tissue origin (synovicitis type A and B, as well as their atypical and decaying forms), which are markers of degenerative-dystrophic changes, to blood cells (neutrophils, lymphocytes, monocytes), which determines the inflammatory nature of the pathological process.
The above examples indicate that, in principle, based on objective data on the state of synovial joints elements, it is possible with a certain degree of accuracy to diagnose a patient with synovial joints pathology (regardless of much of his personal data) and to plan its treatment at various stages based on standardized clinical protocols. However, as stated in the osteoarthritis part of the World Health Organization (WHO) report: “The current methods of clinical diagnosis and X-rays are not precise enough to effectively measure status and progression of the condition, which presents serious difficulties in evaluating both the impact of risk factors and the effectiveness of potential therapies” [12]. This is one of the main reasons why osteoarthritis remains the most common synovial joints disease and, according to the WHO, is among the ten most disabling diseases in developed countries [12]. In this regard, at the WHO level, the need to develop new technologies for imaging, diagnostics and biomarkers is noted for more effective measurement of the status and progression of osteoarthritis [13]. At the same time, other issues concerning the anatomy, physiology and treatment of synovial joints in general and their structural elements remain relevant.
It should be noted that the anatomy and physiology of the joints has a long history, the beginning of which is associated with Hippocrates (born around 460 BC). Since then, a huge amount of scientific research has been carried out, the results of which have made it possible to obtain almost complete information about joints (including synovial joints) at various levels. Despite this, interest in this area of research is constantly growing, as evidenced by the graphs of publication activity on topics synovial joints, articular cartilage and synovial fluid from 1950 to 2020, shown in Figure 4.
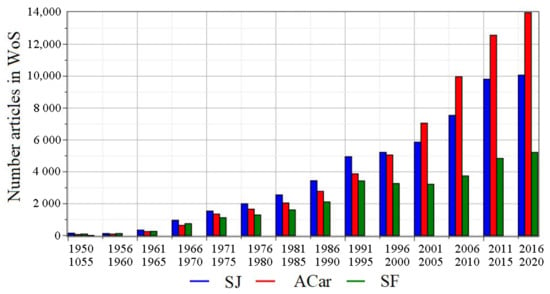
Figure 4.
Dynamics of publications on topics synovial joints (SJ), articular cartilage (ACar) and synovial fluid from 1950 to 2020 (according to Web of Science data).
In our opinion, the reasons for this interest are due to many factors, including: the need to create effective pharmacological agents for the treatment of osteoarthritis, improving the technologies of tissue engineering articular cartilage, developing effective technologies for regenerating damaged articular cartilage, design of biosimilar synovial joints replacements and new technologies for their implantation, etc.
In this article paying tribute and memory to the outstanding scientist D. Dowson who made a significant contribution to the development of the science of synovial joints, we discuss the new problems that need to be solved for the development of new biomaterials, scaffolds, implants, rehabilitation devices, as well as intelligent diagnostic technologies with which to prevent and improve the effectiveness of treatment of synovial joints at various stages of osteoarthritis.
2. Materials and Methods
2.1. Articular Cartilage as a Basis of Synovial Joints
Articular cartilage is a type of connective tissue covering the ends of long bones, which performs bearing functions into the synovial joints while ensuring high wear resistance and low coefficient of friction of articular surfaces. It provides the ease of relative movement of the bones that form the synovial joints and its high durability, provided that the body remains in a healthy state.
The main cells of articular cartilage are chondrocytes, located in a hydrated extracellular matrix, consisting mainly of collagen II and proteoglycans. The swelling proteoglycans tend to create osmotic swelling pressure in articular cartilage, while collagen II counteracts this, thereby providing articular cartilage’s functional integrity, its longitudinal (tensile and compressive) and shear stiffness. Thanks to the combined action of collagen II and proteoglycans, articular cartilage is able to resist many times the load acting on it during the operation of a synovial joint.
Articular cartilage is a heterogeneous, anisotropic, viscoelastic material with a porous structure, in which the density and organization of cells change markedly during growth and maturation. The biochemical and biomechanical properties of articular cartilage also change significantly in depth (from the surface to the area of attachment to the subchondral bone), which is a consequence of cell and extracellular matrix changes. This results in a non-linear response to external forces [14].
In the process of functioning, the synovial joints elements, contacting along articular surfaces, are subjected to compression, shear and sliding relative to each other. Since articular cartilage has a very low permeability, during compression, the hydrostatic pressure of the interstitial fluid present in it rapidly increases, which allows bearing the external load. As the compressive load increases, interstitial fluid begins to be released from the articular cartilage, which leads to a redistribution of some of the load on the solid matrix and to the consolidation of the cartilage. Once equilibrium is reached, the interstitial fluid flow from articular cartilage stops and the entire load is taken up by the solid matrix. This effect is known as stress relaxation in articular cartilage and characterizes one of its most important features that determine the compression process and bearing functions [15]. This effect, as well as the viscoelastic properties of cartilage, can be explained on the basis of a two-phase model [16], in which it is assumed that articular cartilage contains a small number of cells (~1% of the tissue mass) and its mechanical characteristics are mainly determined by extracellular matrix, which consists of liquid and solid phases. The liquid phase (~80% by mass) is represented by interstitial fluid, and the composite solid phase, as a porous, permeable, fiber-bonded material, is represented by macromolecules, among which collagen II and proteoglycans predominate.
It should be noted that articular cartilage is a well-studied biological tissue, complete information about which can be found, for example, in [17], as well as in many other sources. But even the features of articular cartilage, briefly described above, allow us to note that its properties determine the normal physiology of synovial joints. Changes in extracellular matrix, such as collagen II and/or proteoglycans degradation, can lead to a variety of diseases. At the same time, the low regenerative potential of articular cartilage, determined by the peculiarities of its histological structure, may lead to an early development of total osteoarthritis even with local damage.
The mechanisms of articular cartilage damage in osteoarthritis and the conditions for their occurrence (or non-occurrence) are still not fully understood and require further study. At the same time, it is known that osteoarthritis is polyetiologic pathology of synovial joints, the pathogenesis of which can be interpreted in different ways. However, there is no doubt that the development of osteoarthritis is based on the articular cartilage lesion, which occurs in stages [18,19].
2.2. Lubrication and Friction in Synovial Joints
2.2.1. Lubrication and Friction Modes
The lubricating medium of synovial joints is synovial fluid filling articular cartilage. It can be considered as a mobile medium that carries out mass transfer between the synovial joints elements and unites them into a single biophysical and biochemical system [4]. That is, synovial fluid is a kind of reservoir in which nutrients and signaling molecules of cell populations are located in synovial joints. In addition, it houses high molecular weight molecules that are retained in the joint due to their large size, contributing to the maintenance of synovial fluid volume during synovial joints operating [20,21]. In a healthy body, the entire complex of molecular components of synovial fluid determines its unique properties and functions of maintaining synovial joints homeostasis.
One of the most important functions of the synovial fluid (but not the only one) is to provide the synovial joints lubrication, which contributes to the low friction and wear of the articular surfaces, and therefore the locomotion efficiency of the synovial joints. A number of facts indicate that this paradigm was recognized in ancient times. Therefore, for example, in one of the treatises published in the middle of the 18th century, the following is noted: “Human body is a subject so much the more entertaining, as it must strike every one that considers it attentively with an idea of fine mechanical compositions. Where ever the motion of one bone upon another is requisite, there we find an excellent apparatus for rendering that motion safe and free: we see, for instance, the extremity of one bone moulded into an orbicular cavity, to receive the head of another, in order to afford in an extensive play. Both are covered with a smooth elastic crust to prevent mutual abrasion; connected with strong ligaments, to prevent dislocation and enclosed in a bag that contains a proper fluid deposited there, for lubricating the two contiguous surfaces” [22]. Since then and until now, many attempts have been made to uncover the mechanisms underlying biolubrication and friction of synovial joints [23,24,25,26,27,28].
A significant contribution in this direction of research was made by D. Dowson and colleagues [29,30,31,32,33,34,35,36,37,38]. They were able to prove that elastohydrodynamic lubrication (EHL) is the dominant lubrication mode in synovial joints [39,40,41], which led to significant progress in the study of friction mechanisms in synovial joints. However, it was later shown that EHL is not realized in all modes, and at high contact pressure or at a decrease in sliding speed synovial fluid is slowly squeezed out of the intra-articular space. The resistance forces that arise due to the synovial fluid viscosity do not allow it to free itself from this space quickly. As a result, the remaining liquid film is compressed and takes up the load acting on the synovial joints, at least for a short period of time. This process is called squeeze-film lubrication. Experimentally, its existence was confirmed by R.S. Fein [42] and then by the method of asymptotic analysis by J.S. Hou and colleagues [43].
In the model used in [43], the following assumptions were made:
- articular cartilage is a linear porous-permeable two-phase material filled with a linear viscous (Newtonian) fluid;
- synovial fluid is also a Newtonian fluid;
- articular cartilage is a homogeneous layer of thickness H, and the thickness of the synovial fluid film (h) is significantly less than H; h << H;
- the radius of curvature R of the bearing articular surfaces is much larger than H; R >> H;
- the compression of the synovial fluid film is provided by a stepped load in the form of a Heaviside function applied to both bearing articular surfaces.
This allowed the authors to use two small parameters for the asymptotic analysis of the problem: geometric () and physical (), where —apparent viscosity of the interstitial fluid, —diffusive drag in articular cartilage and . For such values at : As a result, they obtained two coupled nonlinear partial differential equations: one for synovial fluid (similar to the Reynolds equation) and one for articular cartilage, the analysis of the numerical solution of which led to the following conclusions [43]:
- articular cartilage material deforms, while the load transfer area increases;
- articular cartilage deformation leads to a decrease in the synovial fluid velocity, thus increasing the time for the formation of the squeezed film;
- synovial fluid in the gap is forced from the central high-pressure region into articular cartilage, and expelled from the tissue at the low-pressure periphery of the load-bearing region;
- tensile hoop stress exists at the cartilage surface despite the compressive squeeze-film loading condition.
It is these features that correspond to the synovial fluid lubrication.
It should be noted that the synovial fluid lubrication mode allows simulating the behavior of synovial joints at different stages of osteoarthritis, which makes it possible to evaluate various options for its treatment, considering many personal factors inherent in a particular patient. From this point of view, the studies by M. Hlavachek published in [44,45,46] are of interest.
The author used a two-phase articular cartilage model, represented by a mixture of an ideal interstitial fluid and a poro-elastic homogeneous isotropic incompressible matrix, which allows one to study the case of early osteoarthritis, when the intact surface zone of normal articular cartilage, which is more rigid than the base material, is already destroyed or worn out. He found that under these conditions, under normal displacement of articular surfaces, the liquid film is rapidly depleted and turns into a synovial gel, which in the case of sliding motion should behave like boundary lubrication [45]. It was shown in [46] that, due to the high viscosity of normal synovial fluid, at very low shear rates, the squeezed film at a fixed time after applying a constant load turns out to be much thicker in a small central part of the lubricated contact region. The rest of the film is thin, since it corresponds to a Newtonian fluid with the same viscosity at high shear rate. At the same time, the filtration is lower for normal articular cartilage with an intact surface zone, due to its lower permeability and compressive rigidity. But even in the case of zero filtration, the effect of thixotropy (liquefaction) on an increase in the minimum thickness of the liquid film appears within a fairly short period of time after the application of a physiological load.
It should be noted that a complete analytical solution to the problem of synovial joints operating in the synovial fluid lubrication mode cannot be found, due to the complexity of the model. However, taking into account some conditions (assumptions), the problem can be simplified significantly. For example, A. Ruggiero managed to reduce the problem of the synovial fluid lubrication of the human ankle joint with synovial fluid filtrated by articular cartilage to an approximate analytical model and find its numerical solution for synovial fluid, represented as Newtonian lubricant [47]. Using the example of the knee joint, as mentioned above, this problem was solved by J.S. Hou and colleagues [43]; in [34] the results of its solution for the hip joint were presented; in [48] for the case of contact of two planes (with reference to the lubricant synovial fluid lubrication of synovial joints). In one of the latest works carried out with the participation of D. Dowson, the mode of pore-hyperelastic lubrication articular cartilage in natural synovial joints was considered. According to the authors, this model describes all modes, including synovial fluid lubrication and boundary lubrication that occurs with increasing load, which represents major progress in modeling the mechanics of articular cartilage [49].
In [50], a short, but rather informative history of the formation of the science branch devoted to friction and lubrication of synovial joints was presented. It is noted that in a natural joint, depending on its state and conditions of operating, various modes can be observed, including boundary, mixed and liquid lubrication. Therefore, when solving applied problems, there is a need for a preliminary assessment of the most probable mode. The most typical synovial joints lubrication mechanisms are shown schematically in Figure 5.
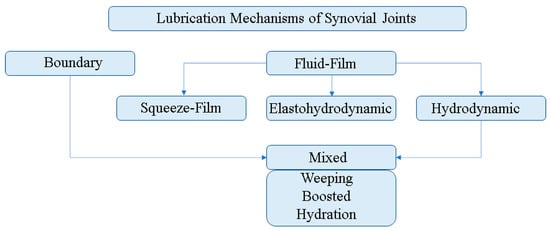
Figure 5.
Most typical synovial joints lubrication mechanisms.
In this article, we analyze the models of synovial joints operating in synovial fluid lubrication mode. Solutions to such problems are extremely important for various applications, such as: development of artificial analogues of synovial fluid, new designs of joint implants, biomaterials, scaffolds for regenerative technologies, for optimal synthesis of regenerative rehabilitation devices, etc.
2.2.2. Mathematical Models of Squeeze Film Lubrication
In [47], considering an approximate analytical model of the synovial fluid lubrication of the ankle joint with porous articular cartilage, the authors obtained the following differential equation:
where is a function describing the change in load on a joint over the time in a walking cycle, is a function characterizing the force perceived by articular surfaces, depending on the size of the gap and the rate of its change , which has the following form:
The parameter notations used in (2) correspond to [47]: —effective radius curvature of the contact of talus (with radius curvature ) and tibia (with radius curvature ): ; —length of the cylindrical joint model; —clearance; —polar angle; —tibial length; —shear modulus of the cartilage matrix; —permeability of the cartilage matrix.
In this model, it is assumed that two rigid infinite cylinders, representing the tibia and talus of the ankle, covered with a thin layers of articular cartilage of equal thickness, are in internal contact with each other [51]. In this case, articular surfaces of the talus is conventionally immobile, while articular surface of the tibia performs exclusively compressive movement , which leads to reduction of the gap in the joint filled with a thin film of synovial fluid.
Equation (1) corresponds to the linear model articular cartilage, in which a geometrically linear (small deformations), homogeneous and isotropic elastic porous matrix is filled with an ideal (Newtonian) interstitial fluid [16]. The effects arising from the deformation of articular cartilage are not taken into account in it. The advantages of such a model are that it is quite simple to use for solving many applied problems, including optimization ones, without using the complex mathematical apparatus necessary for solving systems of non-linear partial differential equations. In this case, the numerical solution of Equation (1) can be obtained by a variety of known methods for various laws of change in the external load .
Later, a modified version of this model was presented, in which the synovial fluid was considered as non-Newtonian [52], which led to the need to take into account coupled stresses [53].
Indeed, if we consider the movements of the elements of the synovial joint only in the sagittal plane, then its model in the first approximation can be represented by two rigid infinite cylinders covered with a porous elastic material and separated by a layer of liquid that can penetrate into the pores. So, for example, the model of the ankle joint is presented as a movable joint of the talus and tibia, the surfaces of which, being in internal contact with each other, are close to cylindrical with radii ( (talus) and (tibia) and are covered with thin layers of poro-elastic articular cartilage the same thickness (). In this case, the talus, which can be conventionally considered motionless, perceives the action of an external load applied to the tibia (Figure 6).
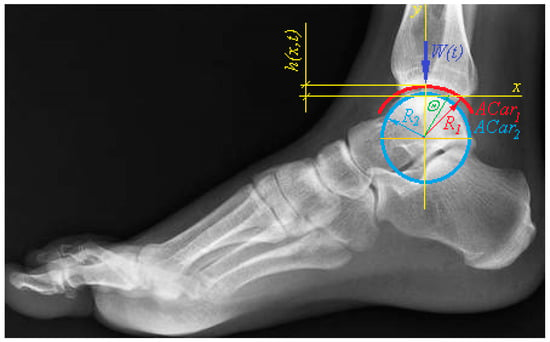
Figure 6.
Coordinate system and location of the main model elements ( are articular cartilages). Adopted from [54].
It is assumed that the external load is set kinematically, by compressing a liquid film with a thickness located between the articular surfaces’s of the joint, i.e.,:
where —total layer thickness of synovial fluid.
If we neglect the inertia and mass forces of synovial fluid and assume that the synovial fluid layer in the joint is a thin film, then the Stokes moment equations in Cartesian coordinates [53] can be represented as follows:
These equations must satisfy the continuity of the liquid medium
and boundary conditions:
where are the velocity field components, ; is a synovial fluid pressure, Pa; is a synovial fluid dynamic viscosity, ; is a couple stress synovial fluid constant, ; is a synovial fluid constant with the dimension of length, [53].
General solution to Equation (3):
where are integration constants.
Giving the boundary conditions (7, 8), expression (9) takes the following form:
Let us now consider the porous structure of articular cartilage and the filtration of synovial fluid through it. In accordance with Darcy’s law for synovial fluid (as a non-Newtonian fluid) [53], we write down the conditions on the boundaries:
where Φ is a articular cartilage permeability, ; , . Integrating (6) over , we write:
or
From this expression, using condition (11), we obtain:
In this way,
Finally, from (14), using condition (12), we obtain the following expression:
To simplify further transformations and the possibility of obtaining an approximate analytical solution, we go over to the polar coordinate system ( and reduce the differential Equation (15) to a dimensionless form using the following dimensionless variables:
where c is the joint clearance; is a normal displacement of the articular surfaces of the tibia towards the articular surfaces of the talus. Substituting (15) into (16), we obtain:
Integrating (17) twice over θ and taking into account the boundary conditions:
we obtain an expression for the dimensionless pressure synovial fluid inside the joint:
To determine the resistance force to the action of an external load, it is necessary to calculate the integral:
In order to find an approximate analytical expression for , we expand in Maclaurin Series in :
where
After substituting (20) in (19) and integrating, we obtain the following expression:
This model is more suitable from a biological point of view. Indeed, it is known that synovial fluid ingredients such as globulin, lubricin, hyaluronic acid, albumin, mucin, surface active phospholipids [4] play an important role in synovial joints lubrication, which contribute to the implementation of various modes of synovial joints lubrication both individually and in combination with each other. With a strong load on the joint, the combination and concentration of lubricant molecules adhered to articular surfaces gives a synergistic effect that helps to reduce the friction coefficient and the rate of wear of articular cartilage under boundary and mixed modes of cartilage lubrication [55]. It is these molecules with a large molecular weight that give synovial fluid the properties of a non-Newtonian liquid, the viscosity of which decreases with an increase in the sliding speed. This is especially typical for synovial fluid in synovial joints affected by arthritis and osteoarthritis, which is explained by a change in the concentration of proteins and polysaccharides on articular surfaces in these pathologies.
In addition, it was found that the properties of synovial fluid, and, consequently, the mechanisms of lubrication, change depending on the value of the contact pressure, temperature, and the rate of protein deposition [56]. This implies the use of methods of the moment theory of elasticity and non-Newtonian properties of synovial fluid, which considers the appearance of coupled stresses in a compressed liquid film [53,57,58].
It should be noted that in recent years it has become practically the norm to represent synovial fluid as a non-Newtonian fluid, since the results of solving most problems become more plausible even with significant simplifications of other elements and parameters of lubrication models [52,59,60,61,62,63]. The only problem that arises in this case is a certain complication of the mathematical side of the problem. However, with modern software, this problem becomes insignificant.
Note that the models described above are not unique and, if necessary, can be refined/changed by formulating new hypotheses and assumptions. However, as practice shows, the complication of the initial data that are used in the formulation of mathematical models does not always lead to a more accurate description of the subject or the modeling process, which, first of all, is explained by the lack of accurate information about their real state and change. For example, the shape of articular surfaces, the parameters of articular cartilage and of synovial fluid differ significantly depending on a large number of factors, and the coefficient of friction in synovial joints, measured in vivo, can never be detected in vitro. This prevents synovial joints models from being built with a predetermined accuracy. Nevertheless, such models allow reliable qualitative characteristics of synovial joints, and in some cases, quantitative ones, to be obtained.
2.3. Regeneration and Regenerative Rehabilitation of Articular Cartilage
The morphology of articular cartilage determines its weak ability to regenerate, which, as a rule, does not allow spontaneous full restoration of defects to be achieved, because in the damaged area, fibrous tissue or fibrous cartilage is formed, which differ significantly in architectonics, biochemical composition, and mechanical properties [64]. In addition, despite the knowledge of the etiopathogenetic mechanisms of articular cartilage lesion, determining the tactics of its treatment and recovery technology is a difficult task with the outcome difficult to predict. Nevertheless, all modern surgical technologies recommended for the treatment of articular cartilage are focused primarily on providing optimal conditions for tissue regeneration, which is close in properties to natural articular cartilage. Moreover, most of them include postoperative rehabilitation, as a necessary procedure for the treatment of the disease, the phases of which are recommended to correlate with the biological phases of tissue regeneration.
This is explained by the fact that articular cartilage is susceptible to mechanical stress, although to a lesser extent than other biological tissues. Moreover, it has been established that physiological mechanical stress is a decisive factor for the development of zonally defined cartilage in adults and vertebrates. This feature of articular cartilage develops during skeletal maturation in postnatal development and is formed by articular movements resulting in a combined load, including compression, extension, and shear [65].
Forced external mechanical influences can also have a significant effect on the biosynthesis of extracellular matrix, chondrocytes, and chondrogenic differentiation of mesenchymal stem cells during repair and regeneration of articular cartilage. In particular, it has been shown that the type, frequency, magnitude, and duration of mechanical stimuli affect the response of chondrocytes and mesenchymal stem cells’ differentiation [66].
It was found that a strong prochondrogenic stimulus for the articular cartilage is its compression in various ways. In particular, dynamic compression causes a reaction of chondrocytes, accompanied by enhanced synthesis of extracellular matrix molecules, including proteoglycans and collagen II [67,68,69], which largely depends on the rate of deformation, frequency, amplitude, and loading history. The response to dynamic hydrostatic pressure is similar to dynamic compression [70,71]. At the same time, it was shown that mechanical stimuli, the parameters of which exceed physiological ones by more than 20%, do not enhance the production of the extracellular matrix [67], and static or very low-frequency load generally suppresses its synthesis [72].
It is also known that articular cartilage responds to mechanical stimuli that promote the formation of shear deformations [73]. The results of a number of in vitro experiments indicate that shear loads, applied simultaneously with compressive ones, lead to a significant increase in the expression of chondrogenic mesenchymal stem cell genes, including proteoglycans-4, which leads to the formation of articular cartilage with a high modulus of elasticity. In this case, the phenotype of the new tissue depends on the frequency and amplitude of mechanical stimuli that simultaneously contribute to shear and compression [74,75,76].
The aforementioned effects of the occurrence of biochemical processes at the cellular and molecular levels in response to the action of mechanical stimuli, which are commonly called mechanotransduction, are well known, but the mechanisms of their occurrence are still poorly understood. There are still no answers to questions regarding the determination of specific parameters of forced external mechanical influences that would contribute to improving the quality and reliability of regenerative processes using regenerative rehabilitation technologies; it is not clear how to apply mechanical stimuli to the affected tissue area in vivo in order to achieve the course of biochemical processes in the desired direction, etc. Answers to these questions can be obtained only on the basis of systematic experimental and theoretical studies, in which studies of tissue regeneration models can play an important role. In this case, both in mathematical models and in their experimental analogs, it is desirable to reproduce the loading of articular cartilage in a non-invasive way by reproducing the natural conditions of articular surfaces contact in different lubrication modes. It can be assumed that the synovial fluid lubrication model of poroelastic articular cartilage in combination with EHL will be the most suitable in such cases.
3. Results
Considering the fact that the most dangerous disease of the synovial joints is osteoarthritis, characterized by degenerative damage to the articular cartilage, a large number of studies in this area are focused on solving problems focused on the prevention and treatment of cartilage diseases, including the development of methods for the regeneration of cartilage tissue, the creation of artificial analogues of synovial fluid and extracellular matrix. In recent years, increasing attention has been paid to the development of regenerative rehabilitation technologies which, as shown above, use the targeted action of mechanical stimuli on the damaged area of the cartilaginous tissue in order to create the best conditions for its regeneration. Despite the fact that the results of a large number of experimental and theoretical studies indicate the high potential of such technologies, it has not yet been possible to achieve significant results in this direction. This is not least due to the peculiarities of the histological structure of the articular cartilage and the complexity of the transmission of the necessary stimuli to the local area of the joint using external sources of their generation. In this regard, the methods of modeling the synovial joints, in terms of exposure to mechanical stimuli created with the help of external generators, are especially relevant. In this case, various lubrication modes can be taken into account, including the squeeze-film lubrication mode.
As a result of the analysis of such models, such important characteristics as the components of the velocity field (10, 14), the pressure of interstitial fluid (18) both on the surface and inside the cartilage, as well as the total force perceived by the articular surfaces (19) at a certain amplitude of kinematic disturbance. In the future, these characteristics can serve as initial data for assessing the stress state of the cartilaginous tissue, which is necessary for the study of models of regenerative rehabilitation. It is clear that they can be obtained as a result of research and more detailed models, but a possible increase in their accuracy will be offset by the fact that numerical models of articular cartilage regeneration are very approximate, since they are based on hypotheses about mechanotransduction and idealization of the structure of cartilage tissue.
Thus, at this stage, one of the most effective ways of researching and designing technologies for regenerative rehabilitation of cartilaginous tissue should include at least two stages: obtaining approximate theoretical data and comparing them with data obtained as a result of experiments. The final result of such studies should be a refined model of the regenerative rehabilitation of articular cartilage, which makes it possible to study the processes of regeneration of cartilage tissue at different stages of the development of pathology, taking into account the effect on it of different nature stimuli.
The approximate squeeze-film lubrication model described above makes it easy to estimate the parameters required for the process analysis. At the same time, Equation (2) obtained on its basis can be solved by many known methods, including those built into the analytical computing system Maple: dverk78 (seventh-eighth order continuous Runge–Kutta method), rkf45 (Fehlberg fourth-fifth order Runge–Kutta method), rosenbrock (Implicit Rosenbrock third-fourth order Runge–Kutta method). When using them, practically identical solutions were obtained, which indicates that the structure of Equation (2) is relatively simple and its numerical solution does not present any computational problems.
The solutions were obtained for an external load, the graph of the change of which during a walking cycle in a dimensionless form is shown in Figure 7. However, in principle, this problem is easily solved with loads of other types, including oscillating ones. The numerical values of the parameters used in the calculations are given in Table A1.
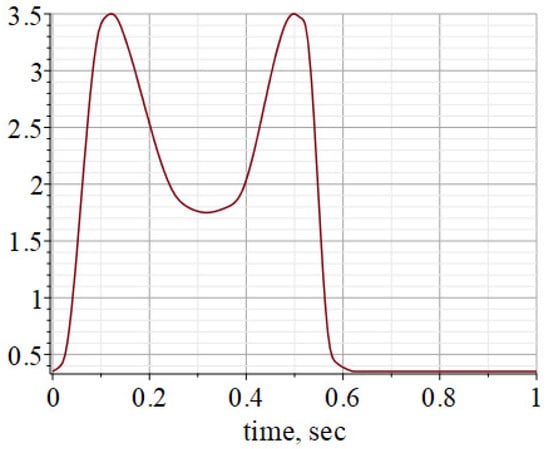
Figure 7.
Graph of changes the external load in a dimensionless form during a normal human walking cycle.
Figure 8 shows graphs of changes in intra-articular pressure at different points in time; Figure 9 is a graph of the change in the thickness of the squeezed fluid film; Figure 10 is a graph of the change in the rate of compression of the ankle joint fluid film.
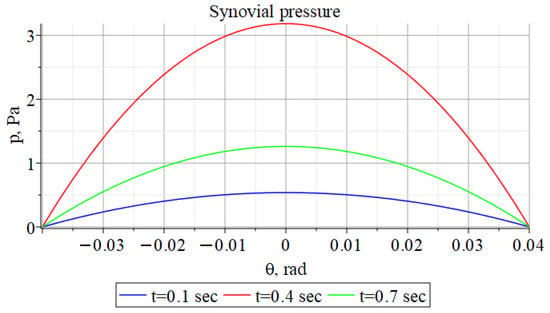
Figure 8.
Graphs of pressure changes in the squeezed fluid film of the ankle joint at different points in the gait cycle.
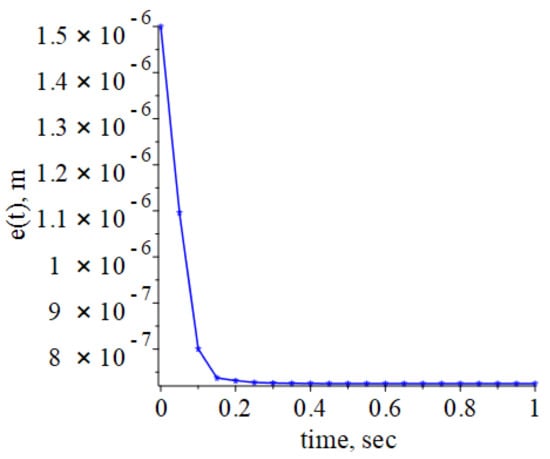
Figure 9.
Graph of the change in the thickness of the squeezed fluid film of the ankle.
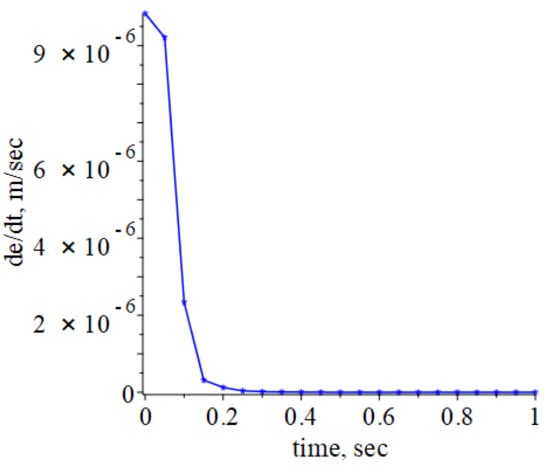
Figure 10.
Graph of the change in the rate of compression of the fluid film of the ankle.
The shapes of the graphs shown in Figure 9 and Figure 10 differ in shape from the similar graphs given in [47]. However, given the small size of the joint gap, these differences can be considered insignificant.
We also investigated the synovial fluid lubrication model of an ankle joint filled with synovial fluid, which has the properties of a non-Newtonian fluid. Figure 11 shows a graph of the function , showing the change in the dimensionless distributed load applied to the elements of the ankle joint during its kinematic loading depending on the variables .
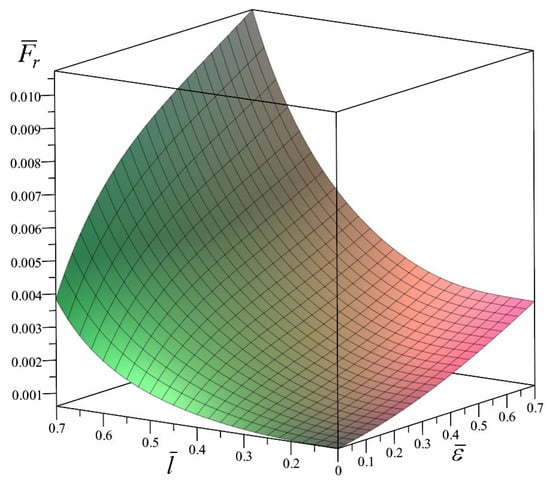
Figure 11.
Change in the dimensionless distributed load applied to the elements of the ankle joint under kinematic loading.
Figure 12 shows graphs of changes in the dimensionless intra-articular pressure at constant and variable values of the dimensionless displacement , and Figure 13 at constant and variable .
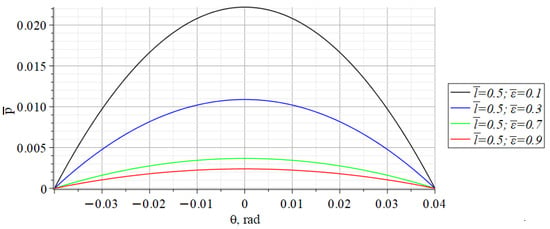
Figure 12.
Graphs of the dimensionless pressure distribution on the contact surfaces of the ankle joint elements at constant and variable values of dimensionless displacement .
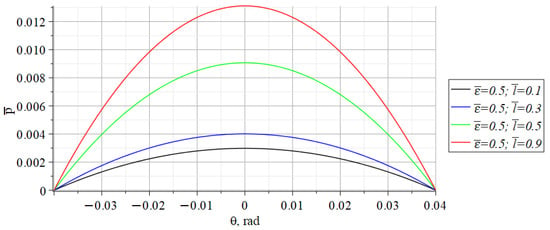
Figure 13.
Graphs of the dimensionless pressure distribution on the contact surfaces of the ankle joint elements at constant values of dimensionless displacement and constant .
Thus, using an approximate model of the contact interaction of articular surfaces covered with porous cartilaginous tissue and separated by a thin layer of synovial fluid, it is possible to determine the law of distribution of fluid pressures in the cartilage and, therefore, to estimate the stress-strain state at each point. This will allow calculating the criterion index of molecular differentiation, for example, the osteogenic index (OI) proposed by D. Carter [77]
where is the number of the type of stimulating effect; is the number of cycles of the i-th type; are hydrostatic and tangential octahedral stresses under stimulating action of the i-th type, respectively. It is noted that at sufficiently large OI values, cells differentiate into bone tissue, and at relatively low values, into cartilaginous tissue. Obviously, as a result of experiments planned based on the results of the study of models of regenerative rehabilitation, criterion indices can be proposed that more accurately determine the direction of differentiation of cartilage tissue models.
4. Conclusions
Analysis of literature sources shows that the development, condition and regeneration of all biological tissues is largely determined by the mechanical loads acting on them. First of all, these are natural physiological loads characteristic of the daily activity of a person. Many examples can be cited indicating that the properties of tissues change significantly when, for various reasons, the effect of external loads on them ceases, for example: in a state of weightlessness, with post-traumatic and postoperative immobilization, with aging and changes in lifestyle, etc. In such cases, the internal structure of tissues changes along with a change in their cellular structure, physical, chemical and mechanical properties. This indicates a phenomenon observed in nature inherent in biological organisms—mechanotransduction, in which, as a result of the action of mechanical stimuli on tissues, a response occurs at the cellular and molecular levels. Taking this fact into account, it can be reasonably assumed that mechanotransduction can be very effective in the processes of regeneration of damaged tissues. And, as noted above, these assumptions are not without foundation. In particular, it was shown that mechanical stimuli applied to cartilaginous tissues in vitro actually enhance the biosynthesis of the extracellular matrix, chondrocytes and chondrogenic differentiation of mesenchymal stem cells in articular cartilage. In the context of health promotion, prevention and treatment of synovial joints, taking into account and using the effects inherent in mechanotransduction can be very useful procedures.
When constructing theoretical models of regenerative processes, poroelastic tissue models are used, the features of which are most often described in the framework of the theory of consolidation by M. Biot [78,79,80,81,82,83,84,85]. In particular, on the basis of such models, algorithms for structural rearrangement and regeneration of bone and cartilaginous tissues can be constructed [86]. They are much more complicated than models based on Darcy’s law, but they allow one to represent the dynamics of structural rearrangement processes in two-phase porous media with much higher accuracy. For tissues with a well-studied microstructure, which include articular cartilage, it is possible to avoid using the methods of the theory of elasticity for calculating anisotropic effective constants of compliance [87]. This is ensured by directly taking into account experimental data on the structure of tissue pores in their poroelastic models.
It should be noted that the results of the study of a number of mathematical models of tissue restructuring, built on the basis of M. Biot’s theory, are currently available for analysis. Among them, the works of L. Maslov [88,89,90,91], D. Carter [92,93,94,95,96,97] and other researchers are of interest, in which, among other things, hypotheses and algorithms for the theoretical study of regenerative processes are presented. However, the use of these and other theoretical results to create conditions for practical repair or regeneration of articular cartilage presents serious difficulties. Not least, this is due to the impossibility of creating a stress-strain state of the desired type in the local area of the damaged tissue.
Information about the pressure in interstitial fluid, on the surface and within the articular cartilage, obtained from the study of the lubrication and contact models of articular surfaces, can only be used as an initial condition for the tissue regeneration process. This is due to the fact that as the distance from articular surfaces increases, the stress-strain state of the tissue also changes dramatically, since the interstitial fluid is released mainly from the surface layer of articular cartilage [95,96]. That is, linear poroelastic models are incapable of assessing the deformations of articular cartilage as a whole, since they are based on the assumption that there is no interstitial fluid flow inside the tissue. At the same time, such models describe quite well the behavior of interstitial fluid released in vivo from articular cartilage under load in the intra-articular space. The interstitial fluid is trapped between two mating synovial joints elements and maintains a high level of pressure, preventing high contact stresses and ensuring low friction between the extracellular matrix elements of the two mating articular surfaces. An experimental confirmation of this effect is given in references [97,98].
It should be noted that synovial joints are striking examples of the optimality of biological systems characterized by high functional efficiency and resistance to external factors. However, when normal conditions of operating are violated, such systems lose their unique properties and their structural elements quickly degrade. In synovial joints, first of all, degradation of articular cartilage and synovial fluid occurs, which, in turn, leads to joint disease and an increase in the rate of degradation. In the early stages of the disease, this situation can be corrected by conservative methods of treatment, the stages of which should be combined with various rehabilitation procedures, including mechanotherapy. This medical field, which has received the name regenerative rehabilitation, is gaining increasing popularity and recognition in the medical community [99]. However, the effectiveness of regenerative rehabilitation is manifested to a greater extent in applications focused on tissue regeneration. With regard to articular cartilage, this boils down to the impact on its damaged areas of such mechanical stimuli that would provide an increase in the biosynthesis of extracellular matrix, chondrocytes and chondrogenic differentiation of mesenchymal stem cells.
The currently known models of tissue restructuring and regeneration under the influence of mechanical stimuli cannot be considered sufficient to develop optimal regenerative rehabilitation technologies on their basis. This is partly due to the fact that they are built mainly on a mechanistic basis and the biological component is poorly represented in them. This also applies to the models of lubrication and articular surfaces’ contact interaction. Such models allow one to perform an approximate assessment of the functional state of the synovial joints, predict the development of destructive and pathological processes in it, and also have an idea of the initial conditions of the processes of articular cartilage regenerative rehabilitation. At the same time, they do not take into account the death and survival of mesenchymal stem cells inhabited in articular cartilage for the purpose of its regeneration, changes in the extracellular matrix structure, the qualitative composition of synovial fluid, and other biological processes. In this regard, in order to increase the efficiency of the reliability of the regeneration process, scaffolds are introduced into the damaged area of articular cartilage, which are populated in vitro in mesenchymal stem cell bioreactors, thereby providing better conditions for cell proliferation and survival. As practice shows, the combination of this approach with the simultaneous action of mechanical stimuli on articular cartilage contributes to the emergence of the best conditions for its regeneration.
However, the currently used articular cartilage regeneration and regenerative rehabilitation technologies can be considered effective only for the restoration of small areas of the affected tissue located closer to articular surfaces. Unfortunately, with osteoarthritis at the last stages of development, it has not yet been possible to ensure the repair or regeneration of articular cartilage. The most effective medical procedure in such cases is synovial joints arthroplasty, which consists in replacing it with an artificial analogue—an endoprosthesis. Despite the fact that modern endoprostheses are made from special biomaterials similar in properties to biological tissues [100], and their designs create high-tech products [101,102], they do not fully ensure the functionality of natural joints. First of all, they do not provide the lubrication conditions inherent in natural synovial joints and the natural coefficient of friction, which leads to their wear and, as a result, to metalosis, and ultimately to the need for reprosthetics. This and other potential pathologies that may arise after synovial joints arthroplasty do not allow this surgery to be considered as a complete replacement for a natural joint. However, the technical means and technologies of synovial joints arthroplasty are being perfected, which is achieved by bringing artificial joints closer to the natural ones by way of their more detailed study both at the level of experiments and on the basis of the study of new mathematical models.
Author Contributions
Conceptualization, V.L.P., A.M.P. and V.I.P.; investigation, A.M.P. and V.I.P.; writing, review and editing, V.L.P., A.M.P. and V.I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Foundation for Basic Research (grant No. 20-03-00046A).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Tibial length | |
| Clearance | |
| Integration constants | |
| Gap between articular surfaces | |
| Rate change in the gap between articular surfaces | |
| Function characterizing the force perceived by articular surfaces | |
| Dimensionless resistance force to the action of an external load | |
| Articular cartilage layer thickness | |
| Thicknes of poro-elastic articular cartilage layers | |
| Total layer thickness of synovial fluid | |
| Synovial film thickness | |
| Dimensionless parameters and | |
| Diffusive drag in articular cartilage | |
| Length of the cylindrical joint model | |
| Synovial fluid constant with the dimension of length: | |
| Dimensionless parameters and | |
| p | Synovial fluid pressure |
| Dimensionless parameter p | |
| Effective radius of curvature of the contact of talus and tibia: | |
| Radius of talus curvature | |
| Radius of tibia curvature | |
| Time | |
| u, v, w | Velocity field components of fluid media |
| Law of change of an external load for unit of length | |
| Cartesian coordinates of the ankle model | |
| Parameter: | |
| Polar angle: | |
| Small parameter: | |
| Small parameter: | |
| Dimensionless parameter: | |
| Couple stress synovial fluid constant | |
| Polar angle of the ankle model | |
| Synovial fluid dynamic viscosity | |
| Apparent viscosity of the interstitial fluid | |
| Φ | Permeability of the cartilage matrix |
| Dimensionless parameter Φ |
Appendix A

Table A1.
Numerical values used for the calculations [45].
Table A1.
Numerical values used for the calculations [45].
| Parameters | Numerical Values | Units |
|---|---|---|
| a | [m] | |
| L | [m] | |
| c | [m] | |
| R | [m] | |
| R1 | [m/s] | |
| Ф | [m2] | |
| [rad] | ||
| [Pa s] |
References
- Pavlova, V.N. Components of the internal environment of the joints and their functional interaction. Adv. Mod. Biol. 1989, 107, 238–242. (In Russian) [Google Scholar]
- Pawlak, Z.; Pai, R.; Mrela, A.; Kaczmarek, M.; Yusuf, K.Q.; Urbaniak, W. Natural articular cartilage: A smart biointerface. J. Comput. Methods Sci. Eng. 2019, 19, 479–489. [Google Scholar] [CrossRef]
- Chernyakova, Y.M.; Pinchuk, L.S. The synovial joint as a “smart” friction unit. Frict. Wear 2007, 28, 410–417. (In Russian) [Google Scholar]
- Pinchuk, L.S.; Chernyakova, Y.M.; Ermakov, S.F. Tribo Physics of Synovial Fluid, 1st ed.; Belarusian Science: Minsk, Belarus, 2010; pp. 3–381. (In Russian) [Google Scholar]
- Turovskaya, E.F.; Alekseeva, L.I.; Filatova, E.G. Modern ideas about the pathogenetic mechanisms of pain in osteoarthritis. Sci. Pract. Rheumatol. 2014, 52, 438–444. (In Russian) [Google Scholar] [CrossRef]
- Sakovets, T.G. Features of neuropathic pain with joint damage. Pract. Med. 2014, 4, 103–106. (In Russian) [Google Scholar]
- Lim, A.Y.; Doherty, M. What of guidelines for osteoarthritis? Int. J. Rheum. Dis. 2011, 14, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Kraus, V.B.; Kilfoil, M.; Hash, T.W.; McDaniel, G.; Renner, J.B.; Carrino, J.A.; Adams, S. Atlas of radiographic features of osteoarthritis of the ankle and hindfoot. Osteoarthritis Cartilage 2015, 14, 2059–2085. [Google Scholar] [CrossRef]
- Knee Osteoarthritis: Forms, Diseases, Primary Analyzes, Stages. Available online: https://gp195.ru/bolezni/osteoartrit-lechenie.html (accessed on 15 December 2020).
- Kotelkina, A.A.; Struchko, G.Y.; Merkulova, L.M.; Kostrova, O.Y.; Stomenskaya, I.S.; Timofeeva, N.Y. Characteristics of synovial fluid in normal conditions and in some pathological processes. Acta Med. Eurasica 2017, 4, 24–30. [Google Scholar]
- Netyaga, S.V.; Dubrovin, G.M.; Netyaga, A.A. The role of cytological examination of synovial fluid in the diagnosis of degenerative-dystrophic changes in the joints. Man His Health 2005, 1, 45–49. (In Russian) [Google Scholar]
- WHO. Department of Chronic Diseases and Health Promotion. Available online: http://www.who.int/chp/topics/rheumatic/en/ (accessed on 23 September 2020).
- Kaplan, W.; Wirtz, V.J.; Mantel-Teeuwisse, A.; Stolk, P.; Duthey, B.; Laing, R. Priority Medicines for Europe and the World 2013 Update; World Health Organization: Geneva, Switzerland, 2013. [Google Scholar]
- Dabiri, Y.; Li, L.P. Influences of the depth-dependent material inhomogeneity of articular cartilage on the fluid pressurization in the human knee. Med. Eng. Phys. 2013, 35, 1591–1598. [Google Scholar] [CrossRef]
- Mow, V.C.; Gu, W.Y.; Chen, F.H. Structure and Function of Articular Cartilage and Meniscus. In Basic Orthopaedic Biomechanics and Mechano-Biology, 3rd ed.; Mow, V.C., Huiskes, R., Eds.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2005; pp. 181–258. [Google Scholar]
- Mow, V.C.; Kuei, S.C.; Lai, W.M.; Armstrong, C.G. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. J. Biomech. Eng. 1980, 102, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Pavlova, V.N.; Kopyeva, T.N.; Slutsky, L.I.; Pavlov, G.G. Cartilage, 1st ed.; Medicine: Moscow, Russia, 1988; pp. 3–320. (In Russian) [Google Scholar]
- Brandt, K.D.; Dieppe, P.; Radin, E.L. Etiopathogenesis of Osteoarthritis. Rheum. Dis. Clin. N. Am. 2008, 34, 531–559. [Google Scholar] [CrossRef] [PubMed]
- Davies-Tuck, M.L.; Wluka, A.E.; Wang, Y.; Teichtahl, A.J.; Jones, G.; Ding, C.; Cicuttini, F.M. The natural history of cartilage defects in people with knee osteoarthritis. Osteoarthr. Cartil. 2008, 16, 337–342. [Google Scholar] [CrossRef]
- Scott, D.; Coleman, P.J.; Mason, R.M.; Levick, J.R. Concentration Dependence of Interstitial Flow Buffering by Hyaluronan in Synovial Joints. Microvasc. Res. 2000, 59, 345–353. [Google Scholar] [CrossRef] [PubMed]
- Scott, D.; Coleman, P.J.; Mason, R.M.; Levick, J.R. Interaction of intraarticular hyaluronan and albumin in the attenuation of fluid drainage from joints. Arthritis Rheum. 2000, 43, 1175–1182. [Google Scholar] [CrossRef]
- Hunter, W. Of the structure and diseases of articulating cartilages, by William Hunter, surgeon. Philos. Trans. R. Soc. Lond. 1743, 42, 514–521. [Google Scholar] [CrossRef]
- Dedinaite, A. Biomimetic lubrication. Soft Matter 2012, 8, 273–284. [Google Scholar] [CrossRef]
- Klein, J. Molecular mechanisms of synovial joint lubrication. J. Eng. Tribol. 2006, 220, 691–710. [Google Scholar] [CrossRef]
- Wang, M.; Liu, C.; Thormann, E.; Dėdinaitė, A. Hyaluronan and Phospholipid Association in Biolubrication. Biomacromolecules 2013, 14, 4198–4206. [Google Scholar] [CrossRef]
- Dėdinaitė, A.; Wieland, D.C.F.; Bełdowski, P.; Claesson, P.M. Biolubrication synergy: Hyaluronan—Phospholipid interactions at interfaces. Adv. Colloid Interface Sci. 2019, 274, 102050. [Google Scholar] [CrossRef]
- Pradal, C.; Yakubov, G.E.; Williams, M.A.K.; McGuckin, M.A.; Stokes, J.R. Lubrication by biomacromolecules: Mechanisms and biomimetic strategies. Bioinspiration Biomim. 2019, 14, 051001. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.; Smith, D.W.; Miramini, S.; Gardiner, B.S.; Zhang, L. A coupled contact model of cartilage lubrication in the mixed-mode regime under static compression. Tribol. Int. 2020, 1–11, 106185. [Google Scholar] [CrossRef]
- Dowson, D.; Unsworth, A.; Wright, V. Analysis of ‘boosted lubrication’ in human joints (reprinted from vol 1, 1959). Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 71–76. [Google Scholar]
- Dowson, D. Paper 12: Modes of Lubrication in Human Joints. Proc. Inst. Mech. Eng. Conf. Proc. 1966, 181, 45–54. [Google Scholar] [CrossRef]
- Dowson, D.; Wright, V.; Longfield, M.D. Human joint lubrication. Biomed. Eng. 1969, 4, 160–165. [Google Scholar] [PubMed]
- Wright, V.; Dowson, D.; Unsworth, A. The lubrication and stiffness of joints. Mod. Trends Rheumatol. 1971, 2, 30–45. [Google Scholar] [PubMed]
- Unsworth, A.; Dowson, D.; Wright, V. Some new evidence on human joint lubrication. Ann. Rheum. Dis. 1973, 32, 587–588. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.M.; Dowson, D.; Fisher, J. The Effect of Porosity of Articular Cartilage on the Lubrication of a Normal Human Hip Joint. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1992, 206, 117–124. [Google Scholar] [CrossRef] [PubMed]
- Jalali-Vahid, D.; Jagatia, M.; Jin, Z.M.; Dowson, D. Prediction of lubricating film thickness in a ball-in-socket model with a soft lining representing human natural and artificial hip joints. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2001, 215, 363–372. [Google Scholar] [CrossRef]
- Jin, Z.M.; Dowson, D. Elastohydrodynamic Lubrication in Biological Systems. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2005, 219, 367–380. [Google Scholar] [CrossRef]
- Dowson, D. Bio-tribology. Faraday Discuss. 2009, 156, 9–30. [Google Scholar] [CrossRef] [PubMed]
- Ghanbarzadeh, A.; Wilson, M.; Morina, A.; Dowson, D.; Neville, A. Development of a new mechano-chemical model in boundary lubrication. Tribol. Int. 2016, 93, 573–582. [Google Scholar] [CrossRef]
- Medley, J.B.; Dowson, D.; Wright, V. Transient Elastohydrodynamic Lubrication Models for the Human Ankle Joint. Eng. Med. 1984, 13, 137–151. [Google Scholar] [CrossRef] [PubMed]
- Dowson, D.; Jin, Z.-M. Micro-Elastohydrodynamic Lubrication of Synovial Joints. Eng. Med. 1986, 15, 63–65. [Google Scholar] [CrossRef]
- Dowson, D. Elastohydrodynamic and micro-elastohydrodynamic lubrication. Wear 1995, 190, 125–138. [Google Scholar] [CrossRef]
- Fein, R.S. Research Report 3: Are Synovial Joints Squeeze-Film Lubricated? Proc. Inst. Mech. Eng. Conf. Proc. 1966, 181, 125–128. [Google Scholar] [CrossRef]
- Hou, J.S.; Mow, V.C.; Lai, W.M.; Holmes, M.H. An analysis of the squeeze-film lubrication mechanism for articular cartilage. J. Biomech. 1992, 25, 247–259. [Google Scholar] [CrossRef]
- Hlaváček, M. The role of synovial fluid filtration by cartilage in lubrication of synovial joints—II. Squeeze-film lubrication: Homogeneous filtration. J. Biomech. 1993, 26, 1151–1160. [Google Scholar] [CrossRef]
- Hlavachek, M. Squeeze-film lubrication of the human ankle joint with synovial fluid filtrated by articular cartilage with the superficial zone worn out. J. Biomech. 2000, 33, 1415–1422. [Google Scholar]
- Hlavachek, M. The thixotropic effect of the synovial fluid in squeeze-film lubrication of the human hip joint. Biorheology 2001, 38, 319–334. [Google Scholar]
- Ruggiero, A.; Gòmez, E.; D’Amato, R. Approximate Analytical Model for the Squeeze-Film Lubrication of the Human Ankle Joint with Synovial Fluid Filtrated by Articular Cartilage. Tribol. Lett. 2011, 41, 337–343. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Savitramma, G.K. Squeeze Film Lubrication between Rough Poroelastic Rectangular Plates with Micropolar Fluid: A Special Reference to the Study of Synovial Joint Lubrication. ISRN Tribol. 2013, 2013, 431508. [Google Scholar] [CrossRef]
- De Boer, G.N.; Raske, N.; Soltanahmadi, S.; Dowson, D.; Bryant, M.G.; Hewson, R.W. A porohyperelastic lubrication model for articular cartilage in the natural synovial joint. Tribol. Int. 2020, 149, 105760. [Google Scholar] [CrossRef]
- Ruggiero, A. Milestones in Natural Lubrication of Synovial Joints. Front. Mech. Eng. 2020, 6, 52. [Google Scholar] [CrossRef]
- Medley, J.B.; Dowson, D.; Wright, V. Surface Geometry of the Human Ankle Joint. Eng. Med. 1983, 12, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Ruggiero, A.; Gomez, E.; Roberto, D. Approximate closed-form solution of the synovial fluid film force in the human ankle joint with non-Newtonian lubricant. Tribol. Int. 2013, 57, 156–161. [Google Scholar] [CrossRef]
- Stokes, V.K. Couple Stresses in Fluids. Phys. Fluids 1966, 9, 1709. [Google Scholar] [CrossRef]
- Ankle X-ray: Indications, Conduct, Results. Available online: https://ocrb.ru/lechenie/rentgenografiya-golenostopnogo-sustava.html (accessed on 15 December 2020).
- Schmidt, T.A.; Gastelum, N.S.; Nguyen, Q.T.; Schumacher, B.L.; Sah, R.L. Boundary lubrication of articular cartilage: Role of synovial fluid constituents. Arthritis Rheum. 2007, 56, 882–891. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; Dipankar, C.; Nabangshu, S.; Belinda, P.-M. Tribological role of synovial fluid compositions on artificial joints—A systematic review of the last 10 years. Lubr. Sci. 2014, 26, 387–410. [Google Scholar] [CrossRef]
- Lin, J.R. Couple-stress effect on the squeeze film characteristics of hemi-spherical bearings with reference to synovial joints. Appl. Mech. Eng. 1996, 1, 317–332. [Google Scholar]
- Meziane, A.; Bou-Saïd, B.; Tichy, J. Modelling human hip joint lubrication subject to walking cycle. Lubr. Sci. 2008, 20, 205–222. [Google Scholar] [CrossRef]
- Yousfi, M.; Bou-Saïd, B.; Tichy, J. An analytical study of the squeezing flow of synovial fluid. Mech. Ind. 2013, 14, 59–69. [Google Scholar] [CrossRef]
- De Boer, G.N.; Raske, N.; Soltanahmadi, S.; Bryant, M.G.; Hewson, R.W. Compliant-poroelastic lubrication in cartilage-on-cartilage line contacts. Tribol. Mater. Surf. Interfaces 2020, 14, 151–165. [Google Scholar] [CrossRef]
- Ruggiero, A.; Sicilia, A. A Mixed Elasto-Hydrodynamic Lubrication Model for Wear Calculation in Artificial Hip Joints. Lubricants 2020, 8, 72. [Google Scholar] [CrossRef]
- Naduvinamani, N.B.; Hiremath, P.S.; Fathima, S.T. On the squeeze film lubrication of long porous journal bearings with couple stress fluids. Ind. Lubr. Tribol. 2005, 57, 12–20. [Google Scholar] [CrossRef]
- Ateshian, G.A.; Hung, C.T. The natural synovial joint: Properties of cartilage. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2006, 220, 657–670. [Google Scholar] [CrossRef]
- Gill, T.J.; Asnis, P.D.; Berkson, E.M.; Gill, T.J. The Treatment of Articular Cartilage Defects Using the Microfracture Techniques. J. Orthop. Sports Phys. Ther. 2006, 10, 728–738. [Google Scholar] [CrossRef]
- Julkunen, P.; Livarinen, J.; Brama, P.A.; Arokoski, J.; Jurvelin, S.; Helminen, H.J. Maturation of collagen fibril network structure in tibial and femoral cartilage of rabbits. Osteoarthr. Cartil. 2010, 18, 406–415. [Google Scholar] [CrossRef]
- Steward, A.J.; Kelly, D.J. Mechanical regulation of mesenchymal stem cell differentiation. J. Anat. 2015, 227, 717–731. [Google Scholar] [CrossRef]
- Wong, M.; Siegrist, M.; Cao, X. Cyclic compression of articular cartilage explants is associated with progressive consolidation and altered expression pattern of extracellular matrix proteins. Matrix Biol. 1999, 18, 391–399. [Google Scholar] [CrossRef]
- Mauck, R.L.; Soltz, M.A.; Wang, C.C.B.; Wong, D.D.; Chao, P.-H.G.; Valhmu, W.B.; Hung, C.T.; Ateshian, G.A. Functional Tissue Engineering of Articular Cartilage Through Dynamic Loading of Chondrocyte-Seeded Agarose Gels. J. Biomech. Eng. 2000, 122, 252–260. [Google Scholar] [CrossRef] [PubMed]
- Ng, K.W.; Mauck, R.L.; Wang, C.C.-B.; Kelly, T.-A.N.; Ho, M.M.-Y.; Chen, F.H.; Ateshian, G.A.; Hung, C.T. Duty Cycle of Deformational Loading Influences the Growth of Engineered Articular Cartilage. Cell. Mol. Bioeng. 2009, 2, 386–394. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Smith, R.L.; Lin, J.; Trindade, M.C.D.; Shida, J.; Kajiyama, G.; Vu, T.; Hoffman, A.R.; Van Der Meulen, M.C.H.; Goodman, S.B.; Schurman, D.J.; et al. Time-dependent effects of intermittent hydrostatic pressure on articular chondrocyte type II collagen and aggrecan mRNA expression. J. Rehabil. Res. Dev. 2000, 37, 153–161. [Google Scholar] [PubMed]
- Smith, R.L.; Rusk, S.F.; Ellison, B.E.; Wessells, P.; Tsuchiya, K.; Carter, D.R.; Caler, W.E.; Sandell, L.J.; Schurman, D.J. In vitro stimulation of articular chondrocyte mRNA and extracellular matrix synthesis by hydrostatic pressure. J. Orthop. Res. 1996, 14, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Guilak, F.; Meyer, B.C.; Ratcliffe, A.; Mow, V.C. The effects of matrix compression on proteoglycan metabolism in articular cartilage explants. Osteoarthr. Cartil. 1994, 2, 91–101. [Google Scholar] [CrossRef]
- Nugent, G.E.; Aneloski, N.M.; Schmidt, T.A.; Schumacher, B.L.; Voegtline, M.S.; Sah, R.L. Dynamic shear stimulation of bovine cartilage biosynthesis of proteoglycan 4. Arthritis Rheum. 2006, 54, 1888–1896. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Yao, S.-J.; Alini, M.; Stoddart, M.J. Chondrogenesis of Human Bone Marrow Mesenchymal Stem Cells in Fibrin–Polyurethane Composites Is Modulated by Frequency and Amplitude of Dynamic Compression and Shear Stress. Tissue Eng. Part A 2010, 16, 575–584. [Google Scholar] [CrossRef] [PubMed]
- Schätti, O.; Grad, S.; Goldhahn, J.; Salzmann, G.; Li, Z.; Alini, M.; Stoddart, M.J. A combination of shear and dynamic compression leads to mechanically induced chondrogenesis of human mesenchymal stem cells. Eur. Cells Mater. 2011, 22, 214–225. [Google Scholar] [CrossRef] [PubMed]
- Huang, A.H.; Baker, B.M.; Ateshian, G.A.; Mauck, R.L. Sliding contact loading enhances the tensile properties of mesenchymal stem cell-seeded hydrogels. Eur. Cell Mater. 2012, 24, 29–45. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.R.; Blenman, E.R.; Beaupré, G.S. Correlations between mechanical stress history and tissue differentiation in initial fracture healing. J. Orthop. Res. 1988, 6, 736–748. [Google Scholar] [CrossRef] [PubMed]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Elasticity and Consolidation for a Porous Anisotropic Solid. J. Appl. Phys. 1955, 26, 182–185. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Biot, M.A.; Willis, D.G. The elastic coefficients of the theory of consolidation. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar]
- Biot, M.A. Generalized Theory of Acoustic Propagation in Porous Dissipative Media. J. Acoust. Soc. Am. 1962, 34, 1254–1264. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of finite deformation of porous solid. Indiana Univ. Math. J. 1972, 21, 597–620. [Google Scholar] [CrossRef]
- Biot, M.A. Generalized Lagrangian equations of non-linear reaction-diffusion. Chem. Phys. 1982, 66, 11–26. [Google Scholar] [CrossRef]
- Cowin, S.C. Bone poroelasticity. J. Biomech. 1999, 32, 217–238. [Google Scholar] [CrossRef]
- Cowin, S.C. Anisotropic poroelasticity: Fabric tensor formulation. Mech. Mater. 2004, 36, 665–677. [Google Scholar] [CrossRef]
- Maslov, L.B. Algorithm for the numerical analysis of biological tissues based on a two-phase medium model. Bull. Ivanovo State Power Univ. 2005, 3, 1–9. (In Russian) [Google Scholar]
- Maslov, L.B. Poroelastic models of vibrations of biological tissues. Bull. Nizhny Novgorod Univ. 2011, 4, 499–501. (In Russian) [Google Scholar]
- Maslov, L.B. Mathematical model of bone tissue structural rearrangement. Russ. J. Biomech. 2013, 17, 39–63. (In Russian) [Google Scholar]
- Maslov, L.B. Mathematical Model of Bone Regeneration. Mech. Compos. Mater. 2017, 53, 399–414. [Google Scholar] [CrossRef]
- Carter, D.R.; Rapperport, D.J.; Fyhrie, D.P.; Schurman, D.J. Relation of coxarthrosis to stresses and morphogenesis: A finite element analysis. Acta Orthop. Scand. 1987, 58, 611–619. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.R.; Wong, M. The role of mechanical loading histories in the development of diarthrodial joints. J. Orthop. Res. 1988, 6, 804–816. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.R.; Beaupre, C.S. Linear elastic and poroelastic models of cartilage can produce comparable stress results: A comment on Tanck et al. (J. Biomech. 32, 153–161, 1999). J. Biomech. 1999, 32, 1255–1257. [Google Scholar]
- Carter, D.R.; Wong, M. Modelling cartilage mechanobiology. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2003, 358, 1461–1471. [Google Scholar] [CrossRef]
- Carter, D.R.; Beaupré, G.S.; Wong, M.; Smith, R.L.; Andriacchi, T.P.; Schurman, D.J. The Mechanobiology of Articular Cartilage Development and Degeneration. Clin. Orthop. Relat. Res. 2004, 427S, S69–S77. [Google Scholar] [CrossRef]
- Soltz, M.A.; Ateshian, G.A. Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. J. Biomech. 1998, 31, 927–934. [Google Scholar] [CrossRef]
- Soltz, M.A.; Ateshian, G.A. Interstitial fluid pressurization during confined compression cyclical loading of articular cartilage. Ann. Biomed. Eng. 2000, 28, 150–159. [Google Scholar] [CrossRef] [PubMed]
- Rose, L.F.; Wolf, E.J.; Brindle, T.; Cernich, A.; Dean, W.K.; Dearth, C.L.; Grimm, M.; Kusiak, A.; Nitkin, R.; Potter, K.; et al. The convergence of regenerative medicine and rehabilitation: Federal perspectives. npj Regen. Med. 2018, 10, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Poliakov, A.; Pakhaliuk, V.; Popov, V.L. Current Trends in Improving of Artificial Joints Design and Technologies for Their Arthroplasty. Front. Mech. Eng. 2020, 6, 4. [Google Scholar] [CrossRef]
- Poliakov, O.; Olinichenko, G.; Pashkov, Y.; Kalinin, M.; Kramar, V.; Burkov, D. A new design of a unipolar hip endoprosthesis focused on the best quality of life of the patients during the postoperative period. In Proceedings of the 2012 International Conference on Biomedical Engineering, Penang, Malaysia, 27–28 February 2012; pp. 22–27. [Google Scholar] [CrossRef]
- Polyakov, A.; Pakhaliuk, V.; Kalinin, M.; Kramar, V.; Kolesova, M.; Kovalenko, O. System Analysis and Synthesis of Total Hip Joint Endoprosthesis. Procedia Eng. 2015, 100, 530–538. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).