Dynamic Characteristics of Cylindrical Roller Bearing with Cage Pocket Deformation
Abstract
1. Introduction
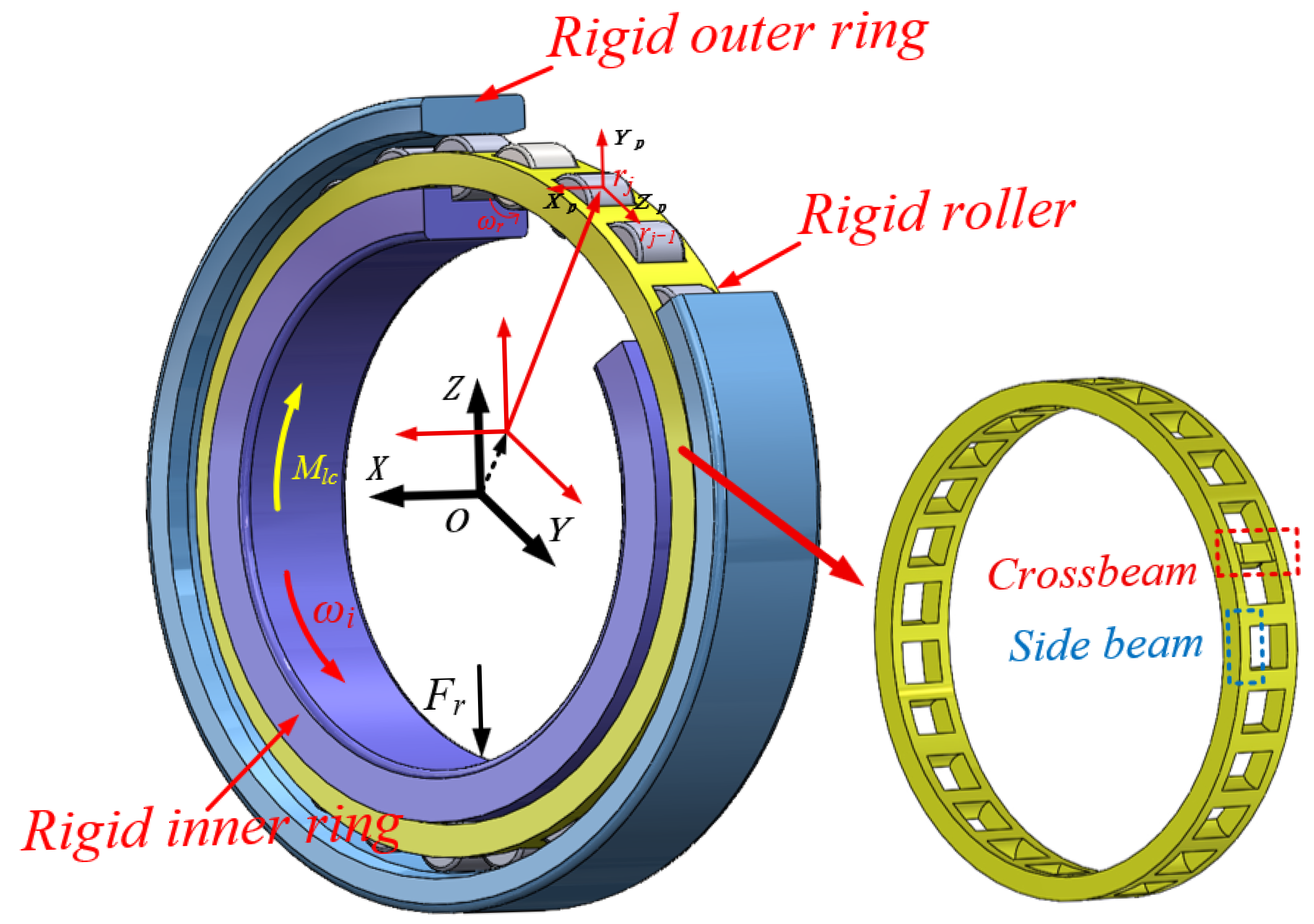
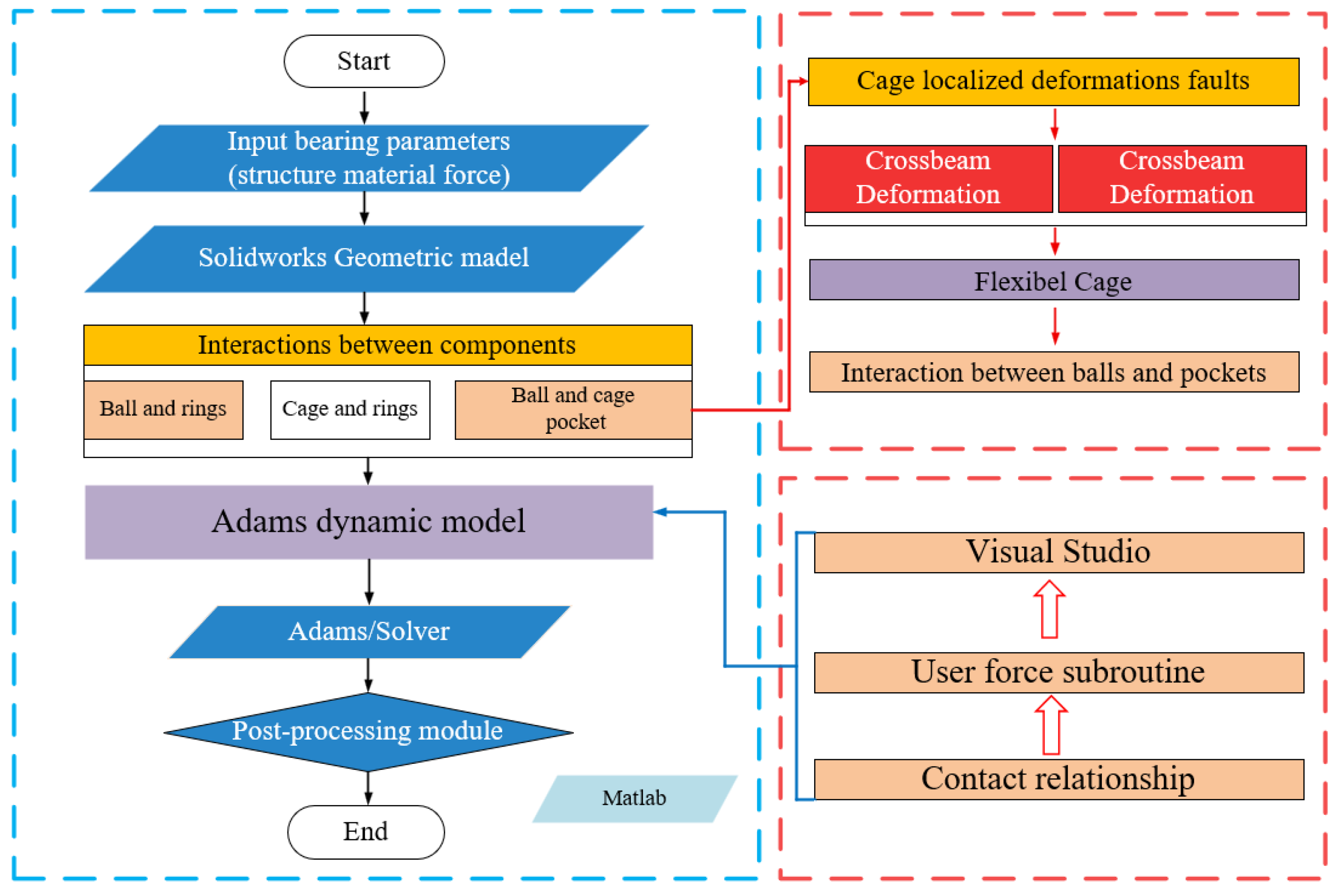
2. Rigid–Flexible Coupled Dynamic Model of a Cylindrical Roller Bearing
2.1. Dynamic Characterization of Cage Localized Deformation
2.1.1. Model Assumptions
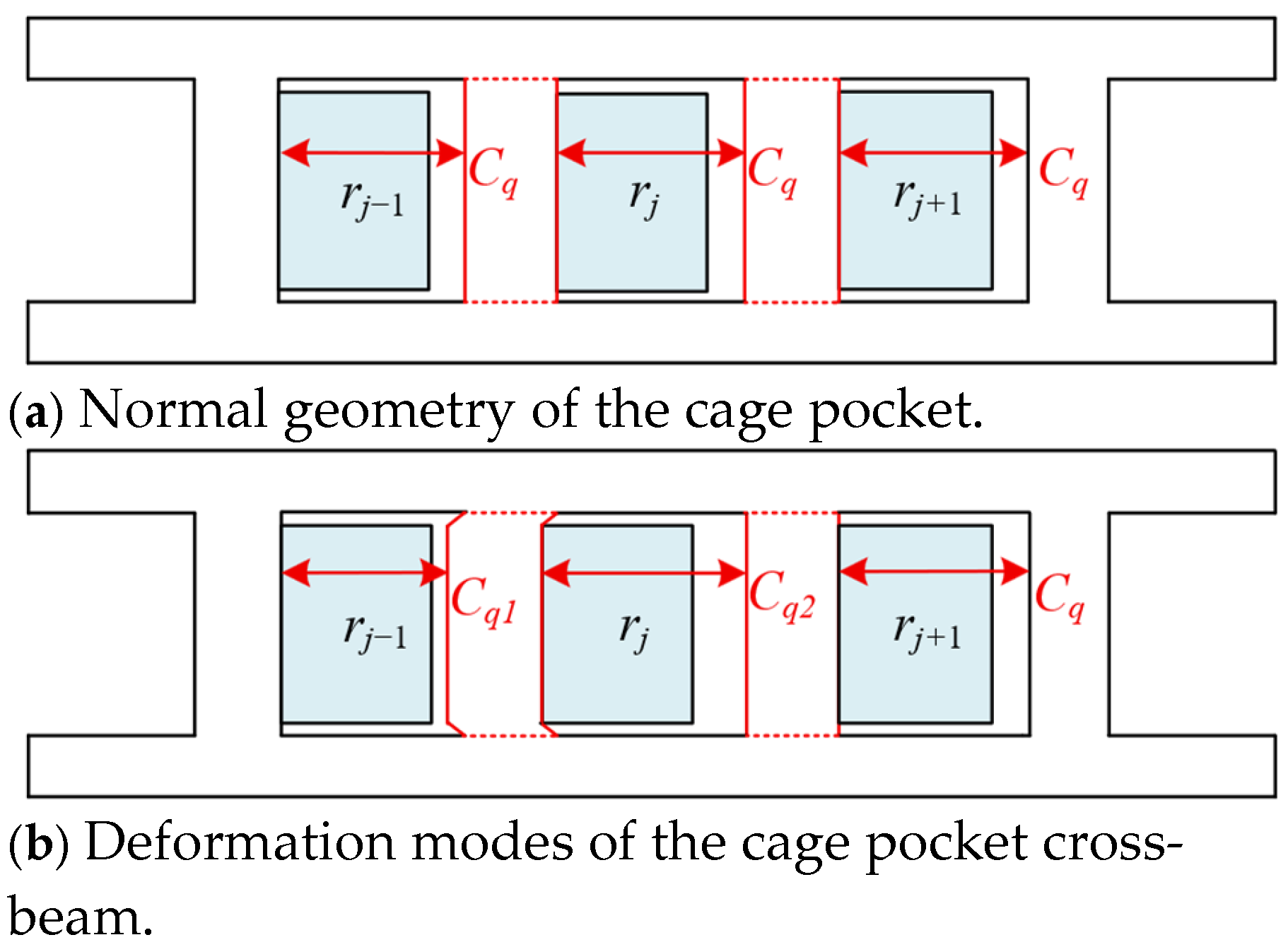
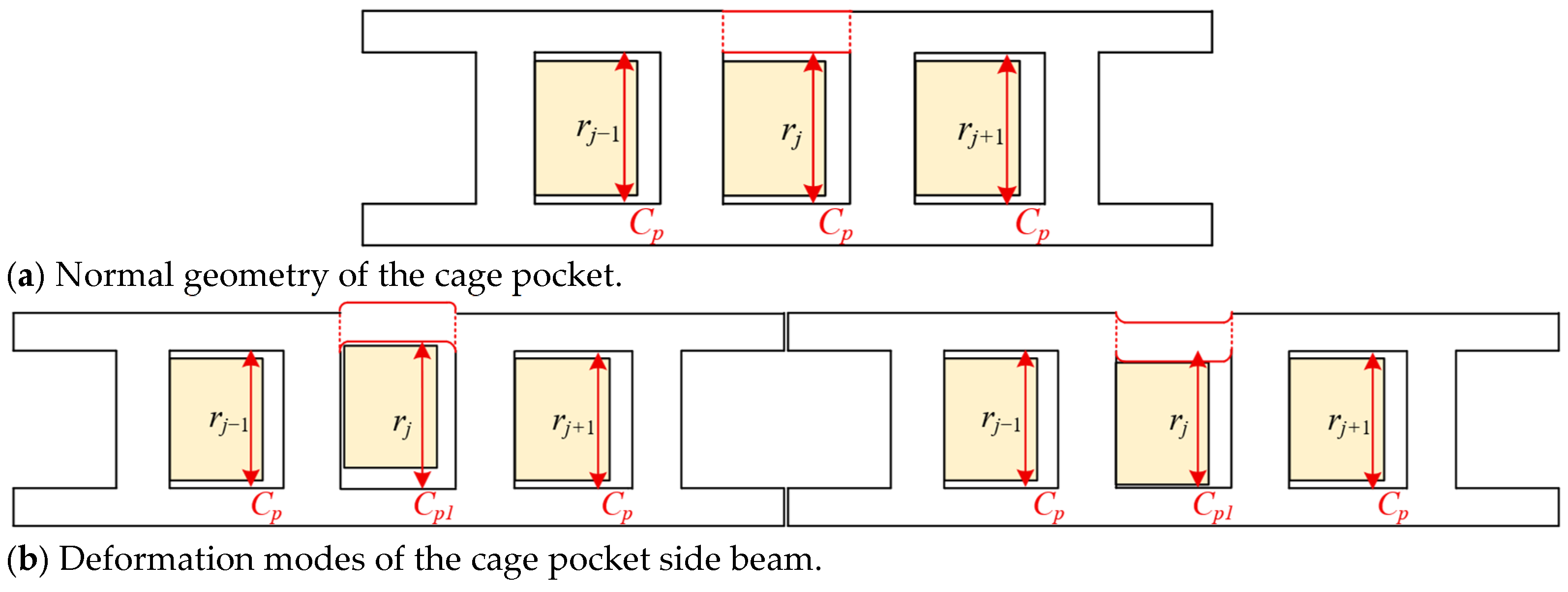
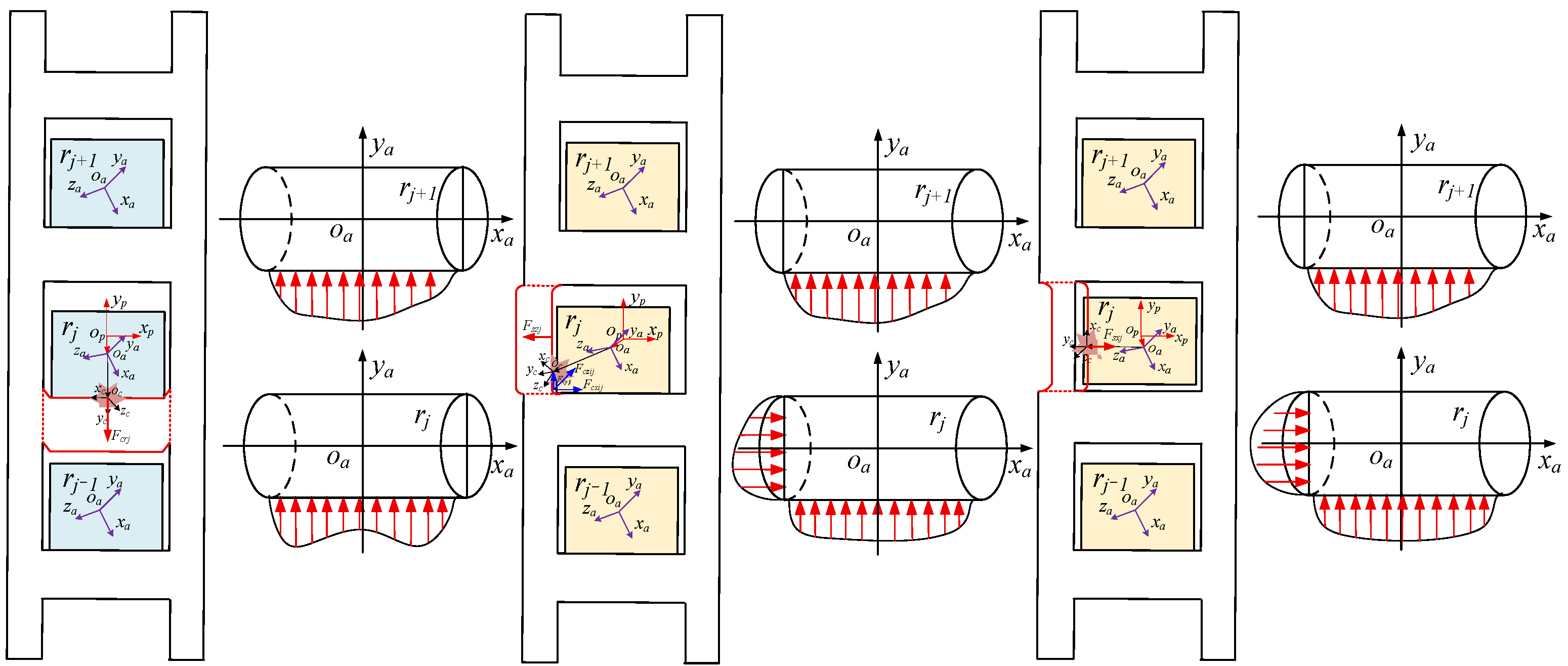
2.1.2. Cage Local Deformation Characterization
2.2. Rigid–Flexible Dynamic Model of a Cylindrical Roller Bearing Considering Cage Deformation
2.2.1. Interaction Forces Among Bearing Components
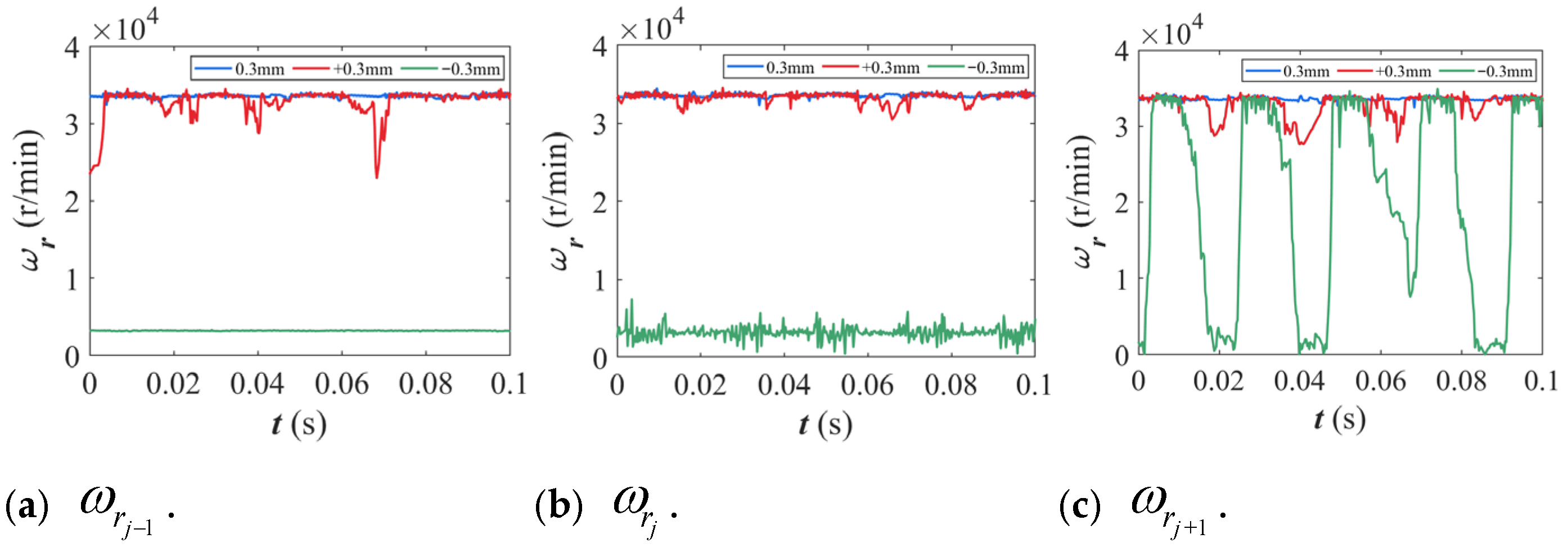
2.2.2. Roller Slip Ratio Calculation
2.3. Rigid–Flexible Coupling Dynamics Theory
2.3.1. Flexible Treatment of Cage
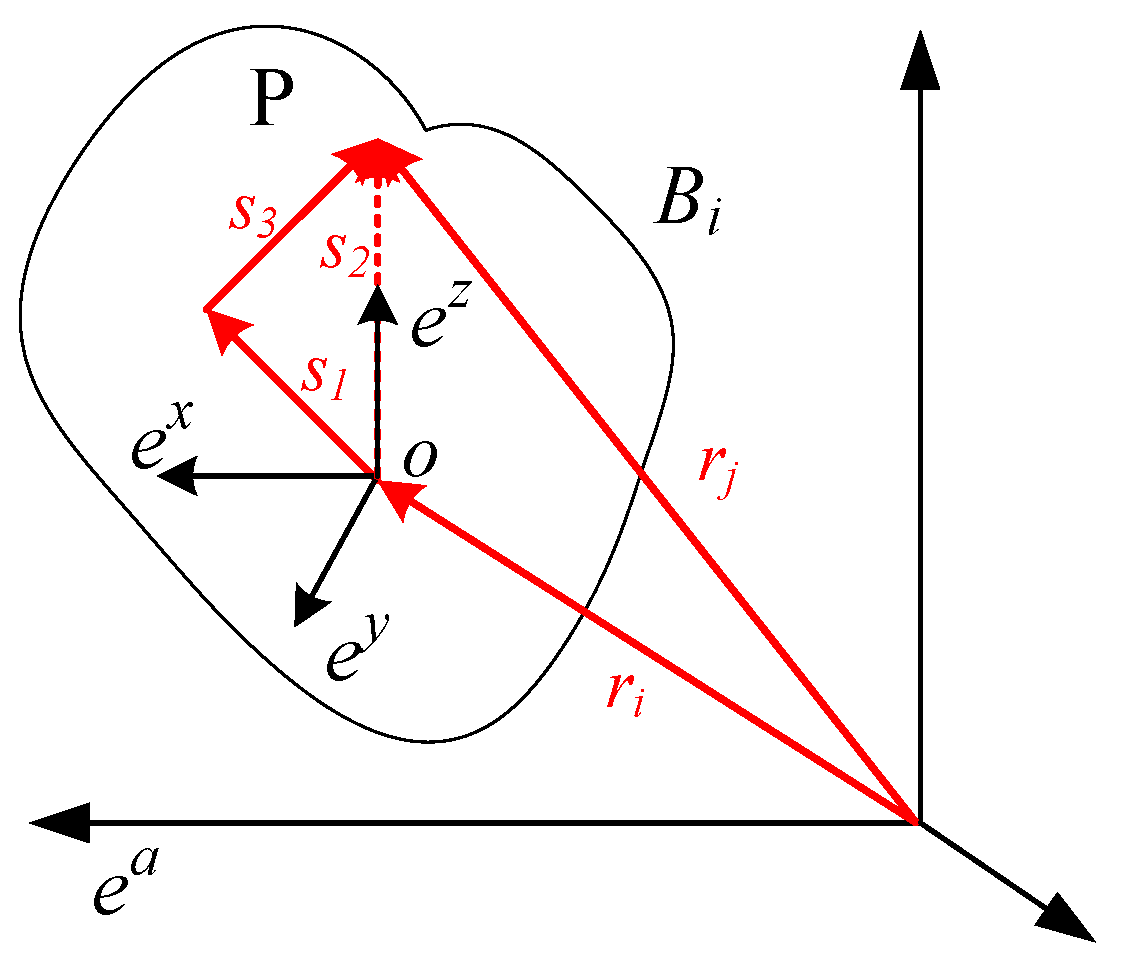
2.3.2. Velocity and Acceleration of Flexible Body at Arbitrary Points
2.3.3. Rigid–Flexible Coupling Motion Equations
3. Dynamic Analysis of Cylindrical Roller Bearing Under Cage Localized Deformation
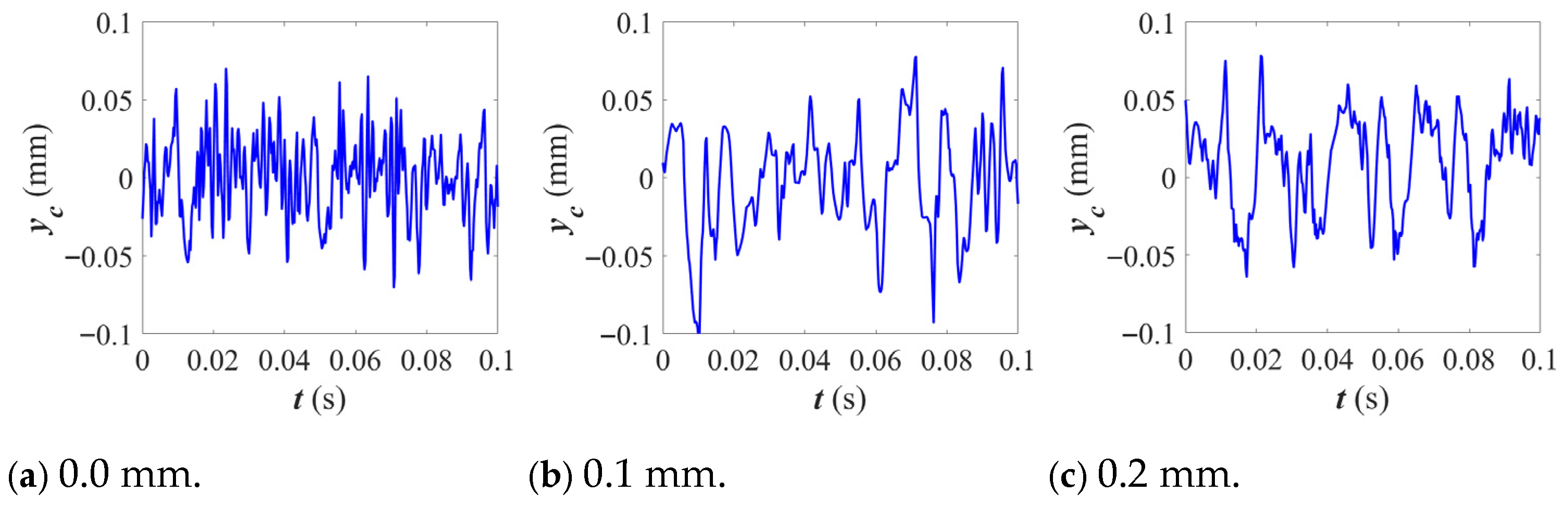
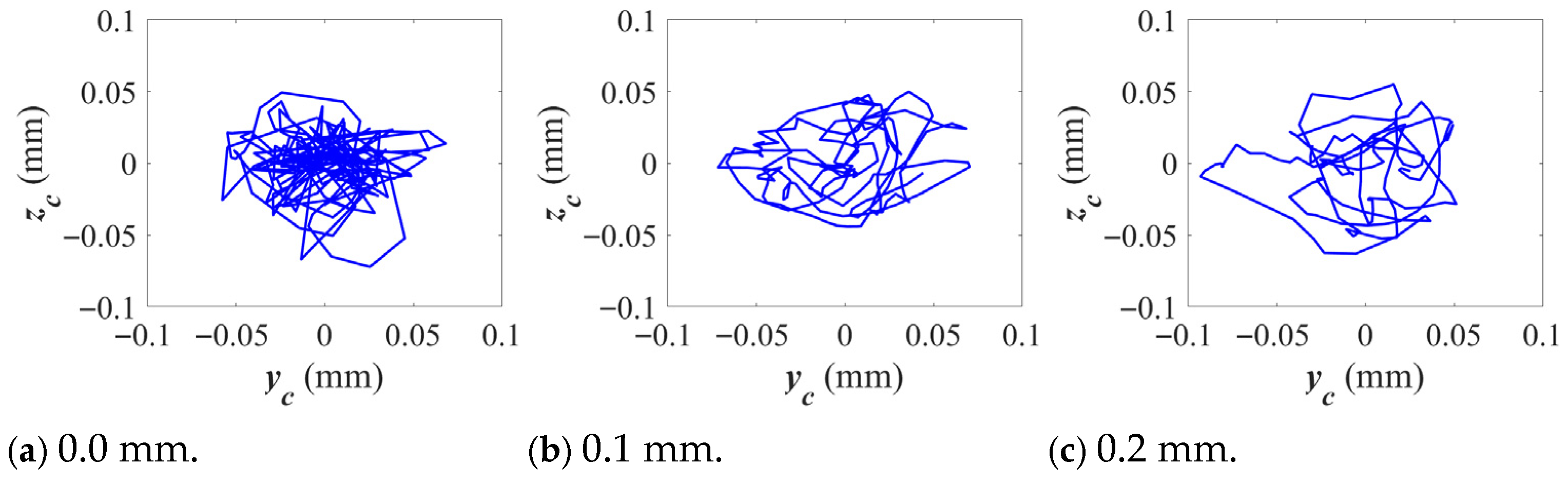
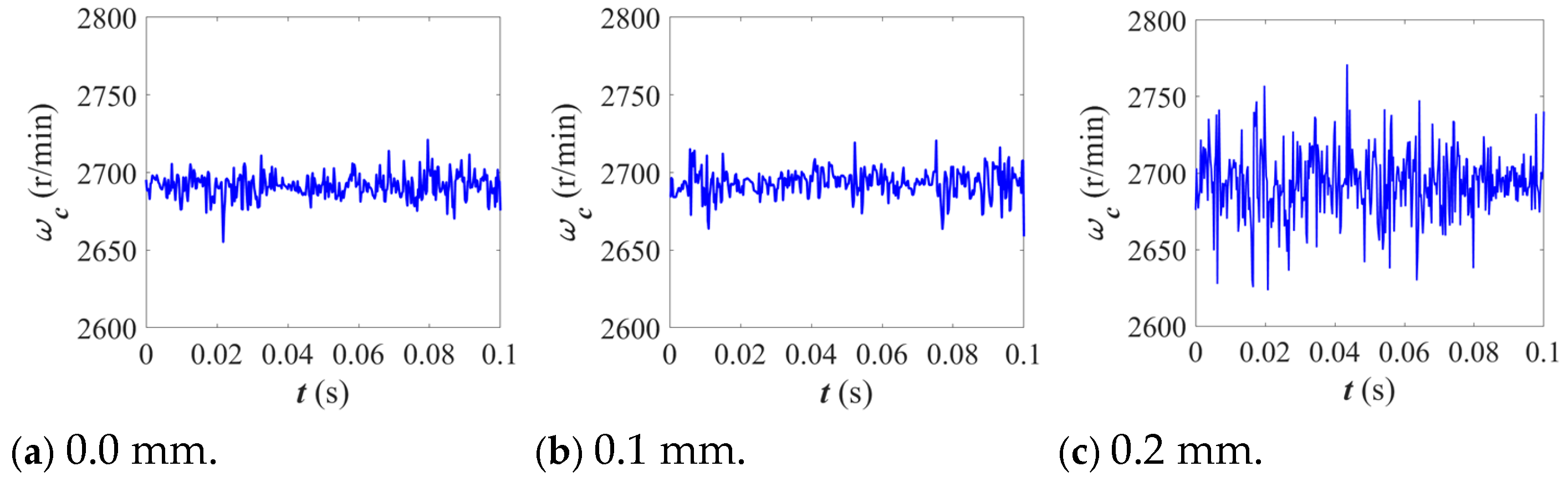
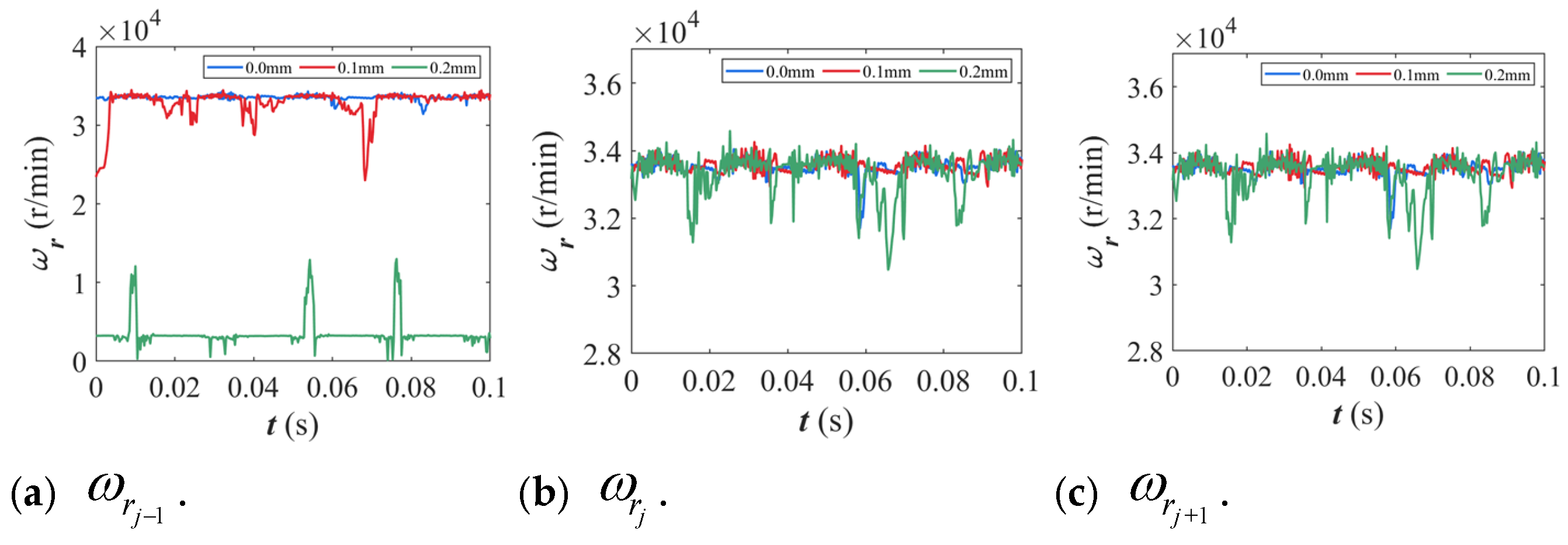
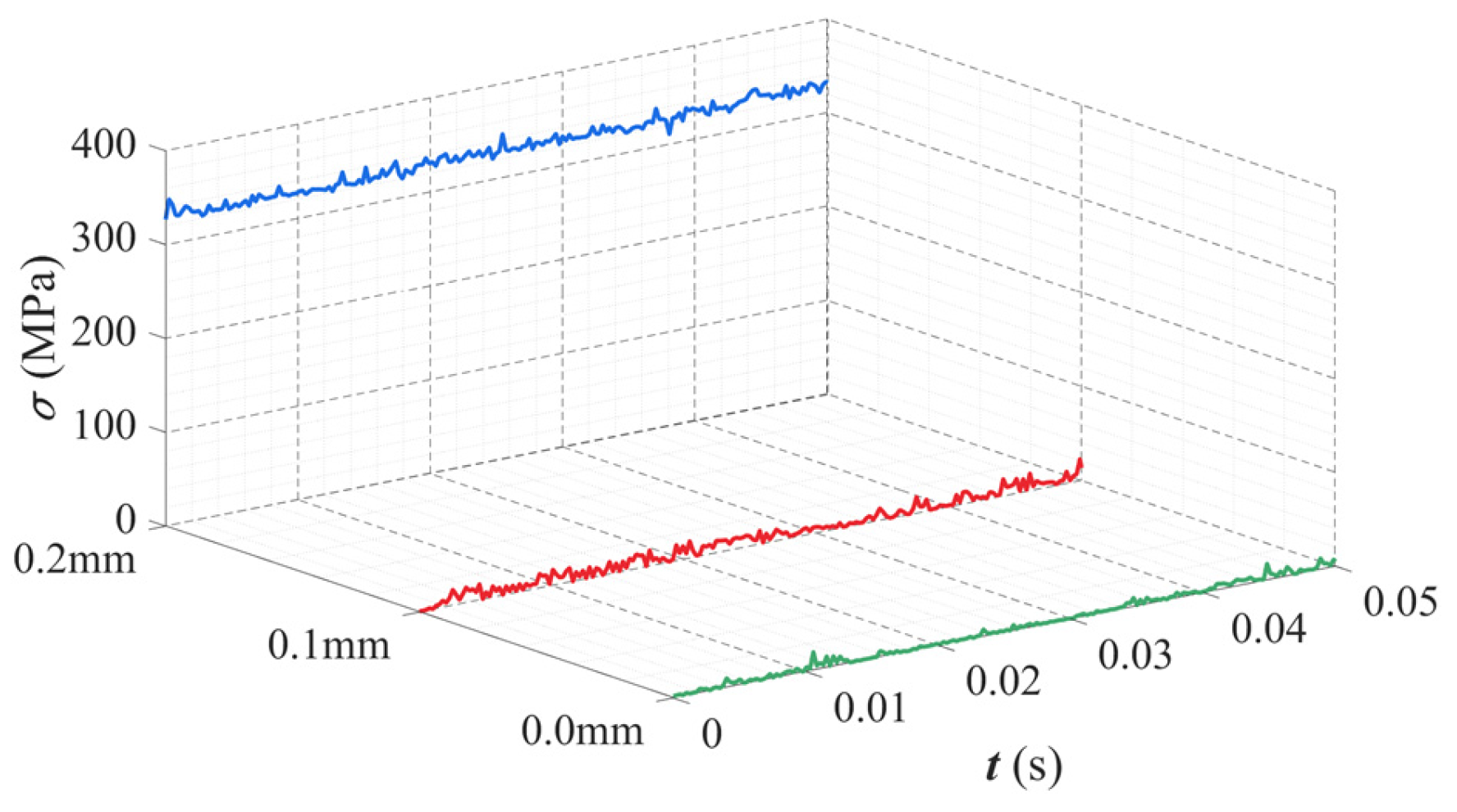
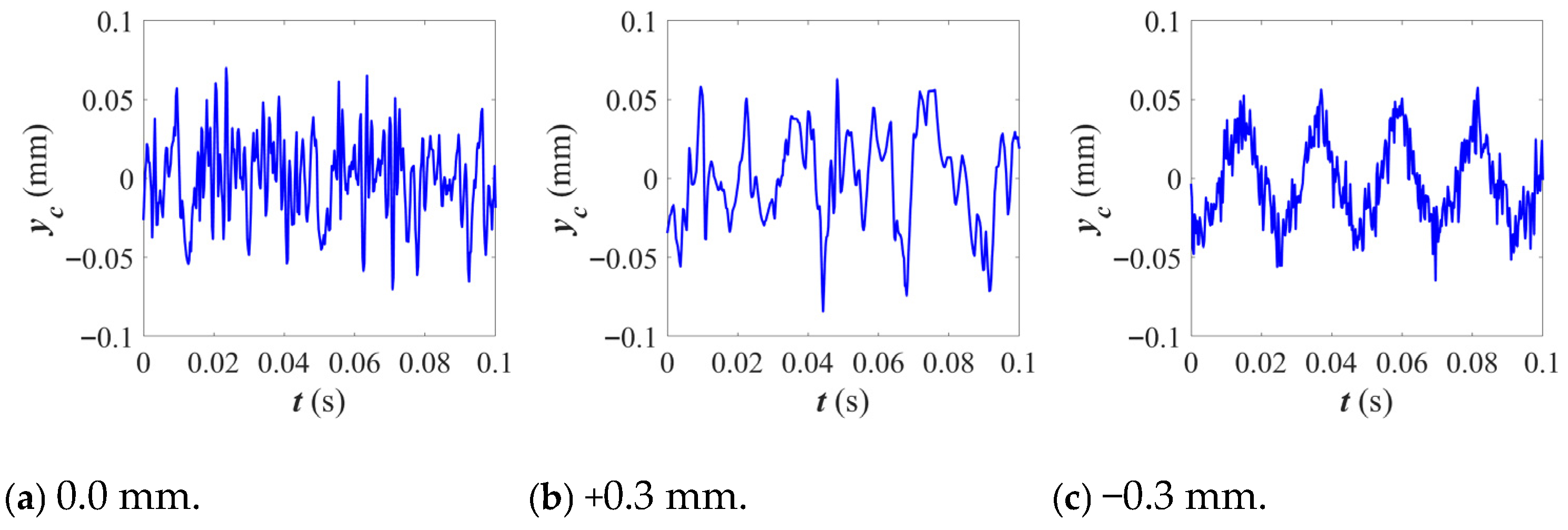
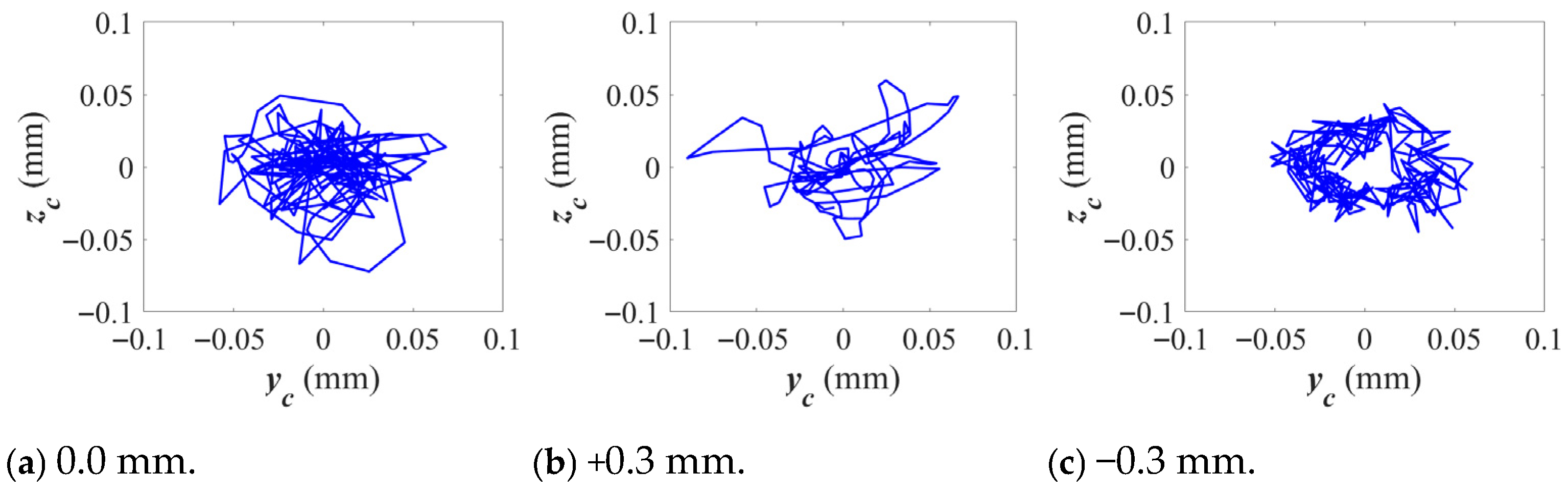
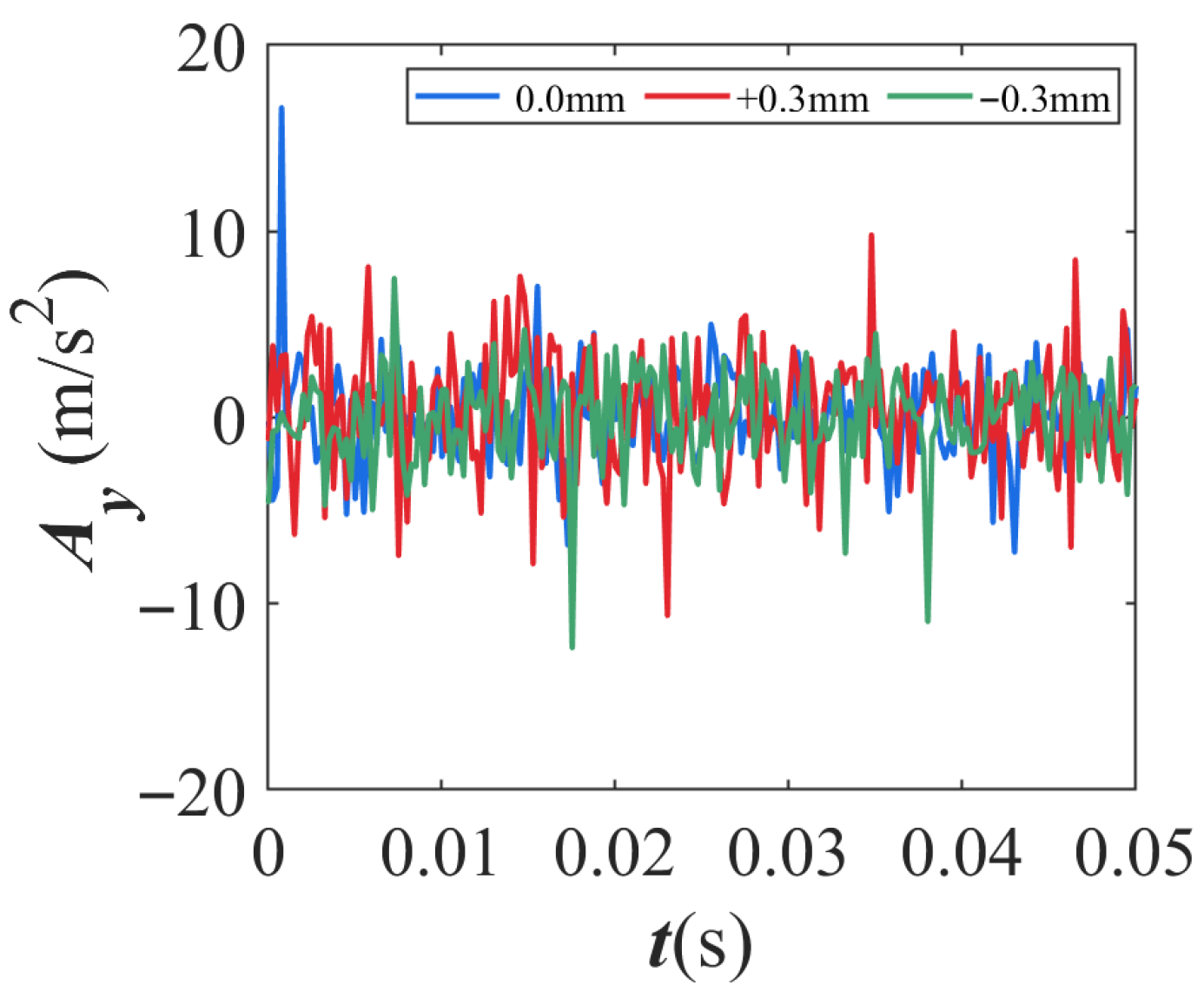
3.1. Influence of Cage Pocket Crossbeam Deformation on the Dynamic Characteristics of Bearings
3.2. Influence of Cage Pocket Side Beam Deformation on the Dynamic Characteristics of Bearings
4. Conclusions
- (1)
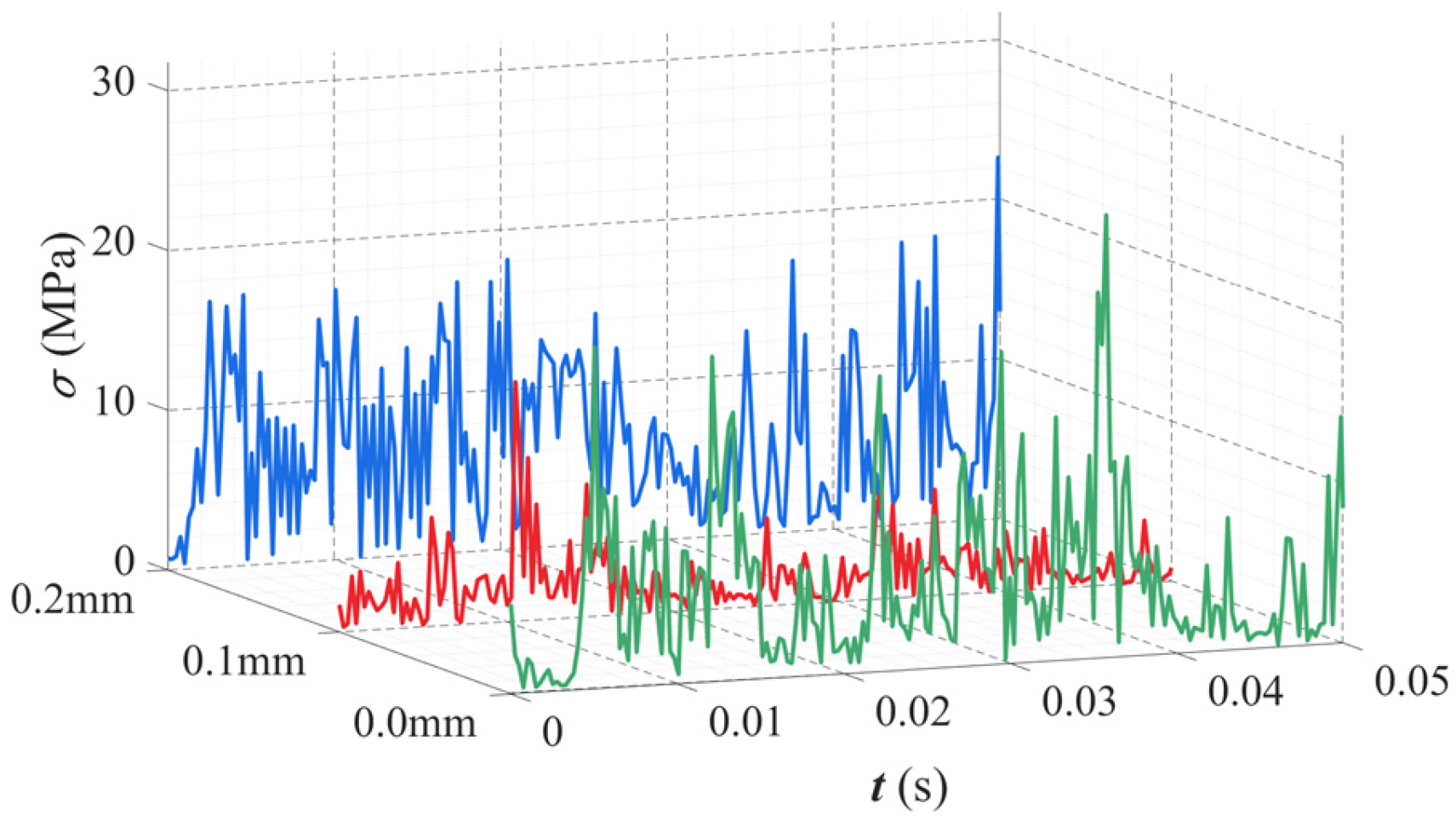
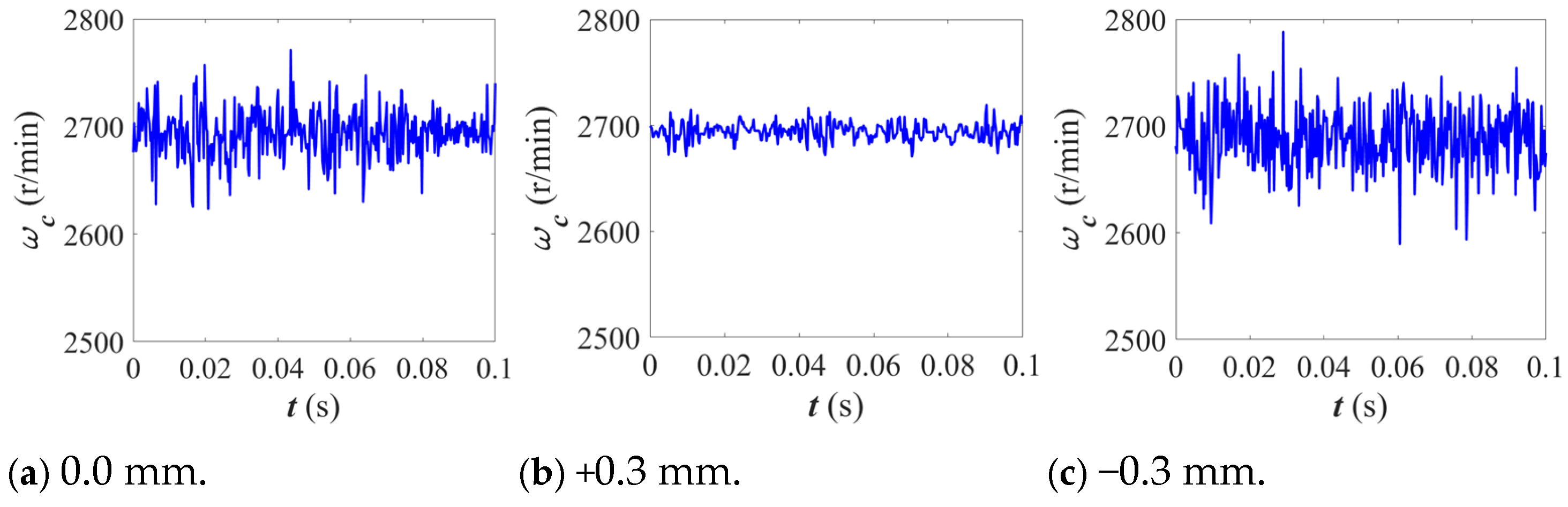
- The deviation in cage length exerts a significant influence on the dynamic performance of the bearing. Negative deviation reduces the amplitude of equivalent stress on the cage, indicating stricter constraints on its motion. As the deformation increases, the cage’s motion range diminishes while the inner ring and rollers’ rotational speed fluctuates intensifies. Negative deviations make the bearing’s overall dynamic response more sensitive; this is mainly due to the reduced clearance between the cage and rollers, which enhances friction and contact forces. The resulting restriction on cage motion causes a rotational speed imbalance, leading to greater fluctuations.
- (2)
- The deformation of the cage pocket crossbeam exhibits distinct influence patterns. Negative deformation of the side beam significantly increases the root stress of the cage, which stabilizes at approximately 320.51 MPa. Meanwhile, the cage centroid’s motion transitions from irregular oscillations to sinusoidal fluctuations at characteristic frequencies, accompanied by a reduction in whirl amplitude. When the side beam undergoes positive deformation, the clearance between the cage and rollers increases, which weakens their interactions. As a result, the variation in root stress becomes negligible, and the system’s dynamic stability improves. However, positive deformation of the side beam also induces irregular, large-amplitude fluctuations in the outer ring’s vibration response, indicating that local cage deformation can compromise the stability of outer ring vibrations.
- (3)
- Negative deviation significantly affects the performance of cylindrical roller bearings by reducing the clearance between the rolling elements and the cage. This leads to increased contact, which in turn amplifies friction and impact forces among the components, especially with side beam deviation. Negative deviation increases stress, restricts mobility, and alters interaction characteristics, severely disrupting the bearing’s equilibrium and resulting in pronounced fluctuations in speed and motion. In contrast, positive deviation enlarges clearance, facilitating smoother interactions, reducing stress, and enhancing the system’s overall stability.
- (4)
- In the practical design and assembly of bearings, the influence of negative deviation should be minimized because the location and direction of local cage deformation directly affect roller clearance and the slip ratio. As deformation increases, the load conditions of the rollers change, restricting their normal motion. Furthermore, roller motion in both deformed and undeformed regions is affected, thereby inducing a cascading effect in roller slip. Ultimately, this dynamic interference severely deteriorates bearing performance and shortens its service life.
- (5)
- The influence of local cage deformation defects on the dynamic characteristics of cylindrical roller bearings was analyzed. The insights gained from this study provide valuable guidance for improving the design and manufacturing processes of cylindrical roller bearings, thereby ensuring their greater reliability and durability. Future research may explore the effects of multiple coupled faults, such as the interaction between local cage deformation, surface damage, and assembly deviations, on the bearing system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghaisas, N.; Wassgren, C.R.; Sadeghi, F. Cage Instabilities in Cylindrical Roller Bearings. Journal of Tribology. J. Tribol. 2004, 126, 681–689. [Google Scholar] [CrossRef]
- Kumbhar, S.G.; Sudhagar P, E.; Desavale, R.G. An overview of dynamic modeling of rolling-element bearings. Noise Vib. Worldw. 2021, 52, 3–18. [Google Scholar] [CrossRef]
- Guo, Z.; Ju, H.; Wang, K. A Novel Explicit Canonical Dynamic Modeling Method for Multi-Rigid-Body Mechanisms Considering Joint Friction. Aerospace 2024, 11, 368. [Google Scholar] [CrossRef]
- Pesterev, D.; Druzhina, O.; Pchelintsev, A.; Nepomuceno, E.; Butusov, D. Numerical integration schemes based on composition of adjoint multistep methods. Algorithms 2022, 15, 463. [Google Scholar] [CrossRef]
- Xin, J.; Wang, Z.; Hao, X.; Qi, X.; Wang, Y.; Wen, B. Dynamic Characteristics Analysis of Cylindrical Roller Bearing with Dimensional Deviations in Cage Pocket. Appl. Sci. 2024, 14, 9433. [Google Scholar] [CrossRef]
- Zhang, L.; Xiang, Z.; Zhang, H.; Liu, W.; Huang, C.; Qian, T.; Wang, C.; Liu, J. An Investigation of the Effect of the Fault Degree on the Dynamic Characteristics and Crack Propagation of Rolling Bearings. Appl. Sci. 2025, 15, 1198. [Google Scholar] [CrossRef]
- Yang, Y.; Qi, X.; Wang, Y.; Wang, M.; Wen, B.; Zhai, J. Dynamic Characteristics of a Cylindrical Roller Bearing with Cage Cracks. Lubricants 2025, 13, 25. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, S.; Duan, D. Fracture Analysis and Working Stress Calculation of Bearing Cage Used in Charging Pump in a Nuclear Power Plant. Metals 2023, 13, 1380. [Google Scholar] [CrossRef]
- Li, H.; Liu, H.; Liu, Y.; Qi, S.; Wang, F. On the dynamic characteristics of ball bearing with cage broken. Lubr. Tribol. 2020, 72, 881–886. [Google Scholar] [CrossRef]
- Wen, B.; Ren, H.; Zhang, H.; Han, Q. Experimental investigation of cage motions in an angular contact ball bearing. Part J J. Eng. Tribol. 2017, 231, 1041–1055. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Liang, H.; Wang, W. The collision and cage stability of cylindrical roller bearing considering cage flexibility. Tribol. Int. 2024, 192, 109219. [Google Scholar] [CrossRef]
- Dai, P.; Liang, X.; Lin, X.; Wang, F.; Wang, J. Investigation on stability and slip characteristic of the cage in cylindrical roller bearing with localized failure on raceways. Mech. Syst. Signal Process. 2023, 199, 110469. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, X.; Hao, W.; Miao, C.; Hu, X.; Fang, C. Tribo-Dynamic Behavior of Double-Row Cylindrical Roller Bearings Under Raceway Defects and Cage Fracture. Lubricants 2025, 13, 80. [Google Scholar] [CrossRef]
- Zarei, A.; Farahani, S.; Pradeep, S.A.; Driscoll, J.; Lukasiewicz, R.; Pilla, S. Design and manufacturing of roller bearing polymeric cages and development of a theoretical model for predicting the roller push-out force. Sci. Rep. 2022, 12, 1017. [Google Scholar] [CrossRef]
- Pederson, B.M.; Sadeghi, F.; Wassgren, C. The effects of cage flexibility on ball-to-cage pocket contact forces and cage instability in deep groove ball bearings. SAE Trans. 2006, 115, 260–271. [Google Scholar]
- Weinzapfel, N.; Sadeghi, F. A discrete element approach for modeling cage flexibility in ball bearing dynamics simulations. J. Tribol. 2009, 131, 021101. [Google Scholar] [CrossRef]
- Ma, S.; Tian, C.; Yang, C.; Yan, K.; Stefano, L.; Hong, J. New bearing model with flexible cage and study of dynamic behavior under variable-speed. Mech. Syst. Signal Process. 2024, 208, 111045. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Tang, L.; Zhai, W. Skidding dynamic performance of rolling bearing with cage flexibility under accelerating conditions. Mech. Syst. Signal Process. 2021, 150, 107257. [Google Scholar] [CrossRef]
- Wang, M.; Yan, K.; Tang, Q.; Guo, J.; Zhu, Y.; Hong, J. Dynamic modeling and properties analysis for ball bearing driven by structure flexible deformations. Tribol. Int. 2023, 179, 108163. [Google Scholar] [CrossRef]
- Neglia, S.G.; Culla, A.; Fregolent, A. Bearing Cage Dynamics: Cage Failure and Bearing Life Estimation. In Nonlinear Dynamics, Volume 1: Proceedings of the 33rd IMAC, A Conference and Exposition on Structural Dynamics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Guo, Y.; Parker, R. Rolling Element Bearing Stiffness Matrix Determination (Presentation); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014. [Google Scholar]
- Qin, Y.; Li, C.; Wu, X.; Wang, Y.; Chen, H. Multiple-degree-of-freedom dynamic model of rolling bearing with a localized surface defect. Mech. Mach. Theory 2020, 154, 104047. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Ma, H.; Xu, H.; Li, X.; Luo, Z.; Wen, B. Vibration characteristics of rotor-bearing system with angular misalignment and cage fracture: Simulation and experiment. Mech. Syst. Signal Process. 2023, 182, 109545. [Google Scholar] [CrossRef]
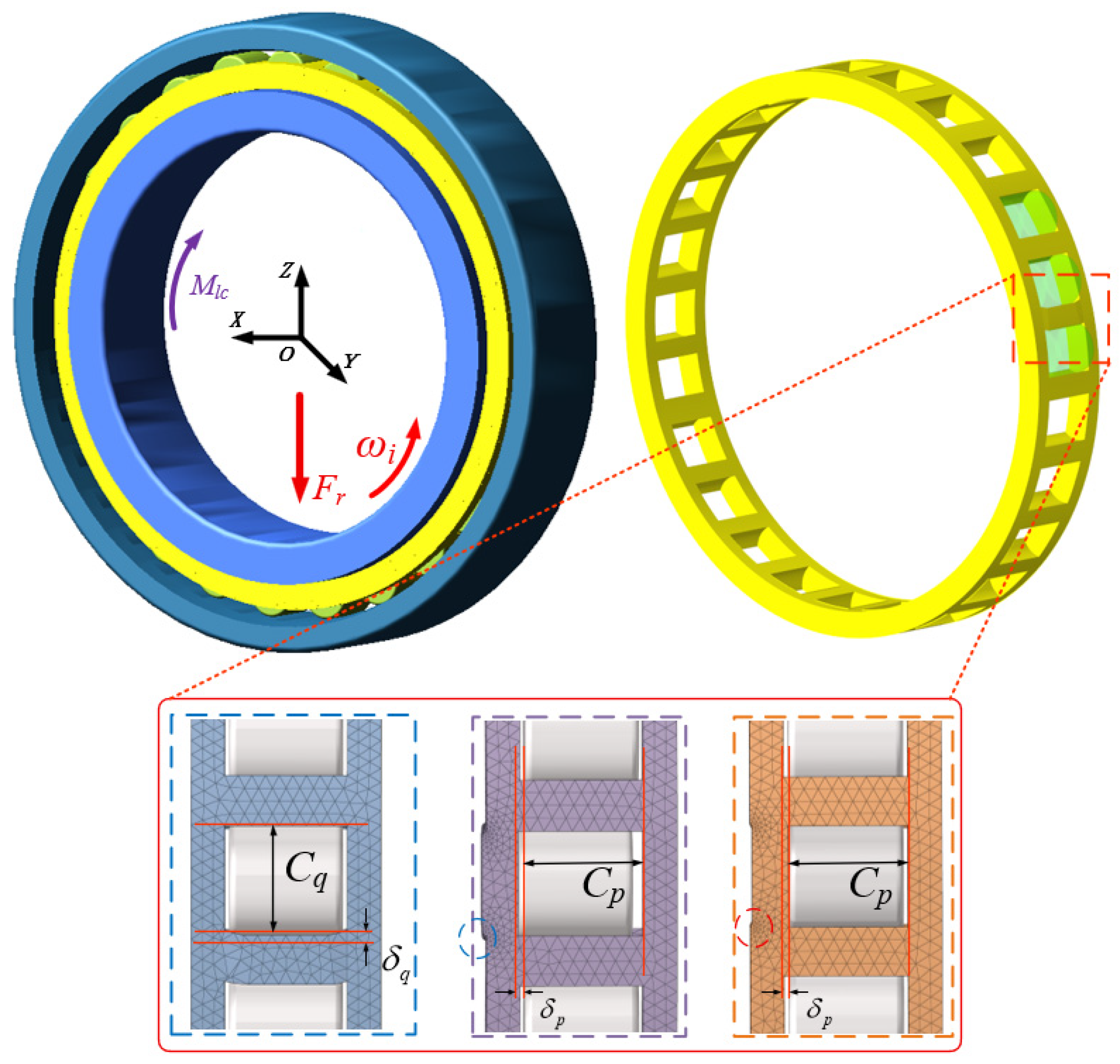

| Component Name | Cage | Inner and Roller |
|---|---|---|
| Material | Brass | GCr15 |
| Density | 8.545 × 103 (kg/m3) | 7.83 × 103 (kg/m3) |
| Elastic Modulus | 1.06 × 105 (N/mm2) | 2.19 × 105 (N/mm2) |
| Poisson’s Ratio | 0.324 | 0.3 |
| Roller | 0.0 mm | 0.1 mm | 0.2 mm |
|---|---|---|---|
| 10.80% | 8.72% | 90.55% | |
| 9.59% | 8.58% | 8.66% | |
| 9.21% | 8.58% | 8.69% |
| Roller | 0.0 mm | +0.3 mm | −0.3 mm |
|---|---|---|---|
| 9.59% | 8.60% | 91.24% | |
| 9.21% | 8.59% | 91.29% | |
| 10.70% | 8.58% | 44.40% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, B.; Li, S.; Qi, X.; Zhang, Z.-G.; Wang, M.; Zhai, J. Dynamic Characteristics of Cylindrical Roller Bearing with Cage Pocket Deformation. Lubricants 2025, 13, 495. https://doi.org/10.3390/lubricants13110495
Wen B, Li S, Qi X, Zhang Z-G, Wang M, Zhai J. Dynamic Characteristics of Cylindrical Roller Bearing with Cage Pocket Deformation. Lubricants. 2025; 13(11):495. https://doi.org/10.3390/lubricants13110495
Chicago/Turabian StyleWen, Baogang, Song Li, Xiaoye Qi, Zhan-Ge Zhang, Meiling Wang, and Jingyu Zhai. 2025. "Dynamic Characteristics of Cylindrical Roller Bearing with Cage Pocket Deformation" Lubricants 13, no. 11: 495. https://doi.org/10.3390/lubricants13110495
APA StyleWen, B., Li, S., Qi, X., Zhang, Z.-G., Wang, M., & Zhai, J. (2025). Dynamic Characteristics of Cylindrical Roller Bearing with Cage Pocket Deformation. Lubricants, 13(11), 495. https://doi.org/10.3390/lubricants13110495




