Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations
Abstract
:1. Introduction
1.1. Research Objectives
1.2. Problem Context
1.3. Problem Description
2. Materials and Methods
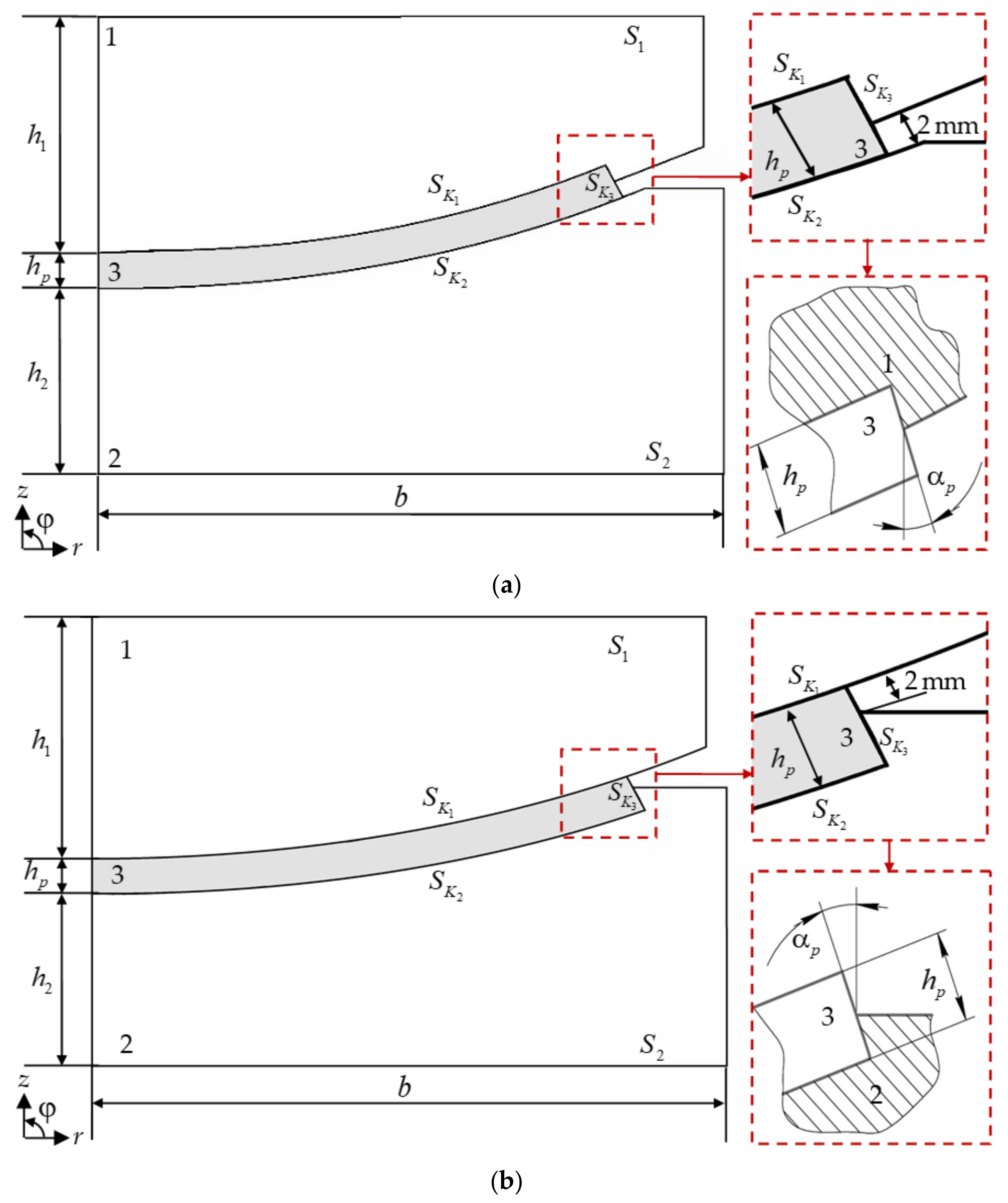
2.1. Model
2.2. Materials
- −
- materials cannot be produced in the required volume;
- −
- materials have a very heterogeneous set of properties;
- −
- significantly nonlinear compressibility of materials under constrained compression has been discovered;
- −
- additional experimental studies with different histories of long-term multistage loading are required, etc.
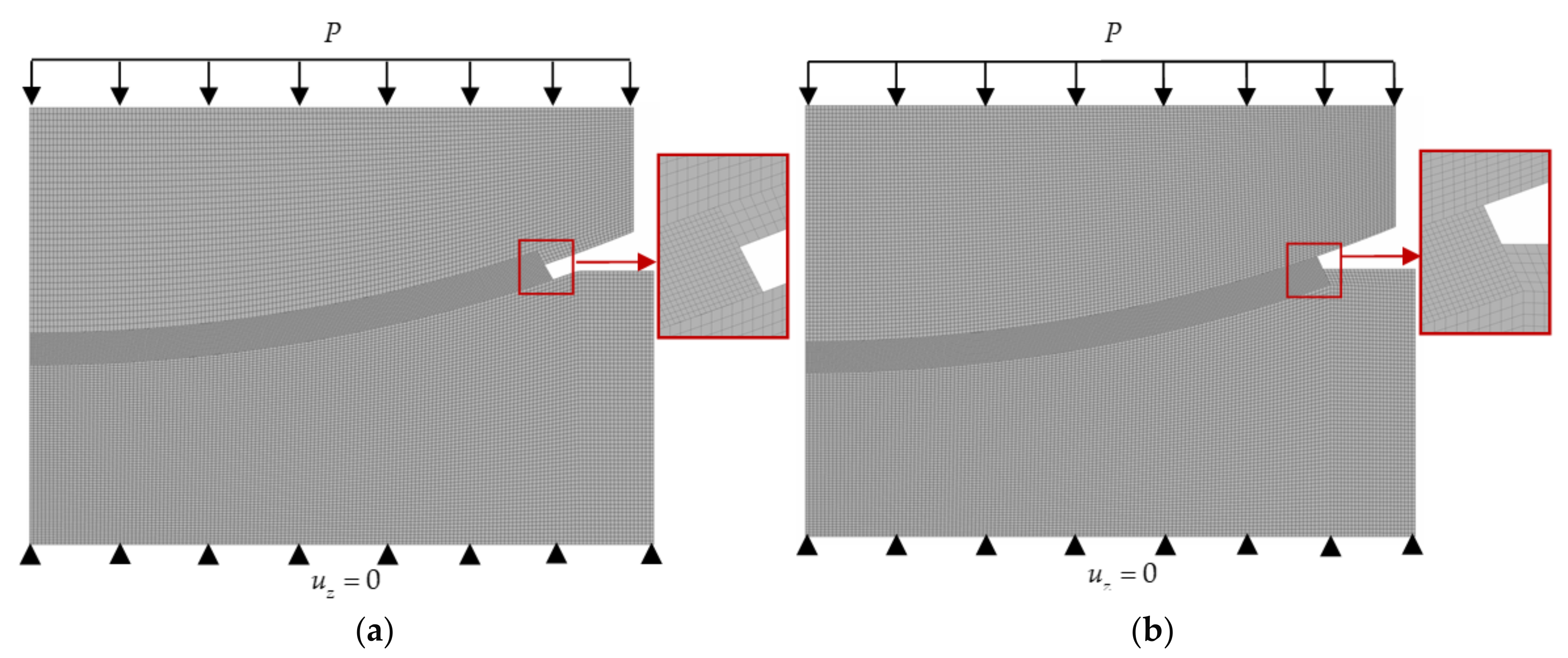
2.3. Mathematical Setting, Boundary Conditions and Methods
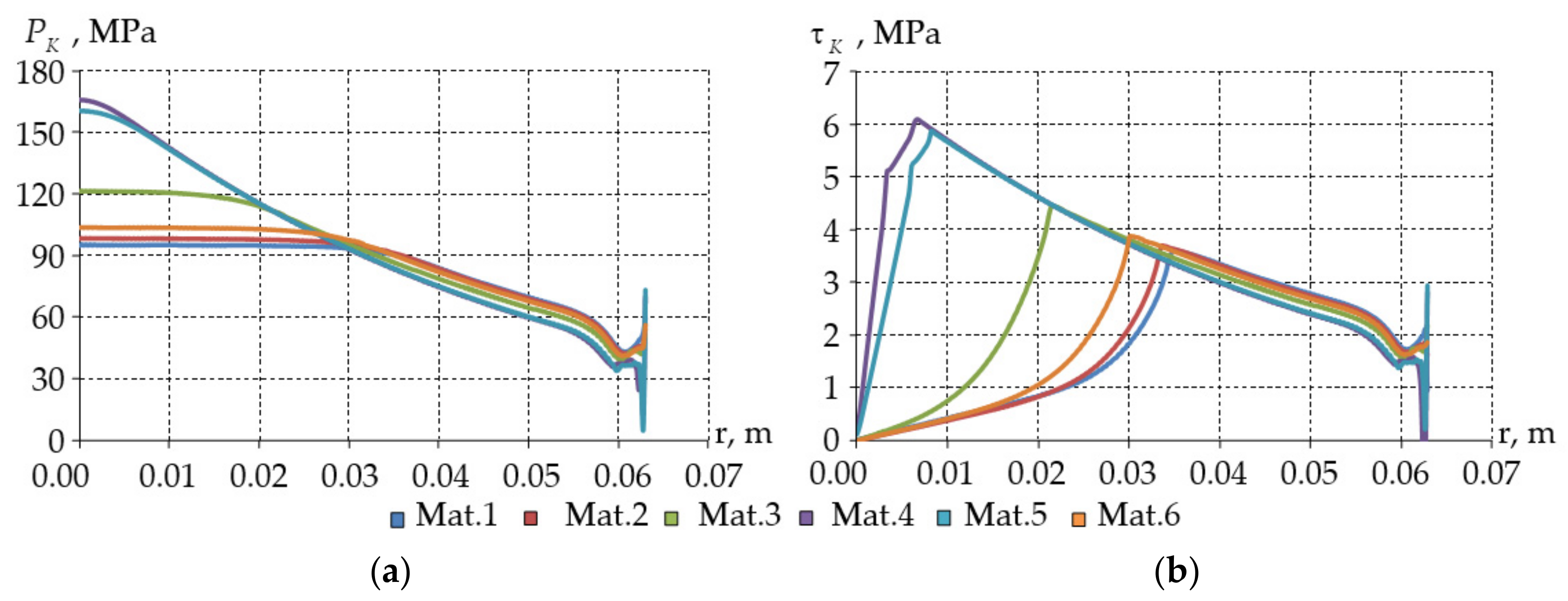
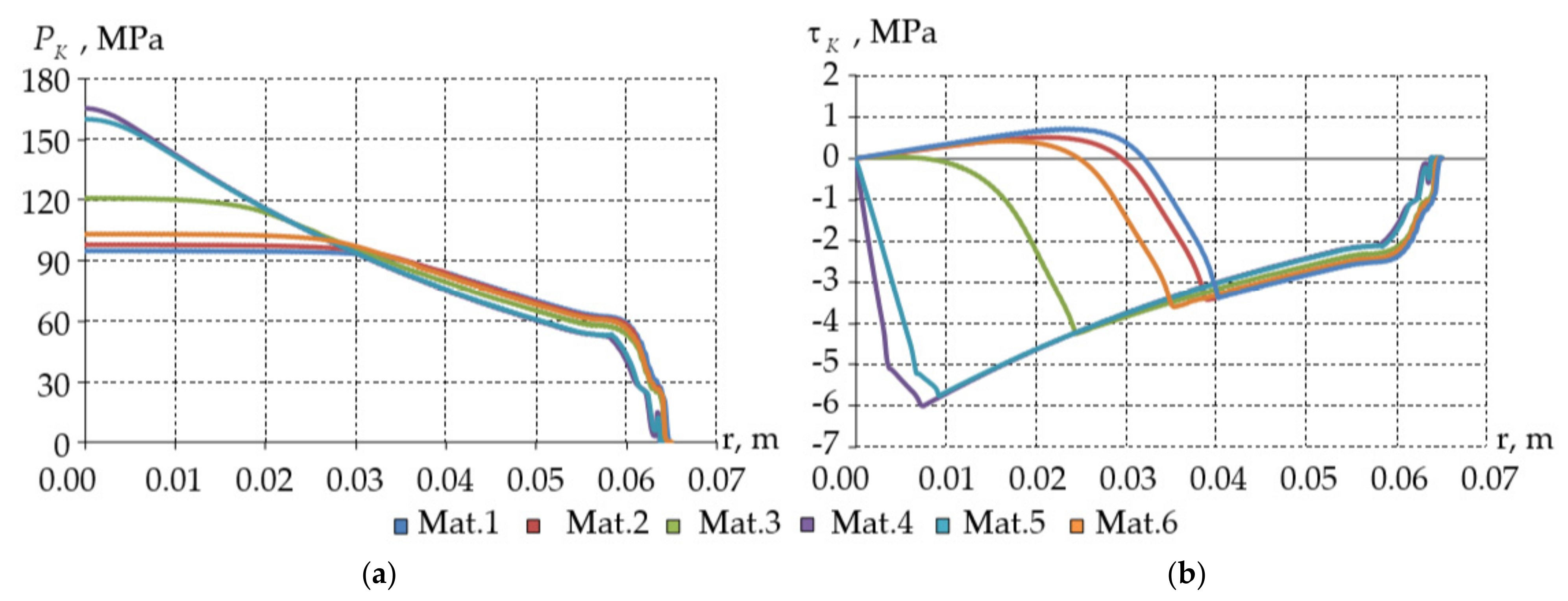
3. Results
- −
- “pressed surface” is contact surface pressed into steel plates ( in model A, in model B);
- −
- “turning surface” is the contact surface along which the rotation of the spherical segment is possible ( in model A, in model B);
- −
- “end face surface” is relatively free end face of the interlayer ( in model A and B);
- −
- is area that is contact with full adhesion;
- −
- is area of the zone of “no contact” (divergence) of mating surfaces.
- −
- an increase in the area of full “adhesion” of mating surfaces;
- −
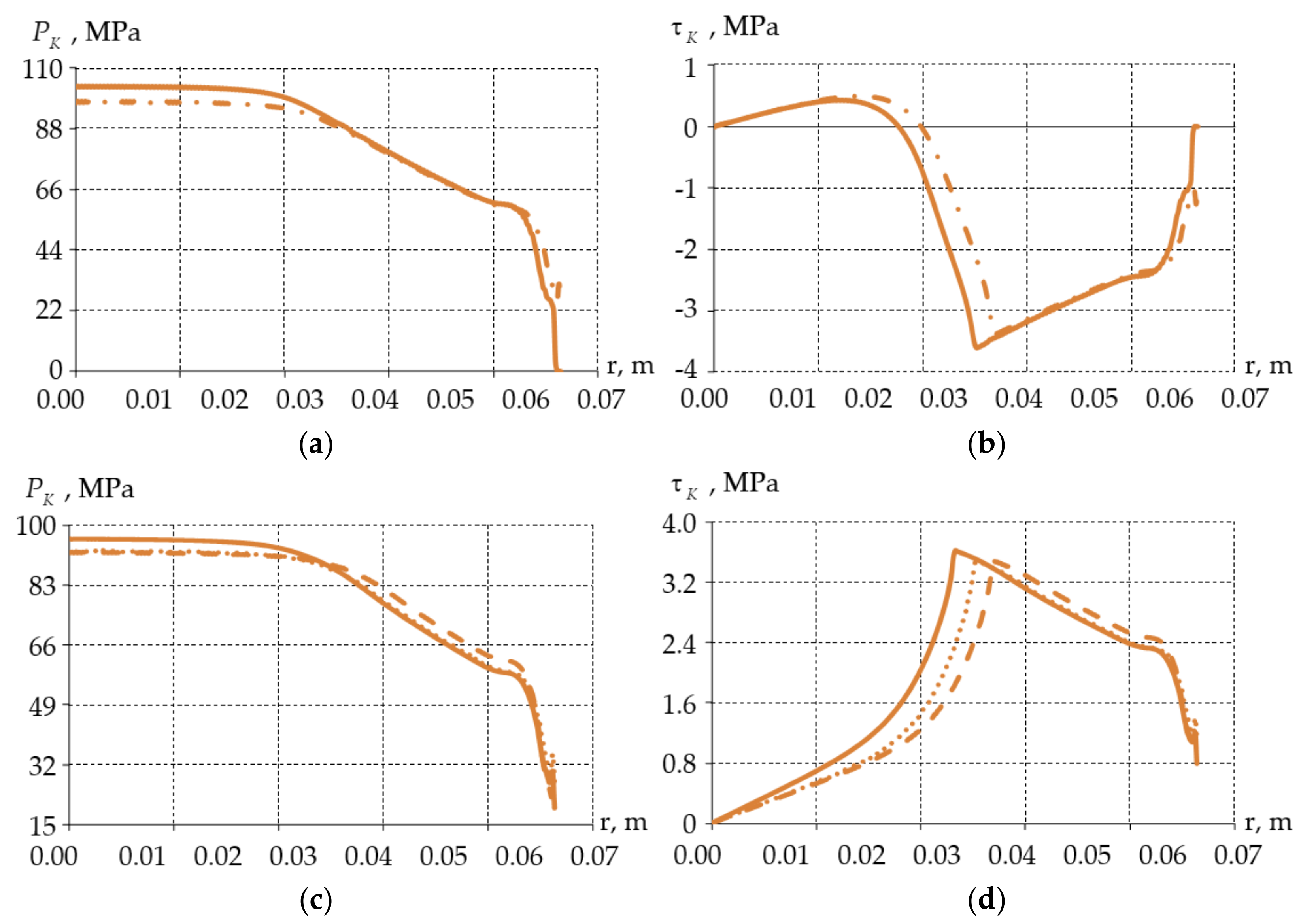
- lowering the maximum level of contact parameters;
- −
- absence of “no contact” zone near the end face of the model A layer.
4. Discussion
4.1. The Compared Results to PTFE Interlayer
4.2. About Materials
5. Conclusions
- −
- a higher level of maximum parameters on all interfaces of steel plates of structure with an interlayer;
- −
- the “no contact” zones on the “turning surface”;
- −
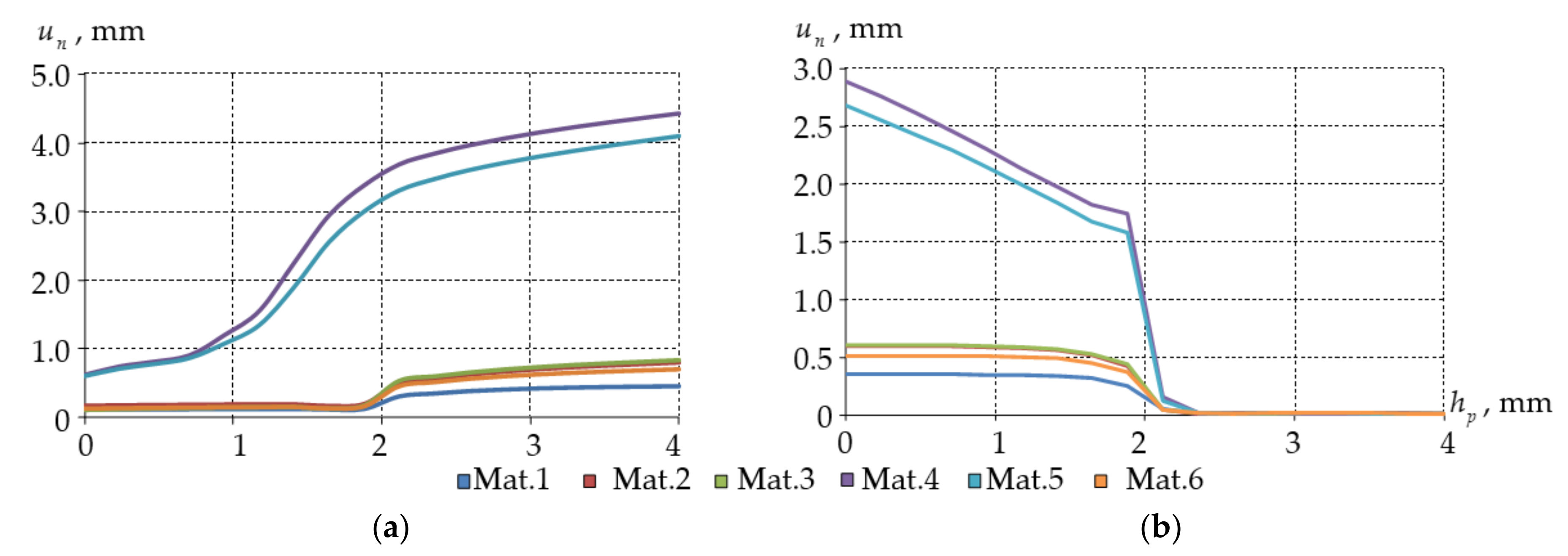
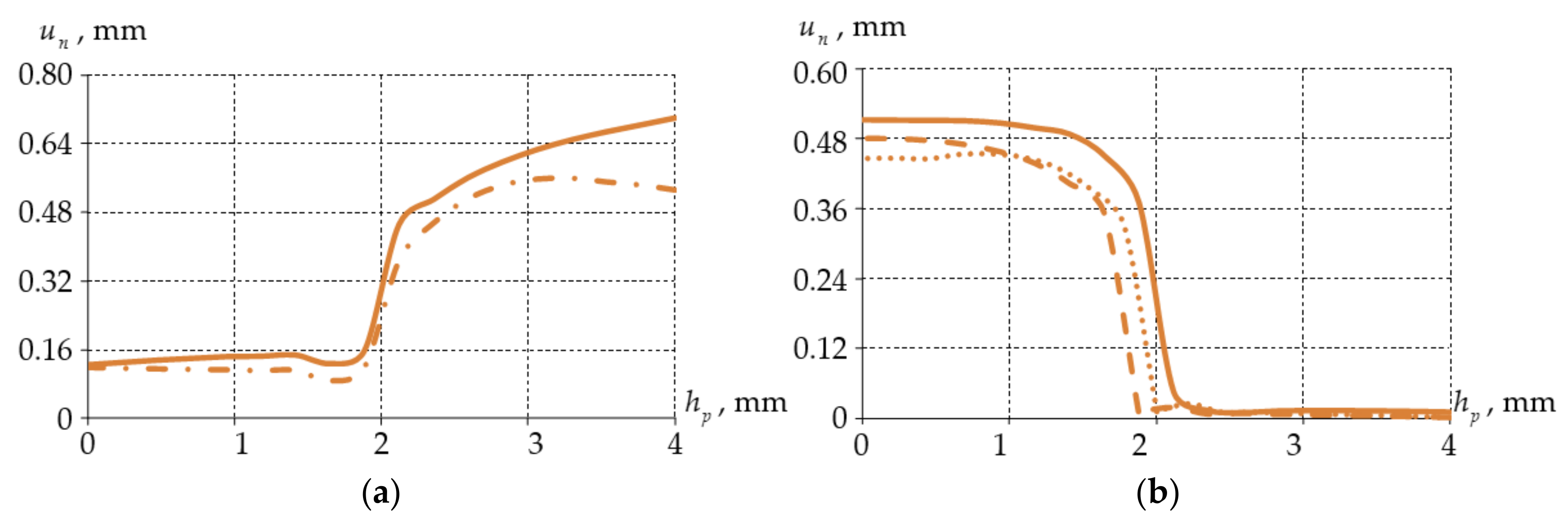
- the maximum level of displacements along the normal to the “end face surface” is greater;
- −
- the plastic flow of interlayer materials from the steel plate recess, material shearing during the structure operation is possible;
- −
- the draft level of the structure is greater.
- −
- the reduction of the maximum level of contact and deformation characteristics;
- −
- the increase in the “adhesion” area of mating surfaces: the volume of the interlayer material working within the framework of the elasticity theory increases;
- −
- the absence of a “no contact” zone in interlayer from polymeric materials (mat. 1–3, 6) or a decrease in % of the “no contact” area in interlayer from composites (mat. 4–s5).
- −
- The construction with a layer placed in lower steel plate shows better performance compared to model A.
- −
- Interlayers from materials 1, 2, and 6 show a better distribution of contact parameters compared to other materials.
- −
- The constructions that have an inclination angle of the end face of 0° for model A and 25° for model B have more distributed contact parameters and lower draft values. Thus, it may be concluded that structures with these angles perform better than those with standard angles.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| inclination angle of the antifriction layer end face; | |
| antifriction layer thickness; | |
| central section height of the upper steel plate; | |
| central section height of the lower steel plate; | |
| structure height; | |
| maximum length of bearing half; | |
| maximum length of bearing; | |
| upper surface of the steel plate; | |
| lower surface of the steel plate; | |
| vertical force applied to ; | |
| pressure; | |
| upper contact surface; | |
| lower contact surface; | |
| antifriction layer end face; | |
| contact pressure; | |
| maximum contact pressure; | |
| maximum contact pressure for the “turning surface”; | |
| relative difference of contact pressure of models A and B; | |
| contact tangential stress; | |
| maximum modulo contact tangential stress; | |
| maximum modulo contact tangential stress for the “turning surface”; | |
| relative difference of maximum modulo contact tangential stress of models A and B; | |
| normal displacements on ; | |
| maximum normal displacements on ; | |
| maximum normal displacements on ; | |
| relative difference of maximum normal displacements on of models A and B; | |
| structure draft; | |
| relative difference of structure draft of models A and B; | |
| area that is contact with full adhesion; | |
| area that is contact with full adhesion for the “turning surface”; | |
| area of the zone of “no contact” (divergence) of mating surfaces; | |
| area of the zone of “no contact” (divergence) of mating surfaces for the “turning surface”. |
References
- Arêde, A.; Costa, C. Proceedings of ARCH 9th International Conference on Arch Bridges; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Vayas, I.; Liopoulos, A. Design of Steel-Concrete Composite Bridges to Eurocodes; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Vaidya, S.M. Bridge Bearings; Railways Institute of Civil Engineering: Pune, India, 2014.
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimisation and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Xie, H.-B.; Wu, W.-J.; Wang, Y.-F. Life-time reliability based optimization of bridge maintenance strategy considering LCA and LCC. J. Clean. Prod. 2018, 176, 36–45. [Google Scholar] [CrossRef]
- Wu, C.; Wu, P.; Wang, J.; Jiang, R.; Chen, M.; Wang, X. Critical review of data-driven decision-making in bridge operation and maintenance. Struct. Infrastruct. Eng. 2020, 18, 47–70. [Google Scholar] [CrossRef]
- Calvert, G.; Neves, L.; Andrews, J.; Hamer, M. Incorporating defect specific condition indicators in a bridge life cycle analysis. Eng. Struct. 2021, 246, 113003. [Google Scholar] [CrossRef]
- Peel, H.; Luo, S.; Cohn, A.; Fuentes, R. Localisation of a mobile robot for bridge bearing inspection. Autom. Constr. 2018, 94, 244–256. [Google Scholar] [CrossRef]
- Petcherdchoo, A.; Neves, L.A.; Frangopol, D.M. Optimizing Lifetime Condition and Reliability of Deteriorating Structures with Emphasis on Bridges. J. Struct. Eng. 2006, 134, 544–552. [Google Scholar] [CrossRef]
- Higuchi, S.; Macke, M. Cost-benefit analysis for the optimal rehabilitation of deteriorating structures. Struct. Saf. 2008, 30, 291–306. [Google Scholar] [CrossRef]
- Colford, B.; Chiarello, M.; Hendy, C.; Sandberg, J. Bearing replacement and strengthening of Forth road bridge approach viaducts. In Proceedings of the Sixth International IABMAS Conference, Lake Como, Italy, 8–12 July 2012; pp. 81–92. [Google Scholar] [CrossRef]
- Redpath, J. Pendel bearing replacement at A9 Kessock Bridge, Scotland. In Proceedings of the Institution of Civil Engineers-Bridge Engineering; Thomas Telford Ltd.: London, UK, 2007; Volume 160, pp. 195–203. [Google Scholar] [CrossRef]
- Ma, F.; Cheng, X.; Zhu, X.; Wu, G.; Feng, D.-C.; Hou, S.; Kang, X. Safety Monitoring of Bearing Replacement for a Concrete High-Speed Railway Bridge Based on Acoustic Emission. J. Perform. Constr. Facil. 2022, 36, 04022014. [Google Scholar] [CrossRef]
- Proske, D. Bridge Collapse Frequencies Versus Failure Probabilities; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Beben, D. Soil-Steel Bridges; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Ye, S.; Lai, X.; Bartoli, I.; Aktan, A.E. Technology for condition and performance evaluation of highway bridges. J. Civ. Struct. Health Monit. 2020, 10, 573–594. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A. Structural Health Monitoring for Suspension Bridges; Springer: Singapore, 2019. [Google Scholar] [CrossRef]
- Okamoto, N.; Kinoshita, T.; Futagi, T. Development of new embedded expansion joint using high flexibility stone mastic asphalt. In International Symposium on Testing and Characterization of Sustainable and Innovative Bituminous Materials; Springer: Dordrecht, The Netherlands, 2016; Volume 11, pp. 837–849. [Google Scholar] [CrossRef]
- Eggert, H.; Kauschke, W. Structural Bearings; Ernst & Sohn: Berlin, Germany, 2002. [Google Scholar]
- Kamenskih, A.; Trufanov, N. Numerical analysis of the stress state of a spherical contact system with an interlayer of antifriction material. Comput. Contin. Mech. 2013, 6, 54–61. [Google Scholar] [CrossRef]
- Jiang, L.; He, W.; Wei, B.; Wang, Z.; Li, S. The shear pin strength of friction pendulum bearings (FPB) in simply supported railway bridges. Bull. Earthq. Eng. 2019, 17, 6109–6139. [Google Scholar] [CrossRef]
- Kuznetsov, D.N.; Grigorash, V.V.; Sventikov, A.A. Work power of the support unit of the steel I-beam. Russ. J. Build. Constr. Arch. 2021, 1, 19–29. [Google Scholar] [CrossRef]
- Kim, S.; Kim, T. Machine-learning-based prediction of vortex-induced vibration in long-span bridges using limited information. Eng. Struct. 2022, 266, 114551. [Google Scholar] [CrossRef]
- Pipinato, A. Innovative Bridge Design Handbook; Elsevier: Oxford, UK, 2021. [Google Scholar] [CrossRef]
- Blinkin, M.; Koncheva, E. Transport Systems of Russian Cities: Ongoing Transformations; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Wetzk, V. Brückenlager. 1850–1950. Ph.D. Thesis, Brandenburgische Technische Universität Cottbus-Senftenberg, Cottbus, Germany, 25 November 2010. [Google Scholar]
- Huang, X.; Hou, S.; Liao, M.; Zhu, Z. Bearing Capacity Evaluation and Reinforcement Analysis of Bridge Piles under Strong Earthquake Conditions. KSCE J. Civ. Eng. 2018, 22, 1295–1303. [Google Scholar] [CrossRef]
- Devitofranceschi, A.; Paolieri, E. Integral Bridges: A Construction Method to Minimize Maintenance Problems. Lect. Notes Civ. Eng. 2020, 42, 515–529. [Google Scholar] [CrossRef]
- Huang, W.; Pei, M.; Liu, X.; Wei, Y. Design and construction of super-long span bridges in China: Review and future perspectives. Front. Struct. Civ. Eng. 2020, 14, 803–838. [Google Scholar] [CrossRef]
- Su, M.; Wang, J.; Peng, H.; Cai, C.S.; Dai, G. State-of-the-art review of the development and application of bridge rotation construction methods in China. Sci. China Technol. Sci. 2020, 64, 1137–1152. [Google Scholar] [CrossRef]
- Kollegger, J.; Reichenbach, S. Balanced Lift Method—Building Bridges without Formwork. Lect. Notes Civ. Eng. 2018, 10, 200–215. [Google Scholar] [CrossRef]
- Yu, X.-M.; Chen, D.-W.; Bai, Z.-Z. A New Method for Analysis of Sliding Cable Structures in Bridge Engineering. KSCE J. Civ. Eng. 2018, 22, 4483–4489. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskih, A.A.; Pankova, A.P. Numerical analysis of the spherical bearing geometric configuration with antifriction layer made of different materials. PNRPU Mech. Bull. 2020, 4, 15–26. [Google Scholar] [CrossRef]
- Ono, K. Structural materials: Metallurgy of bridges. In Metallurgical Design and Industry; Springer: Cham, Switzerland, 2018; pp. 193–269. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J. Effect of Material Characteristics of High Damping Rubber Bearings on Aseismic Behaviors of a Two-Span Simply Supported Beam Bridge. Adv. Mater. Sci. Eng. 2020, 2020, 9231382. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, Y.; Wang, W. Influence of the cage on the migration and distribution of lubricating oil inside a ball bearing. Friction 2022, 10, 1035–1045. [Google Scholar] [CrossRef]
- Choi, E.; Lee, J.S.; Jeon, H.-K.; Park, T.; Kim, H.-T. Static and dynamic behavior of disk bearings for OSPG railway bridges under railway vehicle loading. Nonlinear Dyn. 2010, 62, 73–93. [Google Scholar] [CrossRef]
- Itoh, Y.; Gu, H.S. Prediction of Aging Characteristics in Natural Rubber Bearings Used in Bridges. J. Bridge Eng. 2009, 14, 122–128. [Google Scholar] [CrossRef]
- Beyer, E.; Wintergerst, L. New bridge storage, new pillar shape. Bauingenleur 1960, 35, 227–230. [Google Scholar]
- Block, T.; Eggert, H.; Kauschke, W. Lager im Bauwesen; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Eggert, H.; Grote, J.; Kauschke, W. Lager im Bauwesen; Ernst & Sohn: Berlin, Germany, 1974. [Google Scholar]
- Wei, W.; Yuan, Y.; Igarashi, A.; Zhu, H.; Luo, K. Generalized hyper-viscoelastic modeling and experimental characterization of unfilled and carbon black filled natural rubber for civil structural applications. Constr. Build. Mater. 2020, 253, 119211. [Google Scholar] [CrossRef]
- Sánchez, M.A.G.; Giraldo-Vásquez, D.H.; Sánchez, R.M. Rheometric, transient, and cyclic tests to assess the viscoelastic behavior of natural rubber-based compounds used for rubber bearings. Mater. Today Commun. 2020, 22, 100815. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, S.; Tan, P.; Zhu, H. Mechanical performance and shear constitutive model study of a new high-capacity polyurethane elastomeric bearing. Constr. Build. Mater. 2020, 232, 117227. [Google Scholar] [CrossRef]
- Niemierko, A. Modern Bridge Bearings and Expansion Joints for Road Bridges. Transp. Res. Procedia 2016, 14, 4040–4049. [Google Scholar] [CrossRef]
- Askari, E.; Flores, P. Coupling multi-body dynamics and fluid dynamics to model lubricated spherical joints. Arch. Appl. Mech. 2020, 90, 2091–2111. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P. Influence Analysis of the Antifriction Layer Materials and Thickness on the Contact Interaction of Spherical Bearings Elements. Lubricants 2022, 10, 30. [Google Scholar] [CrossRef]
- Dhanumalayan, E.; Joshi, G.M. Performance properties and applications of polytetrafluoroethylene (PTFE)—A review. Adv. Compos. Hybrid. Mater. 2018, 1, 247–268. [Google Scholar] [CrossRef]
- Sadovskaya, N.V.; Obvintsev, A.Y.; Khatipov, R.S.; Seliverstov, D.I.; Khatipov, S.A. Effect of irradiation on interfacial interaction and structure formation in filled PTFE composites. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2016, 10, 917–924. [Google Scholar] [CrossRef]
- Yi, X.; Du, S.; Zhang, L. Composite Materials Engineering, Volume 1: Fundamentals of Composite Materials; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Wang, Q.J.; Chung, Y.W. Encyclopedia of Tribology; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Martynov, M.A.; Gol’Dman, A.Y.; Il’Chenko, P.A.; Polyakov, Y.S.; Andreeva, A.I. Effect of thermal treatment on the mechanical properties and accumulation of submicrocracks in fluoroplastics. Strength Mater. 1975, 7, 1390–1393. [Google Scholar] [CrossRef]
- Pavlenko, V.I.; Bondarenko, G.G.; Tarasov, D.G.; Edamenko, O.D. Gamma modification of radiation-resistant fluoroplastic composite. Inorg. Mater. Appl. Res. 2013, 4, 389–393. [Google Scholar] [CrossRef]
- Shelestova, V.A.; Grakovich, P.N.; Danchenko, S.G.; Smirnov, V.A. New antifriction materials of the Fluvis group based on modified carbon fibers. Chem. Pet. Eng. 2006, 42, 663–666. [Google Scholar] [CrossRef]
- Balyakin, V.B.; Khatipov, S.A.; Pilla, C.K. Experimental studies of tribotechnical characteristics of radiation-modified polytetrafluoroethylene to use in rotor supports. J. Frict. Wear 2015, 36, 346–349. [Google Scholar] [CrossRef]
- Adamov, A.; Kamenskikh, A.; Strukova, V. Numerical analysis of the effect of the antifriction layer face angle on the deformation behavior of spherical support parts of different geometric configurations. AIP Conf. Proc. 2021, 2371, 020004. [Google Scholar] [CrossRef]
- Adamov, A.A.; Kamenskikh, A.A.; Strukova, V.I. Influence of geometry and configuration of the spherical sliding layer of bridge bearings on the structure working capacity. Comput. Contin. Mech. 2021, 14, 289–299. [Google Scholar] [CrossRef]
- Gajewski, M.D.; Miecznikowski, M. Assessment of the Suitability of Elastomeric Bearings Modeling Using the Hyperelasticity and the Finite Element Method. Materials 2021, 14, 7665. [Google Scholar] [CrossRef]
- Heggade, V.N. Bearings & Their Configurations Within Bridge System. Bridge Struct. Eng. 2013, 43, 23–35. [Google Scholar]
- Kamenskih, A.A.; Trufanov, N.A. Regularities interaction of elements contact spherical unit with the antifrictional polymeric interlayer. J. Frict. Wear 2015, 36, 170–176. [Google Scholar] [CrossRef]
- Wang, Q.J.; Chung, Y.W. Antifriction Materials and Composites; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Gooch, J.W. Encyclopedic Dictionary of Polymers; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Wang, H.; Sun, A.; Qi, X.; Dong, Y.; Fan, B. Experimental and Analytical Investigations on Tribological Properties of PTFE/AP Composites. Polymers 2021, 13, 4295. [Google Scholar] [CrossRef] [PubMed]
- Mnif, R.; Ben Jemaa, M.C.; Kacem, N.H.; Elleuch, R. Impact of Viscoelasticity on the Tribological Behavior of PTFE Composites for Valve Seals Application. Tribol. Trans. 2013, 56, 879–886. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Zhang, Q.; Zhou, Y. Experimental and Theoretical Research on the Stress-Relaxation Behaviors of PTFE Coated Fabrics under Different Temperatures. Adv. Mater. Sci. Eng. 2015, 2015, 319473. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, D.; Chen, K. In situ microscopic observations of dynamic viscoelastic contact and deformation at a friction interface. Mater. Express 2019, 9, 235–244. [Google Scholar] [CrossRef]
- Tan, B.; Stephens, L.S. Evaluation of viscoelastic characteristics of PTFE-Based materials. Tribol. Int. 2019, 140, 105870. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, K.; Ye, J.; Li, X.; Zhao, X.; Qu, T.; Liu, Q.; Gao, B. The effects of filler type on the friction and wear performance of PEEK and PTFE composites under hybrid wear conditions. Wear 2022, 490, 204178. [Google Scholar] [CrossRef]
- Samad, M.A. Recent Advances in UHMWPE/UHMWPE Nanocomposite/UHMWPE Hybrid Nanocomposite Polymer Coatings for Tribological Applications: A Comprehensive Review. Polymers 2021, 13, 608. [Google Scholar] [CrossRef]
- Mageba. Available online: https://www.mageba-group.com (accessed on 20 July 2022).
- Maurer. Available online: https://www.maurer.eu (accessed on 20 July 2022).
- Lampman, S. Characterization and Failure Analysis of Plastics; ASM International: Almere, The Netherlands, 2003. [Google Scholar]
- Friedrich, K. Polymer composites for tribological applications. Adv. Ind. Eng. Polym. Res. 2018, 1, 3–39. [Google Scholar] [CrossRef]

| Parameter | Material 1 (UHMWPE with Carbon Additive) | Material 2 (UHMWPE Produced in Germany) | Material 3 (UHMWPE Produced in Russia) | Material 4 (MAK Composite with Dendritic Bronze Inclusions) | Material 5 (MAK Composite with Spherical Bronze Inclusions) | Material 6 (Modified PTFE) |
|---|---|---|---|---|---|---|
| , MPa | 1420 | 706 | 1050 | 903 | 860.52 | 863.8 |
| 0.440 | 0.470 | 0.452 | 0.447 | 0.439 | 0.461 |
| Parameter | Material | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Model A | ||||||
| , MPa | 95.487 | 98.264 | 121.200 | 166.030 | 160.520 | 103.500 |
| , MPa | 3.629 | 3.702 | 4.451 | 6.101 | 5.871 | 3.877 |
| 26.315 | 26.547 | 27.232 | 27.214 | 27.341 | 26.693 | |
| Model B | ||||||
| , MPa | 90.559 | 92.095 | 110.39 | 148.32 | 135.44 | 96.193 |
| , MPa | 3.060 | 3.166 | 3.810 | 5.276 | 4.717 | 3.291 |
| 29.599 | 29.093 | 28.971 | 28.111 | 28.716 | 29.228 | |
| Comparison Models A and B | ||||||
| , % | 5.161 | 6.278 | 8.919 | 11.856 | 15.624 | 7.060 |
| , % | 15.684 | 14.481 | 14.389 | 15.785 | 19.663 | 15.121 |
| Parameter | Material | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Model A | ||||||
| , MPa | 95.217 | 98.087 | 121.070 | 165.620 | 160.230 | 103.390 |
| , MPa | 3.362 | 3.415 | 4.239 | 6.009 | 5.759 | 3.593 |
| 28.321 | 28.724 | 28.564 | 27.561 | 27.815 | 28.773 | |
| Model B | ||||||
| , MPa | 90.803 | 92.216 | 110.390 | 148.460 | 135.570 | 96.268 |
| , MPa | 3.421 | 3.475 | 4.085 | 5.396 | 4.852 | 3.621 |
| 26.540 | 26.539 | 27.024 | 27.514 | 27.944 | 26.587 | |
| Comparison Models A and B | ||||||
| , % | 4.636 | 5.986 | 8.813 | 10.361 | 15.390 | 6.888 |
| , % | 1.755 | 1.757 | 3.633 | 10.201 | 15.749 | 0.779 |
| Parameter | Material | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Model A | ||||||
| , % | 37.55 | 35.27 | 13.77 | 1.18 | 1.86 | 28.87 |
| , % | 1.49 | 2.97 | 2.97 | 4.73 | 4.44 | 2.23 |
| Model B | ||||||
| , % | 31.39 | 29.31 | 14.64 | 2.78 | 5.34 | 26.28 |
| , % | 0.00 | 0.00 | 0.00 | 5.17 | 4.44 | 0.00 |
| Parameter | Material | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Model A | ||||||
| , mm | 0.451 | 0.802 | 0.834 | 4.423 | 4.093 | 0.700 |
| Model B | ||||||
| , mm | 0.358 | 0.594 | 0.607 | 2.894 | 2.680 | 0.513 |
| Comparison Models A and B | ||||||
| , % | 20.621 | 25.935 | 27.218 | 34.569 | 34.522 | 26.714 |
| Parameter | Material | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Model A | ||||||
| , mm | 0.120 | 0.190 | 0.147 | 0.318 | 0.312 | 0.142 |
| Model B | ||||||
| , mm | 0.108 | 0.162 | 0.102 | 0.243 | 0.252 | 0.123 |
| Comparison Models A and B | ||||||
| , % | 11.135 | 17.260 | 44.046 | 30.876 | 23.522 | 15.833 |
| Parameter | Material | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Model A | |||||||
| , MPa | 0 | 90.888 | 100.090 | 99.848 | 142.510 | 120.610 | 97.690 |
| 30 | 95.217 | 98.087 | 121.070 | 165.620 | 160.230 | 103.390 | |
| , MPa | 0 | 3.173 | 3.493 | 3.494 | 5.080 | 4.257 | 3.393 |
| 30 | 3.362 | 3.415 | 4.239 | 6.009 | 5.759 | 3.593 | |
| Model B | |||||||
| , MPa | 25 | 87.417 | 94.860 | 93.021 | 124.540 | 114.140 | 92.495 |
| 30 | 90.803 | 92.216 | 110.390 | 148.460 | 135.570 | 96.268 | |
| 40 | 87.878 | 94.400 | 93.434 | 126.870 | 115.650 | 92.886 | |
| , MPa | 25 | 3.306 | 3.532 | 3.493 | 4.563 | 4.204 | 3.483 |
| 30 | 3.421 | 3.475 | 4.085 | 5.396 | 4.852 | 3.621 | |
| 40 | 3.322 | 3.520 | 3.514 | 4.658 | 4.286 | 3.487 | |
| Parameter | Material | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Model A | |||||||
| , % | 0 | 42.81 | 28.87 | 30.10 | 4.83 | 12.94 | 33.07 |
| 30 | 37.55 | 35.27 | 13.77 | 1.18 | 1.86 | 28.87 | |
| , % | 0 | 0.00 | 0.00 | 0.00 | 3.71 | 2.97 | 0.00 |
| 30 | 1.49 | 2.97 | 2.97 | 4.73 | 4.44 | 2.23 | |
| Model B | |||||||
| , % | 25 | 38.36 | 29.80 | 27.21 | 9.39 | 14.17 | 33.10 |
| 30 | 31.39 | 29.31 | 14.64 | 2.78 | 5.34 | 26.28 | |
| 40 | 35.69 | 27.21 | 27.97 | 7.59 | 12.11 | 29.51 | |
| , % | 25 | 0.00 | 0.00 | 0.00 | 4.33 | 4.33 | 0.00 |
| 30 | 0.00 | 0.00 | 0.00 | 5.17 | 4.44 | 0.00 | |
| 40 | 0.00 | 0.00 | 0.00 | 3.55 | 2.84 | 0.00 | |
| Parameter | Material | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Model A | |||||||
| , mm | 0 | 0.400 | 0.688 | 0.679 | 2.596 | 2.200 | 0.560 |
| 30 | 0.451 | 0.802 | 0.834 | 4.423 | 4.093 | 0.700 | |
| Model B | |||||||
| , mm | 25 | 0.353 | 0.585 | 0.569 | 2.224 | 2.066 | 0.480 |
| 30 | 0.358 | 0.594 | 0.607 | 2.894 | 2.680 | 0.513 | |
| 40 | 0.334 | 0.553 | 0.536 | 2.550 | 2.262 | 0.454 | |
| Parameter | Material | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Model A | |||||||
| , mm | 0 | 0.116 | 0.136 | 0.138 | 0.240 | 0.243 | 0.133 |
| 30 | 0.120 | 0.190 | 0.147 | 0.318 | 0.312 | 0.142 | |
| Model B | |||||||
| , mm | 25 | 0.100 | 0.114 | 0.116 | 0.218 | 0.217 | 0.113 |
| 30 | 0.108 | 0.162 | 0.102 | 0.243 | 0.252 | 0.123 | |
| 40 | 0.112 | 0.130 | 0.130 | 0.224 | 0.233 | 0.127 | |
| Model | Parameter | |||||
|---|---|---|---|---|---|---|
MPa | MPa | % | % | mm | mm | |
| A | 168.95 | 6.02 | 3.59 | 7.05 | 5.77 | 0.41 |
| B | 156.58 | 5.05 | 14.59 | 5.72 | 3.90 | 0.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adamov, A.A.; Kamenskikh, A.A.; Pankova, A.P.; Strukova, V.I. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants 2022, 10, 207. https://doi.org/10.3390/lubricants10090207
Adamov AA, Kamenskikh AA, Pankova AP, Strukova VI. Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants. 2022; 10(9):207. https://doi.org/10.3390/lubricants10090207
Chicago/Turabian StyleAdamov, Anatoliy A., Anna A. Kamenskikh, Anastasia P. Pankova, and Veronika I. Strukova. 2022. "Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations" Lubricants 10, no. 9: 207. https://doi.org/10.3390/lubricants10090207
APA StyleAdamov, A. A., Kamenskikh, A. A., Pankova, A. P., & Strukova, V. I. (2022). Comparative Analysis of the Work of Bridge Spherical Bearing at Different Antifriction Layer Locations. Lubricants, 10(9), 207. https://doi.org/10.3390/lubricants10090207





