Abstract
The ‘relativity with a preferred frame’, designed to reconcile the relativity principle with the existence of the cosmological preferred frame, incorporates the preferred frame at the level of special relativity (SR) while retaining the fundamental spacetime symmetry, which, in the standard SR, manifests itself as Lorentz invariance. In this paper, the processes, accompanying the propagation of cosmic rays and gamma rays through the background radiation from distant sources to Earth, are considered on the basis of particle dynamics and electromagnetic field dynamics developed within the framework of the ‘relativity with a preferred frame’. Applying the theory to the photopion-production and pair-production processes shows that the modified particle dynamics and electrodynamics lead to measurable signatures in the observed cosmic and gamma-ray spectra which can provide an interpretation of some puzzling features found in the observational data. Other processes responsible for gamma-ray attenuation are considered. It is found, in particular, that electromagnetic cascades, developing on cosmic microwave background and extragalactic background light, may be reduced or suppressed due to the preferred frame effects which should influence the shape of the very high-energy gamma-ray spectra. Other possible observational consequences of the theory, such as the birefringence of light propagating in vacuo and dispersion, are discussed.
1. Introduction
Lorentz symmetry is arguably the most fundamental symmetry of physics, at least in its modern conception. Physical laws are Lorentz-covariant among inertial frames; namely, the form of a physical law is invariant under the Lorentz group of spacetime transformations. Therefore, the Lorentz symmetry sets a fundamental constraint for physical theories. Nevertheless, modifications of special relativity (SR) and possible violations of Lorentz invariance have recently obtained increased attention. Although the success of general relativity (GR) to describe all observed gravitational phenomena proves the fundamental importance of Lorentz invariance in our current understanding of gravitation, some of the modern theories (unification theories, extensions of the standard model, and so on) suggest a violation of special relativity. The aim of most of the Lorentz-violating theories is to modify a Lorentz-invariant theory by introducing small phenomenological Lorentz-violating terms into the basic relations of the theory (Lagrangian density, dispersion relation, and so on) and predict what can be expected from it (see, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] for the most popular approaches to parameterizing Lorentz violating physics). Some of those studies are discussed in the following sections in relation to the results obtained in the present paper.
The theory termed ‘relativity with a preferred frame’, developed in [27,28,29], represents a very special type of a Lorentz-violating theory that is conceptually different from others found in the literature. It is not even a preferred frame that makes a difference—all violations of Lorentz invariance, made by distorting Lorentz-invariant relations of the theory, imply the existence of a preferred frame for the formulation of the physical laws, the one in which all the calculations need to be carried out, since breaking relativistic invariance also invalidates the transformations that allow us to change reference frame. The first major difference of the present analysis from the abovementioned studies is that the Lorentz violation is not introduced into the theory. The theory is based on the same principles as the standard relativity theory, relativity principle, and the principle of universality of speed of light, but the latter is applied in a more general form using a freedom in formulation of the principle. Lorentz violation arises as a result of the analysis revealing itself in the form of the spacetime transformations between inertial frames, which differs from the Lorentz transformations. In other terms, Lorentz violation is ingrained into the framework of the theory at some fundamental level. The second major difference is that the relativistic invariance, in the sense that the form of a physical law is invariant under the spacetime transformations between inertial frames, is not violated—it is a Lorentz violation without violation of relativistic invariance.
To outline the framework of the theory named ‘relativity with a preferred frame’, one has to start from the definition of the preferred frame. In the ‘relativity with a preferred frame’, the preferred frame is defined as the only frame where propagation of light is isotropic, while it is anisotropic in all other frames moving relative to the preferred one (it is a common definition in the studies investigating the fundamentals of special relativity and its potential breaking). When discussing the anisotropy of propagation of light, one has to distinguish between the two-way speed of light, i.e. the average speed from source to observer and back, and the one-way speed, which is the speed of light in one direction—either from source to observer or back.1 In ‘relativity with a preferred frame’, it is the one-way speed of light that is assumed to be anisotropic in all the frames except for the preferred frame, while the two-way speed of light is isotropic and equal to c in all inertial frames.2 The analysis is based on invariance of the equation of (anisotropic) light propagation with respect to the spacetime transformations between inertial frames; the group structure of the transformations plays a central role in the analysis. Although the existence of the preferred frame seems to be in contradiction both with the basic principles of special relativity and with the group property of the transformations, in the framework of the ‘relativity with a preferred frame’, those principles are retained. The crucial element, which allows retaining of the relativistic invariance and the group property of the spacetime transformations, is that the anisotropy parameter k, figuring in the equation of the anisotropic light propagation, is treated as a variable that takes part in the group transformations (for more details, see Section 2). Then, the preferred frame, in which , enters the analysis on equal footing with other frames, as nothing distinguishes the transformations to/from that frame from the transformations between two frames with . In the modified relativity theory, designed in such a way, all the features of the standard relativity are present. Besides the relativity principle, universality of the light propagation, and group property, it is the spacetime symmetry expressed by the existence of a combination invariant under the transformations (a counterpart of the interval of the standard SR)—only the form of the invariant combination is modified. Such a ’modified spacetime symmetry’ paves the way to extensions of the kinematics of the ‘relativity with a preferred frame’ to free-particle dynamics, general relativity, and electromagnetic field theory.
The generalization of special relativity described above cannot be validated by experiments measuring speed of light, since only the two-way speed of light, the same in all the frames, can be measured. For creating a physical theory, predictions of which can be compared with observational data, it is necessary to identify the preferred frame of the present analysis, which is defined by the property of isotropy of the one-way speed of light, with a frame possessing the property that the velocity of any other frame relative to it can be measured using some other physical phenomena. In the present analysis, that preferred frame is a comoving frame of cosmology, or the CMB frame. Note that identifying the preferred frame with the CMB frame is usually implied in Lorentz-violating theories (see, e.g., [44,45,46]). As a matter of fact, it is the only frame possessing the property whereby motion of any other frame relative to it is distinguishable and, in addition, this frame, similar to the preferred frame of the present analysis, is defined based on the isotropy property. As a result of specifying the preferred frame, all the relations of the ‘relativity with a preferred frame’, as well as of its extensions, contain only one universal constant, b, which is a parameter to be adjusted for fitting the results of the theory to observational data.
The fact that, in the present analysis, the preferred frame is the cosmological comoving frame dictates applying the theory on cosmological scales.3 In [28], special relativity with a preferred frame is extended to general relativity, and the cosmological models based on the modified general relativity are developed. The results allow explanation of the SNIa observational data (see, e.g., [48]) without introducing dark energy. The baryon acoustic oscillations (BAO) data can be also fit to the theory. It is found that there exists the interval of the values of the single parameter of the theory b, within which the theory fits both the BAO and the SNIa data. In [29], the kinematics of relativity with a preferred frame is extended to the free particle dynamics, and the modified dynamics is applied to the problem of interactions of the ultra-high-energy cosmic rays (UHECR) with universal diffuse background radiation (see, e.g., review articles [49,50,51]). In this respect, the Greisen–Zatsepin–Kuzmin (GZK) cutoff [52,53], which describes a well-defined energy threshold for the energy suppression due to pion photoproduction by UHECR protons, is the most remarkable phenomenon. It is shown in [29] that the results of applying the modified particle dynamics to defining the GZK cutoff, combined with constraints on the values of b from cosmology, may provide an explanation of the much debated data [54,55] on the mass composition of UHECR.
The purpose of the present study is twofold. First, to construct the electromagnetic field theory within the framework of the ‘relativity with a preferred frame’. Implementing this task yields the modified Maxwell equations for describing electromagnetic phenomena which is of general theoretical interest in view of the special type of Lorentz-violating theory which the ‘relativity with a preferred frame’ represents. In particular, studying the electromagnetic waves on the basis of the modified Maxwell equations reveals some features that are not found in other Lorentz-violating theories involving the electromagnetic phenomena.
The second aim of the present study, partially related to the first, is to apply relativity with a preferred frame to the processes accompanying the gamma-rays propagation from distant sources to Earth. In the interactions of the gamma-rays high-energy photons () with the photons of the extragalactic background light (), the process of pair production , which has the effect of a significant energy attenuation in the flux of high-energy gamma rays, is of the utmost importance. Such interaction takes place for gamma rays with energies above the threshold of pair production (in other terms, the threshold defines the minimum energy of the background photons needed for the process to occur). Calculating the threshold for the pair-production process on the basis of the dynamics of relativity with a preferred frame yields a correction factor to the standard threshold value which influences the value of the optical depth for the gamma-rays propagation. The preferred frame effects also influence the cosmological part of the expression for the optical depth which is analyzed using the results from the cosmology of relativity with a preferred frame developed in [28]. The possibility of the vacuum dispersion and vacuum birefringence effects that are considered in the literature as major features of the behavior of electromagnetic waves in vacuum in the presence of Lorentz violation is discussed on the basis of the modified Maxwell equations and the electromagnetic wave equation, obtained in the present paper. The analysis is also aimed at revealing constraints on the vales of the parameter of the theory b that the astrophysical tests using those phenomena could impose.
The presentation is organized as follows. To make the presentation self-contained, in the first two sections (Section 2.1 and Section 2.2) following the introduction, the kinematics and dynamics of the ‘relativity with a preferred frame’, developed in the earlier papers [27,28], are outlined. In Section 3, the electromagnetic field dynamics is developed, and in Section 4, the modified electromagnetic field equations are applied to the problem of electromagnetic waves propagation. The processes accompanying the gamma-rays propagation through the universal diffuse background radiation are considered in Section 5. The results and some related issues are discussed in the concluding Section 6.
2. Special Relativity
2.1. Kinematics
Kinematics of relativity with a preferred frame is developed using the group property of the spacetime transformations as a primary tool. The transformations between two arbitrary inertial reference frames S and , with the coordinate systems and in the standard configuration (with the y- and z-axes parallel to the Y- and Z-axes and moving relative to S with the velocity v in the positive direction of the common x-axis), are considered. The groups of transformations are sought using the condition of invariance of the equation of anisotropic light propagation [35,36,38]:
where k is the anisotropy parameter. The analysis deals with groups of transformations which involve both the space and time coordinates and the anisotropy parameter k, as follows:
where a is the group parameter and k and K are the anisotropy parameters in the frames and S, respectively. The group from Equation (2) is defined from the requirement that the transformations convert the equation of light propagation in the frame S
into the equation of light propagation in the frame
In accordance with the infinitesimal Lie group technique (see, e.g., [56,57]), the infinitesimal group generators for the variables are introduced as follows:
See [28,29,30,31,32,33,34,35,36,37,38] for arguments regarding justification and generality of Equations (1) and (5). Having the group generators defined, one can determine the finite group transformations and then determine invariants of the group (see [27,28] for details). As a result, a counterpart of the interval of the standard SR, the combination, invariant under the group transformations, is identified as follows:
where is the group generator for the variable (see Equation (5)). Introducing the new variables
converts the invariant combination (6) into the Minkowski interval
while the transformations take the form of Lorentz transformations. However, in applications to physical effects, one has to use the ’true’ time and space intervals in the ’physical’ variables obtained using transformations inverse to Equation (8).
Next, the dependence of the anisotropy parameter k in an arbitrary inertial frame on the frame velocity relative to the preferred frame can be approximated by
where b is an arbitrary constant. Approximation (10) is valid up to the third order in on the grounds of the argument that a sign of k should change to the opposite with the direction of relative motion reversed, and therefore the expansion of the function should not include even powers of . With that approximation, the factor takes the form (see [27,28] for details of calculations)
Upon introducing Equation (10) into Equation (11), the function becomes the function of the frame velocity relative to the preferred frame, as follows:
Thus, all equations of the theory contain only one universal parameter b.
2.2. Free Particle Dynamics
In this section, the free particle dynamics of the ‘relativity with a preferred frame’ developed in [29] is presented in a shortened form. The modified dynamics is developed based on the existence of the invariant combination (a counterpart of the interval of the standard SR) defined by Equation (6). Then, the action integral for a free material particle is [58]
where the integral is along the world line between two given world points, and L represents the Lagrange function. The invariant defined by Equation (6) can be represented in the form
where
and
are components of the velocity vector. Then, the Lagrange function is defined by
which is used to obtain expressions for the momentum and energy E of a particle, as follows:
and
Proceeding with the four-dimensional formulation, we will use the variables defined by Equation (8) which allows to convert the invariant combination (Equation (6)) into the form (Equation (9)) of the Minkowski interval. Introducing the four-dimensional contrainvariant radius vector by
we define the contrainvariant four-velocity vector as
where the superscript i runs from 0 to 3. Using Equation (20) and Equation (14) in Equation (21) yields
where is defined by Equation (15). Correspondingly, covariant four-dimensional radius vector and velocity vector are defined by
and the following relations hold
where a common rule of summation over repeated indexes is assumed.
Next, recalling that the momentum four-vector is defined by
and using the principle of the least action [58], we find (see [29] for details) that
while the contravariant components of the four-momentum vector are
Then, from the identity Equation (26), we obtain
Recalling that
with allowance for Equations (20) and (27), we have
which, upon using Equations (24) and (28), yields Relations (18) and (19) for the three-momentum and energy. Solving Equation (32) for the components of the four momentum vector, we obtain
Then, using Equation (33) in Equation (30) yields a dispersion relation for a free particle which can be represented in the form
where the quantities
are speeds of light in the positive and negative x-directions [27]. It follows from Equation (34) that for massless particles moving along the x-axis in the positive x direction,
while for massless particles moving in the negative x direction,
3. Electromagnetic Field Dynamics
The invariant action integral for a charged material particle in the electromagnetic field is made up of two parts: the action for the free particle defined by Equation (13) and a term describing the interaction of the particle with the field. The invariance is provided by using the combinations that are invariant in the Minkowskian variables (Equation (20)) so that the action integral takes the form [58]
where the coordinates are related to physical coordinates by Equation (20), and are components of the (covariant) four-potential vector expressed through the contravariant components by
Upon representing the four-potential as
where is a scalar potential and the three-dimensional vector is the vector potential of the field, the electromagnetic part of the action integral can be written in the form
Here, and in what follows, ’tilde’ indicates that variables and operations are in Minkowskian spacetime variables (Equation (20)). Note that, while scalars and components of three-dimensional vectors in the Minkowskian formulation appear with ’tilde’, four-dimensional Minkowskian variables are not supplied with ’tilde’. This does not lead to any confusion, as the four-dimensional notation is not applicable to the formulation in physical variables.
In the electrodynamics of the standard special relativity (which, in our case, is electrodynamics in Minkowskian variables), the electric and magnetic fields intensities are defined on the basis of equations of motion of a charged particle obtained from the Lagrange equations.
where, in the Lagrange function , a part related to the electromagnetic field is given by the integrand of (41). Then, the electric and magnetic field intensities and are introduced by separating the right-hand side of the vector equation of motion (the force) into two parts, one of which does not depend on the velocity of the particle and the second depends on the velocity, being proportional to the velocity and perpendicular to it, as follows:
where is the momentum vector. The electric and magnetic field intensities are related to the potentials by
The same line of argument is used to derive equations describing the electromagnetic field in physical variables . The action integral is represented in the form
where t is the ’physical’ time related to the Minkowskian variables via Equation (20), and L is the Lagrangian in physical variables. The free particle part of L is defined by Equations (15)–(17). To obtain the electromagnetic field part of the Lagrangian, the right-hand side of Equation (41) is transformed to physical spacetime variables and then the new variables (modified potentials) are introduced by the relations
As the result, the Lagrangian function L in the action integral Equation (45) takes the form
where is the free particle part of L defined by Equations (15)–(17). Substituting Equation (47) into the Lagrange equations
yields
Thus, upon using the modified potentials, the equations of motion in physical variables have the same form as in the standard relativity with the physical electric and magnetic field intensities expressed through the modified potentials by the relations
of the same form (Equation (44)) as in the standard relativity. Then, the first pair of the Maxwell equations in physical variable derived from Equation (50) have the same form as in the standard relativity:
To obtain the second pair of Maxwell equations in physical variables, let us calculate the components of the electromagnetic field tensor , defined by
Expressing on the right-hand side of Equation (52) through the modified potentials by Equation (46) and then transforming the result to physical spacetime variables using Equation (20), with a subsequent use of Equation (50), yields the expressions for the components of the electromagnetic field tensor in terms of physical electric and magnetic field intensities. The result can be written as a matrix in which the index labels the rows, and the index labels the columns, as follows:
while
Note that the terms containing the anisotropy parameter k in Equations (53) and (54) spoil the property that when of the standard relativity electrodynamics.
The electromagnetic field equations are obtained with the aid of the principle of least action [58] in the form
(only fields in vacuum that are relevant to the subject of this paper are considered). Substituting Equation (54) into Equation (55) and transforming the equations to physical spacetime variables, upon combining equations with different ‘i’ and using the first pair of the Maxwell Equation (51), yields the second pair of the Maxwell equations in the three-dimensional form
An important feature of Equations (51) and (56) is their linearity in and , and hence in . The Lorentz-violating terms thereby avoid the complications of nonlinear modifications to the Maxwell equations, which are known to occur in some physical situations, such as nonlinear optics or when vacuum polarization effects are included. Another feature is that the extra Lorentz-violating terms involve only the electric field, as well as its derivatives.
Note the existence of an alternative way of derivation of the modified Maxwell Equations (51) and (56). Based on Equations (44), (46), and (50), the electric and magnetic field intensities and in Minkowskian formulation can be related to the physical electric and magnetic field intensities and , as follows:
4. Electromagnetic Waves
The equation describing electromagnetic waves in electrodynamics of relativity with a preferred frame can be derived straight from the modified Maxwell equations in the same way as it is done for the electromagnetic wave equation of standard relativity electrodynamics (the modified Maxwell equations are reproduced below for convenience).
Eliminating by taking ’curl’ from the second equation of Equation (61) and substituting from the second equation of Equation (62) with a subsequent use of differential consequences of the first equation of Equation (62) for eliminating mixed space derivatives yields
where represents any component of . It is readily verified that the wave equation for obtained from the modified Maxwell equations in a similar way has the same form (Equation (63)).
Alternatively, the wave Equation (63) can be derived from Equation (55) expressed in terms of the potentials using Equation (52) while imposing the Lorentz gauge condition
Converting the derivatives in the resulting equation
into derivatives in physical spacetime variables yields equations of the form Equation (63) with f being any component of . In view of the fact that Equations (46) and (50), relating to the modified potentials and then to and , are linear, it is evident that any of those variables obeys Equation (63).
It is worth noting that the fact that the wave Equation (63) can be derived straight from the modified Maxwell Equations (61) should be considered as a proof of their validity (within the framework of the relativity with a preferred frame). Indeed, the form Equation (63), being derived from the form Equation (65) in Minkowskian variables which mimics the form of the Minkowsky interval, can be guessed in view of the expected linear relations between the Minkowslian potentials and the physical field intensities. At the same time, the derivation of the modified Maxwell equations involves many steps and their final form cannot be guessed.
Much of the propagation behavior of the electromagnetic wave is encoded in its dispersion relation, which provides spectral information for the modes. To find the dispersion relation, the ansatz in the form of monochromatic plane waves is used as follows:
where and can be regarded as the frequency and wave vector of the mode or as the associated energy and momentum (taking the real part is understood, as usual). Substituting Equation (66) into Equation (63) yields the dispersion relation
The dispersion relation Equation (67) can be also represented in the form
where
are speeds of light in the positive and negative x-directions [27]. The form Equation (68) adheres to the dispersion relation Equation (34) for free massless particles with E and replaced by and .
In the standard relativity, the polynomial Equation (67) determining reduces to one with two quadruply degenerate roots which correspond to the opposite directions of the group velocity. In the modified electrodynamics, the polynomial also has two roots
Similar to in the standard relativity case, the two roots (70) are obtained from each other by changing sign of , but, in the case of , it is accompanied by a change of sign of the anisotropy parameter k.
More insight about the wave motion implied by Equation (63) can be gained from the modified Maxwell Equations (61) and (62). The expressions of Equation (61), which are unaffected by the modifications, reduce with the ansatz (Equation (66)) to
The first of these equations shows that the magnetic field remains transverse to despite the Lorentz violation. The second equation shows that the magnetic field is perpendicular to the electric field . The first equation of Equation (62) reduces to
Equation (72) implies the existence of two modes.
The first one corresponds to the electric field with . Then, it follows from Equation (72) that the electric field is perpendicular to . Further, the condition implies that the vector lies in the plane and so the vector is directed along the x-axis (the direction of the anisotropy vector ). Therefore, and also, based on rotational symmetry in the plane , it can be set , which implies . In such a case, the first equation of Equation (61) and the first equation of Equation (62) are satisfied identically in view of . Then, the second equation of Equation (61) and the second equation of Equation (62) reduce to the system of equations for the two nonzero components of the electric and magnetic field intensities and , while the requirement of vanishing the determinant of the system yields the dispersion relation Equation (67). Thus, the mode with represents a usual electromagnetic plane wave (but with the unusual dispersion relation), with the magnetic and electric fields transverse to the direction of propagation of the wave and perpendicular to each other, which propagates along the direction of the anisotropy vector.
The second mode corresponds to the case . Then, it follows from Equation (72) that the electric field vector is not normal to . Since, according to the second equation of Equation (71), is normal to the plane of and , one can choose, without loosing generality, the direction of to be along the y-axis and the plane of the vectors and to be the -plane. Then, the first equation of Equation (71) gives , and it is readily verified that the remaining equations of Equations (61) and (62) can be satisfied only if with , , and obeying the dispersion relation Equation (67) for . Note the particular case when is directed along the x-axis ()4 and the dispersion relation degenerates to
Thus, the second mode represents electromagnetic wave, in which the magnetic field is transverse to direction of propagation and perpendicular to the electric field , similar to in the regular wave, but, as distinct from the regular wave, the electric field is not normal to . Another characteristic feature of such a wave that distinguishes it from the first mode is that the direction of propagation is not along the anisotropy vector and so not along the velocity of relative motion of the source and the observer. It implies that, in the case when the relative motion velocity is only the cosmological recession velocity, such a wave does not propagate along a line of sight.
It is worthwhile to note a distinguishing feature of the above analysis as compared with other studies of electromagnetic waves in the presence of the Lorentz violation. Typically, different modes arising due to the Lorentz violation correspond to different roots of the modified dispersion relation (see, e.g., [6,59,60,61]). The present analysis provides an unusual example when two different modes correspond to the same root of the dispersion relation (for the waves propagating to the observer, it is the second root of Equation (70)). The existence of two modes is revealed only when one studies the corresponding solutions of the modified Maxwell equations. It is also worth noting that the present analysis is performed solely in terms of field intensities and , while studies of electromagnetic waves in the presence of the Lorentz violation mostly also involve the electromagnetic field potentials which are accompanied by extensive discussions of different gauge choices and their influence on the results.
5. Gamma-Ray Propagation
5.1. Attenuation due to the Pair-Production Process
Gamma rays () propagating from distant sources to Earth interact with the photons of the extragalactic background light () being able to produce through the process of pair production
which has the effect of a significant energy attenuation in the flux of high-energy gamma rays. Such interaction takes place for gamma rays with energies () above the threshold of pair production. The existence of a threshold can be also expressed as the minimum energy () that a needs to produce a .
Calculation of the threshold value of the gamma-ray photons energy proceeds along the same lines as the calculation of the GZK threshold for the photopion production by the UHECR protons in [29]. It is based on the equation expressing conservation of the total 4 - momentum of the system: the square of the total 4 - momentum in the lab frame before the collision is equal to the square of the total 4 - momentum of the outgoing particles in their center of mass frame after the collision as follows:
In the threshold calculations, in order to minimize the energy needed, the momenta of the gamma rays and background light photons in the lab frame should be pointing in opposite directions while the outgoing particles should be produced at rest in their center of mass frame after the collision.
To calculate the right-hand side of Equation (75), components of the 4 - momentum vectors are expressed through the three-momenta and energies using Equation (33) to give
Then, the three-momenta and energies, given by Equations (18), (19), and (15), with for both particles, are substituted into Equation (76), which yields
The left-hand side of Equation (75) is to be expressed in terms of the high-energy and background photon energies using the relations between the particle momentum and energies obtained from the dispersion relation Equation (34). The high-energy photons move to the observer in the direction opposite to the direction of velocity of the lab frame relative to the observer (relative to the preferred frame), which is chosen to be a positive direction of the x-axis. Thus, the high-energy photon moves along the x-axis in the negative x direction, while the background photon moves, according to the threshold assumption (ii), in the positive x direction. Thus, the photons momenta are related to their energies using Equation (36), as follows:
where k is the anisotropy parameter in the lab frame. Then, the left-hand side of Equation (75) is calculated as follows (head on collision):
Then, using Equations (80) and (77) in Equation (75) and solving the resulting equation for , one obtains the expression for the threshold energy of the high-energy photon
or the expression for the threshold energy of the background photon (minimum energy to produce ):
It is worth noting that the above derivation of the threshold Equation (82) does not involve any approximations, while the derivation of the expression for the GZK threshold (both modified [29] and standard) is made using the ultrarelativistic approximation for protons.
The factor can be represented as a function of the frame velocity relative to a preferred frame which, with an accuracy up to , is given by Equation (12). In a cosmological context, where is a recession velocity of a source, depends on the cosmological redshift of an object z and, with the accuracy of Equation (12), can be replaced by . Then, the threshold equation takes the form
where is the modified value of the threshold and is the standard value of the threshold. It is seen that the expression, Equation (83), for the threshold energy of the background photon differs from the standard one by the factor . The universal constant b is negative, as it is found by fitting the cosmological model developed in the framework of the ‘relativity with a preferred frame’ to the observational data [28], which means that the threshold energy of the background photon decreases with the distance to the source (the redshift z).
Attenuation of gamma rays with the energy from the source at redshift due to the pair production process is characterized by the optical depth . For not to be too large, one typically has so that the Universe is optically thin along the line of sight of the source, and if it happens that , the Universe becomes optically thick at some point along the line of sight. The value such that defines the -ray horizon for a given , and sources beyond the horizon tend to become progressively invisible as further increases. The optical depth is evaluated by
where is the -ray absorption coefficient, which represents the probability per unit path length, l, that a -ray will be destroyed by the pair-production process. The absorption coefficient is calculated by convolving the spectral number density of background photons at a redshift z with the cross section of the pair production process ( is the angle between the direction of propagation of both photons) for fixed values of and and next integrating over these variables [47], as follows:
Then, the integral over distance l in Equation (84) is represented as an integral over z to arrive at the expression for the optical depth in the form
The threshold energy of background photons taking part in the expressions Equations (85) and (86) is corrected according to Equation (83) such that decreases with the distance to the source (the redshift z). The cumulative outcome of this phenomenon may result in measurable variations in the expected attenuation of the gamma rays flux reducing the expected flux.
The preferred frame effects may also influence the cosmological part of the expression Equation (86). The distance element is defined by , where and are the scale factor and radial distance element in the Robertson–Walker metric. These quantities are calculated on the basis of the GR equations (more specifically, Friedman equations) and the result depends on the cosmological model accepted. Commonly, the quantity is calculated within the standard ’concordance’ ΛCDM cosmological model [48], as follows:
where is the value of the Hubble parameter at the present moment, and is defined by
where G is Newton’s gravitational constant, is the present energy density of nonrelativistic matter, and is the critical energy density. Equation (88) has been derived under the assumption of the flat Universe (the curvature ). In the cosmology of relativity with a preferred frame, one has [28]
where the quantity is to be calculated using several other equations. The result is represented as series in z, as follows:
In the concordance model relation of Equation (87), the value , obtained from the observational data (see [28] for references), is used. In the present model, there is an interval of allowed values of and the corresponding values of b, within which the results fit both the SNIa and BAO data [28]. The curvature in the present model is not obligatory zero, but the value of corresponding to the flat Universe is within the interval of allowed values of .
Although Equations (87) and (90) defining dependence on z in the concordance model and in the present model look completely different, the corresponding dependencies practically coincide, as it is seen from Figure 1. Thus, the preferred frame effects influence only via the threshold value in Equation (85), similar to in other Lorentz-violating theories (see, e.g., [62,63,64]).
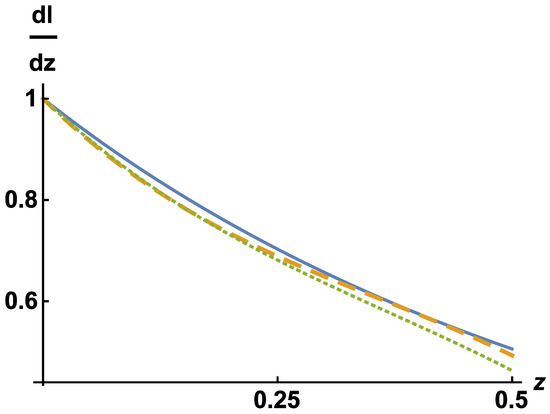
Figure 1.
The dependence of (multiplied by ) on z for the concordance model with (solid) and for the cosmological model, based on ‘relativity with a preferred frame’ [28], with , (dashed) and , (dotted) where the values of the parameters and b are chosen from those consistent with both the SNIa and BAO data (see [28]).
5.2. Attenuation due to Other Processes
5.2.1. Attenuation Processes
The pair production process considered in the previous section is the basic attenuation process in photon–photon collisions for photons of energy eV traversing cosmic matter, with the 3 K blackbody radiation being the principal component of the ambient photon gas. It may seem that, due to that process, the Universe should be opaque for the -ray photons with energies above the threshold for the pair production. However, it is not valid since the pair-production cross section decreases with the photon energy, roughly as . In view of that, one may be led to the opposite conclusion that the Universe is transparent for the high-energy photons, as photons with energies as high as the most energetic photons observed may have a mean free part comparable with the ’Hubble radius’. Nevertheless, it is also not correct, as, for the high-energy photons, other processes start to dominate the pair production. First of all, it is the double-pair production (DPP) process . For interactions with cosmic microwave background, the DPP begins to dominate the single-pair production above eV. When the single-pair cross section is small, the double-pair cross section adds a constant (in energy) absorption probability as the DPP cross section rapidly increases with near the threshold and quickly approaches the asymptotic value [65,66] (for more recent estimates of the DPP cross section, see, e.g., [67,68]). As a result, no further increase in the mean free part occurs. Thus, there is an energy range where DPP is the main attenuation mechanism for - rays. The double-pair production process has been extensively studied in various astrophysical contexts, including the propagation of high-energy photons [67,69].
Another process that may substantially modify the photon spectrum at the energies above the threshold for pair production is the electromagnetic (EM) cascade developing on cosmic microwave background and extragalactic background light radiations (the first works in this field were [70,71]; for the latest developments, see, e.g., [72,73]). When a very-high-energy extragalactic photon collides with low-energy background photons , then (in the Klein–Nishina regime, ) either electron or positron, produced in a pair-production event , typically carries almost all of the initial total energy. The produced electron (positron) then undergoes inverse Compton scattering (ICS) (here, e stands for either or ), losing more than 90% of energy, and finally, the upscattered background photon carries away almost all of the initial energy of the UHE photon, producing the new generation of cascade photons. The number of cycles in this kind of a cascade may be considerably higher than unity if the energy of the primary photon is high enough and the source is sufficiently distant. It should be remarked, however, that in the presence of an extragalactic magnetic field (EGMF), the above scenario changes somewhat. The electrons may lose a substantial part of their energy by emitting synchrotron radiation, which may lead to the suppression of the electromagnetic cascade development.
The pair production and inverse Compton scattering are the main processes that drive the EM cascade at the energies above the pair-production threshold. However, at the energies eV, the DPP process may be also significant at the first stage of the cycle, substantially influencing the development and propagation of the EM cascade. Another second-order process, called triplet pair production (TPP) , may occur together with inverse Compton scattering. Its role in the propagation of high-energy photons has long been recognized [74,75,76,77]. This process starts to become important at eV, for cosmological distances. The contribution of TPP to the energy attenuation is comparable to, or even greater than, ICS above eV.
5.2.2. The Preferred Frame Effects
First, note the influence of the preferred frame effects on the threshold energy for the DPP process. Calculations, implemented along the lines of the analysis of Section 5.1 (they are not included in order not to overload the presentation) show that the DPP threshold energy of the high-energy photon differs from the standard one by the same factor as for the single-pair production. As the universal constant b is negative, as it is found by fitting the cosmological model developed in the framework of the ‘relativity with a preferred frame’ to the observational data [28], the threshold energy decreases with the distance (the redshift z) to the place where the process occurs.
Next, consider a mechanism by which the preferred frame effects may influence the electromagnetic cascade development and propagation. The mechanism is driven by the dependence of the threshold energy on pair production (single or double) on z. For implementing the EM cascade cycle, the energy of both the photons initiating the cascade cycle and the secondary photons produced at the second stage of the cascade should be above the threshold for pair production. If the EGMF is small, the cascade particles propagate in the same direction as the parent photon, and then the next cycle of the cascade starts at smaller z than the previous cycle. Correspondingly, the threshold energy needed for initiating the next cycle appears to be higher than that for the previous cycle. Thus, even if, according to the standard analysis, the secondary photon energy is above the threshold for pair production so that the next cycle of the cascade can be initiated, it may be lower than the modified pair-production threshold. It is evident that this mechanism may lead to either reducing the number of cycles in the EM cascade or suppression of the cascade. It should result, in particular, in hardening of the gamma-ray spectrum of discrete sources.
This effect can be considered in the context of the repeatedly debated issue of anomalous transparency of the Universe to very-high-energy (VHE) –rays (see, e.g., [78,79,80,81,82,83]). Some recent observations have been interpreted as evidence that the Universe may be more transparent to VHE -rays than expected based on all existing EBL models [84,85,86,87]. Furthermore, several studies have found that, after correction for EBL absorption, the VHE -ray spectra of several blazars appear to be unexpectedly hard and/or exhibit marginal hints of spectral upturns toward the highest energies [88,89]. Different mechanisms, including the existence of some nonconventional physical effects, such as conversions of photons into axionlike particles (see, e.g., [90,91,92]), have been suggested to resolve the controversy. The above-described mechanism of reducing or suppression of the EM cascade development by the preferred frame effects, which should result in hardening of the VHE photon spectra, might be seen as a contribution to the issue.
5.3. Astrophysical Tests for Vacuum Dispersion and Vacuum Birefringence
In the literature on Lorentz violation, as major features of the behavior of electromagnetic waves in vacuum in the presence of Lorentz violation, vacuum dispersion and vacuum birefringence are considered. Astrophysical tests for vacuum dispersion of light from astrophysical sources seek differences in the velocity of light at different wavelengths due to Lorentz violation, which should result in observed arrival-time differences. For differences in the arrival times of different wavelengths to be interpreted as caused by differences in the light velocities, explosive or pulsed sources of radiation that produce light over a wide range of wavelengths in a short period of time, such as gamma-ray bursts, pulsars, or blazars, are to be used. All those are point sources, which have the disadvantage (for the purpose of imposing constraints on Lorentz violation) that a single line of sight is involved, which provides sensitivity to only a restricted portion of space for free coefficients of the Lorentz violating models.
The same is valid for the present theory leading to the dispersion relation, Equation (67). In the case of the waves propagating along the x-axis (aligned with the anisotropy vector k), when and , the two routs (Equation (70)) become
which corresponds to the waves propagating in the opposite directions. For a wave propagating to the observer from a cosmological source, with the x-axis directed from the observer to the source, the group velocity is
It does not depend on q, and so there is no place for vacuum dispersion.
Another test that is commonly used for setting constraints on the parameters of the Lorentz-violating theories in electrodynamics is the vacuum birefringence test. In birefringent scenarios, the two eigenmodes propagate at slightly different velocities. This implies that the superposition of the modes is altered as light propagates in free space. As the two modes differ in polarization, the change in superposition causes a change in the net polarization of the radiation. However, it is not applicable to the present theory leading to the dispersion relation of Equation (67). The two roots of the dispersion relation correspond to the waves propagating in different directions. Thus, there are no two eigenmodes propagating in the same direction and so there is no possibility for vacuum birefringence. Thus, neither tests for vacuum dispersion nor tests for vacuum birefringence can impose restrictions, additional to those imposed by cosmological data, on the values of the only parameter of the theory b.
The vacuum birefringence and vacuum dispersion are widely discussed in the literature as astrophysical tests of Lorentz violation in the pure photon sector of the standard-model extension (e.g., [6,59,93,94,95,96]). Therefore it is of interest, in that context, to compare the Lorentz-violating terms, appearing in the Lagrangian due to the preferred frame effects in the present study, with those introduced as a formal SME extension. Extracted from the SME, the Lorentz-violating electrodynamics can be written in terms of the usual field strength , defined by Equation (52) and the potentials , as follows:
In the following, we calculate the Lagrangian of the electrodynamics with a preferred frame and compare the Lorentz violating terms in that Lagrangian with those in Equation (93). Calculating using Equations (53) and (54) yields
It is seen that the form Equation (94) is, in a sense, more general than Equation (93) because of the Lorentz violating multiplier . However, since the multiplier does not depend on the field variables and so does not influence the form of the field equations, it can be disregarded. Then, the Lorentz-violating terms in Equation (94) can be written based on Equation (54) in terms of the field strength, as follows:
which fits the form Equation (93) with the coefficients
while other , as well as all , are zeros. As a matter of fact, the second term on the right-hand side of Equation (93), not contributing to the Lagrangian of the present theory, could be disregarded from the beginning on the grounds that it has theoretical difficulties associated with negative contributions to the energy [6,59]. The Lagrangian defined by Equation (95) (or Equation (96)) provides an example of the Lorentz-violating SME (in a pure photon sector) which leads to equations of the electromagnetic wave propagation not exhibiting the vacuum birefringence and vacuum dispersion effects.
6. Discussion
In the present paper, the ‘relativity with a preferred frame’ is extended to the electromagnetic field dynamics. The extension is not as straightforward as the extension to the free particle dynamics developed in [28], although both rely on the existence of the modified spacetime symmetry. The analysis reveals that a consistent transition from the modified kinematics and dynamics to the electromagnetic field should be based on the requirement that the expression for the force acting on a particle placed in the field were of the same form as in the standard electromagnetic field theory. It allows one to define the relations between the Minkowskian electric and magnetic field potentials and the ’physical’ electric and magnetic field intensities. Then, the same arguments as in the standard SR unambiguously lead to the modified Maxwell equations. A validity of those equations (within the framework of the ‘relativity with a preferred frame’) is proved by the fact that applying them to the field in vacuum yields the electromagnetic wave equation of the same form as that obtained by transforming the wave equation in Minkowskian variables to the ’physical’ variables. The modified particle dynamics and modified electromagnetic field dynamics are used to study the influence of the preferred frame effects on the processes accompanying propagation of gamma rays from distant sources to Earth. Those issues are also related to the problem of verification of the ’relativity of the preferred frame’ by observations and, in particular, to the problem of defining allowed values of the only parameter b of the theory.
The problem of defining allowed values of b is to be considered in the context of applications of the theory, as nothing (except for maybe some intuitive arguments regarding the sign of b) in the theory itself imposes constraints on the values of b. First, the cosmological models, developed in [28] on the basis of the properly modified general relativity, being applied to the data on cosmological scales, lead to constraints on the values of b. Quantitative results are provided by applications of the cosmological models to the type Ia supernova (SNIa) data and the baryon acoustic oscillations (BAO) data. Discussing the results of application of the cosmological models to the SNIa data, one can separate the conceptual and quantitative aspects. The conceptual aspect is related to the interpretation of the luminosity distance versus redshift relation obtained from the SNIa data, which has played a revolutionary role in the development of the modern cosmology concepts. That relation, corresponding to the negative acceleration parameter, cannot be explained using cosmological matter dominated models (Friedman–Robertson–Walker models) based on the standard general relativity. To explain the data, in modern cosmology, dark energy, a new type of energy with the equation of state corresponding to a negative pressure, is introduced. In the cosmological models based on the ‘relativity with a preferred frame’, the Friedman models are corrected such that the theory fits the SNIa data well and there is no need to introduce the dark energy. The quantitative aspect is that, for any reasonable value of the parameter (see Equation (88) for the definition of ), there exists a value of b such that the luminosity distance versus redshift relation of the present theory fits the SNIa data with high accuracy.
Regarding the BAO data, it should be noted that the BAO observations provide two different sets of data: BAO scales in transverse and line-of-sight directions. Measurements of the angular distribution of galaxies yield the quantity , which is the comoving angular diameter distance. Measurements of the redshift distribution of galaxies yield the value of the Hubble parameter . The recently released galaxy clustering dataset of the Baryon Oscillation Spectroscopic Survey (BOSS), part of the Sloan Digital Sky Survey III (SDSS III), allowed us to obtain the BAO scales in both transverse and line-of-sight directions. In [97], the results of several studies studying that sample with a variety of methods are combined into a set of the final consensus constraints that optimally capture all of the information. In Reference [27], the results yielded by the present model are compared with the consensus constraints derived from the BAO data in [97] (see Figure 4 in Reference [27]). The comparison shows that the predictions of the present theory are consistent with the constraints on and if the values of and b are confined with a quite narrow region in the plane (, b) defined by overlapping the two regions within which the predictions of the present theory fit both the data and the data. The results are also consistent with the SNIa data—a segment of the line in the plane (, b), on which the results of the present model fit the SNIa data, lies within that narrow overlapping region. —only two points, ’A’ and ’B’, of the segment are shown in order not to overload the figure. The points ’C’ and ’D’ correspond to the values of the parameters for which the deviation from the SNIa data is substantial. Therefore, as distinct from the points ’A’ and ’B’ where the deviation is negligible, the points ’C’ and ’D’ are far from the overlapping region. Thus, the results obtained by applying the cosmological models of the ‘relativity with a preferred frame’ fit three different sets of observational data well, with the values of the theory parameter b confined within a quite narrow interval (approximately to ). It is worth remarking again that, in the present theory, the dark energy is not needed to fit the data.
Next, it might be expected that more constraints on allowed values of b could arise as a result of applying the theory to the cosmic rays data. In the propagation of the ultra-high-energy cosmic rays (UHECR) from distant sources to Earth, the most remarkable effect is the attenuation due to pion photoproduction by UHECR protons, which is characterized by a well-defined energy threshold for the energy suppression—the Greisen–Zatsepin–Kuzmin (GZK) cutoff [52,53]. Derivation of the GZK limit within the framework of relativity with a preferred frame (see [29] for details) results in the expression which differs from the GZK limit, obtained on the basis of the standard relativity theory, by a correction factor as follows:
where is the GZK threshold calculated using equations of relativity with a preferred frame and is the standard value of the GZK threshold calculated using equations of the standard relativity. Since , as the cosmological data, discussed above, show, the threshold energy decreases as the distance to the source of the particles (the redshift z) increases. Although a comparison of that prediction of the theory with the data on the UHECR flux does not straightforwardly lead to constraints on the values of b, another issue, namely the data on the mass composition of UHECR, provides an indirect confirmation of the present theory. The mass composition of UHECR became a matter of lively debate after the Pierre Auger Collaboration (Auger) released its data [54,55]. Those data, showing that the UHECR mass composition is dominated by protons only at energies around and below eV, and then the fraction of protons is progressively decreasing up to energies of eV, contradicted the previous consensus that UHECRs are mostly protons and that sources should accelerate them to eV. After a common effort of the Auger and the Telescope Array (TA) collaborations, the evidence for decreasing a fraction of protons towards higher energies became well established, which stimulated development of the new complex scenario acceleration models. This is in stark contrast to the previously accepted paradigm of the UHECR mass composition dominated by protons when both the acceleration models and the models of interaction of UHECR with the astrophysical background are much simpler.
The prediction of the ‘relativity with a preferred frame’, in which the GZK threshold energy decreases with the distance to the source of the particles, allows resolution of (at least, partially) the contradiction between the view that the primary UHECR flux is mostly protons accelerated to very high energies and the observational data showing that the fraction of protons in the UHECR is decreasing towards higher energies. Protons emitted with some energy can reach the Earth observer only if the GZK threshold value is larger than . Therefore, a decrease of the GZK threshold with the distance results in the available sources being confined within a sphere of the radius corresponding to the GZK threshold value equal to . As the result, the number of sources contributing to the observed flux of protons at a given energy should be progressively decreasing with the energy increasing (see [29] for a more detailed discussion). Thus, reducing the fraction of protons in the observed UHECR flux towards the higher energies can be considered as a consequence of that effect.
Applying the modified particle dynamics to the pair-production process, which is responsible for attenuation of the gamma-rays flux, does not provide quantitative constraints on the values of the parameter b or indirect confirmations of the theory. At the same time, the finding that the preferred frame effects could result in hardening of the VHE photon spectra due to reduction or suppression of the EM cascades may be considered as favorable for the theory in view of the evidence that the VHE -ray spectra of several blazars appear to be unexpectedly hard. In addition, the results of applying the modified electromagnetic field dynamics to the behavior of electromagnetic waves in vacuum may be counted as a kind of indirect confirmation of the theory. The vacuum birefringence and vacuum dispersion are the features present in the popular Lorentz-violating theories (e.g., [6,59,93,94,95,96]), and the fact that no indications of existence of those phenomena are found in observations imposes constraints on the values of numerous parameters of those theories. On the contrary, the present theory does not predict such features as the vacuum birefringence and vacuum dispersion, and thus the absence of the observational evidence for the existence of those phenomena may be considered as an argument in favor of the theory, even though it is possible that present-day instruments are technologically not capable of detecting them, while future observatories might provide that possibility.
Possible future applications and extensions of the present framework could provide other confirmations of the theory and/or restrictions on the values of the parameter b. Application of the modified electromagnetic field theory and the modified particle dynamics of relativity with a preferred frame to the processes accompanying the propagation of cosmic and gamma rays in the presence of intergalactic magnetic fields (IGMFs) should be mentioned first as a potential development. In this respect, high-energy gamma rays are of utmost interest as they provide one of the most promising ways to probe IGMFs through secondary gamma rays produced in electromagnetic cascades. It follows immediately from the idea of cascades that magnetic fields can interfere with their development, because the charged component of the cascade is sensitive to magnetic fields. Thus, gamma-ray observations of distant objects such as blazars can be used to constrain IGMF properties (see review [73]). Since the preferred frame effects modify the magnetic field strength and the particle momentum, the deflection angles of the pairs produced in cascades by intervening IGMFs will be also modified as compared with the standard theory. It should influence the interpretation of the relevant gamma-ray observables, the spectrum, angular distribution, light curves, and time delays.
In addition, applying the theory to gravitational waves suggests itself in the light of the well-known analogy between the equations for electromagnetism and relativistic gravitation; specifically, between Maxwell’s field equations and a weak gravitational field approximation of the Einstein field equations. The conceptual basis for that application is provided by the extension of the framework of relativity with a preferred frame to general relativity developed in [28].
In general, the fact that applying the theory containing only one universal parameter to a number of different phenomena does not lead to any contradictions proves a consistency of its basic principles. Actually, the presence of only one parameter in the theory is a consequence of the fact that, as distinct from the popular Lorentz-violating theories, where Lorenz violation is introduced phenomenologically by adding Lorentz-violating terms to the Lorentz invariant relations, the ‘relativity with a preferred frame’ starts from the physically reasonable modification of the basic postulates of the SR. The generalized relativistic invariance, and therefore the Lorentz invariance violation, are ingrained in the theory at the most fundamental level being embedded into the metric. It is also worth emphasizing that the conceptual basis of the theory has been developed without having in mind possible applications. It is aimed at designing the framework which would allow incorporation of the preferred frame into special relativity while retaining the relativity principle and the fundamental spacetime symmetry. Nevertheless, the theory provides explanations of some observational data that were regarded as puzzling after their discovery (such as the SNIa luminosity distance—redshift relation indicating the acceleration of the Universe and the absence of high-energy protons in the UHECR flux). As a result, the new concepts (among which the dark energy is the most striking one), introduced to explain those puzzling features, become redundant. All the above justifies treating the ‘relativity with a preferred frame’ as an alternative to some currently accepted theories.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author is indebted to the Reviewers for valuable comments which led to significant improvements in the presentation.
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | For a discussion of the one-way vs. two-way speed of light issue and the related issues of conventionality of simultaneity and clock synchronization, see, e.g., [30,31,32,33,34,35,36,37]; a discussion of those issues in the context of the ‘relativity with a preferred frame’ can be found in [27,38]. Here, it is only worth noting that the transformations derived in the present framework differ conceptually from other transformations incorporating the anisotropy of the one-way speed of light that are repeatedly derived in the literature (e.g., [30,31,32,33]). In the latter, the anisotropy is a feature that emerges due to changing the synchronization procedure, which is equivalent to a change of coordinates, while, in the present framework, the anisotropy is governed entirely by a physical law. |
| 2 | In the modern versions of the experiments designed to test special relativity and the so-named ‘test theories’ (e.g., [39,40,41,42], see also [43], and a discussion in [27,28,38]), the tests are meant to detect the anisotropy of the two-way speed of light. |
| 3 | It should be noted in this connection that, in the cosmological context, the rest frame is defined by the large-scale structure; in particular, when the terms ’rest frame’ or ’CMB frame’ are used in cosmological applications, the frame more or less coinciding with our galaxy is meant. Thus, using the terms ’rest frame’ or ’CMB frame’ in that context inevitably implies the space (and time) averaging over the scales on which the assumptions of homogeneity and isotropy accepted in the cosmological models are valid. The same is implied for the theories treating propagation of astroparticles on cosmological scales, moreover that those theories should include effects of the cosmological expansion which are calculated on the basis of homogeneous and isotropic cosmological models [47]. Therefore, the experiments on the solar system scale intended to detect phenomena related to motion of the Earth, as, for example, asymmetry of lifetimes of particles parallel and antiparallel to the direction of motion of the Earth with respect to the CMB frame [44], are irrelevant to the frameworks (such as the present one) designed to describe phenomena on cosmological scales. |
| 4 |
References
- Kostelecky, V.A.; Samuel, S. Spontaneous breaking of Lorentz symmetry in string theory. Phys. Rev. D 1989, 39, 683. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A.; Samuel, S. Gravitational phenomenology in higher–dimensional theories and strings. Phys. Rev. D 1989, 40, 1886. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A. (Ed.) Proceedings of the Second Meeting on CPT and Lorentz Symmetry, Bloomington, IN, USA, 15–18 August 2001; World Scientific: Singapore, 2002. [Google Scholar]
- Oriti, D. Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Colladay, D.; Kostelecky, V.A. CPT violation and the standard model. Phys. Rev. D 1997, 55, 6760. [Google Scholar] [CrossRef]
- Colladay, D.; Kostelecky, V.A. Lorentz-violating extension of the standard model. Phys. Rev. D 1998, 58, 116002. [Google Scholar] [CrossRef]
- Kostelecky, V.A. Gravity, Lorentz violation, and the standard model. Phys. Rev. D 2004, 69, 105009. [Google Scholar] [CrossRef]
- Jacobson, T.; Mattingly, D. Gravity with a dynamical preferred frame. Phys. Rev. D 2001, 64, 024028. [Google Scholar] [CrossRef]
- Jacobson, T.; Mattingly, D. Einstein-ether waves. Phys. Rev. D 2004, 70, 024003. [Google Scholar] [CrossRef]
- Jacobson, T. Einstein-ather gravity: A status report. In Proceedings of the Conference ’From Quantum to Emergent Gravity: Theory and Phenomenology’, Trieste, Italy, 11–15 June 2007; SISSA: Trieste, Italy, 2007. v.2: PoS QG-Ph:020,2007; Sissa Medialab srl Partita IVA. [Google Scholar]
- Oost, J.; Mukohyama, S.; Wang, A. Constraints on Einstein-aether theory after GW170817. Phys. Rev. D 2018, 97, 124023. [Google Scholar] [CrossRef]
- Jacobson, T.; Liberati, S.; Mattingly, D. Threshold effects and Planck scale Lorentz violation: Combined constraints from high energy astrophysics. Phys. Rev. D 2003, 67, 124011. [Google Scholar] [CrossRef]
- Coleman, S.R.; Glashow, S.L. High-Energy Tests of Lorentz Invariance. Phys. Rev. D 1999, 59, 116008. [Google Scholar] [CrossRef]
- Liberati, S. Tests of Lorentz invariance: A 2013 update. Class. Quantum Gravity 2013, 30, 133001. [Google Scholar] [CrossRef]
- Aloisio, R.; Blasi, P.; Ghia, P.L.; Grillo, A.F. Probing the structure of space-time with cosmic rays. Phys. Rev. D 2000, 62, 053010. [Google Scholar] [CrossRef]
- Mattingly, D. Modern tests of lorentz invariance. Living Rev. Relativ. 2005, 8, 5. [Google Scholar] [CrossRef]
- Scully, S.T.; Stecker, F.W. Lorentz invariance violation and the observed spectrum of ultrahigh energy cosmic rays. Astropart. Phys. 2009, 31, 220. [Google Scholar] [CrossRef]
- Bi, X.J.; Cao, Z.; Li, Y.; Yuan, Q. Testing Lorentz invariance with ultra high energy cosmic ray spectrum. Phys. Rev. D 2009, 79, 083015. [Google Scholar] [CrossRef]
- Maccione, L.; Taylor, A.M.; Mattingly, D.M. Planck-scale Lorentz violation constrained by Ultra-High-Energy Cosmic Rays. J. Cosmol. Astropart. Phys. 2009, 2009, 022. [Google Scholar] [CrossRef]
- Scully, S.T.; Stecker, F.W. Testing Lorentz invariance with neutrinos from ultrahigh energy cosmic ray interactions. Astropart. Phys. 2011, 34, 575. [Google Scholar] [CrossRef]
- Saveliev, A.; Maccione, L.; Sigl, G. Lorentz invariance violation and chemical composition of ultrahigh-energy cosmic rays. J. Cosmol. Astropart. Phys. 2011, 2011, 046. [Google Scholar] [CrossRef]
- Stecker, F.W.; Scully, S.; Liberati, S.; Mattingly, D. Searching for traces of Planck-scale physics with high energy neutrinos. Phys. Rev. D 2015, 91, 045009. [Google Scholar] [CrossRef]
- Boncioli, D.; di Matteo, A.; Salamida, F.; Aloisio, R.; Blasi, P.; Ghia, P.L.; Grillo, A.F.; Petrera, S.; Pierog, T. Future prospects of testing Lorentz invariance with UHECRs. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), Hague, The Netherlands, 30 July–6 August 2015. [Google Scholar]
- Stecker, F.W. Testing Lorentz symmetry using high energy astrophysics observations. Symmetry 2017, 9, 201. [Google Scholar] [CrossRef]
- Boncioli, D.; Pierre Auger Collaboration. Probing Lorentz symmetry with the Pierre Auger Observatory. In Proceedings of the 35th International Cosmic Ray Conference (ICRC2017), Bexco, Busan, Korea, 12–20 July 2017. [Google Scholar]
- Lang, R.G.; Filipčič, A.; Kukec Mezek, G.; Stanič, S.; Trini, M.; Vorobiov, S.; Yang, L.; Zavrtanik, D.; Zavrtanik, M.; Zehrer, L. Testing Lorentz Invariance Violation at the Pierre Auger Observatory. In Proceedings of the 36th International Cosmic Ray Conference, Madison, WI, USA, 24 July–1 August 2019. [Google Scholar]
- Burde, G.I. Special Relativity with a Preferred Frame and the Relativity Principle. J. Mod. Phys. 2018, 9, 1591. [Google Scholar] [CrossRef][Green Version]
- Burde, G.I. Cosmological models based on relativity with a privileged frame. Int. J. Mod. Phys. D 2020, 29, 2050038. [Google Scholar] [CrossRef]
- Burde, G.I. Particle dynamics and GZK limit in relativity with a preferred frame. Astropart. Phys. 2021, 126, 102526. [Google Scholar] [CrossRef]
- Edwards, W.F. Special relativity in anisotropic space. Am. J. Phys. 1963, 31, 482. [Google Scholar] [CrossRef]
- Winnie, J.A. Special relativity without one-way velocity assumptions: Part II. Phil. Sci. 1970, 37, 223. [Google Scholar] [CrossRef]
- Tangherlini, F.R. The Velocity of Light in Uniformly Moving Frame. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1958. Reproduced in: Abraham Zelmanov J. 2009, 2, 44. [Google Scholar]
- Ungar, A.A. The Lorentz transformation group of the special theory of relativity without Einstein’s isotropy convention. Phil. Sci. 1986, 53, 395. [Google Scholar] [CrossRef]
- Ungar, A.A. Formalism to deal with Reichenbach’s special theory of relativity. Found. Phys. 1991, 21, 691. [Google Scholar] [CrossRef]
- Anderson, R.; Vetharaniam, I.; Stedman, G.E. Conventionality of synchronisation, gauge dependence and test theories of relativity. Phys. Rep. 1998, 295, 93. [Google Scholar] [CrossRef]
- Minguzzi, E. On the conventionality of simultaneity. Found. Phys. Lett. 2002, 15, 153. [Google Scholar] [CrossRef][Green Version]
- Rizzi, G.; Ruggiero, M.L.; Serafini, A. Synchronization gauges and the principles of special relativity. Found. Phys. 2004, 34, 1835. [Google Scholar] [CrossRef]
- Burde, G.I. Special relativity kinematics with anisotropic propagation of light and correspondence principle. Found. Phys. 2016, 46, 1573. [Google Scholar] [CrossRef]
- Robertson, H.P. Postulate versus observation in the special theory of relativity. Rev. Mod. Phys. 1949, 21, 378. [Google Scholar] [CrossRef]
- Mansouri, R.; Sexl, S.U. A test theory of special relativily: I. Simultaneity and slow clock synchronization. Gen. Rel. Grav. 1977, 8, 497. [Google Scholar] [CrossRef]
- Mansouri, R.; Sexl, S.U. A test theory of special relativily: II. First order tests. Gen. Rel. Grav. 1977, 8, 515. [Google Scholar] [CrossRef]
- Mansouri, R.; Sexl, S.U. A test theory of special relativily: III. Second order tests. Gen. Rel. Grav. 1977, 8, 809. [Google Scholar] [CrossRef]
- Lammerzahl, C. Test theories for Lorentz invariance. Lect. Notes Phys. 2006, 702, 349. [Google Scholar]
- de Angelis, A.; Maria, M.d.; Antonelli, M.; Dreucci, M. A search for directional violations of the Lorentz invariance through the study of a possible anisotropy of particle lifetimes. IL Nuovo Cimento 2011, 34 C, 323. [Google Scholar]
- Alhulaimi, B.; Coley, A.; Sandin, P. Anisotropic Einstein–aether cosmological models. J. Math. Phys. 2013, 54, 042503. [Google Scholar] [CrossRef]
- Kanno, S.; Soda, J. Lorentz violating inflation. Phys. Rev. D 2006, 74, 063505. [Google Scholar] [CrossRef]
- De Angelis, A.; Galanti, G.; Roncadelli, M. Transparency of the Universe to gamma rays. Mon. Not. Roy. Astron. Soc. 2013, 432, 3245. [Google Scholar] [CrossRef]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Aloisio, R. Acceleration and propagation of ultra-high energy cosmic rays. Prog. Theor. Exp. Phys. 2017, 12, 12A102. [Google Scholar] [CrossRef]
- Aloisio, R.; Blasi, P.; Mitri, I.D.; Petrera, S. Selected Topics in Cosmic Ray Physics. In Multiple Messengers and Challenges in Astroparticle Physics; Aloisio, R., Coccia, E., Vissani, F., Eds.; Springer International Publishing AG: Cham, Switzerland, 2018; pp. 1–96. [Google Scholar]
- Anchordoqui, L.A. Ultra-High-Energy Cosmic Rays. Phys. Rept. 2019, 801, 1. [Google Scholar] [CrossRef]
- Greisen, K. End to the cosmic-ray spectrum? Phys. Rev. Lett. 1966, 16, 748. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuzmin, V.A. Upper limit of the spectrum of cosmic rays. Pisma Zh. Ekps. Teor. Fiz. 1966, 4, 114, English translation: JETP Lett. 1966, 4, 78. [Google Scholar]
- Aab, A.; Abreu, P.; Aglietta, M.A.R.C.O.; Ahn, E.J.; Al Samarai, I.; Albuquerque, I.F.M.; Allekotte, I.; Allen, J.; Allison, P.; Almela, A.; et al. Depth of maximum of air-shower profiles at the Pierre Auger Observatory II: Composition implications. Phys. Rev. D 2014, 90, 122006. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.A.R.C.O.; Ahn, E.J.; Al Samarai, I.; Albuquerque, I.F.M.; Allekotte, I.; Allison, P.; Almela, A.; Alvarez Castillo, J.; et al. Evidence for a mixed mass composition at the ‘ankle’ in the cosmic-ray spectrum. Phys. Lett. B 2016, 762, 288. [Google Scholar] [CrossRef]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations, Applied Mathematical Sciences; Springer: New York, NY, USA, 1989; Volume 81. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations (Graduate Texts in Mathematics: Volume 107); Springer: New York, NY, USA, 1993. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1971. [Google Scholar]
- Carroll, S.M.; Field, G.B.; Jackiw, R. Limits on a Lorentz- and parity-violating modification of electrodynamics. Phys. Rev. D 1990, 41, 1231. [Google Scholar] [CrossRef]
- Kostelecky’, V.A.; Mewes, M. Signals for Lorentz violation in electrodynamics. Phys. Rev. D 2002, 66, 056005. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Electrodynamics with Lorentz-violating operators of arbitrary dimension. Phys. Rev. D 2009, 80, 015020. [Google Scholar] [CrossRef]
- Lang, R.G.; Martnez-Huerta, H.; de Souza, V. Limits on the Lorentz Invariance Violation from UHECR astrophysics. Astrophys. J. 2018, 853, 23. [Google Scholar] [CrossRef]
- Lang, R.G.; Martnez-Huerta, H.; de Souza, V. Improved limits on Lorentz invariance violation from astrophysical gamma-ray sources. Phys. Rev. D 2019, 99, 043015. [Google Scholar] [CrossRef]
- Martnez-Huerta, H.; Lang, R.G.; de Souza, V. Lorentz Invariance Violation Tests in Astroparticle Physics. Symmetry 2020, 12, 1232. [Google Scholar] [CrossRef]
- Cheng, H.; Wu, T.T. Cross Sections for Two-Pair Production at Infinite Energy. Phys. Rev. D 1970, 2, 2103–2104. [Google Scholar] [CrossRef]
- Brown, R.W.; Hunt, W.F.; Mikaelian, K.O.; Muzinich, I.J. Role of γ + γ⟶ e+ + e− + e+ + e− in Photoproduction, Colliding Beams, and Cosmic Photon Absorption. Phys. Rev. D 1973, 8, 3083–3102. [Google Scholar] [CrossRef]
- Demidov, S.V.; Kalashev, O.E. Double pair production by ultra–high–Energy Cosmic Ray Photons. J. Exp. Theor. Phys. 2009, 108, 764. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.; Xue, S.-S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys. Rep. 2010, 487, 1. [Google Scholar] [CrossRef]
- Ruffini, R.; Vereshchagin, G.V.; Xue, S.S. Cosmic absorption of ultra high energy particles. Astrophys. Space Sci. 2016, 361, 82. [Google Scholar] [CrossRef][Green Version]
- Jelley, J.V. High-energy γ-ray absorption in Space by a 3.5°K microwave field. Phys. Rev. Lett. 1966, 16, 479–481. [Google Scholar] [CrossRef]
- Gould, R.J.; Schreder, D. Opacity of the Universe to High-Energy Photons. Phys. Rev. Lett. 1966, 16, 252. [Google Scholar] [CrossRef]
- Berezinsky, V.; Kalashev, O. High-energy electromagnetic cascades in extragalactic space: Physics and features. Phys. Rev. D 2016, 94, 023007. [Google Scholar] [CrossRef]
- Alves Batista, R.; Saveliev, A. The Gamma-ray Window to Intergalactic Magnetism. Universe 2021, 7, 223. [Google Scholar] [CrossRef]
- Bonometto, S.A.; Marcolungo, P. Metagalactic opacity to photons of energy larger than 1017 eV. Lett. Nuovo C. 1972, 5, 595–603. [Google Scholar] [CrossRef]
- Bonometto, S.A.; Lucchin, F.; Marcolungo, P. Induced Pair Production and Opacity Due to Black-body Radiation. Astron. Astrophys. 1974, 31, 41. [Google Scholar]
- Dermer, C.D.; Schlickeiser, R. Effects of triplet pair production on ultrarelativistic electrons in a soft photon field. Astron. Astrophys. 1991, 252, 414. [Google Scholar]
- Mastichiadis, A.; Protheroe, R.J.; Szabo, A.P. The Effect of Triplet Production on Pair/Compton Cascades in Thermal Radiation. Mon. Not. R. Astron. Soc. 1994, 266, 910. [Google Scholar] [CrossRef][Green Version]
- De Angelis, A.; Mansutti, O.; Persic, M.; Roncadelli, M. Photon propagation and the very high energy γ–ray spectra of blazars: How transparent is the Universe? Mon. Not. R. Astron. Soc. Lett. 2009, 394, L21–L25. [Google Scholar] [CrossRef]
- Costamante, L. Gamma-Rays from Blazars and the Extragalactic Background Light. Int. J. Mod. Phys. D 2013, 22, 1330025. [Google Scholar] [CrossRef]
- Horns, D.; Jacholkowska, A. Gamma rays as probes of the Universe. Comptes Rendus Phys. 2016, 17, 632648. [Google Scholar] [CrossRef]
- Abdalla1, H.; Bottcher, M. EBL Inhomogeneity and Hard-Spectrum Gamma-Ray Sources. Astrophys. J. 2017, 835, 237. [Google Scholar] [CrossRef]
- Dzhatdoev, T.A.; Khalikov, E.V.; Kircheva, A.P.; Lyukshin, A.A. Electromagnetic cascade masquerade: A way to mimic γ–axion–like particle mixing effects in blazar spectra. Astron. Astrophys. 2017, 603, A59. [Google Scholar] [CrossRef]
- Franceschini, A. Photon–photon interactions and the opacity of the universe in gamma rays. Universe 2021, 7, 146. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; et al. Very-high-energy gamma rays from a distant quasar: How transparent is the universe? Science 2008, 320, 1752–1754. [Google Scholar] [CrossRef]
- Horns, D.; Meyer, M. Indications for a pair-production anomaly from the propagation of VHE gamma-rays. J. Cosmol. Astropart. Phys. 2012, 2, 33. [Google Scholar] [CrossRef][Green Version]
- Meyer, M.; Horns, D.; Raue, M. First lower limits on the photon-axion-like particle coupling from very high energy gamma-ray observations. Phys. Rev. D 2013, 87, 035027. [Google Scholar] [CrossRef]
- Archambault, S.; Aune, T.; Behera, B.; Beilicke, M.; Benbow, W.; Berger, K.; Bird, R.; Biteau, J.; Bugaev, V.; Byrum, K.; et al. Deep broadband observations of the distant gamma–ray Blazar PKS 1424+240. Astrophys. J. Lett. 2014, 785, L16. [Google Scholar] [CrossRef]
- Finke, J.D.; Razzaque, S.; Dermer, C.D. Modeling the extragalactic background Llight from stars and dust. Astrophys. J. 2010, 712, 238. [Google Scholar] [CrossRef]
- Furniss, A.; Williams, D.A.; Danforth, C.; Fumagalli, M.; Prochaska, J.X.; Primack, J.; Urry, C.M.; Stocke, J.; Filippenko, A.V.; Neely, W. The firm redshift lower limit of the most distant TeV-detected blazar PKS 1424+240. Astrophys. J. Lett. 2013, 768, L31. [Google Scholar] [CrossRef]
- Horns, D.; Maccione, L.; Meyer, M.; Mirizzi, A.; Montanino, D.; Roncadelli, M. Hardening of TeV gamma spectrum of AGNs in galaxy clusters by conversions of photons into axionlike particles. Phys. Rev. D 2012, 86, 075024. [Google Scholar] [CrossRef]
- Troitsky, S. Towards discrimination between galactic and intergalactic axion-photon mixing. Phys. Rev. D 2016, 93, 045014. [Google Scholar] [CrossRef]
- Galanti, G.; Tavecchio, F.; Roncadelli, M.; Evoli, C. Blazar VHE spectral alterations induced by photon–ALP oscillations. Mon. Not. R. Astron. Soc. 2019, 487, 123132. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Mewes, M. Cosmological constraints on Lorentz violation in electrodynamics. Phys. Rev. Lett. 2001, 87, 251304. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A.; Mewes, M. Sensitive polarimetric search for relativity violations in gamma-ray bursts. Phys. Rev. Lett. 2006, 97, 140401. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A.; Mewes, M. Lorentz-violating electrodynamics and the cosmic microwave background. Phys. Rev. Lett. 2007, 99, 011601. [Google Scholar] [CrossRef] [PubMed]
- Kostelecky, V.A.; Mewes, M. Astrophysical tests of Lorentz and CPT violation with photons. Astrophys. J. 2008, 689, L1. [Google Scholar] [CrossRef]
- Alam, S.; Ata, M.; Bailey, S.; Beutler, F.; Bizyaev, D.; Blazek, J.A.; Bolton, A.S.; Brownstein, J.R.; Burden, A.; Chuang, C.-H.; et al. The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).