The Validity of Machine Learning Procedures in Orthodontics: What Is Still Missing?
Abstract
:1. Introduction
2. Challenging Interface between Machine Learning Models and Orthodontic Features
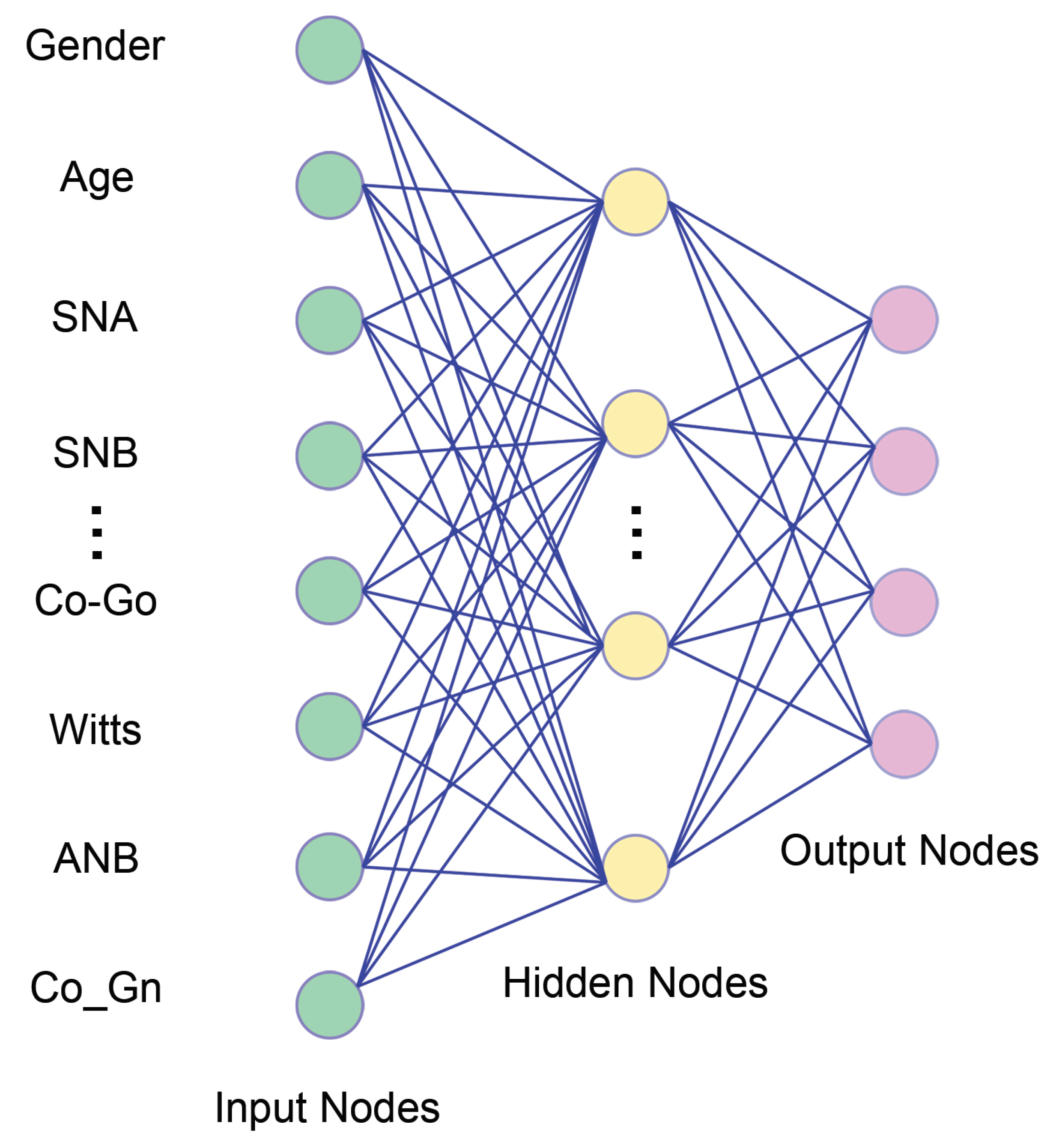
3. How Can Orthodontic Input Be Incorporated into the Machine Learning Process?
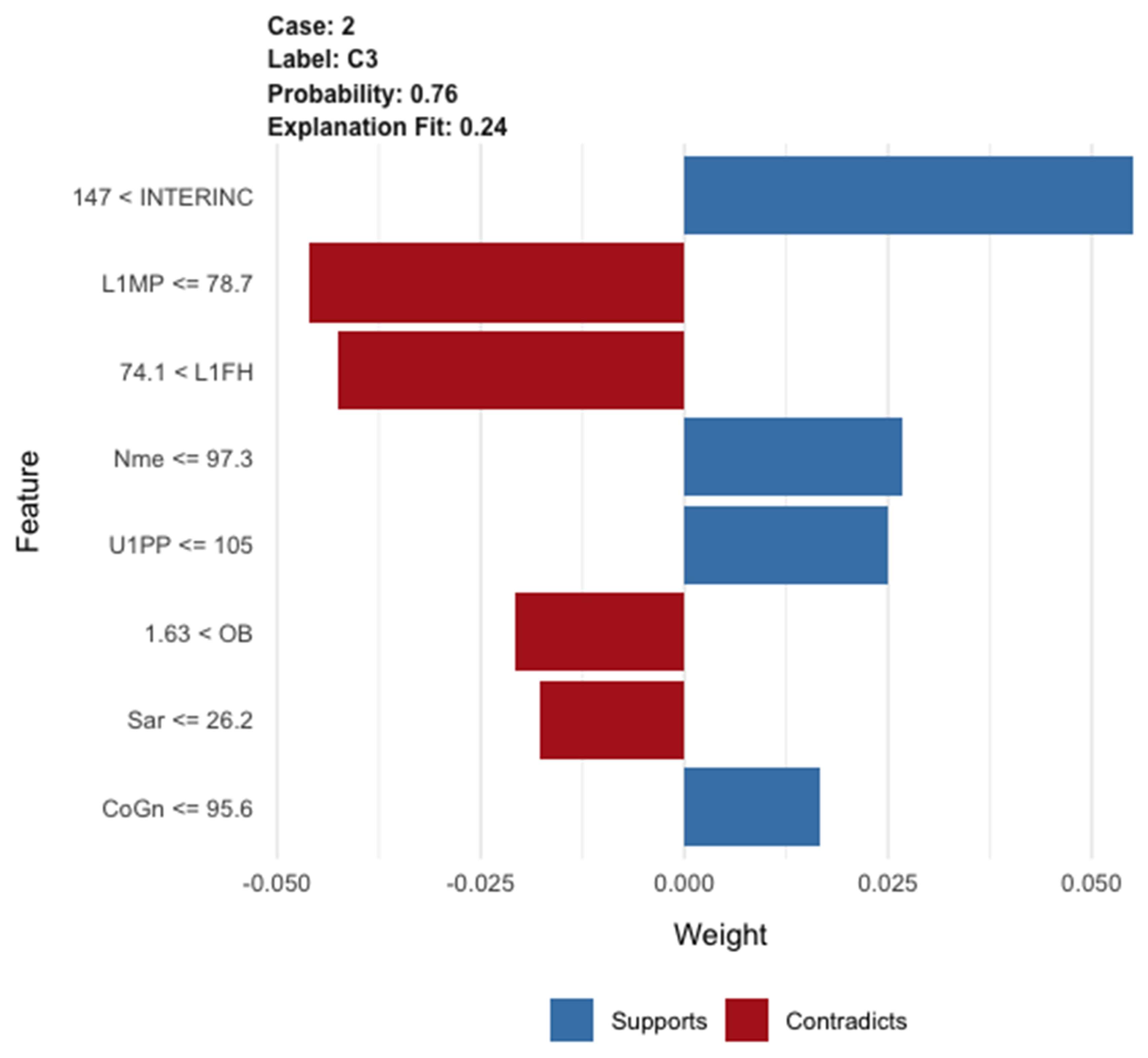
4. Tell Me What You Have Understood about This Patient
5. A Matter of Trust
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
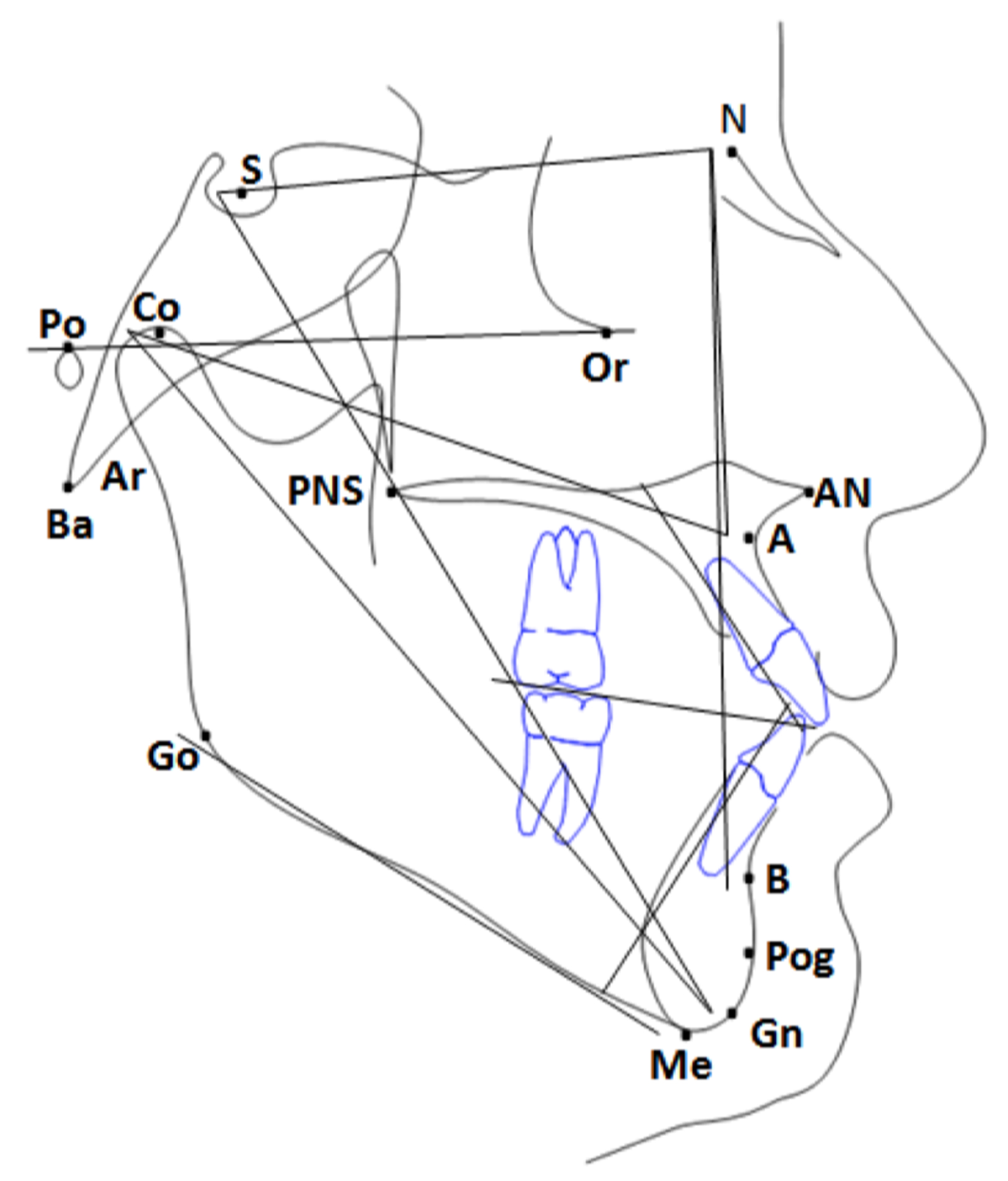
Appendix A. Translating from Orthodontic to ML Models
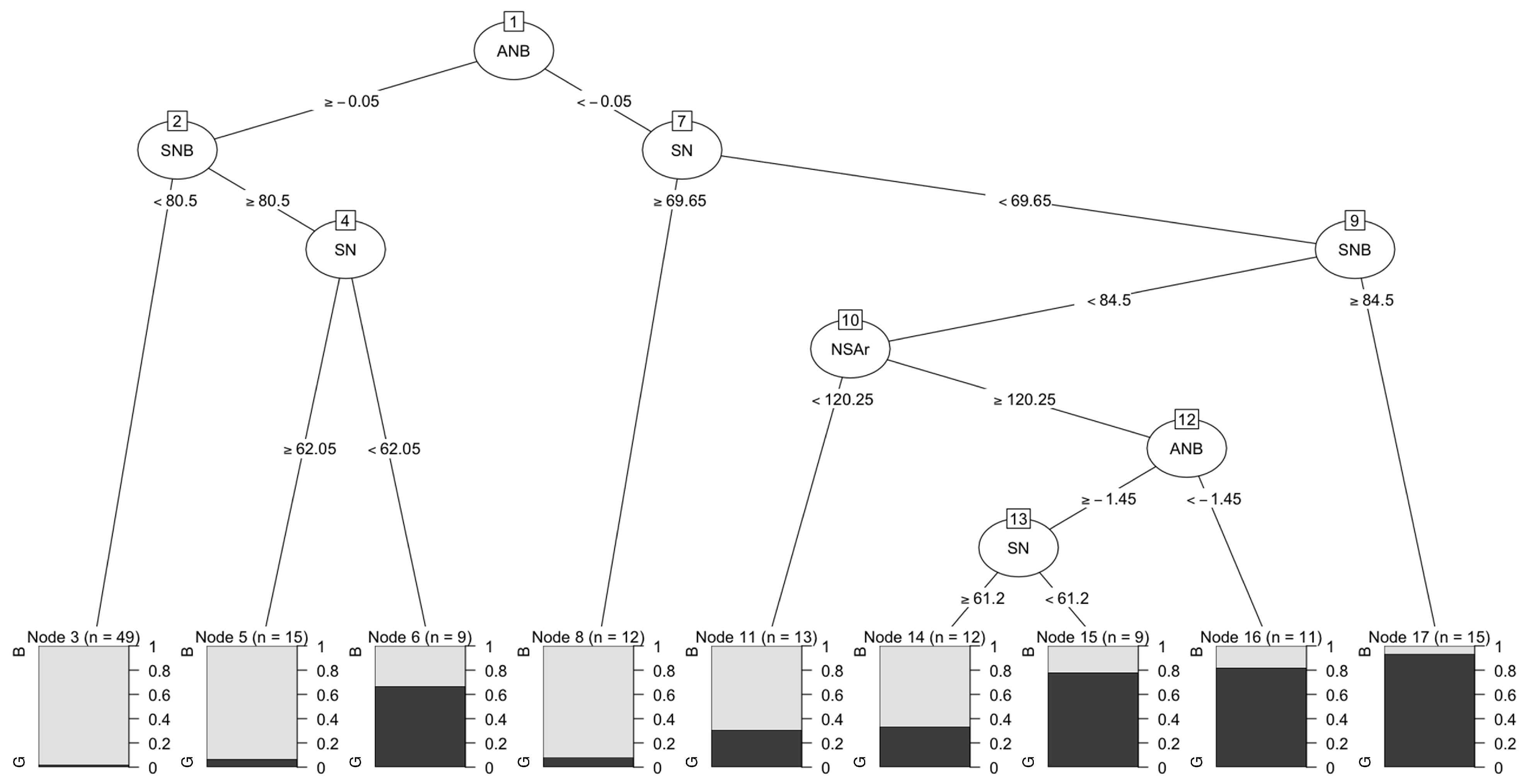
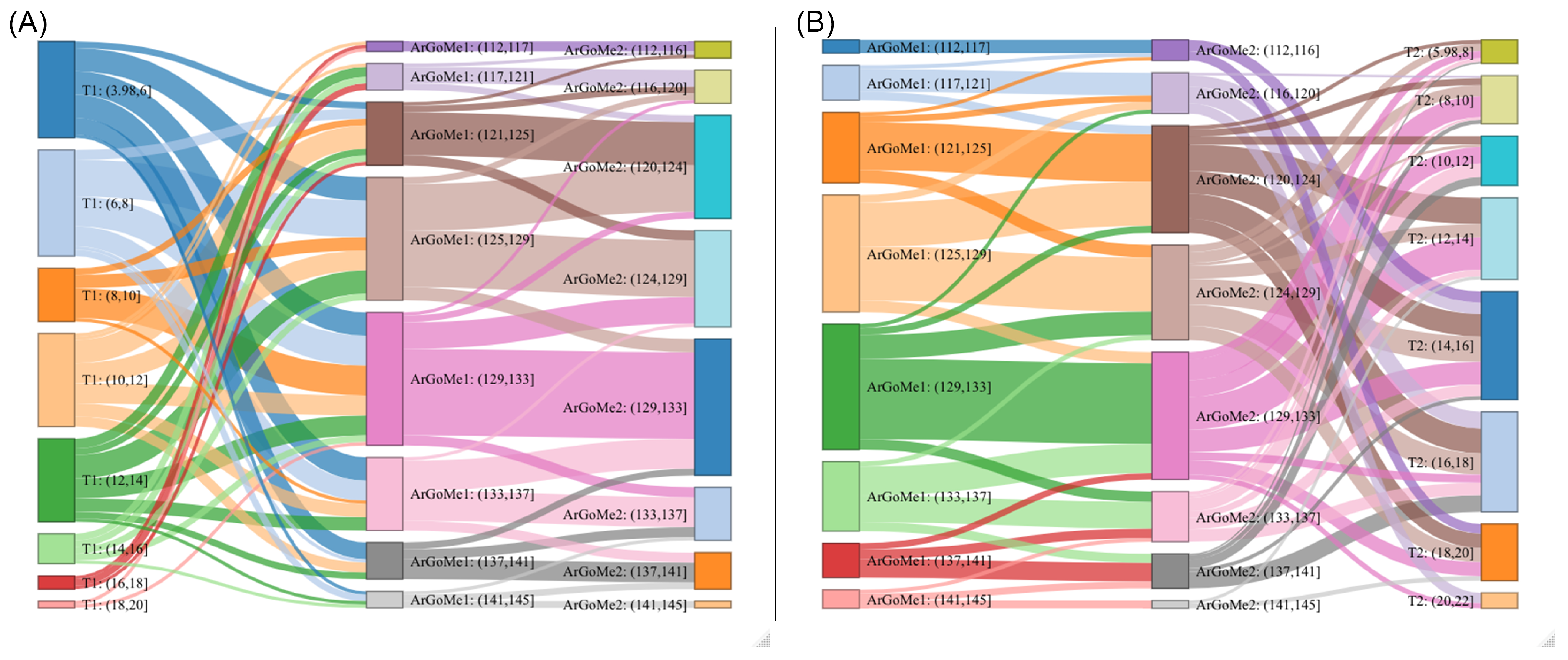
Appendix B. Machine Learning Programs Can Uncover Effects of Hidden Relationships between Components
References
- Rajkomar, A.; Dean, J.; Kohane, I. Machine learning in medicine. N. Engl. J. Med. 2019, 380, 1347–1358. [Google Scholar] [CrossRef] [PubMed]
- Deo, R.C. Machine learning in medicine. Circulation 2015, 132, 1920–1930. [Google Scholar] [CrossRef] [PubMed]
- Handelman, G.S.; Kok, H.K.; Chandra, R.V.; Razavi, A.H.; Lee, M.J.; Asadi, H. eDoctor: Machine Learning and the Future of Medicine. J. Intern. Med. 2018, 284, 603–619. [Google Scholar] [CrossRef] [PubMed]
- Weinberger, D. Everyday Chaos: Technology, Complexity, and How We’re Thriving in a New World of Possibility; Harvard Business Press: Boston, MA, USA, 2019. [Google Scholar]
- Obermeyer, Z.; Lee, T.H. Lost in Thought—The Limits of the Human Mind and the Future of Medicine. N. Engl. J. Med. 2017, 377, 1209–1211. [Google Scholar] [CrossRef]
- Miotto, R.; Li, L.; Kidd, B.A.; Dudley, J.T. Deep Patient: An Unsupervised Representation to Predict the Future of Patients from the Electronic Health Records. Sci. Rep. 2016, 6, 26094. [Google Scholar] [CrossRef]
- Bellazzi, R.; Zupan, B. Predictive data mining in clinical medicine: Current issues and guidelines. Int. J. Med. Inform. 2008, 77, 81–97. [Google Scholar] [CrossRef] [PubMed]
- Topol, E.J. High-performance medicine: The convergence of human and artificial intelligence. Nat. Med. 2019, 25, 44–56. [Google Scholar] [CrossRef]
- Sajda, P. Machine learning for detection and diagnosis of disease. Annu. Rev. Biomed. Eng. 2006, 8, 537–565. [Google Scholar] [CrossRef]
- Kononenko, I. Machine learning for medical diagnosis: History, state of the art and perspective. Artif. Intell. Med. 2001, 23, 89–109. [Google Scholar] [CrossRef]
- Freitas, A.A. Understanding the crucial role of attribute interaction in data mining. Artif. Intell. Rev. 2001, 16, 177–199. [Google Scholar] [CrossRef]
- Bzdok, D.; Altman, N.; Krzywinski, M. Points of Significance: Statistics versus machine learning. Nat. Methods 2018, 15, 233–234. [Google Scholar] [CrossRef] [PubMed]
- Goldemberg, J.; Ferguson, C.; Prud’homme, A. The World’s Energy Supply: What Everyone Needs to Know; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Arik, S.Ö.; Ibragimov, B.; Xing, L. Fully automated quantitative cephalometry using convolutional neural networks. J. Med. Imaging 2017, 4, 014501. [Google Scholar] [CrossRef] [PubMed]
- Marcus, G.; Davis, E. Rebooting AI: Building Artificial Intelligence We Can Trust; Pantheon Books: New York, NY, USA, 2019. [Google Scholar]
- Finlay, S. Predictive Analytics, Data Mining and Big Data; Palgrave Macmillan: New York, NY, USA, 2014; p. 248. [Google Scholar] [CrossRef]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning; Number September; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018; p. 218. [Google Scholar]
- Kelso, J.A.S.; Engstrom, D.A. The Complementary Nature; MIT Press: Cambridge, MA, USA, 2018; p. 317. [Google Scholar] [CrossRef]
- Blastland, M. The Hidden Half: The Unseen Forces That Influence Everything; Atlantic Books: London, UK, 2020. [Google Scholar]
- Pelaccia, T.; Forestier, G.; Wemmert, C. Deconstructing the diagnostic reasoning of human versus artificial intelligence. CMAJ 2019, 191, E1332–E1335. [Google Scholar] [CrossRef]
- Bichu, Y.M.; Hansa, I.; Bichu, A.Y.; Premjani, P.; Flores-Mir, C.; Vaid, N.R. Applications of artificial intelligence and machine learning in orthodontics: A scoping review. Prog. Orthod. 2021, 22, 18. [Google Scholar] [CrossRef]
- Nanda, S.B.; Kalha, A.S.; Jena, A.K.; Bhatia, V.; Mishra, S. Artificial neural network (ANN) modeling and analysis for the prediction of change in the lip curvature following extraction and non-extraction orthodontic treatment. J. Dent. Spec. 2015, 3, 217. [Google Scholar] [CrossRef]
- Asiri, S.N.; Tadlock, L.P.; Schneiderman, E.; Buschang, P.H. Applications of artificial intelligence and machine learning in orthodontics. APOS Trends Orthod. 2020, 10, 17–24. [Google Scholar] [CrossRef]
- Li, P.; Kong, D.; Tang, T.; Su, D.; Yang, P.; Wang, H.; Zhao, Z.; Liu, Y. Orthodontic Treatment Planning based on Artificial Neural Networks. Sci. Rep. 2019, 9, 2037. [Google Scholar] [CrossRef]
- Allareddy, V.; Rengasamy Venugopalan, S.; Nalliah, R.P.; Caplin, J.L.; Lee, M.K.; Allareddy, V. Orthodontics in the era of big data analytics. Orthod. Craniofacial Res. 2019, 22, 8–13. [Google Scholar] [CrossRef]
- Bahaa, K.; Noor, G.; Yousif, Y. The Artificial Intelligence Approach for Diagnosis, Treatment and Modelling in Orthodontic. In Principles in Contemporary Orthodontics; InTech: London, UK, 2011. [Google Scholar] [CrossRef]
- Faber, J.; Faber, C.; Faber, P. Artificial intelligence in orthodontics. APOS Trends Orthod. 2019, 9, 201–205. [Google Scholar] [CrossRef]
- Murata, S.; Lee, C.; Tanikawa, C.; Date, S. Towards a fully automated diagnostic system for orthodontic treatment in dentistry. In Proceedings of the 13th IEEE International Conference on eScience, eScience 2017, Auckland, New Zealand, 24–27 October 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Lux, C.J.; Stellzig, A.; Volz, D.; Jäger, W.; Richardson, A.; Komposch, G. A neural network approach to the analysis and classification of human craniofacial growth. Growth Dev. Aging 1998, 62, 95–106. [Google Scholar] [PubMed]
- Deo, R.C.; Nallamothu, B.K. Learning about Machine Learning: The Promise and Pitfalls of Big Data and the Electronic Health Record. Circ. Cardiovasc. Qual. Outcomes 2016, 9, 618–620. [Google Scholar] [CrossRef] [PubMed]
- Obermeyer, Z.; Emanuel, E.J. Predicting the Future—Big Data, Machine Learning, and Clinical Medicine. N. Engl. J. Med. 2016, 375, 1216–1219. [Google Scholar] [CrossRef] [PubMed]
- Ledley, R.S.; Lusted, L.B. Reasoning foundations of medical diagnosis. Science 1959, 130, 9–21. [Google Scholar] [CrossRef]
- Holzinger, A. Trends in Interactive Knowledge Discovery for Personalized Medicine: Cognitive Science meets Machine Learning. IEEE Intell. Inform. Bull. 2014, 15, 6–14. [Google Scholar]
- Wood, R.; Baxter, P.; Belpaeme, T. A review of long-term memory in natural and synthetic systems. Adapt. Behav. 2012, 20, 81–103. [Google Scholar] [CrossRef]
- Crawford, J.; Greene, C.S. Incorporating biological structure into machine learning models in biomedicine. Curr. Opin. Biotechnol. 2020, 63, 126–134. [Google Scholar] [CrossRef]
- Zitnik, M.; Nguyen, F.; Wang, B.; Leskovec, J.; Goldenberg, A.; Hoffman, M.M. Machine learning for integrating data in biology and medicine: Principles, practice, and opportunities. Inf. Fusion 2019, 50, 71–91. [Google Scholar] [CrossRef]
- Saria, S.; Butte, A.; Sheikh, A. Better medicine through machine learning: What’s real, and what’s artificial? PLoS Med. 2018, 15, e1002721. [Google Scholar] [CrossRef]
- Martínez-Abraín, A. Statistical significance and biological relevance: A call for a more cautious interpretation of results in ecology. Acta Oecologica 2008, 34, 9–11. [Google Scholar] [CrossRef]
- Lovell, D.P. Biological importance and statistical significance. J. Agric. Food Chem. 2013, 61, 8340–8348. [Google Scholar] [CrossRef] [PubMed]
- Bray, D. Limits of computational biology. Silico Biol. 2015, 12, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Auconi, P.; Scazzocchio, M.; Defraia, E.; Mcnamara, J.A.; Franchi, L. Forecasting craniofacial growth in individuals with class III malocclusion by computational modelling. Eur. J. Orthod. 2014, 36, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Barelli, E.; Ottaviani, E.; Auconi, P.; Caldarelli, G.; Giuntini, V.; McNamara, J.A.; Franchi, L. Exploiting the interplay between cross-sectional and longitudinal data in Class III malocclusion patients. Sci. Rep. 2019, 9, 6189. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Iguyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Baumrind, S. Clinical judgment versus prediction: Towards a new paradigm for orthodontic research. In Science and Clinical Judgment in Orthodontics; Vig PS, R.K., Ed.; Center for Human Growth and Development, The University of Michigan: Ann Arbor, MI, USA, 1985; pp. 149–162. [Google Scholar]
- Auconi, P.; McNamara, J.A.; Franchi, L. Computer-aided heuristics in orthodontics. Am. J. Orthod. Dentofac. Orthop. 2020, 158, 856–867. [Google Scholar] [CrossRef]
- Gigerenzer, G.; Brighton, H. Homo Heuristicus: Why Biased Minds Make Better Inferences. Top. Cogn. Sci. 2009, 1, 107–143. [Google Scholar] [CrossRef]
- Cabitza, F.; Ciucci, D.; Rasoini, R. A giant with feet of clay: On the validity of the data that feed machine learning in medicine. In Lecture Notes in Information Systems and Organisation; Springer: Cham, Switzerland, 2019; Volume 28, pp. 121–136. [Google Scholar] [CrossRef]
- Benítez, J.M.; Castro, J.L.; Requena, I. Are artificial neural networks black boxes? IEEE Trans. Neural Netw. 1997, 8, 1156–1164. [Google Scholar] [CrossRef]
- Zhang, G.P. Avoiding pitfalls in neural network research. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 3–16. [Google Scholar] [CrossRef]
- Lipton, Z.C. The Mythos of Model Interpretability. Queue 2018, 16, 31–57. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Kim, B.; Khanna, R.; Koyejo, O. Examples are not enough, learn to criticize! Criticism for interpretability. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; Volume 29, pp. 2288–2296. [Google Scholar]
- Bien, J.; Tibshirani, R. Prototype selection for interpretable classification. Ann. Appl. Stat. 2011, 5, 2403–2424. [Google Scholar] [CrossRef]
- Bergadano, F.; Matwin, S.; Michalski, R.S.; Zhang, J. Learning two-tiered descriptions of flexible concepts: The POSEIDON system. Mach. Learn. 1992, 8, 5–43. [Google Scholar] [CrossRef]
- Vassie, K.; Morlino, G. Natural and artificial systems: Compare, model or engineer? In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; Volume 7426, pp. 1–11. [Google Scholar] [CrossRef]
- Cabitza, F.; Rasoini, R.; Gensini, G.F. Unintended consequences of machine learning in medicine. Jama 2017, 318, 517–518. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C. The End of Theory: The Data Deluge Makes the Scientific Method Obsolete. Wired Mag. 2008, 16, 1–2. [Google Scholar]
- Shortliffe, E.H.; Buchanan, B.G. A model of inexact reasoning in medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
- Di Carlo, G.; Gili, T.; Caldarelli, G.; Polimeni, A.; Cattaneo, P.M. A community detection analysis of malocclusion classes from orthodontics and upper airway data. Orthod. Craniofacial Res. 2021, 24, 172–180. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Auconi, P.; Gili, T.; Capuani, S.; Saccucci, M.; Caldarelli, G.; Polimeni, A.; Di Carlo, G. The Validity of Machine Learning Procedures in Orthodontics: What Is Still Missing? J. Pers. Med. 2022, 12, 957. https://doi.org/10.3390/jpm12060957
Auconi P, Gili T, Capuani S, Saccucci M, Caldarelli G, Polimeni A, Di Carlo G. The Validity of Machine Learning Procedures in Orthodontics: What Is Still Missing? Journal of Personalized Medicine. 2022; 12(6):957. https://doi.org/10.3390/jpm12060957
Chicago/Turabian StyleAuconi, Pietro, Tommaso Gili, Silvia Capuani, Matteo Saccucci, Guido Caldarelli, Antonella Polimeni, and Gabriele Di Carlo. 2022. "The Validity of Machine Learning Procedures in Orthodontics: What Is Still Missing?" Journal of Personalized Medicine 12, no. 6: 957. https://doi.org/10.3390/jpm12060957
APA StyleAuconi, P., Gili, T., Capuani, S., Saccucci, M., Caldarelli, G., Polimeni, A., & Di Carlo, G. (2022). The Validity of Machine Learning Procedures in Orthodontics: What Is Still Missing? Journal of Personalized Medicine, 12(6), 957. https://doi.org/10.3390/jpm12060957









