An Innovative Approach for Extraction of Smoking Addiction Levels Using Physiological Parameters Based on Machine Learning: Proof of Concept
Abstract
1. Introduction
2. Materials and Methods
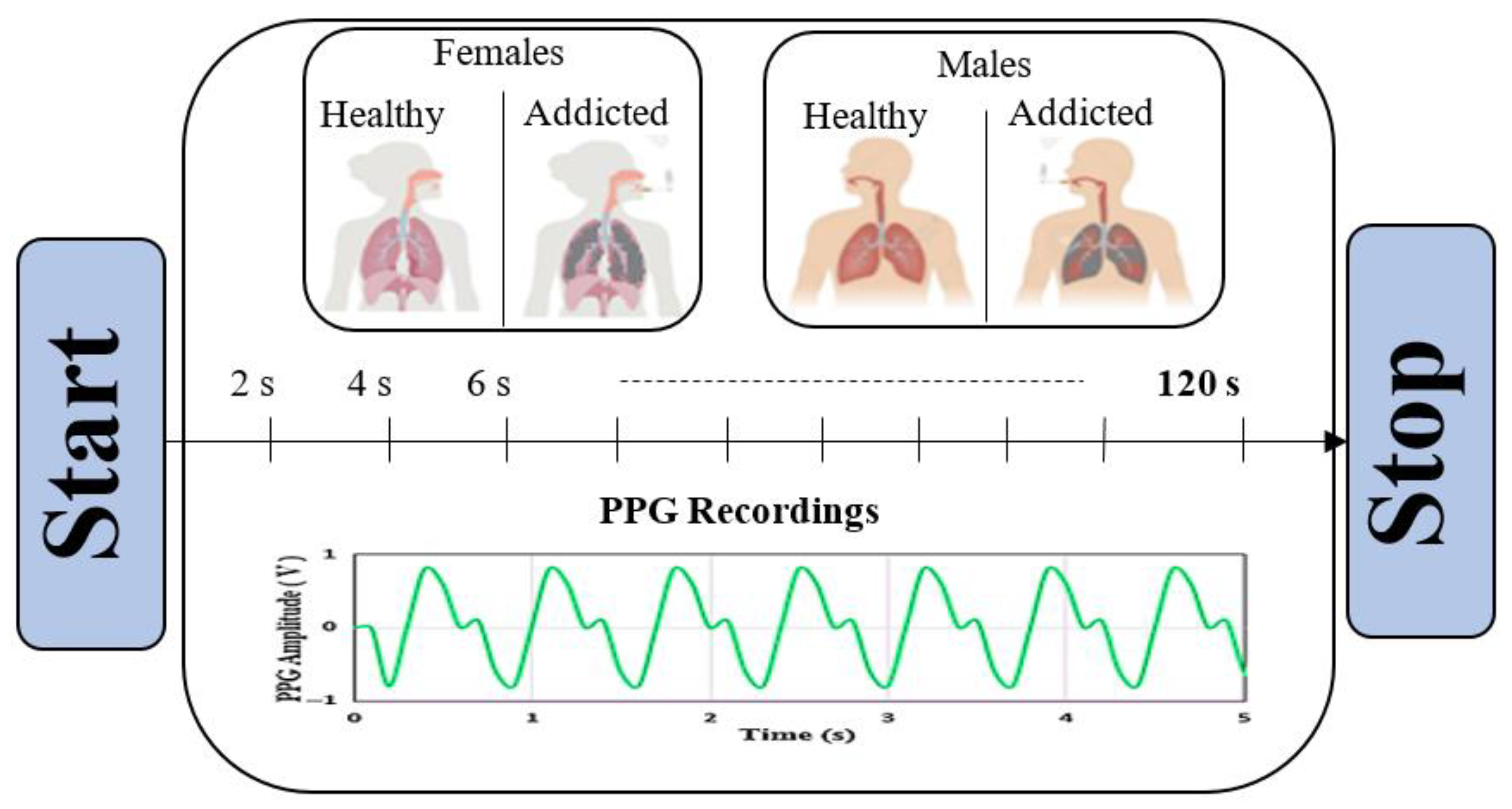
2.1. Dataset
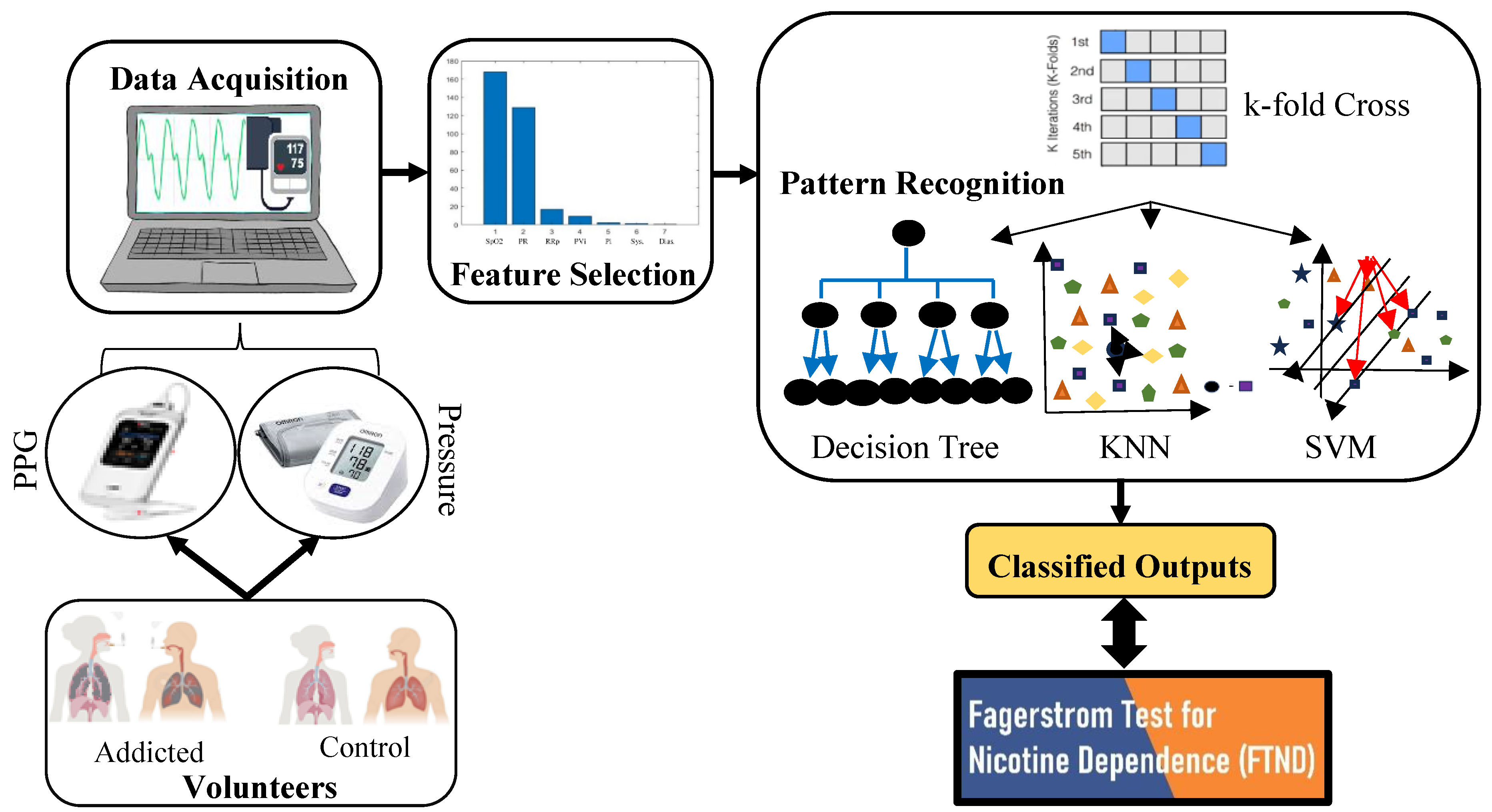
2.2. Method
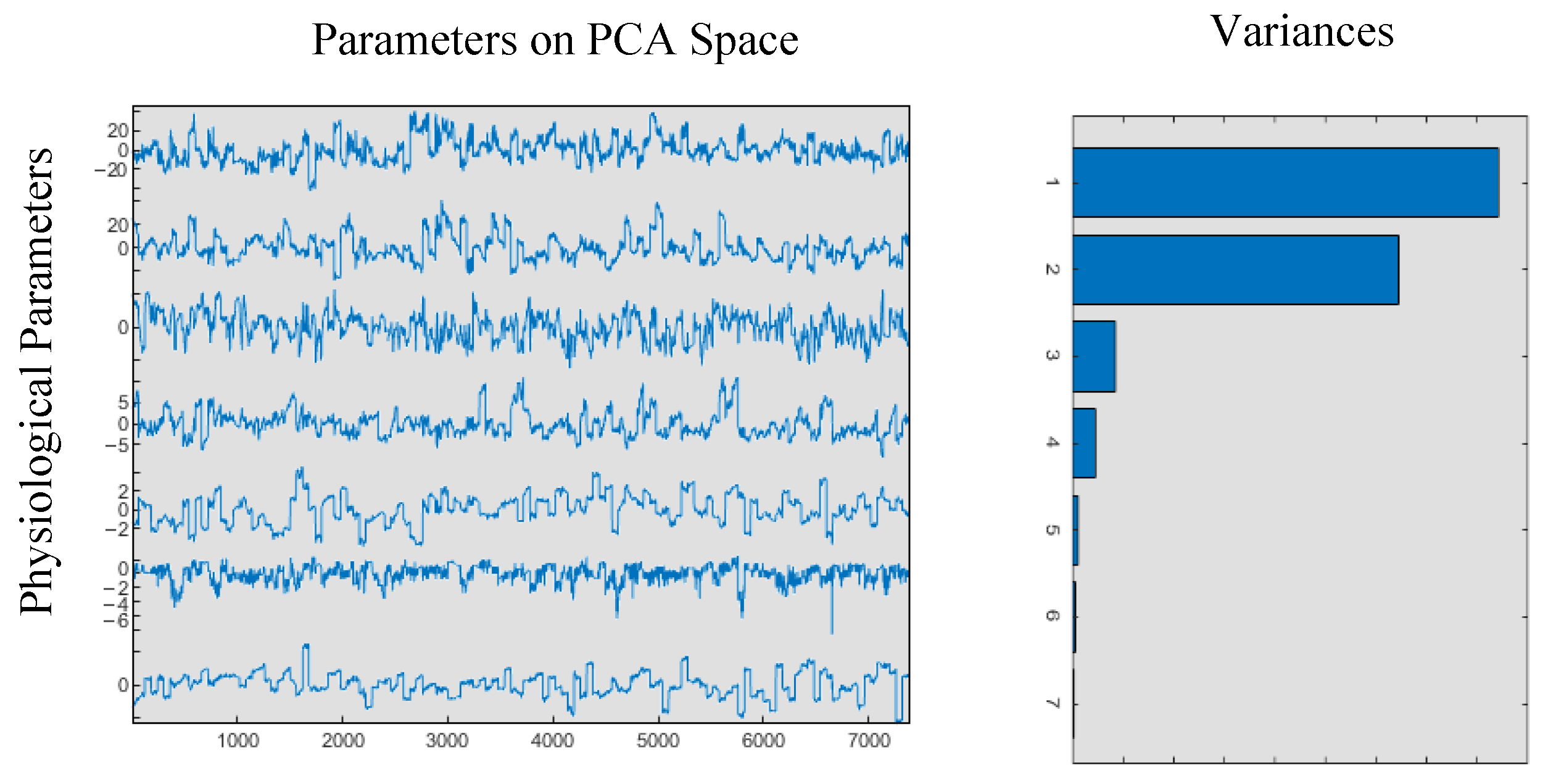
2.3. Principal Component Analysis (PCA)
2.4. Synthetic Minority Over-Sampling Technique (SMOTE)
2.5. Class-Weighting Technique for Imbalanced Data
2.6. Machine Learning
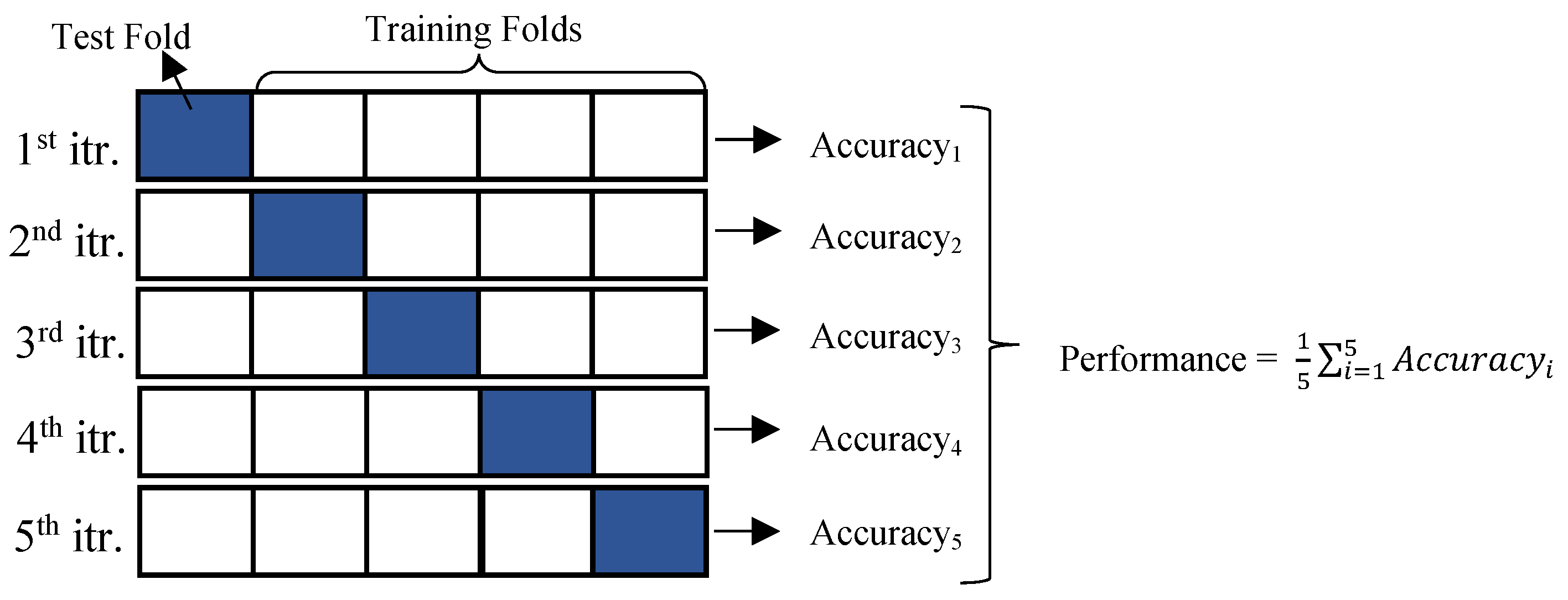
2.6.1. k-Fold Cross-Validation Technique
2.6.2. Decission Tree
2.6.3. K-Nearest Neighbor (KNN)
2.6.4. Support Vector Machine (SVM)
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Available online: https://www.who.int/news-room/fact-sheets/detail/tobacco?utm_source=chatgpt.com (accessed on 23 September 2025).
- Our World in Data. Available online: https://ourworldindata.org/grapher/number-of-deaths-from-tobacco-smoking#sources-and-processing (accessed on 23 September 2025).
- Dai, X.; Gakidou, E.; Lopez, A.D. Evolution of the global smoking epidemic over the past half century: Strengthening the evidence base for policy action. Tob. Control 2022, 31, 129–137. [Google Scholar] [CrossRef]
- De Silva, R.; Silva, D.; Piumika, L.; Abeysekera, I.; Jayathilaka, R.; Rajamanthri, L.; Wickramaarachchi, C. Impact of global smoking prevalence on mortality: A study across income groups. BMC Public Health 2024, 24, 1786. [Google Scholar] [CrossRef]
- Marakoğlu, K.; Çivi, S.; Şahsıvar, Ş.; Özdemir, S. The Relationship between Smoking Status and Depression Prevalence among First and Second Year Medical Students. J. Depend. 2006, 7, 129–134. [Google Scholar]
- Yazıcı, H.; Ak, İ. Depressive symptoms, personal health behaviors and smoking among university students. Anatol. J. Psychiatry 2008, 9, 224–231. [Google Scholar]
- Zincir, S.B.; Zincir, N.; Sünbül, E.A.; Kaynak, E. Relationship between nicotine dependence and temperament and character traits in adults with cigarette smoking. J. Mood Disord. 2012, 2, 160–166. [Google Scholar] [CrossRef]
- Çelepkolu, T.; Atli, A.; Palancı, Y.; Yılmaz, A.; Demir, S.; Ibiloglu, A.O.; Ekin, S. The relationship between nicotine dependence level and age-gender among the smokers: Diyarbakir sample. Dicle Med. J. 2014, 41, 712–716. [Google Scholar] [CrossRef]
- Kim, S. Overview of Cotinine Cutoff Values for Smoking Status Classification. Int. J. Environ. Res. Public Health 2016, 13, 1236. [Google Scholar] [CrossRef] [PubMed]
- Zettergren, A.; Sompa, S.; Palmberg, L.; Ljungman, P.; Pershagen, G.; Andersson, N.; Lindh, C.; Georgelis, A.; Kull, I.; Melen, E.; et al. Assessing tobacco use in Swedish young adults from self-report and urinary cotinine: A validation study using the BAMSE birth cohort. BMJ Open 2023, 13, e072582. [Google Scholar] [CrossRef]
- Pariyadath, V.; Stein, E.A.; Ross, T.J. Machine learning classification of resting state functional connectivity predicts smoking status. Front. Hum. Neurosci. 2014, 8, 425. [Google Scholar] [CrossRef] [PubMed]
- Wetherill, R.R.; Rao, H.; Hager, N.; Wang, J.; Franklin, T.R.; Fan, Y. Classifying and characterizing nicotine use disorder with high accuracy using machine learning and resting-state fMRI. Addict. Biol. 2019, 24, 811–821. [Google Scholar] [CrossRef]
- Eken, A.; Çalışkan, Ş.; Çivilibal, S.; Tosun, P.D. Prediction of smoking status by using multi-physiological measures and machine learning techniques. Dokuz Eylul Univ. Fac. Eng. J. Sci. Eng. 2021, 23, 55–69. [Google Scholar] [CrossRef]
- Çay, T.; Ölmez, E.; Tanık, N.; Altın, C. EEG based cigarette addiction detection with deep learning. Trait. Du Signal 2024, 41, 1183–1192. [Google Scholar] [CrossRef]
- Carreiro, S.; Ramanand, P.; Akram, W.; Stapp, J.; Chapman, B.; Smelson, D.; Indic, P. Developing a Wearable Sensor-Based Digital Biomarker of Opioid Dependence. Anesth. Analg. 2025, 141, 393–402. [Google Scholar] [CrossRef] [PubMed]
- Horvath, M.; Pittman, B.; O’Malley, S.S.; Grutman, A.; Khan, N.; Gueorguieva, R.; Brewer, J.A.; Garrison, K.A. Smartband-based smoking detection and real-time brief mindfulness intervention: Findings from a feasibility clinical trial. Ann. Med. 2024, 56, 2352803. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Xiang, L.; Fekete, G.; Baker, J.S.; Mao, Z.; Gu, Y. Data-Driven Approach for Fatigue Detection during Running Using Pedobarographic Measurements. Appl. Bionics Biomech. 2023, 2023, 7022513. [Google Scholar] [CrossRef]
- Mahoney, J.M.; Rhudy, M.B. Methodology and validation for identifying gait type using machine learning on IMU data. J. Med. Eng. Technol. 2019, 43, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Kunutsor, S.K.; Spee, J.M.; Kieneker, L.M.; Gansevoort, R.T.; Dullaart, R.P.F.; Voerman, A.J.; Touw, D.J.; Bakker, S.J. Self-Reported Smoking, Urine Cotinine, and Risk of Cardiovascular Disease: Findings From the PREVEND (Prevention of Renal and Vascular End-Stage Disease) Prospective Cohort Study. J. Am. Heart Assoc. 2018, 7, e008726. [Google Scholar] [CrossRef]
- Murriky, A.; Allam, E.; Alotaibi, H.; Alnamasy, R.; Alnufiee, A.; AlAmro, A.; Al-Hammadi, A. The relationship between nicotine dependence and willingness to quit smoking: A cross-sectional study. Prev. Med. Rep. 2025, 53, 103066. [Google Scholar] [CrossRef]
- Masimo. Rad-G: Continuous Pulse Oximeter Opretors Manual. Available online: https://techdocs.masimo.com/globalassets/techdocs/pdf/lab-10076a_master.pdf (accessed on 23 September 2025).
- Hartmann Veroval Compact Upper Arm Blood Pressure Monitor. Available online: https://www.veroval.info/-/media/country/website/archive/diagnostics/veroval/pdfs/new-pdfs/instructions-for-use/veroval_compact_bpu_22.pdf?rev=7ab70eb24ab44ce5a52b69682dc797d1&sc_lang=en (accessed on 23 September 2025).
- Fagerström, K.O. Measuring degree of physical dependence to tobacco smoking with reference to individualization of treatment. Addict. Behav. 1978, 3, 235–241. [Google Scholar] [CrossRef]
- Heatherton, T.F.; Kozlowski, L.T.; Frecker, R.C.; Fagerstrom, K.O. The Fagerstrom Test for Nicotine Dependence: A revision of the Fagerstrom Tolerance Questionnaire. Br. J. Addict. 1991, 86, 1119–1127. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Cao, L.J.; Chua, K.; Chong, W.K.; Lee, H.P.; Gu, O.M. A comparison of PCA, KPCA and ICA for dimensionality reduction in support vector machine. Neurocomputing 2003, 55, 321–336. [Google Scholar] [CrossRef]
- Howley, T.; Madden, M.G.; O’Connell, M.L.; Ryder, A.G. The effect of principal component analysis on machine learning accuracy with high-dimensional spectral data. Knowl.-Based Syst. 2006, 19, 363–370. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Fernandez, A.; Garcia, S.; Herrera, F.; Chawla, N.V. SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-year Anniversar. J. Artif. Intell. Res. 2018, 61, 863–905. [Google Scholar] [CrossRef]
- Benkendorf, D.J.; Schwartz, S.D.; Cutler, D.R.; Hawkins, C.P. Correcting for the effects of class imbalance improves the performance of machine-learning based species distribution models. Ecol. Model. 2023, 483, 110414. [Google Scholar] [CrossRef]
- Bakırarar, B.; Ehan, A.H. Class Weighting Technique to Deal with Imbalanced Class Problem in Machine Learning: Methodological Research. Turk. Klin. J. Biostat. 2023, 15, 19–29. [Google Scholar] [CrossRef]
- Bascil, M.S. A New Approach on HCI Extracting Conscious Jaw Movements Based on EEGSignals Using Machine Learnings. J. Med. Syst. 2018, 42, 169. [Google Scholar] [CrossRef]
- Ozer, I.; Karaca, A.C.; Ozer, C.K.; Gorur, K.; Kocak, I.; Cetin, O. The exploration of the transfer learning technique for Globotruncanita genus against the limited low-cost light microscope images. Signal Image Video Process. 2024, 18, 6363–6377. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lee, S.; Lee, C.; Mun, K.G.; Kim, D. Decision Tree Algorithm Considering Distances Between Classes. IEEE Access 2022, 10, 69750–69756. [Google Scholar] [CrossRef]
- D’Ambrosio, A.; Tutore, V.A. Conditional Classification Trees by Weighting the Gini Impurity Measure. In Proceedings of the 7th Conference of the Classification and Data Analysis Group of the Italian Statistical Society, Catania, Italy, 9–11 September 2009. [Google Scholar] [CrossRef]
- Görür, K.; Bozkurt, M.R.; Bascil, M.S.; Temurtas, F. Tongue-Operated Biosignal over EEG and Processing with Decision Tree and kNN. Acad. Platf.-J. Eng. Sci. 2021, 9, 112–125. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Peterson, L.E. K-Nearest Neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Ali, N.; Neagu, D.; Trundle, P. Evaluation of k-nearest neighbour classifier performance for heterogeneous data sets. SN Appl. Sci. 2019, 1, 1559. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Weston, J.A. User’s guide to support vector machines. Methods Mol. Biol. 2009, 609, 223–239. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; The MIT Press: Cambridge, MA, USA, 2001. [Google Scholar] [CrossRef]
- Hidayaturrohman, Q.A.; Hanada, E. A Comparative Analysis of Hyper-Parameter Optimization Methods for Predicting Heart Failure Outcomes. Appl. Sci. 2025, 15, 3393. [Google Scholar] [CrossRef]
- Last, F.; Douzas, G.; Bacao, F. Oversampling for Imbalanced Learning Based on K-Means and SMOTE. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F.; Kamalov, F. A theoretical distribution analysis of synthetic minority oversampling technique (SMOTE) for imbalanced learning. Mach. Learn. 2024, 113, 4903–4923. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Batista, G.; Prati, R.C.; Monard, M.C. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Y.Q.; Chawla, N.V.; Krasser, S. SVMs modeling for highly imbalanced classification. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 281–288. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Li, Y.; Shang, J.; Gu, M.; Huang, Y.; Gong, B. Learning from class-imbalanced data: Review of methods and applications. Expert Syst. Appl. 2017, 73, 220–239. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2009, 3, 1157–1182. [Google Scholar]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists, 1st ed.; O’Reilly Media: Sebastopol, CA, USA, 2018. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Kharabsheh, M.; Meqdadi, O.; Alabed, M.; Veeranki, S.; Abbadi, A.; Alzyoud, S. A machine learning approach for predicting nicotine dependence. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 179–184. [Google Scholar] [CrossRef]
- Choi, J.; Jung, H.T.; Ferrell, A.; Woo, S.; Haddad, L. Machine learning-based nicotine addiction prediction models for youth e-cigarette and waterpipe (hookah) users. J. Clin. Med. 2021, 10, 972. [Google Scholar] [CrossRef]
- Issabakhsh, M.; Sánchez-Romero, L.M.; Le, T.; Liber, A.C.; Tan, J.; Li, Y.; Meza, R.; Mendez, D.; Levy, D.T. Machine learning application for predicting smoking cessation among US adults: An analysis of waves 1–3 of the PATH study. PLoS ONE 2023, 18, e0286883. [Google Scholar] [CrossRef] [PubMed]
- Aishwarya, S.; Siddalingaswamy, P.C.; Chadaga, K. Explainable artificial intelligence driven insights into smoking prediction using machine learning and clinical parameters. Sci. Rep. 2025, 15, 24069. [Google Scholar] [CrossRef] [PubMed]
- Qananwah, Q.; Quran, H.; Dagamseh, A.; Blazek, V.; Leonhardt, S. Investigating the correlation between smoking and blood pressure via photoplethysmography. BioMed. Eng. OnLine 2025, 24, 57. [Google Scholar] [CrossRef]







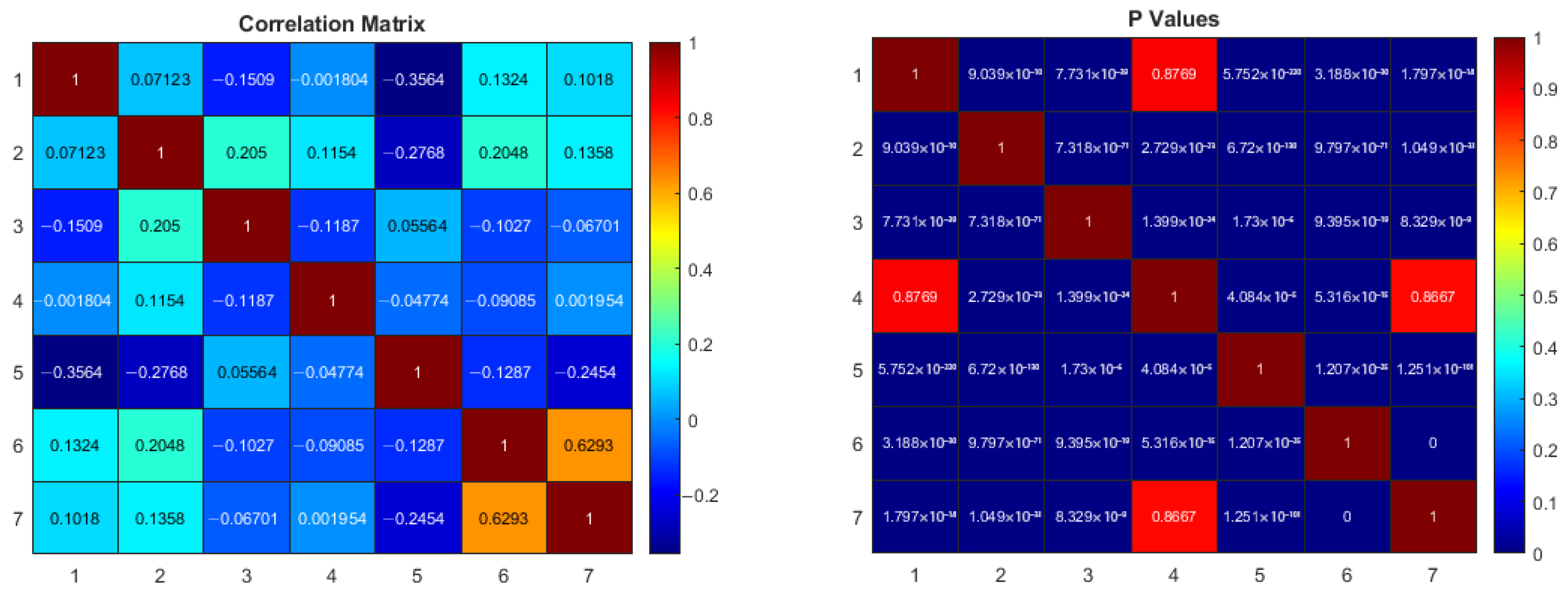
| Class | SpO2 Mean | SpO2 SD | PR Mean | PR SDNN | RRp Mean | RRp CV% |
|---|---|---|---|---|---|---|
| Class 1 | 98.1 ± 1.3 | 1.3 | 79.8 ± 8.2 | 36.4 | 16.8 ± 2.9 | 16.8 |
| Class 2 | 95.2 ± 2.9 | 2.9 | 92.4 ± 10.1 | 30.7 | 20.2 ± 4.1 | 20.1 |
| Class 3 | 91.8 ± 4.7 | 4.7 | 104.9 ± 12.3 | 25.2 | 24.3 ± 6.2 | 25.3 |
| Class 4 | 87.1 ± 6.4 | 6.4 | 118.3 ± 14.8 | 20.1 | 27.9 ± 8.7 | 31.1 |
| Class | SDNN (ms) | RMSSD (ms) | LF/HF Ratio | pNN50 (%) | HRV Index |
|---|---|---|---|---|---|
| Class 1 | 36.4 ± 8.2 | 31.5 ± 7.1 | 1.52 ± 0.4 | 25.8 ± 6.3 | 13.4 ± 2.8 |
| Class 2 | 30.7 ± 7.4 | 24.3 ± 6.2 | 2.01 ± 0.5 | 17.2 ± 5.1 | 10.7 ± 2.4 |
| Class 3 | 25.2 ± 6.8 | 18.7 ± 5.4 | 2.68 ± 0.6 | 11.4 ± 4.2 | 8.3 ± 2.1 |
| Class 4 | 20.1 ± 6.1 | 14.2 ± 4.9 | 3.41 ± 0.8 | 6.3 ± 3.1 | 6.2 ± 1.9 |
| Class | Respiration Rate (Breaths/Min) | RR Coefficient of Variation (%) | Breath Interval SD (Seconds) | Rapid Shallow Breathing Index |
|---|---|---|---|---|
| Class 1 | 16.8 ± 2.9 | 16.8 ± 4.2 | 1.9 ± 0.4 | 37.3 ± 8.1 |
| Class 2 | 20.2 ± 4.1 | 20.1 ± 5.7 | 2.9 ± 0.7 | 48.1 ± 10.4 |
| Class 3 | 24.3 ± 6.2 | 25.3 ± 7.8 | 4.3 ± 1.1 | 63.9 ± 14.2 |
| Class 4 | 27.9 ± 8.7 | 31.1 ± 9.5 | 5.8 ± 1.6 | 85.8 ± 19.7 |
| Methods | Performance Metrics (%), (k = 5 Fold) | |||||
|---|---|---|---|---|---|---|
| Recall | Specificity | Precision | F-Score | Accuracy | ||
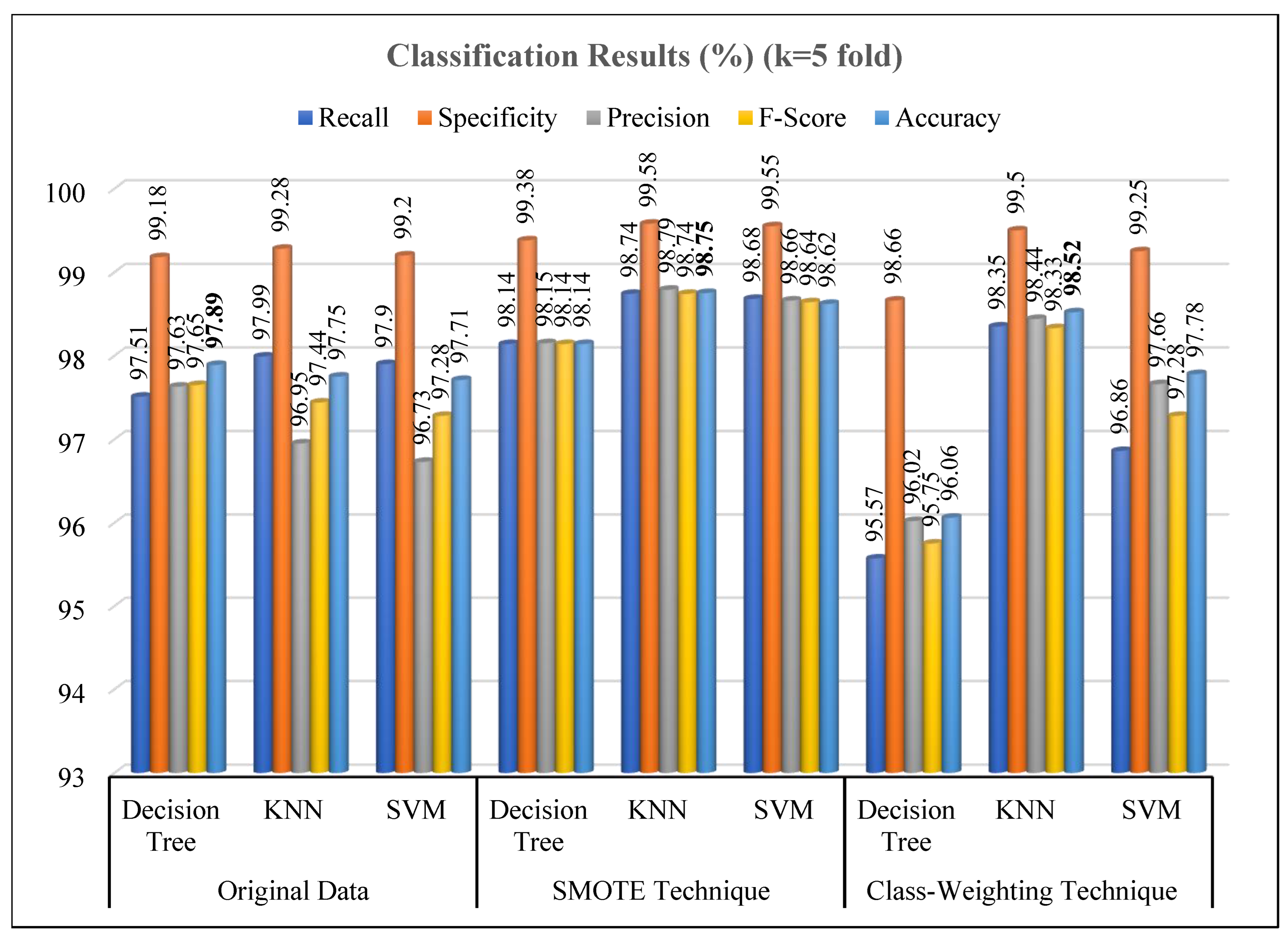
| Original Data | Decision Tree | 97.51 ± 0.55 | 99.18 ± 0.16 | 97.63 ± 0.53 | 97.65 ± 0.52 | 97.89 ± 0.45 |
| KNN | 97.99 ± 0.33 | 99.28 ± 0.11 | 96.95 ± 0.48 | 97.44 ± 0.39 | 97.75 ± 0.33 | |
| SVM | 97.90 ± 0.26 | 99.28 ± 0.08 | 96.73 ± 0.32 | 97.28 ± 0.26 | 97.71 ± 0.22 | |
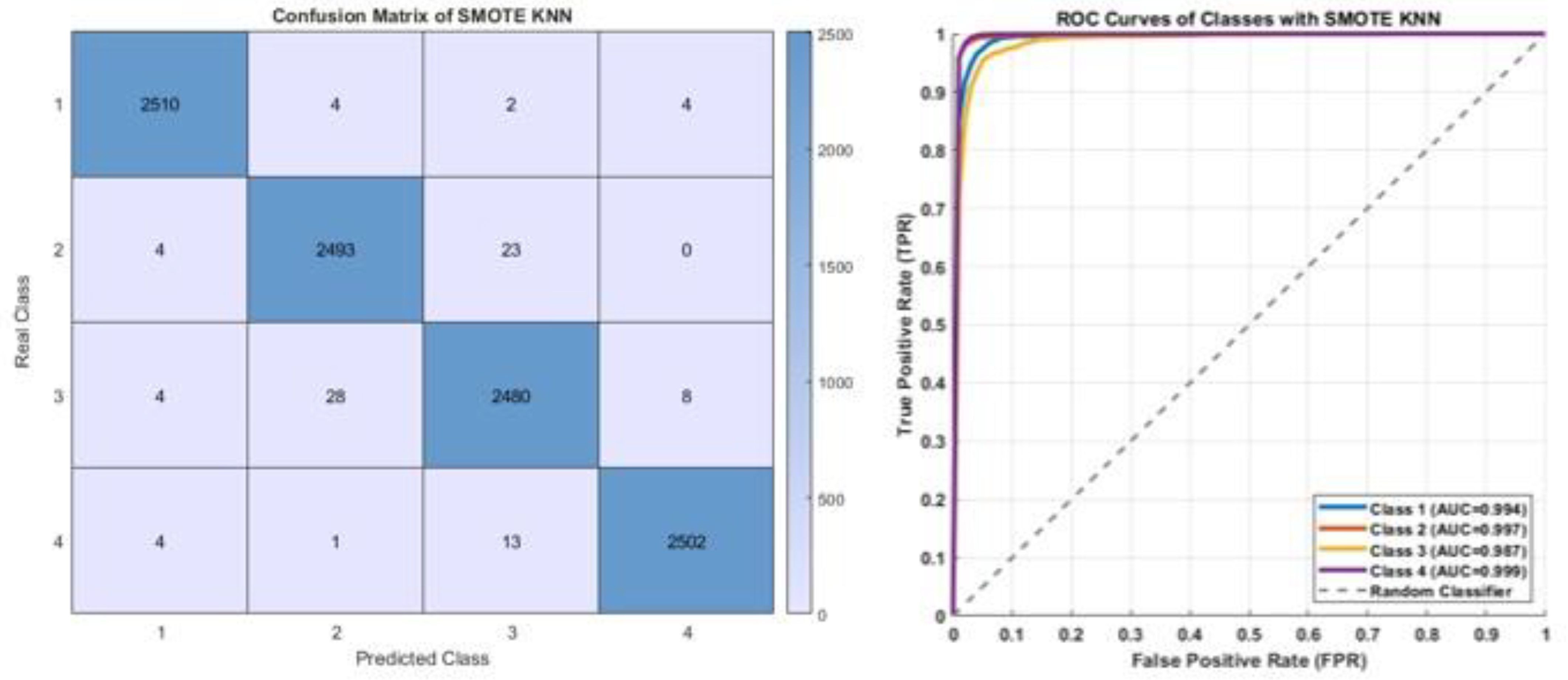
| SMOTE Technique | Decision Tree | 98.14 ± 0.31 | 99.38 ± 0.10 | 98.15 ± 0.31 | 98.14 ± 0.31 | 98.14 ± 0.31 |
| KNN | 98.74 ± 0.22 | 99.58 ± 0.07 | 98.79 ± 0.24 | 98.74 ± 0.22 | 98.75 ± 0.22 | |
| SVM | 98.68 ± 0.12 | 99.55 ± 0.05 | 98.66 ± 0.16 | 98.64 ± 0.15 | 98.62 ± 0.16 | |
| Class-Weighting Technique | Decision Tree | 95.57 ± 1.52 | 98.66 ± 0.41 | 96.02 ± 1.44 | 95.75 ± 1.41 | 96.06 ± 1.27 |
| KNN | 98.35 ± 0.63 | 99.5 ± 0.11 | 98.44 ± 0.58 | 98.33 ± 0.51 | 98.52 ± 0.41 | |
| SVM | 96.86 ± 0.73 | 99.25 ± 0.26 | 97.66 ± 0.40 | 97.28 ± 0.59 | 97.78 ± 0.44 | |
| Methods | Classification Results (%) with PCA (99%), (k = 5 Fold) | |||||
|---|---|---|---|---|---|---|
| Recall | Specificity | Precision | F-Score | Accuracy | ||
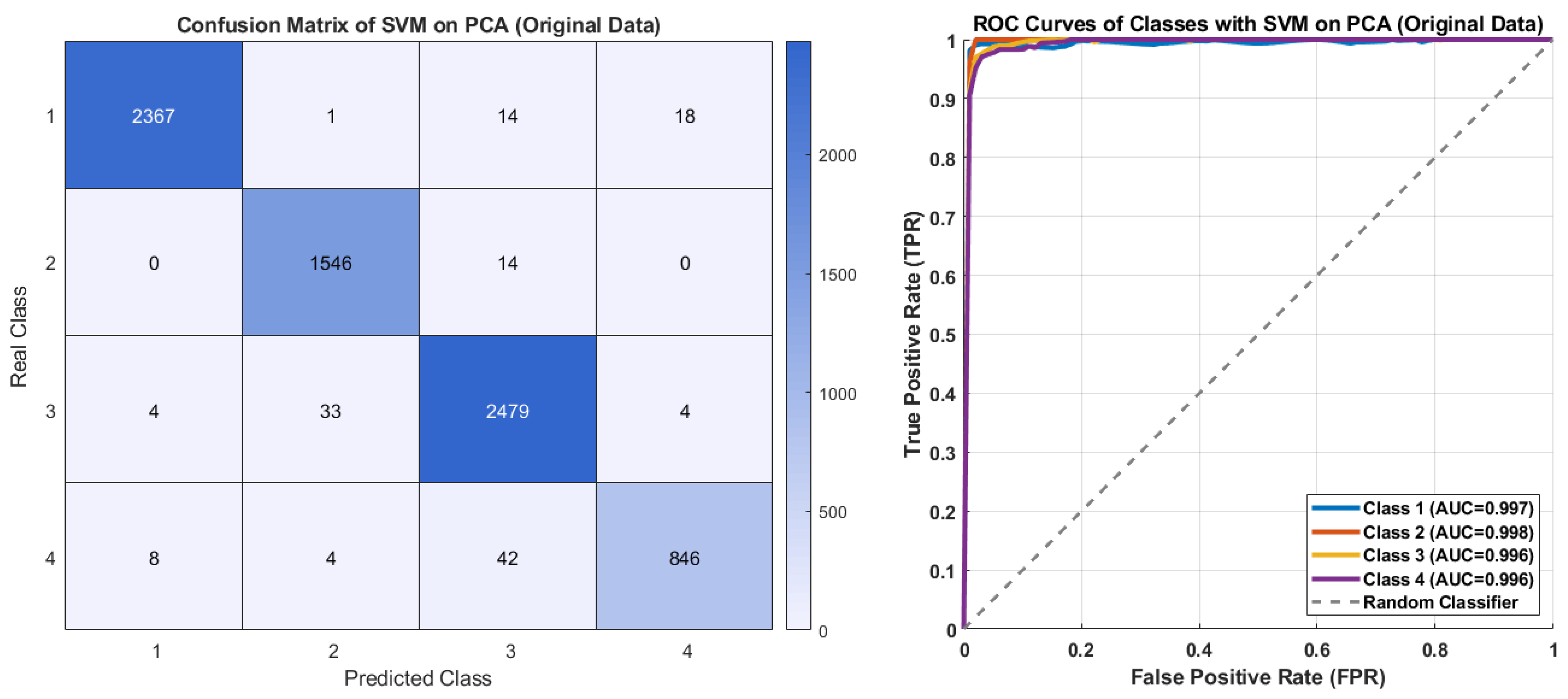
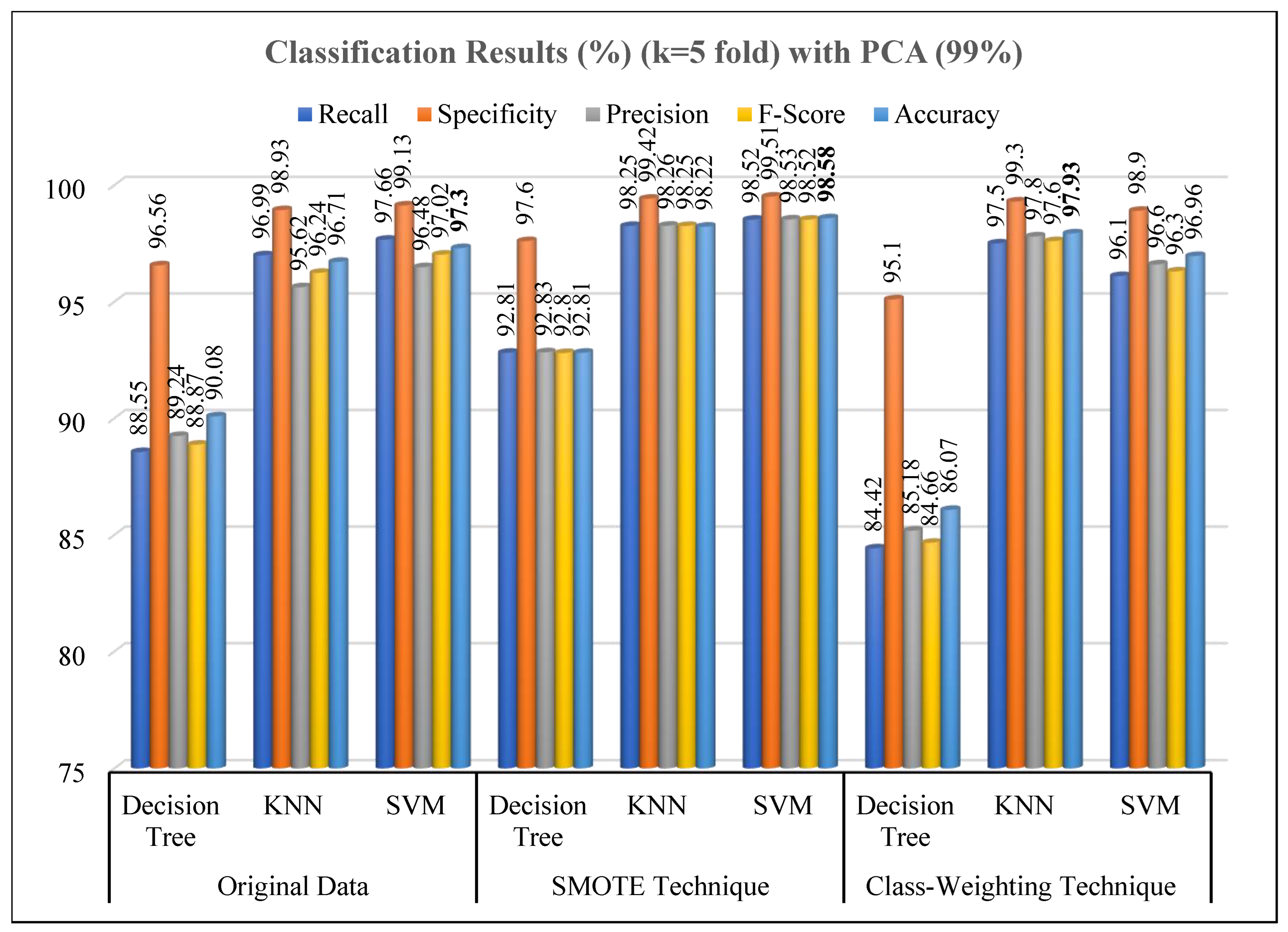
| Original Data (Reduced by PCA) | Decision Tree | 88.55 ± 0.86 | 96.56 ± 0.25 | 89.24 ± 0.87 | 88.87 ± 0.85 | 90.08 ± 0.72 |
| KNN | 96.99 ± 0.40 | 98.93 ± 0.13 | 95.62 ± 0.55 | 96.24 ± 0.46 | 96.71 ± 0.39 | |
| SVM | 97.66 ± 0.16 | 99.13 ± 0.06 | 96.48 ± 0.38 | 97.02 ± 0.27 | 97.30 ± 0.20 | |
| SMOTE Technique | Decision Tree | 92.81 ± 0.53 | 97.60 ± 0.17 | 92.83 ± 0.53 | 92.80 ± 0.53 | 92.81 ± 0.52 |
| KNN | 98.25 ± 0.26 | 99.42 ± 0.09 | 98.26 ± 0.26 | 98.25 ± 0.26 | 98.22 ± 0.28 | |
| SVM | 98.52 ± 0.25 | 99.51 ± 0.08 | 98.53 ± 0.25 | 98.52 ± 0.22 | 98.58 ± 0.23 | |
| Class-Weighting Technique | Decision Tree | 84.42 ± 2.73 | 95.10 ± 0.61 | 85.18 ± 1.85 | 84.66 ± 2.19 | 86.07 ± 1.64 |
| KNN | 97.5 ± 0.16 | 99.3 ± 0.20 | 97.8 ± 0.41 | 97.6 ± 0.75 | 97.93 ± 0.51 | |
| SVM | 96.1 ± 1.3 | 98.9 ± 0.31 | 96.6 ± 0.92 | 96.3 ± 1.11 | 96.96 ± 0.83 | |
| Study | Data Source | Machine Learnings | Classes | Accuracy | Paticipant | Focus |
|---|---|---|---|---|---|---|
| Kharabsheh et al. (2019) [54] | Survey Data (WTSQ) | Dec.Tree, SVM, k-Star, Naive Bayes | 3 | 82% | 108 | Survey-based dependence classification |
| Choi et al. (2021) [55] | Survey Data (NYTS) | RF, LASSO | 4 | 73.42% | 6511 | Risk factor analysis in adolescents |
| Issabakhsh et al. (2023) [56] | Basic Vital Signs | Random Forest, XGBoos | 2 | 81% | 5000 | Biomarker-based smoking status classification |
| Aishwarya et al. (2025) [57] | Clinical/Biological Data | RF, LR, Dec.Tree, KNN, CatBoost, ANN | 2 | 85% | 2000 | Binary smoking status classification (Smoker/Non-smoker) |
| Qananwah et al. (2025) [58] | PPG+EKG | Gaussian Process Regression | 3 | 99.7% | 84 | Predicting smoking’s acute effect on blood pressure |
| This Study (2025) | PPG (SpO2, PR, RRp, Pi, Pvi, BP) | Dec.Tree, KNN, SVM | 4 | 98.75% | 123 | PPG-based multi-level nicotine dependence severity assessment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bascil, M.S.; Iscanli, I.N. An Innovative Approach for Extraction of Smoking Addiction Levels Using Physiological Parameters Based on Machine Learning: Proof of Concept. Diagnostics 2025, 15, 2839. https://doi.org/10.3390/diagnostics15222839
Bascil MS, Iscanli IN. An Innovative Approach for Extraction of Smoking Addiction Levels Using Physiological Parameters Based on Machine Learning: Proof of Concept. Diagnostics. 2025; 15(22):2839. https://doi.org/10.3390/diagnostics15222839
Chicago/Turabian StyleBascil, Muhammet Serdar, and Irem Nur Iscanli. 2025. "An Innovative Approach for Extraction of Smoking Addiction Levels Using Physiological Parameters Based on Machine Learning: Proof of Concept" Diagnostics 15, no. 22: 2839. https://doi.org/10.3390/diagnostics15222839
APA StyleBascil, M. S., & Iscanli, I. N. (2025). An Innovative Approach for Extraction of Smoking Addiction Levels Using Physiological Parameters Based on Machine Learning: Proof of Concept. Diagnostics, 15(22), 2839. https://doi.org/10.3390/diagnostics15222839





