On Torque Vectoring Control: Review and Comparison of State-of-the-Art Approaches

Abstract

Torque vectoring is a widely known technique to improve vehicle handling and to increase stability in limit conditions. With the advent of electric vehicles, this is becoming a key topic since it is possible to have distributed powertrains, i.e., multiple motors are adopted, in which each motor is controlled separately from the others. Moreover, electric motors deliver the torque required by the controller faster and more precisely than internal combustion engines, active differentials and conventional hydraulic brakes. The state of the art of Direct Yaw Moment Control (DYC) techniques, ranging from classical to modern control theories, are analyzed and discussed in this paper. The aim is to give an overview of the currently available approaches while identifying their drawbacks regarding performances and robustness when dealing with common issues like model uncertainties, external disturbances, friction limit and common state estimation problems. This contribution analyzes all the steps from the lateral dynamics reference generation to the desired control action computation and allocation to the available actuators. In addition, some of the presented control logic is evaluated in a simulation environment for a passenger car. Results of both open-loop and closed-loop maneuvers allow the comparison and clarification of each control strategy’s key advantages.

1. Introduction

In recent years, Electric Vehicles (EVs) have become an increasingly popular alternative to conventional internal combustion engine vehicles [1]. To both governments and the mass public, they appear as a solution for reducing air pollution and its consequences on human health [2].

In this context, the powertrain has been redesigned to exploit all the features offered by electric motors [3]. In fact, more than one motor can be fitted in the vehicle. Among distributed motor powertrains, a common approach is that of In-Wheel Motors (IWMs), which allows for effective packaging and high efficiency [4]. Moreover, using distributed motors allows significant improvements from the vehicle dynamics point of view. The possibility of independently controlling the torque on each wheel quickly and precisely makes applying Torque Vectoring Control (TVC) strategies easy. Indeed, Torque Vectoring (TV) consists in applying different longitudinal forces to the wheels of the same axle, resulting in a yaw moment that is used to control the vehicle lateral dynamics. Different powertrain layouts have been compared in the literature [5,6,7,8], and it is generally agreed that the best performing one is that with a four independent wheel drive system. Moreover, in certain cases, TV control is also combined with Active Front Steering (AFS) [9], Active Rear Steering (ARS) [10] and Four-Wheel Steering (4WS) [11,12].

This paper presents a review of torque vectoring control systems. Conversely to other vehicle chassis control reviews already present in the literature [13,14,15,16,17], this paper focuses on torque vectoring, providing an overview of the available techniques and including a comparison of simulation results to highlight advantages and disadvantages of the most relevant strategies. Furthermore, this contribution analyzes all three levels of the cascaded control, reporting the different approaches used in the literature.

TV potential in enhancing vehicle handling is so significant [18,19] that these control strategies were adopted before the advent of electric motors. At that time, TV was either actuated through active and semi-active differentials [20,21,22,23,24,25] or through individually controlled wheel brakes [21,26,27,28,29,30], as it is still used nowadays in some applications [31,32]. Nevertheless, both actuation systems are less effective than electric motors because of slower dynamics, lower efficiency and flexibility, while also showing an increased integration complexity.

Regarding TV control architecture, most of the literature proposes a multilayer cascaded control composed by three main blocks, as in Figure 1, which include the following:

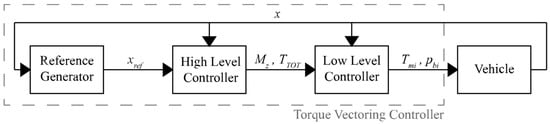
Figure 1. Torque vectoring control scheme.

• reference generator;
• high-level controller;
• low-level controller.

The three components of the TV controller are briefly introduced hereafter, while a more in-depth description is given in the following sections, with the main focus being the high-level controller.

The reference generator obtains the driver inputs and the vehicle states ($x$) to generate a reference ($x_{ref}$) for yaw rate and/or sideslip angle, which are the relevant quantities related to vehicle lateral dynamics. Most of the times, the reference quantity for vehicle-handling improvement is the yaw rate. In the most straightforward approach, based on the tuning of the understeer gradient, the reference yaw rate is a linear function of the driver steering angle input [21,33,34,35,36,37,38,39,40]. An evolution of this approach accounts for a variable desired understeer gradient [41], that is selected based on driver intention recognition when entering or exiting a curve. Nevertheless, this approach does not account for the non-linear dynamics characterizing the vehicle at high acceleration levels. For this reason, the authors in [42] proposed a correction factor based on a feedforward neural network adopting the steering angle and the vehicle speed as inputs. Later, a more advanced approach was proposed in [24] and adopted by many other authors in a slightly modified formulation [6,28,43,44,45,46,47,48] where the idea is to fully design the understeer characteristics of the vehicle with any shape not limited to the linear behavior. Using this approach, different vehicle behaviors can be obtained, corresponding to different understeer characteristics, being denoted as the driving modes [45,49]. Driving modes are sometimes selectable by drivers to adjust the vehicle behavior to their actual desires, such as a sport mode that improves the fun-to-drive experience. Driving modes can be designed to target not only vehicle handling performances but also energy efficiency requirements. In fact, some works have as their primary target the energetic efficiency of the vehicle, which is achieved by a proper design of the vehicle’s understeer characteristics [50,51].

The vehicle sideslip angle is often considered along with the yaw rate as a reference quantity since it provides an indication about vehicle lateral stability. It must be pointed out that, in general, controlling the yaw rate and sideslip angle simultaneously can be a challenging task since the two requirements are often conflicting. In general, two approaches can be found for the integration of sideslip angle control, which are:

• the sideslip angle reference is an additional control objective independent from the yaw rate reference [48,52], scheduling the control action based on driving conditions to manage conflicting requirements, e.g., sideslip angle contribution is only introduced when it exceeds a threshold value [46,53];
• the yaw rate reference is modified based on the sideslip angle value to increase vehicle stability [54,55].

The high-level controller takes as input the driver commands, the vehicle states and the output quantities from the reference generator. These inputs then define the total driving torque ($T_{TOT}$) and yaw moment ($M_z$) to be applied to the vehicle. Two parallel logics generally compute the two outputs of the high-level controller. The total torque demand is obtained through a drivability controller, while the yaw moment is obtained through the torque vectoring controller. The drivability controller uses drivability maps to define the amount of total driving torque to be delivered to the wheels to fulfill the driver demands, i.e., the accelerator pedal position is converted into a total torque reference for the engine or the motors. Instead, the torque vectoring controller computes the total desired yaw moment to be applied to the vehicle according to various approaches. The simplest method consists in a Proportional–Integral–Derivative (PID) controller [56,57,58] based on the error between the reference and the actual value of the yaw rate and/or sideslip angle. Alternatively, optimal controllers can be used to track state references [59,60]. This approach generally requires a reliable vehicle model, which allows it to outperform the simple PID approach. Conversely to optimal approaches, it is possible to mention Sliding Mode Control (SMC) [61,62] or also fuzzy logic control [63,64]. Through the years, Model Predictive Control (MPC) [65,66] has also become widespread thanks to the improved computational capabilities of micro-processors. As in other fields, the last trend in vehicle dynamics yaw control also concerns the adoption of Reinforcement Learning (RL) techniques [67,68].

The low-level controller takes the total driving torque and yaw moment demand as inputs. Then, it generates a torque demand for each motor ($T_{m,i}$) and, if necessary, a braking pressure for each brake caliper ($p_{b,i}$). This level is necessary because, in over-actuated vehicles, the high-level requests are not met in a straightforward manner, but it is necessary to properly allocate the single actuator efforts to meet the virtual high-level requests [69]. In torque vectoring studies, the low-level torque distributor is designed in two alternative ways. The first considers a front-to-rear distribution, which the designer fixes a priori, while the second considers an optimal torque allocation to wheels. The optimal approach deals alternatively with the equal exploitation of tire adherence or the energy efficiency of the whole vehicle. In some cases, where the target is energy efficiency, the high-level and the low-level controllers are designed together. In this way, the required yaw moment is also computed to save energy while giving less importance to the vehicle handling performance.

This paper is organized as follows: First, different torque vectoring control approaches are presented. Then, the simulation models are defined. Finally, the simulation results of relevant TVC strategies are reported.

2. Torque Vectoring Control

This section presents in detail the three main components that constitute torque vectoring controllers, making reference to the approaches employed in a wide range of the literature. To focus on the control strategy, all vehicle states are assumed to be available to the controller, and the state estimation issue is not addressed in this paper. This assumption is significant since, in the context of passenger vehicles, crucial quantities like vehicle sideslip angle or tire–road contact forces and friction coefficient are not directly measurable but require estimation. A comprehensive overview of techniques and approaches for tire and vehicle state estimation can be found in [70,71,72,73], where an exhaustive literature review is provided.

2.1. Reference Generator

The reference generator aims to define the desired vehicle lateral dynamics behavior, thereby generating references for the controller. When dealing with vehicle lateral dynamics, the most common approach considers yaw rate and sideslip angle responses, which are the two state variables representative of cornering performance and stability. Two approaches are commonly employed for defining the reference yaw rate. The first establishes a linear relationship between the yaw rate and the input steering angle, while the second defines a piecewise function linking the yaw rate to the input steering angle.

The simplest method for determining reference values for yaw rate and sideslip angle involves the linearization of the steady-state equations of motion of a single-track vehicle model [21,33,34,35,36,37,38,39,40,74,75,76,77]. This approach results in the reference yaw rate being expressed as a linear function of the input steering angle and thus reads:

$${\dot{\psi }}_{ref}=\frac{V}{l(1+k_{US}{V}^2)}\delta$$

(1)

where ${\dot{\psi }}_{ref}$ is the reference yaw rate; $V$ the vehicle speed; $l$ the vehicle wheelbase; $k_{US}$ the understeering coefficient and $\delta$ the wheels steering angle. The understeering coefficient is, in turn, a function of vehicle and tire properties and is defined as follows:

$$k_{US}=\frac{m}{l^2}\left(\frac{b}{k_{TF}}-\frac{a}{k_{TR}}\right)$$

(2)

where $m$ represents the vehicle mass, $a$ and $b$ denote the distances between the vehicle center of mass and the front and rear axle, respectively, and $k_{TF}$ and $k_{TR}$ are the cornering stiffnesses of the front and rear axle, respectively. This approach enables the manipulation of the vehicle’s cornering response by acting on the understeering coefficient ($k_{US}$). However, the linear nature of this approach for the reference yaw rate has limitations due to the inherent linearization and is thus effective within the linear region of tires (typically below 4 m/s² lateral acceleration). Notably, this method does not account for tire–road friction, which physically restricts the maximum attainable yaw rate. To address this limitation, a more sophisticated approach is introduced, allowing for a detailed design of the reference understeer characteristic [6,24,28,43,44,45,46,47,48,49,78,79,80,81,82]. In relation to that, a piecewise function defines the relationship between the dynamic steering angle ${\delta }_{dyn}$ and the lateral acceleration $a_y$, which, under quasi-steady-state conditions, is directly associated with the reference yaw rate (${\dot{\psi }}_{ref}=a_y/V$). This approach originates from defining the steering angle $\delta$ as the sum of dynamic ${\delta }_{dyn}$ and kinematic ${\delta }_{kin}$ components, with the latter obtained from the Ackermann formula, as in the following:

$$\delta ={\delta }_{dyn}+{\delta }_{kin}={\delta }_{dyn}+\frac{l}{R_c}={\delta }_{dyn}+\frac{l{·a}_y}{V^2}$$

(3)

where $R_c$ represents the curvature radius of the vehicle trajectory. Then, the piecewise function defining the relationship between the dynamic steering angle and the lateral acceleration retains a linear trait defined as in the previous approach. However, it introduces an upper limit associated with the maximum lateral acceleration, constrained by the available tire–road friction. To avoid any discontinuity, the two linear traits are interconnected using an exponential function, yielding the following set of expressions:

$$a_y=\left\{\begin{array}{c}\begin{array}{cc}\frac{1}{k_U}{\delta }_{dyn}& {\delta }_{dyn}\le {k_{U}a}_y^{*}\end{array}\\ \begin{array}{cc}{a}_{y,max}+\left(a_y^{*}-a_{y,max}\right)e^{\left(\frac{k_U{a}_y^{*}-{\delta }_{dyn}}{k_U\left(a_{y,max}-a_y^{*}\right)}\right)}& {\delta }_{dyn}>{k_{U}a}_y^{*}\end{array}\end{array}\right.$$

(4)

where $k_U=\partial {\delta }_{dyn}/\partial a_y=k_{US}l$ is the understeer gradient, $a_y^{*}$ denotes the lateral acceleration at the limit of the linear region of the understeering characteristic and $a_{y,max}$ represents the maximum lateral acceleration achievable with the available tire–road friction. These three parameters hold a clear physical meaning, and tuning them allows the accomplishment of three design objectives for the vehicle understeer characteristic, as illustrated in Figure 2:

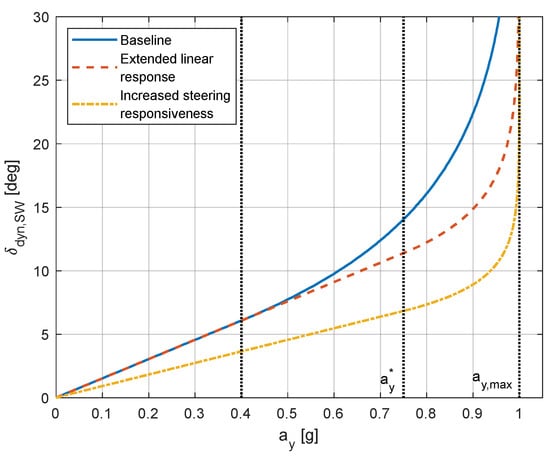
Figure 2. TV control objectives.

• reduction in the understeer gradient k_U compared with the baseline vehicle, leading to increased steering responsiveness, which is characteristic of a vehicle closer to neutral behavior;
• extension of the linear cornering response region by increasing the lateral acceleration limit $a_y^{*}$ for the transition between the linear trait and the saturation region;
• increase in the maximum achievable lateral acceleration $a_{y,max}$, maximizing the utilization of available tire–road friction. This objective is feasible because the maximum lateral acceleration occurs when the vehicle experiences a yaw moment, as detailed in the Milliken Moment Method (MMM) diagrams in [83].

It is worth mentioning that the cornering responses depicted in Figure 2 do not represent the response of an actual vehicle, but they serve for elucidating potential enhancements in the steady-state vehicle cornering response. These improvements are typically attainable through a proper vehicle setup or by incorporating an active vehicle lateral dynamics control and setting the desired vehicle cornering response as the reference quantity to be tracked. As the reference cornering response is derived under steady-state conditions, precise tracking is crucial in quasi-steady-state conditions. Conversely, when addressing transient conditions, the same reference can be adopted to mitigate the undesired variability in the vehicle’s cornering response even though the tracking results less precise.

Translating the control reference in terms of lateral acceleration into the equivalent yaw rate reference is straightforward, as the two quantities are linked by a precise relationship in steady-state conditions. This implies that the maximum attainable yaw rate is the maximum achievable lateral acceleration normalized by the actual vehicle speed (${\dot{\psi }}_{max}=a_{y,max}/V$). Designating ${\dot{\psi }}^{*}$ as the yaw rate value at which the transition between the linear and saturation regions occurs, and knowing that this phenomenon happens at a steering angle ${\delta }^{*}={k_{U}a}_y^{*}$, the yaw rate reference can be expressed as:

$${\dot{\psi }}_{ref}=\left\{\begin{array}{c}\begin{array}{cc}\frac{V}{l(1+k_{US}{V}^2)}\delta =\alpha \delta & \delta \le {\delta }^{*}\end{array}\\ \begin{array}{cc}{\dot{\psi }}_{max}+\left({\dot{\psi }}^{*}-{\dot{\psi }}_{max}\right)e^{\left(\frac{-\alpha \left(\delta -{\delta }^{*}\right)}{\left({\dot{\psi }}_{max}-{\dot{\psi }}^{*}\right)}\right)}& \delta >{\delta }^{*}\end{array}\end{array}\right.$$

(5)

where all the mentioned quantities are already known. When following the presented approach, it is crucial to consider that the maximum vehicle acceleration is constrained by the available tire–road friction. Consequently, a longitudinal acceleration results in a reduction in the maximum attainable lateral acceleration. Thus, the yaw rate reference (${\dot{\psi }}_{ref}$) can be derived as the function of steering wheel angle input (${\delta }_{SW}$), vehicle speed ($V$) and longitudinal acceleration ($a_x$), as illustrated in Figure 3.

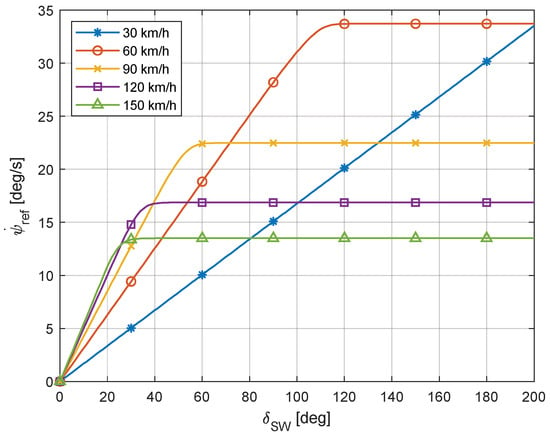
Figure 3. Reference yaw rate at different running speeds for null longitudinal acceleration.

In some cases, a combined control on yaw rate and sideslip angle is proposed, as a lower sideslip angle corresponds to improved vehicle drivability. The simplest approach for defining the reference sideslip angle is still based on the linearization of the steady-state equations of motion of a single-track vehicle model [38,48,76,77,79,84,85]. This approach allows for the definition of the reference sideslip angle (${\beta }_{ref}$) as a function of the reference yaw rate, leading to either a linear or a saturating expression depending on the definition of the reference yaw rate.

$${\beta }_{ref}=\left(\frac{b}{V}-\frac{m a V}{l k_{TR}}\right){\dot{\psi }}_{ref}$$

(6)

Another widely used approach to limit the sideslip angle value, with the aim of ensuring vehicle stability, is to impose a null reference value [86,87,88,89]. This usually requires an extremely high control effort, and thus, a more relaxed formulation has been proposed in the literature. This defines the vehicle sideslip angle reference as a maximum absolute value not to be exceeded, eventually as a function of vehicle states, meaning that this quantity is controlled only when overcoming a certain threshold [39,46,90]. This approach activates the sideslip angle control only for specific handling conditions, whereas it would be desirable to have a continuously active control for ensuring vehicle safety. For a continuously active controller, a new reference should be defined because a steep variation in the reference occurs when switching from positive to negative sideslip angle values and vice versa, due to the sudden shift from a positive to a negative constant reference value and vice versa. This can lead to discontinuous control action and abrupt changes in vehicle behavior, so, more recently, a novel approach has been introduced. In relation to that, the reference vehicle sideslip angle is based on the actual value of the sideslip angle $\beta$, still with the aim of limiting it to a constant maximum value but avoiding discontinuities for a change in sign of the vehicle sideslip angle [52]. The following expression can be adopted:

$${\beta }_{ref}={\beta }_{max}\tanh \left(\frac{\beta }{{\beta }_{max}}\right)$$

(7)

where ${\beta }_{max}$ is the maximum sideslip angle. This upper bound to the sideslip angle is the one that allows for the stability of the vehicle and can be selected based on the controller designer’s expertise [84] or by considering a reasonable margin with respect to the phase plane stability boundary [91].

2.2. High-Level Controllers

The high-level controller aims to define the amount of yaw moment to be applied to the vehicle to effectively control its lateral dynamics. Numerous approaches are available in the literature, drawing from both classical and modern control theories.

While the majority of controllers operate on feedback loops, there are instances where a feedforward contribution is added to the control action to ensure a faster response. The feedforward component is typically scheduled based on offline simulation results. The simplest approach involves scheduling the feedforward yaw moment control action according to the steering wheel angle commanded by the driver [24,35,56]. This entails defining the feedforward yaw moment based on the single-track vehicle model with the aim of enhancing vehicle lateral dynamics, typically by tracking a reference state. A more sophisticated approach consists in conducting offline simulations to optimize the yaw moment feedforward control actions as function of various parameters such as steering wheel angle, longitudinal acceleration and the tire–road friction coefficient [43,92]. Within the latter category, a novel offline optimization procedure for designing the feedforward control action of the vehicle dynamics controller for a fully electric vehicle is presented in [6]. The novelty lies in the objective function formulation, which is based on energy efficiency criteria and constrained by a reference vehicle handling performance.

The rest of this section summarizes and analyzes the most common approaches in the literature for vehicle lateral dynamics control, highlighting the pros and cons of each method. The examined controllers are categorized in subsections based on the adopted control methodology.

2.2.1. PID Controllers

The simplest approach for applying torque vectoring involves the use of a Proportional–Integral–Derivative (PID) control logic, which tracks yaw rate and/or sideslip angle. In general, PID controllers have the advantage of being easy to implement and tune. Moreover, they exhibit robustness to external disturbances, noises and changes in plant characteristics. However, the drawbacks of PIDs are associated with changes in the model, as they are designed for Linear Time-Invariant (LTI) systems.

In [56], a TV proportional (P) controller, based on a linearized single-track vehicle model, is proposed. The control strategy draws from previous studies on vehicle lateral dynamics control where the control input was the steering angle [93,94,95]. The controller comprises a feedforward part proportional to the steering angle ($\delta$) and a feedback part proportional to the yaw rate ($\dot{\psi }$), as schematized in Figure 4. The feedback gain $k_{\psi }$ is designed to obtain a damping ratio that is independent of vehicle speed, while the feedforward gain $k_{\delta }$ is designed to achieve a null steady-state value of the vehicle sideslip angle. The desired yaw moment ($M_z$) is then actuated by defining individual motor torques ($T_{m,i}$) through a low-level controller, also accounting for the total driving torque ($T_{TOT}$) required by the driver.

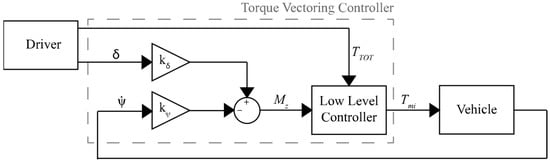
Figure 4. TV control scheme of Chong et al. [56].

To consider yaw moment limitations due to wheel slip that may be induced by excessive wheel torque, a control strategy with two components is proposed in [34]. The first controller is a wheel slip controller acting separately on each tire to maximize the produced force by limiting the applied torque and, consequently, the wheel slip. The second controller is a stability controller that generates a yaw moment proportional to the difference between the actual yaw acceleration and its desired value, inferred from the driver commanded steer angle rate. The torque distribution to each wheel is then performed according to the torque limit factors set by the traction controller. Similar contributions that incorporate an anti-skid controller into the torque vectoring logic can be found in [20,36,37,96].

To further adapt the controller to system non linearities and time-variant parameters, the authors of [36] present a control strategy consisting in an inner-loop Anti-Skid Contribution (ASC) together with an outer-loop direct yaw moment contribution. The scheme of this controller is depicted in Figure 5. The advantage of the proposed controllers is that they are based on disturbance observers, eliminating the need for parameters such as vehicle velocity, sideslip angle or tire cornering stiffness, which can be challenging to measure or observe. The Direct Yaw Control (DYC) part of the control law generates a yaw moment ($M_{z,PI}$) based on a Proportional–Integral (PI) controller that tracks a yaw rate reference value (${\dot{\psi }}_r$) dependent upon the steering input. Subsequently, the disturbance observer corrects the yaw moment by the PI controller to compensate for disturbances, defining the yaw moment ($M_z$) to be applied to the vehicle.

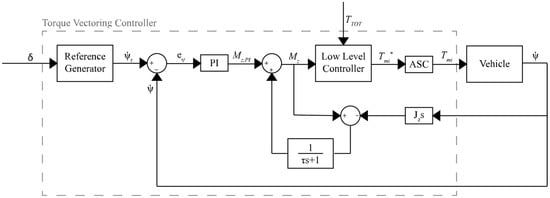
Figure 5. TV control scheme of Fujimoto et al. [36].

Since PID is a feedback control, many authors have suggested adding a feedforward contribution to allow a quicker system response. Indeed, while the feedback aims to guarantee robust stability and disturbance rejection, the feedforward contribution allows a faster system response [25,28,29,43,45,46,97]. For instance, the authors in [45] propose a control logic for vehicle lateral dynamics consisting of a feedforward and a feedback contribution, as depicted in Figure 6. The feedforward part is based on a multi-dimensional map containing the optimal yaw moment ($M_{z,FF}$) required for the desired vehicle cornering response, also named as driving mode. The feedback contribution ($M_{z,FB}$), on the other hand, is based on a gain-scheduled PID controller tracking the yaw rate reference value specific to the selected driving mode, with an anti-windup contribution for the management of integral term saturation. The feedback gains are scheduled as a function of vehicle speed using a Particle Swarm Optimization (PSO) algorithm. An extension of the work is presented in [46], where a dynamic feedforward contribution is added together with the Active Vibration Controller (AVC) from [98] and the sideslip controller from [43]. This combination, used together with the suboptimal Second Order Sliding Mode (SOSM), defines the yaw rate and sideslip angle integrated controller. The purpose of the dynamic feedforward contribution is to modify the vehicle’s dynamic response without altering the steady-state gain in the static feedforward contribution. The design of this dynamic feedforward contribution is fulfilled through a transfer function that depends on front and rear axle cornering stiffness as well as on vehicle speed. For ease of implementation and to ensure stability, the scheduling is performed only on vehicle speed since cornering stiffness estimation can suffer from stability problems.

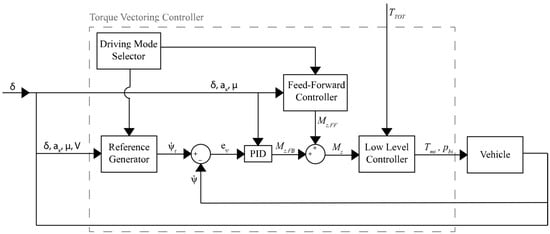
Figure 6. TV control scheme of De Novellis et al. [45].

When the tire–road friction is correctly estimated, a torque vectoring control acting on yaw rate error is sufficient to ensure vehicle stability. However, in the event of a drop in friction, there is the risk of tailspin. This risk can be mitigated by also controlling the vehicle sideslip angle together with the yaw rate [99]. Given that torque vectoring is a single actuation means with the need to fulfill two objectives (yaw rate and sideslip angle control), it is necessary to properly combine the two references into one single input to the system. This is fundamental since it can happen that the two targets conflict with each other. The authors in [54,55] proposed a Single-Input Single-Output (SISO) control strategy for vehicle lateral dynamics that aims to control both the yaw rate and vehicle sideslip angle. The approach is based on a yaw rate reference generator composed of two subsystems, as schematized in Figure 7. The first subsystem is the handling yaw rate generator that defines the vehicle cornering response (${\dot{\psi }}_h$) as a function of steering wheel angle and vehicle speed. The second subsystem applies a correction to the output of the first one based on the actual values of sideslip angle and yaw rate. Then, the error ($e_{\psi }$) between the reference-corrected yaw rate (${\dot{\psi }}_r$) and the actual yaw rate ($\dot{\psi }$) becomes the input of a PI controller to generate the desired yaw moment ($M_z$), which is then obtained by means of an even torque distribution strategy between front and rear wheels on the same vehicle side. The simulation results show that this approach can extend the stable region of vehicle operation. An alternative solution is proposed in [74,90], where a control strategy simultaneously controls vehicle sideslip angle and yaw rate by combining rear axle torque vectoring with Rear Wheel Steering (RWS). The definition of the yaw moment and of the rear wheels’ steering angle is performed by using four PI controllers in parallel, each one considering one actuator and tracking a single reference. The two results for the same actuator are then condensed in the control action through weighting coefficients. When control actions commanded by the yaw rate and the sideslip angle error are opposite, an anti-windup procedure is used to reset the integral parts of the controllers to avoid a slow response. Moreover, when a certain threshold of vehicle sideslip angle is exceeded, the yaw rate control is deactivated to ensure vehicle stability, accepting a slight degradation in performances. Using state portraits, the effects of the two controllers on modifying lateral dynamics are studied, and a performance index is assigned to them, acting as the weight for control actions. Performance index maps are generated offline for different combinations of front steering angle and vehicle speed values, but only for a small portion of the phase portrait about the equilibrium point.

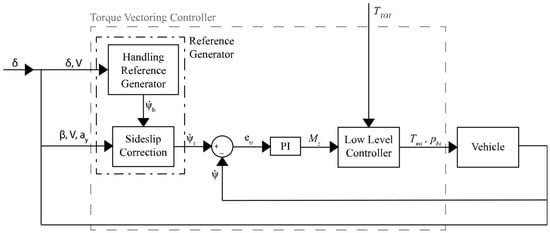
Figure 7. TV control scheme of Lenzo et al. [54,55].

Torque vectoring is widely regarded as an effective tool in improving vehicle dynamics, prompting the design of controllers that also address uncommon road-driving situations. In [100], a controller assisting the driver during drift maneuvers is proposed by imposing an appropriate yaw moment through torque vectoring at the rear axle, according to the scheme of Figure 8. To define a suitable control strategy, the effects of steering angle, gas pedal and torque vectoring on vehicle lateral dynamics were studied. The steering wheel angle has a strong influence in all driving conditions, with the gas pedal having comparable effects only in drifting conditions, and torque vectoring being able to control the yaw rate in any condition. This analysis explains why, instead of modifying driver inputs like steering angle and gas pedal, it is better to assist him by using torque vectoring. The yaw moment generated by the controller is proportional to the yaw index (YI) as in [48], and it is activated only when the drift condition is detected, meaning a precise series of inputs coming from the driver related to the actual vehicle yaw rate. Trying to minimize the value of the yaw index, as done here, means trying to maintain the vehicle close to steady-state cornering, or equivalently, to prevent excessive increases in lateral velocity. In fact, the yaw index ($I_y$) is defined as follows:

$$I_y=\frac{a_y}{V}-\dot{\psi }$$

(8)

where $a_y$ is the vehicle lateral acceleration, $V$ is the vehicle forward speed and $\dot{\psi }$ is the yaw rate. The developed control strategy relies only on measured quantities, making it robust and not requiring any kind of estimator.

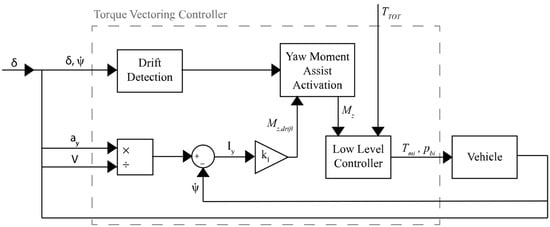
Figure 8. TV control scheme of Vignati et al. [100].

Other contributions, similar to the ones presented above, are reported in Table 1, where the most innovative aspects of each paper at the time of writing are highlighted.

Table 1. Proportional–Integral–Derivative torque vectoring controllers.

Authors	Controller	Method
Sakai et al. [33]	PI	The yaw moment is defined based on yaw rate error with the aim of making the vehicle follow a yaw rate reference, while no consideration about vehicle sideslip angle is made. Nevertheless, the focus of the paper is on torque distribution since, for a four-wheel drive vehicle, the two equations provided by the high-level controller are not sufficient to determine the torque to allocate to each wheel.
Nishio et al. [27]	P	The same approach adopted in [56] is proposed with an extension regarding vehicle sideslip angle estimation that accounts for tire–road friction, road bank and vehicle spinout judgements.
Wheals et al. [20]	PI	A combined control strategy composed of a traction controller and a yaw rate controller is proposed. The latter is a PI controller that generates a yaw moment based on the difference between the actual yaw rate and its desired value, with the gains scheduled according to vehicle speed.
Fujimoto et al. [37]	PI	The control strategy proposed in [36] is extended in the disturbance observer part. In particular, tire cornering stiffness is estimated through a recursive least squares algorithm and is assumed to be equal for the front and rear axles. This estimated quantity is then used in the disturbance compensator, resulting in an adaptive DYC that outperforms the previous version.
Osborn et al. [101]	PI	A Multiple-Input Multiple-Output (MIMO) control for vehicle lateral dynamics is proposed based on the results of a sensitivity analysis conducted using a simplified non-linear double-track vehicle model. With the target of using only control parameters directly measurable on a vehicle, yaw rate and lateral acceleration are the selected control variables. From the Box–Behnken matrix of experiments, it turns out that yaw rate is most influenced by front-to-rear torque distribution, while lateral acceleration is affected almost equally by front-to-rear and left-to-right torque distributions. Because of this, a dual PI controller is proposed using a neutral steering vehicle in steady-state cornering conditions as reference. The front-to-rear torque distribution is regulated with yaw rate error feedback, while the left-to-right torque distribution is governed by the lateral acceleration error feedback. A satisfactory tuning of the dual PI feedback gains is achieved through an iterative search approach.
Kakalis et al. [28]	PID	The proposed control logic consists of a feedforward and a feedback part. The feedforward component aims to guarantee a quick response and is based on 3D maps whose point values correspond to the maximum oversteering moment tolerable by the vehicle for various adherence levels. The feedback component, instead, aims to guarantee stability and disturbance rejection properties and is based on a PID controller on yaw rate error.
Cheli et al. [25]	PID	A similar approach to that presented in [28] is proposed, except for rear tire slips, which is controlled in feedback, attempting to maximize the longitudinal force at the axle using a PI controller. The main focus of the article is on torque distribution, attempting to keep the torque on the rear axle at a level saturating the tires, with the remaining required amount sent to the front axle through the actuation of a center clutch. Based on vehicle sideslip angle and angular velocity estimation, an oversteer management algorithm is developed, for which, if those two quantities are above a prescribed value, the torque transmitted to the front axle is prevented from decreasing to ensure vehicle stability and not worsen its dynamic properties at the handling limits.
Sabbioni et al. [29]	PID	The Brake Torque Vectoring (BTV) control strategy proposed in [28] is improved by adding the friction estimation through instrumented tires. According to the authors, the improvement in the results achievable by knowing tire friction and tire vertical load is due to the possibility of using a less conservative tuning of control system parameters.
Ando et al. [96]	PI	The control logic in [37] is retrieved, and active front steering is added as an actuation system, proposing a distribution algorithm that tries to equalize tire workloads.
Pinto et al. [39]	PID	A PID controller is proposed to generate a yaw moment on the vehicle based on the error between reference and actual yaw rate. The control intervention is then limited in case of excessive vehicle sideslip angle or angular velocity, with the threshold levels that are updated according to vehicle speed and tire–road friction coefficient. The vehicle sideslip angle is estimated by means of a combination of an observer based on a double-track vehicle model and direct integration when non-stationary conditions are detected.
Braghin et al. [102]	PI	A control system aiming to dampen out yaw rate and sideslip angle oscillations, especially during transients, is proposed. A PI controller is designed to minimize the vehicle sideslip angle rate, estimated by measuring yaw rate and longitudinal and lateral accelerations, while estimating the vehicle speed. The desired yaw moment is then achieved by having an even and opposite longitudinal force distribution on a given axle, with the distribution among axles obtained using a PI controller on the absolute value of the sideslip angular velocity. To prevent wheel spin and lockup, as well as in case of motor saturation, alternative control strategies are implemented for the distribution of driving/braking torques.
Sill et al. [103]	PID	The desired yaw moment to be applied to the vehicle is obtained by means of a PID controller acting on the error between actual and desired yaw rate. The required torque to generate the yaw moment is then distributed across the axle with more lateral force capability, according to axle saturation definition. The saturation balancing control aims to obtain the same saturation on the front and rear axles to approach a neutral steer behavior, and this is achieved through a PI control on axle saturation factors’ difference to manage front-to-rear torque bias. The proposed method enabled stabilization of a nominally over-steering vehicle while retaining yaw responsiveness. Simulation results reveal the benefits of each component of the control scheme: the stable completion of the extreme avoidance maneuver thanks to the saturation balancing control, as well as an improved response due to direct yaw-moment control.
Sill et al. [104]	PID	The yaw moment to be applied to the vehicle is computed by applying a PID controller on front-to-rear axle saturation difference. This approach does not need the definition of a reference model for the desired response, but the saturation balancing approach internalizes the computation of an equivalent desired yaw rate, which also has the advantage of automatically adapting to the available tire–road friction without the need for direct estimation.
Braghin et al. [85]	P	The presented control strategy is composed of a steady-state contribution to enhance vehicle-handling performance and a transient contribution to ensure stability in limit maneuvers. The steady-state part of the controller generates a yaw moment by using a P control on the error between actual and reference steering angle by scheduling the gain as function of vehicle speed and including an activation coefficient based on fuzzy rules. The transient control strategy, instead, is an LQR controller like that proposed in [48].
Sabbioni et al. [105]	P + P	The control strategy in [85] is retrieved and modified by substituting the transient part of the controller with the P control on the yaw index from [48].
De Novellis et al. [43]	PID	Different vehicle lateral dynamics controllers are proposed for the generation of a corrective yaw moment. The proposed control strategies to determine the control action are a PID, an adaptive PID, a suboptimal Second Order Sliding Mode (SOSM), and a twisting SOSM, all based on the error between the actual yaw rate and its reference value, which is also used to determine the PID adaptive gains. In the case of PID controllers, a single-track vehicle model is used to analyze the yaw rate frequency response characteristics, and it is concluded that no gain scheduling is necessary for compensating the yaw rate response for varying longitudinal and lateral acceleration, while gain scheduling is required for different vehicle speeds. Both the PID and the adaptive PID feedback controllers are used in combination with a feedforward controller that is based on multi-dimensional maps containing the results of an optimization routine to derive the appropriate yaw moment that yields the desired understeer characteristic.
Moseberg et al. [106]	P + PD	A cascaded control structure for the horizontal motion of a vehicle with single-wheel actuators is presented. A feedforward controller generates a reference trajectory for vehicle in-plane motion together with the necessary forces and yaw moment to obtain it. Then, the outer horizontal dynamics controller realizes the desired vehicle motion despite external disturbances, being a P controller on longitudinal and lateral acceleration errors for longitudinal and lateral forces, respectively, while a PD controller on yaw rate error for the yaw moment. In the end, the inner single-wheel controller stabilizes the rotational speeds of the wheels despite unknown tire–road friction conditions.
Park et al. [97]	P	A control strategy for torque vectoring of a Front-Wheel-Drive (FWD) vehicle is proposed and comprises two control modes. One is named the agile mode and aims to improve vehicle controllability, while the other is named the safe mode and aims to improve vehicle stability. A supervisory controller oversees the selection of the appropriate control mode by comparing the actual vehicle yaw rate with its steady-state value for the maximum steering angle and its limit value, accounting for the available friction. The target yaw rate is composed of the usual steady-state linear function of the driver’s steering angle and a transient contribution computed using a transfer function approach like that in [46]. The desired yaw moment is obtained using a P control on yaw rate error against the reference value, which is computed using an appropriate understeering coefficient for the considered control mode.
Park et al. [107]	P	A vehicle lateral dynamics controller is proposed for a vehicle with IWMs at the front axle and an Electronic Limited Slip Differential (eLSD) at the rear axle. The controller features parallel yaw moment controllers for each of the actuators, with a supervisory controller that oversees the understeering gradient improvement selection and thus the reference for the two high-level controllers. The high-level controller for the front IWMs is a feedforward on vehicle lateral acceleration, where the control action is defined to achieve the desired improvement in vehicle understeer gradient based on the steady-state single-track model, whose front and rear axles’ cornering stiffnesses are mapped as function of lateral acceleration. The high-level controller for the rear eLSD is instead a P controller on the difference between the actual yaw rate and its reference value with the objective to prevent vehicle oversteer.

2.2.2. Optimal Controllers

Optimal controllers are model-based controllers. Therefore, in contrast to PID regulators, they require a vehicle model and often an estimation of vehicle states for proper operation. The effectiveness of these controllers strongly depends on vehicle model reliability and on the capability to estimate model parameters, such as the tire–road friction coefficient. Moreover, obtaining the controller optimality conditions demands a thorough and precise knowledge of the system. Indeed, disturbances together with the variance in parameters can significantly impact both the performance and stability of the controller. Various techniques have been proposed in the literature to achieve optimal solutions, with the most common being LQR, LQG, LPV and numerical optimization tools. Linear Quadratic Regulators (LQRs) are optimal controllers aiming at the minimization of a quadratic cost function, which usually includes terms for vehicle state deviation from the reference and terms for actuation effort in torque vectoring applications. The typical plant model for these applications is either linear or linearized and expressed in state–space formulation. Letting ${\underset{\_}{x}}_d$ represent the desired state vector, $\underset{\_}{x}$ the actual state vector and $\underset{\_}{u}$ the control input vector, the quadratic cost function ($J$) is defined as:

$$J=\frac{1}{2}{\int }_0^{\infty }\left[{\left({\underset{\_}{x}}_d-\underset{\_}{x}\right)}^T\left[Q\right]\left({\underset{\_}{x}}_d-\underset{\_}{x}\right)+{\underset{\_}{u}}^T\left[R\right]\underset{\_}{u}\right]$$

(9)

where $\left[Q\right]$ is a symmetric and positive semi-definite matrix that weights state deviation in the cost definition and $\left[R\right]$ is a symmetric and positive definite matrix that weights the actuation effort. The gains for this controller type are derived for a linear system by solving the corresponding Riccati equation. Nevertheless, LQRs are highly sensitive to both modelling errors and disturbances, leading to the introduction of a Linear Quadratic Gaussian (LQG) controller, which models uncertainties as Gaussian noise. A limitation of both techniques is their reliance on linear models despite vehicles’ strong non-linear dynamics, which oblige the control designer to adopt a linearized vehicle model. Linearization can be alternatively performed only once at the beginning of the control process or cyclically at each iteration step. The latter approach requires a great computational effort but offers improved performance since the linearized model better represents the actual vehicle dynamics. Another tool ensuring controller stability even in the case of changes in vehicle parameters is the Linear Parameter Varying (LPV) modelling, which allows the synthesis of the optimal controller considering confidence ranges for key vehicle parameters.

All described optimal controller types adhere to a uniform scheme, as illustrated in Figure 9, where the only difference lies in the optimization algorithm. Additionally, the objective functions may vary, commonly focusing on:

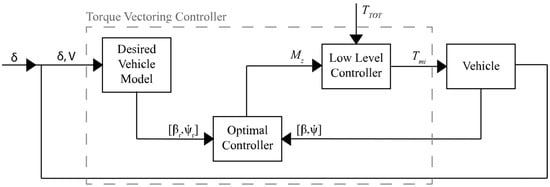
Figure 9. Typical optimal TV control scheme.

• state reference tracking, where the controller aims to follow a reference for yaw rate (${\dot{\psi }}_r$) and/or sideslip angle (${\beta }_r$);
• energy consumption minimization, which may or may not involve following a reference in yaw rate and/or sideslip angle, sometimes also considering the low-level distribution of torques in the optimization routine.

Significant contributions to the field of torque vectoring optimal control are summarized in Table 2, highlighting the unique aspects of each study.

Table 2. Optimal torque vectoring controllers.

Authors	Controller	Method
Sakai et al. [108]	LQR	A Robustified Model-Matching Controller (R-MMC) based on a linearized single-track vehicle model is proposed. The robustified approach aims to suppress the steady-state error inherent to classic MMC by augmenting the state with the control input’s time derivative and subsequently determining the optimal feedback gains via LQR theory. Vehicles equipped with the proposed controller have demonstrated proficiency in rejecting wind gust disturbances and safely managing acceleration and deceleration on μ-split road surfaces.
Sakai et al. [109]	LQR	The instability encountered on low friction surfaces, as discussed in [108], is addressed through the adoption of a skid-detection method. This enables the implementation of a traction control system for each driving wheel, preventing tires’ saturation and ensuring vehicle stability by limiting the maximum torque deliverable to each wheel.
Esmailzadeh et al. [35]	LQR	An optimal control law for yaw moment based on a linearized single-track vehicle model is proposed. This control law incorporates a feedforward component on the steering angle and a feedback component on both yaw rate and lateral velocity. The determination of feedforward and feedback gains is achieved through the analytical solution of an LQR problem, where the performance index accounts for both yaw rate error and control effort. Additionally, a semi-optimal control law is defined excluding the feedback branch on the lateral velocity for more feasible real-vehicle implementation. Comparative simulations between the optimal and semi-optimal control laws highlight the latter’s suitability, particularly given its simpler implementation. However, the primary limitation of the proposed approach lies in its applicability solely in the linear region of vehicle dynamics.
Hancock et al. [21]	LQR	A control algorithm based on double feedback is proposed, with the primary feedback aiming at minimizing deviations from desired vehicle states and the secondary feedback focused on reducing the errors between the vehicle and a reference linear model. The primary feedback relies on a single-track linear vehicle model, employing a quadratic cost function to achieve neutral steer characteristics while considering the requested yaw moment suitability with respect to the maximum attainable without tires’ saturation. The secondary feedback relies on an updated linearization of the non-linear vehicle model since its purpose is to compensate for errors caused by the non-linearities that are not considered in the primary feedback. This is achieved through another cost function aimed at minimizing the yaw rate error while also considering the margin between the requested yaw moment and the one attainable at tires’ saturation.
Geng et al. [110]	LQR	A control law based on a linearized single-track vehicle model is presented, which relies on feedback on measured yaw rate and estimated vehicle sideslip angle. This estimation is performed using a non-linear observer, which is linearized at each operating point to reconduct to the theory of linear observers. Gains are determined using the LQR theory with a quadratic cost function accounting for an actuation effort contribution and prioritizing errors on yaw rate and sideslip angle, adjusting their importance based on system state. The proposed weighting coefficient gives high importance to the yaw rate error for low values of sideslip angle, while, at high sideslip angle values or on low friction surfaces, it is the sideslip angle error assuming high importance.
Xiong et al. [111]	LQR	A control logic comprising feedforward and feedback contributions is proposed. The feedforward compensator generates a yaw moment to obtain a null steady-state vehicle sideslip angle during cornering. Instead, the feedback contribution, designed according to LQR theory, aims to minimize deviations in actual yaw rate and vehicle sideslip angle from their reference values.
Geng et al. [112]	LQR	The work extends the findings in [110] for vehicle sideslip angle estimation, which is performed employing two local observers based on Kalman filter approach, which run in parallel and are then combined into a single observer by means of fuzzy rules. The two proposed local observers rely on two local linear tire models, consisting in a small-slip region linearization and a large-slip region linearization, respectively.
Baslamisli et al. [113]	LPV	An optimal control law leveraging a double-track vehicle model is proposed. To account for model uncertainties, the vehicle in-plane dynamics are expressed in the Linear Parameter-Varying (LPV) form with also a methodology for predicting parameter bounds. The objective of the proposed controller is to minimize the error between the desired and actual values of yaw rate and vehicle sideslip angle. The controller’s design process results in a set of Linear Matrix Inequalities (LMIs), allowing the definition of a convex optimization problem. Simulation results have proven the logic to be robust against speed and road conditions variations.
Kaiser et al. [114]	LQG	The proposed control law adopts a flatness-based feedforward component to enhance transient dynamics, while an optimal feedback component addresses lateral dynamics errors stemming from model uncertainties and parameters variations. The feedback controller, based on LQG control theory, aims at yaw rate and vehicle sideslip angle errors minimization.
Liu et al. [115]	LPV	A self-scheduled LPV control is proposed to address the torque vectoring problem. Utilizing an LPV single-track vehicle model, the gain scheduling for the controller reduces to the solution of a system of LMIs, aiming for reference yaw rate tracking. The controller integrates a feedforward component for reference tracking and a feedback component to mitigate disturbances and model uncertainties effects. Both controllers are synthesized in a unified optimization process, complemented by an anti-windup scheme for actuator limit management. The proposed LPV controller demonstrates superior performance over another strategy [114], which combines a flat feedforward with an LQG feedback.
Cheli et al. [48,78]	LQR	A couple of control strategies are proposed, and their results compared. The first employs optimal control theory, whereas the second relies on an index correlated with the vehicle’s oversteer/understeer dynamics. The optimal control law is based on LQR control theory and leverages a linear single-track vehicle model to define the yaw moment. This is achieved by minimizing a quadratic cost function including both the state deviation from the reference and the actuation effort. In contrast, the control law based on the so-called Yaw Index (YI) is a proportional regulator aiming to maintain the index close to the unit value. This approach seeks to preserve near-steady-state cornering conditions, thereby preventing excessive vehicle sideslip angles. The YI control holds an advantage over LQR as it does not require a precise estimation of the friction coefficient, which is necessary in the LQR to avoid excessive tire slip. Moreover, no sideslip angle estimation is required for the YI control. Front-to-rear yaw moment distribution is based on a coefficient that varies with both vehicle speed and steering angle.
Lu et al. [47]	H∞	An H∞ control strategy is proposed for vehicle lateral dynamics based on the error between actual and reference yaw rate values, with the latter determined from a multi-dimensional table. The H∞ controller consists of a pre-filter for yaw rate reference smoothing, a PI controller acting as a pre-compensator for yaw rate error, a constant gain ensuring unit steady-state gain between reference and actual yaw rate and an H∞ compensator designed from solving two algebraic Riccati equations. The H∞ method enhances the robustness of the PI compensator, enabling the calculation of stability margins, which results in negligible penalties for the omission of gain scheduling as a function of the axles’ cornering stiffness. Simulations demonstrate the H∞ controller’s superior tracking performances compared to PI and PI+FF controllers.
Lu et al. [53]	H∞	An approach integrating sideslip angle control into a continuously active yaw rate controller is proposed, aiming to enhance vehicle cornering stability by tolerating higher vehicle sideslip angle values. Two control strategies are compared. The first is that in [46], which employs two parallel control strategies for yaw rate and vehicle sideslip angle, with the resulting yaw moment being a weighted sum of the two. The second, instead, is the extension of the H∞ controller in [47] for Multiple-Input Single-Output (MISO) multivariable robust design. Additionally, two activation policies for the sideslip angle controller are proposed, including a fixed threshold, as in [46], and a variable threshold scheme based on stability boundaries in the phase plane investigating the sideslip angle relationship with its time-derivative. To resolve conflicts between sideslip and yaw rate control, it is proposed to adjust the reference yaw rate by an amount equivalent to the reduction caused by the sideslip contribution.
Vignati et al. [7,52]	LQR	A control law combining an optimal controller with a control logic relying on an index obtained from measured quantities and being related to vehicle understeer/oversteer is proposed. During transients, characterized by a high Yaw Index (YI), the control action is dominated by the YI controller, while at steady-state, the optimal controller, whose parameters are updated during transients, is predominant. The steady-state optimal control strategy employs the LQR theory and uses a single-track vehicle model, linearized at each evaluation step, to minimize sideslip angle and yaw rate deviations from their reference while also limiting the control action. The transient control strategy revises the YI-based approach proposed in [48], incorporating high-pass filtering of the lateral acceleration to remove an eventual bank angle effect. The longitudinal force distribution across axles considers the front/rear vertical forces ratio and the yaw index to allocate more longitudinal force to the axle that would less influence stability for a decrease in lateral force. The study is further extended in [5], exploring the impact of two different weight distributions between front and rear axles.
De Filippis et al. [51]	Fuzzy (Rule-Based)	An analytical solution is derived for defining the yaw moment leading to the minimization of drivetrain power losses, assuming that they strictly monotonically increase with wheel torque demand. The results of the analytical procedure are a yaw moment and the rules for torque distribution across active motors. This typically provides multiple solutions that can be narrowed down by considering longitudinal and lateral tire slips in the cost function. However, since tire slip power losses are generally less significant than drivetrain power losses under most driving conditions, a sub-optimal control law is proposed minimizing drivetrain power losses only and then selecting the best solution in terms of tire slip power losses among the redundant options.
Beal et al. [116]	Maps	The conventional 2D phase-plane analysis is extended to a 3D state portrait for vehicle lateral dynamics control, incorporating vehicle sideslip angle, yaw rate and longitudinal velocity. The proposed control law comprises a look-ahead path-following function determining the target cornering radius to keep the vehicle on the roadway. This results in the definition of a planar surface in the state space that is representative of the roadway geometric constraints, on which vehicle states must move while also respecting the limits given by yaw stability surfaces. Lateral dynamics control is performed using an optimal mapping of control inputs to track the sliding surface, which is obtained by adding sideslip angle and longitudinal velocity errors to the planar surface defined through the path-following function.
Wang et al. [60]	RLQR	A Robust Linear Quadratic Regulator (RLQR) is proposed for guaranteeing proper control performance even in the case of unmodelled dynamics and parameter uncertainties by adding an extra term to the feedback contribution of a usual LQR. This adjustment limits the closed-loop tracking error and enhances its robustness. In addition, control gains are scheduled to optimally vary with velocity, adapting to inherent changes in the vehicle model with velocity. The superior robustness of the proposed RLQR over a traditional LQR is demonstrated analytically, with further validation through numerical and experimental tests.
Sun et al. [117]	Maps	An energy efficient yaw moment control strategy for quasi-steady-state cornering is proposed, using motor efficiency maps based solely on the requested torque over a narrow speed range. The minimization of power losses is ensured using a double level controller. The first level deals with the optimization of the torque distribution for each yaw moment, while the second deals with the optimization of the yaw moment. Offline rules for torque distribution are defined based on yaw moment intervals, with the optimal yaw moment in the possible range determined using the Golden Section Search method to minimize the total power consumption. The proposed controller results in terms of energy efficiency are benchmarked against a stability DYC controller based on SMC, highlighting its effectiveness.
Mangia et al. [49]	LQR	A control framework is proposed, allowing the driver to select between handling and energy-efficient driving modes. The handling mode adapts the control logic in [52] by adding the distribution of torques according to the principle of speed-scheduled switching torque defined in [50]. The energy efficiency mode, instead, is obtained by an extension of the study in [51]. Simulation results indicate that, even without the imposition of a specific understeer characteristic in the energy efficient mode, the maximum lateral acceleration can be increased.
Morera-Torres et al. [118]	H∞ and LPV	An H∞ and an LPV controller are proposed based on a single-track vehicle model, incorporating tire non-linearities through cornering stiffness parametrization on vehicle sideslip angle based on experimental data. Both controllers aim to track a yaw rate reference, with the H∞ controller designed based on a single-track model linearized around a prescribed operating point and the LPV controller designed based on a non-linear single-track model, where some of the non-linear terms have been considered as disturbances. This approach allows for a reduction in the optimization problem complexity but yields satisfactory results when setting appropriate control effort weighting. The torque distribution is performed through an optimization problem to meet both driver and high-level controller demands. From simulation results, the LPV controller exhibits a better yaw rate tracking ability with also a lower control effort with respect to the H∞ controller.
Liang et al. [119]	H∞ + Fuzzy	An H∞ controller is proposed to enhance vehicle-handling characteristics through four independently driven IWMs, employing Takagi–Sugeno fuzzy modelling to address vehicle non-linearities. Indeed, this modelling approach allows representing the non-linear model as the combination of a set of linear models, facilitating the design of a multi-objective H∞ controller that prioritizes reference yaw rate tracking or minimizes vehicle sideslip angles based on proximity to the vehicle stability limit. This limit is defined based on the tires’ slip angles phase plane, which allows identification of tires’ saturation. Hardware-In-the-Loop (HIL) simulations show that the proposed controller outperforms a MPC controller while showing lower power consumption by properly privileging the handling or the stability objective.

2.2.3. Sliding Mode Controllers

Sliding Mode Control (SMC) is a discontinuous control technique that translates control objectives for a given plant into state constraints, typically forming a sliding surface for system state evolution. Usually, the sliding surface is defined with the objective of following the reference states for the system, and upon reaching this surface, the system state evolves by “sliding” over it. This type of controller is considered robust against modelling uncertainties but has the drawback of being continuously active when applied to vehicles for torque vectoring control. The output of the control strategy in its classical formulation can assume only a null or an arbitrary high value, meaning the control is a switching control that most of the times causes actuator saturation, which is then responsible for the typical chattering behavior. This issue is traditionally mitigated by low-pass filtering the control action or by performing the SMC at an integral or at a second-order level to produce a continuous control action.

Even in the case of sliding mode control, variations in vehicle parameters can impact the control strategy performance. In this light, the authors of [120] presented a Variable Torque Distribution (VTD) Direct Yaw Control (DYC) strategy that uses rear axle torque vectoring while adjusting front-to-rear axle torque distribution for extending the linear vehicle response region. The yaw moment to track the neutral steering response of the linearized single-track reference vehicle model is obtained using a sliding mode control due to its robustness against the controlled plant’s non-linearities. For an increased robustness, the controller gains have been tuned according to the operational range for vehicle parameters, which are obtained through an uncertainty analysis. Challenges such as motor torque limitation and tire saturation are addressed in the controller design, with the tire control force limited according to the friction ellipse concept to reduce tire saturation occurrences.

In view of avoiding discontinuous control, the Second Order Sliding Mode (SOSM) is applied, defining the control action’s first time derivative with a switching function. A contribution in this field comes from [121], where a torque vectoring control strategy for a vehicle equipped with a Rear Active Differential (RAD) is proposed. The controller combines feedforward and feedback contributions designed based on a single-track vehicle model according to the scheme in Figure 10. The feedforward contribution improves the transient response, while the feedback contribution ensures robust stability. In particular, the aim of this paper is to compare two different techniques for the robust feedback control, which are Internal Model Control (IMC) and second order sliding mode. The feedforward controller determines the control yaw moment through a linear filter built to match the desired open-loop yaw rate behavior of the vehicle. The IMC feedback controller is designed based on an H_∞ approach to guarantee robustness in presence of model uncertainties and adding an anti-windup part to account for actuator saturation. The SOSM feedback controller, instead, is designed using the yaw rate error as sliding variable ($S$), with the first-time derivative of the yaw moment (${\dot{M}}_z$) that is defined using the typical sliding mode switching function. This guarantees that a continuous control action ($M_z$) can be achieved, by moving the discontinuity to its first time derivative, while retaining the same robustness against uncertainties that are typical of first order sliding mode control. The desired yaw moment is then generated by setting the RAD locking torque ($T_{diff}$).

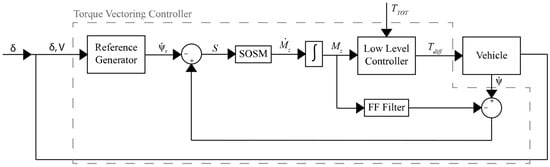
Figure 10. TV control scheme by Canale et al. [121].

When controlling multiple states, decoupling them and employing parallel control logics allows the definition of several control actions, also presenting the possibility of dealing with multiple actuators. This type of approach is schematized in Figure 11 according to the controller developed in [89], where a control strategy is proposed to jointly determine the control actions to be allocated to Active Rear Steering (ARS) and direct yaw moment control, avoiding any implicit allocation algorithm. A Multiple-Input Multiple-Output (MIMO) sliding mode controller, based on a linear single-track vehicle model, is designed for simultaneously tracking vehicle sideslip angle and yaw rate references. The proposed MIMO sliding mode controller adopts separate switching functions for each state, considering the coupled yaw and lateral dynamics. Moreover, the controller replaces the sign function from the classical sliding mode theory with a saturation function to smoothen out the control action.

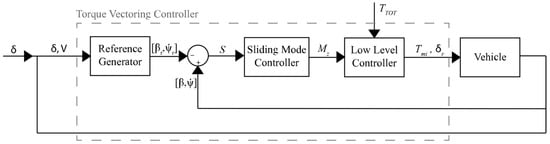
Figure 11. TV control scheme by Fu et al. [89].

Table 3 presents additional findings on torque vectoring sliding mode control, outlining the peculiarities and order of the SMC method used in each study.

Table 3. Sliding mode torque vectoring controllers.

Authors	Order	Method
Drakunov et al. [122]	1	A Sliding Mode Control (SMC) strategy, actuated through independent wheel brakes, is proposed. In this controller, the front-to-rear braking torque distribution is fixed, while the right-to-left distribution is the control variable. The right-to-left torque distribution is determined via SMC utilizing a switching function based on the difference between actual and desired yaw moment and its integral. By appropriately defining the desired yaw moment as a function of yaw rate error and first-time derivative of desired yaw rate, the convergence of yaw moment error leads to the actual yaw rate converging to the desired value.
Zhang et al. [123]	1	A sliding mode control is proposed to track the vehicle desired yaw rate using differential braking. In this contribution, the controlled variable is the error between the actual vehicle yaw rate and its desired value. The paper defines a proportional switching law with a gain depending on yaw rate error and its first time derivative, with the switching function also obtained from the composition of yaw rate error and its first time derivative.
Zhang et al. [124]	1	A fuzzy sliding mode controller is proposed for the control of vehicle lateral dynamics through torque vectoring. The sliding surface is defined as the weighted sum of the errors between actual and desired values of vehicle sideslip angle and yaw rate. The yaw moment is then constituted by two contributions, the first being the yaw moment required to move on the sliding surface and the second being the additional yaw moment necessary to fulfill the reaching condition, defined through a switching function. The switching gain is adaptively tuned to account for state deviation from the sliding surface by using a fuzzy logic to reduce chattering.
De Novellis et al. [43]	2	Different vehicle lateral dynamics controllers are proposed for the generation of a corrective yaw moment. These include a PID, an adaptive PID, a suboptimal Second Order Sliding Mode (SOSM) and a twisting SOSM, all based on the error between the actual yaw rate and its reference value. As additional option, the suboptimal SOSM is combined with a sideslip angle control based on a sliding mode algorithm to limit its maximum value. In general, a yaw rate controller allows the vehicle sideslip angle to remain within the stability limits, provided that the tire–road friction coefficient is accurately estimated, and a correct reference yaw rate is generated. Thus, the additional control on vehicle sideslip angle turns out to be extremely useful in limit conditions where the available friction coefficient is not properly estimated. The SOSM, both in the suboptimal and in the twisting implementation, considers the application of the SMC law to the first time derivative of the yaw moment to avoid discontinuities. For the integrated yaw rate and sideslip angle controller, the SMC control law on the vehicle sideslip angle is instead applied to the yaw moment and it is used as an alternative to the control on yaw rate when overcoming a prescribed sideslip angle value. The transition between the two different yaw moment controllers is performed using an exponential law to smoothen the discontinuities when switching between the two control actions.
Goggia et al. [44]	−1 (Integral)	A torque vectoring control strategy for yaw rate control based on Integral Sliding Mode (ISM) is proposed. The yaw moment is generated based on the error between actual and desired yaw rate incorporating two contributions. The first is a PID controller for stabilizing the ideal system in the absence of uncertainties and external perturbations, while the second is an SMC dealing with uncertainties and thus guaranteeing robustness. The yaw moment obtained from the SMC is then low-pass filtered to reduce chattering.
Song et al. [84]	1	A sliding mode control strategy for enhancing the stability of four wheel independent-driven electric vehicles is proposed. The sliding surface combines yaw rate and sideslip angle errors, with the yaw moment defined by the sum of a switching function contribution and a contribution proportional to the sliding surface amplitude. To reduce chattering, the standard sign function is replaced by a steep saturation function.
Fu et al. [125]	1	A sliding mode controller with adaptive gains based on a linear single-track vehicle model is proposed. The switching function is defined as the error between the actual and reference yaw rate values. The control yaw moment is determined based on the sign of the switching function, considering a gain defined as the weighted sum of the front and rear axle slip angles. The weighting coefficients, constituting the adaptive part of the algorithm, are selected to be proportional to the absolute value of the switching function.
Saikia et al. [126]	2	A sliding mode vehicle lateral dynamics controller, combining Active Front Steering (AFS) and DYC, is proposed. The sliding surface is designed as the sum of a proportional and an integral contribution on the tracking error for both yaw rate and vehicle sideslip angle. The front steering angle and yaw moment are then obtained using a SOSM control law that is based on a reaching law comprising a proportional and a switching term.
Zhang et al. [127]	2	An Adaptive Second Order Sliding Mode (ASOSM) controller is proposed for tracking a weighted sum of yaw rate and sideslip angle references based on a single-track vehicle model. Unlike traditional approaches using the Lyapunov direct method, the authors adopted backstepping design techniques. Moreover, the switching gain is adaptively obtained without requiring the knowledge of the uncertain term bound, which is typically a key factor for usual SOSM controllers. Simulation results demonstrate the robustness of the proposed method together with its advantage over classic SOSM controllers of requiring lower control actions thanks to the adaptive switching gain.
Sun et al. [128]	1	A Non-singular Terminal Sliding Mode (NTSM) controller is proposed for controlling the vehicle lateral dynamics. Yaw rate and sideslip angle tracking are considered in parallel, with each separate yaw moment defined based on a sliding surface comprising the error function and an exponential evaluation of its first time derivative. This exponential reaching law allows for faster convergence of the controlled system towards the reference state. The two control actions for yaw rate and sideslip angle tracking are then merged into the actual control action through a weighted sum, where the weighting coefficient is obtained through a Particle Swarm Optimization (PSO) algorithm aiming to minimize vehicle lateral instability. Simulation results show the effectiveness of the proposed controller in tracking the reference state and in improving vehicle stability according to the phase-plane analysis.

2.2.4. Model Predictive Controllers

Model Predictive Control (MPC) is a widely employed control framework for the solution of non-linear constrained optimal control problems. Similarly to optimal control techniques presented before, the primary objective is to achieve a suitable balance between tracking ability and actuation effort. However, a distinctive feature lies in the fact that the optimization problem is addressed within a finite time horizon, as opposed to an infinite duration. This similarity with optimal controllers is also evident when examining their typical scheme illustrated in Figure 12. MPC relies on a dynamic model of the system and employs the receding horizon control principle to predict the future response. At each control cycle, a series of control actions to be applied for the predictive horizon is calculated, with only the first one actually applied to the system. The computation of the control input profile is iteratively updated at each control step, incorporating new information from sensors. Consequently, the computational burden of this technique is substantial when compared to classic control strategies. Hence, due to the rapid nature of vehicle dynamics, implementing real-time control techniques was not feasible some years ago. Nonetheless, advancements in microprocessor technology and innovative computation algorithms now render this feasible.

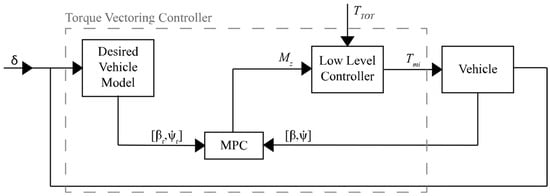
Figure 12. Typical model predictive control TV control scheme.

Significant contributions in the field of model predictive control for vehicle lateral dynamics are reported in Table 4, which provides detailed descriptions of controller designs and the associated vehicle models used for this purpose.

Table 4. Model predictive control torque vectoring controllers.

Authors	Controller	Method
Ghike et al. [86]	NLPC	The Non-Linear Predictive Control (NLPC) theory is used in combination with an 8 DOFs non-linear vehicle model to establish a wheel torque management strategy. This strategy combines drive–brake torque distribution and emergency individual brake application (ESP), considering physical limits for control variables in the logic designs. Traction and braking torque distribution are achieved using a front-rear distribution factor and then a right-left distribution factor for each axle, which are modified by the controller to track the reference neutral steer vehicle response. Through simulations, the controller performance is assessed, demonstrating its robustness against variations in tire–road friction coefficient. Notably, without any knowledge of the friction coefficient, the logic effectively prevents vehicle spin, while incorporating such knowledge results in smoother and quicker control actions.
Canale et al. [129]	NMPC	A Non-linear Model Predictive Control (NMPC) is designed to track a reference yaw rate with constraints on the maximum allowable vehicle sideslip angle. The control problem is solved relying on a single-track vehicle model with non-linear tires while imposing both state and control action constraints. At each sampling time, the control action is determined by minimizing a performance index, defined as a weighted sum of yaw rate error and control effort over the predictive horizon. However, due to its computational burden, the optimization problem cannot be solved in real time, so it is solved offline for specific conditions using typical maneuvers. The Fast Model Predictive Control (FMPC) then uses these data and the Nearest Point (NP) approach to approximate the optimal online solution, ensuring controller stability and performance.
Kwangseok et al. [130]	MPC	A yaw stability controller is proposed to track the desired vehicle yaw rate response, defined as the value assumed in quasi-steady-state maneuvers. Starting from a non-linear double-track vehicle model, the linear error dynamics and predictive output are obtained based on the discretized error dynamic equation. The optimal control action is determined through the minimization of a cost function accounting for both yaw rate error and control effort terms. A Quadratic Programming (QP) approach is used for the solution of the optimization problem, where tire friction and motor torque limits are incorporated for deriving realistic inputs to the model.
Guo et al. [131]	NMPC	A real-time NMPC logic based on a single-track vehicle model with non-linear tires is presented for enhancing vehicle handling. The MPC problem for yaw control aims to minimize a cost function, considering state error and control effort, along with the terminal cost to drive the state to the reference at the predictive horizon. The proposed highly non-linear control problem is efficiently solved using the Continuation/Generalized Minimal Residual (C/GMRES) algorithm, where inequality constraints are transformed into penalty costs to account for actual limits in states and control action. Additionally, the predictive duration is set as variable to further expedite the algorithm.
Han et al. [132]	MPC	A model predictive control structure is proposed to improve vehicle cornering performance without calculating a reference yaw rate but only based on the difference between front and rear axle sideslip angles, that are defined analytically using a single-track vehicle model. Since most production vehicles are understeering for safety reasons, the controller aims to increase the rear axle sideslip angle to approach the front one, thus aiming at a neutral vehicle behavior. The MPC problem minimizes a cost function composed of state error, control effort and rate of change in the control action. Constraints are added to ensure vehicle stability and prevent it from becoming oversteering while also avoiding the front axle assuming a too high sideslip angle, meaning it will be in the unstable region of tire forces.
Parra et al. [133]	NMPC	A controller using torque vectoring to enhance vehicles’ energy efficiency is presented. Based on a 7 DOFs vehicle model, the NMPC problem is formulated by using a cost function considering total longitudinal force and yaw rate tracking performance, energy efficiency related to powertrain and tire slip power losses, and rear-to-total torque distribution for each side of the vehicle. These terms are weighted to form the cost function, with the weights that are defined using a fuzzy logic based on vehicle sideslip angle and yaw rate errors, prioritizing the control objective between energy efficiency and handling at each control time step.
Liu et al. [66]	NMPC	A non-linear model predictive control is proposed to track a reference yaw rate while minimizing the vehicle sideslip angle using a combination of torque vectoring and rear wheel steering. The optimal control action is determined by minimizing a cost function accounting both for states deviation from the reference and control efforts. The vehicle model used for prediction is a single-track vehicle model with a non-linear Fiala tire model. The motor torque for yaw moment generation is allocated evenly across the axles and in an even and opposite way to the wheels of the same axle. The rear wheel-steering angle is, instead, determined through a lookup table approach, selecting the wheel steering angle to achieve the tire slip angle corresponding to the desired lateral force.
Svec et al. [134]	KMPC	A Koopman operator Model Predictive Control (KMPC) is proposed to track a yaw rate reference. The defined controller employs a standard MPC where the innovation lies in the vehicle model definition. Indeed, a finite-dimensional approximation of the Koopman operator is introduced for transforming the non-linear vehicle dynamics into a higher-dimensional space where its evolution becomes linear. Simulation results indicate the improved performance of the proposed KMPC compared to LTV-MPC but not compared to NMPC, while being more computationally efficient than both of them.

2.2.5. Fuzzy Controllers

Fuzzy logic is employed as a black-box approach to map an input space into an output space based on specific rules, often articulated in natural language. Typically, a fuzzy logic controller comprises three fundamental steps: fuzzification of inputs, processing of the fuzzified inputs, and defuzzification into outputs. The fuzzification of inputs consists in converting them into a qualitative value assuming a high or low value. The processing involves the application of the natural language rules established by the designer leveraging their knowledge about the system to be controlled to aggregate inputs into outputs. The defuzzification entails defining the control action according to output rules, still defined by the designer based on their knowledge. The application of this control process for vehicle lateral dynamics is illustrated in Figure 13.

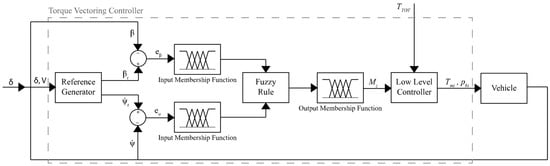
Figure 13. Typical fuzzy TV control scheme.

Table 5 outlines various contributions in the literature related to torque vectoring control using fuzzy logic, where the fuzzy inference process proposed by each paper is described.

Table 5. Fuzzy torque vectoring controllers.

Authors	Method
Pusca et al. [135]	A fuzzy controller for a 4WD vehicle with independent motors is developed. The command signals, determining which wheel needs to be braked, are defined using a comprehensive table that incorporates estimated tire slips, reference yaw rate, actual yaw rate, actual steering angle and other parameters. This control system is integrated with a slip controller capable of considering both for tire slips and front and rear sideslip angles.
Kim et al. [38,63]	A fuzzy logic control law for the stability control of a four-wheel-drive vehicle is proposed in combination with an optimal wheel torque distribution using regenerative braking of the rear motor and an Electro-Hydraulic Brake (EHB). The desired direct yaw moment is determined through a fuzzy controller, taking the errors of vehicle sideslip angle and yaw rate as input variables, with the reference quantities inferred from actual steering angle and vehicle velocity. The performance of the proposed control logic is compared to that of fixed regenerative braking and optimal regenerative braking during a single lane change maneuver. Simulation results indicate that the proposed distribution can achieve increased energy recuperation while maintaining vehicle stability.
Jaafari et al. [91]	An integrated vehicle lateral dynamics control is proposed, featuring two alternative control strategies that are proposed for handling improvement and stability control. The first control layer selects the appropriate strategy based on judgements about the sideslip angle rate phase plane, while the second control layer defines the yaw moment according to the selected control strategy. The stability control strategy relies on fuzzy logic, receiving as input the distance of the vehicle state from the phase plane reference region and its derivative. The control strategy for handling improvement also relies on fuzzy logic, but receiving as input the yaw rate error and its derivative with respect to a reference model.
Parra et al. [88]	A fuzzy logic controller is proposed for the control of vehicle lateral dynamics, aiming to match a reference vehicle response. The right-to-left torque distribution is the output of the fuzzy logic, which receives as input the yaw rate error and its derivative together with the vehicle sideslip angle error, using an always null reference value for the latter. The torque distribution also incorporates the front-to-rear torque distribution factor, defined based on the ratio between the vertical load on one axle and the total vertical load of the vehicle. In particular, tire vertical forces are estimated using an Adaptive Neuro-Fuzzy Inference System (ANFIS). The proposed control logic is assessed for its performances in [8], considering different powertrain architectures and demonstrating its adaptability without the need for parameter tuning.
Parra et al. [64]	The control logic proposed in [88] is extended by introducing a regenerative braking contribution activated only when the vehicle sideslip angle reaches high values. The torque to be generated by regenerative braking is predetermined and applied based on the lateral torque distribution required by the fuzzy yaw moment controller. Simulation results indicate that the proposed approach can enhance vehicle stability, improve handling characteristics, while also providing a lower energy consumption.

2.3. Low-Level Controllers

The low-level controller defines the torque to be supplied by each motor to meet the total longitudinal force required by the driver and the desired yaw moment specified by the high-level controller. Several approaches are documented in the literature for this task, ranging from fixed distribution logics to optimized logics aiming at the equalization of tire workloads or at energy consumption minimization.

Fixed distribution logics, known for their simplicity in definition and implementation at the vehicle level, offer a straightforward approach. The simplest approach, applicable to 2WD vehicles, involves generating the desired yaw moment by allocating the torque to the driving wheels with the same magnitude and opposite sign [33]. This enables the application of TV with theoretically no energy consumption, as the power consumed on one side of the vehicle is recovered on the other side. The advanced version of fixed distribution algorithms for 4WD independently driven vehicles, instead, requires tuning a couple of parameters, namely the front-to-rear and left-to-right distributions, or, equivalently, the front-to-rear distribution for each side of the vehicle. A contribution from this field is presented in [136], where the left-to-right distribution is fixed at the design stage, while the front-to-rear distribution is regulated through a PD controller on yaw rate error, accounting for the influence of longitudinal forces on vehicle lateral dynamics. Another example of rule-based distribution logic is presented in [137], where a hierarchical approach using a decision tree is introduced. The concept is to generate the desired yaw moment by exploiting the maximum available friction at the minimum possible number of tires. Moreover, different tire selection orders are employed based on whether the actual vehicle yaw rate exceeds the reference value or not.

Much more interesting are the approaches dealing with the optimization of torque allocation to driving motors. As previously mentioned, two distinct methods can be identified: the first aims to minimize the imbalance of tire workloads, while the second focuses on minimizing energy consumption while ensuring a proper handling performance. Table 6 provides a summary of various contributions with the objective of defining an optimal torque allocation.

Table 6. Optimal wheel torque allocation controllers.

Authors	Method
Sakai et al. [33]	A torque distribution logic for torque vectoring applications is proposed, as the two quantities provided by the high-level controller are insufficient for determining the torque allocation to each wheel in a four-wheel-drive vehicle. To ensure vehicle stability even on slippery roads, a distribution algorithm is introduced to minimize the load imbalances between tires. The algorithm distributes longitudinal forces accounting for the lateral force already required to each tire. Although the proposed algorithm is an approximate solution, its results are compared with numerical solutions, revealing negligible differences between approximate and optimal solutions. Moreover, a comparison between the approximate solution and the even distribution approach demonstrates the effectiveness of the proposed method.
Ono et al. [138]	Similar to [33], an integrated control for four-wheel-distributed steering and four-wheel-distributed traction/braking systems is proposed. The control strategy aims to minimize tires workload, ensuring it is the same for all the tires. Tire grip margin and friction circle radius are estimated based on the relationship between Self-Aligning Torque (SAT) and the longitudinal and lateral forces for each tire. The distribution algorithm calculates the direction and magnitude of each tire force, satisfying constraints from the high-level controller regarding total force and yaw moment while minimizing the μ-rate of each tire, which is an index defining tire usage.
Xiong et al. [111]	An effectiveness matrix for control allocation is proposed through the analysis of tire characteristics under combined longitudinal and lateral forces, considering the impact of the longitudinal force on the lateral force. The longitudinal force at each wheel is optimally allocated using a Quadratic Programming (QP) method, where the first objective is minimizing the allocation error, and the second objective is minimizing the energy consumption from the actuator.
Moseberg et al. [106]	Tire forces distribution is performed minimizing the weighted square sum of the tire adhesion utilization, being the ratio between the developed force and the maximum force ideally sustainable by the tire. Furthermore, the wheel torque allocation addresses actuator failures by adding constraints equations related to the detected failure.
Zhang et al. [139]	An optimal torque distribution strategy for 4WD Electric Vehicles (EVs) is proposed, considering both vehicle stability performance and energy consumption. The vehicle stability objective function is based on the friction circle concept, being the sum of squared tire in-plane forces normalized by the maximum squared force that the tire can develop. The energy consumption objective function is the ratio between the motor output power and efficiency at the operating point. Constraints for both vehicle stability and energy consumption operation include driver torque request, motor torque limits and tire slip. For vehicle stability enhancement, instead, the requested yaw moment from the high-level controller should also be applied. The two objective functions are combined using a weighting coefficient obtained through a fuzzy logic algorithm based on vehicle sideslip angle and yaw rate.
Dizqah et al. [50]	An analytical solution of the control allocation problem, aiming to maximize energy efficiency, is provided under the assumption of strictly monotonically increasing power losses with wheel torque demand. The optimization problem is formulated as a multiparametric Non-Linear Programming (mp-NLP) problem. Moreover, the optimal solution, in the case of equal drivetrains, is made parametric with respect to vehicle speed. Simulations reveal that, given the assumption on power losses trend, the minimum consumption is achieved using one single motor on each side of the vehicle up to a threshold in torque demand; then, an even torque distribution among front and rear motors maximizes efficiency above that threshold.

3. Simulation Models

To enable a quantitative comparison among the various TV control methods previously discussed, some controllers for each method are considered and implemented in MATLAB/Simulink R2022b environment using a co-simulation approach featuring VI-Car Real Time for implementing the vehicle equations of motion. The simulation model accounts for the following elements:

• vehicle (14 DOFs);
• in-wheel electric motors (one per wheel);
• control strategy.

While the preceding paragraph extensively covered the aspect of control strategy, the current section provides a concise yet comprehensive overview of the controllers employed for simulation purposes. Three different high-level controllers are compared:

• LQR+YI;
• SOSM;
• PID+ISM.

It is noteworthy that the low-level controller, used for wheel torque allocation purposes and addressing tire forces saturation, remains consistent across all the high-level controllers that are the subjects of comparison.

3.1. Vehicle Model

The vehicle model is developed using VI-Grade CarRealTime 2022 software, thus accounting for five rigid bodies and 14 degrees of freedom. The rigid bodies consist of the four wheels and the vehicle chassis, while the degrees of freedom include:

• three displacements of the vehicle center of mass, namely x, y and z;
• three rotations about the principal axes passing through the vehicle center of mass, namely yaw, pitch and roll;
• four vertical displacements of unsprung masses;
• four wheel angular velocities about the hub axis.

This modeling approach addresses typical non-linearities in vehicle behavior, such as those associated with suspension elasto-kinematics, by incorporating multiple look-up tables. This enables achieving high fidelity without necessitating a substantial increase in the number of bodies and degrees of freedom. A detailed model including all the links and bodies present in the actual vehicle would otherwise require such an increase. For the present study, the vehicle parameters have been tuned to replicate a D-segment passenger car. The main vehicle data are reported in Table 7.

Table 7. Main vehicle data.

Description	Symbol	Unit	Value
Vehicle mass	m	kg	1680
Vehicle yaw inertia moment	Jz	kg m2	2600
Wheelbase	l	mm	2700
Vehicle c.o.m to front axle distance	a	mm	1160
Vehicle c.o.m to rear axle distance	b	mm	1540
Front track half-width	tF	mm	756
Rear track half-width	tR	mm	748
Vehicle c.o.m height from ground	hG	mm	580

Tires are modelled based on the Pacejka MF-Tire model [140]. The specific version employed in this paper is the PAC2002, which accounts both for combined slip conditions and relaxation lengths.

The driver model is the one embedded into VI-CarRealTime, employing a single-track model-based predictive control technique to define driver inputs. Given a target trajectory, the controller defines a connecting contour compatible with the initial position and orientation of the vehicle, smoothly linking to the reference trajectory at a predetermined preview distance. Subsequently, this connecting contour is used as a dynamic vehicle trajectory, imposed as input, ultimately leading to the computation of the corresponding steering control action through the inversion of equations.

3.2. Electric Motor Model

The four in-wheel electric motors driving the vehicle are modelled from a mechanical point of view. Figure 14 illustrates the motor mechanical characteristics in terms of torque versus speed, establishing upper and lower bounds for the available motor torque in the simulation. The dynamics of the motor, coupled with the electronic drive, is introduced through a first-order time lag transfer function (${TF}_{mot}$) of the form:

$$\mathrm{T}{\mathrm{F}}_{\mathrm{m}\mathrm{o}\mathrm{t}}(s)=\frac{T_{m,DYN}\left(s\right)}{T_{m,SS}\left(s\right)}=\frac{1}{{\tau }_{mot}s+1}$$

(10)

where ${\tau }_{mot}$ denotes the time constant. This transfer function is employed by providing the desired steady-state motor torque ($T_{m,SS}$) as input and obtaining the actual motor torque ($T_{m,DYN}$) as output, ensuring adherence to the actual system dynamics.

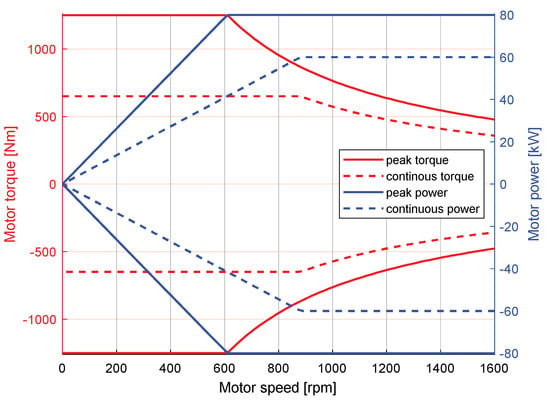
Figure 14. IWM mechanical characteristic curves.

3.3. Control Strategy

Among the wide variety of controllers presented for the high-level control task associated with yaw moment definition, three have been selected for comparison. The common objective for each controller is to track the same state reference quantities, enabling a direct comparison of simulation results.

3.3.1. References

The proposed controllers aim to control both yaw rate and sideslip angle, thus, necessitating the definition of references for both these quantities. Concerning the yaw rate reference, it is determined according to Equation (5), considering an understeering coefficient $k_{US}=0.3·{10}^{-3} \mathrm{r}\mathrm{a}\mathrm{d}/{\left(\mathrm{m}/\mathrm{s}\right)}^2$, a maximum lateral acceleration $a_{y,max}=0.9·\mu ·\mathrm{g}$ and a limit lateral acceleration $a_y^{*}=0.65 a_{y,max}$ for the vehicle linear response. The sideslip angle reference is defined according to Equation (7), where a limit sideslip angle ${\beta }_{max}=5 \mathrm{d}\mathrm{e}\mathrm{g}$ is considered.

3.3.2. High-Level Yaw Moment Generator—Strategy 1

The first controller is an optimal controller from [52], comprising the sum of a steady-state and a dynamic contribution.

$$M_{z,LQR+YI}=M_{z,DYN}+{\zeta }_{I_y}{M}_{z,SS}$$

(11)

The steady-state contribution ($M_{z,SS}$) is obtained in the form of an LQR where the vehicle model is linearized at each time instant. This contribution is multiplied by the activation factor ${\zeta }_{I_y}$, which diminishes the steady-state contribution during transients. The dynamic contribution ($M_{z,DYN}$) relies on the yaw index ($I_y$), directly associated with the vehicle understeer/oversteer behavior. This index is employed in a proportional controller to determine the appropriate yaw moment to be applied to the vehicle.

$$I_y=\frac{a_y}{V}-\dot{\psi }$$

(12)

$$M_{z,DYN}=k_y·I_y$$

(13)

This control logic is denoted as LQR+YI henceforth.

3.3.3. High-Level Yaw Moment Generator—Strategy 2

The second control strategy is presented in [43] and combines a suboptimal second order sliding mode for yaw rate control with a first order sliding mode for sideslip angle control.

$$M_{z,SOSM}={{\rho }_1(M}_{z,SOSM,\dot{\psi }}-M_{z,SOSM,\beta })+M_{z,SOSM,\beta }$$

(14)

The suboptimal second order sliding mode uses the sliding surface $S_{\dot{\psi }}$, defined as the difference between the actual yaw rate ($\dot{\psi }$) and its reference value (${\dot{\psi }}_{ref}$).

$$S_{\dot{\psi }}=\dot{\psi }-{\dot{\psi }}_{ref}$$

(15)

This sliding surface is employed to define the yaw moment first time derivative (${\dot{M}}_{z,SOSM,\dot{\psi }}$).

$${\dot{M}}_{z,SOSM,\dot{\psi }}=-J_z{k}_{r}sign\left[S_{\dot{\psi }}\left(t\right)-0.5·S_{\dot{\psi }}\left(t_{Mk,\dot{\psi }}\right)\right]$$

(16)

In particular, $t_{Mk,\dot{\psi }}$ corresponds to the time of the last singular value of $S_{\dot{\psi }}\left(t\right)$, meaning that ${\dot{S}}_{\dot{\psi }}\left(t_{Mk}\right)=0$. Similarly, the controller on the vehicle sideslip angle employs a sliding surface $S_{\beta }$ to define the control action ($M_{z,SOSM,\beta }$), characterized by a discontinuous term.

$$S_{\beta }=\beta -{\beta }_{ref}$$

(17)

$$M_{z,SOSM,\beta }=J_z{k}_{\beta }sign\left[S_{\beta }\left(t\right)-0.5·S_{\beta }\left(t_{Mk,\beta }\right)\right]$$

(18)

As before, $t_{Mk,\beta }$ corresponds to the time of the last singular value of $S_{\beta }\left(t\right)$, meaning that $S_{\beta }\left(t_{Mk,\beta }\right)=0$. The transition between the two control logics is managed by the multiplying factor ${\rho }_1$, determined based on the actual value of vehicle sideslip angle.

$${\rho }_1=e^{-{\rho }_2{e}_{\beta }}$$

(19)

Here, $e_{\beta }$ represents the error in the sideslip angle, and ${\rho }_2$ is a constant parameter selected by the designer. This control logic is referred to as SOSM hereafter.

3.3.4. High-Level Yaw Moment Generator—Strategy 3

The third control algorithm is from [44] and computes the yaw moment ($M_{z,ISM}$) by combining a PID contribution ($M_{z,PID}$) and a filtered integral sliding mode contribution ($M_{z,SM,fil}$). The latter is obtained by filtering the yaw moment ($M_{z,SM}$) derived by a standard sliding mode controller through a first-order transfer function with a ${\tau }_{SM}$ time constant.

$$M_{z,ISM}=M_{z,PID}+M_{z,SM,fil}$$

(20)

$$M_{z,SM}=-J_z{k}_{SM}sign\left(S\right)$$

(21)

$${\tau }_{SM}{\dot{M}}_{z,SM,fil}+M_{z,SM,fil}=M_{z,SM}$$

(22)

Here, the sliding variable $S$ is defined as the sum of the sliding surface $S_0$, representing the difference between the actual and reference yaw rates, and of an integral sliding mode variable ($z$). The latter also includes the time derivative of the yaw rate reference (${\ddot{\psi }}_{ref}$) in its definition.

$$S=S_0+z$$

(23)

$$\dot{z}=-\frac{d{S}_0}{d\left(\dot{\psi }-{\dot{\psi }}_{ref}\right)}\left[-{\ddot{\psi }}_{ref}+\frac{1}{J_z}\left(M_{z,ISM}-M_{z,SM}\right)\right]$$

(24)

This control logic has been enhanced with the incorporation of a proportional sideslip angle controller for better alignment with the other methods, and it is designated as PID+ISM moving forward.

3.3.5. Low-Level Torque Distribution Strategy

Concerning the low-level torque distribution logic, a uniform approach is adopted for all the simulations to ensure fairness in comparing different high-level controllers. The driving torque ($T_{TOT}$) specified by the driver through the throttle position is evenly distributed to the front axle across both wheels, given that the validated vehicle model represents a Front-Wheel Drive (FWD) car. The differential torque necessary to meet the yaw moment requirement is then added to the former contribution on the front axle and is the sole contribution on the rear axle. The left-to-right torque distribution on a given axle is performed with an even approach, where the torque allocated to the left and right motors to achieve the desired yaw moment is equal in magnitude and opposite in sign. Conversely, the front-to-rear torque distribution among axles is performed proportionally to the force that can be generated before saturating the axle, based on the friction circle principle. The axle saturation (${sat}_{a,F/R}$) is obtained as the average of the tire saturation factors (${sat}_{t,i}$) belonging to that axle. The tire saturation factor is defined as follows:

$${sat}_{t,i}=\frac{F_{z,i}}{\sqrt[2]{F_{x,i}^2+F_{y,i}^2}}$$

(25)

where $F_{z,i}$ is the vertical force at the i-th tire, while $F_{x,i}$ and $F_{y,i}$ are the longitudinal and lateral force at the i-th tire, respectively. The distribution factor between the front and rear axle is then determined as a function of the normalized front and rear axle saturations, ensuring their sum corresponds to the unit value.

$${\sigma }_F=\frac{{sat}_{a,F}}{{sat}_{a,F}+{sat}_{a,R}} ; {\sigma }_R=1-{\sigma }_F$$

(26)

Here, ${\sigma }_F$ and ${\sigma }_R$ represent the fraction of motor torque for yaw moment generation applied to the front and rear axles, respectively. Consequently, the torque allocated to each wheel is expressed as:

$$T_{m,FR}=\frac{T_{m,req}}{2}+{\sigma }_F\frac{M_z R_w}{2t}$$

(27)

$$T_{m,FL}=\frac{T_{m,req}}{2}-{\sigma }_F\frac{M_z R_w}{2t}$$

(28)

$$T_{m,RR}={\sigma }_R\frac{M_z R_w}{2t}$$

(29)

$$T_{m,RL}=-{\sigma }_R\frac{M_z R_w}{2t}$$

(30)

where $R_w$ is the mean wheel radius, $t$ is the mean vehicle half-track width, and the subscript for each IWM torque ($T_m$) first indicates the axle (F/R) and then the side concerning the vehicle’s forward travelling direction (R/L).

In this paper, the yaw moment defined by the high-level controller leverages the capabilities of 4 IWMs. However, the same high-level controllers can be effectively deployed to any vehicle featuring torque vectoring capabilities. This includes vehicles using brakes as actuators or also vehicles exploiting torque vectoring at only two wheels, such as those equipped with active differentials or featuring a pair of independent motors on a single axle. It is evident that a change in vehicle topology requires a redesign of the low-level controller according to the available actuators for yaw moment generation.

3.3.6. Controller Tuning

The three proposed controllers from the literature were tuned to attain similar performances in both steady-state and transient conditions. Given the combined tracking of yaw rate and sideslip angle, yaw rate is selected as the primary state variable for tracking, accepting larger errors in sideslip angle. The tuning aspect is crucial for evaluating the advantages and disadvantages of each of the presented controllers. However, it is essential to acknowledge that variations in vehicle dynamics with the compared controllers are certain due to their different nature.

4. Results

The effectiveness of the control strategies presented above is assessed through numerical simulations, encompassing both transient and steady-state maneuvers, spanning from open-loop to closed-loop modalities. These same maneuvers are simulated under both high friction (μ = 1.0) and low friction (μ = 0.4) conditions to comprehensively investigate the entire operational range during typical vehicle operation on the road.

4.1. Open-loop Maneuvers

The steady-state performance of the proposed controllers under high friction conditions is evaluated through an ISO 4138 [141] steering pad constant speed maneuver, where the speed is kept constant at approximately 100 km/h. During this maneuver, the steering wheel angle increases at a constant rate up to 90 degrees within a 200-second timeframe. The selection of the maximum steering wheel angle is conducted through incremental adjustments in 5-degree steps until the selected vehicle reference response achieves a minimum of 99% of the maximum achievable lateral acceleration. The duration for increasing the steering wheel angle from straight to the maximum value is selected based on the authors’ prior knowledge to comply with the steady-state maneuver limits outlined in the ISO 4138 standard [141]. The results of these simulations are reported in Figure 15.

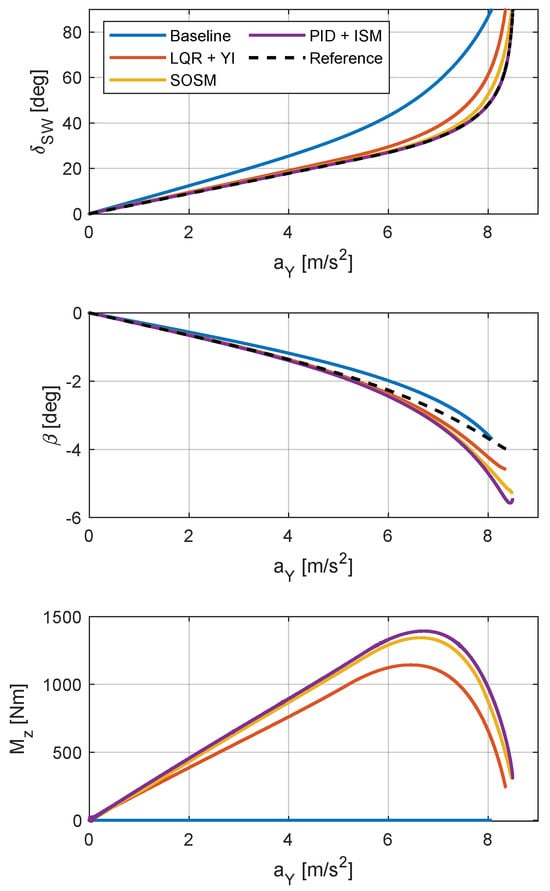
Figure 15. Steering pad constant speed maneuver on high friction road (μ = 1).

Analyzing the quasi-steady-state simulations under high friction conditions, it is evident that the handling properties of the uncontrolled vehicle have been improved. All controllers demonstrate the ability to increase the maximum achievable lateral acceleration, ensuring a more responsive vehicle at low lateral acceleration while still guaranteeing a smooth vehicle behavior. The SOSM and PID+ISM controllers closely track the reference for steering angle against lateral acceleration or, equivalently, yaw rate. In contrast, the LQR+YI controller deviates from the yaw rate reference due to conflicting objectives related to concurrent yaw rate and sideslip angle reference tracking. However, the LQR+YI controller excels in drivability at handling limits, providing a smooth increase in vehicle sideslip angle and thus a more predictable behavior for the driver. On the other hand, SOSM and PID+ISM generate results that are farther from the sideslip angle reference, and this is expected since that variable becomes progressively controlled when the sideslip angle increases. Given the consistent reference across all the controllers, the observed differences across them are attributed to variations in the proportional weight of errors on yaw rate and sideslip angle, reflecting the different tuning requirements of each controller.

The steady-state performances of the same controllers under low friction conditions are still evaluated using a steering pad constant speed maneuver at 70 km/h, progressively increasing the steering angle at a constant rate up to 60 degrees within 200 seconds. Once again, the selection of the maximum steering wheel angle is based on achieving the maximum steady-state lateral acceleration performance of the reference vehicle. The execution time for the maneuver is maintained constant to ensure quasi-steady-state conditions, especially in more challenging scenarios, such as on surfaces with reduced friction. The results of these simulations are presented in Figure 16.

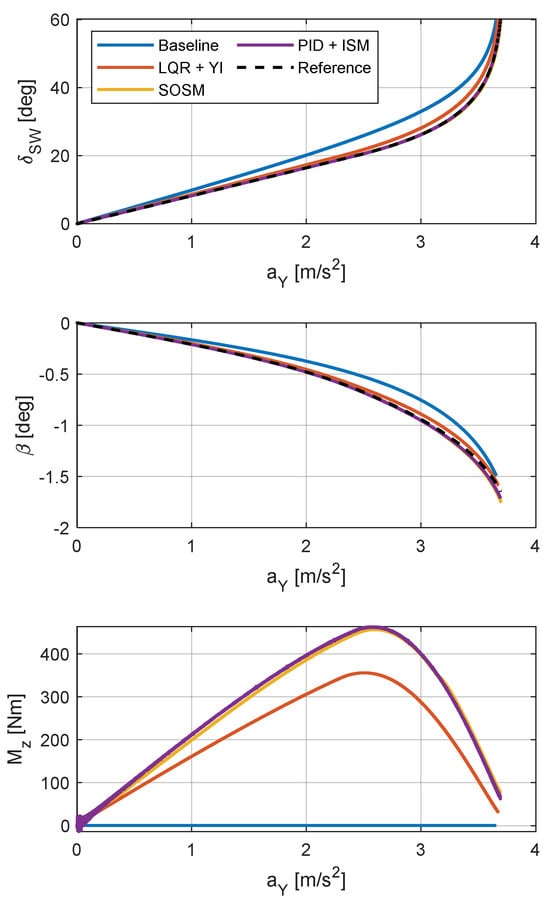
Figure 16. Steering pad constant speed maneuver on low friction road (μ = 0.4).

Under low friction conditions, similar considerations to those under high friction apply. The main difference is the reduced variation between the three control strategies due to the lower margin against the total available friction which can be exploited to modify the vehicle handling characteristics. Drawing conclusions, it can be asserted that the LQR+YI controller has the potential to enhance steady-state vehicle dynamics. However, its dependence on a linearized vehicle model prevents it attaining optimal performance at handling limits. Conversely, both the SOSM and the PID+ISM controllers enhance steady-state vehicle dynamics, even in proximity of handling limits, with the PID+ISM controller exhibiting a superior yaw rate tracking performance. However, the PID+ISM controller induces a sudden variation in sideslip angle at handling limits, particularly under high-friction conditions. Consequently, the SOSM controller emerges as the preferable choice, as it achieves good handling performance while ensuring the predictability of the vehicle’s behavior. This quality translates to enhanced drivability, making the SOSM controller a more suitable option.

Transient performances of the controllers under high friction conditions are assessed using an ISO 7401 [142] step steer maneuver, starting in straight line at 100 km/h and applying a sudden steer of 60 degrees while maintaining a fixed throttle position. The steering wheel angle at the end of the maneuver is predetermined, while the speed is systematically incremented in 10 km/h steps, stopping just before the point where the baseline vehicle could no longer complete the maneuver due to tailspin. The results for these maneuvers on high friction surface are reported in Figure 17.

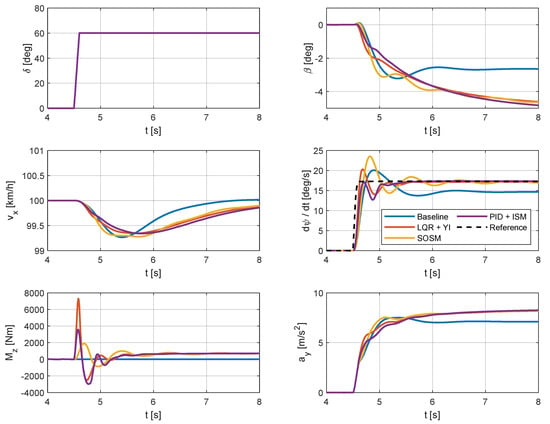
Figure 17. Step steer maneuver on high friction road (μ = 1).

Examining the simulated transient maneuver under high friction conditions, torque vectoring, irrespective of the algorithm, enhances yaw rate and lateral acceleration responses compared to the uncontrolled vehicle. Regarding the yaw rate, the controlled vehicle damps out oscillations faster than the baseline vehicle. Moreover, the PID+ISM controller strongly reduces the yaw rate overshoot, while the other controllers are not able to do this. In general, the vehicle sideslip angle is also much smoother for the controlled vehicle than for the uncontrolled one, meaning easier handling for the driver. The SOSM is the worst performing controller in this scenario, generating oscillations in both yaw rate and sideslip angle responses. Notably, the SOSM controller exhibits a larger yaw rate overshoot than the uncontrolled vehicle, with yaw rate oscillations also not being better dampened out.

The transient performances of the controllers under low friction conditions are also assessed using a step steer maneuver, starting from a speed of 70 km/h and applying a sudden steer of 60 degrees while maintaining a fixed throttle position. The criteria for selecting the speed and the steering wheel angle at the conclusion of the maneuver align with those applied for the high-friction maneuver. The results for these maneuvers on low friction surface are presented in Figure 18.

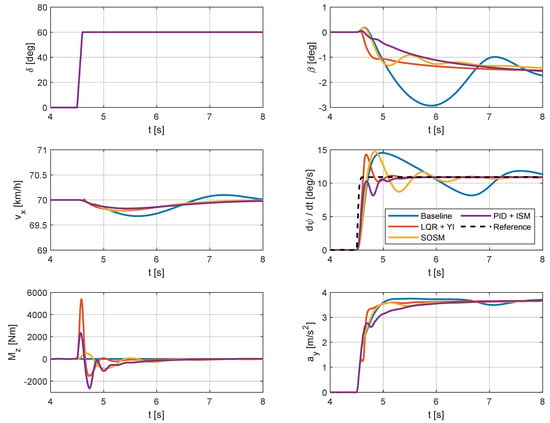
Figure 18. Step steer maneuver on low friction road (μ = 0.4).

Under low friction conditions, the lateral acceleration achieved by the controlled vehicle is comparable to that of the uncontrolled vehicle. In this case, the LQR+YI controller generates a peaky overshoot of yaw rate and a rapid increase in the vehicle sideslip angle. This may cause drivability issues for the driver, who may not be prepared to react to such a sudden variation in vehicle handling properties. The SOSM controller achieves a similar yaw rate overshoot to the uncontrolled vehicle but settles to the steady-state value faster and with smaller oscillations in the vehicle sideslip angle. The PID+ISM controller outperforms the other methods, guaranteeing no overshoot in yaw rate and providing a smooth shape of the vehicle sideslip angle, contributing to ease the vehicle handling.

4.2. Close-Loop Maneuvers

Transient performances of the proposed controllers are assessed through steering wheel closed-loop simulations involving an ISO 3888 [143] double lane-change maneuver. Under high friction conditions, the vehicle enters the testing track at 125 km/h and maintains that speed throughout the maneuver; meanwhile, under low friction conditions, the speed is set to 90 km/h. The maneuver speed is determined by incrementing it in 5 km/h steps and halting the process when the baseline vehicle strikes at least one cone of the ISO 3888 [143] test course. The results for high friction and low friction conditions are presented in Figure 19 and Figure 20, respectively.

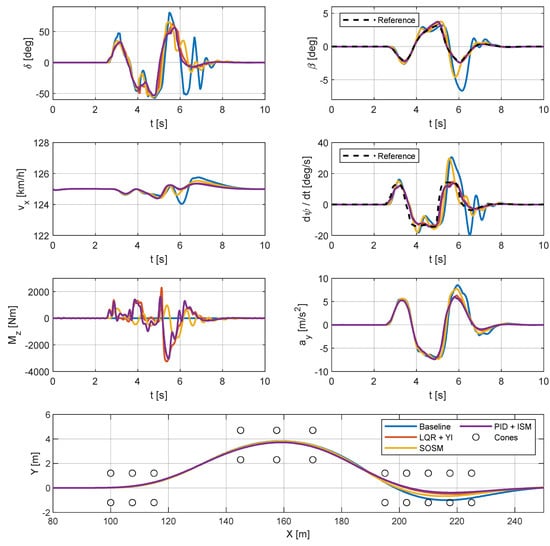
Figure 19. Double lane-change maneuver on high friction road (μ = 1).

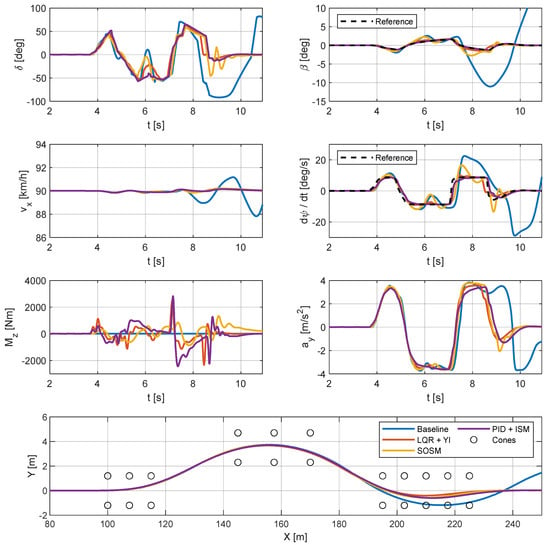
Figure 20. Double lane-change maneuver on low friction road (μ = 0.4).

Upon examining the results under both high and low friction conditions, it is evident that the uncontrolled vehicle struggles to maintain the course, while the controlled ones successfully complete the maneuver without striking any cones in the last section of the test track. Particularly under low friction conditions, the uncontrolled vehicle exhibits strong oscillations even after completing the maneuver, while the controlled vehicle remains safely stable. In both low and high friction conditions, an undesirable interaction is observed between the SOSM torque vectoring controller and the steering wheel angle controller. Indeed, at the most critical point of the maneuver, there is a slightly oscillating behavior in the steering angle, yaw rate and vehicle sideslip angle time histories. Nevertheless, this undesired oscillation is promptly dampened out through proper steering wheel angle correction. Aside from these issues, all the controllers can effectively track the reference quantities for yaw rate and sideslip angle, resulting in a vehicle that is safer and easier to drive compared to the baseline one. Overall, the PID+ISM controller emerges as the top-performing option, slightly surpassing the performance of the LQR+YI controller, particularly in proximity to the maximum achievable lateral acceleration.

5. Conclusions

A review of direct yaw moment control techniques available in the literature is performed in this article. To ensure proper reliability, most of these techniques employ feedback controllers. Nevertheless, it has been demonstrated that incorporating a feedforward component into the control action is beneficial for achieving a fast response. The simplest approach to vehicle direct yaw moment control relies on PID controllers, known for their ease of design and tuning, as well as their robustness against external disturbances. The primary drawback lies in potential stability issues arising from unmodeled dynamics at the tuning stages. Modelling uncertainties can instead be properly handled by sliding mode controllers, which employ a discontinuous control technique. Nonetheless, this discontinuity poses a significant disadvantage in vehicle lateral dynamics control as it can lead to substantial vehicle oscillations. Several strategies have been proposed over the years to mitigate this effect, although they profoundly influence the controller’s nature and disturbance rejection capabilities. The controllers recognized for achieving the best performances are optimal controllers, which require a vehicle model for properly working. Consequently, their actual performance is heavily dependent on the vehicle model reliability. This also explains the evolution from LQR, sensitive to both modelling errors and external disturbances, to LQG, which models uncertainties as Gaussian noise, and LPV vehicle modelling, incorporating confidence ranges for main vehicle parameters. Similarly, Model Predictive Control (MPC) addresses optimization problems over a finite time horizon, distinguishing itself from infinite horizon optimization typical for optimal controllers. This feature makes MPC superior to infinite horizon optimization methods since the dynamics predicted by the adopted vehicle model are much more reliable over a short time horizon. However, it comes at the cost of a high computational power for real-time implementation, which is now becoming available thanks to technological advancements. At last, it is worth mentioning fuzzy logic control, which does not rely on any vehicle model but only on the designer’s knowledge. This characteristic, while offering flexibility, makes it challenging to ensure proper stability across various driving conditions.

In the second part of the paper, some of the presented yaw moment control techniques are tested on an electric vehicle with four independent motors, one for each wheel. The testing maneuvers range from steady-state to transient ones under both high and low friction conditions. The comparison highlights that, in steady-state conditions, the results in terms of yaw rate tracking are similar for the proposed algorithms. Nevertheless, some differences arise due to the variation in relative weights of yaw rate and sideslip angle errors in defining the control action. This happens because, in many situations, the two tracking objectives are conflicting, and thus, to define a single control action, it is necessary to make a compromise between them. In general, accepting decreased handling performance in yaw rate tracking is necessary to achieve a safer and more predictable vehicle in which sideslip angle is prevented from an excessive increase. Moreover, different kinds of controllers have different tuning requirements for being stable and robust against uncertainties, further contributing to differences in controller performances. Overall, the most effective torque vectoring controller among the compared ones is the PID+ISM, with its primary strength lying in its high responsiveness and robustness against disturbances. In contrast, the LQR+YI controller has worse performances at handling limits and during fast transients due to its dependency on a linearized vehicle model, which does not accurately represent the vehicle dynamics in extreme conditions. On the other hand, the SOSM controller is susceptible to inducing oscillations in extreme conditions due to its discontinuous nature. Indeed, looking at close-loop driving maneuvers, it is also possible to notice bad interactions between the SOSM torque vectoring controller and the driver, potentially causing an undesired vehicle behavior. For this reason, future works will concentrate on the interaction between vehicle handling control logics and human drivers using a dynamic driving simulator.