Featured Application
Robot Pneumatic System.
Abstract
Due to advantages such as a high power-to-weight ratio, a simple structure, and low cost, pneumatic systems are widely applied in automation. However, precise position control of pneumatic actuators is challenging because of factors such as friction, compressibility, and external disturbances. This paper presents a backstepping sliding mode control (BSMC) strategy based on the extended state observer (ESO) for pneumatic cylinder position tracking. A nonlinear model of the pneumatic system is first established, then system states and disturbances are estimated by an ESO, next the BSMC approach is developed using backstepping method and sliding mode control theory, and the stability of the ESO and controller is analyzed using Lyapunov theory. Finally, simulations and experiments on a pneumatic testbed are performed to compare the effectiveness of the proposed approach with PID control. The results show that the proposed strategy improves tracking accuracy and robustness against disturbances, with a 77.04% reduction in root mean square error (RMSE). This research provides a promising control solution for automated pneumatic polishing robots.
1. Introduction
Polishing is a surface finishing process that aims to enhance the appearance or the functionality of a workpiece through material removal or shape modification [1]. It is widely applied in various fields, including metal processing, mold manufacturing, aero-space engineering, and biomedical engineering [2,3]. However, the traditional manual polishing process heavily depends on skilled labor, resulting in inconsistent quality and low productivity. Consequently, there has been a growing interest in automating the polishing process to achieve higher throughput, repeatability, and consistency [4,5]. Among the popular methods for automated polishing, pneumatic polishing systems integrated with robotic arms have emerged as a preferred approach. An essential aspect of automatic polishing is the precise control of the end effector within the pneumatic system of the polishing robot [3,6].
Pneumatic systems offer several advantages, such as a simple structure, low cost, fast response, and a high power-to-weight ratio [7,8]. However, they also present challenges, including nonlinear characteristics, parameter uncertainty, complex friction forces, and unknown disturbances. Therefore, it is crucial to develop an effective control method for pneumatic systems to achieve precise automatic polishing. Proportion-al-Integral-Derivative (PID) control is a widely employed method in the industrial field due to its simplicity and robustness [5,9]. PID control has been successfully implemented in various polishing applications, such as robotic belt grinding and robotic abrasive flow machining. Nevertheless, despite its extensive use, PID control has limitations, such as sensitivity to parameter variations, suboptimal performance under nonlinear conditions, and limited disturbance rejection capabilities. As a result, it may be inadequate for highly nonlinear systems such as pneumatic polishing [10].
In order to overcome these limitations, alternative control methods, such as sliding mode control, have been investigated. Sliding mode control is a nonlinear robust control method that can effectively handle parameter uncertainty and external disturbance by utilizing a discontinuous switching function [11]. Compared to PID control, sliding mode control offers advantages, such as fast convergence speed, strong robustness, and easy implementation. It has been applied in various pneumatic system applications, such as pneumatic servo positioning, pneumatic artificial muscle actuation, and pneumatic hammering force regulation [12,13,14].
However, sliding mode control also has some drawbacks, such as the chattering phenomenon caused by high-frequency switching functions, the difficulty of designing a sliding surface for high-order systems, and the requirement of accurate system model in-formation [15,16]. The polishing pneumatic system is a high-order, strongly nonlinear system that involves complex dynamics, including friction forces and random disturbances. Therefore, traditional sliding mode control may not achieve satisfactory performance for the polishing pneumatic system. To address these problems, backstepping control is introduced to enhance the performance of sliding mode control. Backstepping control is a recursive design method that can handle high-order nonlinear systems by decomposing them into lower-order subsystems and applying feedback stabilization at each step [17,18,19]. It offers several advantages, such as a systematic design procedure, a flexible structure, and good tracking performance. Backstepping control has been successfully applied in various sliding mode control applications, such as robot manipulator control, induction motor control, and spacecraft attitude control [20,21].
In addition to the challenges mentioned earlier, another factor that contributes to the in-accurate control of the polishing pneumatic system is the presence of unknown disturbances that affect the system dynamics [22,23]. These unknown disturbances in the pneumatic system can result from various factors, such as load variation, air leakage, valve dead zone, and more [15,23]. Consequently, it becomes crucial to eliminate or compensate for these unknown disturbances during the control process. By effectively addressing the impact of these disturbances, the control performance can be enhanced and more accurate and reliable control of the polishing pneumatic system can be achieved.
Various methods have been employed to address the issue of unknown disturbances in the control process, including adaptive control, robust control, and disturbance observer [24,25]. However, these methods often come with certain disadvantages, such as complex design procedures, conservative performance, and high computational burdens. A promising approach to tackle these challenges is the extended state observer (ESO), which is a novel method capable of estimating and compensating for unknown disturbances by augmenting the system state with an additional variable that represents the total disturbance [26,27]. The ESO offers several advantages over other methods, including its simple structure, low computational cost, wide applicability, and strong robustness [28,29]. The ESO has been successfully applied in various control applications, such as servo motor control, magnetic levitation system control, and flexible joint robot control [30,31]. However, there is a limited amount of literature available on the application of an ESO to polishing pneumatic system control. Therefore, in this paper, a backstepping sliding mode control (BSMC) method based on an ESO for the polishing pneumatic system is proposed. The proposed method only requires the measurement of the displacement of the pneumatic cylinder, enabling it to estimate and compensate for the velocity, acceleration, and composite disturbance signal. By effectively suppressing and compensating for unmodeled friction forces and random disturbances in the system, the proposed method demonstrates strong engineering practicability, high control accuracy, and robustness. The effectiveness of the proposed method is validated through simulation and experimental results.
The rest of this paper is organized as follows: Section 2 develops the mathematical model of the polishing robot pneumatic system and presents the expression of the state equation. Section 3 designs the observer and controller. Based on the Lyapunov stability theory, the stability of the observer and controller is proved. Section 4 establishes an AMESim and MATLAB/Simulink co-simulation model of the polishing robot pneumatic system, compares the simulation results of the traditional PID control method and the BSMC method proposed in this paper, and quantitatively analyzes the experimental effects of the two algorithms. Section 5 summarizes the main contributions of this paper and discusses the application significance of the proposed method.
2. Construction of System Modeling
This paragraph describes the structure of the pneumatic control system of a polishing robot, as shown in Figure 1. The system consists of a pressure source, a relief valve, a pneumatic cylinder, and a displacement sensor. The pressure source supplies gas pressure for the entire system, while the relief valve serves as a protective function. The pneumatic cylinder acts as an actuator and the displacement sensor is mounted at the end of the pneumatic cylinder to feed back its displacement. The controller outputs a control signal to the proportional valve based on the displacement error of the pneumatic cylinder, which controls its position.
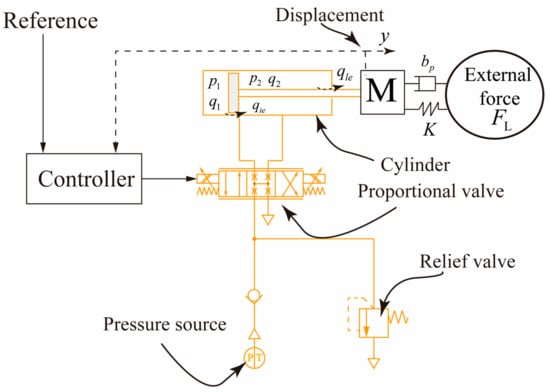
Figure 1.
Structure diagram of the pneumatic control system.
The dynamic equation of the pneumatic cylinder is derived from Newton’s second law:
In Equation (1), is the area of the rear end of the pneumatic cylinder, ; is the area of the rod end of the pneumatic cylinder, ; is the air pressure in the rod-less chamber of the pneumatic cylinder, Pa; is the air pressure in the rod chamber of the pneumatic cylinder, Pa; is the equivalent mass of the load and air cylinder, kg; is the displacement of the pneumatic cylinder, m; is the load force and difficult-to-model interference force N.
Since the improvement of sealing technology, the external leakage of the pneumatic cylinder is so minor that it can be ignored. The pressure-flow equation of the pneumatic cylinder can be expressed as follows [23]:
In Equations (2) and (3), is the gas elastic modulus, Pa; and are the initial volumes of the air cylinder with and without rod, respectively, ; is the internal leakage coefficient of the pneumatic cylinder, ; and are the gas flows in the pneumatic cylinder without and with the rod, respectively. The flow equation of the proportional valve is expressed as [12]:
In Equations (4) and (5), ; ; and are the area gradients of the proportional valve; is the gas density, ; is the displacement of the proportional valve spool, m; is the pressure of the pressure source, Pa; is the return air tank pressure of the proportional valve.
Then, s (·) is a symbolic function expressed as:
Since the frequency response of a proportional valve is typically much faster than that of a pneumatic cylinder, it is often assumed that the displacement of the valve core and the input voltage have an approximately linear relationship. In other words, this relationship can be expressed as follows:
In Equation (7), ki is the amplification factor, and Equations (4) and (5) can be simplified as follows:
where , , .
If the equation of variable can be expressed as , then the system state equation is:
In Equation (10), , , , is a compound disturbance.
3. Design of the Backstepping Sliding Mode Pneumatic Cylinder Position Controller
The control objective of a pneumatic system is to achieve accurate tracking of the desired trajectory for the pneumatic cylinder in different environments, regardless of the influence of external disturbances. In this section, a backstepping sliding mode position controller for the pneumatic cylinder is designed by incorporating an extended state observer (ESO). However, before proceeding with the design, the following assumptions are established:
Assumption 1.
The third derivative of y of the displacement signal of the pneumatic cylinder exists and is derivable, that is, and
. and
are constants.
Assumption 2.
The first-order differential of perturbation force exists and is upper bounded (the lower bound is, as we commonly know, 0), that is, . is constant.
Remark 1.
Assumption 2 is widely accepted by researchers and can be proved in literature [32,33].
Another important work of this paper is the stability analysis of the designed controller, which includes the stability analysis of both an ESO and BSMC. Stability analysis is crucial for assessing the reliability and robustness of the control system, and it plays a key role in ensuring the stability of the designed controller. The Lyapunov method is a important technique for stability analysis, which involves analyzing the properties of a Lyapunov function. By examining the derivative of this function, the stability of the system can be established. Applying the Lyapunov method to the designed controller can ensure accurate state estimation and robust control performance.
3.1. The Extended State Observer
Before designing, it is necessary to expand the complex disturbance into a new state variable and define the following: .
Then, Equation (10) is rewritten as [34]:
The variable is defined as the estimated value of the ESO for each state, and the ESO is constructed according to the mathematical model of Equation (11):
where are all positive numbers.
3.2. Stability Analysis of the ESO
Define as the ESO estimation error. The observer error equation can be obtained by subtracting Equation (12) from Equation (11):
According to Equation (13):
where , , is a bounded variable. Then, there is that makes .
When , if Hurwitz polynomial can be satisfied by , then is a Hurwitz matrix, and there is a real symmetric positive definite matrix and a positive definite matrix to make , that is, the existence of makes Therefore, the observer has an upper bound boundary, and its stability can be proved.
3.3. Backstepping Sliding Mode Control
The backstepping sliding mode controller for the pneumatic cylinder position is designed as follows:
Step 1: According to the pneumatic cylinder’s displacement and expected displacement , the tracking error can be expressed as:
Derivation of Equation (15):
Define the first Lyapunov function V1:
Derivation of the first Lyapunov function:
Define , where is the virtual control variable. To make negative, let . If , then:
If , then . The controller is stable. The next design goal is to make .
Step 2: Define the second Lyapunov function :
Take the derivative of and bring Equation (20) into:
where , define , where is the virtual control variable. To make negative, let . If , then:
Step 3: Define the synovial function:
Derivation of Equation (23) gives:
Set , and bring e1, e2 into the equation to obtain the control law:
3.4. Stability Analysis of Backstepping Sliding Mode Control
From , it can be obtained:
From Equations (25) and (26), it can be obtained:
Define Lyapunov function:
Take the derivative of Equation (27) and bring it into Equation (28):
From , and the Young inequality [35], it can be obtained that:
From Equation (30), it can be obtained that [36]:
where
From Equation (32), it can be seen that , meaning the controller designed has an upper bound and the controller is stable.
The control strategy of the algorithm designed in this paper is illustrated in Figure 2. The speed, acceleration, and complex disturbance force of the pneumatic cylinder are estimated by the extended state observer (ESO) based on the controller output and displacement of the cylinder. The estimation information from the ESO and the displacement tracking error of the pneumatic cylinder are fed into the controller, which then calculates and outputs the control signal. The control signal is received by the electric proportional valve to regulate the gas flow into the pneumatic cylinder, thus enabling precise control of its position. This is successfully accomplished by making the high pressure gas entering the left chamber (red dotted line) and the low pressure gas leaving the right chamber (blue dotted line).

Figure 2.
Schematic diagram of the proposed control strategy.
4. Simulation and Experimental Results and Discussion of the Pneumatic System
4.1. Simulation Setup
A co-simulation model combining AMESim and MATLAB/Simulink was established to verify the control method proposed in this paper, as shown in Figure 3. The pneumatic system was modeled using AMESim, while the control algorithm was implemented using MATLAB/Simulink. This approach takes full advantage of the capabilities of both software tools to improve the accuracy of the simulation. Controller1 is a PID controller, while Controller2 is a backstepping sliding mode controller based on an extended state observer (ESO).
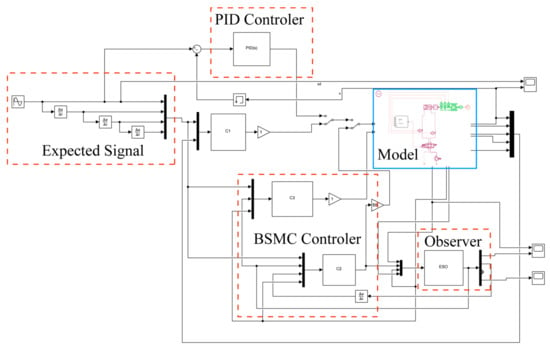
Figure 3.
AMESim and MATLAB/Simulink Co-simulation model.
Table 1 shows some of the modeling parameters of the co-simulation model. The dimensional parameters, such as the mass, diameter of the piston and rod of the pneumatic cylinder, are obtained by direct measurement in the three-dimensional modeling software (Solidworks 2020). Another part of the parameters describes the state and properties of the working medium, which is important for the pneumatic system, as it is sensitive to the environment, especially the temperature. However, these parameters are not easy to determine, as there are no professional tools available for measurement. The parameter range is determined by referring to some literature [37,38,39] and user manuals, and then iteratively debugging the simulation model.

Table 1.
Values of simulation model system parameters.
The reference signal is set as a composite signal: . Initially, the piston of the pneumatic cylinder is in the middle of the air cylinder. The piston dis-placement is positive with the extension stroke of the pneumatic cylinder, and negative with the retract stroke. In the simulation process, the model is subjected to a sinusoidal disturbance force of Nonlinear Coulomb Friction with and .
Table 2 shows the parameter values of the two controllers in this paper. The performance of the PID controller depends on three parameters: the proportional gain Kp, the integral gain Ki, and the differential gain Kd. Due to its few control parameters, a classic trial-and-error method, Ziegler-Nichols, is used to obtain the values of Kp, Ki, and Kd [40]. This method is simple and easy to use, but it is slightly inferior in terms of accuracy and stability. The performance of the backstepping sliding mode controller depends on parameters such as the backstepping transformation function, the sliding mode surface function, and the sliding mode control law function. The determination method of these parameters is more complicated. In Section 3, the control law was derived by an analytical method. Based on this, some parameters were adjusted by referring to some literature [41,42] and combining with our model.

Table 2.
Parameter values of the controllers.
4.2. Simulation Results and Discussions
According to the simulation setup of the proposed method, Figure 4 and Figure 5 show the comparison of the control effects of two controllers under external disturbance forces. Figure 4 compares the displacement tracking results of the pneumatic cylinder. As shown in Figure 4, the ESO-based BSMC method has a faster response speed, higher control accuracy, and smaller tracking error than the traditional PID control method. This is also confirmed by the comparison of the pneumatic cylinder displacement error in Figure 5. The displacement tracking simulation results of the pneumatic cylinder demonstrate that the proposed control algorithm has better control performance.

Figure 4.
Displacement simulation results of the pneumatic cylinder.
Figure 5.
Displacement tracking error of the pneumatic cylinder.
Figure 6 shows the comparison of the outputs of two controllers, indicating that the proposed backstepping sliding mode controller (BSMC) can still ensure stable output under external disturbances. Figure 7, Figure 8 and Figure 9 compare the simulated and estimated values of the displacement, velocity, and acceleration of the pneumatic cylinder, respectively. The solid lines represent the simulated signals, while the dashed lines represent the estimated signals. The comparison results at each observation point show that the estimation effect using the extended state observer (ESO) method is satisfactory. As the simulation time increases, the estimation error gradually decreases, ensuring control accuracy. Therefore, the observer designed in this paper can realize sensorless information estimation, providing convenience for some application scenarios where sensors are not convenient to install. Figure 10 shows the estimated value of the comprehensive disturbance force on the pneumatic cylinder. It can be seen that the disturbance force is sinusoidal and nonlinear, consistent with the disturbance signal set in Section 4.1. Therefore, the observer designed in this paper is also effective for complex disturbance estimation.
Figure 6.
Comparison of the controllers’ output.

Figure 7.
Displacement estimation results of the ESO.

Figure 8.
Velocity estimation results of the ESO.
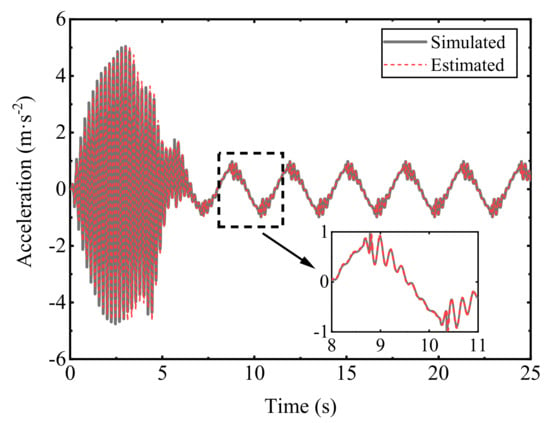
Figure 9.
Acceleration estimation results of the ESO.

Figure 10.
Disturbance force observation results of the ESO.
To evaluate the control effect of the two controllers qualitatively, the following three indicators are introduced to assess the displacement tracking error of the pneumatic cylinder [43]:
- (1)
- Mean absolute error (MAE):
- (2)
- Root mean square error (RMSE):
- (3)
- Integrated time and absolute error (ITAE):
The MAE value indicates the average level of the control error, as it represents the mean absolute error between the actual and the expected displacement of the pneumatic cylinder. The RMSE value reflects the dispersion of the displacement control error, as it is computed from the square root of the ratio of the squared deviation between the actual and the expected displacement of the pneumatic cylinder and the number of measurements n. The RMSE value is sensitive to the outliers of the error. The ITAE value is obtained by weighting the displacement control error of the pneumatic cylinder with time. This indicator is insensitive to the initial error but sensitive to the later error. Table 3 presents the calculation results of three indicators for two control algorithms. It can be observed that the ESO-based backstepping sliding mode controller has better indicators than the traditional PID controller. The result demonstrates that the proposed method has higher control accuracy and robustness, as it is less affected by errors.

Table 3.
Comparison of performance evaluation indexes.
4.3. Experimental Setup
The test bench (Figure 11) enables the horizontal orientation of the pneumatic cylinder, using the rod as the moving element, and Figure 12 shows the test bench scheme, which illustrates the experimental bench designed and constructed in this work. This scheme, which is used in typical industrial applications, allows for the analysis of the behavior of the pneumatic cylinder in a realistic application environment. Moreover, a special structure is designed inside the hydraulic cylinder to achieve accurate measurement of the cylinder displacement.

Figure 11.
Test bench of pneumatic cylinder experiments.

Figure 12.
Scheme of the test bench.
The system components implemented in the test bench are as follows:
- SPEEDAIRE® Single-acting pneumatic cylinder, model 6CPZ8, which is made from stainless steel, and has a cylinder body with a diameter of 5/16 in, a stroke length 1 in.
- Two miniature pressure sensors, type XMLPM60RC23F, for measuring the pressure in the two chambers of the pneumatic cylinder.
- 5/2 solenoid valve B522ADA53C, to control the pneumatic cylinder.
- 24 volts push button to activate the 5/2 proportional solenoid valve.
- A dSPACE DS1104 data acquisition system for receiving sensor signals and triggering control signals.
- A power supply to provide electrical energy.
- A Lenovo Notebook G15, for operation control.
The pressure source of the pneumatic system, Ps, is supplied by a gas tank, which is regulated and maintained at a constant pressure by a regulating valve. The input voltage of the proportional solenoid valve is changed by a push button, allowing the pneumatic cylinder rod to move to the expected position. Two pressure sensors, model XMLPM60RC23F, are mounted 10 cm from the cylinder to measure the pressure in the pneumatic cylinder chambers. The dSPACE 1104 data acquisition board, with a real-time data acquisition rate of 0.2 kHz, can receive the analog voltage generated by the sensors and send commands to the push button with the help of a computer. A linear optical encoder is used to measure the displacement of the pneumatic cylinder, connected to the pneumatic cylinder on one end and to the dSPACE DS1104 on the other. The encoder has a resolution of 200 lines per inch and is fixed to the end of the cylinder’s moving rod to ensure correct alignment with the coding strip affixed to the inside of the protective housing. Vibration damping devices such as sponges and brackets are used to protect the encoder, ensuring that the movement of the cylinder rod is accurately captured during sudden strong air pressure shocks. Real-time interaction and recording of data are performed by MATLAB/Simulink (R2017b), which is commonly used in industry.
4.4. Experimental Design
To verify the advantages of the proposed control strategy, comparative experiments were conducted using the same parameters as the simulation as much as possible. However, it should be noted that due to the existence of various disturbances in the experiments, the experimental environment was difficult to be consistent with the simulation. It should also be mentioned that for a polishing robot pneumatic system, low-pressure control has obvious benefits in reducing throttling loss, but it also poses challenges to control stability. PID control is the most widely used algorithm in engineering due to its simplicity, ease of operation, and stability. Therefore, PID control was chosen to validate the designed control algorithm. To verify the effectiveness of the proposed control algorithm, four cases were designed as follows:
Case 1: Sinusoidal trajectory test condition. xd = 200sin(0.5πt) with F = 40 N and the gas source pressure is set to 4 MPa
Case 2: Ramp trajectory test condition. The trajectory consists of two slopes with speed of 20 mm/s and the gas source pressure are set to 4 MPa.
Case 3: Step trajectory test condition. The amplitude and frequency of the trajectory are 200 mm and 0.25 Hz, respectively.
Case 4: Sinusoidal trajectory test condition. xd = 200sin(0.5πt) with F = 40 N and the gas source pressure is set to 3 MPa.
The parameters of the experimental platform are provided in Table 4. As pneumatic systems are time-varying systems, some parameters are difficult to obtain precisely. Therefore, only some values from manufacturers’ samples or from experimental measurements are listed here, which were experimentally determined.

Table 4.
System parameter of experiment.
In the experiment, the gas source pressure was set to 4 MPa and the parameters shown in Table 5 were adopted for both controllers as an example. All controller parameters were adjusted to achieve the best possible control performance. The performance metrics used in the simulation were also applied to evaluate the experimental results. However, for the sake of experimental simplicity and repeatability, the RMSE metric was chosen as the evaluation criterion, which is also commonly used in experimental design. It is important to note that although only one metric was used to evaluate the performance of the two controllers in the experiment, the simulation results showed that all 3 performance metrics had a consistent trend. Therefore, this experimental approach, which used only the RMSE to evaluate the experimental results, was sufficiently convincing.

Table 5.
Parameter values of the controllers used in experiment.
4.5. Experimental Results and Discussions
Before discussing the results of the experimental tests, it should be clarified that in Cases 1 to 4, different expected trajectory signals were also tested. The main purpose was to verify the validity of the two algorithms in different test environments. To better compare the control effects of the two control algorithms under different cases, the same hydraulic cylinder displacement (200 mm) was finally selected.
In this operating condition, where limited space on the test bench restricts the placement of an adequate number of sensors for detailed measurements of each information, the extended state observer (ESO) demonstrates excellent applicability. The estimation capability of the ESO for system information was first tested. In the experimental setup, external forces were controllable, making the force signal a suitable criterion for evaluation. Figure 13 illustrates the interference force estimation during the test. The black curve represents the output force of the ESO, which is nonsmooth due to environmental noise and other disturbances. The red curve represents the filtered and smoothed result. From approximately 0 to 0.25 s, the estimated force rises from 0 N to around 60 N and fluctuates in the vicinity until 2 s. Subsequently, it stabilizes around 50 N. This can be explained by the fact that within the initial 0.25 s, the pneumatic system is just starting and is in an unstable state. Due to factors such as frictional forces within the pneumatic cylinder and medium resistance, the estimated interference force fluctuates within a larger range. After 2 s, the entire system tends to stabilize, and additional interference forces decrease. Therefore, the estimated force is observed to stabilize around a smaller value. Finally, an external force of approximately 48 N is obtained, which is larger than the set value of 40 N. This indicates that a portion of the interference force, including frictional forces, can also be indirectly estimated, demonstrating the accuracy of the ESO method in testing.

Figure 13.
Estimation of interference forces in testing.
In addition to the trajectory tracking error, the control performance is also assessed using the maximum error percentage (MEP), which is obtained by dividing the maximum error by the maximum position value [44]. The trajectory results for Cases 1 to 4, comparing BSMC and PID, are shown in Figure 14, Figure 15, Figure 16 and Figure 17.
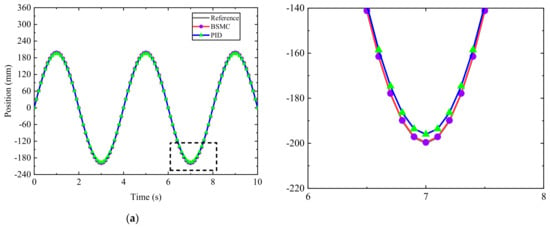
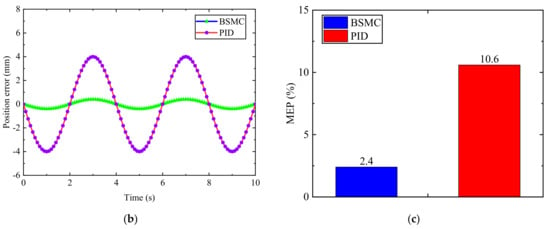
Figure 14.
Experimental results under the sinusoidal test condition with gas pressure 4 MPa. (a) Trajectory tracking result. (b) Trajectory tracking error. (c) Result of MEP.
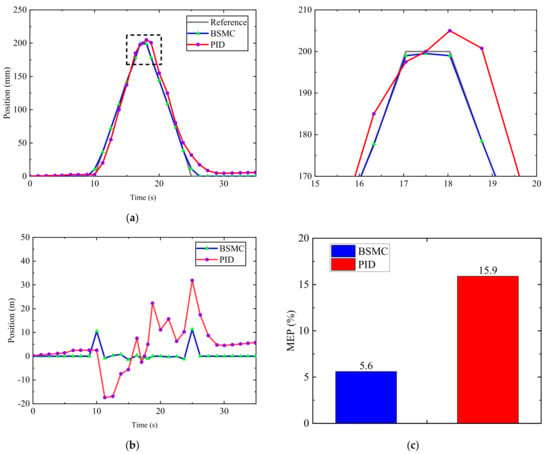
Figure 15.
Experimental results under the ramp test condition with gas pressure 4 MPa. (a) Trajectory tracking result. (b) Trajectory tracking error. (c) Result of MEP.

Figure 16.
Experimental results under the step test condition with gas pressure 4 MPa. (a) Trajectory tracking result. (b) Trajectory tracking error. (c) Result of MEP.
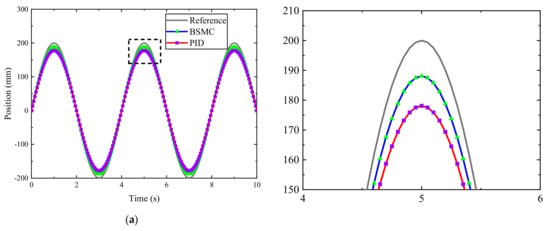

Figure 17.
Experimental results under the sinusoidal test condition with gas pressure 3 MPa. (a) Trajectory tracking result. (b) Trajectory tracking error. (c) Result of MEP.
The MEP chart and displacement tracking curves show that both the BSMC algorithm and the PID algorithm achieved good control performance, but the two algorithms exhibit significant differences for different test conditions. When the test conditions are stable and the reference is smooth, as shown in Figure 14, both the PID and BSMC tracking results are satisfactory and show no significant performance differences. However, when the reference signal is a ramp excitation, as shown in Figure 15, the BSMC algorithm outperforms the PID algorithm in terms of tracking speed and accuracy. This result is attributed to the ability of the BSMC algorithm to more accurately and quickly observe and compensate for errors and uncertainties through the ESO, with the advantage of fast adjustment of the observed state of the ESO. In addition, the BSMC controller achieves stability faster and the error converges to 0, which has a clear advantage over PID. Compared to Figure 14 and Figure 17, the accuracy of either the BSMC or PID control decreases when the gas pressure becomes smaller in the experiment. The decrease in gas pressure results in a reduction of the drive force applied to the cylinder, thereby amplifying the impact of cylinder friction and overall system nonlinearity. Consequently, controlling the position of the pneumatic system at low speeds and low pressures becomes a crucial and challenging task.
As mentioned above, the RMSE values of the two algorithms under the four cases are calculated as shown in Table 6. Compared to the PID, the average RMSE of the BSMC is reduced by 77.04% ((6.7 − 1.54)/6.7), with smaller RMSE values indicating higher control accuracy. This result strongly supports the analysis presented and demonstrates the effectiveness of the BSMC algorithm in achieving higher control accuracy and robustness.

Table 6.
The RMSE value under different cases.
5. Conclusions
This paper proposes an effective backstepping sliding mode control scheme based on the extended state observer for pneumatic position control of polishing robots. Both simulations and experiments demonstrate its advantages over conventional PID in trajectory tracking accuracy and disturbance rejection. The main research elements and conclusions are as follows:
- (1)
- A mathematical model of the polishing robot pneumatic system is established, considering factors such as cylinder dynamics, valve flow characteristics, and friction.
- (2)
- An extended state observer is designed to estimate unmeasured states such as velocity, acceleration and total disturbance. Stability analysis proves that the estimation error is bounded.
- (3)
- A backstepping sliding mode controller is systematically designed and stability is proved using Lyapunov theory, and the controller achieves robust tracking against disturbances.
- (4)
- Co-simulations in AMESim and MATLAB verify the effectiveness of the proposed control method in tracking various trajectories under friction and load disturbances. It demonstrates superior performance over PID control. Comparative experiments on a test bench further validate the proposed method, showing an over 77% average reduction in tracking error compared to PID control.
The method proposed in this paper is simple and practical. However, it should be noted that although the method has proven to be effective in bench tests, its effectiveness in a real working environment still needs further investigation. Therefore, future work may focus on implementing the control scheme on an actual polishing robot and evaluating its performance improvement in industrial polishing tasks. The observer and control gains could also be adaptively tuned online to further enhance robustness, and extending the approach to pneumatic systems with multiple actuators is another worthwhile research direction.
Author Contributions
Conceptualization, Q.L.; methodology, Q.L.; software, Q.L.; validation, Q.L.; formal analysis, Q.L.; investigation, Q.L.; resources, Q.L.; data curation, Q.L.; writing—original draft preparation, Q.L.; writing—review and editing, Q.L. and B.D.; visualization, Q.L.; supervision, Q.L.; project administration, Q.L.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Research Project of Colleges and Universities in Anhui Province (No. 2022AH052356).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data in this study is available on request from the corresponding author.
Acknowledgments
The authors thank the editor and the reviewers for their useful feedback that improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xia, Z.; Fang, F.; Ahearne, E.; Tao, M. Advances in Polishing of Optical Freeform Surfaces: A Review. J. Mater. Process. Technol. 2020, 286, 116828. [Google Scholar] [CrossRef]
- Zhu, Z.-Q.; Chen, Z.-T.; Zhang, Y. A Novel Polishing Technology for Leading and Trailing Edges of Aero-Engine Blade. Int. J. Adv. Manuf. Technol. 2021, 116, 1871–1880. [Google Scholar] [CrossRef]
- Dai, S.; Li, S.; Ji, W.; Wang, R.; Liu, S. Adaptive Friction Compensation Control of Robotic Pneumatic End-Effector Based on LuGre Model. Ind. Robot Int. J. Robot. Res. Appl. 2023, 50, 848–860. [Google Scholar] [CrossRef]
- Mahamed, H.; Duan, J.; Dai, Z. An Automatic Control of Robotic Polishing for a Compound Surface Composed of a Plane and Curved Parts. Res. Sq. 2023. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Zhao, J.; Zhao, J. The Hybrid Force/Position Anti-Disturbance Control Strategy for Robot Abrasive Belt Grinding of Aviation Blade Base on Fuzzy PID Control. Int. J. Adv. Manuf. Technol. 2021, 114, 3645–3656. [Google Scholar] [CrossRef]
- Qin, Y.; Wu, H.; Li, Z.; Sun, N.; Sun, L. Design and Analysis of a Compliant End-Effector for Robotic Polishing Using Flexible Beams. Actuators 2022, 11, 284. [Google Scholar] [CrossRef]
- Su, X.; Xie, Y.; Sun, L.; Jiang, B. Constant Force Control of Centrifugal Pump Housing Robot Grinding Based on Pneumatic Servo System. Appl. Sci. 2022, 12, 9708. [Google Scholar] [CrossRef]
- Huilcapi, V.; Cajo, R.; Orellana, J.; Cascante, A. Nonlinear Identification and Position Control of a Pneumatic System. In Intelligent Technologies: Design and Applications for Society; Robles-Bykbaev, V., Mula, J., Reynoso-Meza, G., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 127–138. [Google Scholar]
- Fan, C.; Xue, C.; Zhang, L.; Wang, K.; Wang, Q.; Gao, Y.; Lei, L. Design and Control of the Belt-Polishing Tool System for the Blisk Finishing Process. Mech. Sci. 2021, 12, 237–248. [Google Scholar] [CrossRef]
- Tokat, S.; Fadali, M.S.; Eray, O. A Classification and Overview of Sliding Mode Controller Sliding Surface Design Methods. In Recent Advances in Sliding Modes: From Control to Intelligent Mechatronics; Yu, X., Önder Efe, M., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 417–439. ISBN 978-3-319-18290-2. [Google Scholar]
- Yang, J.; Li, S.; Yu, X. Sliding-Mode Control for Systems with Mismatched Uncertainties via a Disturbance Observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Song, J.; Ishida, Y. A Robust Sliding Mode Control for Pneumatic Servo Systems. Int. J. Eng. Sci. 1997, 35, 711–723. [Google Scholar] [CrossRef]
- Tran, X.B.; Nguyen, V.L.; Nguyen, N.C.; Pham, D.T.; Phan, V.L. Sliding Mode Control for a Pneumatic Servo System with Friction Compensation. In Advances in Engineering Research and Application; Sattler, K.-U., Nguyen, D.C., Vu, N.P., Tien Long, B., Puta, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 648–656. [Google Scholar]
- Fan, C.; Hong, G.S.; Zhao, J.; Zhang, L.; Zhao, J.; Sun, L. The Integral Sliding Mode Control of a Pneumatic Force Servo for the Polishing Process. Precis. Eng. 2019, 55, 154–170. [Google Scholar] [CrossRef]
- Dao, Q.-T.; Mai, D.-H.; Nguyen, D.-K.; Ly, N.-T. Adaptive Parameter Integral Sliding Mode Control of Pneumatic Artificial Muscles in Antagonistic Configuration. J. Control Autom. Electr. Syst. 2022, 33, 1116–1124. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Mehmood, A.; Bhatti, A.I. Robust Backstepping Sliding Mode Control Design for a Class of Underactuated Electro–Mechanical Nonlinear Systems. J. Electr. Eng. Technol. 2020, 15, 1821–1828. [Google Scholar] [CrossRef]
- Deutscher, J. A Backstepping Approach to the Output Regulation of Boundary Controlled Parabolic PDEs. Automatica 2015, 57, 56–64. [Google Scholar] [CrossRef]
- Binh, N.T.; Tung, N.A.; Nam, D.P.; Quang, N.H. An Adaptive Backstepping Trajectory Tracking Control of a Tractor Trailer Wheeled Mobile Robot. Int. J. Control Autom. Syst. 2019, 17, 465–473. [Google Scholar] [CrossRef]
- Deutscher, J. Output Regulation for General Linear Heterodirectional Hyperbolic Systems with Spatially-Varying Coefficients. Automatica 2017, 85, 34–42. [Google Scholar] [CrossRef]
- Lin, F.-J.; Shen, P.-H.; Hsu, S.-P. Adaptive Backstepping Sliding Mode Control for Linear Induction Motor Drive. Electr. Power Appl. IEE Proc. 2002, 149, 184–194. [Google Scholar] [CrossRef]
- Chunmei, Y.; Kunfeng, L.; Yuanqing, X.; Hailiang, L. Sliding Mode Control Attitude Tracking of Rigid Spacecraft Using Adaptive Back-Stepping Method. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28 July 2015; pp. 3281–3286. [Google Scholar]
- Zhang, J.; Xu, F.; Liu, X.; Gu, S.; Geng, H. Fixed-Time Dynamic Surface Control for Pneumatic Manipulator System with Unknown Disturbances. IEEE Robot. Autom. Lett. 2022, 7, 10890–10897. [Google Scholar] [CrossRef]
- Li, A.; Meng, D.; Lu, B.; Li, Q. Nonlinear Cascade Control of Single-Rod Pneumatic Actuator Based on an Extended Disturbance Observer. J. Cent. South Univ. 2019, 26, 1637–1648. [Google Scholar] [CrossRef]
- Ding, L.; Liu, K.; Zhu, G.; Wang, Y.; Li, Y. Adaptive Robust Control via a Nonlinear Disturbance Observer for Cable-Driven Aerial Manipulators. Int. J. Control Autom. Syst. 2023, 21, 604–615. [Google Scholar] [CrossRef]
- Ahmed, N.; Chen, M. Disturbance Observer-Based Robust Adaptive Control for Uncertain Actuated Nonlinear Systemwith Disturbances. Assem. Autom. 2021, 41, 567–576. [Google Scholar]
- Ran, M.; Li, J.; Xie, L. A New Extended State Observer for Uncertain Nonlinear Systems. Automatica 2021, 131, 109772. [Google Scholar] [CrossRef]
- Talole, S.E.; Kolhe, J.P.; Phadke, S.B. Extended-State-Observer-Based Control of Flexible-Joint System with Experimental Validation. IEEE Trans. Ind. Electron. 2010, 57, 1411–1419. [Google Scholar] [CrossRef]
- Özkal, F.M. Evolutionary Structural Optimization—A Trial Review. In Nature-Inspired Metaheuristic Algorithms for Engineering Optimization Applications; Carbas, S., Toktas, A., Ustun, D., Eds.; Springer: Singapore, 2021; pp. 277–308. ISBN 978-981-336-773-9. [Google Scholar]
- Pourdehi, S.; Naghavi, S.V.; Safavi, A.A. Observer-Based Robust Model Predictive Control of a Class of Nonlinear Systems with Both State and Input Delays. In Proceedings of the 3rd International Conference on Control, Instrumentation, and Automation, Tehran, Iran, 28–30 December 2013; pp. 65–70. [Google Scholar]
- Hosseini-Pishrobat, M.; Keighobadi, J. Extended State Observer-Based Robust Non-Linear Integral Dynamic Surface Control for Triaxial MEMS Gyroscope. Robotica 2019, 37, 481–501. [Google Scholar] [CrossRef]
- Qi, G.; Li, X.; Chen, Z. Problems of Extended State Observer and Proposal of Compensation Function Observer for Unknown Model and Application in UAV. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 2899–2910. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, Y.; Celler, B.G.; Su, S.W. Backstepping Control of Electro-Hydraulic System Based on Extended-State-Observer with Plant Dynamics Largely Unknown. IEEE Trans. Ind. Electron. 2016, 63, 6909–6920. [Google Scholar] [CrossRef]
- Yao, J.; Jiao, Z.; Ma, D. Extended-State-Observer-Based Output Feedback Nonlinear Robust Control of Hydraulic Systems with Backstepping. IEEE Trans. Ind. Electron. 2014, 61, 6285–6293. [Google Scholar] [CrossRef]
- Humaidi, A.J. Experimental Design and Verification of Extended State Observers for Magnetic Levitation System Based on PSO. Open Electr. Electron. Eng. J. 2018, 12, 110–120. [Google Scholar] [CrossRef]
- Furuichi, S.; Minculete, N. Refined Young Inequality and Its Application to Divergences. Entropy 2021, 23, 514. [Google Scholar] [CrossRef]
- Doudou, S.; Khaber, F. Adaptive Fuzzy Sliding Mode Control for a Class of Uncertain Nonaffine Nonlinear Strict-Feedback Systems. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 33–45. [Google Scholar] [CrossRef]
- Kurpaska, S.; Sobol, Z.; Pedryc, N.; Hebda, T.; Nawara, P. Analysis of the Pneumatic System Parameters of the Suction Cup Integrated with the Head for Harvesting Strawberry Fruit. Sensors 2020, 20, 4389. [Google Scholar] [CrossRef] [PubMed]
- Harris, P.G.; O’Donnell, G.E.; Whelan, T. Modelling and Identification of Industrial Pneumatic Drive System. Int. J. Adv. Manuf. Technol. 2012, 58, 1075–1086. [Google Scholar] [CrossRef]
- Trentini, R.; Campos, A.; Espindola, G.; Da Silveira, A.S. Parameter Identification of a Pneumatic Proportional Pressure Valve. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 69–77. [Google Scholar] [CrossRef]
- Deželak, K.; Bracinik, P.; Sredenšek, K.; Seme, S. Proportional-Integral Controllers Performance of a Grid-Connected Solar PV System with Particle Swarm Optimization and Ziegler–Nichols Tuning Method. Energies 2021, 14, 2516. [Google Scholar] [CrossRef]
- Ren, H.; Fan, J. Adaptive Backstepping Slide Mode Control of Pneumatic Position Servo System. Chin. J. Mech. Eng. 2016, 29, 1003–1009. [Google Scholar] [CrossRef]
- Sun, C.; Dong, X.; Wang, M.; Li, J. Sliding Mode Control of Electro-Hydraulic Position Servo System Based on Adaptive Reaching Law. Appl. Sci. 2022, 12, 6897. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.; Jurman, G. The Coefficient of Determination R-Squared Is More Informative than SMAPE, MAE, MAPE, MSE and RMSE in Regression Analysis Evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, H.; Zhang, P.; Ouyang, X.; Xu, L.; Ge, Y.; Yao, Y.; Yang, H. High-Precision Control Solution for Asymmetrical Electro-Hydrostatic Actuators Based on the Three-Port Pump and Disturbance Observers. IEEE/ASME Trans. Mechatron. 2023, 28, 396–406. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).