Optimal Design of a Five-Bar Planar Manipulator and Its Controller by Using Different Algorithms for Minimum Shaking Forces and Moments for the Largest Trajectory in a Usable Workspace

Abstract

In this paper, a structural design and controller optimization process for a five-bar planar manipulator are studied using three different population-based optimization techniques: particle swarm optimization, genetic algorithm, and differential evolution. First, the desired kinematic properties of the manipulator, such as the position, velocity, and acceleration of the endpoint, are determined using inverse kinematics. Then, an optimization problem is created to minimize the shaking force and moments, and the desired kinematic quantities are implemented as constraints. All the link properties of the manipulator are defined as design variables, and the optimization results are obtained. The results show that it is possible to significantly reduce the shaking force and moment significantly thanks to the optimal design parameters. Finally, the controller is optimized to find the best PID gains considering the forward kinematics of the manipulator. It is observed that the shaking force and shaking moment can be reduced by 99% and 54%, respectively, which has a very positive effect on the accuracy of the trajectory tracking. Moreover, the performances of the optimization methods are compared by using the same number of iterations in the calculations, and thus, it can be seen that the GA method achieves the best results compared to the others. Therefore, the results of this study are of utmost importance for a manufacturer, who wants to design a five-bar planar manipulator and its controller.

1. Introduction

In the last two decades, five-bar planar manipulators have been extensively used in various industrial fields, especially in robotic applications for mass production such as assembly, transportation, and positioning, as well as haptic and medical devices. There are a variety of five-bar planar manipulators depending on whether the actuators are rotary or linear [1].

In designing such a mechanism, several problems related to kinematics and dynamics must be solved. The determination of workspace (including singularity points) and trajectory planning are the main kinematic issues [1,2,3,4,5,6,7,8,9,10,11,12,13], while determination and minimization of the shaking forces and torques, together with the torques of the actuators, are the crucial dynamic issues [14,15,16,17,18,19,20,21,22,23]. In [2,3], the singularity and workspace of the 5R (revolute joint) symmetrical parallel mechanism are studied. Cervantes et al. found all the working space and singularity curves of a 2-DOF, 5R manipulator [2]. On the other hand, X.-J. Liu et al. determined the optimal design criteria for the maximum working space, which is only suitable for working conditions with an upward configuration [3]. Stan et al. [6] addressed a kinematic optimization problem for a microparallel RPRPR robot (two linear actuators and three revolute joints). In their kinematic optimization, the most suitable dimensions of the bipod model were found for the largest workspace.

For fast-moving parallel mechanisms, trajectory planning is also of great importance. Oarcea et al. [10] studied two motion profiles (constant velocity and trapezoidal velocity) using the Dassault Systems Solidworks and Simulink Simscape Multibody Software. In [11,12], the integration of non-circular gears is specifically used to operate on only one precise trajectory. In particular, in [11], the dimensions of a five-bar mechanism were obtained by genetic optimization as a function of the trajectory. Uzunoglu et al. [13] integrated the five-bar mechanism into laser-cutting machines to accelerate short movements. They designed a new algorithm by adding the U and V axes to the five-bar mechanism, in addition to the X and Y main axes, to the G-codes, which is known as the communication language of the CNC systems.

High-speed mechanisms are designed to eliminate or minimize shaking forces and shaking moments. Berkoff [14] has shown that an inertial counterweight and a physical pendulum joint can provide a complete balance of force and moment for a specific case of inline joints. In addition, the conditions for redistribution of mass and the inclusion of additional masses required to fully balance the inertial loads of the linkage were determined.

Alici and Shirinzadeh [17] analyzed the dynamic equilibrium of the five-bar linkage to optimize the sum of squared values of the bearing forces, driving torques, shaking moment, and the sum of angular momentum by considering the lengths and angles of the mechanism. Ilia and Sinatra [20] used a novel simplified approach for the dynamic balancing of five-bar linkages. They derived the dynamic model of the five-bar mechanism by restoring the natural-orthogonal complement method and then determined the shaking force acting in the workspace. A system of seven equations and four inequality constraints with twelve linkage parameters expressed the dynamic balancing conditions of the five-bar linkage.

The population-based optimization methods are very effective tools for determining the correct kinematic and dynamic parameters of the mechanism. The most commonly used stochastic optimization methods in the literature are the genetic algorithm (GA), particle swarm optimization (PSO), and differential evolution (DE). These methods have numerous applications regarding the mechanism and machine design [24,25,26,27,28,29,30,31,32,33,34,35]. Yildiz [28] used these methods to optimize the four-bar linkages used in the mechanism to open and close the trunk lid of sedans. Sergiu, Maties, and Balan [9] solved an optimization problem using a genetic algorithm to create the largest workspace; as a result, they determined the symmetric link length. Alici and Shirinzadeh [18] used a genetic algorithm for the dynamic balancing of the five-bar linkage. In their study, they determined which components were more important in the objective function by giving the weight factors the value “0” or “1”.

In practice, the control of a manipulator is also an important issue. Among the numerous works in this field, some important ones related to the present work will be mentioned here. In [36], the prototype of a planar parallel manipulator with five-bars was created by a multi-disciplinary study, and the simulation results were compared with the measurement results by performing the PI control. Tao and Sadler [37] developed the constant speed control of a four-bar mechanism driven by a motor using a state-space representation, and several modified PID-type rules were implemented. In recent years, various control algorithms seem to work together or nested. [38,39,40]. In [40], the extreme learning machine-PID controller has shown that it outperforms the pure P and PID controllers with the adaptive tuning of the control parameters. Optimization methods such as GA [38] and PSO [39] are used, especially to select the coefficients of the widely used PID controller. In this study, the gains of the PID controllers are determined using an optimization technique after solving the problem of balancing the shaking forces and moments.

This work differs from the previous studies in three aspects. First, in solving the balancing problem of the manipulator, all the properties of the joints, such as the lengths, masses, inertias, and centers of gravity of the bars, are considered optimization parameters. Second, in this optimization problem, the largest desired trajectory is tracked in the reachable workspace (without singularity) with the constraint functions. Third, the PID gains of the developed controller are also obtained by optimization. The balancing and control of the manipulator could be posed as a single multi-objective optimization problem. However, the combination of these two stages of the problem could make the optimization algorithm become more complicated. Hence, the manipulator control problem was defined as a secondary optimization problem. The layout of the simulation of the optimization algorithms has seen in Figure 1. Three different optimization techniques have been used to compare their performances for both optimization problems.

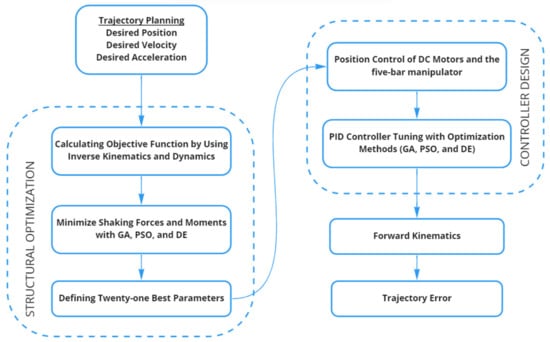
Figure 1. The layout of the simulation of the optimization algorithm.

2. Modeling of the Five-Bar Planar Manipulator

The general view of the five-bar manipulator used in this paper is illustrated in Figure 2. Provided that the physical features and positions of the links and the desired motion profile of point P are known, the angular position, velocity, and acceleration values are determined from inverse kinematic analysis.

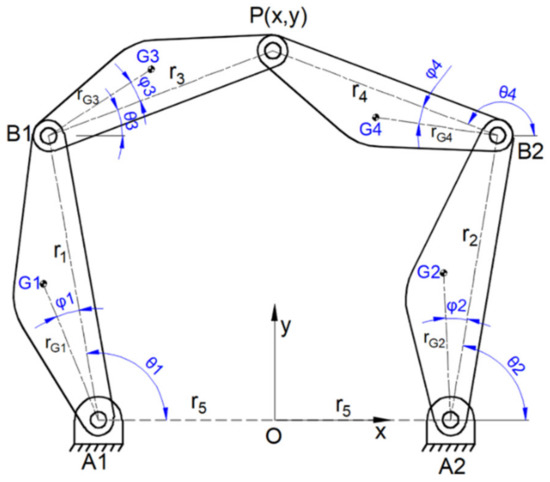
Figure 2. The five-bar manipulator.

2.1. Inverse Kinematics of the Five-Bar Planar Manipulator

The loop equation of the five-bar manipulator can be written as follows:

$$\overrightarrow{OP}=\overrightarrow{O{A}_1}+\overrightarrow{A_1{B}_1}+\overrightarrow{B_{1}P}=\overrightarrow{O{A}_2}+\overrightarrow{A_2{B}_2}+\overrightarrow{B_{2}P}$$

(1)

or in form of complex numbers,

$$r_5{e}^{i\pi }+r_1{e}^{i{\theta }_1}+r_3{e}^{i{\theta }_3}=x+iy$$

(2)

$$r_5{e}^0+r_2{e}^{i{\theta }_2}+r_4{e}^{i{\theta }_4}=x+iy$$

(3)

In the above equations, r_i (i = 1…5) denote the lengths of the links and θ_i (i = 1…4) their rotation angles. Besides, the terms x and y define the position of point P. The solution of the inverse kinematic problem can be expressed with the following equations:

$$r_3^2={\left(x+r_5-r_{1}cos{\theta }_1\right)}^2+{\left(y-r_1\mathit{sin}{\theta }_1\right)}^2$$

(4)

$$r_4^2={\left(x-r_5-r_{2}cos{\theta }_2\right)}^2+{\left(y-r_2\mathit{sin}{\theta }_2\right)}^2$$

(5)

where θ₁ and θ₂ are the input angles of the mechanism. These are obtained from either Equations (4) and (5):

$${\theta }_i=2{\mathit{tan}}^{-1}\left(z_i\right), \mathrm{for} i=1,2$$

(6)

where

$$z_i=\frac{-b_i+{\sigma }_i\sqrt{b_i^2-4a_i{c}_i}}{2a_i}, \mathrm{for} i=1,2$$

(7)

in which

$$\begin{gathered} a_1=x^2+y^2+r_5{}^2+r_1{}^2-r_3{}^2+2x{r}_5+2r_5{r}_1+2x{r}_1 \\ {b}_1=-4y{r}_1 \\ {c}_1=x^2+y^2+r_5{}^2+r_1{}^2-r_3{}^2+2x{r}_5-2r_5{r}_1-2x{r}_1 \\ {a}_2=x^2+y^2+r_5{}^2+r_2{}^2-r_4{}^2-2x{r}_5-2r_5{r}_2+2x{r}_2 \\ {b}_2=-4y{r}_2 \\ {c}_2=x^2+y^2+r_5{}^2+r_2{}^2-r_4{}^2-2x{r}_5+2r_5{r}_2-2x{r}_2 \end{gathered}$$

(8)

Five-bar planar parallel manipulators have four inverse kinematics solutions [3]. These solution configurations have (+ −), (+ +), (− −), and (− +) models according to the sign of (σ₁ σ₂) values. In this paper, the inverse kinematics solution is obtained by considering the operation in the (+ −) model; that is, σ₁ = + 1 and σ₂ = −1 are taken. θ₃ and θ₄ are obtained by substituting the values of θ₁ and θ₂ in Equations (2) and (3).

The relationship between the link angular velocities and the linear velocity components of point P is given by the following matrix equation:

$$\left[\begin{array}{c}{\omega }_1\\ {\omega }_2\\ {\omega }_3\\ {\omega }_4\end{array}\right]={\left[\begin{array}{cccc}-r_1\mathit{sin}{\theta }_1& 0& -r_3\mathit{sin}{\theta }_3& 0\\ r_1\mathit{cos}{\theta }_1& 0& r_3\mathit{cos}{\theta }_3& 0\\ 0& -r_2\mathit{sin}{\theta }_2& 0& -r_4\mathit{sin}{\theta }_4\\ 0& r_2\mathit{cos}{\theta }_2& 0& r_4\mathit{cos}{\theta }_4\end{array}\right]}^{-1}\left[\begin{array}{c}{V}_x\\ V_y\\ V_x\\ V_y\end{array}\right]$$

(9)

where ω_i (i = 1…4) are links’ angular velocities. V_x and V_y are the x- and y-components of point P.

Similarly, the angular accelerations are given as follows:

$$\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ {\alpha }_3\\ {\alpha }_4\end{array}\right]={\left[\begin{array}{cccc}-r_1\mathit{sin}{\theta }_1& 0& -r_3\mathit{sin}{\theta }_3& 0\\ r_1\mathit{cos}{\theta }_1& 0& r_3\mathit{cos}{\theta }_3& 0\\ 0& -r_2\mathit{sin}{\theta }_2& 0& -r_4\mathit{sin}{\theta }_4\\ 0& r_2\mathit{cos}{\theta }_2& 0& r_4\mathit{cos}{\theta }_4\end{array}\right]}^{-1}\left[\begin{array}{c}{a}_x+r_1{\omega }_1{}^2\mathit{cos}{\theta }_1+r_3{\omega }_3{}^2\mathit{cos}{\theta }_3\\ a_y+r_1{\omega }_1{}^2\mathit{sin}{\theta }_1+r_3{\omega }_3{}^2\mathit{sin}{\theta }_3\\ a_x+r_2{\omega }_2{}^2\mathit{cos}{\theta }_2+r_4{\omega }_4{}^2\mathit{cos}{\theta }_4\\ a_y+r_2{\omega }_2{}^2\mathit{sin}{\theta }_2+r_4{\omega }_4{}^2\mathit{sin}{\theta }_4\end{array}\right]$$

(10)

where α_i (i = 1…4) are links’ angular accelerations. a_x and a_y are linear acceleration components of point P in the x- and y-directions. The accelerations of the center of gravities can be obtained as follows:

$$\left[\begin{array}{c}{a}_{G1x}\\ a_{G1y}\\ a_{G3x}\\ a_{G3y}\\ a_{G2x}\\ a_{G2y}\\ a_{G4x}\\ a_{G4y}\end{array}\right]=\left[\begin{array}{c}\begin{array}{l}\begin{array}{c}\hfill -r_{G1}{\alpha }_1\mathit{sin}\left({\theta }_1+{\phi }_1\right)-r_{G1}{\omega }_1^2\mathit{cos}\left({\theta }_1+{\phi }_1\right)\hfill \\ \hfill r_{G1}{\alpha }_1\mathit{cos}\left({\theta }_1+{\phi }_1\right)-r_{G1}{\omega }_1^2\mathit{sin}\left({\theta }_1+{\phi }_1\right)\hfill \\ \hfill -r_1{\alpha }_1\mathit{sin}{\theta }_1-r_1{\omega }_1^2\mathit{cos}{\theta }_1-r_{G3}{\alpha }_3\mathit{sin}\left({\theta }_3+{\phi }_3\right)-r_{G3}{\omega }_3^2\mathit{cos}\left({\theta }_3+{\phi }_3\right)\hfill \\ \hfill r_1{\alpha }_1\mathit{cos}{\theta }_1-r_1{\omega }_1^2\mathit{sin}{\theta }_1+r_{G3}{\alpha }_3\mathit{cos}\left({\theta }_3+{\phi }_3\right)-r_{G3}{\omega }_3^2\mathit{sin}\left({\theta }_3+{\phi }_3\right)\hfill \end{array}\\ \hfill -r_{G2}{\alpha }_2\mathit{sin}\left({\theta }_2+{\phi }_2\right)-r_{G2}{\omega }_2{}^2\mathit{cos}\left({\theta }_2+{\phi }_2\right)\hfill \end{array}\\ r_{G2}{\alpha }_2\mathit{cos}\left({\theta }_2+{\phi }_2\right)-r_{G2}{\omega }_2^2\mathit{sin}\left({\theta }_2+{\phi }_2\right)\\ -r_2{\alpha }_2\mathit{sin}{\theta }_2-r_2{\omega }_2^2\mathit{cos}{\theta }_2-r_{G4}{\alpha }_4\mathit{sin}\left({\theta }_4+{\phi }_4\right)-r_{G4}{\omega }_4^2\mathit{cos}\left({\theta }_4+{\phi }_4\right)\\ r_2{\alpha }_2\mathit{cos}{\theta }_2-r_2{\omega }_2^2\mathit{sin}{\theta }_2+r_{G4}{\alpha }_4\mathit{cos}\left({\theta }_4+{\phi }_4\right)-r_{G4}{\omega }_4^2\mathit{sin}\left({\theta }_4+{\phi }_4\right)\end{array}\right]$$

(11)

where r_gi and φ_i (i = 1…4) are the magnitudes and orientation angles of the local position vectors of the centers of gravity.

2.2. Inverse Dynamics of the Five-Bar Planar Manipulator

In this part, to determine the shaking forces and moments transmitted to the machine foundation, the dynamic analysis of the mechanism is carried out by using the well-known Newton–Euler principle. The free-body diagrams are given in Figure 3.

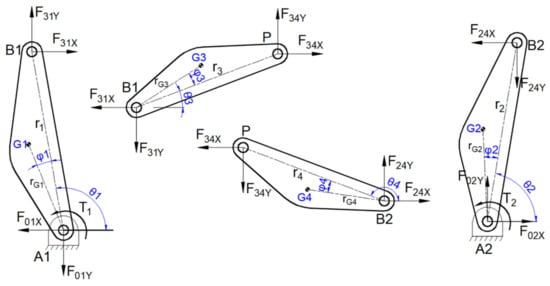
Figure 3. Free body diagrams of the five-bar planar manipulator.

The following equations of motion are written for link 1:

$$-F_{01x}+F_{31x}=m_1{a}_{G1x}$$

(12)

$$-F_{01y}+F_{31y}=m_1{a}_{G1y}$$

(13)

$$\overrightarrow{T_1}+\overrightarrow{G{A}_1}x\overrightarrow{F_{01}}+\overrightarrow{G{B}_1}x\overrightarrow{F_{31}}=I_{G1}\overrightarrow{{\alpha }_1}$$

(14)

where

$$\overrightarrow{G{A}_1}=-\overrightarrow{A_{1}G}=-(r_{G1}\mathit{cos}({\theta }_1+{\phi }_1)\overrightarrow{i}+r_{G1}\mathit{sin}({\theta }_1+{\phi }_1)\overrightarrow{j})$$

(15)

$$\overrightarrow{G{B}_1}=\overrightarrow{r_1}-\overrightarrow{r_{G1}}=\left(r_1\mathit{cos}{\theta }_1-r_{G1}\mathit{cos}({\theta }_1+{\phi }_1)\right)\overrightarrow{i}+\left(r_1\mathit{sin}{\theta }_1-r_{G1}\mathit{sin}({\theta }_1+{\phi }_1)\right)\overrightarrow{j}$$

(16)

Substituting Equations (15) and (16) in Equation (14) yields the following equation:

$$\begin{array}{ll}{T}_1& +r_{G1}\mathit{cos}({\theta }_1+{\phi }_1)F_{01y}-r_{G1}\mathit{sin}({\theta }_1+{\phi }_1)F_{01x}+\left(r_1\mathit{cos}{\theta }_1-r_{G1}\mathit{cos}({\theta }_1+{\phi }_1)\right)F_{31y}\\ & -\left(r_1\mathit{sin}{\theta }_1-r_{G1}\mathit{sin}({\theta }_1+{\phi }_1)\right)F_{31x}=I_{G1}{\alpha }_1\end{array}$$

(17)

Similar equations must be written for other links. All the equations of motion are given in the matrix form (Appendix A). The number of motion equations is twelve. It should be noted that the dynamic equations of the system are derived by considering zero friction conditions.

2.3. Shaking Force and Moment of the Five-Bar Planar Manipulator

The five-bar manipulator is connected to the ground at two fixed pivot points, A₁ and A₂. The sum of the forces transmitted to the ground via the fixed joints is defined as the shaking force. This shaking force is given in Equation (20).

$$F_{01}=\sqrt{F_{01x}{}^2+F_{01y}{}^2}$$

(18)

$$F_{02}=\sqrt{F_{02x}{}^2+F_{02y}{}^2}$$

(19)

$$F_s=-\left(F_{02}-F_{01}\right)$$

(20)

The shaking moment transmitted to the ground is as follows:

$$M_s=-\left(T_1+T_2+2r_{5}x{F}_{02y}\right)$$

(21)

3. Structural Optimization of Five-Bar Planar Manipulator

3.1. Desired Trajectory Planning

The largest circular trajectory in two-dimensional space is assumed to be tracked by point P in the reachable workspace (no singular points), as illustrated in Figure 4.

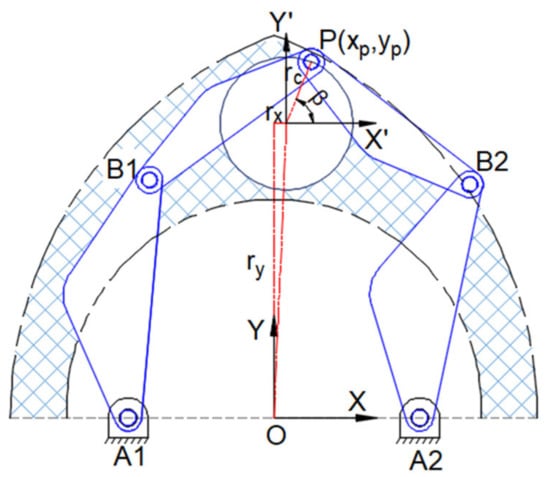
Figure 4. Applied trajectory.

The trapezoidal motion program is one of the most widely used motions in industrial robots. In the trapezoidal velocity profile, the endpoint P moves with maximum constant velocity during most of the operation time. The desired motion profile equations are presented in Equations (22)–(24).

$$\beta \left(t\right)=\left\{\begin{array}{c}\frac{a_c}{2}{t}^2 0\le t\le t_1\\ a_c{t}_1\left(t_2-t_1\right) t_1\le t\le t_2\\ \frac{a_c}{2}{(t-t_2)}^2 t_2\le t\le t_f\end{array}\right.$$

(22)

$$\dot{\beta }\left(t\right)=\left\{\begin{array}{c}{a}_{c}t 0\le t\le t_1\\ a_c{t}_1 t_1\le t\le t_2\\ a_c{t}_f-a_{c}t t_2\le t\le t_f\end{array}\right.$$

(23)

$$\ddot{\beta }\left(t\right)=\left\{\begin{array}{c}{a}_c 0\le t\le t_1\\ 0 t_1\le t\le t_2\\ -a_c t_2\le t\le t_f\end{array}\right.$$

(24)

The trajectory is comprised of three main parts, as shown in Figure 5a. These plots represent the angular position, angular velocity, and angular acceleration of the endpoint P. For a circular trajectory, the endpoint P position, velocity, and acceleration according to the motion as defined in Figure 5a are given in Figure 5b.

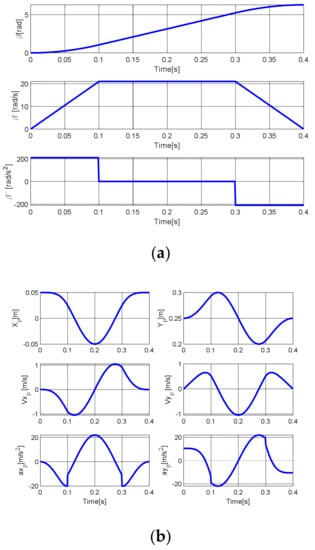
Figure 5. (a) The trapezoidal motion profile, (b) position, velocity, and acceleration of the endpoint P.

3.2. Definition of the Objective Function, Design Variables, and Constraints

The optimization problem can be defined as re-dimensioning the five-bar manipulator such that the shaking forces and shaking moments become minimized while following the desired trajectory. The objective function is selected as follows:

$$F=w_1{f}_1+w_2{f}_2$$

(25)

where $w_1$ and $w_2$ are the weighting factors, $f_1$ and $f_2$ are the first and second objective functions, respectively. The weighting factors’ sum should be equal to one. The first objective function is the sum of the absolute values of shaking force, while the sum of the absolute shaking moment is the second objective function.

$$f_1=\sum \overrightarrow{\parallel F_s\parallel }$$

(26)

$$f_2=\sum \overrightarrow{\parallel M_s\parallel }$$

(27)

This object function includes twenty-one design variables given in the following:

$$[\begin{array}{ccccccccccccccccccccc}{r}_{g1}& r_{g2}& r_{g3}& r_{g4}& m_1& m_2& m_3& m_4& I_g{}_1& I_g{}_2& I_g{}_3& I_g{}_4& {\phi }_1& {\phi }_2& {\phi }_3& {\phi }_4& r_1& r_2& r_3& r_4& r_5]\end{array}$$

(28)

The constraint functions contain keeping the desired trajectory within the workspace and balancing the five-bar manipulator.

$$\begin{gathered} g_1={\left(x+r_5\right)}^2+y^2-{\left(r_1+r_3\right)}^2\le 0 \\ {g}_2={\left(x-r_5\right)}^2+y^2-{\left(r_2+r_4\right)}^2\le 0 \\ {g}_3=x-\left(r_{1}cos{\theta }_1+r_{2}cos{\theta }_2\right)/2\le 0 \\ {g}_4=y-\left(r_{1}sin{\theta }_1+r_{2}sin{\theta }_2\right)/2\le 0 \\ {g}_5=m_1{r}_{G1}\mathit{cos}{\phi }_1+m_3{r}_1+m_4{r}_{G4}\mathit{cos}{\phi }_4\frac{r_1}{r_4}\le 0 \\ {g}_{6=}{r}_{G1}\mathit{sin}{\phi }_1+m_4{r}_{G4}\mathit{sin}{\phi }_4\frac{r_1}{r_4}\le 0 \\ {g}_7=m_3{r}_{G3}\mathit{cos}{\phi }_3+m_4{r}_{G4}\mathit{cos}{\phi }_4\frac{r_3}{r_4}\le 0 \\ {g}_8=r_{G3}\mathit{sin}{\phi }_3+m_4{r}_{G4}\mathit{sin}{\phi }_4\frac{r_3}{r_4}\le 0 \\ {g}_9=m_2{r}_{G2}\mathit{cos}{\phi }_2+m_4{r}_2-m_4{r}_{G4}\mathit{cos}{\phi }_4\frac{r_2}{r_4}\le 0 \end{gathered}$$

(29)

where g₁ and g₂ are the equations of the outer circle of the workspace. g₃ and g₄ show the singularity created by the locus of point P when B1PB2 is completely extended. Other functions are related to mass balancing.

In order to limit the solution space, the following constraints are also added to the above-mentioned ones.

$$\begin{array}{ll}0\le r_{gi}& \mathrm{for} i=1\dots 4\\ 0.7m_i\le m_i\le 1.3m_i& \mathrm{for} i=1\dots 4\\ 0.7I_{gi}\le I_{gi}\le 1.3I_{gi}& \mathrm{for} i=1\dots 4\\ 0\le {\phi }_i\le 2\pi & \mathrm{for} i=1\dots 4\\ 0.9r_i\le r_i\le 1.1r_i& \mathrm{for} i=1\dots 5\end{array}$$

(30)

3.3. Applied Optimization Methods

In this study, we have used three optimization procedures. These were, namely, genetic algorithm (GA) [36], particle swarm optimization (PSO) [37], and differential evolution (DE) [38,39]. GA procedure is inspired by reproduction processes and natural selection. This method aims to solve the extremum problems with a randomly generated population of individuals called chromosomes. GA reproduces new generations of those chromosomes by considering the natural selection approach, which can be summarized as survival of the fittest. The PSO method, which is a stochastic optimization algorithm, was inspired by the group behavior of birds and fishes. In this method, a random group of particles is submitted to search for the extreme point of the objective function. Then, the particles follow the nearest ones to obtain the best value of the target through the reproduced velocities. This process continues until the final criteria are satisfied. DE algorithm uses real numbers to represent each variable’s value. Its speed, tenacity, and basic structure are the most important assets of this method. Equations of the PSO and DE methods are given in Appendix B.

For each optimization method, the objective function is calculated until the maximum number of iterations is reached and the best solution is found. The pseudocode and parameters of the optimization methods are given in Table 1.

Table 1. Optimization pseudo-codes and the optimization parameters.

Pseudo-codes
GA		PSO		DE
START Generate the initial population Compute fitness REPEAT Selection Crossover Mutation Compute fitness UNTIL population has converged STOP		START Initialize Parameters Initialize Population For each particle Update velocity and position Evaluate Update local best Update global best UNTIL the stopping criterion is met STOP		START Generate the initial population Evaluation REPEAT Mutation Recombination Evaluation Selection UNTIL the stopping criterion is met STOP
The optimization parameters
				Population Size	100
Population Size	100			Crossover Operator	0.4
Crossover Operator	0.5	Swarm Size	100	Low Bound of Scaling Factor	0.2
Mutation Operator	0.03	Function Tolerance	1 × 10−5	Upper Bound of Scaling Factor	0.8
Number of Iteration	200	Number of Iteration	200	Number of Iteration	200

3.4. Structural Optimization Results

In this optimization study, the objective functions are solved using different weighting factors according to a single objective function. Table 2 shows the sum of the absolute values of shaking force and shaking moment according to the change of weighting factors using three different optimization methods.

Table 2. The total objective function for different weighting factors for three methods.

Weight ing Factor	Un-optimized	GA			PSO			DE
	F Obj. Fun.	F(1)	F(2)	F Obj. Fun.	F(1)	F(2)	F Obj. Fun.	F(1)	F(2)	F Obj. Fun.
$w_1$ = 1 and $w_2$ = 0	4215.3	33.4	634.1	33.4	7.1	622.1	7.1	26.1	582.6	26.1
$w_1$ = 0.9 and $w_2$ = 0.1	3895.8	61.1	623.5	117.2	0.43	497.4	50.1	14.8	462.3	59.5
$w_1$ = 0.8 and $w_2$ = 0.2	3576.3	51.0	482.9	137.4	0.05	479.3	95.9	65.9	381.4	129.0
$w_1$ = 0.7 and $w_2$ = 0.3	3256.9	25.8	436.1	148.9	0.10	432.5	129.8	75.6	361.6	161.4
$w_1$ = 0.6 and $w_2$ = 0.4	2937.4	10.0	359.1	149.6	0.01	352.3	140.9	88.9	347.7	192.4
$w_1$ = 0.5 and $w_2$ = 0.5	2617.9	21.4	358.7	190.1	36.1	351.8	193.9	138.8	325.9	232.4
$w_1$ = 0.4 and $w_2$ = 0.6	2298.4	201.81	297.8	259.4	100.7	339.0	243.7	195.3	297.4	256.6
$w_1$ = 0.3 and $w_2$ = 0.7	1978.9	254.45	259.9	258.3	245.0	278.2	268.2	278.9	224.7	214.0
$w_1$ = 0.2 and $w_2$ = 0.8	1659.5	416.60	218.1	257.8	421.5	211.9	253.9	423.8	210.8	253.4
$w_1$ = 0.1 and $w_2$ = 0.9	1340.0	800.40	212.4	271.2	717.1	208.4	259.2	709.5	210.3	260.2
$w_1$ = 0 and $w_2$ = 1	1020.5	3564.5	197.1	244.7	2275.5	163.8	163.8	2379.8	157.5	157.5

When the multi-objective function is used singularly, the best result is determined in two ways. First, by displaying the objective function one versus function two on a graph, the closest value to the origin can be chosen. Secondly, the minimum value can be found by taking the square root of the sum of the squares of the objective functions. The graphical representation of the obtained objective function one and objective function two values are given in Figure 6.

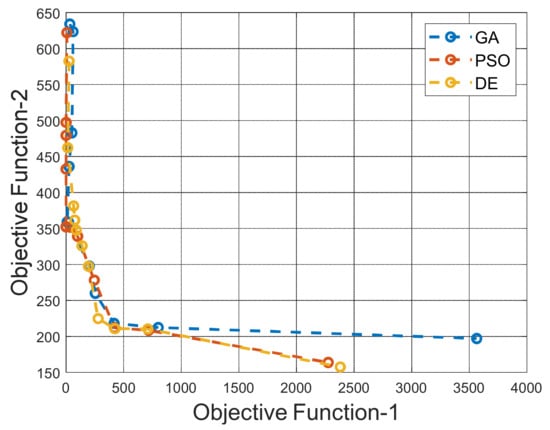
Figure 6. Relationship between number values of two objective functions.

The PSO method using $w_1$ = 0.6 and $w_2$ = 0.4 as the weighting factors gives the best results. The change in the design variables, which yields these results is shown in Table 3.

Table 3. The change in design variables.

Link i	mi (kg)		ri (m)		Igi (kgm2)		rgi (m)		φi (rad)
	Initial	Optimum	Initial	Optimum	Initial	Optimum	Initial	Optimum	Initial	Optimum
1	1.8711	2.1438	0.180	0.189	0.0093	0.0075	0.0772	0.0216	0	3.1387
2	1.8711	1.5887	0.180	0.196	0.0093	0.0075	0.0772	0.0346	0	3.1440
3	0.3269	0.2615	0.150	0.165	0.0008	0.0006	0.075	0.0110	0	0.0408
4	0.3276	0.2621	0.150	0.164	0.0008	0.0006	0.0801	0.0109	0	3.1826
5	-	-	0.110	0.111	-	-	-	-	-	-

While following the circular trajectory, the shaking force, shaking moment, and driving torques in the initial state, and after optimization are shown in Figure 7.

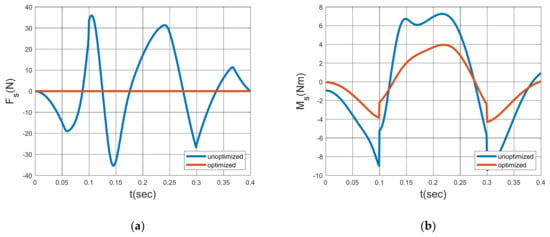
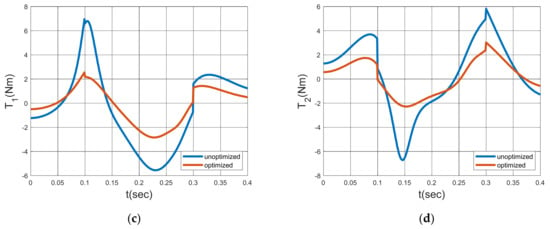
Figure 7. Results of optimization: shaking force (a), shaking moment (b), driving torque 1 (c), and driving torque 2 (d).

A reduction of 99.99% in the sum of the absolute values of the shaking force, 54.44% in the sum of the absolute values of the shaking moment, 52.56% in the sum of the absolute values of the first driving torque, and 48.54% in the sum of the absolute values of the second driving torque have been determined.

4. Controller Design

As mentioned above, the control of a manipulator is essential to practical applications. Therefore, this section is devoted to the design of the controller based on the PID algorithm. The block diagram of this system is presented in Figure 8.

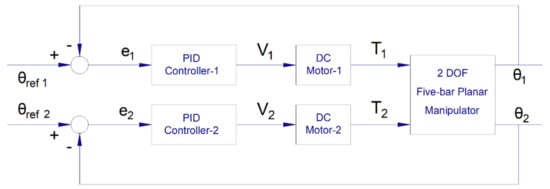
Figure 8. Block diagram of PID controlled system.

The equations of motion of the manipulator are obtained using the Lagrange method. The angles of the driving links ${\theta }_1$ and ${\theta }_2$ are defined as active joint angles, while the angles ${\theta }_3$ and ${\theta }_4$ are called passive joint angles. The passive angles can be expressed as the functions of active angles as follows:

$$\begin{gathered} {\theta }_3=f_3\left({\theta }_1,{\theta }_2\right) \\ {\theta }_4=f_4\left({\theta }_1,{\theta }_2\right) \end{gathered}$$

(31)

The influence coefficients of the angular velocities and angular accelerations of the passive angles are shown in Equations (32) and (33) as follows:

$$\begin{gathered} {\dot{\theta }}_3=\frac{\partial f_3}{\partial {\theta }_1}{\dot{\theta }}_1+\frac{\partial f_3}{\partial {\theta }_2}{\dot{\theta }}_2 \\ {\dot{\theta }}_4=\frac{\partial f_4}{\partial {\theta }_1}{\dot{\theta }}_1+\frac{\partial f_4}{\partial {\theta }_2}{\dot{\theta }}_2 \end{gathered}$$

(32)

$$\begin{gathered} {\ddot{\theta }}_3=\frac{\partial f_3}{\partial {\theta }_1}{\ddot{\theta }}_1+\frac{{\partial }^2{f}_3}{\partial {\theta }_1{}^2}{\dot{\theta }}_1{}^2+2\frac{{\partial }^2{f}_3}{\partial {\theta }_1\partial {\theta }_2}{\dot{\theta }}_1{\dot{\theta }}_2+\frac{\partial f_3}{\partial {\theta }_2}{\ddot{\theta }}_2+\frac{{\partial }^2{f}_3}{\partial {\theta }_2{}^2}{\dot{\theta }}_2{}^2 \\ {\ddot{\theta }}_4=\frac{\partial f_4}{\partial {\theta }_1}{\ddot{\theta }}_1+\frac{{\partial }^2{f}_4}{\partial {\theta }_1{}^2}{\dot{\theta }}_1{}^2+2\frac{{\partial }^2{f}_4}{\partial {\theta }_1\partial {\theta }_2}{\dot{\theta }}_1{\dot{\theta }}_2+\frac{\partial f_4}{\partial {\theta }_2}{\ddot{\theta }}_2+\frac{{\partial }^2{f}_4}{\partial {\theta }_2{}^2}{\dot{\theta }}_2{}^2 \end{gathered}$$

(33)

Considering ${\theta }_1$ and ${\theta }_2$ as principal generalized coordinates, Lagrange’s equations can be written as follows:

$$\frac{\partial }{\partial t}\left[\frac{\partial K}{\partial {\dot{\theta }}_i}\right]-\frac{\partial K}{\partial {\theta }_i}=T_i$$

(34)

where $K$ is kinetic energy and $T_i$ are input torques.

The kinetic energy is expressed as follows:

$$K={\displaystyle \sum }_{i=1}^4(\frac{1}{2}{m}_i\left(V_{ix}{}^2+V_{iy}{}^2\right)+\frac{1}{2}{I}_i{\dot{\theta }}_i{}^2$$

(35)

These equations were obtained as follows. The derivation of these equations is given in Appendix C.

$$T_1=k_1{\ddot{\theta }}_1+k_2{\ddot{\theta }}_2+k_3{\dot{\theta }}_1{}^2+k_4{\dot{\theta }}_1{\dot{\theta }}_2+k_5{\dot{\theta }}_2{}^2$$

(36)

$$T_2=l_1{\ddot{\theta }}_1+l_2{\ddot{\theta }}_2+l_3{\dot{\theta }}_1{}^2+l_4{\dot{\theta }}_1{\dot{\theta }}_2+l_5{\dot{\theta }}_2{}^2$$

(37)

4.1. Mathematical Model of DC Motor

The mathematical model of the DC gear motor is specified in the following equations:

$$V_s{}_i=V_{Ra}{}_i+V_{La}{}_i+E_{emf}{}_i \mathrm{for} i=1,2$$

(38)

where $V_{Ra}, V_{La}$, $E_{emf}$ in Equation (38), $V_{Ra}=R_a{I}_a$, $V_{La}=L_a\frac{d{I}_a}{dt}$, $E_{emf}=K_b\stackrel{.}{{\theta }_m}$, and $V_s$ is input voltage

$$T_s{}_i=T_e{}_i-J_m\stackrel{..}{{\theta }_m{}_i}-T_w{}_i-T_{L_i} \mathrm{for} i=1,2$$

(39)

where $T_e$, $T_w$, T_L in Equation (39), $T_e=K_t{I}_a$, $T_w=B_m\stackrel{.}{{\theta }_m}$, T_L is constant mechanical load and $T_s$ is system output torque. DC gear motor properties in Table 4.

Table 4. Motor properties.

Motor Properties	GPX37-DCX32L
$R_a$-Armature resistance (ohm) $L_a$-Armature inductance (H) $K_t$- Torque constant (Nm/A) $K_b$-Back emf constant (Vs./rad) $J_m$-Rotor Inertia (kgm2) $B_m$-Viscous friction coefficient (Nms/rad) n-Reducer ratio	0.331 0.103 × 10−3 27.3 × 10−3 2.85 × 10−3 72.8 × 10−7 1 × 10−5 26

Substituting Equations (36) and (37) in Equation (39) yields

$$k_1\stackrel{..}{{\theta }_1}+k_2\stackrel{..}{{\theta }_2}+k_3{\stackrel{.}{{\theta }_1}}^2+k_4\stackrel{.}{{\theta }_1}\stackrel{.}{{\theta }_2}+k_5{\stackrel{.}{{\theta }_2}}^2=K_t{I}_1-J_m\stackrel{..}{{\theta }_1}-B\stackrel{.}{{\theta }_1}-T_L$$

(40)

$$l_1\stackrel{..}{{\theta }_1}+l_2\stackrel{..}{{\theta }_2}+l_3{\stackrel{.}{{\theta }_1}}^2+l_4\stackrel{.}{{\theta }_1}\stackrel{.}{{\theta }_2}+l_5{\stackrel{.}{{\theta }_2}}^2=K_t{I}_2-J_m\stackrel{..}{{\theta }_2}-B\stackrel{.}{{\theta }_2}-T_L$$

(41)

State variables are defined as follows:

$$x\left(1\right)={\theta }_1, x\left(2\right)={\theta }_2, x\left(3\right)=\dot{{\theta }_1}, x\left(4\right)=\dot{{\theta }_2, } x\left(5\right)=I_1, x\left(6\right)=I_2$$

(42)

Equations (38), (40) and (41) in the state-space form become as follows:

$$\begin{gathered} \dot{x}\left(1\right)=x\left(3\right) \\ \dot{x}\left(2\right)=x\left(4\right) \\ \dot{x}\left(3\right)=\frac{K_{t}x\left(5\right)-B_{m}x\left(3\right)-k_2\stackrel{.}{x\left(4\right)}-k_{3}x{(3)}^2-k_{4}x\left(3\right)x\left(4\right)-k_{5}x{(4)}^2}{k_1+J_m} \\ \dot{x}\left(4\right)=\frac{K_{t}x\left(6\right)-B_{m}x\left(4\right)-l_1\stackrel{.}{x\left(3\right)}-l_{3}x{(3)}^2-l_{4}x\left(3\right)x\left(4\right)-l_{5}x{(4)}^2}{l_2+J_m} \\ \dot{x}\left(5\right)=\frac{1}{L_a}\left(V_1-R_{a}x\left(5\right)-K_{b}x\left(3\right)\right) \\ \dot{x}\left(6\right)=\frac{1}{L_a}\left(V_2-R_{a}x\left(6\right)-K_{b}x\left(4\right)\right) \end{gathered}$$

(43)

4.2. Tuning of PID Controller Using Optimization Methods

Since the five-bar manipulator system with two DC motors is nonlinear, numerical optimization methods are used to determine the PID controller gains. The following objective function is used to find their optimal gain:

$$f_{obj}=\sqrt{IA{E}_1{}^2+IA{E}_2{}^2}$$

(44)

where $IA{E}_1$ and $IA{E}_2$ are the integral absolute errors. These are given in Equations (45) and (46). Angular position values in inverse kinematics are used as reference position values.

$$IA{E}_1={{\displaystyle \int }}_0^{\infty }\left(\left|{\theta }_{ref1}\left(t\right)-{\theta }_1\left(t\right)\right|\right)dt={{\displaystyle \int }}_0^{\infty }\left|e_1\left(t\right)\right|dt$$

(45)

$$IA{E}_2={{\displaystyle \int }}_0^{\infty }\left(\left|{\theta }_{ref2}\left(t\right)-{\theta }_2\left(t\right)\right|\right)dt={{\displaystyle \int }}_0^{\infty }\left|e_2\left(t\right)\right|dt$$

(46)

Here, optimization aims to minimize the position errors of the motors in the five-bar manipulator. Optimized PID coefficients give the minimum position error in a trajectory.

Tuning the PID gains is a very important issue, and there are different methods to find them. In our study, they will be obtained by using population-based algorithm methods. The PID gains (Kp₁, Kd₁, Ki₁, Kp₂, Kd₂, Ki₂) are defined as design variables, and their ranges are as follows:

$$\begin{array}{l}0\ll K_p{}_j\ll 50\\ 0\ll K_d{}_j\ll 50\hspace{1em}\mathrm{for} j=1,2\\ 0\ll K_i{}_j\ll 100\end{array}$$

(47)

4.3. PID-Controller Simulation Results

The center of the circular trajectory chosen is (x_c, y_c) = (0 m, 0.25 m), and the circle radius is r_c = 0.50 m. The center is chosen so that there is no singularity.

The PID gains obtained after the optimization procedures are shown in Table 5.

Table 5. PID gains.

	GA		PSO		DE
	Motor-1	Motor-2	Motor-1	Motor-2	Motor-1	Motor-2
Kp	36,282	49,929	36,347	40,904	41,771	47,353
Kd	49,989	50,000	22,591	38,205	46,534	37,040
Ki	72,884	99,996	80,320	100,00	100,00	62,028

The angular positions of the motors and the trajectory obtained by applying PID gains are shown in Figure 9.

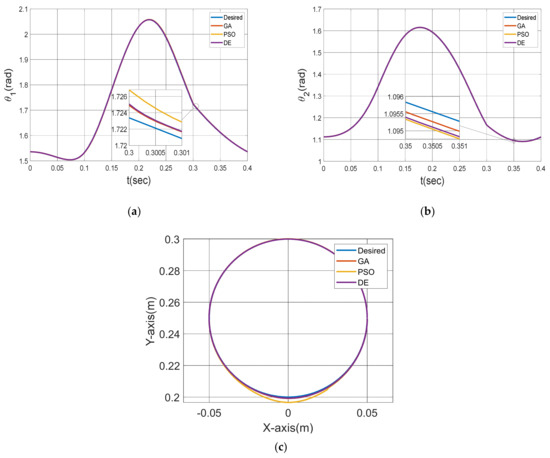
Figure 9. Control results, first motor angle (a) and second motor angle (b), applied trajectory (c).

5. Conclusions

This study focuses on finding the design parameters that minimize the shaking force and moment and provide the most accurate trajectory tracking with PID position control. To achieve this, the largest trajectory to follow was identified. In the meantime, the desired maximum working speed and acceleration values were determined.

First, the objective function of structural optimization consists of two objective functions. A single objective function is created by applying the weighting factor. Optimization is performed using GA, PSO, and DE. Here, different results are obtained such that the sum of the weighting factor values is one. When all the results are compared, the optimum design is found using the PSO method and giving $w_1$ = 0.6 and $w_2$ = 0.4. The shaking force is balanced, and the shaking moment is minimized.

Secondly, there are two objective functions when finding the PID Controller gains by optimization. Here, the square root of the sum of the squares of IAE₁ and IAE₂ is converted to a single objective function. Consistent results are obtained without applying the weighting factor. The most accurate trajectory tracking is found with GA optimization.

The application of these three different optimization methods shows that different optimization methods give better results in various optimization problems.