Generic Homeomorphisms with Shadowing of One-Dimensional Continua

Abstract

In this article, we show that there are homeomorphisms of plane continua whose conjugacy class is residual and have the shadowing property.

1. Introduction

Let $(X,dist)$ be a compact metric space and denote by $\mathcal{H}\left(X\right)$ the space of homeomorphisms $f:X\to X$ with the $C^0$ distance

$${dist}_{C^0}(f,g)=sup\{dist(f\left(x\right),g\left(x\right)),dist(f^{-1}\left(x\right),g^{-1}\left(x\right)):x\in X\}.$$

A property is said to be generic if it holds on a residual subset of $\mathcal{H}\left(X\right)$. Recall that a set is $G_{\delta }$ if it is a countable intersection of open sets and it is residual if it contains a dense $G_{\delta }$ subset. For instance, it is known that the shadowing property is generic for X a compact manifold ([1], Theorem 1) or a Cantor set ([2], Theorem 4.3). Recall that $f\in \mathcal{H}\left(X\right)$ has the shadowing property if for all $\epsilon >0$, there is $\delta >0$ such that if ${\left\{x_i\right\}}_{i\in \mathbb{Z}}$ is a $\delta$-pseudo orbit, then there is $y\in X$ such that $dist(f^i\left(y\right),x_i)<\epsilon$ for all $i\in \mathbb{Z}$. We say that ${\left\{x_i\right\}}_{i\in \mathbb{Z}}$ is a $\delta$-pseudo orbit if $dist(f\left(x_i\right),x_{i+1})<\delta$ for all $i\in \mathbb{Z}$.

A remarkable result, proved in [3,4], states that if X is a Cantor set, then there is a homeomorphism of X whose conjugacy class is a dense $G_{\delta }$ subset of $\mathcal{H}\left(X\right)$. That is, a generic homeomorphism of a Cantor set is conjugate to this special homeomorphism. We say that $f,g\in \mathcal{H}\left(X\right)$ are conjugate if there is $h\in \mathcal{H}\left(X\right)$ such that $f\circ h=h\circ g$ and the conjugacy class of f is the set of all the homeomorphisms conjugate to f. This result gives rise to a natural question: besides the Cantor set,

which compact metric spaces have a G_δ dense conjugacy class?

On a space with a $G_{\delta }$ dense conjugacy class, the study of generic properties (invariant under conjugacy, as the shadowing property) is reduced to determine whether a representative of this class has the property or not.

In Theorem 2, we show that there are one-dimensional plane continua with a $G_{\delta }$ dense conjugacy class whose members have the shadowing property. The proof of this result is based on Theorem 1, where we show that for a compact interval I there is a $G_{\delta }$ conjugacy class in $\mathcal{H}\left(I\right)$ which is dense in the subset of orientation preserving homeomorphisms of I. In addition, the proof of Theorem 2 depends on Propositions 2 and 3, where we give sufficient conditions for the existence of a residual conjugacy class and for a homeomorphism to have the shadowing property, respectively. The following open question has an affirmative answer in the examples known by the authors:

if a homeomorphism has a G_δ dense conjugacy class, does it have the shadowing property?

2. Generic Dynamics on a Closed Segment

Let $I=[0,1]$ and define ${\mathcal{H}}^{+}\left(I\right)=\{f\in \mathcal{H}\left(I\right):f\mathrm{preserves}\mathrm{orientation}\}$. In this section, we show the following result.

Theorem 1.

There is $f_{*}\in {\mathcal{H}}^{+}\left(I\right)$ whose conjugacy class is a $G_{\delta }$ dense subset of ${\mathcal{H}}^{+}\left(I\right)$.

Remark 1.

The generic dynamics of circle homeomorphisms is studied in detail in [5], Theorem 9.1. The proof of Theorem 1 follows the same ideas. As we could not find this result in the literature, we include the details.

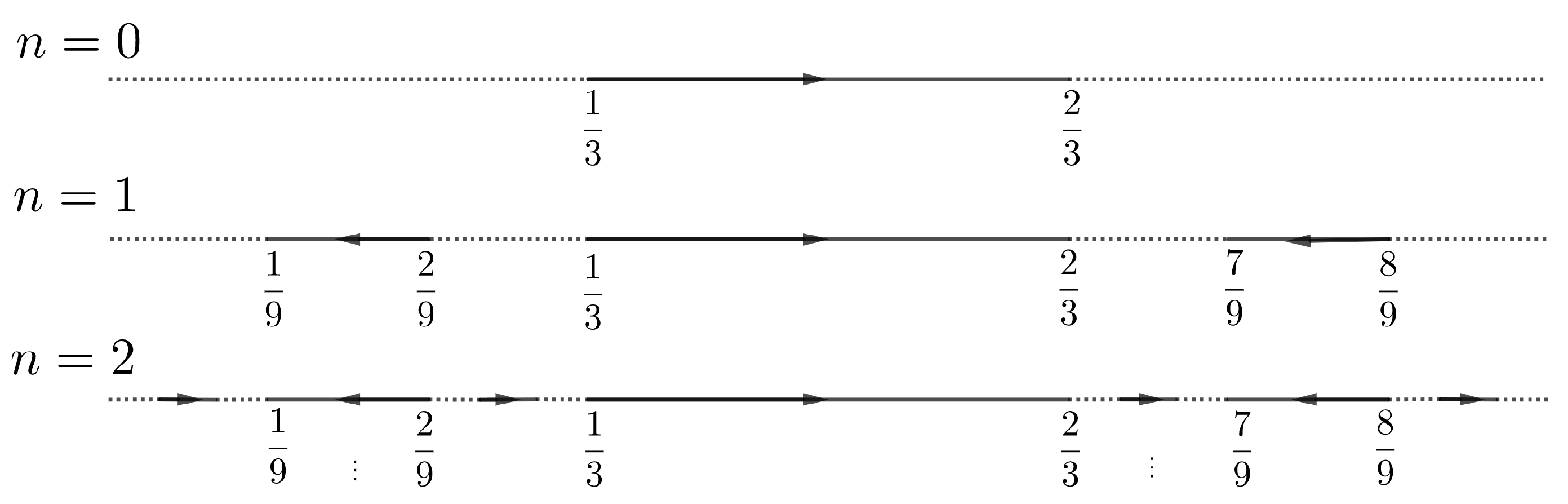
To prove Theorem 1, we start by defining the homeomorphism $f_{*}$. For this purpose, we introduce some definitions. For $f\in {\mathcal{H}}^{+}\left(I\right)$ let $fix\left(f\right)=\{x\in X:f(x)=x\}$. A connected component of $I\backslash fix\left(f\right)$ will be called a wandering interval. Following [6], we say that a wandering interval $(a,b)$ is an r-interval if ${lim}_{n\to +\infty }{f}^n\left(x\right)=b$ for all $x\in (a,b)$. Analogously, it is an l-interval if ${lim}_{n\to +\infty }{f}^n\left(x\right)=a$ for all $x\in (a,b)$. For each interval $[a,b]$, fix a homeomorphism $f_r^{[a,b]}:[a,b]\to [a,b]$ such that $(a,b)$ is an r-interval. Analogously, we consider $f_l^{[a,b]}$ with $(a,b)$ an l-interval.

For $n\ge 0$ and $0\le k<3^n$, define the closed interval

$$J(n,k)=\left[\frac{3k+1}{3^{n+1}},\frac{3k+2}{3^{n+1}}\right].$$

For x in the ternary Cantor set, define $f_{*}\left(x\right)=x$. In another case, there is a minimum integer $n_x\ge 0$ such that $x\in J(n_x,k)$ for some $0\le k<3^{n_x}$ and define

$$f_{*}\left(x\right)=\left\{\begin{array}{cc}{f}_l^{J(n_x,k)}\left(x\right)\hfill & \mathrm{if}{n}_x\mathrm{is}\mathrm{odd},\hfill \\ f_r^{J(n_x,k)}\left(x\right)\hfill & \mathrm{if}{n}_x\mathrm{is}\mathrm{even}.\hfill \end{array}\right.$$

For example, $(\frac{1}{3},\frac{2}{3})$ is an r-interval, while $(\frac{1}{3^2},\frac{2}{3^2})$ and $(\frac{7}{3^2},\frac{8}{3^2})$ are l-intervals. See Figure 1.

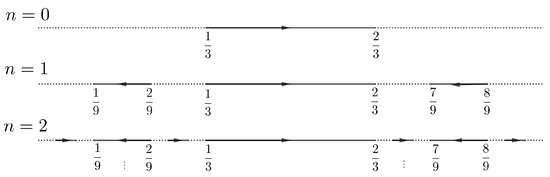
Figure 1. A sketch of the phase diagram of $f_{*}$.

Remark 2.

From [7], Theorem 8, we know that $f_{*}$, and every homeomorphism conjugate to $f_{*}$, has the shadowing property.

The next result gives a useful characterization of the conjugacy class of $f_{*}$. Given $\epsilon >0$, we say that $g\in {\mathcal{H}}^{+}\left(I\right)$ satisfies the property $P_{\epsilon }$ if there are intervals $J_i=(a_i,b_i)$, $i=1,\cdots ,n$, such that:

• $0<a_1<b_1<a_2<b_2<a_3<\cdots <b_n<1$;
• $J_i$ is an r-interval for i odd and an l-interval for i even;
• $max\{a_1,1-b_n\}<\epsilon$ and $max\{a_{i+1}-b_i:1\le i<n\}<\epsilon$.

Proposition 1.

A homeomorphism $g\in {\mathcal{H}}^{+}\left(I\right)$ is conjugate to $f_{*}$ if and only if it satisfies $P_{\epsilon }$ for all $\epsilon >0$.

Proof. 

The direct part of the proof is clear from the construction of $f_{*}$.

To prove the converse, suppose that g satisfies $P_{\epsilon }$ for all $\epsilon >0$. From Condition (3), we see that $fix\left(g\right)$ is totally disconnected. Suppose that $p\in I$ is an isolated fixed point. If $p=0$, then there is a wandering interval $(0,x)$. Taking $\epsilon \in (0,x)$, we have a contradiction with (3), because $a_1<\epsilon$. Analogously we show that p cannot be 1. If $p\in (0,1)$, then p is in the boundary of two wandering intervals. Taking $\epsilon$ smaller than the length of these intervals, we contradict (1) and (3). Thus, $fix\left(g\right)$ has no isolated point and is a Cantor set. Condition (2) (applied for a suitable $\epsilon$ small) implies that between two wandering intervals there is an r-interval and an l-interval.

Let $\mathcal{R}$ and $\mathcal{L}$ be the families of r-intervals and l-intervals of g, respectively. We define an order in $\mathcal{R}\cup \mathcal{L}$ in the following way: $I_{\alpha }<I_{\beta }$ if $x<y$ for all $x\in I_{\alpha }$, $y\in I_{\beta }$. We will make the conjugacy by induction. For the first step, name $I_{1/2}\in \mathcal{R}$ which satisfies $diam\left(I_{1/2}\right)\ge diam\left(I\right)$ for every $I\in \mathcal{R}$. In the case that there exists more than one interval which verifies this condition, we choose any of them. Let $J_c$ be a wandering interval of $f_{*}$ such that c is the midpoint of $J_c$. By construction, $J_{1/2}$ is an r-interval of $f_{*}$, thus we can consider a conjugacy $h_{1/2}:I_{1/2}\to J_{1/2}$ of g and $f_{*}$ restricted to these intervals. Notice that $1/6$ and $5/6$ are the midpoints of $(1/9,2/9)$ and $(7/9,8/9)$, respectively. Take $I_{1/6}\in \mathcal{L}$ satisfying $I_{1/6}<I_{1/2}$ and $diam\left(I_{1/6}\right)\ge diam\left(I\right)$ for every $I\in \mathcal{L}$ such that $I<I_{1/2}$. In addition, take $I_{5/6}\in \mathcal{L}$ satisfying $I_{1/2}<I_{5/6}$ and $diam\left(I_{5/6}\right)\ge diam\left(I\right)$ for every $I\in \mathcal{L}$ such that $I>I_{1/2}$. Then, consider $h_{1/6}:I_{1/6}\to J_{1/6}$ to be a conjugacy from g to $f_{*}$ restricted to the corresponding intervals. Similarly, define $h_{5/6}$. Then, we go on defining $2^{k-1}$ homeomorphisms on each step. If $k-1$ is even, we choose r-intervals, otherwise we choose l-intervals. Notice that since in each step we choose the largest interval of the r or l-intervals of g, every wandering interval of g is eventually chosen. In this way, the conjugacies $h_{j/k}$ give rise to a conjugacy h of g and $f_{*}$ in the whole interval $[0,1]$ and the proof ends. □

Proof of Theorem 1.

Given $n\ge 1$, let ${\mathcal{U}}_n$ be the set of increasing homeomorphisms of I satisfying $P_{1/n}$. Notice that $P_{\epsilon }$ implies $P_{{\epsilon }^{\prime }}$ for all ${\epsilon }^{\prime }>\epsilon >0$. Thus, from Proposition 1 we have that the conjugacy class of $f_{*}$ is the countable intersection ${\bigcap }_{n\ge 1}{\mathcal{U}}_n$. To finish the proof, applying Baire’s Theorem, we show that each ${\mathcal{U}}_n$ is open and dense in ${\mathcal{H}}^{+}\left(I\right)$.

To prove that ${\mathcal{U}}_n$ is open, consider $f\in {\mathcal{U}}_n$. It is clear that there is $\delta >0$ such that $f\in {\mathcal{U}}_{n-4\delta }$. Consider the intervals $(a_i,b_i)$ from the definition of property $P_{\epsilon }$, for $\epsilon =1/n$. For each odd $i=1,\cdots ,n$, take $x_i\in (a_i,a_i+\delta )$ and for i even take $y_i\in (b_i-\delta ,b_i)$. Consider $m\in \mathbb{N}$ large such that $f^m\left(x_i\right)\in (b_i-\delta ,b_i)$ and $f^m\left(y_i\right)\in (a_i,a_i+\delta )$ for all i. Take a neighborhood $\mathcal{V}$ of f such that ${dist}_{C^0}(f^m,g^m)<\delta$ for all $g\in \mathcal{V}$ and $g^m\left(x_i\right)>x_i$, $g^m\left(y_i\right)<y_i$ for all i. This implies that $(x_i,g^m\left(x_i\right))$ is contained in an r-interval for g and $(g^m\left(y_i\right),y_i)$ is contained in an l-interval for g. For all $g\in \mathcal{V}$ and i odd, we have

$$\begin{array}{ccc}|g^m\left(x_i\right)-g^m\left(y_{i+1}\right)\left)\right|\hfill & \le \hfill & |g^m\left(x_i\right)-f^m\left(x_i\right)|+|f^m\left(x_i\right)-f^m\left(y_{i+1}\right)|\hfill \\ & & +|f^m\left(y_{i+1}\right)-g^m\left(y_{i+1}\right)|\hfill \\ & <\hfill & \delta +|f^m\left(x_i\right)-b_i|+|b_i-a_{i+1}|+|a_{i+1}-f^m\left(y_{i+1}\right)|+\delta \hfill \\ & <\hfill & 2\delta +(1/n-4\delta )+2\delta =1/n.\hfill \end{array}$$

Arguing analogously for i even, we conclude that $g\in {\mathcal{U}}_n$ and ${\mathcal{U}}_n$ is open.

To prove that ${\mathcal{U}}_n$ is dense in ${\mathcal{H}}^{+}\left(I\right)$, the following remark is sufficient. Given $f\in {\mathcal{H}}^{+}\left(I\right)$, $p\in fix\left(f\right)\cap (0,1)$ and $\delta >0$ small, we can define $g\in {\mathcal{H}}^{+}\left(I\right)$ close to f such that:

• ${f|}_{[0,p]}$ and ${g|}_{[0,p-\delta ]}$ are conjugate;
• ${f|}_{[p,1]}$ and ${g|}_{[p+\delta ,1]}$ are conjugate; and
• g has an r or l-interval at $[p-\delta ,p+\delta ]$.

That is, a fixed point can be exploded into a small wandering interval with an arbitrarily small perturbation. By finitely performing many such explosions, the density of ${\mathcal{U}}_n$ is obtained. □

3. Genericity on a Plane One-Dimensional Continuum

In this section, we show that there are some particular one-dimensional plane continua with a $G_{\delta }$ dense conjugacy class whose members have the shadowing property. We start with a sufficient condition for the existence of a $G_{\delta }$ dense conjugacy class. An open subset $U\subset X$ is a free arc if it is homeomorphic to $\mathbb{R}$.

Proposition 2.

If X is a compact metric space such that

• $X={\cup }_{n\ge 1}{a}_n$, where each $a_n$ is a compact arc with extreme points $p_n,q_n\in X$ for all $n\ge 1$;
• $a_n\backslash \{p_n,q_n\}$ is a free arc for all $n\ge 1$; and
• for all $f\in \mathcal{H}\left(X\right)$, it holds that $f\left(a_n\right)=a_n$ and $p_n,q_n\in fix\left(f\right)$ for all $n\ge 1;$

then $\mathcal{H}\left(X\right)$ has a $G_{\delta }$ dense conjugacy class.

Proof. 

For each $n\ge 1$, let $X_n=clos(X\backslash a_n)$ and define

$${\mathcal{H}}_n=\{f\in \mathcal{H}\left(X_n\right):p_n,q_n\in fix\left(f\right)\},$$

and the map ${\phi }_n:\mathcal{H}\left(X\right)\to {\mathcal{H}}^{+}\left(a_n\right)\times {\mathcal{H}}_n$ as ${\phi }_n\left(f\right)=f{{|}_{a_n}\times f|}_{X_n}$. In ${\mathcal{H}}^{+}\left(a_n\right)\times {\mathcal{H}}_n$, we consider the product topology. It is clear that ${\phi }_n$ is a homeomorphism for each $n\ge 1$. Let ${\mathcal{R}}_n$ be the $G_{\delta }$ dense conjugacy class of ${\mathcal{H}}^{+}\left(a_n\right)$ given by Theorem 1 and define ${\mathcal{S}}_n={\mathcal{R}}_n\times {\mathcal{H}}_n$. Thus, ${\cap }_{n\ge 1}{\phi }_n^{-1}\left({\mathcal{S}}_n\right)$ is a $G_{\delta }$ dense conjugacy class in $\mathcal{H}\left(X\right)$. □

Remark 3.

Notice that a representative $g_{*}$ of the $G_{\delta }$ dense conjugacy of Proposition 2 is obtained by considering a conjugate of $f_{*}$ on each arc $a_n$ of X.

Now, we prove a sufficient condition for a homeomorphism to have the shadowing property. For this purpose, we need some definitions and a lemma. Suppose that $(X,dist)$ is a compact metric space and take $f\in \mathcal{H}\left(X\right)$. A compact f-invariant subset $A\subset X$ is a quasi-attractor if for every open neighborhood U of A there is an open subset $V\subset U$ such that $A\subset V$ and $clos\left(f\right(V\left)\right)\subset V$. If, in addition, $f:A\to A$ has the shadowing property, we say that A is a quasi-attractor with shadowing.

Lemma 1.

If $A\subset X$ is a quasi-attractor with shadowing, then for all $\epsilon >0$ there is $\delta >0$ such that if ${\left\{x_n\right\}}_{n\ge 0}$ is a δ-pseudo-orbit with $x_0\in B_{\delta }\left(A\right)$, then there is $y\in A$ that ε-shadows ${\left\{x_n\right\}}_{n\ge 0}$.

Proof. 

Given $\epsilon >0$, take ${\delta }_1>0$ such that every ${\delta }_1$-pseudo-orbit in A is $\epsilon /2$-shadowed by a point in A. Consider $0<\alpha <min\{\epsilon /2,{\delta }_1/3\}$ such that $dist(a,b)<\alpha$ implies $dist(f\left(a\right),f\left(b\right))<{\delta }_1/3$. Since A is a quasi-attractor, for $U=B_{\alpha }\left(A\right)$ there exists an open set V such that $A\subset V\subset U$ and $clos\left(f\right(V\left)\right)\subset V$. Take $\delta \in (0,{\delta }_1/3)$ such that $B_{\delta }(clos\left(f\left(V\right)\right))\subset V$.

Suppose that ${\left\{x_n\right\}}_{n\ge 0}$ is a $\delta$-pseudo-orbit with $x_0\in B_{\delta }\left(A\right)$. Since $f\left(x_0\right)\in f\left(V\right)$, we have that $x_1\in B_{\delta }\left(f\left(V\right)\right)$ and $x_1\in V$. In this way, we prove that $x_n\in V$ for all $n\ge 0$. For each $n\ge 0$, take $y_n\in A$ such that $dist(y_n,x_n)<\alpha$. We have that

$$\begin{array}{cc}dist(f\left(y_n\right),y_{n+1})\hfill & \le dist(f\left(y_n\right),f\left(x_n\right))+dist(f\left(x_n\right),x_{n+1})+dist(x_{n+1},y_{n+1})\hfill \\ & \le {\delta }_1/3+\delta +\alpha <3{\delta }_1/3={\delta }_1.\hfill \end{array}$$

This proves that ${\left\{y_n\right\}}_{n\ge 0}$ is a ${\delta }_1$-pseudo-orbit contained in A. There exists $z\in A$ that $\epsilon /2$-shadows ${\left\{y_n\right\}}_{n\ge 0}$. Thus,

$$dist(f^n\left(z\right),x_n)\le dist(f^n\left(z\right),y_n)+dist(y_n,x_n)<\epsilon /2+\alpha \le \epsilon .$$

Therefore, the proof ends. □

Proposition 3.

If every point of X belongs to a quasi-attractor with shadowing, then f has shadowing.

Proof. 

Suppose that $\epsilon >0$ is given. For each $x\in X$, let $A_x\subset X$ be a quasi-attractor with shadowing containing x. Let ${\delta }_x>0$ be given by Lemma 1 such that for every ${\delta }_x$-pseudo-orbit ${\left\{x_n\right\}}_{n\ge 0}$ with $x_0\in B_{{\delta }_x}\left(A_x\right)$ there is a point in $A_x$ that $\epsilon$-shadows ${\left\{x_n\right\}}_{n\ge 0}$. As X is compact, there is a finite sequence $x_1,\cdots ,x_k\in X$ such that ${\cup }_{i=1}^k{B}_{{\delta }_i}\left(A_i\right)=X$, where $A_i=A_{x_i}$ and ${\delta }_i={\delta }_{x_i}$. If we take $\delta =min\{{\delta }_1,\cdots ,{\delta }_k\}$, we have that for every $\delta$-pseudo-orbit ${\left\{x_n\right\}}_{n\ge 0}$ in X, there is j such that $x_0\in B_{{\delta }_j}\left(A_j\right)$. Then, there is a point in $A_j$ that $\epsilon$-shadows ${\left\{x_n\right\}}_{n\ge 0}$ and the proof ends. □

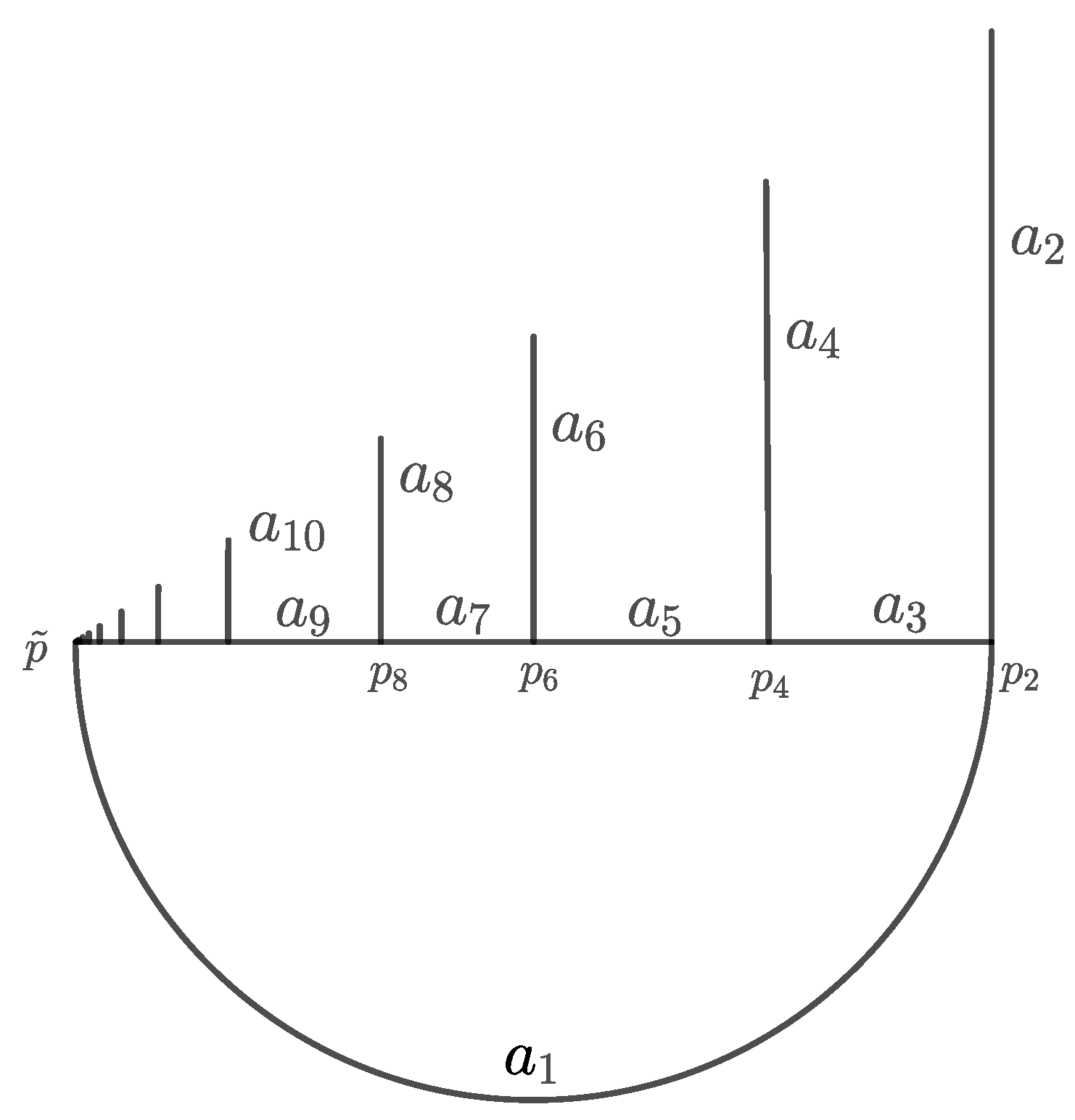
Let $Y\subset {\mathbb{R}}^2$ be the union of

• the circle arc $x^2+y^2=1$, $y\le 0$;
• the horizontal segment $[-1,1]\times \left\{0\right\}$; and
• the vertical segments $\{-1+\frac{2}{n}\}\times [0,1/n]$, for $n\ge 1$.

See Figure 2.

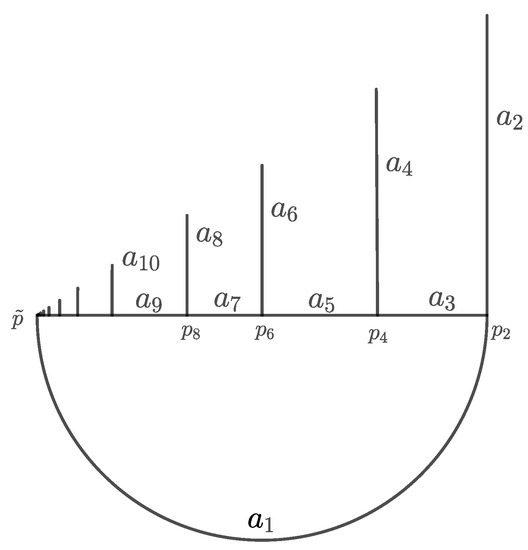
Figure 2. The continuum Y can be decomposed as a union of arcs as in Proposition 2.

Theorem 2.

For the continuum Y, there is a $G_{\delta }$ conjugacy class which is dense in $\mathcal{H}\left(Y\right)$ and whose members have the shadowing property. In particular, the shadowing property is generic in $\mathcal{H}\left(Y\right)$.

Proof. 

The continuum Y satisfies the hypothesis of Proposition 2. Indeed, the conditions (1) and (2) are directly from the construction of Y. Consider the points $p_n,\tilde{p}$ indicated in Figure 2. It is clear that $\tilde{p}\in fix\left(f\right)$ for all $f\in \mathcal{H}\left(Y\right)$. This implies that $a_1$ is invariant and $p_2\in fix\left(f\right)$. In turn, this implies that $a_2$ is invariant under each $f\in \mathcal{H}\left(Y\right)$. In this way, it is shown that condition (3) of Proposition 2 holds. Therefore, $\mathcal{H}\left(Y\right)$ contains a $G_{\delta }$ dense conjugacy class.

As explained in Remark 3, a representative $g_{*}\in \mathcal{H}\left(Y\right)$ of this conjugacy class is obtained by taking a conjugate of $f_{*}$ on each arc $a_n$. It only remains to prove that $g_{*}$ has the shadowing property. By Remark 2, we know that $g_{*}:a_n\to a_n$ has the shadowing property. By construction, each $a_n$ is a quasi-attractor for $g_{*}$. Since the arcs $a_n$ cover Y, we can apply Proposition 3 to conclude that $g_{*}$ has the shadowing property. □