1. Introduction
Let
be a compact metric space and denote by
the space of homeomorphisms
with the
distance
A property is said to be
generic if it holds on a residual subset of
. Recall that a set is
if it is a countable intersection of open sets and it is
residual if it contains a dense
subset. For instance, it is known that the shadowing property is generic for
X a compact manifold ([
1], Theorem 1) or a Cantor set ([
2], Theorem 4.3). Recall that
has the
shadowing property if for all
, there is
such that if
is a
-pseudo orbit, then there is
such that
for all
. We say that
is a
-
pseudo orbit if
for all
.
A remarkable result, proved in [
3,
4], states that if
X is a Cantor set, then there is a homeomorphism of
X whose conjugacy class is a dense
subset of
. That is, a generic homeomorphism of a Cantor set is conjugate to this special homeomorphism. We say that
are
conjugate if there is
such that
and the
conjugacy class of
f is the set of all the homeomorphisms conjugate to
f. This result gives rise to a natural question: besides the Cantor set,
On a space with a dense conjugacy class, the study of generic properties (invariant under conjugacy, as the shadowing property) is reduced to determine whether a representative of this class has the property or not.
In Theorem 2, we show that there are one-dimensional plane continua with a
dense conjugacy class whose members have the shadowing property. The proof of this result is based on Theorem 1, where we show that for a compact interval
I there is a
conjugacy class in
which is dense in the subset of orientation preserving homeomorphisms of
I. In addition, the proof of Theorem 2 depends on Propositions 2 and 3, where we give sufficient conditions for the existence of a residual conjugacy class and for a homeomorphism to have the shadowing property, respectively. The following open question has an affirmative answer in the examples known by the authors:
2. Generic Dynamics on a Closed Segment
Let and define . In this section, we show the following result.
Theorem 1. There is whose conjugacy class is a dense subset of .
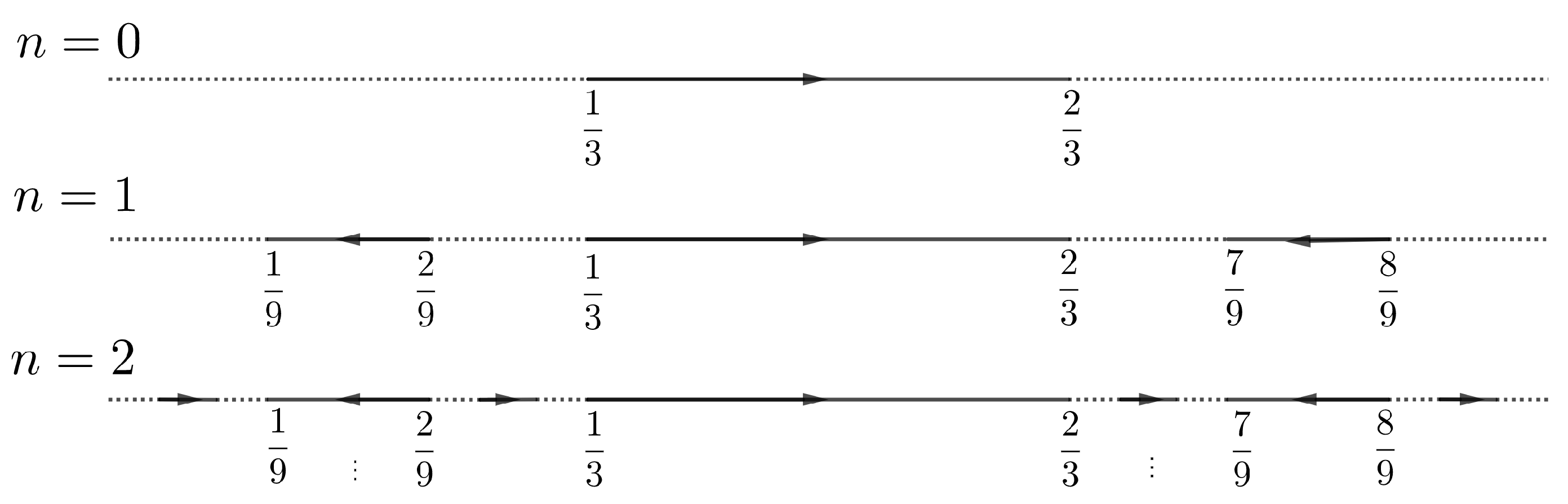
Remark 1. The generic dynamics of circle homeomorphisms is studied in detail in [5], Theorem 9.1. The proof of Theorem 1 follows the same ideas. As we could not find this result in the literature, we include the details. To prove Theorem 1, we start by defining the homeomorphism
. For this purpose, we introduce some definitions. For
let
. A connected component of
will be called a
wandering interval. Following [
6], we say that a wandering interval
is an
r-
interval if
for all
. Analogously, it is an
l-
interval if
for all
. For each interval
, fix a homeomorphism
such that
is an
r-interval. Analogously, we consider
with
an
l-interval.
For
and
, define the closed interval
For
x in the ternary Cantor set, define
. In another case, there is a minimum integer
such that
for some
and define
For example,
is an
r-interval, while
and
are
l-intervals. See
Figure 1.
Remark 2. From [7], Theorem 8, we know that , and every homeomorphism conjugate to , has the shadowing property. The next result gives a useful characterization of the conjugacy class of . Given , we say that satisfies the property if there are intervals , , such that:
;
is an r-interval for i odd and an l-interval for i even;
and .
Proposition 1. A homeomorphism is conjugate to if and only if it satisfies for all .
Proof. The direct part of the proof is clear from the construction of .
To prove the converse, suppose that g satisfies for all . From Condition (3), we see that is totally disconnected. Suppose that is an isolated fixed point. If , then there is a wandering interval . Taking , we have a contradiction with (3), because . Analogously we show that p cannot be 1. If , then p is in the boundary of two wandering intervals. Taking smaller than the length of these intervals, we contradict (1) and (3). Thus, has no isolated point and is a Cantor set. Condition (2) (applied for a suitable small) implies that between two wandering intervals there is an r-interval and an l-interval.
Let and be the families of r-intervals and l-intervals of g, respectively. We define an order in in the following way: if for all , . We will make the conjugacy by induction. For the first step, name which satisfies for every . In the case that there exists more than one interval which verifies this condition, we choose any of them. Let be a wandering interval of such that c is the midpoint of . By construction, is an r-interval of , thus we can consider a conjugacy of g and restricted to these intervals. Notice that and are the midpoints of and , respectively. Take satisfying and for every such that . In addition, take satisfying and for every such that . Then, consider to be a conjugacy from g to restricted to the corresponding intervals. Similarly, define . Then, we go on defining homeomorphisms on each step. If is even, we choose r-intervals, otherwise we choose l-intervals. Notice that since in each step we choose the largest interval of the r or l-intervals of g, every wandering interval of g is eventually chosen. In this way, the conjugacies give rise to a conjugacy h of g and in the whole interval and the proof ends. □
Proof of Theorem 1. Given , let be the set of increasing homeomorphisms of I satisfying . Notice that implies for all . Thus, from Proposition 1 we have that the conjugacy class of is the countable intersection . To finish the proof, applying Baire’s Theorem, we show that each is open and dense in .
To prove that
is open, consider
. It is clear that there is
such that
. Consider the intervals
from the definition of property
, for
. For each odd
, take
and for
i even take
. Consider
large such that
and
for all
i. Take a neighborhood
of
f such that
for all
and
,
for all
i. This implies that
is contained in an
r-interval for
g and
is contained in an
l-interval for
g. For all
and
i odd, we have
Arguing analogously for
i even, we conclude that
and
is open.
To prove that is dense in , the following remark is sufficient. Given , and small, we can define close to f such that:
and are conjugate;
and are conjugate; and
g has an r or l-interval at .
That is, a fixed point can be exploded into a small wandering interval with an arbitrarily small perturbation. By finitely performing many such explosions, the density of is obtained. □
3. Genericity on a Plane One-Dimensional Continuum
In this section, we show that there are some particular one-dimensional plane continua with a dense conjugacy class whose members have the shadowing property. We start with a sufficient condition for the existence of a dense conjugacy class. An open subset is a free arc if it is homeomorphic to .
Proposition 2. If X is a compact metric space such that
, where each is a compact arc with extreme points for all ;
is a free arc for all ; and
for all , it holds that and for all
then has a dense conjugacy class.
Proof. For each
, let
and define
and the map
as
. In
, we consider the product topology. It is clear that
is a homeomorphism for each
. Let
be the
dense conjugacy class of
given by Theorem 1 and define
. Thus,
is a
dense conjugacy class in
. □
Remark 3. Notice that a representative of the dense conjugacy of Proposition 2 is obtained by considering a conjugate of on each arc of X.
Now, we prove a sufficient condition for a homeomorphism to have the shadowing property. For this purpose, we need some definitions and a lemma. Suppose that is a compact metric space and take . A compact f-invariant subset is a quasi-attractor if for every open neighborhood U of A there is an open subset such that and . If, in addition, has the shadowing property, we say that A is a quasi-attractor with shadowing.
Lemma 1. If is a quasi-attractor with shadowing, then for all there is such that if is a δ-pseudo-orbit with , then there is that ε-shadows .
Proof. Given , take such that every -pseudo-orbit in A is -shadowed by a point in A. Consider such that implies . Since A is a quasi-attractor, for there exists an open set V such that and . Take such that .
Suppose that
is a
-pseudo-orbit with
. Since
, we have that
and
. In this way, we prove that
for all
. For each
, take
such that
. We have that
This proves that
is a
-pseudo-orbit contained in
A. There exists
that
-shadows
. Thus,
Therefore, the proof ends. □
Proposition 3. If every point of X belongs to a quasi-attractor with shadowing, then f has shadowing.
Proof. Suppose that is given. For each , let be a quasi-attractor with shadowing containing x. Let be given by Lemma 1 such that for every -pseudo-orbit with there is a point in that -shadows . As X is compact, there is a finite sequence such that , where and . If we take , we have that for every -pseudo-orbit in X, there is j such that . Then, there is a point in that -shadows and the proof ends. □
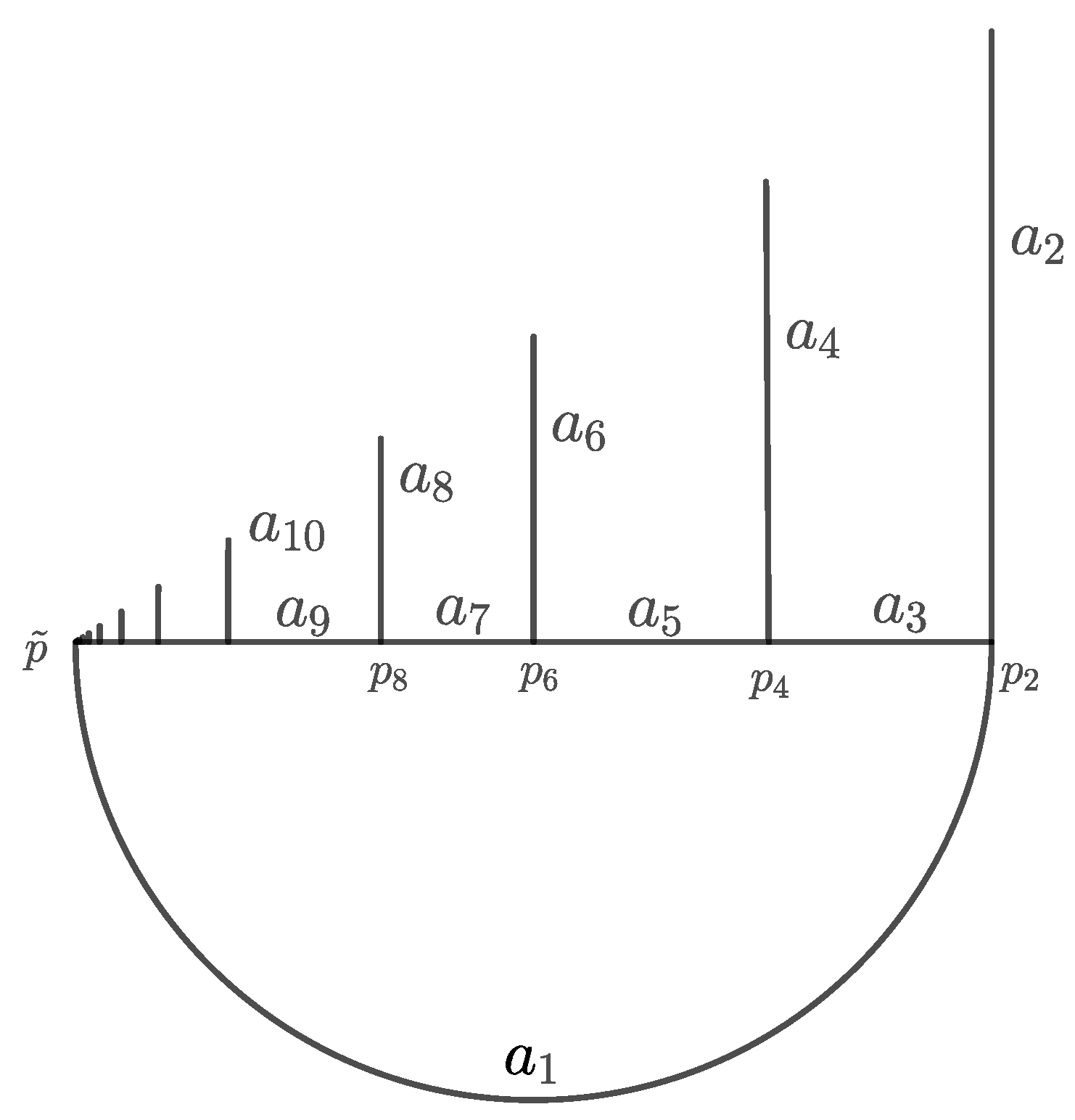
Let be the union of
the circle arc , ;
the horizontal segment ; and
the vertical segments , for .
Theorem 2. For the continuum Y, there is a conjugacy class which is dense in and whose members have the shadowing property. In particular, the shadowing property is generic in .
Proof. The continuum
Y satisfies the hypothesis of Proposition 2. Indeed, the conditions (1) and (2) are directly from the construction of
Y. Consider the points
indicated in
Figure 2. It is clear that
for all
. This implies that
is invariant and
. In turn, this implies that
is invariant under each
. In this way, it is shown that condition (3) of Proposition 2 holds. Therefore,
contains a
dense conjugacy class.
As explained in Remark 3, a representative of this conjugacy class is obtained by taking a conjugate of on each arc . It only remains to prove that has the shadowing property. By Remark 2, we know that has the shadowing property. By construction, each is a quasi-attractor for . Since the arcs cover Y, we can apply Proposition 3 to conclude that has the shadowing property. □