Abstract
Tickysim is a clock tick-based simulator for the inter-chip interconnection network of the SpiNNaker architecture. Network devices such as arbiters, routers, and packet generators store, read, and write forward data through fixed-length FIFO buffers. At each clock tick, every component executes a “read” phase followed by a “write” phase. The structures of any finite graph which represents numerical quantities are known as topological indices. In this paper, we compute degree-based topological indices of the Tickysim SpiNNaker Model () sheet.
Keywords:
degree; topological indices; multiple Zagreb indices; Zagreb polynomials; Tickysim SpiNNaker Model MSC:
97K30
1. Introduction
Neural networks are applicable in many solutions for classification, prediction, control, etc. The variety of purposes is growing but with each new application the expectations are higher. We want neural networks to be more precise independently of the input data. Efficiency of the processing in a large manner depends on the training algorithm. Basically this procedure is based on the random selection of weights in which neurons connections are burdened. During training process we implement a method which involves modification of the weights to minimize the response error of the entire structure see details in [1,2].
Convolutional neural network (CNN) is an essential model to achieve high accuracy in various machine learning applications, such as image recognition and natural language processing. One of the important issues for CNN acceleration with high energy efficiency and processing performance is efficient data reuse by exploiting the inherent data locality. Recurrent neural networks (RNNs) are powerful models of sequential data. They have been successfully used in domains such as text and speech. However, RNNs are susceptible to overfitting; regularization is important [3]. Motivated by these networks we consider the Tickysim SpiNNaker Model(network) for utilization its topological properties.
In this paper all graphs are finite, simple, and undirected. Let and be the vertex set and edge set of a graph G. The vertices are adjacent (or neighbors) if u and v are endpoints of and e is incident with the vertices u and v and e is said to connect u and The set of all neighbors of a vertex u of G denoted by is called the neighborhood of The degree of a vertex in an undirected simple graph is the number of edges incident with it. The degree of the vertex u is denoted by and is the sum of degrees of all vertices adjacent to the vertex In other words, where All the concepts of graph theory and combinatorics are used from the book of Harris et al. [4,5].
The application of molecular structure descriptors is now a standard procedure in the study of structure–property relations, especially in QSPR/QSAR study. In the past couple of years, the amount of proposed nuclear descriptors is rapidly increases as a result of the significance of the creation of these descriptors. They interface the particular physico-substance properties of mixture blends. A most seasoned, considered, and prominent topological record among all degree-based topological lists is the Randić index, which was presented by Randić in 1975 [6]. This record was discovered to be reasonable with the end goal of a medication plan [7]. The numerical elements of the Randić index incorporates its association with the standardized Laplacian framework [8,9,10]. The formal definition of the Randić index of a graph G is given as follows:
Soon after the discovery of Randić index, the general Randić index was introduced. It is denoted by , and its formula is given as:
where is a nonzero real number. Zhou et al. [11] introduced the general sum-connectivity index and defined it as:
where is a real number. Shirdel et al. introduced a new degree-based Zagreb index named the “hyper-Zagreb index” which is defined in [12], and is also known as general sum-connectivity index The first general Zagreb index was studied in [13].
Estrada et al. invented the atom-bond connectivity index, abbreviated as the index [14]. index is of much importance due to its correlation with the thermodynamic properties of alkanes (see [15,16]). The definition of the index is as follows:
The fourth version of the index was introduced by Ghorbani and Hosseinzadeh [17], and is defined as:
Another important degree-based topological index is the geometric-arithmetic index ( index) and is of much importance due to its application to acyclic, unicyclic, and bicyclic molecular graphs [18]. The formal definition of the index is as follows:
Recently, the fifth version of was introduced by Graovac el al. [19], defined as:
In [20], Ghorbani and Azimi defined first multiple Zagreb index and second multiple Zagreb index , defined as:
These multiple Zagreb indices are studied for some chemical structures in [21,22,23,24,25]. The first Zagreb polynomial and second Zagreb polynomial are defined as:
2. Applications of Topological Indices
To relate with certain physico-concoction properties, the index has much preferred prescient control over the prescient energy of the Randić connectivity index [26]. The first and second Zagreb indexes were found to be helpful for calculation of the aggregate -electron energy of the particles inside particular rough articulations [27]. These are among the graph invariants that were proposed for estimation of the skeleton of stretching of the carbon atom [28]. The Randić index is a topological descriptor that has related with a great deal of the synthetic qualities of atoms and has been discovered parallel to processing the boiling point and Kovats constants of the particles. The particle bond network index gives a decent connection to the security of direct alkanes and also the stretched alkanes and for processing the strain vitality of cyclo alkanes [29,30].
In the past two decades, analysts contemplated certain substance diagrams and arrangement s and processed their particular indices. W. Gao and M. R. Farahani figured degree-based indices of synthetic structures by utilizing an edge-separated technique [31]. Gao et al. [32] contemplated concoction structures in medications and some medication structures, and processed the overlooked topological indices. Some different utilizations of the atomic descriptors of sub-atomic diagrams and systems are given in the reference list and the references [33]. These applications and writing survey inspired us to investigate some new substance diagrams and process their topological indices [34,35,36,37].
3. Materials and Methods
At the highest level of abstraction, inter-chip architectures are basically mathematical graphs where each device is considered as vertex and the topology used between these devices reflects the edges and in total nature of graph. One of the network topologies used in this model is 12 × 12 hexagonal torus. In this topology, each node is connected to six incident nodes. We also consider the finite Tickysim SpiNNaker Model sheet which is obtained by hexagonal torus. For more details, see [38].
The Second of the network topology consists of a set of a hexagonal segments of a hexagonal mesh of nodes. Each node in the simulation represents a SpiNNaker chip that contains a router, packet generator, packet consumer, and a tree of two-input round-robin arbiters which arbitrates between the inputs to the router. The router always consists of a four-stage pipeline. If a packet cannot be forwarded to its requested output after 50 cycles at the head of the router, it is dropped. The packet generator generates packets for each node of the system. If the output buffer is full, the packet generator waits until a space becomes available. The packet consumer receives incoming packets immediately, but the packet consumer will wait 10 cycles before accepting another packet. The arbiter tree is based on SpiNNaker’s NoC aspects. In each cycle, the arbiter selects a waiting packet on one of its inputs and forwards it to its output if there is space in the output buffer.
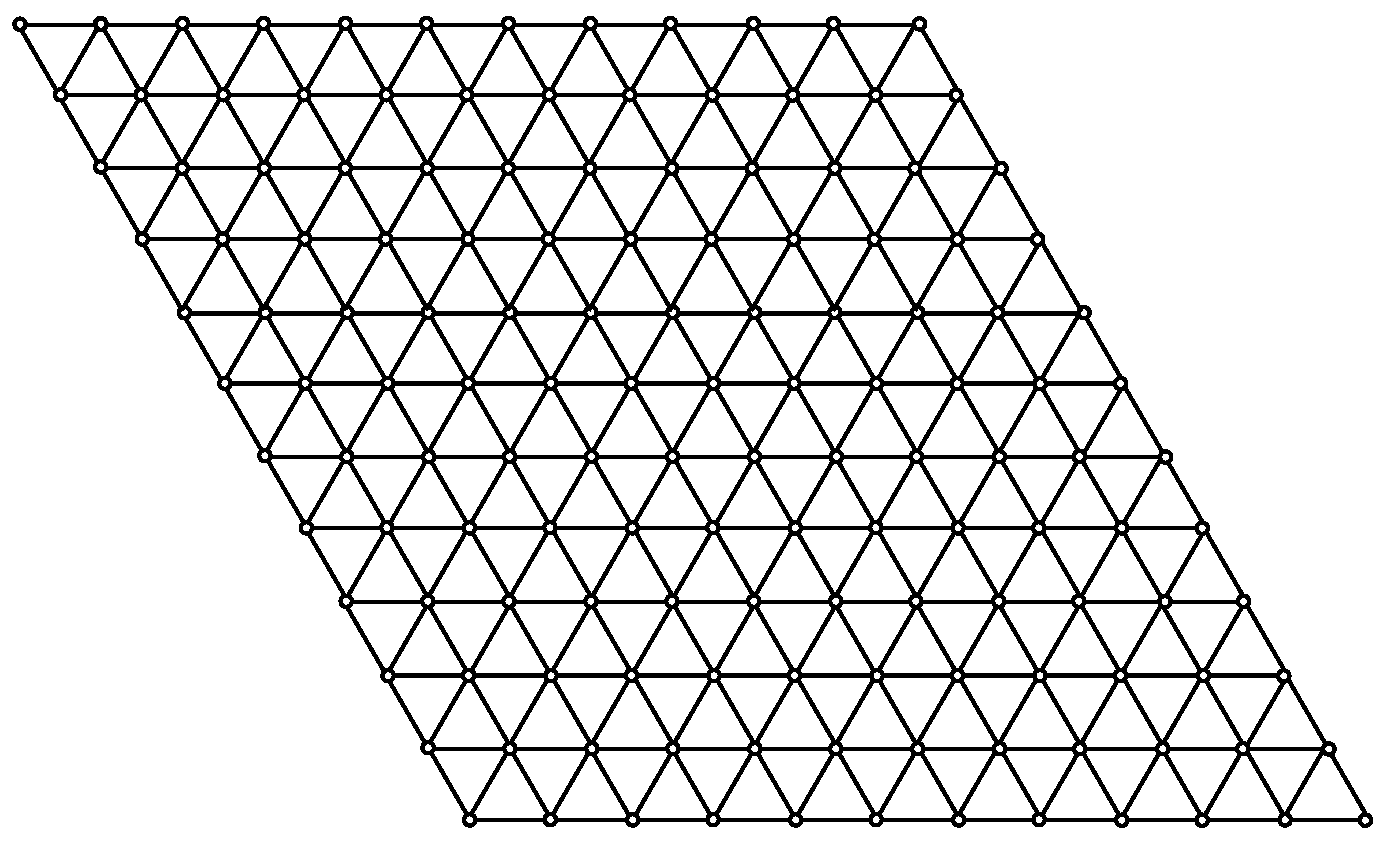
The graph of a Tickysim SpiNNaker Model sheet is shown in Figure 1. The number of vertices in the Tickysim SpiNNaker Model sheet are , and the vertex partition of the graph sheet based on the degree of vertices is shown in Table 1.
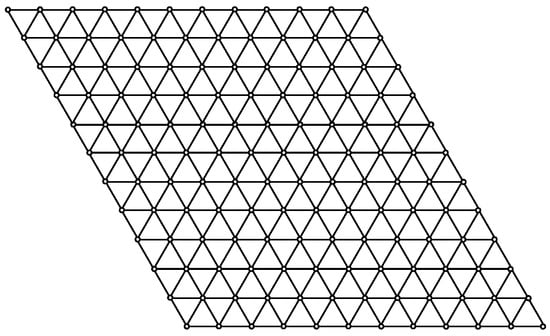
Figure 1.
Graph of the Tickysim SpiNNaker Model sheet for m = n = 12.

Table 1.
The vertex partition of the graph sheet based on the degree of vertices.
4. Main Results
Theorem 1.
Let be a Tickysim SpiNNaker Model sheet, then
- 1.
- ,
- 2.
- ,
- 3.
- ,where α is a real number.
Proof.

The number of edges of the sheet graph is The edge partition based on the degree of the end vertices of each edge are shown in Table 2. Since the formula of the general Randić index is
it implies that
and the formula of the general sum-connectivity index is
which implies that

Table 2.
The edge partition of a graph sheet based on the degree of end vertices of each edge.
This completes the proof. □
Theorem 2.
The atom-bond connectivity index sheet is given by
Proof.
The number of , and edges are mentioned in Table 2. Since the atom-bond connectivity index is defined as
it implies that
This completes the proof. □
Theorem 3.
The geometric-arithmetic index of the sheet is given by
Proof.
The numbers of , and edges are mentioned in Table 2. Since the geometric-arithmetic index is defined as
it implies that
This completes the proof. □
In the next two theorems, we calculated the fourth atom-bond connectivity index and the fifth geometric-arithmetic index . There are eighteen types of edges on the degree-based sum of neighbors vertices of each edge in the Tickysim SpiNNaker Model sheet. We used this partition of edges to calculate and indices. Table 3 gives such types of edges of the Tickysim SpiNNaker Model sheet. The edge set is divided into eighteen edge partitions based on the degree of end vertices. The edge partition contains edges where , , and

Table 3.
The edge partition of the graph sheet based on the degree sum of neighbor vertices of the end vertices of each edge.
Theorem 4.
The fourth atom-bond connectivity index of the Tickysim SpiNNaker Model sheet is given by
Proof.
Let denote the number of edges of the Tickysim SpiNNaker Model sheet with and It is easy to see that the summation of the degree of the edge endpoints of a given graph has eighteen edge types , and , which are shown in Table 3. The fourth atom-bond connectivity index is defined as:
This implies that
This completes the proof. □
Theorem 5.
The fifth geometric-arithmetic index of the Tickysim SpiNNaker Model sheet is given by
Proof.
Let denote the number of edges of the Tickysim SpiNNaker Model sheet with and It is easy to see that the summation of the degree of edge endpoints of given graph has eighteen edge types , and , which are shown in Table 3. The fifth geometric-arithmetic index is defined as:
This implies that
This completes the proof. □
We compute the hyper-Zagreb index first multiple Zagreb index second multiple Zagreb index and Zagreb polynomials for the Tickysim SpiNNaker Model sheet in the following theorem.
Theorem 6.
Let be a Tickysim SpiNNaker Model sheet, then
- 1.
- 2.
- 3.
- 4.
- 5.
Proof.
Let be a Tickysim SpiNNaker Model sheet. The edge set is divided into six edge partitions based on degree of end vertices. The first edge partition contains 4 edges where The second edge partition contains m edges where , The third edge partition contains 2 edges where The fourth edge partition contains edges where The fifth edge partition contains edges where The sixth edge partition contains edges where
Since
after putting the values of edge partitions, we get
Since,
Now, since
After simplification, we get
As,
As
By inserting the values, we obtain
This completes the proof. □
5. Conclusions
In this paper, we deal with a Tickysim SpiNNaker Model sheet and study its topological indices. We determined the first general Zagreb index , general Randić connectivity index , general sum-connectivity index , atom-bond connectivity index , geometric-arithmetic index , fourth atom-bond connectivity index , fifth geometric-arithmetic index , hyper-Zagreb index , first multiple Zagreb index , second multiple Zagreb index , and Zagreb polynomials
In the future, we are interested in designing some incipient architectures/networks and then studying their topological indices, which will be quite auxiliary to understanding their underlying topology.
Author Contributions
M.I. contribute for supervision, funding and analyzed the data curation. M.K.S. contribute for conceptualization, visualization, project administration and wrote the initial draft of the paper. A.A. contribute for Investigation, visualization and Methodology. U.A. and N.H. contribute for designing the experiments, validation, conceptualization, formal analysing experiments, resources, software and some computations. All authors read and approved the final version of the paper.
Funding
This research is supported by the Start-Up Research Grant 2016 of United Arab Emirates University (UAEU), Al Ain, United Arab Emirates via Grant No. G00002233, UPAR Grant of UAEU via Grant No. G00002590 and by the Summer Undergraduate Research Experience (SURE) plus 2017 research Grant via Grant No. G00002412.
Acknowledgments
The authors are grateful to the anonymous referees for their valuable comments and suggestions that improved this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- PoLap, D.; Woźniak, M.; Wei, W.; Damaševičius, R. Multi-threaded learning control mechanism for neural networks. Future Gener. Comput. Syst. 2018, 87, 16–34. [Google Scholar] [CrossRef]
- Woźniak, M.; PoLap, D. Hybrid neuro-heuristic methodology for simulation and control of dynamic systems over time interval. Neural Netw. 2017, 93, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Ando, K.; Takamaeda-Yamazaki, S.; Ikebe, M.; Asai, T.; Motomura, M. Multithreaded CGRA for Convolutional Neural Network Processing. Circuits Syst. 2017, 8, 1–22. [Google Scholar] [CrossRef]
- Harris, J.M.; Hirst, J.L.; Mossinghoff, M.J. Combinatorics and Graph Theory; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Rosen, K.H. Discrete Mathematics and Its Applications, 7th ed.; The McGraw-Hill Companies, Inc.: New York, NY, USA, 2012. [Google Scholar]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar] [CrossRef]
- Gutman, I.; Ruščić, B.; Trinajstić, N.; Wilcox, C.F. Graph Theory and Molecular Orbitals. XII. Acyclic Polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar] [CrossRef]
- Bozkurt, B.; Güngör, A.D.; Gutman, I.; Çevik, A.S. Randić matrix and Randić energy. MATCH Commun. Math. Comput. Chem. 2010, 64, 239–250. [Google Scholar]
- Cavers, M.; Fallat, S.; Kirkland, S. On the normalized Laplacian energy and general Randić index R-1 of graphs. Linear Algebra Appl. 2010, 433, 172–190. [Google Scholar] [CrossRef]
- Gutman, I.; Furtula, B.; Bozkurt, S.B. On Randić energy. Linear Algebra Appl. 2014, 442, 50–57. [Google Scholar] [CrossRef]
- Zhou, B.; Trinajstic, N. On general sum-connectivity index. J. Math. Chem. 2010, 47, 210–218. [Google Scholar] [CrossRef]
- Shirdel, G.H.; Pour, H.R.; Sayadi, A.M. The Hyper-Zagreb index of graph operations. Iran. J. Math. Chem. 2013, 4, 213–220. [Google Scholar]
- Li, X.; Zhao, H. Trees with the first three smallest and largest generalized topological indice. MATCH Commun. Math. Comput. Chem. 2004, 50, 57–62. [Google Scholar]
- Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Estrada, E. Atom–bond connectivity and the energetic of branched alkanes. Chem. Phys. Lett. 2008, 463, 422–425. [Google Scholar] [CrossRef]
- Gutman, I.; Tošović, J.; Radenković, S.; Marković, S. On atom-bond connectivity index. and its chemical applicability. Indian J. Chem. 2012, 51A, 690–694. [Google Scholar]
- Ghorbani, M.; Hosseinzadeh, M.A. Computing ABC4 index of nanostar dendrimers. Optoelectron. Adv. Mater. Rapid Commun. 2010, 4, 1419–1422. [Google Scholar]
- Du, Z.; Zhou, B.; Trinajstić, N. On Geometric-Arithmetic Indices of (Molecular) Trees, Unicyclic Graphs and Bicyclic Graphs. MATCH Commun. Math. Comput. Chem. 2011, 66, 681–697. [Google Scholar]
- Gravovac, A.; Ghorbani, M.; Hosseinzadeh, M.A. Computing fifth geometric-arithmetic index for nanostar dendrimers. J. Math. Nano. 2011, 1, 33–42. [Google Scholar]
- Ghorbani, M.; Azimi, N. Note on multiple Zagreb indices. Iran. J. Math. Chem. 2012, 3, 137–143. [Google Scholar]
- Liu, J.B.; Siddiqui, M.K.; Zahid, M.A.; Naeem, M.; Baig, A.Q. Topological Properties of Crystallographic Structure of Molecules. Symmetry 2018, 10, 265. [Google Scholar] [CrossRef]
- Shao, Z.; Siddiqui, M.K.; Muhammad, M.H. Computing Zagreb Indices and Zagreb Polynomials for Symmetrical Nanotubes. Symmetry 2018, 10, 244. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Imran, M.; Ahmad, A. On Zagreb indices, Zagreb polynomials of some nanostar dendrimers. Appl. Math. Comput. 2016, 280, 132–139. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K.; Naeem, M.; Rehman, N.A. Topological Characterization of Carbon Graphite and Crystal Cubic Carbon Structures. Molecules 2017, 22, 1496. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Siddiqui, M.K.; Imran, M.; Jamil, M.K.; Farahani, M.R. Forgotten Topological Index of Chemical Structure in Drugs. Saudi Pharm. J. 2016, 24, 258–267. [Google Scholar] [CrossRef] [PubMed]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Imran, M.; Siddiqui, M.K.; Naeem, M.; Iqbal, M.A. On Topological Properties of Symmetric Chemical Structures. Symmetry 2018, 10, 173. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Gharibi, W. On Zagreb Indices, Zagreb Polynomials of Mesh Derived Networks. J. Comput. Theor. Nanosci. 2016, 13, 8683–8688. [Google Scholar] [CrossRef]
- Ahmad, A. On the degree based topological indices of benzene ring embedded in P-type-surface in 2D network. Hacet. J. Math. Stat. 2018, 47, 9–18. [Google Scholar] [CrossRef]
- Siddiqui, M.K.; Naeem, M.; Rahman, N.A.; Imran, M. Computing topological indicesof certain networks. J. Optoelectron. Adv. Mater. 2016, 18, 884–892. [Google Scholar]
- Hayat, S.; Imran, M. Computation of certain topological indices of nanotubes. J. Comput. Theor. Nanosci. 2015, 12, 70–76. [Google Scholar] [CrossRef]
- Gao, W.; Siddiqui, M.K. Molecular Descriptors of Nanotube, Oxide, Silicate, and Triangulene Networks. J. Chem. 2017, 2017, 6540754. [Google Scholar] [CrossRef]
- Hayat, S.; Imran, M. Computation of certain topological indices of nanotubes covered by C5 and C7. Comput. Theor. Nanosci. 2015, 12, 533–541. [Google Scholar] [CrossRef]
- Gao, W.; Imran, M.; Siddiqui, M.K.; Naeeme, M.; Jamil, F. Molecular Description of Copper (I) Oxide and Copper (II) Oxide. Quimica. Nova. 2018, 41, 874–879. [Google Scholar]
- Riaz, M.; Gao, W.; Baig, A.Q. M-polynomials and degree-based topological indices of some families of convex polytopes. Open J. Math. Sci. 2018, 2, 18–28. [Google Scholar] [CrossRef]
- Basavanagoud, B.; Gao, W.; Patil, S.; Desai, V.R.; Mirajkar, K.G.; Pooja, B. Computing First Zagreb index and F-index of New C-products of Graphs. Appl. Math. Nonlinear Sci. 2017, 2, 285–298. [Google Scholar] [CrossRef]
- Bača, M.; Horvràthovà, J.; Mokrišovà, M.; Suhànyiovà, A. On topological indices of fullerenes. Appl. Math. Comput. 2015, 251, 154–161. [Google Scholar]
- Stojmenovic, I. Honeycomb Networks: Topological Properties and Communication Algorithms. IEEE Trans. Parallel Distrib. Syst. 1997, 8, 1036–1042. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).