Abstract
The need for organizations to evaluate their environmental practices has been recently increasing. This fact has led to the development of many approaches to appraise such practices. In this paper, a novel decision model to evaluate company’s environmental practices is proposed to improve traditional evaluation process in different facets. Firstly, different reviewers’ collectives related to the company’s activity are taken into account in the process to increase company internal efficiency and external legitimacy. Secondly, following the standard ISO 14031, two general categories of environmental performance indicators, management and operational, are considered. Thirdly, since the assumption of independence among environmental indicators is rarely verified in environmental context, an aggregation operator to bear in mind the relationship among such indicators in the evaluation results is proposed. Finally, this new model integrates quantitative and qualitative information with different scales using a multi-granular linguistic model that allows to adapt diverse evaluation scales according to appraisers’ knowledge.
1. Introduction
Corporate Social Responsibility has a pivotal role in Business models and although it has been differently defined along years, all definitions have five dimensions on common: The environmental, the social, the economic, the stakeholder and the voluntariness dimension. Focusing on the environmental dimension, in recent years companies and institutions have born environmental pressures from regulators. This fact has forced many corporations to expand their attention to environmental responsible practices and to manage their environmental issues as a strategic competitive issue. Therefore, companies need to implement strategies to reduce their environmental impacts and to contribute to environmental sustainability. As a result, the environmentally conscious practices have emerged in form of systems (environmental management systems) and programs to improve processes and products by means of internal policies, actions and plans like design for environment, recycling, waste management, life cycle analysis, green supply chain management and so on (e.g., see [1,2]). Aside from environmental pressures from regulators, companies implement environmentally conscious practices due to the fact that there is a link between carrying on environmental strategies and improving business performance (see [3,4,5], among other).
In order to reflect the company’s efforts and achievements in relation with its environmental performance, many environmental performance indicators (EPI) have been developed. These are used for environmental performance evaluation because they allow communication at different organizational levels and also they provide a basis for making decisions to reach specific goals. Traditionally, environmental indicators are composite indicators, that is, they are a mathematical combination of a set of indicators or criteria that have no common meaningful unit of measurement. EPIs have taken a great importance and they are being used in different ways like the considerable literature in this area shows (e.g., see [6,7], among other). Moreover, there are many works focused on examining some specific indicators (see [7,8,9,10,11,12,13,14,15]). From another angle, the existence of intertwined relations among the components and elements of the environmental practices is a relevant aspect of environmental evaluation problem and it has called attention in the technical literature (see [16,17,18,19]). Such relationships are not easy to take into account in the evaluation process and they have been partially addressed by hierarchical process (see [1,20]).
From the methodology perspective, the evaluation of companies’ environmental performance has been addressed from different approaches (see [12,21,22,23], among other). This paper follows the viewpoint of the Multi-Criteria Decision Making Theory because it facilitates an structured approach to identify solutions to complex evaluation problems (see Figure 1). Decision Analysis is a renowned discipline to accomplish this kind of processes since allows to consider different criteria and several experts. In detail, this contribution is influenced by the Fuzzy Set Theory because it allows to handle simultaneously the qualitative and quantitative information included in environmental performance evaluation process and it has got good results in similar context (see [24,25]).
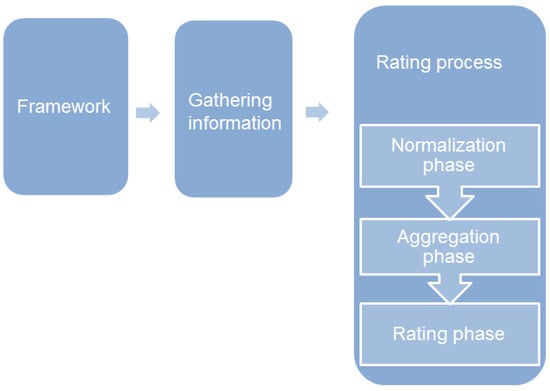
Figure 1.
Scheme of the novel evaluation model.
Taking into account the aforementioned wide spectrum of issues, the main aims of this contribution can be summarized as follows. Firstly, proposing a new environmental integral evaluation model for companies, general enough to integrate indicators built over diverse standpoints. Non-focused on selecting a particular environmental indicator set. Secondly, overcoming the limitations associated with some previous models to evaluate environmental practices proposing a model where different sets of reviewers could evaluate company’s environmental practices attending to different criteria. Thirdly, presenting a flexible evaluation framework allowing appraisers may express their assessments by means of numerical or linguistic information according to the criteria nature. Finally, for addressing the interdependence among criteria/EPIs in a flexible way, the discrete Choquet integral is adopted in the model-like aggregation operator (see [26]).
The novelty of this model is not only its generality but also its capacity to deal with evaluation frameworks in which different set of reviewers (internal and external, experts and non-experts) can assess criteria of diverse nature conforming a flexible heterogeneous framework where different domains of information (numerical, linguistic) are allowed. Finally another important improvement offered by this novel procedure is the management of interdependence among criteria by using the discrete Choquet integral. Therefore, this proposal for an environmental integral evaluation model is versatile enough to be applied under various settings.
The outline of this paper is as follows. In Section 2, we present a roughly overview of previous works. Section 3 is devoted to detail our proposal of environmental integral evaluation model and Section 4 provides with an illustrative application on a manufacturing company. The paper ends pointing out some concluding remarks.
2. Related Works
Before proposing our new approach to carry out evaluation of company’s environmental practices, a short review of the context of environmental evaluation and previous works are included. Initially environmental issues are alluded and then the methodology traditionally used it.
2.1. Evaluating Corporate Environmental Practices
Companies have usually performed different environmental policies from reactive to proactive strategies, some of them react to institutional pressures and stringent environmental regulations (see [9,27]). In many instances, companies respond to influences from large corporate buyers, that demand environmental information to their suppliers. However, a lot of companies voluntarily implement environmental programs, in some cases devoting attention to diverse stakeholder or pursuing environmental reputation (e.g., see [2,28]). For these reasons different authors agree to include stakeholder in the environmental evaluation process (see [1,2,29,30]). Therefore, it is relevant to take into account multiple viewpoints of the concerned parties in the evaluation.
From another point of view, the increasing acceptance of ISO 14001 environmental standards, has caused thousands of facilities worldwide to have adopted Environmental Management System (EMS) that is required to be certified to ISO 14001 (see [31,32]). The environmental standards involve an explicit commitment for improvement of environmental performance (EP). Although there is not a compulsory way of building performance indicators, ISO 14001 gives guidance in environmental performance evaluation through environmental performance indicators, defined as the “specific expression that provides information about an organization’s environmental performance”. In the standard ISO 14031, there are three basic types of EP indicators (EPI): operational (OEPI), management (MEPI) and environmental condition indicators (ECI) (see [33]). The latter intend to provide information about the local, regional, national or global condition of the environment. The MEPIs provide information about management activities in reference to the strategic policy, staffing policy, practices, procedures, decisions and actions at all levels of the organization. The OEPIs provide information about environmental performance of the operations of the organization relative to organization’s physical facilities and equipment (material and energy flows).
Although there is not a discussion about this classification, the ECIs are rarely applied by companies while the OEPIs have been reported more widely than the MEPIs, as is shown in different works (see e.g., [16,18,21,34]). It is relevant to point out that those indicators are quite general and they can encompass results of other more specific environmental evaluation tools such as life cycle assessment, environmental risk assessment and so on.
Diverse approaches have been introduced and a great variety of measurement items may be used in the construction of environmental performance indicators (EPIs) (see [16,17,35]). In the literature, a large number of studies have reported a broad range of such indicators (see [7,8,9,10,11,12,13,14], among other).
Another relevant aspect of environmental evaluation context is the existence of intertwined relations among the components and elements of the environmental practices. This is a notable feature and it has deserved certain attention in the literature (see [16,17,18,19]). It is not easy to take into account such relationships in the evaluation procedure. One way of addressing partially this issue has been through organizing environmental aspects or factors or components that arise from other subcomponents or elements in a hierarchical way. This common practice has also an inherent interest in the environmental matter (see [1,20]).
2.2. Evaluation Methodologies
Many works have addressed the evaluation of corporate environmental performance with different tools (see e.g., [21,23], among other). This contribution focuses on the use of the Multi-Criteria Decision Making Theory to deal with environmental issues. Some approaches are based on traditional methods like Multi-Attribute Analysis technique (MAA) (see e.g., [12]), Analytical Hierarchy Process (AHP) (see e.g., [10,36]), Analytical Network Process (ANP) (see [1,11]) and others specifically developed models (see e.g., [22]). Several references to diverse applications of multi-criteria analysis can be foun to specific issues in corporate environmental evaluation in [15].
Usually it is necessary to handle qualitative information as well as quantitative one in environmental performance evaluation. Given the difficulty of mixing imprecise knowledge in a common way, the Fuzzy Set Theory is expanding in this area. Some proposals in this line are the Fuzzy Extended Analytical Hierarchy Process (see e.g., [36]), the Fuzzy TOPSIS (Technique for Order Performance by Similarity to Ideal Solution ) (see e.g., [37]), the adaptation of Grey Relational Analysis (see e.g., [38]) and another more general works such as [39].
Some contributions in the environmental evaluation context discuss how to integrate the interdependence relations in the evaluation process (e.g., see [19,20,40,41]).
3. A Multi-Criteria Decision Integral Model for Evaluating Environmental Practices
Taking into account the aforementioned goals of the paper, a new proposal of environmental integral evaluation model is introduced in further detail below and its novelties and improvements.
Generally speaking, the main issue of an evaluation process is to compute a set of overall assessments that summarizes information and provides useful knowledge on evaluated elements. Decision analysis is an excellent field to carried out evaluation processes since includes a wide variety of methods for appraising a set of alternatives considering different criteria and involving several experts. It has got good results as it can be seen in the literature (see [24,25]).
Therefore, in this paper an environmental evaluation process based on a classical decision analysis approach is proposed. It consists of three main stages: establishing a framework suitable for the environmental evaluation, gathering information and rating process. In an heterogeneous information context like environmental evaluation, the rating process begins with a normalization of the information [42]. After that, it is possible to carry out an aggregation in an appropriate way. And, finally, we are in the position to make an assessment of the outcomes. Figure 1 shows a graphical scheme of the proposed model. All this steps are going to be explained in coming subsections.
3.1. Evaluation Framework
The evaluation framework fixes actors and elements that may be considered to evaluate environmental practices of a company with n facility sites, . The type of criteria, appraisers and domains used in our proposal are described below.
3.1.1. Criteria Selection
EPIs depict vast quantity of environmental information, relevant attributes or environmental criteria, in a comprehensive and concise way (see [12,13]).
According to the standard ISO 14031, this contribution considers two general categories of EPIs: management performance indicators (MEPI) and operational performance indicators (OEPI). Hence, two types of criteria associated to them are distinguished: management performance criteria, and operational performance criteria, Consequently, there are almost criteria.
Both sets of criteria could have a qualitative and quantitative nature. Due to this fact, the set of all criteria C is split into two subsets: one subset of quantitative criteria, , and another one of qualitative, . The criteria structure is then the following one:
- Management performance criteria:
- Operational performance criteria:
Notice and .
Generally, information provided by reviewers is expressed by means of crisp values (to evaluate quantitative criteria) or by means of words based on Liker’s methodology (see [43]) (to evaluate qualitative criteria) (see [14,22]). In this novel model the appraisers express their assessments with different linguistic descriptors to asses qualitative criteria. So, our proposal is to manage the qualitative criteria using different scales with a multi-granular linguistic model that allow to adapt the evaluation scales and model the linguistic information by using the fuzzy linguistic approach (see [44]).
3.1.2. Reviewers’ Selection
Following the standard ISO 14001, company’s environmental practices are assessed from diverse collectives related to the company activity and not only from the top technical environmental managers. This fact increases company internal efficiency and external legitimacy (see [27,30]).
Thus, a method that distinguishes between experts and non-experts reviewers is developed. Moreover, two general set of reviewers, the internal and the external ones are considered due to the importance to include several information sources related to the company environmental practices. These reviewers are classified based on their knowledge and their information about criteria. Therefore, the following collectives of reviewers take part in the evaluation process (see Figure 2 for a symbolic summary):
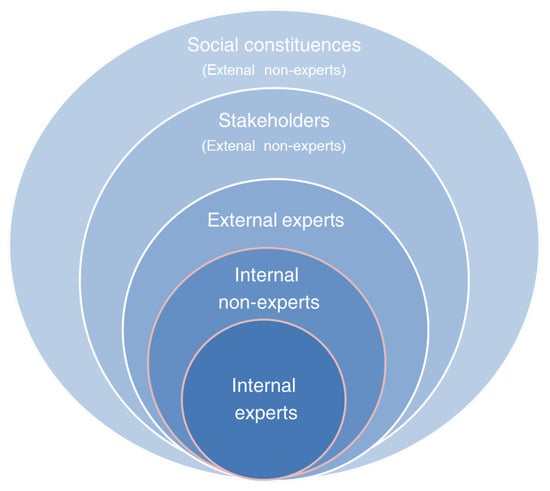
Figure 2.
Reviewers of a facility site.
- A set of internal reviewers:
- -
- A set of company’s internal experts:
- -
- A set of company’s internal non-expert (such as managers, staff, employees, etc.):
- A set of external reviewers:
- -
- A set of company’s external experts such as auditors:
- -
- A set of company’s external non-experts evaluators, , which is split in two types depending on their relation to the company:
- A set of general stakeholders (shareholders, suppliers, government regulators, local communities, intermediate customers, large retailers, final consumers):
- A set of social constituents (community groups, trade associations, labor unions, environmental groups):
Therefore,
3.2. Gathering Information
Once criteria and reviewers have been established, the next step consists of gathering reviewer’s assessments about each facility site with regards to each criterion and attending to their knowledge on them. These evaluations are denoted as follows:
- Let and be the internal reviewers’ evaluations, experts and non-experts respectively, on the facility site by the j-th reviewer regarding the criterion . Abusing notation, on occasions we refer to criterion k as , where superscript denotes M or O, the criterion type.where is the set of non-negative real numbers and and are the linguistic term sets used by the internal experts and non-experts reviewers, respectively, to evaluate the criterion k.
- In the same way, let , , and be the external reviewers’ evaluations, experts and non-experts from stakeholders and social constituencies, respectively, on the facility site by the j-th reviewer with regard to the criterion .where is the set of non-negative real numbers and , and are the linguistic term sets used by the external experts and non-experts reviewers, respectively, to evaluate the criterion k.
Note that any appropriate linguistic term set, , is characterized by its cardinality . In order to keep the notation as simple as possible we use , the subscript denotes the reviewers collective.
3.3. Rating Process
To deal with the information gathered, we adapt the proposal presented in [42] to our aim. Each step of this process is described in the following subsections and its scheme is depicted in Figure 1.
3.3.1. Normalization Phase
In order to manage properly the assessments from reviewers, all gathered heterogeneous information should be unified in the normalization phase. Due to the fact that criteria used to evaluate environmental practices could have different domains, it is necessary to achieve the normalization process by means of different ways, depending on the criterion nature.
Firstly, if the compiled information is regarded to a qualitative criterion , the registered values are linguistic labels that belong to a linguistic term set. Each collective of reviewers can use different linguistic term sets to evaluate qualitative criteria for each facility site. Therefore, we need to bring all the linguistic labels into a unique expression domain, a common linguistic term set called Basic Linguistic Term Set (BLTS). The BLTS is selected with the aim of keeping as much knowledge as possible. It is denoted by and its granularity is g (see [42]). This procedure conducts the heterogeneous information into fuzzy sets and later into linguistic 2-tuples in the BLTS (see [44,45] for more details). The definition of the 2-tuples is recalled below.
Definition 1.
([44]) Let be a set of linguistic terms. The 2-tuple set associated with is determined for . The function is given by,
where round assigns to the integer number closest to .
Secondly, if gathered information is on a quantitative criterion , we have to distinguish between benefit or cost criterion to accomplish accurately the normalization process.
Let be the assessment to the facility site of the reviewer j, on the criterion k, This assessment is normalized in :
where is the maximum assessment expressed for all reviewers over all facility sites attending to the k-th criterion, that is, .
Then, is conducted it into the BLTS by means of linguistic 2-tuples following [42,46].
Once the information is normalized and unified, we proceed to the next step of the rating process, the aggregation.
3.3.2. Aggregation Phase
In this phase, the individual assessments are aggregated by means of aggregation operators according to the step of the aggregation phase and considering their properties. We focus especially on proposing the OWA and discrete Choquet integral as aggregation operators. The former does not distinguish the origin of the values (they are anonymous). This allows to manage properly information from different reviewers. The latter operator is useful to manage interdependence among criteria which are commonly found in environmental evaluation.
In the environmental evaluation literature the existence of relations among environmental indicators is well-known but it is rarely explicitly defined. Obviously, not to take into account these relations it could have consequences over outcomes and it could disturb company’s environmental final decisions. With the aim of overcoming this drawback, our proposal manages such a relationship by means of discrete Choquet integral (see [26,47,48]). This aggregation operator allows us to take into account interactions among criteria or EPIs and, also, the global importance of each criteria or EPI.
Then, each stage of the aggregation process is developed. The Figure 3 displays an outline of this phase.
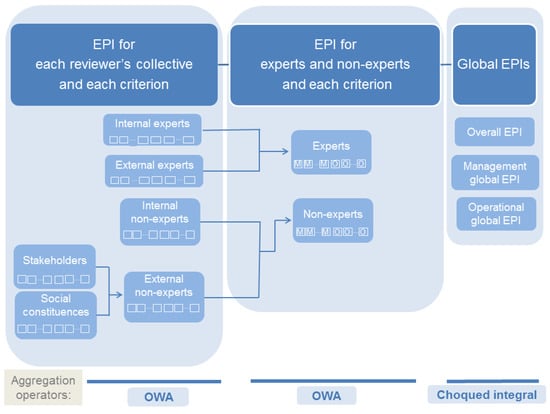
Figure 3.
Multi-step aggregation scheme.
- Computing EPIs for each reviewers’ collective and each criterion.Since we assume that the reviewers give their evaluations individually, we propose to use the 2-tuple OWA operator from [46]. We reproduce its definition below.Definition 2.Let be a vector of linguistic 2-tuples and be a weighting vector such that . The 2-tuple OWA operator associated with is the function defined bywhere is the i-th largest element of .In order to apply this operator, the weighting vector can be computed using the well-known non-decreasing quantifiers proposed by Yager (see [49]). It is important to note that each concrete aggregation procedure with OWA operators can use a different quantifier, in other words, a different weighting vector. This adds flexibility to the model.The reviewers’ assessments are aggregated for each criterion and each collective (see Figure 3) by means of a 2-tuple OWA operator, . Then, for each collective and for every criterion , the process is conducted as follows:
- -
- For internal reviewers (experts and non-experts, respectively):
- -
- For external reviewers (experts and non-experts, respectively):where is the environmental performance indicator for stakeholder reviewers:and is the environmental performance indicator for social constituents reviewers:
- Computing EPIs for experts/non-experts reviewers and each criterion.As in the preceding step, the OWA operator is used. The previous environmental performance indicators for the facility site: , , and are aggregated for each criterion taking into account if the reviewers are experts or not (see Figure 3). The previous indicators belonging to the experts reviewers are then aggregated by means of an OWA operator for each criterion .Analogously to the experts reviewers, an environmental performance indicator is computed for each criterion by aggregating the opinions of all non-experts reviewers.
- Computing global EPIs.The proposed environmental integral evaluation model puts forward the computation of three global environmental performance indicators: an overall that includes all the issues, a management one relative to management issues and an operational one for the operational issues considered. In this way, the major recommendations issued by the ISO 14001 is followed and the model takes the most advantage of the gathered information.From the previous step, there are two values for every single criterion, one from experts reviewers and another from non-experts reviewers for each facility site.Now to aggregate the values corresponding to different criteria, we propose to use the discrete Choquet integral as aggregation operator. It allows for consideration of the interrelations among criteria through the choice of an specific fuzzy measure.
- (a)
- An overall global EPI.In order to cover better the possible interdependences among criteria when we compute an overall global EPI, we do not distinguish between management and operational criteria because we could have interdependences among some management criteria with some operational criteria. Therefore, we do not limit to consider the interdependence among management criteria on the one hand, or only among operational criteria on the another hand.We propose to determine a fuzzy measure, , over the set of all criteria,And then, this fuzzy measure is used to calculate the associated Choquet integrals. Theoretical aspects of Choquet Integral are included in Appendix A. We must do twice, one for the values coming from the experts reviewers and another one for the values coming from the non-experts reviewers. Afterwards, a convex linear combination of both is computed which is the overall global EPI. The parameter is chosen arbitrary taking into account the interest of the company. It stands for the relative importance assigned for the expert reviewers assessments versus the non-expert reviewers assessments.
- (b)
- Management and operational global EPIS.At this point we are interested in calculating two more global indicators, a management global EPI and an operational global EPI, with the aim of conforming to the standard ISO 14001. The criteria are divided according to their type, management and operational. Each type of criteria is aggregated separately by means of two discrete Choquet integrals because it can have interrelations (see Figure 3).In this case, we take the fuzzy measure previously built on the set of all criteria, C, and we derive from it two new fuzzy measures, one on the set of management criteria, , and another on the set of operational criteria, , called and , respectively. So, they are coherent to the previous one, . These are defined as followsNow, from these fuzzy measures we proceed to calculate the mentioned indicators using a discrete Choquet integral for each one.
- Management global environmental performance indicator (MEPI). In order to calculate this indicator we aggregate the experts and non-experts indicators for management criteria, by means of a Choquet integral based on the fuzzy measure previously defined. We then compute a convex linear combination of both of them. is selected depending on the interest of the company (see Figure 3).
- Operational global environmental performance indicator (OEPI). Analogously to management global EPI, an operational global environmental performance indicator is computed for operational criteria, adopting the same strategy to aggregate the experts and no-experts indicators for such criteria. We use the Choquet integral based on the fuzzy measure defined above and a convex linear combination of both with a constant chosen according of the interest of the company (see Figure 3).
All these indicators obtained in each step of the aggregation process, , , , , , , , , and are used for evaluating company environmental practices, not only the overall global EPI for each facility site.
3.3.3. Rating Phase
In the rating phase, the management team shall classify and order facility sites according to the environmental performance indicators obtained in the previous phase. Since those values are linguistic 2-tuples over the BLTS, the sorting and ranking of facility sites are carried out according to the ordinary lexicographic order presented in [46].
One of the most important points of an environmental practices evaluation process is providing feedback to facility sites. With this environmental integral evaluation model, several indicators are obtained for each facility site. Among them are the MEPI and OEPI recommended in the standard ISO14001. In this way, manager team know comprehensive results in the process evaluation and they can use them to formulate environmental policy and programs in order to improve company’s environmental practices.
4. An Illustrative Application
A manufacturing company which is carrying out an evaluation on their environmental practices is considered. This company involves in the evaluation process assessments from internal and external reviewers.
To begin with, the evaluation framework is presented. Without loss of generality a company with two facility sites to be evaluated: is considered according to the criteria described below.
- : Extension in pollution control initiatives.
- : Green purchasing. Assessing how far they incorporate environmental considerations in the purchasing process.
- : Proportion of research and development funds applied to projects with environmental significance.
- : The amount of CO emissions measured in Kg of CO/m.
- : The scope of use of renewable power sources.
- : The electric power consumption in KWh/m.
The criteria can be sorted out according to different issues. We can classify them by the criteria nature and based on the type of information gathered (see Section 3.1.1). In this case, these classifications of the cited criteria are shown in Table 1.

Table 1.
Criteria along with their classifications considered in the example.
These criteria are assessed by diverse reviewers’ collectives:
- Internal reviewers. This reviewers’ collective is made up of:
- -
- A set of three company’s internal experts:
- -
- A set of two company’s internal non-experts:
- External reviewers. This collective consists of:
- -
- A set of two company’s external experts such as auditors: .
- -
- A set of five company’s external non-experts evaluators which is made up of two different reviewers’ collectives:
- A set of three general stakeholders: .
- A set of two social constituents: .
It is worth noticing that each group of reviewers express their appraisals on the facility sites, but not necessarily attending to the same criteria. For example, the non-experts do not assess the criterion relative to funds in research projects because they do not have enough knowledge.
In relation with the expression domains used specifically in the assessments, there are three quantitative and three qualitative criteria. The term set referred to criteria , (, , , , ) have seven linguistic terms whose semantics {Very poor (VP), Medium poor (MP), Fair(F), Medium good (MG), Very good (VG)} is shown in Figure 4 (left). For the criterion the term sets (, , , , ) have five linguistic terms {Very poor (VP), Medium poor(MP), Fair(F), Medium good (MG), Very good (VG)} whose semantics is included in Figure 4 (right).
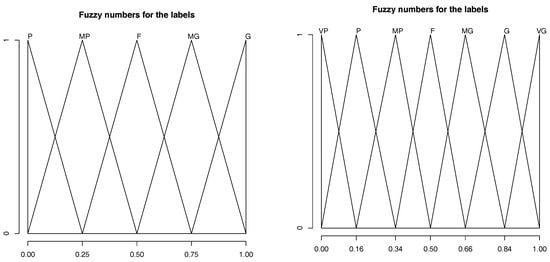
Figure 4.
Left: label set for criteria and its associated fuzzy numbers; Right: label set for criteria and and its associated fuzzy numbers.
When the evaluation framework has been fixed, the reviewers express their opinions about each facility site in relation to each criterion. The values are shown in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7.

Table 2.
Appraisals from the reviewers for criterion .

Table 3.
Appraisals from the reviewers for criterion .

Table 4.
Appraisals from the reviewers for criterion .

Table 5.
Appraisals from the reviewers for criterion .

Table 6.
Appraisals from the reviewers for criterion .

Table 7.
Appraisals from the reviewers for criterion .
After gathering the appraisals, the rating process begins. According to the proposed environmental evaluation process in Section 3, the three phases of the rating process are carried out.
The first phase of the rating process is the normalization phase, whose target is unified all the information gathered from reviewers. We begin by transforming the numerical values into the interval as it was stated in Section 3.3.1. Let us recall that and are cost criteria and is a benefit criterion. After that, both numerical and linguistic values will be conducted into a unique linguistic term set called BLTS by means of fuzzy sets. In this case the BLTS is . Following the procedure described previously, all the values are conducted into linguistic 2-tuples in . The results are not shown here because of the length (see complementary material).
Now, a global assessment for each facility site in a multi-step aggregation process is computed like it was proposed in Section 3.3.2 (see Figure 3).
- Computing environmental performance indicators for each reviewers’ collective and each criterion.In the first step of this process, we apply the 2-tuple OWA operator, which requires a weighting vector. This vector can be chosen in different ways. Particularly, in this example, we use the weighting vector determined by a fuzzy linguistic quantifier (see [50]), the quantifier “most” whose parameters are .The aggregation value with these OWA operators is computed for each criterion for the collectives of internal expert and internal non-experts and for each site ( and ), see Table 8.
 Table 8. Environmental indicators for internal reviewers for each criterion.The environmental performance indicators for general stakeholder reviewers and for social constituents reviewers are obtained by aggregating the values associated to them for each criterion and for each site and ). They are used to compute the indicators for each criterion for external non-experts and for each site (). In addition, the aggregation value is obtained for each criterion for the external experts and for each site (). As noted above, all these calculations have been made using OWA operators with the appropriated weights. The results are showed in Table 9.
Table 8. Environmental indicators for internal reviewers for each criterion.The environmental performance indicators for general stakeholder reviewers and for social constituents reviewers are obtained by aggregating the values associated to them for each criterion and for each site and ). They are used to compute the indicators for each criterion for external non-experts and for each site (). In addition, the aggregation value is obtained for each criterion for the external experts and for each site (). As noted above, all these calculations have been made using OWA operators with the appropriated weights. The results are showed in Table 9. Table 9. Environmental indicators for external reviewers for each criterion.
Table 9. Environmental indicators for external reviewers for each criterion. - Computing environmental performance indicators for experts/non-experts reviewers and each criterion.In the second step of the process, the 2-tuple OWA operator is also applied using the weighting vector calculated before. It is worth pointing out that there is the possibility to use another one attending to the specific characteristics of a particular case study. After these calculations, an environmental performance indicator is computed for experts and non-experts, for each criterion about each facility site. These results are shown in Table 10. The Figure 5a, displays those values for each criteria.
 Table 10. EPIs for experts and non experts for each criterion.
Table 10. EPIs for experts and non experts for each criterion.
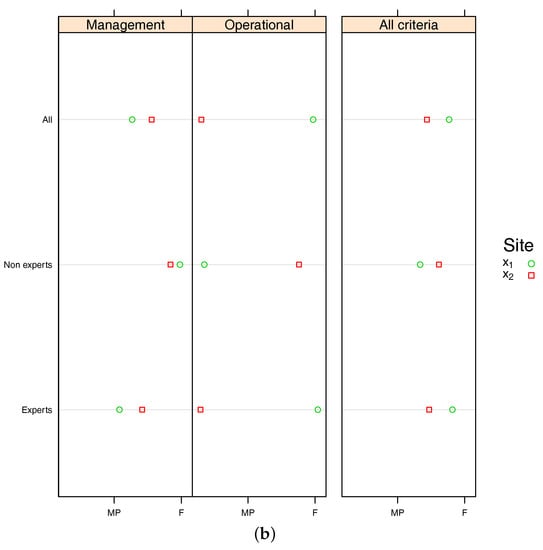 Figure 5. EPIs for site and . (a) EPIs for each criteria for experts and non-experts; (b) Partial and global EPIs.
Figure 5. EPIs for site and . (a) EPIs for each criteria for experts and non-experts; (b) Partial and global EPIs. - Computing global environmental performance indicators.In this step, the values in Table 10 are aggregated for each facility site. At this point, it is needed to aggregate the indicators from different criteria. Therefore, according to the proposed environmental integral evaluation model, the 2-tuple Choquet integral operator is used, which is able to cope with interaction among criteria. Consequently, specific fuzzy measures suited for this example are required and included in Appendix B.
- (a)
- An overall global environmental performance indicator.Now, the fuzzy measures from Table A2 and from Table A4 are employed to calculate the associated 2-tuple Choquet integral for experts and for non experts, respectively, in each site ( and ). These computed values are shown in Table 11.
 Table 11. Experts and non-experts EPIs for sites and .Finally, the overall global environmental performance indicator for each facility site is computed from previous indicators as it was established in the Section 3.3.2, using for example . They are shown in Table 12.
Table 11. Experts and non-experts EPIs for sites and .Finally, the overall global environmental performance indicator for each facility site is computed from previous indicators as it was established in the Section 3.3.2, using for example . They are shown in Table 12. Table 12. Overall global EPI for sites and .
Table 12. Overall global EPI for sites and . - (b)
- Management and operational global environmental performance indicators.In the last step of the process, a management global indicator and an operational global indicator for each facility site are derived. In a similar way to the previous step, the values for several criteria are aggregated using a 2-tuple Choquet integral separately for the management criteria and for operational criteria. In the latter calculation it is used both the fuzzy measure for management and the fuzzy measure for operational criteria , respectively. The results are in Table 13. In order to compute the final values by the proposed procedure, both types of criteria are aggregated for experts and non experts using . The resultant management and operational global performance indicators are shown in Table 14.
 Table 13. Partial EPIs for sites and .
Table 13. Partial EPIs for sites and . Table 14. Management and operational global EPIs for sites and .
Table 14. Management and operational global EPIs for sites and .
In order to ease the evaluation of the outcomes, the partial and global results obtained in the aggregation process are displayed in Figure 5b.
Finally, a classification between the facility sites is established with the purpose of identifying the best one, both overall as global management and operational issues. Using the ordinary lexicographic order on , the facility site , with a value , is the best globally carrying out environmental practices with this evaluation. As well, the results show the facility site is slightly better than facility site in management issues, but not in operational ones. These indicators make visible different facets of the environmental strategies, as suggested by the standard ISO 14001 guidelines. Also note that both experts and non-experts consider better the site . The company now knows the partial and global results which indicate the weak points of the facility sites and it allows to synchronize environmental facility site goals with company’s environmental goals.
5. Conclusions
The evaluation of environmental practices allows companies and organizations to determine their efficiency and effectiveness of their efforts concerning environmental aspects. In this paper, an environmental integral evaluation model has been presented facilitating the comprehensive analysis. This new approach ensures the most relevant issues are regarded in the evaluation process. So, it can deal with different reviewers’ collectives related to the company’s activity. These reviewers express their objective and subjective perceptions presenting different degrees of knowledge about evaluated facility sites. Thus in our proposal, appraisers could express their assessments in different scales according to their knowledge and criteria nature. In addition, this model handles the interdependence among environmental criteria by means of the use of the discrete Choquet integral. It is worth emphasizing that the proposed model is quite flexible to be adapted easily to different settings. A computational experiment for making sensitivity analysis on fuzzy measures could be considered as future research.
Finally, the proposed model not only produces an overall global environmental performance indicator for each facility site, but also a management global and an operational global environmental performance indicators. In addition, it generates intermediate environmental performance indicators according to the opinions of each set of reviewers and each criterion. These are useful for the organization in its environmental improvement effort.
In the following appendixes some definitions and explanations are included to better understand our approach and our illustrative application.
Acknowledgments
The authors thank the anonymous reviewers and Academic Editor for their valuable comments and recommendations. The authors acknowledge financial support by the Spanish Ministerio de Economía y Competitividad under Projects ECO2016-77900-P (R. de Andrés Calle and T. González-Arteaga) and TIN2015-66524-P (L. Martínez).
Author Contributions
Teresa González-Arteaga, Rocio de Andrés Calle and Luis Martínez have contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. A Short Survey on Discrete Choquet Integral for Dealing with Dependencies of EPIs
The application of the Choquet integral in multiple criteria decision making problems has been expanding and the main advances can be seen in [26,47]. When criteria have inter-dependent characteristics, it is not suitable to aggregate them by traditional aggregation operators based on additive measures because it would cause some bias effects in results. Then, we can use alternative operators that has been developed for this distinctive feature. These operators are based on fuzzy measures (or capacities), which only fulfil a monotonicity instead of additivity property. In this appendix, some definitions and important needed results are included for this application.
Definition A1.
Let be a finite universe. A fuzzy measure or capacity is a set function which satisfies:
- 1.
- and ,
- 2.
- ,
where is the set of all subsets of C.
Definition A2.
Let μ a fuzzy measure on C, the representation of μ is a set function given by
We note that if it is known the representation, it is easy to recover the fuzzy measure from which was derived , .
Definition A3.
Let be a function with for . The discrete Choquet integral of f with respect to a fuzzy measure μ is given by
where ⋀ denote the minimum.
Remark A1.
From a mathematical point of view, the discrete Choquet integral is a linear expression up to a reordering of the elements. In addition, as it has been proved in several references such as [26,51,52], among others, the Choquet integral fulfills very significant mathematical properties like idempotence, continuity, non-decreasing monotonicity, stability under the same positive linear transformation, decomposability and compensativeness.
In this paper, we underscore the importance of the latter because it is essential for our application. Compensativeness indicates that:
This allows us to transform the results of the aggregation by means of the Choquet integral into 2-tuples in the linguistic term set using the results in [46], faciliting understanding. It proves suitable the following definition.
Definition A4.
[53] Let be a vector of linguistic 2-tuple, a finite universe and μ a fuzzy measure on C, then the 2-tuples Choquet integral operator is defined as:
here ⋀ denote the minimum.
It is relevant to point out that the fuzzy measure plays a key role in the Choquet integral comparable with the choice of weights in the weighted mean. Moreover, the weighted mean and the OWA aggregation operator are special cases of the Choquet integral for specific fuzzy measures which are connected with the weighting vector (see [52]).
The value, which the fuzzy measure assigns to a set A of criteria, defines the weight of one combination of criteria, but it does not give the global importance of the criteria not either the degree of interaction among them. The overall importance of one or more criteria is given through all the measures where A contains such criteria. On the basis of this idea, it has been proposed different indexes being the most common the Shapley index, which expresses the relative importance of a single criterion or a number of criteria into the decision problem. Thus, those indexes help to analyse the behavioral properties of the aggregation operator (see [51]).
In order to use the Choquet integral in our approach, we need to have at our disposal a fuzzy measure. Since it is convenient to choose one adjusted to our decision problem, we put forward identifying an appropriate fuzzy measure from its concrete characteristics. The main possibilities to do that are enclosed below. Once a fuzzy measure is identified the associated Choquet integral can be used as an aggregation tool.
Identification of the Fuzzy Measure
The identification of a suitable fuzzy measure to a particular Multi-Criteria Decision problem is the great importance since all the knowledge concerning the criteria is embedded into the fuzzy measure. As we manage a problem with n criteria, real numbers in is needed to be completely determined. It seems obvious that these coefficients are hard to be provided by the decision makers. In order to address this issue a number of strategies have been considered in the literature. The fuzzy measure identification methods have been studied by many authors (see [26,47,54,55]). The key point is to use optimization methods to build the fuzzy measure belonging to a particular family with the aim of reducing the initial requirements. The most relevant family is the k-additive fuzzy measures. This allows us to model interaction among at most k criteria.
A fuzzy measure is k-additive if its representation verifies for each with and there exist at least one subset A of cardinality k such that .
An optimization problem in order to obtain an specific fuzzy measure is posed for our problem. The alternative optimization methods differ among them with respect to the objective function and with respect to the input information used to establish constrains. The latter usually come from the monotonicity of fuzzy measures, the particular characteristics of the family of fuzzy measures used. It is also usual to use learning data that may include semantical considerations. An overview is provided in [47].
From a practical point of view these methods can be applied by means of the Kappalab R package (see [56]). This package contains high-level routines for R, which is free software environment release under GNU (GNU is a recursive acronym for “GNU is Not Unix”) for statistical computing and graphics [57]. As a consequence, this software smooths the way for the applications of the Choquet integral, in particular, in the environmental context.
Finally, it is important to emphasize the advantage of allowing decision makers the flexibility to incorporate major interdependencies among criteria through the formulation of the fuzzy measure identification problem.
Appendix B. Computing Some Fuzzy Measures for the Illustrative Example
This appendix is devoted to computing the needed fuzzy measures used in the illustrative application of Section 4.
As we stated in Appendix A, there are several methods to achieve a suited fuzzy measure which collects the distinctive features of the evaluation context. In order to build a particular fuzzy measure for the application, we look for a 2-additive fuzzy measures using the minimum variance method (see [47]). Therefore, some initial requirements are considered. The choice made is just to show some potentials that may be interesting, but there are plenty of possibilities.
- Firstly, we have a clear orientation to criteria relative to practices in outputs of the company (, , ). We translate this through some constrains in the optimization problem. Let us consider Table A1 that contains a learning set of possible normalized criteria values. We demand that the aggregated values, with Choquet integral for its rows, satisfy this orderHere the aggregation values for rows 1 and 2 are greater than for rows 3, 4, and 5 because the outputs criteria have bigger values whatever are the rest of criteria. Besides, when the output criteria have equal values we prefer to have a greater value in criteria , , relative to practices in inputs of the company than in . This implies that Row 1 has an aggregation value greater than Row 2 and the same happens with Rows 4 and 5.
 Table A1. A learning set used for determining the fuzzy measure (criteria reordered).Table A1. A learning set used for determining the fuzzy measure (criteria reordered).
Table A1. A learning set used for determining the fuzzy measure (criteria reordered).Table A1. A learning set used for determining the fuzzy measure (criteria reordered).Output Input Row 1 G MP MP G MP MP Row 2 G MP MP MP MP G Row 3 MP MP MP G MP G Row 4 MP MP MP G MP MP Row 5 MP MP MP MP MP G This means the following constraints:. - Secondly, the decision maker brings some ideas about the interactions of some criteria. The pairs and have to interact in a redundancy way. That is, the contribution of the pair should be inferior to the sum of the contribution of the criterion into it. However, the pair has to interact in a complementary way, i.e., it has a contribution superior to the sum of the contributions of the criteria in it. This means the following constraints on the Shapley indexes:, and
- Thirdly, due to the fact that the emissions are the great importance for the company, it is imposed that the overall importance of this criterion should be at least 0.15 over 1. This adds a new constraint through the Shapley value for this criterion.This implies the constraint on the Shapley value .
In order to get the fuzzy measure we are looking for we incorporate all the previous requirements in the routine for minimum variance method implemented in the kappalab R package. As the resulting fuzzy measure has values we show its Mobius transformation, which is shorter, in Table A2. Analogously, Table A3 contains the Mobius transformation of the associated fuzzy measures and .

Table A2.
Möbius transformation for the fuzzy measure for expert reviewers.
Table A2.
Möbius transformation for the fuzzy measure for expert reviewers.
| {} | {} | {} | {} | {} | {} | |
| 0.503 | 0.203 | 0.036 | 0.266 | 0.109 | 0.222 | |
| {, } | {, } | {, } | {, } | {, } | {, } | |
| −0.003 | −0.003 | −0.219 | 0.100 | −0.197 | 0.131 | |
| {, } | {, } | {, } | {, } | {, } | {, } | |
| −0.047 | −0.099 | −0.025 | 0.000 | −0.010 | 0.000 | |
| {, } | {, } | {, } | ||||
| 0.006 | 0.028 | 0.000 |

Table A3.
Mobius for and for management and for operational criteria, respectively (for experts).
Table A3.
Mobius for and for management and for operational criteria, respectively (for experts).
| {} | {} | {} | {, } | {, } | {, } | |
| 0.58 | 0.23 | 0.04 | −0.00 | −0.00 | 0.15 | |
| {} | {} | {} | {, } | {, } | {, } | |
| 0.42 | 0.17 | 0.35 | 0.01 | 0.04 | 0.00 |
Besides, since some of the criteria cannot be assessed by non-experts, we need to compute another fuzzy measure suited for the aggregation step that implies those criteria appraised by non-experts (, , ). Hence, we adapt the previous requirements in appropriate way. The results are shown in Table A4

Table A4.
Mobius transformation for the fuzzy measure for non-expert reviewers.
Table A4.
Mobius transformation for the fuzzy measure for non-expert reviewers.
| {} | {} | {} | {, } | {, } | {, } | |
|---|---|---|---|---|---|---|
| 0.29 | 0.35 | 0.29 | −0.01 | 0.10 | −0.01 | |
| 0.47 | 0.56 | - | −0.02 | - | - | |
| - | - | 1 | - | - | - |
In order to understand better the role of each criteria in the aggregation operator we obtain the Shapley values associated to those previous fuzzy measures (see Table A5). These values shows the global involvement of each criteria in the results obtained with the Choquet integral. So, the criterion (pollution control initiatives) is the more relevant for the expert reviewers but not for the non experts.

Table A5.
Shapley values for fuzzy measure , and for experts (right) and non-experts (left).
Table A5.
Shapley values for fuzzy measure , and for experts (right) and non-experts (left).
| Non-Experts | Experts | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.34 | 0.18 | 0.10 | 0.15 | 0.11 | 0.12 | 0.33 | 0.33 | 0.33 | ||
| 0.58 | 0.31 | 0.12 | 0.45 | 0.55 | ||||||
| 0.45 | 0.18 | 0.37 | 1 | |||||||
References
- Sarkis, J. Evaluating environmentally conscious business practices. Eur. J. Oper. Res. 1998, 107, 159–174. [Google Scholar] [CrossRef]
- Darnall, N.; Henriques, I.; Sadorsky, P. Do environmental management systems improve business performance in an international setting? J. Int. Manag. 2008, 14, 364–376. [Google Scholar] [CrossRef]
- Stanwick, P.; Stanwick, S. CEO compensation: Does it pay to be green? Bus. Strategy Environ. 2001, 10, 176–182. [Google Scholar] [CrossRef]
- Rivera, J. Assessing a voluntary environmental initiative in the developing world: The Costa Rican Certification for Sustainable Tourism. Policy Sci. 2002, 35, 333–360. [Google Scholar] [CrossRef]
- Iraldo, F.; Testa, F.; Frey, M. Is an environmental management system able to influence environmental and competitive performance? The case of the eco-management and audit scheme (EMAS) in the European union. J. Clean. Prod. 2009, 17, 1444–1452. [Google Scholar] [CrossRef]
- Jørgensen, S.; Burkhard, B.; Müller, F. Twenty volumes of ecological indicators: An accounting short review. Ecol. Indic. 2013, 28, 4–9. [Google Scholar] [CrossRef]
- Rahdari, A.; Rostamy, A. Designing a general set of sustainability indicators at the corporate level. J. Clean. Prod. 2015, 108, 757–771. [Google Scholar] [CrossRef]
- Jasch, C. Environmental performance evaluation and indicators. J. Clean. Prod. 2000, 8, 79–88. [Google Scholar] [CrossRef]
- Lin, B.; Jones, C.; Hsieh, C. Environmental practices and assessment: A process perspective. Ind. Manag. Data Syst. 2001, 101, 71–79. [Google Scholar] [CrossRef]
- Handfield, R.; Walton, S.; Sroufe, R.; Melnyk, S. Applying environmental criteria to supplier assessment: A study in the application of the Analytical Hierarchy Process. Eur. J. Oper. Res. 2002, 141, 70–87. [Google Scholar] [CrossRef]
- Sarkis, J. A strategic decision framework for green supply chain management. J. Clean. Prod. 2003, 11, 397–409. [Google Scholar] [CrossRef]
- Humphreys, P.; Wong, Y.; Chan, F. Integrating environmental criteria into the supplier selection process. J. Mater. Process. Technol. 2003, 138, 349–356. [Google Scholar] [CrossRef]
- Zhu, Q.; Sarkis, J.; Lai, K.H. Confirmation of a measurement model for green supply chain management practices implementation. Int. J. Prod. Econ. 2008, 111, 261–273. [Google Scholar] [CrossRef]
- Jabbour, A.B.L.S.; Jabbour, C.J.C. Are supplier selection criteria going green? Case studies of companies in Brazil. Ind. Manag. Data Syst. 2009, 109, 477–495. [Google Scholar] [CrossRef]
- Herva, M.; Roca, E. Review of combined approaches and multi-criteria analysis for corporate environmental evaluation. J. Clean. Prod. 2013, 39, 355–371. [Google Scholar] [CrossRef]
- Olsthoorn, X.; Tyteca, D.; Wehrmeyer, W.; Wagner, M. Environmental indicators for business: A review of the literature and standardisation methods. J. Clean. Prod. 2001, 9, 453–463. [Google Scholar] [CrossRef]
- Niemeijer, D.; de Groot, R.S. A conceptual framework for selecting environmental indicator sets. Ecol. Indic. 2008, 8, 14–25. [Google Scholar] [CrossRef]
- Brunklaus, B.; Malmqvist, T.; Baumann, H. Managing Stakeholders or the Environment? The Challenge of Relating Indicators in Practice. Corp. Soc. Responsib. Environ. Manag. 2009, 16, 27–37. [Google Scholar] [CrossRef]
- Gandhi, S.; Mangla, S.; Kumar, P.; Kumar, D. Evaluating factors in implementation of successful green supply chain management using DEMATEL: A case study. Int. Strateg. Manag. Rev. 2015, 3, 96–109. [Google Scholar] [CrossRef]
- Tseng, M.L. Using a hybrid MCDM model to evaluate firm environmental knowledge management in uncertainty. Appl. Soft Comput. 2011, 11, 1340–1352. [Google Scholar] [CrossRef]
- Xie, S.; Hayase, K. Corporate Environmental Performance Evaluation: A Measurement Model and a New Concept. Bus. Strategy Environ. 2007, 16, 148–168. [Google Scholar] [CrossRef]
- Tsoulfas, G.T.; Pappis, C.P. A model for supply chains environmental performance analysis and decision making. J. Clean. Prod. 2008, 16, 1647–1657. [Google Scholar] [CrossRef]
- Ho, W.; Xu, X.; Dey, P.K. Multi-criteria decision making approaches for supplier evaluation and selection: A literature review. Eur. J. Oper. Res. 2010, 202, 16–24. [Google Scholar] [CrossRef]
- Arfi, B. Fuzzy decision making in politics: A linguistic fuzzy-set approach. Political Anal. 2005, 13, 23–56. [Google Scholar] [CrossRef]
- Martínez, L. Sensory evaluation based on linguistic decision analysis. Int. J. Approx. Reason. 2007, 44, 148–164. [Google Scholar] [CrossRef]
- Grabisch, M. The application of fuzzy integrals in multicriteria decision making. Eur. J. Oper. Res. 1996, 89, 445–456. [Google Scholar] [CrossRef]
- Darnall, N.; Seol, I.; Sarkis, J. Perceived stakeholder influences and organizations’ use of environmental audits. Acc. Organ. Soc. 2009, 34, 170–187. [Google Scholar] [CrossRef]
- King, A.; Lenox, M.; Terlaak, A. The strategic use of decentralized institutions: Exploring certification with the ISO 14001 management standard. Acad. Manag. J. 2005, 48, 1091–1106. [Google Scholar] [CrossRef]
- Kain, J.H.; Saderberg, H. Management of complex knowledge in planning for sustainable development: The use of multi-criteria decision aids. Environ. Impact Assess. Rev. 2008, 28, 7–21. [Google Scholar] [CrossRef]
- Nawrocka, D.; Parker, T. Finding the connection: Environmental management systems and environmental performance. J. Clean. Prod. 2009, 17, 601–607. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Environmental Management Systems–Requirements with Guidance for Use (ISO 14001:2004); ISO: Geneva, Switzerland, 2004. [Google Scholar]
- To, W.; Lee, P. Diffusion of ISO 14001 environmental management system: Global, regional and country-level analyses. J. Clean. Prod. 2014, 66, 489–498. [Google Scholar] [CrossRef]
- International Organization for Standardization (ISO). Standards 14031. Environmental Management Environmental Performance Evaluation: Guidelines; ISO: Geneva, Switzerland, 1999. [Google Scholar]
- Henri, J.F.; Journeault, M. Environmental performance indicators: An empirical study of Canadian manufacturing firms. J. Environ. Manag. 2008, 87, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Thoresen, J. Environmental performance evaluation—A tool for industrial improvement. J. Clean. Prod. 1999, 7, 365–370. [Google Scholar] [CrossRef]
- Lee, A.H.; Kang, H.Y.; Hsu, C.F.; Hung, H.C. A green supplier selection model for high-tech industry. Expert Syst. Appl. 2009, 36, 7917–7927. [Google Scholar] [CrossRef]
- Awasthi, A.; Chauhan, S.S.; Goyal, S. A fuzzy multicriteria approach for evaluating environmental performance of suppliers. Int. J. Prod. Econ. 2010, 126, 370–378. [Google Scholar] [CrossRef]
- Tseng, M.L.; Chiu, A.S. Evaluating firm’s green supply chain management in linguistic preferences. J. Clean. Prod. 2013, 40, 22–31. [Google Scholar] [CrossRef]
- Espinilla, M.; de Andres, R.; Martinez, F.J.; Martinez, L. A Heterogeneous Evaluation Model for the Assessment of Sustainable Energy Policies; MeloPinto, P., Couto, P., Serodio, C., Fodor, J., DeBaets, B., Eds.; Advances in Intelligent and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2011; Volume 107, pp. 209–220. [Google Scholar]
- Tseng, M.L.; Chiang, J.H.; Lan, L.W. Selection of optimal supplier in supply chain management strategy with analytic network process and choquet integral. Comput. Ind. Eng. 2009, 57, 330–340. [Google Scholar] [CrossRef]
- Buyukozkan, G.; Cifci, G. A novel fuzzy multi-criteria decision framework for sustainable supplier selection with incomplete information. Comput. Ind. 2011, 62, 164–174. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L.; Sánchez, P. Managing non-homogeneous information in group decision making. Eur. J. Oper. Res. 2005, 166, 115–132. [Google Scholar] [CrossRef]
- Likert, R. A Technique for the measumerement of attitudes. Arch. Psychol. 1932, 140, 1–55. [Google Scholar]
- Herrera, F.; Herrera-Viedma, E.; Martínez, L. A fusion approach for managing multi-granularity linguistic term sets in decision making. Fuzzy Sets Syst. 2000, 114, 43–58. [Google Scholar] [CrossRef]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Grabisch, M.; Kojadinovic, I.; Meyer, P. A review of methods for capacity identification in Choquet integral based multi-attribute utility theory: Applications of the Kappalab R package. Eur. J. Oper. Res. 2008, 186, 766–785. [Google Scholar] [CrossRef]
- Klement, E.; Mesiar, R. Discrete Integrals and Axiomatically Defined Functionals. Axioms 2012, 1, 9–20. [Google Scholar] [CrossRef]
- Yager, R. On Ordered Weighted Averaging Operators in Multicriteria Decision Making. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Zadeh, L. A Computational Approach to Fuzzy Quantifiers in Natural Languages. Comput. Math. Appl. 1983, 9, 149–184. [Google Scholar] [CrossRef]
- Marichal, J.L. Behavioral analysis of aggregation in multicriteria decision aid. In Preferences and Decisions under Incomplete Knowledge; Fodor, J., De Baets, B., Perny, P., Eds.; Studies in Fuzziness and Soft Computing; Physica Verlag: Heidelberg, Germany, 2000; Volume 51, pp. 153–178. [Google Scholar]
- Beliakov, G.; Pradera, A.; Calvo, T. Aggregation Functions: A Guide for Practitioners; Springer: Berlin, Germany, 2007. [Google Scholar]
- Yang, W.; Chen, Z. New aggregation operators based on the Choquet integral and 2-tuple linguistic information. Expert Syst. Appl. 2012, 39, 2662–2668. [Google Scholar] [CrossRef]
- Meyer, P.; Roubens, M. Choice, Ranking and Sorting in Fuzzy Multiple Criteria Decision Aid. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; International Series in Operations Research and Management Science; Springer: New York, NY, USA, 2005; Volume 78, pp. 471–503. [Google Scholar]
- Wu, J.Z.; Zhang, Q. 2-order additive fuzzy measure identification method based on diamond pairwise comparison and maximum entropy principle. Fuzzy Optim. Decis. Mak. 2010, 9, 435–453. [Google Scholar] [CrossRef]
- Grabisch, M.; Kojadinovic, I.; Meyer, P. Kappalab: Non-Additive Measure and Integral Manipulation Functions, R package version 0.4-7; Repository CRAN; 2015. Available online: https://cran.r-project.org/web/packages/kappalab/index.html (accessed on 20 September 2017).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; ISBN 3-900051-07-0. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).