Estimating Covariances and Goodness of Fit Plots for Accelerated Failure Time Models

Abstract

Let the response variable Y be the time until an event such as death. Assume that there are p predictors $x_1,\dots ,x_p$ and that the response variable is right censored. Several survival regression models, including accelerated failure time models, have the form $Z=log\left(Y\right)={\alpha }_Z+{\mathit{x}}_i^T{\mathit{\beta }}_Z+e$. This paper gives a simple method for estimating the covariances $Cov(x_i,Z)$ for some of these models. Plots are given for checking the goodness of fit of accelerated failure time models. Plots for checking the proportional hazards regression model are often harder to use.

1. Introduction

This section reviews some survival regression models, including plots for checking the models. The response variable $Y>0$ is the time until an event such as death. Let the $p\times 1$ vector of predictor variables $\mathit{x}={(x_1,\dots ,x_p)}^T$. Let the sufficient predictor $SP=\alpha +{\mathit{x}}^T\mathit{\beta }$, and let the estimated sufficient predictor $ESP=\widehat{\alpha }+{\mathit{x}}^T\widehat{\mathit{\beta }}$ where it is possible that $\alpha =\widehat{\alpha }=0$. The ESP is sometimes called the estimated risk score.

Assume that the response variable is right censored so Y is not observed. Instead, the right censored survival time $T_i=min(Y_i,W_i)$ where $Y_i$ is independent of the censoring time $W_i$. Also ${\delta }_i=0$ if $T_i=W_i$ is censored and ${\delta }_i=1$ if $T_i=Y_i$ is uncensored. Hence the data is $(T_i,{\delta }_i,x_i)$ for $i=1,\dots ,n.$

For an accelerated failure time model, the log transformation of the response variable results in a multiple linear regression model. Hence multiple linear regression models will be useful. Now let the response variable Y be for multiple linear regression, so Y need not be a nonnegative time until event. A useful multiple linear regression model is $Y|{\mathit{x}}^T\mathit{\beta }=\alpha +{\mathit{x}}^T\mathit{\beta }+e$ or

$$Y_i=\alpha +x_{i,1}{\beta }_1+\dots +x_{i,p}{\beta }_p+e_i=\alpha +{\mathit{x}}_i^T\mathit{\beta }+e_i$$

(1)

for $i=1,\dots ,n.$ Assume that the $e_i$ are independent and identically distributed (iid) with expected value $E\left(e_i\right)=0$ and variance $V\left(e_i\right)={\sigma }^2$. In matrix form, this model is

$$\mathit{Y}=\mathit{X}\mathit{\varphi }+\mathit{e},$$

(2)

where Y is an $n\times 1$ vector of dependent variables, X is an $n\times (p+1)$ matrix with ith row $(1,{\mathit{x}}_i^T)$, $\mathit{\varphi }={(\alpha ,{\mathit{\beta }}^T)}^T$ is a $(p+1)\times 1$ vector, and e is an $n\times 1$ vector of unknown errors. Also $E\left(\mathit{e}\right)=0$ and Cov($e)={\sigma }^2{\mathit{I}}_n$ where ${\mathit{I}}_n$ is the $n\times n$ identity matrix.

For a multiple linear regression model with heterogeneity, assume model (1) holds with $E\left(\mathit{e}\right)=0$ and Cov$\left(\mathit{e}\right)={\Sigma }_{\mathit{e}}=diag\left({\sigma }_i^2\right)=diag({\sigma }_1^2,\dots ,{\sigma }_n^2)$ is an $n\times n$ positive definite matrix. When the ${\sigma }_i^2$ are known, weighted least squares is often used. Under regularity conditions, the ordinary least squares (OLS) estimator ${\widehat{\mathit{\varphi }}}_{OLS}={\left({\mathit{X}}^T\mathit{X}\right)}^{-1}{\mathit{X}}^T\mathit{Y}$ can be shown to be a consistent estimator of $\mathit{\varphi }$.

For estimation with ordinary least squares, let the $p\times p$ covariance matrix of x be $\mathrm{Cov}\left(\mathit{x}\right)={\Sigma }_{\mathit{x}}=E\left[(\mathit{x}-E\left(\mathit{x}\right)){(\mathit{x}-E\left(\mathit{x}\right))}^T\right]$ and let the $p\times 1$ vector $\mathrm{Cov}(\mathit{x},Y)={\Sigma }_{\mathit{x}Y}=E[(\mathit{x}-E\left(\mathit{x}\right)(Y-E\left(Y\right))]={(\mathrm{Cov}(x_1,Y),\dots ,\mathrm{Cov}(x_p,Y))}^T.$ Let

$${\widehat{\Sigma }}_{\mathit{x}}={\displaystyle \frac{1}{n-1}}\sum _{i=1}^n({\mathit{x}}_i-\overline{\mathit{x}}){({\mathit{x}}_i-\overline{\mathit{x}})}^T\mathrm{and}{\widehat{\Sigma }}_{\mathit{x}Y}={\displaystyle \frac{1}{n-1}}\sum _{i=1}^n({\mathit{x}}_i-\overline{\mathit{x}})(Y_i-\overline{Y}).$$

Then the OLS estimators for model (1) are ${\displaystyle {\widehat{\mathit{\varphi }}}_{OLS}={\left({\mathit{X}}^T\mathit{X}\right)}^{-1}{\mathit{X}}^T\mathit{Y}}$, ${\displaystyle {\widehat{\alpha }}_{OLS}=\overline{Y}-{\widehat{\mathit{\beta }}}_{OLS}^T\overline{\mathit{x}}}$, and

$${\widehat{\mathit{\beta }}}_{OLS}={\widehat{\Sigma }}_{\mathit{x}}^{-1}{\widehat{\Sigma }}_{\mathit{x}Y}.$$

For a multiple linear regression model with iid cases, ${\widehat{\mathit{\beta }}}_{OLS}$ is a consistent estimator of ${\mathit{\beta }}_{OLS}={\Sigma }_{\mathit{x}}^{-1}{\Sigma }_{\mathit{x}Y}$ under mild regularity conditions, while ${\widehat{\alpha }}_{OLS}$ is a consistent estimator of $E\left(Y\right)-{\mathit{\beta }}_{OLS}^{T}E\left(\mathit{x}\right)$.

For a parametric accelerated failure time (AFT) model,

$$Z_i=log\left(Y_i\right)=\alpha +{\mathit{\beta }}_A^T{\mathit{x}}_i+\sigma e_i$$

(3)

where the $e_i$ are iid from a location scale family. The parameters are estimated by maximum likelihood.

The Weibull proportional hazards regression model or Weibull regression model is

$$Y|SP\sim W(\gamma =1/\sigma ,{\lambda }_{0}exp\left(SP\right))$$

where Y has a Weibull $W(\gamma ,\lambda )$ distribution if the probability density function of Y is

$$f\left(y\right)=\lambda \gamma y^{\gamma -1}exp[-\lambda y^{\gamma }]$$

for $y>0,\gamma >0,$ and $\lambda >0.$ This regression model can also be fit using the Cox (1972) [1] proportional hazards regression model. Let the sufficient predictor $SP={\mathit{x}}^T{\mathit{\beta }}_P$. If $Y|x^T{\mathit{\beta }}_P$ satisfies a Weibull regression model, then $Z=log\left(Y\right)=\alpha +x^T{\mathit{\beta }}_A+e_i$ satisfies a Weibull AFT with ${\lambda }_0=exp(-\alpha /\sigma )$ and ${\mathit{\beta }}_P=-{\mathit{\beta }}_A/\sigma$. Exponential regression is the special case where $\sigma =1$.

Two other important AFTs are (i) the lognormal AFT where $log\left(Y\right)|{\mathit{x}}^T{\mathit{\beta }}_A\sim N(\alpha +{\mathit{x}}^T{\mathit{\beta }}_A,{\sigma }^2)$, where the $Y_i$ are lognormal and the $e_i\sim N(0,1)$ are normal, and (ii) the loglogistic AFT where $log\left(Y\right)|{\mathit{x}}^T{\mathit{\beta }}_A\sim L(\alpha +{\mathit{x}}^T{\mathit{\beta }}_A,\sigma )$, where the $Y_i$ are loglogistic and the $e_i\sim L(0,1)$ are logistic. For the loglogistic AFT, Y follows a proportional odds model. Y does not follow a proportional hazards regression model for the loglogistic and lognormal AFTs.

The Buckley and James (1979) [2] estimator $({\widehat{\alpha }}_{BJ},{\widehat{\mathit{\beta }}}_{BJ})$ is a nonparametric survival regression method for models of the form (3), and is a competitor for the parametric AFTs. When there is no censoring, this estimator is equivalent to the ordinary least squares estimator for multiple linear regression.

Often the log transformation results in a linear model with heterogeneity:

$$Z_i=log\left(Y_i\right)={\alpha }_Z+{\mathit{x}}_i^T{\mathit{\beta }}_Z+e_i$$

(4)

where the $e_i$ are independent with expected value $E\left(e_i\right)=0$ and variance $V\left(e_i\right)={\sigma }_i^2.$ For the AFT and the Buckley James estimator, the variance is constant: $V\left(e_i\right)={\sigma }^2$ does not depend on i.

The Cox (1972) [1] proportional hazards regression model is a semiparametric model with $SP={\mathit{\beta }}_C^T\mathit{x}$ and hazard function

$$h_{Y|SP}\left(t\right)=exp\left({\mathit{\beta }}_C^T\mathit{x}\right)h_0\left(t\right)=exp\left(SP\right)h_0\left(t\right)$$

where the baseline hazard function $h_0\left(t\right)$ is left unspecified. The survival function is

$$S_{Y|SP}\left(t\right)=P(Y>t|SP={\mathit{\beta }}_C^T\mathit{x})={\left[S_0\left(t\right)\right]}^{exp\left({\mathit{\beta }}_C^T\mathit{x}\right)}={\left[S_0\left(t\right)\right]}^{exp\left(SP\right)}$$

(5)

where $S_0\left(t\right)$ is the baseline survival function. If $\mathit{x}=\mathbf{0}$ is within the range of the predictors, then the baseline survival and hazard functions correspond to the survival and hazard functions of $\mathit{x}=\mathbf{0}.$ The cumulative hazard function $H_{Y|SP}\left(t\right)=-log\left(S_{Y|SP}\left(t\right)\right)$ for $t>0$, and the hazard function $h_{Y|SP}\left(t\right)={\displaystyle \frac{d}{dt}}{H}_{Y|SP}\left(t\right)$ for $t>0.$ High hazard implies low survival times while low hazard implies long survival times.

The literature for checking the goodness of fit of the proportional hazards model is fairly large. See, for example, Arjas (1988) [3], Feng et al. (2017) [4], Gill and Schumaker (1987) [5], Kay (1984) [6], Lin and Wei (1991) [7], Marzec and Marzec (1997) [8], Ng’andu (1997) [9], Quantin et al. (1996) [10], and Yu et al. (2008) [11].

Grambsch and Therneau (1994) [12] give a useful graphical check. Suppose the ith case had an uncensored survival time $t_i$. Let the scaled Schoenfeld residual for the ith observation and jth variable $x_j$ be $r_{P,j}^{*}\left(t_i\right)$. For each variable, plot the $t_i$ versus the $r_{P,j}^{*}\left(t_i\right)+\widehat{{\beta }_j}$ and add the loess curve. If the loess curve is approximately horizontal for each of the p plots, then the proportional hazards assumption is reasonable. Alternatively, fit a line to each plot and test that each of the p slopes is equal to 0. The R function cox.zph makes both the plots and tests.

2. Materials and Methods

2.1. Estimating ${\Sigma }_{\mathit{x}Z}$ for Some Censored Survival Regression Models

This subsection derives an estimator for ${\Sigma }_{\mathit{x}Z}=\mathrm{Cov}(\mathit{x},Z)$ where the right censored $Z_i$ are not observed. Let the ordinary least squares (OLS) estimator be ${\widehat{\mathit{\beta }}}_{OLS}$. Assume that the cases $({\mathit{x}}_i,Y_i)$ are iid. Since model (4) is a multiple linear regression model, under mild regularity conditions, the population parameter vectors are equal: ${\mathit{\beta }}_Z={\mathit{\beta }}_{OLS}={\Sigma }_{\mathit{x}}^{-1}{\Sigma }_{\mathit{x}Z}$. Thus ${\Sigma }_{\mathit{x}Z}=\mathrm{Cov}\left(\mathit{x}\right){\mathit{\beta }}_Z={\Sigma }_{\mathit{x}}{\mathit{\beta }}_Z.$ When the response $Y_i$ is censored, several survival regression models give consistent estimators ${\widehat{\mathit{\beta }}}_Z$ of ${\mathit{\beta }}_Z$. Hence

$${\widehat{\Sigma }}_{\mathit{x}Z}={\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_Z.$$

(6)

The Buckley James estimator is equivalent to the OLS estimator when there is no censoring, and censoring does not change the population parameter. Although the population parameters are the same, the estimators are very different. The OLS estimator is not a consistent estimator of ${\mathit{\beta }}_Z={\mathit{\beta }}_{OLS}$ when censoring occurs. Hence ${\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_{OLS}$ is not a consistent estimator of ${\Sigma }_{\mathit{x}Z}$ if the response variable is censored.

If an accelerated failure time model is used, then two estimators are ${\widehat{\Sigma }}_{\mathit{x}Z}\left(A\right)={\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_A$ and ${\widehat{\Sigma }}_{\mathit{x}Z}\left(B\right)={\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_{BJ}$. These two estimators require consistent estimators of ${\mathit{\beta }}_Z={\Sigma }_{\mathit{x}}^{-1}{\Sigma }_{\mathit{x}Z}$, which occurs, for example, if the cases $({\mathit{x}}_i,Y_i)$ are iid from some population with covariance matrix ${\Sigma }_{\mathit{x}}$ and covariance vector ${\Sigma }_{\mathit{x}Z}$. The survival times $Y_i$ can be right censored, but the predictor variables $x_1,\dots ,x_p$ are not censored. Note that the predictor variables that have the highest absolute correlation with Z have the highest values of $|\widehat{\mathrm{Cov}}(x_i,Z)|/\sqrt{\widehat{V}\left(x_i\right)}$.

Although this technique is a simple plug in estimator, to our knowledge, the technique has not been suggested previously for survival regression models. In the literature, there are several estimators for the correlation $Cor(X,Y)$, where X and Y are survival times. These estimators usually use maximum likelihood estimation or multiple imputation assuming that $(X,Y)$ are iid from a bivariate normal distribution. See, for example, Barchard and Russell (2024) [13], Li et al. (2018) [14], and Lyles, Fan, and Chuachoowong (2001) [15]. For covariance estimation, see references in Pesonen, Pesonen, and Nevalainen (2015) [16].

2.2. The EE Plot

It is important to check that a parametric AFT model is reasonable with the Buckley James estimator before using Equation (6). Make an EE plot of $ESPBJ={\mathit{x}}^T{\widehat{\mathit{\beta }}}_{BJ}$ versus $ESPA={\mathit{x}}^T{\widehat{\mathit{\beta }}}_A$. For the Weibull AFT, also plot $ESPPH=-\widehat{\sigma }{\mathit{x}}^T{\widehat{\mathit{\beta }}}_P$ versus the above two ESPs, where PH stands for the Cox proportional hazards estimator. The plotted points in the EE plot should scatter tightly about the identity line with zero intercept and unit slope. Lack of fit is suggested if the plotted points do not cluster tightly about the identity line. The identity line is included in the EE plots as a visual aid. Suppose the two estimators of $\mathit{\beta }={\mathit{\beta }}_Z$ are consistent. Then as $n\to \infty$, the correlation of the plotted points goes to 1 in probability for any finite interval, e.g., from the 1st percentile to the 99th percentile of ${\mathit{x}}^T{\widehat{\mathit{\beta }}}_{BJ}$.

For the Exponential regression model, $\sigma =1$ and ${\mathit{\beta }}_P=-{\mathit{\beta }}_A$. Since the Exponential regression model with ${\widehat{\mathit{\beta }}}_E$ is a special case of the Weibull regression model with ${\widehat{\mathit{\beta }}}_W$, plots can use $ESPE={\mathit{x}}^T{\widehat{\mathit{\beta }}}_E$, $ESPBJ$, $ESPPH$ or $-{\mathit{x}}^T{\widehat{\mathit{\beta }}}_P$, and $ESPA=ESPW$ where $A=W$ is the Weibull regression that estimates $\widehat{\sigma }$.

The EE plots are much easier to use than other plots in the literature, since tight clustering about the identity line suggests goodness of fit.

3. Some Other Plots

Let $log\left(T_i\right)=\widehat{\alpha }+{\widehat{\mathit{\beta }}}_A^T{\mathit{x}}_i+r_i$ where the $r_i$ are residuals. Collett (2003, p. 231) [17] defines a standardized residual $r_{Si}=r_i/\widehat{\sigma }.$ For accelerated failure time models, a log censored response (LCR) plot is a plot of $\widehat{\alpha }+{\widehat{\mathit{\beta }}}_A^T{\mathit{x}}_i$ versus log($T_i)$ on the vertical axis with plotting symbol 0 for censored cases and + for uncensored cases. The identity line with unit slope and zero intercept is added to the plot, and the vertical deviations from the identity line = $r_i$. This plot is useful to check for cases with unusual survival times. The plot is also useful for checking for linearity (which is often rather weak due to the censored response and skewed data).

Ritov (1990) [18] and Tsiatis (1990) [19] consider the censored survival regression model $Z=t\left(Y\right)={\alpha }_Z+{\mathit{x}}_i^T{\mathit{\beta }}_Z+e$ where t is a known monotone function. Then a plot of ${\widehat{\alpha }}_Z+{\mathit{x}}_i^T{\widehat{\mathit{\beta }}}_Z$ versus $t\left(T_i\right)$ is useful. A power transformation has the form $W=t_{\lambda }\left(T\right)=T^{\lambda }$ for $\lambda \ne 0$ and $W=t_0\left(T\right)=log\left(T\right)$ for $\lambda =0$ where

$$\lambda \in {\mathrm{\Lambda }}_L=\{-1,-1/2,-1/3,0,1/3,1/2,1\}.$$

The modified power transformation family

$$t_{\lambda }\left(T_i\right)\equiv T_i^{\left(\lambda \right)}={\displaystyle \frac{T_i^{\lambda }-1}{\lambda }}$$

(7)

for $\lambda \ne 0$ and $T_i^{\left(0\right)}=log\left(T_i\right)$.

A graphical method for response transformations makes the transformation plot of $\widehat{\alpha }+{\mathit{x}}_i^T\widehat{\mathit{\beta }}$ versus $t_{\lambda }\left(T_i\right)$ using the Buckley James estimator with $W=t_{\lambda }\left(T\right)$ as the “response” for $\lambda \in {\mathrm{\Lambda }}_L$. Then a candidate response transformation $Z=t_{{\lambda }^{*}}\left(T\right)$ has the transformation plot that suggests a linear model is appropriate.

Smith (2002, p. 191) [20] notes that the Buckley James estimator replaces the censored $T_i$ by their estimated conditional expected values, resulting in a renovated response variable $T_i^{*}$. Using the $T_i^{*}$ instead of the $T_i$ may increase the linearity of the plot.

The slice survival plot divides the ESP into J groups of roughly the same size. For each group j with $n_j$ cases, the model estimated survival function ${\widehat{S}}_j\left(t\right)$ is computed using the x corresponding to the “median ESP” of the group (the kth order statistic of the ESP in group j, where $k=1+floor[(n_j-1)/2]$). Let ${\widehat{S}}_{KMj}\left(t\right)$ be the Kaplan Meier estimator computed from the survival times $(T_i,{\delta }_i)$ in the jth group. For each group, ${\widehat{S}}_j\left(t\right)$ is plotted and ${\widehat{S}}_{KMj}\left(t_i\right)$ is plotted as circles at the uncensored event times $t_i$. The survival regression model is reasonable if the circles “track ${\widehat{S}}_j$ well” in each of the J plots.

If the slice widths go to zero, but the number of cases per slice increases to ∞ as $n\to \infty ,$ then the Kaplan Meier estimator and the model estimator converge to $S_{Y|SP}\left(t\right)$ if the model holds. Simulations suggest that the two survival functions are “close” for moderate n and nine slices. For small n and skewed predictors, some slices may be too wide in that the model is correct but ${\widehat{S}}_{KMj}\left(t\right)$ is not a good approximation of $S_{Y|SP}\left(t\right)$ where $SP$ corresponds to the x used to compute ${\widehat{S}}_j\left(t\right).$

For the Cox model, if pointwise confidence interval (CI) bands are added to the plot, then ${\widehat{S}}_{KMj}$ “tracks ${\widehat{S}}_j$ well” if most of the plotted circles do not fall very far outside the pointwise CI bands since these pointwise bands are not as wide as simultaneous bands. Collett (2003, pp. 241–243) [17] places several observed Kaplan Meier curves with fitted curves on the same plot.

Survival regression is the study of the conditional survival $S_{Y|SP}\left(t\right)$, and the slice survival plot is a useful tool for visualizing $S_{Y|SP}\left(t\right)$ in the background of the data. Suppose the jth slice is narrow so that $ESP\approx w_j$. If the model is reasonable, $ESP\approx SP$, and the number of uncensored cases in the jth slice is not too small, then $S_{Y|SP=w_j}\left(t\right)\approx {\widehat{S}}_j\left(t\right)\approx {\widehat{S}}_{KMj}\left(t\right).$ (These quantities approximate ${\left[{\widehat{S}}_0\left(t\right)\right]}^{exp\left(w_j\right)}$ for the Cox model.) Thus the nonparametric Kaplan Meier estimator is used to check the model estimator ${\widehat{S}}_j\left(t\right)$ in each slice.

The slice survival plot tailored to the Cox model is closely related to the May and Hosmer (1998) [21] test. Also, van Houwelingen et al. (2006) [22] use similar ideas but place the J Kaplan Meier curves on one plot and the J Cox survival curves on another plot. The ESP is a scalar while x is a $p\times 1$ vector. Using the ESP instead of x in plots is an important dimension reduction technique (and is similar to using a scalar valued minimal sufficient statistic instead of the p-dimensional sufficient statistic x.) Plots have been suggested by several authors with x divided into J groups instead of the ESP. For example, see Miller (1981, p. 168) [23]. Hosmer and Lemeshow (1999, pp. 141–145) [24] suggest making plots based on the quartiles of the ith predictor $x_i$, and note that a problem with Cox survival curves, ${\displaystyle {\widehat{S}}_{\mathit{x}}\left(t\right)={\left[{\widehat{S}}_0\left(t\right)\right]}^{exp\left({\widehat{\mathit{\beta }}}_C^T\mathit{x}\right)}={\left[{\widehat{S}}_0\left(t\right)\right]}^{exp\left(ESP\right)}}$, is that they may use inappropriate extrapolation. Using the ESP results in narrow slices with many cases, and adding Kaplan Meier curves shows if there is extrapolation.

3.1. Examples and Simulations

Example 1.

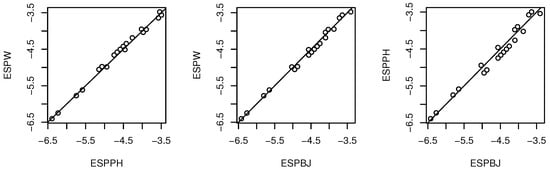
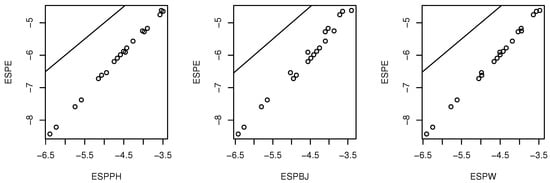
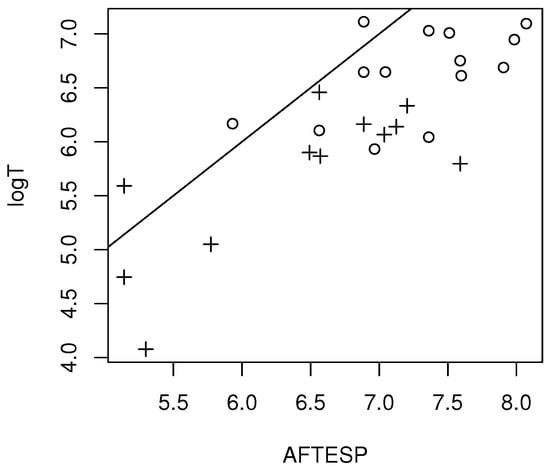
The ovarian cancer data is from Collett (2003, pp. 187–190) [17] and Edmunson et al. (1979) [25]. The response variable is the survival time of $n=26$ ovarian cancer patients in days, with predictors age in years and treat (1 for cyclophosphamide alone and 2 for cyclophosphamide combined with adriamycin). See Figure 1 for the three EE plots for the ovarian cancer data, where ESPW=ESPA. The Weibull AFT appears to be appropriate for this data set. Then $\widehat{Cov}(age,Z)=-0.1286$, $\widehat{Cov}(treat,Z)=-7.90408$, $\widehat{Cov}(age,Z)/\sqrt{\widehat{V}\left(age\right)}=-0.2522$, and $\widehat{Cov}(treat,Z)/\sqrt{\widehat{V}\left(treat\right)}=-0.7840.$ Hence $|\widehat{Cor}(treat,Z)|\approx 3|\widehat{Cor}(age,Z)|.$ Figure 2 shows the EE plots when an Exponential AFT is used instead of the Weibull AFT. Now the plotted points do not cluster about the identity line. Hence the Exponential AFT should not be used. Figure 3 shows the LCR plot using the Weibull AFT.

Figure 1. Three EE plots for the ovarian cancer data.

Figure 2. Three EE plots with the exponential AFT.

Figure 3. LCR plot for ovarian cancer data.

Example 2.

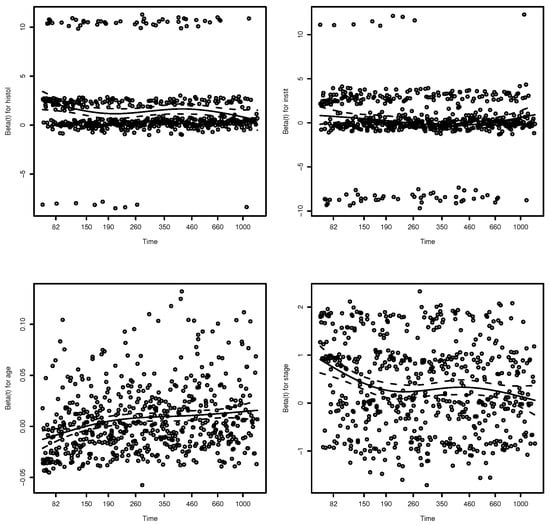
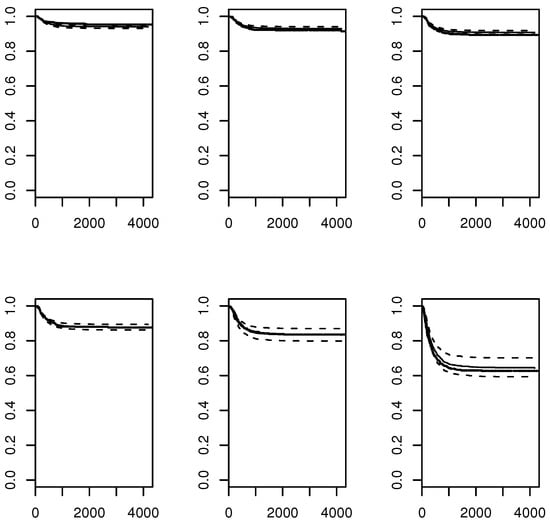
R contains a data set nwtco where the response variable Y is the time until relapse with $n=4028$. The model used predictors histol = tumor histology from central lab, instit = tumor histology from local institution, age in months, and stage of disease from 1 to 4 (treated as a continuous variable). In Figure 4, the Grambsch and Therneau (1994) [12] plots suggest that the Cox model is not valid since not all of the loess curves are flat, and the global test has p-value $\approx 0.$ The slice survival plot in Figure 5 shows that the Cox survival estimators and Kaplan Meier estimators are nearly identical in the six slices, suggesting that the Cox model is a reasonable approximation to the data. The greatest contributors to lack of fit seem to be the predictors age and stage corresponding to the bottom two plots of Figure 4, and survival for small ESP corresponding to the upper left plot in Figure 5.

Figure 4. Grambsch and Therneau plots for NWTCO data.

Figure 5. Slice survival plot for NWTCO data: dashes are pointwise CI bands.

3.2. ${\widehat{\Sigma }}_{xZ}$ Simulation

An R code similar to that of Zhou (2001) [26] was used to generate a Weibull regression data set with parameter vector ${\mathit{\beta }}_P$. Then the Weibull AFT parameter vector $\mathit{\beta }={\mathit{\beta }}_Z={\mathit{\beta }}_A=-\sigma {\mathit{\beta }}_P=-(1/\gamma ){\mathit{\beta }}_P.$ Hence ${\Sigma }_{\mathit{x}Z}=-\gamma \mathrm{Cov}\left(\mathit{x}\right){\mathit{\beta }}_P$. The simulation used ${\mathit{\beta }}_A=-{(1/\gamma ,\dots ,1/\gamma ,0,\dots ,0)}^T$ with $p-k$ zeroes and ${\mathit{\beta }}_P={(1,\dots ,1,0,\dots ,0)}^T$ with k ones and $p-k$ zeroes. The population ${\Sigma }_{\mathit{x}Z}={\Sigma }_{\mathit{x}}{\mathit{\beta }}_A$ was computed.

In the simulations, for $i=1,\dots ,n$, we generated $w_i\sim N_p(0,\mathit{I})$ where the p elements of the vector ${\mathit{w}}_i$ are iid N(0,1). Let the $p\times p$ matrix $\mathit{A}=\left(a_{ij}\right)$ with $a_{ii}=1$ and $a_{ij}=\psi$ where $0\le \psi <1$ for $i\ne j$. Then the vector ${\mathit{x}}_i=\mathit{A}{\mathit{w}}_i$ so that $\mathrm{Cov}\left({\mathit{x}}_i\right)={\Sigma }_{\mathit{x}}=\mathit{A}{\mathit{A}}^T=\left({\sigma }_{ij}\right)$ where the diagonal entries ${\sigma }_{ii}=[1+p{\psi }^2]$ and the off diagonal entries ${\sigma }_{ij}=[2\psi +(p-1){\psi }^2]$. Hence the correlations are $cor(x_i,x_j)=\rho =(2\psi +(p-1){\psi }^2)/(1+p{\psi }^2)$ for $i\ne j$. If $\psi =1/\sqrt{cp}$, then $\rho \to 1/(c+1)$ as $p\to \infty$ where $c>0$. As $\psi$ gets close to 1, the predictor vectors ${\mathit{x}}_i$ cluster about the line in the direction of ${(1,\dots ,1)}^T.$

Then 5000 runs are used to obtain the estimators. The means and standard deviations of the estimators are given. In the simulation, the uncensored values of Z are known. Hence the first estimator is the usual sample covariance vector ${\widehat{\Sigma }}_{\mathit{x}Z}$. For real data, this estimator cannot be computed since only censored values of Z are known. The second estimator is ${\widehat{\Sigma }}_{\mathit{x}Z}\left(A\right)={\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_A$ from the Weibull AFT. The third estimator is ${\widehat{\Sigma }}_{\mathit{x}Z}\left(BJ\right)={\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_{BJ}$ using the Buckley James estimator. Let ${\Sigma }_{\mathit{x}Z}={({\sigma }_{1Z},\dots ,{\sigma }_{pZ})}^T$. Table 1 gives 2 lines per simulation scenario. The first line gives the means while the second line gives the standard deviations. A value of $0+$ means the absolute value was less than 0.0005. Table 2 gives similar results with $p=5$. Table 3 used correlated predictors. The simulation needed roughly $n>25p$ to avoid convergence problems in the 5000 runs.

Table 1. ${\Sigma }_{\mathit{x}Z}={(-1,0,0,0)}^T$.

$(\mathit{n},\mathit{\psi },\mathit{k})$	est	${\mathit{\sigma }}_{1\mathit{Z}}$	${\mathit{\sigma }}_{2\mathit{Z}}$	${\mathit{\sigma }}_{3\mathit{Z}}$	${\mathit{\sigma }}_{4\mathit{Z}}$
(100,0,1)	samp	−0.999	−0.002	−0.002	−0.001
	SD	0.194	0.162	0.162	0.163
(100,0,1)	AFT	−1.003	−0.001	−0.001	$0+$
	SD	0.186	0.149	0.150	0.151
(100,0,1)	BJ	−1.002	−0.002	−0.002	−0.001
	SD	0.202	0.169	0.169	0.169
(500,0,1)	samp	−1.000	0.001	0.002	$0+$
	SD	0.087	0.073	0.073	0.074
(500,0,1)	AFT	−1.001	0.001	0.001	$0+$
	SD	0.082	0.065	0.066	0.066
(500,0,1)	BJ	−1.000	0.001	0.002	$0+$
	SD	0.090	0.075	0.075	0.076
(1000,0,1)	samp	−1.001	$0+$	0.001	$0+$
	SD	0.061	0.051	0.051	0.051
(1000,0,1)	AFT	−1.001	0.001	0.001	$0+$
	SD	0.056	0.047	0.047	0.046
(1000,0,1)	BJ	−1.000	$0+$	0.001	0.020
	SD	0.064	0.053	0.053	0.053

Table 2. ${\Sigma }_{\mathit{x}Z}={(-0.2,-0.2,-0.2,-0.2,-0.2)}^T$.

$(\mathit{n},\mathit{\psi },\mathit{k})$	est	${\mathit{\sigma }}_{1\mathit{Z}}$	${\mathit{\sigma }}_{2\mathit{Z}}$	${\mathit{\sigma }}_{3\mathit{Z}}$	${\mathit{\sigma }}_{4\mathit{Z}}$	${\mathit{\sigma }}_{5\mathit{Z}}$
(150,0,5)	samp	−0.1999	−0.2002	−0.2015	−0.1984	−0.1998
	SD	0.0613	0.0622	0.0615	0.0615	0.0622
(150,0,5)	AFT	−0.2004	−0.2004	−0.2018	−0.1998	−0.2008
	SD	0.0569	0.0574	0.0572	0.0570	0.0569
(150,0,5)	BJ	−0.2005	−0.2002	−0.2019	−0.1988	−0.2001
	SD	0.0639	0.0646	0.0642	0.0640	0.0646
(500,0,5)	samp	−0.2001	−0.1999	−0.2003	−0.2000	−0.2000
	SD	0.0339	0.03366	0.0342	0.0337	0.0338
(500,0,5)	AFT	−0.2006	−0.1999	−0.2006	−0.2004	−0.2002
	SD	0.0312	0.0309	0.0311	0.0311	0.0307
(500,0,5)	BJ	−0.2000	−0.1999	−0.2003	−0.2001	−0.2000
	SD	0.0351	0.0349	0.0355	0.0348	0.0350
(1000,0,5)	samp	−0.2003	−0.1999	−0.2002	−0.2001	−0.2010
	SD	0.0234	0.0239	0.0239	0.0237	0.0237
(1000,0,5)	AFT	−0.2004	−0.2002	−0.2002	−0.2000	−0.2007
	SD	0.0215	0.0218	0.0217	0.0216	0.0216
(1000,0,5)	BJ	−0.2003	−0.1998	−0.2001	−0.1999	−0.2009
	SD	0.0243	0.0247	0.0247	0.0244	0.0245

Table 3. ${\Sigma }_{\mathit{x}Z}={(-1,-0.2136,-0.2136,-0.2136)}^T$.

$(\mathit{n},\mathit{\psi },\mathit{k})$	est	${\mathit{\sigma }}_{1\mathit{Z}}$	${\mathit{\sigma }}_{2\mathit{Z}}$	${\mathit{\sigma }}_{3\mathit{Z}}$	${\mathit{\sigma }}_{4\mathit{Z}}$
(100,0.1,5)	samp	−0.9977	−0.2116	−0.2121	−0.2136
	SD	0.1913	0.1608	0.1655	0.1640
(100,0.1,5)	AFT	−1.0026	−0.2122	−0.2124	−0.2137
	SD	0.1834	0.1470	0.1526	0.1528
(100,0.1,5)	BJ	−1.0003	−0.2119	−0.2123	−0.2148
	SD	0.2001	0.1670	0.1718	0.1707

All three estimators worked well. It is not surprising that a correctly specified AFT would slightly outperform the Buckley James estimator (have the smallest standard deviations).

4. Discussion

The Harrell (2015) [27] rms library is useful for the Buckley James estimator. For more on estimators for model (4), see, for example, Heller and Simonoff (1990) [28], James and Smith (1984) [29], Lai and Ying (1991) [30], Lin and Wei (1992) [31], and Zeng and Lin (2007) [32]. The Kaplan Meier estimator is due to Kaplan and Meier (1958) [33].

Next, we provide some directions for further research.

(a) Under iid cases, ${\mathit{\beta }}_{OLS}={\Sigma }_{\mathit{x}}^{-1}{\Sigma }_{\mathit{x}Y}$ even if heterogeneity is present. Hence ${\widehat{\Sigma }}_{\mathit{x}Z}={\widehat{\Sigma }}_{\mathit{x}}{\widehat{\mathit{\beta }}}_Z$ where, for example, ${\widehat{\mathit{\beta }}}_Z$ is one of the estimators studied by Yu, Liu, and Chen (2024) [34].

(b) Similar ideas can be used for other censored regression models, such as a Tobit regression, provided that the cases are iid, and the population parameter vector $\mathit{\beta }={\mathit{\beta }}_{OLS}$.

(c) The Buckley James estimator can also be used for the survival regression model $Z=t\left(Y\right)={\alpha }_Z+{\mathit{x}}_i^T{\mathit{\beta }}_Z+e$ where t is a known monotone function and Z is right censored.

(d) Better large sample theory would be useful so confidence intervals can be made for $Cov(x_i,Y)$.

(e) More resistance to outliers would be useful, although the LCR plot is somewhat useful for detecting outliers.

(f) When the Grambsch and Therneau test and the slice survival plot give contradictory evidence on the proportional hazards assumption, how should that evidence be used?

Software

The R software 4.4.1 was used in the simulations. See R Core Team (2024) [35]. Programs are in the collection of R functions survpack.txt, available from (http://parker.ad.siu.edu/Olive/survpack.txt, accessed on 29 October 2025). The function BJcovxz generates a Weibull regression data set with right censored survival times. The function BJcovxzsim was used for Table 1. The function vnwtco was used to produce plots for Example 2. The function vovar is useful for Example 1. The function bphgfit makes a slice survival plot if there is a single covariate $x=1$ for group (treatment) 1 and $x=0$, otherwise. The function bphsim3 simulates the above function. The function phgfit2 makes a slice survival plot when x is a $p\times 1$ vector. Both of these functions are for the Cox model. The function phsim5 simulates the above function. The function wphsim simulates the slice survival plot for Weibull regression. The function wregsim2 simulates EE plots for Weibull regression.

Some R code for producing the simulation and Figure 1 appears in Johana Lemonge (2025) [36].