Generating Dynamical Systems with Iterated Torus Knots as Solutions

Abstract

The occurrence of knots as solutions of dynamical systems has been widely studied in the literature. In particular, ways to determine families of knots as solutions of differential equations have been described in several papers. In this article, an infinite family of dynamical systems, based on torus knots, is built each of which has the property that an infinite number of cable knots from torus knots (i.e., iterated torus knots) are obtained as solutions. One such dynamical system, based on the trefoil knot, is explicitly constructed. The methodology described herein may also be applied to any torus knot, and even to any other knot as long as a parametrization is provided for the latter. An example of application of the method is presented for the case of the figure eight knot, which is not a torus knot. Also, a possible application in cryptography is sketched.

1. Introduction

The relations between knot theory and dynamical systems have been studied in several articles. For example, in [1] Silver and Williams show that, given the group G of an oriented knot k, the set $\mathrm{Hom}(K,\mathsf{\Sigma })$ of representations of the commutator subgroup $K=[G,G]$ into any finite group $\mathsf{\Sigma }$ has the structure of a shift of finite type ${\mathsf{\Phi }}_{\mathsf{\Sigma }}$, which is a special type of dynamical system. Moreover, some invariants of ${\mathsf{\Phi }}_{\mathsf{\Sigma }}$ determine invariants of the knot. Also, in [2] Pinsky, [3] Bonatti & Pinsky, showed that the Lorenz system, extended to $S^3$, has an invariant knotted curve which is not a periodic orbit but is the union of invariant manifolds of the singular points. They also showed that different parameters yield different knotted curves. In particular, they proved that when the invariant curve is the trefoil knot and it is removed, the new flow is topologically equivalent to a geodesic flow on the modular surface.

Additional examples of dynamical systems have been studied and their analysis has shown that that they admit whole families of knots as solutions. In [4], Birman and Williams analyzed Lorenz equations and showed that knots and links, called Lorenz knots, appear as solutions. They showed that all torus and algebraic knots are Lorenz knots, and they noticed that some iterated knots occur as solutions as well. In [5], Ghrist and Holmes proved, by using branched 2-manifold theory, that there exists a family of ODEs each element of which contains as solutions all knots (and links); this family was first proposed by Chua et al. in [6] while analyzing the double scroll, which is a strange attractor, in order to rigorously prove that it is chaotic. In [7], Chen and Banks proved the existence of a dynamical system which contains every torus knot. On the other hand, given an arbitrary knot, Song et al. in [8] constructed explicit differential equations for dynamical systems which contain a braid whose closure yields the given knot.

In this paper, our focus is on generating a dynamical system whose solutions contain an infinite family of iterated torus knots. Moreover, it is shown that an infinite family of dynamical systems with this property can be constructed by varying some of the parameters involved in the construction. To the extent of our knowledge, this method for obtaining such classes of knots has not yet been presented in the literature. All plots included in the sequel were generated using the GNU Octave software (ver. 2022).

This paper is organized as follows. In Section 2, we review some preliminaries about knots and spun dynamical systems; using these results, we then describe a procedure to construct a new dynamical system which contains all torus knots as solutions. Building on this dynamical system, in Section 3 we present a method that yields a new dynamical system with iterated torus knots as solution and prove that the same method may also be applied to obtain cable knots. Finally, closing remarks and conclusions are included in Section 4.

2. Preliminaries

A well known area in topology is knot theory, which studies properties of knots in ${\mathbb{R}}^3$. All the definitions used in this paper are well known, and can be found, for example in [9]. A definition of knot, particularly adapted to the present setting, is as follows:

Definition 1.

A subset $N\subset {\mathbb{R}}^3$ is a knot if it is homeomorphic to the unit circle

$$S^1=\{(x,y)\in {\mathbb{R}}^2\mid x^2+y^2=1\}.$$

Definition 2.

A torus knot , as illustrated in Figure 1a, is a knot contained in the surface $T^2$ , where:

$$T^2=\{(x,y,z)\in {\mathbb{R}}^3\mid {(\sqrt{x^2+y^2}-2)}^2+z^2=1\}.$$

Figure 1. (a) The surface $T^2$; and (b) in red there is a torus knot example.

A $(p,q)$-torus knot, also denoted $T(p,q)$, where $p,q\in \mathbb{N}$ are relatively prime integers, i.e., $gcd(p,q)=1$, is a simple closed curve on $T^2$ that rotates p times in the longitudinal direction and q times in the transversal direction. In particular, the torus knot $T(3,2)$, displayed in Figure 2b, is called trefoil knot. In Figure 1b the torus knot $T(5,3)$ is shown. It is well known that knots $T(p,q)$ and $T(q,p)$ are equivalent, see for instance [10]. Therefore, unless otherwise stated (see Section 3.2), in the sequel we shall exclusively consider pairs of admissible natural numbers p and q, in the sense that $gcd(p,q)=1$ and ${\displaystyle \frac{p}{q}}<1$.

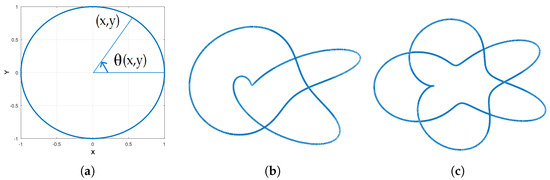
Figure 2. (a) The angle function; (b) the torus knot $T(2,3)$ obtained with $h_2^3$; and (c) the torus knot $T(2,5)$ obtained with $h_2^5$.

Given a pair of admissible numbers r and s, there is a well-known family of differentiable mappings which embed elements from the torus knot family into ${\mathbb{R}}^3$:

$$h_r^s:S^1\to {\mathbb{R}}^3$$

$$h_r^s(x,y)=\left(a_r^s(x,y),b_r^s(x,y),sin(s·\theta (x,y))\right).$$

The functions $a_r^s$ and $b_r^s$ are given by

$$\begin{array}{c}{a}_r^s(x,y)=(2+cos(s·\theta (x,y)))cos(r·\theta (x,y)),\hfill \\ b_r^s(x,y)=-(2+cos(s·\theta (x,y)))sin(r·\theta (x,y)),\hfill \end{array}$$

(1)

and $\theta (x,y)$ is the angle function, see Figure 2a. In this case the torus knot obtained is $h_r^s\left(S^1\right)=T(r,s)$. It is worth noticing that each function $h_r^s$ is a diffeomorphism between $S^1$ and its image $h_r^s\left(S^1\right)$. Figure 2b,c depict examples of knots built using different pairs of admissible numbers.

Given any two knots, the so-called satellite knot construction is a procedure to create a third knot using the properties of given ones. Here we are interested in two particular cases of satellite knots, namely cable knots and iterated torus knots.

Definition 3.

The$(r,s)$-cable of a knot K , denoted $K_{(r,s)}$, is the knot obtained by taking the knot $T(r,s)$ on a K-tubular neighborhood boundary. When $K=T(p,q)$ the $(r,s)$-cable of K is called the iterated torus knot of type$(p,q,r,s)$, which we will denote by ${\mathcal{K}}_{(p,q,r,s)}$.

An example of how an iterated knot is constructed is shown in Figure 3.

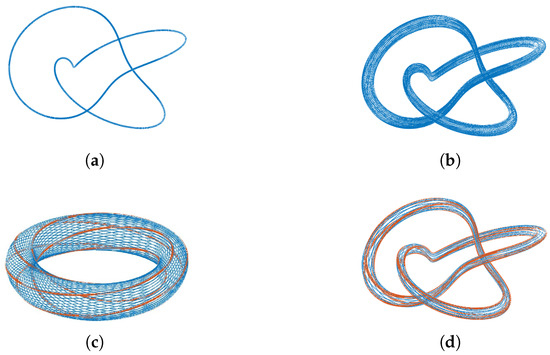
Figure 3. (a) The trefoil knot $K=T(2,3)$; (b) a tubular neighborhood of K; (c) in red is the torus knot $T(3,5)$; and (d) the cable ${\mathcal{K}}_{(2,3,3,5)}$ also in red.

This construction will be useful in Section 3.1, where one deals with iterated torus knots.

2.1. Spun Dynamical Systems

In [7], the ideas behind the spun of a dynamical system in order to obtain knotted trajectories are discussed. Let us to start with the dynamical system (2):

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& f_1(x_1,\dots ,x_n)\hfill \\ \hfill & ⋮& \hfill \\ \hfill {\dot{x}}_n& =& f_n(x_1,\dots ,x_n)\hfill \end{array}$$

(2)

Notice that a necessary condition to spin system (2) around the hyperplane $x_n=0$ is that (3) below holds:

$$f_n(x_1,\dots ,x_{n-1},0)=0\mathrm{for}\mathrm{all}{x}_1,\dots ,x_{n-1}\in \mathbb{R}.$$

(3)

When $n=2$, this means that system (2) will spin around the axis $x_2=0$. Under the stated conditions we define a new dynamical system, the spun of system (2), as:

$$\begin{array}{ccc}\hfill {\dot{x}}_1& =& f_1(x_1,\dots ,x_{n-1},\sqrt{x_n^2+x_{n+1}^2})\hfill \\ \hfill & ⋮& \hfill \\ \hfill {\dot{x}}_{n-1}& =& f_{n-1}(x_1,\dots ,x_{n-1},\sqrt{x_n^2+x_{n+1}^2})\hfill \\ \hfill {\dot{x}}_n& =& f_n(x_1,\dots ,x_{n-1},\sqrt{x_n^2+x_{n+1}^2})·{\displaystyle \frac{x_n}{\sqrt{x_n^2+x_{n+1}^2}}}-c(x_1,\dots ,x_n,x_{n+1})x_{n+1}\hfill \\ \hfill {\dot{x}}_{n+1}& =& f_n(x_1,\dots ,x_{n-1},\sqrt{x_n^2+x_{n+1}^2})·{\displaystyle \frac{x_{n+1}}{\sqrt{x_n^2+x_{n+1}^2}}}+c(x_1,\dots ,x_n,x_{n+1})x_n.\hfill \end{array}$$

(4)

In the above equations, $c:{\mathbb{R}}^{n+1}\to \mathbb{R}$ is a smooth function that determines the spinning velocity. In [7], the spun of the Volterra-Lotka system was studied and, by considering a specific smooth function c, they proved that every torus knot appears as a solution of the associated spun dynamical system. In the next subsection we will illustrate this concept with a useful example.

2.2. A New Dynamical System Admitting All Torus Knots as Solutions

In this subsection we show how to obtain another dynamical system that contains all torus knots as solutions. Following the line of ideas in Section 2.1, we start with the dynamical system (5):

$$\begin{array}{c}\dot{x}=y-a_0,\hfill \\ \dot{y}=-x+a_0.\hfill \end{array}$$

(5)

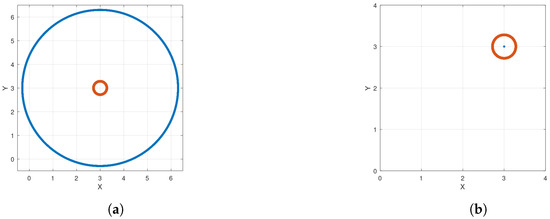
Although the method is valid for any $a_0>0$, for definiteness we select and fix a value $a_0=3$. Note that all solutions of system (5) define circles around the point $(a_0,a_0)$ with period $2\pi$ and, hence, it does not satisfy condition (3), as it can be seen from the blue solution in Figure 4a, which crosses the $\mathrm{Y}$-axis. Therefore, in order to fulfill this condition, the function $\rho$ in (6), similar to the tube function used in [8], is composed over system (5) to obtain the new system (7), which will indeed satisfy condition (3). The function $\rho$ is defined as follows.

Figure 4. (a) Two solutions for system (5) with $a_0=3$; and (b) a solution of system (7).

Given real numbers $m_0$, $n_0$ and $a_0$ satisfying $0<m_0<n_0<a_0$, let us define

$$\rho (x,y)=\left({\displaystyle {\int }_{d_{a_0}(x,y)}^{n_0}g\left(r\right)dr}\right)/\left({\displaystyle {\int }_{m_0}^{n_0}g\left(r\right)dr}\right)x,y\in \mathbb{R},$$

(6)

with

$$d_{a_0}(x,y)=\sqrt{{(x-a_0)}^2+{(y-a_0)}^2}\mathrm{and}g\left(r\right)=\left\{\begin{array}{ccc}\hfill e^{\left({\displaystyle \frac{1}{r-n_0}}-{\displaystyle \frac{1}{r-m_0}}\right)}& & m_0<r<n_0,\hfill \\ \hfill 0& & \mathrm{otherwise}.\hfill \end{array}\right.$$

Note that $d_{a_0}(x,y)$ is the distance between the point $(x,y)$ and $(a_0,a_0)$. Also note that g, whose graph is in Figure 5a, is a bump function, such functions are known for having continuous derivatives of all orders. In (6) we have that the denominator is a constant used to obtain $\rho (x,y)=1$ whenever $d_{a_0}(x,y)<m_0$, this can be seen in the green part of Figure 5b where the graph of $\rho$ is shown. Since g has continuous derivatives of all orders, by using the Fundamental theorem of calculus it can be proved that $\rho$ is, at least, differentiable.

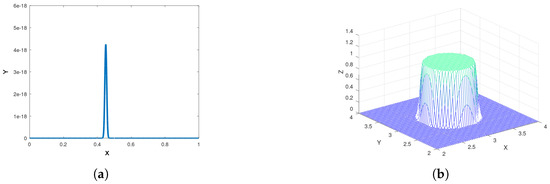
Figure 5. (a) Graphs of g; and (b) $\rho$ in the case when $m_0=0.4$, $n_0=0.5$ and $a_0=3$.

By setting from now on $a_0=3$, $m_0=0.4$ and $n_0=0.5$, let us generate a new dynamical system by applying $\rho$ to the system (5):

$$\begin{array}{c}\hfill \begin{array}{c}\dot{x}=\rho (x,y)(y-a_0),\hfill \\ \dot{y}=\rho (x,y)(-x+a_0).\hfill \end{array}\end{array}$$

(7)

Note that, given an initial condition within the circle

$$C=\{(x,y)\in {\mathbb{R}}^2:{(x-a_0)}^2+{(y-a_0)}^2\le n_0^2\},$$

the solution consists of a circular trajectory around the center $(a_0,a_0)$, as illustrated in Figure 4b. Moreover, if $(x,y)\notin C$ then $d_{a_0}(x,y)\ge n_0$ and $\rho (x,y)=0$, hence $(x,y)$ will be a fixed point of system (7), thus satisfying the necessary condition (3).

Now, after applying the spinning method to (7), the associated dynamical system reads:

$$\begin{array}{c}\hfill \begin{array}{c}\dot{x}=\rho (x,\sqrt{y^2+z^2})\left(\sqrt{y^2+z^2}-a_0\right),\hfill \\ \dot{y}=\rho (x,\sqrt{y^2+z^2})(-x+a_0)({\displaystyle \frac{y}{\sqrt{y^2+z^2}}})-\rho (x,\sqrt{y^2+z^2})c_1(x,y,z)z,\hfill \\ \dot{z}=\rho (x,\sqrt{y^2+z^2})(-x+a_0)({\displaystyle \frac{z}{\sqrt{y^2+z^2}}})(+\rho (x,\sqrt{y^2+z^2})c_1(x,y,z)y\hfill \end{array}\end{array}$$

(8)

It is to be noted that the function $c(x,y,z)$ defined in (4) in this case is $\rho (x,\sqrt{y^2+z^2})$$c_1(x,y,z)$ and, because of the definition of $\rho$, we only need from $c_1$ to be differentiable on $(x,y,z)$ where $\rho (x,\sqrt{y^2+z^2})\ne 0$. System (8) will also be referred as $\dot{X}=G\left(X\right)$.

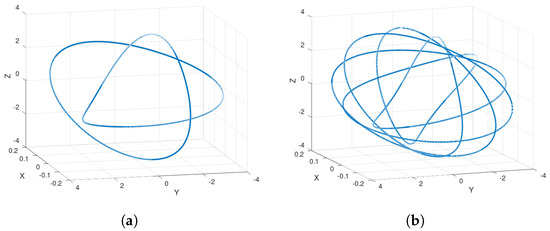
On the one hand, note that when $c_1(x,y,z)=1$, all the solutions of system (8) with initial conditions within the circle

$$C^{\prime }=\{(x,y,0):{(x-a_0)}^2+{(y-a_0)}^2\le {\left(n_0\right)}^2\},$$

will generate the torus $T_1$, shown in Figure 6a, with inner radius $n_0$ and outer radius $a_0$. One easily shows that, for an initial condition $(x_0,y_0,z_0)\notin T_1$, one has $\rho (x_0,\sqrt{y_0^2+z_0^2})=0$; therefore, given any smooth function $c_1$, $(x_0,y_0,z_0)$ is a fixed point for system (8). The same applies when the initial condition lies on the boundary $\partial \left(T_1\right)$.

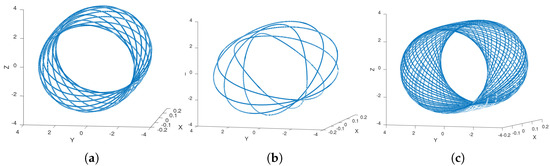
Figure 6. (a) The torus $T_1$; (b) the knotted solution $T(5,7)$; and (c) a solution when $c_1(x,y,z)=\sqrt{2}/2$.

On the other hand, in the case of the constant function $c_1(x,y,z)=5/7$ and the initial condition $(3.2,3.2,0.3)\in T_1$, the solution is the torus knot $T(5,7)$, which is depicted in Figure 6b. Note, however, that since $c_1$ is a constant function, any initial condition within $T_1$ will yield the torus knot $T(5,7)$ as a solution. This is due to the fact that the solutions of system (7) are periodic and when the spinning velocity is $5/7\sim 0.7142$, or any other rational number $p/q$, the solutions of system (8) are also periodic. In contrast, when $c_1(x,y,z)=\sqrt{2}/2\sim 0.7071$ the resultant solution is not periodic, as it can be seen in Figure 6c. Moreover, if $c_1(x,y,z)=p/q$ with p and q a pair of admissible numbers, we obtain the torus knot $T(p,q)$ as a solution for (8). Therefore, in order to produce all torus knots $T(p,q)$ as solutions, instead of a constant function one uses a function $c_1$ which includes the interval $(0,1)$ in its range.

In order to define such a function $c_1$, given $0\le \lambda \le n_0$, let $C_{\lambda }$ be the set

$$C_{\lambda }=\{(x,y)\in {\mathbb{R}}^2\mid {(x-a_0)}^2+{(y-a_0)}^2={\lambda }^2\},$$

and let $T_{\lambda }$ be the torus generated by rotating $C_{\lambda }$ around the $\mathrm{Y}$-axis. Note that function $\rho$ is constant along every $T_{\lambda }$ and also note that

$$T_1=\bigcup _{0\le \lambda \le n_0}{T}_{\lambda }.$$

Then the mapping $c_1$ is defined by

$$c_1(x,y,z)=\left\{\begin{array}{ccc}{\displaystyle \frac{5}{2}}\lambda \hfill & & \mathrm{if}(x,y,z)\in T_{\lambda }\hfill \\ {\displaystyle \frac{5}{4}}\hfill & & \mathrm{otherwise}.\hfill \end{array}\right.$$

(9)

Another way of defining $c_1$, when $(x,y,z)\in T_{\lambda }$, is:

$$c_1(x,y,z)={\displaystyle \frac{5}{2}}\sqrt{{(a_0-\sqrt{x^2+z^2})}^2+{(a_0-y)}^2}.$$

(10)

Note that from (9) it follows that function $c_1$ constant along every $T_{\lambda }$, while from (10), it follows that $c_1$ is continuous and differentiable in

$$\bigcup _{\lambda <n_0}{T}_{\lambda }.$$

Hence $\rho (x,\sqrt{y^2+z^2})c_1(x,y,z)$ is also continuous and differentiable in ${\mathbb{R}}^3$.

From (9) it follows that if $(x,y,z)\in T_{\lambda }$ with $\lambda ={\displaystyle \frac{2p}{5q}}$ then $c_1(x,y,z)={\displaystyle \frac{p}{q}}$ and the knot obtained as a solution is $T(p,q)$. Since $(0,1)\subset c_1\left([0,m_0]\right)=[0,1]$ then every torus knots will appear as a particular solution.

Theorem 1.

Given the dynamical system (8), where $c_1$ is defined as in (10), it contains every torus knot as solution.

Proof. 

Given the torus knot $T(p,q)$ we are going to show an explicit initial condition whose solution is such a knot. Define $r=a_0-{\displaystyle \frac{p}{q}}{\displaystyle \frac{2}{5\sqrt{2}}}$. Hence, for

$${\lambda }_r=d_{a_0}(r,r)=(a_0-r)\sqrt{2},$$

we have that the initial condition $(r,r,0)\in T_{{\lambda }_r}$. Then, by (10), one has

$$c_1(r,r,0)={\displaystyle \frac{5}{2}}{\lambda }_r={\displaystyle \frac{p}{q}}.$$

The latter entails that the solution issued from the initial condition $(r,r,0)$ is the torus knot $T(p,q)$. □

Example 1.

When $r_1=a_0-{\displaystyle \frac{2}{3}}{\displaystyle \frac{2}{5\sqrt{2}}}$ one has $c_1(r_1,r_1,0)={\displaystyle \frac{2}{3}}$, and the trajectory of the system (8) with initial condition $(r_1,r_1,0)$ is the trefoil knot $T(2,3)$, shown in Figure 7a. Similarly, when $r_2=a_0-{\displaystyle \frac{5}{7}}{\displaystyle \frac{2}{5\sqrt{2}}}$, we obtain the torus knot $T(5,7)$, shown in Figure 7b, for the initial condition $(r_2,r_2,0)$.

Figure 7. (a) The knots $T(2,3)$; and (b) $T(5,7)$ as solutions for (8).

3. Main Results

In this section we construct a diffeomorphism between the torus $T_1$, which contains all torus knots as solutions of system (8), and a trefoil knotted torus $T_2$. This diffeomorphism is then used to obtain a dynamical system, defined to be identically zero on the complement of $T_2$, and admitting the iterated torus knots ${\mathcal{K}}_{(2,3,r,s)}$ as solutions. It also will be shown that this method can be easily extended to other knotted tori, obtained from torus knots that differ from the trefoil knot, in order to obtain iterated torus knots of the form ${\mathcal{K}}_{(p,q,r,s)}$. At the end of this section, it will be shown that these ideas can be extended to produce cable knots different from iterated torus knots as solutions.

3.1. Iterated Torus Knots

Since system (8) admits all torus knots as solutions, we would like to have a diffeomorphism from $T_1$ to a solid knotted torus $T_2$. Using this diffeomorphism we shall define a new system whose dynamics is identically zero on the complement of $T_2$, and a conjugation on $T_2$. In order to construct the sought diffeomorphism, let us consider the following diffeomorphisms:

$$F:{\mathbb{R}}^3\to {\mathbb{R}}^3$$

$$F(x,y,z)=\left(x-a_0,y,z\right).$$

And

$$H_2^3:F\left(T_1\right)\to T_2$$

$$H_2^3(x,y,z)=\left(k(x,y)·a_2^3(x,y),k(x,y)·b_2^3(x,y),k(x,y)·sin\left(3\theta \right(x,y\left)\right)+z\right),$$

where $a_2^3$ and $b_2^3$ are defined as in (1), $k(x,y)=\sqrt{x^2+y^2}$ and $T_2=(H_2^3\circ F)\left(T_1\right)$. With these definitions at hand, one has the following:

Theorem 2.

Given the dynamical system:

$$\dot{X}=\left\{\begin{array}{cc}(H_2^3\circ F)\circ G\circ {(H_2^3\circ F)}^{-1}\left(X\right),\hfill & \hfill \mathrm{for}X\in T_2\\ 0,\hfill & \hfill \mathit{otherwise};\end{array}\right.$$

(11)

where G is as in system (8), $H_2^3$ and F are the previously defined diffeomorphisms and $T_2=(H_2^3\circ F)\left(T_1\right)$. Then all the iterated knots of the form ${\mathcal{K}}_{(2,3,r,s)}$ are solutions of the system.

Proof. 

Note that F and $H_2^3$ are diffeomorphisms and, hence, $F\circ H_2^3:T_1\to T_2$ is also a diffeomorphism. We will denote:

$$\mathsf{\Theta }=F\circ H_2^3\mathrm{and}\mathsf{\Phi }=(H_2^3\circ F)\circ G\circ {(H_2^3\circ F)}^{-1}.$$

Then, it is clear that

$$\mathsf{\Phi }=\mathsf{\Theta }\circ G\circ {\mathsf{\Theta }}^{-1}\mathrm{and}\mathrm{thus}\mathsf{\Phi }\circ \mathsf{\Theta }=\mathsf{\Theta }\circ G.$$

Therefore $\dot{X}=G\left(X\right)$ and $\dot{X}=\mathsf{\Phi }\left(X\right)$ are topologically conjugate dynamical systems defined over $T_1$ and $T_2$, correspondingly. Moreover, since the bump function $\rho$ is implicit in G then $\mathsf{\Phi }(x,y,z)=0$ for any $(x,y,z)\in \partial \left(T_2\right)$. Since system (11) is defined as 0 whenever $X\notin T_2$ we can conclude that it is smooth. It is well known that being topologically conjugate implies that any torus knot solution $T(r,s)$ of system $\dot{X}=G\left(X\right)$ is mapped, under the $\mathsf{\Theta }$ function, to a periodic solution of system $\dot{X}=\mathsf{\Phi }\left(X\right)$ which lies on the knotted torus $T_2$. Thereby, yielding the iterated torus knot solution ${\mathcal{K}}_{(2,3,r,s)}$. □

Figure 8 shows some iterated knot examples obtained by applying Theorem 2. Where $(r,s)$ take values $(3,5)$, $(5,7)$ and $(15,17)$ in (a), (b) and (c), respectively.

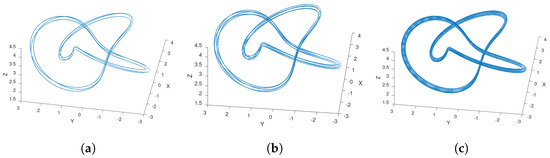
Figure 8. Iterated knots (a) ${\mathcal{K}}_{(2,3,3,5)}$; (b) ${\mathcal{K}}_{(2,3,5,7)}$; and (c) ${\mathcal{K}}_{(2,3,15,17)}$ as solutions for system (8).

As a particular case we are using $H_2^3$, clearly based on $h_2^3$, to obtain the tubular neighborhood of the trefoil knot. Similarly, instead of $h_2^3$ we could also use any $h_p^q$ to obtain a new dynamical system with iterated torus knot ${\mathcal{K}}_{(p,q,r,s)}$ as a solution; by adjusting, if necessary, the inner radius $n_0$ in order to avoid self intersections of the knotted torus $T_2$. In Figure 9 it is shown the iterated knot ${\mathcal{K}}_{(5,9,15,31)}$ obtained by using several inner radius. Since the core of the knotted torus is the same in all cases, by varying $n_0$ from $0.5$ to $2.5$ the knotted torus $T_2$ gets thicker. Thus, in order to avoid self-intersections, a proper $n_0$ must be chosen.

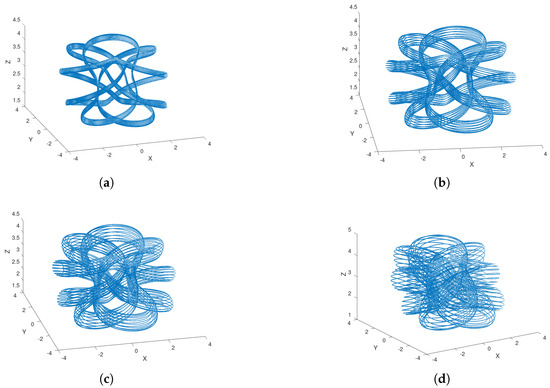
Figure 9. (a) Iterated knot ${\mathcal{K}}_{(5,9,15,31)}$ with inner radius $n_0=0.5$; (b) $n_0=1.0$; (c) $n_0=1.5$; and (d) $n_0=2.5$ respectively.

3.2. Cable Knots of Other Knots

The previous results can also be applied to obtain cable knots $K_{(r,s)}$, where K is not a torus knot, as long as a diffeomorphism between the knot K and $S^1$ is known. As an example we have the following family of diffeomorphisms, each of which defines a knot.

$$g_p^q(x,y)=\left(a_p^q(x,y),b_p^q(x,y),sin\left(4\theta (x,y)\right)\right).$$

In this case, with the aim of obtaining knots which are not torus knots, the numbers p and q satisfy $gcd(p,q)=1$ and ${\displaystyle \frac{p}{q}}>1$.

Note that $g_3^2$ will give rise to the figure eight knot $K_1$, which is not a torus knot. And, by applying the method in this case, one obtains another dynamical system in which the associated $T_2$ is the figure eight knotted torus. In Figure 10a is shown the $T(5,11)$ knot on $T_2$, denoted $K_{1(5,11)}$. In contrast, if $K_2$ is the knot associated to $g_5^3$, we are able to obtain the cable knot $K_{2(5,11)}$ shown in Figure 10b.

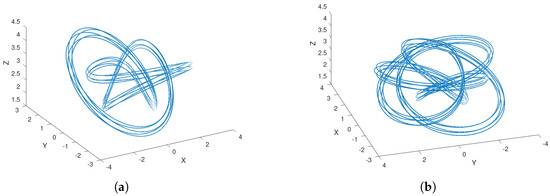
Figure 10. (a) Cable knots $K_{1(5,11)}$; and (b) $K_{2(5,11)}$ obtained with the proposed method.

4. Concluding Remarks

In this paper we presented an explicit way to construct a dynamical system for which the knotted trajectories ${\mathcal{K}}_{(2,3,r,s)}$, which belong to the iterated torus knots family, occur as solutions. Although the computations were made for the pair of numbers 2 and 3, the ideas can be extended to any pair of admissible numbers p and q. Therefore, our methodology provides an explicit way to construct an infinite number of dynamical systems, one for each admissible pair p and q, each of which admits all the iterated torus knots ${\mathcal{K}}_{(p,q,r,s)}$ as solutions.

We also showed that the exposed ideas can easily be extended to other parametrized knots which are not torus knots, for example the figure eight knot, by modifying the inner radius if necessary. This procedure to construct iterated torus knots as solutions of a dynamical system, as far as we know, has not been previously reported in the literature.

On the other hand, whereas other references prove the existence of dynamical systems admitting all knots as solution, they do not necessarily provide explicit ways to produce specified knots, unlike our results in this paper. We believe that this explicit form of producing iterated torus knots could be used, for example, to cipher messages, images, etc. Below we outline this idea.

One way of encrypting and decrypting data can be done since any message can be seen as a binary string $s_1$. Suppose that the message w has associated the binary string:

$$s_1=010011111000010101110011011111110001011110010111$$

And, in order to encrypt $s_1$ we need a way to generate another binary string $s_2$, with the same length of $s_1$, which will be the key used to encrypt and decrypt the message. For example, we cloud use the string:

$$s_2=010000111111001101100100011010010110011101101111$$

Note that, in this case, both strings have length 48. Next, we add the strings $s_1$ and $s_2$ ($mod2$). This is performed, digit by digit, on the strings $s_1$ and $s_2$ using the following rules:

$$0+0=00+1=1+0=11+1=0.$$

Then $s_1+s_2$ will generate the encrypted string $s_3$:

$$\begin{gathered} +\begin{array}{c}010011111000010101110011011111110001011110010111s_1\\ 010000111111001101100100011010010110011101101111s_2\end{array} \\ \hspace{1em}\begin{array}{c}—————————————————————\hfill \\ 000011000111011000010111000101100111000011111000s_3\end{array} \end{gathered}$$

Note that $s_2+s_2=\overline{0}$ where $\overline{0}$ is a string with 48 zeros. Therefore, if someone possesses the encrypted string $s_3$ and the string $s_2$, then by noticing that

$$s_3+s_2=(s_1+s_2)+s_2=s_1+(s_2+s_2)=s_1+\overline{0}=s_1,$$

also possesses the original message w.

We can use a knotted torus to generate the encrypting string $s_2$. This can be done by initially considering a cubic grid of length l for ${\mathbb{R}}^3$ and by assigning 0 or 1 to each cube, akin to a “3-dimensional chess board”. Then, integers $p,q,l$ are selected along with a constant time $t_0$, and Theorems 1 and 2 are used to construct the knotted torus where all the iterated torus knot ${\mathcal{K}}_{(p,q,r,s)}$ appears as solutions. For example, for $p=4$ and $q=7$, given two different close initial conditions we obtain distinct solutions, namely the iterated knot ${\mathcal{K}}_{(4,7,7,13)}$ shown in Figure 11a and the non-periodic solution seen in Figure 11b.

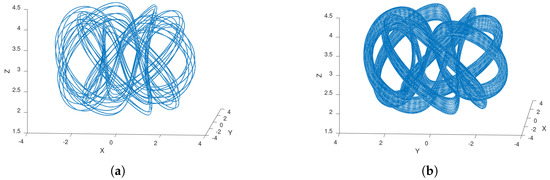
Figure 11. Two solutions obtained from different close initial conditions: (a) the iterated knot ${\mathcal{K}}_{(4,7,7,13)}$; and (b) a non-periodic solution.

Then, if $y\left(t\right)$ is the solution associated to the initial condition $x_0$, either 0 or 1 is assigned depending on the cube, of length side l, that $x_0=y\left(0\right)$ belongs to. Then the procedure is repeated for the solution at time $n·t_0$, where $n\in \mathbb{N}$, and 0 or 1 is assigned depending on the position of the point $x_n=y(n·t_0)$ in the cubic greed. Evidently, if we modify the length l of the greed then the resulting encrypting string will also change.

Naturally, albeit the generation of ciphering strings using this procedure would require more in-depth analysis to determine its suitability as an encryption (and decryption) mechanism, this may outline a possible line of further research.