Abstract
Let be the finite classical polar space of rank over , and be the set of all
m-dimensional subspaces of . In this paper, we introduce the (m, 2)-graph with as its
vertex set, and two vertices P, Q are adjacent if and only if P + Q is an (m + 2)-dimensional
subspace of . The full automorphism group of (m, 2)-graph is determined.
MSC:
05C60; 05E14
1. Introduction
Finite classical polar spaces arise from the classification of non-degenerate sesquilinear and nonsingular quadratic forms defined on vector spaces over a finite field. There are six fundamental types of forms to consider, which naturally induce three geometric structures. Alternating forms yield symplectic geometries, Hermitian forms generate unitary geometries, and quadratic forms produce orthogonal geometries. Given a form on a finite vector space V, all totally isotropic subspaces of V form the associated polar space . The rank of the polar space is defined as the dimension of its maximal subspaces. The collection of all m-dimensional subspaces of is denoted by .
Table 1 classifies all isomorphism types of finite classical polar spaces with rank over finite fields . The table specifies type symbols for each polar space class, dimension n of the corresponding projective space , a uniformity parameter facilitating consistent enumeration across types, and the collineation group G. In particular, the Hermitian polar spaces only exist for squares q. For more details on finite classical polar spaces, readers can refer to [1,2,3].

Table 1.
Finite classical polar spaces of rank .
The -graph in finite classical polar spaces is the graph with as its vertex set, and two vertices are adjacent if and only if is an -dimensional subspace of . It is easy to verify that the union of -graph and generalized symplectic, unitary or orthogonal graph is a Grassmann graph of the corresponding polar spaces. The properties and automorphism groups of generalized symplectic, unitary, and orthogonal graphs have been extensively studied by many scholars [4,5,6,7,8,9,10,11,12,13]. In this paper, we determine the full automorphism group of the -graph. For convenience, we denote the -graph in by . There is an edge in graph if and only if . Therefore, we only consider these cases. The main theorems are as follows.
Theorem 1.
The graph Γ is a -regular graph where
and
Theorem 2.
Let ; the full automorphism group of the graph Γ is the collineation group G in Table 1, that is, every automorphism of Γ has the following form:
where , , and T belongs to the projective generalized classical group of the corresponding polar space.
In the following sections of this paper, we will take the symplectic polar space as an example and give proofs of Theorems 1 and 2. The cases on unitary and orthogonal polar spaces are similar. Section 2 introduces the preliminaries on the symplectic polar space. In Section 3, we investigate the properties of the -graph in the symplectic polar space. Section 4 determines the full automorphism group of the -graph. Finally, in Section 5, we summarize our work and propose two open questions for further research.
2. Preliminaries on the Symplectic Polar Space
Let K be an nonsingular alternate matrix over . As we know, n is even. From now on, we assume that . A matrix T over is called a symplectic matrix with respect to K if , where is the transpose of the matrix T. Clearly, symplectic matrices form a group with respect to the matrix multiplication, called the symplectic group of degree with respect to K over and denoted by . It is easy to verify that the symplectic groups of degree with respect to different nonsingular alternate matrices are isomorphic. Thus, in discussing symplectic groups, without loss of generality, we can choose any particular nonsingular alternate matrix K. In this paper, let us take
where is the identity matrix. Denote the symplectic group with respect to K simply by . Consider the -dimensional row vector space over the finite field . The symplectic group acts naturally on this space via right matrix multiplication, as expressed by the group action map:
The vector space , together with the above group action, forms the -dimensional symplectic space over .
Let P denote an m-dimensional subspace of . A matrix representation of P is any matrix whose row space spans P. Note that such representations are unique up to left multiplication by invertible matrices. Two matrices and of rank m represent the same subspace if and only if for some , denoted by . The m-dimensional subspace P is classified as type if the rank of is , that is, rk. The existence of such subspaces is constrained by the inequalities [14]. Notably, when i.e., , P is called totally isotropic. The collection of all totally isotropic subspaces constitutes the symplectic polar space of rank , denoted by . For brevity, we still adopt for , for the set of m-dimensional totally isotropic subspaces, and for the dimension of P.
Lemma 1
([14]). Let . Then the number of m-dimensional vector subspaces of is
(ii) The number of subspaces in is equal to
Lemma 2
([15]). Let , and . Then and
Let . Then and if and only if there exists such that and .
Let ; the number of vertices in the set
is independent of the choice of P, since the symplectic group acts transitively on the subspaces of the same type. Denote this set by .
Lemma 3
([15]). Let Then the number of vertices in is
The generalized symplectic graph over is the graph with as its vertex set, and two vertices P and Q are adjacent if and only if
To introduce the full automorphism group of , we give the definition of the projective generalized symplectic group. The set of matrices T over the finite field satisfying the condition , where , forms the generalized symplectic group of degree over with respect to the matrix multiplication, denoted by The projective quotient is obtained by factoring the modulo its central subgroup , called the projective generalized symplectic group.
Lemma 4
([6]). The full automorphism group of the generalized symplectic graph is , that is, every automorphism of has the following form:
where , , and .
3. Properties of -Graph in the Symplectic Polar Space
The -graph in the symplectic polar space is the graph with as its vertex set, and two vertices are adjacent if and only if is an -dimensional totally isotropic subspace. From the conditions for the existence of an subspace, it follows that there is an edge in the graph if and only if .
Since the symplectic group acts transitively on the subspaces of the same type, the graph is vertex-transitive. It is obvious that the number of vertices in is in Lemma 1, and the degree of each vertex is in Lemma 3. By simple calculation, Theorem 1 is proved, where .
Let be the distance between two vertices P and Q in . Denote by when P and Q are adjacent, and otherwise. For , let be the set of neighbors of P. Then we have the following theorem.
Theorem 3.
Let , be two vertices of Γ satisfying and ; then, if and only if
where when .
Proof.
Since the symplectic group is an automorphism group of , without loss of generality, we can assume that
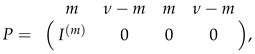 where the numbers above the matrix are the numbers of columns. If and , then and
by Lemma 1, and we can choose a special vertex Q to compute its distance with P by Lemma 2. Next, let us discuss d with the following cases.
where the numbers above the matrix are the numbers of columns. If and , then and
by Lemma 1, and we can choose a special vertex Q to compute its distance with P by Lemma 2. Next, let us discuss d with the following cases.
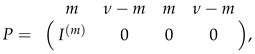
If , then by and
When , we can assume that
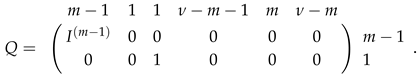
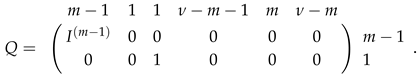
When , we can assume that
 , that is, . Let
, that is, . Let
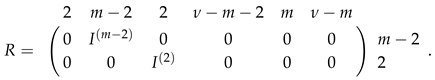 It is to easy to verify that ; thus, .
It is to easy to verify that ; thus, .

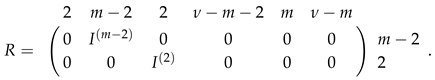
If , then .
When , , that is, .
When or 2, similar to the discussion in case (i), we could find a vertex R satisfying for each special Q. Thus, .
If , then (this case occurs only when ).
When or 2, similar to the discussion in case (i), we have .
When , we can assume
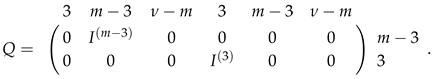 For each , it has the following matrix representation
For each , it has the following matrix representation
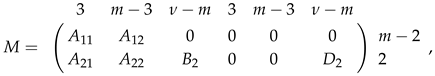 where rk, and Thus,
where rk, and Thus,

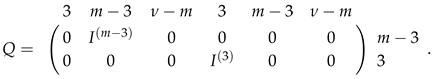
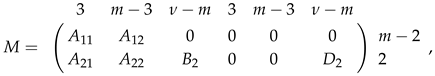

Since rk and , rk. This means that . Therefore, . In addition, let
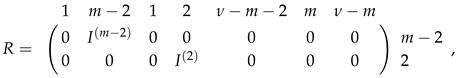
 where and are the first and second unit vectors, respectively. It is easy to verify that , then
where and are the first and second unit vectors, respectively. It is easy to verify that , then
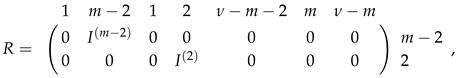

If , then (this case occurs only when ).
Similar to the discussion in case (iii), we have when or 2, and when or 4.
If , then (this case occurs only when ).
Similar to the discussion in case (iii), we have .
Above all, if and only if , , or when or . The theorem now follows. □
From the proof of the above theorem, we have the following corollary.
Corallary 1.
Let the diameter of Γ be . Then, when , and when or 4.
4. Automorphisms of -Graph in the Symplectic Polar Space
In this section, we will determine the full automorphism group of the -graph in the symplectic polar space. For the given d and r, let P and Q be any two vertices of satisfying Then, by Lemma 2, the number of common neighbors of P and Q is independent of the choice of P and Q, which is denoted by . We have the following theorem.
Theorem 4.
Let
where when . Then,
.
where or 1, .
Proof.
The conditions that d and r satisfy are precisely those stated in Theorem 3. Without loss of generality, let
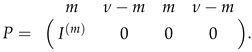
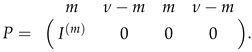
If and as in the theorem, then . Suppose , then M has the matrix representation
 where
where

is the number of common neighbors of P and Q, i.e., the number of vertices M such that . Next, we will compute by choosing the special Q for each pair .
When , let


is the number of M satisfying . if and only if


This means that , and then
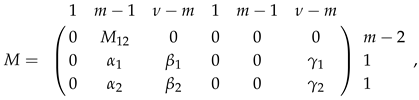 where . Therefore,
where . Therefore,
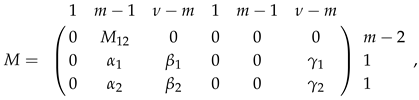
Through similar computations, we could get
Above all, we can verify that , , , , for . Then, the theorem follows. □
Finally, we present the proof of Theorem 2.
Proof of Theorem 2.
It is easy to verify that the group is an automorphism group of . Conversely, let be an automorphism of , and satisfies Then, by Theorem 3. Since preserves the distance between two vertices in , , and
Therefore, by Theorem 4, which means that is also an automorphism of the generalized symplectic graph . Thus, by Lemma 4. The theorem now follows. □
5. Conclusions and Further Study
In this paper, we introduce the -graph in finite classical polar spaces. Taking the symplectic polar space as an example, we establish fundamental properties of the -graph , proving its regularity and characterizing distance metric, completely determining its full automorphism group. In the following study, we will consider the spectral properties of , and examine whether similar results extend to the general -graph with . These investigations will deepen the connections between finite geometry, algebraic graph theory, and group theory.
Author Contributions
Y.Z., S.L., and L.Z.: Conceptualization, Methodology, Validation, Writing—Original Draft, Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
Research supported by NSFC (No.12171139).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
All authors declare no conflicts of interest in this paper.
References
- Beule, J.D.; Klein, A.; Metsch, K. Substructures of finite classical polar spaces. In Current Research Topics in Galois Geometry; Storme, L., De Beule, J., Eds.; Mathematics Research Developments, Nova Science: Hauppauge, NY, USA, 2012; pp. 35–61. [Google Scholar]
- Ball, S. Finite Geometry and Combinatorial Applications, Number 82 in London Mathematical Society Student Texts; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Brouwer, A.E.; Maldeghem, H.V. Strongly Regular Graphs, Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2022; p. 182. [Google Scholar]
- Wan, Z.X.; Tang, Z.M. Symplectic graphs and their automorphisms. Eur. J. Combin. 2006, 27, 38–50. [Google Scholar][Green Version]
- Tits, J. Buildings of Spherical Type and Finite BN-Pairs; Lecture Notes in Math; Springer: Berlin/Heidelberg, Germany, 1974; p. 386. [Google Scholar]
- Zeng, L.W.; Chai, Z.; Feng, R.Q.; Ma, C.L. Full autommrphism group of generalized symplectic group. Sci. China Math. 2013, 56, 1509–1520. [Google Scholar] [CrossRef]
- Wan, Z.X.; Zhou, K. Unitary graphs and their automorphisms. Ann. Comb. 2010, 14, 367–395. [Google Scholar] [CrossRef]
- Liu, W.; Ma, C.L.; Wang, K.S. Full automorphism group of generalized unitary graphs. Linear Algebra Appl. 2012, 437, 684–691. [Google Scholar] [CrossRef]
- Gu, Z.H.; Wan, Z.X. Orthogonal graphs of odd characteristic and their automorphisms. Finite Fields Appl. 2008, 14, 291–313. [Google Scholar] [CrossRef]
- Wan, Z.X.; Zhou, K. Orthogonal graphs of characteristic 2 and their automorphisms. Sci. China Ser. A 2009, 52, 361–380. [Google Scholar] [CrossRef]
- Li, F.G.; Wang, Y.X. Subconstituents of dual polar graph in finite classical space III. Linear Algebra Appl. 2002, 349, 105–123. [Google Scholar] [CrossRef]
- Huo, L.J.; Guo, W.N.; Ma, C.L. Automorphisms of generalized orthogonal graphs with odd characteristic. Acta Math. Sin. Chin. Ser. 2014, 57, 71–88. [Google Scholar][Green Version]
- Huo, L.J.; Guo, W.N.; Zhang, G.S. Automorphisms of generalized orthogonal graphs of characteristic 2. Front. Math. China 2014, 9, 303–319. [Google Scholar] [CrossRef]
- Wan, Z.X. Geometry of Classical Groups over Finite Fields; Science Press: Beijing, China; New York, NY, USA, 2002. [Google Scholar]
- Wei, H.Z.; Wang, Y.X. Suborbits of the transitive set of subspaces of type (m, 0) under finite classical groups. Algebra Colloq. 1996, 3, 73–84. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).