Fuzzy Signature from Computational Diffie–Hellman Assumption in the Standard Model

Abstract

Fuzzy signature (${\mathsf{SIG}}_{\mathsf{F}}$) is a type of digital signature that preserves the core functionalities of traditional signatures, while accommodating variations and non-uniformity in the signing key. This property enables the direct use of high-entropy fuzzy data, such as biometric information, as the signing key. In this paper, we define the m-existentially unforgeable under chosen message attack ($\mathfrak{m}{-\mathrm{EUF}-\mathrm{CMA}}^{\ast }$) security of fuzzy signature. Furthermore, we propose a generic construction of fuzzy signature, which is composed of a homomorphic secure sketch ($\mathsf{SS}$) with an error-recoverable property, a homomorphic average-case strong extractor ($\mathsf{Ext}$), and a homomorphic and key-shift* secure signature scheme ($\mathsf{SIG}$). By instantiating the foundational components, we present a $\mathfrak{m}{-\mathrm{EUF}-\mathrm{CMA}}^{\ast }$ secure fuzzy signature instantiation based on the Computational Diffie–Hellman (CDH) assumption over bilinear groups in the standard model.

1. Introduction

1.1. Digital Signature and Fuzzy Signature

A digital signature [1,2] is a fundamental cryptographic primitive that ensures integrity, authentication, and non-repudiation in digital communication. Traditional signature algorithms [3] generally require the signing keys to be uniformly random and precisely accurate. When using a digital signature for authentication, users need to take care to retain their signing key. They may store the signing key on devices such as a smart card [4,5] or a USB token [6,7]. Hence, it is unavoidable for users to carry an additional device.

Fuzzy signature [8] is an advanced digital signature scheme that permits non-uniformity and approximate matching of the signing key. This property enables fuzzy signatures to leverage fuzzy data (e.g., biometric information) as the signing key. Note that the same individual’s biometric information [9,10,11] (e.g., fingerprints, iris scans, and facial features) may vary slightly with each capture due to environmental conditions, equipment differences, and measurement noise. Additionally, the distribution of biometric information is not uniform, but has high entropy.

Fuzzy signature (${\mathsf{SIG}}_{\mathsf{F}}$) consists of four algorithms, as depicted in Figure 1. The setup algorithm ${\mathsf{Setup}}_{\mathsf{F}}$ takes the security parameter as input, and it outputs the public parameters $pp$. Given the public parameters $pp$ and a fuzzy signing key $sk$, such as a sample of biometric data, the key-generation algorithm ${\mathsf{KeyGen}}_{\mathsf{F}}$ computes the verification key $vk$. The signing algorithm ${\mathsf{Sign}}_{\mathsf{F}}$ takes ${sk}^{\prime }$ (a new sample of the same biometric data), a message m, and the public parameters $pp$ as inputs, and it outputs a signature $\sigma$. The verification algorithm ${\mathsf{Verify}}_{\mathsf{F}}$ takes $pp$, $vk$, a message m, and a signature $\sigma$ as inputs, and it outputs 1 (valid) or 0 (invalid). The signature $\sigma$ is guaranteed to be valid when the signing keys $sk$ and $s{k}^{\prime }$ are sufficiently close.

The notion of fuzzy signature was first introduced by Takahashi et al. [8]. In their work, they proposed a general construction of fuzzy signature based on a tool called linear sketch and a signature with homomorphic properties regarding keys and signatures. However, their security model assumes that the differences between different samples drawn from identical biometric data are independent of the biometric data itself, which deviates from real-world applications. In addition, their fuzzy signature has a critical limitation: it requires biometric information to be uniformly distributed, a condition that is clearly unrealistic in practical scenarios. Furthermore, their fuzzy signature requires bilinear groups and has large public parameters (proportional to the security parameter), making it less practical for real-world deployment.

Matsuda et al. [12] relaxed the constraints imposed on the underlying linear sketch and homomorphic signature scheme. Through this relaxation, they constructed a new fuzzy signature scheme based on the Schnorr signature scheme [13] and an improved linear sketch. Their construction operates under the assumption that the fuzzy data has high average min-entropy, even in the presence of information leakage. Thanks to the use of the Schnorr signature scheme, their fuzzy signature scheme achieves greater efficiency. Nevertheless, its security is guaranteed only in the random oracle model.

In 2021, Katsumata et al. [14] proposed a simple and efficient generic construction of fuzzy signature based on linear sketch and the tweaked Schnorr signature scheme. In their work, the linear sketch is formalized using lattice theory [15]. The security of the scheme relies on the ${\mathrm{DL}}^{\mathrm{sketch}}$ assumption, which combines the hardness of the discrete logarithm problem (DLP) [16] with the security of the sketch mechanism. Analysis shows that under a low Conditional False Matching Rate (ConFMR), ${\mathrm{DL}}^{\mathrm{sketch}}$ reduces to the standard DLP, and remains unconditionally secure in the generic group model, even for higher ConFMR values. To connect theory with practice, the authors develop a statistical framework using extreme value analysis and t-tests to estimate the ConFMR for real biometric data. However, their fuzzy signature is secure only in the random oracle model [17]. Similarly to previous works, their fuzzy signature requires that the differences between different samples drawn from identical biometric data are independent of the biometric data itself, which is not compatible with real-world applications.

Song et al. [18] introduced a novel security model called $\mathfrak{m}$-existentially unforgeable under chosen message attack ($\mathfrak{m}-\mathrm{EUF}-\mathrm{CMA}$) security for fuzzy signature, which requires only that the fuzzy signing key $sk$ possesses sufficient entropy [19] and that the error distribution across different biometric samples can be arbitrarily correlated to the biometric data. In addition, they proposed a generic construction of fuzzy signature based on a fuzzy extractor [20] and a signature scheme with a simple key-generation process. By instantiating their framework with different signature schemes, they presented two concrete constructions: one based on the Computational Diffie–Hellman (CDH) assumption [21] in the standard model, and another based on lattice assumptions which is post-quantum secure in the random oracle model.

However, their signature generation algorithm requires the verification key $vk$ as an additional input, which may impose a usability burden on the user. For instance, consider a scenario where a user signs messages using biometric data (e.g., a fingerprint or iris scan) as the signing key. If $vk$ is required during signing, the user must securely store $vk$ and may need to carry an external device (e.g., a smart card or USB token), which introduces usability challenges and potential security risks. Is such a device is compromised, it could undermine the overall security of the system. In contrast, if $vk$ is not required during the signing process, the user can generate signatures solely based on biometric data, without the need to manage or protect the verification key. This leads to a more practical, user-friendly, and device-free signing experience.

With the advancement of quantum computing, growing attention has been devoted to the development of post-quantum secure cryptographic algorithms. Tian et al. [22] presented a new reusable fuzzy signature based on a reusable fuzzy extractor from LWE [23,24,25] and lattice-based digital signatures [26]. While their fuzzy signature scheme achieves post-quantum security, its security is established in the random oracle model.

In 2023, zheng et al. [27] proposed another efficient quantum-resistant fuzzy signature scheme based on the small integer solution problem (SIS) [28] by employing a modified linear sketch. Although their security proof is more rigorous than that of prior work, it can only be established under the random oracle model.

The aforementioned fuzzy signature schemes typically employ either a linear sketch or a fuzzy extractor as the core technique to bridge the gap between fuzzy biometric data and cryptographic primitives (e.g., signing keys).

A fundamental limitation of fuzzy signature schemes [8,12,14,27] based on linear sketches is the requirement that the errors across different biometric samples are statistically independent of the biometric data itself. This assumption is difficult to justify in practice, as real-world biometric variations are typically correlated with the underlying data, rendering such schemes impractical for real-life applications.

On the other hand, fuzzy extractor–based constructions face their own limitations. For instance, the scheme proposed in [22] is only proven secure in the random oracle model, while the one in [18] requires the verification key as input during signing, which introduces usability and security challenges.

Motivated by these observations, we are naturally led to the following question:

Does there exist a construction of a fuzzy signature scheme that (1) relaxes the assumptions on the distribution of fuzzy data, (2) does not require the verification key as input during signing, and (3) achieves security in the standard model without relying on random oracles?

1.2. Our Contributions

In this work, we provide an affirmative answer to the above question. The principal contributions of our work are as follows:

–

First, we redefine the notion of fuzzy signature and propose a new security model, which we call $\mathfrak{m}$-existential unforgeability under chosen-message attack ($\mathfrak{m}{-\mathrm{EUF}-\mathrm{CMA}}^{\ast }$), for fuzzy signatures. Compared with previous work [18], this new definition eliminates the requirement for the signing algorithm to take a verification key as input, thereby reducing the burden on users to maintain the verification key. Furthermore, our new security model is stronger than the one proposed by Matsuda et al. [12], because our security model allows the adversary to determine the differences between different biometric samples.

–

We formally define the error-recoverable property of the secure sketch and show that the syndrome-based secure sketch possesses the error recoverable property. We redefine the homomorphic property and define the key-shift* security of the signature scheme. In our key-shift* security model, the adversary can modify not only the signing key $sk$, but also the verification key $vk$. We also prove that the Waters signature scheme ${\mathsf{SIG}}_{\mathsf{Wat}}$ is homomorphic and key-shift* secure.

–

We present a generic construction of a fuzzy signature scheme, built upon three core primitives: a homomorphic secure sketch ($\mathsf{SS}$) with error recovery, a homomorphic average-case strong extractor ($\mathsf{Ext}$), and a homomorphic signature scheme ($\mathsf{SIG}$) satisfying key-shift security.

–

Instantiating these primitives yields a fuzzy signature scheme that achieves $\mathfrak{m}{-\mathrm{EUF}-\mathrm{CMA}}^{\ast }$ security under the Computational Diffie–Hellman (CDH) assumption in the standard model over bilinear groups, and, notably, does not require the verification key as input to the signing algorithm.

In

Table 1. An overview of representative fuzzy signature schemes. “${\mathsf{SIG}}_{\mathsf{F}}$” is the abbreviation of fuzzy signature scheme. “Method” represents the primary cryptographic primitive utilized in the construction of ${\mathsf{SIG}}_{\mathsf{F}}$. “Correlation” explains the relationship between the error distribution e and the biometric information W, where e captures the deviation between the fuzzy signing key $sk$ and $s{k}^{\prime }$ (i.e., two readings derived from identical biometric input W). “$vk$” indicates that the signing algorithm does not need $vk$ as input. “Assumption” specifies the cryptographic assumption underlying the ${\mathsf{SIG}}_{\mathsf{F}}$. “Standard Model” asks whether the ${\mathsf{SIG}}_{\mathsf{F}}$ achieves security in the standard model.

${\mathsf{SIG}}_{\mathsf{F}}$	Method	Correlation	$vk$	Assumption	Standard Model
TMMHN15 [8]	Linear Sketch	Independent	✓	CDH	✓
MTMH16 [12]	Linear Sketch	Independent	✓	DL	✗
KK21 [14]	Linear Sketch	Independent	✓	DL	✗
ZLM23 [27]	Linear Sketch	Independent	✓	SIS	✗
SW21 [18]	Fuzzy Extractor	Arbitrary	✗	CDH	✓
TLDSY21 [22]	Fuzzy Extractor	Adversary-Selected	✓	LWE, SIS	✗
Our Scheme	Secure Sketch	Adversary-Selected	✓	CDH	✓

, we present an overview of our constructions compared with existing fuzzy signature schemes.

1.3. Our Approach

Our generic construction of fuzzy signature consists of a homomorphic secure sketch with an error-recoverable property, a homomorphic average-case strong extractor, and a $\mathsf{SIG}$ with a homomorphic property and a simple key-generation process.

In the setup algorithm ${\mathsf{Setup}}_{\mathsf{F}}$, the seed i of extractor $\mathsf{Ext}$ and public parameters $pp$, generated by the underlying signature scheme’s setup algorithm $\mathsf{Setup}$, serve as the public parameters $p{p}_{\mathsf{F}}$ of the entire fuzzy signature ${\mathsf{SIG}}_{\mathsf{F}}$. In the key-generation algorithm ${\mathsf{KeyGen}}_{\mathsf{F}}$, the public parameters $p{p}_{\mathsf{F}}$ and a biometric sample $\mathrm{w}$ are taken as input, and the verification key $v{k}_{\mathsf{F}}$ of ${\mathsf{SIG}}_{\mathsf{F}}$ is generated. Specifically, $\mathrm{w}$ is first computed by the sketch generation algorithm $\mathsf{SS}.\mathsf{Gen}$ to produce a sketch $\mathsf{s}$, and then the extractor $\mathsf{Ext}$ is used to extract the secret key $sk$ from $\mathrm{w}$ for the underlying signature scheme ($\mathsf{SIG}$). Subsequently, the $\mathsf{SIG}$’s simple key-generation process enables the verification key $vk$ of the $\mathsf{SIG}$ to be derived. Therefore, the final verification key of the ${\mathsf{SIG}}_{\mathsf{F}}$ is given by $v{k}_{\mathsf{F}}=(vk,\mathsf{s})$.

The signing algorithm ${\mathsf{Sign}}_{\mathsf{F}}$ uses a new biometric sample ${\mathrm{w}}^{\prime }$ as the signing key of fuzzy signature to sign the message m. Specifically, the process begins by computing a new sketch ${\mathsf{s}}^{\prime }$ from ${\mathrm{w}}^{\prime }$, while the extractor $\mathsf{Ext}$ is used to extract the new $s{k}^{\prime }$ as the secret key (signing key) for the underlying signature scheme $\mathsf{SIG}$. Subsequently, the message m and the sketch ${\mathsf{s}}^{\prime }$ are signed together using the $\mathsf{SIG}$ to obtain $\sigma$. The final signature ${\sigma }_{\mathsf{F}}$ is then given by $(\sigma ,{\mathsf{s}}^{\prime })$. In ${\mathsf{Verify}}_{\mathsf{F}}$, utilizing the values of $\mathsf{s}$ and ${\mathsf{s}}^{\prime }$ generated during the ${\mathsf{KeyGen}}_{\mathsf{F}}$ and ${\mathsf{Sign}}_{\mathsf{F}}$, the error-recovery property of $\mathsf{SS}$ allows us to compute $\Delta \mathrm{w}={\mathrm{w}}^{\prime }-\mathrm{w}$. This enables the extractor $\mathsf{Ext}$ to calculate $\Delta sk=s{k}^{\prime }-sk$. Next, thanks to the homomorphic property of the $\mathsf{SIG}$, we can obtain the verification key $v{k}^{\prime }$ corresponding to $s{k}^{\prime }$, thereby ensuring the correctness of $\mathsf{SIG}$. Consequently, the correctness of the entire fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$ is also guaranteed. In addition, the security of our ${\mathsf{SIG}}_{\mathsf{F}}$ is ensured by $\mathsf{Ext}$ and $\mathsf{SIG}$. More precisely, the security of $\mathsf{Ext}$ guarantees the uniform randomness of the secret key in $\mathsf{SIG}$, thereby guaranteeing the security of $\mathsf{SIG}$. Furthermore, the $\mathfrak{m}{-\mathrm{EUF}-\mathrm{CMA}}^{\ast }$ security we defined for ${\mathsf{Sign}}_{\mathsf{F}}$ can be reduced to the key-shift* security of $\mathsf{SIG}$, which is further guaranteed by the homomorphic property and EUF-CMA security of $\mathsf{SIG}$. Detailed information on this is presented in Section 4.

2. Preliminaries

Throughout this paper, we denote the set of integers by $\mathbb{Z}$ and the set of real numbers by $\mathbb{R}$. The notation “$u\leftarrow v$” denotes a deterministic assignment of the value v to the variable u. Given a finite set $\mathcal{D}$, we use $d{\leftarrow }_{\$}\mathcal{D}$ to indicate that d is drawn uniformly at random from $\mathcal{D}$. The cardinality of a set $\mathcal{D}$ is denoted by $\left|\mathcal{D}\right|$. For any bit strings a and b, we write $\left|a\right|$ for the bit-length of a, and write $a \Vert b$ to denote the concatenation of a and b. A probabilistic algorithm that operates in polynomial time is referred to as a $\mathrm{PPT}$ algorithm. For a natural number k, we write $\left[k\right]$ for the index set $\{1,2,\dots ,k\}$. Let $\mathcal{A}$ be a randomized procedure; we express $\rho \leftarrow \mathcal{A}(x;r)$ to represent the outcome $\rho$ when $\mathcal{A}$ is executed on input x with internal randomness r. A function $\mathsf{negl}\left(n\right)$ is called negligible if for every positive polynomial $q(·)$, there exists an integer $n_0$, such that for all $n>n_0$, it holds that $\mathsf{negl}\left(n\right)\le {\displaystyle \frac{1}{q\left(n\right)}}$.

2.1. Metric Spaces

Definition 1 (Metric Space [29]). 

A metric space is a set $\mathcal{W}$ equipped with a distance function $\mathrm{dis}:\mathcal{W}\times \mathcal{W}\to {\mathbb{R}}_{\ge 0}$, where $\mathrm{dis}$ satisfies the following properties for all ${\mathrm{w}}_1,{\mathrm{w}}_2,{\mathrm{w}}_3\in \mathcal{W}$:

(i) 

$\mathrm{dis}({\mathrm{w}}_1,{\mathrm{w}}_2)=0$ if, and only if, ${\mathrm{w}}_1={\mathrm{w}}_2$;

(ii) 

$\mathrm{dis}({\mathrm{w}}_1,{\mathrm{w}}_2)=\mathrm{dis}({\mathrm{w}}_2,{\mathrm{w}}_1)$ (symmetry);

(iii) 

$\mathrm{dis}({\mathrm{w}}_1,{\mathrm{w}}_3)\le \mathrm{dis}({\mathrm{w}}_1,{\mathrm{w}}_2)+\mathrm{dis}({\mathrm{w}}_2,{\mathrm{w}}_3)$ (triangle inequality).

2.2. Min-Entropy and Statistical Distance

Definition 2 (Min-Entropy [29]). 

Let ξ be a discrete random variable over a finite set $\mathcal{D}$. The min-entropy of ξ is defined as

$$H_{\infty }\left(\xi \right)=-log\left(\underset{d\in \mathcal{D}}{max}Pr[\xi =d]\right).$$

Definition 3 (Average Min-Entropy [20]). 

Let A and B be two discrete random variables over finite sets $\mathcal{A}$ and $\mathcal{B}$, respectively. The average min-entropy of A given B is defined as

$${\tilde{H}}_{\infty }(A\mid B)=-log\left({\mathbb{E}}_{b\leftarrow B}\left[\underset{a\in \mathcal{A}}{max}Pr[A=a\mid B=b]\right]\right).$$

Definition 4 (Statistical Distance [20]). 

Let U and V be two random variables taking values in a finite set $\mathcal{W}$. The statistical distance between U and V is defined as

$$\mathrm{SD}(U,V)={\displaystyle \frac{1}{2}}\sum _{\mathrm{w}\in \mathcal{W}}\left|Pr[U=\mathrm{w}]-Pr[V=\mathrm{w}]\right|.$$

2.3. Computational Diffie–Hellman (CDH) Assumption

Let $\mathcal{IG}$ be an algorithm that outputs $(p,g,\mathbb{G})$, where $\mathbb{G}$ is a cyclic group with order p, and $g\in \mathbb{G}$ is a generator.

Definition 5 (CDH Problem). 

Given the four-tuple $(\mathbb{G},g,g^a,g^b)$, compute $g^{ab}$, where $(p,g,\mathbb{G})\leftarrow \mathcal{IG}$ and $a,b\in {\mathbb{Z}}_p$.

Definition 6 (CDH Assumption). 

The CDH assumption w.r.t. $(p,g,\mathbb{G})$ is ϵ-hard if, for any PPT adversary $\mathcal{A}$, the following holds:

$${\mathsf{Adv}}_{\mathcal{A}}^{\mathrm{CDH}}:=Pr[\mathcal{A}(\mathbb{G},g,g^a,g^b)\to g^{ab}]\le ϵ,$$

where $(p,g,\mathbb{G})\leftarrow \mathcal{IG}$ and $a,b\in {\mathbb{Z}}_p$.

2.4. Secure Sketch and Average-Case Strong Extractor

Definition 7 (Secure Sketch [20]). 

A $(\mathcal{W},\mathfrak{m},\widehat{\mathfrak{m}},t)$-secure sketch $\left(\mathsf{SS}\right)$ consists of two efficient algorithms, defined as follows:

–

$\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)$ on input $\mathrm{w}\in \mathcal{W}$, outputs a sketch $\mathsf{s}\in \mathcal{S}$.

–

$\mathsf{SS}.\mathsf{Rec}({\mathrm{w}}^{\prime },\mathsf{s})$ on input ${\mathrm{w}}^{\prime }\in \mathcal{W}$ and a sketch $\mathsf{s}\in \mathcal{S}$, outputs a recovered value $\tilde{\mathrm{w}}$.

These algorithms must satisfy the following properties:

–

$\mathrm{Correctness}:$ When $\mathrm{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$, then $\mathrm{w}=\mathsf{SS}.\mathsf{Rec}({\mathrm{w}}^{\prime },\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right))=\tilde{\mathrm{w}}$.

–

$\mathrm{Security}:$ For any distribution W over $\mathcal{W}$, if $H_{\infty }\left(W\right)>\mathfrak{m}$, ${\tilde{H}}_{\infty }\left(W\right|\mathsf{SS}.\mathsf{Gen}\left(W\right))>\widehat{\mathfrak{m}}$.

A secure sketch is regarded as homomorphic if for all $\mathsf{u},\mathsf{v}\in \mathcal{W}$, it holds that

$$\mathsf{SS}.\mathsf{Gen}(\mathsf{u}+\mathsf{v})=\mathsf{SS}.\mathsf{Gen}\left(\mathsf{u}\right)+\mathsf{SS}.\mathsf{Gen}\left(\mathsf{v}\right).$$

Definition 8 (Error-Recoverable Property). 

Let $\mathsf{SS}=(\mathsf{SS}.\mathsf{Gen},\mathsf{SS}.\mathsf{Rec})$ be a $(\mathcal{W},\mathfrak{m},\widehat{\mathfrak{m}},t)$-secure sketch and $\mathrm{w},{\mathrm{w}}^{\prime }\in \mathcal{W}$, such that $\mathsf{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$. Let $\Delta \mathrm{w}={\mathrm{w}}^{\prime }-\mathrm{w}$ and $\mathsf{s}=\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)$, ${\mathsf{s}}^{\prime }=\mathsf{SS}.\mathsf{Gen}\left({\mathrm{w}}^{\prime }\right)$. We say that the secure sketch has the error-recoverable property if there is a deterministic function $f_{rec}$, such that $\Delta \mathrm{w}=f_{rec}({\mathsf{s}}^{\prime },\mathsf{s})$.

Remark 1. 

In our fuzzy signature scheme, the user needs to compute the error between the fuzzy data $\mathrm{w}$ sampled during the generation of the verification key and ${\mathrm{w}}^{\prime }$ used for signing, by utilizing the values $\mathsf{s}$ and ${\mathsf{s}}^{\prime }$. Here, $\mathsf{s}$ is included in the verification key, while ${\mathsf{s}}^{\prime }$ is part of the signature. Through this mechanism, the scheme can verify the validity of the signature. The details can be found in Section 4 of our paper. The error-recoverable property ensures that the user can perform the above operations reliably.

Lemma 1. 

The error-recoverable property mentioned above is satisfied by the syndrome-based secure sketch construction.

Proof. 

This lemma is a straightforward consequence of the inherent properties of the syndrome-based secure sketch construction [20]. Recall that the syndrome-based secure sketch is as follows. The generation algorithm $\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)=\mathrm{syn}\left(\mathrm{w}\right)=\mathsf{s}$, and the recovery algorithm $\mathsf{SS}.\mathsf{Rec}({\mathrm{w}}^{\prime },\mathsf{s})={\mathrm{w}}^{\prime }-\mathsf{decode}(\mathrm{syn}\left({\mathrm{w}}^{\prime }\right)-\mathsf{s})={\mathrm{w}}^{\prime }-\mathsf{decode}({\mathsf{s}}^{\prime }-\mathsf{s})$, where $\mathsf{decode}$ is an efficient and deterministic function to find the unique $e\in \mathcal{W}$, where $\mathsf{dis}(e,0)\le t$ such that $\mathrm{syn}\left(e\right)=\mathrm{syn}\left({\mathrm{w}}^{\prime }\right)-\mathsf{s}$. By the correctness of the secure sketch, if $\mathsf{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$, then $\mathrm{w}=\mathsf{SS}.\mathsf{Rec}({\mathrm{w}}^{\prime },\mathsf{s})={\mathrm{w}}^{\prime }-\mathsf{decode}({\mathsf{s}}^{\prime }-\mathsf{s})$. It is obvious that $\Delta \mathrm{w}={\mathrm{w}}^{\prime }-\mathrm{w}=\mathsf{decode}({\mathsf{s}}^{\prime }-\mathsf{s})$. The lemma follows. □

For completeness, we provide the details of the syndrome-based secure sketch in Appendix A.

Definition 9 (Average-Case Strong Extractor [20]). 

A function $\mathsf{Ext}:\mathcal{W}\times \mathcal{R}\to \mathcal{V}$ is called an average-case $(\mathcal{W},m,\mathcal{V},{\epsilon }_{ext})$-strong extractor with randomness $R\in \mathcal{R}$ if for every random variable W over $\mathcal{W}$ and any auxiliary information Z, the following holds:

$$\mathrm{SD}\left(\left(\mathsf{Ext}(W,R),R,Z\right),\left(U,R,Z\right)\right)\le {\epsilon }_{ext},$$

where R and U are independently and uniformly sampled from $\mathcal{R}$ and $\mathcal{V}$, respectively.

Definition 10 (Homomorphic Average-Case Strong Extractor). 

An average-case $(\mathcal{W},m,\mathcal{V},\epsilon )$-strong extractor $\mathsf{Ext}:\mathcal{W}\times \mathcal{R}\to \mathcal{V}$ is said to be homomorphic if for all ${\mathrm{w}}_1,{\mathrm{w}}_2\in \mathcal{W}$ and all seeds $r\in \mathcal{R}$, it satisfies

$$\mathsf{Ext}({\mathrm{w}}_1+{\mathrm{w}}_2,r)=\mathsf{Ext}({\mathrm{w}}_1,r)+\mathsf{Ext}({\mathrm{w}}_2,r).$$

One instantiation of an average-case strong extractor [30] is defined as follows:

$$\mathsf{Ext}(\mathrm{w},\mathbf{r})={\mathrm{w}}_0+r_1{\mathrm{w}}_1+\dots +r_l{\mathrm{w}}_l,$$

(1)

where $\mathbf{r}=(r_1,\dots ,r_l)\in {\mathbb{Z}}_p^l$ denotes the seed, and $\mathrm{w}=({\mathrm{w}}_0,{\mathrm{w}}_1,\dots ,{\mathrm{w}}_l)\in {\mathbb{Z}}_p^{l+1}$ represents the input. Note that

$$\begin{array}{ccc}\hfill \mathsf{Ext}({\mathrm{w}}_{\mathbf{0}}+{\mathrm{w}}_{\mathbf{1}},\mathbf{r})& =& ({\mathrm{w}}_{0,0}+{\mathrm{w}}_{1,0})+r_1({\mathrm{w}}_{0,1}+{\mathrm{w}}_{1,1})+\dots +r_l({\mathrm{w}}_{0,l}+{\mathrm{w}}_{1,l})\hfill \\ & =& {\mathrm{w}}_{0,0}+r_1{\mathrm{w}}_{0,1}+\dots +r_l{\mathrm{w}}_{0,l}+{\mathrm{w}}_{1,0}+r_1{\mathrm{w}}_{1,1}+\dots +r_l{\mathrm{w}}_{1,l}\hfill \\ & =& \mathsf{Ext}({\mathrm{w}}_{\mathbf{0}},\mathbf{r})+\mathsf{Ext}({\mathrm{w}}_{\mathbf{1}},\mathbf{r}).\hfill \end{array}$$

Then we have that Equation (1) is a homomorphic average-case strong extractor.

2.5. Signature Scheme

Definition 11 (Signature Scheme). 

A digital signature scheme $\mathsf{SIG}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Sign},\mathsf{Verify})$ consists of four probabilistic polynomial-time (PPT) algorithms.

• $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$: On input the security parameter λ, $\mathsf{Setup}$ outputs public parameters $pp$.
• $(vk,sk)\leftarrow \mathsf{KeyGen}\left(pp\right)$: On input $pp$, $\mathsf{KeyGen}$ generates a key pair consisting of a verification key $vk\in \mathcal{VK}$ and a signing key $sk\in \mathcal{SK}$.
• $\sigma \leftarrow \mathsf{Sign}(pp,sk,m)$: On input $pp$, $sk$, and a message $m\in \mathcal{M}$, $\mathsf{Sign}$ outputs a signature σ.
• $b\leftarrow \mathsf{Verify}(pp,vk,m,\sigma )$: On input $pp$, $vk$, m, and σ, $\mathsf{Verify}$ outputs a bit $b\in \{0,1\}$ indicating whether the signature is valid (1) or invalid (0).

Correctness. 

For any message $m\in \mathcal{M}$, let $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, $(vk,sk)\leftarrow \mathsf{KeyGen}\left(pp\right)$, and signature $\sigma \leftarrow \mathsf{Sign}(pp,sk,m)$; then

$$Pr\left[\mathsf{Verify}\right(pp,vk,m,\sigma )=1]\ge 1-\mathsf{negl}\left(\lambda \right).$$

Definition 12 (EUF-CMA Security). 

We say that a digital signature $\mathsf{SIG}$ achieves existentially unforgeable under adaptive chosen-message attack (EUF-CMA) security if for any PPT adversary, it holds that

$${\mathsf{Adv}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{EUF}-\mathsf{CMA}}\left(1^{\lambda }\right):=Pr[{\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{EUF}-\mathsf{CMA}}\left(1^{\lambda }\right)\Rightarrow 1]⩽\mathsf{negl}\left(\lambda \right),$$

where ${\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{EUF}-\mathsf{CMA}}\left(1^{\lambda }\right)$ is defined as follows.

${\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{EUF}-\mathsf{CMA}}\left(1^{\lambda }\right)$:

1. 

The challenger $\mathcal{C}$ runs $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, generates $(vk,sk)\leftarrow \mathsf{KeyGen}\left(pp\right)$, initializes an empty query set $\mathcal{Q}=\varnothing$, and sends $pp$ and $vk$ to the adversary $\mathcal{A}$.

2. 

Throughout the experiment, $\mathcal{A}$ may adaptively query a signing oracle:

• $\mathcal{A}$ submits a message $m_j\in \mathcal{M}$ to $\mathcal{C}$.
• $\mathcal{C}$ computes ${\sigma }_j\leftarrow \mathsf{Sign}(pp,sk,m_j)$, adds $m_j$ to $\mathcal{Q}$, and returns ${\sigma }_j$ to $\mathcal{A}$.

3. 

Finally, $\mathcal{A}$ outputs a forgery $(m^{\ast },{\sigma }^{\ast })$. The experiment outputs 1 if, and only if,

$$m^{\ast }\notin \mathcal{Q}and\mathsf{Verify}(pp,vk,m^{\ast },{\sigma }^{\ast })=1.$$

Otherwise, it outputs 0.

Definition 13 

(Simple Key-Generation Process [8]). We say that a digital signature scheme $\mathsf{SIG}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Sign},\mathsf{Verify})$ supports a simple key-generation process if the public parameters $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$ implicitly define the signing key space $\mathcal{SK}$, and there exists a deterministic polynomial-time ($\mathrm{PPT}$) algorithm $\mathsf{KG}$ such that $\mathsf{KeyGen}\left(pp\right)$ is functionally equivalent to the following procedure:

$$\mathsf{KeyGen}\left(pp\right):\left[sk{\leftarrow }_{\$}\mathcal{SK},vk\leftarrow \mathsf{KG}(pp,sk),return(vk,sk)\right].$$

Definition 14 (Homomorphic Signature). 

A signature scheme $\mathsf{SIG}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Sign},\mathsf{Verify})$, equipped with a simple key-generation process $\mathsf{KG}$, is said to be homomorphic if the following properties are satisfied:

1. 

For all $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, the signing key space $\mathcal{SK}$ constitutes an abelian group $(\mathcal{SK},+)$.

2. 

For all $sk,\Delta sk\in \mathcal{SK}$, there exists a deterministic and efficient algorithm ${\mathsf{A}}_{\mathsf{vk}}$ such that

$$\mathsf{KG}(pp,sk+\Delta sk)={\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta sk),$$

where $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, $vk\leftarrow \mathsf{KG}(pp,sk)$.

3. 

Suppose the random space of the signing algorithm is $\mathcal{R}$. For all $r\in \mathcal{R}$, $m\in \mathcal{M}$ and $sk,\Delta sk\in \mathcal{SK}$, there exists a deterministic and efficient algorithm ${\mathsf{A}}_{\mathsf{Sign}}$ such that

$$\mathsf{Sign}(pp,sk+\Delta sk,m,r)={\mathsf{A}}_{\mathsf{Sign}}(pp,m,\sigma ,\Delta sk),$$

where $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, $\sigma \leftarrow \mathsf{Sign}(pp,sk,m,r)$.

Remark 2. 

For simplicity, we sometimes omit r and say that there exists a deterministic and efficient algorithm ${\mathsf{A}}_{\mathsf{Sign}}$ such that

$$\mathsf{Sign}(pp,sk+\Delta sk,m)={\mathsf{A}}_{\mathsf{Sign}}(pp,m,\sigma ,\Delta sk).$$

where $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, $\sigma \leftarrow \mathsf{Sign}(pp,sk,m)$.

Remark 3. 

Our definition of a homomorphic signature differs from the definition provided in [8] in three aspects.

1. 

The first difference lies in the inputs required by the algorithm ${\mathsf{A}}_{\mathsf{Sign}}$. In our definition, ${\mathsf{A}}_{\mathsf{Sign}}$ takes $pp,m,\sigma ,\Delta sk$ as input and generates a valid signature of m under the signing key $sk+\Delta sk$. However, in [8], the algorithm additionally requires $vk$ as part of its input.

2. 

The second difference is that in our definition with the same random number r, $\mathsf{Sign}(pp,sk+\Delta sk,m,r)={\mathsf{A}}_{\mathsf{Sign}}(pp,m,\mathsf{Sign}(pp,sk,m,r),\Delta sk),$ while in [8], the distribution of $\{{\sigma }^{\prime }\leftarrow \mathsf{Sign}(pp,sk+\Delta sk,m):{\sigma }^{\prime }\}$ and $\{\sigma \leftarrow \mathsf{Sign}(pp,sk,m);{\sigma }^{\prime }\leftarrow {\mathsf{A}}_{\mathsf{Sign}}(pp,m,\sigma ,\Delta sk):{\sigma }^{\prime }\}$ is required to be identical.

3. 

The third difference is that our definition omits the requirement that for all $sk,\Delta sk$ and all pairs $(m,\sigma )$ satisfying $\mathsf{Verify}(pp,\mathsf{KG}(pp,sk),m,\sigma )=1$, it holds that $\mathsf{Verify}(pp,\mathsf{KG}(pp,sk+\Delta sk),m,{\mathsf{A}}_{\mathsf{Sign}}(pp,m,\sigma ,\Delta sk))=1$.

Next, we will formally define the key-shift* security of a signature scheme. In the traditional related-key attack (RKA) security experiment [31], only the signing key $sk$ can be changed by the adversary $\mathcal{A}$. More precisely, the adversary is allowed to modify the secret key $sk$ using a predefined set of transformations, and obtains signatures under the modified keys on adaptively chosen messages, while the verification key $vk$ remains unchanged. The adversary’s goal is to produce a valid forgery—a message–signature pair $(m,\sigma )$—such that $\sigma$ verifies correctly under the corresponding verification key $vk$. If the adversary succeeds in producing such a forgery, it is said to have broken the scheme under related-key attacks. These transformations can include various functions, such as affine transformations, bitwise operations, or other structured modifications. A more detailed RKA security definition is given in Appendix B.

The key-shift security notion is a special case of RKA security, in which the adversary is restricted to applying only additive shifts to the secret key. That is, the adversary can choose a shift value $\Delta sk$ and obtain signatures under $sk+\Delta sk$.

Our proposed key-shift* security strengthens the key-shift model by also allowing the adversary to submit not only a forged message–signature pair $(m,\sigma )$, but also a corresponding secret key shift $\Delta sk$. The adversary succeeds if the signature $\sigma$ verifies correctly with respect to the verification key associated with the shifted secret key $sk+\Delta sk$. This captures a stronger adversarial capability and provides a more refined security guarantee in settings where both the signing and verification keys may be subject to related-key manipulations.

Definition 15 (Key-Shift* Security). 

A signature scheme $\mathsf{SIG}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Sign},\mathsf{Verify})$ with a simple key-generation process $\mathsf{KG}$ is key-shift* secure if for all $\mathrm{PPT}$ adversaries $\mathcal{A}$, it holds that

$${\mathsf{Adv}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right):=Pr[{\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right)\Rightarrow 1]⩽\mathsf{negl}\left(\lambda \right),$$

where ${\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right)$ is defined as follows.

${\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right)$:

1. 

The challenger $\mathcal{C}$ runs $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, generates $(vk,sk)\leftarrow \mathsf{KeyGen}\left(pp\right)$, initializes an empty query set $\mathcal{Q}=\varnothing$, and sends $pp$ and $vk$ to the adversary $\mathcal{A}$.

2. 

Throughout the experiment, $\mathcal{A}$ may adaptively query a signing oracle with pairs $(m_j,\Delta s{k}_j)$, where $m_j\in \mathcal{M}$ and $\Delta s{k}_j$ is a key shift:

• $\mathcal{A}$ submits $(m_j,\Delta s{k}_j)$ to $\mathcal{C}$.
• $\mathcal{C}$ computes the signature ${\sigma }_j\leftarrow \mathsf{Sign}(pp,sk+\Delta s{k}_j,m_j)$, adds $m_j$ to $\mathcal{Q}$, and returns ${\sigma }_j$ to $\mathcal{A}$.

3. 

Finally, $\mathcal{A}$ outputs a forgery $(m^{\ast },{\sigma }^{\ast })$ and a final shift $\Delta s{k}^{\ast }$. The experiment outputs 1 if, and only if,

$$m^{\ast }\notin \mathcal{Q}and\mathsf{Verify}\left(pp,\mathsf{KG}(pp,sk+\Delta s{k}^{\ast }),m^{\ast },{\sigma }^{\ast }\right)=1.$$

Otherwise, it outputs 0.

Remark 4. 

Compared to standard key-shift security, key-shift* security captures a stronger adversarial capability. In this work, key-shift* security is specifically designed to support the construction of fuzzy signature schemes, where secret keys are often derived from noisy or biometric data that may vary across different uses.

Lemma 2. 

Let $\mathsf{SIG}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Sign},\mathsf{Verify})$ be a signature scheme with a simple key-generation process $\mathsf{KG}$ and a signing key space $\mathcal{SK}$. If $\mathsf{SIG}$ is EUF-CMA secure and homomorphic, then $\mathsf{SIG}$ is key-shift* secure.

Proof. 

We prove the key-shift* security of $\mathsf{SIG}$ via a reduction to its EUF-CMA security, leveraging the homomorphic property of the scheme $\mathsf{SIG}$. Suppose there exists a probabilistic polynomial-time (PPT) adversary $\mathcal{A}$ that breaks the key-shift* security of $\mathsf{SIG}$ with a non-negligible advantage. Then, we construct a new adversary $\mathcal{B}$ that uses $\mathcal{A}$ as a subroutine to break the EUF-CMA security of $\mathsf{SIG}$.

The adversary $\mathcal{B}$ interacts with its own EUF-CMA challenger and simulates the key-shift* experiment for $\mathcal{A}$ as follows:

• Upon receiving the public parameters $pp$ and verification key $vk$ from its EUF-CMA challenger, $\mathcal{B}$ forwards $(pp,vk)$ to $\mathcal{A}$.
• For each j-th signing query $(m_j,\Delta s{k}_j)$ made by $\mathcal{A}$, $\mathcal{B}$ proceeds as follows:
  • $\mathcal{B}$ queries its signing oracle on $m_j$ and receives a signature $\widetilde{{\sigma }_j}\leftarrow \mathsf{Sign}(pp,sk,m_j)$.
  • $\mathcal{B}$ computes ${\sigma }_j\leftarrow {\mathsf{A}}_{\mathsf{Sign}}(pp,m_j,\widetilde{{\sigma }_j},\Delta s{k}_j)$ using the homomorphic signing algorithm, and returns ${\sigma }_j$ to $\mathcal{A}$.
• In the final phase, when $\mathcal{A}$ outputs a forgery $(m^{\ast },{\sigma }^{\ast })$ and a shift $\Delta s{k}^{\ast }$, $\mathcal{B}$ computes

  $$\widetilde{{\sigma }^{\ast }}\leftarrow {\mathsf{A}}_{\mathsf{Sign}}(pp,m^{\ast },{\sigma }^{\ast },-\Delta s{k}^{\ast }),$$

  and submits $(m^{\ast },\widetilde{{\sigma }^{\ast }})$ to its challenger. $\mathcal{B}$ then outputs whatever its challenger returns.

We now argue that the simulation is perfect. By the homomorphic property of $\mathsf{SIG}$, we have

$$\mathsf{Sign}(pp,sk+\Delta s{k}_j,m_j)={\mathsf{A}}_{\mathsf{Sign}}(pp,m_j,\widetilde{{\sigma }_j},\Delta s{k}_j),$$

where $\widetilde{{\sigma }_j}=\mathsf{Sign}(pp,sk,m_j)$. Therefore, the signatures returned by $\mathcal{B}$ are distributed identically to those in the real key-shift* experiment.

Next, we will show that $\mathcal{B}$ has the same advantage of $\mathcal{A}$.

Note that if $\mathcal{A}$’s forgery $(m^{\ast },{\sigma }^{\ast })$ is valid under the shifted key $sk+\Delta s{k}^{\ast }$, i.e.,

$$m^{\ast }\notin \mathcal{Q}\wedge \mathsf{Verify}(pp,\mathsf{KG}(pp,sk+\Delta s{k}^{\ast }),m^{\ast },{\sigma }^{\ast })=1,$$

by the homomorphic property, we have

$$\widetilde{{\sigma }^{\ast }}={\mathsf{A}}_{\mathsf{Sign}}(pp,m^{\ast },{\sigma }^{\ast },-\Delta s{k}^{\ast })=\mathsf{Sign}(pp,sk+\Delta s{k}^{\ast }-\Delta s{k}^{\ast },m^{\ast })=\mathsf{Sign}(pp,sk,m^{\ast }).$$

This implies that $\widetilde{{\sigma }^{\ast }}$ is a valid signature of $m^{\ast }$ under the signing key $sk$. As a result, if $\mathcal{A}$ wins the key-shift* experiment, then $\mathcal{B}$ wins the EUF-CMA experiment. So we have

$${\mathsf{Adv}}_{\mathsf{SIG},\mathcal{A}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right)\le {\mathsf{Adv}}_{\mathsf{SIG},\mathcal{B}}^{\mathsf{EUF}-\mathsf{CMA}}\left(1^{\lambda }\right)\le \mathsf{negl}\left(\lambda \right).$$

□

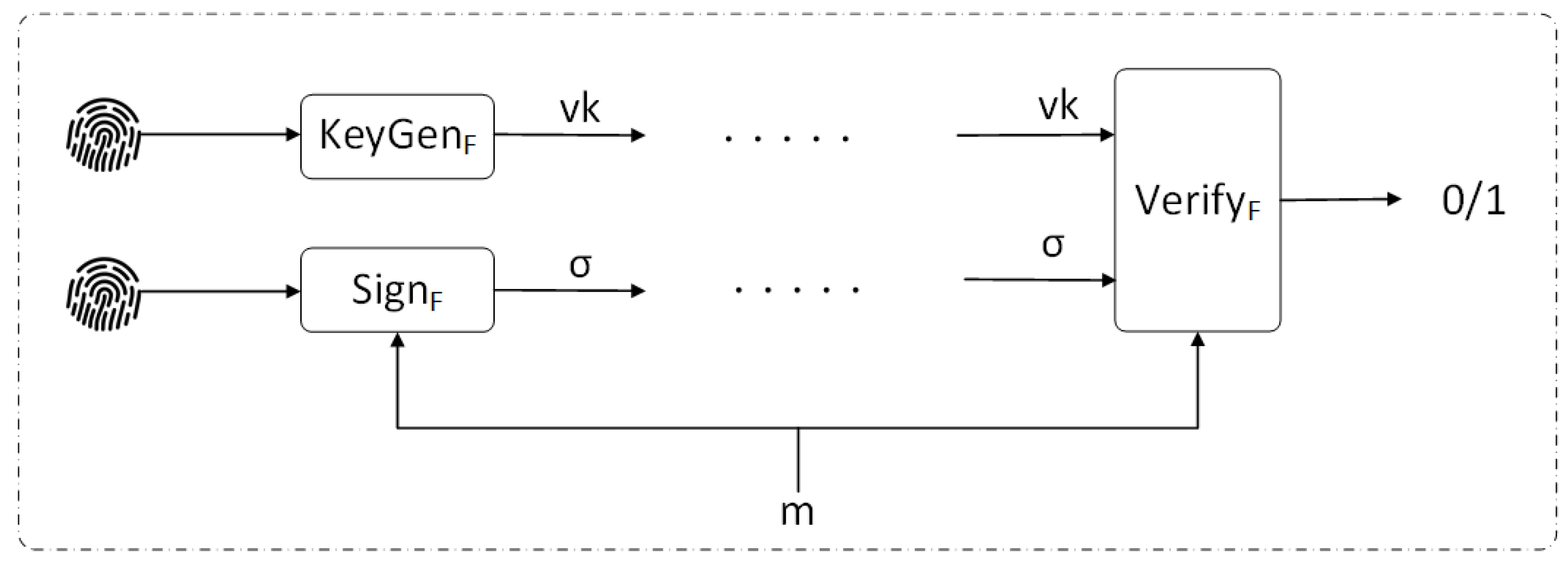
3. Fuzzy Signature

A fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$ differs from a traditional digital signature scheme $\mathsf{SIG}$ in that the signing key is no longer required to be uniformly random or precisely reproducible. Instead, the signing key in a fuzzy signature can be any high-entropy fuzzy data, such as biometric inputs (e.g., facial scans or fingerprints). The key-generation algorithm takes a fuzzy signing key $\mathrm{w}\in \mathcal{W}$ (e.g., an initial facial scan) and outputs a verification key $v{k}_{\mathsf{F}}$. Any signature generated using ${\mathrm{w}}^{\prime }\in \mathcal{W}$ (e.g., a later facial scan of the same person) will verify successfully under $v{k}_{\mathsf{F}}$, provided that $\mathrm{w}$ and ${\mathrm{w}}^{\prime }$ are sufficiently close according to an appropriate distance metric. Below, we formally define a fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$.

Definition 16(Fuzzy Signature). 

Let $\mathcal{W}$ be the fuzzy signing key space, $\mathcal{M}$ the message space, and $t\in \mathbb{N}$ a threshold parameter governing the acceptable distance between keys. A $(\mathcal{W},\mathcal{M},t)$-fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}=({\mathsf{Setup}}_{\mathsf{F}},{\mathsf{KeyGen}}_{\mathsf{F}},{\mathsf{Sign}}_{\mathsf{F}},{\mathsf{Verify}}_{\mathsf{F}})$ consists of four probabilistic polynomial-time ($\mathrm{PPT}$) algorithms:

• $p{p}_{\mathsf{F}}\leftarrow {\mathsf{Setup}}_{\mathsf{F}}\left(1^{\lambda }\right)$. Upon input of the security parameter $1^{\lambda }$, this algorithm outputs public parameters $p{p}_{\mathsf{F}}$.
• $v{k}_{\mathsf{F}}\leftarrow {\mathsf{KeyGen}}_{\mathsf{F}}(p{p}_{\mathsf{F}},\mathrm{w})$. Given the public parameters $p{p}_{\mathsf{F}}$ and a fuzzy signing key $\mathrm{w}\in \mathcal{W}$ (e.g., a biometric template), this algorithm generates a verification key $v{k}_{\mathsf{F}}$.
• ${\sigma }_{\mathsf{F}}\leftarrow {\mathsf{Sign}}_{\mathsf{F}}(p{p}_{\mathsf{F}},{\mathrm{w}}^{\prime },m)$. To sign a message $m\in \mathcal{M}$, the signer uses a (possibly different) fuzzy key ${\mathrm{w}}^{\prime }\in \mathcal{W}$ close to the original $\mathrm{w}$, along with $p{p}_{\mathsf{F}}$, to produce a signature ${\sigma }_{\mathsf{F}}$.
• $b\leftarrow {\mathsf{Verify}}_{\mathsf{F}}(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}},m,{\sigma }_{\mathsf{F}})$, where $b\in \{0,1\}$. This algorithm checks the validity of the signature ${\sigma }_{\mathsf{F}}$ on message m under the verification key $v{k}_{\mathsf{F}}$ and public parameters $p{p}_{\mathsf{F}}$, returning 1 if valid and 0 otherwise.

Correctness. 

For any $m\in \mathcal{M}$, $\mathrm{w},{\mathrm{w}}^{\prime }\in \mathcal{W}$, if $p{p}_{\mathsf{F}}\leftarrow {\mathsf{Setup}}_{\mathsf{F}}\left(1^{\lambda }\right)$, $v{k}_{\mathsf{F}}\leftarrow {\mathsf{KeyGen}}_{\mathsf{F}}(p{p}_{\mathsf{F}},\mathrm{w})$, ${\sigma }_{\mathsf{F}}\leftarrow \mathsf{Sign}(p{p}_{\mathsf{F}},{\mathrm{w}}^{\prime },m)$, $\mathsf{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$, we have

$$Pr[\mathsf{Verify}(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}},m,{\sigma }_{\mathsf{F}})=1]\ge 1-\mathsf{negl}\left(\lambda \right).$$

Next, we present a new security model in which the adversary can adaptively determine the differences between biometric samples.

Definition 17 

($\mathfrak{m}{-\mathrm{EUF}-\mathrm{CMA}}^{\ast }$ Security). A $(\mathcal{W},\mathcal{M},t)$-fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$ is said to be $\mathfrak{m}$-existentially unforgeable under adaptive chosen-message attacks secure ($\mathfrak{m}$-EUF-${\mathrm{CMA}}^{\ast }$) if no efficient adversary $\mathcal{A}$ can produce a valid forgery with non-negligible probability when the signing key is sampled from an arbitrary distribution W over $\mathcal{W}$ with min-entropy of at least $\mathfrak{m}$, i.e., $H_{\infty }\left(W\right)\ge \mathfrak{m}$.

Formally, for all probabilistic polynomial-time (PPT) adversaries $\mathcal{A}$, we require that

$${\mathsf{Adv}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right):=Pr[{\mathsf{Expt}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-\mathsf{CMA}}\left(1^{\lambda }\right)\Rightarrow 1]⩽\mathsf{negl}\left(\lambda \right),$$

where ${\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)$ is defined as follows.

${\mathsf{Expt}}_{\mathsf{SIG},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)$:

1. 

The challenger $\mathcal{C}$ runs $p{p}_{\mathsf{F}}\leftarrow {\mathsf{Setup}}_{\mathsf{F}}\left(1^{\lambda }\right)$; samples a signing key $\mathrm{w}\leftarrow W$, where W is a distribution over $\mathcal{W}$ with $H_{\infty }\left(W\right)\ge \mathfrak{m}$; computes $v{k}_{\mathsf{F}}\leftarrow {\mathsf{KenGen}}_{\mathsf{F}}(p{p}_{\mathsf{F}},\mathrm{w})$; and initializes an empty query set $\mathcal{Q}=\varnothing$. Next, it returns $p{p}_{\mathsf{F}}$ and $v{k}_{\mathsf{F}}$ to $\mathcal{A}$.

2. 

Over the course of the experiment, $\mathcal{A}$ is allowed to adaptively make signing oracle queries in the following form:

• $\mathcal{A}$ sends a message $m_j\in \mathcal{M}$ and a shift $\Delta {\mathrm{w}}_j\in \mathcal{W}$ to $\mathcal{C}$.
• If $\mathsf{dis}(\Delta {\mathrm{w}}_j,0)>t$, $\mathcal{C}$ returns ⊥ (invalid shift). Else, $\mathcal{C}$ invokes ${\sigma }_{\mathsf{F},j}\leftarrow {\mathsf{Sign}}_{\mathsf{F}}(p{p}_{\mathsf{F}},\mathrm{w}+\Delta {\mathrm{w}}_j,m_j)$, adds $m_j$ to the query set $\mathcal{Q}$, and returns ${\sigma }_{\mathsf{F},j}$ to $\mathcal{A}$.

3. 

In the final phase, $\mathcal{A}$ outputs a forgery $(m^{\ast },{\sigma }_{\mathsf{F}}^{\ast })$. The experiment returns 1 if $m^{\ast }\notin \mathcal{Q}\wedge {\mathsf{Verify}}_{\mathsf{F}}(pp,vk,m^{\ast },{\sigma }_{\mathsf{F}}^{\ast })=1$; otherwise, it returns 0.

Remark 5. 

In our security model, the shift $\Delta {\mathrm{w}}_j$ between different samples of the same noisy source is adaptively chosen by the adversary $\mathcal{A}$. Note that, before the adversary submits a shift $\Delta w_j$, the adversary has received $p{p}_{\mathsf{F}},v{k}_{\mathsf{F}}$, and $({\sigma }_{\mathsf{F},1},\dots ,{\sigma }_{\mathsf{F},j-1})$. Since $v{k}_{\mathsf{F}}$ and $({\sigma }_{\mathsf{F},1},\dots ,{\sigma }_{\mathsf{F},j-1})$ are dependent on W, $\Delta w_j$ can be dependent on W. However, due to $\mathcal{A}$’s limited computational ability, the shift $\Delta {\mathrm{w}}_j$ cannot depend on the biometric data in an arbitrary manner. Nevertheless, our security model is still stronger than the security model in [12], which requires the errors between different samples to be independent of the noisy source.

Remark 6. 

From a theoretical perspective, the adversary-selected shift model subsumes the scenario of independent errors, provided that the adversary chooses the shifts randomly and independently. From a practical perspective, however, we argue that modeling only independent errors may not be sufficient to capture real-world threats. For instance, in biometric-based systems, an adversary could manipulate the sampling device to deterministically flip or fix certain bits of the biometric data. Consider, for example, the i-th bit of the biometric template:

• If the original bit is 1, it remains unchanged.
• If the original bit is 0, it is flipped to 1.

This type of deterministic bit manipulation cannot be captured by independent random-error models, as the error is not random, but depends on the biometric template. In contrast, our adversary-selected shift model is specifically designed to account for such scenarios, thereby providing a stronger and more realistic security guarantee in the presence of active and targeted distortions.

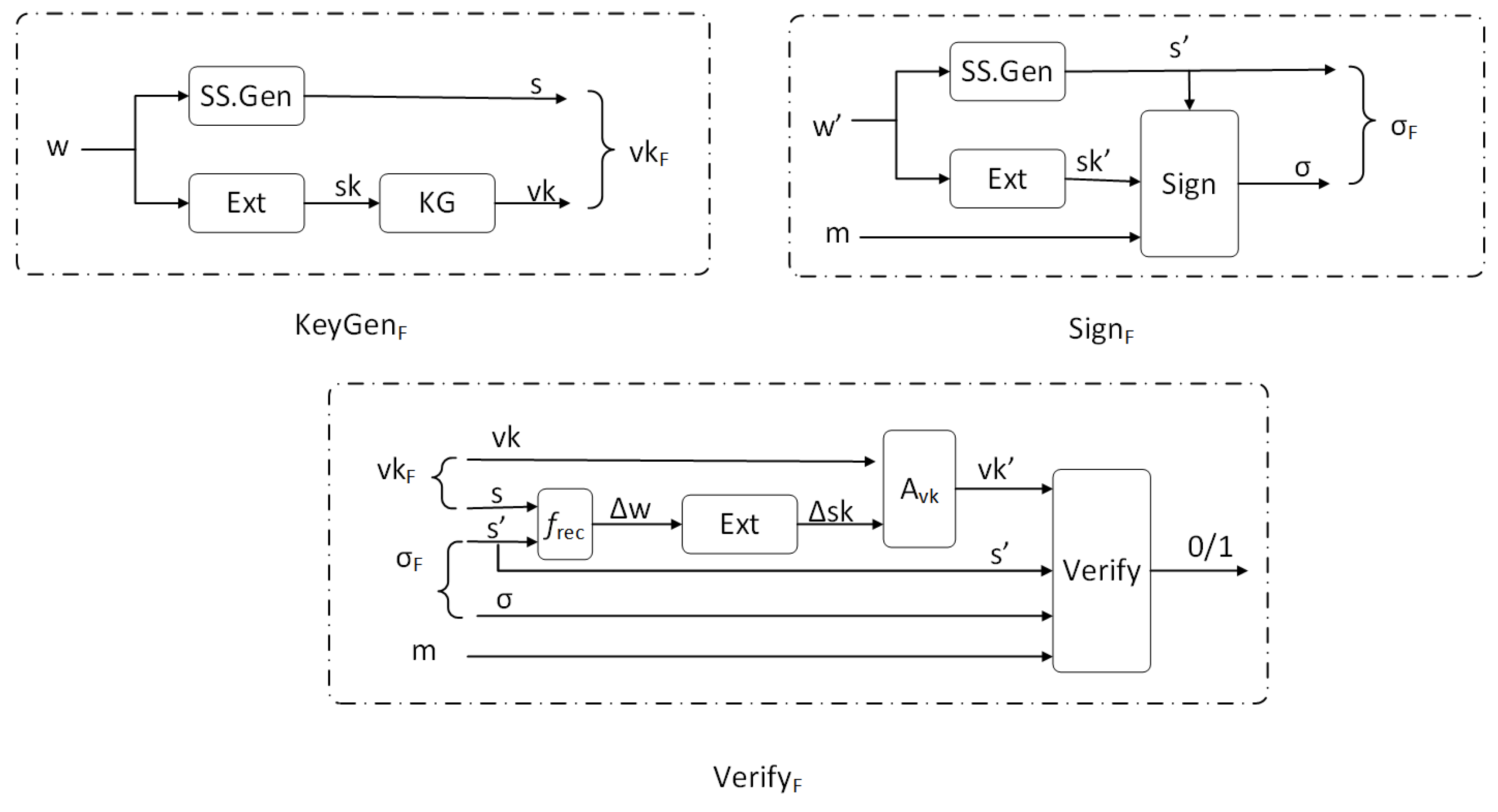
4. Construction of Fuzzy Signature

4.1. Construction

Our fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}=({\mathsf{Setup}}_{\mathsf{F}},{\mathsf{KeyGen}}_{\mathsf{F}},{\mathsf{Sign}}_{\mathsf{F}},{\mathsf{Verify}}_{\mathsf{F}})$, which is depicted in Figure 2, is composed of the following building blocks.

• A homomorphic $(\mathcal{W},\mathfrak{m},\tilde{\mathfrak{m}},t)$-secure sketch $\mathsf{SS}=(\mathsf{SS}.\mathsf{Gen},\mathsf{SS}.\mathsf{Rec})$ with a sketching space $\mathcal{S}$ that satisfies the error-recoverable property.
• A key-shift* secure and homomorphic $\mathsf{SIG}=(\mathsf{Setup},\mathsf{KeyGen},\mathsf{Sign},\mathsf{Verify})$ with a secret key space $\mathcal{SK}$ and a message space $\mathcal{M}\times \mathcal{S}$.
• A homomorphic average-case $(\mathcal{W},\tilde{\mathfrak{m}},\mathcal{SK},{\epsilon }_{ext})$-strong extractor $\mathsf{Ext}$ with seed space $\mathcal{I}$.

For better clarity and understanding of our construction, we have added Figure 3 to visually depict the key components and their interactions.

4.2. Correctness

Theorem 1. 

If $\mathsf{SS}$ is a homomorphic $(\mathcal{W},\mathfrak{m},\tilde{\mathfrak{m}},t)$-secure sketch with a sketch space $\mathcal{S}$ and the error-recoverable property, $\mathsf{Ext}$ is a homomorphic average-case $(\mathcal{W},\tilde{\mathfrak{m}},\mathcal{SK},{\epsilon }_{\mathrm{ext}})$-strong extractor with a seed space $\mathcal{I}$, and the signature scheme $\mathsf{SIG}$ is homomorphic with the secret key space $\mathcal{SK}$ and message space $\mathcal{M}\times \mathcal{S}$, then the constructed fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$ is correct.

Proof. 

To establish the correctness of the fuzzy signature scheme, we need to show that for any $m\in \mathcal{M}$ and $\mathrm{w},{\mathrm{w}}^{\prime }\in \mathcal{W}$, if $\mathsf{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$, the verification algorithm accepts the signature. Specifically, it holds that ${\mathsf{Verify}}_{\mathsf{F}}(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}},m,{\sigma }_{\mathsf{F}})=1$, where $p{p}_{\mathsf{F}}\leftarrow {\mathsf{Setup}}_{\mathsf{F}}\left(1^{\lambda }\right)$, $v{k}_{\mathsf{F}}\leftarrow {\mathsf{KeyGen}}_{\mathsf{F}}(p{p}_{\mathsf{F}},\mathrm{w})$, and ${\sigma }_{\mathsf{F}}\leftarrow {\mathsf{Sign}}_{\mathsf{F}}(p{p}_{\mathsf{F}},{\mathrm{w}}^{\prime },m)$.

Note that verification algorithm accepts the signature if, and only if, the underlying signature scheme successfully verifies. That is, $\mathsf{Verify}(pp,v{k}^{\prime },M,\sigma )=1$, where $\sigma \leftarrow \mathsf{Sign}(pp,{sk}^{\prime },M)$, ${\mathsf{s}}^{\prime }\leftarrow \mathsf{SS}.\mathsf{Gen}\left({\mathrm{w}}^{\prime }\right)$, ${sk}^{\prime }\leftarrow \mathsf{Ext}({\mathrm{w}}^{\prime },i)$, and $M\leftarrow (m,{\mathsf{s}}^{\prime })$.

By the correctness of the underlying signature $\mathsf{SIG}$, if $v{k}^{\prime }=\mathsf{KG}(pp,s{k}^{\prime })$, then $\mathsf{Verify}(pp,v{k}^{\prime },M,\sigma )=1$, since $\sigma \leftarrow \mathsf{Sign}(pp,{sk}^{\prime },M)$. So we need to prove that if $\mathsf{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$, $v{k}^{\prime }=\mathsf{KG}(pp,s{k}^{\prime })$.

Recall that $\Delta \mathrm{w}\leftarrow f_{rec}(\mathsf{s},{\mathsf{s}}^{\prime })$, $\Delta sk\leftarrow \mathsf{Ext}(\Delta \mathrm{w},i)$, $v{k}^{\prime }\leftarrow {\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta sk)$, where $\mathsf{s}\leftarrow \mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)$ and ${\mathsf{s}}^{\prime }\leftarrow \mathsf{SS}.\mathsf{Gen}\left({\mathrm{w}}^{\prime }\right)$. Due to the the error-recoverable property of the secure sketch $\mathsf{SS}$, for any $\mathrm{w},{\mathrm{w}}^{\prime }\in \mathcal{W}$, if $\mathsf{dis}(\mathrm{w},{\mathrm{w}}^{\prime })\le t$, it holds that $\Delta \mathrm{w}={\mathrm{w}}^{\prime }-\mathrm{w}=f_{rec}(\mathsf{s},{\mathsf{s}}^{\prime })$.

Due to the homomorphic property of $\mathsf{Ext}$, we have

$$s{k}^{\prime }=\mathsf{Ext}\left({\mathrm{w}}^{\prime }\right)=\mathsf{Ext}(\mathrm{w}+\Delta \mathrm{w})=\mathsf{Ext}\left(\mathrm{w}\right)+\mathsf{Ext}(\Delta \mathrm{w})=sk+\Delta sk.$$

Similarly, due to the homomorphic property of $\mathsf{SIG}$, it follows that

$$v{k}^{\prime }={\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta sk)=\mathsf{KG}(pp,sk+\Delta sk)=\mathsf{KG}(pp,s{k}^{\prime }).$$

As a result, the fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$ is correct. □

4.3. Security

Theorem 2. 

If $\mathsf{SS}$ is a homomorphic $(\mathcal{W},\mathfrak{m},\tilde{\mathfrak{m}},t)$-secure sketch with a sketching space $\mathcal{S}$ and it satisfies the error-recoverable property, $\mathsf{Ext}$ is a homomorphic average-case $(\mathcal{W},\tilde{\mathfrak{m}},\mathcal{SK},{\epsilon }_{ext})$-strong extractor with a seed space $\mathcal{I}$, $\mathsf{SIG}$ is a homomorphic signature scheme with a secret key space $\mathcal{SK}$, message space $\mathcal{M}\times \mathcal{S}$ and key-shift* security, then the construction of fuzzy signature ${\mathsf{SIG}}_{\mathsf{F}}$ in Figure 2 is a $(\mathcal{W},\mathcal{M},t)$-fuzzy signature satisfying $\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }$ security. In addition,

$${\mathsf{Adv}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)\le {\mathsf{Adv}}_{\mathsf{SIG}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right)+{\epsilon }_{ext}.$$

Proof. 

Let $\mathcal{A}$ be an arbitrary PPT adversary that attacks the $\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }$ security of fuzzy signature ${\mathsf{SIG}}_{\mathsf{F}}$. We will prove this theorem by a sequence of games, where the first game Game 0 is the original game ${\mathsf{Expt}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)$. For $\mathsf{i}\in \{0,1,2\}$, let ${\mathsf{S}}_{\mathsf{i}}$ denote the event that $\mathcal{A}$ wins (i.e., the experiment returns 1) in Game $\mathsf{i}$. Our goal is to show that ${\mathsf{Adv}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right):=Pr[{\mathsf{Expt}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)\Rightarrow 1]$ is negligible. Differences between adjacent games are highlighted with underline.

Game 0. 

Game 0 is identical to the $\mathfrak{m}$-EUF-${\mathrm{CMA}}^{\ast }$ experiment ${\mathsf{Expt}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathrm{EUF}-{\mathrm{CMA}}^{\ast }}\left(1^{\lambda }\right)$. Specifically, it proceeds as follows:

• Challenger $\mathcal{C}$ samples $i{\leftarrow }_{\$}\mathcal{I}$, invokes $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, sets $p{p}_{\mathsf{F}}\leftarrow (i,pp)$, then samples $\mathrm{w}\leftarrow W$, computes $\mathsf{s}\leftarrow \mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)$, $sk\leftarrow \mathsf{Ext}(\mathrm{w},i)$, $vk\leftarrow \mathsf{KG}(pp,sk)$, and sets $v{k}_{\mathsf{F}}\leftarrow (\mathsf{s},vk)$. Next, it initializes the query set $\mathcal{Q}=\varnothing$, which denotes the set of queries selected by $\mathcal{A}$. Afterwards, $\mathcal{C}$ returns $(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}})$ to $\mathcal{A}$.
• The adversary $\mathcal{A}$ may adaptively make signing queries.
  • $\mathcal{A}$ submits a message $m_j\in \mathcal{M}$ and a shift $\Delta {\mathrm{w}}_j\in \mathcal{W}$ to $\mathcal{C}$.
  • If $\mathsf{dis}(\Delta {\mathrm{w}}_j,0)>t$, $\mathcal{C}$ returns ⊥. Else, $\mathcal{C}$ parses $p{p}_{\mathsf{F}}=(\mathsf{i},pp)$, invokes ${\mathsf{s}}_j\leftarrow \mathsf{SS}.\mathsf{Gen}(\mathrm{w}+\Delta {\mathrm{w}}_j)$ and $s{k}_j\leftarrow \mathsf{Ext}(\mathrm{w}+\Delta {\mathrm{w}}_j,i)$, then sets $M_j\leftarrow (m_j,{\mathsf{s}}_j)$, invokes ${\sigma }_j\leftarrow \mathsf{Sign}(pp,s{k}_j,M_j)$, sets ${\sigma }_{\mathsf{F},j}\leftarrow ({\mathsf{s}}_j,{\sigma }_j)$, adds $m_j$ to the set $\mathcal{Q}$, and returns ${\sigma }_{\mathsf{F},j}$ to $\mathcal{A}$.
• Finally, $\mathcal{A}$ submits a forgery $(m^{\ast },{\sigma }_{\mathsf{F}}^{\ast })$. $\mathcal{C}$ parses $p{p}_{\mathsf{F}}=(i,pp)$, $v{k}_{\mathsf{F}}=(\mathsf{s},vk)$, ${\sigma }_{\mathsf{F}}^{\ast }=({\mathsf{s}}^{\ast },{\sigma }^{\ast })$, then sets $M^{\ast }\leftarrow (m^{\ast },{\mathsf{s}}^{\ast })$, and computes $\Delta {\mathrm{w}}^{\ast }\leftarrow f_{rec}({\mathsf{s}}^{\ast },\mathsf{s})$, $\Delta s{k}^{\ast }\leftarrow \mathsf{Ext}(\Delta {\mathrm{w}}^{\ast },i)$ and $v{k}^{\ast }\leftarrow {\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta s{k}^{\ast })$. If $m^{\ast }\notin \mathcal{Q}\wedge \mathsf{Verify}(pp,v{k}^{\ast },M^{\ast },{\sigma }^{\ast })=1$, the experiment outputs 1; else, it outputs 0.
  Obviously,

  $${\mathsf{Adv}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)=Pr[{\mathsf{Expt}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)\Rightarrow 1]=Pr\left[{\mathsf{S}}_0\right].$$

  (2)

Game 1. 

This game behaves equivalently to Game 0, apart from some conceptual changes. More precisely,

• The adversary $\mathcal{A}$ may adaptively make signing queries.
  • $\mathcal{A}$ submits a message $m_j\in \mathcal{M}$ and a shift $\Delta {\mathrm{w}}_j\in \mathcal{W}$ to $\mathcal{C}$.
  • If $\mathsf{dis}(\Delta {\mathrm{w}}_j,0)>t$, $\mathcal{C}$ returns ⊥. Else, $\mathcal{C}$ parses $p{p}_{\mathsf{F}}=(\mathsf{i},pp)$, invokes ${\mathsf{s}}_j\leftarrow \mathsf{s}+\mathsf{SS}.\mathsf{Gen}(\Delta {\mathrm{w}}_j)$ and $s{k}_j\leftarrow sk+\mathsf{Ext}(\Delta {\mathrm{w}}_j,i)$, then sets $M_j\leftarrow (m_j,{\mathsf{s}}_j)$, invokes ${\sigma }_j\leftarrow \mathsf{Sign}(pp,s{k}_j,M_j)$, sets ${\sigma }_{\mathsf{F},j}\leftarrow ({\mathsf{s}}_j,{\sigma }_j)$, adds $m_j$ to the set $\mathcal{Q}$, and returns ${\sigma }_{\mathsf{F},j}$ to $\mathcal{A}$.

Lemma 3. 

$Pr\left[{\mathsf{S}}_0\right]=Pr\left[{\mathsf{S}}_1\right]$.

Proof. 

Due to the homomorphic property of $\mathsf{Ext}$, it follows that

$$s{k}_j=\mathsf{Ext}(\mathrm{w}+\Delta {\mathrm{w}}_j,i)=\mathsf{Ext}(\mathrm{w},i)+\mathsf{Ext}(\Delta {\mathrm{w}}_j,i)=sk+\mathsf{Ext}(\Delta {\mathrm{w}}_j,i).$$

Similarly, due to the homomorphic property of $\mathsf{SS}$, it follows that

$${\mathsf{s}}_j=\mathsf{SS}.\mathsf{Gen}(\mathrm{w}+\Delta {\mathrm{w}}_j)=\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)+\mathsf{SS}.\mathsf{Gen}(\Delta {\mathrm{w}}_j)=\mathsf{s}+\mathsf{SS}.\mathsf{Gen}(\Delta {\mathrm{w}}_j).$$

Therefore, in both games, the signing key $s{k}_j$ and the sketch ${\mathsf{s}}_j$ used in response to each query are computed correctly according to the homomorphic property. Since all oracle responses are identically distributed in ${\mathsf{Game}}_0$ and ${\mathsf{Game}}_1$, it follows that $Pr\left[{\mathsf{S}}_0\right]=Pr\left[{\mathsf{S}}_1\right]$. The lemma is thus established. □

Game 2. 

This game is identical to Game 1, except that in step 1, $sk$ is uniformly chosen from $\mathcal{SK}$ other than $sk\leftarrow \mathsf{Ext}(\mathrm{w},i)$. More specifically,

• Challenger $\mathcal{C}$ samples $i{\leftarrow }_{\$}\mathcal{I}$, invokes $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, sets $p{p}_{\mathsf{F}}\leftarrow (i,pp)$, then samples $\mathrm{w}\leftarrow W$, computes $\mathsf{s}\leftarrow \mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)$, randomly chooses $sk{\leftarrow }_{\$}\mathcal{SK}$, computes $vk\leftarrow \mathsf{KG}(pp,sk)$, and sets $v{k}_{\mathsf{F}}\leftarrow (\mathsf{s},vk)$. Next, it initializes the query set $\mathcal{Q}=\varnothing$, which denotes the set of queries selected by $\mathcal{A}$. Afterwards, $\mathcal{C}$ returns $(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}})$ to $\mathcal{A}$.

Lemma 4. 

$|Pr\left[{\mathsf{S}}_1\right]-Pr\left[{\mathsf{S}}_2\right]|\le {\epsilon }_{ext}$.

Proof. 

Note that $H_{\infty }\left(W\right)\ge \mathfrak{m}$; by the security of the $(\mathcal{W},\mathfrak{m},\tilde{\mathfrak{m}},t)$-secure sketch, we have ${\tilde{H}}_{\infty }\left(W\right|\mathsf{SS}\left(W\right)\ge \tilde{\mathfrak{m}}$. Since $\mathsf{Ext}$ is a average-case $(\mathcal{W},\tilde{\mathfrak{m}},\mathcal{SK},{\epsilon }_{ext})$-strong extractor with a seed space $\mathcal{I}$, then we have

$$\mathrm{SD}((\mathsf{Ext}(\mathrm{w},i),i,\mathsf{s}=\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)),(u,i,\mathsf{s}=\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)))\le {\epsilon }_{ext},$$

where $u{\leftarrow }_{\$}\mathcal{SK}$.

Next we show that if there exists an adversary $\mathcal{A}$ that the difference between the probability of $\mathcal{A}$ winning in Game 1 and the probability of $\mathcal{A}$ winning in Game 2 is non-negligible, then we can construct an algorithm $\mathcal{B}$ that can distinguish $\left(\mathsf{Ext}\right(\mathrm{w},i),i,\mathsf{s}=\mathsf{SS}.\mathsf{Gen}(\mathrm{w}\left)\right)$ and $(u,i,\mathsf{s}=\mathsf{SS}.\mathsf{Gen}(\mathrm{w}\left)\right)$ with a non-negligible advantage. Assume that $\mathcal{B}$ is given $(d,i,\mathsf{s})$, where d is either $\mathsf{Ext}(\mathrm{w},i)$ or an element $u{\leftarrow }_{\$}\mathcal{SK}$. The aim of $\mathcal{B}$ is to tell which case it is. Adversary $\mathcal{B}$ proceeds as follows:

• $\mathcal{B}$ invokes $pp\leftarrow \mathsf{Setup}\left(1^{\lambda }\right)$, sets $p{p}_{\mathsf{F}}\leftarrow (i,pp)$, then sets $sk=d$, computes $vk\leftarrow \mathsf{KG}(pp,sk)$, and sets $v{k}_{\mathsf{F}}\leftarrow (\mathsf{s},vk)$. Next, it initializes the query set $\mathcal{Q}=\varnothing$, which denotes the set of queries selected by $\mathcal{A}$. Afterwards, $\mathcal{C}$ returns $(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}})$ to $\mathcal{A}$.
• $\mathcal{A}$ may adaptively interact with the signing oracle in the following manner.
  • $\mathcal{A}$ submits a message $m_j\in \mathcal{M}$ and a shift $\Delta {\mathrm{w}}_j\in \mathcal{W}$ to $\mathcal{B}$.
  • If $\mathsf{dis}(\Delta {\mathrm{w}}_j,0)>t$, $\mathcal{B}$ returns ⊥. Else, $\mathcal{B}$ parses $p{p}_{\mathsf{F}}=(i,pp)$, invokes ${\mathsf{s}}_j\leftarrow \mathsf{s}+\mathsf{SS}.\mathsf{Gen}(\Delta {\mathrm{w}}_j)$ and $s{k}_j\leftarrow sk+\mathsf{Ext}(\Delta {\mathrm{w}}_j,i)$, then sets $M_j\leftarrow (m_j,{\mathsf{s}}_j)$, invokes ${\sigma }_j\leftarrow \mathsf{Sign}(pp,s{k}_j,M_j)$, sets ${\sigma }_{\mathsf{F},j}\leftarrow ({\mathsf{s}}_j,{\sigma }_j)$, adds $m_j$ to the set $\mathcal{Q}$, and returns ${\sigma }_{\mathsf{F},j}$ to $\mathcal{A}$.
• In the finalization phase, $\mathcal{A}$ outputs a forgery $(m^{\ast },{\sigma }_{\mathsf{F}}^{\ast })$. $\mathcal{B}$ parses $p{p}_{\mathsf{F}}=(i,pp)$, $v{k}_{\mathsf{F}}=(\mathsf{s},vk)$, ${\sigma }_{\mathsf{F}}^{\ast }=({\mathsf{s}}^{\ast },{\sigma }^{\ast })$, then sets $M^{\ast }\leftarrow (m^{\ast },{\mathsf{s}}^{\ast })$, and computes $\Delta {\mathrm{w}}^{\ast }\leftarrow f_{rec}({\mathsf{s}}^{\ast },\mathsf{s})$, $\Delta s{k}^{\ast }\leftarrow \mathsf{Ext}(\Delta {\mathrm{w}}^{\ast },i)$, and $v{k}^{\ast }\leftarrow {\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta s{k}^{\ast })$. If $m^{\ast }\notin \mathcal{Q}\wedge \mathsf{Verify}(pp,v{k}^{\ast },M^{\ast },{\sigma }^{\ast })=1$, $\mathcal{B}$ returns 1; else, $\mathcal{B}$ returns 0.

If $d=\mathsf{Ext}(\mathrm{w},i)$, then $\mathcal{B}$ accurately simulates Game 1 for $\mathcal{A}$; if $d=u$, where $u{\leftarrow }_{\$}\mathcal{SK}$, then $\mathcal{B}$ perfectly simulates Game 2 for $\mathcal{A}$. As a result, we have

$$|Pr\left[{\mathsf{S}}_1\right]-Pr\left[{\mathsf{S}}_2\right]|\le \mathrm{SD}((\mathsf{Ext}(\mathrm{w},i),i,\mathsf{s}),(u,i,\mathsf{s}))\le {\epsilon }_{ext}.$$

The lemma follows. □

Lemma 5 

$|Pr\left[{\mathsf{S}}_2\right]|\le {\mathsf{Adv}}_{\mathsf{SIG}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right).$

Proof. 

We prove this lemma by showing that if there exists a PPT adversary $\mathcal{A}$ who wins in Game 2, then we can construct a PPT adversary $\mathcal{B}$ who can win in the key-shift* experiment of the underlying signature $\mathsf{SIG}$.

• Upon receiving $(pp,vk)$ from its key-shift* challenger, $\mathcal{B}$ samples $i{\leftarrow }_{\$}\mathcal{I}$, $\mathrm{w}\leftarrow W$, then calculates $\mathsf{s}=\mathsf{SS}.\mathsf{Gen}\left(\mathrm{w}\right)$, sets $p{p}_{\mathsf{F}}\leftarrow (i,pp),v{k}_{\mathsf{F}}\leftarrow (\mathsf{s},vk)$, and returns $(p{p}_{\mathsf{F}},v{k}_{\mathsf{F}})$ to adversary $\mathcal{A}$.
• When $\mathcal{A}$ makes a signing query on $(m_j,\Delta {\mathrm{w}}_j)\in \mathcal{M}\times \mathcal{W}$, $\mathcal{B}$ responds to $\mathcal{A}$’s query in the following manner:
  • If $\mathsf{dis}(\Delta {\mathrm{w}}_j,0)>t$, $\mathcal{B}$ returns ⊥. Else, $\mathcal{B}$ computes $\Delta s{k}_j\leftarrow \mathsf{Ext}(\Delta {\mathrm{w}}_j,i)$ and ${\mathsf{s}}_j=\mathsf{s}+\mathsf{SS}.\mathsf{Gen}(\Delta {\mathrm{w}}_j)$, sets $M_j=(m_j,{\mathsf{s}}_j)$, and sends $(M_j,\Delta s{k}_j)$ to its key-shift* challenger.
  • Upon receiving ${\sigma }_j$ from its key-shift* challenger, $\mathcal{B}$ sets ${\sigma }_{\mathsf{F},j}=({\mathsf{s}}_j,{\sigma }_j)$ and returns ${\sigma }_{\mathsf{F},j}$ to $\mathcal{A}$.
• In the finalization phase, $\mathcal{A}$ outputs a forgery $(m^{\ast },{\sigma }_{\mathsf{F}}^{\ast })$ to $\mathcal{B}$. $\mathcal{B}$ parses ${\sigma }_{\mathsf{F}}^{\ast }=({\mathsf{s}}^{\ast },{\sigma }^{\ast })$, sets $M^{\ast }\leftarrow (m^{\ast },{\mathsf{s}}^{\ast })$, computes $\Delta {\mathrm{w}}^{\ast }\leftarrow f_{rec}({\mathsf{s}}^{\ast },\mathsf{s})$ and $\Delta s{k}^{\ast }\leftarrow \mathsf{Ext}(\Delta {\mathrm{w}}^{\ast },i)$, submits $(M^{\ast },{\sigma }^{\ast })$ and a shift $\Delta s{k}^{\ast }$ to its challenger, and returns what its challenger returns.

It is obvious that $\mathcal{B}$ perfectly simulates Game 2 for $\mathcal{A}$. As a result, if $\mathcal{A}$ wins in Game 2, then $\mathcal{B}$ wins the key-shift* experiment. Consequently,

$$|Pr\left[{\mathsf{S}}_2\right]|\le {\mathsf{Adv}}_{\mathsf{SIG}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right).$$

□

Taking Equation (2) and Lemmas 3–5 together, we have

$${\mathsf{Adv}}_{{\mathsf{SIG}}_{\mathsf{F}},\mathcal{A}}^{\mathfrak{m}-\mathsf{EUF}-{\mathsf{CMA}}^{\ast }}\left(1^{\lambda }\right)\le {\mathsf{Adv}}_{\mathsf{SIG}}^{\mathsf{key}-{\mathsf{shift}}^{\ast }}\left(1^{\lambda }\right)+{\epsilon }_{ext}.$$

Theorem 2 follows.

5. Instantiation

In this section, we instantiate the generic construction presented in Section 4 using the Waters signature scheme. We choose the Waters signature scheme for this instantiation as it is one of the few schemes that simultaneously supports both the homomorphic property and key-shift* security—two desirable features that are seldom found together in existing signature schemes. To this end, we first recall ${\mathsf{SIG}}_{\mathsf{Wat}}$, as depicted in Figure 4. Subsequently, we prove that ${\mathsf{SIG}}_{\mathsf{Wat}}$ is both homomorphic and key-shift* secure.

Waters [32] proved that the Waters signature scheme ${\mathsf{SIG}}_{\mathsf{Wat}}$ is EUF-CMA secure under the computational Diffie-Hellman (CDH) assumption in $\mathbb{G}$ (Further details regarding $\mathbb{G}$ can be found in Appendix C).

Theorem 3 

([32,33]). Suppose there exists a forger $\mathcal{A}$ that $(t,q,ϵ)$-breaks the EUF-CMA security of ${\mathsf{SIG}}_{\mathsf{Wat}}$. Then, there exists an algorithm $\mathcal{B}$$({ϵ}^{\prime },t^{\prime })$-solving the computational Diffie–Hellman problem in $\mathbb{G}$ in time $t^{\prime }\approx t$ with success probability ${ϵ}^{\prime }\ge ϵ·O\left({\displaystyle \frac{1}{\sqrt{\ell q}}}\right)$.

Lemma 6. 

${\mathsf{SIG}}_{\mathsf{Wat}}$ is homomorphic. More precisely, ${\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta sk)=vk·g^{\Delta sk},$${\mathsf{A}}_{\mathsf{Sign}}(pp,m,({\sigma }_1,{\sigma }_2),\Delta sk)=(h^{\Delta sk}·{\sigma }_1,{\sigma }_2).$

Proof. 

We now show that ${\mathsf{SIG}}_{\mathsf{Wat}}$ is homomorphic by demonstrating that it satisfies Definition 14. It is straightforward to see that ${\mathsf{SIG}}_{\mathsf{Wat}}$ has a simple key-generation process,

$$vk=\mathsf{KG}(pp,sk)=g^{sk}.$$

• Note that $sk{\leftarrow }_{\$}{\mathbb{Z}}_p.$ The signing key space $\mathcal{SK}={\mathbb{Z}}_p$, equipped with addition modulo p, constitutes an abelian group.
• Note that $\mathsf{KG}(pp,sk+\Delta sk)=g^{sk+\Delta sk}=g^{sk}·g^{\Delta sk}=vk·g^{\Delta sk}$, so there exsits a deterministic and efficient algorithm ${\mathsf{A}}_{\mathsf{vk}}$, such that

  $${\mathsf{A}}_{\mathsf{vk}}(pp,vk,\Delta sk)=vk·g^{\Delta sk}=\mathsf{KG}(pp,sk+\Delta sk).$$
• Given a message M and a fixed random number $r{\leftarrow }_{\$}{\mathbb{Z}}_p$, the signature $\sigma$ of M under signing key $sk$ with random number r is

  $$\sigma =({\sigma }_1=h^{sk}·{(u^{\prime }·\prod _{i\in \left[l\right]}{u}_i^{M_i})}^r,{\sigma }_2\leftarrow g^r).$$
  The signature $\tilde{\sigma }$ of M under signing key $sk+\Delta sk$ with the same random number r is

  $$\tilde{\sigma }=(\widetilde{{\sigma }_1}=h^{sk+\Delta sk}·{(u^{\prime }·\prod _{i\in \left[l\right]}{u}_i^{M_i})}^r,\widetilde{{\sigma }_2}\leftarrow g^r).$$
  Note that

  $$\widetilde{{\sigma }_1}=h^{sk+\Delta sk}·{(u^{\prime }·\prod _{i\in \left[l\right]}{u}_i^{M_i})}^r=h^{sk}·h^{\Delta sk}·{(u^{\prime }·\prod _{i\in \left[l\right]}{u}_i^{M_i})}^r=h^{\Delta sk}·{\sigma }_1,$$

  and

  $${\sigma }_2=\widetilde{{\sigma }_2}.$$
  So there exisits a deterministic and efficient algorithm ${\mathsf{A}}_{\mathsf{Sign}}$, such that

  $${\mathsf{A}}_{\mathsf{Sign}}(pp,m,({\sigma }_1,{\sigma }_2),\Delta sk)=(h^{\Delta sk}·{\sigma }_1,{\sigma }_2)=\mathsf{Sign}(pp,sk+\Delta sk,m,r).$$
  The lemma follows. □

It follows from Theorem 3 that ${\mathsf{SIG}}_{\mathsf{Wat}}$ achieves EUF-CMA security under the CDH assumption. Moreover, Lemma 6 demonstrates that ${\mathsf{SIG}}_{\mathsf{Wat}}$ possesses the homomorphic property. In addition, Lemma 2 states that any signature scheme that is both homomorphic and EUF-CMA secure also satisfies key-${\mathrm{shift}}^{\ast }$ security. Therefore, by combining Theorem 3, Lemma 6, and Lemma 2, we derive the following corollary.

Corollary 1. 

${\mathsf{SIG}}_{\mathsf{Wat}}$ is key-${\mathrm{shift}}^{\ast }$ secure under the computational Diffie–Hellman (CDH) assumption in $\mathbb{G}$.

We use the homomorphic average-case strong extractor $\mathsf{Ext}$ in Equation (1), the syndrome-based secure sketch introduced in Section 2.4, and the Waters signature scheme ${\mathsf{SIG}}_{\mathsf{Wat}}$ as fundamental components to instantiate the generic construction presented in Figure 2. The detailed construction is illustrated in Figure 5. This results in a fuzzy signature scheme ${\mathsf{SIG}}_{\mathsf{F}}$ that is secure under the CDH assumption over a bilinear group in the standard model. Moreover, the signing algorithm of this scheme does not require the verification key as extra input.

Corollary 2. 

The instantiation illustrated in Figure 5 constitutes a $(\mathcal{W},\mathcal{M},t)$-${\mathsf{SIG}}_{\mathsf{F}}$, for which $\mathfrak{m}$-EUF-${\mathrm{CMA}}^{\ast }$ security is established in the standard model, assuming the hardness of the CDH problem in bilinear groups.

6. Future Work

One main limitation of our scheme is its reliance on pairing operations, which may impact efficiency in practice. Constructing a more efficient fuzzy signature scheme—potentially based on alternative assumptions such as lattices or hash-based primitives—is an important direction for future work.

Moreover, while our security model allows the adversary to choose errors adaptively, designing a fuzzy signature scheme in which the errors can be arbitrarily correlated with the biometric data itself remains an open and challenging problem.