High Relative Accuracy for Corner Cutting Algorithms

Abstract

Corner cutting algorithms are important in computer-aided geometric design and they are associated to stochastic non-singular totally positive matrices. Non-singular totally positive matrices admit a bidiagonal decomposition. For many important examples, this factorization can be obtained with high relative accuracy. From this factorization, a corner cutting algorithm can be obtained with high relative accuracy. Illustrative examples are included.

1. Introduction

Bidiagonal decompositions of a matrix arise in two apparently separate fields of mathematics: in total positivity theory and in computer-aided geometric design (CAGD). In the first case, the bidiagonal decomposition is a remarkable property of a non-singular totally positive matrix. Moreover, this decomposition provides a parametrization of the matrix that has been the starting point for the construction of algorithms with high relative accuracy (see [1,2,3,4,5,6]). In fact, if one knows the bidiagonal decomposition of a non-singular totally positive matrix, then one can construct such algorithms for the computation of all eigenvalues and singular values of the matrix and also to calculate the inverse (see also [7]) and the solution of some linear systems.

High relative accuracy (HRA) is a very desirable goal in numerical analysis and it can be assured when the subtractions in the algorithm only involve initial data (see [8]). The mentioned parameters of the bidiagonal decomposition come from an elimination procedure known as Neville elimination. But this procedure uses, in fact, subtractions, so that an alternative method is usually necessary to obtain the parameters of the bidiagonal decomposition with HRA.

In CAGD, decompositions of a matrix also play a crucial role. In fact, they are associated with the main family of algorithms in this field, which are called corner cutting algorithms (see [9,10,11,12]). For instance, evaluation algorithms and reduction and elevation degree algorithms are corner cutting algorithms. The matrix associated with these algorithms is totally positive as well as stochastic, and all bidiagonal factors of the decomposition are also stochastic matrices.

In [13] it was shown that, if a corner cutting algorithm is known with high relative accuracy, then the bidiagonal decomposition of the corresponding matrix can also be obtained with high relative accuracy. Here, the more practical converse question is considered. Let us assume that the bidiagonal decomposition of a given stochastic matrix is known. This has been achieved with many important classes of matrices. Then, it is proved that the corresponding corner cutting algorithm can also be obtained with high relative accuracy.

The layout of this paper is as follows. In Section 2, totally positive matrices and bidiagonal decompositions are introduced, relating them to Neville elimination. Section 3 is devoted to recall some basic facts concerning high relative accuracy. Section 4 deals with corner cutting algorithms and relates them with stochastic non-singular totally positive matrices. Section 5 proves the result mentioned above, which provides the parameters for corner cutting algorithms with high relative accuracy. Section 6 includes some illustrative examples and shows applications to curve evaluation. Finally, Section 7 summarizes the main conclusions of this paper.

2. Totally Positivity and Bidiagonal Decompositions

A matrix is called totally positive (TP) when all its minors are non-negative. They are often called totally non-negative matrices (see [14,15]). This class of matrices has relevance in many fields like approximation theory, statistics, mechanics, economics, combinatorics, biology, computer-aided geometry design, lie group theory, or graph theory (see [14,16,17,18,19]).

One of the properties of non-singular matrices TP with more computational advantages is given by their following bidiagonal decomposition, although this property can be defined for more general matrices. We say that an $n\times n$ non-singular matrix A has a bidiagonal decomposition $\mathcal{BD}\left(A\right)$ when it can be expressed in the following form:

$$A=L^{\left(1\right)}\cdots L^{(n-1)}D{U}^{(n-1)}\cdots U^{\left(1\right)},$$

(1)

where $D=diag(d_1,\dots ,d_n)$, and, for $k=1,\dots ,n-1$, $L^{\left(k\right)}$ and $U^{\left(k\right)}$ are unit diagonal lower and upper bidiagonal matrices, respectively, with off-diagonal entries $l_i^{\left(k\right)}:={\left(L^{\left(k\right)}\right)}_{i+1,i}$ and $u_i^{\left(k\right)}:={\left(U^{\left(k\right)}\right)}_{i,i+1}$, $(i=1,\dots ,n-1)$ satisfying

• $d_i\ne 0$ for all i,
• $l_i^{\left(k\right)}=u_i^{\left(k\right)}=0$ for $i<n-k$,
• $l_i^{\left(k\right)}=0\Rightarrow l_{i+s}^{(k-s)}=0$ and $u_i^{\left(k\right)}=0\Rightarrow u_{i+s}^{(k-s)}=0$, for $s=1,2,\dots ,k-1$.

Therefore, the bidiagonal matrices of the bidiagonal decomposition $\mathcal{BD}\left(A\right)$ have the following form:

$$L^{\left(k\right)}=\left(\begin{array}{ccccccc}1& & & & & & \\ 0& 1& & & & & \\ & \ddots & \ddots & & & & \\ & & 0& 1& & & \\ & & & l_{n-k}^{\left(k\right)}& 1& & \\ & & & & \ddots & \ddots & \\ & & & & & l_{n-1}^{\left(k\right)}& 1\end{array}\right),U^{\left(k\right)}=\left(\begin{array}{ccccccc}1& 0& & & & & \\ & \ddots & \ddots & & & & \\ & & 1& 0& & & \\ & & & 1& u_{n-k}^{\left(k\right)}& & \\ & & & & \ddots & \ddots & \\ & & & & & 1& u_{n-1}^{\left(k\right)}\\ & & & & & & 1\end{array}\right),$$

where $k=1,\dots ,n-1$.

In general, the bidiagonal decomposition of a matrix is not unique. However, Proposition 2.2 in [20] guarantees that $\mathcal{BD}\left(A\right)$ is unique.

Proposition 1.

Let A be a non-singular matrix. If a bidiagonal decomposition $\mathcal{BD}\left(A\right)$ exists, then it is unique.

When the matrix A is TP, its bidiagonal decomposition $\mathcal{BD}\left(A\right)$ satisfies more specific conditions, which characterize non-singular matrices TP as shown by the following result. This result can be derived from Theorem 4.2 in [21].

Theorem 1.

An $n\times n$ non-singular matrix A is TP if and only if there exists a (unique) $\mathcal{BD}\left(A\right)$ such that

1. 

$d_i>0$ for all i;

2. 

$l_i^{\left(k\right)}\ge 0$, $u_i^{\left(k\right)}\ge 0$ for $1\le k\le n-1$ and $n-k\le i\le n-1$.

The next simple example illustrates the applications of Theorem 1.

Example 1.

Given the matrix

$$A=\left(\begin{array}{cc}1/2& 1/2\\ 1/3& 2/3\end{array}\right)$$

its $\mathcal{BD}\left(A\right)$ is given by

$$A=\left(\begin{array}{cc}1& 0\\ 2/3& 1\end{array}\right)\left(\begin{array}{cc}1/2& 0\\ 0& 1/3\end{array}\right)\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right),$$

so by Theorem 1 it is TP. Examples of higher dimensions can be seen in Section 6.

The representation $\mathcal{BD}\left(A\right)$ for a non-singular matrix TP A arises in the process of the complete Neville elimination (CNE), where the entries $l_i^{\left(k\right)}$, $u_i^{\left(k\right)}$ of the previous matrices coincide with the multipliers of the CNE and the entries $d_i$ with the diagonal pivots (see [21,22]).

The following section shows that $\mathcal{BD}\left(A\right)$ leads to many accurate computations with non-singular matrices TP.

3. High Relative Accuracy

Let us recall that an algorithm can be performed with high relative accuracy if it does not include subtractions (except of the initial data), that is, if it only includes products, divisions, sums (of numbers of the same sign), and subtractions of the initial data (cf. [8,23]). In case of an algorithm without any subtraction, it is called a subtraction free (SF) algorithm and it can be performed with HRA.

For a non-singular matrix TP, the non-trivial entries of the matrices in $\mathcal{BD}\left(A\right)$ (see (1)) have been considered in [4,5,6] as natural parameters associated with A in order to perform many linear algebra computations with A to HRA. In fact, if we know $\mathcal{BD}\left(A\right)$ with HRA, then we can compute with HRA the singular values of A, its eigenvalues, its inverse (using also [7]), or the solution of linear systems $Ax=b$ where b has alternating signs.

Moreover, for many subclasses of non-singular matrices TP it has been possible to obtain the bidiagonal decomposition $\mathcal{BD}\left(A\right)$ of their matrices A with HRA, so that the remaining mentioned linear algebra computations can also be obtained with HRA. Among these subclasses, we can mention (cf. [24,25,26]) the collocation matrices of the Bernstein basis of polynomials (also called Bernstein–Vandermonde matrices). Other subclasses of non-singular matrices TP for which this has also been possible are the collocation matrices of the Said–Ball basis of polynomials [27], the collocation matrices of rational bases using the Bernstein or the Said–Ball basis [28], the collocation matrices of the q-Bernstein basis [29], or the collocation matrices of the h-Bernstein basis [30]. All these mentioned bases are very useful in the field of computer-aided geometric design (see [9]). In the next section, we recall a crucial algorithms in this field.

4. Stochastic Matrices TP and Corner Cutting Algorithms

A matrix is call stochastic if it is non-negative and the entries of each row sum up to 1. We will pay special attention to the non-singular matrices TP that are also stochastic, because they are very important in CAGD. In fact, their bidiagonal factorization can lead to corner cutting algorithms, which form the most relevant family of algorithms in this subject. These algorithms have an important geometric interpretation. They start from a polygon and refine this polygon cutting its corners iterability. These algorithms, depending on how the corners are cut, can finish at a point, like the de Casteljau evaluation algorithm, or at another polygon. In this later case, one can have the elevation degree algorithms or some subdivision-type algorithms like the Chaikin algorithm (cf. [31]). In addition, corner cutting algorithms have very good stability properties. So let us now recall the definition of these algorithms.

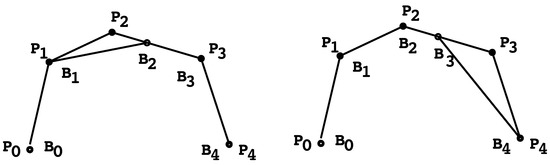
An elementary corner cutting is a transformation that maps any polygon $P_0\dots P_n$ into another polygon $B_0\dots B_n$ defined by one of the following ways:

$$\begin{array}{ccc}{B}_j\hfill & =\hfill & P_j,j\ne i,\hfill \\ B_i\hfill & =\hfill & (1-\lambda )P_i+\lambda P_{i+1},\hfill \end{array}$$

(2)

for some $i\in \{0,\dots ,n-1\}$, $0\le \lambda <1$, or 

$$\begin{array}{ccc}{B}_j\hfill & =\hfill & P_j,j\ne i,\hfill \\ B_i\hfill & =\hfill & (1-\lambda )P_i+\lambda P_{i-1},\hfill \end{array}$$

(3)

for some $i\in \left\{1,\dots ,n\right\}$, $0\le \lambda <1$ (see Figure 1). Then, a corner cutting algorithm is any composition of elementary corner cuttings (see [10]).

Figure 1. Elementary corner cuttings (2) and (3).

The matrix form of the elementary corner cutting given by (2) is

$${(B_0,\dots ,B_n)}^T=U\left({\lambda }_i\right){(P_0,\dots ,P_n)}^T,$$

where $U\left({\lambda }_i\right)$ is the non-singular, stochastic, bidiagonal and upper triangular matrix

$$U\left({\lambda }_i\right)=\left(\begin{array}{ccccccc}1& 0& & & & & \\ & 1& 0& & & & \\ & & \ddots & \ddots & & & \\ & & & 1-{\lambda }_i& {\lambda }_i& & \\ & & & & \ddots & \ddots & \\ & & & & & 1& 0\\ & & & & & & 1\end{array}\right).$$

Analogously to the previous case, a lower triangular matrix can also be used for the elementary corner cutting (3).

Therefore, a corner cutting algorithm is given by a product of matrices that are all bidiagonal, non-singular, TP, and stochastic. In particular, any upper triangular bidiagonal, non-singular, TP and stochastic matrix leads to a corner cutting algorithm by the composition

$$\left(\begin{array}{ccccccc}1-{\lambda }_0& {\lambda }_0& & & & & \\ & 1-{\lambda }_1& {\lambda }_1& & & & \\ & & \ddots & \ddots & & & \\ & & & 1-{\lambda }_i& {\lambda }_i& & \\ & & & & \ddots & \ddots & \\ & & & & & 1-{\lambda }_{n-1}& {\lambda }_{n-1}\\ & & & & & & 1\end{array}\right)=U\left({\lambda }_{n-1}\right)U\left({\lambda }_{n-2}\right)\cdots U\left({\lambda }_0\right).$$

Likewise, there exists an analogous factorization for the lower triangular case (3).

A corner cutting algorithm coming from a non-singular stochastic matrix TP can be expressed as a product of bidiagonal non-singular stochastic matrices TP, as can be seen by the following result, which corresponds to Theorem 4.5 in [21].

Theorem 2.

An $n\times n$ nonsingular matrix A is TP stochastic if and only if it can be decomposed as

$$A=F_{n-1}{F}_{n-2}\cdots F_1{G}_1\cdots G_{n-2}{G}_{n-1},$$

(4)

with

$$F_i=\left(\begin{array}{ccccccc}1& & & & & & \\ 0& 1& & & & & \\ & \ddots & \ddots & & & & \\ & & 0& 1& & & \\ & & & {\alpha }_{i+1,1}& 1-{\alpha }_{i+1,1}& & \\ & & & & \ddots & \ddots & \\ & & & & & {\alpha }_{n,n-i}& 1-{\alpha }_{n,n-i}\end{array}\right)$$

and

$$G_i=\left(\begin{array}{ccccccc}1& 0& & & & & \\ & \ddots & \ddots & & & & \\ & & 1& 0& & & \\ & & & 1-{\alpha }_{1,i+1}& {\alpha }_{1,i+1}& & \\ & & & & \ddots & \ddots & \\ & & & & & 1-{\alpha }_{n-i,n}& {\alpha }_{n-i,n}\\ & & & & & & 1\end{array}\right),$$

where, $\forall (i,j),$ $0\le {\alpha }_{i,j}<1$ satisfies

$$\begin{array}{c}{\alpha }_{ij}=0\Rightarrow {\alpha }_{hj}=0\forall h>ifori>j,\\ {\alpha }_{ij}=0\Rightarrow {\alpha }_{ik}=0\forall k>jfori<j.\end{array}$$

(5)

Under these conditions, the factorization is unique.

We now can back to the matrix to Example 1 to illustrate Theorem 2.

Example 2.

Let A the matrix given in Example 1. Then, its decomposition associated to a corner cutting algorithm is given by

$$A=\left(\begin{array}{cc}1/2& 1/2\\ 1/3& 2/3\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 2/3& 1/3\end{array}\right)\left(\begin{array}{cc}1/2& 1/2\\ 0& 1\end{array}\right).$$

Examples of higher dimensions will be presented in Section 6.

Remark 1.

A corner cutting algorithm corresponding to a stochastic matrix TP A as this of Theorem 2 can be expressed in compact form using the following matrix notation:

$$\mathcal{CCA}\left(A\right)=\left(\begin{array}{ccccc}1& {\alpha }_{1,2}& \dots & \dots & {\alpha }_{1,n}\\ {\alpha }_{2,1}& 1& \ddots & & ⋮\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ ⋮& & \ddots & \ddots & {\alpha }_{n-1,n}\\ {\alpha }_{n,1}& \dots & \dots & {\alpha }_{n,n-1}& 1\end{array}\right).$$

With an analogous distribution to that of the off-diagonal entries of the compact form of the corner cutting algorithm $\mathcal{CCA}\left(A\right)$, we can define the compact form of the bidiagonal decomposition $\mathcal{BD}\left(A\right)$, but including in the main diagonal the diagonal pivots of the CNE of A (see Section 2 of [5]).

Observe that the restrictions for the ${\alpha }_{ij}$’s in Theorem 2 are imposed to assure the unicity of the decomposition, in the same way as the restrictions of zero entries in $\mathcal{BD}\left(A\right)$.

Many essential algorithms used in curve design, such as evaluation, subdivision, degree elevation, and knot insertion, are corner cutting algorithms (see [9,10]). In particular, it is well known that all bases mentioned in the previous section, which are useful in CAGD, have non-singular stochastic collocation matrices TP. Therefore, they satisfy the hypotheses of Theorem 2 and so it leads to an evaluation corner cutting algorithm for the simultaneous evaluation of $n+1$ points, as illustrated in Section 6.

5. Construction of Corner Cutting Algorithms with HRA

It has already been studied [13] how to obtain an accurate bidiagonal decomposition of a matrix A from a corner cutting algorithm. In this section, we consider the converse problem, that is, how to obtain with HRA the associated corner cutting algorithm if we start with an accurate bidiagonal decomposition $\mathcal{BD}\left(A\right)$ (which has been obtained in many important examples, as recalled in Section 3). The following result gives a constructive answer proving that, from an accurate $\mathcal{BD}\left(A\right)$, we can construct with HRA the corner cutting algorithm of the associated $n\times n$ non-singular stochastic matrix TP A.

Theorem 3.

Let A a non-singular stochastic matrix TP. If we know the entries of $D,L^{\left(k\right)},U^{\left(k\right)}$, for $k=1,2,\dots ,n-1$ from the bidiagonal decomposition $\mathcal{BD}\left(A\right)$ (1) with HRA, then we can compute a corner cutting algorithm associated to the matrix decomposition (4) with a SF algorithm and, hence, to HRA.

Proof. 

Since $U^{\left(1\right)}$ is non-singular and non-negative, its row sums are positive, and so we can rewrite $U^{\left(1\right)}$ as

$$U^{\left(1\right)}=D_1^{\left(U\right)}{\overline{U}}^{\left(1\right)},$$

where $D_1^{\left(U\right)}=diag\left({\sum }_{j=1}^n{u}_{1j}^{\left(1\right)},{\sum }_{j=1}^n{u}_{2j}^{\left(1\right)},\dots ,{\sum }_{j=1}^n{u}_{nj}^{\left(1\right)}\right)$ has positive diagonal entries, formed by the row sums of $U^{\left(1\right)}$. In addition, ${\overline{U}}^{\left(1\right)}$ is a stochastic matrix. Since $U^{\left(k\right)}$ for $k=2,3,\dots ,n-1$ is non-singular and non-negative, the previous process can be iterated obtaining

$$U^{\left(k\right)}{D}_{k-1}^{\left(U\right)}=D_k^{\left(U\right)}{\overline{U}}^{\left(k\right)},$$

where $D_k^{\left(U\right)}$ is the diagonal matrix whose i-th diagonal entry is the sum of the entries in the i-th row of the matrix $U^{\left(k\right)}{D}_{k-1}^{\left(U\right)}$. Since this matrix is non-negative and non-singular, the diagonal entries of $D_k^{\left(U\right)}$ are positive. Moreover, ${\overline{U}}^{\left(k\right)}$ are stochastic matrices, for $k=2,3,\dots ,n-1$. After iterating this process, we obtain

$$A=L^{\left(1\right)}\cdots L^{(n-1)}\underset{=:\overline{D}}{\underbrace{D{D}_{n-1}^{\left(U\right)}}}{\overline{U}}^{(n-1)}\cdots {\overline{U}}^{\left(1\right)}=L^{\left(1\right)}\cdots L^{(n-1)}\overline{D}{\overline{U}}^{(n-1)}\cdots {\overline{U}}^{\left(1\right)}.$$

Now, since $L^{(n-1)}\overline{D}$ is non-singular and non-negative, its row sums are positive, and it can be expressed by

$$L^{(n-1)}\overline{D}=D_{n-1}^{\left(L\right)}{\overline{L}}^{(n-1)},$$

where ${\overline{L}}^{(n-1)}$ is an stochastic matrix. Iterating this procedure the following factorization of A is obtained by

$$A=D_1^{\left(L\right)}{\overline{L}}^{\left(1\right)}\cdots {\overline{L}}^{(n-1)}{\overline{U}}^{(n-1)}\cdots {\overline{U}}^{\left(1\right)},$$

(6)

where $D_1^{\left(L\right)}$ is a diagonal non-negative matrix. Taking into account that the matrices A, ${\overline{L}}^{\left(k\right)}$ and ${\overline{U}}^{\left(k\right)}$ are stochastic, we have

$$Ae=e,{\overline{L}}^{\left(k\right)}e=e\mathrm{and}{\overline{U}}^{\left(k\right)}e=e,$$

where $e={(1,\dots ,1)}^T$. From (6) and using the previous formulas, we can write

$$D_1^{\left(L\right)}e=D_1^{\left(L\right)}\underset{=e}{\underbrace{\left({\overline{L}}^{\left(1\right)}\cdots {\overline{L}}^{(n-1)}{\overline{U}}^{(n-1)}\cdots {\overline{U}}^{\left(1\right)}\right)e}}=Ae=e.$$

So, $D_1^{\left(L\right)}$ is a diagonal stochastic matrix. Hence, the identity matrix and factorization (6) must be as follows:

$$A={\overline{L}}^{\left(1\right)}\dots {\overline{L}}^{(n-1)}{\overline{U}}^{(n-1)}\cdots {\overline{U}}^{\left(1\right)},$$

(7)

where ${\overline{L}}^{\left(k\right)}$ (resp., ${\overline{U}}^{\left(k\right)}$) are stochastic and lower (resp., upper) bidiagonal matrices as in (4) of Theorem 2 (for $k=1,2,\dots ,n-1$, $F_k={\overline{L}}^{(n-k)}$ and $G_k={\overline{U}}^{(n-k)}$).

Taking into account that, for the construction of the corner cutting factorization (7), only products, quotients, and sum of non-negative numbers have been used, the corner cutting algorithm associated to (7) is an SF algorithm and so, it can be obtained with HRA.    □

Algorithm 1 shows a pseudocode of the recursive algorithm introduced in the proof of the previous theorem.

Algorithm 1 Computation of a corner cutting algorithm from a bidiagonal factorization

Require: $\mathcal{BD}\left(A\right)$ of a stochastic non-singular matrix TP A Ensure: ${\left({\alpha }_{i,j}\right)}_{1\le i,j\le n,i\ne j}$ entries of the corner cutting algorithm   $D_{aux}=I_n$   for  $k=1:n-1$  do     $U^{\left(k\right)}=U^{\left(k\right)}{D}_{aux}$     $aux=U^{\left(k\right)}e$     $D_{aux}=diag\left(aux\right)$     for $i=1:k$ do         ${\alpha }_{i,n-k+i}=U^{\left(K\right)}(n-k+i-1,n-k+i)/aux(n-k+i-1)$     end for   end for   $D_{aux}=D{D}_{aux}$   for  $k=1:n-1$  do     $L^{(n-k)}=L^{(n-k)}{D}_{aux}$     $aux=L^{(n-k)}e$     $D_{aux}=diag\left(aux\right)$     for $i=k+1:n$ do         ${\alpha }_{i,i-k}=L^{(n-k)}(i,i-1)/aux\left(i\right)$     end for   end for

6. Examples

This section presents examples illustrating the result and the algorithm of the previous section. For example, let us consider the basis of the space of polynomials of degree at most n given by the Bernstein polynomials of degree n:

$$b_i^n\left(x\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{n}{i}}\right)x^i{(1-x)}^{n-i},x\in [0,1],i=0,1,\dots ,n.$$

Example 3.

For the first example, let us consider the collocation matrix of the Bernstein basis for $n=3$ at the points $0,1/3,2/3,1$, which is given by

$$M_3:=M\left(\begin{array}{c}{b}_0^3,b_1^3,b_2^3,b_3^3\\ 0,1/3,2/3,1\end{array}\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ {\displaystyle \frac{8}{27}}& {\displaystyle \frac{4}{9}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{1}{27}}\\ {\displaystyle \frac{1}{27}}& {\displaystyle \frac{2}{9}}& {\displaystyle \frac{4}{9}}& {\displaystyle \frac{8}{27}}\\ 0& 0& 0& 1\end{array}\right).$$

This matrix is stochastic, non-singular, and totally positive. It can be checked that its bidiagonal decomposition is given in compact form by

$$\mathcal{BD}\left(M_3\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ {\displaystyle \frac{8}{27}}& {\displaystyle \frac{4}{9}}& {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{6}}\\ {\displaystyle \frac{1}{8}}& {\displaystyle \frac{3}{8}}& {\displaystyle \frac{1}{3}}& {\displaystyle \frac{2}{3}}\\ 0& 0& 0& 1\end{array}\right),$$

that is,

$$\begin{array}{c}\hfill M_3=\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & 1& \\ & & 0& 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & {\displaystyle \frac{1}{8}}& 1& \\ & & 0& 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ {\displaystyle \frac{8}{27}}& 1& & \\ & {\displaystyle \frac{3}{8}}& 1& \\ & & 0& 1\end{array}\right)·\\ \hfill ·\left(\begin{array}{cccc}1& & & \\ & {\displaystyle \frac{4}{9}}& & \\ & & {\displaystyle \frac{1}{3}}& \\ & & & 1\end{array}\right)·\left(\begin{array}{cccc}1& 0& & \\ & 1& {\displaystyle \frac{1}{2}}& \\ & & 1& {\displaystyle \frac{2}{3}}\\ & & & 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ & 1& 0& \\ & & 1& {\displaystyle \frac{1}{6}}\\ & & & 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & 1& 0\\ & & & 1\end{array}\right).\end{array}$$

Applying Algorithm 1 to the previous bidiagonal decomposition of $M_3$, the following corner cutting algorithm is obtained:

$$\begin{array}{c}\hfill M\left(\begin{array}{c}{b}_0^3,b_1^3,b_2^3,b_3^3\\ 0,1/3,2/3,1\end{array}\right)=\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & 1& \\ & & 0& 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & {\displaystyle \frac{1}{8}}& {\displaystyle \frac{7}{8}}& \\ & & 0& 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ {\displaystyle \frac{8}{27}}& {\displaystyle \frac{19}{27}}& & \\ & {\displaystyle \frac{19}{63}}& {\displaystyle \frac{44}{63}}& \\ & & 0& 1\end{array}\right)·\\ \hfill ·\left(\begin{array}{cccc}1& 0& & \\ & {\displaystyle \frac{12}{19}}& {\displaystyle \frac{7}{19}}& \\ & & {\displaystyle \frac{7}{11}}& {\displaystyle \frac{4}{11}}\\ & & & 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ & 1& 0& \\ & & {\displaystyle \frac{6}{7}}& {\displaystyle \frac{1}{7}}\\ & & & 1\end{array}\right)·\left(\begin{array}{cccc}1& & & \\ & 1& & \\ & & 1& 0\\ & & & 1\end{array}\right).\end{array}$$

Taking into account Remark 1, this bidiagonal representation of the corner cutting algorithm can be written in compact form as

$$\mathcal{CCA}\left(M_3\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ {\displaystyle \frac{8}{27}}& 1& {\displaystyle \frac{7}{19}}& {\displaystyle \frac{1}{7}}\\ {\displaystyle \frac{1}{8}}& {\displaystyle \frac{19}{63}}& 1& {\displaystyle \frac{4}{11}}\\ 0& 0& 0& 1\end{array}\right).$$

Example 4.

In this example, we consider the collocation matrix of the Bernstein basis of the space of polynomials of degree less than or equal to 7 at the points ${\{i/7\}}_{i=0}^7$. Let us denote it by $M_7$. It can be checked that its bidiagonal decomposition can be expressed in compact form as

$$\mathcal{BD}\left(M_7\right)=\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ \frac{279936}{823543}& \frac{46656}{117649}& \frac{1}{2}& \frac{5}{18}& \frac{1}{6}& \frac{1}{10}& \frac{1}{18}& \frac{1}{42}\\ \frac{78125}{279936}& \frac{109375}{279936}& \frac{3125}{16807}& \frac{2}{3}& \frac{2}{5}& \frac{6}{25}& \frac{2}{15}& \frac{2}{35}\\ \frac{16384}{78125}& \frac{24576}{78125}& \frac{7168}{15625}& \frac{256}{2401}& \frac{3}{4}& \frac{9}{20}& \frac{1}{4}& \frac{3}{28}\\ \frac{2187}{16384}& \frac{3645}{16384}& \frac{729}{2048}& \frac{567}{1024}& \frac{27}{343}& \frac{4}{5}& \frac{4}{9}& \frac{4}{21}\\ \frac{128}{2187}& \frac{256}{2187}& \frac{160}{729}& \frac{32}{81}& \frac{56}{81}& \frac{4}{49}& \frac{5}{6}& \frac{5}{14}\\ \frac{1}{128}& \frac{3}{128}& \frac{1}{16}& \frac{5}{32}& \frac{3}{8}& \frac{7}{8}& \frac{1}{7}& \frac{6}{7}\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right)$$

Applying Algorithm 1 to the previous bidiagonal decomposition, the following corner cutting algorithm is obtained:

$$\mathcal{CCA}\left(M_7\right)=\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ \frac{279936}{823543}& 1& \frac{217015}{543607}& \frac{53719}{217015}& \frac{8359}{53719}& \frac{799}{8359}& \frac{43}{799}& \frac{1}{43}\\ \frac{78125}{279936}& \frac{8493859375}{23742862339}& 1& \frac{592578372}{1270750247}& \frac{15807156}{49381531}& \frac{272388}{1317263}& \frac{2724}{22699}& \frac{12}{227}\\ \frac{16384}{78125}& \frac{445376}{1552041}& \frac{40664007904}{107878368199}& 1& \frac{703547955}{1493652451}& \frac{5096295}{15634399}& \frac{22455}{113251}& \frac{45}{499}\\ \frac{2187}{16384}& \frac{45009189}{221828125}& \frac{916951}{3157481}& \frac{1493652451}{3765658771}& 1& \frac{12765680}{28400079}& \frac{46320}{159571}& \frac{80}{579}\\ \frac{128}{2187}& \frac{14197}{131776}& \frac{3157481}{17496875}& \frac{224053}{796633}& \frac{9466693}{22912743}& 1& \frac{109350}{268921}& \frac{50}{243}\\ \frac{1}{128}& \frac{2059}{92583}& \frac{5599}{103456}& \frac{796633}{6795625}& \frac{28629}{124979}& \frac{268921}{660961}& 1& \frac{40}{121}\\ 0& 0& 0& 0& 0& 0& 0& 1\end{array}\right)$$

In computer-aided geometric design, the usual representation to work with polynomial curves is the Bézier representation. So a Bézier curve of degree n is given by

$$\gamma \left(t\right)=\sum _{i=0}^n{P}_i{b}_i^n\left(t\right),t\in [0,1],$$

where $P_i\in {\mathbb{R}}^k$, $k=2$ or 3, are called the control points of the curve. The usual algorithm in CAGD to evaluate a Bézier curve is the de Casteljau algorithm. This algorithm is a corner cutting algorithm; that is, all its steps are formed by linear convex combinations. Corner cutting algorithms are desirable algorithms since they are very stable from a numerical point of view. The de Casteljau algorithm evaluates a Bézier curve of degree n at a certain value $t\in [0,1]$ with a computational cost of $\mathcal{O}\left(n^2\right)$ elementary operations. So it evaluates the Bézier curve at a sequence of points $0\le t_0<t_1<\dots <t_n\le 1$ with a computational cost of $\mathcal{O}\left(n^3\right)$ elementary operations. Taking into account Examples 3 and 4, we can obtain another corner cutting algorithm to evaluate Bézier curves. Let us consider a Bézier function of degree n

$$f\left(t\right)=\sum _{i=0}^n{f}_i{b}_i^n\left(t\right),t\in [0,1],$$

where $f_i\in \mathbb{R}$ for $i=0,1,\dots ,n$. Then, we can consider the collocation matrix of the Bernstein basis of degree n at $0\le t_0<t_1<\dots <t_n\le 1$:

$$M_n:=M\left(\begin{array}{c}{b}_0^n,b_1^n,\dots ,b_n^n\\ t_0,t_1,\dots ,t_n\end{array}\right).$$

The previous matrix is stochastic, non-singular, and totally positive. By the results in [26], its bidiagonal decomposition can be computed to HRA. Then, using Theorem 3, from this bidiagonal decomposition, a corner cutting algorithm representation like this of Theorem 2 can be obtained for $M_n$:

$$M_n=F_n{F}_{n-2}\dots F_1{G}_1\dots G_{n-2}{G}_n.$$

Then, we can deduce that

$$\left(\begin{array}{c}f\left(t_0\right)\\ f\left(t_1\right)\\ ⋮\\ f\left(t_n\right)\end{array}\right)=M_n\left(\begin{array}{c}{f}_0\\ f_1\\ ⋮\\ f_n\end{array}\right)=F_n{F}_{n-2}\dots F_1{G}_1\dots G_{n-2}{G}_n\left(\begin{array}{c}{f}_0\\ f_1\\ ⋮\\ f_n\end{array}\right)$$

Hence, in fact we have a corner cutting algorithm to evaluate Bézier curves alternative to the de Casteljau algorithm. In addition, the new algorithm has a computational cost of $\mathcal{O}\left(n^2\right)$ elementary operations to evaluate the function at the $n+1$ points in contrast to the computational cost of $\mathcal{O}\left(n^3\right)$ elementary operations of the de Casteljau algorithm.

The two previous examples have shown how the algorithm provides a corner cutting algorithm from the bidiagonal decomposition of a non-singular stochastic matrix TP. So, in the next example, it will be illustrated that when Algorithm 1 is carried out in floating point arithmetic, the parameters of the corner cutting algorithm are obtained with high relative accuracy.

Example 5.

In Example 4, the corner cutting algorithm $\mathcal{CCA}\left(M_7\right)$ from $\mathcal{BD}\left(M_7\right)$ was obtained applying the algorithm with exact computations. Then, $\mathcal{CCA}\left(M_7\right)$ were computed in double precision floating point arithmetic with a Python (3.10.9) implementation of Algorithm 1. Then, the component-wise relative errors were calculated obtaining:

$$\left(\begin{array}{cccccccc}-& 0& 0& 0& 0& 0& 0& 0\\ 0& -& 0& 1.12\times {10}^{-16}& 1.78\times {10}^{-16}& 2.9\times {10}^{-16}& 3.87\times {10}^{-16}& 0\\ 0& 1.55\times {10}^{-16}& -& 0& 1.73\times {10}^{-16}& 2.68\times {10}^{-16}& 0& 0\\ 0& 1.93\times {10}^{-16}& 0& -& 1.18\times {10}^{-16}& 1.7\times {10}^{-16}& 1.4\times {10}^{-16}& 1.54\times {10}^{-16}\\ 0& 0& 1.91\times {10}^{-16}& 1.4\times {10}^{-16}& -& 1.23\times {10}^{-16}& 0& 0\\ 0& 0& 0& 0& 0& -& 1.37\times {10}^{-16}& 0\\ 0& 0& 1.28\times {10}^{-16}& 1.18\times {10}^{-16}& 1.21\times {10}^{-16}& 0& -& 0\\ 0& 0& 0& 0& 0& 0& 0& -\end{array}\right).$$

As it can be observed, all the parameters of the corner cutting algorithm are obtained with an error of the order of the unit roundoff of the double precision floating point arithmetic system. So, all the parameters are obtained with HRA as Theorem 3 states.

7. Conclusions

The bidiagonal decomposition with high relative accuracy is known for many non-singular matrices TP. If the non-singular matrix TP is also stochastic, then it provides a corner cutting algorithm. It is proved that, if we have the bidiagonal decomposition with high relative accuracy, then we can obtain the corner cutting algorithm through a SF algorithm, and so with high relative accuracy. Hence, the method presented in this paper provides a source for constructing corner cutting algorithms with high relative accuracy. Examples of its use as curve evaluation algorithms are included.