Mathematical Modeling of the Influence of Equilibrium Coefficient Variation on the Steady-State Transport of a Binary Electrolyte in the Cross-Section of a Desalination Channel

Abstract

This paper presents the first theoretical investigation of the effect of a variable equilibrium coefficient on the steady-state transport of a binary electrolyte in a desalination channel cross-section of the electrodialyzer. To address this problem, we developed a new mathematical model in the form of a boundary value problem for an extended system of stationary Nernst–Planck–Poisson equations. We obtained a numerical solution to this problem using the finite element method. Analysis of this solution revealed that the channel cross-section has a complex structure: it is divided into seven regions dominated by different processes, and, consequently, the solution to the boundary value problem behaves differently in each of them. Existing models of the diffusion layer or channel cross-section typically assume a constant equilibrium coefficient. In this paper, we demonstrated that in the channel cross-section, the velocity change corresponding to the equilibrium constant is related not only to the field strength but also to the magnitude of the space charge. In the space-charge region, in the boundary layers near the ion-exchange membranes, intense dissociation of water molecules occurs, and the higher the equilibrium coefficient, the more intense this dissociation is. We have shown that an internal boundary layer (recombination region) arises deep within the solution, associated with the recombination reaction of H+ and OH− ions. In this study, we found that with increasing equilibrium coefficient, fluxes increase, while with increasing fluxes, the electric field strength decreases proportionally, and equilibrium is reached. We demonstrate that by calibrating a single fitting parameter in the model, the simulation results can be matched to experimental data with high accuracy. Thus, our proposed model and its numerical solution provide a completely new understanding of the ion transport process in electromembrane systems, taking into account the influence of the dissociation/recombination reaction of water molecules.

1. Introduction

Currently, there is an acute shortage of clean water, more than 40% of the world’s population does not have access to clean water. Even more important is the problem of water scarcity in technological processes, as well as in agriculture [1,2,3]. The most effective method of solving this problem is electromembrane methods of water purification [4,5,6,7,8,9]. One of the promising directions is the use of electrodialysis machines, which are alternating concentration and desalination chambers separated by anion exchange and cation exchange membranes [10,11,12,13,14,15,16,17].

Let us consider the steady-state transport of binary salt ions, such as $NaCl$. The mathematical models for the diffusion layer [18] and the one-dimensional channel cross-section differ significantly. For instance, the diffusion layer model cannot be considered a submodel of the channel cross-section, although physically there are two diffusion layers in the channel cross-section, near the anion-exchange and cation-exchange membranes. Indeed, let us consider the diffusion layer near one of the membranes, for example, a cation-exchange membrane. The equations describing the mathematical models of ion transport in the diffusion layer and the channel cross-section are identical (1–4), as are the boundary conditions at the solution/cation-exchange membrane boundary at $x=H$. The boundary conditions of these models differ at $x=0$, since the physical processes at this point differ. In the channel cross-section, the anion-exchange membrane is located at point $x=0$, while for the diffusion layer, point $x=0$ represents the depth of the solution where the concentrations are known and the electroneutrality condition is satisfied. Diffusion layer models assume that the solution is perfectly mixed at point $x=0$, so the concentration of cations and anions is the same and corresponds to the initial solution concentration. Thus, transport in the diffusion layer retains some features of the two-dimensional model. When considering a channel cross-section, the fundamental assumption is that the solution is immobile. This leads to fundamental differences in the mathematical models of ion transport in the channel cross-section and in the diffusion layer. For example, under the natural assumption of ideal selectivity of ion-exchange membranes, the anion flux through the cation-exchange membrane is zero, and all current is carried by cations. The magnitude of this current can be arbitrary, depending on the potential drop at points $x=0$ and $x=H$ (Figure 1). In channel cross-section models, in addition to the anion current being zero, the cation current is also zero, since the anion-exchange membrane is also perfectly selective. Thus, the salt ion current in channel cross-section models is zero, unlike diffusion layer models, where the current can have an arbitrary value. Each model has its own advantages and disadvantages. For example, channel cross-section models allow one to consider the recombination/dissociation process in the extreme steady-state case, when the influence of salt ions is minimal, since the salt ion current is zero. Furthermore, the mathematical model of binary electrolyte transport in a channel cross-section provides a more detailed description of ion flows and interactions, allowing for complex geometric and physical conditions to be taken into account. This leads to increased prediction accuracy and process optimization compared to the diffusion layer model.

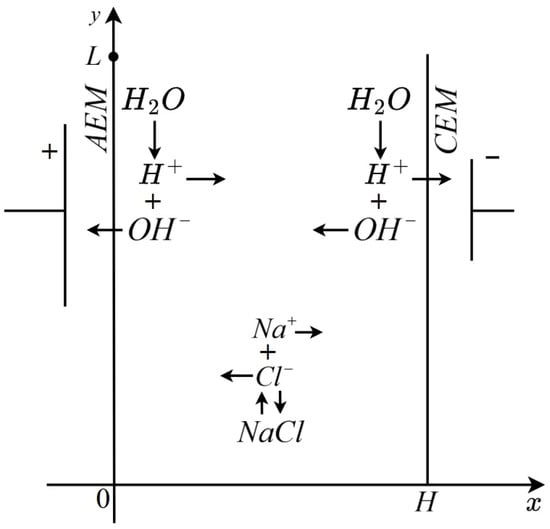
Figure 1. Scheme of the desalination channel and the simulated phenomena, the Ox axis is directed across the channel, at x = 0, the AEM is located, and at x = H-CEM, the Oy axis is directed along the channel, y = 0 is the entrance to the channel, y = L is the exit from the channel. A certain potential jump is applied to the system. OH⁻ ions formed near the anion exchange membrane are transferred through this membrane and do not participate in further transfer processes, H⁺ ions move deeper into the solution. A similar process occurs near the cation exchange membrane, and OH⁻ go towards H⁺ and recombine with them in the depth of the solution.

Water dissociation at interfaces and changes in the equilibrium coefficient are important for understanding the processes occurring during substance transfer through selective ion-exchange membranes. Changes in the rate coefficient of water molecule dissociation at interfaces (membrane/solution or membrane/membrane) can have several causes, as indicated in [19]. This paper examines the effect of an electric field on the equilibrium coefficient of the dissociation/recombination reaction of water molecules using a new mathematical model of steady-state salt ion transport in a channel cross-section, taking into account the dissociation/recombination reaction of water molecules, in contrast to work [20], where the equilibrium coefficient was assumed to be constant.

In the works of Onsager L. [19], Timashev S.F., and Sheldeshov N.V. [21,22], the change in the equilibrium coefficient is associated with the magnitude of the electric field strength. In some studies [18,20], in contrast to the above-mentioned studies, the change in the equilibrium coefficient is associated not simply with the magnitude of the electric field strength but with the magnitude of the space charge.

This is particularly relevant in monopolar membrane systems, where—unlike in bipolar systems—the space charge occupies a small yet macroscopic region at overlimiting current densities [23] and therefore it is necessary to take into account changes in the equilibrium coefficient for the spatial variable.

A change in the equilibrium coefficient, according to the proposed mathematical model, leads to a significant increase in the fluxes of $H^{+}$ and $O{H}^{-}$ ions. This leads to a local increase in the equilibrium coefficient, for example, in the quasi-equilibrium boundary layer region by a factor of 10–30, which corresponds in order of magnitude to experimental data [24].

The extended Nernst–Planck–Poisson (NPP) system has long been the cornerstone for modeling ion transport in membrane systems [25,26]. However, accurately capturing the phenomenon of water splitting at ion-exchange membranes, which becomes critical at overlimiting currents, requires going beyond the description of simple salt ion transport. The fundamental understanding of this process was laid by Onsager L. [19], who theorized that strong electric fields could enhance the dissociation of weak electrolytes like water by suppressing the recombination of $H^{+}$ and $O{H}^{-}$ ions.

This theory was successfully applied to model the dramatically enhanced water splitting observed in bipolar membranes (BPMs) [4,5,21,22]. In these systems, the electric field is concentrated in a sharp junction, and the dissociation rate constant $k_d$ is often expressed as an exponential function of the local electric field strength $E$.

In monopolar membrane systems, the situation is more complex. While high fields exist in the depletion boundary layers, the region of significant space charge—a direct consequence of concentration depletion—is also a key feature. Recent advanced models have begun to incorporate water dissociation. For instance, the work by Nikonenko V. et al. [24] provided crucial experimental evidence linking enhanced $H^{+}$ and $O{H}^{-}$ ions fluxes to the structure of the depleted diffusion layer. The model by Kovalenko A. et al. [20] represented a significant step forward by explicitly including water dissociation/recombination reactions in a electrodialysis model, though it assumed a constant equilibrium coefficient.

The pivotal consideration, which our present work introduces and explores, is that in monopolar systems, the primary driver for the local enhancement of water dissociation may not be the electric field alone, but the magnitude of the local space charge density. This concept is supported by the idea that the space charge itself can screen the Coulombic potential between the $H^{+}$ and $O{H}^{-}$ ions, facilitating their separation, as suggested by Onsager’s original work [19] and discussed in the context of membrane systems [23]. This leads to a functional dependence of the form $k_w=k_w(\rho )$.

Therefore, this study fills a critical gap by developing a model for the channel cross-section that incorporates a space-charge-dependent equilibrium coefficient. This allows us to move beyond the BPM-inspired field-dependent models and provide a more physically grounded description of water splitting in monopolar electrodialysis systems, offering a direct mechanistic link to the observed experimental fluxes [24].

2. The Mathematical Model of the Influence of the Dependence of the Dissociation Coefficient on the Magnitude of the Space Charge on the Stationary Transport of Salt Ions in the Channel Cross-Section

According to the concepts developed by Onsager L., Timashev S.F., Sheldeshov N.V. et al. [19,21,22] for bipolar membranes, the current density of $H^{+}$ ($O{H}^{-}$) ions generated in the membrane system is determined by an empirical formula, where the equilibrium coefficient exponentially depends on the strength of the external electric field.

In electrodialysis systems with monopolar membranes, few studies have been devoted to the study of this dependence [18,20].

There are considerations from which it follows that, in contrast to the above-mentioned works, in systems with monopolar membranes, the change in the equilibrium coefficient can be associated not simply with the magnitude of the electric field strength, but with the magnitude of the space charge; that is, $k_w(\rho )=k_{w_0}+b\left|\rho \right|$, where $k_{w_0}={\displaystyle \frac{k_d}{k_r}}(0)C_{H_{2}O}={10}^{-8}$, $\rho =F(C_1(x)-C_2(x)+C_3(x)-C_4(x))$ the value of the space charge at point $x$, $b$ is an adjustable parameter, $k_d$ dissociation coefficient, $k_r$ recombination coefficient, $C_i(x)$ as the concentrations, of the i-th ion, $C_{H_{2}O}$—water concentration, $F$ is Faraday’s constant. Let us denote $b_0=bF{C}_{H_{2}O}=\lambda C_{H_{2}O}$, where $\lambda =bF$ ($\lambda$ is a dimensionless quantity and, accordingly, has the dimensions of concentration); then we obtain $k_w(\rho )=k_{w_0}+\lambda {\displaystyle \sum _{i=1}^n{z}_i{C}_i}$. Thus, we obtain just one, dimensionless, adjustable parameter $\lambda$, which has a clear and simple physical meaning: the influence of the magnitude of the space charge on the increase in the dissociation rate of water molecules.

The linear dependence of the coefficient on the magnitude of the space charge is taken as a first approximation and in order to be able to find analytical solutions, see Section 4.2.

The dependence of ion flows on the magnitude of space charge was first mentioned in the work of V.V. Nikonenko et al. [24]. To explain the influence of the magnitude of space charge on the equilibrium coefficient, let us consider the process of increasing dissociation of water molecules near the anion-exchange membrane. In this region, the space charge is determined by the predominance of the concentration of $C{l}^{-}$ ions over the concentrations of all other ions. As is known, a water molecule is a dipole, at one end of which are located $H^{+}$ and $O{H}^{-}$. $C{l}^{-}$ ions surround the water molecule from the $H^{+}$ side, weakening (shielding) and breaking its bond with $O{H}^{-}$. As a result, the resulting free $O{H}^{-}$ ions are transferred unhindered through the anion-exchange membrane and do not participate in further processes, while $H^{+}$ ions move into the solution, and the higher the concentration of $C{l}^{-}$ ions, the greater the flow of $H^{+}$ ions. Thus, the greater the magnitude of the space charge, the more intense this process, which is in fact the electrolytic dissociation of water molecules, occurs; that is, the equilibrium coefficient kw depends on the magnitude of the space charge. This corresponds to the point of view of Onsager L., that the increase in the equilibrium coefficient is due to the gradual screening of the ion’s electric field by the surrounding space charge [2]. In the region of the space charge in the vicinity of the cation exchange membrane (CEM), similar processes occur, only the role of $C{l}^{-}$ ions is played by $N{a}^{+}$ or $K^{+}$ ions, $O{H}^{-}$ ions are injected into the solution, and $H^{+}$ ions are transferred through the CEM and do not participate in further transfer processes.

2.1. System of Equations

Under the above conditions, the steady-state transfer of salt ions for a 1:1 electrolyte into the channel cross-section, taking into account the space charge and the dissociation/recombination reaction, taking into account the dependence of the dissociation coefficient on the magnitude of the space charge, is described by the extended system of Nernst–Planck–Poisson equations [25].

Let us denote $\phi (x,\epsilon )$ as the potential, $j_i(x,\epsilon )$, $C_i(x,\epsilon )$, $D_i$ as the flux, concentrations, and diffusion coefficients of the i-th ion, respectively. In the steady-state case $j_1=j_2=0$ [25]. Therefore, the current carried by the salt ions is equal to zero, and, consequently, the total current $I=F{\displaystyle \sum _{i=1}^4{z}_i{j}_i}$ is equal to the current carried by the $H^{+}$ and $O{H}^{-}$ ions: $I_c=j_3-j_4$. Thus, the steady-state transport in the one-dimensional cross-section of the desalination channel can only be equilibrium with respect to the salt ions.

Thus, the system of equations has the form

$$-{\displaystyle \frac{d{j}_i}{dx}}+R_i=0, i=1,\dots ,4$$

(1)

$$j_i=-z_i{\displaystyle \frac{F}{RT}}{D}_i{C}_i{\displaystyle \frac{d\varphi }{dx}}-D_i{\displaystyle \frac{d{C}_i}{dx}}, i=1,\dots ,4$$

(2)

$${\displaystyle \frac{d^2\varphi }{d{x}^2}}=-{\displaystyle \frac{\rho }{{\epsilon }_r}}$$

(3)

$$R_3=R_4=k_d(\rho )C_{H_{2}O}-k_r{C}_3{C}_4=k_r(k_w(\rho )-C_3{C}_4)$$

(4)

$$z_1=1, z_2=-1, z_3=1, z_4=-1$$

Here, (1) represents the material balance equations; (2) are the Nernst–Planck equations for the fluxes of potassium or sodium ions ($i=1$), chloride ions ($C{l}^{-},\hspace{1em}i=2$), hydrogen ions ($H^{+},\hspace{1em}i=3$), and hydroxide ions ($O{H}^{-},\hspace{1em}i=4$); (3) is the Poisson equation for the electric potential; (4) are the formulas describing the dissociation/recombination reaction of water molecules; (5) is the current flow equation, which states that the current density $I$ through the cross-section of the desalination channel is determined by the ionic fluxes, i.e., it corresponds to the Faraday current density.

Here, ${\epsilon }_r$ is the dielectric permittivity of the solution, $R$ is the universal gas constant, $\varphi$ is the potential, $z_i$ charge numbers, T—absolute temperature of the solution, $R_i$—reaction speed, $E=-{\displaystyle \frac{d\varphi }{dx}}$ is the electric field strength, $k_r(0)=1.1\cdot {10}^8$ m³/s mol is the recombination rate constant, $k_d(0)=2\cdot {10}^{-5}$ is the dissociation rate constant of water molecules, and, consequently, $k_{w_0}={\displaystyle \frac{k_d}{k_r}}(0)C_{H_{2}O}={10}^{-8}$ mol² m⁻⁶ is the equilibrium coefficient (ionic product of water).

2.2. Boundary Conditions

At $x=0$:

$$C_2(0)=C_{2a},$$

(5)

$${\left.\left(-{\displaystyle \frac{F}{RT}}{C}_1{D}_1{\displaystyle \frac{\partial \phi }{\partial x}}-D_1{\displaystyle \frac{\partial C_1}{\partial x}}\right)\right|}_{x=0}=0,$$

(6)

$${\left.\left(-{\displaystyle \frac{F}{RT}}{C}_3{D}_3{\displaystyle \frac{\partial \varphi }{\partial x}}-D_3{\displaystyle \frac{\partial C_3}{\partial x}}\right)\right|}_{x=0}=j_{3a},$$

(7)

$${\displaystyle \frac{d{C}_4(0)}{dx}}=0,$$

(8)

$$\varphi (0)=d.$$

(9)

At $x=H$:

$$C_1(H)=C_{1k},$$

(10)

$${\left.\left({\displaystyle \frac{F}{RT}}{C}_2{D}_2{\displaystyle \frac{\partial \varphi }{\partial x}}-D_2{\displaystyle \frac{\partial C_2}{\partial x}}\right)\right|}_{x=H}=0,$$

(11)

$${\displaystyle \frac{d{C}_3(H)}{dx}}=0,$$

(12)

$${\left.\left({\displaystyle \frac{F}{RT}}{C}_4{D}_4{\displaystyle \frac{\partial \varphi }{\partial x}}-D_4{\displaystyle \frac{\partial C_4}{\partial x}}\right)\right|}_{x=H}=j_{4k},$$

(13)

$$\varphi (H)=0.$$

(14)

The concentrations of anions (5) and cations (10) at the membrane surfaces are determined by their exchange capacity, with the membranes assumed to be ideally selective (6), (11). It is assumed that in the surface layer of the membranes the generation of $H^{+}$ and $O{H}^{-}$ ions occurs, and these ions freely pass through the cation-exchange and anion-exchange membranes (8), (12), no longer participating in the subsequent transport processes. At the same time, from the surface of the anion-exchange membrane a flux of $H^{+}$ ions is injected into the solution, determined by condition (7), while from the surface of the cation-exchange membrane a flux of $O{H}^{-}$ ions is injected (13). The membrane surfaces are considered equipotential, and the potential jump is defined by relations (9), (14).

3. Analysis of the Numerical Solution

The finite element method was applied to obtain a numerical solution. To analyze the results, calculations were performed with a wide range of initial data, the fitting parameter $b$, and so on. The most representative results are presented below: in each figure, the results for $b=0$ are shown on the left, while those for $b=0.0001$ are generally shown on the right.

To analyze the results of the numerical solution, we will use the following functions:

• the charge distribution density normalized by Faraday’s constant ${\rho }_0={\displaystyle \frac{\rho }{F}}=C_1(x)-C_2(x)+C_3(x)-C_4(x)$,
• the equilibrium function $P_w=k_{w_0}+bF\left|C_1-C_2+C_3-C_4\right|-C_3{C}_4$, or $P_w=k_{w_0}+b_0\left|C_1-C_2+C_3-C_4\right|-C_3{C}_4$, where $b_0=bF$,
• the equilibrium coefficient $k_w(\rho )=k_{w_0}+b\left|\rho \right|$.

3.1. Concentration Distribution

As shown in Figure 2a,b, the qualitative behavior of the concentrations of all four ion species for $b=0$ and $b=0.0001$ is similar. Specifically, near the ion-exchange membranes, boundary layers ($U_A=[0,x_1)$, $U_K=(x_4,H]$) are observed where the concentrations of chloride ions $C{l}^{-}$ and hydrogen ions $H^{+}$ at the anion-exchange membrane ($x=0$), as well as sodium ions $N{a}^{+}$ and hydroxide ions $O{H}^{-}$ at the cation-exchange membrane ($x=H$), vary at an exponential rate. Beyond these layers, there are relatively large regions adjacent to the boundaries ($U_1=(x_1,x_2)$, $U_3=(x_3,x_4)$) where the concentrations of the above-mentioned ions change linearly or are nearly zero. Moreover, the concentrations of $C{l}^{-}$ and $H^{+}$ match with high accuracy, as do those of $N{a}^{+}$ and $O{H}^{-}$. In the central part of the channel, there exists a region $U_2=(x_2,x_3)$ with nearly constant concentration distributions, the values of which are practically independent of $b$.

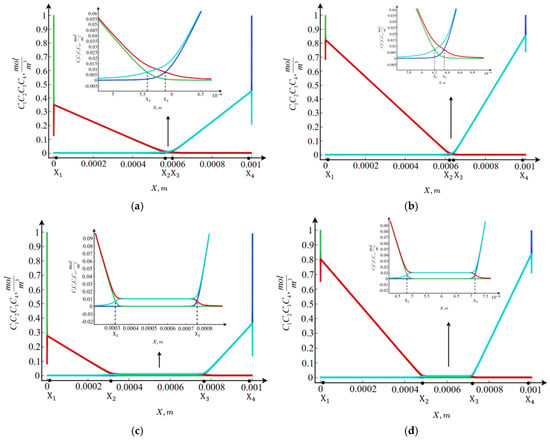
Figure 2. Concentrations: (a) for $b=0$, $d=0.3$; (b) for $b=0.0001$, $d=0.3$; (c) for $b=0$, $d=1.5$; (d) for $b=0.0001$, $d=1.5$. $C_1$—blue line, $C_2$—green line, $C_3$—red line, $C_4$—light-blue line.

Despite this qualitative similarity, there are several quantitative differences between the concentration distributions at $b=0$ and $b=0.0001$. The size and location of the central region differ at $b=0.0001$, it shifts to the right and becomes smaller. In addition, although the central region is narrower at $b=0.0001$, the linear concentration distributions are steeper, since the concentration value at the boundary of the adjacent layer is significantly higher.

From the analysis of the concentration distributions, it can be concluded that the cross-section of the desalination channel consists of at least seven regions: two boundary layers $U_A=[0,x_1)$, $U_K=(x_4,H]$, two regions of linear concentration variation $U_1=(x_1,x_2)$ $U_3=(x_3,x_4)$, and one region of nearly constant concentrations $U_2=(x_2,x_3)$, as well as two intermediate layers between the regions of linear variation and the constant region $(x_2-\delta ,x_2+\delta )$, $(x_3-\delta ,x_3+\delta )$. To fully understand the significance of these regions, it is necessary to consider additional characteristics of the transport processes.

Furthermore, unlike the diffusion layer (for example, near the cation-exchange membrane), where the steady state may be nonequilibrium—that is, the salt-ion current may not equal zero, and therefore the cation concentration may decrease almost to zero—in the cross-sectional domain of the desalination channel, the steady state can only be equilibrium. In other words, the salt-ion current is zero, which means that salt ions cannot be completely removed. Consequently, during the transport of $H^{+}$ and $O{H}^{-}$ ions, the redistribution of salt ions occurs, but they are not carried beyond the channel boundaries.

3.2. Spatial Charge Distribution

In Figure 3, the spatial charge distribution shows that the cross-sectional domain of the desalination channel can also be divided into seven intervals. The boundary layers represent regions of spatial charge associated with the properties of the interfacial boundary, that is, part of the conventional electric double layer [24], with the anion-exchange membrane carrying a negative charge and the cation-exchange membrane a positive charge. In the regions of linear concentration distribution, the condition of electroneutrality is satisfied with high accuracy. In the central part of the channel, however, an additional region of spatial charge appears (internal boundary layers), which is not related to the interfacial boundaries. To explain the emergence of these internal boundary layers, it is necessary to consider the function $P_W$ (the rate of water molecule dissociation/recombination reaction).

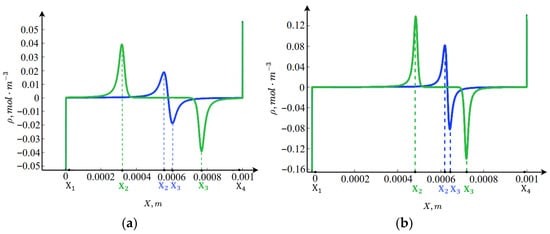
Figure 3. Spatial charge $\rho$: (a) for $b=0$, (b) for $b=0.0001$. Blue curve: $d=0.3$; green curve: $d=1.5$.

3.3. Graphs of the Equilibrium Function $P_w$

Figure 4 shows that in the regions of spatial charge, within the boundary layers near the ion-exchange membranes, intense water molecule dissociation occurs, as the electric field strength in these regions reaches very high values. Moreover, for $b=0.0001$, water dissociation is more intense than for $b=0$. In region $[0,x_1)$, the ions $O{H}^{-}$ are completely transported through the anion-exchange membrane (boundary condition 19a), so their concentration is practically zero. At the same time, the concentration of ions $H^{+}$ rapidly increases. The concentration of ions $C{l}^{-}$ decreases exponentially from $K^{+}$, while the concentration of (formula) remains practically zero.

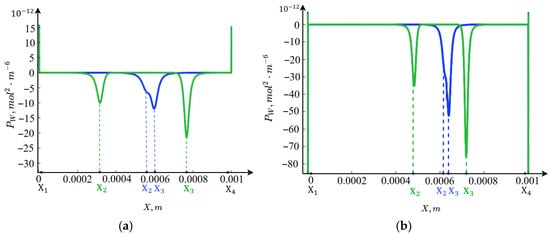
Figure 4. Equilibrium function $P_W$: (a) for $b=0$, (b) for $b=0.0001$. Blue curve: $d=0.3$; green curve: $d=1.5$.

In $(x_4, H]$, the situation occurs in the opposite manner: the ions $H^{+}$ are completely transported through the cation-exchange membrane (boundary condition 12), so their concentration is practically zero. At the same time, the concentration of ions $O{H}^{-}$ increases rapidly. The concentration of ions $K^{+}$ grows exponentially toward $C_{1k}$, while the concentration of $C{l}^{-}$ remains practically zero.

The spatial charge concentration distribution in the central part of the channel, as shown above, significantly depends on the potential jump. Let us first consider the case when the potential is below the limiting value, for example, 0.3 V. In this case, a region $(x_2,x_4)$ forms in the central part of the channel where recombination dominates over dissociation; we will refer to this as the recombination region. The structure of the recombination region is almost symmetric with respect to the channel center for a $KCl$ solution, with a slight rightward shift, since the diffusion coefficients of potassium and chloride ions are nearly equal. However, for a $NaCl$ solution, a significant asymmetry is observed because the diffusion coefficient of sodium ions is smaller than that of chloride ions.

A characteristic feature of this region is the presence of a deep, single local minimum of the equilibrium function, caused by the dominance of recombination over dissociation. The minimum point is defined by the location where the hydrogen ion concentration equals the hydroxide ion concentration, which is why recombination is maximal at this point. To the left of the minimum point, the hydrogen ion concentration exceeds that of hydroxide ions. Since in the recombination region the concentrations of potassium and chloride ions are much lower than those of hydrogen and hydroxide ions, an excess of hydrogen ions occurs to the left of the minimum point, creating a region of positive spatial charge. Similarly, to the right of the minimum point, a region of negative spatial charge forms due to an excess of hydroxide ions.

This leads to the conclusion that the internal space charge boundary layer form due to the finite rate of the recombination reaction. Specifically, $H^{+}$ ions approach from the left and $O{H}^{-}$ ions from the right, and they recombine. Since the recombination rate is finite, albeit very high, not all ions recombine immediately, so they accumulate in a “queue” for recombination. This results in a positively charged spatial region on the left due to $H^{+}$ ions and a negatively charged spatial region on the right due to $O{H}^{-}$ ions.

At a potential jump of ${\Delta }_r\varphi =1.5 B$, a characteristic feature is the presence of two local minima in the equilibrium function (Figure 4), which is due to the very high electric field strength between these points. This causes dissociation to be so enhanced that near-equilibrium conditions are almost reached between the two local minima of the equilibrium function.

3.4. Graphs of the Fluxes $j_3$ ($H^{+}$) and $j_4$ ($O{H}^{-}$)

Figure 5 and Figure 6 shows that accounting for the dependence of the equilibrium coefficient on the spatial charge leads to an increase in the fluxes: for $b=0.0001$, the fluxes rise by an order of magnitude in the boundary layers near the membranes and approximately double in the central part of the channel. By selecting an appropriate value of bb, the flux can be increased by 10–30 times, as observed in experiments shown in Figure 4 and Figure 5 of [24]. Thus, choosing the dependence of the equilibrium coefficient on the spatial charge, along with a proper fitting parameter $b$, allows for both qualitatively and quantitatively accurate description of the enhancement of the fluxes of the products of water molecule dissociation.

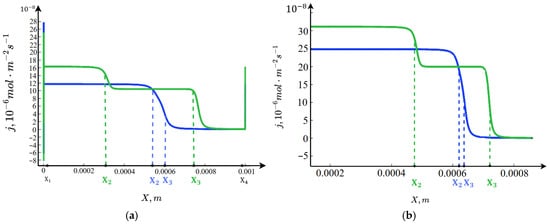
Figure 5. Fluxes $j_3$: (a) for $b=0$, (b) for $b=0.0001$. Blue curve: $d=0.3$; green curve: $d=1.5$.

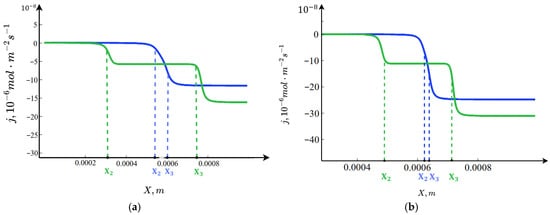
Figure 6. Fluxes $j_4$: (a) for $b=0$, (b) for $b=0.0001$. Blue curve: $d=0.3$; green curve: $d=1.5$.

In the electroneutral region, one of the fluxes is zero while the other proportional to the current I. In the equilibrium region, where the concentrations are practically constant, both fluxes take constant values, which are different from zero. This leads to the formation of two boundary layers for each flux in the vicinity of points $x_1$ and $x_4$.

3.5. Graphs of the Electric Field Intensity E

Figure 7 shows that the electric field intensity decreases numerically in the boundary layers with increasing parameter $b$. This is because, as noted above, the release of $H^{+}$ ions at the anion-exchange membrane and $O{H}^{-}$ ions near the cation-exchange membrane is enhanced. Since the spatial charges near the anion- and cation-exchange membranes are negative and positive, respectively, the $H^{+}$ and $O{H}^{-}$ ions reduce the magnitude of these spatial charges, leading to a corresponding decrease in the electric field intensity in these regions. To explain the increase in the electric field intensity in the middle of the channel, it should be noted that the concentrations in this region are constant and do not depend on $b$, while the fluxes increase. After a series of transformations, we obtain ${\displaystyle \frac{d(C_1-C_2+C_3-C_4)}{dx}}=(C_1+C_2+C_3+C_4)E-{\displaystyle \frac{1}{D_3}}{j}_3+{\displaystyle \frac{1}{D_4}}{j}_4$.

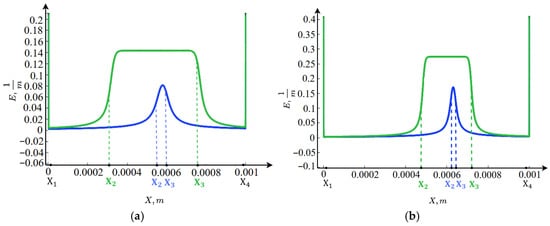
Figure 7. Electric field intensity $E$ (a) for $b=0$. (b) for $b=0.0001$. Blue curve: $d=0.3$; green curve: $d=1.5$.

Since the concentrations are practically constant, ${\displaystyle \frac{d(C_1-C_2+C_3-C_4)}{dx}}\approx 0$; therefore

$$(C_1+C_2+C_3+C_4)E-{\displaystyle \frac{1}{D_3}}{j}_3+{\displaystyle \frac{1}{D_4}}{j}_4\approx 0$$

$$E\approx {\displaystyle \frac{1}{D_4{D}_3}}{\displaystyle \frac{D_4{j}_3-D_3{j}_4}{C_1+C_2+C_3+C_4}}$$

(15)

Thus, with an increase in b, the fluxes increase, the numerator grows while the denominator remains constant, and consequently, the electric field intensity increases proportionally with the fluxes.

3.6. Equilibrium Constant $k_w$

For $b=0$, the equilibrium constant $k_w$ is constant, whereas for $b=0.0001$ it becomes variable and behaves similarly to the spatial charge, except that $k_w$ is positive and its maximum value depends on $b$, increasing as $b$ increases. Thus, for $b=0.0001$, the equilibrium constant increased by approximately 57 times. It can be shown that by selecting $b$, the maximum value of the equilibrium constant can be made arbitrarily large, which leads to an increase in the fluxes of $H^{+}$ and $O{H}^{-}$ ions. The increase in $H^{+}$ and $O{H}^{-}$ fluxes reduces the magnitude of the spatial charge near the anion- and cation-exchange membranes, since the signs of the spatial charge near the membranes and those of the $H^{+}$ and $O{H}^{-}$ ions are opposite. This, in turn, diminishes the effect of the spatial charge on enhancing the fluxes of $H^{+}$ and $O{H}^{-}$ ions, leading to a certain equilibrium. As a result, neither the electric field intensity nor the fluxes can increase indefinitely.

4. The Structure of the Cross-Section of the Desalination Channel and the Analytical Solution

4.1. Structure of the Desalination Channel Cross-Section

From the analysis of the numerical solution above, it is clear that the cross-sectional domain of the desalination channel can be divided into 7 intervals:

• Boundary layers near the anion-$U_A=[0,x_1)$ and cation-exchange $U_K=(x_4,H]$ membranes, which are quasi-equilibrium regions of spatial charge for $b=0$ and their analogs for $b=0.0001$. In addition, there are two internal boundary layers of spatial charge, whose formation is associated with the recombination reaction of water molecules.
• Between the two internal boundary layers, there is an internal equilibrium region $U_2=(x_2,x_3)$ where the concentrations and electric field intensity are constant. The electric field intensity in this region is relatively high, which is associated with the increased fluxes of $H^{+}$ and $O{H}^{-}$ ions.
• In the remaining two regions, the conditions of equilibrium (Figure 5) and local electroneutrality (Figure 4) are satisfied, and the concentration distribution is linear with high accuracy. We will designate these regions, respectively, $U_1=(x_1,x_2)$ and $U_3=(x_3,x_4)$.

Using this structure of the desalination channel cross-section, in the next section an approximate analytical solution to the boundary value problem is found. Analytical solutions play a key role in the study of singularly perturbed equations [27,28,29,30], allowing one to gain a deep understanding of the structure of solutions and their properties.

4.2. Analytical Solution Algorithm

To find the analytical solution, the solution is found in each of the described regions $U_A=[0,x_1)$, $U_1=(x_1,x_2)$, $U_2=(x_2,x_3)$, $U_3=(x_3,x_4)$ independently, which are then merged, i.e., constants are found and the region boundaries are refined.

(1)

The solution in region $U_2=(x_2,x_3)$ was actually given above (see Formula (15)), and the concentrations are constant.

(2)

The solution in region $U_1=(x_1,x_2)$ is found assuming that the equilibrium and electroneutrality conditions are satisfied, with $C_1$, $C_4$, being small compared to $C_2$ and $C_3$, the latter being close to linear functions (see Section 4.1 and Figure 3), and the fluxes being constant (Figure 6). Therefore, to find $C_2$ and $C_3$, we obtain Equations (16)–(18).

$$j_2={\displaystyle \frac{F}{RT}}{D}_2{C}_2{\displaystyle \frac{d\varphi }{dx}}-D_2{\displaystyle \frac{d{C}_2}{dx}}$$

(16)

$$j_3=-{\displaystyle \frac{F}{RT}}{D}_3{C}_3{\displaystyle \frac{d\varphi }{dx}}-D_3{\displaystyle \frac{d{C}_3}{dx}}$$

(17)

$$-C_2+C_3=0$$

(18)

From where, after a series of transformations, we find

$$C_2=C_3=\beta -{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{j_2}{D_2}}+{\displaystyle \frac{j_3}{D_3}}\right)x$$

(19)

$$E=-{\displaystyle \frac{RT}{F}}{\displaystyle \frac{D_3{j}_2-D_2{j}_3}{D_2{D}_3(C_2+C_3)}}$$

(20)

$$E=-{\displaystyle \frac{RT}{F}}{\displaystyle \frac{D_3{j}_2-D_2{j}_3}{D_2{D}_3(2\beta -\left(\frac{j_2}{D_2}+\frac{j_3}{D_3}\right)x)}}$$

(21)

$$E={\displaystyle \frac{RT}{F}}{\displaystyle \frac{D_2{j}_3-D_3{j}_2}{2D_2{D}_3\beta -\left(D_3{j}_2+D_2{j}_3\right)x}}$$

(22)

The solution in the region $U_2=(x_2,x_3)$ is found similarly.

(3)

Solution in the boundary layer region $U_A=[0,x_1)$. In this region, as in the region $U_2=(x_2,x_3)$, $C_1$, $C_4$ are small compared to $C_2$ and $C_3$. However, in this region, the equilibrium condition is violated: namely, the dissociation reaction predominates over the recombination reaction, and there is a negative space charge, with the concentration gradients $C_2$ and $C_3$ very large. Therefore, the solution in this region is significantly more complicated.

Taking into account all the above assumptions, we obtain the system (16), (17), (23), (24)

$${\displaystyle \frac{d{j}_3}{dx}}=k_r(k_{w_0}-b(-C_2+C_3))$$

(23)

$${\epsilon }_r{\displaystyle \frac{d^2\varphi }{d{x}^2}}=-F(-C_2+C_3)$$

(24)

From (25) we substitute into (24)

$${\displaystyle \frac{d{j}_3}{dx}}=k_r(k_{w_0}+{\displaystyle \frac{b{\epsilon }_r}{F}}{\displaystyle \frac{d^2\varphi }{d{x}^2}})$$

By integrating, we find one of the first integrals

$$j_3=k_r{k}_{w_0}x+{\displaystyle \frac{k_{r}b{\epsilon }_r}{F}}{\displaystyle \frac{d\varphi }{dx}}+{\gamma }_1$$

${\gamma }_1$—the integration constant.

From this, it is clear that at $b>0$, there is an additional increase in flux $j_3$, which linearly depends on the field strength.

Using this relationship, after a series of transformations, we obtain the equation for the potential:

$${\epsilon }_r{\displaystyle \frac{d^3\varphi }{d{x}^3}}=({\displaystyle \frac{{\epsilon }_r}{2}}{\displaystyle \frac{F^2}{R^2{T}^2}}{({\displaystyle \frac{d\varphi }{dx}})}^2-{\displaystyle \frac{1}{2\epsilon }}{\displaystyle \frac{F^2}{RT}}{k}_r{k}_w{x}^2-{\displaystyle \frac{b_0{k}_r{\epsilon }_{r}F}{RT}}\varphi -{\displaystyle \frac{F^2}{RT}}{\gamma }_{1}x+{\gamma }_2){\displaystyle \frac{d\varphi }{dx}}+{\displaystyle \frac{a}{\epsilon }}{k}_{w_0}x-b_0{\displaystyle \frac{d\varphi }{dx}}+{\gamma }_{1}F$$

The last equation is a third-order nonlinear ordinary equation, which in special cases can be solved analytically using the Airy function. In general, we solve it numerically using software packages such as Wolfram Mathematica 14.2.

5. Conclusions

The study established that in systems with monopolar membranes, the change in the equilibrium constant can be linked not merely to the electric field strength but to the magnitude of the spatial charge. According to the proposed mathematical model, variations in the equilibrium constant lead to a significant increase in the fluxes of $H^{+}$ and $O{H}^{-}$ ions. In particular, the equilibrium constant locally increases, for example in the quasi-equilibrium boundary layer region, by a factor of 10–30, which is in the same order of magnitude as the experimental data [24,26].

The work demonstrated that in the regions of spatial charge, within the boundary layers near the ion-exchange membranes, intense water molecule dissociation occurs, with higher values of the parameter $b$ leading to stronger dissociation.

Furthermore, it was analytically demonstrated that hydrogen and hydroxyl ion fluxes increase linearly with increasing electric field strength. Using this relationship, a third-order differential equation for the potential was derived, free of unknown concentrations and fluxes. Regions of electroneutrality arise near the space charge regions, in which equilibrium conditions are additionally satisfied. This results in a nearly linear concentration distribution, enabling an analytical solution to be found in this region. It was shown that an equilibrium region arises deep within the solution, in which concentrations are virtually constant and the electric field strength is quite high. Using these properties, an approximate analytical solution to the boundary value problem in this region was found.

It was also shown that an internal boundary layer (the recombination region) forms deeper in the solution, associated with the recombination of $H^{+}$ and $O{H}^{-}$ ions. Furthermore, with an increase in b, the flows increase and the electric field strength increases proportionally.