An Online Generalized Multiscale Method for Embedded Discrete Fracture Model

Abstract

This study concerns an online generalized multiscale method for flow in fractured porous media that is based on an embedded discrete fracture model. We first convert a two-point flux-approximation scheme into an equivalent discrete weak formulation that results in the same linear algebraic system for the unknown pressure. Then, by the use of a suitable local snapshot space and a well-designed spectral decomposition, we compute offline basis functions to capture local heterogeneity information on account of the presence of various fractures in each coarse cell. After that, we compute residual-based online basis functions that contain global multiscale information to enrich the multiscale space and thus achieve higher accuracy of the multiscale solution. Meanwhile, theoretical analyses are conducted to show the convergence behavior, and a number of numerical tests with different fracture configurations are performed to investigate the performance of online enrichment.

1. Introduction

For the practical applications of underground engineering, such as unconventional oil and gas reservoir management, porous media of concern are generally filled with conductive fractures [1,2,3,4] that may have great impacts on the behavior of fluids flowing through them. Discrete fracture models [5,6,7] are some of the most commonly used models for modeling flow in fractured porous media, which treat fractures as lower-dimensional features within the surrounding matrix and can characterize fractures exactly. In addition, the mixed formulation of this modeling approach has also been presented [8,9,10]. However, the discrete fracture model needs to generate conforming grids such that fractures are aligned with the interface of matrix cells, usually resulting in complex unstructured grids. Alternatively, to alleviate the difficulty of the conforming grid generation, an embedded discrete fracture model [11,12,13] is devised, where the matrix and fracture grids can be generated independently, and this is also the main advantage of this modeling approach; please see [14,15,16,17] for recent works. The fractures not only have complex spatial distributions but also exhibit disparities in their orientation, direction, aperture, length, and permeability. All these lead to the fractured porous media having strong heterogeneities, and the fluid flowing through them represents an essentially multiscale problem. In order to precisely characterize complicated fractures, a sufficiently fine mesh is commonly required, which results in a large number of grid cells, greatly increasing the difficulty of numerical simulations. Therefore, efficient multiscale model reduction methods are required to substantially save computational resources for the numerical simulation of flow in fractured porous media with high accuracies.

There have been many multiscale model reduction methods proposed for flow in fractured porous media, with parts of them subjected to the embedded discrete fracture model that are broadly stated as follows. In the framework of a multiscale finite volume method, to begin with, an iterative multiscale finite volume method makes use of only one basis function to characterize each fracture network, which is especially suitable for fracture networks with short spatial length scales [18]. Afterwards, an algebraic multiscale method is applied so that the matrix and fracture basis functions can be coupled in different levels, which is accurate for embedded fractures with various length scales [19]. At the same time, a multiscale restriction smoothed basis method that enables general couplings of fracture and matrix basis functions is proposed, which can efficiently deal with fractures in various conductivities [20]. In [21], a generalized multiscale finite element method is employed for solving the discrete fracture model, embedded discrete fracture model and to further their combinations, which captures the heterogeneity of fractures by multiple multiscale basis functions that represent the fracture network with long spatial length scales, and it homogenizes the fracture network with short spatial length scales. In [22], for the simulation of multiphase flow in fractured porous media, multiscale basis functions are computed through the integration of an multiscale mimetic method, which can effectively represent the complicated interactions between the matrix and fractures.

For the generalized multiscale finite element method mentioned above, initially proposed in [23,24], it provides a systematic and flexible framework that enriches the multiscale space by additional multiscale basis functions so that it is able to capture more heterogeneity information and thereby obtain more accurate multiscale solutions; moreover, it has been extended to the constraint energy minimizing generalized multiscale finite element method [25,26,27], whose convergence is mesh-size-dependent and not dependent on the contrast by making use of the appropriate oversampling parameter. Subsequently, taking into account the influence of distant effects, the residual-based online basis functions are devised to carry the related global information and also enrich the multiscale space, then the rate of convergence is significantly improved [28]. For more details and applications of the generalized multiscale finite element method, please see [29] for a comprehensive review; and see [30,31,32,33] for more applications of the online generalized multiscale finite element method. Meanwhile, some other examples of the online enrichment have also been proposed for the mixed generalized multiscale finite element method [34,35], generalized multiscale discontinuous Galerkin method [36], constraint energy minimizing generalized multiscale finite element method [37,38], mixed generalized multiscale finite element method with velocity elimination [39,40,41], and so on.

In this paper, we propose an online generalized multiscale method for flow in fractured porous media through the use of an embedded discrete fracture model, where the fine-scale system is discretized by a basic finite volume method, the two-point flux-approximation scheme, which is widely used in the reservoir simulation [42,43,44]. Firstly, according to the linear algebraic system, with respect to the two-point flux-approximation scheme, we obtain the corresponding discrete weak formulation, thereby the embedded discrete fracture model can be conveniently integrated into the framework of generalized multiscale finite element methods. Next, for each coarse cell, we solve a range of local problems with specific boundary conditions to establish the local snapshot space, and reduce the dimension by a selected eigenvalue problem to obtain the dominant modes, i.e., the offline basis functions. We can find that on each coarse cell, per fracture network corresponds to one offline basis function. Then, by taking these offline basis functions to form the initial multiscale space and solving the discrete weak formulation on the coarse grid, we obtain the initial multiscale solution. Subsequently, depending on the residual of the initial multiscale solution, online basis functions are iteratively computed on each coarse cell to enrich the multiscale space and thereby reduce the impact of distant effects on the accuracy of the multiscale solution. Accordingly, in light of [28], convergence analyses and numerical examples are also given, and the initial multiscale space is vital to the online enrichment in that more initial basis functions contribute to faster convergence rates. Conversely, when offline basis functions, with respect to the extremely small eigenvalues, are not included in the initial multiscale space, the online enrichment shows a very slow convergence rate.

The remaining parts of this paper are arranged as follows. Section 2 states the basic embedded discrete fracture model, fine-scale discretization by the two-point flux-approximation scheme, and the equivalent discrete weak formulation. Section 3 discusses the detailed procedures and ingredients of the proposed online generalized multiscale method. A variety of numerical examples are presented in Section 4. Section 5 concludes the paper.

2. Embedded Discrete Fracture Model

2.1. Mathematical Formulation

Let $\Omega$ be a fractured porous medium domain in ${\mathbb{R}}^2$, and ${\Omega }_m$ and ${\Omega }_f$ be, respectively, the matrix domain and fracture domain. The governing equations of the embedded discrete fracture model can be written as

$$-\nabla ·({\kappa }^m\nabla p^m)+{\Psi }^{mf}=Q^m\mathrm{in}{\Omega }_m,$$

(1)

$$-\nabla ·({\kappa }^f\nabla p^f)+{\Psi }^{fm}=Q^f\mathrm{in}{\Omega }_f,$$

(2)

where ${\kappa }^i$, $p^i$ and $Q^i$ are, respectively, the permeability, pressure, and source term in ${\Omega }_i$, $i=m,f$, ${\Psi }^{mf}$ and ${\Psi }^{fm}$ are the cross-media flux interactions between the matrix and fractures.

For the embedded discrete fracture model, computational grids for the matrix and fractures are constructed independently so that the matrix grids do not need to match the fractures. Let ${\mathcal{K}}_h^m$ be the uniform fine-grid partition of ${\Omega }_m$, which is composed of rectangles, and ${\mathcal{K}}_h^f$ be the fine-grid partition of ${\Omega }_f$. For simplicity, we suppose that for each fracture cell, it is completely contained in one matrix cell, and we use ${\mathcal{I}}_h^{mf}$ to denote the set of all pairs of connected matrix and fracture cells. To conduct the multiscale model reduction, we also introduce the coarse grid, which is denoted by ${\mathcal{K}}_H$, a uniform partition of the fractured porous medium domain $\Omega$, such that each coarse cell is exactly the combination of several matrix and fracture cells.

2.2. Two-Point Flux-Approximation Scheme

By the fine grids ${\mathcal{K}}_h^m$ for the matrix and ${\mathcal{K}}_h^f$ for the fractures, for each pair of matrix cells k and fracture cells e, such that $(k,e)\in {\mathcal{I}}_h^{mf}$, the cross-media flux interactions ${\Psi }^{mf}$ and ${\Psi }^{fm}$ between k and e are, respectively, defined as

$${\Psi }_{ke}^{mf}=C{I}_{ke}{\overline{\kappa }}_{ke}(p_k^m-p_e^f)/s_k\mathrm{and}{\Psi }_{ke}^{fm}=C{I}_{ke}{\overline{\kappa }}_{ke}(p_e^f-p_k^m)/l_e,$$

(3)

where ${\overline{\kappa }}_{ke}$ is the harmonic average of ${\kappa }_k^m$ and ${\kappa }_e^f$, the matrix permeability in k and the fracture permeability in e; $s_k$ is the area of k; $l_e$ is the length of e; $C{I}_{ke}$ is the connectivity index for k and e, depending on the grids for the matrix and fractures, and is calculated as

$$C{I}_{ke}={\displaystyle \frac{l_e}{{⟨d⟩}_{ke}}},$$

(4)

${⟨d⟩}_{ke}$ is the average distance between e and k, taking the form as

$${⟨d⟩}_{ke}={\displaystyle \frac{{\int }_k{d}_e\mathrm{d}s}{s_k}},$$

(5)

with $d_e$ being the distance between integral volume $\mathrm{d}s$ and fracture cell e.

Then, the flux between the connected fracture cell e and matrix cell k are, respectively, defined as

$$F_{ke}={\int }_k{\Psi }_{ke}^{mf}\mathrm{d}s=T_{ke}(p_k^m-p_e^f)\mathrm{and}{F}_{ek}={\int }_e{\Psi }_{ke}^{fm}\mathrm{d}l=T_{ek}(p_e^f-p_k^m),$$

(6)

where the matrix-fracture transmissibility $T_{ke}=C{I}_{ke}{\overline{\kappa }}_{ke}=T_{ek}$. In other words, the total flux between matrix cell k and fracture cell e should be conserved. We define the jump of p between k and e as $⟦p{⟧}_{ke}=p_k^m-p_e^f$.

For each pair of neighbouring matrix cells $k_i$ and $k_j$ with the common edge e, the half transmissibilities are, respectively, defined as

$$T_{k_{i}e}={\displaystyle \frac{l_e{\kappa }_{k_i}^m}{{⟨d⟩}_{k_{i}e}}},T_{k_{j}e}={\displaystyle \frac{l_e{\kappa }_{k_j}^m}{{⟨d⟩}_{k_{j}e}}},$$

(7)

where ${⟨d⟩}_{k_{i}e}$ is the average distances from $k_i$ to e. Note that we also use the notation e to denote a fine-grid edge, which is the same as a fracture cell throughout this paper.

Accordingly, the flux across e between the neighbouring matrix cells $k_i$ and $k_j$ is defined as

$$F_e={(T_{k_{i}e}^{-1}+T_{k_{j}e}^{-1})}^{-1}(p_{k_i}^m-p_{k_j}^m)=T_e(p_{k_i}^m-p_{k_j}^m),$$

(8)

where $T_e={(T_{k_{i}e}^{-1}+T_{k_{j}e}^{-1})}^{-1}$ is the matrix-matrix transmissibility. We define the jump cross e as $⟦p{⟧}_e=p_{k_i}^m-p_{k_j}^m$, and constants $s_{e{k}_i}=1$, $s_{e{k}_j}=-1$.

In the same way, for each pair of neighbouring fracture cells $e_i$ and $e_j$ with the common node r, the half transmissibilities are, respectively, defined as

$$T_{e_{i}r}^n={\displaystyle \frac{d_{e_i}^f{\kappa }_{e_i}^f}{{⟨d⟩}_{e_{i}r}}},T_{e_{j}r}^n={\displaystyle \frac{d_{e_j}^f{\kappa }_{e_j}^f}{{⟨d⟩}_{e_{j}r}}},$$

(9)

where $d_{e_i}^f$ is the width of fracture cell $e_i$, ${⟨d⟩}_{e_{i}r}$ is the average distance from $e_i$ to r, i.e., the half length of $e_i$.

And the flux across r between the neighbouring fracture cells $e_i$ and $e_j$ is defined as

$$F_r^n={\left({\left(T_{e_{i}r}^n\right)}^{-1}+{\left(T_{e_{j}r}^n\right)}^{-1}\right)}^{-1}(p_{e_i}^f-p_{e_j}^f)=T_r^n(p_{e_i}^f-p_{e_j}^f),$$

(10)

where $T_r^n={\left({\left(T_{e_{i}r}^n\right)}^{-1}+{\left(T_{e_{j}r}^n\right)}^{-1}\right)}^{-1}$ is the neighbouring fracture-fracture transmissibility. We define the jump cross r as $⟦p{⟧}_r^n=p_{e_i}^f-p_{e_j}^f$, and constants $s_{r{e}_i}=1$, $s_{r{e}_j}=-1$.

For each pair of intersecting fracture cells $e_i$ and $e_j$, with the intersection point r, we define

$$T_{e_{i}r}^c={\displaystyle \frac{2d_{e_i}^f{\kappa }_{e_i}^f}{l_{e_i}}},T_{e_{j}r}^c={\displaystyle \frac{2d_{e_j}^f{\kappa }_{e_j}^f}{l_{e_j}}},$$

(11)

then the flux between $e_i$ and $e_j$ is defined as

$$F_r^c={\left({\left(T_{e_{i}r}^c\right)}^{-1}+{\left(T_{e_{j}r}^c\right)}^{-1}\right)}^{-1}(p_{e_i}^f-p_{e_j}^f)=T_r^c(p_{e_i}^f-p_{e_j}^f)=T_{e_i{e}_j}^c(p_{e_i}^f-p_{e_j}^f),$$

(12)

where $T_r^c=T_{e_i{e}_j}^c={\left({\left(T_{e_{i}r}^c\right)}^{-1}+{\left(T_{e_{j}r}^c\right)}^{-1}\right)}^{-1}$ is the intersecting fracture-fracture transmissibility. We define the jump between $e_i$ and $e_j$ as $⟦p{⟧}_r^c=p_{e_i}^f-p_{e_j}^f$, and for each fracture cell e, we use $\mathcal{C}\left(e\right)$ to denote the set of intersecting fracture cells with it.

In the two-point flux-approximation scheme of the finite volume method, by the mass conversion for each grid cell, the discretized equations for matrix cells are expressed as

$$\sum _{e\in \partial k}{T}_e{s}_{ek}⟦p{⟧}_e+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ke}(p_k^m-p_e^f)=Q_k^m,\forall k\in {\mathcal{K}}_h^m,$$

(13)

and the discretized equations for fracture cells are formulated in the same way that

$$\sum _{r\in \partial e}{T}_r^n{s}_{re}⟦p{⟧}_r^n+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ek}(p_e^f-p_k^m)+\sum _{e_0\in \mathcal{C}\left(e\right)}{T}_{e{e}_0}^c(p_e^f-p_{e_0}^f)=Q_e^f,\forall e\in {\mathcal{K}}_h^f,$$

(14)

where $Q_k^m$ and $Q_e^f$ are, respectively, the integrals of source terms over matrix cell $k\in {\mathcal{K}}_h^m$ and fracture cell $e\in {\mathcal{K}}_h^f$.

On the matrix and fracture grids ${\mathcal{K}}_h^m$ and ${\mathcal{K}}_h^f$, we introduce the following discrete spaces,

$$\begin{array}{cc}\hfill V_h^m& =\{q^m\in L^2\left({\Omega }_m\right):q_k^m\in {\mathbb{P}}_0\left(k\right),\forall k\in {\mathcal{K}}_h^m\},\hfill \\ \hfill V_h^f& =\{q^f\in L^2\left({\Omega }_f\right):q_e^f\in {\mathbb{P}}_0\left(e\right),\forall e\in {\mathcal{K}}_h^f\},\hfill \end{array}$$

(15)

where ${\mathbb{P}}_0$ means the constant function space, and we define the global discrete space for pressure as

$$V_h=V_h^m\times V_h^f.$$

(16)

For any function $q\in V_h$, by multiplying each equation in (13) and (14) with each component of q that corresponds to the same grid cell, and taking a summation, we obtain

$$\begin{array}{cc}\hfill & \sum _{k\in {\mathcal{K}}_h^m}\sum _{e\in \partial k}{T}_e{s}_{ek}⟦p{⟧}_e{q}_k^m+\sum _{k\in {\mathcal{K}}_h^m}\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ke}(p_k^m-p_e^f)q_k^m+\sum _{e\in {\mathcal{K}}_h^f}\sum _{r\in \partial e}{T}_r^n{s}_{re}⟦p{⟧}_r^n{q}_e^f\hfill \\ \hfill & +\sum _{e\in {\mathcal{K}}_h^f}\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ek}(p_e^f-p_k^m)q_e^f+\sum _{e\in {\mathcal{K}}_h^f}\sum _{e_0\in \mathcal{C}\left(e\right)}{T}_{e{e}_0}^c(p_e^f-p_{e_0}^f)q_e^f\hfill \\ \hfill & =\sum _{k\in {\mathcal{K}}_h^m}{Q}_k^m{q}_k^m+\sum _{e\in {\mathcal{K}}_h^f}{Q}_e^f{q}_e^f.\hfill \end{array}$$

(17)

By calculation, we derive that

$$\begin{array}{cc}\hfill & \sum _{e\in {\mathcal{E}}_h^m}{T}_e⟦p{⟧}_e⟦q{⟧}_e+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ke}⟦p{⟧}_{ke}⟦q{⟧}_{ke}+\sum _{r\in {\mathcal{N}}_h^f}{T}_r^n⟦p{⟧}_r^n⟦q{⟧}_r^n+\sum _{r\in {\mathcal{C}}_h^f}{T}_r^c⟦p{⟧}_r^c⟦q{⟧}_r^c\hfill \\ \hfill & =\sum _{k\in {\mathcal{K}}_h^m}{Q}_k^m{q}_k^m+\sum _{e\in {\mathcal{K}}_h^f}{Q}_e^f{q}_e^f,\hfill \end{array}$$

(18)

where ${\mathcal{E}}_h^m$ is the matrix edge set of ${\mathcal{K}}_h^m$, ${\mathcal{N}}_h^f$ is the fracture node set of ${\mathcal{K}}_h^f$, and ${\mathcal{C}}_h^f$ is the intersection point set of all fractures.

By virtue of the above equation, we can obtain the following discrete bilinear form, written as

$$\begin{array}{cc}\hfill a(p,q)& =\sum _{e\in {\mathcal{E}}_h^m}{T}_e⟦p{⟧}_e⟦q{⟧}_e+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ke}⟦p{⟧}_{ke}⟦q{⟧}_{ke}\hfill \\ \hfill & +\sum _{r\in {\mathcal{N}}_h^f}{T}_r^n⟦p{⟧}_r^n⟦q{⟧}_r^n+\sum _{r\in {\mathcal{C}}_h^f}{T}_r^c⟦p{⟧}_r^c⟦q{⟧}_r^c,\forall p,q\in V_h,\hfill \end{array}$$

(19)

and we use ${\parallel ·\parallel }_a=\sqrt{a(·,·)}$ to denote the deduced norm. Correspondingly, we acquire the discrete weak formulation as: find $p_h=(p_h^m,p_h^f)\in V_h$, such that

$$a(p_h,q)=(Q,q),\forall q=(q^m,q^f)\in V_h,$$

(20)

which has the same linear algebraic system as the two-grid approximation-scheme.

3. Coarse-Grid Approximation

3.1. Snapshot Space

For each coarse cell $K_i\in {\mathcal{K}}_H$, we denote the set of matrix edges on $\partial K_i$ by $\partial {\mathcal{E}}_i^m$, set of fracture nodes on $\partial K_i$ by $\partial {\mathcal{E}}_i^f$, set of fracture endpoints inside $K_i$ by $\partial {\mathcal{E}}_{i,0}^f$, and suppose that there are $N_i^m$ fine-grid edges in $\partial {\mathcal{E}}_i^m$, $N_i^f$ fracture nodes in $\partial {\mathcal{E}}_i^f$.

To begin with, in light of [45], a total number of $N_i^m+N_i^f$ snapshot basis functions are solved on $K_i$, through the local problem written as: find ${\phi }_j^i=({\phi }_j^{i,m},{\phi }_j^{i,f})\in V_h\left(K_i\right)$, such that

$$\begin{array}{cc}\hfill -\nabla ·({\kappa }^m\nabla {\phi }_j^{i,m})+{\Psi }^{mf}& =Q^m\mathrm{in}{K}_i\cap {\Omega }_m,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill -\nabla ·({\kappa }^f\nabla {\phi }_j^{i,f})+{\Psi }^{fm}& =Q^f\mathrm{in}{K}_i\cap {\Omega }_f,\hfill \end{array}$$

(22)

with the boundary conditions being set as: for $j=1,\cdots ,N_i^m$,

$$\left\{\begin{array}{c}{\phi }_j^{i,m}=\left\{\begin{array}{c}1\mathrm{on}{e}_j\in \partial {\mathcal{E}}_i^m,\hfill \\ 0\mathrm{on}\mathrm{other}\mathrm{edges}\mathrm{of}\partial {\mathcal{E}}_i^m,\hfill \end{array}\right.\hfill \\ {\phi }_j^{i,f}=0\mathrm{on}\mathrm{all}\mathrm{points}\mathrm{of}\partial {\mathcal{E}}_i^f,\hfill \\ \partial {\phi }_j^{i,f}·\tau =0\mathrm{on}\mathrm{all}\mathrm{points}\mathrm{of}\partial {\mathcal{E}}_{i,0}^f,\hfill \end{array}\right.$$

(23)

and for $j=N_i^m+1,\cdots ,N_i^m+N_i^f$,

$$\left\{\begin{array}{c}{\phi }_j^{i,m}=0\mathrm{on}\mathrm{all}\mathrm{edges}\mathrm{of}\partial {\mathcal{E}}_i^m,\hfill \\ {\phi }_j^{i,f}=\left\{\begin{array}{c}1\mathrm{on}{r}_{j_0}\in \partial {\mathcal{E}}_i^f,\hfill \\ 0\mathrm{on}\mathrm{other}\mathrm{points}\mathrm{of}\partial {\mathcal{E}}_i^f,\hfill \end{array}\right.\hfill \\ \partial {\phi }_j^{i,f}·\tau =0\mathrm{on}\mathrm{all}\mathrm{points}\mathrm{of}\partial {\mathcal{E}}_{i,0}^f,\hfill \end{array}\right.$$

(24)

where $j_0=j-N_i^m$, and $\tau$ is the unit-tangent vector of the fracture at endpoints.

For each coarse cell $K_i\in {\mathcal{K}}_H$, the local snapshot space is obtained by the span of the above snapshot basis functions, read as

$$V_{\mathrm{snap}}^i=\mathrm{span}\{{\phi }_j^i=({\phi }_j^{i,m},{\phi }_j^{i,f}):j=1\cdots N_i^m+N_i^f\}.$$

(25)

We introduce the following local bilinear form on the local snapshot space $V_{\mathrm{snap}}^i$,

$$\begin{array}{cc}\hfill a_i(p,q)& =\sum _{e\in {\mathcal{E}}_h^m\left(K_i^0\right)}{T}_e⟦p{⟧}_e⟦q{⟧}_e+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}\left(K_i\right)}{T}_{ke}⟦p{⟧}_{ke}⟦q{⟧}_{ke}\hfill \\ \hfill & +\sum _{r\in {\mathcal{N}}_h^f\left(K_i^0\right)}{T}_r^n⟦p{⟧}_r^n⟦q{⟧}_r^n+\sum _{r\in {\mathcal{C}}_h^f\left(K_i\right)}{T}_r^c⟦p{⟧}_r^c⟦q{⟧}_r^c,\forall p,q\in V_{\mathrm{snap}}^i,\hfill \end{array}$$

(26)

with the deduced local norm, written as

$$\begin{array}{cc}\hfill {\parallel q\parallel }_{a,i,0}^2& =\sum _{e\in {\mathcal{E}}_h^m\left(K_i^0\right)}{T}_e⟦q{⟧}_e^2+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}\left(K_i\right)}{T}_{ke}⟦q{⟧}_{ke}^2\hfill \\ \hfill & +\sum _{r\in {\mathcal{N}}_h^f\left(K_i^0\right)}{T}_r^n{(⟦q{⟧}_r^n)}^2+\sum _{r\in {\mathcal{C}}_h^f\left(K_i\right)}{T}_r^c{(⟦q{⟧}_r^c)}^2,\forall q\in V_{\mathrm{snap}}^i,\hfill \end{array}$$

(27)

where ${\mathcal{I}}_h^{mf}\left(K_i\right)$ and ${\mathcal{C}}_h^f\left(K_i\right)$ are, respectively, the subsets of ${\mathcal{I}}_h^{mf}$ and ${\mathcal{C}}_h^f$ restricted to $K_i$, ${\mathcal{E}}_h^m\left(K_i^0\right)$ is the set of matrix edges inside $K_i$, and ${\mathcal{N}}_h^f\left(K_i^0\right)$ is the set of fracture nodes inside $K_i$.

We can easily find the relation between the global norm ${\parallel ·\parallel }_a$ below (19), and the local norm ${\parallel ·\parallel }_{a,i,0}$ in (27), that is

$${\parallel q\parallel }_a^2={\parallel q\parallel }_{a,i,0}^2+\sum _{e\in \partial {\mathcal{E}}_i^m}{T}_e⟦q{⟧}_e^2+\sum _{r\in \partial {\mathcal{E}}_i^f}{T}_r^n{(⟦q{⟧}_r^n)}^2,\forall q\in V_{\mathrm{snap}}^i.$$

(28)

Note that $\partial {\mathcal{E}}_i^m$ is the set of matrix edges on $\partial K_i$, and $\partial {\mathcal{E}}_i^f$ is the set of fracture nodes on $\partial K_i$.

Moreover, suppose there are $N_K$ coarse cells in ${\mathcal{K}}_H$, and ${\mathcal{E}}_H$ is the union of ${\mathcal{E}}_h^m(\partial K_i)$ with respect to all coarse cells, thereby, we can reformulate the global norm ${\parallel ·\parallel }_a$ as

$${\parallel q\parallel }_a^2=\sum _{i=1}^{N_C}{\parallel q\parallel }_{a,i,0}^2+\sum _{e\in {\mathcal{E}}_H}{T}_e⟦q{⟧}_e^2+\sum _{r\in {\mathcal{E}}_H\cap {\mathcal{N}}_h^f}{T}_r^n{(⟦q{⟧}_r^n)}^2,\forall q\in V_h,$$

(29)

and it is straight that ${\sum }_{i=1}^{N_C}{\parallel q\parallel }_{a,i,0}^2\le {\parallel q\parallel }_a^2$, for all $q\in V_h$.

3.2. Offline Space

The spectral decomposition is conducted to extract the main multiscale information locally so as to reduce the dimension of the local snapshot space for each coarse cell. For this purpose, on the matrix and fracture grids ${\mathcal{K}}_h^m$ and ${\mathcal{K}}_h^f$, the following piecewise constant functions ${\overline{\kappa }}^m$ and ${\overline{\kappa }}^f$ are firstly introduced, written as

$$\begin{array}{cc}\hfill {\overline{\kappa }}_k^m& =\sum _{e\in \partial k}{T}_e+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ke},\forall k\in {\mathcal{K}}_h^m,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\overline{\kappa }}_e^f& =\sum _{r\in \partial e}{T}_r^n+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}}{T}_{ek}+\sum _{e_0\in \mathcal{C}\left(e\right)}{T}_{e{e}_0}^c,\forall e\in {\mathcal{K}}_h^f,\hfill \end{array}$$

(31)

via these two piecewise constant functions, a bilinear form $s(·,·)$ is brought in together, formulated as

$$s(p,q)=({\overline{\kappa }}^m{p}^m,q^m)+({\overline{\kappa }}^f{p}^f,q^f),\forall p,q\in V_h,$$

(32)

and we use ${\parallel ·\parallel }_s=\sqrt{s(·,·)}$ to denote the deduced norm.

Therefore, on each coarse cell $K_i$, the eigenvalue problem for the spectral decomposition is read as: find ${\lambda }_t^i$ and ${\varphi }_t^i$, $t=1,\cdots ,N_i^m+N_i^f$, such that

$$a_i({\varphi }_t^i,q)={\lambda }_t^{i}s({\varphi }_t^i,q),\forall q\in V_{\mathrm{snap}}^i.$$

(33)

Note that all eigenfunctions can be normalized, such that $s({\varphi }_t^i,{\varphi }_t^i)=1$, $t=1,\cdots ,N_i^m+N_i^f$. To select the dominant modes, we arrange all eigenfunctions such that their corresponding eigenvalues are sorted in ascending order, i.e., from small to large. By choosing the first $N_i$ eigenfunctions as the offline basis functions, we have the local offline space as follows

$$V_{\mathrm{off}}^i=\mathrm{span}\{{\varphi }_t^i:t=1\cdots N_i\}.$$

(34)

And the global offline space is the direct sum of all local offline spaces, that is

$$V_{\mathrm{off}}=\underset{i=1}{\overset{N_C}{⨁}}{V}_{\mathrm{off}}^i.$$

(35)

For the source term $Q=(Q^m,Q^f)$, correction functions are utilized to capture the information stemmed from them. We obtain the coarse block $K_i^{+}$ for each coarse cell $K_i$ by combining several fine-grid layers around. Through solving ${\widehat{\varphi }}^i=({\widehat{\varphi }}^{i,m},{\widehat{\varphi }}^{i,f})\in V_h({\widehat{K}}_i)$, such that

$$\begin{array}{cc}\hfill -\nabla ·({\kappa }^m\nabla {\widehat{\varphi }}^{i,m})+{\Psi }^{mf}& =Q^m\mathrm{in}{\widehat{K}}_i\cap {\Omega }_m,\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill -\nabla ·({\kappa }^f\nabla {\widehat{\varphi }}^{i,f})+{\Psi }^{fm}& =Q^f\mathrm{in}{\widehat{K}}_i\cap {\Omega }_f,\hfill \end{array}$$

(37)

where the homogeneous Neumann boundary condition and the integral of ${\widehat{\varphi }}^i$ being zero are imposed, restricting them to $K_i$ and taking a summation, we then derive the global correction function, written as

$${\widehat{p}}_g=\sum _{i=1}^{N_C}{\widehat{\varphi }}^i\left(K_i\right).$$

(38)

The global offline space will be served as the initial multiscale space, that is

$$V_g=V_{\mathrm{off}}.$$

(39)

Therefore, we obtain the generalized multiscale method for the two-point flux-approximation scheme to solve the embedded discrete fracture model: find ${\overline{p}}_g=({\overline{p}}_g^m,{\overline{p}}_g^f))\in V_g$, such that

$$\begin{array}{cc}\hfill a({\overline{p}}_g,q)& =(Q,q)-a({\widehat{p}}_g,q),\forall q=(q^m,q^f)\in V_g,\hfill \end{array}$$

(40)

then the multiscale solution $p_g={\overline{p}}_g+{\widehat{p}}_g$, that is, we find the multiscale solution $p_g\in {\widehat{p}}_g+V_g$, such that

$$a(p_g,q)=(Q,q),\forall q=(q^m,q^f)\in V_g.$$

(41)

3.3. Online Enrichment

For each coarse cell $K_i$, we define the following operator on the local snapshot space $V_{\mathrm{snap}}^i$,

$$R_{i}q={\int }_{K_i\cap {\Omega }_m}{Q}^m{q}^m+{\int }_{K_i\cap {\Omega }_f}{Q}^f{q}^f-a(p_g,q),\forall q=(q^m,q^f)\in V_{\mathrm{snap}}^i,$$

(42)

which is referred as the residual operator, and the operator norm measured by the space norm ${\parallel ·\parallel }_a$ is defined as

$$\parallel R_i{\parallel }_a=\underset{q\in V_{\mathrm{snap}}^i}{sup}{\displaystyle \frac{|R_{i}q|}{{\parallel q\parallel }_a}}.$$

(43)

In addition, a projection operator $P_i$: $V_{\mathrm{snap}}^i\to V_{\mathrm{off}}^i$ is introduced, satisfying

$$s(P_{i}p,q)=s(p,q),\forall q\in V_{\mathrm{off}}^i.$$

(44)

Obviously, we can use eigenfunctions of the spectral decomposition (33) to represent any function in $V_{\mathrm{snap}}^i$, that is

$$q=\sum _{t=1}^{N_i^m+N_i^f}{c}_t{\varphi }_t^i,\forall q\in V_{\mathrm{snap}}^i.$$

(45)

By the normalization and orthogonality of these eigenfunctions, for the projection operator $P_i$, we obtain

$$P_{i}q=\sum _{t=1}^{N_i}{c}_t{\varphi }_t^i,q-P_{i}q=\sum _{t=N_i+1}^{N_i^m+N_i^f}{c}_t{\varphi }_t^i.$$

(46)

Then, for any $q\in V_{\mathrm{snap}}^i$,

$$\begin{array}{cc}\hfill \parallel q-P_i{q\parallel }_s^2& =s(q-P_{i}q,q-P_{i}q)=\sum _{t=N_i+1}^{N_i^m+N_i^f}{c}_t^{2}s({\varphi }_t^i,{\varphi }_t^i)=\sum _{t=N_i+1}^{N_i^m+N_i^f}{c}_t^2\hfill \\ \hfill & \le {\left({\lambda }_{N_i+1}^i\right)}^{-1}\sum _{t=N_i+1}^{N_i^m+N_i^f}{\lambda }_t^i{c}_t^2\le {\left({\lambda }_{N_i+1}^i\right)}^{-1}\sum _{t=1}^{N_i^m+N_i^f}{\lambda }_t^i{c}_t^2\le {\left({\lambda }_{N_i+1}^i\right)}^{-1}{\parallel q\parallel }_{a,i,0}^2.\hfill \end{array}$$

(47)

On the other hand,

$$\begin{array}{cc}\hfill {\parallel q\parallel }_a^2& =\sum _{e\in {\mathcal{E}}_h^m\left(K_i\right)}{T}_e⟦q{⟧}_e^2+\sum _{(k,e)\in {\mathcal{I}}_h^{mf}\left(K_i\right)}{T}_{ke}⟦q{⟧}_{ke}^2+\sum _{r\in {\mathcal{N}}_h^f\left(K_i\right)}{T}_r^n{(⟦q{⟧}_r^n)}^2+\sum _{r\in {\mathcal{C}}_h^f\left(K_i\right)}{T}_r^c{(⟦q{⟧}_r^c)}^2\hfill \\ \hfill & \le 2\sum _{k\in {\mathcal{K}}_h^m\left(K_i\right)}(\sum _{e\in \partial k}{T}_e+\sum _{e\in {\mathcal{K}}_h^f,e\cap k\ne \varnothing }{T}_{ke}){(q_k^m)}^2\hfill \\ \hfill & +2\sum _{e\in {\mathcal{K}}_h^f\left(K_i\right)}(\sum _{r\in \partial e}{T}_r^n+\sum _{k\in {\mathcal{K}}_h^m,k\cap e\ne \varnothing }{T}_{ke}+\sum _{e_0\in \mathcal{C}\left(e\right)}{T}_{e{e}_0}^c){(q_e^f)}^2\hfill \\ \hfill & \le 2(\sum _{k\in {\mathcal{K}}_h^m\left(K_i\right)}{\overline{\kappa }}_k^m{\left(q_k^m\right)}^2+\sum _{e\in {\mathcal{K}}_h^f\left(K_i\right)}{\overline{\kappa }}_e^f{(q_e^f)}^2)=2s(q,q)=2{\parallel q\parallel }_s^2,\hfill \end{array}$$

(48)

which implies that

$$\parallel q-P_i{q\parallel }_a\le \sqrt{2}{\parallel q-P_{i}q\parallel }_s,$$

(49)

together with (47), we derive

$$\parallel q-P_i{q\parallel }_a\le \sqrt{2}{\left({\lambda }_{N_i+1}^i\right)}^{-{\displaystyle \frac{1}{2}}}{\parallel q\parallel }_{a,i,0},i=1,\cdots ,N_C.$$

(50)

Lemma 1.

Let $p_h$ be the fine-grid solution of (20) and $p_g$ be the initial multiscale solution of (41), then we have

$$\parallel p_h-p_g{\parallel }_a^2\le 2\sum _{i=1}^{N_C}{\parallel R_i\parallel }_a^2{\left({\lambda }_{N_i+1}^i\right)}^{-1}.$$

(51)

Proof. 

For any $q\in V_{\mathrm{snap}}$, written as $q={\sum }_{i=1}^{N_C}{q}^i$, with $q^i\in V_{\mathrm{snap}}^i$, $i=1,\cdots ,N_C$. Since $P_i{q}^i\in V_{\mathrm{off}}^i\subset V_{\mathrm{off}}=V_g$, by (41), we get

$$a(p_g,P_i{q}^i)=(Q,P_i{q}^i).$$

(52)

Making use of (20) and (41), we obtain

$$\begin{array}{cc}\hfill & a(p_h-p_g,q)=(Q,q)-a(p_g,q)\hfill \\ \hfill & =(Q,\sum _{i=1}^{N_C}(q^i-P_i{q}^i))+(Q,\sum _{i=1}^{N_C}{P}_i{q}^i)-a(p_g,\sum _{i=1}^{N_C}{P}_i{q}^i)-a(p_g,\sum _{i=1}^{N_C}(q^i-P_i{q}^i))\hfill \\ \hfill & =\sum _{i=1}^{N_C}(Q,q^i-P_i{q}^i)-\sum _{i=1}^{N_C}a(p_g,q^i-P_i{q}^i)\hfill \\ \hfill & =\sum _{i=1}^{N_C}((Q,q^i-P_i{q}^i)-a(p_g,q^i-P_i{q}^i))\hfill \\ \hfill & =\sum _{i=1}^{N_C}{R}_i(q^i-P_i{q}^i).\hfill \end{array}$$

(53)

With the help of the approximation property of $P_i$ in (50), it attains

$$|a(p_h-p_g,q)|\le \sum _{i=1}^{N_C}\parallel R_i{\parallel }_a\parallel q^i-P_i{q}^i{\parallel }_a\le \sqrt{2}\sum _{i=1}^{N_C}\parallel R_i{\parallel }_a{\left({\lambda }_{N_i+1}^i\right)}^{-{\displaystyle \frac{1}{2}}}{\parallel q\parallel }_{a,i,0}.$$

(54)

Let $q=p_h-p_g$, and by ${\sum }_{i=1}^{N_C}{\parallel q\parallel }_{a,i,0}^2\le {\parallel q\parallel }_a^2$, the proof is completed. □

In the following, based on the initial multiscale space and the related multiscale solution, we construct online basis functions and enrich the multiscale space iteratively. Suppose that we have already known $V_g^l$ and $p_g^l$, the multiscale space and solution in the l-th level, respectively. For any coarse cell $K_i\in {\mathcal{K}}_H$, by solving the following local problem on the coarse block ${\tilde{K}}_i$ formed by adding one fine-grid layer around: find $\tilde{\varphi }=({\tilde{\varphi }}^m,{\tilde{\varphi }}^f)\in V_h({\tilde{K}}_i)$ such that

$$\begin{array}{cc}\hfill -\nabla ·({\kappa }^m\nabla {\tilde{\varphi }}^m)+{\Psi }^{mf}& =Q^m\mathrm{in}{\tilde{K}}_i\cap {\Omega }_m,\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill -\nabla ·({\kappa }^f\nabla {\tilde{\varphi }}^f)+{\Psi }^{fm}& =Q^f\mathrm{in}{\tilde{K}}_i\cap {\Omega }_f,\hfill \end{array}$$

(56)

and having the same value as $p_g^l$ on the added fine-grid layer, then we can obtain the online basis function, denoted by $\varphi =\tilde{\varphi }\left(K_i\right)-p_g^l\left(K_i\right)$.

Since online basis functions can only be computed simultaneously on the non-adjacent coarse cells, all coarse cells are divided into disjoint subsets $S_1$, $S_2$, $S_3$, and $S_4$ so that the coarse cells are non-adjacent in each subset. Accordingly, there are four sub-iterations in each level of the online enrichment, i.e., to compute online basis functions on coarse cells of $S_1$, $S_2$, $S_3$, and $S_4$ periodically.

For each coarse cell set $S_j$, $j=1,2,3,4$, we use ${\Lambda }_{min,j}={min}_{i\in S_j}{\lambda }_{N_i+1}^i$ to denote the minimum value of eigenvalues that the related eigenfunctions on the coarse cells of $S_j$ are not contained in the initial multiscale space (offline space) $V_g$.

Theorem 1.

Let $p_h$ be the fine-grid solution of (20) and $p_g^l$ ($l\ge 1$) be the multiscale solution after online enrichments, then it holds that

$$\parallel p_h-p_g^{l+1}{\parallel }_a^2\le \prod _{j=1}^4(1-{\displaystyle \frac{{\Lambda }_{min,j}}{2}}{\displaystyle \frac{{\sum }_{i\in S_j}{\parallel R_i\parallel }_a^2{({\lambda }_{N_i+1}^i)}^{-1}}{{\sum }_{i=1}^{N_C}{\parallel R_i\parallel }_a^2{({\lambda }_{N_i+1}^i)}^{-1}}}){\parallel p_h-p_g^l\parallel }_a^2.$$

(57)

Proof. 

We consider adding only one online basis function into the multiscale space, because online basis functions are computed independently at each sub-iteration. Suppose $\varphi$ is the newly computed online basis function on the coarse cell $K_i$. $V_g^{l+1}$ and $p_g^{l+1}$ are the resulting multiscale space and solution.

It is known that $p_g^{l+1}={\overline{p}}_g^{l+1}+{\widehat{p}}_g$, with ${\widehat{p}}_g$ being the global correction function in (38), and ${\overline{p}}_g^{l+1}\in V_g^{l+1}$ satisfying

$$\begin{array}{cc}\hfill a({\overline{p}}_g^{l+1},q)& =(Q,q)-a({\widehat{p}}_g,q),\forall q\in V_g^{l+1}.\hfill \end{array}$$

(58)

From (20), we end up with

$$\begin{array}{cc}\hfill a({\overline{p}}_g^{l+1},q)& =a(p_h,q)-a({\widehat{p}}_g,q)=a(p_h-{\widehat{p}}_g,q),\forall q\in V_g^{l+1}.\hfill \end{array}$$

(59)

In other words, ${\overline{p}}_g^{l+1}$ is actually the projection of $p_h-{\widehat{p}}_g$. Since $a(·,·)$ is symmetric and coercive, we have

$$\parallel p_h-p_g^{l+1}{\parallel }_a^2=a(p_h-p_g^{l+1},p_h-p_g^{l+1})=\underset{q\in {\widehat{p}}_g+V_g^{l+1}}{inf}a(p_h-q,p_h-q).$$

(60)

Let $q=p_g^l+\beta \varphi$, with $\beta \in \mathbb{R}$, it attains

$$\begin{array}{cc}\hfill \parallel p_h-p_g^{l+1}{\parallel }_a^2& \le a(p_h-p_g^l-\beta \varphi ,p_h-p_g^l-\beta \varphi )\hfill \\ \hfill & =a(p_h-p_g^l,p_h-p_g^l)-2\beta a(p_h-p_g^l,\varphi )+{\beta }^{2}a(\varphi ,\varphi )\hfill \\ \hfill & =\parallel p_h-p_g^l{\parallel }_a^2-2\beta a(p_h-p_g^l,\varphi )+{\beta }^{2}a(\varphi ,\varphi ).\hfill \end{array}$$

(61)

By selecting

$$\beta ={\displaystyle \frac{a(p_h-p_g^l,\varphi )}{a(\varphi ,\varphi )}},$$

(62)

which maximizes

$$2\beta a(p_h-p_g^l,\varphi )-{\beta }^{2}a(\varphi ,\varphi ),$$

(63)

then

$$\parallel p_h-p_g^{l+1}{\parallel }_a^2\le {\parallel p_h-p_g^l\parallel }_a^2-{\displaystyle \frac{|a(p_h-p_g^l,\varphi ){|}^2}{a(\varphi ,\varphi )}}.$$

(64)

The above inequality (64) can also be reformulated via the fact that $\varphi \in V_h\left(K_i\right)\subset V_h$ and applying (20) as follows

$$\parallel p_h-p_g^{l+1}{\parallel }_a^2\le {\parallel p_h-p_g^l\parallel }_a^2-{\displaystyle \frac{|(Q,\varphi )-a(p_g^l,\varphi ){|}^2}{a(\varphi ,\varphi )}}.$$

(65)

Due to the definition of the global correction function ${\widehat{p}}_g$, the online basis function $\varphi \in V_{\mathrm{snap}}^i$, moreover, by the residual operator $R_i$ in (42), the operator norm ${\parallel ·\parallel }_a$ in (43), and its construction in (55) and (56), it actually maximizes

$${\displaystyle \frac{|(Q,\varphi )-a(p_g^l,\varphi ){|}^2}{a(\varphi ,\varphi )}},$$

(66)

with

$$|(Q,\varphi )-a(p_g^l,\varphi )|=a(\varphi ,\varphi )={\parallel \varphi \parallel }_a^2={\parallel R_i\parallel }_a^2.$$

(67)

Therefore,

$$\parallel p_h-p_g^{l+1}{\parallel }_a^2\le \parallel p_h-p_g^l{\parallel }_a^2-{\parallel R_i\parallel }_a^2.$$

(68)

It is obvious that the initial multiscale space is included in the multiscale space $V_g^l$, according to Lemma 1, we obtain

$$\parallel p_h-p_g^l{\parallel }_a^2\le 2\sum _{i=1}^{N_C}{\parallel R_i\parallel }_a^2{\left({\lambda }_{N_i+1}^i\right)}^{-1},$$

(69)

then, by integrating (69) into, the inequality (68) becomes

$$\parallel p_h-p_g^{l+1}{\parallel }_a^2\le (1-{\displaystyle \frac{{\lambda }_{N_i+1}^i}{2}}{\displaystyle \frac{\parallel R_i{\parallel }_a^2{({\lambda }_{N_i+1}^i)}^{-1}}{{\sum }_{i=1}^{N_C}{\parallel R_i\parallel }_a^2{({\lambda }_{N_i+1}^i)}^{-1}}}){\parallel p_h-p_g^l\parallel }_a^2.$$

(70)

As a result, through the enrichment by online basis functions with respect to all coarse cells of $S_j$, $j=1,2,3,4$, in sequence, and using the same argument as above, we complete the proof. □

4. Numerical Examples

We provide several numerical examples of the proposed online generalized multiscale method to solve the embedded discrete fracture models (1) and (2). The fractured porous medium domain is set as $\Omega ={[0,1]}^2$, which is divided into a $50\times 50$ structured Cartesian grid for ${\mathcal{K}}_h^m$, and a $5\times 5$ structured Cartesian grid for ${\mathcal{K}}_H$. Furthermore, for all fractures, we set their widths to be $0.01$. The relative errors of the multiscale solution measured by $\parallel ·\parallel$ and ${\parallel ·\parallel }_a$ are, respectively, denoted by $E_0$ and $E_a$, that is

$$E_0:=\parallel p_g-p_h\parallel \parallel p_h\parallel ,E_a:=\parallel p_g-p_h{\parallel }_a{\parallel p_h\parallel }_a.$$

(71)

Example 1.

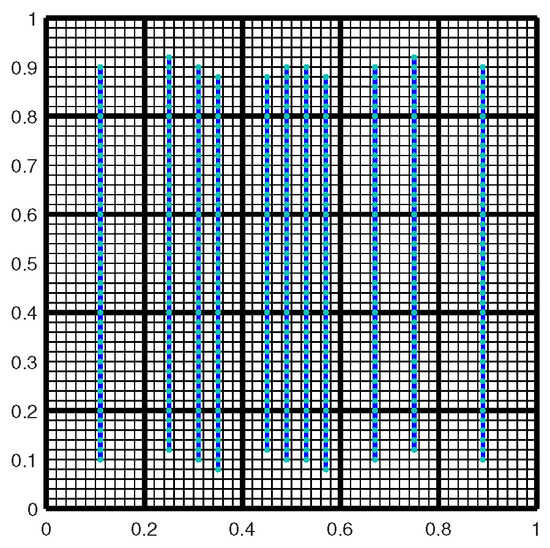
The fracture configuration is shown in Figure 1 with 11 vertical fractures, and the related mesh is also presented. The boundary condition is

$$p=1\mathrm{on}x=0,p=0\mathrm{on}x=1,{\displaystyle \frac{\partial p}{\partial n}}=0\mathrm{on}y=0\mathrm{and}y=1,$$

(72)

where n is the outward unit-normal vector on $\partial \Omega$. We take the matrix permeability ${\kappa }^m=1$ and consider three different fracture permeabilities ${\kappa }^f=$$1\times {10}^2,1\times {10}^4,1\times {10}^6$.

Figure 1. The fracture configuration fracture 1 in Example 1. The blue lines indicate fractures; the light green dots indicate grid nodes of the fractures.

The convergence histories of online enrichment by selecting 1, 2, 3, and 4 offline basis functions per coarse cell as the initial basis functions are, respectively, shown in Table 1, Table 2, Table 3 and Table 4, where `#Dofs’ means the number of multiscale basis functions in $V_g$, and ${\Lambda }_{min}={min}_{j=1,2,3,4}{\Lambda }_{min,j}$ is the minimum value of eigenvalues that the related eigenfunctions are not included in the initial multiscale space.

Table 1. (Example 1) The online enrichment with 1 initial basis function per coarse cell.

#Dofs	${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^2$, ${\mathbf{\Lambda }}_{min}=0.0021$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^4$, ${\mathbf{\Lambda }}_{min}=2.5631\times {10}^{-5}$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^6$, ${\mathbf{\Lambda }}_{min}=2.5686\times {10}^{-7}$
	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$
25	0.0745	3.0000	0.0745	3.0000	0.0745	3.0000
50	0.0673	0.7300	0.0782	0.7819	0.0784	0.7826
75	0.0610	0.5252	0.0852	0.6512	0.0854	0.6525
100	0.0303	0.3270	0.0871	0.6155	0.0877	0.6182
125	0.0124	0.1619	0.0921	0.5880	0.0933	0.5917

Table 2. (Example 1) The online enrichment with 2 initial basis functions per coarse cell.

#Dofs	${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^2$, ${\mathbf{\Lambda }}_{min}=0.0072$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^4$, ${\mathbf{\Lambda }}_{min}=8.0721\times {10}^{-5}$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^6$, ${\mathbf{\Lambda }}_{min}=8.0807\times {10}^{-7}$
	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$
50	0.1037	1.3101	0.1013	1.5461	0.2074	2.0073
75	0.0148	0.2534	0.0311	0.3569	0.0679	0.5138
100	0.0061	0.1126	0.0062	0.1245	0.0561	0.3616
125	0.0020	0.0358	0.0040	0.0657	0.0300	0.2527
150	7.9617 × 10−4	0.0151	0.0040	0.0565	0.0171	0.1812

Table 3. (Example 1) The online enrichment with 3 initial basis functions per coarse cell.

#Dofs	${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^2$, ${\mathbf{\Lambda }}_{min}=0.0123$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^4$, ${\mathbf{\Lambda }}_{min}=1.2434\times {10}^{-4}$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^6$, ${\mathbf{\Lambda }}_{min}=1.2432\times {10}^{-6}$
	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$
75	0.0759	0.6927	0.0823	0.7418	0.1336	0.8385
100	0.0142	0.1958	0.0143	0.2007	0.0384	0.3188
125	0.0055	0.0735	0.0058	0.0760	0.0243	0.1923
150	0.0020	0.0257	0.0039	0.0515	0.0097	0.1099
175	8.2117 × 10−4	0.0112	0.0033	0.0469	0.0040	0.0633

Table 4. (Example 1) The online enrichment with 4 initial basis functions per coarse cell.

#Dofs	${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^2$, ${\mathbf{\Lambda }}_{min}=0.0147$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^4$, ${\mathbf{\Lambda }}_{min}=0.0135$		${\mathit{\kappa }}^{\mathit{f}}=1\times {10}^6$, ${\mathbf{\Lambda }}_{min}=0.0135$
	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$
100	0.0616	0.5955	0.0720	0.5902	0.0722	0.5907
125	0.0145	0.2025	0.0115	0.1922	0.0115	0.1925
150	0.0047	0.0688	0.0027	0.0520	0.0027	0.0520
175	0.0017	0.0214	8.0132 × 10−4	0.0132	8.0084 × 10−4	0.0132
200	4.4674 × 10−4	0.0071	1.5293 × 10−4	0.0033	1.4898 × 10−4	0.0032

For example, in Table 1, we use 1 initial basis function per coarse cell. Since there are $5\times 5=25$ coarse cells, the initial multiscale space includes 25 Dofs. By the initial multiscale space, we solve the initial multiscale solution and by which we compute online basis functions iteratively to enrich the initial multiscale space, i.e., obtain the multiscale space in the next level, which has 50 Dofs. Similarly, by the new multiscale space, we solve the corresponding multiscale solution, and by which we compute online basis functions to enrich the multiscale space again. For the multiscale solution in each level, we calculate the relative errors $E_0$ and $E_a$ compared to the fine-grid solution by use of (71).

From these tables, we observe that for different fracture permeabilities, the values of ${\Lambda }_{min}$ with 4 initial basis functions per coarse cell are similar, while they are distinctive with 1, 2, and 3 initial basis functions per coarse cell, and the former are greater than the later. Accordingly, the convergence rates with 4 initial basis functions per coarse cell are similar for different fracture permeabilities, and the relative error reductions are visibly faster than the relative error reductions with 1, 2, and 3 initial basis functions per coarse cell. This example shows that initial basis functions are vitally important for the online enrichment, and with enough number of initial basis functions, convergence rates are independent of the matrix-fracture permeability contrasts, coinciding with the result in Theorem 1.

Example 2.

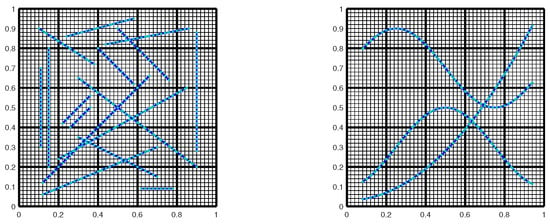
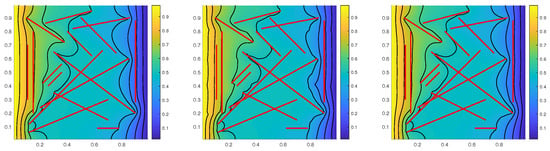
We test two different fracture configurations: Fracture 2 and Fracture 3, as shown in Figure 2. In Fracture 2, the fractures are intersected with each other, having different orientations, directions and lengths, and some of them are completely immersed, partially immersed or not immersed in one coarse cell. In Fracture 3, the fractures are curvilinear and also intersected with each other. The boundary condition is the same as (72). The matrix permeability and fracture permeability are, respectively, taken as ${\kappa }^m=1$ and ${\kappa }^f=$$1\times {10}^6$. We use 3 initial basis functions per coarse cell for the online enrichment, and the convergence history is shown in Table 5. The relative errors reduce rapidly for these two fracture configurations. Figure 3 and Figure 4 present comparisons for the pressure and contours between the fine-grid solution and multiscale solutions with 4 and 5 basis functions per coarse cell (including 3 initial basis functions), and we find that multiscale solutions supply good approximations after the addition of two online basis functions per coarse cell.

Figure 2. Two fracture configurations Fracture 2 (left) and Fracture 3 (right) in Example 2. The blue lines indicate fractures; the light green dots indicate grid nodes of the fractures.

Table 5. (Example 2) The online enrichment with 3 initial basis functions per coarse cell.

#Dofs	Fracture 2		Fracture 3
	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$	${\mathit{E}}_{\mathbf{0}}$	${\mathit{E}}_{\mathit{a}}$
75	0.1156	0.7277	0.1098	0.7177
100	0.0175	0.1812	0.0141	0.1989
125	0.0027	0.0529	0.0028	0.0401
150	3.9197 × 10−4	0.0108	8.4589 × 10−4	0.0108
175	7.2413 × 10−5	0.0027	1.8707 × 10−4	0.0032

Figure 3. (Example 2) The fine-grid solution (left), multiscale solutions with 4 (middle) and 5 (right) basis functions per coarse cell of Fracture 2.

Figure 4. (Example 2) The fine-grid solution (left), multiscale solutions with 4 (middle) and 5 (right) basis functions per coarse cell of Fracture 3.

Example 3.

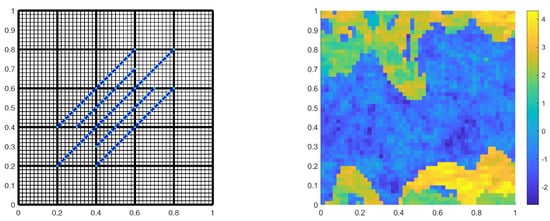
The fracture configuration is shown in the left graph of Figure 5, the matrix permeability ${\kappa }^m$ is heterogeneous, as shown in the right graph of Figure 5, the fracture permeability ${\kappa }^f=$$1\times {10}^6$, the boundary condition is taken as

$${\displaystyle \frac{\partial p}{\partial n}}=0\mathrm{on}\partial \Omega ,$$

(73)

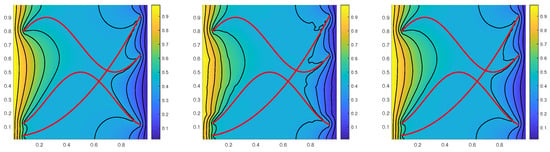
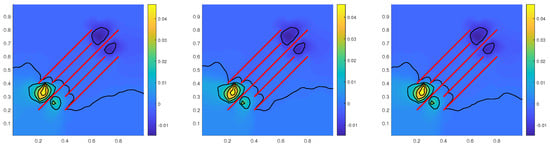
the matrix source term $Q^m$ takes values 1 and $-1$ in the subdomains ${[0.2,0.4]}^2$ and ${[0.6,0.8]}^2$, respectively, and 0 in other places, the fracture source term $Q^f=0$. As Example 2, with 3 initial basis functions per coarse cell, the relative errors also reduce rapidly, which are presented in Table 6. Figure 6 gives comparisons for the fine-grid solution and multiscale solutions with 4, 5 basis functions per coarse cell (including 3 initial basis functions), multiscale solutions still approximate the fine-grid solution well when the matrix rock is of high heterogeneity.

Figure 5. The fracture configuration Fracture 4 (left) and the matrix permeability (right, logarithmic scale) in Example 3. In the left graph, the blue lines indicate fractures; the light green dots indicate grid nodes of the fractures.

Table 6. (Example 3) The online enrichment with 3 initial basis functions per coarse cell.

#Dofs	${\mathit{E}}_0$	${\mathit{E}}_{\mathit{a}}$
75	0.3127	0.4936
100	0.1025	0.1079
125	0.0445	0.0451
150	0.0159	0.0145
175	0.0032	0.0037

Figure 6. (Example 3) The fine-grid solution (left), multiscale solutions with 4 (middle) and 5 (right) basis functions per coarse cell of Fracture 4.

5. Conclusions

In this paper, for the simulation of flow in fractured porous media by utilizing an embedded discrete fracture model, an online generalized multiscale method has been proposed to improve the computational efficiency, which can well cope with the various fractures with different orientations, directions, lengths, and permeabilities, and also highly heterogeneous matrix rock. Based on the linear algebraic system results from the two-point flux-approximation scheme of the finite volume method, we derive the corresponding discrete weak formulation so that the framework of generalized multiscale finite element methods can be conveniently integrated. To build the initial multiscale space, we solved a series of local problems with specific boundary conditions and a given eigenvalue problem for the spectral decomposition on each coarse cell, which contains the dominant multiscale information owing to local fractures. We calculated online basis functions, relying on the residuals to enrich the multiscale space so that the global multiscale information could be captured to reduce the impact of distant effects. Convergence analyses and many numerical examples are also given, which are consistent with the notion that the more initial basis functions, the faster the rates of convergence.