Sensitivity Analysis of Eigenvalues for PDNT Toeplitz Matrices

Abstract

This study focuses on a class of perturbed Dirichlet–Neumann tridiagonal (PDNT) Toeplitz matrices, mainly exploring their eigenvalue sensitivity and inverse problems. By the explicit expressions for eigenvalues and eigenvectors of PDNT Toeplitz matrices, an analytical formula for the eigenvalue condition number is proposed, and numerical experiments are presented based on the theoretical results. Meanwhile, the stability of eigenvalues is analyzed with respect to structured perturbations and pseudospectral properties, and finally, two inverse eigenvalue problems are discussed.

1. Introduction

The structured distance of PDNT Toeplitz matrices has been discussed [1]. This paper mainly studies the eigenvalue sensitivity of such matrices and explores their inverse eigenvalue problems.

Tridiagonal Toeplitz matrices find significant applications in resistance network modeling [2], quantum anomalous Hall effect analysis [3], and molecular orbital theory [4]. They are also widely used in partial differential equations [5,6,7,8], time series decomposition [9], and Tikhonov regularization of discrete ill-posed problems [10,11]. Thus, studying their fundamental computational properties is essential.

Previous studies have achieved fruitful results in the numerical algebra of banded and quasi-banded matrices. Refs [12,13,14] systematically investigate efficient solvers for linear systems arising from such matrices and propose fast algorithms for determinant evaluation. Ref [15] focuses on tridiagonal Toeplitz matrices, analyzes their pivoting patterns under various diagonal-dominance conditions, and constructs an efficient block LU factorization accordingly. In addition, [16] independently addresses the eigenvalue problem of a class of symmetric tridiagonal matrices.

Norm equalities and inequalities for perturbed tridiagonal Toeplitz matrices are concentrated on in [17], while closed-form expressions and fast algorithms for the determinants, inverses, and eigenpairs of periodical or border-perturbed tridiagonal Toeplitz matrices are focused on in [18,19,20,21]. Meanwhile, systematic analysis approaches for two regular matrix pairs are presented in [22,23,24]. With respect to $\epsilon$-pseudospectral separations in banded Toeplitz matrices, works [25,26,27] reveal characteristic spectral behaviors through investigation. Tridiagonal Toeplitz matrix operators have become a research focus due to their dual strengths: efficient computation of key metrics and multidisciplinary applicability. In foundational works such as [28,29,30,31], Biswa Datta was the first to investigate multiple themes, among which are the inverse eigenvalue problems discussed here.

The structure of this paper is as follows: First, we clarify the definitions and related lemmas employed in this research. The study of eigenvalue sensitivity is placed in Section 3, and Section 4 presents numerical examples. The main task of Section 5 is to solve the inverse eigenvalue problem.

2. Main Concepts and Definitions

This paper employs the Euclidean norm ${\parallel ·\parallel }_2$ and the Frobenius norm ${\parallel ·\parallel }_F$ to quantify vectors and matrices, respectively.

Definition 1

([1]).

$$\begin{array}{c}\hfill \mathbb{E}=\left(\begin{array}{ccccccc}{\gamma }_0-\sqrt{{\gamma }_1{\gamma }_2}& {\gamma }_1& & & & & O\\ {\gamma }_2& {\gamma }_0& {\gamma }_1& & & & \\ & {\gamma }_2& ·& ·& & & \\ & & ·& ·& ·& & \\ & & & ·& ·& ·& \\ & & & & ·& ·& \sqrt{2}{\gamma }_1\\ O& & & & & \sqrt{2}{\gamma }_2& {\gamma }_0\end{array}\right)\in {\mathbf{C}}^{z\times z}.\end{array}$$

(1)

As a z-order square matrix satisfying Equation (1), the PDNT Toeplitz matrix has the standardized form $\mathbb{E}$ = (z;$-\sqrt{{\gamma }_1{\gamma }_2}$,${\gamma }_2$,${\gamma }_0$,${\gamma }_1$,$\sqrt{2}{\gamma }_2$,$\sqrt{2}{\gamma }_1$). The phase parameters are further defined as follows:

$$\begin{array}{c}\hfill {\varpi }_1=arg{\gamma }_2,{\varpi }_2=arg{\gamma }_1,{\varpi }_3=arg{\gamma }_0.\end{array}$$

(2)

In particular, when ${\gamma }_0=0$, ${\mathbb{E}}_0=(z;-\sqrt{{\gamma }_1{\gamma }_2},{\gamma }_2,0,{\gamma }_1,\sqrt{2}{\gamma }_2,\sqrt{2}{\gamma }_1)$.

Lemma 1

([1]). Let $\mathbb{E}$ be a PDNT Toeplitz matrix. Then, the right eigenvector $v^{\left(j\right)}={[v_1^{\left(j\right)},\dots ,v_z^{\left(j\right)}]}^T$ corresponding to the eigenvalue ${\lambda }_j\left(\mathbb{E}\right)$ of matrix $\mathbb{E}$ is given by

$$\begin{array}{c}\hfill v_k^{\left(j\right)}={\displaystyle \frac{2}{\sqrt{2z-1}}}{d}_k{d}_j{\left(\sqrt{{\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}}\right)}^{k-1}sin{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}},k=1,\dots ,z,j=1,\dots ,z.\end{array}$$

(3)

Similarly, the left eigenvector $u^{\left(j\right)}={[u_1^{\left(j\right)},\dots ,u_z^{\left(j\right)}]}^T$ is expressed as

$$\begin{array}{c}\hfill u_k^{\left(j\right)}={\displaystyle \frac{2}{\sqrt{2z-1}}}{d}_k{d}_j{\left(\sqrt{{\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}}\right)}^{k-1}sin{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}},k=1,\dots ,z,j=1,\dots ,z,\end{array}$$

(4)

where

$$\begin{array}{c}\hfill {\lambda }_j\left(\mathbb{E}\right)={\gamma }_0+2\sqrt{{\gamma }_1{\gamma }_2}cos{\displaystyle \frac{(2j-1)\pi }{2z-1}},j=1,\dots ,z.\end{array}$$

(5)

And $d_r=\left\{\begin{array}{cc}1\hfill & \hfill r\ne z,\\ {\displaystyle \frac{\sqrt{2}}{2}}\hfill & \hfill r=z,\end{array}\right.$ ${\overline{\gamma }}_1$ and ${\overline{\gamma }}_2$ represent the complex conjugates of ${\gamma }_1$ and ${\gamma }_2$, respectively.

${\mathbb{E}}^{*}$ denotes the normal PDNT matrix minimizing the Frobenius norm distance to $\mathbb{E}$, with parameters ${\gamma }_0^{*}={\gamma }_0$, ${\gamma }_1^{*}=\Pi e^{i{\varpi }_2}$, and ${\gamma }_2^{*}=\Pi e^{i{\varpi }_1}$, where ${\varpi }_1$ and ${\varpi }_2$ are given by $\left(2\right)$, and

$$\Pi ={\displaystyle \frac{\sqrt{\left|{\gamma }_1{\gamma }_2\right|}+z(\left|{\gamma }_1\right|+\left|{\gamma }_2\right|)}{2z+1}}.$$

Furthermore, the eigenvalues of ${\mathbb{E}}^{*}$ are explicitly expressed as follows:

$${\lambda }_j\left({\mathbb{E}}^{*}\right)={\gamma }_0+2\Pi e^{{\displaystyle \frac{\left({\varpi }_1+{\varpi }_2\right)i}{2}}}cos{\displaystyle \frac{(2j-1)\pi }{2z-1}},j=1,\dots ,z.$$

(6)

3. Eigenvalue Sensitivity

Regarding eigenvalue analysis of general matrices, extensive research has been conducted on various aspects, such as condition numbers and sensitivity, see references [32,33,34,35]. Ref. [36] derives bounds for structured eigenvalue condition numbers and analyzes the effect of different algebraic structures on eigenvalue sensitivity. In references [37,38], the zero-structured, patterned, and traditional condition numbers of simple eigenvalues are compared, and the eigenvalue sensitivities of Toeplitz and Hankel matrices under patterned perturbations are analyzed through numerical experiments.

We examine the eigenvalue sensitivity of matrices ${\mathbb{E}}_0$ and $\mathbb{E}$ from various perspectives.

To quantify the sensitivity of eigenvalue set

$$\overrightarrow{A}\left({\mathbb{E}}_0\right)=[{\lambda }_1\left({\mathbb{E}}_0\right),\dots ,{\lambda }_z\left({\mathbb{E}}_0\right)]$$

to perturbations in ${\gamma }_1$ and ${\gamma }_2$, we introduce a mapping

$$o:H\subset {\mathbf{C}}^2\to o\left(H\right)\subset {\mathbf{C}}^z,H=\{({\gamma }_1,{\gamma }_2)\in {\mathbf{C}}^2:{\gamma }_1{\gamma }_2\ne 0\}:\overrightarrow{A}\left({\mathbb{E}}_0\right)=o({\gamma }_1,{\gamma }_2).$$

The sensitivity of $\overrightarrow{A}\left({\mathbb{E}}_0\right)$ to ${\gamma }_1$ and ${\gamma }_2$ perturbations is directly related to the Jacobian matrix of o, with the detailed analysis proceeding as follows:

$$\begin{array}{c}\hfill {\displaystyle \sum _{j=1}^z}{cos}^2{\displaystyle \frac{(2j-1)\pi }{2z-1}}=\left\{\begin{array}{cc}1,\hfill & z=1,\hfill \\ {\displaystyle \frac{2z+1}{4}},\hfill & z>1.\hfill \end{array}\right.\end{array}$$

(7)

From (5), the Jacobian matrix of o takes the following form.

$$D_o({\gamma }_1,{\gamma }_2)=\left(\begin{array}{cc}\sqrt{{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}}cos{\displaystyle \frac{\pi }{2z-1}}& \sqrt{{\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}}cos{\displaystyle \frac{\pi }{2z-1}}\\ \sqrt{{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}}cos{\displaystyle \frac{3\pi }{2z-1}}& \sqrt{{\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}}cos{\displaystyle \frac{3\pi }{2z-1}}\\ ⋮& ⋮\\ \sqrt{{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}}cos{\displaystyle \frac{(2z-3)\pi }{2z-1}}& \sqrt{{\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}}cos{\displaystyle \frac{(2z-3)\pi }{2z-1}}\\ -\sqrt{{\displaystyle \frac{{\gamma }_1}{{\gamma }_2}}}& -\sqrt{{\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}}\end{array}\right)\in {\mathbb{E}}^{z\times 2}.$$

(8)

After substituting Equations $\left(7\right)$ and $\left(8\right)$ into the Frobenius norm operation, the derivation results in

$${∥D_o({\gamma }_1,{\gamma }_2)∥}_F=\left\{\begin{array}{c}\sqrt{{\displaystyle \frac{\left|{\gamma }_1\right|}{\left|{\gamma }_2\right|}}+{\displaystyle \frac{\left|{\gamma }_2\right|}{\left|{\gamma }_1\right|}}},z=1,\hfill \\ {\displaystyle \frac{\sqrt{2z+1}}{2}}\sqrt{{\displaystyle \frac{\left|{\gamma }_1\right|}{\left|{\gamma }_2\right|}}+{\displaystyle \frac{\left|{\gamma }_2\right|}{\left|{\gamma }_1\right|}}},z>1.\hfill \end{array}\right.$$

(9)

When considering relative errors in ${\gamma }_1$, ${\gamma }_2$ and ${\lambda }_j\left({\mathbb{E}}_0\right)$, the analogue to $\left(8\right)$ becomes a $z\times 2$ matrix.

$${\mathrm{X}}_o({\gamma }_1,{\gamma }_2)=\left(\begin{array}{cc}{\displaystyle \frac{{\gamma }_2}{{\lambda }_1\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{1,1}& {\displaystyle \frac{{\gamma }_1}{{\lambda }_1\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{1,2}\\ {\displaystyle \frac{{\gamma }_2}{{\lambda }_2\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{2,1}& {\displaystyle \frac{{\gamma }_1}{{\lambda }_2\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{2,2}\\ ⋮& ⋮\\ {\displaystyle \frac{{\gamma }_2}{{\lambda }_{z-1}\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{z-1,1}& {\displaystyle \frac{{\gamma }_1}{{\lambda }_{z-1}\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{z-1,2}\\ {\displaystyle \frac{{\gamma }_2}{{\lambda }_z\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{z,1}& {\displaystyle \frac{{\gamma }_1}{{\lambda }_z\left(E_0\right)}}{\left(D_o({\gamma }_1,{\gamma }_2)\right)}_{z,2}\end{array}\right)=\left(\begin{array}{cc}{\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\\ ⋮& ⋮\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\\ {\displaystyle \frac{1}{2}}& {\displaystyle \frac{1}{2}}\end{array}\right).$$

The matrix ${\mathrm{X}}_o({\gamma }_1,{\gamma }_2)$ is found to possess the following properties

$${\mathrm{X}}_o{({\gamma }_1,{\gamma }_2)}^H{\mathrm{X}}_o({\gamma }_1,{\gamma }_2)={\displaystyle \frac{z}{4}}\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right),$$

where ${\mathrm{X}}_o{({\gamma }_1,{\gamma }_2)}^H$ is the Hermitian adjoint of ${\mathrm{X}}_o({\gamma }_1,{\gamma }_2)$.

With both its spectral norm and Frobenius norm yielding

$${∥{\mathrm{X}}_o({\gamma }_1,{\gamma }_2)∥}_2={∥{\mathrm{X}}_o({\gamma }_1,{\gamma }_2)∥}_F=\sqrt{{\displaystyle \frac{z}{2}}}.$$

We introduce the ratio g as

$$g=\left\{\begin{array}{cc}{\displaystyle \frac{|{\gamma }_2|}{|{\gamma }_1|}},\hfill & |{\gamma }_2|<|{\gamma }_1|,\hfill \\ {\displaystyle \frac{|{\gamma }_1|}{|{\gamma }_2|}},\hfill & |{\gamma }_1|<|{\gamma }_2|.\hfill \end{array}\right.$$

(10)

Remark 1.

The norm of $X_o$ remains immune to changes in ${\gamma }_1$ and ${\gamma }_2$, while the norm of $D_o$ is governed by g. Notably, as g decreases, the Frobenius norm of $D_o({\gamma }_1,{\gamma }_2)$ approaches positive infinity. Moreover, if and only if $|{\gamma }_1|=|{\gamma }_2|$,

$${∥D_o({\gamma }_1,{\gamma }_2)∥}_F=\left\{\begin{array}{c}\sqrt{2},z=1,\hfill \\ \sqrt{{\displaystyle \frac{2z+1}{2}}},z>1.\hfill \end{array}\right.$$

3.1. Individual Eigenvalue Condition Numbers

This section focuses on the analysis of individual eigenvalue condition numbers.

We first prove an essential trigonometric identity

$${\displaystyle \sum _{k=1}^z}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}=\left\{\begin{array}{c}1,z=1,\hfill \\ {\displaystyle \frac{2z+1}{4}},z>1.\hfill \end{array}\right.$$

(11)

Proof. 

For $z=1$, we have

$${sin}^2{\displaystyle \frac{(2j-1)\pi }{2}}=1.$$

For $z>1$, using the identity ${sin}^2\theta =\frac{1}{2}(1-cos2\theta )$, we obtain

$${\displaystyle \sum _{k=1}^z}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}={\displaystyle \frac{1}{2}}{\displaystyle \sum _{k=1}^z}\left(1-cos{\displaystyle \frac{(2k-1)(2j-1)\pi }{2z-1}}\right).$$

Thus,

$${\displaystyle \sum _{k=1}^z}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}={\displaystyle \frac{z}{2}}-{\displaystyle \frac{1}{2}}{\displaystyle \sum _{k=1}^z}cos{\displaystyle \frac{(2k-1)(2j-1)\pi }{2z-1}}.$$

By the formula for the sum of cosines of equally spaced angles, it follows that

$${\displaystyle \sum _{k=1}^z}cos{\displaystyle \frac{(2k-1)(2j-1)\pi }{2z-1}}=-{\displaystyle \frac{1}{2}}.$$

Substituting this result, we get

$${\displaystyle \sum _{k=1}^z}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}={\displaystyle \frac{2z+1}{4}}.$$

□

When ${\gamma }_1{\gamma }_2\ne 0$, a series of subsequent results are derived from Equations (3), (4), and (11).

For $j=1,\dots ,z,$

$$\begin{array}{cc}\hfill {\parallel v^{\left(j\right)}\parallel }_2^2& ={\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{|{\gamma }_2|}{|{\gamma }_1|}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\parallel u^{\left(j\right)}\parallel }_2^2& ={\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{|{\gamma }_1|}{|{\gamma }_2|}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}},\hfill \end{array}$$

(13)

and

$$\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)={\displaystyle \frac{\parallel v^{\left(j\right)}{\parallel }_2{\parallel u^{\left(j\right)}\parallel }_2}{|{\left(u^{\left(j\right)}\right)}^H{v}^{\left(j\right)}|}}.$$

(14)

If $|{\gamma }_1|=|{\gamma }_2|$, the PDNT Toeplitz matrix $\mathbb{E}$ is normal, and its eigenvectors satisfy

$${∥v^{\left(j\right)}∥}_2^2={∥u^{\left(j\right)}∥}_2^2={\displaystyle \sum _{k=1}^z}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}=\left\{\begin{array}{c}1,z=1,\hfill \\ {\displaystyle \frac{2z+1}{4}},z>1,\hfill \end{array}\right.j=1,2,\dots ,z.$$

The eigenvalue condition number then reduces to

$$\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)=\left\{\begin{array}{c}\begin{array}{c}1,j=1,\hfill \\ {\displaystyle \frac{2z-1}{2z+1}},2\le j\le z-1,\hfill \end{array}\hfill \\ {\displaystyle \frac{2\left(2z-1\right)}{2z+1}},j=z.\hfill \end{array}\right.$$

(15)

To prove the subsequent theorem, we first derive the following identities from Euler’s formula

$$\begin{array}{cc}\hfill {\displaystyle \sum _{k=0}^z}{n}^{k}sinkx& ={\displaystyle \frac{n^{z+2}sinzx-n^{z+1}sin(z+1)x+nsinx}{n^2-2ncosx+1}},\hfill \\ \hfill {\displaystyle \sum _{k=0}^z}{n}^{k}coskx& ={\displaystyle \frac{1-ncosx-n^{z+1}cos(z+1)x+n^{z+2}coszx}{n^2-2ncosx+1}}.\hfill \end{array}$$

(16)

Furthermore, the following trigonometric relations hold immediately, let $p={\displaystyle \frac{(2j-1)\pi }{2z-1}},$

$$\begin{array}{cccc}\hfill sin\left(2(z-1)p\right)& =sinp,\hfill & \hfill cos\left(2(z-1)p\right)& =-cosp,\hfill \\ \hfill sin\left(2zp\right)& =-sinp,\hfill & \hfill cos\left(2zp\right)& =-cosp.\hfill \end{array}$$

(17)

Theorem 1.

For a PDNT Toeplitz matrix $\mathbb{E}$, assuming $|{\gamma }_1|>|{\gamma }_2|$ without loss of generality, the eigenvalue condition number $\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)$ exhibits two cases.

For $z=1$: ${∥v^{\left(j\right)}∥}_2^2={∥u^{\left(j\right)}∥}_2^2=1$, $\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)=1$.

For $z>1$: if $j=z$,

$$\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)={\displaystyle \frac{2\sqrt{2-6g^z+2g^{2z}+2g-g^{z+1}-g^{z-1}+2g^{2z-1}}}{g^{\left(z-1\right)/2}\left(2z+1\right)\left(1-g\right)}};$$

(18)

if $j\ne z$,

$$\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)={\displaystyle \frac{2\sqrt{4M-2N+1}}{2z+1}};$$

(19)

where M and N are defined as

$$M=\Phi \Omega ,N={\displaystyle \frac{\Phi }{g^{z-1}}}+g^{z-1}\Omega .$$

And

$$\Phi ={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1-g^z}{1-g}}-{\displaystyle \frac{cosp-gcosp+g^{z}cos2p-g^{z+1}}{g^2-2gcos2p+1}}\right),$$

$$\Omega ={\displaystyle \frac{1}{2g^{z-1}}}\left({\displaystyle \frac{1-g^z}{1-g}}-{\displaystyle \frac{g^{z+1}cosp-g^{z}cosp+gcos2p-1}{g^2-2gcos2p+1}}\right).$$

Here, $p={\displaystyle \frac{(2j-1)\pi }{2z-1}}$ ($j=1,2,\dots ,z-1$), and g is defined in Equation (10).

Proof. 

When $z>1$ and $|{\gamma }_1|>|{\gamma }_2|$, then $g={\displaystyle \frac{|{\gamma }_2|}{|{\gamma }_1|}}$. For an eigenvalue ${\lambda }_j$ with $j=1,2,\dots ,z$, define $p={\displaystyle \frac{(2j-1)\pi }{2z-1}}$. By trigonometric half-angle identities, the summation simplifies to

$${\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{|{\gamma }_2|}{|{\gamma }_1|}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}={\displaystyle \frac{1}{2}}({\displaystyle \sum _{k=1}^z}{g}^{k-1}-{\displaystyle \sum _{k=0}^{z-1}}{g}^{k}cos(2k+1)p).$$

(20)

From Equations (16) and (17), we derive the following:

$$\begin{array}{cc}\hfill {\displaystyle \sum _{k=0}^{z-1}}{g}^{k}cos(2k+1)p& =cosp{\displaystyle \sum _{k=0}^{z-1}}{g}^{k}cos2kp-sinp{\displaystyle \sum _{k=0}^{z-1}}{g}^{k}sin2kp\hfill \\ \hfill & ={\displaystyle \frac{cosp-gcosp+g^{z}cos2p-g^{z+1}}{g^2-2gcos2p+1}}.\hfill \end{array}$$

(21)

Let $\Phi$ denote ${\sum }_{k=1}^z{\left({\displaystyle \frac{|{\gamma }_2|}{|{\gamma }_1|}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}$ and $\Omega$ denote ${\sum }_{k=1}^z{\left({\displaystyle \frac{|{\gamma }_1|}{|{\gamma }_2|}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}.$ Consequently, the following conclusion can be drawn based on Equations (20) and (21):

$$\Phi ={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{1-g^z}{1-g}}-{\displaystyle \frac{cosp-gcosp+g^{z}cos2p-g^{z+1}}{g^2-2gcos2p+1}}\right),$$

(22)

and analogously,

$$\Omega ={\displaystyle \frac{1}{2g^{z-1}}}\left({\displaystyle \frac{1-g^z}{1-g}}-{\displaystyle \frac{g^{z+1}cosp-g^{z}cosp+gcos2p-1}{g^2-2gcos2p+1}}\right).$$

(23)

Using Equations (12) and (13), the following can be obtained:

$$\begin{array}{c}\hfill {∥v^{\left(j\right)}∥}_2^2=\left\{\begin{array}{c}{\displaystyle \frac{4}{2z-1}}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}-{\displaystyle \frac{2}{2z-1}}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{z-1},j\ne z,\hfill \\ {\displaystyle \frac{2}{2z-1}}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{k-1}-{\displaystyle \frac{1}{2z-1}}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{z-1},j=z,\hfill \end{array}\right.\\ \hfill {∥u^{\left(j\right)}∥}_2^2=\left\{\begin{array}{c}{\displaystyle \frac{4}{2z-1}}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}-{\displaystyle \frac{2}{2z-1}}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{z-1},j\ne z,\hfill \\ {\displaystyle \frac{2}{2z-1}}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{k-1}-{\displaystyle \frac{1}{2z-1}}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{z-1},j=z.\hfill \end{array}\right.\end{array}$$

(24)

By (3) and (4), we can get

$$\left|{u^{\left(j\right)}}^H{v}^{\left(j\right)}\right|=\left\{\begin{array}{c}\begin{array}{c}{\displaystyle \frac{2z+1}{2z-1}},j\ne z,\hfill \end{array}\hfill \\ {\displaystyle \frac{2z+1}{2(2z-1)}},j=z.\hfill \end{array}\right.$$

(25)

Based on the preceding results and substituting Equations (24) and (25) into Equation (14), we obtain the expression for the condition number of the j-th eigenvalue as

$$\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)=\left\{\begin{array}{c}{\displaystyle \frac{2\sqrt{4M-2N+1}}{2z+1}},j\ne z,\hfill \\ {\displaystyle \frac{2\sqrt{4\left({\displaystyle \sum _{k=1}^z}{\left(\frac{{\gamma }_2}{{\gamma }_1}\right)}^{k-1}{\displaystyle \sum _{k=1}^z}{\left(\frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}\right)}^{k-1}\right)-2\left({\left(\frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}\right)}^{z-1}{\displaystyle \sum _{k=1}^z}{\left(\frac{{\gamma }_2}{{\gamma }_1}\right)}^{k-1}+{\left(\frac{{\gamma }_2}{{\gamma }_1}\right)}^{z-1}{\displaystyle \sum _{k=1}^z}{\left(\frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}\right)}^{k-1}\right)+1}}{2z+1}},j=z,\hfill \end{array}\right.$$

where

$$\begin{array}{c}M={\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}},\hfill \\ N={\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{z-1}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}}+{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{z-1}{\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{k-1}{sin}^2{\displaystyle \frac{(2k-1)(2j-1)\pi }{2(2z-1)}},\hfill \\ {\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\gamma }_2}{{\gamma }_1}}\right)}^{k-1}={\displaystyle \frac{1-{\left(\frac{{\gamma }_2}{{\gamma }_1}\right)}^z}{1-\frac{{\gamma }_2}{{\gamma }_1}}},\hfill \\ {\displaystyle \sum _{k=1}^z}{\left({\displaystyle \frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}\right)}^{k-1}={\displaystyle \frac{1-{\left(\frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}\right)}^z}{1-\frac{{\overline{\gamma }}_1}{{\overline{\gamma }}_2}}}.\hfill \end{array}$$

Substituting Equations (22) and (23) yields the desired result.

When $z=1$, $\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)=1$ obviously holds. □

Remark 2.

For $z>1$, Equation (19) can be rewritten via algebraic manipulation as follows:

When $j\ne z$,

$$\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)={\displaystyle \frac{1}{(2z+1)g^{(z-1)/2}(1-g)}}{K}_2,$$

(26)

where $K_2=2g^{\left(z-1\right)/2}\left(1-g\right)\sqrt{4M-2N+1}$, $p={\displaystyle \frac{(2j-1)\pi }{2z-1}}$.

Though the explicit forms of polynomial combinations M and N are omitted, theoretical analysis and numerical experiments confirm $K_2\ge 0.$

3.2. The Global Eigenvalue Condition Number

This section systematically investigates the global condition number:

$${\kappa }_F\left(\lambda \right)={\displaystyle \sum _{k=1}^z}\kappa \left({\lambda }_k\left(\mathbb{E}\right)\right).$$

(27)

This property provides an explicit analytical method for computation.

By substituting Equations (18) and (19) into Equation (27), we obtain expression for the global condition number ($z>1$):

$${\kappa }_F\left(\lambda \right)={\displaystyle \sum _{j=1}^{z-1}}\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)+\kappa \left({\lambda }_z\left(\mathbb{E}\right)\right).$$

For PDNT Toeplitz matrices $\mathbb{E}$ satisfying $|{\gamma }_1|=|{\gamma }_2|$, their parameter bounds can be determined through Equations (3) and (4).

For PDNT Toeplitz matrices $\mathbb{E}$ with $|{\gamma }_1|\ne |{\gamma }_2|$, we are able to the bounds: ${\kappa }_F\left(\lambda \right)\ge 0.$

3.3. The $\epsilon$-Pseudospectrum

Given $\epsilon >0$, follow [27], the $\epsilon$-pseudospectrum of $\mathbb{E}$$\in {\mathbf{C}}^{z\times z}$ is defined as the set ${\Theta }_{\epsilon }\left(\mathbb{E}\right)$

$${\Theta }_{\epsilon }\left(\mathbb{E}\right)={\{y:\Vert (yI-\mathbb{E})}^{-1}{\Vert }_2\ge {\epsilon }^{-1}\}.$$

An alternative, equivalent definition that will be utilized in Section 5 is as follow:

$${\Theta }_{\epsilon }\left(\mathbb{E}\right)=\{y:\exists l\in {\mathbf{C}}^z{,\Vert l\Vert }_2={1,\mathrm{such}\mathrm{that}\Vert (yI-\mathbb{E})l\Vert }_2\le \epsilon \},$$

(28)

the vectors l in this definition are referred to as $\epsilon$-pseudoeigenvectors.

First, define the function

$$f\left(y\right)={\gamma }_{1}y+{\gamma }_0+{\gamma }_2{y}^{-1},$$

and then further construct the ellipse

$$f\left(S\right)=\left\{f\right(y):y\in \mathbf{C},\mid y\mid =1\}.$$

(29)

This ellipse is precisely the spectral boundary of ${\mathbb{E}}_{\infty }=(\infty ;-\sqrt{{\gamma }_1{\gamma }_2},{\gamma }_2,{\gamma }_0,{\gamma }_1,\sqrt{2}{\gamma }_2,\sqrt{2}{\gamma }_1).$ Regarding the ellipse $f\left(S\right)$, its major axis can be characterized by

$$S_1=\{{\gamma }_0+b{e}^{i({\varpi }_1+{\varpi }_2)/2},b\in \mathbf{R},\left|b\right|\le {\displaystyle \frac{2\sqrt{\left|{\gamma }_1{\gamma }_2\right|}+2z(\left|{\gamma }_1\right|+\left|{\gamma }_2\right|)}{2z+1}}\}.$$

(30)

Similarly, the interval between its foci is defined according to

$$S_2=\{{\gamma }_0+b{e}^{i({\varpi }_1+{\varpi }_2)/2},b\in \mathbf{R},\left|b\right|\le 2\sqrt{|{\gamma }_1{\gamma }_2|}\}.$$

When $z\ge 1$ and is finite, the spectral containment of the matrix $\mathbb{E}$ is contained in $S_2$, and $S_2$ is the smallest interval with this property. With the help of Equation (6), it can be determined that the interval where the spectrum of the normal PDNT Toeplitz matrix ${\mathbb{E}}^{*}$ closest to $\mathbb{E}$ lies is (30).

3.4. Structured Perturbations

Under the condition $|{\gamma }_2|<|{\gamma }_1|$, we investigate ${\mathbb{E}}_c=(z;\sqrt{c{\gamma }_1},-c,0,0,-\sqrt{2}c,0)$ of the original matrix $\mathbb{E}$ = (z;$-\sqrt{{\gamma }_1{\gamma }_2}$,${\gamma }_2$,${\gamma }_0$,${\gamma }_1$,$\sqrt{2}{\gamma }_2$,$\sqrt{2}{\gamma }_1$). For the parameter $c=\alpha {\gamma }_2$ with $0<\alpha <1$, we obtain a family of diagonalizable matrices $\mathbb{E}+{\mathbb{E}}_c$ possessing simple eigenvalues. As the parameter $\alpha ⟶1$, the family of matrices $\mathbb{E}+{\mathbb{E}}_c$ converges to a defective matrix ${\mathbb{E}}^{+}=(z;0,0,{\gamma }_0,{\gamma }_1,0,\sqrt{2}{\gamma }_1)$. This matrix possesses only one eigenvalue ${\gamma }_0$ with a geometric multiplicity of one. The structured perturbation

$${\mathbb{E}}_{{\gamma }_2}=(z;\sqrt{{\gamma }_1{\gamma }_2},-{\gamma }_2,0,0,-\sqrt{2}{\gamma }_2,0),{\Vert {\mathbb{E}}_{{\gamma }_2}\Vert }_F=\sqrt{z|{\gamma }_2{|}^2+\left|{\gamma }_1{\gamma }_2\right|},$$

shifts all eigenvalues of matrix $\mathbb{E}$, such that they all become ${\gamma }_0$.

Under $0<|{\gamma }_2|\le |{\gamma }_1|$, the rate of change of the j-th eigenvalue of $\mathbb{E}$ with respect to the perturbation is given by

$${\displaystyle \frac{\mid {\lambda }_j(\mathbb{E}+{\mathbb{E}}_{{\gamma }_2})-{\lambda }_j\left(\mathbb{E}\right)\mid }{\Vert {\mathbb{E}}_{{\gamma }_2}{\Vert }_F}}={\displaystyle \frac{2\sqrt{\mid {\gamma }_1{\gamma }_2\mid }\mid cos\frac{(2j-1)\pi }{2z-1}\mid }{\sqrt{z|{\gamma }_2{|}^2+\left|{\gamma }_1{\gamma }_2\right|}}}={\displaystyle \frac{2\mid cos\frac{(2j-1)\pi }{2z-1}\mid }{\sqrt{zg+1}}}.$$

(31)

Let $c=\alpha {\gamma }_2$, $d=\alpha {\gamma }_1$ with $0<\alpha <1$, and define ${\mathbb{E}}_{c,d}=(z;\sqrt{cd},-c,0,-d,-\sqrt{2}c,-\sqrt{2}d)$. It follows that

$$\underset{\alpha \to 1}{lim}(\mathbb{E}+{\mathbb{E}}_{c,d})={\gamma }_{0}I,$$

where I denotes the identity matrix, implying that $\mathbb{E}+{\mathbb{E}}_{c,d}$ is normal. The limit matrix is achieved via the perturbation

$${\mathbb{E}}_{{\gamma }_1,{\gamma }_2}=(z;\sqrt{{\gamma }_1{\gamma }_2},-{\gamma }_2,0,-{\gamma }_1,-\sqrt{2}{\gamma }_2,-\sqrt{2}{\gamma }_1),{\Vert {\mathbb{E}}_{{\gamma }_1,{\gamma }_2}\Vert }_F=\sqrt{z\left(\right|{\gamma }_1{|}^2+|{\gamma }_2{|}^2)+|{\gamma }_1{\gamma }_2|}.$$

For $j=1,2,\dots ,z$, the relative eigenvalue variation rate is characterized by

$${\displaystyle \frac{\mid {\lambda }_j(\mathbb{E}+{\mathbb{E}}_{{\gamma }_1,{\gamma }_2})-{\lambda }_j\left(\mathbb{E}\right)\mid }{\Vert {\mathbb{E}}_{{\gamma }_1,{\gamma }_2}{\Vert }_F}}={\displaystyle \frac{2\sqrt{|{\gamma }_1{\gamma }_2|}|cos\frac{(2j-1)\pi }{2z-1}|}{\sqrt{z\left(\right|{\gamma }_1{|}^2+|{\gamma }_2{|}^2)+|{\gamma }_1{\gamma }_2|}}}=\left\{\begin{array}{c}{\displaystyle \frac{2}{\sqrt{D_o{({\gamma }_1,{\gamma }_2)}^2+1}}},z=1,\hfill \\ {\displaystyle \frac{2\sqrt{2z+1}|cos\frac{(2j-1)\pi }{2z-1}|}{\sqrt{4z{D}_o{({\gamma }_1,{\gamma }_2)}^2+2z+1}}},z>1.\hfill \end{array}\right.$$

The derived results reveal an inverse relationship between the rate and the Frobenius norm of the Jacobian matrix (9). The rate reaches its maximum when $\mathbb{E}$ is normal, as shown in Remark 1.

4. Examples of Eigenvalue Sensitivity

This section numerically verifies the properties of PDNT Toeplitz matrices and their eigenvalues as analyzed previously. For the matrix ${\mathbb{E}}_{\left(g\right)}$ defined in

$${\mathbb{E}}_{\left(g\right)}=(50;-\sqrt{-5g(4+3i)},(4+3i)g,16-3i,-5,\sqrt{2}(4+3i)g,-5\sqrt{2}),$$

(32)

with $0<g<1$, where g is the ratio in (10). It is observed that ${\mathbb{E}}_{\left(0\right)}$ is defective, while ${\mathbb{E}}_{\left(1\right)}$ is normal. The eigenvalues of ${\mathbb{E}}_{\left(g\right)}$ and ${\mathbb{E}}_{\left(g\right)}^{*}$ are visualized in Figure 1, Figure 2, Figure 3 and Figure 4, where horizontal and vertical axes represent the real and imaginary parts of eigenvalues, respectively. The eigenvalues are determined by resorting to Equations (5) and (6). The figures depict the image of the unit circle under the matrices ${\mathbb{E}}_{\left(g\right)}$, and the detailed information can be referred to in Equation (29). Figure 5 demonstrates the spectra of the matrices ${\mathbb{E}}_{\left(0.1\right)}^T$ and ${\left({\mathbb{E}}_{\left(0.1\right)}^T\right)}^{*}$ obtained by executing the QR algorithm. In the first five figures, each green elliptical curve is the spectral boundary of

$${\mathbb{E}}_{\infty }=(\infty ;-\sqrt{-5g(4+3i)},(4+3i)g,16-3i,-5,\sqrt{2}(4+3i)g,-5\sqrt{2}).$$

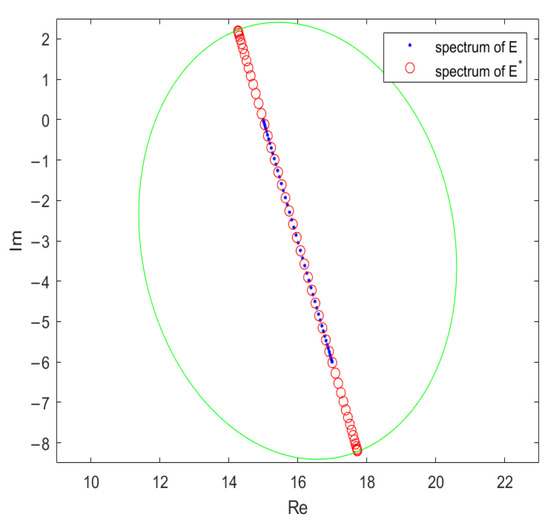
Figure 1. The spectra of matrix ${\mathbb{E}}_{\left(g\right)}$ and the closest normal PDNT Toeplitz matrix ${\mathbb{E}}_{\left(g\right)}^{*}$ at $g=0.1$.

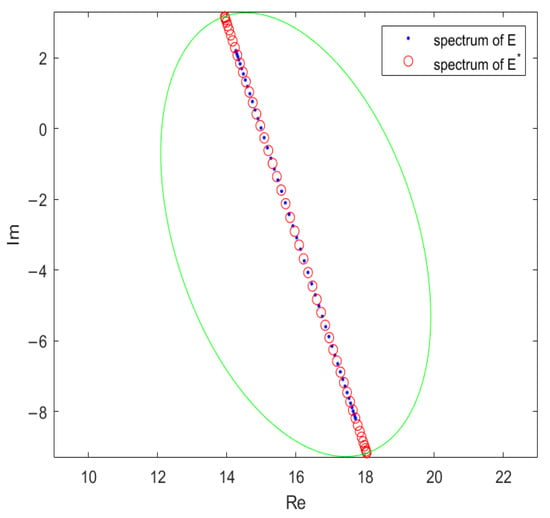
Figure 2. The spectra of matrix ${\mathbb{E}}_{\left(g\right)}$ and the closest normal PDNT Toeplitz matrix ${\mathbb{E}}_{\left(g\right)}^{*}$ at $g=0.3$.

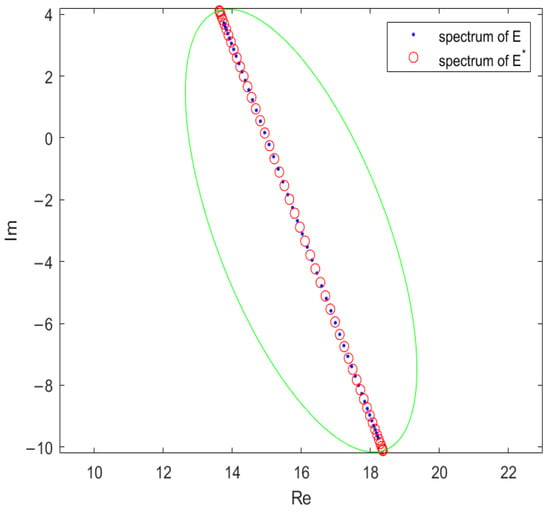
Figure 3. The spectra of matrix ${\mathbb{E}}_{\left(g\right)}$ and the closest normal PDNT Toeplitz matrix ${\mathbb{E}}_{\left(g\right)}^{*}$ at $g=0.5$.

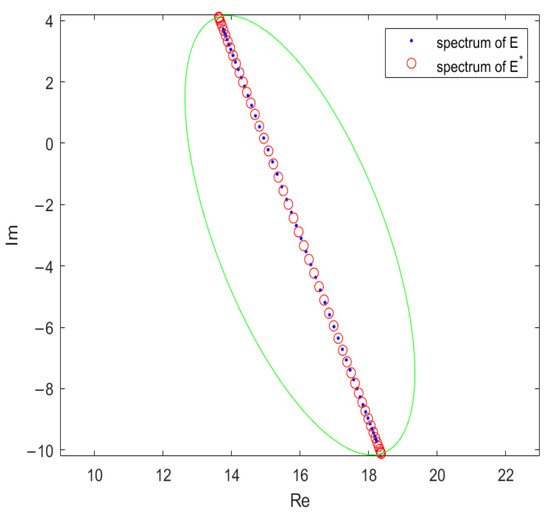
Figure 4. The spectra of matrix ${\mathbb{E}}_{\left(g\right)}$ and the closest normal PDNT Toeplitz matrix ${\mathbb{E}}_{\left(g\right)}^{*}$ at $g=0.9$.

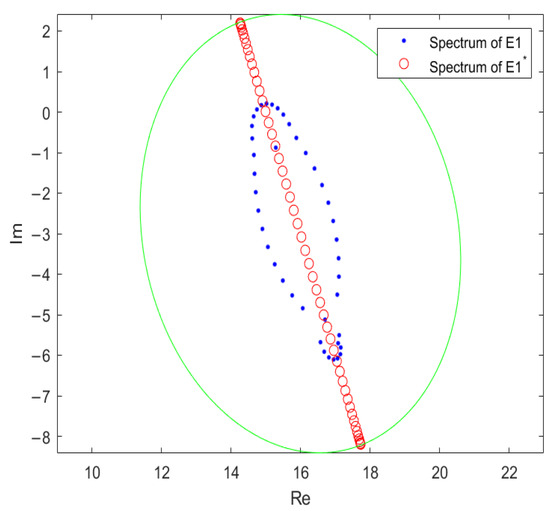
Figure 5. The spectra of ${\mathbb{E}}_{\left(g\right)}^T$ and ${\left({\mathbb{E}}_{\left(g\right)}^T\right)}^{*}$ at $g=0.1$, denoted $\mathbb{E}1$ and $\mathbb{E}{1}^{*}$ in the legend.

In the process of solving eigenvalues, due to the differences in calculation methods, the visualization effects will also differ. By comparing Figure 1 and Figure 5, it is difficult to discern that the matrices ${\mathbb{E}}_{\left(0.1\right)}$ and ${\mathbb{E}}_{\left(0.1\right)}^T$ have identical eigenvalues. As can be seen from Figure 5, when $\epsilon$ is set to the machine epsilon $2\times {10}^{-16}$, the spectrum of the matrix ${\mathbb{E}}_{\left(0.1\right)}^T$ is nearly adjacent to the boundary of the $\epsilon$-pseudospectrum. Figure 6 displays the $\epsilon$-pseudospectra of ${\mathbb{E}}_{\left(0.1\right)}$ under progressively increasing $\epsilon$-values. Figure 7 depicts the variation of the average forward and backward errors of ${\mathbb{E}}_{\left(0.1\right)}$ with matrix dimension z after adding tiny random perturbations. Figure 8 and Figure 9 plot the condition number $\kappa \left({\lambda }_j\left(\mathbb{E}\right)\right)$ versus the parameter g at $z=50$, corresponding to the two distinct cases $j=49$ and $j=50$, respectively.

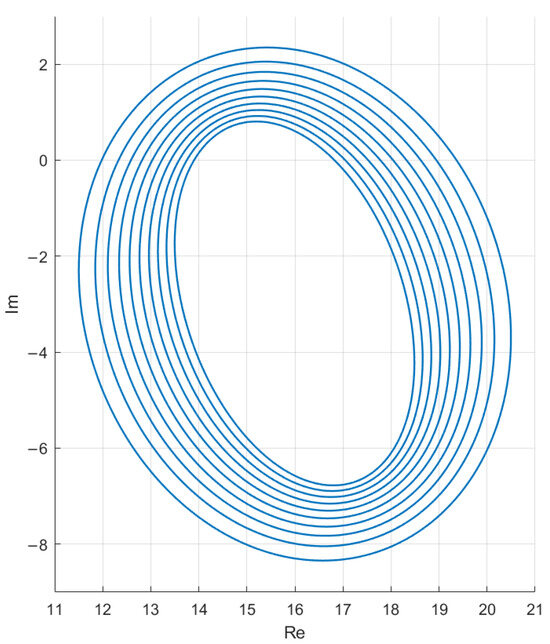
Figure 6. The figure shows the $\epsilon$-pseudospectrum of ${\mathbb{E}}_{\left(g\right)}$ at $g=0.1$, consisting of ten contours whose $\epsilon$-values increase by one order of magnitude from ${10}^{-10}$ (innermost) to ${10}^{-1}$ (outermost).

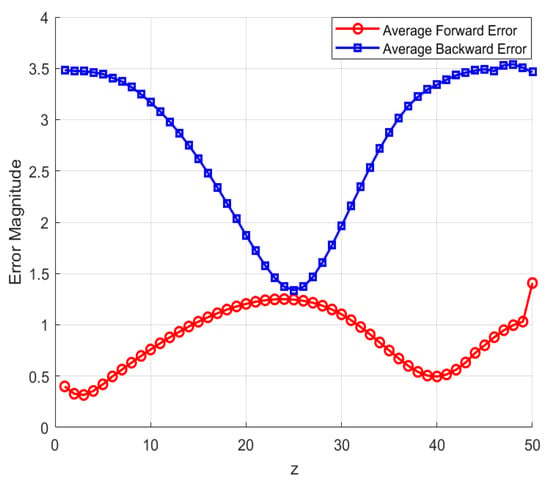
Figure 7. The variation of the average forward and backward errors of ${\mathbb{E}}_{\left(g\right)}$ at g = 0.1 with matrix dimension z. Red circles represent the average forward error, and blue squares represent the average backward error.

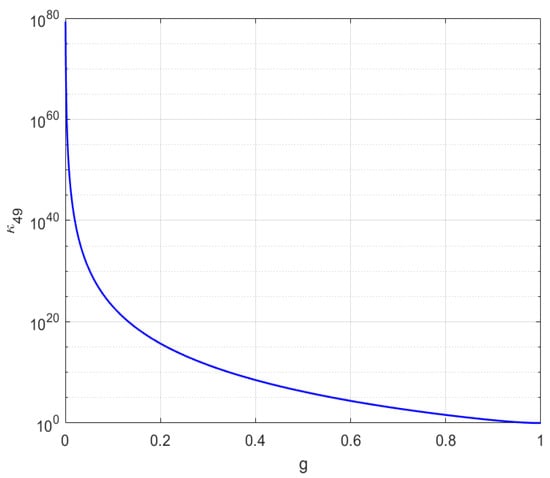
Figure 8. Logarithmic plot of the condition number $\kappa \left({\lambda }_{49}\left(\mathbb{E}\right)\right)$ (${\kappa }_{49}$) versus the parameter g for $j=49$ and $z=50$.

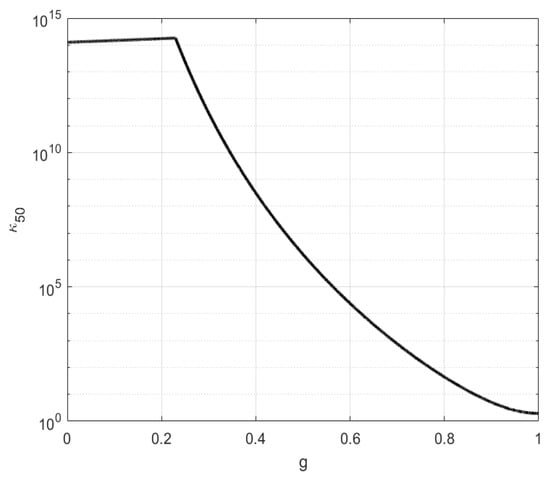
Figure 9. Logarithmic plot of the condition number $\kappa \left({\lambda }_{50}\left(\mathbb{E}\right)\right)$ (${\kappa }_{50}$) versus the parameter g for $j=50$ and $z=50$.

5. Inverse Problems for $\mathbb{E}$

This section first addresses the inverse eigenvalue problems for PDNT Toeplitz matrices, followed by an investigation of their inverse vector counterparts. In the latter problem, a trapezoidal PDNT Toeplitz matrix is determined by minimizing the matrix-vector product norm with a specified vector.

Problem 1.

Given two distinct complex numbers $u_1$, $u_2$ and a natural number z, construct a PDNT Toeplitz matrix $\mathbb{E}$ = (z;$-\sqrt{{\gamma }_1{\gamma }_2}$,${\gamma }_2$,${\gamma }_0$,${\gamma }_1$,$\sqrt{2}{\gamma }_2$,$\sqrt{2}{\gamma }_1$) with the requirement that its extremal eigenvalues are $z_1$ and $z_2$.

While no unique solution exists for this problem, it is crucial to emphasize that the eigenvalues of $\mathbb{E}$ are fully determined by the given data. Given the eigenvalues

$${\lambda }_1=z_1={\gamma }_0+2\sqrt{{\gamma }_1{\gamma }_2}cos{\displaystyle \frac{\pi }{2z-1}},{\lambda }_z=z_2={\gamma }_0-2\sqrt{{\gamma }_1{\gamma }_2},$$

the ${\gamma }_0$ and the product ${\gamma }_1{\gamma }_2$ are uniquely determined by

$$\sqrt{{\gamma }_1{\gamma }_2}={\displaystyle \frac{z_1-z_2}{2(cos\frac{\pi }{2z-1}+1)}},{\gamma }_0={\displaystyle \frac{z_1+z_{2}cos\frac{\pi }{2z-1}}{1+cos\frac{\pi }{2z-1}}}.$$

The given data determines both the magnitude $|{\gamma }_1{\gamma }_2|$ and the phase angle $arg\left({\gamma }_1\right)+arg\left({\gamma }_2\right)$. Both the choice of subdiagonal or superdiagonal element arguments and the ratio g ($0<g\le 1$) defined in Equation (10) can be freely assigned. The ill-conditioning of the eigenvalues increases as the parameter g approaches 0. When the parameter $g=1$ is chosen, the resulting matrix becomes normal. By selecting different phase angles for subdiagonal or superdiagonal elements, distinct normal matrices can be constructed.

Problem 2.

For a given vector $\overrightarrow{\tau }\in {\mathbf{C}}^z$, construct a trapezoidal PDNT Toeplitz matrix

$$\left(\begin{array}{ccccccc}{\gamma }_2& 1-\sqrt{{\gamma }_1{\gamma }_2}& {\gamma }_1& & & & 0\\ & {\gamma }_2& 1& {\gamma }_1& & & \\ & & \ddots & \ddots & \ddots & & \\ & & & {\gamma }_2& 1& {\gamma }_1& \\ 0& & & & \sqrt{2}{\gamma }_2& 1& \sqrt{2}{\gamma }_1\end{array}\right)\in {\mathbf{C}}^{(z-2)\times z},$$

such that $\mathbb{E}$ attains

$$\begin{array}{c}\hfill \underset{{\gamma }_1,{\gamma }_2}{min}{∥\mathbb{E}\overrightarrow{\tau }∥}_2.\end{array}$$

(33)

By defining the vector $\overrightarrow{\tau }={[{\omega }_1,{\omega }_2,\dots ,{\omega }_z]}^T$, the problem $\left(33\right)$ transforms to

$$\begin{array}{c}\hfill \underset{{\gamma }_1,{\gamma }_2}{min}{∥\left[\begin{array}{cc}{\omega }_1& {\omega }_3\\ {\omega }_2& {\omega }_4\\ .& .\\ .& .\\ \sqrt{2}{\omega }_{z-2}& \sqrt{2}{\omega }_z\end{array}\right]\left[\begin{array}{c}{\gamma }_2\\ {\gamma }_1\end{array}\right]+\left[\begin{array}{c}(1-\sqrt{{\gamma }_1{\gamma }_2}){\omega }_2\\ {\omega }_3\\ .\\ .\\ {\omega }_{z-1}\end{array}\right]∥}_2.\end{array}$$

(34)

When the columns of matrix (34) are linearly independent, this least-squares problem admits a unique solution.

Proof. 

Assume, for contradiction, that the least squares solution is not unique. Then, there exist two distinct solutions $x_1\ne x_2$, such that

$$\parallel A{x}_1{-b\parallel }_2^2=\parallel A{x}_2{-b\parallel }_2^2=\underset{x}{min}{\parallel Ax-b\parallel }_2^2,$$

where $A=\left[\begin{array}{cc}{\omega }_1& {\omega }_3\\ {\omega }_2& {\omega }_4\\ ⋮& ⋮\\ ⋮& ⋮\\ \sqrt{2}{\omega }_{z-2}& \sqrt{2}{\omega }_z\end{array}\right]$, $x=\left[\begin{array}{c}{\gamma }_2\\ {\gamma }_1\end{array}\right]$ and $b=-\left[\begin{array}{c}(1-\sqrt{{\gamma }_1{\gamma }_2}){\omega }_2\\ {\omega }_3\\ .\\ .\\ {\omega }_{z-1}\end{array}\right]$.

Consider the convex combination $x_t=t{x}_1+(1-t)x_2$. We have

$$\parallel A{x}_t{-b\parallel }_2^2=\parallel tA{x}_1+(1-t)A{x}_2{-b\parallel }_2^2={\parallel t(A{x}_1-b)+(1-t)(A{x}_2-b)\parallel }_2^2.$$

Since both $x_1$ and $x_2$ are minimizers, denote $\parallel A{x}_1{-b\parallel }_2={\parallel A{x}_2-b\parallel }_2=T_{min}$. By convexity,

$$\parallel A{x}_t{-b\parallel }_2^2\le T_{min}\forall t\in [0,1].$$

Equality holds only if

$$A(x_1-x_2)=0.$$

However, since A has full column rank, $ker\left(A\right)=\left\{0\right\}$, which implies $x_1-x_2=0\Rightarrow x_1=x_2$, contradicting $x_1\ne x_2$. Therefore, the solution must be unique. □

The columns are linearly dependent if, and only if, there exists a complex number $\gamma \in \mathbf{C}$ such that the components of $\overrightarrow{\tau }$ satisfy

$${\omega }_{k+2}=\gamma {\omega }_k,k=1,\dots ,z-2.$$

In the process of solving for the solution $\mathbb{E}$ of $\left(33\right)$, a key question is how to characterize the unit vectors $\overrightarrow{\tau }$, for which ${∥\mathbb{E}\overrightarrow{\tau }∥}_2$ remains small. Given that $\widehat{\mathbb{E}}\in {\mathbf{C}}^{z\times z}$ is the PDNT Toeplitz matrix constructed by prepending and appending appropriately chosen rows to $\mathbb{E}$, the definition in Equation (28) implies that the $ϵ$-pseudoeigenvectors of $\widehat{\mathbb{E}}$ corresponding to $y=0$ is contained within

$$\{l:\parallel \mathbb{E}l{\parallel }_2\le \epsilon ,\parallel l{\parallel }_2=1\}.$$