Co-Secure Domination Number in Some Graphs

Abstract

Let G be a graph and $S\subseteq V\left(G\right).$ If S is a dominating set of G, and for each vertex $u\in V\left(G\right)-S,$ there is a neighbor of u in $S,$ denoted by $v,$ such that $(S\setminus \{v\left\}\right)\cup \left\{u\right\}$ is a dominating set of $G,$ then S is a secure dominating set (SDS) of $G.$ Conversely, S is a co-secure dominating set (CSDS) of G if S is a dominating set of G and for each vertex v in $S,$ $V\left(G\right)-S$ contains a neighbor of $v,$ denoted by $u,$ such that $(S\setminus \{v\left\}\right)\cup \left\{u\right\}$ is a dominating set of $G.$ The minimum cardinality of a CSDS (resp. SDS) of G is the co-secure (resp. secure) domination number of $G.$ We use ${\gamma }_{cs}\left(G\right)$ and ${\gamma }_s\left(G\right)$ to denote the co-secure domination number and secure domination number of $G,$ respectively. Arumugam et al. proposed two questions: (1) Characterize a graph G with ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right),$ where $\alpha \left(G\right)$ is the independence number of $G;$ (2) Characterize a graph G with ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right).$ In this paper, we characterize some forbidden induced subgraphs for a graph G with ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)$; moreover, we obtain that ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right)$ for each $\{K_3,C_5,P_5\}$-free graph G with $\delta \left(G\right)\ge 2.$ Our conclusions can generalize some known results.

1. Introduction

We consider only simple graphs in this paper. For notation and terminology not defined here, readers are referred to [1]. Let G be a graph and $S\subseteq V\left(G\right).$ We use $G\left[S\right]$ and $E\left(G\right[S\left]\right)$ to denote the subgraph of G induced by $S,$ and the edge set of $G\left[S\right],$ respectively. Let $N_S\left(v\right)=\{u\in S:uv\in E\left(G\right)\}$ and $d_S\left(v\right)=\left|N_S\left(v\right)\right|;$ and if there is no confusion, we set $N\left(v\right)=N_G\left(v\right)$ and $d\left(v\right)=d_G\left(v\right)$ for brevity. Let $N\left[v\right]=N\left(v\right)\cup \left\{v\right\}.$ For an induced subgraph $H_1$ of G and a graph $H_2,$ let $H_1=H_2$ if $H_1$ is isomorphic to $H_2.$ A complete graph of order n is denoted by $K_n,$ and a complete bipartite graph with two color classes $A,B$ is denoted by $K_{p,q},$ where $\left|A\right|=p$ and $\left|B\right|=q.$G is H-free if G contains no induced subgraph isomorphic to a graph $H.$ Figure 1 shows some of the forbidden induced subgraphs of G in this paper. A claw is a graph isomorphic to $K_{1,3}.$ We use $G[v,v_1,v_2,v_3]$ to denote an induced subgraph H of G with $H=K_{1,3}$ such that the degree sequence of H is $d_H\left(v\right)=3,d_H\left(v_i\right)=1$ for each $i\in \{1,2,3\}.$ Let $K_4^{-}$ denote the graph obtained from $K_4$ by deleting an edge. We use $C_4,C_5,$ and $P_5$ to denote a 4-cycle, 5-cycle, and a path of order 5, respectively. Let $P=v_1{v}_2\cdots v_k$ denote a path P of order $k\ge 2$ from $v_1$ to $v_k$ in $G.$ The bull graph, denoted by $B_{1,1},$ is a graph obtained by joining two disjoint vertices to two distinct vertices of a triangle. If an induced subgraph H of G consisting of $v_i,1\le i\le 5,$ and isomorphic to $B_{1,1},$ then let $G\left[\{v_1,v_2,v_3,v_4,v_5\}\right]=H$ such that $d_H\left(v_1\right)=2,d_H\left(v_2\right)=d_H\left(v_3\right)=3,d_H\left(v_4\right)=d_H\left(v_5\right)=1,$ and $v_4{v}_2,v_3{v}_5\in E\left(H\right).$ If an induced subgraph H of G consisting of $w_i,1\le i\le 5,$ and isomorphic to $Z_2$, then let $G\left[\{w_1,w_2,w_3,w_4,w_5\}\right]=H$ such that $d_H\left(w_1\right)=3,d_H\left(w_2\right)=d_H\left(w_3\right)=d_H\left(w_4\right)=2,d_H\left(v_5\right)=1,$ and $w_1{w}_4{w}_5$ is an induced path of order 3 in H. For two graphs $H_1$ and $H_2,$ let $G_1=H_1\vee H_2$ denote the join of $H_1$ and $H_2$ such that $V\left(G_1\right)=V\left(H_1\right)\cup V\left(H_1\right)$ and $E\left(G_1\right)=E\left(H_1\right)\cup E\left(H_2\right)\cup \{uv\in E\left(G_1\right):u\in V\left(H_1\right),v\in V\left(H_2\right)\}.$ The diameter of G, denoted by diam$\left(G\right),$ is the maximum distance of a pair of vertices in $G.$ Let $\alpha \left(G\right)$ denote the independence number of G.

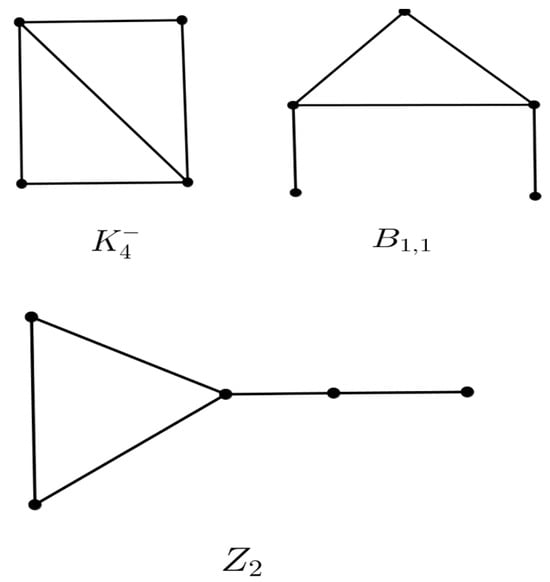
Figure 1. The forbidden induced subgraphs in this paper $K_4^{-},$ $B_{1,1}$ and $Z_2$.

If each vertex of G is in S or adjacent to some vertex in $S,$ then S is a dominating set (DS) of $G.$ If S is a dominating set of G, and for each vertex $u\in V\left(G\right)-S,$ there is a neighbor of u in $S,$ denoted by $v,$ such that $(S\setminus \{v\left\}\right)\cup \left\{u\right\}$ is a dominating set of $G,$ then S is a secure dominating set (SDS) of $G.$ Conversely, S is a co-secure dominating set (CSDS) of G if S is a dominating set of G and for each vertex v in $S,$ $V\left(G\right)-S$ contains a neighbor of $v,$ denoted by $u,$ such that $(S\setminus \{v\left\}\right)\cup \left\{u\right\}$ is a dominating set of $G.$ The minimum cardinality of a CSDS (resp. SDS) of G is the co-secure (resp. secure) domination number of $G.$ Let ${\gamma }_{cs}\left(G\right)$ and ${\gamma }_s\left(G\right)$ denote the co-secure domination number and secure domination number of $G,$ respectively. Let $G=K_m\vee (K_2\cup K_1),m\ge 3.$ It is easy to verify that ${\gamma }_{cs}\left(G\right)=1$ and ${\gamma }_s\left(G\right)=2,$ which implies there is no implication between SDS and CSDS.

The secure domination and co-secure domination problems have practical applications, such as the assignment of guards for locations. We can obtain a graph G in the following way: the given locations consist of the vertex set of G, and if two locations are connected by a street, then there is an edge between them in G. We assume that if a location u has a guard, then each neighbor of u is protected by the guard. The secure domination problem is that we assign a minimum number of guards for a subset of locations, denoted by S, such that for each location u in $V\left(G\right)-S,$ S contains a neighbor v of u such that the guard in v can move to $u,$ and then the guard team can also protect all the locations. The problem with the co-secure domination number is that we assign a minimum number of guards for a subset S of locations such that for each location u in $S,$ its guard can move to a neighbor of u, and then the guard team can also protect all the locations.

Cockayne et al. introduced the concept of a secure dominating set and secure domination number. The exact values of secure domination number for paths, cycles, complete multipartite graphs and some other graph classes were given in [2], and the bounds of secure domination number for different graph classes were given in [3,4,5,6,7,8,9]. The concept of co-secure domination was introduced by Arumugan et al. [10]. They also determined the co-secure domination number of some families of graphs, such as paths and cycles, and gave sharp upper and lower bounds of graphs; moreover, they proved that the decision problem for ${\gamma }_{cs}\left(G\right)$ of a graph G is NP-complete even if G is a bipartite, chordal or planar graph. Joseph and Sangeetha [11] gave some bounds for the co-secure domination number of some classes of graphs.

Arumugan et al. [10] proved that for a connected graph $G,$ the independence number is an upper bound of ${\gamma }_{cs}\left(G\right)$ as follows.

Theorem 1 ([10]).

Every maximum independent set is a co-secure dominating set of G for each non-trivial graph $G,$ i.e., ${\gamma }_{cs}\left(G\right)\le \alpha \left(G\right).$

Moreover, in [10], they gave the upper bound ${\gamma }_s\left(G\right)$ for ${\gamma }_{cs}\left(G\right)$ of a graph G as follows.

Theorem 2 ([10]).

${\gamma }_{cs}\left(G\right)\le {\gamma }_s\left(G\right)$ for each graph G with $\delta \left(G\right)\ge 2.$

Based on Theorems 1 and 2, Arumugan et al. [10] asked the following two problems.

Problem 1 ([10]).

Characterize a graph G with ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right).$

Problem 2 ([10]).

Characterize a graph G with ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right).$

Inspired by Theorems 1 and 2 and Problems 1 and 2, in the Section 2, we give sufficient conditions for a graph G that satisfies ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)$ and ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right),$ respectively.

2. Main Results and Their Proofs

Suppose that S is a dominating set of a graph G with $v\in S,u\in N_{G-S}\left(v\right).$ If $N_S\left(u\right)=\left\{v\right\},$ then u is an external private neighbor of v with respect to $S.$ If $(S\setminus \{v\left\}\right)\cup \left\{u\right\}$ is a dominating set of $G,$ then u is S-defended by v, and we can say u is S-defended for brevity. If for each vertex $u^{\prime }\in S,$ u is not S-defended by $u^{\prime },$ then u is S-undefended. Let $epn(v,S)=\{u\in V(G)-S:u$ is an S-external private neighbor of $v\}$ and $rpn(v,S)=\{w\in V(G)-S:wisS$-defended by $v\}.$ It is easy to verify that $u\in rpn(v,S)$ if and only if $epn(v,S)\subseteq N\left[u\right].$ By the definitions of secure dominating set and co-secure dominating set, if S is a secure dominating set of G, it is easy to verify that for each $u\in G-S,$ $u\in rpn(v,S)$ and $epn(v,S)\subseteq N\left[u\right]$ for some vertex $v\in S;$ if S is a co-secure dominating set of G, then for each vertex $v\in S,$ $rpn(v,S)\ne \varnothing$ and $epn(v,S)\subseteq N\left[u\right]$ for each vertex $u\in rpn(v,S).$ We mainly applied the previous definitions and properties to the proof of our main results in this section.

According to Problem 1, we obtain Theorems 3 and 4, which gives an infinite family $\mathcal{F}$ of graphs with ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)$ if $G\in \mathcal{F}.$

Theorem 3. 

Every non-trivial $\{K_4^{-},C_4,P_5,B_{1,1}\}$-free graph contains a minimum co-secure dominating set which is a maximum independent set.

Proof. 

Let G be a non-trivial $\{K_4^{-},C_4,P_5\}$-free graph. Suppose that G consists of k components $G_1,\cdots ,G_k$ with $k\ge 1.$ Clearly, ${\sum }_{i=1}^{i=k}{\gamma }_{cs}\left(G_i\right)={\gamma }_{cs}\left(G\right).$ Thus, without loss of generality, we assume that G is connected, i.e., $k=1.$ We begin with the following result.

Claim 1. 

For a vertex x in a CSDS S of G, if $epn(x,S)\ne \varnothing ,$ then $G\left[epn\right(x,S\left)\right]$ is a clique.

Proof. 

Suppose that S is a CSDS of G and $x\in S$ with $epn(x,S)\ne \varnothing .$ If $\left|epn\right(x,S\left)\right|=1,$ then we are done. Let $\left|epn\right(x,S\left)\right|\ge 2.$ Suppose on the contrary that $x_1,x_2\in epn(x,S)$ and $x_1{x}_2\notin E\left(G\right).$ By the definition of a CSDS, we have $rpn(x,S)\ne \varnothing$ and $x_1,x_2\notin rpn(x,S).$ Assume that $y\in rpn(x,S).$ Then, $y\notin \{x_1,x_2\}$ and $x_{1}y,x_{2}y\in E\left(G\right),$ which implies $G\left[\{x,x_1,x_2,y\}\right]=K_4^{-},$ a contradiction. Thus, $G\left[epn\right(x,S\left)\right]$ is a clique. □

For a CSDS S of G, since $u\in rpn(v,S)$ if and only if $epn(v,S)\subseteq N\left[u\right]$ for a vertex $v\in S$ and a vertex $u\in N_{G-S}\left(v\right),$ we can obtain the following claim by Claim 1.

Claim 2. 

For a vertex x in a CSDS S of G, $epn(x,S)\subseteq rpn(x,S).$

By the definition of a CSDS and Claims 1 and 2, we can obtain the following result.

Claim 3. 

Let S be a dominating set such that $d_{G-S}\left(x\right)\ge 1$ for each vertex $x\in S.$ If S is not a CSDS of G, then S contains a vertex x such that $rpn(x,S)=\varnothing ,$ and $epn(x,S)$ contains two non-adjacent vertices.

Claim 4. 

If S is a minimum CSDS of G with $E\left(G\right[S\left]\right)\ne \varnothing ,$ then there is a vertex $x\in S$ with $d_S\left(x\right)\ge 1$ such that $epn(x,S)\ne \varnothing$.

Proof. 

Suppose on the contrary that $epn(x,S)=\varnothing$ for each vertex $x\in S$ with $d_S\left(x\right)\ge 1.$ Let $u,v\in S$ such that $uv\in E\left(G\right).$ Then, by the hypothesis, we have $epn(u,S)=epn(v,S)=\varnothing .$ Let $S^{\prime }=S\setminus \left\{u\right\}.$ Since S is a CSDS of $G,$ we have $rpn(x,S)\ne \varnothing$ and $N_{G-S}\left(x\right)\ne \varnothing$ for each vertex $x\in S.$ Moreover, since $epn(u,S)=\varnothing$ and $uv\in E\left(G\right),$ we have $d_{S^{\prime }}\left(x\right)\ge 1$ for each vertex $x\in V\left(G\right)-S^{\prime }.$ Thus, $S^{\prime }$ is a dominating set of $G.$ Since S is a minimum CSDS of G and $|S^{\prime }| < |S|,$ $S^{\prime }$ is not a CSDS of $G.$ Thus, by Claim 3, there exists a vertex y in $S^{\prime }$ with $epn(y,S^{\prime })\ne \varnothing$ and $rpn(y,S^{\prime })=\varnothing .$ Moreover, let $y_1,y_2\in epn(y,S^{\prime })$ with $y_1{y}_2\notin E\left(G\right).$ By $y\in S^{\prime },$ we have $y\ne u.$ Suppose that $y_1,y_2\notin epn(y,S).$ Then, $N_S\left(y_i\right)=\{u,y\}$ for each $i\in \{1,2\}.$ If $uy\notin E\left(G\right),$ then $G\left[\{y_1,y_2,y,u\}\right]=y_{1}u{y}_{2}y{y}_1$ is a 4-cycle by $y_1{y}_2\notin E\left(G\right),$ a contradiction. Thus, $uy\in E\left(G\right),$ which implies $G\left[\{y_1,y_2,y,u\}\right]=K_4^{-},$ a contradiction. Thus, $epn(y,S)$ contains at least one vertex in $\{y_1,y_2\}$. Moreover, by Claim 1 and $y_1{y}_2\notin E\left(G\right),$ we have $|\{y_1,y_2\}\cap epn(y,S)| =1.$

Without loss of generality, assume that $y_1\in epn(y,S)$ and $y_2\notin epn(y,S).$ Then, $N_S\left(y_2\right)=\{u,y\}$ by $y_2\in epn(y,S^{\prime }).$ Since $y_1\in epn(y,S),$ we have $d_S\left(y\right)=0$ by $epn(x,S)=\varnothing$ for each vertex $x\in S$ with $d_S\left(x\right)\ge 1.$ Thus, $y\ne v$ and $yu,yv\notin E\left(G\right).$ By $y\ne v$ and $N_S\left(y_2\right)=\{u,y\},$ we have $y_{2}v\notin E\left(G\right).$ We have $y_{1}u,y_{1}v\notin E\left(G\right)$ by $y_1\in epn(y,S)$ and $y\notin \{u,v\}.$ It follows that $G\left[\{v,u,y,y_1,y_2\}\right]=vu{y}_{2}y{y}_1=P_5,$ a contradiction. Thus, $epn(x,S)\ne \varnothing$ for some vertex $x\in S$ with $d_S\left(x\right)\ge 1.$ □

Claim 5. 

G contains a minimum CSDS S such that S is an independent set.

Proof. 

Suppose to the contrary that each minimum CSDS of G is not an independent set. We choose a minimum CSDS S of G such that $\left|E\right(G\left[S\right]\left)\right|$ is minimum. Since S is not an independent set, we have $\left|E\right(G\left[S\right]\left)\right|\ge 1,$ which implies ${\gamma }_{cs}\left(G\right)=\left|S\right|\ge 2.$ By Claim 4, without loss of generality, assume that $d_S\left(u\right)\ge 1$ and $u^{\prime }\in epn(u,S).$ Let $S_1=(S\setminus \left\{u\right\})\cup \left\{u^{\prime }\right\}.$ By Claim 1, $epn(u,S)\subseteq N\left[u^{\prime }\right].$ Moreover, $rpn(x,S)\ne \varnothing$ for each vertex $x\in S_1\setminus \left\{u^{\prime }\right\}.$ Thus, $S_1$ is a dominating set of G with $d_{S_1}\left(x\right)\ge 1$ for each vertex $x\in S_1.$ We have $d_{S_1}\left(u^{\prime }\right)=0$ by $u^{\prime }\in epn(u,S),$ which implies $|E\left(G\left[S_1\right]\right)| < |E\left(G\left[S\right]\right)|.$ Thus, by the choice of $S,$ $S_1$ is not a CSDS of $G.$ By Claim 3, there is a vertex $w\in S_1$ and $z_1,z_2\in epn(w,S_1)$ such that $rpn(w,S_1)=\varnothing$ and $z_1{z}_2\notin E\left(G\right).$ By $u\notin S_1,$ we have $w\ne u.$ By Claim 1 and $z_1{z}_2\notin E\left(G\right)$, at least one vertex in $\{z_1,z_2\}$ is not in $epn(w,S).$ In the following, we claim that there is a contradiction if $\{z_1,z_2\}\cap epn(w,S)=\varnothing$ or $|\{z_1,z_2\}\cap epn(w,S)|=1.$

Suppose that $\{z_1,z_2\}\cap epn(w,S)=\varnothing .$ Then, $N_S\left(z_i\right)=\{u,w\}$ for each $i\in \{1,2\}.$ If $wu\in E\left(G\right),$ then $G\left[\{z_1,u,z_2,w\}\right]=K_4^{-},$ a contradiction. If $wu\notin E\left(G\right),$ then $G\left[\{z_1,u,z_2,w\}\right]=z_{1}w{z}_{2}u{z}_1$ is a 4-cycle, a contradiction. Thus, $|\{z_1,z_2\}\cap epn(w,S)| =1.$ Without loss of generality, assume that $z_1\notin epn(w,S)$ and $z_2\in epn(w,S).$ Then, $N_S\left(z_1\right)=\{u,w\}.$ By $u^{\prime }\in epn(u,S)$ and $z_2\in epn(w,S),$ we have $u^{\prime }w,z_{2}u\notin E\left(G\right).$ Suppose that $uw\in E\left(G\right).$ We have $u^{\prime }{z}_2\in E\left(G\right)$ by $G\left[\{u^{\prime },u,z_1,w,z_2\}\right]\ne B_{1,1},$ a contradiction to $z_2\in epn(w,S_1).$ Suppose that $uw\notin E\left(G\right).$ Then, we have $u^{\prime }{z}_2\in E\left(G\right)$ by $u^{\prime }u{z}_{1}w{z}_2\ne P_5,$ a contradiction to $z_2\in epn(w,S_1).$ Thus, the claim is true. □

Let us resume the proof of Theorem 3. If G contains a minimum CSDS which is a maximum independent set of $G,$ then we are done. Thus, we assume that each minimum CSDS of G is not a maximum independent set. Then, ${\gamma }_{cs}\left(G\right)<\alpha \left(G\right)$ by Theorem 1, which implies $\alpha \left(G\right)\ge 2.$ We have ${\gamma }_{cs}\left(G\right)\ge 2.$ Otherwise, suppose $S=\left\{v\right\}$ is a minimum CSDS of $G.$ Then, each vertex in $V\left(G\right)-\left\{v\right\}$ is adjacent to $v,$ i.e., $epn(v,S)=V\left(G\right)\setminus \left\{v\right\}.$ Then, by Claim 1, G is a complete graph, a contradiction to $\alpha \left(G\right)\ge 2.$

Let $S^{\prime }$ be a maximum independent of G. By Claim 5, we take a minimum CSDS S of G such that S is an independent set and $|S \cap S^{\prime }|$ is maximum. Then, $\left|S\right| < |S^{\prime }|$ by ${\gamma }_{cs}\left(G\right)<\alpha \left(G\right),$ and hence $S^{\prime }-S\ne \varnothing$ and $|S^{\prime }-S| > |S-S^{\prime }|.$ Since S is a dominating set of G, each vertex in $S^{\prime }-S$ is adjacent to a vertex of $S-S^{\prime }.$ The rest proof boils down to two cases as follows.

Case 1. $d_S\left(x\right)\ge 2$ for each vertex $x\in S^{\prime }-S.$

Since $|S^{\prime }-S| > |S-S^{\prime }|$ and S is a dominating set of $G,$ there is a vertex $v\in S-S^{\prime }$ such that $d_{S^{\prime }-S}\left(v\right)\ge 2.$ Assume that $v_1,v_2\in N_{S^{\prime }-S}\left(v\right).$ By the hypothesis of the case, $d_S\left(v_i\right)\ge 2$ for each $i\in \{1,2\}.$ Suppose that $|N_S\left(v_1\right)\cap N_S\left(v_2\right)| \ge 2$ and assume $w\in (N_S\left(v_1\right)\cap N_S\left(v_2\right))\setminus \left\{v\right\}.$ Since $v_1,v_2$ are in the independent set $S^{\prime },$ $v_1{v}_2\notin E\left(G\right).$ We have $vw\notin E\left(G\right)$ since S is an independent set. Thus, $G\left[\{v,v_1,w,v_2\}\right]=v_{1}v{v}_{2}w{v}_1$ is a 4-cycle, a contradiction. Thus, $N_S\left(v_1\right)\cap N_S\left(v_2\right)=\left\{v\right\}.$ Suppose $w_i\in N_S\left(v_i\right)\setminus \left\{v\right\},i\in \{1,2\}.$ By $N_S\left(v_1\right)\cap N_S\left(v_2\right)=\left\{v\right\},$ we have $w_1\ne w_2$ and $v_1{w}_2,v_2{w}_1\notin E\left(G\right).$ Moreover, since S is an independent set, $G\left[\{w_1,v_1,v,v_2,w_2\}\right]=w_1{v}_{1}v{v}_2{w}_2=P_5,$ a contradiction.

Case 2. There is a vertex $u\in S^{\prime }-S$ and a vertex $v\in S$ such that $u\in epn(v,S).$

Let $S_1=(S\setminus \left\{v\right\})\cup \left\{u\right\}.$ By $u\in epn(v,S),$ $ux\notin E\left(G\right)$ for each vertex $x\in S\setminus \left\{v\right\},$ which implies that $S_1$ is an independent set with $|S_1| = |S|.$ Since $rpn(x,S)\ne \varnothing$ for each vertex $x\in S$ and $u\in epn(v,S),$ $S_1$ is a dominating set of G with $d_{G-S_1}\left(x^{\prime }\right)\ge 1$ for each vertex $x^{\prime }\in S_1$ by Claim 1. If $S_1$ is a CSDS of $G,$ then $|S_1\cap S^{\prime }| > |S\cap S^{\prime }|,$ a contradiction to the choice of $S^{\prime }.$ Thus, $S_1$ is not a CSDS of $G.$ By Claim 3, there exists a vertex $x\in S_1$ and $x_1,x_2\in epn(x,S_1)$ such that $rpn(x,S_1)=\varnothing ,$ and $x_1{x}_2\notin E\left(G\right).$ Since $v\notin S_1,$ we have $x\ne v.$ Moreover, it is easy to verify that $v\in rpn(u,S_1),$ and hence $u\ne x$ by $rpn(x,S_1)=\varnothing .$ By Claim 1 and $x_1{x}_2\notin E\left(G\right),$ we have $|\{x_1,x_2\}\cap epn(x,S)| \le 1.$

Suppose that $x_1,x_2\notin epn(x,S).$ Then, $N_S\left(x_i\right)=\{v,x\}$ for each $i\in \{1,2\}.$ Since S is an independent set and $v\ne x,$ we have $xv\notin E\left(G\right),$ which implies that $G\left[\{x_1,v,x_2,x\}\right]=x_{1}v{x}_{2}x{x}_1$ is a 4-cycle, a contradiction. Thus, $|\{x_1,x_2\}\cap epn(x,S)| =1.$ Without loss of generality, assume that $x_1\in epn(x,S)$ and $x_2\notin epn(x,S).$ Then, $N_S\left(x_2\right)=\{v,x\}.$ By $x_1\in epn(x,S)$ and $u\in epn(v,S),$ we have $x_{1}v,ux\notin E\left(G\right).$ Since $uv{x}_{2}x{x}_1\ne P_5$ and $vx,x_{1}v,u{x}_2,x_1{x}_2,ux\notin E\left(G\right),$ we have $x_{1}u\in E\left(G\right),$ which implies $d_{S_1}\left(x_1\right)\ge 2,$ a contradiction to $x_1\in epn(x,S_1).$

It follows that Theorem 3 is true. □

By Theorems 1 and 3, we can obtain the following corollary, which characterizes a graph G with ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right).$

Corollary 1. 

Let G be a non-trivial $\{K_4^{-},C_4,P_5,B_{1,1}\}$-free graph. Then, ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right).$

By Corollary 1, it is obvious that G contains an induced subgraph isomorphic to $K_4^{-},C_4,P_5$ or $B_{1,1}$ if ${\gamma }_{cs}\left(G\right)\ne \alpha \left(G\right)$ for a graph G. Clearly, a tree contains no induced subgraph in $\{K_4^{-},B_{1,1},C_4\}$. Thus, by Corollary 1, we have that if T is a tree with diam $\left(T\right)\le 3,$ then ${\gamma }_{cs}\left(T\right)=\alpha \left(T\right).$ Let T be a star or double star of order n. Clearly, $\alpha \left(T\right)=n-2$ and diam $\left(T\right)\le 3.$ Thus, ${\gamma }_{cs}\left(T\right)=n-2$ by Corollary 1, which is obtained by Arumugan in [10].

In the following we consider some other forbidden induced subgraphs in $\mathcal{F}=\{K_{1,3},B_{1,1},Z_2\}$ for a graph $G,$ such that if G is $\mathcal{F}$-free, i.e., G contains no any induced subgraph in $\mathcal{F},$ then ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right).$

Theorem 4. 

${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)$ for every $\{K_{1,3},B_{1,1},Z_2\}$-free graph G with $\delta \left(G\right)\ge 3$ if $\alpha \left(G\right)\ne 2.$

Proof. 

We assume that G is connected and $\{K_{1,3},B_{1,1},Z_2\}$-free graph with $\alpha \left(G\right)\ne 2.$ As the proof of Theorem 3, it suffices to prove that there is a minimum CSDS of $G,$ which is a maximum independent set of G. If G is a complete graph, i.e., $\alpha \left(G\right)=1,$ then ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)=1,$ and we are done. Suppose on the contrary that ${\gamma }_{cs}\left(G\right)<\alpha \left(G\right).$ Then, $\alpha \left(G\right)\ge 3.$

Claim 1. 

${\gamma }_{cs}\left(G\right)\ge 2.$

Proof. 

Suppose on the contrary that ${\gamma }_{cs}\left(G\right)=1.$ Let $S=\left\{v\right\}$ be a CSDS of $G.$ Then, each vertex in $G\setminus \left\{v\right\}$ is adjacent to v and each vertex in $G\setminus \left\{v\right\}$ is adjacent to $v.$ Since $\delta \left(G\right)\ge 3,$ $\left|V\right(G\left)\right|\ge 4.$ Then, by $\alpha \left(G\right)\ge 3,$ let $v_1,v_2,v_3\in V\left(G\right)\setminus \left\{v\right\}$ such that $\{v_1,v_2,v_3\}$ is an independent set. Then, $G[v,v_1,v_2,v_3]=K_{1,3},$ a contradiction. Thus, $\alpha \left(G\right)\le 2,$ a contradiction. □

Let S be a minimum CSDS of G such that $\left|E\right(G\left[S\right]\left)\right|$ is minimum. By Claim 1, $\left|S\right|\ge 2.$

Claim 2. 

There exists a vertex $x\in S$ with $d_S\left(x\right)\ge 1$ such that $epn(x,S)\ne \varnothing$ if $E\left(G\right[S\left]\right)\ne \varnothing .$

Proof. 

Suppose to the contrary that $epn(x,S)=\varnothing$ for each vertex $x\in S$ with $d_S\left(x\right)\ge 1.$ We assume that $uv\in E\left(G\right)$ with $u,v\in S.$ Then, $epn(u,S)=epn(v,S)=\varnothing .$ Let $S^{\prime }=S\setminus \left\{u\right\}.$ Since S is a CSDS of $G,$ $N_{G-S}\left(x\right)\ne \varnothing$ for each vertex $x\in S.$ Moreover, by $epn(u,S)=\varnothing$ and $uv\in E\left(G\right),$ we have $S^{\prime }$ is a dominating set of G such that $d_{G-S^{\prime }}\left(x\right)\ge 1$ for each vertex $x\in S^{\prime }.$ By the minimality of $\left|S\right|$ and $|S^{\prime }| < |S|,$ $S^{\prime }$ is not a CSDS of $G.$ Then, by Claim 3 of Theorem 3, let $x\in S^{\prime }$ such that $rpn(x,S^{\prime })=\varnothing$ and $x_1,x_2\in epn(x,S^{\prime })$ with $x_1{x}_2\notin E\left(G\right).$ We have $|\{x_1,x_2\}\cap epn(x,S)|<2$ since $rpn(x,S)\ne \varnothing .$ Clearly, $u\in N_S\left(x_i\right)$ if $x_i\notin epn(x,S),$ where $i\in \{1,2\}.$

Suppose $\{x_1,x_2\}\cap epn(x,S)=\varnothing .$ Then, $\{u,x\}=N_S\left(x_i\right)$ for each $i\in \{1,2\}.$ We have $x=v$; otherwise, $x_1,x_2\notin N\left(v\right)$ by $N_{S^{\prime }}\left(x_i\right)=\left\{x\right\},$ and so $G[u,x_1,x_2,v]=K_{1,3},$ a contradiction. Thus, $epn(v,S^{\prime })\ne \varnothing$ by $x=v$ and $\{x_1,x_2\}\in epn(x,S^{\prime }).$ We have $epn(v,S^{\prime })\subseteq N\left[u\right]$ by $epn(v,S)=\varnothing .$ Thus, $u\in rpn(v,S^{\prime }),$ a contradiction to $rpn(v,S^{\prime })=\varnothing .$ It follows that $|\{x_1,x_2\}\cap epn(x,S)|=1$ by $|\{x_1,x_2\}\cap epn(x,S)|<2$.

Without loss of generality, assume $x_1\notin epn(x,S)$ and $x_2\in epn(x,S).$ Then, $x\ne v$ and $N_S\left(x\right)=\varnothing$ by the hypothesis that $epn(x^{\prime },S)=\varnothing$ for each vertex $x^{\prime }\in S$ with $d_S\left(x^{\prime }\right)\ge 1.$ Note that $N_S\left(x_1\right)=\{u,x\}.$ By $d\left(x\right)\ge 3$ and $N_S\left(x\right)=\varnothing ,$ assume $N_{G-S}\left(x\right)\setminus \{x_1,x_2\}\ne \varnothing .$ We claim that $y{x}_2\notin E\left(G\right),$ and $y{x}_1,yu\in E\left(G\right)$ for each vertex $y\in N_S\left(x\right)\setminus \{x_1,x_2\}.$ Let $x_3\in N_{G-S}\left(x\right)\setminus \{x_1,x_2\}.$ We have $x_1{x}_3\in E\left(G\right)$ or $x_2{x}_3\in E\left(G\right)$ by $G[x,x_1,x_2,x_3]\ne K_{1,3}$ and $x_1{x}_2\notin E\left(G\right).$ Assume $x_2{x}_3\in E\left(G\right).$ Suppose $x_{3}v\in E\left(G\right).$ Then, we have $x_1{x}_3\in E\left(G\right)$ by $G[x_2,x_3,x,v,x_1]\ne B_{1,1}$ and $vx,x_1{x}_2,x_{2}v,x_{1}v\notin E\left(G\right),$ and hence $G[x_3,x_1,v,x_2]=K_{1,3},$ a contradiction. Thus, $x_{3}v\notin E\left(G\right).$ If $x_{3}u\in E(\left(G\right),$ then $G[x_3,x_2,x,u,v]=Z_2$ by $x_{2}u,x_{2}v,x_{3}v,xu,xv\notin E\left(G\right),$ a contradiction. Thus, $x_{3}u\notin E(\left(G\right),$ which implies $G[x,x_2,x_3,$ $x_1,u]=Z_2,$ a contradiction. It follows that $x_2{x}_3\notin E\left(G\right)$ and then $x_1{x}_3\in E\left(G\right).$ By $G[x_3,x,x_1,x_2,u]\ne B_{1,1}$ and $x_3{x}_2,x_2{x}_1,x_{2}u\notin E\left(G\right),$ we have $x_{3}u\in E\left(G\right).$

We have $N_{G-S}\left(v\right)\cap N_{G-S}\left(x\right)=\varnothing .$ Otherwise, without loss of generality, let $y\in N_{G-S}\left(v\right)\cap N_{G-S}\left(x\right).$ Then, $y{x}_1,yu\in E\left(G\right)$ and $y{x}_2\notin E\left(G\right)$ by the above result. Thus, $G[y,u,v,x,x_2]=Z_2,$ a contradiction. Moreover, we claim that $N_{G-S}\left(v\right)\cap N_{G-S}\left(x_1\right)=\varnothing .$ Otherwise, let $v_1\in N_{G-S}\left(v\right)\cap N_{G-S}\left(x_1\right).$ Then, $v_{1}x\notin E\left(G\right)$ by $N_{G-S}\left(v\right)\cap N_{G-S}\left(x\right)=\varnothing .$ We have $v_{1}u\in E\left(G\right)$ by $G[x_1,u,x,v_1]\ne K_{1,3}$ and $ux,v_{1}x\notin E\left(G\right).$ Thus, $v_1{x}_2\in E\left(G\right)$ by $G[x_1,u,v_1,x,x_2]\ne Z_2$ and $x_{2}u,x_2{x}_1,x{v}_1,xu\notin E\left(G\right).$ Then, we have $G[v_1,x_1,x_2,v]=K_{1,3},$ a contradiction. We have $N_{G-S}\left(v\right)\cap N_{G-S}\left(u\right)=\varnothing .$ Otherwise, assume $v_2\in N_{G-S}\left(v\right)\cap N_{G-S}\left(u\right).$ Then, $x_1{v}_2\notin E\left(G\right)$ by $N_{G-S}\left(v\right)\cap N_{G-S}\left(x_1\right)=\varnothing$ and $v_{2}x\notin E\left(G\right)$ by $N_{G-S}\left(v\right)\cap N_{G-S}\left(x\right)=\varnothing .$ Thus, $G[u,v_2,v,x_1,x]=Z_2,$ a contradiction. Let $v^{\prime }\in N_{G-S}\left(v\right)$ by $N_{G-S}\left(v\right)\ne \varnothing .$ Then, $v^{\prime }x,v^{\prime }u,v^{\prime }{x}_1\notin E\left(G\right)$ by the previous proof, and hence $x_3{v}^{\prime }\in E\left(G\right)$ by $G[u,x_1,x_3,v,$ $v^{\prime }]\ne Z_2.$ It follows that $G[x_3,v^{\prime },x,u]=K_{1,3},$ a contradiction. □

Claim 3. 

S is an independent set.

Proof. 

Suppose on the contrary that S is not an independent set. By Claim 2, assume $u,v\in S$ with $uv\in E\left(G\right),$ and $u_1\in epn(u,S).$ Clearly, $u_{1}v\notin E\left(G\right).$ Let $S_2=(S\setminus \left\{u\right\})\cup \left\{u_1\right\}.$ For each vertex $u^{\prime }\in N_{G-S}\left(u\right)\setminus \left\{u_1\right\},$ we have $u^{\prime }{u}_1\in E\left(G\right)$ or $u^{\prime }v\in E\left(G\right)$ by $G[u,u_1,v,u^{\prime }]\ne K_{1,3}$ and $u_{1}v\notin E\left(G\right).$ Thus, $S_2$ is a dominating set with $\left|S\right| = |S_2|$ and $|E\left(G\left[S_2\right]\right)| < |E\left(G\left[S\right]\right)|,$ which implies $S_2$ is not a CSDS by the choice of $S.$ Clearly, $u\in rpn(u_1,S_2).$ By Claim 3 of Theorem 3, let $x\in S_2\setminus \left\{u_1\right\}$ such that $rpn(x,S_2)=\varnothing ,$ and let $x_1,x_2\in epn(x,S_2)$ be two distinct non-adjacent vertices such that $|\{x_1,x_2\}\cap epn(x,S)|<2.$ By $x_1,x_2\in epn(x,S_2),$ we have $x_1{u}_1,x_2{u}_1\notin E\left(G\right).$ By $\{x_1,x_2\}⊈epn(x,S),$ without loss of generality, assume that $x_2\notin epn(x,S).$ Then, $N_S\left(x_2\right)=\{u,x\}.$ We have $x_{2}v\in E\left(G\right)$ by $G[u,x_2,v,u_1]\ne K_{1,3}$ and $x_2{u}_1,v{u}_1\notin E\left(G\right),$ which implies $x=v$. We claim $x_1\in epn(v,S).$ Otherwise, $N_S\left(x_1\right)=N_S\left(x_2\right)=\{u,v\}.$ Then, $x_2{x}_1\in E\left(G\right)$ by $G[u,x_2,x_1,u_1]\ne K_{1,3}$ and $x_1,x_2\notin N\left(u_1\right),$ a contradiction. Thus, $N_S\left(x_1\right)=\left\{v\right\}$ and then $x_{1}u\notin E\left(G\right).$ By $G[x_2,u,v,u_1,x_1]\ne B_{1,1}$ and $u_{1}v,x_{1}u,u_1{x}_2,x_1{x}_2\notin E\left(G\right),$ we have $u_1{x}_1\in E\left(G\right),$ a contradiction to $x_1\in epn(v,S_2).$ □

Let $S_1$ be a maximum independent set of G. By Claim 3, we choose a minimum CSDS S of G such that S is an independent set and $|S\cap S_1|$ is maximum. Then, $|S_1\setminus S| > |S\setminus S_1|$ by ${\gamma }_{cs}\left(G\right)<\alpha \left(G\right).$ Since S is a dominating set and $|S_1\setminus S| > |S\setminus S_1|,$ there are two vertices in $S_1\setminus S$ having a common neighbor in $S\setminus S_1.$ Assume $u,v\in S_1\setminus S$ and $w\in S\setminus S_1$ such that $u,v\in N\left(w\right).$

Claim 4. 

If $z\in epn(w,S)$, then $z\notin rpn(w,S),$ where $z\in \{u,v\}.$

Proof. 

Without loss of generality, let $u\in epn(w,S)$ and suppose on the contrary that $u\in rpn(w,S).$ Let $S^{\prime }=(S\setminus \left\{w\right\})\cup \left\{u\right\}.$ Since $u\in epn(w,S),$ $S^{\prime }$ is an independent set. We have $epn(w,S)\subseteq N\left[u\right]$ by $u\in rpn(w,S).$ Thus, $S^{\prime }$ is a dominating set with $|S^{\prime }| = |S|.$ By $|S^{\prime }\cap S_1| > |S\cap S_1|$ and the choice of $S,$ $S^{\prime }$ is not a CSDS of $G.$ Clearly, $w\in rpn(u,S^{\prime }).$ Thus, by Claim 3 of Theorem 3, let $x\in S^{\prime }\setminus \left\{u\right\}$ such that $rpn(x,S^{\prime })=\varnothing$ and $x_1,w_1\in epn(x,S^{\prime })$ such that $x_1{w}_1\notin E\left(G\right)$ and $|\{x_1,w_1\}\cap epn(x,S)|<2.$ Since $x_1,w_1\in epn(x,S^{\prime })$ and $u\in S^{\prime }\setminus \left\{x\right\},$ we have $x_{1}u,w_{1}u\notin E\left(G\right).$ By $|\{x_1,w_1\}\cap epn(x,S)|<2,$ without loss of generality, assume $w_1\notin epn(x,S).$ Then, $N_S\left(w_1\right)=\{w,x\}.$

We claim that $|\{x_1,w_1\}\cap epn(x,S)|=1.$ Suppose $x_1\notin epn(x,S).$ Then, $N_S\left(x_1\right)=N_S\left(w_1\right)=\{u,x\},$ and hence $G[w,u,x_1,w_1]=K_{1,3},$ a contradiction. Thus, $x_1\in epn(x,S).$

We claim that each vertex in $N_{G-S}\left(w\right)\setminus \{u,w_1\}$ is nonadjacent to u and adjacent to $w_1.$ Let $w_2\in N_{G-S}\left(w\right)\setminus \{w_1,u\}$ since $d\left(w\right)\ge 3$ and S is an independent set. Then, $w_2{w}_1\in E\left(G\right)$ or $w_{2}u\in E\left(G\right)$ by $G[w,w_1,w_2,u]\ne K_{1,3}$ and $u{w}_1\notin E\left(G\right).$ Suppose $u{w}_2\in E\left(G\right).$ Assume $w_2\in epn(w,S).$ Then, $w_{2}x\notin E\left(G\right),$ which implies $w_2{w}_1\in E\left(G\right)$ by $G[w,u,w_2,w_1,x]\ne Z_2$ and $wx,ux,u{w}_1\notin E\left(G\right).$ Thus, $w_2{x}_1\in E\left(G\right)$ by $G[w_1,w_2,w,x,x_1]\ne Z_2$ and $wx,x_{1}w,x_1{w}_1,w_{2}x\notin E\left(G\right).$ It follows that $G[w_2,u,w_1,x_1]=K_{1,3},$ a contradiction. Thus, $w_2\notin epn(w,S),$ and moreover, we have $d_S\left(w_2\right)=2$ since G is claw-free and S is an independent set. Let $\{y,w\}=N_S\left(w_2\right).$ Suppose $y\ne x.$ Then, $w_{2}x\notin E\left(G\right),$ which implies $w_2{w}_1\in E\left(G\right)$ by $G[w,u,w_2,w_1,x]\ne Z_2$. Since $u\in epn(w,S)$ and $N_S\left(w_1\right)=\{u,x\},$ we have $uy,w_{1}y\notin E\left(G\right),$ and hence $G[w_2,y,u,w_1]=K_{1,3},$ a contradiction. Thus, $y=x,$ i.e., $N_S\left(w_2\right)=\{w,x\}.$ By $G[x,w_1,w_2,x_1]\ne K_{1,3}$ and $w_1{x}_1\notin E\left(G\right),$ we have $x_1{w}_2\in E\left(G\right)$ or $w_1{w}_2\in E\left(G\right).$ If $w_1{w}_2\in E\left(G\right),$ then $w_2{x}_1\in E\left(G\right)$ by $G[w_1,w_2,x,u,x_1]\ne B_{1,1}$ and $u{w}_1,u{x}_1,w_1{x}_1,ux\notin E\left(G\right),$ which implies $G[w_2,u,w_1,x_1]=K_{1,3},$ a contradiction. Thus, $w_2{w}_1\notin E\left(G\right),$ and $w_2{x}_1\in E\left(G\right),$ which implies $G[x_1,w_2,x,u,w_1]=B_{1,1},$ a contradiction. It follows that $w_{2}u\notin E\left(G\right),$ and $w_2{w}_1\in E\left(G\right).$ In the following we use the result to obtain a contradiction.

Since $u\in epn(w,S)$ and $d\left(u\right)\ge 3,$ let $u_1,u_2\in N_{G-S}\left(u\right).$ By the above result, we have $u_1,u_2\notin N\left(w\right)$; otherwise, there is a vertex in $N\left(w\right)\setminus \{u,w_1\}$ adjacent to u, a contradiction. Thus, $u_1{u}_2\in E\left(G\right)$ by $G[u,u_1,u_2,w]\ne K_{1,3}.$ Moreover, we have $w_1{u}_i\in E\left(G\right)$ for some $i\in \{1,2\}$ by $G[u,u_1,u_2,w,w_1]\ne Z_2.$ Without loss of generality, assume $w_1{u}_1\in E\left(G\right).$ Then, $u_{1}x\in E\left(G\right)$ by $G[w_1,u_1,w,x]\ne K_{1,3}$ and $u_{1}w,wx\notin E\left(G\right).$ We have $u_1{x}_1\in E\left(G\right)$ by $G[w_1,u_1,x,u,x_1]\ne B_{1,1}$ and $ux,u{x}_1,u{w}_1,w_1{x}_1\notin E\left(G\right).$ Thus, $G[u_1,w_1,u,x_1]=K_{1,3},$ a contradiction. □

Claim 5. 

$\{u,v\}\cap epn(w,S)=\varnothing .$

Proof. 

Without loss of generality, suppose on the contrary that $u\in epn(w,S).$ Then, by Claim 4, $u\notin rpn(w,S),$ and hence let $w_1\in epn(w,S)\setminus \left\{u\right\}$ such that $u{w}_1\notin E\left(G\right).$ Since S is a CSDS of $G,$ $rpn(w,S)\ne \varnothing .$

Let $w_2\in rpn(w,S).$ We have $w_2\notin \{u,w_1\}$ by $u,w_1\in epn(w,S)$ and $u{w}_1\notin E\left(G\right).$ Moreover, $w_1{w}_2,w_{2}u\in E\left(G\right)$ by $w_2\in rpn(w,S)$ and $u,w_1\in epn(w,S).$ We claim $rpn(w,S)\subseteq epn(w,S).$ Suppose $w_2\notin epn(w,S).$ Then, $d_S\left(w_2\right)\ge 2.$ Let $x\in N_S\left(w_2\right)\setminus \left\{w\right\}.$ We have $ux,w_{1}x\notin E\left(G\right)$ by $u,w_1\in epn(w,S),$ and hence $G[w_2,w_1,u,x]=K_{1,3},$ a contradiction. Thus, $w_2\in epn(w,S).$

We claim that $N\left(w\right)=epn(w,S)$ by reduction to absurdity. Suppose $N\left(w\right)\setminus epn(w,S)\ne \varnothing ,$ and assume $w_3\in N\left(w\right)\setminus epn(w,S).$ Then, $d_S\left(w_3\right)\ge 2,$ and $w_3\notin \{u,w_1,w_2\}$ by $\{u,w_1,w_2\}\subseteq epn(w,S).$ Let $y\in N_S\left(w_3\right)\setminus \left\{w\right\}.$ Then, $w_{3}u\in E\left(G\right)$ or $w_3{w}_1\in E\left(G\right)$ by $G[w,w_1,u,w_3]\ne K_{1,3}$ and $w_{1}u\notin E\left(G\right).$ Assume $w_{3}u\in E\left(G\right).$ Then, by $G[u,w,w_3,w_1,y]\ne B_{1,1}$ and $u{w}_1,uy,wy,w_{1}y\notin E\left(G\right),$ we have $w_1{w}_3\in E\left(G\right),$ and hence $G[w_3,w_1,u,y]=K_{1,3},$ a contradiction. Thus, $w_{3}u\notin E\left(G\right)$ and similarly, $w_1{w}_3\notin E\left(G\right),$ which implies a contradiction.

Since $\left|S\right|\ge 2$ and G is connected, assume that $x_1\in N_{G-S}\left(w\right),$ $x_2\in V\left(G\right)-S$ such that $x_1{x}_2\in E\left(G\right)$ and $N_S\left(x_2\right)\setminus \left\{w\right\}\ne \varnothing .$ Moreover, by $epn(w,S)=N\left(w\right),$ we have $x_{2}w\notin E\left(G\right).$ Let $z\in N_S\left(x_2\right).$ Then, $z\ne w.$ Suppose $x_1\notin rpn(w,S).$ Then, without loss of generality, assume $x_1=w_1.$ By $x_{2}z\in E\left(G\right)$ and $N\left(w\right)=epn(w,S),$ we have $x_{2}w,w_{1}z,uz,w_{2}z\notin E\left(G\right).$ Thus, $w_2{x}_2\in E\left(G\right)$ by $G[w_1,w_2,w,x_2,z]\ne Z_2,$ which implies $u{x}_2\in E\left(G\right)$ by $G[w_2,u,w,x_2,z]\ne Z_2.$ It follows that $G[x_2,w_1,u,z]=K_{1,3},$ a contradiction. Thus, $x_1\in rpn(w,S),$ and then $x_{2}u\notin E\left(G\right).$ Without loss of generality, let $x_1=w_2.$ Then, $G[w_2,u\left(w_1\right),w,x_2,z]=Z_2$ by $x_2{w}_1,x_{2}u\notin E\left(G\right),$ a contradiction. □

Claim 6. 

$epn(x,S)\ne \varnothing$ for each vertex x in $N_S\left(u\right)\cap N_S\left(v\right).$

Proof. 

Without loss of generality, suppose on the contrary that $epn(w,S)=\varnothing .$ Since $d\left(w\right)\ge 3,$ let $w_1\in N_{G-S}\left(w\right)\setminus \{u,v\}.$ Then, $w_{1}u\in E\left(G\right)$ or $w_{1}v\in E\left(G\right)$ by $G[w,u,v,w_1]\ne K_{1,3}$ and $uv\notin E\left(G\right).$ Without loss of generality, assume that $w_{1}u\in E\left(G\right).$ Since $epn(w,S)=\varnothing ,$ $min\{d_S\left(u\right),d_S\left(v\right)\}\ge 2.$ Moreover, since G is claw-free and S is an independent set, $d_S\left(u\right)=d_S\left(v\right)=2.$ Assume $N_S\left(u\right)=\{w,x\}$ and $N_S\left(v\right)=\{w,y\}.$

We claim that $y=x.$ Suppose $y\ne x.$ By $G[w,w_1,u,v,y]\ne Z_2$ and $uy,uv,wy\notin E\left(G\right),$ we have $v{w}_1\in E\left(G\right)$ or $w_{1}y\in E\left(G\right).$ Suppose that $y{w}_1\in E\left(G\right).$ Then, $w_{1}x\notin E\left(G\right);$ otherwise, $G[w_1,w,y,x]=K_{1,3},$ a contradiction. Thus, $G[w,w_1,u,y,x]=B_{1,1},$ a contradiction. It follows that $y{w}_1\notin E\left(G\right)$, and then $w_{1}v\in E\left(G\right).$ Since $epn(w,S)=\varnothing ,$ we assume that $z\in N_S\left(w_1\right)\setminus \left\{w\right\}.$ By $w_{1}y\notin E\left(G\right),$ we have $z\ne y.$ Moreover, we have $G[w,v,w_1,y,z]=B_{1,1}$ by $N_S\left(v\right)=\{y,w\},$ a contradiction. Thus, $y=x.$

Let $S^{\prime }=(S\setminus \{w,x\})\cup \{u,v\}.$ Since $N_S\left(u\right)=N_S\left(v\right)=\{w,x\},$ $S^{\prime }$ is an independent set with $|S^{\prime }| = |S|.$ Moreover, each vertex in $N\left(w\right)\cup N\left(x\right)$ is adjacent to u or $v,$ since G is claw-free. Clearly, $w,x\notin S_1$ and then $|S^{\prime }\cap S_1| > |S\cap S_1|.$ Thus, $S^{\prime }$ is not a CSDS of G by the choice of $S.$ Then, let $z\in S^{\prime }$ such that $rpn(z,S^{\prime })=\varnothing$ and let $x_1,x_2$ be two non-adjacent vertices in $epn(z,S^{\prime })$ such that $|\{x_1,x_2\}\cap epn(z,S)| <2.$ Without loss of generality, assume that $x_1\notin epn(z,S).$ Then, $x_1\cap \{w,x\}\ne \varnothing ,$ which implies $x_{1}u\in E\left(G\right)$ or $x_{1}v\in E\left(G\right).$ In the following, we claim that $z\in \{u,v\},$ and then obtain a forbidden subgraph to give a contradiction.

Suppose $z\notin \{u,v\}.$ Then, $d_{S^{\prime }}\left(x_1\right)\ge 2$ by $x_1\in N\left(u\right)\cup N\left(v\right)$, a contradiction to $x_1\in epn(z,S^{\prime }).$ Without loss of generality, assume that $z=u.$ Then, $x_{i}v\notin E\left(G\right)$ by $x_i\in epn(u,S^{\prime }),$ and $N\left(x_i\right)\cap \{w,x\}\ne \varnothing$ for each $i\in \{1,2\}.$ Suppose that $x_1$ and $x_2$ has a common neighbor in $\{w,x\}.$ Without loss of generality, assume that $w\in N\left(x_1\right)\cap N\left(x_2\right).$ Then, $x_{1}v$ or $x_{2}v\in E\left(G\right)$ by $G[w,v,x_1,x_2]\ne K_{1,3}$ and $x_1{x}_2\notin E\left(G\right),$ a contradiction. Thus, $N\left(x_1\right)\cap N\left(x_2\right)=\varnothing .$ Without loss of generality, assume that $x_{1}w,x_{2}x\in E\left(G\right).$ Then, $x_{1}x,x_{2}w\notin E\left(G\right).$ It follows that $G[x_2,x,u,v,x_1]=B_{1,1},$ a contradiction. Thus, the claim is true. □

Claim 7. 

If a vertex in $\{u,v\}$ is in $rpn(x,S)$, then $N_S\left(u\right)=N_S\left(v\right),$ where $x\in N_S\left(u\right)\cap N_S\left(v\right).$

Proof. 

Without loss of generality, let $u\in rpn(w,S).$ We have $epn(w,S)\ne \varnothing$ by Claim 6. Then, each vertex in $epn(w,S)$ is adjacent to $u.$ By Claim 5, $d_S\left(u\right)=d_S\left(v\right)=2$ since G is claw-free. Assume $N_S\left(u\right)=\{w,x\}$ and $N_S\left(v\right)=\{w,y\}.$ It suffices to prove $x=y.$ Suppose $x\ne y.$ We claim that $v\in rpn(w,S).$ Otherwise, let $w_1\in epn(w,S)$ such that $w_{1}v\notin E\left(G\right).$ By $u\in rpn(w,S),$ we have $w_{1}u\in E\left(G\right).$ Moreover, $w_{1}y\notin E\left(G\right)$ by $w_1\in epn(w,S).$ Thus, $G[w,u,w_1,v,y]=Z_2,$ a contradiction, and then $v\in rpn(w,S).$

Let $w_1\in epn(w,S).$ Then, $w_{1}v,w_{1}u\in E\left(G\right)$ by $\{u,v\}\subseteq rpn(w,S).$ We claim that $v\in rpn(y,S)$. Otherwise, let $y_1\in epn(y,S)$ such that $v{y}_1\notin E\left(G\right).$ Clearly, $w_{1}y,y_{1}w\notin E\left(G\right)$ by $w_1\in epn(w,S)$ and $y_1\in epn(y,S).$ Thus, we have $w_1{y}_1\in E\left(G\right)$ by $G[v,w_1,w,y,y_1]\ne Z_2.$ Then, $u{y}_1\in E\left(G\right)$ since $G[w_1,u,w,y_1,y]\ne Z_2.$ Since $y_1\in epn(y,S),$ we have $y_{1}x,y_{1}w\notin E\left(G\right),$ which implies $G[u,x,w,y_1]=K_{1,3},$ a contradiction. Similarly, $u\in rpn(x,S).$ Moreover, each vertex in $N\left(w\right)\setminus \{u,v\}$ is adjacent to u or v since G is claw-free. Let $S^{\prime }=(S\setminus \{w,x,y\})\cup \{u,v\}.$ By the previous result, $S^{\prime }$ is a dominating set of G. Moreover, $S^{\prime }$ is an independent set.

We claim that $z_{1}u\in E\left(G\right)$ or $z_{1}v\in E\left(G\right)$ for each vertex in $z_1\in N\left(z\right)\setminus (N\left(w\right)\cup epn(z,S))$ and each $z\in \{x,y\}.$ Otherwise, without loss of generality, suppose that $z_1\in N\left(x\right)\setminus (N\left(w\right)\cup epn(x,S))$ and $z_{1}u,z_{1}v\notin E\left(G\right).$ Then, we have $w_1{z}_1\in E\left(G\right)$ by $G[u,w_1,w,x,z_1]\ne Z_2,$ and hence $G[w_1,z_1,u,v]=K_{1,3},$ a contradiction. It follows that $z^{\prime }\notin epn(z,S^{\prime })$ if $N_S\left(z^{\prime }\right)\setminus \{w,x,y\}\ne \varnothing$ for each $z^{\prime }\in N\left(z\right),$ where $z\in \{x,y,w\}.$

By $|S^{\prime }| < |S|,$ $S^{\prime }$ is not a CSDS of $G.$ Then, let $z^{\prime }\in S^{\prime }$ such that $rpn(z^{\prime },S^{\prime })=\varnothing$ and let $z_1,z_2$ be two non-adjacent vertices in $epn(z^{\prime },S^{\prime })$ such that $|\{z_1,z_2\}\cap epn(z^{\prime },S)|<2.$ Suppose that $z^{\prime }\notin \{u,v\}.$ By $|\{z_1,z_2\}\cap epn(z^{\prime },S)| <2,$ without loss of generality, assume that $z_1\notin epn(z^{\prime },S).$ Then, $N\left(z_1\right)\cap \{w,x,y\}\ne \varnothing$ by the above result. Since $N\left(z_1\right)\cap \{u,v\}\ne \varnothing ,$ we obtain a contradiction to $z_1\in epn(z^{\prime },S^{\prime }).$ Thus, $z^{\prime }\in \{u,v\}.$ Without loss of generality, assume that $z^{\prime }=u.$ Then, $z_{1}v,z_{2}v\notin E\left(G\right)$ by $z_1,z_2\in epn(u,S^{\prime }).$ We have $z_{1}x\in E\left(G\right)$ or $z_{2}x\in E\left(G\right)$ by $G[u,z_1,z_2,x]\ne K_{1,3}.$ Without loss of generality, assume that $z_{1}x\in E\left(G\right).$ Then, we have $z_{1}w\in E\left(G\right)$ by $G[u,z_1,x,w,v]\ne Z_2,$ which implies $z_{1}y\in E\left(G\right)$ by $G[w,u,z_1,v,y]\ne Z_2.$ Thus, $G[z_1,w,x,y]=K_{1,3},$ a contradiction. It follows that $x=y.$ □

Now we come to complete the theorem. We claim that $N_S\left(u\right)=N_S\left(v\right).$ By Claim 7, it suffices to prove $N_S\left(u\right)=N_S\left(v\right)$ if no vertex of $\{u,v\}$ is in $rpn(w^{\prime },S)$ for each vertex $w^{\prime }\in N_S\left(u\right)\cap N_S\left(v\right).$ Assume $\{u,v\}\cap rpn(w,S)=\varnothing .$ Then, by Claim 6, let $w_1\in epn(w,S)$ such that $w_{1}u\notin E\left(G\right).$ We have $w_{1}v\in E\left(G\right)$ by $G[w,u,v,w_1]\ne K_{1,3}$ and $uv\notin E\left(G\right).$ We have $d_S\left(u\right)=d_S\left(v\right)=2$ since G is claw-free and by Claim 5. Assume that $N_S\left(u\right)=\{w,x\}.$ Clearly, $w_{1}x\notin E\left(G\right)$ by $w_1\in epn(w,S).$ Then, $vx\in E\left(G\right)$ by $G[w,v,w_1,u,x]\ne Z_2.$ Thus, $N_S\left(u\right)=N_S\left(v\right)=\{w,x\}.$

Let $S^{\prime }=(S\setminus \{w,x\})\cup \{u,v\}.$ Since G is claw-free and $uv\notin E\left(G\right),$ each vertex in $N\left(w\right)\cup N\left(x\right)$ is adjacent to u or $v.$ Thus, $S^{\prime }$ is a dominating set, and moreover, $S^{\prime }$ is an independent set by $N_S\left(u\right)=N_S\left(v\right)=\{w,x\}.$ Clearly, $x,w\notin S_1$ and then $|S^{\prime }\cap S_1| > |S\cap S_1|.$ Thus, $S^{\prime }$ is not a CSDS of G by the choice of $S.$ Then, let $y\in S^{\prime }$ such that $rpn(y,S^{\prime })=\varnothing ,$ and let $y_1,y_2\in epn(y,S^{\prime })$ such that $y_1{y}_2\notin E\left(G\right)$ and $|\{y_1,y_2\}\cap epn(y,S)| <2.$

Without loss of generality, assume that $y_1\notin epn(y,S).$ Then, $d_S\left(y_1\right)\ge 2$ and $N_S\left(y_1\right)\cap \{w,x\}\ne \varnothing .$ Thus, $N\left(y_1\right)\cap \{u,v\}\ne \varnothing .$ It follows that $d_{S^{\prime }}\left(y_1\right)\ge 2$ if $y\notin \{u,v\},$ a contradiction to $y_1\in epn(y,S^{\prime }).$ Thus, $y\in \{u,v\}.$ Without loss of generality, assume that $y=u.$ Then, $y_{1}v,y_{2}v\notin E\left(G\right)$ by $y_1,y_2\in epn(u,S^{\prime }).$ We have $y_{1}w\in E\left(G\right)$ or $y_{2}w\in E\left(G\right)$ by $G[u,w,y_1,y_2]\ne K_{1,3}.$ Without loss of generality, assume that $y_{1}w\in E\left(G\right).$ Then, $w{y}_2\notin E\left(G\right).$ Otherwise, $G[w,y_1,y_2,v]=K_{1,3},$ a contradiction. It follows that $G[y_1,u,w,y_2,v]=B_{1,1},$ a contradiction. Thus, the theorem is true. □

Let $G=K_m\vee (K_2\cup K_1),m\ge 3.$ Then, G is a $\{K_{1,3},B_{1,1},Z_2\}$-free graph with $\delta \left(G\right)\ge 3$ and $\alpha \left(G\right)=2.$ It is easy to verify that ${\gamma }_{cs}\left(G\right)=1.$ Thus, the condition that $\alpha \left(G\right)\ne 2$ in Theorem 4 is necessary.

By Theorem 4, if ${\gamma }_{cs}\left(G\right)<\alpha \left(G\right)$ for a graph G with $\delta \left(G\right)\ge 3,$ then G contains an induced subgraph isomorphic to $K_{1,3}$, $Z_2,$ or $B_{1,1}$. Moreover, by Theorems 1 and 4, it is easy to obtain the following corollary.

Corollary 2. 

Let G be a non-trivial every $\{K_{1,3},B_{1,1},Z_2\}$-free graph G with $\delta \left(G\right)\ge 3$ and $\alpha \left(G\right)\ne 2.$ Then, every maximum independent set of G is a minimum co-secured dominating set of $G.$

According to Problem 2, we give the following result.

Theorem 5. 

${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right)$ for every $\{K_3,C_5,P_5\}$-free graph G with $\delta \left(G\right)\ge 2.$

Proof. 

Let G be a $\{K_3,C_5,P_5\}$-free graph with $\delta \left(G\right)\ge 2.$ By Theorem 2, it suffices to prove G contains a minimum CSDS S such that S is a SDS, i.e., ${\gamma }_{cs}\left(G\right)\ge {\gamma }_s\left(G\right).$ Suppose to the contrary that each minimum CSDS of G is not a SDS of $G.$ Let S be a minimum CSDS S of G. Then, there is an S-undefended vertex in $G-S.$

Firstly, we claim that for each vertex $u\in S,$ $\left|epn\right(u,S\left)\right|\le 1.$ Suppose that there is a vertex $x\in S$ such that $\left|epn\right(x,S\left)\right|\ge 2.$ Assume that $x_1,x_2\in epn(x,S).$ We have $x_1{x}_2\notin E\left(G\right)$, otherwise, $G\left[\{x,x_1,x_2\}\right]=K_3,$ a contradiction. Thus, $x_i\notin rpn(x,S)$ for each $i\in \{1,2\}.$ By the definition of a CSDS, $rpn(x,S)\ne \varnothing .$ Assume that $y\in rpn(x,S).$ Then, $y\notin \{x_1,x_2\}$ by $\{x_1,x_2\}\cap rpn(x,S)=\varnothing ,$ and hence $y{x}_i\in E\left(G\right)$ for each $i\in \{1,2\}.$ It follows that $G\left[\{y,x_i,x\}\right]=K_3$ for each $i\in \{1,2\},$ a contradiction. Thus, $\left|epn\right(x,S\left)\right|\le 1$ and $rpn(x,S)=\left\{x^{\prime }\right\}$ if $epn(x,S)=\left\{x^{\prime }\right\}.$ It follows that if a vertex $z\in V\left(G\right)-S$ is S-undefended, then $d_S\left(z\right)\ge 2$.

Suppose $z\in V\left(G\right)-S$ is S-undefended. Then, for each vertex w in $N_S\left(z\right),$ $epn(w,S)\ne \varnothing$ and the exactly one vertex in $epn(w,S)$ is non-adjacent to $z.$ By $d_S\left(z\right)\ge 2,$ we assume $w_1,w_2\in N_S\left(z\right).$ Let $u_1\in epn(w_1,S),u_2\in epn(w_2,S).$ Then, $u_1{w}_2,u_2{w}_1\notin E\left(G\right).$ By $G\left[\{z,w_1,w_2\}\right]\ne K_3$, we have $w_1{w}_2\notin E\left(G\right).$ Then, $u_1{u}_2\in E\left(G\right)$ by $G\left[\{u_1,w_1,z,w_2,u_2\}\right]\ne P_5,$ which implies $G[\{u_1,w_1,z,w_2,u_2\}=C_5,$ a contradiction. Thus, each vertex in $G-S$ is S-defended, and S is a SDS of $G.$ We have ${\gamma }_{cs}\left(G\right)\ge {\gamma }_s\left(G\right),$ and the theorem is true. □

By Theorem 5, if ${\gamma }_{cs}\left(G\right)<{\gamma }_s\left(G\right)$ for a graph G with $\delta \left(G\right)\ge 2,$ then G contains an induced subgraph isomorphic to $K_3,$ $C_5,$ or $P_5.$ Since a bipartite graph G contains no odd cycles, G is $\{K_3,C_5\}$-free. Thus, by Theorem 5, we can obtain the following corollary.

Corollary 3. 

If G is a bipartite graph with $\delta \left(G\right)\ge 2$ and contains no induced subgraph isomorphic to $P_5,$ then ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right).$

By Corollary 3, we have ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right)$ for a complete bipartite graph $G=K_{p,q}$ with $2\le p\le q.$ This generalizes Proposition 2.15 in [10].

3. Conclusions

Arumugam et al. [10] proposed two questions: (1) Characterize a graph G with ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right);$ (2) Characterize a graph G with ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right).$ In this paper, according to question (1), we prove that ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)$ for every non-trivial $\{K_4^{-},C_4,B_{1,1},P_5\}$-free graph; moreover, we obtain that ${\gamma }_{cs}\left(G\right)=\alpha \left(G\right)$ for every non-trivial $\{K_{1,3},B_{1,1},Z_2\}$-free graph G with $\delta \left(G\right)\ge 3$ and $\alpha \left(G\right)\ne 2$; according to question (2), we obtain that ${\gamma }_{cs}\left(G\right)={\gamma }_s\left(G\right)$ for each $\{K_3,C_5,P_5\}$-free graph G with $\delta \left(G\right)\ge 2.$ Our conclusions can generalize some results on the bounds of co-secure domination number of some families of trees and bipartite graphs.