Solutionsof Fuzzy Goursat Problems with Generalized Hukuhara (gH)-Differentiability Concept

Abstract

In this manuscript, we will discuss the solutions of Goursat problems with fuzzy boundary conditions involving gH-differentiability. The solutions to these problems face two main challenges. The first challenge is to deal with the two types of fuzzy gH-differentiability: $\left(i\right)$-differentiability and $\left(ii\right)$-differentiability. The sign of coefficients in Goursat problems and gH-differentiability produces sixteen possible cases. The existing literature does not afford a solution method that addresses all the possible cases of this problem. The second challenge is the mixed derivative term in Goursat problems with fuzzy boundary conditions. Therefore, we propose to discuss the solutions of fuzzy Goursat problems with gH-differentiability. We will discuss the solutions of fuzzy Goursat problems in series form with natural transform and Adomian decompositions. To demonstrate the usability of the established solution methods, we will provide some numerical examples.

1. Introduction

Fuzzy calculus has valuable applications in many physical problems, particularly those involving uncertainty [1]. It also has important contributions in other fields like banking [2], optimization [3], resources allocations [4], decision-making [5], linear programming and engineering. In fuzzy calculus, ordinary and partial fuzzy differential equations have an important role. But in the phenomena of the physical world, several independent variables are involved, and therefore partial differential equations perform better than ordinary differential equations. In the physical world, any physical measure contains uncertainty. Buckley and Feuring [6] used the concept of fuzziness to address uncertainty in partial differential equations. After this work, the concept of fuzzy partial differential equations has been used by many researchers for different processes such as heat equations [7,8], advection equations [9], advection-diffusion equations [10,11] and fractional differential equations [12].

In wave phenomena, hyperbolic partial differential equations have second-order mixed derivative terms, these problems are known as Goursat problems. Goursat problems have many applications in physics, engineering and other fields. The authors of [13,14,15,16] discussed some applications and solution methods for Goursat problems. In paper [17], the authors discussed the conditions for Goursat problems with fuzzy boundary conditions to ensure unique solutions.

The existing literature has various processes to solve differential equations (DEs) such as integral transforms (Laplace, Sumudu, natural transform, etc.) and series processes (Taylor’s series, Adomian decomposition, Homotopy, etc.). George Adomian [18] was the first one to introduce the method of Adomian decomposition. Later on, many researchers used Adomian decomposition [19,20,21] and its various modifications [22,23] for the solutions of various differential equations. In [24], the authors introduced the concept of natural transform. The natural transform directly produced the Laplace and Sumudu transforms only by providing unity values to the transformation parameters.

To solve fuzzy partial DEs with gH-differentiability, the existing solution process faces difficulties due to the two types of gH-differentiability: $\left(i\right)$-differentiability and $\left(ii\right)$-differentiability. Moreover, the sign of coefficients in Goursat problems and mixed gH-derivative terms produces many possibilities. Therefore, the existing literature does not have a solution method that deals with all possible cases of Goursat problems with fuzzy boundary conditions.

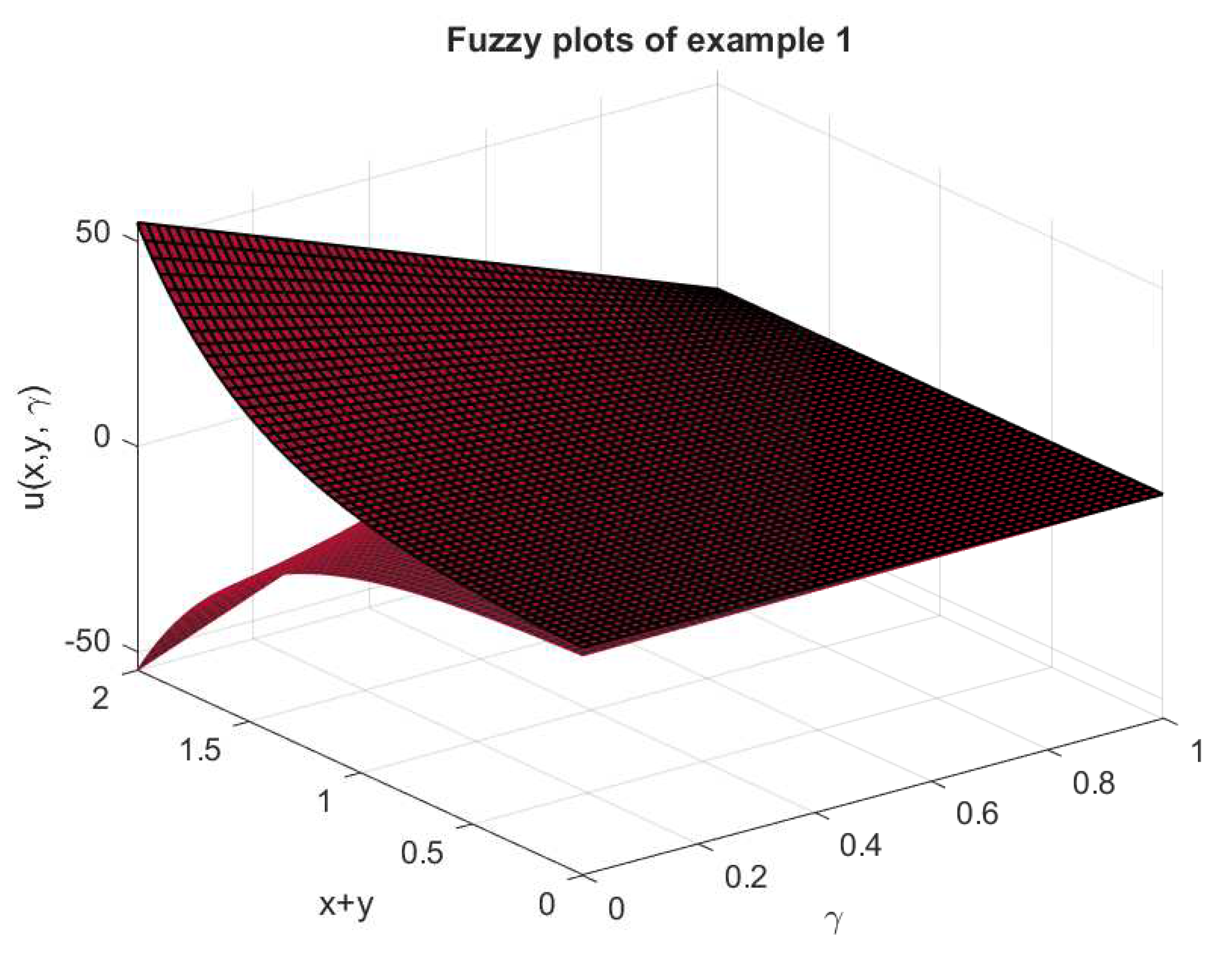
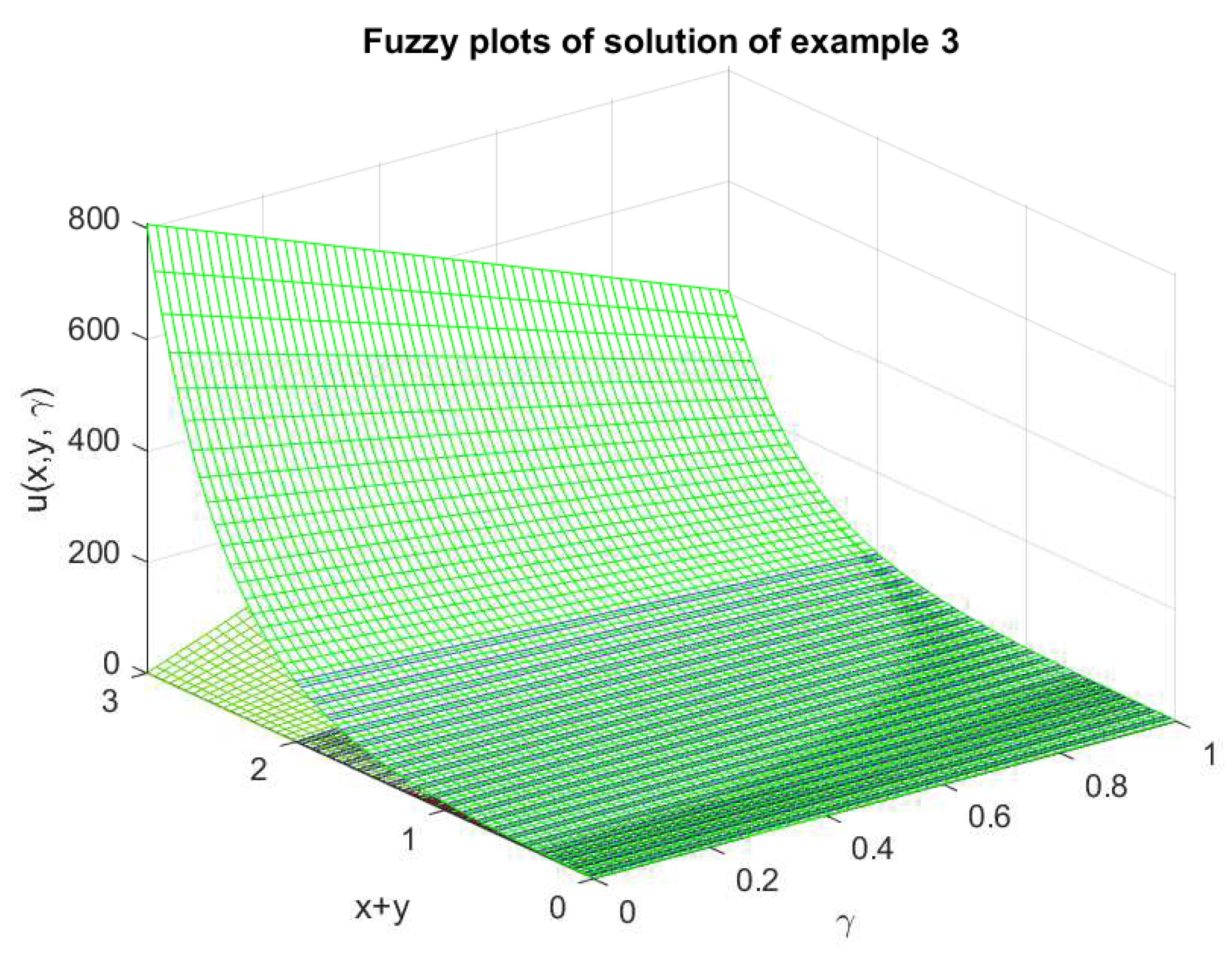
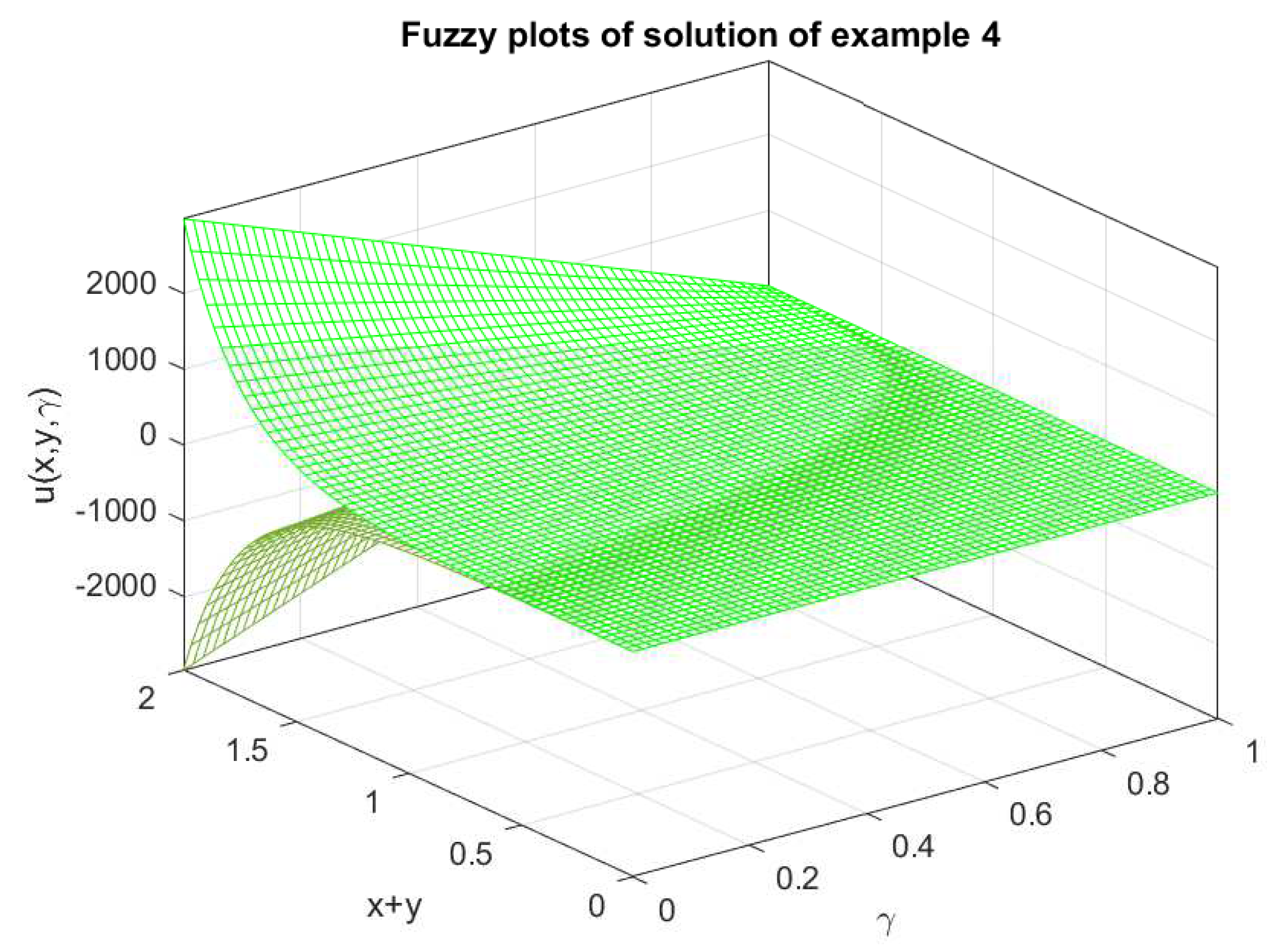
In this paper, we will discuss the solutions of Goursat problems with fuzzy boundary conditions in series form with natural Adomian decomposition. This work is the first effort to discuss all possible solutions of Goursat problems with gH-differentiability. In the literature on fuzzy partial differential equations mostly the solutions of special cases of fuzzy problems are discussed due to the complex nature of fuzzy differentiability, but our work has potential to discuss all possible cases of the fuzzy Goursat problems. In the solutions of fuzzy Goursat problems with gH-differentiability, sixteen different cases arise due to the sign of coefficients and the nature of said differentiability. Natural transform is the generalization of Laplace and Sumudu transforms. Therefore, in this solution method, we propose natural transform with Adomian decomposition to save the time of researchers because if the natural transform of problems obtained, then the Laplace transform directly obtain from it only by taking the transform parameter $r=1$ and Sumudu transform by $s=1$. This new algorithm is not only limited to Goursat problems, but it is also applicable to all fuzzy partial differential equations. For the usability of the proposed solution method, we will also provide some numerical examples.

2. Preliminaries

Now, we recall some definitions, remarks and results from fuzzy set theory and calculus. In this manuscript, $R_F$ denotes the space of fuzzy numbers.

Definition 1.

[25] A fuzzy set is a fuzzy number if its membership function ψ satisfies the conditions given below

(i) 

ψ is upper semi-continuous;

(ii) 

ψ is convex;

(iii) 

ψ is normal;

(iv) 

The support of ψ is compact.

For $0\le \alpha \le 1$ the $\alpha$-level set is given by ${\left[\psi \right]}^{\alpha }=\{\sigma \in R|\psi \left(\sigma \right)\ge \alpha \}.$

Definition 2.

[26] The gH-difference of fuzzy number $\psi ,\varphi$, is defined as

$$\psi {\ominus }_{gH}\phi =\phi \iff \left\{\begin{array}{c}\hfill \psi =\varphi \oplus \phi ,\\ \hfill \varphi =\psi \oplus (-\phi ).\end{array}\right.$$

Moreover, $\psi \ominus \varphi =\psi {\ominus }_{gH}\varphi$ if the $H-$ difference $\psi \ominus \varphi$ exists.

Definition 3.

[26,27] Let $\tau :I\to R_F$, and $\vartheta \in I$ is said to be generalized Hukuhara (gH) differentiable at ϑ if there exists ${\tau }^{\prime }\left(\vartheta \right)\in R_F$ such that either

(1) 

The limits exist in the fuzzy metric space and H-difference $\tau (\vartheta +\delta )\ominus \tau \left(\vartheta \right)$, $\tau \left(\vartheta \right)\ominus \tau (\vartheta -\delta )$ exist for sufficiently small $\delta >0$.

$$\begin{array}{ccc}\hfill \underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau \left(\vartheta \right)\ominus \tau (\vartheta +\delta )}{\delta }}& =& \underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau (\vartheta -\delta )\ominus \tau \left(\vartheta \right)}{\delta }}={\tau }^{\prime }\left(\vartheta \right)\hfill \end{array}$$

(2) 

The limits exist in the fuzzy metric space and H-difference, $\tau \left(\vartheta \right)\ominus \tau (\vartheta +\delta ),$$\tau (\vartheta -\delta )\ominus \tau \left(\vartheta \right)$ exist for sufficiently small $\delta >0.$

$$\begin{array}{ccc}\hfill \underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau (\vartheta +\delta )\ominus \tau \left(\vartheta \right)}{(-\delta )}}& =& \underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau \left(\vartheta \right)\ominus \tau (\vartheta -\delta )}{(-\delta )}}={\tau }^{\prime }\left(\vartheta \right)\hfill \end{array}$$

These are respectively $\left(i\right)$-differentiable and $\left(ii\right)$-differentiable.

Lemma 1.

[28] Let $\tau :I\to R_F,$ is a continuous fuzzy function with ${\left[\tau \left(\theta \right)\right]}^{\alpha }=\left[{\underline{\tau }}^{\alpha }\left(\theta \right),{\overline{\tau }}^{\alpha }\left(\theta \right)\right]$, and $0\le \alpha \le 1$.

$\left(i\right)$

If ${\left[\tau \left(\theta \right)\right]}^{\alpha }$ is $\left(i\right)$-differentiable, then ${\underline{\tau }}^{\alpha }\left(\theta \right),{\overline{\tau }}^{\alpha }\left(\theta \right)$ are differentiable

and ${\left[{\tau }^{\prime }\left(\theta \right)\right]}^{\alpha }=\left[{\left({\underline{\tau }}^{\alpha }\right)}^{\prime }\left(\theta \right),{\left({\overline{\tau }}^{\alpha }\right)}^{\prime }\left(\theta \right)\right].$

$\left(ii\right)$

If ${\left[\tau \left(\theta \right)\right]}^{\alpha }$ is $\left(ii\right)$-differentiable, then ${\underline{\tau }}^{\alpha }\left(\theta \right),{\overline{\tau }}^{\alpha }\left(\theta \right)$ are differentiable

and ${\left[{\tau }^{\prime }\left(\theta \right)\right]}^{\alpha }=\left[{\left({\overline{\tau }}^{\alpha }\right)}^{\prime }\left(\theta \right),{\left({\underline{\tau }}^{\alpha }\right)}^{\prime }\left(\theta \right)\right].$

Now, we present the partial generalized Hukuhara derivative for fuzzy functions.

Definition 4.

[7] The $gH$-differentiability of $\tau :I\times J\to R_F,$ with respect to ϑ exists at $({\vartheta }_0,{\kappa }_0)\in I\times J$ if one of the following holds

$\left(i\right)$

The limits exist in the fuzzy metric space and H-difference $\tau ({\vartheta }_0+\delta ,{\kappa }_0)\ominus \tau ({\vartheta }_0,{\kappa }_0),$

$\tau ({\vartheta }_0,{\kappa }_0)\ominus \tau ({\vartheta }_0-\delta ,{\kappa }_0)$ exist for sufficiently small $\delta >0.$

$$\begin{array}{ccc}\hfill \underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau ({\vartheta }_0+\delta ,{\kappa }_0)\ominus \tau ({\vartheta }_0,{\kappa }_0)}{\delta }}=\underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau ({\vartheta }_0,{\kappa }_0)\ominus \tau ({\vartheta }_0-\delta ,{\kappa }_0)}{\delta }}& =& D_{\vartheta }^i\tau ({\vartheta }_0,{\kappa }_0).\hfill \end{array}$$

$\left(ii\right)$

The limits exist in the fuzzy metric space and H-difference $\tau ({\vartheta }_0,{\kappa }_0)\ominus \tau ({\vartheta }_0+\delta ,{\kappa }_0),$$\tau ({\vartheta }_0-\delta ,{\kappa }_0)\ominus \tau ({\vartheta }_0,{\kappa }_0)$ exist for sufficiently small $\delta >0.$

$$\begin{array}{ccc}\hfill \underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau ({\vartheta }_0,{\kappa }_0)\ominus \tau ({\vartheta }_0+\delta ,{\kappa }_0)}{(-\delta )}}=\underset{\delta \to 0^{+}}{lim}{\displaystyle \frac{\tau ({\vartheta }_0-\delta ,{\kappa }_0)\ominus \tau ({\vartheta }_0,{\kappa }_0)}{(-\delta )}}& =& D_{\vartheta }^{ii}({\vartheta }_0,{\kappa }_0).\hfill \end{array}$$

The first one, ${D^i}_{\vartheta }({\vartheta }_0,{\kappa }_0)$, is referred to as $\left(i\right)$-differentiable and the second one, $D_{\vartheta }^{ii}({\vartheta }_0,{\kappa }_0)$, as $\left(ii\right)$-differentiable.

According to Lemma 1, we have the following result

Lemma 2.

[7] Let $\tau :I\times J\to R_F,$ be a continuous fuzzy function with ${\left[\tau (\kappa ,\vartheta )\right]}^{\alpha }=[{\underline{\tau }}^{\alpha }(\kappa ,\vartheta ),{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )]$; then, the following identity holds for $(\kappa ,\vartheta )\in I\times J.$

$\left(i\right)$

If ${\left[D_{\kappa }^i\tau (\kappa ,\vartheta )\right]}^{\alpha }$ exist on $I\times J,$ then $D_{\kappa }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )$, $D_{\kappa }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )$ are differentiable with respect to κ and ${\left[D_{\kappa }^i\tau (\kappa ,\vartheta )\right]}^{\alpha }=\left[D_{\kappa }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta ),D_{\kappa }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )\right].$

$\left(ii\right)$

If ${\left[D_{\vartheta }^i\tau (\kappa ,\vartheta )\right]}^{\alpha }$ exist on $I\times J,$ then $D_{\vartheta }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )$, $D_{\vartheta }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )$ are differentiable with respect to ϑ and ${\left[D_{\vartheta }^i\tau (\kappa ,\vartheta )\right]}^{\alpha }=\left[D_{\vartheta }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta ),D_{\vartheta }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )\right].$

$\left(iii\right)$

If ${\left[D_{\kappa }^{ii}\tau (\kappa ,\vartheta )\right]}^{\alpha }$ exist on $I\times J,$ then $D_{\kappa }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )$, $D_{\kappa }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )$ are differentiable with respect to κ and ${\left[D_{\kappa }^{ii}\tau (\kappa ,\vartheta )\right]}^{\alpha }=\left[D_{\kappa }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta ),D_{\kappa }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )\right].$

$\left(iv\right)$

If ${\left[D_{\vartheta }^{ii}\tau (\kappa ,\vartheta )\right]}^{\alpha }$ exist on $I\times J,$ then $D_{\vartheta }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )$, $D_{\vartheta }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )$ are differentiable with respect to ϑ and ${\left[D_{\vartheta }^{ii}\tau (\kappa ,\vartheta )\right]}^{\alpha }=\left[D_{\vartheta }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta ),D_{\vartheta }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )\right].$

Definition 5.

[17] Let $j,l\in \{i,ii\}$ and $u:I\times J\to F_R$ be such that $D_{\kappa }^{j}u$ exists on $I\times J$. The function u is second-order $(j,l)$-partial differentiable with respect to κ and $\vartheta ,$ at $({\kappa }_0,{\vartheta }_0)\in \left\{{\kappa }_0\right\}\times I$, if $D_{\kappa }^{j}u$ where $j\in \{i,ii\}$ exists in a neighborhood of $({\kappa }_0,{\vartheta }_0)\in \left\{{\kappa }_0\right\}\times J$ and $l-$ differentiable with respect to ϑ at $({\kappa }_0,{\vartheta }_0)$ where $l\in \{i,ii\}$.

Let the second-order fuzzy partial gH-derivative of u be denoted by $D_{\kappa \vartheta }^{j,l}u(\kappa ,\vartheta ),$ $D_{\kappa \kappa }^{j,l}u,$ $D_{\kappa \vartheta }^{j,l}u,$ and $D_{\vartheta \vartheta }^{j,l}u,$ with $j,l\in \{i,ii\}$. If $j=l$ with $j,l\in \{i,ii\}$, then it is denoted by $D_{\kappa \vartheta }^{j}u,$ $D_{\kappa \kappa }^{j}u,$ $D_{\kappa \vartheta }^{j}u$ and $D_{\vartheta \vartheta }^{j}u$.

Lemma 3.

[17] Let a continuous fuzzy function, $\tau :I\times J\to R_F,$ such that ${\left[\tau (\kappa ,\vartheta )\right]}^{\alpha }=[{\underline{\tau }}^{\alpha }(\kappa ,\vartheta ),{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )]$ and $0\le \alpha \le 1$ such that $D_{\kappa \vartheta }^{j,l}\tau (\kappa ,\vartheta )$ exist on $I\times J$; then,

$\left(i\right)$

$\left[D_{\kappa \vartheta }^{j,l}{\tau }^{\alpha }(\kappa ,\vartheta )\right]=[D_{\kappa \vartheta }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta ),D_{\kappa \vartheta }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta )]$ if $j=l$ where $j,l\in \{i,ii\}.$

$\left(ii\right)$

$\left[D_{\kappa \vartheta }^{j,l}{\tau }^{\alpha }(\kappa ,\vartheta )\right]=[D_{\kappa \vartheta }{\overline{\tau }}^{\alpha }(\kappa ,\vartheta ),D_{\kappa \vartheta }{\underline{\tau }}^{\alpha }(\kappa ,\vartheta )]$ if $j\ne l$ where $j,l\in \{i,ii\}.$

Lemma 4.

[17] Let $\tau :(0,S)\times (0,T)\to F_R$ be defined in the neighborhood $(0,S)\times (0,T)\in R^2$ of point $({\theta }_0,{\vartheta }_0)\in R^2.$ Assume that $D_{\theta }^i\tau ,$ $D_{\vartheta }^i\tau ,$ $D_{\theta \vartheta }^i\tau$ exist in $(0,S)\times (0,T),$ $D_{\theta }^i\tau (\theta ,\vartheta )$ is continuous on θ(for fixed ϑ) $D_{\vartheta }^i\tau (\theta ,\vartheta )$ is continuous on ϑ(for fixed θ) and $D_{\theta \vartheta }^i\tau$ is continuous at $({\theta }_0,{\vartheta }_0).$ If for all $\theta \in (0,S)$, the following H-Differences exist close enough to ${\theta }_0.$

$$\left(\tau (\theta +\kappa ,{\vartheta }_0+r)\ominus \tau (\theta +\kappa ,{\vartheta }_0)\right)\ominus \left(\tau (\theta ,{\vartheta }_0+r)\ominus \tau (\theta ,{\vartheta }_0)\right)\ominus \kappa r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

$$\left(\tau (\theta ,{\vartheta }_0+r)\ominus \tau (\theta ,{\vartheta }_0)\right)\ominus \left(\tau (\theta -\kappa ,{\vartheta }_0+r)\ominus \tau (\theta -\kappa ,{\vartheta }_0)\right)\ominus \kappa r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

$$\left(\tau (\theta ,{\vartheta }_0)\ominus \tau (\theta ,{\vartheta }_0-r)\right)\ominus \left(\tau (\theta -\kappa ,{\vartheta }_0)\ominus \tau (\theta -\kappa ,{\vartheta }_0-\kappa )\right)\ominus \kappa r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

$$\left(\tau (\theta +\kappa ,{\vartheta }_0)\ominus \tau (\theta +\kappa ,{\vartheta }_0-r)\right)\ominus \left(\tau (\theta ,{\vartheta }_0)\ominus \tau (\theta ,{\vartheta }_0-\kappa )\right)\ominus \kappa r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0).$$

And for all $\vartheta \in (0,T)$, the following H-Differences exist close enough to ${\vartheta }_0.$

$$\left(D_{\theta }^i\tau ({\theta }_0+\kappa ,\vartheta +r)\ominus D_{\theta }^i\tau ({\theta }_0+\kappa ,\vartheta )\right)\ominus r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

$$\left(D_{\theta }^i\tau ({\theta }_0+\kappa ,\vartheta )\ominus D_{\theta }^i\tau ({\theta }_0+\kappa ,\vartheta -r)\right)\ominus r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

$$\left(D_{\theta }^i\tau ({\theta }_0-\kappa ,\vartheta +r)\ominus D_{\theta }^i\tau ({\theta }_0-\kappa ,\vartheta )\right)\ominus r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

$$\left(D_{\theta }^i\tau ({\theta }_0-\kappa ,\vartheta )\ominus D_{\theta }^i\tau ({\theta }_0-\kappa ,\vartheta -r)\right)\ominus r{D}_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0),$$

For $\kappa \in [0,\kappa ]$ and $\kappa ,r>0$ small enough that $D_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0)$ exist and $D_{\theta \vartheta }^i\tau ({\theta }_0,{\vartheta }_0)=D_{\vartheta \theta }^i\tau ({\theta }_0,{\vartheta }_0).$

Remark 1.

[17] Since $D_{\theta }^i$ exist in $(0,S)\times (0,T)\in R^2$, then $\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0+r)\right)$$\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0)\ominus \tau ({\theta }_0,{\vartheta }_0)\right)$ exist for $\kappa ,r>0$ small enough. The H-Differences

$$\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0+\kappa ,{\vartheta }_0)\right)\ominus \left(\tau ({\theta }_0,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0)\right),$$

$$\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0+r)\right)\ominus \left(\tau ({\theta }_0+\kappa ,{\vartheta }_0)\ominus \tau ({\theta }_0,{\vartheta }_0)\right),$$

exist and $\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0+\kappa ,{\vartheta }_0)\right)\ominus \left(\tau ({\theta }_0,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0)\right)=\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0+r)\right)\ominus \left(\tau ({\theta }_0+\kappa ,{\vartheta }_0)\ominus \tau ({\theta }_0,{\vartheta }_0)\right).$ Using Lemma 4, one can get

$$\begin{array}{ccc}\hfill \underset{(\kappa ,r)\to (0^{+},0^{+})}{lim}{\displaystyle \frac{\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0+\kappa ,{\vartheta }_0)\right)\ominus \left(\tau ({\theta }_0,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0)\right)}{\kappa r}}& =& D_{\vartheta \theta }^i\tau ({\theta }_0,{\vartheta }_0).\hfill \end{array}$$

Similarly,

$$\begin{array}{ccc}\hfill \underset{(\kappa ,r)\to (0^{+},0^{+})}{lim}{\displaystyle \frac{\left(\tau ({\theta }_0+\kappa ,{\vartheta }_0+r)\ominus \tau ({\theta }_0,{\vartheta }_0+r)\right)\ominus \left(\tau ({\theta }_0+\kappa ,{\vartheta }_0)\ominus \tau ({\theta }_0,{\vartheta }_0)\right)}{\kappa r}}& =& D_{\vartheta \theta }^i\tau ({\theta }_0,{\vartheta }_0)\hfill \end{array}$$

Note that H-difference some time does not exist, but if the H-difference and the limit in the Remark 1 exist for a fuzzy function, then the fuzzy function is gH-differentiable.

Definition 6.

[24] Let $N\left(u\right(\vartheta \left)\right)=U(s,r)$ where N is a natural transform with transform parameters s and r defined as follows,

$$U(s,r)=N\left\{u\left(\vartheta \right)\right\}={\int }_0^{\infty }{e}^{-s\vartheta }u\left(r\vartheta \right)d\vartheta .$$

(1)

Theorem 1.

[10] Let $e^{-s\vartheta }{\left[D_{\theta }^l\tau (r\vartheta ,\theta )\right]}^{\gamma }$ where $l\in \{i,ii\}$ is a fuzzy Riemann integrable in $[0,\infty )$ where $\tau :[0,\infty )\times [0,\infty )\to R_F,$ is a continuous fuzzy function; then,

$$N\left(D_{\theta }^l{\left[\tau (\vartheta ,\theta )\right]}^{\gamma }\right)=D_{\theta }^l\left(N{\left[\tau (\vartheta ,\theta )\right]}^{\gamma }\right),$$

where N is a natural transform with respect to $\vartheta .$

Theorem 2.

[17] The Goursat problem (2) has unique solutions in the spaces of continuous fuzzy functions $C_{(j,l)}(I,F_R)$ if $u(\upsilon ,0)$ is j-differentiable and $u(0,\theta )$ is l-differentiable, where $j,l\in \{i,ii\}.$

Definition 7.

[17] If $u(\upsilon ,\theta )$ satisfies the Goursat problem (2), then $u(\upsilon ,\theta )$ is a solution of the problem (2) in the spaces of continuous functions $C_{(j,l)}(I,F_R).$

3. Fuzzy Goursat Problems with Natural Transform and Adomian Decomposition

In this section, we will discuss the solutions to the following Goursat problem with fuzzy boundary conditions by natural Adomian decomposition.

$$\left\{\begin{array}{ccc}\hfill D_{\upsilon \theta }^{j,l}u(\upsilon ,\theta )& =\hfill & a_1{D}_{\upsilon }^{j}u(\upsilon ,\theta )+a_2{D}_{\theta }^{l}u(\upsilon ,\theta )+a_{3}u(\upsilon ,\theta )+G(\upsilon ,\theta ),\\ \hfill u(\upsilon ,0)& =\hfill & u_1\left(\upsilon \right),0\le \upsilon \le {\upsilon }_0,\\ \hfill u(0,\theta )& =\hfill & u_2\left(\theta \right),0\le \theta \le {\theta }_0,\end{array}\right.$$

(2)

where, $a_1,a_2,a_3:\Pi \to R$ are continuous functions on the closed rectangle $\Pi =(0,{\upsilon }_0)\times (0,{\theta }_0),$ and $j,l\in \{i,ii\}.$

From the two types gH-differentiability, $\left(i\right)$-differentiability and $\left(ii\right)$-differentiability, and the sign of coefficients $a_1,a_2,a_3$ in fuzzy Goursat problems, sixteen possible cases arises. The following table summarizes all the possible cases of fuzzy Goursat problems.

The literature of fuzzy differential equations does not have a solution method which discusses all possible cases of the problem (2). To enrich the literature of fuzzy differential equations with the solutions of fuzzy Goursat problems, we decided to discuss the solutions of said problems. For the solutions of the problem (2), we will use natural transform with Adomian decomposition as follows: In the natural Adomian decomposition method, first of all, we take the natural transform of the fuzzy Goursat problem. In the second step, we rearrange the transform of required function, transformed terms and the term whose natural transform is difficult or has the second type of gH-differentiability. Then apply the inverse natural transform. The complex term whose inverse natural transform as well as natural transform does not evaluate are set for the Adomian decomposition. The terms whose inverse natural transform is obtained are used for the first iteration of the Adomian decomposition. The solution to the problem is obtained from the series. The

Table 1. This table shows all possible cases of fuzzy Goursat problems with gH-differentiability.

	$a_1>0$	$a_2\ge 0$	$a_3\ge 0$	$l=i$	$j=i$
Case: 1.1						OR
	$a_1<0$	$a_2\le 0$	$a_3<0$	$l=i$	$j=ii$
	$a_1\ge 0$	$a_2\ge 0$	$a_3\ge 0$	$l=ii$	$j=i$
Case: 1.2						OR
	$a_1>0$	$a_2\le 0$	$a_3<0$	$l=ii$	$j=ii$
	$a_1>0$	$a_2\ge 0$	$a_3>0$	$l=i$	$j=ii$
Case: 1.3						OR
	$a_1\ge 0$	$a_2\le 0$	$a_3<0$	$l=i$	$j=i$
	$a_1\ge 0$	$a_2\ge 0$	$a_3>0$	$l=ii$	$j=ii$
Case: 1.4						OR
	$a_1\ge 0$	$a_2\le 0$	$a_3<0$	$l=ii$	$j=i$
	$a_1<0$	$a_2\ge 0$	$a_3<0$	$l=i$	$j=i$
Case: 2.1						OR
	$a_1<0$	$a_2\le 0$	$a_3>0$	$l=i$	$j=ii$
	$a_1>0$	$a_2\ge 0$	$a_3<0$	$l=i$	$j=ii$
Case: 2.2						OR
	$a_1<0$	$a_2\le 0$	$a_3>0$	$l=i$	$j=i$
	$a_1<0$	$a_2\ge 0$	$a_3<0$	$l=ii$	$j=i$
Case: 2.3						OR
	$a_1<0$	$a_2\le 0$	$a_3>0$	$l=ii$	$j=ii$
	$a_1\le 0$	$a_2\ge 0$	$a_3<0$	$l=ii$	$j=ii$
Case: 2.4						OR
	$a_1\le 0$	$a_2\le 0$	$a_3>0$	$l=ii$	$j=i$
	$a_1>0$	$a_2\le 0$	$a_3\ge 0$	$l=i$	$j=i$
Case: 3.1						OR
	$a_1>0$	$a_2\ge 0$	$a_3\le 0$	$l=i$	$j=ii$
	$a_1\ge 0$	$a_2\le 0$	$a_3>0$	$l=i$	$j=ii$
Case: 3.2						OR
	$a_1\ge 0$	$a_2\ge 0$	$a_3<0$	$l=i$	$j=i$
	$a_1>0$	$a_2\le 0$	$a_3\ge 0$	$l=ii$	$j=i$
Case: 3.3						OR
	$a_1>0$	$a_2\ge 0$	$a_3<0$	$l=ii$	$j=ii$
	$a_1\ge 0$	$a_2\le 0$	$a_3>0$	$l=ii$	$j=ii$
Case: 3.4						OR
	$a_1\ge 0$	$a_2\ge 0$	$a_3<0$	$l=ii$	$j=i$
	$a_1\le 0$	$a_2\ge 0$	$a_3>0$	$l=i$	$j=i$
Case: 4.1						OR
	$a_1\le 0$	$a_2\le 0$	$a_3<0$	$l=i$	$j=ii$
	$a_1<0$	$a_2\ge 0$	$a_3\ge 0$	$l=i$	$j=ii$
Case: 4.2						OR
	$a_1>0$	$a_2\le 0$	$a_3\le 0$	$l=i$	$j=i$
	$a_1\le 0$	$a_2\ge 0$	$a_3>0$	$l=ii$	$j=i$
Case: 4.3						OR
	$a_1\le 0$	$a_2\le 0$	$a_3<0$	$l=ii$	$j=ii$
	$a_1<0$	$a_2\ge 0$	$a_3\ge 0$	$l=ii$	$j=ii$
Case: 4.4						OR
	$a_1<0$	$a_2\le 0$	$a_3\le 0$	$l=ii$	$j=i$

show all possible cases Goursat problems.

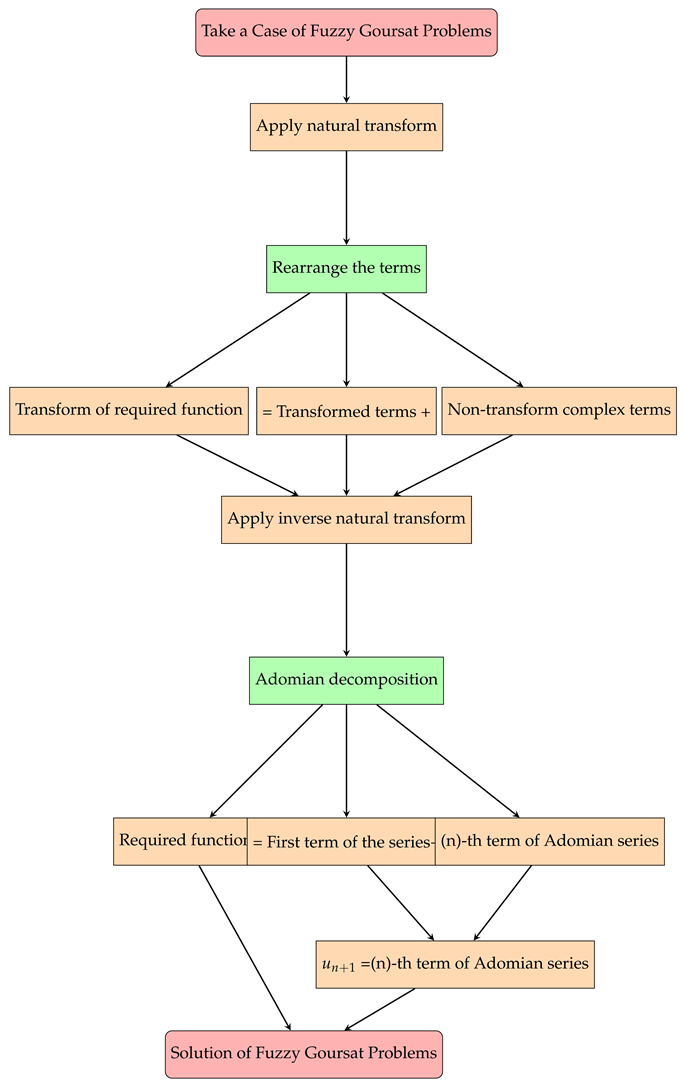
The following flowchart show the solution method investigate in this manuscript.

Case (1.1): If $a_1>0,a_2,a_3\ge 0,$ and $j=l=i,$ or $a_2\le 0,a_3<0,a_1>0,$ and $j=ii$ and $l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

(3)

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{a_1}{s{a}_1+r{a}_3}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\\ \hfill +\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}\right)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{a_1}{s{a}_1+r{a}_3}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\\ \hfill +\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}\right)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

By taking the inverse natural transform, one can find $\underline{u}(\upsilon ,\theta )$ and $\overline{u}(\upsilon ,\theta ),$ as follows.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^i\underline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\right),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^i\overline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\right).\end{array}\right.$$

We obtain the recursive relation by the Adomain decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^i\underline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^i\overline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(4)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i{\underline{U}}_n(s,r,\theta ,\gamma )\right)=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right),\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i{\overline{U}}_n(s,r,\theta ,\gamma )\right)=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right).\end{array}\right.$$

(5)

Case (1.2): If $a_1,a_2,a_3\ge 0,$ and $j=i$ and $l=ii,$ or $a_2\le 0,a_3<0,a_1>0,$ and $j=l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

(6)

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{a_1}{s{a}_1+r{a}_3}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\\ \hfill +\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}\right)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{a_1}{s{a}_1+r{a}_3}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\\ \hfill +\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}\right)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

By taking the inverse natural transform, one can find the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\right),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\right).\end{array}\right.$$

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_1}}{e}^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(7)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}{\underline{U}}_n(s,r,\theta ,\gamma )\right)=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right),\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}{\overline{U}}_n(s,r,\theta ,\gamma )\right)=N^{-1}\left({\displaystyle \frac{s-r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right).\end{array}\right.$$

(8)

Case (1.3): If $a_1,a_2\ge ,a_3>0,$ where $j=ii$ and $l=i,$ or $a_2\le 0,a_3<0,a_1>0,$ and $j=l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\underline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\overline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, we can obtain the following.

$$\left\{\begin{array}{c}\hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(9)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(10)

$$\left\{\begin{array}{c}\hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(11)

The problem (2) has the following solution in series form

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (1.4): If $a_1,a_2\ge 0,a_3>0,$ and $j=l=ii$ or $a_2\le 0,a_3<0,a_1\ge 0,$ and $j=i$ and $l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\underline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\overline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, one can find $\underline{u}(\upsilon ,\theta )$ and $\overline{u}(\upsilon ,\theta ),$ as follows.

$$\left\{\begin{array}{c}\hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(12)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(13)

$$\left\{\begin{array}{c}\hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(14)

The solution of the Goursat problem (2) in series form is obtained, as

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (2.1): If $a_1,a_3<0,a_2\ge 0,$ and $j=l=i,$ or $a_1,a_2\le 0,a_3>0,$ and $j=ii$ and $l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

(15)

$$\left\{\begin{array}{ccc}\hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )=\left\{{\displaystyle \frac{1}{s-\frac{-a_{3}r}{a_1}}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{a_1(s-\frac{-a_{3}r}{a_1})}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )=\left\{{\displaystyle \frac{1}{s-\frac{-a_{3}r}{a_1}}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{a_1(s-\frac{-a_{3}r}{a_1})}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

(16)

The inverse transform of Equation (16) produces the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(17)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(18)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(19)

The problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (2.2): If $a_1,a_3<0,a_2\ge 0,$ and $j=ii$ and $l=i,$ or $a_1,a_2\le 0,a_3>0,$ and $j=l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, one can find $\underline{u}(\upsilon ,\theta )$ and $\overline{u}(\upsilon ,\theta ),$ as follows.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(20)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(21)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(22)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (2.3): If $a_1,a_3<0,a_2\ge 0,$ where $j=i$ and $l=ii,$ or $a_1,a_2\le 0,a_3>0,$ and $j=l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill \left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

(23)

$$\left\{\begin{array}{ccc}\hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )=\left\{{\displaystyle \frac{1}{s-\frac{-a_{3}r}{a_1}}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{a_1(s-\frac{-a_{3}r}{a_1})}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )=\left\{{\displaystyle \frac{1}{s-\frac{-a_{3}r}{a_1}}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{a_1(s-\frac{-a_{3}r}{a_1})}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

(24)

The inverse transform produces the following

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(25)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(26)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{\left(s-r{a}_2\right)}{\left(s{a}_1+r{a}_3\right)}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(27)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (2.4): If $a_1,a_3<0,a_2\ge 0,$ where $j=l=ii,$ or $a_1,a_2\le 0,a_3>0,$ and $j=i$ and $l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )\ominus N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform produces the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_2}{a_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(28)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(29)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{a_{3}r}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_2}{a_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{a_{1}s}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(30)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (3.1): If $a_1,a_3>0,a_2<0,$ and $j=l=i,$ or $a_1,a_2\ge 0,a_3<0,$ where $j=ii$ and $l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & \left({\displaystyle \frac{s}{r}}{a}_1+a_3\right)\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

From the above, the following system is obtained

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(31)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(32)

The Goursat problem (2) has the following solution.

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (3.2): If $a_1,a_3>0,a_2<0,$ where $j=ii$ and $l=i,$ or $a_1,a_2\ge 0,a_3<0,$ and $j=l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, we can obtain the following system.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(33)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(34)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(35)

We obtain the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (3.3): If $a_1,a_3>0,a_2\le 0,$ where $j=i$ and $l=ii,$ or $a_1,a_2\ge 0,a_3<0,$ where $j=l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

From the above, we obtain the following system.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\right\}\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(36)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(37)

From the above, we obtain the following solution of the Goursat problem (2).

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (3.4): If $a_1,a_3>0,a_2\le 0,$ where $j=l=ii,$ or $a_1,a_2\ge 0,a_3<0,$ where $j=i$ and $l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, we obtain

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(38)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(39)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(40)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (4.1): If $a_2\ge 0,a_3>0,a_1\le 0,$ and $j=l=i,$ or $a_1,a_2,a_3<0$ and $j=ii$ and $l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )& =\hfill & {\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill & +\hfill & a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, we obtain the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(41)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^i\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(42)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(43)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (4.2): If $a_2\ge ,a_3>0,a_1<0,$ and $j=ii$ and $l=i,$ or $a_1,a_2,a_3<0$ and $j=l=i,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{c}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )={\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\\ \hfill +a_2{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )={\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\\ \hfill +a_2{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^i\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

Taking the inverse natural transform, we obtain the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^i\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^i\overline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(44)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^i\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(45)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^i{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(46)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (4.3): If $a_2\ge ,a_3>0,a_1<0,$ where $j=i$ and $l=ii$ or $a_1,a_2,a_3<0$ and $j=l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{c}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )={\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\\ \hfill +a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )={\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\\ \hfill +a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{ccc}\hfill \underline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill \overline{U}(s,r,\theta ,\gamma )& =\hfill & {\displaystyle \frac{1}{a_3}}\left\{{\displaystyle \frac{a_1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill & +\hfill & {\displaystyle \frac{1}{a_3}}\left\{\left({\displaystyle \frac{s}{r}}-a_2\right)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

Taking the inverse natural transform, we obtain the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\overline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right)\\ \hfill +N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)D_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}\underline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(47)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right),\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )={\displaystyle \frac{a_1}{a_3}}\underline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}{D}_{\theta }^{ii}\overline{u}(0,\theta )\ominus {\displaystyle \frac{1}{a_3}}\left(G(\upsilon ,\theta )\right).\end{array}\right.$$

(48)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{1}{a_3}}({\displaystyle \frac{s}{r}}-a_2)N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{s{a}_1}{a_{3}r}}N\left({\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(49)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

Case (4.4): If $a_2\ge ,a_3>0,a_1<0,$ and $j=l=ii$ or $a_1,a_2,a_3<0$ and $j=i$ and $l=ii,$ then, using Theorem 1, the natural transform of Equation (2) is obtained as follows

$$\left\{\begin{array}{c}\hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )={\displaystyle \frac{s}{r}}{a}_1\underline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )+a_3\underline{U}(s,r,\theta ,\gamma )\\ \hfill +a_2{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right),\\ \hfill {\displaystyle \frac{s}{r}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )={\displaystyle \frac{s}{r}}{a}_1\overline{U}(s,r,\theta ,\gamma )\ominus a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )+a_3\overline{U}(s,r,\theta ,\gamma )\\ \hfill +a_2{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )+N\left(G(s,r,\theta )\right).\end{array}\right.$$

This produces the following system

$$\left\{\begin{array}{c}\hfill \underline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\underline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\overline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma ),\\ \hfill \overline{U}(s,r,\theta ,\gamma )={\displaystyle \frac{r}{s{a}_1+r{a}_3}}\left\{a_1{\displaystyle \frac{1}{r}}\overline{U}(0,\theta ,\gamma )\ominus {\displaystyle \frac{1}{r}}{D}_{\theta }^{ii}\underline{U}(0,\theta ,\gamma )-N\left(G(s,r,\theta )\right)\right\}\\ \hfill +{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma ).\end{array}\right.$$

Taking the inverse natural transform, we obtain the following.

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}\\ \hfill +N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\underline{U}(s,r,\theta ,\gamma )\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}{D}_{\theta }^{ii}\overline{U}(s,r,\theta ,\gamma )\right\}.\end{array}\right.$$

(50)

We obtain the recursive relation by the Adomian decomposition method with

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\overline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus {\displaystyle \frac{1}{a_1}}{D}_{\theta }^{ii}\underline{u}(0,\theta )e^{-{\displaystyle \frac{a_3}{a_1}}\upsilon }\ominus N^{-1}\left\{{\displaystyle \frac{r}{s{a}_1+r{a}_3}}N\left(G(s,r,\theta )\right)\right\}.\end{array}\right.$$

(51)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\underline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\ominus {\displaystyle \frac{r{a}_2}{s{a}_1+r{a}_3}}N\left(D_{\theta }^{ii}{\overline{u}}_n^{\gamma }(\upsilon ,\theta )\right)\right\}.\end{array}\right.$$

(52)

The Goursat problem (2) has the following solution

$$\left\{\begin{array}{ccc}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\underline{u}}_n}^{\gamma }(\upsilon ,\theta ),\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )& =\hfill & \sum _{n=0}^{\infty }{{\overline{u}}_n}^{\gamma }(\upsilon ,\theta ).\end{array}\right.$$

4. Some Numerical Examples

In this section, we will discuss the useability of the developed algorithms. We will apply the established method to some problems to obtained their solution.

Example 1.

Let us suppose that we have a problem with fuzzy number $A=(-1;0;1),$ as follows

$$\left\{\begin{array}{ccc}\hfill D_{\upsilon \theta }^{j,l}u(\upsilon ,\theta )& =\hfill & u(\upsilon ,\theta ),\\ \hfill u(\upsilon ,0)& =\hfill & A{e}^{\upsilon },0\le \upsilon \le {\upsilon }_0,\\ \hfill u(0,\theta )& =\hfill & A{e}^{\theta },0\le \theta \le {\theta }_0.\end{array}\right.$$

(53)

Theorem 2 ensures the unique solution of problem (53) in the space $C_{(j,l)}(Y,F_R)$ with $j=l=i.$ The solution of this problem is similar to case (4.1); therefore, using Equations (42) and (43), we obtain the solution, as follows (Figure 1)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\ominus (\gamma -1)e^{\theta },\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\ominus (1-\gamma )e^{\theta }.\end{array}\right.\mathit{and}\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s^n}{r^{n+1}}}\left(\ominus (\gamma -1)e^{\theta }\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\displaystyle \frac{s^n}{r^{n+1}}}\left(\ominus (1-\gamma )e^{\theta }\right)\right\}.\end{array}\right.$$

$$\begin{array}{c}\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{({\displaystyle \frac{1}{r}}+{\displaystyle \frac{s}{r^2}}+{\displaystyle \frac{s^2}{r^3}}...{\displaystyle \frac{s^n}{r^{n+1}}})\left(\ominus (\gamma -1)e^{\theta }\right)\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{({\displaystyle \frac{1}{r}}+{\displaystyle \frac{s}{r^2}}+{\displaystyle \frac{s^2}{r^3}}...{\displaystyle \frac{s^n}{r^{n+1}}})\left(\ominus (1-\gamma )e^{\theta }\right)\right\}.\end{array}\right.\hfill \\ \Rightarrow \left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=(\gamma -1)N^{-1}\left\{{\displaystyle \frac{1}{s-r}}{e}^{\theta }\right\}=(\gamma -1)e^{\upsilon +\theta },\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=(1-\gamma )N^{-1}\left\{{\displaystyle \frac{1}{s-r}}{e}^{\theta }\right\}=(1-\gamma )e^{\upsilon +\theta }.\end{array}\right.\hfill \end{array}$$

Example 2.

Let us suppose that we have a problem with fuzzy number $A=(0;1;2),$ as follows

$$\left\{\begin{array}{ccc}\hfill D_{\upsilon \theta }^{j,l}u(\upsilon ,\theta )& =\hfill & u(\upsilon ,\theta ),\\ \hfill u(\upsilon ,0)& =\hfill & A{e}^{-\upsilon },0\le \upsilon \le {\upsilon }_0,\\ \hfill u(0,\theta )& =\hfill & A{e}^{-\theta },0\le \theta \le {\theta }_0.\end{array}\right.$$

(54)

Theorem 2 ensures the unique solution of problem (54) in the space $C_{(j,l)}(Y,F_R)$ with $j=l=ii.$ The solution of this problem is similar to case (1.4); therefore, using Equations (13) and (14), we obtain the solution, as follows (Figure 2)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=\ominus \gamma e^{-\theta },\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=\ominus (2-\gamma )e^{-\theta }.\end{array}\right.\mathit{and}\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{(-1)}^{n+1}{\displaystyle \frac{s^n}{r^{n+1}}}\left(\ominus \gamma e^{-\theta }\right)\right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{(-1)}^{n+1}{\displaystyle \frac{s^n}{r^{n+1}}}\left(\ominus (2-\gamma )e^{-\theta }\right)\right\}.\end{array}\right.$$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{((-1){\displaystyle \frac{1}{r}}+{(-1)}^2{\displaystyle \frac{s}{r^2}}+{(-1)}^3{\displaystyle \frac{s^2}{r^3}}...{(-1)}^{n+1}{\displaystyle \frac{s^n}{r^{n+1}}})\left(\ominus \gamma e^{-\theta }\right)\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{((-1){\displaystyle \frac{1}{r}}+{(-1)}^2{\displaystyle \frac{s}{r^2}}+{(-1)}^3{\displaystyle \frac{s^2}{r^3}}...{(-1)}^{n+1}{\displaystyle \frac{s^n}{r^{n+1}}})\left(\ominus (2-\gamma )e^{-\theta }\right)\right\}.\end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=(1-\gamma )N^{-1}\left\{{\displaystyle \frac{1}{s-(-r)}}{e}^{-\theta }\right\}=\gamma e^{-(\upsilon +\theta )},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=(\gamma -1)N^{-1}\left\{{\displaystyle \frac{1}{s-(-r)}}{e}^{-\theta }\right\}=(2-\gamma )e^{-(\upsilon +\theta )}.\end{array}\right.\end{array}$$

Example 3.

Let us suppose that we have a problem with fuzzy number $A=(0;1;2),$ as follows

$$\left\{\begin{array}{c}\hfill 3D_{\upsilon \theta }^{j,l}u(\upsilon ,\theta )=D_{\upsilon }^{j}u(\upsilon ,\theta )+D_{\theta }^{l}u(\upsilon ,\theta )+u(\upsilon ,\theta ),\\ \hfill u(\upsilon ,0)=A{e}^{\upsilon },0\le \upsilon \le {\upsilon }_0,\\ \hfill u(0,\theta )=A{e}^{\theta },0\le \theta \le {\theta }_0.\end{array}\right.$$

(55)

Theorem 2 ensures the unique solution of problem (55) in the space $C_{(j,l)}(Y,F_R)$ with $j=l=i.$ The solution of this problem is similar to case (1.1); therefore, using Equations (4) and (5), we obtain the solution, as follows (Figure 3)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-\upsilon }\underline{u}(0,\theta )\ominus 3e^{-\upsilon }{D}_{\theta }^i\underline{u}(0,\theta )=\left({\displaystyle \frac{-2}{s+r}}\right)e^{\theta }\gamma ,\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-\upsilon }\overline{u}(0,\theta )\ominus 3e^{-\upsilon }{D}_{\theta }^i\overline{u}(0,\theta )=\left({\displaystyle \frac{-2}{s+r}}\right)e^{\theta }(2-\gamma ).\end{array}\right.$$

And

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^n\left({\displaystyle \frac{-2}{s+r}}\right)e^{\theta }\gamma \right\},\\ \hfill {\overline{u}}_{n+1}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^n\left({\displaystyle \frac{-2}{s+r}}\right)e^{\theta }(2-\gamma )\right\}.\end{array}\right.$$

The solution in series form is the following

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{-2}{s+r}}\right)\left(1+{\displaystyle \frac{3s-r}{s+r}}+{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^2+{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^3...{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^n\right)e^{\theta }\gamma \right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{-2}{s+r}}\right)\left(1+{\displaystyle \frac{3s-r}{s+r}}+{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^2+{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^3...{\left({\displaystyle \frac{3s-r}{s+r}}\right)}^n\right)e^{\theta }(2-\gamma )\right\}.\end{array}\right.$$

From the sum of infinite geometric series, we obtain

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{1}{s-r}}\right)e^{\theta }\gamma \right\}=\gamma e^{\upsilon +\theta },\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{1}{s-r}}\right)e^{\theta }(1-\gamma )\right\}=(2-\gamma )e^{\upsilon +\theta }.\end{array}\right.$$

Example 4.

Let us suppose that we have a problem with fuzzy number $A=(-1;0;1),$ as follows

$$\left\{\begin{array}{c}\hfill D_{\upsilon \theta }^{j,l}u(\upsilon ,\theta )=-{\displaystyle \frac{1}{2}}{D}_{\upsilon }^{j}u(\upsilon ,\theta )+D_{\theta }^{l}u(\upsilon ,\theta )-{\displaystyle \frac{1}{2}}u(\upsilon ,\theta )+\upsilon \theta ,\\ \hfill u(\upsilon ,0)=A{e}^{3\upsilon }+12(e^{-\upsilon }-1)+4\upsilon (e^{-\upsilon }+1),0\le \upsilon \le {\upsilon }_0,\\ \hfill u(0,\theta )=A{e}^{\theta },0\le \theta \le {\theta }_0.\end{array}\right.$$

(56)

Theorem 2 ensures the unique solution of problem (56) in the space $C_{(j,l)}(Y,F_R)$ with $j=l=i.$ The solution of this problem is similar to case (2.1); therefore, using the Equations (18) and (19), we obtain the solution, as follows (Figure 4)

$$\left\{\begin{array}{c}\hfill {\underline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-\upsilon }\underline{u}(0,\theta )\ominus (-2)e^{-\upsilon }{D}_{\theta }^i\overline{u}(0,\theta )\ominus N^{-1}\left\{-{\displaystyle \frac{2r^2}{s^2(s+r)}}\theta \right\}\\ \hfill =\left({\displaystyle \frac{-1}{s+r}}\right)e^{\theta }(\gamma -1)\ominus N^{-1}\left\{-{\displaystyle \frac{2r^2}{s^2(s+r)}}\theta \right\},\\ \hfill {\overline{u}}_0^{\gamma }(\upsilon ,\theta )=e^{-\upsilon }\overline{u}(0,\theta )\ominus (-2)e^{-\upsilon }{D}_{\theta }^i\underline{u}(0,\theta )\ominus N^{-1}\left\{-{\displaystyle \frac{2r^2}{s^2(s+r)}}\theta \right\}\\ \hfill =\left({\displaystyle \frac{-1}{s+r}}\right)e^{\theta }(1-\gamma )\ominus N^{-1}\left\{-{\displaystyle \frac{2r^2}{s^2(s+r)}}\theta \right\}.\end{array}\right.$$

And

$$\left\{\begin{array}{c}\hfill {\underline{u}}_1^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{2(s-r)}{s+r}}\right)\left({\displaystyle \frac{-1}{s+r}}\right)e^{\theta }(\gamma -1)\ominus {\displaystyle \frac{4r^2(s-r)}{s^2{(s+r)}^2}}\right\},\\ \hfill {\overline{u}}_1^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{2(s-r)}{s+r}}\right)\left({\displaystyle \frac{-1}{s+r}}\right)e^{\theta }(1-\gamma )\ominus {\displaystyle \frac{4r^2(s-r)}{s^2{(s+r)}^2}}\right\}.\end{array}\right.$$

$$\left\{\begin{array}{c}\hfill {\underline{u}}_{n+2}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\left({\displaystyle \frac{2(s-r)}{s+r}}\right)}^n\left({\displaystyle \frac{-1}{s+r}}\right)e^{\theta }(\gamma -1)\right\},\\ \hfill {\overline{u}}_{n+2}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{{\left({\displaystyle \frac{2(s-r)}{s+r}}\right)}^n\left({\displaystyle \frac{-1}{s+r}}\right)e^{\theta }(1-\gamma )\right\}.\end{array}\right.$$

The solution in series form is the following

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\{\left({\displaystyle \frac{-1}{s+r}}\right)\left(1+{\displaystyle \frac{2(s-r)}{s+r}}+{\left(2{\displaystyle \frac{s-r}{s+r}}\right)}^2+...{\left(2{\displaystyle \frac{s-r}{s+r}}\right)}^n\right)e^{\theta }(\gamma -1)\\ \hfill -{\displaystyle \frac{2r^2}{s^2(s+r)}}\theta -{\displaystyle \frac{4r^2(s-r)}{s^2{(s+r)}^2}}\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\{\left({\displaystyle \frac{-1}{s+r}}\right)\left(1+{\displaystyle \frac{2(s-r)}{s+r}}+{\left(2{\displaystyle \frac{s-r}{s+r}}\right)}^2+...{\left(2{\displaystyle \frac{s-r}{s+r}}\right)}^n\right)e^{\theta }(1-\gamma )\\ \hfill -{\displaystyle \frac{2r^2}{s^2(s+r)}}\theta -{\displaystyle \frac{4r^2(s-r)}{s^2{(s+r)}^2}}\}.\end{array}\right.$$

By the sum of infinite geometric series and partial fraction decomposition, we can obtain

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{1}{s-3r}}\right)e^{\theta }(\gamma -1)-{\displaystyle \frac{2}{s}}\theta +{\displaystyle \frac{2r}{s^2}}\theta +{\displaystyle \frac{2}{s+r}}\theta -{\displaystyle \frac{12}{s}}+{\displaystyle \frac{4r}{s^2}}+{\displaystyle \frac{12}{s+r}}+{\displaystyle \frac{8r}{{(s+r)}^2}}\right\},\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=N^{-1}\left\{\left({\displaystyle \frac{1}{s-3r}}\right)e^{\theta }(1-\gamma )-{\displaystyle \frac{2}{s}}\theta +{\displaystyle \frac{2r}{s^2}}\theta +{\displaystyle \frac{2}{s+r}}\theta -{\displaystyle \frac{12}{s}}+{\displaystyle \frac{4r}{s^2}}+{\displaystyle \frac{12}{s+r}}+{\displaystyle \frac{8r}{{(s+r)}^2}}\right\}.\end{array}\right.$$

$$\left\{\begin{array}{c}\hfill {\underline{u}}^{\gamma }(\upsilon ,\theta )=(\gamma -1)e^{3\upsilon +\theta }-2\theta +2\upsilon \theta +2e^{-\upsilon }\theta -12+4\upsilon +12e^{-\upsilon }+8\upsilon e^{-\upsilon },\\ \hfill {\overline{u}}^{\gamma }(\upsilon ,\theta )=(1-\gamma )e^{3\upsilon +\theta }-2\theta +2\upsilon \theta +2e^{-\upsilon }\theta -12+4\upsilon +12e^{-\upsilon }+8\upsilon e^{-\upsilon }.\end{array}\right.$$

5. Conclusions and Future Directions

In this work, we studied the solutions of fuzzy Goursat problems with gH-differentiability. The mixed derivative term, two types of gH-differentiability and the sign of the coefficient produce difficulties in the solutions of fuzzy Goursat problems. In the solution of fuzzy Goursat problems with gH-differentiability, different cases arise. Therefore, we discussed sixteen possible cases of fuzzy Goursat problems with gH-differentiability. We discussed the solutions in series form by the combination of natural transform with Adomian decomposition. This work is the first effort to discuss the complete solutions of Goursat problems with boundary conditions. In this manuscript, we discussed the solutions to all cases of said problem. The algorithm developed in this work is not limited only to Goursat problems, but it is also applicable to all fuzzy partial differential equations. It should be noted that in the literature of fuzzy partial differential equations, the solutions of special cases of fuzzy problems are mostly discussed, but our work has a complete process to discuss all possible cases of a fuzzy problem. Moreover, natural transforms directly convert to Laplace and Sumudu transforms only by taking the particular value of the transform parameters. Therefore, we proposed natural transformation in this work to save the time of the research community because it directly produces Laplace and Sumudu transforms. In the last section, we provided examples of the usability of the established work. The difficulties in the solutions of fuzzy Goursat problems with gH-differentiability are not only in the Goursat problems. These difficulties also arise in other partial differential equations and higher-order ordinary differential equations. Therefore, the solution methods discussed in this manuscript are also interesting for other partial differential equations and higher-order ordinary differential equations. The algorithm developed in this work is interesting for fractional fuzzy problems.