On Some Distance Spectral Characteristics of Trees

Abstract

Graham and Pollack in 1971 presented applications of eigenvalues of the distance matrix in addressing problems in data communication systems. Spectral graph theory employs tools from linear algebra to retrieve the properties of a graph from the spectrum of graph-theoretic matrices. The study of graphs with “few eigenvalues” is a contemporary problem in spectral graph theory. This paper studies graphs with few distinct distance eigenvalues. After mentioning the classification of graphs with one and two distinct distance eigenvalues, we mainly focus on graphs with three distinct distance eigenvalues. Characterizing graphs with three distinct distance eigenvalues is “highly” non-trivial. In this paper, we classify all trees whose distance matrix has precisely three distinct eigenvalues. Our proof is different from earlier existing proof of the result as our proof is extendable to other similar families such as unicyclic and bicyclic graphs. The main tools which we employ include interlacing and equitable partitions. We also list all the connected graphs on ν ≤ 6 vertices and compute their distance spectra. Importantly, all these graphs on ν ≤ 6 vertices are determined from their distance spectra. We deliver a distance cospectral pair of order 7, thus making it a distance cospectral pair of the smallest order. This paper is concluded with some future directions.

1. Introduction

All graphs in this article are undirected, finite, connected, and simple.

Spectral graph theory [1] employs tools from linear algebra to retrieve the properties of a graph from the spectrum of graph-theoretic matrices such as the adjacency, the distance, and the Laplacians, among others. In 1970, Doob [2] suggested the study of graphs with a few eigenvalues and proposed, at most, five. A connected regular graph with, at most, three distinct eigenvalues is known to be strongly regular; see, for example [3] for a survey on strongly regular graphs. Connected non-regular graphs with three distinct eigenvalues have been studied by, for example, De Caen, Van Dam and Spence [4], Bridges and Mena [5], Muzychuk and Klin [6], and Van Dam [7].Connected regular graphs with four distinct eigenvalues were studied by Van Dam [8], Van Dam and Spence [9] and Huang and Huang [10], among others. Cioabă et al. [11] (resp. Cioabă et al. [12]) studied connected graphs with, at most, two eigenvalues not equal to 1 and $-1$ (resp. 0 and $-2$). Haemers and Omidi [13] studied generalized adjacency matrices and characterized the graphs admitting two generalized adjacency eigenvalues. In this paper, we study graphs with three distinct generalized adjacency eigenvalues. For applications of graphical and, in general, mathematical models in machine learning and energy research, we refer to [14,15,16,17].

In case of connected graphs, the distance matrix [18] generalizes the adjacency matrix naturally as it delivers more information about pairs of vertices. Graham and Pollack [19], in 1971, put forward a relationship between the problem of addressing in systems of data communications and the number of negative eigenvalues of the distance matrix. In 1978, Graham and Lovász [20] precisely determined the characteristic polynomial of the distance matrix of a graph by providing explicit formulas for its coefficients. Merris [21] used the interlacing theorem to study properties of the distance eigenvalues of trees and their line graphs. The survey by Aouchiche and Hansen [22] covers the known results on the distance matrix and its spectrum till 2014.

The cospectrality of graphs with respect to the distance matrix has received researchers’ attention recently. Lin et al. [23] showed that complete bipartite graphs are determined by their distance spectra and conjectured the same for complete multipartite graphs. Jin and Zhang [24] provided a proof for this conjecture. Heysse [25] proposed a method of constructing distance cospectral graphs. Aouchiche and Hansen [26] generated the distance, Laplacian distance, and signless Laplacian distance spectra of all the graphs up to 10 vertices and identified the ones which are distance cospectral. Zhang [27] investigated graphs with, at most, three distance eigenvalues, of which two are different from $-1$ and $-2$. Moreover, he identified all distance cospectral graphs among this class and showed the remaining can uniquely be determined from their distance spectra. Pokorný et al. [28] showed that non-trivial non-isomorphic trees are never distance integral. They also identify distance integral graphs among the class of complete split graphs.

Research on the study of graphs with few different eigenvalues corresponding to the distance matrix has been initiated recently. Lin et al. [23] classified graphs having three different distance eigenvalues and non-integral distance spectral radius. Aalipour et al. [29] constructed examples of non-regular graphs having a small number of different eigenvalues, showing that not all graphs with few distinct eigenvalues for the distance matrix are regular. Zhang et al. [30] proved some extremal results on the distance spectrum of graphs. They also delivered the first proof for the classification of trees with three distinct distance eigenvalues. In addition, Aalipour et al. [29] precisely determined the spectrum of the distance matrix of all the distance-regular graphs whose positive inertia is exactly one. For each $2\le k\le 11$, Atik and Panigrahi [31] constructed infinite families of graphs with diameter of at least k and precisely k distinct distance eigenvalues. Lu et al. [32] classified graphs with exactly two distance eigenvalues different from $-1$ and $-3$.

In continuation of the study of graphs whose distance matrix has few distinct eigenvalues, in this note, we characterize trees having precisely three different distance eigenvalues. This paper studies the contemporary problem of “few eigenvalues” for the distance matrix of trees. The classification of general graphs with three distinct distance eigenvalues is highly non-trivial. In light of this, we solve this problem for the case of trees. Our proof is extendable to other families of graphs such as unicyclic and bicyclic graphs. The main result of this study is as follows:

Theorem 1.

Let T be a tree on $\nu \ge 2$ vertices. Then, T has three distinct distance eigenvalues if and only if T is a star graph.

The organization of the note goes like this: In Section 2, we define all the necessary terminologies and present preliminary results needed in the subsequent section. Section 3 then provides a proof to Theorem 1.

2. Preliminaries

For standard notations and terminologies, the reader is referred to the standard graph theory textbook by West [33].

Let $\Gamma =(V_{\Gamma },E_{\Gamma })$ be a $\nu$-vertex graph with $V_{\Gamma }$ as its vertex set and $E_{\Gamma }\subseteq \left({\displaystyle \genfrac{}{}{0pt}{}{V_{\Gamma }}{2}}\right)$ as its edge set. The adjacency matrix $A=A_{\Gamma }$ of a graph $\Gamma$ is defined as

$${\left(A\right)}_{xy}=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill xy\in E;\hfill \\ \hfill 0,\hfill & \hfill \mathrm{Otherwise}.\hfill \end{array}\right.$$

Similarly, the distance matrix $\mathcal{D}=\mathcal{D}(\Gamma )$ of an $\nu$-vertex graph $\Gamma$ is defined as vertices of $\Gamma$ and defined as

$${\left(\mathcal{D}\right)}_{xy}=\left\{\begin{array}{cc}\hfill k,\hfill & \hfill d(x,y)=k;\hfill \\ \hfill 0,\hfill & \hfill x=y.\hfill \end{array}\right.$$

Let ${\theta }_0\ge \dots \ge {\theta }_t$ (resp. ${\mu }_0\ge \dots \ge {\mu }_t$) be the eigenvalues of A (resp. $\mathcal{D}$) called A-eigenvalues (resp. $\mathcal{D}$-eigenvalues) of $\Gamma$. Note that both of the adjacency and distance matrices are nonnegative irreducible real symmetric matrices.

Next, we present some tools from linear algebra which we use later on. The following is the so-called Perron–Frobenius Theorem.

Theorem 2.

([1], Theorem 2.2.1) Let M be a nonnegative irreducible matrix of order $\nu \times \nu$. Let $\rho \left(M\right)$ be the largest eigenvalue of M such that $M\mathbf{x}=\rho \mathbf{x}$. Then,

(i)

Both geometric and algebraic multiplicity of $\rho \left(M\right)$ is one. Moreover, $\mathbf{x}$ is a strictly positive real vector.

(ii)

For each eigenvalue θ of M, we have $\rho \ge \left|\theta \right|$. If M is primitive, then $\rho =\left|\theta \right|$ implies $\rho =\theta$.

(iii)

Assume $M_1$ is a nonnegative $\nu \times \nu$ real matrix such that $M-M_1$ is nonnegative. Then, $\rho \left(M\right)\ge \rho \left(M_1\right)$ with $\rho \left(M\right)=\rho \left(M_1\right)$ if and only if $M=M_1$.

The following is the so-called Cauchy Interlacing Theorem of real symmetric matrices.

Theorem 3.

([34], Theorem 9.3.3) Let M be an $m\times m$ principle submatrix of an $\nu \times \nu$ real symmetric matrix N. Assume that ${\theta }_i\left(N\right)(1\le i\le \nu )$ (resp. ${\mu }_i\left(M\right)(1\le i\le m)$ be a non-increasing sequence of the eigenvalues of N (resp. M). Then,

$${\theta }_{\nu -m+i}\left(N\right)\le {\mu }_i\left(M\right)\le {\theta }_i\left(N\right)\mathrm{for}i=1,2,\dots ,m.$$

Let ${\chi }_A\left(x\right)$ be the characteristic polynomial of a matrix A. The proof of the following result is a merely a modification of [34], Theorem 9.1.1.

Theorem 4.

([34], Theorem 9.1.1) Assume π is an equitable partition for a Hermitian matrix M. Let Q be the quotient matrix of M corresponding to π. Then, we have ${\chi }_Q\left(x\right)\mid {\chi }_M\left(x\right).$

In 1971, Graham and Pollack [19] calculated the determinant of $\mathcal{D}\left(T\right)$ of a $\nu$-vertex tree T as follows:

Theorem 5.

([19]) If $\mathcal{D}=\mathcal{D}\left(T\right)$ is the distance matrix of a ν-vertex tree T, where $\nu \ge 2$. Then,

$$det\left(\mathcal{D}\right)={(-1)}^{\nu -1}(\nu -1)2^{\nu -2}.$$

Let A be a real symmetric matrix. Then, the eigenvalues of A are all real. Assume ${\nu }_{+}\left(A\right)$ (resp. ${\nu }_{-}\left(A\right)$) is the number of positive (resp. negative) eigenvalues of A. If ${\nu }_0\left(A\right)$ is the dimension of the null space of A i.e., the number of zero eigenvalues of A, then, $({\nu }_{+}\left(A\right),{\nu }_0\left(A\right),{\nu }_{-}\left(A\right))$ is said to be the inertia of the matrix A.

Theorem 5 immediately implies that the inertia of $\mathcal{D}\left(T\right)$ of a $\nu$-vertex tree T is independent of the structural of T, i.e., only depends on $\nu$.

Corollary 1.

([19]) Let $\mathcal{D}=\mathcal{D}\left(T\right)$ be the distance matrix of a ν-vertex tree T, where $\nu \ge 2$. Then, the inertia of $\mathcal{D}$ is $(1,0,\nu -1)$.

3. Main Results

For a graph $\Gamma$, let ${\delta }_{\Gamma }\left(\mathcal{D}\right)$ be the number of distinct distance eigenvalues of $\Gamma$. Note that the distance matrix $\mathcal{D}$ is an irreducible nonnegative integer symmetric (and thus Hermitian) matrix. Thus, if $\mathcal{D}$ has one distinct eigenvalue $\mu$, then, its minimal polynomial $m\left(x\right)=x-\mu$. This implies that $\mathcal{D}=\mu I$, and since the main diagonal of $\mathcal{D}$ is zero, we obtain that $\mu =0$ and $\mathcal{D}=\mathbf{0}$. This shows that $\Gamma$ is an isolated vertex, as $\Gamma$ is connected. Thus, we have the following lemma.

Lemma 1.

Let Γ be a connected graph. Then, ${\delta }_{\Gamma }\left(\mathcal{D}\right)=1$ if and only if $\Gamma =K_1$.

Stevanović and Indulal [35] calculated the distance spectra of the combination of two regular graphs and, as its application, computed the distance spectra of the complete bipartite graphs. Here, we provide a different proof of this result using equitable partitions of the distance matrix.

Lemma 2.

Let $K_{s,t}$ be the complete bipartite graph. Then, the distance spectrum of $K_{s,t}$ is as follows:

$$\left\{{[s+t-2+\sqrt{s^2-st+t^2}]}^1,{[-2]}^{s+t-2},{[s+t-2-\sqrt{s^2-st+t^2}]}^1\right\}.$$

Proof. 

Consider the equitable partition $\pi =\{V_1,V_2\}$, where $V_1$ and $V_2$ are the partite sets of $K_{s,t}$. The quotient matrix Q of $\pi$ is

$$Q=\left(\begin{array}{cc}2(s-1)& t\\ s& 2(t-1)\end{array}\right).$$

The eigenvalues of Q are $s+t-2\pm \sqrt{s^2-st+t^2}$. By Theorem 4, these are also the distance eigenvalues of $K_{s,t}$ each with multiplicity 1. By Lemma 3.4 in [23], $K_{s,t}$ has three distinct eigenvalues. By using the trace of the distance matrix of $K_{s,t}$, we obtain that $-2$ with multiplicity $s+t-2$ is the other distinct distance eigenvalue of $K_{s,t}$. □

Indulal [36] characterized graphs with two distinct distance eigenvalues. We provide a short proof of this characterization.

Lemma 3.

([36]) A graph Γ has ${\delta }_{\Gamma }\left(\mathcal{D}\right)=2$ if and only if $\Gamma =K_{\nu }$, $\nu \ge 2$.

Proof. 

If $\Gamma =K_{\nu }$, then $\mathcal{D}(\Gamma )=A(\Gamma )$ where $A(\Gamma )$ is the adjacency matrix of $\Gamma$. Thus, $\Gamma$ has two distinct distance eigenvalues i.e., $\nu -1$ and $-1$.

For the converse, assume that $\Gamma$ has two distinct distance eigenvalues, say, ${\mu }_0>{\mu }_1$. Let $m_i$ be the multiplicity of ${\mu }_i$. By Theorem 2, $m_1=1$, and thus, $m_2=\nu -1$. We show that $\Gamma$ does not contain $K_{1,2}$ as an induced subgraph. On the contrary, we assume that it is true. Let P be the principle submatrix of $\mathcal{D}(\Gamma )$ induced by $K_{1,2}$. Then, by Theorem 3, we obtain that P has only two distinct distance eigenvalues. However, by Lemma 2, $\mathcal{D}\left(K_{1,2}\right)$ has precisely three distinct distance eigenvalues. This implies that $K_{1,2}$ is not an induced subgraph of $\Gamma$. And thus, $D(\Gamma )=1$ and $\Gamma =K_{\nu }$, $\nu \ge 2$. □

The problem of characterizing graphs with three distinct distance eigenvalues is, in fact, very hard. This problem was solved for trees by Zhang and Lin [30] in 2023. Here, we deliver an alternative proof which is extendable to other families of graphs such as unicyclic and bicyclic graphs.

Proof of Theorem 1.

The ‘only if part’ of the statement follows from Lemma 2 by considering either $s=1$ or $t=1$.

For the ‘if part’ of the statement, we assume T to be a tree with three distinct distance eigenvalues. Let D (resp. $\mathcal{D}$) be the diameter (resp. distance matrix) of T. Since T is non-complete, we obtain that T is non-regular. Let ${\mu }_0>{\mu }_1>{\mu }_2$ be the distinct eigenvalues of T with respective multiplicities $m_0,m_1,m_2$. By the Perron–Frobenius Theorem 2, we have $m_0=1$. Moreover, by Corollary 1, we have ${\mu }_0>0$ and ${\mu }_1<0$. Let $\mathbf{x}>0$ be the Perron–Frobenius eigenvector of $\mathcal{D}$, then

$$(J-I)\mathbf{x}\le \mathcal{D}\mathbf{x}\le D(J-I)\mathbf{x},$$

and $\mathcal{D}\mathbf{x}=D(J-I)\mathbf{x}$ if and only if $D=1$. This implies that ${\mu }_0\le D(\nu -1)$. We discuss the following two possible cases:

Case 1.

${\mu }_0$ is not an integer.

Since ${\mu }_0$ is simple and non-integral, one of ${\mu }_i$ ($1\le i\le 2$) is also simple. Let $\{\mu ,{\mu }^{\prime }\}=\{{\mu }_1,{\mu }_2\}$, and assume $\mu$ is the simple eigenvalue. This implies that ${\mu }^{\prime }\in \mathbb{Z}$ and has multiplicity $\nu -2$. Since $\left(\mathcal{D}\right)=0$, we obtain that ${\mu }_0+{\mu }_1=-{\mu }^{\prime }(\nu -2).$ Note that $\mathrm{rank}(\mathcal{D}-{\mu }^{\prime }I)=2$. Moreover, $K_{1,2}$ is an induced subgraph of T as it is non-regular and non-complete. This implies that

$$\mathrm{rank}\left(D\left(K_{1,2}\right)-{\mu }^{\prime }I\right)\le 2,$$

where $\mathcal{D}\left(K_{1,2}\right)$ is a principle submatrix of $\mathcal{D}\left(T\right)$. Therefore, by interlacing, ${\mu }^{\prime }\in \{1\pm \sqrt{3},-2\}$ since $Spe{c}_{\mathcal{D}}\left(K_{1,2}\right)=\{1\pm \sqrt{3},-2\}$. However, since ${\mu }^{\prime }\in \mathbb{Z}$, we obtain that ${\mu }^{\prime }=-2$. By Theorem 2.6 from [23], T is a complete multipartite graph. Since T is a non-regular graph having three distinct distance eigenvalues, by Lemma 3.4 from [23], $T=K_{s,t}$, $s,t\ge 2$ is complete bipartite. By Lemma 2 and Corollary 1, we obtain that ${\mu }_1=s+t-2-\sqrt{s^2-st+t^2}<0$ and ${\mu }_2=s+t-2+\sqrt{s^2-st+t^2}>0$. By solving these inequalities, we obtain that either $s=1$ or $t=1$. This implies that T is the star graph.

Case 2.

${\mu }_0$ is an integer.

In this case, we may assume that $m_i\ge 2$ for $i=1,2$. Based on $m_i$, we consider the following subcases.

Subcase 2.1. Assume that $m_1\ne m_2$.

In this case, the corresponding distance eigenvalues ${\mu }_1$ and ${\mu }_2$ are integral such that ${\mu }_1\ge 0$ and ${\mu }_2\le -2$. If ${\mu }_2=-2$, then, by Theorem 2.6 from [23], T is a complete multipartite graph. Since T is a non-regular graph having three distinct distance eigenvalues, by Lemma 3.4 from [23], $T=K_{s,t}$, $s,t\ge 2$ is complete bipartite. By Lemma 2 and Corollary 1, we obtain that ${\mu }_1=s+t-2-\sqrt{s^2-st+t^2}<0$ and ${\mu }_2=s+t-2+\sqrt{s^2-st+t^2}>0$. By solving these inequalities, we obtain that either $s=1$ or $t=1$. This implies that T is a star graph.

Thus, we have ${\mu }_1\ge 0$ and ${\mu }_2\le -3$. By Corollary 1, this is not possible, as the graph is a tree.

Subcase 2.2. Assume that $m_1=m_2\ge 2$.

Then, $m_1=m_2=m={\displaystyle \frac{1}{2}}(\nu -1)$, and hence, $\nu =2m+1$ is odd. Note that $\left(\mathcal{D}\right)=0$ implies that ${\displaystyle \sum _{i=1}^{\nu }}{\mu }_i=0$. This gives us

$${\mu }_0+{\displaystyle \frac{1}{2}}(\nu -1)({\mu }_1+{\mu }_2)=0.$$

(1)

As ${\mu }_1+{\mu }_2\in {\mathbb{Z}}^{-}$, we obtain ${\mu }_0=c{\displaystyle \frac{1}{2}}(\nu -1)$, where c is a positive integer by Equation (1). Since T is non-complete, there exist vertices $x,y$, and z in T such that $x\sim y\sim z$. Note that the set $S=\{x,y,z\}$ induces a path of length two in T. This implies that, by interlacing, we obtain $-1<{\mu }_1<0$, as $Spe{c}_D\left(K_{1,2}\right)=\{1\pm \sqrt{3},-2\}$. Moreover, since $\nu$ is odd and $m_1=m_2=m={\displaystyle \frac{1}{2}}(\nu -1)$, by Theorem 5, we obtain

$$2^{2m}=-{\left({\mu }_1{\mu }_2\right)}^m({\mu }_1+{\mu }_2).$$

(2)

By Equation (2), we obtain that ${\mu }_1{\mu }_2\in \{1,2,4\}$ as ${\mu }_1+{\mu }_2\in {\mathbb{Z}}^{-}$. Next, we discuss all these possibilities one by one:

Subsubcase 2.2.1. ${\mu }_1{\mu }_2=4$.

By Equation (2), we obtain that ${\mu }_1+{\mu }_2=-1$, which is not possible as ${\mu }_1>-1$ and ${\mu }_2\le -2$.

Subsubcase 2.2.2. ${\mu }_1{\mu }_2=1$.

In this case, by Equation (2), we obtain ${\mu }_1+{\mu }_2=-2^{2m}$. As a consequence of Theorem 5, one could show that T has $⌈{\displaystyle \frac{D}{2}}⌉$ distinct distance eigenvalues. Using this fact with ${\mu }_0\le D(\nu -1)$, we find that ${\mu }_0\le D(\nu -1)\le 12m$. By using ${\mu }_0\le 12m$ and Theorem 2, we obtain

$$12m\ge |{\mu }_2|>2^{2m}-1$$

This implies that $m\le 3$ and, thus, $\nu \le 7$. Table 1 and Table 2 present all the trees on $\nu \le 7$ vertices and their distance spectra. It is easy to check that this case is not possible.

Table 1. Trees on $\nu \le 7$ vertices and their distance spectra.

$\mathit{\nu }$	Tree	Distance Spectrum
2		$\{{\left[1\right]}^1,{[-1]}^1\}$
3		$\{{\left[2.7320\right]}^1,{[-0.7320]}^1,{[-2]}^1\}$
4		$\{{\left[4.6457\right]}^1,{[-0.6457]}^1,{[-2]}^2,\}$
4		$\{{\left[5.1623\right]}^1,{[-0.5858]}^1,{[-1.1623]}^1,{[-3.41421]}^1,\}$
5		$\{{\left[6.60555\right]}^1,{[-0.60555]}^1,{[-2]}^3\}$
5		$\{{\left[7.45929\right]}^1,{[-0.51198]}^1,{[-1.0846]}^1,{[-2]}^1,{[-3.8627]}^1\}$
5		$\{{\left[8.2882\right]}^1,{[-0.5578]}^1,{[-0.7639]}^1,{[-1.7304]}^1,{[-5.2361]}^1\}$
6		$\{{\left[8.5826\right]}^1,{[-0.5826]}^1,{[-2]}^4\}$
6		$\{{\left[9.6702\right]}^1,{[-0.4727]}^1{[-1.0566]}^1,{[-2]}^2,{[-4.1409]}^1\}$
6		$\{{\left[11.0588\right]}^1,{[-0.5114]}^1,{[-0.67301]}^1,{[-1.7026]}^1{[-2]}^1,{[-6.1717]}^1\}$
6		$\{{\left[10\right]}^1,{[-0.4384]}^1,{[-1]}^1,{[-2]}^2,{[-4.5615]}^1\}$
6		$\{{\left[10.7424\right]}^1,{[-0.4754]}^1,{[-0.7639]}^1,{[-1.3363]}^1,{[-5.2360]}^1\}$
6		$\{{\left[12.1093\right]}^1,{[-0.5358]}^1,{[-0.6798]}^1,{[-1]}^1,{[-2.4295]}^1,{[-7.4641]}^1\}$
7		$\{{\left[10.5678\right]}^1,{[-0.5678]}^1,{[-2]}^5\}$
7		$\{{\left[11.8281\right]}^1,{[-0.4488]}^1,{[-1.0423]}^1,{[-2]}^3,{[-4.3368]}^1\}$
7		$\{{\left[13.6353\right]}^1,{[-0.4703]}^1,{[-0.6481]}^1,{[-1.6923]}^1,{[-2]}^2,{[-6.8245]}^1\}$
7		$\{{\left[12.3945\right]}^1,{[-0.3973]}^1,{[-0.9692]}^1,{[-2]}^3,{[-5.02789]}^1\}$

Table 2. Trees on $\nu \le 7$ vertices and their distance spectra.

$\mathit{\nu }$	Tree	Distance Spectrum
7		$\{{\left[14.1759\right]}^1,{[-0.5073]}^1,{[-0.5359]}^1,{[-1.6687]}^1,{[-2]}^2,{[-7.464]}^1\}$
7		$\{{\left[13.0698\right]}^1,{[-0.4307]}^1,{[-0.7639]}^1,{[-1.2626]}^1,{[-2]}^1,{[-3.3764]}^1,{[-5.2360]}^1\}$
7		$\{{\left[15.4048\right]}^1,{[-0.4943]}^1,{[-0.62420]}^1,{[-0.9174]}^1,{[-2]}^1,{[-2.4757]}^1,{[-8.8932]}^1\}$
7		$\{{\left[14.863\right]}^1,{[-0.4749]}^1,{[-0.6461]}^1,{[-0.9171]}^1,{[-1.7796]}^1,{[-3.3529]}^1,{[-7.6929]}^1\}$
7		$\{{\left[13.6346\right]}^1,{[-0.43245]}^1,{[-0.6651]}^1,{[-1.3089]}^1,{[-2]}^1,{[-3.0055]}^1,{[-6.223]}^1\}$
7		$\{{\left[14.2969\right]}^1,{[-0.4559]}^1,{[-0.76393]}^2,{[-1.8410]}^1,{[-5.2361]}^2\}$
7		$\{{\left[16.6253\right]}^1,{[-0.52720]}^1,{[-0.6159]}^1,{[-0.8405]}^1,{[-1.2862]}^1,{[-3.2576]}^1,{[-10.0978]}^1\}$

Subsubcase 2.2.3. ${\mu }_1{\mu }_2=2$.

In this case, we obtain that ${\mu }_1+{\mu }_2=-2^m$. By using a similar argument as in Subcase 2.1, we find that, in this case, we have $m\le 6$. Note that ${\mu }_1$ and ${\mu }_2$ are the roots of

$$x^2-({\mu }_1+{\mu }_2)x+{\mu }_1{\mu }_2=0.$$

(3)

From (3), we obtain ${\mu }_1,{\mu }_2={\displaystyle \frac{-2^m\pm \sqrt{2^{2m}-8}}{2}}$. For $m\le 6$, the number $2^{2m}-8$ is not a perfect square. Thus, ${\mu }_i$ ($i=1,2$) is not integral which is a contradiction to the fact that all ${\mu }_i$’s are integral. This shows that ${\mu }_0$ is not integral which completes the proof. □

4. Distance Spectra of Small Graphs

In this section, we deliver all the connected graphs (excluding trees) on $\nu \le 6$ vertices and their distance spectra. For trees, we refer to Table 1 and Table 2. Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16 comprise these data. Note that these data are generated by using nauty-geng generators on Sage [37] software. The first column depicts their unique graph6 string. Researchers may use these data for their research on spectral graph theory of the distance matrix.

Table 3. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
Bw	3		$\{{\left[2\right]}^1,{[-1]}^2\}$
CV	4		$\{{\left[4.0996\right]}^1,{[-0.7165]}^1,{[-1]}^1,{[-2.3832]}^1\}$
C]	4		$\{{\left[4.0\right]}^1,{\left[0.0\right]}^1,{[-2.0]}^2,\}$
C^	4		$\{{\left[3.5616\right]}^1,{[-0.5616]}^1,{[-1.0]}^1,{[-2.0]}^1,\}$
C~	4		$\{{\left[3.0\right]}^1,{[-1.0]}^3\}$

Table 4. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
DC{	5		$\{{\left[6.1764\right]}^1,{[-0.6378]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-2.5387]}^1\}$
DEw	5		$\{{\left[6.5381\right]}^1,{\left[0.0\right]}^1,{[-1.0534]}^1,{[-2.0]}^1,{[-3.4847]}^1\}$
DEk	5		$\{{\left[6.6375\right]}^1,{[-0.5858]}^1,{[-0.8365]}^1,{[-1.801]}^1,{[-3.4142]}^1\}$
DE{	5		$\{{\left[5.7596\right]}^1,{[-0.558]}^1,{[-0.7667]}^1,{[-2.0]}^1,{[-2.4348]}^1\}$
DFw	5		$\{{\left[5.6458\right]}^1,{\left[0.3542\right]}^1,{[-2.0]}^3\}$
DF{	5		$\{{\left[5.3723\right]}^1,{[-0.3723]}^1,{[-1.0]}^1,{[-2.0]}^2\}$
DQw	5		$\{{\left[7.0086\right]}^1,{[-0.5686]}^1,{[-1.0]}^1,{[-1.1774]}^1,{[-4.2626]}^1\}$
DQ{	5		$\{{\left[5.7016\right]}^1,{[-0.7016]}^1,{[-1.0]}^2,{\left[3.0\right]}^1\}$

Table 5. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
DUW	5		$\{{\left[6.0\right]}^1,{[-0.382]}^2,{[-0.618]}^2\}$
DUw	5		$\{{\left[5.6351\right]}^1,{\left[0.0\right]}^1,{[-0.9125]}^1,{[-2.0]}^1,{[-2.7226]}^1\}$
DU{	5		$\{{\left[5.2926\right]}^1,{[-0.382]}^1,{[-0.7217]}^1,{[-1.5709]}^1,{[-2.618]}^1\}$
DTW	5		$\{{\left[6.2161\right]}^1,{[-0.4521]}^1,{[-1.0]}^1,{[-1.1971]}^1,{[-3.5669]}^1\}$
DT{	5		$\{{\left[5.3441\right]}^1,{[-0.7105]}^1,{[-1.0]}^2,{[-2.6336]}^1\}$
DV{	5		$\{{\left[4.9018\right]}^1,{[-0.5122]}^1,{[-1.0]}^2,{[-2.3896]}^1\}$
D}w	5		$\{[{\left[5.2239\right]}^1,{\left[0.1606\right]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-2.3844]}^1\}$
D}{	5		$\{{\left[4.8284\right]}^1,{\left[0.0\right]}^1,{[-0.8284]}^1,{[-2.0]}^2\}$
D^{	5		$\{{\left[4.4495\right]}^1,{[-0.4495]}^1,{[-1.0]}^2,{[-2.0]}^1\}$

Table 6. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
D~{	5		$\{{\left[4.0\right]}^1,{[-1.0]}^4\}$
E?bw	6		$\{{\left[8.2297\right]}^1,{[-0.6009]}^1,{[-1.0]}^1,{[-2.0]}^2,{[-2.6288]}^1\}$
E?ro	6		$\{{\left[8.899\right]}^1,{\left[0.0\right]}^1,{[-0.899]}^1,{[-2.0]}^2,{[-4.0]}^1\}$
E?qw	6		$\{{\left[8.9909\right]}^1,{[-0.512]}^1,{[-0.8175]}^1,{[-1.7801]}^1,{[-2.0]}^1,{[-3.8813]}^1\}$
E?rw	6		$\{{\left[7.8888\right]}^1,{[-0.5542]}^1,{[-0.6926]}^1,{[-2.0]}^2,{[-2.642]}^1\}$
E?zO	6		$\{{\left[9.6569\right]}^1,{\left[0.0\right]}^1,{[-0.7639]}^1,{[-1.6569]}^1,{[-2.0]}^1,{[-5.2361]}^1\}$
E?zo	6		$\{{\left[8.1468\right]}^1,{\left[0.4057\right]}^1,{[-1.0308]}^1,{[-2.0]}^2,{[-3.5217]}^1\}$
E?zW	6		$\{{\left[8.2882\right]}^1,{[-0.5578]}^1,{[-0.5858]}^1,{[-1.7304]}^1,{[-2.0]}^1,{[-3.4142]}^1\}$
E?zw	6		$\{{\left[7.5673\right]}^1,{[-0.358]}^1,{[-0.7507]}^1,{[-2.0]}^2,{[-2.4586]}^1\}$
E?~o	6		$\{{\left[7.4641\right]}^1,{\left[0.5359\right]}^1,{[-2.0]}^4\}$

Table 7. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
E?~w	6		$\{{\left[7.2749\right]}^1,{[-0.2749]}^1,{[-1.0]}^1,{[-2.0]}^3\}$
ECRo	6		$\{{\left[9.3154\right]}^1,{[-0.5023]}^1,{[-1.0]}^1,{[-1.0865]}^1,{[-2.3224]}^1,{[-4.4042]}^1\}$
ECRw	6		$\{{\left[7.8526\right]}^1,{[-0.6303]}^1,{[-1.0]}^2,{[-2.2223]}^1,{[-3.0]}^1\}$
ECr_	6		$\{{\left[9.2606\right]}^1,{\left[0.0\right]}^1,{[-1.0]}^1,{[-1.0898]}^1,{[-3.1708]}^1,{[-4.0]}^1\}$
ECpo	6		$\{{\left[8.8219\right]}^1,{[-0.3559]}^1,{[-0.382]}^1,{[-1.2995]}^1,{[-2.618]}^1,{[-4.1664]}^1\}$
ECqg	6		$\{{\left[9.3852\right]}^1,{[-0.5858]}^2,{[-1.3852]}^1,{[-3.4142]}^2\}$
ECro	6		$\{{\left[8.1822\right]}^1,{\left[0.0\right]}^1,{[-0.8303]}^1,{[-1.3401]}^1,{[-2.5075]}^1,{[-3.5042]}^1\}$
ECrg	6		$\{{\left[8.6632\right]}^1,{[-0.4351]}^1,{[-0.7665]}^1,{[-1.1966]}^1,{[-2.3862]}^1,{[-3.8789]}^1\}$
ECrw	6		$\{{\left[7.5222\right]}^1,{[-0.382]}^1,{[-0.6395]}^1,{[-1.4565]}^1,{[-2.4261]}^1,{[-2.618]}^1\}$
ECZ_	6		$\{{\left[9.9713\right]}^1,{\left[0.0\right]}^1,{[-0.6685]}^1,{[-1.7199]}^1,{[-2.0]}^1,{[-5.5829]}^1\}$

Table 8. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
ECZO	6		$\{{\left[10.668\right]}^1,{[-0.5501]}^1,{[-0.7462]}^1,{[-1.0]}^1,{[-1.8096]}^1,{[-6.562]}^1\}$
ECZG	6		$\{{\left[10.0548\right]}^1,{[-0.552]}^1,{[-0.6878]}^1,{[-1.1178]}^1,{[-2.2283]}^1,{[-5.4689]}^1\}$
ECYW	6		$\{{\left[9.6088\right]}^1,{[-0.4931]}^1,{[-1.0]}^1,{[-1.0924]}^1,{[-2.0]}^1,{[-5.0233]}^1\}$
ECZo	6		$\{{\left[8.497\right]}^1,{\left[0.0\right]}^1,{[-1.0]}^1,{[-1.0613]}^1,{[-2.0]}^1,{[-4.4357]}^1\}$
ECZg	6		$\{{\left[8.9694\right]}^1,{[-0.4807]}^1,{[-0.6851]}^1,{[-1.1687]}^1,{[-2.0]}^1,{[-4.6349]}^1\}$
ECZW	6		$\{{\left[8.5936\right]}^1,{[-0.5686]}^1,{[-0.8339]}^1,{[-1.0]}^1,{[-1.8778]}^1,{[-4.3134]}^1\}$
ECZw	6		$\{{\left[7.4864\right]}^1,{[-0.5574]}^1,{[-0.7551]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-3.1739]}^1\}$
ECfo	6		$\{{\left[8.6378\right]}^1,{[-0.4043]}^1,{[-1.0]}^1,{[-1.1116]}^1,{[-2.0]}^1,{[-4.1219]}^1\}$

Table 9. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
ECfw	6		$\{{\left[7.5546\right]}^1,{[-0.6347]}^1,{[-1.0]}^2,{[-2.0]}^1,{[-2.9199]}^1\}$
ECxo	6		$\{{\left[7.6952\right]}^1,{\left[0.0932\right]}^1,{[-0.382]}^1,{[-2.0]}^1,{[-2.618]}^1,{[-2.7884]}^1\}$
ECzo	6		$\{{\left[7.4058\right]}^1,{\left[0.3642\right]}^1,{[-0.9064]}^1,{[-2.0]}^2,{[-2.8636]}^1\}$
ECzg	6		$\{{\left[8.3569\right]}^1,{[-0.2733]}^1,{[-1.0]}^1,{[-1.0985]}^1,{[-2.0]}^1,{[-3.985]}^1\}$
ECzW	6		$\{{\left[7.9151\right]}^1,{[-0.3566]}^1,{[-0.6712]}^1,{[-1.1846]}^1,{[-2.1064]}^1,{[-3.5963]}^1\}$
ECxw	6		$\{{\left[7.4417\right]}^1,{\left[0.0\right]}^1,{[-0.5595]}^1,{[-2.0]}^2,{[-2.8823]}^1\}$
ECzw	6		$\{{\left[7.1742\right]}^1,{[-0.1943]}^1,{[-0.6764]}^1,{[-1.5289]}^1,{[-2.0]}^1,{[-2.7745]}^1\}$
ECvo	6		$\{{\left[7.837\right]}^1,{\left[0.1708\right]}^1,{[-1.0]}^1,{[-1.0545]}^1,{[-2.377]}^1,{[-3.5763]}^1\}$
ECuw	6		$\{{\left[7.9777\right]}^1,{[-0.5858]}^1,{[-0.8093]}^1,{[-1.0]}^1,{[-2.1683]}^1,{[-3.4142]}^1\}$
ECvw	6		$\{{\left[7.2057\right]}^1,{[-0.5121]}^1,{[-0.763]}^1,{[-1.0]}^1,{[-2.2667]}^1,{[-2.6639]}^1\}$

Table 10. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
EC~o	6		$\{{\left[7.0959\right]}^1,{\left[0.4439\right]}^1,{[-1.0]}^1,{[-2.0]}^2,{[-2.5398]}^1\}$
EC~w	6		$\{{\left[6.8858\right]}^1,{[-0.3426]}^1,{[-1.0]}^2,{[-2.0]}^1,{[-2.5432]}^1\}$
EEr_	6		$\{{\left[8.5704\right]}^1,{\left[0.3566\right]}^1,{[-1.0]}^1,{[-2.0]}^2,{[-3.927]}^1\}$
EEro	6		$\{{\left[7.8759\right]}^1,{\left[0.1611\right]}^1,{[-0.7551]}^1,{[-1.7972]}^1,{[-2.0]}^1,{[-3.4847]}^1\}$
EErw	6		$\{{\left[7.1648\right]}^1,{\left[0.0\right]}^1,{[-0.6718]}^1,{[-2.0]}^2,{[-2.4929]}^1\}$
EEh_	6		$\{{\left[9.0\right]}^1,{\left[0.0\right]}^2,{[-1.0]}^1,{[-4.0]}^2\}$
EEj_	6		$\{{\left[8.4244\right]}^1,{\left[0.0\right]}^2,{[-1.4244]}^1,{[-3.0]}^1,{[-4.0]}^1\}$
EEio	6		$\{{\left[8.5543\right]}^1,{\left[0.0\right]}^1,{[-0.6439]}^1,{[-1.7422]}^1,{[-2.0]}^1,{[-4.1682]}^1\}$
EEho	6		$\{{\left[8.0741\right]}^1,{[-0.3258]}^1,{[-0.382]}^1,{[-0.8858]}^1,{[-2.618]}^1,{[-3.8625]}^1\}$

Table 11. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
EEiW	6		$\{{\left[9.4244\right]}^1,{[-0.4244]}^1,{[-0.7639]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-5.2361]}^1\}$
EEhW	6		$\{{\left[8.5237\right]}^1,{\left[0.0\right]}^1,{[-0.8401]}^1,{[-1.1598]}^1,{[-2.2582]}^1,{[-4.2656]}^1\}$
EEjo	6		$\{{\left[7.8043\right]}^1,{\left[0.0\right]}^1,{[-0.6535]}^1,{[-1.0921]}^1,{[-2.2817]}^1,{[-3.7771]}^1\}$
EEjW	6		$\{{\left[8.2723\right]}^1,{[-0.3698]}^1,{[-0.601]}^1,{[-1.1477]}^1,{[-1.8894]}^1,{[-4.2644]}^1\}$
EEhw	6		$\{{\left[7.4002\right]}^1,{\left[0.0\right]}^1,{[-0.8467]}^1,{[-1.0]}^1,{[-2.5535]}^1,{[-3.0]}^1\}$
EEjw	6		$\{{\left[7.1287\right]}^1,{[-0.279]}^1,{[-0.7025]}^1,{[-1.0]}^1,{[-2.1472]}^1,{[-3.0]}^1\}$
EEz_	6		$\{{\left[7.772\right]}^1,{\left[0.5616\right]}^1,{[-0.772]}^1,{[-2.0]}^2,{[-3.5616]}^1\}$
EEzO	6		$\{{\left[8.2037\right]}^1,{\left[0.1607\right]}^1,{[-1.0]}^1,{[-1.0566]}^1,{[-2.0]}^1,{[-4.3078]}^1\}$
EEzo	6		$\{{\left[7.0425\right]}^1,{\left[0.4744\right]}^1,{[-0.76]}^1,{[-2.0]}^2,{[-2.7569]}^1\}$
EEzg	6		$\{{\left[7.5169\right]}^1,{\left[0.2038\right]}^1,{[-1.0]}^1,{[-1.0737]}^1,{[-2.0]}^1,{[-3.6471]}^1\}$

Table 12. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
EEzw	6		$\{{\left[6.7884\right]}^1,{\left[0.1022\right]}^1,{[-0.7201]}^1,{[-1.4974]}^1,{[-2.0]}^1,{[-2.6732]}^1\}$
EEvo	6		$\{{\left[7.5455\right]}^1,{\left[0.0\right]}^1,{[-0.7465]}^1,{[-1.176]}^1,{[-2.0]}^1,{[-3.6229]}^1\}$
EEuw	6		$\{{\left[7.6235\right]}^1,{[-0.4235]}^1,{[-0.8097]}^1,{[-1.0]}^1,{[-1.8233]}^1,{[-3.567]}^1\}$
EEvw	6		$\{{\left[6.8601\right]}^1,{[-0.4485]}^1,{[-0.7263]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-2.6853]}^1\}$
EEno	6		$\{{\left[7.0835\right]}^1,{\left[0.1639\right]}^1,{[-0.5993]}^1,{[-1.5688]}^1,{[-2.3433]}^1,{[-2.7361]}^1\}$
EElw	6		$\{{\left[7.1231\right]}^1,{[-0.382]}^1,{[-0.382]}^1,{[-1.1231]}^1,{[-2.618]}^1,{[-2.618]}^1\}$
EEnw	6		$\{{\left[6.8289\right]}^1,{[-0.382]}^1,{[-0.5882]}^1,{[-1.0]}^1,{[-2.2407]}^1,{[-2.618]}^1\}$
EEnw	6		$\{{\left[6.8289\right]}^1,{[-0.382]}^1,{[-0.5882]}^1,{[-1.0]}^1,{[-2.2407]}^1,{[-2.618]}^1\}$
EE~w	6		$\{{\left[6.5109\right]}^1,{[-0.3512]}^1,{[-0.7158]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-2.4439]}^1\}$

Table 13. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
EFz_	6		$\{{\left[7.0\right]}^1,{\left[1.0\right]}^1,{[-2.0]}^4\}$
EFzo	6		$\{{\left[6.6961\right]}^1,{\left[0.6888\right]}^1,{[-1.0]}^1,{[-2.0]}^2,{[-2.3849]}^1\}$
EFzW	6		$\{{\left[6.744\right]}^1,{\left[0.3631\right]}^1,{[-0.6703]}^1,{[-2.0]}^2,{[-2.4368]}^1\}$
EFzw	6		$\{{\left[6.4188\right]}^1,{\left[0.3868\right]}^1,{[-0.8056]}^1,{[-2.0]}^3\}$
EF~w	6		$\{{\left[6.1623\right]}^1,{[-0.1623]}^1,{[-1.0]}^2,{[-2.0]}^2\}$
EQj_	6		$\{{\left[9.6964\right]}^1,{[-0.4484]}^1,{[-0.7224]}^1,{[-1.0]}^1,{[-1.7703]}^1,{[-5.7553]}^1\}$
EQjO	6		$\{{\left[9.1962\right]}^1,{[-0.5505]}^1,{[-1.0]}^2,{[-1.1962]}^1,{[-5.4495]}^1\}$
EQjo	6		$\{{\left[8.217\right]}^1,{[-0.4384]}^1,{[-1.0]}^2,{[-1.217]}^1,{[-4.5616]}^1\}$
EQjg	6		$\{{\left[8.6279\right]}^1,{[-0.5617]}^1,{[-1.0]}^2,{[-1.1831]}^1,{[-4.883]}^1\}$

Table 14. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
EQjw	6		$\{{\left[7.1246\right]}^1,{[-0.6959]}^1,{[-1.0]}^3,{[-3.4287]}^1\}$
EQZo	6		$\{{\left[7.772\right]}^1,{\left[0.0\right]}^1,{[-0.772]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-4.0]}^1\}$
EQzo	6		$\{{\left[7.0418\right]}^1,{\left[0.1621\right]}^1,{[-0.912]}^1,{[-1.0]}^1,{[-2.1204]}^1,{[-3.1715]}^1\}$
EQzg	6		$\{{\left[7.9676\right]}^1,{[-0.4017]}^1,{[-1.0]}^1,{[-1.223]}^1,{[-4.3429]}^1\}$
EQzW	6		$\{{\left[7.5165\right]}^1,{[-0.3389]}^1,{[-0.4679]}^1,{[-1.1776]}^1,{[-1.6527]}^1,{[-3.8794]}^1\}$
EQyw	6		$\{{\left[7.0747\right]}^1,{\left[0.0\right]}^1,{[-0.8868]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-3.1879]}^1\}$
EQzw	6		$\{{\left[6.783\right]}^1,{[-0.3274]}^1,{[-0.711]}^1,{[-1.0]}^1,{[-1.6232]}^1,{[-3.1214]}^1\}$
EQ~o	6		$\{{\left[6.7016\right]}^1,{\left[0.2984\right]}^1,{[-1.0]}^2,{[-2.0]}^1,{[-3.0]}^1\}$
EQ~w	6		$\{{\left[6.4641\right]}^1,{[-0.4641]}^1,{[-1.0]}^3,{[-3.0]}^1\}$
EUZ_	6		$\{{\left[7.3594\right]}^1,{\left[0.1919\right]}^1,{[-0.382]}^1,{[-1.8043]}^1,{[-2.618]}^1,{[-2.7471]}^1\}$
EUZO	6		$\{{\left[7.3554\right]}^1,{[-0.2166]}^1,{[-0.382]}^1,{[-1.0]}^1,{[-2.618]}^1,{[-3.1388]}^1\}$

Table 15. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
EUZo	6		$\{{\left[7.0372\right]}^1,{\left[0.0\right]}^1,{[-0.382]}^1,{[-1.2036]}^1,{[-2.618]}^1,{[-2.8336]}^1\}$
EUZw	6		$\{{\left[6.7417\right]}^1,{[-0.382]}^1,{[-0.382]}^1,{[-0.7417]}^1,{[-2.618]}^1,{[-2.618]}^1\}$
EUxo	6		$\{{\left[7.0\right]}^1,{\left[0.0\right]}^2,{[-2.0]}^2,{[-3.0]}^1\}$
EUzo	6		$\{{\left[6.6953\right]}^1,{\left[0.247\right]}^1,{[-0.4698]}^1,{[-1.445]}^1,{[-2.2255]}^1,{[-2.8019]}^1\}$
EUzW	6		$\{{\left[6.7363\right]}^1,{\left[0.0\right]}^1,{[-0.4464]}^1,{[-1.3637]}^1,{[-2.0]}^1,{[-2.9263]}^1\}$
EUzw	6		$\{{\left[6.4114\right]}^1,{\left[0.0\right]}^1,{[-0.687]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-2.7244]}^1\}$
EU~w	6		$\{{\left[6.1012\right]}^1,{[-0.382]}^1,{[-0.5175]}^1,{[-1.0]}^1,{[-1.5837]}^1,{[-2.618]}^1\}$
ETzo	6		$\{{\left[6.7321\right]}^1,{\left[0.187\right]}^1,{[-0.8992]}^1,{[-1.0]}^1,{[-2.1674]}^1,{[-2.8525]}^1\}$
ETzg	6		$\{{\left[7.2426\right]}^1,{[-0.2679]}^1,{[-1.0]}^2,{[-1.2426]}^1,{[-3.7321]}^1\}$

Table 16. Distance spectra of small graphs.

Graph6 String	$\mathit{\nu }$	Graph	Distance Spectrum
ETzw	6		$\{{\left[6.4523\right]}^1,{[-0.2263]}^1,{[-0.7212]}^1,{[-1.0]}^1,{[-1.6828]}^1,{[-2.8221]}^1\}$
ETno	6		$\{{\left[7.2675\right]}^1,{[-0.3691]}^1,{[-1.0]}^2,{[-1.2143]}^1,{[-3.6841]}^1\}$
ETnw	6		$\{{\left[6.5242\right]}^1,{[-0.7074]}^1,{[-1.0]}^3,{[-2.8168]}^1\}$
ET~w	6		$\{{\left[6.1425\right]}^1,{[-0.4913]}^1,{[-1.0]}^3,{[-2.6512]}^1\}$
EV~w	6		$\{{\left[5.7566\right]}^1,{[-0.3629]}^1,{[-1.0]}^3,{[-2.3937]}^1\}$
E]zo	6		$\{{\left[6.3647\right]}^1,{\left[0.2007\right]}^1,{[-0.382]}^1,{[-1.5654]}^1,{[-2.0]}^1,{[-2.618]}^1\}$
E]zg	6		$\{{\left[6.4017\right]}^1,{\left[0.2368\right]}^1,{[-1.0]}^2,{[-2.0]}^1,{[-2.6385]}^1\}$
E]yw	6		$\{{\left[6.3589\right]}^1,{\left[0.4142\right]}^1,{[-1.0]}^2,{[-2.3589]}^1,{[-2.4142]}^1\}$
E]zw	6		$\{{\left[6.0479\right]}^1,{\left[0.1676\right]}^1,{[-0.8252]}^1,{[-1.0]}^1,{[-2.0]}^1,{[-2.3904]}^1\}$
E]~o	6		$\{{\left[6.0\right]}^1,{\left[0.0\right]}^2,{[-2.0]}^3\}$
E]~w	6		$\{{\left[5.7016\right]}^1,{\left[0.0\right]}^1,{[-0.7016]}^1,{[-1.0]}^1,{[-2.0]}^2\}$
E^~w	6		$\{{\left[5.3723\right]}^1,{[-0.3723]}^1,{[-1.0]}^3,{[-2.0]}^1\}$
E^~w	6		$\{{\left[5.3723\right]}^1,{[-0.3723]}^1,{[-1.0]}^3,{[-2.0]}^1\}$
E~~w	6		$\{{\left[5.0\right]}^1,{[-1.0]}^5\}$

There are some interesting observations which we make based on the data in Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16. Before we elaborate these observations, we note some necessary definitions. Two non-isomorphic connected graphs $\Gamma$ and $\Omega$ are said to be distance cospectral (or distance cospectral mates), if both $\Gamma$ and $\Omega$ have the same multiset of distance eigenvalues. A graph $\Gamma$ is said to be determined from its distance spectrum, if it has no distance cospectral mates.

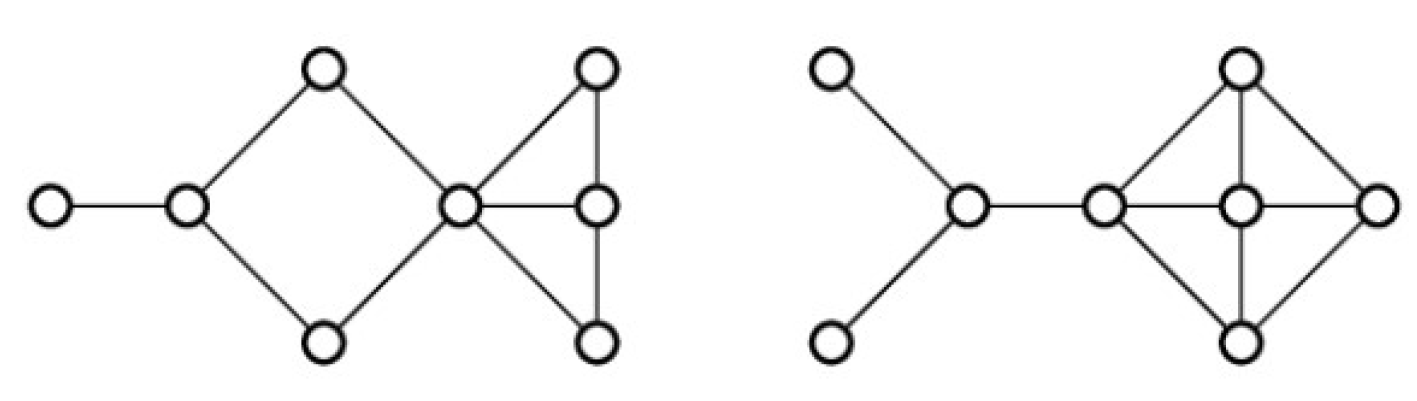
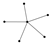
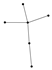
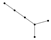
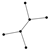
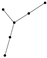
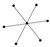
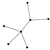
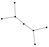
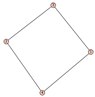
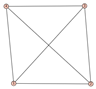
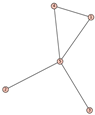
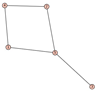
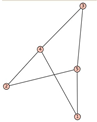
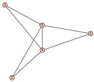
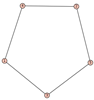
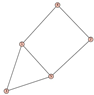
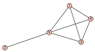
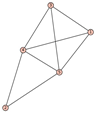
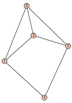
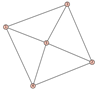
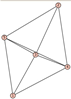
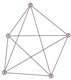
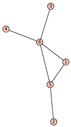
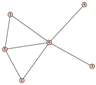
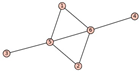
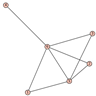
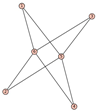
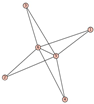
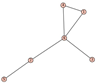
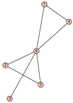
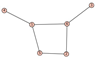
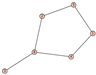
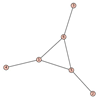
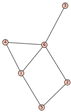
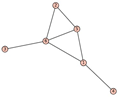
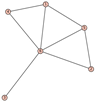
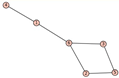
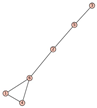
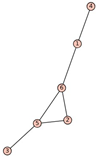
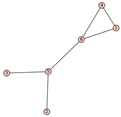
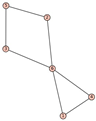
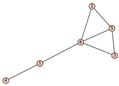
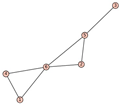
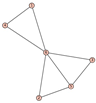
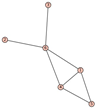
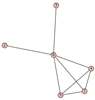
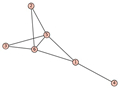
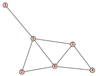
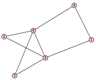
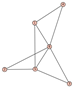
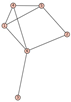
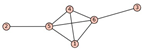
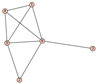
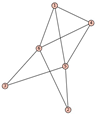
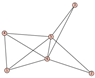
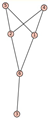
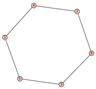
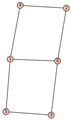
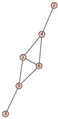
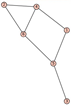
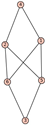
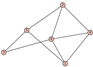
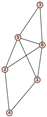
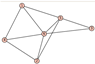
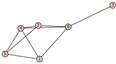
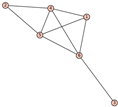
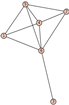
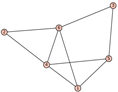
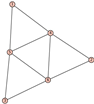
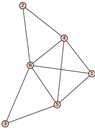
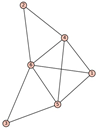
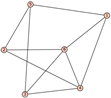
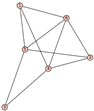
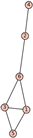
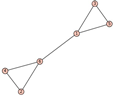
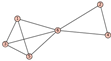
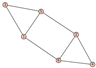
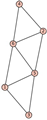
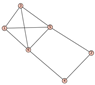
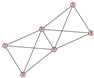
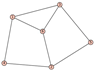
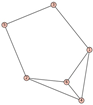
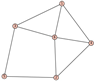
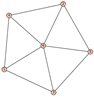
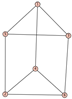
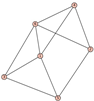
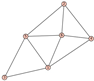
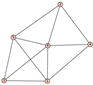
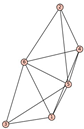
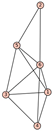
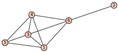
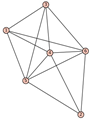
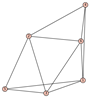
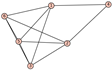
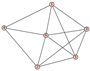
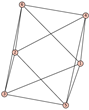
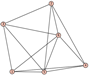
From Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16, we notice that all the connected graphs on $\nu \le 6$ vertices are determined from their distance spectra. We also deliver a distance cospectral pair on $\nu =7$ vertices, making a distance cospectral pair of the smallest possible order. Figure 1 depicts that distance cospectral pair on $\nu =7$ vertices.

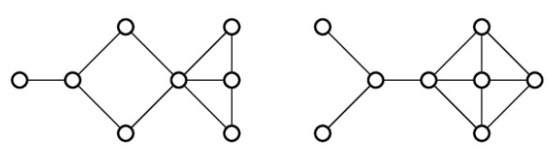
Figure 1. A distance cospectral pair of smallest order.

5. Conclusions

The “few eigenvalues” problem is one of the contemporary problems in spectral graph theory. This paper investigates certain mathematical characteristics of the distance matrix of trees. In particular, this paper studies the “few eigenvalues” problem regarding the distance matrix. The main result of this paper classifies all the trees having precisely three distinct eigenvalues of their distance matrix. Our proof is different from the one delivered by Zhang and Lin [30]. Our proof employs interlacing and equitable partitions and can be extended to other families such as unicyclic and bicyclic graphs. We also list all the connected graphs on $\nu \le 6$ vertices and compute their distance spectra. Some important observations on distance cospectrality are made based on these numerical data.

Based on these remarks, we propose the following open problems for future studies:

Problem 1.

Characterize all unicyclic graphs having precisely three distinct distance eigenvalues.

Problem 2.

Solve Problem 1 for the case of bicyclic graphs.

Problem 3.

Construct an infinite family of non-regular non-bipartite graphs with exactly three distance eigenvalues.