Abstract
Let be a self-similar measure with compact support K. The Hausdorff dimension of K is . The Cauchy transform of is denoted by . For we define the function which compares with the fractional derivative of F of order Let . In this paper, we prove that belongs to for , and belongs to for , where is the Bergman space. At the same time, we give a value distribution property of F, which is similar to the big Picard theorem.
MSC:
28A80; 30C55; 30E20
1. Introduction
The notion of fractals was proposed by Mandelbrot in the 1970s [1]. Soon, the importance of fractals was recognized in many areas of science. In mathematics, a new area called fractal geometry developed quickly on the basis of geometric measure theory, harmonic analysis, dynamical systems and so on. For the aspects of harmonic analysis, the Fourier transform of fractal measures has been investigated by Strichartz [2,3,4,5,6]. For the complex case, more consideration has been given to the Cauchy transform of self-similar measures. The Cauchy transform of a measure in the complex plane plays an important role in geometric measure theory [7,8,9,10]. The study of this transform can be traced back to that of the Cauchy-type integral, which is fundamental in the study of boundary-value problems for analytic functions. Let be a self-similar measure with compact support The Cauchy transform of is defined by In [10], Stricharz et al. studied the Cauchy transform of a self-similar measure with compact support K. From numerical data and computer graphics, they considered the Hölder continuity and analyticity of intuitively. In [11,12,13,14,15], Dong and Lau intensively studied the geometric and analytic properties of F. The precise growth rates of the Laurent coefficients of such F were obtained, and the asymptotic behavior of the coefficients was also discussed in [11]. The geometric properties of F away from K, such as univalence, starlikeness and convexity, were investigated in [14]. Since F is analytic at zero, F has a Taylor expression near zero. The asymptotic behavior of the Taylor coefficients of F was studied in [16,17].
An iterated function system (IFS) consists of a family of contraction mappings, which can represent many fractals that are made up of small images of themselves. For an IFS on , in [18], it is proven that there exists a unique non-empty compact set K that satisfies . K is called the attractor of the IFS. In this paper, we focus on the following IFS:
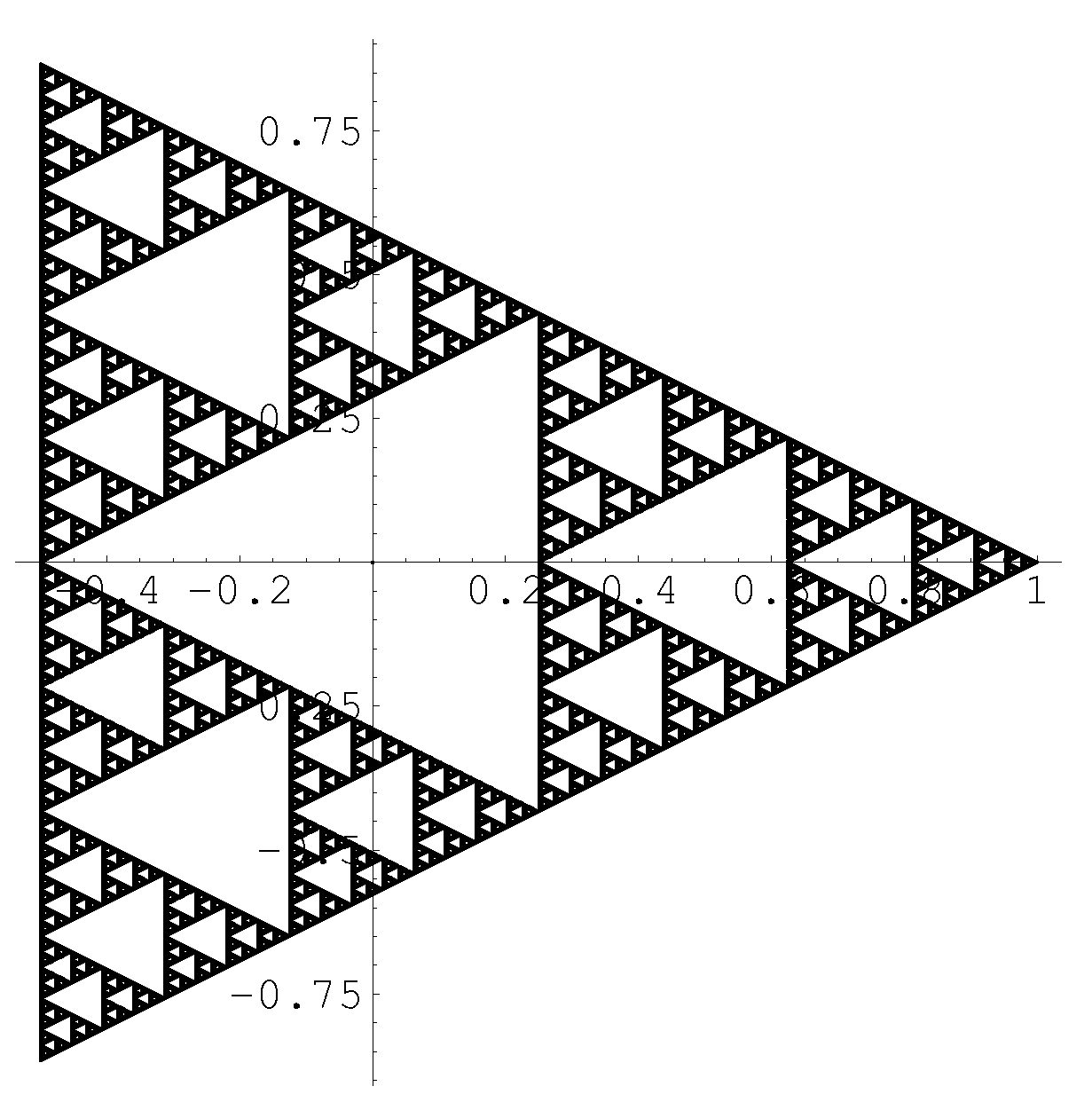
where The attractor of the IFS in (1) is denoted by K, i.e., the unique compact set satisfying . Then, , and K is the Sierpinski gasket (Figure 1). The Cauchy transform of the self-similar measure associated with the IFS was studied by Stricharz et al. in [10]. They proposed several conjectures of F, and these conjectures were partly resolved in [12,13,15]. The Hardy space properties of F were investigated in [19]. In this paper, we consider the Bergman space and multiplier properties of which compares with the fractional derivative of F of order and prove a value distribution property of
Figure 1.
Sierpinski gasket.
2. Preliminaries
In this section, some necessary notations and results are given first. The IFS in (1) satisfies the open-set condition: there exists an open set U such that , and if The Hausdorff dimension of the attractor K of this IFS is . Hutchinson [20] has proven that there exists a unique probability measure with compact support K such that
and is the restriction of the normalized -dimensional Hausdorff measure on K. Theorem 2.1 in [10] proves that the measure is -uniform, i.e., for where C is an absolute positive constant. Notice that is a Hausdorff measure. Therefore, it behaves nicely under translations and dilations: for there exist and [18]. The Cauchy transform of is
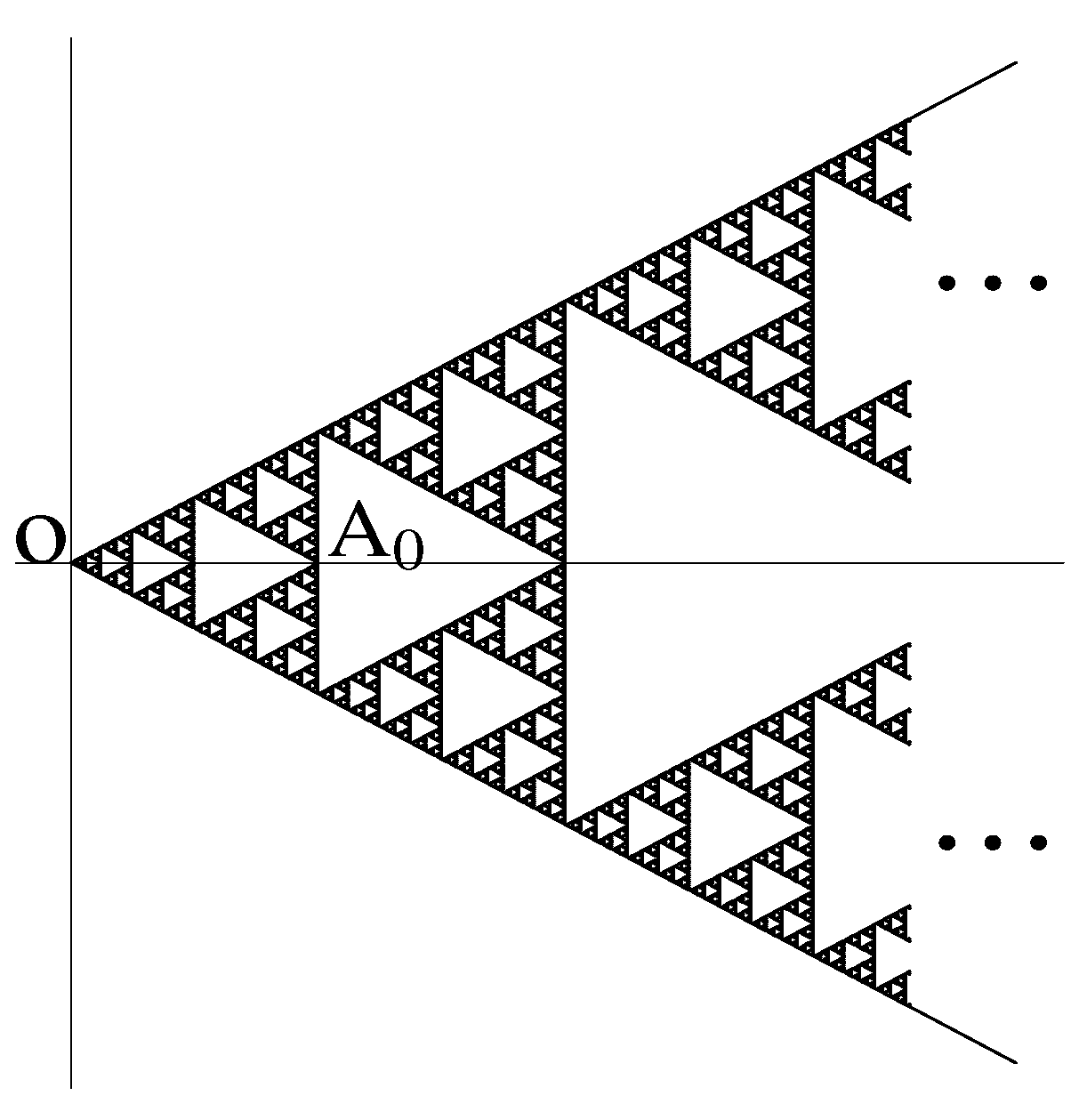
Let And let
This is called the “Sierpinski cones” (Figure 2). For , let . We define auxiliary functions by
where is the principal branch. It is easily seen that by the basic property of the Hausdorff measure.
Figure 2.
Sierpinski cones.
In [11], it is proven that F is analytic in , with , and three-fold symmetric, with , and
where A function f analytic in has the Taylor series expansion The concept of the fractional derivative of f can be described in different ways. For , Hadamard defined the fractional derivative of f of order by
where denotes the gamma function. Hardy and Littlewood [21] described some properties of . MacGregor et al. [22] defined the function by
As shown in [22], it is known that the sequences
have asymptotic expansions , with . Therefore, certain properties of are equivalent to those of .
Let be an analytic function in . It is well known that the Hadamard product of f and g is defined by . Noting that
one can find that is the Hadamard product of f with the function
MacGregor et al. considered the boundary limits of and the limits of of compositions. See [22,23,24].
3. Fractional Derivatives of
Let . Thus, is analytic in . In this section, we will study the Bergman space property of . For a function f analytic in the unit disk , the integral means are defined by
It is well known that the Hardy space [25] consists of analytic functions f in such that
is the class of bounded analytic functions in . For the theory of Hardy spaces, see [24]. The Bergman space [26] consists of all functions f analytic in for which the normalized area integral is finite, where . The norm of a function is defined by
and have many similar properties, and they have the inclusion for In some respects, functions in the Bergman space behave better. See [26,27]. For recent developments in Bergman spaces, the reader can consult [28,29,30,31,32] and references therein.
Theorem 1.
For
Proof.
Firstly, we will show that the Hadamard product of f and g has another integral form,
where f and g are analytic in . In fact,
In terms of integral means, is equivalent to Indeed,
Next, we will prove that the integral is finite. From Theorem 2.1 in [10], we see that is bounded on Using (4), for , we obtain
where C and are positive constants. Hence,
The last integral is convergent for . The result follows. □
Theorem 2.
For , .
Proof.
By (4) and the Hölder inequality, one can have
It follows that
Next, we will consider We denote positive constants by . For fixed , let and Since is -uniform, there exists a positive constant such that Thus,
Notice that is analytic in , and is well defined for The symmetry of and K with respect to the real axis gives
Using (6), for geometric considerations show that
Hence, for , we obtain
It follows that
With (5) and (7), we obtain
for Since
by (8), we have
From the above inequality, it is easy to see that for The proof is complete. □
Below, let us end this section with a multiplier property of . We denote the set of complex-valued Borel measures on by For each let denote the family of functions h having the property that there exists a measure such that
where the logarithm takes the principal branch. For let
where denotes the total variation in the measure . With this norm, is a Banach space. Macgregor introduced the spaces in [33,34]. Several properties of functions in were derived in [35,36]. A multiplier of is an analytic function in such that for all . The family of all such multipliers is denoted by . For , let
With this norm, is a Banach space. The family has been studied in [35,36,37], including the following theorem.
Theorem 3
([36]). Let for If for then .
Theorem 4.
For , if then
Proof.
Note that and
From [38] (p. 79), the inequality
holds. And according to [11] (Theorem 1.2), for , there exists a positive constant C such that Then,
The series is convergent for The result follows from Theorem 3. □
4. A Value Distribution Property
The big Picard theorem shows that if is an isolated essential singularity of an analytic function f, then for any neighborhood of , f assumes every complex number infinitely many times, with, at most, one exception. The Picard theorem can be easily derived from Nevanlinna’s second main theorem, which is an important result in value distribution theory. For more about value distribution theory and its application, see [39,40]. For and let
In this section, we will prove a similar result for F around the non-analytic points . For let We need the following lemma.
Lemma 1
([15]). For any there exists a function such that
where G is continuous on and analytic in and for ; is bounded continuous on and analytic in
For and we write
and
We define the function
where is the principal branch.
Theorem 5.
For each and any there exist infinitely many such that Moreover,
Proof.
To begin with, we prove that for each the function has at least one zero inside for any
Let satisfy By the uniqueness theorem, for some , there exists a disk such that
For all we choose a positive constant R satisfying By Lemma 1, there exists such that
For there exists a positive integer N such that Let
Then,
Due to for from (11) and (12), we conclude that
By Rouche’s theorem, the functions and have the same number of zeros inside . Noting that and , we find that has at least one zero inside . Since is arbitrary, this implies that the function must have an infinite number of zeros inside .
The above shows that for any and The continuity of implies that . Then, one side of the set inclusion in (10) follows. Next, we will prove the reverse inclusion. The multiplicative periodicity of yields the following:
Then, is a compact set by continuity. From Lemma 1, for there exists an absolute constant such that
For arbitrary we choose satisfying If then by (13), where is the —parallel body of It follows that
Since is a compact set, using (14), we find that
It is easy to see that
The proof is complete. □
Remark 1.
If we let
and
the analogous argument to the above yields the same results for the dyadic points
5. Conclusions
In this article, we focus on the Cauchy transform of the self-similar measure on the Sierpinski gasket. We prove that and belong to some Bergman space, where compares with the fractional derivative of the function of order . In addition, we give a value distribution property of F. One can further investigate other analytic properties, such as coefficient estimates, univalence, etc. This topic intersects fractal geometry and geometric function theory. Different from the Cauchy transform of a common measure, the Cauchy transform of a self-similar measure has much more fractal behavior. As is shown in [10] through computer graphics, the image of such a transform is chaotic but regular near the Sierpinski gasket. This is different from the properties in classical analytic function theory and make it possible to construct some unexpected counter examples during one’s research.
Author Contributions
Writing—original draft, S.W.; Writing—review & editing, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the NNSF of China (Grant No. 12101219) and the Hunan Provincial NSF (Grant No. 2022JJ40141).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the referee for his suggestions, which helped to improve the clarity of the paper. Also, the authors really appreciate the helpful suggestions of Xin-Han Dong.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mandelbrot, B.B. Les Objects Fractals: Forme, Hasard et Dimension; Flammarion: Paris, France, 1975. [Google Scholar]
- Strichartz, R.S. Fourier asymptotics of fractal measures. J. Funct. Anal. 1990, 89, 154–187. [Google Scholar] [CrossRef]
- Strichartz, R.S. Self-similar measures and their Fourier transforms I. Indiana Univ. Math. J. 1990, 39, 797–817. [Google Scholar] [CrossRef]
- Strichartz, R.S. Self-similar measures and their Fourier transforms II. Trans. Am. Math. Soc. 1993, 336, 335–361. [Google Scholar] [CrossRef]
- Strichartz, R.S. Self-similar measures and their Fourier transforms III. Indiana Univ. Math. J. 1993, 42, 367–411. [Google Scholar] [CrossRef]
- Strichartz, R.S. Self-similarity in harmonic analysis. J. Fourier Anal. Appl. 1994, 1, 1–37. [Google Scholar] [CrossRef]
- Mattila, P. Geometry Sets and Measures in Euclidean Spaces: Fractals and Rectifiability; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Tolsa, X. Bilipschitz maps, analytic capacity, and the Cauchy integral. Ann. Math. 2005, 162, 1243–1304. [Google Scholar] [CrossRef]
- Tolsa, X. Growth estimates for Cauchy integrals of measures and rectifiability. Geom. Funct. Anal. 2007, 17, 605–643. [Google Scholar] [CrossRef]
- Lund, J.P.; Strichartz, R.S.; Vinson, J.P. Cauchy transforms of self-similar measures. Exp. Math. 1998, 7, 177–190. [Google Scholar] [CrossRef]
- Dong, X.H.; Lau, K.S. Cauchy transforms of self-similar measures: The Laurent coefficients. J. Funct. Anal. 2003, 202, 67–97. [Google Scholar] [CrossRef]
- Dong, X.H.; Lau, K.S. An integral related to the Cauchy transform on the Sierpinski gasket. Exp. Math. 2004, 13, 415–419. [Google Scholar] [CrossRef]
- Dong, X.H.; Lau, K.S.; Liu, J.C. Cantor boundary behavior of analytic functions. Adv. Math. 2013, 232, 543–570. [Google Scholar] [CrossRef]
- Dong, X.H.; Lau, K.S.; Wu, H.H. Cauchy transform of self-similar measures: Starlikeness and univalence. Trans. Am. Math. Soc. 2017, 369, 4817–4842. [Google Scholar] [CrossRef]
- Dong, X.H.; Lau, K.S. Cantor boundary behavior of analytic functions. In Recent Developments in Fractals and Related Fields; Birkhäuser Boston, Inc.: Boston, MA, USA, 2010; pp. 283–294. [Google Scholar] [CrossRef]
- Li, H.P.; Dong, X.H.; Zhang, P.F.; Wu, H.H. Estimates for Taylor coefficients of Cauchy transforms of some Hausdorff measures I. J. Funct. Anal. 2021, 280, 108653. [Google Scholar] [CrossRef]
- Li, H.G.; Dong, X.H.; Zhang, P.F. Estimates for Taylor coefficients of Cauchy transforms of some Hausdorff measures II. J. Funct. Anal. 2021, 280, 108654. [Google Scholar] [CrossRef]
- Folconer, K.J. Fractal Geometry-Mathematical Foundations and Applications; John Wiley & Sons: New York, NY, USA, 1990. [Google Scholar]
- Wang, S.R.; Wang, Z.M. Function space properties of the Cauchy transform on the Sierpinski gasket. AIMS Math. 2023, 8, 6064–6073. [Google Scholar] [CrossRef]
- Hutchinson, J. Fractals and self-similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E. Some properties of fractional integrals II. Math. Zeit. 1932, 34, 403–489. [Google Scholar] [CrossRef]
- MacGregor, T.H.; Sterner, M.P. Limits of fractional derivatives and compositions of analytic functions. J. Aust. Math. Soc. 2017, 103, 104–115. [Google Scholar] [CrossRef]
- TMacGregor, H.; Sterner, M.P. Boundary limits of fractional derivatives of univalent functions. Complex Var. Elliptic Equ. 2018, 63, 1529–1538. [Google Scholar] [CrossRef]
- MacGregor, T.H.; Sterner, M.P. Hadamard products with power functions and multipliers of Hardy spaces. J. Math. Anal. Appl. 2003, 282, 163–176. [Google Scholar] [CrossRef][Green Version]
- Duren, P. Theory of HP Spaces; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Duren, P.; Schuster, A. Bergman Spaces, Mathematical Surveys and Monographs; American Mathematical Society: Providence, RI, USA, 2004; Volume 100. [Google Scholar]
- Hedenmalm, H.; Korenblum, B.; Zhu, K.H. Theory of Bergman Spaces; Springer: New York, NY, USA, 2000. [Google Scholar]
- Peläez, J.A.; Rxaxttyxax, J.; Sierra, K. Embedding Bergman spaces into tent spaces. Math. Z. 2015, 281, 1215–1237. [Google Scholar] [CrossRef]
- Peläez, J.A.; Rxaxttyxax, J.; Sierra, K. Berezin transform and Toeplitz operators on Bergman spaces induced by regular weights. J. Geom. Anal. 2018, 28, 656–687. [Google Scholar] [CrossRef]
- He, B.; Jreis, J.; Lefévre, P.; Lou, Z.J. Absolutely summing Carleson embeddings on Bergman spaces. Adv. Math. 2024, 439, 109495. [Google Scholar] [CrossRef]
- Jreis, J.; Lefévre, P. Some operator ideal properties of Volterra operators on Bergman and Bloch spaces. Integral Equ. Oper. Theory 2024, 96, 1. [Google Scholar] [CrossRef]
- Tong, C.Z.; Li, J.F. Carleson measures on the weighted Bergman spaces with Békollé weights. Chin. Ann. Math. Ser. B 2021, 42, 583–600. [Google Scholar] [CrossRef]
- Macgregor, T.H. Analytic and univalent function with integral representations involving complex measures. Indiana Univ. Math. J. 1987, 86, 109–130. [Google Scholar] [CrossRef]
- Hibschweiler, R.A.; Macgregor, T.H. Closure properties of families of Cauchy-Stieltjes transforms. Proc. Am. Math. Soc. 1989, 105, 615–621. [Google Scholar] [CrossRef]
- Hibschweiler, R.A.; Macgregor, T.H. Multipliers of families of Cauchy- Stieltjes transforms. Trans. Am. Math. Soc. 1992, 331, 377–394. [Google Scholar] [CrossRef]
- Hallenbeck, D.J.; Macgregor, T.H. Fractional Cauchy transforms, inner functions and multipliers. Proc. Lond. Math. Soc. 1996, 72, 157–187. [Google Scholar] [CrossRef]
- Hallenbeck, D.J.; Samotij, K. On Cauchy integrals of logarithmic potentials and their multipliers. J. Math. Anal. Appl. 1993, 174, 614–634. [Google Scholar] [CrossRef][Green Version]
- Gautschi, W. Some elementary inequalities relating to the gamma and incomplete gamma function. J. Math. Phys. 1959, 38, 77–81. [Google Scholar] [CrossRef]
- Cherry, W.; Ye, Z. Nevanlinna’s Theory of Value Distribution; Springer Monographs in Mathematics; Springer: Berlin, Germany, 2001. [Google Scholar]
- Vojta, P. Diophantine Approximation and Nevanlinna Theory; Springer: Berlin, Germany, 2011; pp. 111–230. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).