Bergman Space Properties of Fractional Derivatives of the Cauchy Transform of a Certain Self-Similar Measure

Abstract

Let $\mu$ be a self-similar measure with compact support K. The Hausdorff dimension of K is $\alpha$. The Cauchy transform of $\mu$ is denoted by $F\left(z\right)$. For $0<\beta <1,$ we define the function $F^{\left[\beta \right]},$ which compares with the fractional derivative of F of order $\beta .$ Let $\Phi \left(z\right)=F(1/z),\left|z\right|<1$. In this paper, we prove that ${\Phi }^{\left[\beta \right]}$ belongs to $A^p$ for $0<p<1/(\beta +1)$, and ${\left({\Phi }^{\prime }\right)}^{\left[\beta \right]}$ belongs to $A^p$ for $1\le p<1/\beta \le 1/(2-\alpha )$, where $A^p$ is the Bergman space. At the same time, we give a value distribution property of F, which is similar to the big Picard theorem.

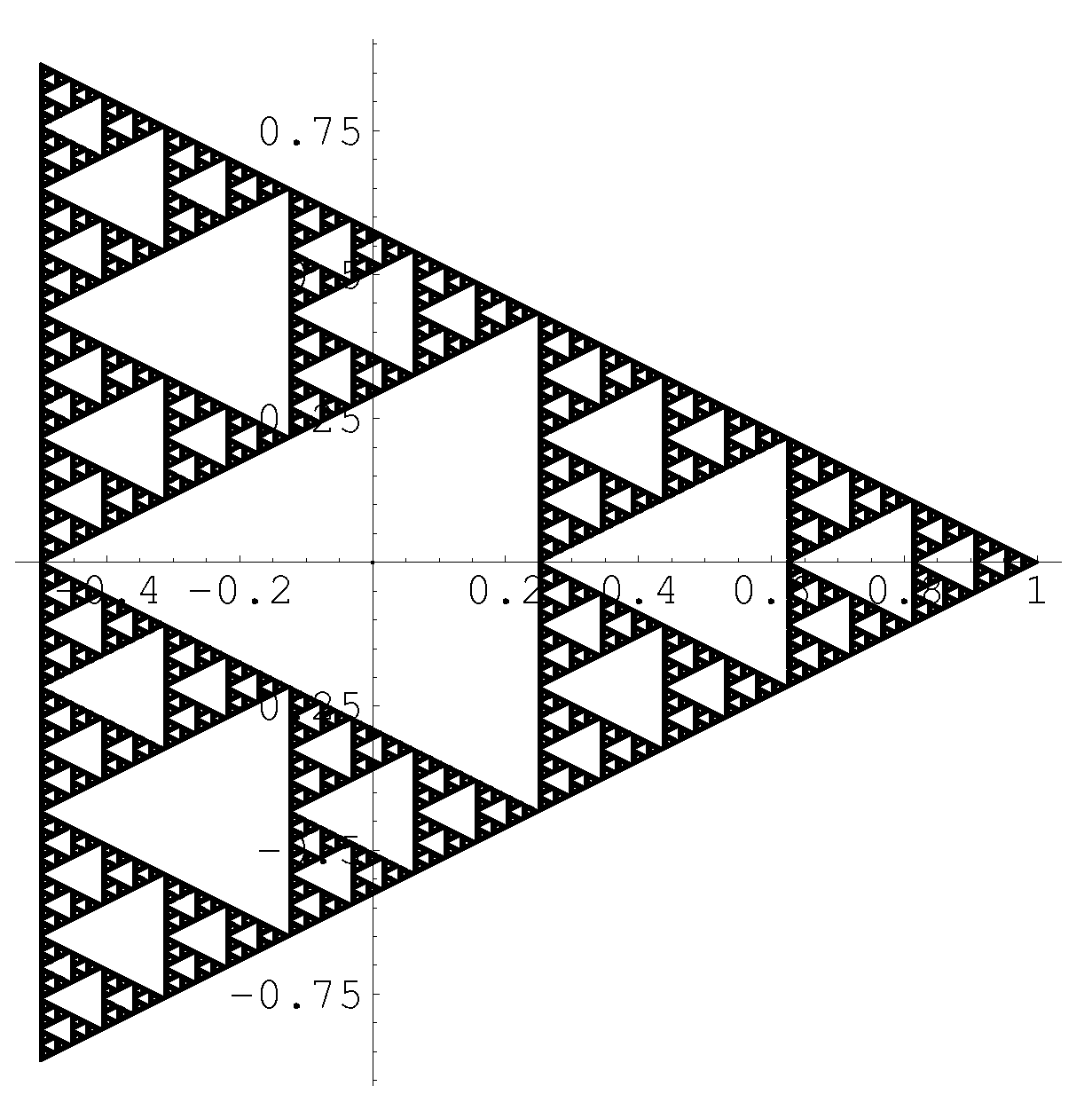
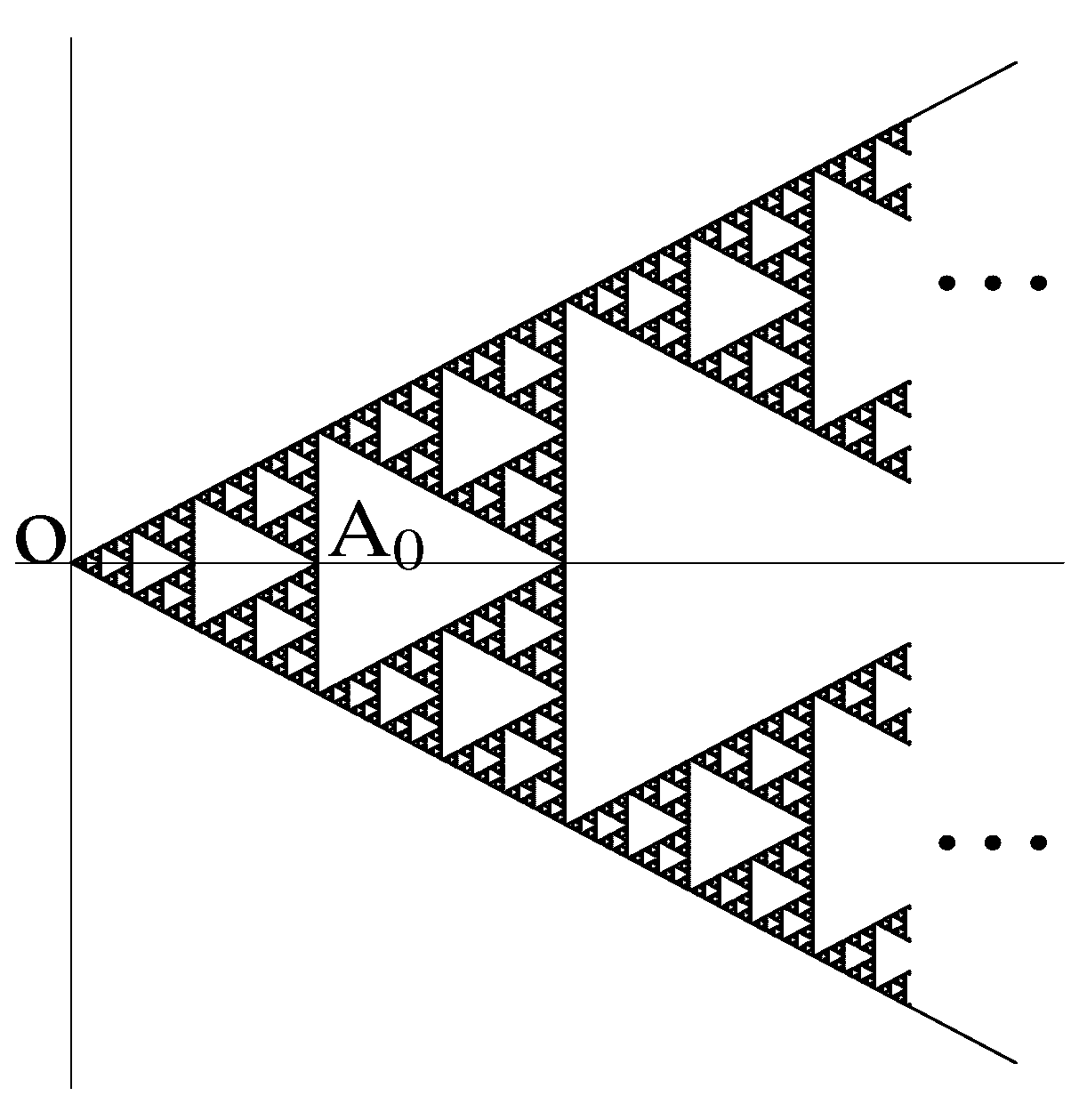
1. Introduction

The notion of fractals was proposed by Mandelbrot in the 1970s [1]. Soon, the importance of fractals was recognized in many areas of science. In mathematics, a new area called fractal geometry developed quickly on the basis of geometric measure theory, harmonic analysis, dynamical systems and so on. For the aspects of harmonic analysis, the Fourier transform of fractal measures has been investigated by Strichartz [2,3,4,5,6]. For the complex case, more consideration has been given to the Cauchy transform of self-similar measures. The Cauchy transform of a measure in the complex plane $\mathbb{C}$ plays an important role in geometric measure theory [7,8,9,10]. The study of this transform can be traced back to that of the Cauchy-type integral, which is fundamental in the study of boundary-value problems for analytic functions. Let $\mu$ be a self-similar measure with compact support $K.$ The Cauchy transform of $\mu$ is defined by $F\left(z\right)={\int }_K{(z-\omega )}^{-1}d\mu \left(\omega \right).$ In [10], Stricharz et al. studied the Cauchy transform of a self-similar measure $\mu$ with compact support K. From numerical data and computer graphics, they considered the Hölder continuity and analyticity of $F\left(z\right)$ intuitively. In [11,12,13,14,15], Dong and Lau intensively studied the geometric and analytic properties of F. The precise growth rates of the Laurent coefficients of such F were obtained, and the asymptotic behavior of the coefficients was also discussed in [11]. The geometric properties of F away from K, such as univalence, starlikeness and convexity, were investigated in [14]. Since F is analytic at zero, F has a Taylor expression near zero. The asymptotic behavior of the Taylor coefficients of F was studied in [16,17].

An iterated function system (IFS) consists of a family of contraction mappings, which can represent many fractals that are made up of small images of themselves. For an IFS ${\left\{S_j\right\}}_{j=1}^m$ on $X\subset {\mathbb{R}}^n$, in [18], it is proven that there exists a unique non-empty compact set K that satisfies $K={\cup }_{j=1}^m{S}_j\left(K\right)$. K is called the attractor of the IFS. In this paper, we focus on the following IFS:

$$\begin{array}{c}\hfill S_j\left(z\right)={\epsilon }_j+\frac{1}{2}(z-{\epsilon }_j),\end{array}$$

(1)

where ${\epsilon }_j=e^{2j\pi i/3},j=0,1,2.$ The attractor of the IFS in (1) is denoted by K, i.e., the unique compact set satisfying $K={\cup }_{j=0}^2{S}_j\left(K\right)$. Then, $K\subset \{z:|z|\le 1\}$, and K is the Sierpinski gasket (Figure 1). The Cauchy transform $F\left(z\right)$ of the self-similar measure associated with the IFS was studied by Stricharz et al. in [10]. They proposed several conjectures of F, and these conjectures were partly resolved in [12,13,15]. The Hardy space properties of F were investigated in [19]. In this paper, we consider the Bergman space and multiplier properties of $F^{\left[\beta \right]},$ which compares with the fractional derivative of F of order $\beta ,$ and prove a value distribution property of $F.$

2. Preliminaries

In this section, some necessary notations and results are given first. The IFS in (1) satisfies the open-set condition: there exists an open set U such that ${\cup }_{j=1}^N{S}_j\left(U\right)\subset U$, and $S_i\left(U\right)\cap S_j\left(U\right)=⌀$ if $i\ne j.$ The Hausdorff dimension of the attractor K of this IFS is $\alpha =\log 3/\log 2$. Hutchinson [20] has proven that there exists a unique probability measure $\mu$ with compact support K such that

$$\begin{array}{c}\hfill \mu =\frac{1}{3}\sum _{j=0}^2\mu \circ S_j^{-1},\end{array}$$

(2)

and $\mu$ is the restriction of the normalized $\alpha$-dimensional Hausdorff measure on K. Theorem 2.1 in [10] proves that the measure $\mu$ is $\alpha$-uniform, i.e., $\mu \left(E\right)\le C\mathrm{diam}{\left(E\right)}^{\alpha }$ for $E\subset \mathbb{C},$ where C is an absolute positive constant. Notice that $\mu$ is a Hausdorff measure. Therefore, it behaves nicely under translations and dilations: for $E\subset \mathbb{C},$ $z_0\in \mathbb{C},$ $0<t<\infty ,$ there exist $\mu (E+z_0)=\mu \left(E\right)$ and $\mu \left(tE\right)=t^{\alpha }\mu \left(E\right)$[18]. The Cauchy transform of $\mu$ is

$$\begin{array}{c}\hfill F\left(z\right)={\int }_K\frac{d\mu \left(w\right)}{z-\omega }.\end{array}$$

(3)

Let $T_j=e^{\pi i}(S_{j}K-1),j=0,1,2.$ And let

$$A_0=\bigcup _{n\in \mathbb{Z}}{2}^n(T_1\cup T_2).$$

This is called the “Sierpinski cones” (Figure 2). For $\ell =1,\cdots ,5$, let $A_{\ell }=e^{\ell \pi i/3}{A}_0$. We define auxiliary functions $G_{\ell }\left(z\right)$ by

$$G_{\ell }\left(z\right)=z^{2-\alpha }{\int }_{A_{\ell }}\frac{d\mu \left(\omega \right)}{\omega (z-\omega )},$$

where $z^{\alpha }$ is the principal branch. It is easily seen that $G_{\ell }\left(2z\right)=G_{\ell }\left(z\right)$ by the basic property of the Hausdorff measure.

In [11], it is proven that F is analytic in $\mathbb{C}\setminus K$, with $F(\infty )=0$, and three-fold symmetric, with $F\left(e^{2\pi i/3}z\right)=e^{-2\pi i/3}F\left(z\right)$, and

$$F\left(\frac{1}{z}\right)=z+\sum _{n=1}^{\infty }{a}_{3n+1}{z}^{3n+1},z<1,$$

where $a_{3n+1}={\int }_K{\omega }^{3n}d\mu \left(\omega \right).$ A function f analytic in $\mathbb{D}$ has the Taylor series expansion $f\left(z\right)={\sum }_{n=0}^{\infty }{a}_n{z}^n.$ The concept of the fractional derivative of f can be described in different ways. For $0<\beta <1$, Hadamard defined the fractional derivative of f of order $\beta$ by

$$f^{\left(\beta \right)}\left(z\right)=z^{-\beta }\sum _{n=0}^{\infty }\frac{\Gamma (n+1)}{\Gamma (n+1-\beta )}{a}_n{z}^n,\left|z\right|<1,$$

where $\Gamma$ denotes the gamma function. Hardy and Littlewood [21] described some properties of $f^{\left(\beta \right)}\left(z\right)$. MacGregor et al. [22] defined the function $f^{\left[\beta \right]}\left(z\right)$ by

$$f^{\left[\beta \right]}\left(z\right)=\sum _{n=0}^{\infty }\frac{\Gamma (n+1+\beta )}{\Gamma (n+1)}{a}_n{z}^n, \left|z\right|<1.$$

As shown in [22], it is known that the sequences

$$\frac{\Gamma (n+1+\beta )}{\Gamma (n+1)} \mathrm{a}\mathrm{n}\mathrm{d} \frac{\Gamma (n+1)}{\Gamma (n+1-\beta )}$$

have asymptotic expansions $n^{\beta }{\sum }_{k=0}^{\infty }{c}_k/n^k$, with $c_0\ne 0$. Therefore, certain properties of $f^{\left[\beta \right]}$ are equivalent to those of $f^{\left(\beta \right)}$.

Let $g\left(z\right)={\sum }_{n=0}^{\infty }{b}_n{z}^n$ be an analytic function in $\mathbb{D}$. It is well known that the Hadamard product of f and g is defined by $(f\ast g)\left(z\right)={\sum }_{n=0}^{\infty }{a}_n{b}_n{z}^n$. Noting that

$$\frac{1}{{(1-z)}^{\beta }}=\sum _{n=0}^{\infty }\frac{\Gamma (n+\beta )}{\Gamma (n+1)\Gamma \left(\beta \right)}{z}^n, \left|z\right|<1,$$

one can find that $f^{\left[\beta \right]}$ is the Hadamard product of f with the function

$$\phi \left(z\right)=\frac{\Gamma (\beta +1)}{{(1-z)}^{\beta +1}},z\in \mathbb{D}.$$

MacGregor et al. considered the boundary limits of $f^{\left[\beta \right]}$ and the limits of $f^{\left[\beta \right]}$ of compositions. See [22,23,24].

3. Fractional Derivatives of $\mathit{F}\mathbf{\left(}\mathit{z}\mathbf{\right)}$

Let $\Phi \left(z\right)=F\left(\frac{1}{z}\right)$. Thus, $\Phi \left(z\right)$ is analytic in $\mathbb{D}$. In this section, we will study the Bergman space property of ${\Phi }^{\left[\beta \right]}\left(z\right)$. For a function f analytic in the unit disk $\mathbb{D}$, the integral means are defined by

$$M_p(r,f)={\left(\frac{1}{2\pi }{\int }_0^{2\pi }f{\left(r{e}^{i\theta }\right)}^{p}d\theta \right)}^{1/p},0<p<\infty .$$

It is well known that the Hardy space [25] $H^p$ consists of analytic functions f in $\mathbb{D}$ such that

$${\parallel f\parallel }_{H^p}={\left(\frac{1}{2\pi }{\int }_0^{2\pi }f{\left(e^{i\theta }\right)}^{p}d\theta \right)}^{1/p}=\underset{0\le r<1}{sup}{M}_p(r,f)<\infty ,0<p<\infty .$$

$H^{\infty }$ is the class of bounded analytic functions in $\mathbb{D}$. For the theory of Hardy spaces, see [24]. The Bergman space [26] $A^p$ consists of all functions f analytic in $\mathbb{D}$ for which the normalized area integral ${\int }_{\mathbb{D}}{\left|f\left(z\right)\right|}^{p}dA\left(z\right)$ is finite, where $dA\left(z\right)=\frac{1}{\pi }dxdy$. The norm of a function $f\in A^p$ is defined by

$${\parallel f\parallel }_{A^p}={\left\{{\int }_{\mathbb{D}}{\left|f\left(z\right)\right|}^{p}dA\left(z\right)\right\}}^{1/p},0<p<\infty .$$

$H^p$ and $A^p$ have many similar properties, and they have the inclusion $H^p\subset A^{2p}$ for $0<p<\infty .$ In some respects, functions in the Bergman space behave better. See [26,27]. For recent developments in Bergman spaces, the reader can consult [28,29,30,31,32] and references therein.

Theorem 1.

For $0<p<1/(\beta +1),{\Phi }^{\left[\beta \right]}\in A^p.$

Proof. 

Firstly, we will show that the Hadamard product of f and g has another integral form,

$$\begin{array}{c}\hfill (f\ast g)\left(r{e}^{i\theta }\right)=\frac{1}{2\pi }{\int }_0^{2\pi }f\left(\sqrt{r}{e}^{it}\right)g\left(\sqrt{r}{e}^{i(\theta -t)}\right)dt,\end{array}$$

(4)

where f and g are analytic in $\mathbb{D}$. In fact,

$$\begin{array}{ccc}& & \frac{1}{2\pi }{\int }_0^{2\pi }f\left(\sqrt{r}{e}^{it}\right)g\left(\sqrt{r}{e}^{i(\theta -t)}\right)dt\hfill \\ & =& \frac{1}{2\pi }{\int }_0^{2\pi }\left(\sum _{n=0}^{\infty }{a}_n{r}^{n/2}{e}^{int}\right)\left(\sum _{n=0}^{\infty }{b}_n{r}^{n/2}{e}^{in(\theta -t)}\right)dt\hfill \\ & =& \sum _{n=0}^{\infty }\frac{1}{2\pi }{\int }_0^{2\pi }\left(\sum _{k=0}^n{a}_k{b}_{n-k}{r}^{n/2}{e}^{i(n-k)\theta }{e}^{i(2k-n)t}\right)dt\hfill \\ & =& \sum _{n=0}^{\infty }{a}_n{b}_n{z}^n.\hfill \end{array}$$

In terms of integral means, ${\Phi }^{\left[\beta \right]}\in A^p$ is equivalent to ${\int }_0^1{\left\{M_p(r,{\Phi }^{\left[\beta \right]})\right\}}^{p}rdr<\infty .$ Indeed,

$$\pi \parallel {\Phi }^{\left[\beta \right]}{\parallel }_{A^p}^p={\int }_0^{2\pi }{\int }_0^1{\left|{\Phi }^{\left[\beta \right]}\left(r{e}^{i\theta }\right)\right|}^{p}rdrd\theta =2\pi {\int }_0^1{\left\{M_p(r,{\Phi }^{\left[\beta \right]})\right\}}^{p}rdr.$$

Next, we will prove that the integral ${\int }_0^1{\left\{M_p(r,F^{\left[\beta \right]})\right\}}^{p}rdr$ is finite. From Theorem 2.1 in [10], we see that $F\left(z\right)$ is bounded on $\mathbb{C}.$ Using (4), for $r<1$, we obtain

$$\begin{array}{ccc}\hfill |{\Phi }^{\left[\beta \right]}\left(r{e}^{i\theta }\right)|& =& \left|\frac{1}{2\pi }{\int }_0^{2\pi }\frac{\Phi \left(\sqrt{r}{e}^{it}\right)}{\Gamma (\beta +1){(1-\sqrt{r}{e}^{i(\theta -t)})}^{\beta +1}}dt\right|\hfill \\ & \le & C{\int }_0^{2\pi }\frac{dt}{|e^{it}-\sqrt{r}{e}^{i\theta }{|}^{\beta +1}}\hfill \\ & =& C{\int }_0^{2\pi }\frac{dt}{{(1+r-2\sqrt{r}\cos (t-\theta ))}^{(\beta +1)/2}}\hfill \\ & \le & \frac{C^{\prime }}{{(1-\sqrt{r})}^{\beta +1}},\hfill \end{array}$$

where C and $C^{\prime }$ are positive constants. Hence,

$${\int }_0^1{\left\{M_p(r,{\Phi }^{\left[\beta \right]})\right\}}^{p}rdr=\frac{1}{2\pi }{\int }_0^1\left({\int }_0^{2\pi }{\Phi }^{\left[\beta \right]}{\left(r{e}^{i\theta }\right)}^{p}d\theta \right)rdr\le C_p{\int }_0^1\frac{r^{3}dr}{{(1-r)}^{p(\beta +1)}}.$$

The last integral is convergent for $0<p<1/(\beta +1)$. The result follows.  □

Theorem 2.

For $1\le p<1/\beta \le 1/(2-\alpha )$, ${\left({\Phi }^{\prime }\right)}^{\left[\beta \right]}\left(z\right)\in A^p$.

Proof. 

By (4) and the Hölder inequality, one can have

$$M_p(r,f\ast g)=M_p(\sqrt{r},f)M_1(\sqrt{r},g),p\ge 1.$$

It follows that

$$\begin{array}{ccc}& & {\int }_0^1{\left\{M_p(r,{\left({\Phi }^{\prime }\right)}^{\left[\beta \right]})\right\}}^{p}rdr\hfill \\ & =& {\int }_0^1{\left\{M_p(r,{\Phi }^{\prime }\ast \phi )\right\}}^{p}rdr\hfill \\ & \le & {\int }_0^1{\left\{M_p(\sqrt{r},{\Phi }^{\prime })\right\}}^p{\left\{M_1(\sqrt{r},\phi )\right\}}^{p}rdr.\hfill \end{array}$$

(5)

Next, we will consider $M_p(\sqrt{r},{\Phi }^{\prime }).$ We denote positive constants by $C,C_1,C_2,\cdots$. For fixed $z\in \mathbb{C}\setminus K$, let $d=\mathrm{dist}(z,K)$ and $E_n=\{w\in K:2^{n}d\le \mid w-z\mid <2^{n+1}d\},n\ge 0.$ Since $\mu$ is $\alpha$-uniform, there exists a positive constant $C_1$ such that $\mu \left(E_n\right)\le C_1{\left(2^{n+2}d\right)}^{\alpha }.$ Thus,

$$\begin{array}{ccc}\hfill |F^{\prime }\left(z\right)|& \le & \sum _{n=0}^{\infty }{\int }_{E_n}\frac{d\mu \left(w\right)}{{|z-w|}^2}\le \sum _{n=0}^{\infty }\frac{{\int }_{E_n}d\mu \left(w\right)}{2^{2n}{d}^2}\hfill \\ & \le & \sum _{n=0}^{\infty }\frac{C_1{\left(2^{n+2}d\right)}^{\alpha }}{2^{2n}{d}^2}\le 4^{\alpha }{C}_1{d}^{\alpha -2}\sum _{n=0}^{\infty }{2}^{(\alpha -2)n}\hfill \\ & =& C_2{d}^{\alpha -2}.\hfill \end{array}$$

(6)

Notice that $\Phi \left(z\right)$ is analytic in $\mathbb{C}\setminus K$, and ${\Phi }^{\prime }\left(e^{i\theta }\right)$ is well defined for $\theta \notin {\left\{{\epsilon }_j\right\}}_{j=0}^2.$ The symmetry of $\mu$ and K with respect to the real axis gives

$$\begin{array}{c}\hfill {\int }_{-\pi }^{\pi }{{\Phi }^{\prime }\left(e^{i\theta }\right)}^{p}d\theta =3{\int }_{-\pi /3}^{\pi /3}{{\Phi }^{\prime }\left(e^{i\theta }\right)}^{p}d\theta =6{\int }_{-\pi /3}^0{{\Phi }^{\prime }\left(e^{i\theta }\right)}^{p}d\theta .\end{array}$$

Using (6), for $-\pi /3<\theta <0,$ geometric considerations show that

$$|{\Phi }^{\prime }\left(e^{i\theta }\right)|\le C_2\mathrm{dist}{(e^{-i\theta },K)}^{\alpha -2}\le C_3{|\theta |}^{\alpha -2}.$$

Hence, for $0<p<1/(2-\alpha )$, we obtain

$$\begin{array}{c}\hfill {\int }_{-\pi }^{\pi }{|{\Phi }^{\prime }\left(e^{i\theta }\right)|}^{p}d\theta \le C_4{\int }_0^{\pi /3}{\theta }^{p(\alpha -2)}d\theta <+\infty .\end{array}$$

It follows that

$$\begin{array}{c}\hfill \parallel {\Phi }^{\prime }{\parallel }_{H^p}=\underset{0\le r<1}{sup}{M}_p(r,{\Phi }^{\prime })<\infty ,0<p<1/(2-\alpha ).\end{array}$$

(7)

With (5) and (7), we obtain

$$\begin{array}{ccc}& & {\int }_0^1{\left\{M_p(r,{\left({\Phi }^{\prime }\right)}^{\left[\beta \right]})\right\}}^{p}rdr\hfill \\ & \le & \parallel {\Phi }^{\prime }{\parallel }_{H^p}{\int }_0^1{M}_1^p(r,\phi )rdr\hfill \\ & =& \parallel {\Phi }^{\prime }{\parallel }_{H^p}{\int }_0^1{\left\{\frac{1}{2\pi }{\int }_0^{2\pi }\frac{d\theta }{\Gamma (\beta +1)|1-\sqrt{r}{e}^{i\theta }{|}^{\beta +1}}\right\}}^{p}rdr\hfill \end{array}$$

(8)

for $1\le p<1/(2-\alpha ).$ Since

$${\int }_0^{2\pi }{|1-\sqrt{r}{e}^{i\theta }|}^{-(\beta +1)}d\theta =O\left({(1-\sqrt{r})}^{-\beta }\right),r⟶1,$$

by (8), we have

$${\int }_0^1{\left\{M_p(r,{\left({\Phi }^{\prime }\right)}^{\left[\beta \right]})\right\}}^{p}rdr\le C{\int }_0^1\frac{rdr}{{(1-\sqrt{r})}^{p\beta }}.$$

From the above inequality, it is easy to see that ${\left({\Phi }^{\prime }\right)}^{\left[\beta \right]}\left(z\right)\in A^p$ for $1\le p<1/\beta \le 1/(2-\alpha ).$ The proof is complete.  □

Below, let us end this section with a multiplier property of ${\Phi }^{\left[\beta \right]}\left(z\right)$. We denote the set of complex-valued Borel measures on $\mathbb{T}=\{z:|z|=1\}$ by $\Lambda .$ For each $\lambda >0,$ let ${\mathfrak{F}}_{\lambda }$ denote the family of functions h having the property that there exists a measure $\mu \in \Lambda$ such that

$$\begin{array}{c}\hfill h\left(z\right)={\int }_{\mathbb{T}}\frac{d\mu \left(\zeta \right)}{{(1-\zeta z)}^{\lambda }},|z|<1,\end{array}$$

(9)

where the logarithm takes the principal branch. For $h\in {\mathfrak{F}}_{\lambda },$ let

$${\parallel h\parallel }_{{\mathfrak{F}}_{\lambda }}=inf\{\parallel \mu \parallel :\mu \in \Lambda \mathrm{such} \mathrm{that} \left(9\right) \mathrm{holds}\},$$

where $\parallel \mu \parallel$ denotes the total variation in the measure $\mu$. With this norm, ${\mathfrak{F}}_{\lambda }$ is a Banach space. Macgregor introduced the spaces ${\mathfrak{F}}_{\lambda }$ in [33,34]. Several properties of functions in ${\mathfrak{F}}_{\lambda }$ were derived in [35,36]. A multiplier of ${\mathfrak{F}}_{\lambda }$ is an analytic function $\upsilon \left(z\right)$ in $\mathbb{D}$ such that $\upsilon \left(z\right)h\left(z\right)\in {\mathfrak{F}}_{\lambda }$ for all $h\in {\mathfrak{F}}_{\lambda }$. The family of all such multipliers is denoted by ${\mathcal{M}}_{\lambda }$. For $\upsilon \in {\mathcal{M}}_{\lambda }$, let

$${\parallel \upsilon \parallel }_{{\mathcal{M}}_{\lambda }}={sup\{\parallel \upsilon h\parallel }_{{\mathfrak{F}}_{\lambda }}:h\in {\mathfrak{F}}_{\lambda }{,\parallel h\parallel }_{{\mathfrak{F}}_{\lambda }}\le 1\}.$$

With this norm, ${\mathcal{M}}_{\lambda }$ is a Banach space. The family ${\mathcal{M}}_{\lambda }$ has been studied in [35,36,37], including the following theorem.

Theorem 3

([36]). Let $f\left(z\right)={\sum }_{n=0}^{\infty }{a}_n{z}^n$ for $\left|z\right|<1.$ If ${\sum }_{n=0}^{\infty }{n}^{1-\lambda }\left|a_n\right|<\infty$ for $0<\lambda <1,$ then $f\in {\mathcal{M}}_{\lambda }$.

Theorem 4.

For $0<\lambda <1$, if $\beta +\lambda >2-\alpha ,$ then ${\Phi }^{\left[\beta \right]}\in {\mathcal{M}}_{\lambda }.$

Proof. 

Note that $\Phi \left(z\right)=z+{\sum }_{n=1}^{\infty }{a}_{3n+1}{z}^{3n+1}$ and

$${\Phi }^{\left[\beta \right]}\left(z\right)=\sum _{n=0}^{\infty }\frac{\Gamma (n+1+\beta )}{\Gamma (n+1)}{a}_n{z}^n.$$

From [38] (p. 79), the inequality

$${\displaystyle \frac{1}{{(n+1)}^{1-s}}\le \frac{\Gamma (n+1+\beta )}{\Gamma (n+1)}\le \frac{1}{n^{1-s}},0\le s\le 1,}$$

holds. And according to [11] (Theorem 1.2), for $n\ge 1$, there exists a positive constant C such that $n^{\alpha }\left|a_n\right|\le C.$ Then,

$$n^{1-\lambda }\left|\frac{\Gamma (n+1+\beta )}{\Gamma (n+1)}{a}_n\right|\le \frac{C{(n+1)}^{\beta }{n}^{1-\lambda }}{n^{\alpha }}=\frac{C{(n+1)}^{\beta }}{n^{\alpha +\lambda -1}}.$$

The series ${\sum }_{n=1}^{\infty }{(n+1)}^{\beta }/n^{\alpha +\lambda -1}$ is convergent for $\beta +\lambda >2-\alpha .$ The result follows from Theorem 3.  □

4. A Value Distribution Property

The big Picard theorem shows that if $z_0\in \mathbb{C}$ is an isolated essential singularity of an analytic function f, then for any neighborhood of $z_0$, f assumes every complex number infinitely many times, with, at most, one exception. The Picard theorem can be easily derived from Nevanlinna’s second main theorem, which is an important result in value distribution theory. For more about value distribution theory and its application, see [39,40]. For $k\in {\mathbb{N}}^{+}$ and $1\le m\le 2^k-1,$ let

$$z_{k,m}=\frac{m}{2^k}{\epsilon }_1+(1-\frac{m}{2^k}){\epsilon }_2=-\frac{1}{2}+\frac{m-2^{k-1}}{2^k}\sqrt{3}i.$$

In this section, we will prove a similar result for F around the non-analytic points $z_{k,m}$. For $0<\theta \le \pi /2,$ let $\Omega \left(\theta \right)=\{z:|\arg z-\pi |<\theta \}.$ We need the following lemma.

Lemma 1

([15]). For any $z_{k,m},$ there exists a function $G=G_1+G_5$ such that

$$F(z+z_{k,m})=F\left(z_{k,m}\right)+G\left(z\right)z^{\alpha -1}+z{P}_{k,m}\left(z\right),0<\arg z<2\pi ,$$

where G is continuous on $\mathbb{C}\setminus \left\{0\right\}$ and analytic in $\Omega (\pi /2),$ and for $0\le \arg z<2\pi ,G\left(2z\right)=G\left(z\right)$; $P_{k,m}$ is bounded continuous on $\mathbb{C}$ and analytic in $\Omega (\pi /2)\cup \{z:|z|<3/2^{k+1}\}.$

For $0<ϵ<1/6$ and $\delta >0,$ we write

$$A_{\delta }\left(ϵ\right)=\{z:|\arg z|<(\frac{1}{6}-ϵ)\pi ,0<\left|z\right|<\delta \}$$

and

$$A_{\delta }^{\ast }\left(ϵ\right)=\{z:|\arg z|\le (\frac{1}{6}-ϵ)\pi ,0<\left|z\right|<\delta \}.$$

We define the function

$$F_{z_{k,m}}\left(z\right):=\frac{F(z+z_{k,m})-F\left(z_{k,m}\right)}{z^{\alpha -1}},$$

where $z^{\alpha }$ is the principal branch.

Theorem 5.

For each $\omega \in G\left(A_{\infty }\left(ϵ\right)\right)$ and any $\delta >0,$ there exist infinitely many $z\in A_{\delta }\left(ϵ\right)$ such that $F_{z_{k,m}}\left(z\right)=\omega .$ Moreover,

$$\begin{array}{c}\hfill G\left(A_{\infty }^{\ast }\left(ϵ\right)\right)=\bigcap _{\delta >0}\overline{F_{z_{k,m}}\left(A_{\delta }\left(ϵ\right)\right).}\end{array}$$

(10)

Proof. 

To begin with, we prove that for each ${\omega }_0\in G\left(A_{\infty }\left(ϵ\right)\right),$ the function $F_{z_{k,m}}\left(z\right)-{\omega }_0$ has at least one zero inside $A_{\delta }\left(ϵ\right)$ for any $\delta >0.$

Let $z_0\in A_{\infty }\left(ϵ\right)$ satisfy $G\left(z_0\right)={\omega }_0.$ By the uniqueness theorem, for some $\rho >0$, there exists a disk $D_{\rho }\left(z_0\right)=\{z:|z-z_0|\le \rho \}\subset A_{\delta }\left(ϵ\right)$ such that

$$\begin{array}{c}\hfill \underset{z\in \partial D_{\rho }\left(z_0\right)}{min}|G\left(z\right)-{\omega }_0|=\tau >0.\end{array}$$

(11)

For all $z\in D_{\rho }\left(z_0\right),$ we choose a positive constant R satisfying $\left|z\right|<R.$ By Lemma 1, there exists ${\delta }_1\in (0,\delta )$ such that

$$\begin{array}{c}\hfill |F_{z_{k,m}}\left(z\right)-G\left(z\right)| = |z^{2-\alpha }{P}_{k,m}\left(z\right)|<\frac{\tau }{2},\forall z\in A_{{\delta }_1}\left(ϵ\right).\end{array}$$

(12)

For ${\delta }_1>0,$ there exists a positive integer N such that $2^{-N}R<{\delta }_1.$ Let

$$D_N≔2^{-N}{D}_{\rho }\left(z_0\right)\subset A_{\delta }\left(ϵ\right).$$

Then,

$$\underset{z\in \partial D_{\rho }\left(z_0\right)}{min}|G\left(z\right)-{\omega }_0|=\underset{z\in \partial D_1}{min}|G\left(2^{N}z\right)-{\omega }_0|.$$

Due to $G\left(2z\right)=G\left(z\right)$ for $0\le \arg z<2\pi ,$ from (11) and (12), we conclude that

$$|(F_{z_{k,m}}\left(z\right)-{\omega }_0)-(G\left(z\right)-{\omega }_0)|<\frac{\tau }{2}<|G\left(2^{N}z\right)-{\omega }_0|=|G\left(z\right)-{\omega }_0|,z\in D_N.$$

By Rouche’s theorem, the functions $F_{z_{k,m}}\left(z\right)-{\omega }_0$ and $G\left(z\right)-{\omega }_0$ have the same number of zeros inside $D_N$. Noting that $G\left(2^{-N}{z}_0\right)-{\omega }_0=G\left(z_0\right)-{\omega }_0=0$ and $2^{-N}{z}_0\in D_N$, we find that $F_{z_{k,m}}\left(z\right)-{\omega }_0$ has at least one zero inside $D_N\subset A_{\delta }\left(ϵ\right)$. Since $\delta$ is arbitrary, this implies that the function $F_{z_{k,m}}\left(z\right)-{\omega }_0$ must have an infinite number of zeros inside $A_{\delta }\left(ϵ\right)$.

The above shows that $G\left(A_{\infty }\left(ϵ\right)\right)\subseteq F_{z_{k,m}}\left(A_{\delta }\left(ϵ\right)\right)$ for any $\delta >0$ and $0<ϵ<1/6.$ The continuity of $G\left(z\right)$ implies that $G\left(A_{\infty }^{\ast }\left(ϵ\right)\right)\subseteq \overline{F_{z_{k,m}}\left(A_{\delta }\left(ϵ\right)\right)}$. Then, one side of the set inclusion in (10) follows. Next, we will prove the reverse inclusion. The multiplicative periodicity of $G\left(z\right)$ yields the following:

$$G\left(A_{\infty }^{\ast }\left(ϵ\right)\right)=G\left(\right\{z:\left|\arg z\right|\le (\frac{1}{6}-ϵ)\pi ,1\le \left|z\right|\le 2\left\}\right).$$

Then, $G\left(A_{\infty }^{\ast }\left(ϵ\right)\right)$ is a compact set by continuity. From Lemma 1, for $\left|\arg z\right|<\pi ,$ there exists an absolute constant $C>0$ such that

$$\begin{array}{c}\hfill |F_{z_{k,m}}{\left(z\right)-G\left(z\right)|\le C|z|}^{2-\alpha }.\end{array}$$

(13)

For arbitrary $\sigma >0,$ we choose $\delta >0$ satisfying $C{\delta }^{2-\alpha }<\sigma .$ If $z\in A_{\delta }\left(ϵ\right),$ then $F_{z_{k,m}}\left(z\right)\in G{\left(A_{\infty }^{\ast }\left(ϵ\right)\right)}_{\sigma }$ by (13), where $G{\left(A_{\infty }^{\ast }\left(ϵ\right)\right)}_{\sigma }$ is the $\sigma$—parallel body of $G\left(A_{\infty }^{\ast }\left(ϵ\right)\right).$ It follows that

$$\begin{array}{c}\hfill F_{z_{k,m}}\left(A_{\delta }\left(ϵ\right)\right)\subseteq G{\left(A_{\infty }^{\ast }\left(ϵ\right)\right)}_{\sigma }\mathrm{for}\mathrm{all}0<\delta <{\left(\sigma C^{-1}\right)}^{\frac{1}{2-\alpha }}.\end{array}$$

(14)

Since $G{\left(A_{\infty }^{\ast }\left(ϵ\right)\right)}_{\sigma }$ is a compact set, using (14), we find that

$$\bigcap _{\delta >0}\overline{F_{z_{k,m}}\left(A_{\delta }\left(ϵ\right)\right)}\subseteq G{\left(A_{\infty }^{\ast }\left(ϵ\right)\right)}_{\sigma },\sigma >0.$$

It is easy to see that

$$\bigcap _{\delta >0}\overline{F_{z_{k,m}}\left(A_{\delta }\left(ϵ\right)\right)}\subseteq \bigcap _{\sigma >0}G{\left(A_{\infty }^{\ast }\left(ϵ\right)\right)}_{\sigma }=G\left(A_{\infty }^{\ast }\left(ϵ\right)\right).$$

The proof is complete.  □

Remark 1.

If we let

$$A_{\delta }\left(ϵ\right)=\{z:(\frac{1}{2}+ϵ)\pi <\arg z<(\frac{3}{2}-ϵ)\pi ,0<\left|z\right|<\delta \}$$

and

$$A_{\delta }^{\ast }\left(ϵ\right)=\{z:(\frac{1}{2}+ϵ)\pi \le \arg z\le (\frac{3}{2}-ϵ)\pi ,0<\left|z\right|<\delta \},$$

the analogous argument to the above yields the same results for the dyadic points $z_{k,m}.$

5. Conclusions

In this article, we focus on the Cauchy transform of the self-similar measure on the Sierpinski gasket. We prove that ${\Phi }^{\left[\beta \right]}$ and ${\left({\Phi }^{\prime }\right)}^{\left[\beta \right]}$ belong to some Bergman space, where ${\Phi }^{\left[\beta \right]}$ compares with the fractional derivative of the function $\Phi$ of order $\beta$. In addition, we give a value distribution property of F. One can further investigate other analytic properties, such as coefficient estimates, univalence, etc. This topic intersects fractal geometry and geometric function theory. Different from the Cauchy transform of a common measure, the Cauchy transform of a self-similar measure has much more fractal behavior. As is shown in [10] through computer graphics, the image of such a transform is chaotic but regular near the Sierpinski gasket. This is different from the properties in classical analytic function theory and make it possible to construct some unexpected counter examples during one’s research.