New Simplified High-Order Schemes for Solving SDEs with Markovian Switching Driven by Pure Jumps

Abstract

New high-order weak schemes are proposed and simplified to solve stochastic differential equations with Markovian switching driven by pure jumps (PJ-SDEwMs). Using Malliavin calculus theory, it is rigorously proven that the new numerical schemes can achieve a high-order convergence rate. Some numerical experiments are provided to show the efficiency and accuracy.

1. Introduction

Let $\left(\mathsf{\Omega },ℱ,{\left\{{ℱ}_t\right\}}_{t\ge 0},P\right)$ be a complete probability space with a filtration ${\left\{{ℱ}_t\right\}}_{t\ge 0}$ generated by a Poisson process. In this paper, we mainly study the second-order weak schemes of the following Equations (PJ-SDEwMs) on the probability space $\left(\mathsf{\Omega },ℱ,{\left\{{ℱ}_t\right\}}_{t\ge 0},P\right)$:

$$X_t=X_0+{\int }_0^{t}a(s,X_s,r_s)ds+{\int }_0^t{\int }_{\mathcal{E}}b(s,X_s,r_s,e)\tilde{N}(de,ds)$$

(1)

with initial value $X_0\in {\mathbb{R}}^d,$ where $r_s$ is Markov chain, $\tilde{N}(de,ds)$ is a compensated Poisson measure, and $\mathcal{E}={\mathbb{R}}^d\setminus \left\{0\right\}$ is equipped with its Borel field E. The drift coefficient is denoted by $a:[0,T]\times {\mathbb{R}}^d\times \mathbb{S}\to {\mathbb{R}}^d$, and the jump diffusion coefficient is represented by $b:[0,T]\times {\mathbb{R}}^d\times \mathbb{S}\times \mathcal{E}\to {\mathbb{R}}^d$.

Recently, the study of SDEs with Markovian switching driven by pure jumps has attracted increasing interest. PJ-SDEwMs can be seen as a generalization of the SDEs with jump. It is also possible to think of it as a generalization of SDEs with Markovian switching, of course. It is not only used in finance but also has a wide range of applications in control systems, bio-mathematics, chemistry and mechanics (see [1,2,3]). The authors [4] study mode coupling in a multimode step-index microstructured polymer optical fibers for potential sensing and communication applications. Ji and Chizeck [5] focused on the control problem for systems with continuous-time Markovian jump parameters. Mao [6] discussed the exponential stability for general nonlinear SDEwMs. Similar to SDEs with jump, it is difficult to obtain an explicit solution for SDEwMs. Therefore, we need effective schemes which are accurate and computationally convenient to approximate the true solutions. Yuan and Mao [7] discovered the convergence of the Euler–Maruyama scheme, which is used to obtain the stationary distribution of SDEwMs in [8]. Mao and Yuan [9] gave the systematic presentation of the theory of SDEs with Markovian switching. Then, the existence and uniqueness of solutions for neutral SDEwMs were proven in [10] under non-Lipschitz conditions, and Euler approximate solutions were provided for solving SDEwMs. Common numerical schemes for solving SDEs with jumps or SDEwMs include Euler–Maruyama scheme [7,9,11,12], Milstein scheme [13,14], and jump-adapted scheme [15,16]. The authors of [17] studied the balanced implicit numerical methods for solving SDEs driven by Poisson jumps. Zhou and Mamon [18] expanded three short-rate models, integrating the switching of economic regimes via a discrete-time finite-state Markov chain.

A high-order model incorporating drift and volatility modulation by a discrete-time weak Markov chain is introduced in [19]. Yang, Yin and Li [20] utilized stochastic approximation techniques to analyze the stability of numerical solutions for jump diffusions with Markovian switching. Furthermore, the authors [21] study the convergence of SDEs differential equations containing delay and Markovian switching, and an Euler scheme for solving SDEwMs under non-Lipschitz conditions is given in [22]. Given the application requirements in finance and related fields, there is an increasing interest in studying high-order numerical schemes for solving SDEs. For instance, Fan [23] developed a strong approximation order 1.5 scheme for solutions of SDEwMs. Liu and Li [24] proved the convergence of the weak stochastic Taylor scheme with an appropriate order. In [25], a new weak scheme for solving SDEwMs driven by Brownian motion was proposed and achieved the convergence rate of second-order. Additionally, the numerical results of several weak schemes are presented, with a focus on the second-order weak stochastic Taylor scheme and the extrapolation of the Euler scheme. We refer to the high-order numerical methods of solving SDEs in [24,25,26,27] to propose novel numerical schemes of pure jump SDEs, which can achieve a weak second-order convergence rate.

The primary contributions of this paper can be succinctly highlighted as follows:

• For PJ-SDEwMs with mark-dependent jump coefficient $b=b(t,X_t,r_t,e)$, we first propose Scheme 1 using Wagner–Platen expansion. However, Scheme 1 contains multiple stochastic integrals, which are not easily computed. Thus, to avoid the use of some double integrals, we propose another new Scheme 2, by employing the trapezoidal rule to approximate the following multiple stochastic integrals

  $${\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_e^{1}a(s,X_s,r_s)\tilde{N}(de,ds)dtand{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{L}^{0}b(s,X_s,r_s,e)ds\tilde{N}(de,dt).$$

  Furthermore, we can use the definition of compound Poisson process to compute

  $${\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_{e_1}b(s,X_s,r_s,e_2)\tilde{N}(d{e}_1,ds)\tilde{N}(d{e}_2,dt),$$

  which has no high-accuracy based on the truncation approximation.
• Especially, for PJ-SDEwMs with mark-independent jump coefficient $b=b(t,X_t,r_t)$, we propose Scheme 3 by using the trapezoidal rule and duality formula, which does not involve multiple stochastic integrals. Moreover, Scheme 3 is not a special case of Scheme 2. Using Malliavin calculus theory, it is strictly proven that Scheme 3 has a local weak order-3.0 convergence rate. The greatest state difference and the upper bound of the state value are connected to the convergence rate.
• The convergence and stability results of Schemes 2 and 3 are validated through numerical experiments, which are also compared with the Euler scheme to verify its effectiveness and accuracy. Scheme 3 is simpler and faster than Scheme 2 in the case of mark-independent PJ-SDEwMs.

The following is a list of some notations to be used later: In Section 2, we give the introduction of fundamental concepts, encompassing the Markov Chain, Itô-Taylor expansion, and Malliavin stochastic calculus which include duality formula and chain rule. Section 3 presents our novel weak second-order numerical schemes, accompanied by a rigorous proof establishing their local weak convergence order of 3.0. In Section 4, we give the practical application of our proposed new schemes, where we present some numerical examples to validate the effectiveness and accuracy of them. The paper concludes with Section 5, providing a succinct summary of our work.

The following notations are listed for future reference:

⧫

$C_b^{l,k}$ is the set of continuously differential functions $\psi :[0,T]\times {\mathbb{R}}^q\to {\mathbb{R}}^q$ with uniformly bounded partial derivatives ${\partial }_t^{l_1}\psi$ and ${\partial }_x^{k_1}\psi$ for $1\le l_1\le l$ and $1\le k_1\le k.$ The notation $C_b^k$ is similarly defined.

⧫

$C_p({\mathbb{R}}^d,\mathbb{R})$ is the set of functions which have at most polynomial growth.

⧫

C is a generic constant depending only on the upper bounds of derivatives of $a,b$, g and the largest state difference.

2. Preliminaries and Notation

2.1. Markov Chain

On the probability space $\left(\mathsf{\Omega },ℱ,{\left\{{ℱ}_t\right\}}_{t\ge 0},P\right),$ we assume that $\left\{r_t,t\ge 0\right\}$ is a right-continuous Markov chain and takes values in a finite state space $\mathbb{S}=\{1,2,\dots ,M\}$ with generator $Q={\left(q_{ij}\right)}_{M\times M}$

$$P\left(r_{t+\delta }=j\mid r_t=i\right)=\left\{\begin{array}{cc}{q}_{ij}\delta +o\left(\delta \right),\hfill & \mathrm{if}i\ne j\hfill \\ 1+q_{ii}\delta +o\left(\delta \right),\hfill & \mathrm{if}i=j\hfill \end{array}\right.$$

(2)

where $\delta >0,q_{ij}\ge 0$ and, for $i\ne j,q_{ii}=-\sum _{i\ne j}{q}_{ij}$. Let $\mathcal{E}=\mathbb{R}\setminus \left\{0\right\}$ be the mark set equipped with its Borel field $\mathcal{B}\left(\mathcal{E}\right).$ Now, on $\mathcal{E}\times [0,T],$ we consider a given intensity measure of the form $\lambda \left(de\right):=\gamma \left(e\right)de$ with kernel function $\gamma \left(e\right)\ge 0$ for all $e\in \mathcal{E}$ and $\lambda \left(de\right):=0$ for $e\notin \mathcal{E}$, and suppose that the total intensity ${\lambda }_{\mathcal{E}}:={\int }_{\mathcal{E}}\gamma \left(e\right)de<\infty .$ Moreover, $d{r}_t={\int }_{\mathcal{E}}h\left(r_{t-},e\right)N(de,dt)$ with $h(i,e)=j-i$ for $e\in {\Delta }_{ij}$ and $h(i,e)=0$ for $e\notin {\Delta }_{ij},$ which the intervals ${\Delta }_{ij}$ have length $q_{ij}$, that is

$$\begin{array}{cc}\hfill & {\Delta }_{12}=\left[0,q_{12}\right),{\Delta }_{13}=\left[q_{12},q_{12}+q_{13}\right),\dots ,{\Delta }_{1M}=\left[\sum _{j=2}^{M-1}{q}_{1j},\sum _{j=2}^M{q}_{1j}\right),\hfill \\ \hfill & {\Delta }_{21}=\left[\sum _{j=2}^M{q}_{1j},\sum _{j=2}^M{q}_{1j}+q_{21}\right),{\Delta }_{23}=\left[\sum _{j=2}^M{q}_{1j}+q_{21},\sum _{j=2}^M{q}_{1j}+q_{21}+q_{23}\right),\dots ,\hfill \\ \hfill & {\Delta }_{2M}=\left[\sum _{j=2}^M{q}_{1j}+\sum _{\begin{array}{c}j=1\\ j\ne 2\end{array}}^{M-1}{q}_{2j},\sum _{j=2}^M{q}_{1j}+\sum _{\begin{array}{c}j=1\\ j\ne 2\end{array}}^M{q}_{2j}\right),\dots ,\hfill \end{array}$$

(3)

and so on (see [9]).

2.2. Wagner–Platen expansion

First, we give Itô’s isometry for jump martingale and multi-dimensional Itô formula for PJ-SDEwMs (see [9,27]).

Lemma 1

(Itô’s isometry for jump martingale, see [27]). If $u(s,e)$ is ${ℱ}_s$-adapted stochastic process, then

$$\mathbb{E}\left[{({\int }_0^T{\int }_{\mathcal{E}}u(s,e)\tilde{N}(de,ds))}^2\right]=\mathbb{E}\left[{\int }_0^T{\int }_{\mathcal{E}}{u}^2(s,e)\lambda \left(de\right)ds\right].$$

(4)

Lemma 2

(Itô formula, see [9]). If $V\in C^{1,2,2}([0,T]\times {\mathbb{R}}^d\times \mathbb{N};\mathbb{R})$, for any $t\ge 0$, we have

$$U(s,X_s,r_s)=U(0,X_0,r_0)+{\int }_0^s{L}^{0}U(t,X_t,r_t)dt+{\int }_0^s{\int }_{\mathcal{E}}{L}_e^{1}U(t,X_t,r_t)\tilde{N}(de,dt),$$

(5)

with the operators

$$\begin{array}{cc}\hfill L_e^{1}U(t,X_t,r_t)=& U\left(t,X_t,i_0+h(r_t,e)\right)-U(t,X_t,r_t),\hfill \\ \hfill L^{0}U(t,X_t,j)=& \frac{\partial }{\partial t}U(t,X_t,j)+\sum _{i=1}^d\frac{\partial }{\partial x_k}U(t,X_t,j)a_k(t,x,j)+\frac{1}{2}trace\left(b{(t,X_t,j)}^{\top }\frac{{\partial }^2}{\partial x^2}U(t,X_t,j)b(t,X_t,j)\right)+\sum _{k\in S}U(t,X_t,j)q_{jk}\hfill \end{array}$$

with $i_0=r_0$ and

$$\begin{array}{c}\hfill \frac{{\partial }^2}{\partial x^2}U(t,X_t,j)={\left(\frac{{\partial }^2}{\partial x_m\partial x_n}U(t,X_t,j)\right)}_{d\times d}.\end{array}$$

A higher order of PJ-SDEwMs can be obtained via the Wagner–Platen expansion. However, there are a few more definitions and notations that must be introduced before we can discuss the order of approximation. When $j_i\in \{0,1\}$ for $i\in \{1,2,...,l\}$, we designate a row vector $\alpha =(j_1,j_2,...,j_l)$ as a multi-index of length $l:l\left(\alpha \right)\in {\mathbb{N}}^{+}$. Then, the set of all multi-indices $\alpha$ is denoted by

$$\mathcal{M}=\{(j_1,j_2,...,j_l):j_i\in \{0,1\},i\in \{0,1,...,l\}forl=1,2,...\}\cup \left\{v\right\}.$$

where v is the multi-index of length zero $\left(l\right(v)=0)$. Assume that ${\mathsf{\Gamma }}_l=\left\{\alpha \in \mathcal{M}:l\left(\alpha \right)\le l\right\}$ is the hierarchical set, and $\mathcal{B}\left({\mathsf{\Gamma }}_l\right)=\left\{\alpha \in \mathcal{M}:l\left(\alpha \right)=l+1\right\}$ is the corresponding remainder set. Given a multi-index $\alpha \in \mathcal{M}$ with $l\left(\alpha \right)>1$, we write $\alpha -$ and $-\alpha$ for the multi-index obtained by eliminating the last component and the first component of $\alpha$, respectively. Let us define recursively the Itô coefficient functions $f_{k,\alpha }$ by

$$f_{k,\alpha }=\left\{\begin{array}{c}{f}_{k,\left(0\right)}=a_k,g_{k,\left(i\right)}=b_k,l=1.\hfill \\ L_e^1{f}_{k,-\alpha },l>1.\hfill \end{array}\right.$$

(6)

Furthermore, let the multiple Itô integral $I_{\alpha }{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,\tau }$ be defined by

$$I_{\alpha }{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,\tau }=\left\{\begin{array}{c}{\int }_{\varrho }^{\tau }{I}_{\alpha -}{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,s}ds,l\ge 1,j_l=0,\hfill \\ {\int }_{\varrho }^{\tau }{\int }_{\mathcal{E}}{I}_{\alpha -}{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,s_l}\tilde{N}(d{e}_l,d{s}_l),l\ge 1,j_l=1.\hfill \end{array}\right.$$

(7)

For $\alpha =(j_1,j_2,j_3)$ and $\varrho ,\tau \in [0,T],$ we assume

$$I_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,\tau }:=\left\{\begin{array}{c}{\int }_{\varrho }^{\tau }{I}_{\alpha -}{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,s}ds,l\ge 1,j_3=0,\hfill \\ {\int }_{\varrho }^{\tau }{\int }_{\mathcal{E}}{I}_{\alpha -}{\left[f_{k,\alpha }(·,X_{·},r_{·},e_{·})\right]}_{\varrho ,s_l}\lambda \left(de\right)ds,l\ge 1,j_3=1.\hfill \end{array}\right.$$

(8)

For example if $\alpha =(1,1,1),$

$$I_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}{\left[H(·,X_{.},r_{.},e)\right]}_{\varrho ,\tau }:={\int }_{\varrho }^{\tau }{\int }_{\mathcal{E}}{\int }_{\varrho }^{s_3}{\int }_{\mathcal{E}}{\int }_{\varrho }^{s_2}{\int }_{\mathcal{E}}H(s_1,X_{s_1},r_{s_1},e_1)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\lambda \left(d{e}_3\right)d{s}_3.$$

2.3. Malliavin Stochastic Calculus

Suppose the operator $D_{t,e}$ is the Malliavin derivative of Poisson process at $(t,e)$. A random variable U is Malliavin differentiable if and only if $U\in {\mathbb{D}}^{l,m}$. Here, the stochastic Sobolev spaces ${\mathbb{D}}^{l,m}$ consist of all ${ℱ}_T-$measurable $U\in L^2\left(P\right)$ with the norm

$${\parallel U\parallel }_{l,m}^2=\mathbb{E}\left[{\left|U\right|}^m\right]+\mathbb{E}\left[{\left({\int }_0^T{\int }_0^{s_l}\cdots {\int }_0^{s_2}{\left|D_{s_1...s_l,e}^{\alpha }U\right|}^{2}d{s}_{1}d{s}_2\cdots d{s}_l\right)}^m\right],$$

(9)

where the Malliavin derivative $D_{s_1...s_l,e}^{\alpha }$ is defined as

$$D_{s_1...s_l,e}^{\alpha }=D_{s_1...s_l,e}^{(j_1,...,j_l)}=D_{s_1,e}^{j_1}···D_{s_l,e}^{j_l}$$

with especially $D_{s_j,e}^0=1$ for $1\le j\le l$.

Lemma 3

(Duality formula, see [28]). Assume $F\in {\mathbb{D}}^{1,2}$ and $u(t,e)\in {\mathbb{D}}^{1,2}$ for $0\le t\le T$, we obtain the duality formula

$$\begin{array}{cc}\hfill & \mathbb{E}\left[F{\int }_0^T{\int }_{\mathcal{E}}u(t,e)\tilde{N}(de,dt)\right]=\mathbb{E}\left[{\int }_0^T{\int }_{\mathcal{E}}u(t,e)D_{t,e}F\lambda \left(de\right)dt\right],\hfill \end{array}$$

Lemma 4

(Chain rule, see [28]). Let $G_1,G_2\in {\mathbb{D}}^{1,2}$, then $G_1{G}_2\in {\mathbb{D}}^{1,2}$ and

$$D_{t,e}\left(G_1{G}_2\right)=G_1{D}_{t,e}{G}_2+G_2{D}_{t,e}{G}_1+D_{t,e}{G}_1{D}_{t,e}{G}_2.$$

Let $G\in {\mathbb{D}}^{1,2}$ and ϕ be a real continuous function on $\mathcal{E}$ and $\varphi \left(G\right)\in {\mathbb{D}}^{1,2}$. Then,

$$D_{t,e}\varphi \left(G\right)=\varphi (G+D_{t,e}G)-\varphi \left(G\right).$$

(10)

Lemma 5

(See [28]). For $t\in [0,T]$ and the stochastic process $u(s,e)\in {\mathbb{D}}^{1,2},$ we have

$$D_{t,e}{\int }_0^T{\int }_{\mathcal{E}}u(s,e)\tilde{N}(de,ds)=u(t,e)+{\int }_t^T{\int }_{\mathcal{E}}{D}_{t,e}u(s,e)\tilde{N}(de,ds),$$

and

$$D_{t,e}{\int }_0^T{\int }_{\mathcal{E}}{\int }_0^{s_2}{\int }_{{\Delta }_{ij}}\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2)={\int }_0^t{\int }_{{\Delta }_{ij}}\tilde{N}(d{e}_1,ds)+I_{{\Delta }_{ij}}\left(e\right){\int }_t^T{\int }_{\mathcal{E}}\tilde{N}(d{e}_1,ds),$$

where $I_{{\Delta }_{ij}}\left(e\right)$ is the indicator function defined by $I_{{\Delta }_{ij}}\left(e\right)=1$ for $e\in {\Delta }_{ij}$ and $I_{{\Delta }_{ij}}\left(e\right)=0$ for $e\notin {\Delta }_{ij}.$

3. Main Results

First, we consider a regular time uniform discretization: $0=t_0<···<t_{N-1}<t_N=T$ with $\Delta t=t_{n+1}-t_n$ for $n=0,1,...,N-1$. For a basic depiction, we consider $r_t^{n,i}:=i+{\int }_{t_n}^t{\int }_{\mathcal{E}}h\left(r_{s-}^{n,i},e\right)N(de,ds)$ and $X_{k,t_{n+1}}^{n,i}:=X_{k,t_{n+1}}^{t_n,X^{n,i}},$ which is the k-th component of $X_{t_{n+1}}^{t_n,X^{n,i}}$. Using the classical Wagner–Platen expansion, we can derive the following Scheme 1 for solving SDEwMs with mark-dependent jump coefficient.

Scheme 1

(Wagner–Platen expansion). Given the initial condition $X^{0,i}$. For $0\le n\le N-1$, we solve $X^{n+1,i}$ with its k-th component $X_k^{n+1,i}$ by

$$X_k^{n+1,i}=X_k^{n,i}+\sum _{\alpha \in {\mathsf{\Gamma }}_2\setminus \left\{v\right\}}{I}_{\alpha }{\left[f_{k,\alpha }(t_n,X^{n,i},i,e)\right]}_{t_n,t_{n+1}}.$$

(11)

From the Wagner–Platen expansion and trapezoidal rule we obtain

$$\begin{array}{cc}\hfill X_{k,t_{n+1}}^{n,i}=& X_k^{n,i}+{\int }_{t_n}^{t_{n+1}}{a}_k(t,X_t^{n,i},r_t^{n,i})dt+{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{b}_k(t,X_t^{n,i},r_t^{n,i},e)\tilde{N}(de,dt)=X_k^{n+1,i}+R_{k,1}^{n,i},\hfill \end{array}$$

(12)

where the truncation error

$$\begin{array}{cc}\hfill R_{k,1}^{n,i}=& {\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\tilde{N}(de,ds)dt-\frac{1}{2}\Delta t\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\tilde{N}(de,dt)\hfill \\ & +{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{L}^0{b}_{k,e}^{n,i}ds\tilde{N}(de,dt)-\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{L}^0{b}_{k,e}^{n,i}\tilde{N}(de,dt)+\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}}\hfill \end{array}$$

(13)

with $L^{i,j}{a}_k^{n,i}=a_k\left(t_n,X^{n,i},j\right)-a_k(t_n,X^{n,i},i).$ Here, we write $a_k^{n,i}$ for $a_k(t_n,X^{n,i},i)$ and $b_{k,e}^{n,i}$ for $b_k(t_n,X^{n,i},i,e)$. Then, by Equation (12), we propose the following second-order new scheme.

Scheme 2.

Given the initial condition $X^{0,i}$. For $0\le n\le N-1$, we solve $X^{n+1,i}$with its k-th component $X_k^{n+1,i}$ by

$$\begin{array}{cc}\hfill X_k^{n+1,i}=& X_k^{n,i}+a_k^{n,i}\Delta t+{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{b}_{k,e}^{n,i}\tilde{N}(de,dt)+\frac{1}{2}{L}^0{a}_k^{n,i}{(\Delta t)}^2+\frac{1}{2}\Delta t\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\tilde{N}(de,dt)\hfill \\ \hfill & +\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{L}^0{b}_{k,e}^{n,i}\tilde{N}(de,dt)+\sum _{j\in S}{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{{\Delta }_{ij}}{L}^{i,j}{b}_{k,e_2}^{n,i}\tilde{N}(d{e}_1,ds)\tilde{N}(d{e}_2,dt)\hfill \end{array}$$

(14)

with $\Delta t=t_{n+1}-t_n$.

Remark 1.

If the jump coefficient function $b=b(t,X_t,r_t,e)$, we generate the compound Poisson process

$$\begin{array}{cc}\hfill {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{b}_{k,e}^{n,i}\tilde{N}(de,dt)=& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}b(t_n,X^{n,i},i,e)(N(de,dt)-\lambda \left(de\right)dt)\hfill \\ \hfill =& \sum _{k=N_{t_n}+1}^{N_{t_{n+1}}}b(t_n,X^{n,i},i,{\xi }_k)-{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}b(t_n,X^{n,i},i,e)\lambda \left(de\right)dt,\hfill \end{array}$$

and the multiple stochastic integral in Scheme 2 can be computed by

$$\begin{array}{cc}& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{{\Delta }_{ij}}\tilde{N}\left(d{e}_1,ds\right)\tilde{N}\left(d{e}_2,dt\right)\hfill \\ \hfill & ={\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\left(N_t^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left(t-t_n\right)\right)\tilde{N}\left(d{e}_2,dt\right)\hfill \\ \hfill & =\sum _{m=N_{t_n}+1}^{N_{t_{n+1}}}\left(N_{{\tau }_m}^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left({\tau }_m-t_n\right)\right)-{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\left(N_t^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left(t-t_n\right)\right)\lambda \left(d{e}_2\right)dt\hfill \\ \hfill & =\sum _{m=N_{t_n}+1}^{N_{t_{n+1}}}\left(N_{{\tau }_m}^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left({\tau }_m-t_n\right)\right)-{\lambda }_{\mathcal{E}}\left({\int }_{t_n}^{t_{n+1}}{N}_t^{{\Delta }_{ij}}dt-N_{t_n}^{{\Delta }_{ij}}\Delta t-\frac{1}{2}{\lambda }_{{\Delta }_{ij}}{(\Delta t)}^2\right),\hfill \end{array}$$

(15)

where the pairs $({\tau }_k,{\xi }_k)$ of k-th jump time and marks are independent uniformly distributed in the planar region $[0,T]\times \mathcal{E}$, ${\tilde{N}}_t^{{\Delta }_{ij}}={\int }_0^t{\int }_{{\Delta }_{ij}}\tilde{N}(d{e}_1,ds),$$N_t^{{\Delta }_{ij}}={\int }_0^t{\int }_{{\Delta }_{ij}}N(d{e}_1,ds)$ and ${\lambda }_{{\Delta }_{ij}}={\int }_{{\Delta }_{ij}}\lambda \left(de\right)={\int }_{{\Delta }_{ij}}\gamma \left(e\right)de.$ For the Lebesgue–Stieltjes stochastic integral ${\int }_{t_n}^{t_{n+1}}{N}_t^{{\Delta }_{ij}}dt,$ we can use trapezoidal rule to approximate it, that is

$${\int }_{t_n}^{t_{n+1}}{N}_t^{{\Delta }_{ij}}dt=\frac{1}{2}(N_{t_n}^{{\Delta }_{ij}}+N_{t_{n+1}}^{{\Delta }_{ij}})\Delta t+R_N^n.$$

In the special case of a mark-independent jump coefficient $b(t,X_t,r_t,e)=b(t,X_t,r_t)$, we use the following discrete-time approximation

$$X_{k,t_{n+1}}^{n,i}=X_k^{n,i}+{\int }_{t_n}^{t_{n+1}}{a}_k(t,X_t^{n,i},r_t^{n,i})dt+{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{b}_k(t,X_t^{n,i},r_t^{n,i})\tilde{N}(de,dt)=X_k^{n+1,i}+R_{k,2}^{n,i}$$

(16)

with the truncation error

$$\begin{array}{cc}\hfill R_{k,2}^{n,i}=& {\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\tilde{N}(de,ds)dt-\frac{1}{2{\lambda }_{\mathcal{E}}}\Delta t\Delta {\tilde{N}}_n\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\hfill \\ & +{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{L}^0{b}_k^{n,i}ds\tilde{N}(de,dt)-\frac{1}{2}{L}^0{b}_k^{n,i}\Delta t\Delta {\tilde{N}}_n\hfill \\ & +{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_{e_1}^1{b}_k^{n,i}\tilde{N}(d{e}_1,ds)\tilde{N}(d{e}_2,dt)-\frac{1}{2{\lambda }_{\mathcal{E}}}\left({(\Delta {\tilde{N}}_n)}^2-{\lambda }_{\mathcal{E}}\Delta t-\Delta {\tilde{N}}_n\right)\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\hfill \\ & +\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i})\right]}_{t_n,t_{n+1}}.\hfill \end{array}$$

(17)

Based on Equation (16), we propose the following simplified scheme for solving mark-independent PJ-SDEwMs.

Scheme 3.

Given the initial condition $X^{0,i}$. For $0\le n\le N-1$, we solve $X^{n+1,i}$ with its k-th component $X_k^{n+1,i}$ by

$$\begin{array}{cc}\hfill X_k^{n+1,i}=& X_k^{n,i}+a_k^{n,i}\Delta t+b_k^{n,i}\Delta {\tilde{N}}_n+\frac{1}{2}{L}^0{a}_k^{n,i}{(\Delta t)}^2+\frac{1}{2{\lambda }_{\mathcal{E}}}\Delta t\Delta {\tilde{N}}_n\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\hfill \\ \hfill & +\frac{1}{2}{L}^0{b}_k^{n,i}\Delta t\Delta {\tilde{N}}_n+\frac{1}{2{\lambda }_{\mathcal{E}}}\left({(\Delta {\tilde{N}}_n)}^2-{\lambda }_{\mathcal{E}}\Delta t-\Delta {\tilde{N}}_n\right)\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}},\hfill \end{array}$$

(18)

where $\Delta t=t_{n+1}-t_n,$$\Delta {\tilde{N}}_n={\tilde{N}}_{t_{n+1}}-{\tilde{N}}_{t_n}$ and ${\lambda }_{{\Delta }_{ij}}={\int }_{{\Delta }_{ij}}\lambda \left(de\right)={\int }_{{\Delta }_{ij}}\gamma \left(e\right)de.$

Remark 2.

Here, $\gamma \left(e\right)$ is a kernel function, which may be symmetric, i.e., $\gamma \left(e\right)=\gamma (-e)$;or non-symmetric, i.e.,

$$\gamma \left(e\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}e\in [-c,c]\hfill \\ 0,\hfill & \mathrm{if}e\notin [-c,c]\hfill \end{array}\right.,c\in {\mathbb{R}}^{+};$$

(19)

or singular, i.e.

$$\gamma \left(e\right)=\left\{\begin{array}{cc}\frac{1}{c^2\sqrt{c\left|e\right|}}\hfill & \mathrm{for}e\in [-c,c]\hfill \\ 0,\hfill & \mathrm{for}e\notin [-c,c]\hfill \end{array}\right.,c\in {\mathbb{R}}^{+}.$$

(20)

Local Weak Convergence Theorems

In this section, using Malliavin stochastic analysis and the Wagner–Platen expansion, we rigorously prove and obtain the local weak order-3.0 convergence of Schemes 1–3.

Theorem 1.

(Local weak convergence) Suppose that $X_{t_{n+1}}^{n,i}$ and $X^{n+1,i}$$(0\le n\le N-1)$ satisfy Equation (12) and Scheme 1, respectively. If the functions $a,b\in C_p({\mathbb{R}}^d,\mathbb{R}),$ $a,b\in C_b^{2,4}$ and $g\in C_b^2,$ then

$$\left|\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\right|\le C(1+{|X^{n,i}|}^m){(\Delta t)}^3,$$

(21)

where $m\in {\mathbb{N}}^{+}$ is a generic constant, which can vary from line to line.

Proof of Theorem 1.

Subtracting Equation (18) from Equation (12) yields

$$X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i}=\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}}.$$

(22)

Then, by the mean value formula of integrals and duality formula, we have

$$\begin{array}{cc}\hfill \mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]=& \sum _{k=1}^d\mathbb{E}\left[F_k^{n+1,i}(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n}\right]\hfill \\ \hfill =& \sum _{k=1}^d\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}\mathbb{E}\left[F_k^{n+1,i}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}}|{ℱ}_{t_n}\right]\hfill \\ \hfill =& \sum _{k=1}^d\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}{\left[\mathbb{E}\left[D_{s_1{s}_2{s}_3,e}^{\alpha }\left(F_k^{n+1,i}\right)f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)|{ℱ}_{t_n}\right]\right]}_{t_n,t_{n+1}}\hfill \end{array}$$

(23)

with

$$F_k^{n+1,i}={\int }_0^1\frac{\partial }{\partial x_k}g(X^{n+1,i}+\mu (X_{t_{n+1}}^{n,i}-X^{n+1,i}))d\mu .$$

(24)

Under the conditions of this theorem, we finally obtain the inequality (21). □

Theorem 2.

Suppose that $X_{t_{n+1}}^{n,i}$ and $X^{n+1,i}$$(0\le n\le N-1)$ satisfy Equation (12) and Scheme 2, respectively. If the functions $a,b\in C_p({\mathbb{R}}^d,\mathbb{R}),$ $a,b\in C_b^{2,4}$ and $g\in C_b^2,$ then

$$\left|\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\right|\le C(1+{|X^{n,i}|}^m){(\Delta t)}^3,$$

(25)

where $m\in {\mathbb{N}}^{+}$ is a generic constant, which can vary from line to line.

Proof of Theorem 2.

Using the multi-dimensional Taylor formula, for ease of proof, we assume

$$I^n=\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]=I_1^n+I_2^n,$$

(26)

where

$$\begin{array}{cc}\hfill I_1^n& =\mathbb{E}[\sum _{k=1}^d\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n}],\hfill \\ \hfill I_2^n& ={\int }_0^1{\int }_0^1\mathbb{E}\left[{\left(\sum _{k=1}^d(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})\frac{\partial }{\partial x_k}\right)}^{2}g\left(X^{n+1,i}+{\mu }_1{\mu }_2(X_{t_{n+1}}^{n,i}-X^{n+1,i})\right)|{ℱ}_{t_n}\right]{\mu }_{1}d{\mu }_{1}d{\mu }_2.\hfill \end{array}$$

(27)

Assume $X_{k,t_{n+1}}^{n,i}$ is the k-th component of explicit solution $X_{t_{n+1}}^{n,i}$. Then, it follows from the Itô–Taylor expansion that

$$\begin{array}{cc}\hfill X_{k,t_{n+1}}^{n,i}& =X_k^{n,i}+\sum _{\alpha \in {\mathsf{\Gamma }}_2\setminus \left\{v\right\}}{I}_{\alpha }{\left[f_{k,\alpha }(t_n,X^{n,i},i,e)\right]}_{t_n,t_{n+1}}+\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}}\hfill \\ \hfill & =X_k^{n,i}+a_k^{n,i}\Delta t+{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{b}_k^{i,e}\tilde{N}(de,dt)+L^0{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}d{s}_{1}d{s}_2+{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\tilde{N}(de,d{s}_1)d{s}_2\hfill \\ \hfill & +{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{L}^0{b}_k^{i,e}d{s}_1\tilde{N}(de,d{s}_2)+{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{L}_{e_1}^1{b}_k^{i,e_2}\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2)\hfill \\ \hfill & +\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}},\hfill \end{array}$$

(28)

which by the fact $L^0{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}d{s}_{1}d{s}_2=\frac{1}{2}{L}^0{a}_k^{n,i}{(\Delta t)}^2$ yields

$$\begin{array}{cc}& X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i}\hfill \\ \hfill =& \sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}}+{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\tilde{N}(de,d{s}_1)d{s}_2-\frac{1}{2}\Delta t\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\tilde{N}(de,ds)\hfill \\ & +{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{L}^0{b}_k^{i,e}d{s}_1\tilde{N}(de,d{s}_2)-\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{L}^0{b}_k^{i,e}\tilde{N}(de,ds)\hfill \\ & +{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{L}_{e_1}^1{b}_k^{i,e_2}\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2)-\sum _{j\in S}{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}{L}^{i,j}{b}_k^{i,e_2}\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2).\hfill \end{array}$$

(29)

It follows from the definition of the operator $L_{e_1}^1$ that

$$\begin{array}{cc}& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{L}_{e_1}^1{b}_k^{i,e_2}\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2)\hfill \\ \hfill =& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}\left(b_k(t_n,X^{n,i},i+h(i,e_1),e_2)-b_k(t_n,X^{n,i},i,e_2)\right)\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2)\hfill \\ \hfill =& \sum _{j\in S}{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\left(b_k(t_n,X^{n,i},j,e_2)-b_k(t_n,X^{n,i},i,e_2)\right)\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2)\hfill \\ \hfill =& \sum _{j\in S}{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}{L}^{i,j}{b}_k^{i,e_2}\tilde{N}(d{e}_1,d{s}_1)\tilde{N}(d{e}_2,d{s}_2).\hfill \end{array}$$

(30)

By the duality formula in Lemma 3 and from Equations (29) and (30), we deduce

$$I_1^n=\mathbb{E}(\sum _{k=1}^d\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n})=\sum _{k=1}^d\sum _{l=1}^3{\zeta }_{g,k}^l,$$

(31)

where

$$\begin{array}{cc}\hfill & {\zeta }_{g,k}^1=\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\left({\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{L}^0{b}_k^{i,e}d{s}_1\tilde{N}(de,d{s}_2)-\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{L}^0{b}_k^{i,e}\tilde{N}(de,ds)\right)|{ℱ}_{t_n}\right],\hfill \\ \hfill & {\zeta }_{g,k}^2=\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\tilde{N}(de,d{s}_1)d{s}_2-\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\tilde{N}(de,ds)\right)|{ℱ}_{t_n}\right],\hfill \\ \hfill & {\zeta }_{g,k}^3=\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)I_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i},e)\right]}_{t_n,t_{n+1}}|{ℱ}_{t_n}\right].\hfill \end{array}$$

By taking Malliavin derivative with respect to $X_k^{n+1,i},$ we obtain

$$\begin{array}{cc}\hfill D_{t,e_2}{X}_k^{n+1,i}=& b_k^{i,e_2}+\frac{1}{2}\Delta t(L^0{b}_k^{i,e_2}+\sum _{j\in S}{L}^{i,j}{a}_k^{n,i})\hfill \\ & +\sum _{j\in S}(L^{i,j}{b}_k^{i,e_2}{\int }_{t_n}^t{\int }_{{\Delta }_{ij}}\tilde{N}(d{e}_1,ds)+I_{{\Delta }_{ij}}\left(e_2\right){\int }_t^{t_{n+1}}{\int }_{\mathcal{E}}{L}^{i,j}{b}_k^{i,e_1}\tilde{N}(d{e}_1,ds))\hfill \end{array}$$

(32)

for $t_n<t\le t_{n+1}$ and $e_2\in \mathcal{E}.$ Furthermore, the chain rule (10) gives

$$D_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)=\frac{\partial }{\partial x_k}g(X^{n+1,i}+D_{t,e}{X}^{n+1,i})-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right).$$

(33)

Then, it follows from Taylor formula and Lemma 5 that

$$\begin{array}{cc}& \frac{\partial }{\partial x_k}g(X^{n+1,i}+D_{t,e_2}{X}^{n+1,i})\hfill \\ \hfill =& \frac{\partial }{\partial x_k}g\left(Y_{i,e_2}^{n+1}\right)+\sum _{j\in S}\sum _{l=1}^d{F}_{g,l,e_2}^{n+1}\left(L^{i,j}{b}_l^{i,e_2}{\int }_{t_n}^t{\int }_{{\Delta }_{ij}}\tilde{N}(d{e}_1,ds)+I_{{\Delta }_{ij}}\left(e_2\right){\int }_t^{t_{n+1}}{\int }_{\mathcal{E}}{L}^{i,j}{b}_l^{i,e_1}\tilde{N}(d{e}_1,ds)\right),\hfill \end{array}$$

(34)

where $Y_{i,e_2}^{n+1}=X^{n+1,i}+b^{i,e_2}+\frac{1}{2}\Delta t\left(L^0{b}^{i,e_2}+\sum _{j\in S}{L}^{i,j}{a}^i\right)$ and

$$F_{g,l,e_2}^{n+1}={\int }_0^1\frac{{\partial }^2}{\partial x_k\partial x_l}g\left(Y_{i,e_2}^{n+1}+\mu \left(X^{n+1,i}+D_{t,e_2}{X}^{n+1,i}-Y_{i,e_2}^{n+1}\right)\right)d\mu .$$

By the duality formula, we have

$$\begin{array}{cc}& \mathbb{E}[F_{g,l,e_2}^{n+1}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\tilde{N}(d{e}_1,d{s}_1)|{ℱ}_{t_n}]={\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]\lambda \left(d{e}_1\right)d{s}_1,\hfill \\ & \mathbb{E}[F_{g,l,e_2}^{n+1}{\int }_{s_2}^{t_{n+1}}{\int }_{\mathcal{E}}{L}^{i,j}{b}_k^{i,e_1}\tilde{N}(d{e}_1,d{s}_1)|{ℱ}_{t_n}]={\int }_{s_2}^{t_{n+1}}{\int }_{\mathcal{E}}\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_k^{i,e_1}\lambda \left(d{e}_1\right)d{s}_1.\hfill \end{array}$$

(35)

Now by Lemma 3, from Equations (33)–(35), we have

$$\begin{array}{cc}\hfill {\zeta }_{g,k}^1=& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}\mathbb{E}[D_{s_2,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}]L^0{b}_k^{i,e}d{s}_1\lambda \left(de\right)d{s}_2\hfill \\ & -\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\mathbb{E}]D_{s,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}[L^0{b}_k^{i,e}\lambda \left(de\right)ds\hfill \\ \hfill =& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}\mathbb{E}]\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}[L^0{b}_k^{i,e}\lambda \left(de\right)d{s}_{1}d{s}_2\hfill \\ & +\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_2}{L}^0{b}_k^{i,e_2}(s_2-t_n)\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & +\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}{\int }_{s_2}^{t_{n+1}}{\int }_{\mathcal{E}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_1}{L}^0{b}_k^{i,e_2}(s_2-t_n)\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & -\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\mathbb{E}[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}]L^0{b}_k^{i,e}\lambda \left(de\right)ds\hfill \\ & -\frac{1}{2}\Delta t\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_2}{L}^0{b}_k^{i,e_2}\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & -\frac{1}{2}\Delta t\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}{\int }_{s_2}^{t_{n+1}}{\int }_{\mathcal{E}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_1}{L}^0{b}_k^{i,e_2}\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2,\hfill \end{array}$$

(36)

which by using the fact

$$\begin{array}{cc}& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]L^0{b}_k^{i,e}\lambda \left(de\right)d{s}_{1}d{s}_2\hfill \\ & =\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]L^0{b}_k^{i,e}\lambda \left(de\right)ds\hfill \\ & =\frac{1}{2}{(\Delta t)}^2{\int }_{\mathcal{E}}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]L^0{b}_k^{i,e}\lambda \left(de\right)\hfill \end{array}$$

yields

$$\begin{array}{cc}\hfill |{\zeta }_{g,k}^1|=& |\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_2}{L}^0{b}_k^{i,e_2}(s_2-t_n)\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & +\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}{\int }_{s_2}^{t_{n+1}}{\int }_{\mathcal{E}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_1}{L}^0{b}_k^{i,e_2}(s_2-t_n)\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & -\frac{1}{2}\Delta t\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_2}{L}^0{b}_k^{i,e_2}\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & -\frac{1}{2}\Delta t\sum _{j\in S}\sum _{l=1}^d{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}{\int }_{s_2}^{t_{n+1}}{\int }_{\mathcal{E}}\left(\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_1}{L}^0{b}_k^{i,e_2}\right)\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2|\hfill \\ \hfill \le & C(1+|X^{n,i}{|}^m){(\Delta t)}^3.\hfill \end{array}$$

(37)

Note that

$$\begin{array}{cc}& {\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right)d{s}_{1}d{s}_2\hfill \\ & =\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right)ds\hfill \\ & =\frac{1}{2}{(\Delta t)}^2{\int }_{{\Delta }_{ij}}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(Y_{i,e}^{n+1}\right)-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right),\hfill \end{array}$$

and we deduce from Lemma 3 that

$$\begin{array}{cc}\hfill {\zeta }_{g,k}^2=& \sum _{j\in S}{L}^{i,j}{a}_k^{n,i}({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[D_{s_1,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right)d{s}_{1}d{s}_2\hfill \\ & -\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[D_{s,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right)ds)\hfill \\ \hfill =& \sum _{j_1\in S}\sum _{j_2\in S}\sum _{l=1}^d{L}^{i,j_1}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_3}{\int }_{{\Delta }_{i{j}_2}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{i{j}_1}}\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j_1}{b}_l^{i,e_1}\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_{2}d{s}_3\hfill \\ \hfill & +\sum _{j\in S}\sum _{l=1}^d{L}^{i,j}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_3}{\int }_{{\Delta }_{ij}}{\int }_{s_2}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e_2}^{n+1}|{ℱ}_{t_n}\right]L^{i,j_1}{b}_l^{i,e_1}\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_{2}d{s}_3\hfill \\ & -\frac{1}{2}\Delta t\sum _{j_1\in S}\sum _{j_2\in S}\sum _{l=1}^d{L}^{i,j_1}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{i{j}_2}}{\int }_{t_n}^{s_2}{\int }_{{\Delta }_{i{j}_1}}\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e}^{n+1}|{ℱ}_{t_n}\right]L^{i,j_1}{b}_l^{i,e_1}\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\hfill \\ & -\frac{1}{2}\Delta t\sum _{j\in S}\sum _{l=1}^d{L}^{i,j}{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{{\Delta }_{ij}}{\int }_{s_2}^{t_{n+1}}{\int }_{{\Delta }_{ij}}\mathbb{E}\left[D_{s_1,e_1}{F}_{g,l,e}^{n+1}|{ℱ}_{t_n}\right]L^{i,j}{b}_l^{i,e_1}\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2,\hfill \end{array}$$

(38)

which gives

$$|{\zeta }_{g,k}^2|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.$$

(39)

Using the duality formula in Lemma 3, we conclude that

$$\begin{array}{c}\hfill |{\zeta }_{g,k}^3|=|\sum _{\alpha \in \mathcal{B}({\mathsf{\Gamma }}_2)}{I}_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}{[\mathbb{E}[D_{s_1{s}_2{s}_3,e}^{\alpha }(\frac{\partial }{\partial x_k}g(X^{n+1,i}))f_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i},e)|{ℱ}_{t_n}]]}_{t_n,t_{n+1}}|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.\end{array}$$

(40)

Combining the inequalities (37)–(40), we obtain

$$|I_1^n|=|\mathbb{E}[\sum _{k=1}^d\frac{\partial }{\partial x_k}g(X^{n+1,i})(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n}]|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.$$

(41)

For $\alpha =(1,1,1)$, applying the Itô isometry Formula (4), we have

$$\begin{array}{cc}& \mathbb{E}\left[{\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_3}{\int }_{t_n}^{s_2}{f}_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i},e_1)d{\tilde{N}}_{s_1}d{\tilde{N}}_{s_2}d{\tilde{N}}_{s_3}\right)}^2|{ℱ}_{t_n}\right]\hfill \\ \hfill & =\mathbb{E}\left[{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_3}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{\left(f_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i},e_1)\right)}^2\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\lambda \left(d{e}_3\right)d{s}_3|{ℱ}_{t_n}\right]\hfill \\ & =I_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}{\left[\mathbb{E}\left[{\left(f_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i},e_1)\right)}^2|{ℱ}_{t_n}\right]\right]}_{t_n,t_{n+1}}.\hfill \end{array}$$

(42)

For $\alpha \ne (1,1,1)$, we obtain

$$\begin{array}{cc}& \sum _{\genfrac{}{}{0pt}{}{\alpha \in \mathcal{B}({\mathsf{\Gamma }}_2)}{\alpha \ne (1,1,1)}}|\mathbb{E}[I_{\alpha }{[f_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i},e_1)]}_{t_n,t_{n+1}}|{ℱ}_{t_n}]{|}^2\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.\hfill \end{array}$$

(43)

By the inequalities (42) and (43), we deduce

$$|I_2^n|=|{\int }_0^1{\int }_0^1\mathbb{E}[{(\sum _{k=1}^d(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})\frac{\partial }{\partial x_k})}^{2}g(X^{n+1,i}+{\mu }_1{\mu }_2(X_{t_{n+1}}^{n,i}-X^{n+1,i}))|{ℱ}_{t_n}]{\mu }_{1}d{\mu }_{1}d{\mu }_2|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.$$

(44)

From the inequalities (41) and (44), we finally obtain

$$\left|\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\right|\le C(1+{|X^{n,i}|}^m){(\Delta t)}^3.$$

□

Theorem 3.

Assume that $X_{t_{n+1}}^{n,i}$ and $X^{n+1,i}$$(0\le n\le N-1)$, respectively, satisfy Equation (16) and Scheme 3. If the functions $a,b\in C_p({\mathbb{R}}^d,\mathbb{R}),$$a,b\in C_b^{2,4}$ and $g\in C_b^2,$ then

$$\left|\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\right|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3,$$

(45)

where $m\in {\mathbb{N}}^{+}$ is a generic constant, which could change line by line.

Proof of Theorem 3.

Using multi-dimensional Taylor formula, to make the proof easier, we have

$$J^n=\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]=J_1^n+J_2^n,$$

(46)

where

$$\begin{array}{cc}\hfill J_1^n& =\mathbb{E}\left[\sum _{k=1}^d\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n}\right],\hfill \\ \hfill J_2^n& ={\int }_0^1{\int }_0^1\mathbb{E}\left[{\left(\sum _{k=1}^d(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})\frac{\partial }{\partial x_k}\right)}^{2}g\left(X^{n+1,i}+{\mu }_1{\mu }_2(X_{t_{n+1}}^{n,i}-X^{n+1,i})\right)|{ℱ}_{t_n}\right]{\mu }_{1}d{\mu }_{1}d{\mu }_2.\hfill \end{array}$$

(47)

Assume $X_{k,t_{n+1}}^{n,i}$ is the k-th component of explicit solution $X_{t_{n+1}}^{n,i}$. Then, from the Itô–Taylor expansion, we can obtain

$$\begin{array}{cc}\hfill X_{k,t_{n+1}}^{n,i}& =X_k^{n,i}+\sum _{\alpha \in {\mathsf{\Gamma }}_2\setminus \left\{v\right\}}{f}_{k,\alpha }(t_n,X^{n,i},i)I_{\alpha }{\left[1\right]}_{t_n,t_{n+1}}+\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i})\right]}_{t_n,t_{n+1}}\hfill \\ \hfill & =X_k^{n,i}+a_k^{n,i}\Delta t+b_k^{n,i}\Delta {\tilde{N}}_n+L^0{a}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{t}dsdt+{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{L}_e^1{a}_k^{n,i}d{\tilde{N}}_{s}dt\hfill \\ \hfill & +L^0{b}_k^{n,i}{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{t}dsd{\tilde{N}}_t+{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{L}_e^1{b}_k^{n,i}d{\tilde{N}}_{s}d{\tilde{N}}_t+\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i})\right]}_{t_n,t_{n+1}},\hfill \end{array}$$

(48)

which yields

$$\begin{array}{cc}\hfill X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i}=& {\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{L}_e^1{a}_k^{n,i}d{\tilde{N}}_{s}dt-\frac{1}{2{\lambda }_{\mathcal{E}}}\Delta t\Delta {\tilde{N}}_n\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\hfill \\ & +L^0{b}_k^{n,i}\left[{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{t}dsd{\tilde{N}}_t-\frac{1}{2}\Delta t\Delta {\tilde{N}}_n\right]+{\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{L}_e^1{b}_k^{n,i}d{\tilde{N}}_{s}d{\tilde{N}}_t\hfill \\ & -\frac{1}{2{\lambda }_{\mathcal{E}}}\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\left({(\Delta {\tilde{N}}_n)}^2-{\lambda }_{\mathcal{E}}\Delta t-\Delta {\tilde{N}}_n\right)+\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i})\right]}_{t_n,t_{n+1}}.\hfill \end{array}$$

(49)

By the duality formula in Lemma 3 and from Equation (49), we deduce

$$\begin{array}{c}\hfill J_1^n=\mathbb{E}\left[\sum _{k=1}^d\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n}\right]=\sum _{k=1}^d\sum _{l=1}^4{ϵ}_{g,k}^l,\end{array}$$

(50)

where

$$\begin{array}{cc}\hfill & {ϵ}_{g,k}^1=L^0{b}_k^i\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{t}dsd{\tilde{N}}_t-\frac{1}{2}\Delta t\Delta {\tilde{N}}_n\right)|{ℱ}_{t_n}\right],\hfill \\ \hfill & {ϵ}_{g,k}^2=\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^s{L}_e^1{a}_k^{n,i}d{\tilde{N}}_{t}ds-\frac{1}{2{\lambda }_{\mathcal{E}}}\Delta t\Delta {\tilde{N}}_n\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\right)|{ℱ}_{t_n}\right],\hfill \\ \hfill & {ϵ}_{g,k}^3=\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{L}_e^1{b}_k^{n,i}d{\tilde{N}}_{s}d{\tilde{N}}_t-\frac{1}{2{\lambda }_{\mathcal{E}}}\left({(\Delta {\tilde{N}}_n)}^2-{\lambda }_{\mathcal{E}}\Delta t-\Delta {\tilde{N}}_n\right)\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\right)|{ℱ}_{t_n}\right],\hfill \\ & {ϵ}_{g,x_k}^4=\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}\mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)I_{\alpha }{\left[f_{k,\alpha }(·,X_{·}^{n,i},r_{·}^{n,i})\right]}_{t_n,t_{n+1}}|{ℱ}_{t_n}\right].\hfill \end{array}$$

For $t_n<s\le t\le t_{n+1},$ by using Malliavin derivative in relation to $X_k^{n+1,i}$, we get

$$\begin{array}{cc}\hfill & D_{t,e}{X}_k^{n+1,i}=b_k^{n,i}+\frac{1}{2}\Delta t{L}^0{b}_k^{n,i}+\frac{1}{2{\lambda }_{\mathcal{E}}}\sum _{j\in S}\left(\Delta t{L}^{i,j}{a}_k^{n,i}+(2\Delta {\tilde{N}}_n-1)L^{i,j}{b}_k^{n,i}\right){\lambda }_{{\Delta }_{ij}},\hfill \\ & D_{s,e}{D}_{t,e}{X}_k^{n+1,i}=\frac{1}{{\lambda }_{\mathcal{E}}}\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}},\hfill \end{array}$$

(51)

which by combining chain rule (10) gives

$$\begin{array}{c}\hfill D_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)=\frac{\partial }{\partial x_k}g(X^{n+1,i}+D_{t,e}{X}^{n+1,i})-\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right):=\mathsf{\Phi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n),\\ \hfill D_{s,e}{D}_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)=D_{s,e}\mathsf{\Phi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n):=\mathsf{\Psi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n),\end{array}$$

where the functions $\mathsf{\Phi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n)$ and $\mathsf{\Psi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n)$ do not depending only on t and e. Furthermore, from Lemma 3, using the notation ${\lambda }_{\mathcal{E}}:={\int }_{\mathcal{E}}\lambda \left(de\right)={\int }_{\mathcal{E}}\gamma \left(e\right)de$, we have

$$\begin{array}{cc}\hfill {ϵ}_{g,k}^1& =L^0{b}_k^{n,i}\left({\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t\mathbb{E}\left[D_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]ds\lambda \left(de\right)dt-\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\mathbb{E}\left[D_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right)dt\right)\hfill \\ \hfill & =L^0{b}_k^{n,i}\mathbb{E}\left[\mathsf{\Phi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n)|{ℱ}_{t_n}\right]\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{\int }_{\mathcal{E}}\lambda \left(de\right)dsdt-\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\lambda \left(de\right)dt\right),\hfill \end{array}$$

(52)

which by using the fact

$${\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{\int }_{\mathcal{E}}\lambda \left(de\right)dsdt=\frac{1}{2}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\lambda \left(de\right)dt=\frac{1}{2}{(\Delta t)}^2{\lambda }_{\mathcal{E}}$$

gives ${\epsilon }_{g,x_k}^1=0$. Similarly, note that

$$\begin{array}{cc}\hfill {\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\lambda \left(de\right)=& \sum _{j\in S}{\int }_{{\Delta }_{ij}}\left(a_k(t_n,X^{n,i},i+h(i,e))-a_k(t_n,X^{n,i},i)\right)\lambda \left(de\right)\hfill \\ \hfill =& \sum _{j\in S}{\int }_{{\Delta }_{ij}}\left(a_k(t_n,X^{n,i},j)-a_k(t_n,X^{n,i},i)\right)\lambda \left(de\right)=\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}},\hfill \end{array}$$

(53)

we deduce

$$\begin{array}{cc}\hfill {ϵ}_{g,k}^2=& {\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^s\mathbb{E}\left[D_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]{\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\lambda \left(de\right)dtds\hfill \\ & -\frac{1}{2{\lambda }_{\mathcal{E}}}\Delta t\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}}{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}\mathbb{E}\left[D_{t,e}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(de\right)dt\hfill \\ \hfill =& \frac{1}{2}{(\Delta t)}^2\left({\int }_{\mathcal{E}}{L}_e^1{a}_k^{n,i}\lambda \left(de\right)-\sum _{j\in S}{L}^{i,j}{a}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\right)\mathbb{E}\left[\mathsf{\Phi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n)|{ℱ}_{t_n}\right]=0.\hfill \end{array}$$

(54)

Using Itô’s formula, we can obtain ${\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{t}d{\tilde{N}}_{s}d{\tilde{N}}_t=\frac{1}{2}\left({(\Delta {\tilde{N}}_n)}^2-{\lambda }_{\mathcal{E}}\Delta t-\Delta {\tilde{N}}_n\right)$, note also that

$$\begin{array}{cc}\hfill {\int }_{\mathcal{E}}{L}_e^1{b}_k^{n,i}\lambda \left(de\right)=& \sum _{j\in S}{\int }_{{\Delta }_{ij}}\left(b_k(t_n,X^{n,i},i+h(i,e))-b_k(t_n,X^{n,i},i)\right)\lambda \left(de\right)\hfill \\ \hfill =& \sum _{j\in S}{\int }_{{\Delta }_{ij}}\left(b_k(t_n,X^{n,i},j)-b_k(t_n,X^{n,i},i)\right)\lambda \left(de\right)=\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}},\hfill \end{array}$$

(55)

by the duality formula we have

$$\begin{array}{cc}\hfill {ϵ}_{g,k}^3=& \mathbb{E}\left[\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{L}_e^1{b}_k^{n,i}d{\tilde{N}}_{s}d{\tilde{N}}_t-\frac{1}{2{\lambda }_{\mathcal{E}}}\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\left({(\Delta {\tilde{N}}_n)}^2-{\lambda }_{\mathcal{E}}\Delta t-\Delta {\tilde{N}}_n\right)\right)|{ℱ}_{t_n}\right]\hfill \\ \hfill =& {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_{e_1}^1{b}_k^{n,i}\mathbb{E}\left[D_{s,e_1}{D}_{t,e_2}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(d{e}_1\right)ds\lambda \left(d{e}_2\right)dt\hfill \\ & -\frac{1}{2{\lambda }_{\mathcal{E}}}\Delta t\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}}{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{\mathcal{E}}\mathbb{E}\left[D_{s,e_1}{D}_{t,e_2}\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]\lambda \left(d{e}_1\right)ds\lambda \left(d{e}_2\right)dt\hfill \\ \hfill =& \frac{1}{2}{(\Delta t)}^2{\lambda }_{\mathcal{E}}\left({\int }_{\mathcal{E}}{L}_e^1{b}_k^{n,i}\lambda \left(de\right)-\sum _{j\in S}{L}^{i,j}{b}_k^{n,i}{\lambda }_{{\Delta }_{ij}}\right)\mathbb{E}\left[\mathsf{\Psi }(t_n,X^n,\Delta t,\Delta {\tilde{N}}_n)|{ℱ}_{t_n}\right]=0.\hfill \end{array}$$

(56)

Applying the duality formula in Lemma 3, we have

$$\begin{array}{c}\hfill |{ϵ}_{g,k}^4|=|\sum _{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{I}_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}{\left[\mathbb{E}\left[D_{s_1{s}_2{s}_3,e}^{\alpha }\left(\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)\right)f_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i})|{ℱ}_{t_n}\right]\right]}_{t_n,t_{n+1}}|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.\end{array}$$

(57)

Combining Equation (50), ${ϵ}_{g,k}^1={ϵ}_{g,k}^2={ϵ}_{g,k}^3=0,$ and inequality (57), we have

$$|J_1^n|=|\mathbb{E}[\sum _{k=1}^d\frac{\partial }{\partial x_k}g\left(X^{n+1,i}\right)(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})|{ℱ}_{t_n}[|\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.$$

(58)

For $\alpha =(1,1,1)$, by using the Itô isometry Formula (4), we obtain

$$\begin{array}{cc}& \mathbb{E}\left[{\left({\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^{s_3}{\int }_{t_n}^{s_2}{f}_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i})d{\tilde{N}}_{s_1}d{\tilde{N}}_{s_2}d{\tilde{N}}_{s_3}\right)}^2|{ℱ}_{t_n}\right]\hfill \\ \hfill & =\mathbb{E}\left[{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_3}{\int }_{\mathcal{E}}{\int }_{t_n}^{s_2}{\int }_{\mathcal{E}}{f}_{k,\alpha }^2(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i})\lambda \left(d{e}_1\right)d{s}_1\lambda \left(d{e}_2\right)d{s}_2\lambda \left(d{e}_3\right)d{s}_3|{ℱ}_{t_n}\right]\hfill \\ & =I_{{\lambda }_{\alpha }}^{{\mathbf{0}}_{\mathbf{3}}}\mathbb{E}\left[f_{k,\alpha }^2(·,X_{·}^{n,i},r_{·}^{n,i})|{ℱ}_{t_n}\right].\hfill \end{array}$$

(59)

For $\alpha \ne (1,1,1)$, we obtain

$$\begin{array}{cc}& \sum _{\genfrac{}{}{0pt}{}{\alpha \in \mathcal{B}\left({\mathsf{\Gamma }}_2\right)}{\alpha \ne (1,1,1)}}|\mathbb{E}\left[I_{\alpha }\left[f_{k,\alpha }(s_1,X_{s_1}^{n,i},r_{s_1}^{n,i})\right]|{ℱ}_{t_n}\right]{|}^2\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.\hfill \end{array}$$

(60)

Combining inequalities (59) and (60), we have

$$J_2^n={\int }_0^1{\int }_0^1\mathbb{E}\left[{\left(\sum _{k=1}^d(X_{k,t_{n+1}}^{n,i}-X_k^{n+1,i})\frac{\partial }{\partial x_k}\right)}^{2}g\left(X^{n+1,i}+{\mu }_1{\mu }_2(X_{t_{n+1}}^{n,i}-X^{n+1,i})\right)|{ℱ}_{t_n}\right]{\mu }_{1}d{\mu }_{1}d{\mu }_2\le C(1+|X^{n,i}{|}^m){(\Delta t)}^3.$$

(61)

From inequalities (58) and (61), we finally obtain

$$|\mathbb{E}\left[g\left(X_{t_{n+1}}^{n,i}\right)-g\left(X^{n+1,i}\right)|{ℱ}_{t_n}\right]|\le C(1+{|X^{n,i}|}^m){(\Delta t)}^3.$$

□

4. Numerical Experiments

Assume that the state space Markov chain $r_t$ is in $\mathbb{S}=\{1,2,3\}$, and the transition probability matrix is

$$P={\left[\begin{array}{ccc}0.3\hfill & 0.6\hfill & 0.1\hfill \\ 0.2\hfill & 0.7\hfill & 0.1\hfill \\ 0.4\hfill & 0.4\hfill & 0.2\hfill \end{array}\right]}_{3\times 3}.$$

We choose $N_{sp}=5000$ as the sample size for our numerical experiments, where $N_{sp}$ is the total number of sample pathways. We can measure the average errors of local weak convergence and the errors of global weak convergence as follows:

$$e_{\Delta t}^{\mathrm{global}}:=\left|\frac{1}{N_{sp}}\sum _{i=1}^{N_{sp}}\left(\phi \left(X_i^N\right)-\phi \left(X_{i,t_N}\right)\right)\right|,e_{\Delta t}^{\mathrm{local}}:=\left|\frac{1}{N_{sp}}\frac{1}{N}\sum _{i=1}^{N_{sp}}\sum _{j=1}^N\left(\phi \left(X_i^j\right)-\phi \left(X_{i,t_j}\right)\right)\right|,$$

where $N=T/\Delta t$, $\Delta t$ are ${\displaystyle \frac{1}{8}},{\displaystyle \frac{1}{16}},{\displaystyle \frac{1}{32}},{\displaystyle \frac{1}{64}},{\displaystyle \frac{1}{128}}$. We let $\phi \left(X_i^j\right)=sin\left(X_i^j\right)$. Let $X^{n,i}$ represent numerical solution and $X_{t_n}$ represent explicit solutions at the time $t_n$, where $j\in \{1,2,...,N\}$.

Now, we give three numerical examples, including mark-dependent PJ-SDEwMs, mark-independent PJ-SDEwMs (Ornstein-Uhlenbeck type) and PJ-SDEwMs (geometrical type).

Example 1.

We consider the following mark-dependent PJ-SDEwMs:

$$\left\{\begin{array}{c}d{X}_t=-\mu X_{t}dt+{\int }_{\mathcal{E}}g\left(r_t\right)e\tilde{N}(de,dt),\hfill \\ X_0=0.5,r_0=0.5,\hfill \end{array}\right.$$

(62)

where $\mu$ is a constant and the Markov chain $r_t$ is in $\mathbb{S}=\{1,2,3\}$. The group coefficients g are given by $g\left(1\right)=0.35,g\left(2\right)=0.3,g\left(3\right)=0.25.$ We use the Itô formula to obtain the explicit solution of Equation (62) which is

$$X_t=X_0·e^{-\mu t}+e^{-\mu t}{\int }_0^t{\int }_{\mathcal{E}}g\left(r_s\right)e^{\mu s}e\tilde{N}(de,ds).$$

Assume $T=1$ and $\mathcal{E}=[0,1],$ and the pairs $({\tau }_m,{\xi }_m)$ ($N_{t_n}+1\le m\le N_{t_{n+1}}$) are independent uniformly distributed in the square $[0,1]\times [0,1].$ Assume the kernel function $\gamma \left(e\right)=e$, we have for ${\Delta }_{ij}=[a_{ij},a_{ij}+q_{ij}]$

$$\begin{array}{cc}\hfill & {\lambda }_{{\Delta }_{ij}}={\int }_{{\Delta }_{ij}}\lambda \left(de\right)={\int }_{{\Delta }_{ij}}ede=\frac{1}{2}{e}^2{|}_{a_{ij}}^{a_{ij}+q_{ij}}=\frac{1}{2}{q}_{ij}(2a_{ij}+q_{ij}),\hfill \\ \hfill & {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}e\tilde{N}(de,ds)=\sum _{m=N_{t_n}+1}^{N_{t_{n+1}}}{\xi }_m,{\int }_{\mathcal{E}}\lambda \left(de\right)={\int }_0^1\gamma \left(e\right)de=\frac{1}{2}.\hfill \end{array}$$

Then, for solving the PJ-SDEwMs (62), we have Scheme 2 with the form

$$\begin{array}{cc}\hfill X^{n+1,i}=& X^{n,i}-\mu X^{n,i}\Delta t+g\left(i\right){\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}e\tilde{N}(de,dt)+\frac{1}{2}{(\Delta t)}^2{\mu }^2{X}^{n,i}+\frac{1}{2}\sum _{j\in S}(g\left(j\right)-g\left(i\right))q_{ij}\Delta t{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}e\tilde{N}(de,dt)\hfill \\ & +{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_{e_1}^{1}g\left(i\right)e_2\tilde{N}\left(d{e}_1,ds\right)\tilde{N}\left(d{e}_2,dt\right),\hfill \end{array}$$

which by the computation of compound Poisson process (see [27]) and the trapezoidal rule gives

$$\begin{array}{cc}\hfill & {\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_{e_1}^{1}g\left(i\right)e_2\tilde{N}\left(d{e}_1,ds\right)\tilde{N}\left(d{e}_2,dt\right)\hfill \\ \hfill & =\sum _{j\in S}(g\left(j\right)-g\left(i\right)){\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{e}_2\left(N_t^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left(t-t_n\right)\right)N\left(d{e}_2,dt\right)\hfill \\ \hfill & -\sum _{j\in S}(g\left(j\right)-g\left(i\right)){\int }_{\mathcal{E}}{e}_2\lambda \left(d{e}_2\right){\int }_{t_n}^{t_{n+1}}\left(N_t^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left(t-t_n\right)\right)dt\hfill \\ \hfill & =\sum _{j\in S}\sum _{m=N_{t_n}+1}^{N_{t_{n+1}}}(g\left(j\right)-g\left(i\right)){\xi }_m\left(N_{{\tau }_m}^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\left({\tau }_m-t_n\right)\right)\hfill \\ & -\frac{1}{6}\sum _{j\in S}(g\left(j\right)-g\left(i\right))\Delta t\left(N_{t_{n+1}}^{{\Delta }_{ij}}-N_{t_n}^{{\Delta }_{ij}}-{\lambda }_{{\Delta }_{ij}}\Delta t+2R_N^n\right),\hfill \end{array}$$

where ${\int }_{\mathcal{E}}{e}_2\lambda \left(d{e}_2\right)={\int }_0^1{e}_2^{2}d{e}_2=\frac{1}{3},$ ${\int }_{t_n}^{t_{n+1}}\left(t-t_n\right)dt=\frac{1}{2}{(\Delta t)}^2,$ ${\tilde{N}}_t^{{\Delta }_{ij}}={\int }_0^t{\int }_{{\Delta }_{ij}}\tilde{N}(de,ds),$ $N_t^{{\Delta }_{ij}}={\int }_0^t{\int }_{{\Delta }_{ij}}N(de,ds),$

$${\int }_{t_n}^{t_{n+1}}{N}_t^{{\Delta }_{ij}}dt=\frac{1}{2}(N_{t_n}^{{\Delta }_{ij}}+N_{t_{n+1}}^{{\Delta }_{ij}})\Delta t+R_N^n.$$

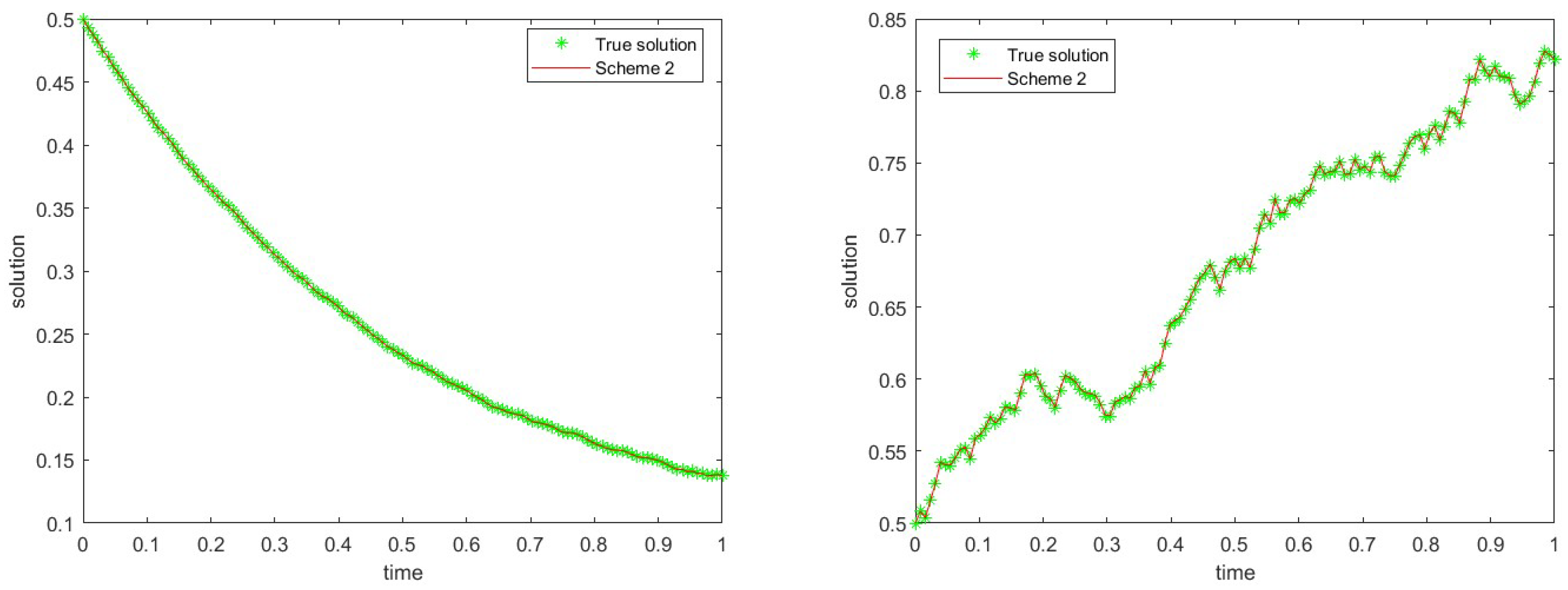
We use CR to represent the rate of convergence over the time step $\Delta t$. To evaluate the performance of Scheme 2, we calculate their global errors and average local errors. It is gratifying to find that the global convergence rate (Glo.CR) has order 2.0, while the average local convergence rate (Avg.local CR) has order 3.0. This means that Scheme 2 has excellent convergence properties and shows the great accuracy in numerical calculations (see Table 1). At the same time, we draw trajectories of numerical and analytical solutions in Figure 1. By comparing different state values, it was found that regardless of how the state values change, the simulation efficacy demonstrated by Scheme 2 remains highly favorable.

Table 1. The results of convergence rates and errors for Scheme 2 in Example 1.

N	Global Errors	CR	Avg. Local Errors	CR
8	1.619 $\times {10}^{-3}$		2.296 $\times {10}^{-4}$
16	4.007 $\times {10}^{-4}$	1.9921	3.001 $\times {10}^{-5}$	2.993
32	8.914 $\times {10}^{-5}$	2.0111	2.967 $\times {10}^{-6}$	3.0846
64	2.107 $\times {10}^{-5}$	2.0237	3.601 $\times {10}^{-7}$	3.1007
128	6.108 $\times {10}^{-6}$	2.1063	5.229 $\times {10}^{-8}$	3.0991

Figure 1. (Left) True solution and numerical solution when $g\left(1\right)=0.35,g\left(2\right)=0.3$. (Right) True solution and numerical solution when $g\left(1\right)=3.5,g\left(2\right)=3$.

Example 2.

Consider the Ornstein–Uhlenbeck (O-U) PJ-SDEwMs as follows:

$$\left\{\begin{array}{c}d{X}_t=-\mu X_{t}dt+{\int }_{\mathcal{E}}g\left(r_t\right)\tilde{N}(de,dt),\hfill \\ X_0=0.5,r_0=0.5,\hfill \end{array}\right.$$

(63)

where $\mu$ is a constant and the Markov chain $r_t$ is in $\mathbb{S}=\{1,2\},$ and the group coefficients g are given by $g\left(1\right)=0.3$ and $g\left(2\right)=0.25.$ It is evident that Equation (63) possesses an explicit solution:

$$X_t=X_0·e^{-\mu t}+{\int }_0^t{\int }_{\mathcal{E}}{e}^{-\mu (t-s)}g\left(r_s\right)\tilde{N}(de,ds).$$

According to the evaluation results presented in Table 2, a detailed analysis was conducted regarding the performance of Schemes 2 and 3. The evaluation included the calculation of their global error and average local error. Interestingly, both Schemes 2 and 3 demonstrated a second-order convergence rate during the global convergence process, indicating a relatively rapid approach towards the optimal solution. Furthermore, in terms of local convergence performance, both schemes exhibited a higher level of convergence with a third-order average convergence rate. This finding suggests that both Schemes 2 and 3 exhibit favorable performance. In Table 3, we compare the global errors and convergence rate of the Euler scheme, Schemes 2 and 3. It is obvious that Scheme 3 makes it simpler and more convenient for us to calculate in comparison to Scheme 2. Equally gratifying is that Scheme 3 greatly reduces the computing time. Scheme 3 takes 3.597104 seconds, while Scheme 2 takes 10.024912 seconds.

Table 2. The results of convergence rates and errors for Scheme 3 in Example 2.

N	Global Errors	CR	Avg. Local Errors	CR
8	1.723 $\times {10}^{-3}$		2.157 $\times {10}^{-4}$
16	3.880 $\times {10}^{-4}$	2.1502	2.430 $\times {10}^{-5}$	3.1497
32	9.239 $\times {10}^{-5}$	2.1103	2.887 $\times {10}^{-6}$	3.1114
64	2.255 $\times {10}^{-5}$	2.0835	3.542 $\times {10}^{-7}$	3.0823
128	5.583 $\times {10}^{-6}$	2.0643	4.350 $\times {10}^{-8}$	3.0651

Table 3. The results of global convergence rates and errors for three schemes in Example 2.

N	8	16	32	64	128	CR	Time (s)
Euler Scheme	1.765 $\times {10}^{-2}$	8.645 $\times {10}^{-3}$	4.277 $\times {10}^{-3}$	2.124 $\times {10}^{-3}$	1.060 $\times {10}^{-3}$	1.0139	0.382757
Scheme 2	1.186 $\times {10}^{-2}$	4.874 $\times {10}^{-4}$	3.115 $\times {10}^{-5}$	2.992 $\times {10}^{-5}$	6.502 $\times {10}^{-6}$	2.0992	10.024912
Scheme 3	1.723 $\times {10}^{-2}$	3.889 $\times {10}^{-4}$	9.249 $\times {10}^{-5}$	2.255 $\times {10}^{-5}$	5.587 $\times {10}^{-6}$	2.0646	3.597104

Example 3.

We consider the following PJ-SDEwMs with mark-independent jump coefficient:

$$\left\{\begin{array}{c}d{X}_t=X_t·f\left(r_t\right)dt+{\int }_{\mathcal{E}}{X}_t·g\left(r_t\right)\tilde{N}(de,dt),\hfill \\ X_0=0.5,r_0=0.5,\hfill \end{array}\right.$$

(64)

where the Markov chain $r_t$ is in $\mathbb{S}=\{1,2\}$, and $\tilde{N}(de,dt)$ represents a compensated Poisson measure in one dimension. Assuming that $N_t$ and $r_t$ are independent, with the group coefficients f and g provided by

$$f\left(1\right)=2,g\left(1\right)=0.3,f\left(2\right)=1.5,g\left(2\right)=0.2.$$

We utilize the Itô formula to derive the explicit solution for Equation (64) as

$$X_t=X_{0}exp\left({\int }_0^{t}f\left(r_s\right)ds\right.\left.+{\int }_0^t{\int }_{\mathcal{E}}ln|1+g\left(r_s\right)|\tilde{N}(de,ds)\right).$$

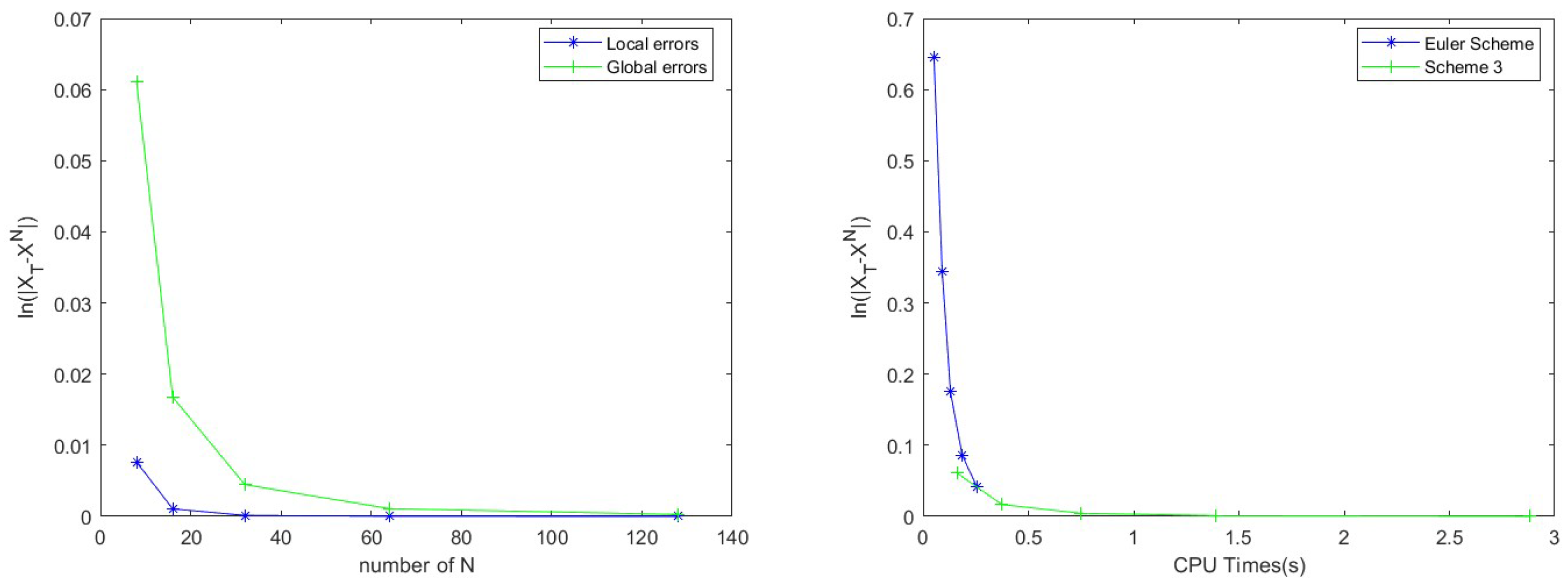
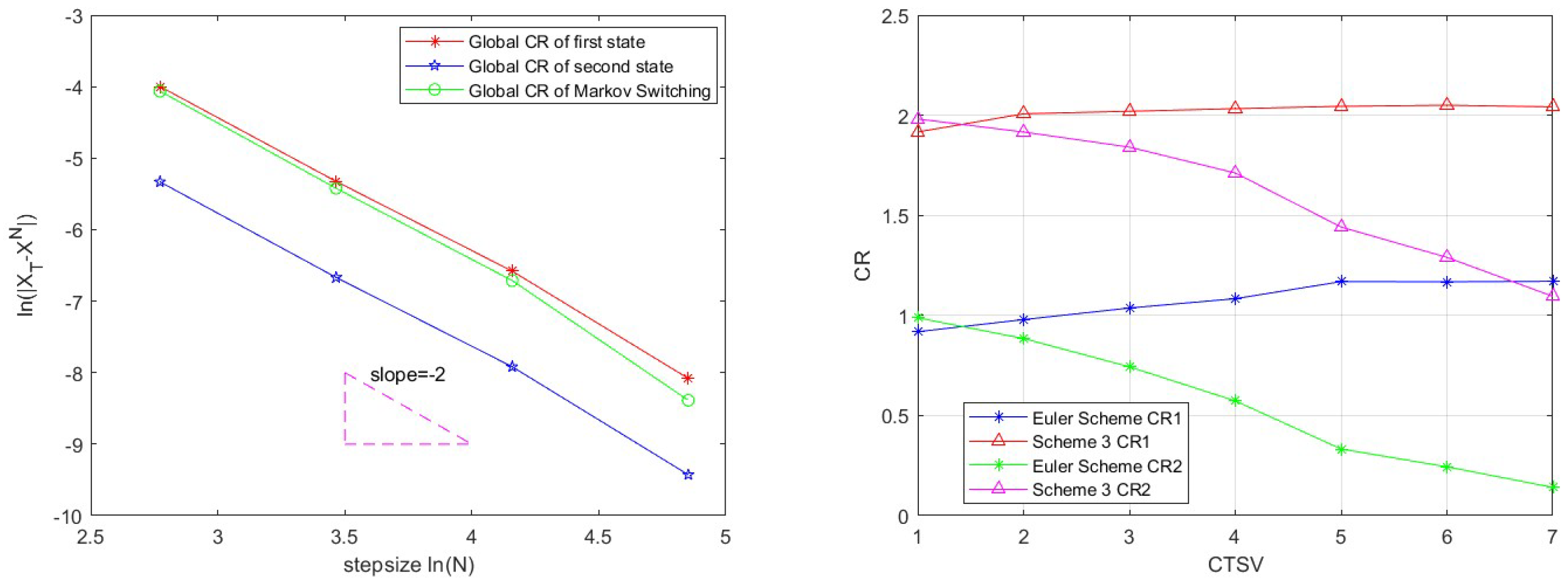
The time $t\in [0,T]$ with $T=1$ is set in Table 4, and we use Scheme 3 to solve the PJ-SDEwMs (64). Scheme 3 has the second-order global convergence rate (Glo.CR) and the third-order average local convergence rate (Avg.local CR). In Table 5 and Table 6, we compare the Euler Scheme with Scheme 3 with different state values. For clearer display, we draw two pictures (errors of the new scheme and CPU times) according to the two tables in Figure 1. In Figure 2 (left), we clearly demonstrate that there are differences in global errors between individual states and transition states. For a more intuitive presentation, Figure 3 (right) illustrates the fluctuation of convergence rates as the number of times changes, showcasing the process of convergence rate variation with the change in state value times (CTSV). These visualizations allow us to gain a clearer understanding of the impact of state changes on convergence rates. The observation enhances our comprehension of the dynamic nature of the system.

Table 4. The results of convergence rates and errors for Scheme 3 in Example 3.

N	Global Errors	CR	Avg. Local Errors	CR
8	6.129 $\times {10}^{-2}$		7.646 $\times {10}^{-3}$
16	1.558 $\times {10}^{-2}$	1.9764	9.623 $\times {10}^{-4}$	2.9902
32	3.931 $\times {10}^{-3}$	1.9814	1.219 $\times {10}^{-4}$	2.9854
64	1.019 $\times {10}^{-3}$	1.9717	1.518 $\times {10}^{-5}$	2.9909
128	1.944 $\times {10}^{-4}$	2.0535	1.825 $\times {10}^{-6}$	3.0051

Table 5. Global convergence rates of multiple groups of different state values for two schemes with $X_0=0.5$.

$\left[\mathit{f}\right(1),\mathit{f}(2\left)\right]$	$[3,2.5]$	$[3,2]$	$[3,1.5]$	$[3,1]$	$[3,0.1]$	$[3,0.05]$	$[3,0.01]$
$\left[\mathbf{g}\right(\mathbf{1}),\mathbf{g}(\mathbf{2}\left)\right]$	$[\mathbf{0}.\mathbf{35},\mathbf{0}.\mathbf{3}]$	$[\mathbf{0}.\mathbf{35},\mathbf{0}.\mathbf{26}]$	$[\mathbf{0}.\mathbf{35},\mathbf{0}.\mathbf{2}]$	$[\mathbf{0}.\mathbf{35},\mathbf{0}.\mathbf{18}]$	$[\mathbf{0.35},\mathbf{0.1}]$	$[\mathbf{0}.\mathbf{35},\mathbf{0}.\mathbf{02}]$	$[\mathbf{0}.\mathbf{35},\mathbf{0}.\mathbf{01}]$
Euler Scheme CR1	0.9187	0.9793	1.0371	1.0837	1.169	1.1682	1.1703
Scheme 3 CR1	1.9163	2.0072	2.0197	2.0328	2.0446	2.0501	2.0418

Table 6. Global convergence rates of multiple groups of different state values in two schemes with $X_0=0.5$.

$\left[\mathit{f}\right(1),\mathit{f}(2\left)\right]$	$[2,1.5]$	$[3.5,3]$	$[5.5,5]$	$[8,7.5]$	$[12.5,12]$	$[15,14.5]$	$[17.5,17]$
$\left[\mathbf{g}\right(\mathbf{1}),\mathbf{g}(\mathbf{2}\left)\right]$	$[\mathbf{0}.\mathbf{3},\mathbf{0}.\mathbf{2}]$	$[\mathbf{0}.\mathbf{4},\mathbf{0}.\mathbf{3}]$	$[\mathbf{0}.\mathbf{6},\mathbf{0}.\mathbf{5}]$	$[\mathbf{1},\mathbf{0}.\mathbf{9}]$	$[\mathbf{1}.\mathbf{8},\mathbf{1}.\mathbf{7}]$	$[\mathbf{2}.\mathbf{8},\mathbf{2}.\mathbf{7}]$	$[\mathbf{3}.\mathbf{5},\mathbf{3}.\mathbf{4}]$
Euler Scheme CR2	0.9881	0.8845	0.7432	0.5731	0.3326	0.2439	0.1410
Scheme 3 CR2	1.9813	1.9160	1.8405	1.7114	1.4414	1.2898	1.0951

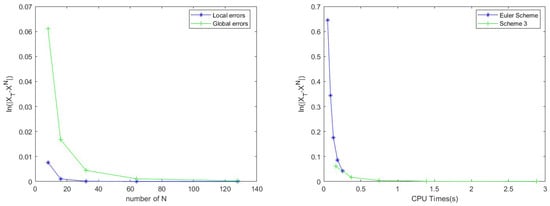
Figure 2. (Left) The results of the global errors and the average local errors for Scheme 3 in Example 3. (Right) The correlations for global errors and CPU time of all schemes.

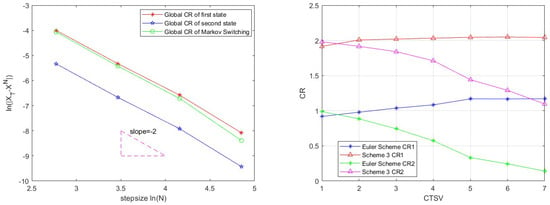
Figure 3. (Left) The convergence rates of different states. (Right) The correlations for global convergence rates and the variation of state values.

5. Discussion

In this work, we mainly study stochastic differential equations with Markovian switching driven by pure jumps (PJ-SDEwMs) and give three numerical schemes. In general, PJ-SDEwMs contains mark-dependent jump coefficient $b=b(t,X_t,r_t,e)$, which we can solve using Schemes 1 and 2. Compared to the Itô-Taylor expansion scheme (Scheme 1), Scheme 2 is easier to calculate by using the trapezoidal rule to approximate the following multiple stochastic integrals:

$${\int }_{t_n}^{t_{n+1}}{\int }_{t_n}^t{\int }_{\mathcal{E}}{L}_e^{1}a(s,X_s,r_s)\tilde{N}(de,ds)dtand{\int }_{t_n}^{t_{n+1}}{\int }_{\mathcal{E}}{\int }_{t_n}^t{L}^{0}b(s,X_s,r_s,e)ds\tilde{N}(de,dt).$$

In particular, PJ-SDEwMs contains mark-independent jump coefficient $b=b(t,X_t,r_t)$, we can compute it in Schemes 2 and 3. Because multidimensional random integrals are avoided, Scheme 3 is simpler and more convenient (Example 2 demonstrates this very well). In addition, by using Malliavin calculus theory, we strictly proved that the proposed new schemes have local weak order-3.0 convergence rates. However, through Example 3, we find that as the upper bound of the state values gradually increases, the simulation effect of Scheme 3 is still good, but the convergence rates will gradually decrease.

6. Conclusions

In this paper, we propose three new weak second-order numerical schemes to solve stochastic differential equations with Markovian switching driven by pure jumps. By using the Malliavin stochastic analysis method, the new schemes are strictly analyzed theoretically, and the second-order convergence rate is proven. Finally, the correctness and effectiveness of the second-order schemes are verified by three numerical experiments. In addition, we find that as the upper bound of the state values increases, the global convergence rate of Scheme 3 gradually decreases to the first-order. Besides, the maximum state difference and the variation of Markov chains have a certain impact on the convergence rate.