Sheffer Stroke Hilbert Algebras Stabilizing by Ideals

Abstract

This manuscript aims to provide a new characterization of Sheffer stroke Hilbert algebras due to their ideals and proposes stabilizers. In the setup of the main results, we construct particular subsets of Sheffer stroke Hilbert algebras and we propose important properties of these subsets by investigating whether these sets are ideals or not. Furthermore, we investigate whether the introduced subsets of Sheffer stroke Hilbert algebras are minimal ideals. Afterwards, we define stabilizers in a Sheffer stroke Hilbert algebra and obtain their set theoretical properties. As an implementation of the theoretical findings, we present numerous examples and illustrative remarks to guide readers.

1. Introduction

Sheffer stroke is a binary operation which was introduced by H. M. Sheffer in his landmark paper [1]. This notion enables mathematicians to reduce and unify the number of axioms and notations in algebraic structures, and it provides compact representations. In the last three decades, Sheffer stroke has attracted remarkable interest from researchers and is extensively applied to algebraic structures. In addition to the theoretical point of view, Sheffer stroke has been utilized in numerous crucial research projects in the engineering sciences. Conducting a quick literature review, one may easily find important applications of Sheffer stroke in the design of chips. We refer readers to the interesting projects found in references [2,3,4,5,6]. Motivated by the application potential of Sheffer stroke, scholars have applied this binary operation in implicational algebras, ortholattices and Boolean algebras. Undoubtedly, there is a vast wealth of literature on this topic and we refer to [7,8,9] as particularly interesting papers.

As an algebraic counterpart of Hilbert’s positive implicative propositional calculus [10], Hilbert algebras were proposed by Henkin and Skolem in [11] and employed in research based on various types of logic. Hilbert algebras have been brought into the spotlight in many papers and their main properties have been investigated. In a recent paper [12], the authors studied the Sheffer stroke operation and Sheffer stroke basic algebra. They presented the Sheffer stroke basic algebra on a given interval, named interval Sheffer stroke basic algebra, and gave some features of an interval Sheffer stroke basic algebra, while, in [13], Hilbert algebras and the relationship between Sheffer stroke and Hilbert algebras was introduced. Subsequently, Sheffer stroke Hilbert algebras are being studied in brand-new papers ([14,15,16]) due to fuzzy filters, fuzzy ideals with t-conorms and neutrosophic structures. We shall highlight that establishing stabilizers for algebraic structures has always been an interesting but gruelling task in theoretical mathematics. This objective has been achieved in many papers regarding residuated lattices and BL-algebras (see [17,18,19,20]). To the best of our knowledge, stabilizers of Hilbert algebras have not been handled so far. Thus, the main objective of this manuscript is to fill this gap by proposing Sheffer stroke stabilizers of Hilbert algebras and improving the ongoing theory on this subject.

The organization of the manuscript is as follows: in the next section, we provide background material on Sheffer stroke Hilbert algebras and ideals. In Section 3, we represent characterizations of Sheffer stroke Hilbert algebras due to ideals. We present the main outcomes of the manuscript and propose stabilizers of Sheffer stroke Hilbert algebras in Section 4.

2. Preliminaries

In this section, we give basic definitions and notions about Sheffer stroke Hilbert algebras and ideals.

Definition 1

([8]). Let $\Im =(T,\circ )$ be a groupoid. The operation ∘ is said to be a Sheffer stroke if it satisfies the following conditions for all $x,y,z\in T.$

(S1)

$x\circ y=y\circ x,$

(S2)

$(x\circ x)\circ (x\circ y)=x,$

(S3)

$x\circ \left(\right(y\circ z)\circ (y\circ z\left)\right)=\left(\right(x\circ y)\circ (x\circ y\left)\right)\circ z$,

(S4)

$(x\circ ((x\circ x)\circ (y\circ y)\left)\right)\circ (x\circ ((x\circ x)\circ (y\circ y)\left)\right)=x$.

In Definition 1, a groupoid can be determined as a group with a partial function which especially states a binary operation in category theory and homotopy theory.

Definition 2

([13]). A Sheffer stroke Hilbert algebra is a structure $(T,\circ )$ of type (2), in which T is a nonempty set and ∘ is Sheffer stroke on T, such that the following identities are satisfied for all $x,y,z\in T$:

(SH_a1)

$(x\circ ((y\circ (z\circ z\left)\right)\circ (y\circ (z\circ z\left)\right)\left)\right)\circ \left(\right((x\circ (y\circ y\left)\right)\circ \left(\right(x\circ (z\circ z))\circ (x\circ (z\circ z)\left)\right))\circ$

$\left(\right(x\circ (y\circ y))\circ ((x\circ (z\circ z\left)\right)\circ (x\circ (z\circ z\left)\right)\left)\right))=x\circ (x\circ x)$

(SH_a2)

If $x\circ (y\circ y)=x\circ (x\circ x)=y\circ (x\circ x),$ then $x=y$.

Lemma 1

([13]). Let $(T,\circ )$ be a Sheffer stroke Hilbert algebra. Then, there exists a unique $1\in T$, such that the following identities hold for all $x\in T$:

1.

$x\circ (x\circ x)=1,$

2.

$x\circ (1\circ 1)=1$,

3.

$1\circ (x\circ x)=1$.

Lemma 2

([13]). Let $(T,\circ )$ be a Sheffer stroke Hilbert algebra. Then, the relation $x\preccurlyeq y$ if and only if $x\circ (y\circ y)=1$ is a partial order on T. Moreover, 1 is the greatest element of T.

Lemma 3

([13]). Let $(T,\circ )$ be a Sheffer stroke Hilbert algebra. Then, the following hold for all $x,y,z\in T$:

(Shb₁)

$x\preccurlyeq y\circ (x\circ x)$,

(Shb₂)

$x\circ \left(\right(y\circ (z\circ z))\circ (y\circ (z\circ z)\left)\right)=(x\circ (y\circ y\left)\right)\circ \left(\right(x\circ (z\circ z))\circ (x\circ (z\circ z)\left)\right)$,

(Shb₃)

$(x\circ (y\circ y\left)\right)\circ (y\circ y)=(y\circ (x\circ x\left)\right)\circ (x\circ x)$,

(Shb₄)

$x\circ \left(\right(y\circ (z\circ z))\circ (y\circ (z\circ z)\left)\right)=y\circ \left(\right(x\circ (z\circ z))\circ (y\circ (z\circ z)\left)\right)$,

(Shb₅)

$x\preccurlyeq (x\circ (y\circ y\left)\right)\circ (y\circ y)$,

(Shb₆)

$\left(\right(x\circ (y\circ y))\circ (y\circ y\left)\right)\circ (y\circ y)=x\circ (y\circ y)$,

(Shb₇)

$x\circ (y\circ y)\preccurlyeq (y\circ (z\circ z\left)\right)\circ \left(\right(x\circ (z\circ z))\circ (x\circ (z\circ z)\left)\right)$, and

(Shb₈)

if $x\preccurlyeq y$, then $z\circ (x\circ x)\preccurlyeq z\circ (y\circ y)$ and $y\circ (z\circ z)\preccurlyeq x\circ (z\circ z)$.

Lemma 4

([13]). Let $(T,\circ )$ be a Sheffer stroke Hilbert algebra with the least element 0, the greatest element 1, and a unary operation * on T be defined by $x^{\ast }=x\circ (0\circ 0)$ for all $x\in T$. Then, the followings hold, for all $x\in T$:

1.

$0\circ 0=1$ and $1\circ 1=0$,

2.

$0^{\ast }=1$ and $1^{\ast }=0$,

3.

$x\circ 1=x\circ x$,

4.

$x^{\ast }=x\circ x$,

5.

$x\circ 0=1$,

6.

${\left(x^{\ast }\right)}^{\ast }=x$, and

7.

$x\circ x^{\ast }=1$.

Lemma 5

([13]). Let $(T,\circ )$ be a Sheffer stroke Hilbert algebra and ≼ be a natural ordering induced by this algebra. Then, $(T,\preccurlyeq )$ is a join-semilattice with the greatest element 1, where $x\vee y=(x\circ (y\circ y\left)\right)\circ (y\circ y)$, for all $x,y\in T$. If $(T,\circ )$ is a Sheffer stroke Hilbert algebra with the least element 0, then $(T,\preccurlyeq )$ is a meet-semilattice, and $x\wedge y=\left(\right(x\circ x)\vee (y\circ y\left)\right)\circ \left(\right(x\circ x)\vee (y\circ y\left)\right)$, for all $x,y\in T$.

Definition 3

([13]). A nonempty subset ℓ of a Sheffer stroke Hilbert algebra $(T,\circ )$ is called an ideal if

(SSHI1)

$0\in \mathcal{\ell }$,

(SSHI2)

$(x\circ (y\circ y\left)\right)\circ (x\circ (y\circ y\left)\right)\in \mathcal{\ell }$ and $y\in \mathcal{\ell }$ imply $x\in \mathcal{\ell }$, for all $x,y\in T$.

Theorem 1

([13]). Let ℓ be a subset of a Sheffer stroke Hilbert algebra $(T,\circ )$ such that $0\in \mathcal{\ell }$. Then, ℓ is an ideal of T if and only if $x\preccurlyeq y$ and $y\in \mathcal{\ell }$ imply $x\in \mathcal{\ell }$, for all $x,y\in T$.

3. Characterizations by Ideals

In this section, we characterize Sheffer stroke Hilbert algebras by ideals. Unless otherwise specified, T denotes a Sheffer stroke Hilbert algebra, and $\overleftrightarrow{xy}:=(x\circ (y\circ y))\circ (x\circ (y\circ y))$ is briefly written.

Define a subset $T_{x,y}$ of a Sheffer stroke Hilbert algebra T by

$$T_{x,y}=\{z\in T:\overleftrightarrow{zy}\preccurlyeq x\},$$

for any $x,y\in T$.

Lemma 6.

Let S be a nonempty subset of T. Then, the following conditions are equivalent:

1.

S is an ideal of T.

2.

$S\supseteq T_{X,Y}$, for all $x,y\in S$.

3.

$\overleftrightarrow{zx}\circ (y\circ y)=1$ implies $z\in S$, for all $x,y\in S$ and $z\in T$.

Proof. 

(1)⇒(2)

Let S be an ideal of T and $x,y\in S$. Suppose that $z\in T_{x,y}$. Then, $\overleftrightarrow{zy}\preccurlyeq x$. By Theorem 1, $\overleftrightarrow{zy}\in S$. Thence, $z\in S$ from (SSHI2).

(2)⇒(3)

Let $S\supseteq T_{x,y}$ and $\overleftrightarrow{zx}\circ (y\circ y)=1$, for any $x,y\in S$. Then, $\overleftrightarrow{zx}\preccurlyeq y\iff \overleftrightarrow{zy}\circ (x\circ x)=1\iff \overleftrightarrow{zy}\preccurlyeq x$ from Lemma 2, (S1) and (Shb₄). Thus, $z\in T_{x,y}$, and so, $z\in S$.

(3)⇒(1)

Let S be a nonempty subset of T such that $\overleftrightarrow{zx}\circ (y\circ y)=1$ implies $z\in S$, for any $x,y\in S$ and $z\in T$. Since $\left(\overleftrightarrow{0x}\right)\circ (y\circ y)=1$ from (S1) and Lemma 4 (5), it is obtained that $0\in S$. Assume that $\overleftrightarrow{xy}\in S$ and $y\in S$. Since $\overleftrightarrow{xx}\circ (y\circ y)=1$ from (S1) and Lemma 1 (1) and (2), it follows that $x\in S$.

□

Lemma 7.

Let T be a Sheffer stroke Hilbert algebra. Then,

1.

$T_{x,y}=T_{y,x}$,

2.

$T_{x,1}=T_{1,x}=T$,

3.

$T_{x,0}=T_{0,x}=\{z\in T:z\preccurlyeq x\}$,

4.

$T_{1,1}=T$,

5.

$T_{0,0}=\left\{0\right\}$,

6.

$0\in T_{x,y}$,

7.

if $x\preccurlyeq y$, then

(i) $T_{u,x}\subseteq T_{u,y}$,

(ii)$T_{x,u}\subseteq T_{y,u}$

for all $u,x,y\in T$.

Proof. 

1.

Since $z\in T_{x,y}\iff \overleftrightarrow{zy}\preccurlyeq x\iff \overleftrightarrow{zx}\preccurlyeq y\iff z\in T_{y,x}$ from Lemma 2, (S1) and (Shb₄), we have $T_{x,y}=T_{y,x}$.

2.

Since $\overleftrightarrow{z1}=1\circ 1=0\preccurlyeq x$ and $\overleftrightarrow{zx}\preccurlyeq 1$ from Lemma 4 (1) and Lemma 2, respectively, it is obtained from (1) that $T_{x,1}=T_{1,x}=T$, for all $x\in T.$

3.

Since $z=\overleftrightarrow{z0}\preccurlyeq x$ from (S2), Lemma 4 (1) and (3), it follows from (1) that $T_{x,0}=T_{0,x}=\{z\in T:z\preccurlyeq x\}$, for all $x\in T.$

4.

$T_{1,1}=\{z\in T:\overleftrightarrow{z1}=1\circ 1=0\preccurlyeq 1\}=T$ from Lemma 2 and Lemma 4 (1).

5.

$T_{0,0}=\{z\in T:z=\overleftrightarrow{z0}\preccurlyeq 0\}=\left\{0\right\}$, from (S2), Lemma 4 (1) and (3).

6.

Since $0=1\circ 1=\overleftrightarrow{0y}\preccurlyeq x$ from (S1), Lemma 4 (1) and (5), we establish that $0\in T_{x,y}$, for any $x,y\in T$.

7.

Let $x\preccurlyeq y$.

(i)

Then, $z\circ (x\circ x)\preccurlyeq z\circ (y\circ y)$ from (Shb₈), and

$$\begin{array}{c}\left(\right(z\circ (y\circ y))\circ (z\circ (y\circ y)\left)\right)\circ \left(\right((z\circ (x\circ x\left)\right)\circ \hfill \\ (z\circ (x\circ x\left)\right))\circ ((z\circ (x\circ x\left)\right)\circ (z\circ (x\circ x\left)\right)\left)\right)\hfill \\ =(z\circ (x\circ x\left)\right)\circ \left(\right(z\circ (y\circ y))\circ (z\circ (y\circ y)\left)\right)\hfill \\ =1\hfill \end{array}$$

from (S1) and (S2). It is obtained from Lemma 2 that $\overleftrightarrow{zy}\preccurlyeq \overleftrightarrow{zx}$, for all $x,y\in T$. Thus, $z\in T_{u,x}\Rightarrow \overleftrightarrow{zx}\preccurlyeq u\Rightarrow \overleftrightarrow{zy}\preccurlyeq \overleftrightarrow{zx}\preccurlyeq u\Rightarrow z\in T_{u,y}$, and so, $T_{u,x}\subseteq T_{u,y}$, for any $z\in T$.

(ii)

$T_{y,u}\preccurlyeq T_{x,u}$ is proved from (1) and (7) (i).

□

Lemma 8.

Let T be a Sheffer stroke Hilbert algebra. Then, $T_{x\vee y,u}\supseteq T_{x,u}\cup T_{y,u}$, for all $u,x,y\in T$.

Proof. 

Since $x\preccurlyeq x\vee y$ and $y\preccurlyeq x\vee y$, for all $x,y\in T$, we arrive at $T_{x,u}\subseteq T_{x\vee y,u}$ and $T_{y,u}\subseteq T_{x\vee y,u}$ from Lemma 7 (ii). Therefore, $T_{x,u}\cup T_{y,u}\subseteq T_{x\vee y,u}$, for all $u,x,y\in T$. □

Example 1

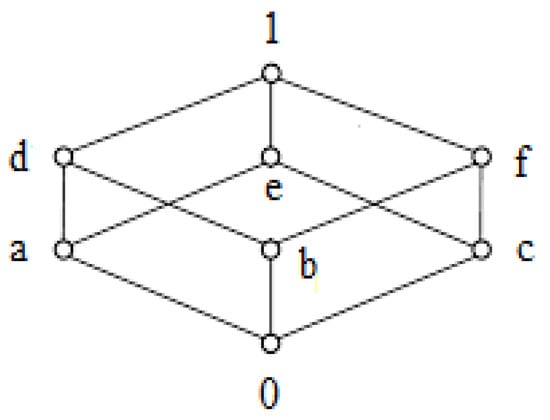
([13]). Consider a Sheffer stroke Hilbert algebra $(T,\circ )$ in which a set $T=\{0,a,b,c,d,e,f,1\}$ has the Hasse diagram in Figure 1 and the Sheffer operation ∘ has the Cayley table in Table 1:

Figure 1. Hasse diagram of T in Example 1.

Table 1. Cayley table of ∘ on T in Example 1.

∘	0	a	b	c	d	e	f	1
0	1	1	1	1	1	1	1	1
a	1	f	1	1	f	f	1	f
b	1	1	e	1	e	1	e	e
c	1	1	1	d	1	d	d	d
d	1	f	e	1	c	f	e	c
e	1	f	1	d	f	b	d	b
f	1	1	e	d	e	d	a	a
1	1	f	e	d	c	b	a	0

Then,

$$T_{a\vee f,e}=T_{1,e}=T\supseteq \{0,b\}=\left\{0\right\}\cup \{0,b\}=T_{a,e}\cup T_{f,e}.$$

Lemma 9.

Let T be a Sheffer stroke Hilbert algebra. Then, $T_{x\wedge y,u}=T_{x,u}\cap T_{y,u}$, for all $u,x,y\in T$.

Proof. 

Let $z\in T_{x,u}\cap T_{y,u}$. Since $z\in T_{x,u}$ and $z\in T_{y,u}$, we obtain $\overleftrightarrow{zu}\preccurlyeq x$ and $\overleftrightarrow{zu}\preccurlyeq y$, and so, $\overleftrightarrow{zu}\preccurlyeq x\wedge y$. Thus, $z\in T_{x\wedge y,u}$. Thence, $T_{x,u}\cap T_{y,u}\subseteq T_{x\wedge y,u}$, for all $u,x,y\in T$. Moreover, $T_{x\wedge y,u}\subseteq T_{x,u}$ and $T_{x\wedge y,u}\subseteq T_{y,u}$ from Lemma 7 (ii). So, $T_{x\wedge y,u}\subseteq T_{x,u}\cap T_{y,u}$, for all $u,x,y\in T$. □

Lemma 10.

Let ℓ be a nonempty subset of T. Then, ℓ is an ideal of T if and only if for all $x,y\in T$,

(SSHI3)

$x,y\in \mathcal{\ell }$ implies $x\vee y\in \mathcal{\ell }$, and

(SSHI4)

$x\preccurlyeq y$ and $y\in \mathcal{\ell }$ imply $x\in \mathcal{\ell }$.

Proof. 

Let ℓ be an ideal of T and $x,y\in \mathcal{\ell }$. Since $\overleftrightarrow{\overleftrightarrow{xy}x}=\overleftrightarrow{\overleftrightarrow{xx}y}=\overleftrightarrow{(y\circ y)\circ 1}=1\circ 1=0\in \mathcal{\ell }$ from (S1), (Shb₄), Lemma 1 (1), Lemma 4 (1) and (SSHI1), it follows from (SSHI2) that $\overleftrightarrow{xy}\in \mathcal{\ell }$, for any $x,y\in T$. Since $\overleftrightarrow{(x\vee y)y}=\overleftrightarrow{xy}\in \mathcal{\ell }$ from Lemma 5 and (Shb₆), we have from (SSHI2) that $x\vee y\in \mathcal{\ell }$, for any $x,y\in T$. Also, (SSHI4) is obvious from Theorem 1.

Conversely, let ℓ be a nonempty subset of T satisfying (SSHI3) and (SSHI4). Since 0 is the least element of T, it is obtained from (SSHI4) that $0\in \mathcal{\ell }$. Let $\overleftrightarrow{xy}\in \mathcal{\ell }$ and $y\in \mathcal{\ell }$, for any $x,y\in T$. Then, $x\vee y=\overleftrightarrow{xy}\vee y\in \mathcal{\ell }$ from Lemma 5, (S2) and (S3) and (SSHI3). Since $x\preccurlyeq x\vee y$, for any $x,y\in T$, we obtain from (SSHI4) that $x\in \mathcal{\ell }$, for any $x,y\in T$. □

Lemma 11.

Let T be a Sheffer stroke Hilbert algebra. Then, $T_{x\circ y,u}\supseteq T_{x\circ x,u}\cup T_{y\circ y,u}$ and $T_{x\circ y,u}\supseteq T_{x\circ x,u}\cap T_{y\circ y,u}$, for all $u,x,y\in T$.

Proof. 

Since $x\circ x\preccurlyeq x\circ y$ and $y\circ y\preccurlyeq x\circ y$ from (S1), (S2) and (Shb₁), it follows from Lemma 7 (ii) that $T_{x\circ x,u}\subseteq T_{x\circ y,u}$ and $T_{y\circ y,u}\subseteq T_{x\circ y,u}$, and so, $T_{x\circ y,u}\supseteq T_{x\circ x,u}\cup T_{y\circ y,u}$ and $T_{x\circ y,u}\supseteq T_{x\circ x,u}\cap T_{y\circ y,u}$, for all $u,x,y\in T$. □

Example 2.

Consider the Sheffer stroke Hilbert algebra $(T,\circ )$ in Example 1. Then, $T_{b\circ c,a}=T_{1,a}=T\supseteq \{0,a,b,c,d,e\}=\{0,a,c,e\}\cup \{0,a,b,d\}=T_{e,a}\cup T_{d,a}$ and $T_{b\circ c,a}=T_{1,a}=T\supseteq \{0,a\}=\{0,a,c,e\}\cap \{0,a,b,d\}=T_{e,a}\cap T_{d,a}$.

Lemma 12.

Let ℓ be a nonempty subset of T. Then, ℓ is an ideal of T if and only if ℓ^u$=\{z\in T:\overleftrightarrow{zu}\in \mathcal{\ell }\}$ is an ideal of T, for all $u\in T$.

Proof. 

Let ℓ be an ideal of T, and ${\mathcal{\ell }}^u=\{z\in T:\overleftrightarrow{zu}\in \mathcal{\ell }\}$ be a subset of T, for any $u\in T$. Since $\overleftrightarrow{0u}=\overleftrightarrow{(u\circ u)1}=1\circ 1=0\in \mathcal{\ell }$ from Lemma 1 (2), Lemma 4 (1) and (5), (S1) and (SSHI1), it is concluded that $0\in {\mathcal{\ell }}^u$. Assume that $\overleftrightarrow{xy}\in {\mathcal{\ell }}^u$ and $y\in {\mathcal{\ell }}^u$. Then, $\overleftrightarrow{\overleftrightarrow{xy}u}\in \mathcal{\ell }$ and $\overleftrightarrow{yu}\in \mathcal{\ell }$. Since $\overleftrightarrow{\left(\overleftrightarrow{xu}\right)\left(\overleftrightarrow{yu}\right)}=\overleftrightarrow{(y\circ (u\circ u\left)\right)(x\circ (u\circ u\left)\right)}=\overleftrightarrow{\overleftrightarrow{xy}u}\in \mathcal{\ell }$ from (S1), (S2) and (Shb₂), we obtain $\overleftrightarrow{xu}\in \mathcal{\ell }$. Thus, $x\in {\mathcal{\ell }}^u$. Hence, ${\mathcal{\ell }}^u$ is an ideal of T.

Conversely, let ${\mathcal{\ell }}^u$ be an ideal of T such that ℓ be a nonempty subset of T, for any $u\in T$. Since $0\in {\mathcal{\ell }}^u$, for any $u\in T$, it follows that $0=1\circ 1=\overleftrightarrow{(u\circ u)1}=\overleftrightarrow{0u}\in \mathcal{\ell }$ from Lemma 1 (2), Lemma 4 (1) and (5), (S1) and (SSHI1). Suppose that $\overleftrightarrow{ps}\in \mathcal{\ell }$ and $s\in \mathcal{\ell }$. Then, there exist $\overleftrightarrow{xy}\in {\mathcal{\ell }}^u$ and $y\in {\mathcal{\ell }}^u$, such that $\overleftrightarrow{ps}=\overleftrightarrow{\overleftrightarrow{xy}u}$ and $s=\overleftrightarrow{yu}$. Since $x\in {\mathcal{\ell }}^u$ and $\overleftrightarrow{\left(\overleftrightarrow{xu}\right)\left(\overleftrightarrow{yu}\right)}=\overleftrightarrow{(y\circ (u\circ u\left)\right)(x\circ (u\circ u\left)\right)}=\overleftrightarrow{\overleftrightarrow{xy}u}=\overleftrightarrow{ps}\in \mathcal{\ell }$ from (SSHI2), (S1), (S2) and (Shb₂), we obtain $p=\overleftrightarrow{xu}\in \mathcal{\ell }$, for any $x\in T$. Therefore, ℓ is an ideal of T. □

Example 3.

Consider the Sheffer stroke Hilbert algebra $(T,\circ )$ in Example 1. For the ideal $\mathcal{\ell }=\{0,c\}$ of T, ℓ^f$=\{0,b,c,f\}$ is an ideal of T.

Theorem 2.

Let ℓ be an ideal of T. Then, ℓ^u is the minimal ideal of T containing ℓ and u, for any $u\in T$.

Proof. 

Let ℓ be an ideal of T. By Lemma 12, ℓ^u is an ideal of T. Assume that $z\in \mathcal{\ell }$. Since $\overleftrightarrow{zu}\circ (z\circ z)=\overleftrightarrow{zz}\circ (u\circ u)=(u\circ u)\circ (1\circ 1)=1$ from (S1), (Shb₄) and Lemma 1 (2), it is obtained from Lemma 2 that $\overleftrightarrow{zu}\preccurlyeq z$. Then, $\overleftrightarrow{zu}\in \mathcal{\ell }$ which means $z\in {\mathcal{\ell }}^u$. So, $\mathcal{\ell }\subseteq {\mathcal{\ell }}^u$, for any $u\in T$. Since $\overleftrightarrow{uu}=1\circ 1=0\in \mathcal{\ell }$ from Lemma 1 (1), Lemma 4 (1) and (SSHI1), we have $u\in {\mathcal{\ell }}^u$, for any $u\in T$. Let $\mathbb{k}$ be an ideal of T containing ℓ and u. Thus, $\overleftrightarrow{zu}\in \mathcal{\ell }\subseteq \mathbb{k}$, for any $z\in {\mathcal{\ell }}^u$. Since $\overleftrightarrow{zu}\in \mathbb{k}$ and $u\in \mathbb{k}$, it follows from (SSHI2) that $z\in \mathbb{k}$. Thence, ${\mathcal{\ell }}^u\subseteq \mathbb{k}$, for any $u\in \xi$. □

Remark 1.

Let ℓ₁ and ℓ₂ be two ideals of a Sheffer stroke Hilbert algebra $(T,\circ )$. Then, ${\mathcal{\ell }}_1\cap {\mathcal{\ell }}_2$ is always an ideal of T. However, ${\mathcal{\ell }}_1\cup {\mathcal{\ell }}_2$ is generally not an ideal of T. If $T=\{0,1\}$, then ${\mathcal{\ell }}_1\cup {\mathcal{\ell }}_2$ is an ideal of T.

Example 4.

Consider the Sheffer stroke Hilbert algebra T in Example 1. For the ideals $\{0,a,b,d\}$ and $\{0,a,c,e\}$ of T, $\{0,a,b,d\}\cap \{0,a,c,e\}=\{0,a\}$ is an ideal of T but $\{0,a,b,d\}\cup \{0,a,c,e\}=\{0,a,b,c,d,e\}$ is not an ideal of T since $f\notin \{0,a,b,c,d,e\}$ when $\overleftrightarrow{fe}\in \{0,a,b,c,d,e\}$ and $e\in \{0,a,b,c,d,e\}$.

Lemma 13.

Let ℓ be a nonempty subset of T. Then, ℓ is an ideal of T if and only if

(SSHI5)

$0\in \mathcal{\ell }$ and

(SSHI6)

$\overleftrightarrow{xy}\in \mathcal{\ell }$ and $\overleftrightarrow{yz}\in \mathcal{\ell }$ imply $\overleftrightarrow{xz}\in \mathcal{\ell }$, for all $x,y,z\in T$.

Proof. 

Let ℓ be an ideal of T. Then, $0\in \mathcal{\ell }$ is obvious from $\left(SSHI1\right)$. Assume that $\overleftrightarrow{xy}\in \mathcal{\ell }$ and $\overleftrightarrow{yz}\in \mathcal{\ell }$, for any $x,y,z\in \mathcal{\ell }$. Since $\overleftrightarrow{\overleftrightarrow{xz}\overleftrightarrow{yz}}=\overleftrightarrow{(y\circ (z\circ z\left)\right)(x\circ (z\circ z\left)\right)}\preccurlyeq \overleftrightarrow{xy}$, from (Shb₇), (S1), (S2) and Lemma 2, it follows from (SSHI4) that $\overleftrightarrow{\overleftrightarrow{xz}\overleftrightarrow{yz}}\in \mathcal{\ell }$. Thus, $\overleftrightarrow{xz}\in \mathcal{\ell }$ from (SSHI2).

Conversely, let ℓ be a nonempty subset of T satisfying (SSHI5) and (SSHI6). Suppose that $x\preccurlyeq y$ and $y\in \mathcal{\ell }$, for any $x,y\in T$. So, $\overleftrightarrow{xy}=1\circ 1=0\in \mathcal{\ell }$ and $\overleftrightarrow{y0}=(y\circ 1)\circ (y\circ 1)=(y\circ y)\circ (y\circ y)=y\in \mathcal{\ell }$ from Lemma 2, (SSHI5), Lemma 4 (1) and (3). Hence, $x=(x\circ x)\circ (x\circ x)=(x\circ 1)\circ (x\circ 1)=\overleftrightarrow{x0}\in \mathcal{\ell }$ from (SSHI6), Lemma 4 (1) and (3). Thereby, ℓ is an ideal of T. □

Theorem 3.

Let ℓ and $\mathbb{k}$ be two ideals of of T. Then,

1.

${\mathcal{\ell }}^u=\mathcal{\ell }$ if and only if $u\in \mathcal{\ell }$,

2.

$u\preccurlyeq v$ implies ${\mathcal{\ell }}^u\subseteq {\mathcal{\ell }}^v$,

3.

$\mathcal{\ell }\subseteq \mathbb{k}$ implies ${\mathcal{\ell }}^u\subseteq {\mathbb{k}}^u$,

4.

${(\mathcal{\ell }\cap \mathbb{k})}^u={\mathcal{\ell }}^u\cap {\mathbb{k}}^u$,

5.

${\mathcal{\ell }}^{(u\circ u)\circ (v\circ v)}={\left({\mathcal{\ell }}^u\right)}^v$,

6.

${\left({\mathcal{\ell }}^u\right)}^v={\left({\mathcal{\ell }}^v\right)}^u$,

7.

${\left({\mathcal{\ell }}^u\right)}^u={\mathcal{\ell }}^u$,

8.

${\mathcal{\ell }}^u\cup {\mathcal{\ell }}^v\subseteq {\mathcal{\ell }}^{u\vee v}$ and ${\mathcal{\ell }}^{u\wedge v}\subseteq {\mathcal{\ell }}^u\cap {\mathcal{\ell }}^v,$

9.

${\mathcal{\ell }}^0=\mathcal{\ell }$ and ${\mathcal{\ell }}^1=T$,

for any $u,v\in T$.

Proof. 

1.

Let ${\mathcal{\ell }}^u=\mathcal{\ell }$. Since $\overleftrightarrow{uu}=1\circ 1=0\in \mathcal{\ell }$ from Lemma 1 (1), Lemma 4 (1) and (SSHI1), we get $u\in {\mathcal{\ell }}^u=\mathcal{\ell }$. Conversely, let $u\in \mathcal{\ell }$. Since $\overleftrightarrow{zu}\circ (z\circ z)=(u\circ u)\circ \overleftrightarrow{zz}=(u\circ u)\circ (1\circ 1)=1$ from (S1), (Shb₄) and Lemma 1 (1) and (2), it is obtained from Lemma 2 that $\overleftrightarrow{zu}\preccurlyeq z$, for any $z\in \mathcal{\ell }$. Then, $\overleftrightarrow{zu}\in \mathcal{\ell }$ from (SSHI2), and so, $z\in {\mathcal{\ell }}^u$. Thus, $\mathcal{\ell }\subseteq {\mathcal{\ell }}^u$. Since $\overleftrightarrow{zu}\in \mathcal{\ell }$, for all $z\in {\mathcal{\ell }}^u$, and $u\in \mathcal{\ell }$, it follows from (SSHI2) that $z\in \mathcal{\ell }$, and so, ${\mathcal{\ell }}^u\subseteq \mathcal{\ell }$. Hence, ${\mathcal{\ell }}^u=\mathcal{\ell }$, for any $u\in T$.

2.

Let $u\preccurlyeq v$ and $z\in {\mathcal{\ell }}^u$. Then, $\overleftrightarrow{zu}\in \mathcal{\ell }$. Since $\overleftrightarrow{zv}\preccurlyeq \overleftrightarrow{zu}$ from (Shb₈), (S1), (S2) and Lemma 2, we have from (SSHI4) that $\overleftrightarrow{zv}\in \mathcal{\ell }$ which implies $z\in {\mathcal{\ell }}^v$. Thence, ${\mathcal{\ell }}^u\subseteq {\mathcal{\ell }}^v$.

3.

Let $\mathcal{\ell }\subseteq \mathbb{k}$, and $z\in {\mathcal{\ell }}^u$. Then, $\overleftrightarrow{zu}\in \mathcal{\ell }\subseteq \mathbb{k}$. Thus, $z\in {\mathbb{k}}^u$, and so, ${\mathcal{\ell }}^u\subseteq {\mathbb{k}}^u$.

4.

Since $\mathcal{\ell }\cap \mathbb{k}\subseteq \mathcal{\ell }$ and $\mathcal{\ell }\cap \mathbb{k}\subseteq \mathbb{k}$, it follows from (3) that ${(\mathcal{\ell }\cap \mathbb{k})}^u\subseteq {\mathcal{\ell }}^u$ and ${(\mathcal{\ell }\cap \mathbb{k})}^u\subseteq {\mathbb{k}}^u$. Then, ${(\mathcal{\ell }\cap \mathbb{k})}^u\subseteq {\mathcal{\ell }}^u\cap {\mathbb{k}}^u$. Let $z\in {\mathcal{\ell }}^u\cap {\mathbb{k}}^u$. Thus, $z\in {\mathcal{\ell }}^u$ and $z\in {\mathbb{k}}^u$ which imply $\overleftrightarrow{zu}\in \mathcal{\ell }$ and $\overleftrightarrow{zu}\in \mathbb{k}$. Since $\overleftrightarrow{zu}\in \mathcal{\ell }\cap \mathbb{k}$, we obtain $z\in {(\mathcal{\ell }\cap \mathbb{k})}^u$. Hence, ${\mathcal{\ell }}^u\cap {\mathbb{k}}^u\subseteq {(\mathcal{\ell }\cap \mathbb{k})}^u$, and so, ${(\mathcal{\ell }\cap \mathbb{k})}^u={\mathcal{\ell }}^u\cap {\mathbb{k}}^u$.

5.

Since

$$\begin{array}{ccc}z\in {\mathcal{\ell }}^{(u\circ u)\circ (v\circ v)}\hfill & \iff & \overleftrightarrow{z\left(\right(u\circ u)\circ (v\circ v\left)\right)}\in \mathcal{\ell }\hfill \\ \hfill & \iff & \overleftrightarrow{\left(\overleftrightarrow{zv}\right)u}=\overleftrightarrow{z\left(\right(u\circ u)\circ (v\circ v\left)\right)}\in \mathcal{\ell }\hfill \\ \hfill & \iff & \overleftrightarrow{zv}\in {\mathcal{\ell }}^u\hfill \\ \hfill & \iff & z\in {\left({\mathcal{\ell }}^u\right)}^v\hfill \end{array}$$

from (S1) and (S3), it follows that ${\mathcal{\ell }}^{(u\circ u)\circ (v\circ v)}={\left({\mathcal{\ell }}^u\right)}^v$.

6.

${\left({\mathcal{\ell }}^u\right)}^v={\mathcal{\ell }}^{(u\circ u)\circ (v\circ v)}={\mathcal{\ell }}^{(v\circ v)\circ (u\circ u)}={\left({\mathcal{\ell }}^v\right)}^u$ from (5) and (S1).

7.

By substituting $[v:=u]$ in (5), it is obtained from (S2) that ${\left({\mathcal{\ell }}^u\right)}^u={\mathcal{\ell }}^{(u\circ u)\circ (u\circ u)}={\mathcal{\ell }}^u$.

8.

They are proved from (2).

9.

${\mathcal{\ell }}^0=\{z\in T:z=(z\circ z)\circ (z\circ z)=(z\circ 1)\circ (z\circ 1)=\overleftrightarrow{z0}\in \mathcal{\ell }\}=\mathcal{\ell }$ and ${\mathcal{\ell }}^1=\{z\in T:0=1\circ 1=\overleftrightarrow{z1}\in \mathcal{\ell }\}=T$ from Lemma 4 (1) and (3), (S2) and Lemma 1 (2).

□

However, ${\mathcal{\ell }}^u\subseteq {\mathcal{\ell }}^v$ does not imply $u\preccurlyeq v$, and ${\mathcal{\ell }}^u\subseteq {\mathbb{k}}^u$ does not satisfy $\mathcal{\ell }\subseteq \mathbb{k}$.

Example 5.

Consider the Sheffer stroke Hilbert algebra T in Example 1. Then, $a\nleqq c$ when ${\mathcal{\ell }}^c=\{0,c\}\subseteq {\mathcal{\ell }}^a=\{0,a,c,e\}$, for an ideal $\mathcal{\ell }=\{0,c\}$ of T. Also, ȷ^a$=\{0,a\}⊈\mathbb{k}=\{0,b,c,f\}$ when $j^a=\{0,a\}\subseteq T={\mathbb{k}}^a$.

Corollary 1.

Let ℓ be an ideal of T. Then,

1.

${\bigcap }_{u\in T}{\mathcal{\ell }}^u=\mathcal{\ell }$ and

2.

${\bigcup }_{u\in T}{\mathcal{\ell }}^u=T$,

for any $u\in T$.

Lemma 14.

Let T be a Sheffer stroke Hilbert algebra. Then $\mho \left(u\right)=\{z\in T:z\preccurlyeq u\}$ is an ideal of T.

Proof. 

Since 0 is the least element of T, we have $0\in \mho \left(u\right)$. Let $\overleftrightarrow{xy}\in \mho \left(u\right)$ and $y\in \mho \left(u\right)$, for any $x,y\in T$. Then, $\overleftrightarrow{xy}\preccurlyeq u$ and $y\preccurlyeq u$. Since

$$\begin{array}{ccc}x\circ (u\circ u)\hfill & =& 1\circ \overleftrightarrow{xu}\hfill \\ \hfill & =& (y\circ (u\circ u\left)\right)\circ \left(\right(x\circ (u\circ u))\circ (x\circ (u\circ u)\left)\right)\hfill \\ \hfill & =& (u\circ u)\circ \overleftrightarrow{xy}\hfill \\ \hfill & =& (u\circ u)\circ (1\circ 1)\hfill \\ \hfill & =& 1\hfill \end{array}$$

from Lemma 1 (2) and (3), (S1) and (S2), Lemma 2 and (Shb₂), it follows from Lemma 2 that $x\preccurlyeq u$, and so, $x\in \mho \left(u\right)$. Thus, $\mho \left(u\right)$ is an ideal of T. □

Lemma 15.

Let T be a Sheffer stroke Hilbert algebra. Then,

1.

$\mho \left(0\right)=\left\{0\right\}$ and $\mho \left(1\right)=T$,

2.

$u\preccurlyeq v$ if and only if $\mho \left(u\right)\subseteq \mho \left(v\right)$,

3.

$\mho \left(\right(u\circ v)\circ (u\circ v\left)\right)=\mho \left(u\right)\cap \mho \left(v\right)$,

Proof. 

1.

Since 0 is the least element and 1 is the greatest element in T, it is clear that $\mho \left(0\right)=\left\{0\right\}$ and $\mho \left(1\right)=\xi$.

2.

Let $u\preccurlyeq v$ and $z\in \mho \left(u\right)$. Since $z\preccurlyeq u\preccurlyeq v$, it is obtained that $z\in \mho \left(v\right)$. Then, $\mho \left(u\right)\subseteq \mho \left(v\right)$. Conversely, let $\mho \left(u\right)\subseteq \mho \left(v\right)$. Since $u\preccurlyeq u$, for all $u\in T$, we deduce that $u\in \mho \left(u\right)$. Since $u\in \mho \left(u\right)\subseteq \mho \left(v\right)$, it follows that $u\preccurlyeq v$.

3.

Since $(u\circ v)\circ (u\circ v)\preccurlyeq u$ and $(u\circ v)\circ (u\circ v)\preccurlyeq v$ from (S1), (S3) and from (1) and (2) from Lemma 1, it is obtained from (2) that $\mho \left(\right(u\circ v)\circ (u\circ v\left)\right)\subseteq \mho \left(u\right)$ and $\mho \left(\right(u\circ v)\circ (u\circ v\left)\right)\subseteq \mho \left(v\right)$. After all, $\mho \left(\right(u\circ v)\circ (u\circ v\left)\right)\subseteq \mho \left(u\right)\cap \mho \left(v\right)$, for any $u,v\in T$. Assume that $z\in \mho \left(u\right)\cap \mho \left(v\right)$. Then, $z\preccurlyeq u$ and $z\preccurlyeq v$. Since $u\circ v\preccurlyeq z\circ v\preccurlyeq z\circ z$ from (S1) and (Shb₈), it follows from (S1), (S2) and Lemma 2 that $z\preccurlyeq (u\circ v)\circ (u\circ v)$. Thus, $z\in \mho \left(\right(u\circ v)\circ (u\circ v\left)\right)$. Hence, $\mho \left(u\right)\cap \mho \left(v\right)\subseteq \mho \left(\right(u\circ v)\circ (u\circ v\left)\right)$, for any $u,v\in T$. Therefore, $\mho \left(\right(u\circ v)\circ (u\circ v\left)\right)=\mho \left(u\right)\cap \mho \left(v\right)$, for any $u,v\in T$.

□

Theorem 4.

Let T be a Sheffer stroke Hilbert algebra. Then,

1.

$\mho (u\wedge v)=\mho \left(\breve{u}\right)\cap \mho \left(\breve{v}\right),$

2.

$\mho \left(u\right)\cup \mho \left(v\right)\subseteq \mho (u\vee v),$

for any $u,v\in T$.

Proof. 

1.

It is obvious from Lemma 15 (2) that $\mho (u\wedge v)\subseteq \mho \left(u\right)\cap \mho \left(v\right)$, for any $u,v\in T$. Let $z\in \mho \left(u\right)\cap \mho \left(v\right)$. Then, $z\preccurlyeq u$ and $z\preccurlyeq v$, and so, $z\preccurlyeq u\wedge v$. Thus, $z\in \mho (u\wedge v)$, which implies $\mho \left(u\right)\cap \mho \left(v\right)\subseteq \mho (u\wedge v)$, for any $u,v\in T$. Thence, $\mho (u\wedge v)=\mho \left(u\right)\cap \mho \left(v\right),$ for any $u,v\in T$.

2.

It is clear from Lemma 15 (2) that $\mho \left(u\right)\cup \mho \left(v\right)\subseteq \mho (u\vee v),$ for any $u,v\in T$.

□

Example 6.

Consider the Sheffer stroke Hilbert algebra T in Example 1. Then, $\mho \left(d\right)\cup \mho \left(f\right)=\{0,a,b,d\}\cup \{0,b,c,f\}=\{0,a,b,c,d,f\}\subseteq T=\mho \left(1\right)=\mho (d\vee f)$.

4. Stabilizers

In this section, we introduce stabilizers in a Sheffer stroke Hilbert algebra.

Definition 4.

Let T be a Sheffer stroke Hilbert algebra and W be a nonempty subset of T. Then, a stabilizer of W is defined as follows:

$$\overbrace{W}=\{u\in T:\overleftrightarrow{xu}=x(or\overleftrightarrow{ux}=u),\forall x\in W\}.$$

Example 7.

Consider the Sheffer stroke Hilbert algebra T in Example 1. For the subsets $W^1=\{a,d\}$ and $W^2=\{0,b\}$ of T, the stabilizer of $W^1$ is $\overbrace{W^1}=\{0,b,c,f\}$ and the stabilizer of $W^2$ is $\overbrace{W^2}=T$, respectively.

Lemma 16.

Let W, X and $W^i$$(i\in I)$ be nonempty subsets of T. Then,

1.

$W\subseteq X$ implies $\overbrace{X}\subseteq \overbrace{W}$,

2.

$\overbrace{T}=\left\{0\right\}$ and $\overbrace{\left\{0\right\}}=T$,

3.

$\overbrace{W}=\bigcap \{\overbrace{\left\{x\right\}}:x\in W\}$,

4.

${\bigcap }_{i\in I}\overbrace{W^i}=\overbrace{{\displaystyle \bigcap _{i\in I}}{W}^i}$ and ${\bigcup }_{i\in I}\overbrace{W^i}=\overbrace{{\displaystyle \bigcup _{i\in I}}{W}^i}$.

Proof. 

1.

Let $W\subseteq X$ and $u\in \overbrace{X}$. Then, $\overleftrightarrow{xu}=x$, for all $x\in X$. Since $W\subseteq X$, we have $\overleftrightarrow{yu}=y$, for all $y\in W$. Thence, $u\in \overbrace{W}$, and so, $\overbrace{X}\subseteq \overbrace{W}$.

2.

Since we have from (S2), Lemma 4 (1) and (3) that $\overleftrightarrow{x0}=(x\circ 1)\circ (x\circ 1)=(x\circ x)\circ (x\circ x)=x$, for all $x\in T$, it is concluded that $0\in \overbrace{T}$, which implies $\left\{0\right\}\subseteq \overbrace{T}$. Let $u\in \overbrace{T}$. Then, $\overleftrightarrow{xu}=x$, for all $x\in T$. Thus, $0=1\circ 1=\overleftrightarrow{uu}=u$ from Lemma 1 (1) and Lemma 4 (1), and so, $u\in \left\{0\right\}$. Hence, $\overbrace{T}\subseteq \left\{0\right\}$. Thereby, $\overbrace{T}=\left\{0\right\}$. Also, it follows from (S1) and (S2), Lemma 1 (2) and Lemma 4 (1) that $\overbrace{\left\{0\right\}}=\{u\in T:\overleftrightarrow{0u}=\overleftrightarrow{(u\circ u)1}=1\circ 1\}=T$, for all $u\in T$.

3.

Since $\left\{x\right\}\subseteq W$, for all $x\in W$, it is obtained from (1) that $\overbrace{W}\subseteq \overbrace{\left\{x\right\}}$, for all $x\in W$, and so, $\overbrace{W}\subseteq \bigcap \{\overbrace{\left\{\breve{x}\right\}}:\breve{x}\in W\}$. Assume that $u\in \bigcap \{\overbrace{\left\{x\right\}}:x\in W\}$. Then, $u\in \overbrace{\left\{x\right\}}$, for all $x\in W$. So, $\overleftrightarrow{xu}=x,$ for all $x\in W$, which implies $u\in \overbrace{W}$. Thus, $\bigcap \{\overbrace{\left\{x\right\}}:x\in W\}\subseteq \overbrace{W}$. Therefore, $\overbrace{W}=\bigcap \{\overbrace{\left\{x\right\}}:x\in W\}$.

4.

Since ${\bigcap }_{i\in I}{W}^i\subseteq W^i$ and $W^i\subseteq {\bigcup }_{i\in I}{W}^i$, for all $i\in I$, we ascertain from (1) that $\overbrace{W^i}\subseteq \overbrace{{\displaystyle \bigcap _{i\in I}}{W}^i}$ and $\overbrace{{\displaystyle \bigcup _{i\in I}}{W}^i}\subseteq \overbrace{W^i}$, and so, ${\bigcap }_{i\in I}\overbrace{W^i}\subseteq \overbrace{{\displaystyle \bigcap _{i\in I}}{W}^i}$ and $\overbrace{{\displaystyle \bigcup _{i\in I}}{W}^i}\subseteq {\bigcup }_{i\in I}\overbrace{W^i}$, for all $i\in I$. Suppose that $u\in \overbrace{{\displaystyle \bigcap _{i\in I}}{W}^i}$, for any $u\in T$. Then, $\overleftrightarrow{xu}=x$, for all $x\in {\bigcap }_{i\in I}{W}^i$. Since $\overleftrightarrow{xu}=x$, for all $x\in W^i$ and $i\in I$, it means that $u\in \overbrace{W^i}$, for all $i\in I$, and so, $u\in {\bigcap }_{i\in I}\overbrace{W^i}$. Thus, $\overbrace{{\displaystyle \bigcap _{i\in I}}{W}^i}\subseteq {\bigcap }_{i\in I}\overbrace{W^i}$. Hence, ${\displaystyle \bigcap _{i\in I}}\overbrace{W^i}=\overbrace{{\bigcap }_{i\in I}{W}^i}$. Let $v\in {\bigcup }_{i\in I}\overbrace{W^i}$. So, $v\in \overbrace{W^{i^{\ast }}}$, for some $i^{\ast }\in I$. Since $\overleftrightarrow{xv}=x$, for all $x\in W^{i^{\ast }}$, it is clear that $\overleftrightarrow{xv}=x$, for all $x\in {\bigcup }_{i\in I}{W}^i$. Then, $v\in \overbrace{{\displaystyle \bigcup _{i\in I}}{W}^i}$, which implies that ${\bigcup }_{i\in I}\overbrace{W^i}\subseteq \overbrace{{\displaystyle \bigcup _{i\in I}}{W}^i}$. Thence, ${\displaystyle \bigcup _{i\in I}}\overbrace{W^i}=\overbrace{{\bigcup }_{i\in I}{W}^i}$.

□

Theorem 5.

Let T be a Sheffer stroke Hilbert algebra and W be a nonempty subset of T. Then, $\overbrace{W}$ is an ideal of T.

Proof. 

Since we obtain from (S2), Lemma 4 (1) and (3) that $\overleftrightarrow{x0}=(x\circ 1)\circ (x\circ 1)=(x\circ x)\circ (x\circ x)=x$, for all $x\in W$, it follows that $0\in \overbrace{W}$. Assume that $\overleftrightarrow{uv}\in \overbrace{W}$ and $v\in \overbrace{W}$. Then, $\overleftrightarrow{x\left(\overleftrightarrow{uv}\right)}=x$ and $\overleftrightarrow{xv}=x$, for all $x\in W$. Since

$$\overleftrightarrow{xu}=\overleftrightarrow{\overleftrightarrow{xv}u}=\overleftrightarrow{(v\circ v)(x\circ (u\circ u\left)\right)}=\overleftrightarrow{(u\circ (v\circ v\left)\right)(x\circ (v\circ v\left)\right)}=\overleftrightarrow{x\left(\overleftrightarrow{uv}\right)}=x$$

from (S1), (S2), (Shb₂) and (Shb₄), it is obtained that $u\in \overbrace{W}$. Hence, $\overbrace{W}$ is an ideal of T. □

However, W is usually not an ideal of T when $\overbrace{W}$ is an ideal of T.

Example 8.

Consider the Sheffer stroke Hilbert algebra T in Example 1. Then, $\overbrace{\{c,e\}}=\{0,a,b,d\}$ is an ideal of T, yet $\{c,e\}$ is not an ideal of T.

Corollary 2.

Let T be a Sheffer stroke Hilbert algebra. Then,

1.

$\overbrace{\left\{1\right\}}=\left\{0\right\}$ and

2.

$\overbrace{\left\{1\right\}}\subseteq \mathcal{\ell }$, for all ideals ℓ of T.

Proof. 

It is obtained from Lemma 1 (1) and (3), Lemma 4 (1) and Theorem 5. □

Definition 5.

Let T be a Sheffer stroke Hilbert algebra, W and X be nonempty subsets of T. Then, a stabilizer of W with respect to X is defined as follows:

$$\overbrace{(W,X)}=\{u\in T:x\wedge u\in X,forallx\in W\}.$$

Example 9.

Consider the Sheffer stroke Hilbert algebra T in Example 1. Then, $\overbrace{(W,X)}=\{a,c,d,f\}$, for the subsets $W=\{b,e\}$ and $X=\{a,c\}$ of T.

Theorem 6.

Let W, X, $W^i$ and $X^i$ be nonempty subsets and ℓ be an ideal of T, for all $i\in I$. Then,

1.

$\overbrace{(W,X)}=T$ implies $W\subseteq X$,

2.

$\overbrace{(\mathcal{\ell },X)}=T$ if and only if $\mathcal{\ell }\subseteq X$,

3.

$\overbrace{(\mathcal{\ell },\mathcal{\ell })}=T$,

4.

$\overbrace{W}\subseteq \overbrace{(W,\mathcal{\ell })}$,

5.

$W^{i_1}\subseteq X^{i_1}$ and $W^{i_2}\subseteq X^{i_2}$ imply $\overbrace{(X^{i_1},W^{i_2})}\subseteq \overbrace{(W^{i_1},X^{i_2})}$,

6.

$\overbrace{(W,\{0\left\}\right)}=\overbrace{W}$,

7.

$\overbrace{\left(\right\{0\},\{0\left\}\right)}=T$,

8.

$\overbrace{(W,{\displaystyle \bigcap _{i\in I}}{X}^i)}={\bigcap }_{i\in I}\overbrace{(W,X^i)}$,

9.

$\overbrace{(W,{\displaystyle \bigcup _{i\in I}}{X}^i)}={\bigcup }_{i\in I}\overbrace{(W,X^i)}$,

10.

$\overbrace{\left(\right\{1\},X)}=X$,

11.

$\overbrace{\left(\right\{1\},\{1\left\}\right)}=\left\{1\right\}$.

Proof. 

1.

Let $\overbrace{(W,X)}=T$. Since $u=u\wedge u\in X$, for all $u\in W$, we obtain $W\subseteq X$.

2.

If $\overbrace{(\mathcal{\ell },X)}=T$, then $\mathcal{\ell }\subseteq X$ from (1). Conversely, let ℓ be an ideal of T, such that $\mathcal{\ell }\subseteq X$, and $u\in T$. Since $x\wedge u\preccurlyeq x$, for all $x\in \mathcal{\ell }$, it follows from (SSHI4) that $x\wedge u\in \mathcal{\ell }$. Then, $x\wedge u\in X$, for all $x\in \mathcal{\ell }$, which implies $u\in \overbrace{(\mathcal{\ell },X)}$. Thus, $\overbrace{(\mathcal{\ell },X)}=T$.

3.

It is proved from (2).

4.

Let $u\in \overbrace{W}$, for any $u\in T$. Then, $\overleftrightarrow{xu}=x$, for all $x\in W$. Since $x\wedge u=\overleftrightarrow{x\overleftrightarrow{xu}}=\overleftrightarrow{xx}=1\circ 1=0\in \mathcal{\ell }$ from Lemma 4 (1), Lemma 5, (S2) and (SSHI1), it is obtained that $u\in \overbrace{(W,\mathcal{\ell })}$, and this means $\overbrace{W}\subseteq \overbrace{(W,\mathcal{\ell })}$.

5.

Let $W^{i_1}\subseteq X^{i_1}$, $W^{i_2}\subseteq X^{i_2}$ and $u\in \overbrace{(X^{i_1},W^{i_2})}$, for any $u\in T$. Since $x\wedge u\in W^{i_2}$, for all $x\in X^{i_1}$, it is concluded that $x\wedge u\in X^{i_2}$, for all $x\in W^{i_1}$. Hence, $u\in \overbrace{(W^{i_1},X^{i_2})}$, and so, $\overbrace{(X^{i_1},W^{i_2})}\subseteq \overbrace{(W^{i_1},X^{i_2})}$.

6.

Since $\left\{0\right\}$ is an ideal of T, we ascertain from (4) that $\overbrace{W}\subseteq \overbrace{(W,\{0\left\}\right)}$. Assume that $u\in \overbrace{(W,\{0\left\}\right)}$, for any $u\in T$. Then, $x\wedge u=0$, for all $x\in W$. Thus, it follows from (Shb₁), Lemma 4 (1), Lemma 5, (S1) and (S2) that $\overleftrightarrow{xu}=x$, for all $x\in W$, and so, $u\in \overbrace{W}$. Hence, $\overbrace{(W,\{0\left\}\right)}\subseteq \overbrace{W}$. Therefore, $\overbrace{(W,\{0\left\}\right)}=\overbrace{W}$.

7.

$\overbrace{\left(\right\{0\},\{0\left\}\right)}=\overbrace{\left\{0\right\}}=T$ from (6) and Lemma 16 (2).

8.

Let $u\in \overbrace{(W,{\displaystyle \bigcap _{i\in I}}{X}^i)}$. Then, $x\wedge u\in {\bigcap }_{i\in I}{X}^i$, for all $x\in W$. Since $x\wedge u\in X^i$, for all $i\in I$ and $x\in W$, we obtain that $u\in \overbrace{(W,X^i)}$, for all $i\in I$, which implies $u\in {\bigcap }_{i\in I}\overbrace{(W,X^i)}$. Thus, $\overbrace{(W,{\displaystyle \bigcap _{i\in I}}{X}^i)}\subseteq {\bigcap }_{i\in I}\overbrace{(W,X^i)}$. Conversely, let $u\in {\bigcap }_{i\in I}\overbrace{(W,X^i)}$. Since $u\in \overbrace{(W,X^i)}$, for all $i\in I$, it follows that $x\wedge u\in X^i$, for all $i\in I$ and $x\in W$, which means $x\wedge u\in {\bigcap }_{i\in I}{X}^i$, for all $x\in W$. Thence, $u\in \overbrace{(W,{\displaystyle \bigcap _{i\in I}}{X}^i)}$, and so, ${\displaystyle \bigcap _{i\in I}}\overbrace{(W,X^i)}\subseteq \overbrace{(W,{\bigcap }_{i\in I}{X}^i)}$. Consequently, $\overbrace{(W,{\displaystyle \bigcap _{i\in I}}{X}^i)}={\bigcap }_{i\in I}\overbrace{(W,X^i)}$.

9.

Let $u\in \overbrace{(W,{\displaystyle \bigcup _{i\in I}}{X}^i)}$. Then, $x\wedge u\in {\bigcup }_{i\in I}{X}^i$, for all $x\in W$. Since $x\wedge u\in X^{i_0}$, for some $i_0\in I$ and $x\in W$, we have $u\in \overbrace{(W,X^{i_0})}$, for some $i_0\in I$, and so, $u\in {\bigcup }_{i\in I}\overbrace{(W,X^i)}$. Hence, $\overbrace{(W,{\displaystyle \bigcup _{i\in I}}{X}^i)}\subseteq {\bigcup }_{i\in I}\overbrace{(W,X^i)}$. Conversely, let $u\in {\bigcup }_{i\in I}\overbrace{(W,X^i)}$. Since $u\in \overbrace{(W,X^{i_{\ast }})}$, for some $i_{\ast }\in I$, it is concluded that $x\wedge u\in X^{i_{\ast }}$, for some $i_{\ast }\in I$ and $x\in W$, which follows $x\wedge u\in {\bigcup }_{i\in I}{X}^i$, for all $x\in W$. Thereby, $u\in \overbrace{(W,{\displaystyle \bigcup _{i\in I}}{X}^i)}$. So, ${\bigcup }_{i\in I}\overbrace{(W,X^i)}\subseteq \overbrace{(W,{\displaystyle \bigcup _{i\in I}}{X}^i)}$. Thereby, $\overbrace{(W,{\displaystyle \bigcup _{i\in I}}{X}^i)}={\bigcup }_{i\in I}\overbrace{(W,X^i)}$.

10.

$\overbrace{\left(\right\{1\},X)}=\{u\in T:u=1\wedge u\in X\}=X$ from Lemma 5, (S2), Lemma 4 (1) and (3).

11.

$\overbrace{\left(\right\{1\},\{1\left\}\right)}=\left\{1\right\}$ from (10).

□

Theorem 7.

Let X, $W^1$ and $W^2$ be nonempty subsets of T. Then, $W^1\subseteq W^2$ implies $\overbrace{(W^2,X)}\subseteq \overbrace{(W^1,X)}$.

Proof. 

Let $W^1\subseteq W^2$, and $u\in \overbrace{(W^2,X)}$. Since $x\wedge u\in X$, for all $x\in W^2$, it follows that $y\wedge u\in X$, for all $y\in W^1$, which means $u\in \overbrace{(W^1,X)}$. Then, $\overbrace{(W^2,X)}\subseteq \overbrace{(W^1,X)}$. □

The following example illustrates that the converse of Theorem 7 is not usually satisfied.

Example 10.

Consider the Sheffer stroke Hilbert algebra T in Example 1. Then, $\overbrace{(W^2,X)}=\varnothing \subseteq \{d,f\}=\overbrace{(W^1,X)}$ but $W^1⊈W^2$, for the subsets $X=\{d,f\},W^1=\{a,b,c,1\}$ and $W^2=\left\{e\right\}$ of T.

Theorem 8.

Let ℓ be a nonempty subset and $\mathbb{k}$ be an ideal of T. Then, $\overbrace{(\mathcal{\ell },\mathbb{k})}$ is an ideal of T.

Proof. 

Let ℓ and $\mathbb{k}$ be two ideals of T. Since we have from Lemma 1 (1), Lemma 4 (1) and (3), Lemma 5, (S2) and (SSHI1) that $x\wedge 0=\overleftrightarrow{x\overleftrightarrow{x0}}=\overleftrightarrow{xx}=1\circ 1=0\in \mathbb{k}$, for all $x\in \mathcal{\ell }$, it follows that $0\in \overbrace{(\mathcal{\ell },\mathbb{k})}$. Assume that $\overleftrightarrow{uv}\in \overbrace{(\mathcal{\ell },\mathbb{k})}$ and $v\in \overbrace{(\mathcal{\ell },\mathbb{k})}$, for any $u,v\in T$. Then, $x\wedge \overleftrightarrow{uv}\in \mathbb{k}$ and $x\wedge v\in \mathbb{k}$, for all $x\in \mathcal{\ell }$. Since

$$\begin{array}{ccc}x\wedge (u\vee v)\hfill & =& x\wedge \left(\right(u\circ (v\circ v))\circ (v\circ v\left)\right)\hfill \\ \hfill & =& x\wedge ((\overleftrightarrow{uv}\circ (v\circ v))\circ (v\circ v))\hfill \\ \hfill & =& x\wedge (\overleftrightarrow{uv}\vee v)\hfill \\ \hfill & =& (x\wedge \overleftrightarrow{uv})\vee (x\wedge v)\in \mathbb{k}\hfill \end{array}$$

from Lemma 5 and (S3), and $x\wedge u\preccurlyeq x\wedge (u\vee v)$, it is obtained from (SSHI4) that $x\wedge u\in \mathbb{k}$, for all $x\in \mathcal{\ell }$. Thus, $u\in \overbrace{(\mathcal{\ell },\mathbb{k})}$. Hence, $\overbrace{(\mathcal{\ell },\mathbb{k})}$ is an ideal of T. □

The following example shows that the converse of Theorem 8 does not hold in general.

Example 11.

Consider the Sheffer stroke Hilbert algebra T in Example 1. Then, $\overbrace{\left(\right\{d\},\{0,a,1\left\}\right)}=\{0,a,c,e\}$ is an ideal of T but $\{0,a,1\}$ is not since $b\notin \{0,a,1\}$ when $\overleftrightarrow{b1}=0\in \{0,a,1\}$ and $1\in \{0,a,1\}$.

5. Concluding Remarks

This manuscript concentrates on Sheffer stroke Hilbert algebras and their main characteristics. The main goal of this study is two-fold: as the first target, a new characterization of Sheffer stroke Hilbert algebras is presented in light of the ideals. In this task, proper subsets of Sheffer stroke Hilbert algebras are introduced, and it is shown that the proposed subsets possess the relationship between lattice and set-theoretical operators. Secondly, we define stabilizers of Sheffer stroke Hilbert algebras for their nonempty subsets and underline their crucial properties. We enhance the theoretical results of the manuscripts with many examples and elaborative discussions.

Regarding future work, we aspire to define various ideals of Sheffer stroke Hilbert algebras by employing more compact and trivial subsets. In this vein, we will be able to construct a comparative approach between different algebraic structures, and this will result in the emergence of new aspects of Hilbert algebras.