Abstract
In this paper, the generalized widest path problem (or generalized maximum capacity problem) is studied. This problem is denoted by the GWPP. The classical widest path problem is to find a path from a source (s) to a sink (t) with the highest capacity among all possible s-t paths. The GWPP takes into account the presence of loss/gain factors on arcs as well. The GWPP aims to find an s-t path considering the loss/gain factors while satisfying the capacity constraints. For solving the GWPP, three strongly polynomial time algorithms are presented. Two algorithms only work in the case of losses. The first one is less efficient than the second one on a CPU, but it proves to be more efficient on large networks if it parallelized on GPUs. The third algorithm is able to deal with the more general case of losses/gains on arcs. An example is considered to illustrate how each algorithm works. Experiments on large networks are conducted to compare the efficiency of the algorithms proposed.
Keywords:
combinatorial optimization; widest path; maximum capacity path; strongly polynomial algorithms; GPU parallelization MSC:
68R10; 90B10; 90C35; 68W10
1. Introduction
Consider a directed and connected network , where represents the set of nodes, A represents the set of arcs (each arc starts from node and terminates at node ), and is a capacity function mapping arcs to non-negative real numbers. Within this network, there are two special nodes: , referred to as the source node; and , referred to as the sink node. Let denote the total number of nodes in the network (|V|) and represent the number of arcs (|A|). A path, denoted as , from a node to a node in network is defined as a sequence of nodes , where is equal to or greater than , and each consecutive pair of nodes is an arc from for every .
Combinatorial optimization is a special class of mathematical program that consists of finding an optimal object among a finite set of specifically structured objects. Some of the most prominent problems of this class are shortest path (SP) problems, maximum reliability path (MRP) problems, and maximum capacity path (MCP) problems/widest path problem (WPP). In these problems, the goal is to find an optimal path from an origin to a destination under a special objective function as follows:
- for SP problems.
- for MRP problems.
- for WPP.
where the set consists of all paths from the origin to the destination. In this context, the parameters , , and represent the length, reliability, and capacity of arc respectively. Fortunately, these problems are tractable and there exist polynomial time algorithms to solve them. For instance, the shortest path problem can be solved using Dijkstra’s algorithm with a Fibonacci heap implementation [1], which has a complexity of if the lengths, , are nonnegative. In case the lengths are negative, the best-known algorithm is a FIFO implementation of the Bellman–Ford algorithm [2,3], with a complexity of , where and represent the number of nodes and arcs, respectively. The maximum reliability path problem can be transformed into a shortest path problem by defining as for every arc . Consequently, it can be solved similarly to the shortest path problem, especially when is less than . Additionally, both the maximum reliability path problem and the widest path problem can be solved directly by modifying the shortest path algorithms. This is because they share similar optimality conditions with the shortest path problem (refer to [4] for more details). However, the best-known algorithm for solving the widest path problem in an undirected network does not rely on this concept. Instead, it employs a recursive algorithm with a linear complexity of [5]. The maximum capacity problem has many applications. The service vehicles and emergency vehicles should use such a path when returning from a service call to the base [6]. Also, the maximum capacity problem could be used to deal with computation problems where only comparison of the graph’s arcs values is permitted [7,8].
The WPP finds its application in various domains. For instance, let us consider a network that represents connections between routers on the Internet. In this context, each arc in the network denotes the bandwidth of the corresponding connection between two routers. With the WPP, the objective is to discover the path between two Internet nodes that offers the highest possible bandwidth. This network routing problem is well-known in the field. Apart from being a fundamental network routing problem, the WPP also plays a crucial role in other areas. One noteworthy application is within the Schulze method, which is utilized for determining the winner of a multiway election [9]. In this method, the WPP aids in resolving ties and determining the strongest path among multiple alternatives. Additionally, the WPP finds application in digital compositing, wherein it assists in combining multiple images or video layers into a final composite image or sequence [10]. By identifying the path with the maximum capacity, the compositing process can ensure the most efficient allocation of computational resources. Moreover, the problem contributes to metabolic pathway analysis, which involves studying chemical reactions within biological systems. In this context, the WPP aids in understanding the flow of metabolites through various pathways and identifying the most influential pathways in terms of capacity [11]. In summary, the WPP has extensive applications ranging from network routing on the Internet, multiway election methods, and digital compositing, to metabolic pathway analysis. Its capability to identify and utilize paths with the highest capacity proves valuable across these diverse domains.
In this paper, a new combinatorial optimization problem called the generalized widest path (GWPP) problem is introduced. It is a more intricate version of the problem that involves finding a directed path from a given source node s to a given sink node t, with the minimum loss among all available directed paths from s to t [12]. To our knowledge, this is the only paper in the literature that studies st-paths in the gain/loss case. The GWPP is defined on a network where each arc is characterized by two attributes: capacity and loss/gain factor.
The capacity of an arc represents the maximum flow value that can be transmitted through it. On the other hand, the loss/gain factor of an arc indicates the flow value that arrives at the tail node when one unit of flow is sent through the arc. The objective of the GWPP is to find a path that is capable of transmitting the maximum flow while considering the loss/gain factors.
This problem is inspired by an extension of the maximum flow problems [13,14] that incorporates loss/gain factors, known as the generalized maximum flow problem. Therefore, the algorithms developed for solving the GWPP can also be utilized as subroutines for addressing generalized maximum flow problems.
Moreover, the GWPP can be viewed as an extension of the maximum reliability path and widest path problems. It becomes equivalent to the MRP problem when capacities are infinite and transforms into the WPP when the loss/gain factors are equal to . Thus, the GWPP upon the scope of both MRP and the WPPs, encompassing their characteristics and generalizations.
In this paper, we introduce the GWPP—a novel combinatorial optimization problem that extends the concept of the WPP by incorporating loss/gain factors. The algorithms developed for the GWPP can be utilized for generalized maximum flow problems, making it a versatile and applicable problem in various contexts.
The rest of this paper is organized as follows. In Section 2, we provide the necessary background information and definitions to lay the foundation for the research work. Section 3 clearly defines the research problem and outlines its significance. Section 4 describes, in detail, the first two proposed algorithms to solve the GWPP in the case of loss factors. In Section 5, the more general case of loss/gain factors is studied, and an algorithm is presented to solve the GWPP in this general case. Section 6 presents the experiments conducted to validate and evaluate the proposed algorithms. Finally, Section 7 summarizes the main findings of the paper.
The current paper is an extension of the paper presented and published in the proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024) [15]. In the current paper, the general case (with loss/gain factors) is studied, and a strongly polynomial algorithm is introduced to solve the GWPP in the general case (see Section 5). Also, in order to illustrate the functionality of the proposed algorithms, the iterations of each of the three algorithms are presented for a given network (see Section 4 and Section 5). The experiments from Section 6 were extended for Algorithm 3 [15] as well.
2. Preliminaries
For the sake of simplicity, from now on, we refer to a path from to as an “-path”.
The capacity of an -path is denoted by and is given by the minimum of its capacities, that is,
In the network is intended to find an -path with the maximum capacity among all -paths:
This problem is also called the widest path problem, the bottleneck shortest path problem, and the max–min path problem in the literature.
3. Problem Formulation
In this section, we will delve into the problem of the generalized widest path. Let us formally define the problem considering a connected and directed network denoted as . Here, is the loss/gain factor parameter.
For each arc , there are two key parameters associated with it. The first one is the capacity, denoted as , which represents the maximum amount of flow that can be sent along the arc. The second parameter is the loss factor if it lies in the interval , or it is the gain factor if . The loss factor captures physical transformations such as evaporation, energy dissipation, breeding, theft, or interest rates [16]. The loss/gain factor could be the exchange rate of two different currencies.
Considering the flow along the arcs, if units of flow enter arc , units of flow are actually delivered to node . If , then this implies that units of flow are absorbed or lost along the arc due to the specified loss factor. If , then this means that flow is increased by units.
The aim of the generalized widest path problem is to find an -path that enables the transmission of the maximum possible flow while taking the loss/gain factors into consideration.
To formulate this problem in a precise manner, we introduce the following variables:
- -
- , representing the flow entering arc .
- -
- , a binary variable that determines whether or not arc carries a positive flow ( if it does, otherwise).
Now, we can express the GWPP as a mixed zero–one linear programming model, which can be stated as follows:
Let us break its points down into separate parts:
- The variables and represent the flow leaving the source node and the flow entering the sink node , respectively.
- Constraints (1b) and (1d) correspond to the balanced flow constraint and the bound constraints commonly found in maximum flow problems [4].
- Constraint (1c) ensures that, at most, one outgoing arc from any node is capable of sending flow. This constraint guarantees that flow is sent only along a single -path.
- The formulation (1) of the GWPP closely resembles that of generalized maximum flow problems, with the added inclusion of zero-one variables and the constraint (1c) [4].
Remark 1.
While we have assumed that, constraint (1d) does not account for the possibility of a flow increment on arcwhen. In such cases, it should be written as. To handle this situation without loss of generality, we can redefine the capacity of arc as .
4. Algorithms for the Case of Losses on Arcs
This section focuses on the development of two algorithms to solve the GWPP in polynomial time. This provides evidence that the problem is tractable, similar to the WPP, SP, and MRP problems.
We start with a simple observation: if we send the maximum flow along a path, then at least one of its arcs will be saturated. The capacity of this saturated arc determines the flow value along the path. Let be the last saturated arc in an -path The flow value along path is then equal to . An interesting insight is that if we remove the arc from the network and add a new arc with capacity , loss factor , we can send the same flow value along the new path . This simple idea leads to a polynomial time algorithm for solving problem (1).
In the first algorithm, disregarding arc capacities, we aim to find a maximum reliability path from s to t, which is a path where the value of the product is maximized. This can be achieved by assigning arc lengths and finding the shortest -path based on these arc lengths. Let be the shortest path obtained. Then, we identify the last arc in that would become saturated if we were to send the maximum flow along . We remove arc from the network and introduce an artificial arc with a loss factor , capacity , and a weight of . We repeat this process until we find a path , in which the last saturated arc is one of the artificial arcs.
Considering the unique characteristics of our algorithm, it is noteworthy to underscore that the negative weights exclusively pertain to arcs emanating from the source node . This crucial distinction enables the seamless application of Dijkstra’s algorithm, as its efficacy is contingent upon the absence of negative cycles within the graph. To further streamline the application of Dijkstra’s algorithm and eliminate negative arcs altogether, we propose a judicious adjustment to the arc weights. Specifically, we suggest augmenting all arcs with the minimum value among the arcs originating from , denoted as for the pair . This augmentation ensures the absence of negative weights in the entire graph, rendering it amenable to Dijkstra’s algorithm without any reservations.
Subsequently, upon identifying the optimal path and obtaining the computed result, we advocate for subtracting the added value, which is representative of the minimum value among the source-emerging arcs. This corrective measure guarantees the restoration of the original, unaltered values on the optimal path while harnessing the benefits of an adjusted graph conducive to the successful application of Dijkstra’s algorithm.
It is important to note that the optimal value of problem (1) is equal to the maximum flow along the last path found by the algorithm. To obtain the optimal path, we need to save the segment of path from to whenever is removed and is added. This can be accomplished by introducing an additional parameter for each artificial arc. Therefore, if the algorithm finds path in the last iteration, the optimal solution will be a path that includes arcs from and , excluding .
Algorithm provides a formal description of our first algorithm. Since an arc is removed in each iteration, the number of iterations is, at most, equal to m (the total number of arcs). Algorithm 1 runs, at most, m times classical Dijkstra’s algorithm in the modified network (by applying –log to the initial values). As a result, we can conclude the following.
Theorem 1.
The complexity of Algorithm is, in which is the complexity of finding the shortest path in the network.
| Algorithm 1 (Alg1) |
| Input: An instance of the generalized WPP Output: An optimal path if Set and else: Set and while True: Find a shortest path with respect to if The optimal path is else: Find the last arc of to be saturated. Remove . Add an artificial arc |
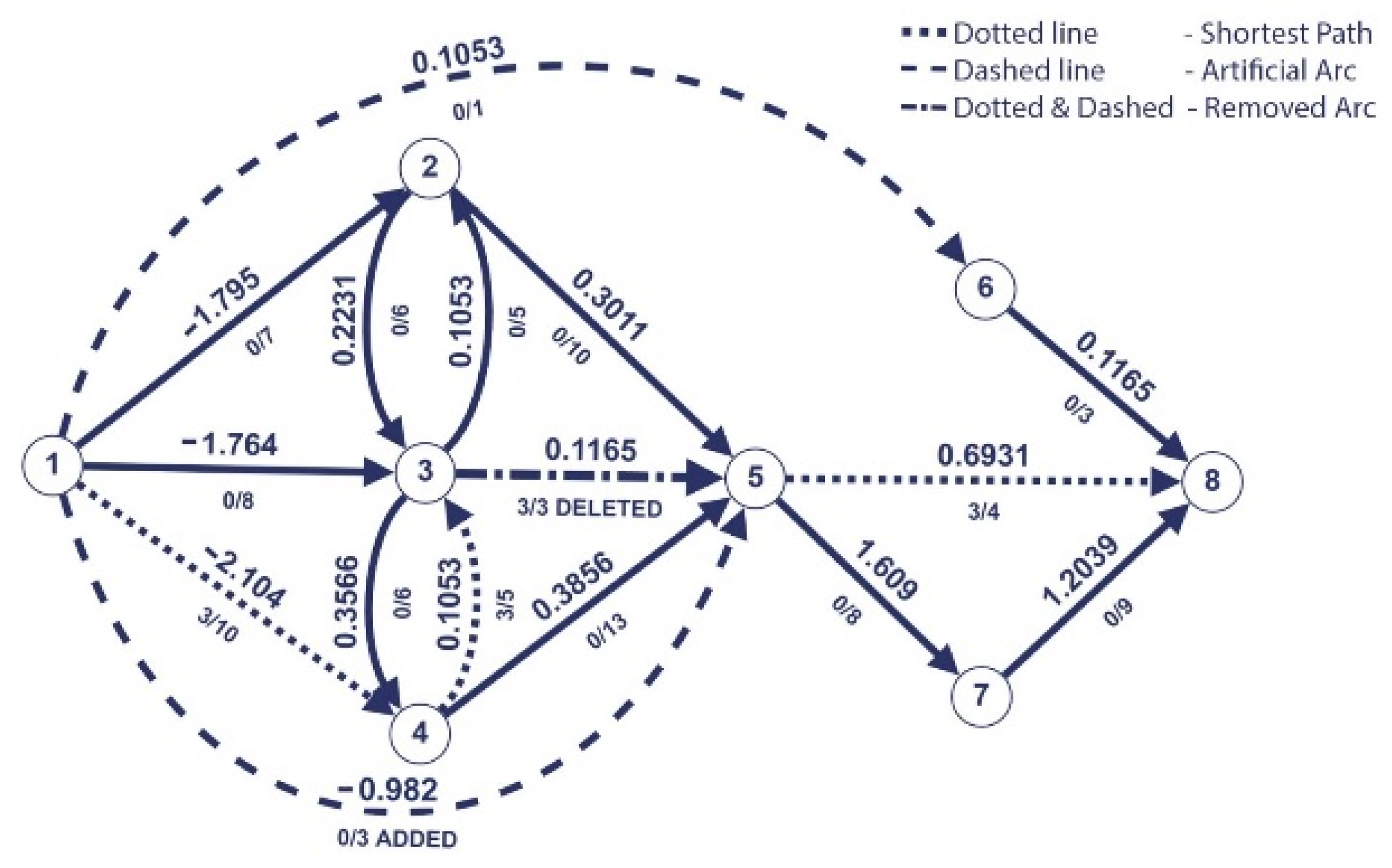
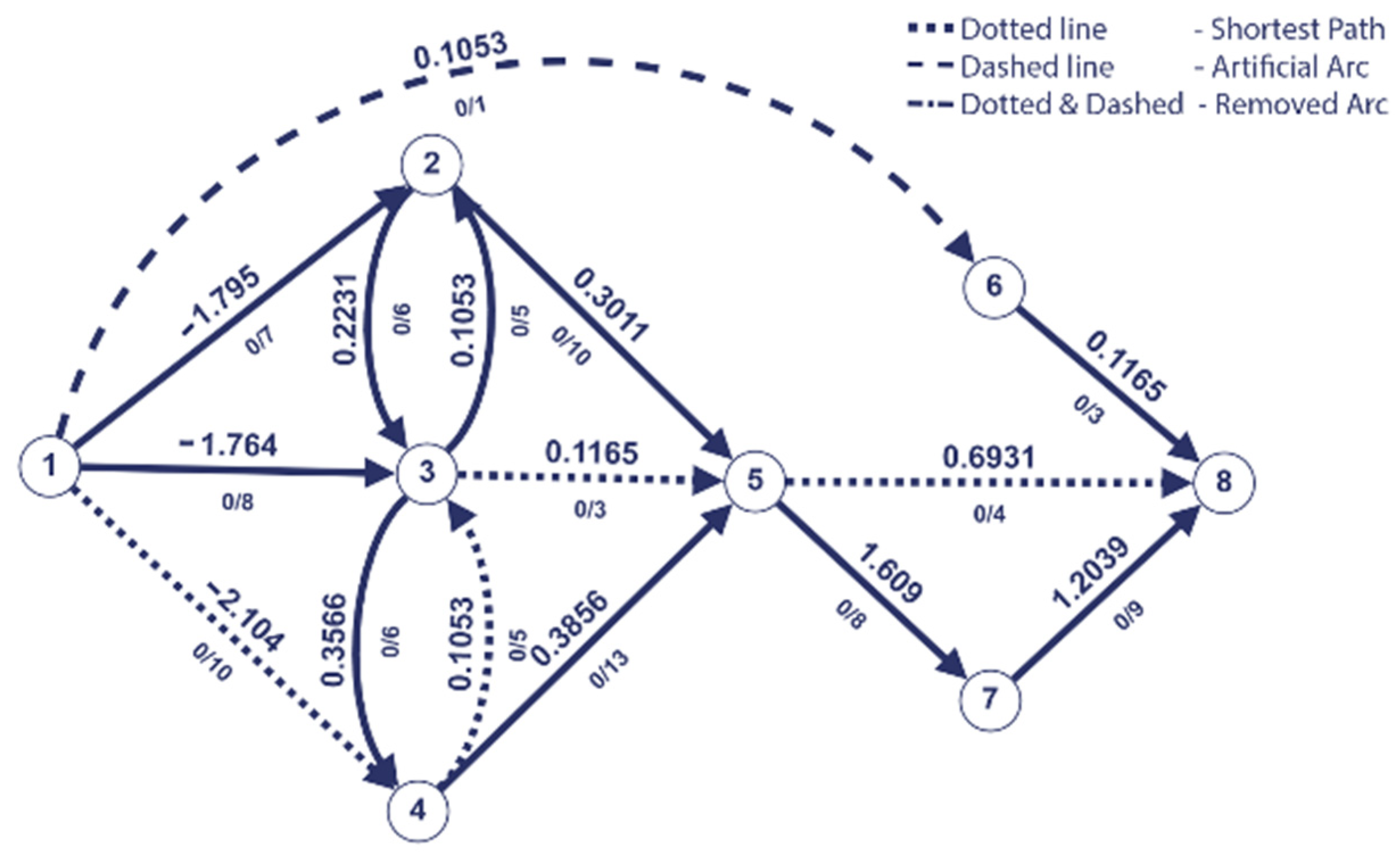
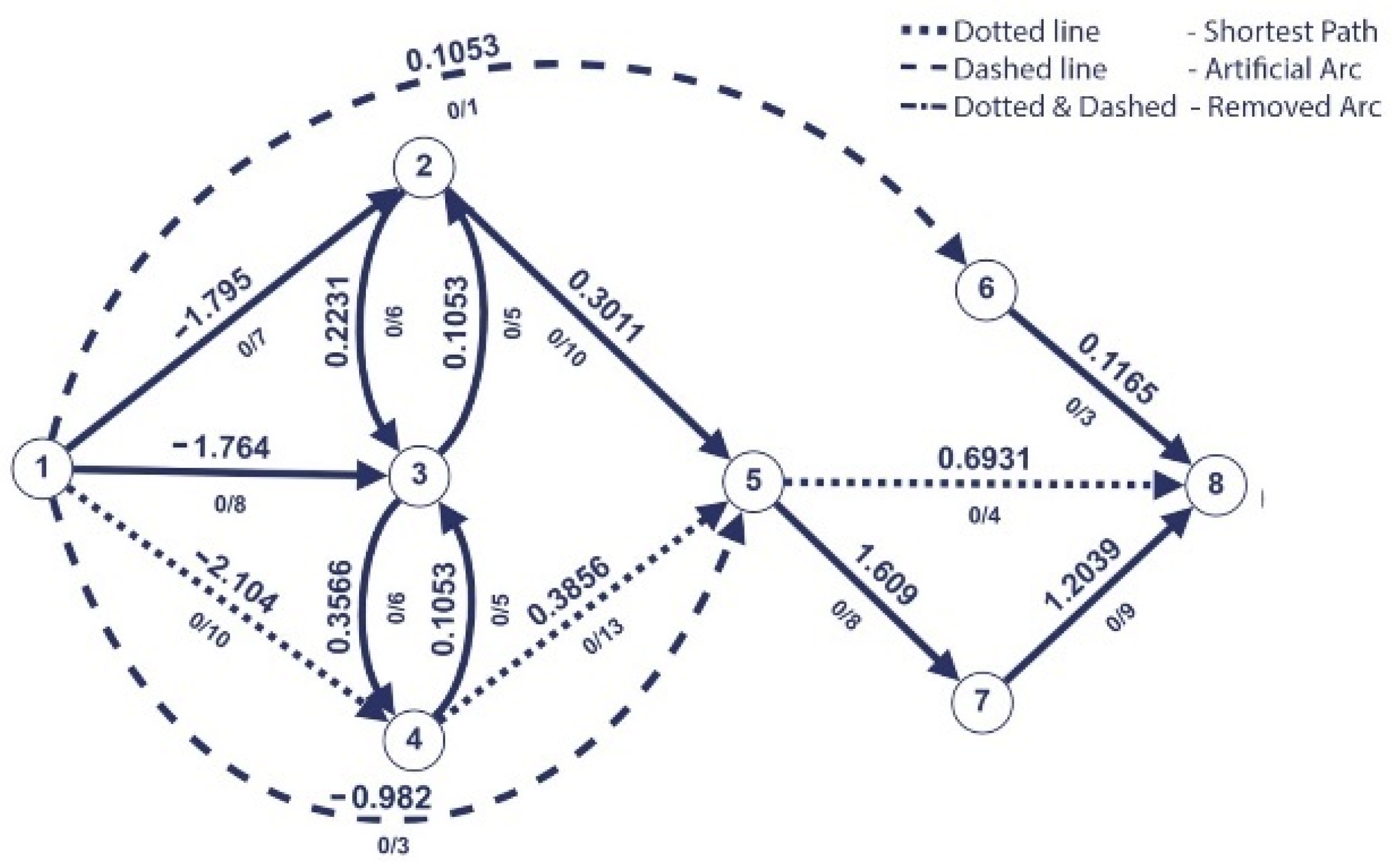
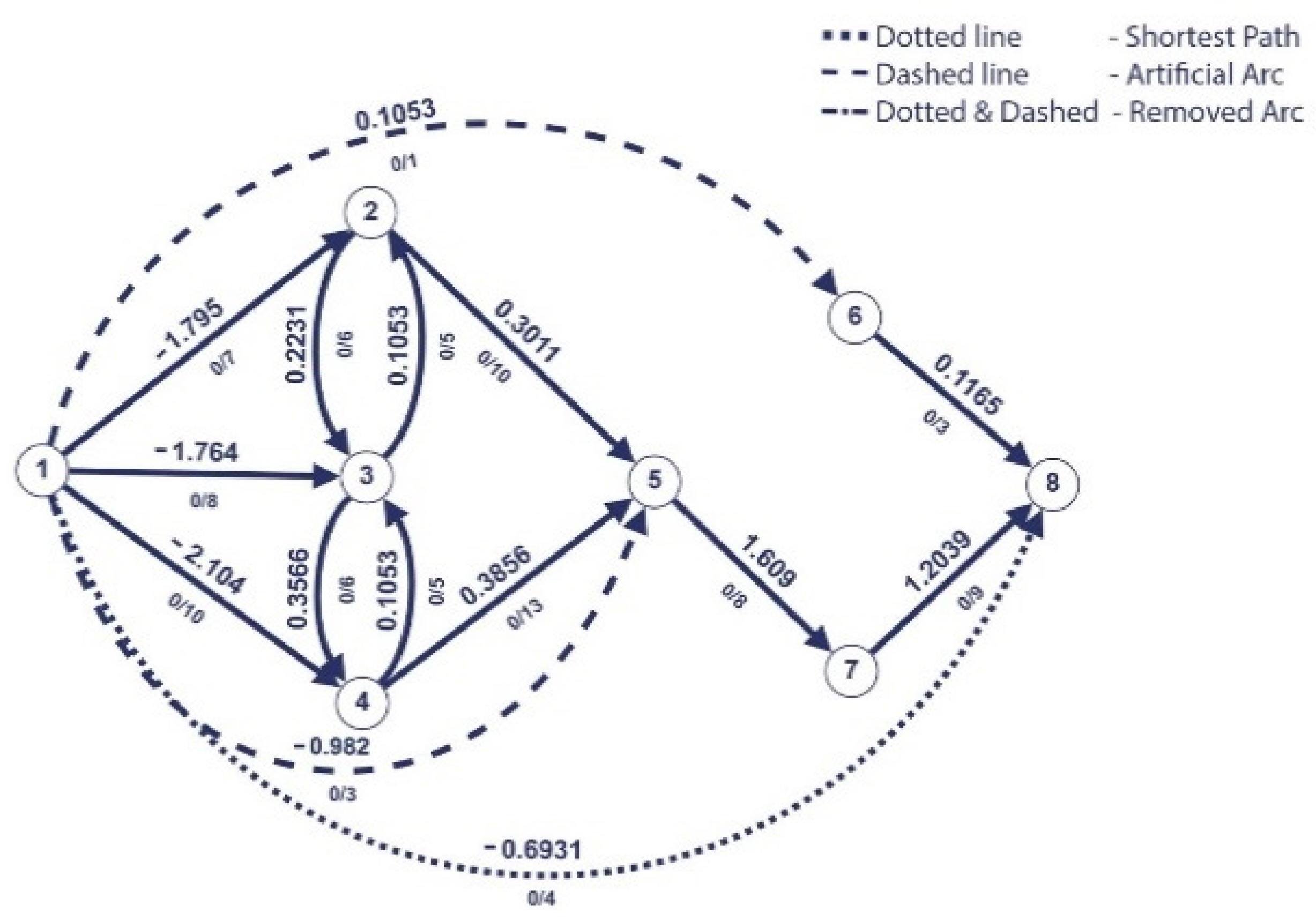
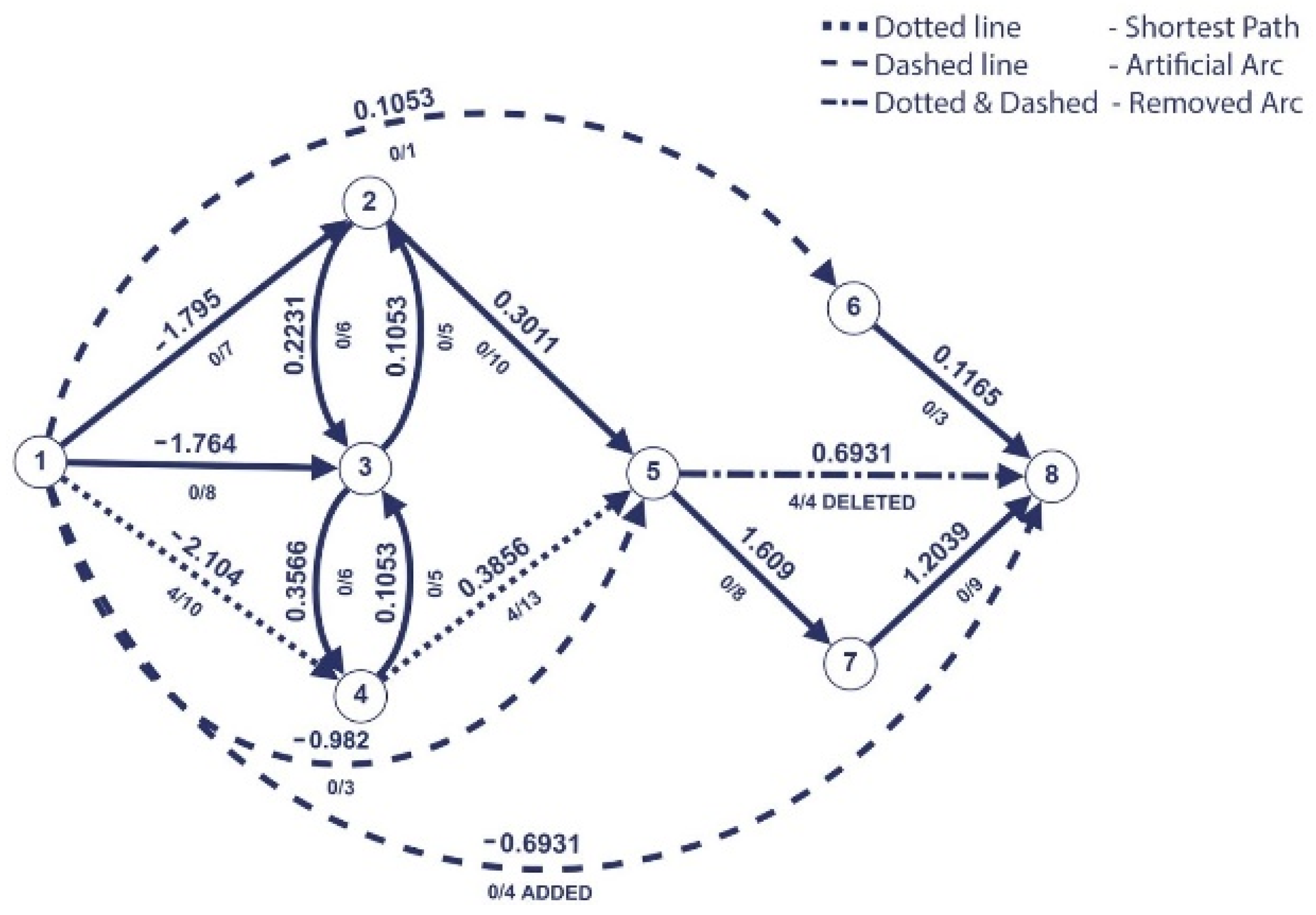
Algorithm 1 iterations (Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 illustrate the iterations of the algorithm):
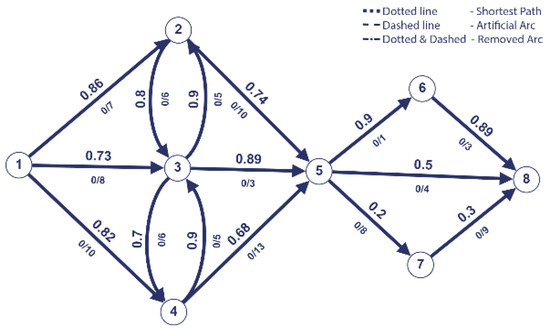
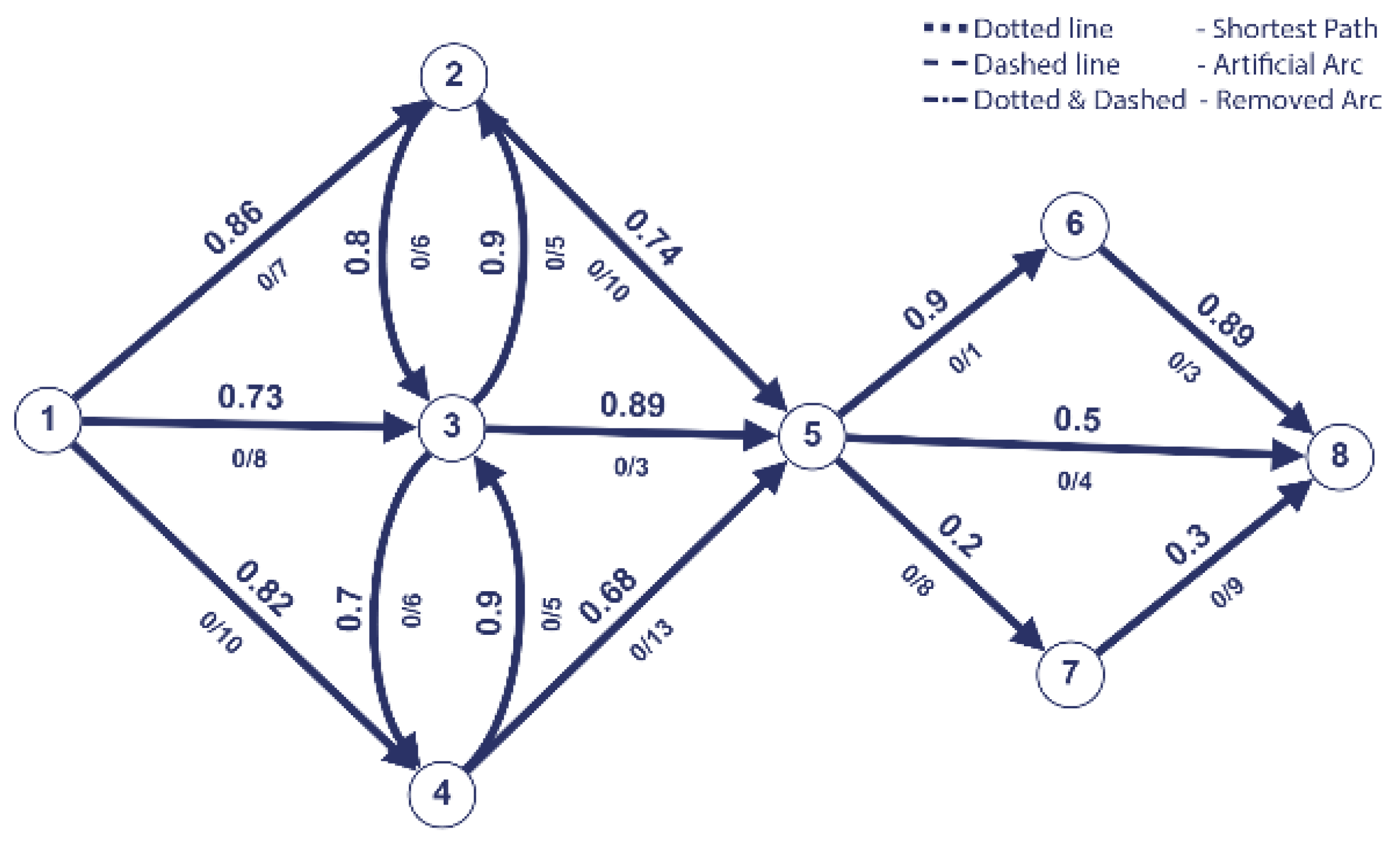
Figure 1.
Initial graph.
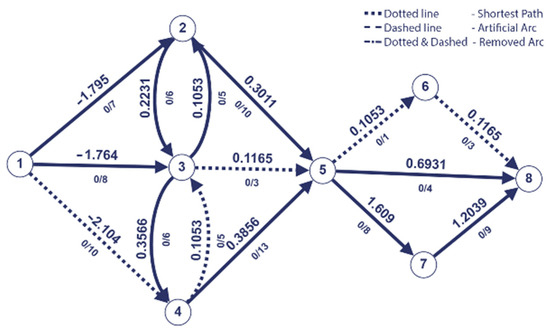
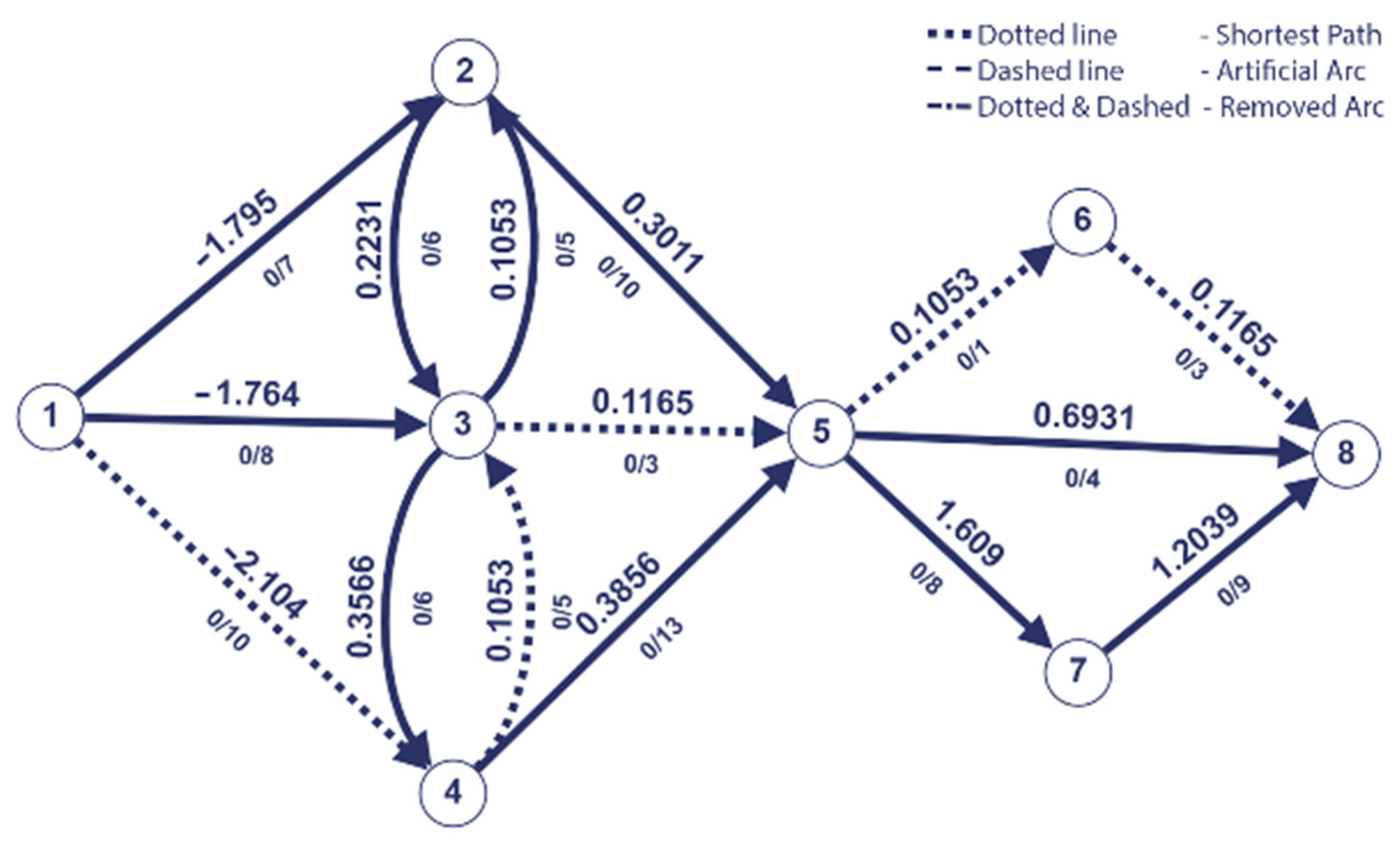
Figure 2.
Transformation of problem (1) into minimization problem.
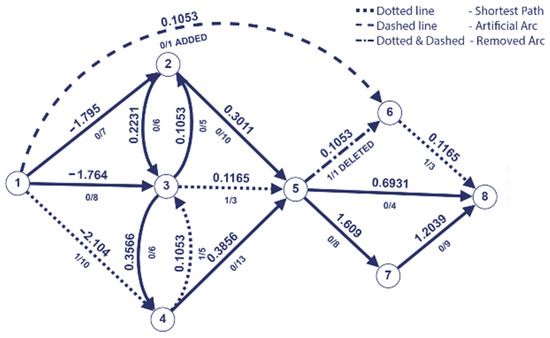
Figure 3.
First iteration of the shortest path.
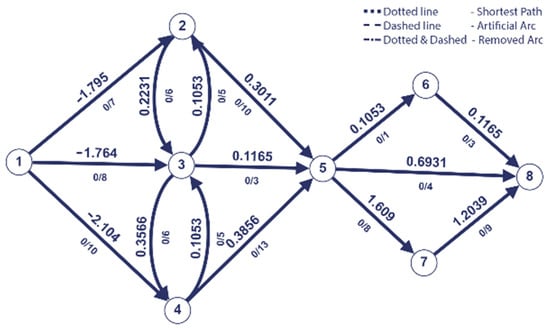
Figure 4.
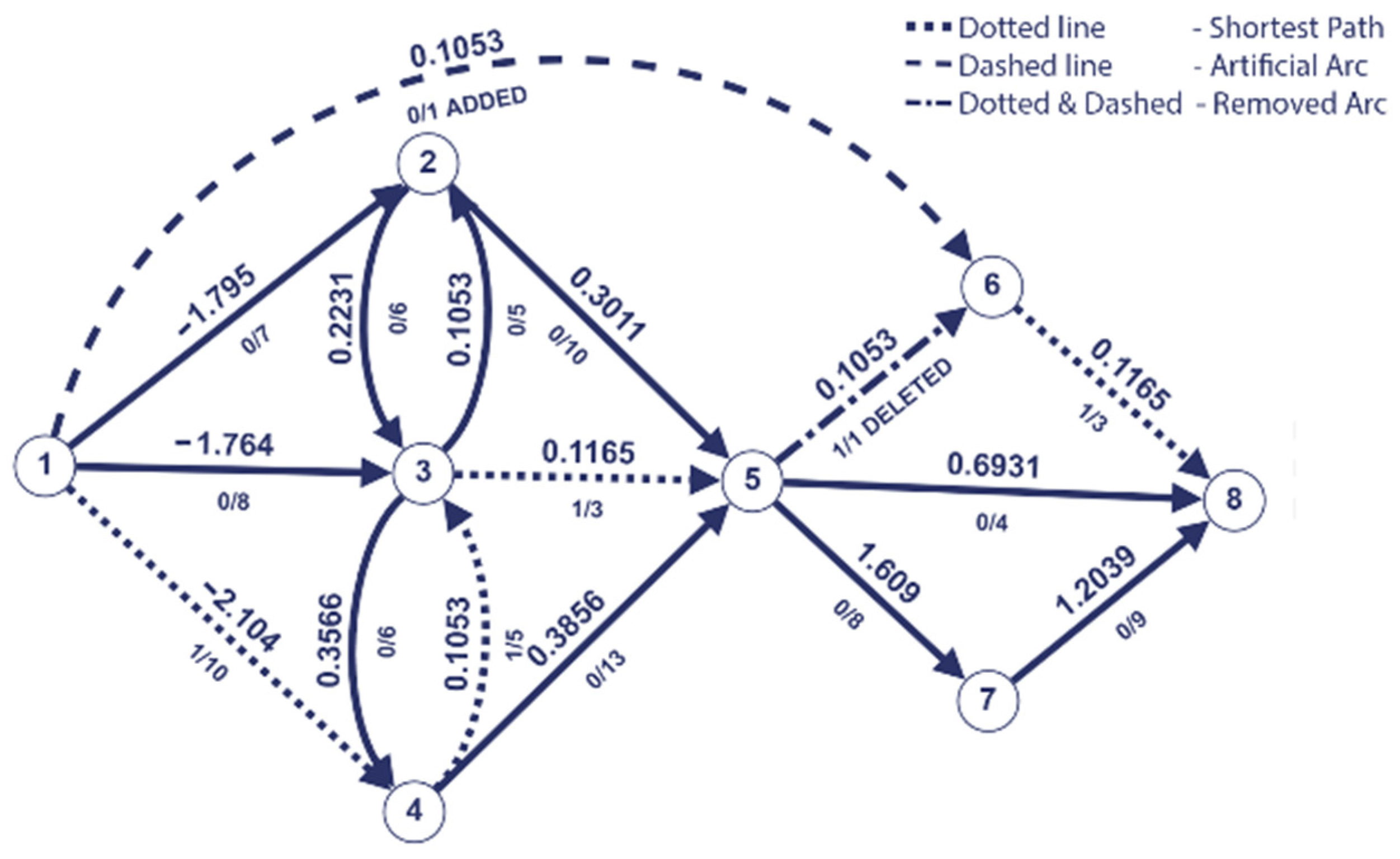
Remove the last saturated arc and add artificial arc.
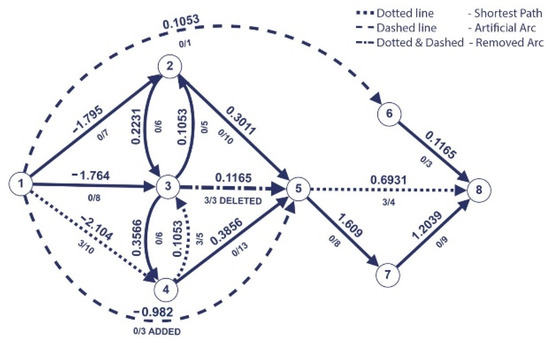
Figure 5.
Second iteration of Dijkstra’s algorithm.
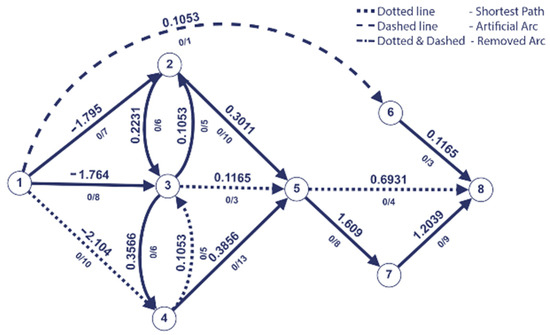
Figure 6.
The last saturated arc is removed and add artificial arc.
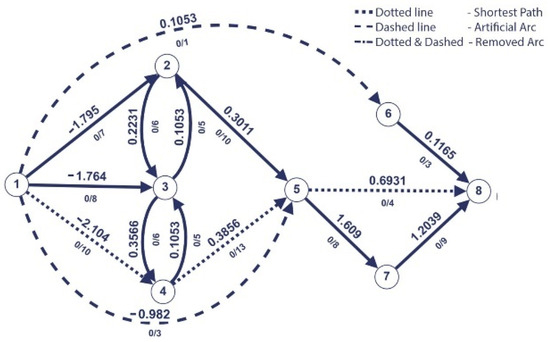
Figure 7.
Third iteration of Dijkstra’s algorithm.
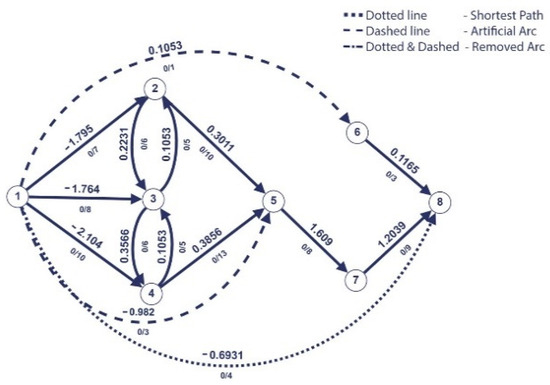
Figure 8.
Remove the last saturated arc and add artificial arc.
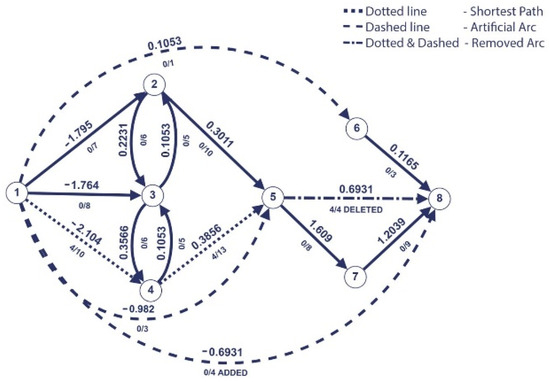
Figure 9.
Last iteration of Dijkstra’s algorithm.
We observe that our graph example contains arcs with negative weights. However, this does not pose a problem as the negative arcs will always exist from the source node. This particularity ensures that Dijkstra’s algorithm performs well.
We applied Dijkstra’s algorithm to find the shortest path from source 1 to the sink 8. The resulting path is marked with dotted line and is = (1,4,3,5,6,8).
The last saturated arc on the shortest path P is eliminated, and the arc (s,6) is added with the capacity of and the weight 0.1503.
The resulted path on the second iteration is = (1,4,3,5,8).
On the new shortest path found, after we push the maximum flow through it, we find that the arc is last saturated. So, it is removed, and the arc (1,5) is added with the same capacity of 3 and the new weight of −0.982.
The resulted path on the third iteration is = (1,4,5,8).
In the third iteration, the arc is found to be the last saturated arc. An artificial arc (1,8) with the capacity 4 and weight −0.6931 is added.
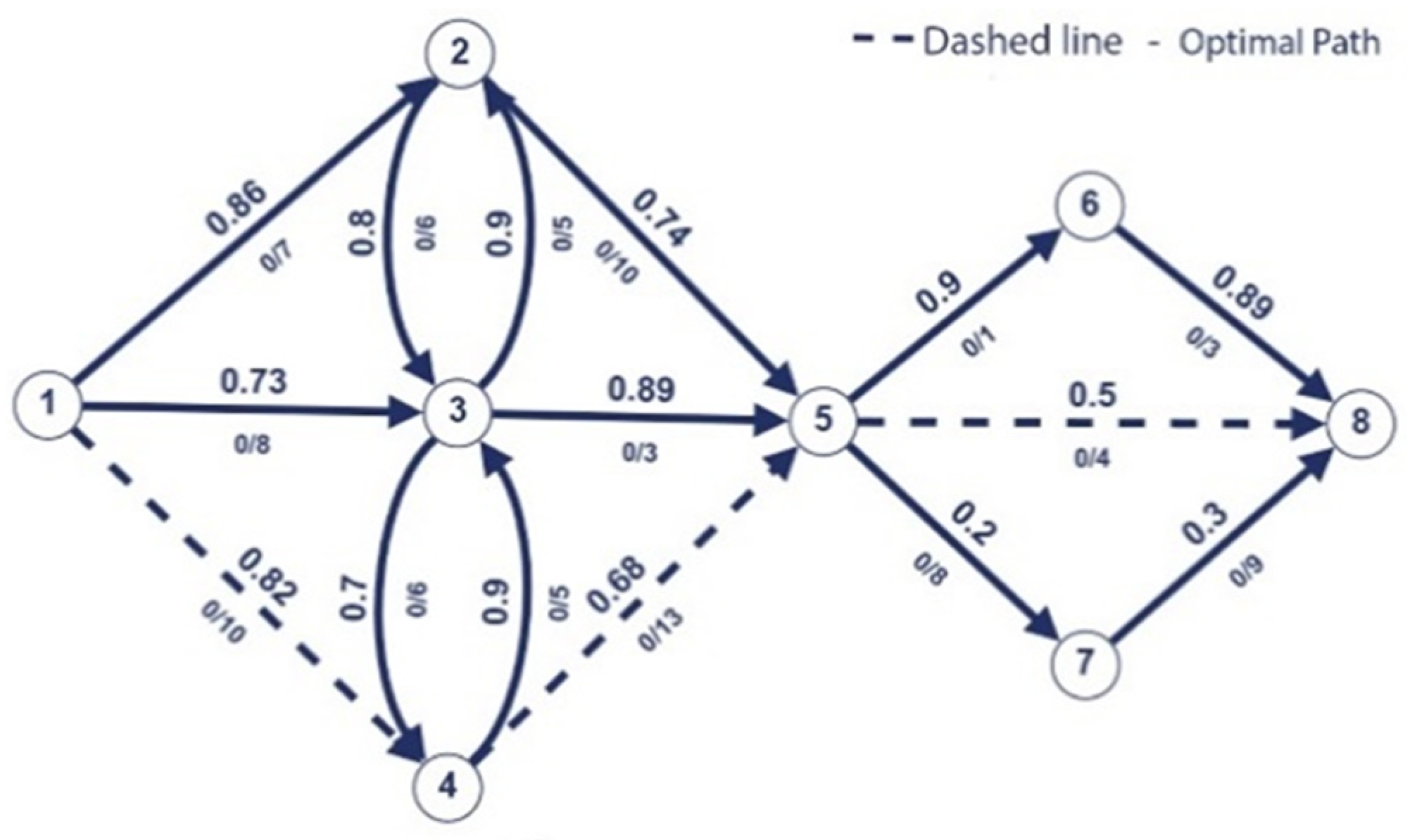
The last saturated arc is one of the artificial arcs; therefore, we stop here. In this scenario, we applied Dijkstra’s algorithm fourth times. After we apply , which, in our scenario, is and = (5,8), we obtain the optimal path (1,4,5,8) as can be seen in Figure 10.
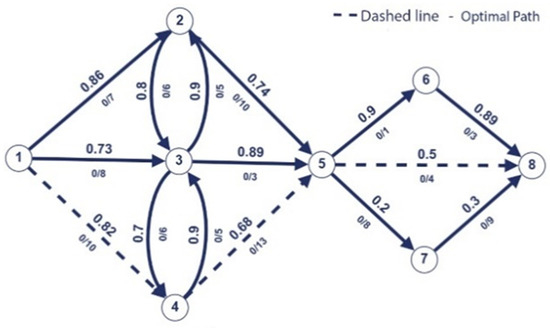
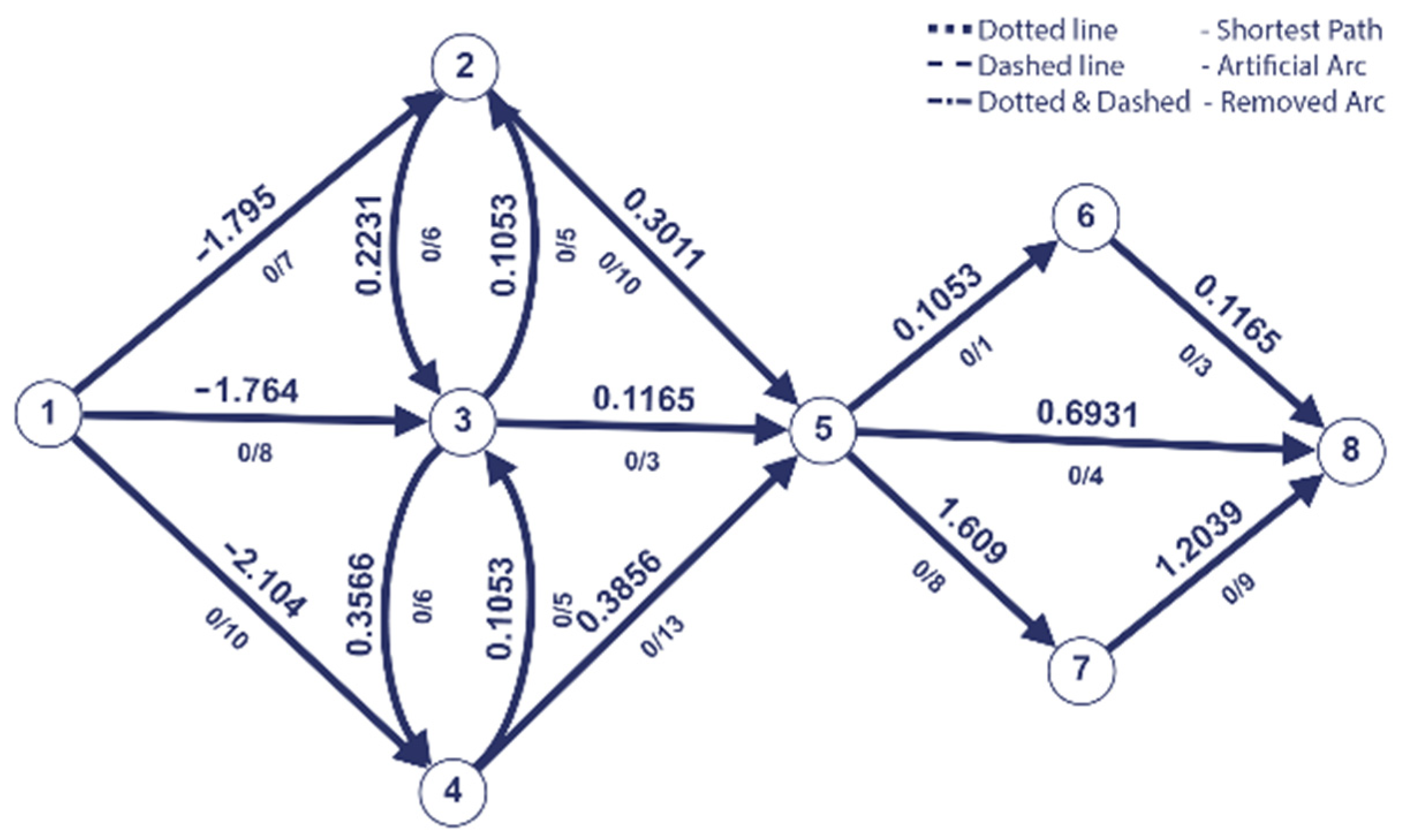
Figure 10.
Optimal path.
In the followings, we discuss optimality conditions for problem (1) and present an algorithm with a time complexity of , which improves the complexity of Algorithm by a factor of .
To begin, we introduce a label for each node . During intermediate stages of computation, the label serves as an estimate (or an upper bound) of the maximum flow sent from the source node s to node j along a single path. At the termination of the algorithm, the label represents the optimal value of problem (1). Our objective is to establish necessary and sufficient conditions for a set of labels to accurately represent the maximum flow.
Let denote the value of the maximum flow sent from the source node to node j (where we set ). In order for the labels to be optimal, they must satisfy the following necessary optimality conditions:
- -
- Constraint (1c): For each node , there exists, at most, one outgoing arc with positive flow. This condition ensures that the flow is sent only along a single -path.
- -
- Capacity Constraint: For each arc , the flow through the arc must not exceed its capacity. Mathematically, this can be written as , where represents the flow on arc and represents the capacity of arc (.
- -
- Flow Conservation: The flow conservation principle must be satisfied at every node (except the source and sink nodes). For any node and , the sum of incoming flows must equal the sum of outgoing flows. Mathematically, this can be expressed as .
- -
- Optimality Condition: For each node , the label represents the maximum flow sent from the source node to node . Therefore, we have where represents the flow on arc and represents the flow on arc .
By satisfying these necessary optimality conditions, we can ensure that the labels accurately represent the maximum flow in the network.
If the labels are optimal, they must satisfy the following necessary optimality conditions:
This is an extension of the optimality conditions of both the WPP and MRP problem. On the optimal path, the inequality is satisfied in the equality form. It states that the label of node is either or . In the case that the flow value arriving at node is less than , (namely, ), this arc is not saturated and consequently . In the other case, is saturated, sending more flow than its capacity. So, in this case.
Since this optimality condition is similar to that of the SP problem, we can apply the concept of Dijkstra’s algorithm to solve problem 1. This is presented in Algorithm 2.
Theorem 2.
Algorithm 2 solves the problem in time.
Proof of Theorem 2.
Considering the provided information, we can deduce that in the while loop, each arc is checked only once. As a result, the number of iterations executed by the two last lines of the loop is, at most, which is also less than or equal to considering the worst-case scenario. □
Conversely, the node selection process, where the node with the minimum label is chosen, requires time in each iteration. Taking into account that the number of iterations is , we can conclude that the most time-consuming operation in this algorithm is the node selection, which takes time. Algorithm 2 is derived from Dijkstra’s algorithm by replacing the classical test with ; then, if necessarily, the update is performed.
| Algorithm 2 (Alg. 2) |
| Input: An instance of the generalized WPP Output: An optimal path Set Set Set while : Let be a node for which ; for each : if : Update Update; |
We can also use the available implementations of Dijkstra’s algorithm for the complexity improvement of Algorithm 2. For example, the Fibonacci heap implementation reduces the complexity to .
- Algorithm 2 iterations:
We will apply Algorithm 2 for the graph from Figure 1. We have the following data structures: d (distance vector), Pred. (predecessor vector), and S (priority queue or a Fibonacci heap, depending on the implementation). It is important to note that all structures are starting from index 1 in this example.
Upon examination of the predecessor vector Pred. represented by [−1, 1, 1, 1, 4, 5, 5, 5], it is obvious that the optimal path is (1, 4, 5, 8). So, both the first and second algorithms yield identical optimal paths (see Figure 10 and Table 1).

Table 1.
Algorithm 2 iterations.
5. Gain/Loss Case of the GWPP
Since the GWPP is reduced to a minimum path search problem in a network with non-negative values on arcs (except for the arcs starting with the source node), Dijkstra’s algorithm was adapted for solving the GWPP. The same optimality conditions may apply to problems involving gain factors (leading to arcs with negative values in the modified network). Therefore, Bellman–Ford’s algorithm can be adapted to address the case when the arcs have gain/loss factors. We used the shortest path faster algorithm (SPFA) implementation of Bellman–Ford [17]. The algorithm iteratively relaxes edges in the graph and updates the optimal path estimates until no further updates are possible. This algorithm is described in Algorithm 3. The correctness of Algorithm 3 is akin to that of the well-known Bellman–Ford algorithm (the modifications performed for the classical Bellman–Ford’s algorithm are similar to those conducted for Dijkstra’s algorithm). For a proof, please refer to [4].
| Algorithm 3 (Alg. 3) |
| Input: An instance of the GWPP with gain/loss factors Output: An optimal path Set Set , while Q has elements: for : if : Update Set if : ; Restore the optimal path by the indices. |
- Algorithm 3 iterations:
| No. itr. | Selected Edge | Structure | Structure Data |
| 0—init. | - | Q | [1] |
| S | [true,false,false,false,false,false,false,false] | ||
| d | [inf, 0, 0, 0, 0, 0, 0, 0] | ||
| Pred. | [−1, −1, −1, −1, −1, −1, −1, −1] | ||
| 1 | (1,2) | Q | [2] |
| S | [false,true,false,false,false,false,false,false] | ||
| d | [inf, 6.02, 0, 0, 0, 0, 0, 0] | ||
| Pred. | [−1, 1, −1, −1, −1, −1, −1, −1] | ||
| 2 | (1,3) | Q | [2, 3] |
| S | [false,true,true,false,false,false,false,false] | ||
| d | [inf, 6.02, 5.84, 0, 0, 0, 0, 0] | ||
| Pred. | [−1, 1, 1, −1, −1, −1, −1, −1] | ||
| 3 | (1,4) | Q | [2, 3, 4] |
| S | [false,true,true,true,false,false,false,false] | ||
| d | [inf, 6.02, 5.84, 8.20, 0, 0, 0, 0] | ||
| Pred. | [−1, 1, 1, 1, −1, −1, −1, −1] | ||
| 3 | (2,3) | Q | [3, 4] |
| S | [false,false,true,true,false,false,false,false] | ||
| d, Pred. | No change | ||
| 4 | (2,5) | Q | [3, 4, 5] |
| S | [false,false,true,true,true,false,false,false] | ||
| d | [inf, 6.02, 5.84, 8.20, 4.45, 0, 0, 0] | ||
| Pred. | [−1, 1, 1, 1, 2, −1, −1, −1] | ||
| 5 | (3,2) | Q | [4, 5] |
| S | [false,false,false,true,true,false,false,false] | ||
| d, Pred. | No change | ||
| 5 | (3,4) | Q, S, d, Pred. | No change |
| 6 | (3,5) | Q, S, d, Pred. | No change |
| 7 | (4,3) | Q | [5] |
| S | [false,false,false,false,true,false,false,false] | ||
| d, Pred. | No change | ||
| 8 | (4,5) | Q, S | No change |
| d | [inf, 6.02, 5.84, 8.20, 5.44, 0, 0, 0] | ||
| Pred. | [−1, 1, 1, 1, 4, −1, −1, −1] | ||
| 9 | (5,6) | Q | [6] |
| S | [false,false,false,false,false,true,false,false] | ||
| d | [inf, 6.02, 5.84, 8.20, 5.44, 0.90, 0, 0] | ||
| Pred. | [−1, 1, 1, 1, 4, 5, −1, −1] | ||
| 10 | (5,7) | Q | [6, 7] |
| S | [false,false,false,false,false,true,true,false] | ||
| d | [inf, 6.02, 5.84, 8.20, 5.44, 0.90, 1.0, 0] | ||
| Pred. | [−1, 1, 1, 1, 4, 5, 5, −1] | ||
| 11 | (5,6) | Q | [6, 7, 8] |
| S | [false,false,false,false,false,true,true,true] | ||
| d | [inf, 6.02, 5.84, 8.20, 5.44, 0.90, 1.0, 2.0] | ||
| Pred. | [−1, 1, 1, 1, 4, 5, 5, 5] | ||
| 12 | (6,8) | Q | [7, 8] |
| S | [false,false,false,false,false,false,true,true] | ||
| d, Pred. | No change | ||
| 13 | (7,8) | Q | [8] |
| S | [false,false,false,false,false,false,false,true] | ||
| d, Pred. | No change | ||
| 14 | (8,-) No neighbors | Q | [EMPTY] |
| S | [false,false,false,false,false,false,false,false] | ||
| d, Pred. | No change |
The complexity of the algorithm is stated in the following theorem.
Theorem 3.
Algorithm 3 solves the GWPP in the presence of loss and gain factors in time.
Proof of Theorem 3.
See [4]. □
While Algorithm 3 is less efficient than Algorithm 2, its ability to handle gain factors makes it a valuable tool in the more general case of gain or loss factors attached to the arcs.
6. Experiments and Discussions
Since the problem studied in the paper is new, the (three) algorithms proposed in the paper were compared with each other. The results of the comparison can be seen below.
Based on the findings presented in Theorems 1 and 2, it is obvious that Algorithm 2 outperforms Algorithm 1 in terms of speed. However, Algorithm 1 offers an advantage in that it can be effectively parallelized on GPUs by utilizing classical Dijkstra’s algorithm [18] in a sequential manner. So, the implementation of CUDA-based Dijkstra’s algorithm resulted in a noteworthy acceleration of Algorithm 1.
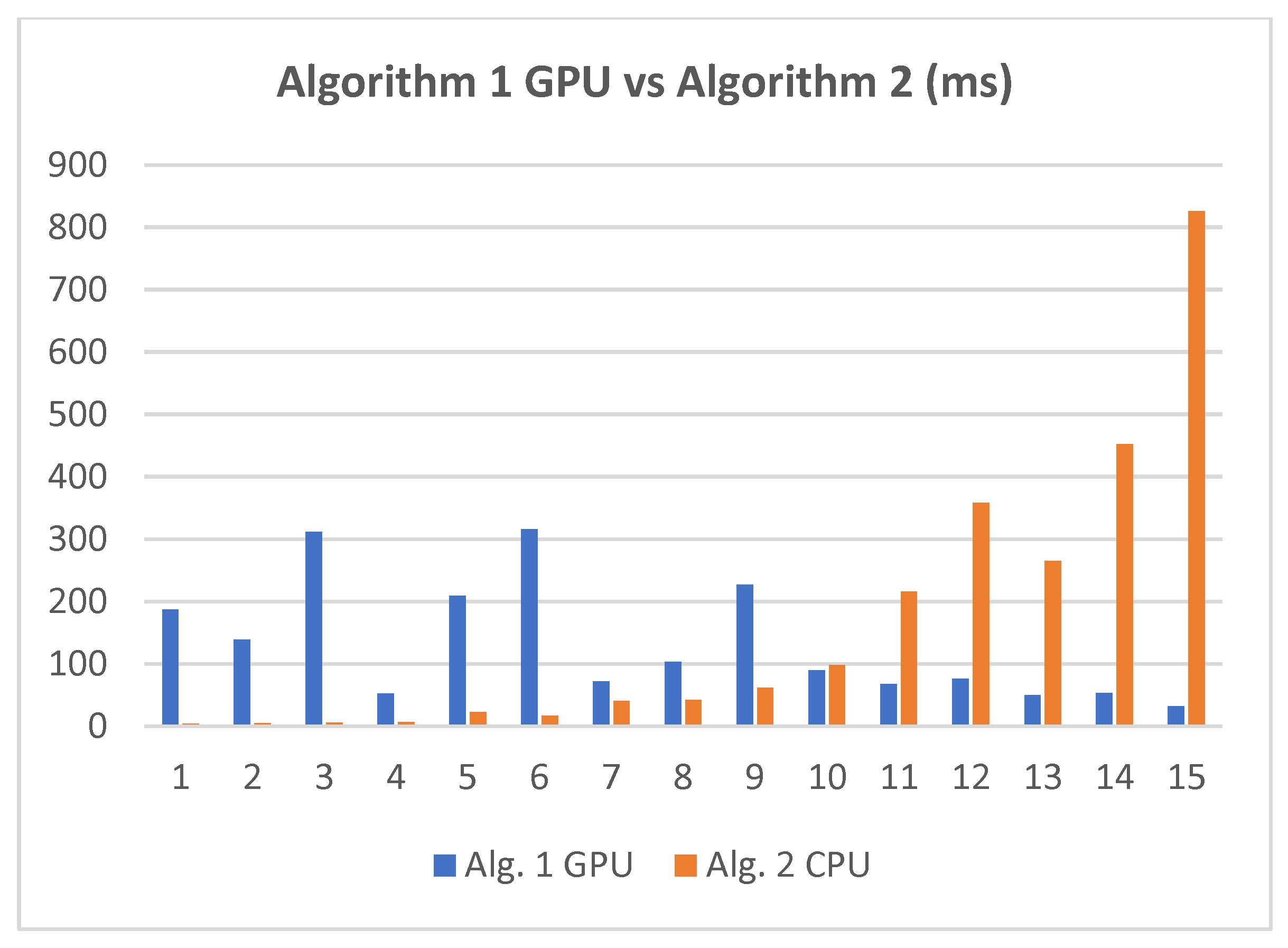
The CUDA version exhibited significantly improved performance compared to Algorithm 2, as shown in Figure 11. Particularly for larger network instances with 10,000 nodes or more, the CUDA implementation of Algorithm 1 was up to 25.7 times faster than that of Algorithm 2.
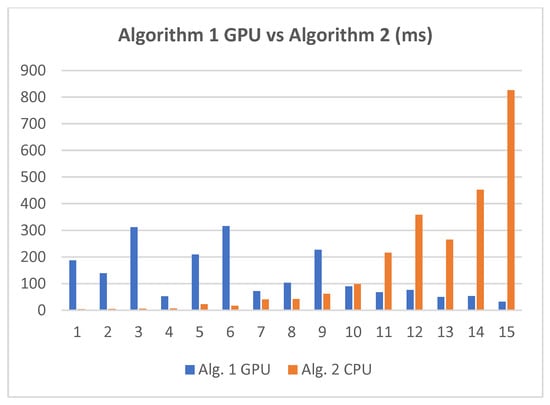
Figure 11.
Running times (ms) comparison between Algorithm 1 GPU and Algorithm 2 CPU.
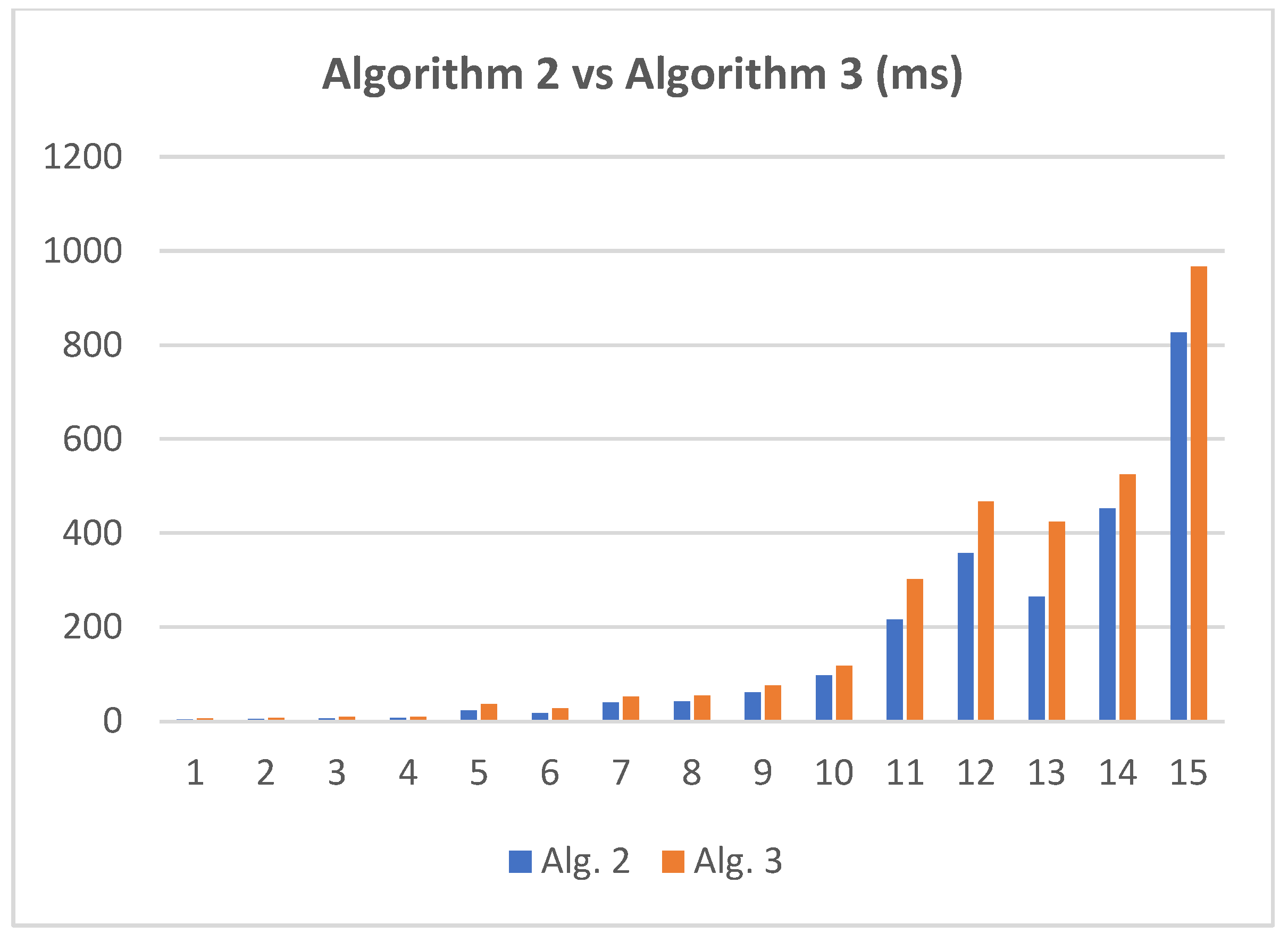
As expected, Algorithm 2 is faster than Algorithm 3 (see Figure 12). The experiments were performed on large networks (see Table 2). They showed that Algorithm 2 runs up to 1.64 times faster than Algorithm 3 (see Table 3).
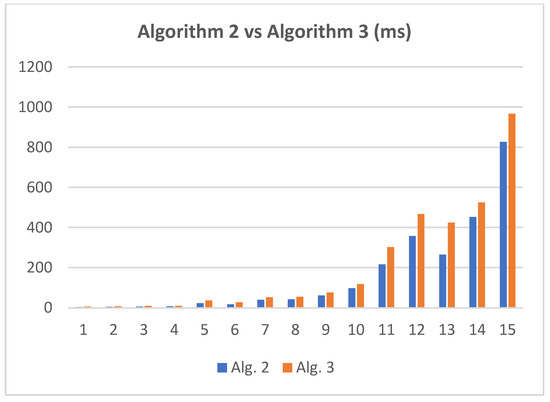
Figure 12.
Running times (ms) comparison between Algorithm 2 and Algorithm 3.

Table 2.
Network generator parameters used for experiments.

Table 3.
Running times (ms) comparison between algorithms.
We used different instances of random generated networks with the number of nodes varying from 1000 to 25,000 (see Table 1). The networks were generated using the network random generator from [19]. It is imperative to acknowledge that throughout various experimental analyses, the graph’s density played an important role and was calibrated using the Erdős–Rényi probability distribution [20]. The Erdős–Rényi variable, a continuous parameter spanning the interval [0, 1], played a pivotal role in these experimental investigations.
In this context, it is essential to elucidate that the Erdős–Rényi variable assumes a value of 0 when the graph lacks any new arcs, signifying minimal density. Conversely, a value of 1 denotes the graph’s attainment of maximum density, highlighting the comprehensive spectrum of density exploration in our experimental framework.
The experiments were performed using a PC with an Intel(R) Core(TM) i5-6500 CPU @ 3.20 GHz, 24 GB RAM, and an NVIDIA GeForce GTX 1070 TI graphics card. The algorithms were programmed in Visual C++ 2022 under Windows 10.
7. Conclusions
In this paper, a novel combinatorial optimization problem was introduced (GWPP). The main objective is to identify a path that can transmit the maximum flow, taking into account both the capacities and loss/gain factors of the arcs.
The paper presented two strongly polynomial algorithms to address the GWPP in the loss factor case and a third algorithm that can be used to solve the GWPP in the general case of gain/loss factors attached to arcs. The first algorithm has a time complexity of , where represents the time complexity of finding the shortest path in the network. On the other hand, the second algorithm has a more efficient time complexity of . However, when the first algorithm is implemented on GPUs, it performs substantially faster than the second algorithm, especially for large network instances. Algorithm 3 has a worse time complexity of compared to that of Algorithm 2, but Algorithm 3 can deal with the more general case of gain/loss factors. To better understand how each of the three algorithms works, an example was considered, and the iterations of each algorithm were presented.
The same experiments were performed for all three algorithms, and the performance was compared. Algorithm 1 is considerably slower than Algorithm 2, both programmed on a CPU. However, Algorithm 1 can be easily and efficiently implemented on GPUs, and in this case, it outperforms Algorithm 2. As expected, Algorithm 3 is slower than Algorithm 2.
Author Contributions
Conceptualization, J.T.; methodology, J.T. and A.M.D.; software, M.-L.R.; validation, A.M.D.; formal analysis, J.T.; data curation, M.-L.R. and A.M.D.; writing—original draft preparation, J.T.; writing—review and editing, J.T., M.-L.R. and A.M.D.; visualization, M.-L.R.; supervision, J.T. and A.M.D.; funding acquisition, A.M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Ford, L.R., Jr.; Fulkerson, D.R. A Shortest Chain Algorithm: Flows in Networks; Princeton University Press: Princeton, NJ, USA, 1962; pp. 130–134. [Google Scholar]
- Ahuja, R.K.; Magnanti, T.L.; Orlin, J.B. Network Flows; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Punnen, A.P. A linear time algorithm for the maximum capacity path problem. Eur. J. Oper. Res. 1991, 53, 402–404. [Google Scholar] [CrossRef]
- Berman, O.; Handler, G.Y. Optimal Minimax Path of a Single Service Unit on a Network to Nonservice Destinations. Transp. Sci. 1987, 21, 115–122. [Google Scholar] [CrossRef]
- Kaibel, V.; Peinhardt, M.A.F. On the Bottleneck Shortest Path Problem; ZIB-Report 06-22; Konrad-Zuse-Zentrum für Informationstechnik Berlin: Berlin, Germany, 2006. [Google Scholar]
- Gabow, H.N.; Tarjan, R.E. Algorithms for two bottleneck optimization problems. J. Algorithms 1988, 9, 411–417. [Google Scholar] [CrossRef]
- Schulze, M. A new monotonic, clone-independent, reversal symmetric, and Condorcet-consistent single-winner election method. Soc. Choice Welf. 2011, 36, 267–303. [Google Scholar] [CrossRef]
- Fernandez, E.; Garfinkel, R.; Arbiol, R. Mosaicking of aerial photographic maps via seams defined by bottleneck shortest paths. Oper. Res. 1998, 46, 293–304. [Google Scholar] [CrossRef]
- Ullah, E.; Lee, K.; Hassoun, S. An algorithm for identifying dominant-edge metabolic pathways. In Proceedings of the 2009 IEEE/ACM International Conference on Computer-Aided Design-Digest of Technical Papers, San Jose, CA, USA, 2–5 November 2009; pp. 144–150. [Google Scholar]
- Deaconu, A.M.; Ciupala, L.; Spridon, D. Finding minimum loss path in big networks. In Proceedings of the 22nd International Symposium on Parallel and Distributed Computing (ISPDC), Bucharest, Romania, 10–12 July 2023; pp. 39–44. [Google Scholar]
- Ford, L.R.; Fulkerson, D.R. Maximal flow through a network. Can. J. Math. 1956, 8, 399–404. [Google Scholar] [CrossRef]
- Edmonds, J.; Karp, R.M. Theoretical improvements in algorithmic efficiency for network flow problems. JACM 1972, 19, 248–264. [Google Scholar] [CrossRef]
- Tayyebi, J.; Rîtan, M.-L.; Deaconu, A.M. Generalized Maximum Capacity Path Problem with Loss Factors. In Proceedings of the 13th International Conference on Operations Research and Enterprise Systems (ICORES 2024), Rome, Italy, 24–26 February 2024; pp. 302–308, ISBN 978-989-758-681-1. ISSN 2184-4372. [Google Scholar]
- Tayyebi, J.; Deaconu, A. Inverse generalized maximum flow problems. Mathematics 2019, 7, 899. [Google Scholar] [CrossRef]
- Moore, E.F. The shortest path through a maze. In Proceedings of the International Symposium on the Theory of Switching; Harvard University Press: Cambridge, MA, USA, 1959. [Google Scholar]
- Ortega-Arranz, H.; Torres, Y.; Llanos, D.R.; Gonzalez-Escribano, A. A new GPU-based approach to the Shortest Path problem. In Proceedings of the 2013 International Conference on High Performance Computing & Simulation (HPCS), Helsinki, Finland, 1–5 July 2013; pp. 505–511. [Google Scholar]
- Deaconu, A.M.; Spridon, D. Adaptation of Random Binomial Graphs for Testing Network Flow Problems Algorithms. Mathematics 2021, 9, 1716. [Google Scholar] [CrossRef]
- Erdős, P.; Rényi, A. On Random Graphs. I. Publ. Math. 1959, 6, 290–297. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).