Abstract
This paper introduces the idea of a cone m-hemi metric space, which extends the idea of an m-hemi metric space. By presenting non-trivial examples, we demonstrate the superiority of cone m-hemi metric spaces over m-hemi metric spaces. Further, we extend the Banach contraction principle and Krasnoselskii, Meir–Keeler, Boyd–Wong, and some other fixed-point results in the setting of complete and compact cone m-hemi metric spaces. Furthermore, we provide several non-trivial examples and applications to the Fredholm integral equation and dynamic market equilibrium to demonstrate the validity of the main results.
MSC:
47H10; 54H25
1. Introduction
Mathematics is a fundamental field of scientific inquiry that influences all areas of life. It combines various sub-fields, with fixed-point theory as a key area in pure and applied mathematics. This theory is broad and adaptable, with applications in numerous disciplines, including mathematical economics, approximation theory, variational inequalities, management, game theory, social sciences, and optimization theory. Over the last 50 to 60 years, fixed-point theory has rapidly become a prominent dynamic and intriguing field of mathematical research. The foundational work in this area began with Poincare [1], who first explored fixed-point theory in 1886. Subsequently, Banach [2] proved in 1922 that contraction mappings in a complete metric space have a unique fixed point. The following is the formulation of the Banach fixed-point theorem.
Consider a metric space and a contraction mapping . For any there exist such that
Under these conditions, T possesses a unique fixed point. In the early phases of fixed-point theory, the Banach contraction principle is acknowledged as a fundamental concept, advancing many subsequent fixed-point theorems.
A significant branch of fixed-point theory is metric fixed-point theory, with applications extending beyond mathematics into other fields. The origins of metric fixed-point theory can be traced back to Banach’s contraction principle introduced in 1922. When this principle falls short, researchers have developed various generalized metric spaces and contraction principles, leading to the establishment of numerous fixed-point theorems. Examples include quasi-metric spaces, which omit the symmetry axioms [3], and semi-metric spaces, which do not require the triangle inequality [4]. Further, partial metric spaces allow for the possibility that the distance between the point and itself does not necessarily need to be zero [5]. In the academic literature, several generalizations of metric spaces have been introduced, including F-metric, b-metric, and modular metric spaces, where numerous theorems concerning fixed points and common fixed points have been formulated [6,7,8,9,10,11,12,13]. The idea of a 2-metric was presented by Gahler [14], derived from geometry involving more than two points, and, subsequently, the topological properties of 2-metric spaces were explored by Lahiri et al. [15]. The idea of G-metric, a generalized metric space based on the geometry of three points, was proposed by Mustafa and Sims [16]. Branciari [17] extended the traditional metric by replacing the standard triangle inequality with four four-point conditions, leading to the notion of a rectangular metric. Additionally, Choi et al. [18] introduced the g-metric with degree n, which characterizes a distance measure involving points. This advancement expands on the traditional distance metrics that involve only two points, and the g-metric incorporates three points.
The concept of an m-hemi metric defined on a set containing at least elements, where m is an integer, was proposed by Deza and Rosenberg [19]. This innovative concept has garnered significant attention from researchers. Studies have explored various topological properties and fixed-point theorems connected to Banach’s contraction principle and its generalizations for mappings defined on m-hemi metric spaces [20].
The idea of cone metric spaces has also garnered considerable interest from researchers. Huang and Zhang [21] were the pioneers in defining cone metric spaces. Rzepecki [22] offered a similar interpretation and, after a detailed exploration of convergence and completeness in these spaces, established multiple fixed-point outcomes for contractive mappings. Later, Liu and Xu [23] extended the idea of cone metric spaces to Banach algebras and applied the Banach contraction principle within this framework. See [24,25,26,27] for more related studies. Ali et al. [28] worked on the approximation of fixed points and the solution of a nonlinear integral equation. Özger et al. [29] proved several fixed-point results and determined the existence and uniqueness of Fredholm-type integral equations by utilizing fixed-point theorems. Firozjah et al. [30] worked on the concept of cone b-metric spaces over Banach algebras and obtained several fixed-point results without the condition of normality of cones. Huang et al. [31] discussed some topological properties and fixed-point results in cone metric spaces over Banach algebras. Firozjah et al. [32] proved several fixed-point results under generalized c-distance in cone b-metric spaces over Banach algebras. Huang et al. [33] generalized a famous result for a Banach-type contractive mapping from to in a cone b-metric space over Banach algebra with coefficient , where is the spectral radius of the generalized Lipshitz constant k. Du and Karapınar [34] investigated the answer to the question regarding whether the results in cone b-metric spaces generalize the existing ones or are equivalent to them. Janković et al. [35] shortened the proofs of fixed-point results in cone metric spaces when the cone is normal and solid. Zabrejko [36] provided a brief overview of fixed-point theorems that extend the Banach–Caccioppoli principle for contractive mapping. Further, they established the presence and uniqueness of fixed points for operators in K-metric or K-normed linear spaces, including local convex spaces and Banach space scales.
In this paper, we present the idea of a cone m-hemi metric space as a generalization of the m-hemi metric space and explore its topological properties. Our main goal is to use complete and compact cone m-hemi metric spaces to prove fixed-point theorems.
The structure of this paper is organized as follows:
- Section 2 introduces the fundamental definitions and examples related to the Banach algebras, metric spaces, cones, cone metric spaces, and m-hemi metric spaces, along with relevant examples for the subsequent sections.
- Section 3 focuses on proving fixed points by utilizing the Banach contraction principle and Krasnoselskii, Meir–Keeler, and Boyd–Wong contraction mapping principles in a complete normal cone m-hemi metric space. This section also includes essential definitions, lemmas, and examples pertinent to our study.
- Section 4 applies the results to Fredholm integral equations and integral equations in dynamic market equilibrium economics to demonstrate the applicability of our main findings. In conclusion, we summarize the key points of the paper.
2. Preliminaries
First, we review some fundamental concepts related to Banach algebra and cone m-hemi metric spaces that are required for the subsequent parts. While researching function spaces, Frechet [24] was the pioneer to introduce the concept of metric space. A function that describes the idea of distance between any two nonempty sets is called a metric.
Definition 1 ([25]).
In metric spaces, an ordered pair represent a set , and Δ is a metric on , often known as a distance function on . This function is defined regarding , and, for every we have
- (S1)
- Δ is finite, non-negative, and real-valued;
- (S2)
- if and only if ;
- (S3)
- (symmetry);
- (S4)
- (triangular inequality).
The sign × stands for the Cartesian product of sets. For the sets , the Cartesian product consists of all the possible ordered pairs , where Therefore, refer to the set of all the ordered pairs formed by elements from .
Example 1 ([25]).
Define the function as follows:
Therefore, Δ is a metric on the real numbers set
To demonstrate that Δ is indeed a metric on the conditions to are straightforward. We only need to verify the condition Let
This demonstrates that Δ is a metric on the set of
Definition 2 ([26]).
If a Banach space ϝ has a multiplication that meets certain properties, it is called a Banach algebra. These properties are as follows: for all ,
- (1)
- (2)
- (3)
- (4)
- Existence of such that
- (5)
- (6)
When there is in such a manner that then an element is considered to be invertible.
Example 2.
The set of complex numbers and the set of real numbers , each equipped with their respective norms defined by absolute values, are both Banach algebras.
Definition 3 ([27]).
A subset ρ of real Banach algebra ϝ is called a cone if it satisfies the following conditions:
- (i)
- ;
- (ii)
- (iii)
For a cone we establish a partial order ≤ on relative to as follows: if and only if We use to denote with and to indicate that ; indicates the interior of The cone is referred to as normal if there exists a number such that, for all
The least positive number that meets the condition above is referred to as the normal constant of . In the subsequent discussion, we assume that is a real Banach algebra, is a cone in with , and ≤ denotes the partial ordering associated with .
If every increasing sequence with upper bounds converges, the cone is referred to as regular. Specifically, if is a sequence such that
there are such that for some Equivalently, if every decreasing sequence with lower bounds converges, the cone is referred to as regular. It is widely recognized that a regular cone is also a normal cone.
Definition 4 ([23]).
Assume that is a nonempty set. The mapping must meet the following conditions:
- (1)
- for all with and if and only if
- (2)
- (3)
Then, Δ is considered to be a cone metric on along with the pair , known as a cone metric space over Banach algebra
Example 3 ([21]).
Suppose represents a constant. Therefore, is said to be a cone metric space.
Definition 5 ([19]).
Assume and E is a set containing at least elements. Δ: is known m-hemi metric if at all possible
- 1.
- (non-negativity);
- 2.
- Δ for any (zero-conditioned);
- 3.
- for any rearrangements π of the set (totally symmetric);
- 4.
- (m-simplex inequality).
Then, called an m-hemi metric space.
The notion of the m-hemi metric serves as a generalization to extend the idea of the semi-metric for the m parameters. An important specific instance of the m-hemi metric is the scenario in which 2.
A function is referred to as a 2-metric if meets the conditions of Definition 5 and the following tetrahedron inequality,
3. Main Results
In cone m-hemi metric space, we formulate a unique fixed-point theorem for contraction mappings and a generalized contraction principle. In addition, we provide a few non-trivial examples to validate our primary findings. Further, we provide some definitions and prove the necessary lemmas.
Definition 6.
Assume and E is set to contain at least elements. Δ: (Banach algebra) is called cone m-hemi metric if at all possible
- 1.
- (non-negativity);
- 2.
- Δ for any (zero-conditioned);
- 3.
- for any rearrangements π of the set (totally symmetric);
- 4.
- (m-simplex inequality).
Then, is called a cone m-hemi metric space.
Now, we discuss that, if is a cone m-hemi metric, then is also a cone m-hemi metric on E.
Lemma 1.
Let Δ be a cone m-hemi metric on E and then be a cone m-hemi metric on E.
Proof.
The non-negativity of ensures the non-negativity . Furthermore, the identity implies axiom and total symmetry
and the fact that exhibits zero-conditioned and totally symmetric aspects. Therefore, we need to demonstrate that satisfies axiom .
Because is strictly increasing in , and since axiom , we have
Moreover, for each , the following inequality holds
Now, we examine if is a cone m-hemi metric, and then is also a cone m-hemi metric on E.
Lemma 2.
Let Δ be a cone m-hemi metric on E, and then is a cone m-hemi metric on E.
Proof.
The properties of non-negativity, axiom , and symmetry for can be derived from the corresponding properties . Therefore, we need to verify that satisfies axiom .
We will examine the different scenarios.
Assume there exists such that
In this case, we have
Therefore, we can assume that, for every , the following hold:
Suppose . In this case, we have for all
and this implies that satisfies axiom .
Next, suppose . Moreover, suppose there is an such that . In this case, we have
Therefore, suppose that for all . Finally, since satisfies axiom , we have
This concludes the proof. □
Example 4.
Let , and
Define
Here, is cone m-hemi metric space but not m-hemi metric space because in a standard cone m-hemi metric space distance function Δ required to map to .
Definition 7.
Consider to be a cone m-hemi metric space. For and
is known as x-open ball with radius ε and centers at .
The topology on E defined by using all x-balls as a sub-basis is referred to as the m-hemi metric topology and is indicated by . Elements of are termed x-open sets, while their complements are called x-closed sets.
Lemma 3.
Let and let be a cone m-hemi metric space. If and only if , then W is an x-open set. There are finite numbers of points and for every
Proof.
The claim’s appropriateness is apparent as the intersection of x-balls is x-open, indicating that the condition is instantly satisfied.
Conversely, let and W be an x-open set. Subsequently, x-open balls exist such that . Given that and , then and . For , choose Afterward, we possess
This concludes the proof. □
Definition 8.
Given a cone m-hemi metric space and a subset W, its x-closure, represented by , is defined as the x-closure of W with regard to the topology τ.
Definition 9.
Consider a cone m-hemi metric space , and ρ denotes a normal cone, where the normal constant is k. In E, let be the sequence.
- 1.
- is said to be x-convergent to a if and only ifTherefore, if and only if converges to y with regard to topology τ, it is x-convergent to y.
- 2.
- A sequence is called x-Cauchy if and only if
- 3.
- is called x-complete if each x-Cauchy sequence in E is x-convergent.
- 4.
- A mapping T is considered to be x-continuous on E if when .
Proposition 1.
Let be sequence in E and be a cone m-hemi metric space.
- (i).
- converges to such that
- (ii).
- For each , so that if is x-Cauchy sequence.
Now, we provide the lemma on the uniqueness of the limit in cone m-hemi metric space.
Lemma 4.
The limit in cone m-hemi metric space is unique.
Proof.
Consider denotes a normal cone, where the normal constant is k, and let be a cone m-hemi metric space. In E, let be an x-convergent sequence. Assume that are both the limits of the sequence . Thus, we obtain for all that there exist such that and there exist such that . Let .
Using m-simplex inequality for all different elements , for ,
Hence, . Since is arbitrary, . Thus, . □
Definition 10.
A cone m-hemi metric space is considered to be compact if each sequence in E contains a convergent subsequence.
Now, we prove the Banach contraction principle in the context of cone m-hemi-metric spaces.
Theorem 1.
Let be an x-complete cone m-hemi-metric space and ρ denote a normal cone, where the normal constant is k and represent an x-continuous self mapping that satisfies
for all , . Then, T has a unique fixed point.
Proof.
Let and be any point. We define a sequence . From (6), we have
Given that is a normal cone with a normal constant k, it follows that
This implies
Hence, is an x-Cauchy sequence. As is x-complete, there exist a with . By x-continuity of T,
and by
and limit’s uniqueness .
We now demonstrate the fixed point’s uniqueness. Assume that T has distinct fixed point with for . By (6), we have
which contradicts . As a result, T possesses a unique fixed point. □
Corollary 1.
Consider to be a complete cone m-hemi metric space, and ρ represents a normal cone, where the normal constant is k. For with and set = Suppose is a mapping that satisfies the contractive condition
for all , , which is a constant. Moreover, assume that Then, T possesses a unique fixed point in
Proof.
We just have to demonstrate that is complete and for all y in .
Suppose is a Cauchy sequence in Then, is also a Cauchy sequence in E. Due to the completeness of E, there is so that We have
Hence, and
Therefore, is complete. For every we have
Since it implies Hence, □
Corollary 2.
Let be a complete cone m-hemi metric space. Let ρ represent a normal cone, where the normal constant is Consider a mapping x-continuous that satisfies for some positive integer u
Where is a constant. Then, T possesses a unique fixed point in E.
Proof.
According to Theorem 1 possesses a unique fixed point, which we denote as However, so is a fixed point of as well. Therefore, , indicating that is a fixed point of As the fixed point of T is also a fixed point of , the fixed point T is unique. □
Example 5.
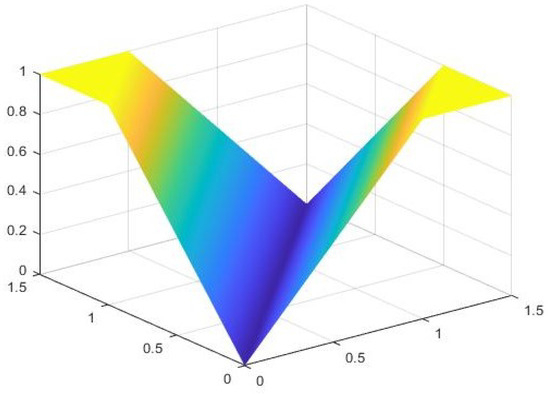
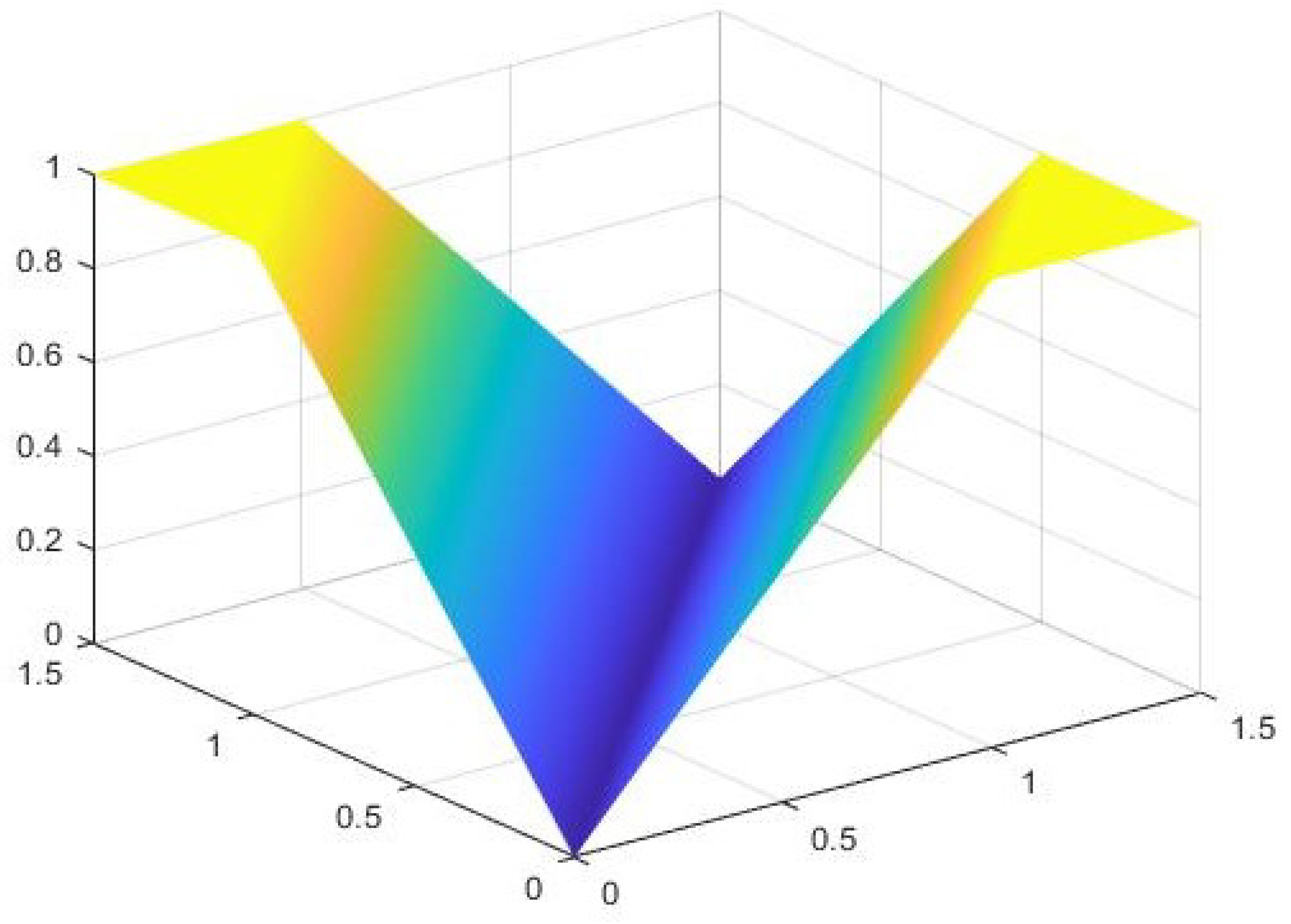
Let . Define and
Then, Δ is an x-complete cone m-hemi metric space on E. Then, (6) is satisfied and T possesses a unique fixed point, which is 0. We depict the graphical behavior of Δ in Figure 1.

Figure 1.
Depicts the graphical behavior of in the above example.
Now, we prove the fixed-point theorem for compact cone m-hemi metric spaces.
Theorem 2.
Consider as a sequentially compact cone m-hemi metric space, and ρ represents a regular cone. Assume that the mapping represents an x-continuous self mapping that satisfies the contractive condition
Then, T possesses a unique fixed point in E.
Proof.
Let and be any point. We define a sequence In the case that, for some u, serves as a fixed point of concluding the proof. Accordingly, we assume for all u that Define and then
Therefore, is a decreasing sequence with a lower bound of 0. Since is a regular, there exists is such that Due to the sequence compactness of E, there is a sub-sequence of and such that . It follows that
So,
where k denotes the normal constant of . By x-continuity of
Moreover, by
and limit’s uniqueness, .
We now demonstrate the fixed point’s uniqueness. Suppose that T has the distinct fixed point with for From (7), we have
which is a contradiction. As a result, T possesses a unique fixed point. □
Example 6.
Consider . Define and
This example demonstrates that the mapping on the sequentially compact cone m-hemi metric space with satisfies the contractive condition, and T possesses a unique fixed point at
Definition 11.
Consider a metric space . A mapping is referred to as a Krasnosalskii mapping if given there exists such that
whenever
Now, we prove the Krasnosalskii fixed-point theorem in the setting of cone m-hemi metric spaces.
Theorem 3.
Let be a complete cone m-hemi metric space and ρ denote a normal cone, where the normal constant is A mapping represent an x-continuous self-mapping that satisfies a Krasnosalskii condition if given there exist such that
whenever Then, T possesses a unique fixed point.
Proof.
We show that T is contractive. Let and let
Since T is Krasnosalskii, there exists
is contractive. Now, let and be any point. We define a sequence .
From (8), we obtain
Given a normal cone with normal constant k, it follows that
This implies
Hence, is an x-Cauchy sequence. Since is x-complete, there exist a with . By x-continuity of T,
and by
and limit’s uniqueness .
Now, we demonstrate the fixed point’s uniqueness. Assume that T has distinct fixed points with for . By using (8), we deduce
which contradicts . As a result, T has a unique fixed point. □
Example 7.
Consider ϝ to be a Banach algebra which consists of all continuous real-valued functions. Let . Then, represents a normal cone, where the normal constant Consider , define , and ,
This example demonstrates that the mapping on the complete cone m-hemi metric space satisfies the Krasnosalskii condition with , so T possesses a unique fixed point at .
Definition 12.
Consider is a metric space and Thus, T is said to satisfy the Meir–Keeler contractive condition if for given so that
Now, we prove fixed-point theorem for Meir–Keeler contraction in the setting of cone m-hemi metric spaces.
Theorem 4.
Let be a complete cone m-hemi metric space and ρ represent a normal cone, where the normal constant is Let represent a x-continuous self-mapping that fulfills the Meir–Keeler contractive condition if for given so that
Then, T possesses a unique fixed point.
Proof.
We demonstrate that T is contractive. Let and then . Since T satisfies the Meir–Keeler contractive condition, such that
⇒T is contractive.
Let and then
Therefore, the sequence is decreasing and has a lower bound of 0.
This implies that is convergent sequence. Let We claim that Suppose that and, taking , so that
Since for so that
In particular, for But,
Applying (11), we obtain
which is a contradiction tot being infimum of Hence,
Now, let and be any point. We define a sequence .
Given that is a normal cone with normal constant k, it follows that,
This implies
Hence, is an x-Cauchy sequence. As is x-complete, there exist a with . By x-continuity of T,
and by
and limit’s uniqueness .
Now, we examine the fixed point’s uniqueness. Assume that T has distinct fixed point with for
Now, denote
By Meir–Keeler condition, for , there exists such that
Applying the condition to we have
which is a contradiction because it implies . As a result, T possesses a unique fixed point. □
Example 8.
Let . Define and
This example demonstrates that the mapping on the x-complete cone m-hemi metric space satisfies the Meir–Keeler condition with , and T possesses a unique fixed point at .
Definition 13.
A function is right-continuous at a point if is defined on an interval lying to the right of δ and if The definition for left-continuous is defined similarly, with lying on the left and
Definition 14.
Consider as a metric space. The mapping is referred to as the Boyd–Wong mapping if there exists a function so that
- (i)
- (ii)
- (iii)
- φ is right-continuous.
Now, we prove Boyd–Wong’s fixed-point theorem in the setting of cone m-hemi metric spaces.
Theorem 5.
Consider as a complete metric space and ρ a normal cone with normal constant k. A mapping represents an x-continuous self-mapping that satisfies the Boyd–Wong condition if there exists a right-continuous function such that if and
for all Then, T possesses a unique fixed point.
Proof.
Let and be any point. We define a sequence .
Let be the function that satisfies Boyd–Wong map condition. So, we assume that, for all Set and then
Therefore, the sequence is decreasing and has a lower bound of 0.
This implies that is a convergent sequence. Let
Suppose . Since is right-continuous function, taking the limit of u on both sides yields
Further, which is contradiction to the fact that Hence, Now, we show that is a Cauchy sequence. On the contrary, we suppose that is not a Cauchy sequence. Then, there exists an such that, for each , we choose integer with So, we have
Since is a decreasing sequence, let be the smallest integer that is greater than l and satisfies . We can choose the smallest possible, meaning that
Now,
Taking the limit as we obtain
implying that from above as and we have
Now,
Taking the limit yields
which implies that
Based on the property, this implies that which is a contradiction. Thus, the sequence is Cauchy. As is x-complete, there exist a with . By x-continuity of T,
and by
and limit’s uniqueness .
Now, we examine the fixed point’s uniqueness. Assume that T has distinct fixed point with for . By using (12), we obtain
which contradicts . As a result, T possesses a unique fixed point. □
Example 9.
Consider to be the algebra of all the u-square real matrices. Let . Then, represents a normal cone, where the normal constant is Let define , and ,
We choose , which satisfies for The fixed point is the zero matrix
4. Applications
In this part, we provide applications to the Fredholm integral equation and dynamic market equilibrium.
4.1. Application to Fredholm Integral Equation
Now, we examine the solution’s uniqueness and existence in the Freholm integral equation in the framework of cone m-hemi metric space. Consider the Fredholm integral equation
and represent the set of continuous functions with cone m-hemi metric
and for
Theorem 6.
Consider an integral Equation (15) and assume
- (i)
- the continuous function
- (ii)
- and for every so that
Then, there exists a unique solution to integral Equation (15).
Proof.
For every , let . According to integral equation formulation, ,
According to Theorem 1, there exists a unique solution to integral Equation (15). □
4.2. Application to Dynamic Market Equilibrium
Now, we demonstrate how to use our proven conclusion to resolve an integral equation uniquely in the context of dynamic market equilibrium economics. Existing prices and pricing patterns (whether prices are rising or declining and whether they are falling or rising at an increasing or decreasing rate) possess an effect on supply and demand in many marketplaces. Determining the current price , the first derivative is and the second derivative Assume
Here, are constants. If prices equilibrate the market continuously over time, we discuss the market’s dynamic stability. In equilibrium, So,
Since
letting in above, we have
When dividing by z, the function is determined by the initial value problem that follows
where is a continuous function. It can be demonstrated that problem (20) is comparable to the integral equation that follows:
where represent a Green’s function, defined as follows:
We will demonstrate that a solution exists for the integral equation as follows:
Let represent the set of continuous real-valued functions defined over the interval . For we define
and for is defined by
Theorem 7.
Consider integral Equation and assume that
- (i)
- ;
- (ii)
- such that
Then, integral Equation possesses a unique solution.
Proof.
Let all such that By the use of assumptions we have
According to Theorem 1, there exists a unique solution to integral Equation (23). □
5. Conclusions
In this study, we introduced the concept of cone m-hemi metric spaces as a generalization of m-hemi metric spaces. Further, we proved several fixed-point results by utilizing generalized contractive conditions, including the Banach contraction principle and Krasnoselskii, Meir–Keeler, and Boyd–Wong contraction mappings in cone m-hemi metric spaces over Banach algebra. We provided several non-trivial examples that show the validity of our main results. Furthermore, regarding applications, we found the existence and uniqueness of the Fredholm integral equation and solution to an integral equation used in dynamic market equilibrium economics with the help of the main results. Our new findings could inspire other researchers to extend and enhance various results in these spaces and explore applications in related fields.
Author Contributions
Conceptualization, L.G., R.B., A.A., E.S., T.K. and U.I.; methodology, L.G., R.B., A.A., E.S., T.K. and U.I.; software, L.G., R.B., A.A., E.S., T.K. and U.I.; validation, L.G., R.B., A.A., E.S., T.K. and U.I.; formal analysis, L.G., R.B., A.A., E.S., T.K. and U.I.; investigation, L.G., R.B., A.A., E.S., T.K. and U.I.; resources, L.G., R.B., A.A., E.S., T.K. and U.I.; data curation, L.G., R.B., A.A., E.S., T.K. and U.I.; writing—original draft preparation, L.G., R.B., A.A., E.S., T.K. and U.I.; writing—review and editing, L.G., R.B., A.A., E.S., T.K. and U.I.; visualization, L.G., R.B., A.A., E.S., T.K. and U.I.; supervision, L.G., R.B., A.A., E.S., T.K. and U.I.; project administration, L.G., R.B., A.A., E.S., T.K. and U.I.; funding acquisition, L.G., R.B., A.A., E.S., T.K. and U.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be available on demand from the corresponding author.
Acknowledgments
The authors are grateful to Princess Nourah bint Abdulrahman University for supporting this research through sabbatical leave program.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Poincare, H. Surless courbes define barles equations differentiate less. J. Math. 1886, 2, 54–65. [Google Scholar]
- Banach, S. Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3, 133–181. [Google Scholar] [CrossRef]
- Bakhtin, I.A. The contraction principle in quasi metric spaces. Funct. Anal. Unianowsk Gos. Ped. Inst. 1989, 30, 26–37. [Google Scholar]
- Wilson, W.A. On semi-metric Spaces. Am. J. Math. 1931, 53, 361–373. [Google Scholar] [CrossRef]
- Matthews, S.G. Partial metric topology. Ann. N. Y. Acad. Sci. 1994, 728, 183–197. [Google Scholar] [CrossRef]
- Abtahi, M.; Kadelburg, Z.; Radenovic, S. Fixed points and coupled fixed points in partially ordered v-generalized metric spaces. Appl. Gen. Topol. 2018, 19, 189–201. [Google Scholar] [CrossRef]
- Chandok, S.; Öztürk, V.; Radenoyic, S. On fixed points in the context of b-metric spaces. Mat. Vesn. 2019, 71, 23–30. [Google Scholar]
- Chistyakov, V.V. Modular metric spaces, I: Basic concepts. Nonlinear Anal. Theory Methods Appl. 2010, 72, 1–14. [Google Scholar] [CrossRef]
- Ozturk, V.; Radenović, S. Some remark on fixed point results of 2 b-metric spaces. Far East J. Math. Sci. 2015, 97, 533–548. [Google Scholar]
- Jahangir, F.; Haghmaram, P.; Nourouzi, K. A note on F-metric spaces. J. Fixed Point Theory Appl. 2021, 23, 2. [Google Scholar] [CrossRef]
- Jleli, M.; Samet, B. On a new generalization of metric spaces. J. Fixed Point Theory Appl. 2018, 20, 128. [Google Scholar] [CrossRef]
- Lateef, D.; Ahmad, J. Dass and Gupta’s fixed point theorem in F-metric spaces. J. Nonlinear Sci. Appl. 2019, 12, 405–411. [Google Scholar] [CrossRef]
- Ozturk, V. Some Results for Ćirić–Prešić Type Contractions in F-Metric Spaces. Symmetry 2023, 15, 1521. [Google Scholar] [CrossRef]
- Gahler, V.S. 2-metrische Raume und ihre topologische Struktur. Math. Nachrichten 1963, 26, 115–118. [Google Scholar] [CrossRef]
- Lahiri, B.K.; Das, P.; Dey, L.K. Cantor’s theorem in 2-metric spaces and its applications to fixed point problems. Taiwan J. Math. 2011, 15, 337–352. [Google Scholar] [CrossRef]
- Mustafa, Z.; Sims, B. A new approach to generalized metric spaces. J. Nonlinear Convex Anal. 2006, 7, 289–297. [Google Scholar]
- Branciari, A. A fixed point theorem of Banach-Caccioppoli type on a class of generalized metric spaces. Publ. Math. Debrecen 2000, 57, 31–37. [Google Scholar] [CrossRef]
- Choi, H.; Kim, S.; Yang, S.Y. Structure for g-Metric Spaces and Related Fixed Point Theorems. arXiv 2018, arXiv:1804.03651. [Google Scholar]
- Deza, M.M.; Rosenberg, I.G. Small cones of m-hemimetrics. Discret. Math. 2005, 291, 81–97. [Google Scholar] [CrossRef][Green Version]
- Ozturk, V.; Radenovic, S. Hemi metric spaces and Banach fixed point theorems. Appl. Gen. Topol. 2024, 25, 175–182. [Google Scholar] [CrossRef]
- Long-Guang, H.; Xian, Z. Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 2007, 332, 1468–1476. [Google Scholar]
- Rzepecki, B. On fixed point theorems of Maia type. Publ. Inst. Math. 1980, 28, 179–186. [Google Scholar]
- Liu, H.; Xu, S. Cone metric spaces with Banach algebras and fixed point theorems of generalized Lipschitz mappings. Fixed Point Theory Appl. 2013, 2013, 320. [Google Scholar] [CrossRef]
- Fréchet, M. Sur quelques points du calcul fonctionnel. Rend. Circ. Mat. Palermo Thése 1906, 22, 1–74. [Google Scholar] [CrossRef]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley and Sons: Hoboken, NJ, USA, 1991; Volume 17. [Google Scholar]
- Cho, S.H. Fixed point theorems in complete cone metric spaces over Banach algebras. J. Funct. Spaces 2018, 2018, 9395057. [Google Scholar] [CrossRef]
- Kutbi, M.A.; Ahmad, J.; Al-Mazrooei, A.E.; Hussain, N. Multivalued fixed point theorems in cone b-metric spaces over Banach Algebra with applications. J. Math. Anal. 2018, 9, 52–64. [Google Scholar]
- Ali, F.; Ali, J.; Rodríguez-López, R. Approximation of fixed points and the solution of a nonlinear integral equation. Nonlinear Funct. Anal. Appl. 2021, 26, 869–885. [Google Scholar]
- Özger, F.; Temizer Ersoy, M.; Ödemiş Özger, Z. Existence of Solutions: Investigating Fredholm Integral Equations via a Fixed-Point Theorem. Axioms 2024, 13, 261. [Google Scholar] [CrossRef]
- Firozjah, A.A.; Rahimi, H.; Rad, G.S. Fixed and periodic point results in cone b-metric spaces over Banach algebras; A survey. Fixed Point Theory 2021, 22, 157–168. [Google Scholar] [CrossRef]
- Huang, H.; Deng, G.; Radenović, S. Some topological properties and fixed point results in cone metric spaces over Banach algebras. Positivity 2019, 23, 21–34. [Google Scholar] [CrossRef]
- Arabnia Firozjah, A.; Rahimi, H.; De la Sen, M.; Soleimani Rad, G. Fixed point results under generalized c-distance in cone b-metric spaces over Banach algebras. Axioms 2020, 9, 31. [Google Scholar] [CrossRef]
- Huang, H.; Radenovic, S.; Deng, G. A sharp generalization on cone b-metric space over Banach algebra. J. Nonlinear Sci. Appl. 2017, 10, 429–435. [Google Scholar] [CrossRef]
- Du, W.S.; Karapınar, E. A note on cone b-metric and its related results: Generalizations or equivalence? Fixed Point Theory Appl. 2013, 2013, 210. [Google Scholar] [CrossRef]
- Janković, S.; Kadelburg, Z.; Radenović, S. On cone metric spaces: A survey. Nonlinear Anal. Theory Methods Appl. 2011, 74, 2591–2601. [Google Scholar] [CrossRef]
- Zabrejko, P.P. K-metric and K-normed linear spaces: Survey. Collect. Math. 1997, 48, 825–859. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).