On Non-Linear Differential Systems with Mixed Boundary Conditions

Abstract

For the constructive analysis of locally Lipschitzian system of non-linear differential equations with mixed periodic and two-point non-linear boundary conditions, a numerical-analytic approach is developed, which allows one to study the solvability and construct approximations to the solution. The values of the unknown solution at the two extreme points of the given interval are considered as vector parameters whose dimension is the same as the dimension of the given differential equation. The original problem can be reduced to two auxiliary ones, with simple separable boundary conditions. To study these problems, we introduce two different types of parametrized successive approximations in analytic form. To prove the uniform convergence of these series, we use the appropriate technique to see that they form Cauchy sequences in the corresponding Banach spaces. The two parametrized limit functions and the given boundary conditions generate a system of algebraic equations of suitable dimensions, the so-called system of determining equations, which give the numerical values of the introduced unknown parameters. We prove that the system of determining equations define all possible solutions of the given boundary value problems in the domain of definition. We established also the existence of the solution based on the approximate determining system, which can always be produced in practice. The theory was presented in detail in the case of a system of differential equations consisting of two equations and having two different solutions.

1. Introduction and Subsidary Statements

For the investigation of solutions of different types of periodic and nonlinear boundary value problems for ordinary differential equations side by side with numerical methods, is often are used an approximate techniques based upon some types of successive approximations constructed in analytic form. See, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19].

We study the following non -linear differential system with mixed, partly periodic and general two-point boundary conditions on the given compact interval

$$\begin{array}{c}\begin{array}{c}{\displaystyle \frac{dx\left(t\right)}{dt}}=f_1\left(t,x\left(t\right),y\left(t\right)\right),t\in \left[a,b\right],x\in {\mathbb{R}}^p,y\in {\mathbb{R}}^q,f_1\in {\mathbb{R}}^p\\ {\displaystyle \frac{dy\left(t\right)}{dt}}=f_2\left(t,x\left(t\right),y\left(t\right)\right),t\in \left[a,b\right],x\in {\mathbb{R}}^p,y\in {\mathbb{R}}^q,f_2\in {\mathbb{R}}^q\end{array}\end{array}$$

(1)

$$\begin{array}{c}x\left(a\right)=x\left(b\right),\end{array}$$

(2)

$$\begin{array}{c}B\left(y\left(a\right),y\left(b\right)\right)=d.\end{array}$$

(3)

Here we suppose that $f_1:\left[a,b\right]\times D_x\times D_y\to {\mathbb{R}}^p,$ $f_2:\left[a,b\right]\times D_x\times D_y\to {\mathbb{R}}^q$ are continuous functions defined on bounded sets $D_x\subset {\mathbb{R}}^p$, $D_y\subset {\mathbb{R}}^q$ and $B:D_a^y\times D_b^y\to {\mathbb{R}}^q$, $d\in {\mathbb{R}}^q$ (the domains $D_x$, $D_y$, $D_a^y$ and $D_b^y$ will be concretized later, see (17), (19) and (21)). Moreover, the functions $f_1$, $f_2$, B are Lipschitzian in the following form:

$$\begin{array}{cc}\hfill \left|f_1(t,x,y)-f_1(t,\tilde{x},\tilde{y})\right|& \le K_1\left|x-\tilde{x}\right|+K_2\left|y-\tilde{y}\right|,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill \left|f_2(t,x,y)-f_2(t,\tilde{x},\tilde{y})\right|& \le K_3\left|x-\tilde{x}\right|+K_4\left|y-\tilde{y}\right|\hfill \end{array}$$

(5)

for any $t\in \left[a,b\right]$, $\left\{x,\tilde{x}\right\}\subset D_x,$ $\left\{y,\tilde{y}\right\}\subset D_y$ and

$$\left|B(u,v)-B(\tilde{u},\tilde{v})\right|\le K_5\left|u-\tilde{u}\right|+K_6\left|v-\tilde{v}\right|$$

(6)

for all $\left\{u,\tilde{u}\right\}\subset D_a^y$, $\left\{v,\tilde{v}\right\}\subset D_b^y$, where $K_1$, $K_2$, $K_3$, $K_4$, $K_5$, $K_6$ are non-negative constant matrices respectively of dimensions $p\times p$, $p\times q$, $q\times p$, $q\times q$, $q\times q$, $q\times q.$

By a solution of problem (1)–(3) we understand a pair of a continuously differentiable functions $x:\left[a,b\right]\to D_x\subset {\mathbb{R}}^p$ and $y:\left[a,b\right]\to D_y\subset {\mathbb{R}}^q$ satisfying Equation (1) on the interval $\left[a,b\right]$ and conditions (2) and (3).

Here and below, the absolute value sign and inequalities between vectors are understood componentwise. A similar convention is adopted for the operations “$\left|·\right|$”, “max”, “min”. The symbol $I_n$ stands for the unit matrix of dimension n, $r\left(K\right)$ denotes a spectral radius of a square matrix $K.$

On the base of matrices $K_1,K_2,K_3,K_4$ let us introduce the $(p+q)\times (p+q)$ dimensional square matrix

$$K=\left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]$$

(7)

Moreover, we suppose that for the maximal in modulus eigenvalue of matrix

$$Q={\displaystyle \frac{3(b-a)}{10}}K$$

(8)

holds

$$r\left(Q\right)<1.$$

(9)

If $w\in {\mathbb{R}}^n$ and $\rho \in {\mathbb{R}}^n$ is a vector with non-negative components, $O_{\rho }\left(w\right)$ stands for the componentwise $\rho$-neighbourhood of $w:$

$$O_{\rho }\left(w\right):=\left\{\xi \in {\mathbb{R}}^n:\left|\xi -w\right|\le \rho \right\}.$$

(10)

Similarly, for a given bounded connected set $\Omega \subset {\mathbb{R}}^n,$ we define its $\rho$-neighbourhood by putting

$$O_{\rho }(\Omega ):=\bigcup _{\xi \in \Omega }{O}_{\rho }\left(\xi \right).$$

(11)

We will use the following statements.

Lemma 1 

([20]). Let $\Lambda \subset$${\mathbb{R}}^k(k\ge 1)$ be a closed bounded set and $u:\left[a,b\right]\times \Lambda \to {\mathbb{R}}^n$ be a continuous function. Then, for an arbitrary $t\in \left[a,b\right]$, $\lambda \in \Lambda$ the componentwise inequality

$$\left|{\int }_a^t\left[u(\tau ,\lambda )-{\displaystyle \frac{1}{b-a}}{\int }_a^{b}u(s,\lambda )ds\right]d\tau \right|\le {\alpha }_1\left(t\right){\displaystyle \frac{{\displaystyle \underset{(s,\lambda )\in \left[a,b\right]\times \Lambda }{max}}u(s,\lambda )-{\displaystyle \underset{(s,\lambda )\in \left[a,b\right]\times \Lambda }{min}}u(s,\lambda )}{2}},$$

(12)

holds, where

$${\alpha }_1\left(t\right)=\left(1-{\displaystyle \frac{t-a}{b-a}}\right){\int }_a^{t}1·ds+{\displaystyle \frac{t-a}{b-a}}{\int }_t^{b}1·ds=2\left(t-a\right)\left(1-{\displaystyle \frac{t-a}{b-a}}\right),$$

(13)

$${\alpha }_1\left(t\right)\le {\displaystyle \frac{b-a}{2}},t\in \left[a,b\right].$$

(14)

Lemma 2 

([21]). Let the sequence of continuous functions ${\left\{{\alpha }_m\right\}}_{m=0}^{\infty }$ be defined by the recurrence relation

$$\begin{array}{cccc}\hfill {\alpha }_{m+1}\left(t\right)& =\left(1-{\displaystyle \frac{t-a}{b-a}}\right){\int }_a^t{\alpha }_m\left(s\right)ds+{\displaystyle \frac{t-a}{b-a}}{\int }_t^b{\alpha }_m\left(s\right)ds,\hfill & \hfill {\alpha }_0\left(t\right)& =1.\hfill \end{array}$$

(15)

Then the following estimates hold for $t\in \left[a,b\right]$:

$$\begin{array}{c}{\alpha }_{m+1}\left(t\right)\le {\displaystyle \frac{10}{9}}{\left({\displaystyle \frac{3(b-a)}{10}}\right)}^m{\alpha }_1\left(t\right),m\ge 0,\\ {\alpha }_{m+1}\left(t\right)\le {\displaystyle \frac{3(b-a)}{10}}{\alpha }_m\left(t\right),m\ge 1.\end{array}$$

(16)

2. Parametrization and Convergence of Successive Approximations

The idea that we are going to employ is based on the reduction of the given problem to a family of simple auxiliary boundary value problems [22]. Let us fix certain compact convex sets $D_a^x=D_b^x\subset {\mathbb{R}}^p$ and $D_a^y\subset {\mathbb{R}}^q$, $D_b^y\subset {\mathbb{R}}^q$$.$ For given bounded connected sets define the sets

$$D_{a,b}^x:=(1-\theta )z+\theta \eta ,z\in D_a^x,\eta \in D_b^x,\theta \in \left[0,1\right].$$

(17)

$$D_{a,b}^y:=(1-\theta )\gamma +\theta \lambda ,\gamma \in D_a^y,\lambda \in D_b^y,\theta \in \left[0,1\right].$$

In practice, it is convenient to choose sets $D_a^x,D_b^x$, $D_a^y$ $,D_b^y$ as parallelepipeds.

The following notations will be required below

$$\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right):={\displaystyle \frac{{\displaystyle \underset{(t,x,y)\in \left[a,b\right]\times D_x\times D_y}{max}}{f}_1(t,x,y)-{\displaystyle \underset{(t,x,y)\in \left[a,b\right]\times D_x\times D_y}{min}}{f}_1(t,x,y)}{2}},\\ {\delta }_{D_x\times D_y}\left(f_2\right):={\displaystyle \frac{{\displaystyle \underset{(t,x,y)\in \left[a,b\right]\times D_x\times D_y}{max}}{f}_2(t,x,y)-{\displaystyle \underset{(t,x,y)\in \left[a,b\right]\times D_x\times D_y}{min}}{f}_2(t,x,y)}{2}}\end{array}$$

(18)

where the domain $D_x$ according to (11) is a componentwise ${\rho }_x$-neighbourhood of the set $D_{a,b}^x$ defined in (17)

$$D_x:=O_{{\rho }_x}\left(D_{a,b}^x\right)$$

(19)

with ${\rho }_x$ such that

$${\rho }_x\ge {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_1\right),$$

(20)

and $D_y$ is the componentwise ${\rho }_y$-neighbourhood of the set $D_{a,b}^y$

$$D_y:=O_{{\rho }_y}\left(D_{a,b}^y\right)$$

(21)

with ${\rho }_y$ such that

$${\rho }_y\ge {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_2\right).$$

(22)

We use an approach that was used also in [23,24] in the case of a different type of boundary value problems. Namely, we introduce the vectors of parameters

$$\begin{array}{ccc}z=col(z_1,z_2,\dots ,z_p),& \gamma =col({\gamma }_1,{\gamma }_2,\dots ,{\gamma }_q),& \lambda =col({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_q)\end{array}$$

(23)

by formally putting

$$\begin{array}{ccc}z=x\left(a\right)=x\left(b\right),\hfill & \gamma =y\left(a\right),\hfill & \lambda =y\left(b\right).\hfill \end{array}$$

(24)

Instead of boundary value problem (1)–(3) we will consider the following two boundary value problems with periodic and two-point linear separated parametrized conditions at a and b:

$$\begin{array}{c}{\displaystyle \frac{dx}{dt}}=f_1\left(t,x,y\right),t\in \left[a,b\right],\end{array}$$

(25a)

$$\begin{array}{c}x\left(a\right)=x\left(b\right)=z\end{array}$$

(25b)

and

$$\begin{array}{c}{\displaystyle \frac{dy}{dt}}=f_2\left(t,x,y\right),t\in \left[a,b\right],\end{array}$$

(26a)

$$\begin{array}{c}y\left(a\right)=\gamma ,y\left(b\right)=\lambda .\end{array}$$

(26b)

We focus on the continuously differentiable solutions $x:\left[a,b\right]\to D_x$ and $y:\left[a,b\right]\to D_y$ of problem (1)–(3) with values $x\left(a\right)\in D_a^x$ and $y\left(a\right)\in D_a^y,y\left(b\right)\in D_b^y.$

As will be seen from statements below, one can then go back to the original problem by choosing the values of the introduced parameters $z,\gamma$ and $\lambda$ appropriately.

Let us connect for problem (25) with the periodic parametrized boundary conditions the sequences of functions

$$\begin{array}{c}{x}_{m+1}(t,z,\gamma ,\lambda )=z+{\int }_a^t{f}_1\left(s,x_m(s,z,\gamma ,\lambda ),y_m(s,z,\gamma ,\lambda )\right)ds\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b{f}_1\left(s,x_m(s,z,\gamma ,\lambda ),y_m(s,z,\gamma ,\lambda )\right)ds,t\in \left[a,b\right],m=0,1,\dots ,\end{array}$$

(27)

and for the investigation of auxiliary problem (27) we introduce the sequence of functions

$$\begin{array}{c}{y}_{m+1}(t,z,\gamma ,\lambda )=\gamma +{\displaystyle \frac{t-a}{b-a}}\left[\lambda -\gamma \right]+{\int }_a^t{f}_2\left(s,x_m(s,z,\gamma ,\lambda ),y_m(s,z,\gamma ,\lambda )\right)ds-\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b{f}_2\left(s,x_m(s,z,\gamma ,\lambda ),y_m(s,z,\gamma ,\lambda )\right)ds,t\in \left[a,b\right],m=0,1,\dots ,\end{array}$$

(28)

satisfying the periodic conditions (25b) and two-point parametrized conditions (26b) for arbitrary $z\in {\mathbb{R}}^p$, $\gamma \in$${\mathbb{R}}^q$ and $\lambda \in$${\mathbb{R}}^q,$ where

$$x_0(t,z)=z,$$

(29)

$$y_0(t,\gamma ,\lambda )=\gamma +{\displaystyle \frac{t-a}{b-a}}\left[\lambda -\gamma \right]$$

(30)

Theorem 1. 

Let conditions (4)–(9) and (19)–(22) be fulfilled. Then, for all fixed $z\in D_a^x$, $\gamma \in D_a^y$, $\lambda \in D_b^y:$

1. 

The functions of the sequence (27) belonging to the domain $D_x$ are continuosly differentiable on the interval $\left[a,b\right]$, and satisfy the two-point periodic boundary conditions (25b) and converges uniformly as $m\to \infty$ with respect to the domain $(t,z,\gamma ,\lambda )\in \left[a,b\right]\times D_a^x\times D_a^y\times D_b^y$ to the limit function

$$x_{\infty }\left(t,z,\gamma ,\lambda \right)=\underset{m\to \infty }{lim}{x}_m(t,z,\gamma ,\lambda ),$$

(31)

which satisfies the periodic boundary conditions (25b).

2. 

The continuously differentiable functions of the sequence (28) belonging to $D_y$ for $t\in \left[a,b\right]$ uniformly converges as $m\to \infty$ with respect to the domain $(t,z,\gamma ,\lambda )\in \left[a,b\right]\times D_a^x\times D_a^y\times D_b^y$ to the limit function

$$y_{\infty }\left(t,z,\gamma ,\lambda \right)=\underset{m\to \infty }{lim}{y}_m(t,z,\gamma ,\lambda ),$$

(32)

which satisfies the boundary conditions (26b).

3. 

The limit functions $x_{\infty }\left(t,z,\gamma ,\lambda \right),y_{\infty }\left(t,z,\gamma ,\lambda \right)$ for all $t\in \left[a,b\right]$ are the unique continuously differentiable solutions of the parametrized integral equations

$$\begin{array}{c}x\left(t\right)=z+{\int }_a^t{f}_1(s,x\left(s\right),y\left(s\right))ds-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b{f}_1(s,x\left(s\right),y\left(s\right))ds,\\ y\left(t\right)=\gamma +{\int }_a^t{f}_2(s,x\left(s\right),y\left(s\right))ds-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b{f}_2(s,x\left(s\right),y\left(s\right))ds+{\displaystyle \frac{t-a}{b-a}}\left[\lambda -\gamma \right]\end{array}$$

(33)

or, equivalently, of the Cauchy problems for the modified system of integro-differential equations:

$$\begin{array}{c}{\displaystyle \frac{dx}{dt}}=f_1(t,x,y)+{\Delta }_x(z,\gamma ,\lambda ),x\left(a\right)=z,\\ {\displaystyle \frac{dy}{dt}}=f_2(t,x,y)+{\Delta }_y(z,\gamma ,\lambda ),y\left(a\right)=\gamma ,\end{array}$$

(34)

where ${\Delta }_x:D_a^x\times D_a^y\times D_b^y\to {\mathbb{R}}^p$ and ${\Delta }_y:D_a^x\times D_a^y\times D_b^y\to {\mathbb{R}}^q$ are the mappings given by the formulas

$$\begin{array}{cc}\hfill {\Delta }_x(z,\gamma ,\lambda )& :=-{\displaystyle \frac{1}{b-a}}{\int }_a^b{f}_1(s,x_{\infty }\left(s,z,\gamma ,\lambda \right),y_{\infty }\left(s,z,\gamma ,\lambda \right))ds,\hfill \\ \hfill {\Delta }_y(z,\gamma ,\lambda )& :={\displaystyle \frac{1}{b-a}}\left[\lambda -\gamma \right]-{\displaystyle \frac{1}{b-a}}{\int }_a^b{f}_2(s,x_{\infty }\left(s,z,\gamma ,\lambda \right),y_{\infty }\left(s,z,\gamma ,\lambda \right))ds.\hfill \end{array}$$

(35)

4. 

The following error estimate holds:

$$\left|x_{\infty }\left(·,z,\gamma ,\lambda \right)-x_m\left(·,z,\gamma ,\lambda \right)\right|\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p,$$

(36)

$$\left|y_{\infty }\left(·,z,\gamma ,\lambda \right)-y_m\left(·,z,\gamma ,\lambda \right)\right|\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q},$$

(37)

where ${\delta }_{D_x\times D_y}\left(f_1\right)$ and ${\delta }_{D_x\times D_y}\left(f_2\right)$ are defined in (18), the matrix Q has form (8) and ${\left\{·\right\}}_i^j$ denotes the components $i,i+1,\dots ,j$ of the vector in the brackets $\left\{·\right\}$.

Proof. 

We will prove that for $z\in D_a^x,\gamma \in$$D_a^y,\lambda \in D_b^y$ and $t\in \left[a,b\right]$ the values of the functions (27) and (28) belong to the domains $D_x$ and $D_y$ respectively and they create the Cauchy sequences in the Banach spaces $C\left(\left[a,b\right],{\mathbb{R}}^p\right),$ and $C\left(\left[a,b\right],{\mathbb{R}}^q\right)$ respectively. Indeed, using the estimate (12) of Lemma 1, relations (13), (14), (27) for $m=0,t\in \left[a,b\right]$ imply that

$$\begin{array}{c}\left|x_1(t,z,\gamma ,\lambda )-x_0\left(t,z\right)\right|\le \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\alpha }_1\left(t\right)\left[{\displaystyle \frac{{\displaystyle \underset{(t,x,y)\in \left[a,b\right]\times D_x\times D_y}{max}}{f}_1(t,x_0(t,z),y_0(t,\gamma ,\lambda ))}{2}}-\right.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.-{\displaystyle \frac{{\displaystyle \underset{(t,x,y)\in \left[a,b\right]\times D_x\times D_y}{min}}{f}_1(t,x_0(t,z),y_0(t,\gamma ,\lambda ))}{2}}\right]\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\alpha }_1\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\le {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_1\right),\hspace{1em}\hspace{1em}\hspace{1em}\end{array}$$

(38)

which means, according to (20), that $x_1\left(t,z,\gamma ,\lambda \right)\in D_x,$ whenever $\left(t,z,\gamma ,\lambda \right)\in \left[a,b\right]\times D_a^x\times D_a^y\times D_b^y.$

We can find similarly to (38) on the base of (28) that

$$\left|y_1(t,z,\gamma ,\lambda )-y_0(t,z,\gamma ,\lambda )\right|\le {\alpha }_1\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\le {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_2\right),$$

(39)

which, according to (22), means that $y_1(t,\gamma ,\lambda )\in D_y.$

By induction, we obtain

$$\left|x_m\left(t,z,\gamma ,\lambda \right)-x_0\left(t,z,\gamma ,\lambda \right)\right|\le {\alpha }_1\left(t\right){\delta }_{\left[a,b\right]\times D_x\times D_y}\left(f_1\right)\le {\displaystyle \frac{b-a}{2}}{\delta }_{\left[a,b\right]\times D_x\times D_y}\left(f_1\right)$$

and

$$\left|y_m(t,z,\gamma ,\lambda )-y_0(t,z,\gamma ,\lambda )\right|\le {\alpha }_1\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\le {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_2\right)$$

which means according to (20) and (22) that all the values of functions (27) are contained in domain $D_x$ for all $m=1,2,3,\dots$ and $\left(t,z,\gamma ,\lambda \right)\in \left[a,b\right]\times D_a^x\times D_a^y\times D_b^y$, and all the values of functions (28) belong to $D_y.$

Estimates (38) and (39) can be rewritten in componentwise vector form

$$\left[\begin{array}{c}\left|x_1\left(t,z,\gamma ,\lambda \right)-x_0\left(t,z,\gamma ,\lambda \right)\right|\\ \left|y_1(t,z,\gamma ,\lambda )-y_0(t,\gamma ,\lambda )\right|\end{array}\right]\le \left[\begin{array}{c}{\alpha }_1\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_1\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right].$$

(40)

Consider now the difference of functions

$$\begin{array}{c}\left|x_2\left(t,z,\gamma ,\lambda \right)-x_1\left(t,z,\gamma ,\lambda \right)\right|=\hfill \\ \hspace{1em}\hspace{1em}=\left|{\int }_a^t\left[f_1\left(s,x_1\left(s,z,\gamma ,\lambda \right),y_1\left(s,z,\gamma ,\lambda \right)\right)-f_1\left(s,x_0\left(s,z,\gamma ,\lambda \right),y_0\left(s,z,\gamma ,\lambda \right)\right)\right]ds\right.\\ \hfill \hspace{1em}-\left.{\displaystyle \frac{t-a}{b-a}}{\int }_a^b\left[f_1\left(s,x_1\left(s,z,\gamma ,\lambda \right),y_1\left(s,z,\gamma ,\lambda \right)\right)-f_1\left(s,x_0\left(s,z,\gamma ,\lambda \right),y_0\left(s,z,\gamma ,\lambda \right)\right)\right]ds\right|\end{array}$$

(41)

and

$$\begin{array}{c}\left|y_2(t,z,\gamma ,\lambda )-y_1(t,z,\gamma ,\lambda )\right|=\hfill \\ \hspace{1em}\hspace{1em}=\left|{\int }_a^t\left[f_2\left(s,x_1\left(s,z,\gamma ,\lambda \right),y_1\left(s,z,\gamma ,\lambda \right)\right)-f_2\left(s,x_0\left(s,z,\gamma ,\lambda \right),y_0\left(s,z,\gamma ,\lambda \right)\right)\right]ds\right.\\ \hfill \hspace{1em}-\left.{\displaystyle \frac{t-a}{b-a}}{\int }_a^b\left[f_2\left(s,x_1\left(s,z,\gamma ,\lambda \right),y_1\left(s,z,\gamma ,\lambda \right)\right)-f_2\left(s,x_0\left(s,z,\gamma ,\lambda \right),y_0\left(s,z,\gamma ,\lambda \right)\right)\right]ds\right|.\end{array}$$

(42)

In view of Lemma 1, Lemma 2 and conditions (4), (5) and estimates (40) from (41) and (42) we obtain

$$\begin{array}{c}\left|x_2\left(t,z,\gamma ,\lambda \right)-x_1\left(t,z,\gamma ,\lambda \right)\right|\le \hfill \\ \hspace{1em}\hspace{1em}|{\int }_a^t\left[K_1\left|x_1\left(s,z,\gamma ,\lambda \right)-x_0\left(s,z,\gamma ,\lambda \right)\right|+K_2\left|y_1\left(s,z,\gamma ,\lambda \right)-y_0\left(s,s,\gamma ,\lambda \right)\right|\right]ds\\ \hspace{1em}-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b\left[K_1\left|x_1\left(s,z,\gamma ,\lambda \right)-x_0\left(s,z,\gamma ,\lambda \right)\right|+K_2\left|y_1\left(s,z,\gamma ,\lambda \right)-y_0\left(s,z,\gamma ,\lambda \right)\right|\right]ds\\ \hfill \hspace{1em}\le K_1{\alpha }_2\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)+K_2{\alpha }_2\left(t\right){\delta }_{\left[a,b\right]\times D_x\times D_y}\left(f_2\right),\end{array}$$

(43)

$$\begin{array}{c}\left|y_2\left(t,z,\gamma ,\lambda \right)-y_1\left(t,z,\gamma ,\lambda \right)\right|\le \hfill \\ \hspace{1em}\hspace{1em}|{\int }_a^t\left[K_3\left|x_1\left(s,z,\gamma ,\lambda \right)-x_0\left(s,z,\gamma ,\lambda \right)\right|+K_4\left|y_1\left(s,z,\gamma ,\lambda \right)-y_0\left(s,z,\gamma ,\lambda \right)\right|\right]ds\\ \hspace{1em}-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b\left[K_3\left|x_1\left(s,z,\gamma ,\lambda \right)-x_0\left(s,z,\gamma ,\lambda \right)\right|+K_4\left|y_1\left(s,z,\gamma ,\lambda \right)-y_0\left(s,z,\gamma ,\lambda \right)\right|\right]ds\\ \hfill \hspace{1em}\le K_3{\alpha }_2\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)+K_4{\alpha }_2\left(t\right){\delta }_{\left[a,b\right]\times D_x\times D_y}\left(f_2\right).\end{array}$$

(44)

Let us rewrite estimates (43) and (44) in the matrix-vector form

$$\begin{array}{cc}\hfill \left|x_2\left(t,z,\gamma ,\lambda \right)-x_1\left(t,z,\gamma ,\lambda \right)\right|& \le \left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]·\left[\begin{array}{c}{\alpha }_2\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_2\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right],\hfill \\ \hfill \left|y_2\left(t,z,\gamma ,\lambda \right)-y_1\left(t,z,\gamma ,\lambda \right)\right|& \le \left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]·\left[\begin{array}{c}{\alpha }_2\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_2\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right].\hfill \end{array}$$

Direct computations give

$$K^2=\left[\begin{array}{cc}{K}_1^2+K_2{K}_3& K_1{K}_2+K_2^2\\ K_3{K}_1+K_4{K}_3& K_3{K}_2+K_4^2\end{array}\right],$$

$$\begin{array}{c}\left[\begin{array}{c}\left|x_3\left(t,z,\gamma ,\lambda \right)-x_2\left(t,z,\gamma ,\lambda \right)\right|\\ \left|y_3(t,z,\gamma ,\lambda )-y_2(t,z,\gamma ,\lambda )\right|\end{array}\right]\le \left[\begin{array}{c}{K}_1^2{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)+K_1{K}_2{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)+\\ K_3{K}_1{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)+K_3{K}_2{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)+\end{array}\right.\hfill \\ \hfill \left.\begin{array}{c}+K_2{K}_3{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)+K_2{K}_4{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\\ +K_4{K}_3{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)+K_4^2{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right], \end{array}$$

(45)

and

$$\begin{array}{c}\left|x_3\left(t,z,\gamma ,\lambda \right)-x_2\left(t,z,\gamma ,\lambda \right)\right|\le {\left\{{\left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]}^2\left[\begin{array}{c}{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p,\\ \left|y_3\left(t,z,\gamma ,\lambda \right)-y_2\left(t,z,\gamma ,\lambda \right)\right|\le {\left\{{\left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]}^2\left[\begin{array}{c}{\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_3\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q},\end{array}$$

(46)

where ${\left\{·\right\}}_1^p$ and ${\left\{·\right\}}_{p+1}^{p+q}$ denotes the $1,2,\dots ,p$ and $p+1,\dots ,p+q$ components of the vector in $\left\{·\right\}.$

By induction using estimate (46), we can establish that

$$\left|x_{m+1}\left(t,z,\gamma ,\lambda \right)-x_m\left(t,z,\gamma ,\lambda \right)\right|\le {\left\{{\left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]}^m\left[\begin{array}{c}{\alpha }_{m+1}\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_{m+1}\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p,$$

(47)

$$\left|y_{m+1}\left(t,z,\gamma ,\lambda \right)-y_m\left(t,z,\gamma ,\lambda \right)\right|\le {\left\{{\left[\begin{array}{cc}{K}_1& K_2\\ K_3& K_4\end{array}\right]}^m\left[\begin{array}{c}{\alpha }_{m+1}\left(t\right){\delta }_{D_x\times D_y}\left(f_1\right)\\ {\alpha }_{m+1}\left(t\right){\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}.$$

Using estimate (16) of Lemma 2, from (47) we obtain

$$\begin{array}{c}\left|x_{m+1}\left(t,z,\gamma ,\lambda \right)-x_m\left(t,z,\gamma ,\lambda \right)\right|\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{\left[\begin{array}{c}{Q}^m{\delta }_{D_x\times D_y}\left(f_1\right)\\ Q^m{\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p,\\ \left|y_{m+1}\left(t,z,\gamma ,\lambda \right)-y_m\left(t,z,\gamma ,\lambda \right)\right|\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{\left[\begin{array}{c}{Q}^m{\delta }_{D_x\times D_y}\left(f_1\right)\\ Q^m{\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}.\end{array}$$

(48)

Let us set

$$\begin{array}{cccc}\hfill r_m\left(x\right)& =\left|x_m(t,z,\gamma ,\lambda )-x_{m-1}(t,z,\gamma ,\lambda )\right|,\hfill & \hfill r_m\left(y\right)& =\left|y_m(t,z,\gamma ,\lambda )-y_{m-1}(t,z,\gamma ,\lambda )\right|.\hfill \end{array}$$

Therefore, in view of (48) from inequalities

$$\begin{array}{c}\left|x_{m+j}(t,z,\gamma ,\lambda )-x_m(t,z,\gamma ,\lambda )\right|\le \\ \le \left|x_{m+j}(t,z,\gamma ,\lambda )-x_{m+j-1}(t,z,\gamma ,\lambda )\right|+\left|x_{m+j-1}(t,z,\gamma ,\lambda )-x_{m+j-2}(t,z,\gamma ,\lambda )\right|+\dots \\ +\left|x_{m+1}(t,z,\gamma ,\lambda )-x_m(t,z,\gamma ,\lambda )\right|,\\ \left|y_{m+j}(t,z,\gamma ,\lambda )-y_m(t,z,\gamma ,\lambda )\right|\le \\ \le \left|y_{m+j}(t,z,\gamma ,\lambda )-y_{m+j-1}(t,z,\gamma ,\lambda )\right|+\left|y_{m+j-1}(t,z,\gamma ,\lambda )-y_{m+j-2}(t,z,\gamma ,\lambda )\right|+\dots \\ +\left|y_{m+1}(t,z,\gamma ,\lambda )-y_m(t,z,\gamma ,\lambda )\right|\end{array}$$

on the base of (9) we have

$$\begin{array}{c}\left|x_{m+j}\left(t,z,\gamma ,\lambda \right)-x_m\left(t,z,\gamma ,\lambda \right)\right|\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \le \sum _{i=1}^j{r}_{m+i}\left(x\right)={\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right)\sum _{i=1}^j{\left\{Q^{m+i}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p\le \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{Q^m\sum _{i=0}^{j-1}{Q}^i\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p\le \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p,\end{array}$$

(49a)

and

$$\begin{array}{c}\left|y_{m+j}\left(t,z,\gamma ,\lambda \right)-y_m\left(t,z,\gamma ,\lambda \right)\right|\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hfill \le \sum _{i=1}^j{r}_{m+i}\left(y\right)={\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right)\sum _{i=1}^j{\left\{Q^{m+i}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}\le \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right){\left\{Q^m\sum _{i=0}^{j-1}{Q}^i\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}\le \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{9}}{\alpha }_1\left(t\right)\left\{Q^m{(I_{p+q}-Q)}^{-1}{\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]}_{p+1}^{p+q}\right\}\end{array}$$

(49b)

Since, due to (9), the maximum eigenvalue of the matrix Q is less than 1, we have

$$\begin{array}{cccc}\hfill \sum _{i=0}^{j-1}{Q}^i& \le {\left(I_{p+q}-Q\right)}^{-1},\hfill & \hfill \underset{m\to \infty }{lim}{Q}^m& =0_{p+q}.\hfill \end{array}$$

(50)

Therefore, we conclude from (49) and (50) that, according to Cauchy convergence test, the sequence ${\left\{x_m\left(t,z,\gamma ,\lambda \right)\right\}}_{m=0}^{\infty }$ of the form (27) uniformly converges in the domain $\left(t,z,\gamma ,\lambda \right)\in \left[a,b\right]\times D_a^x\times D_a^y\times D_b^y$ to the limit function $x_{\infty }\left(t,z,\gamma ,\lambda \right)$ and the sequence ${\left\{y_m\left(t,z,\gamma ,\lambda \right)\right\}}_{m=0}^{\infty }$ of the form (28) uniformly converges in the domain $\left(t,z,\gamma ,\lambda \right)\in \left[a,b\right]\times D_a^x\times D_a^y\times D_b^y$ to the limit function $y_{\infty }\left(t,z,\gamma ,\lambda \right)$. Since all functions of the sequences (27) and (28) satisfy correspondingly the periodic parametrized conditions (25b) and conditions (26b) for all values of the introduced parameters $z\in D_a^x$, $\gamma \in D_a^y$, $\lambda \in D_b^y$ the limit functions $x_{\infty }\left(·,z,\gamma ,\lambda \right)$, $y_{\infty }\left(·,z,\gamma ,\lambda \right)$ also satisfies these conditions. Passing to the limit as $m\to \infty$ in equalities (27), (28) we show that the limit function satisfies both the integral Equation (33) and the Cauchy problem (34).

Passing to the limit as $j\to \infty$ in (49) we get the estimates (36). □

3. Connection of the Limit Functions ${\mathit{x}}_{\mathbf{\infty }}\mathbf{(}\mathit{t}\mathbf{,}\mathit{z}\mathbf{,}\mathit{\gamma }\mathbf{,}\mathit{\eta }\mathbf{)}$, ${\mathit{y}}_{\mathbf{\infty }}\mathbf{(}\mathit{t}\mathbf{,}\mathit{z}\mathbf{,}\mathit{\gamma }\mathbf{,}\mathit{\eta }\mathbf{)}$ to the Solution of the Original Problem

Theorem 2. 

Under the assumptions of Theorem 1, the limit functions

$$\begin{array}{cccc}\hfill x_{\infty }(t,z,\gamma ,\lambda )& =\underset{m\to \infty }{lim}{x}_m(t,z,\gamma ,\lambda ),\hfill & \hfill y_{\infty }(t,z,\gamma ,\lambda )& =\underset{m\to \infty }{lim}{y}_m(t,z,\gamma ,\lambda ),\hfill \end{array}$$

(51)

of the sequences (27), (28) are the solution of the non-linear boundary value problem (1)–(3) if and only if the parameters $\left(z,\gamma ,\lambda \right)$ from (24) satisfy the system of $p+2q$ algebraic or transcendental equations

$$\begin{array}{cc}\hfill {\Delta }_x(z,\gamma ,\lambda )& :={\int }_a^b{f}_1(s,x_{\infty }\left(s,z,\gamma ,\lambda \right),y_{\infty }\left(s,\gamma ,\lambda \right))ds=0,\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill {\Delta }_y(z,\gamma ,\lambda )& :=\lambda -\gamma -{\int }_a^b{f}_2(s,x_{\infty }\left(s,z,\gamma ,\lambda \right),y_{\infty }\left(s,z,\gamma ,\lambda \right))ds=0,\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill \Lambda (z,\gamma ,\lambda )& :=B(y_{\infty }\left(a,\gamma ,\lambda \right),y_{\infty }\left(b,\gamma ,\lambda \right))-d=0.\hfill \end{array}$$

(54)

Proof. 

The proof can be carried out similarly as in [21,22]. □

Remark 1. 

The system of Equations (52)–(54) is usually referred to as a determining equations. In such a manner, the original infinite-dimensional problem (1)–(3) is reduced to a system of $p+2q$ numerical equations.

The method thus consists of two parts, namely, the analytic part, when the integral Equations (33) are dealt with by using the method of successsive approximations (27), (28) and the numerical one, which consists in finding values of the $p+2q$ unknown parameters from Equations (52)–(54).

The next statement proves that the system of determining Equations (52)–(54) defines all possible solutions of the original non-linear boundary value problem (1)–(3) having values in domains $D_x\times D_y$.

Theorem 3. 

Let the assumptions of Theorem 1 hold. Furthermore, assume there exists some triplet of vectors $\left(z^0,{\gamma }^0,{\lambda }^0\right)\in D_a^x\times D_a^y\times D_b^y$ which sytisfy the system of determining Equations (52)–(54).

Then:

1. 

The non-linear boundary value problem (1)–(3) has a solution $x^0(·),y^0(·)$ such that

$$\begin{array}{cccccc}\hfill x^0\left(a\right)& =z^0,\hfill & \hfill y^0\left(a\right)& ={\gamma }^0,\hfill & \hfill y^0\left(b\right)& ={\lambda }^0.\hfill \end{array}$$

(55)

Moreover, this solution is given by the limit function of the sequence (27) and (28):

$$\begin{array}{cc}\hfill x^0(·)& =x_{\infty }\left(·,z^0,{\gamma }^0,{\lambda }^0\right)=\underset{m\to \infty }{lim}{x}_m(·,z^0,{\gamma }^0,{\lambda }^0),t\in \left[a,b\right],\hfill \\ \hfill y^0(·)& =y_{\infty }\left(·,z^0,{\gamma }^0,{\lambda }^0\right)=\underset{m\to \infty }{lim}{y}_m(·,z^0,{\gamma }^0,{\lambda }^0),t\in \left[a,b\right].\hfill \end{array}$$

(56)

2. 

If the non-linear boundary value problem (1)–(3) has a solution $x^0(·),y^0(·)$ then the system of determining Equations (52)–(54) is satisfied with

$$\begin{array}{cccccc}\hfill z& =x^0\left(a\right),\hfill & \hfill \gamma & =y^0\left(a\right),\hfill & \hfill \lambda & =y^0\left(b\right).\hfill \end{array}$$

(57)

Proof. 

The proof can be carried out similarly as in [21,22]. □

4. Solvability Analysis Based on the Approximate Determining System

Although Theorem 2 provides a theoretical answer to the question on the construction of a solution of the original non-linear boundary value problem (1)–(3), its application faces certain difficulties due to the fact that the explicit form of the limit functions $x_{\infty }\left(·,z,\gamma ,\lambda \right)$, $y_{\infty }\left(·,z,\gamma ,\lambda \right)$ and consequently the explicit form of the functions

$$\begin{array}{cccccc}\hfill {\Delta }_x& :D_a^x\times D_a^y\times D_b^y,\hfill & \hfill {\Delta }_y& :D_a^x\times D_a^y\times D_b^y\to {\mathbb{R}}^q,\hfill & \hfill \Lambda & :D_a^y\times D_b^y\to {\mathbb{R}}^q\hfill \end{array}$$

in (52)–(54) is usually unknown. This complication can be overcome by using the so-called approximate determining equations:

$$\begin{array}{cc}\hfill {\Delta }_{x,m}(z,\gamma ,\lambda )& :={\int }_a^b{f}_1(s,x_m\left(s,z,\gamma ,\lambda \right),y_m\left(s,\gamma ,\lambda \right))ds=0,\hfill \end{array}$$

(58)

$$\begin{array}{cc}\hfill {\Delta }_{y,m}(z,\gamma ,\lambda )& :=\lambda -\gamma -{\int }_a^b{f}_2(s,x_m\left(s,z,\gamma ,\lambda \right),y_m\left(s,z,\gamma ,\lambda \right))ds=0,\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill {\Lambda }_m(z,\gamma ,\lambda )& :=B(y_m\left(a,z,\gamma ,\lambda \right),y_m\left(b,z,\gamma ,\lambda \right))-d=0.\hfill \end{array}$$

(60)

for a fixed $m.$

Lemma 3. 

Under the assumptions of Theorem 1 for the exact and approximate determining functions defined by (52)–(54) and (58)–(60) for any $z\in$$D_a^x$, $\eta \in D_a^y$, $\lambda \in D_b^y$, $t\in \left[a,b\right]$ and $m\ge 1$, the following estimates hold:

$$\begin{array}{c}\left|{\Delta }_x\left(z,\gamma ,\lambda \right)-{\Delta }_{x,m}\left(z,\gamma ,\lambda \right)\right|\le \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{27}}{(b-a)}^2{K}_1{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p+\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{10}{27}}{(b-a)}^2{K}_2{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q},\end{array}$$

(61)

$$\begin{array}{c}\left|{\Delta }_y\left(z,\gamma ,\lambda \right)-{\Delta }_{y,m}\left(z,\gamma ,\lambda \right)\right|\le \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{27}}{(b-a)}^2{K}_3{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p+\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{10}{27}}{(b-a)}^2{K}_4{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_2\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q},\end{array}$$

(62)

$$\begin{array}{c}\left|B(y_{\infty }\left(a\right),y_{\infty }\left(b\right))-B(y_m\left(a\right),y_m\left(b\right))\right|\le \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\le K_5{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}+\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+K_6{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_2\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}.\end{array}$$

(63)

Proof. 

Let us fix an arbitrary $\left(z,\gamma ,\lambda \right)\in D_a^x\times D_a^y\times D_b^y.$ Using the Lipschitz conditions (4)–(6) and (52)–(54), (58)–(60), estimates (36) and (37), we have

$$\begin{array}{c}\left[\begin{array}{c}\left|{\Delta }_x\left(z,\gamma ,\lambda \right)-{\Delta }_{x,m}\left(z,\gamma ,\lambda \right)\right|\\ \left|{\Delta }_y\left(z,\gamma ,\lambda \right)-{\Delta }_{y,m}\left(z,\eta ,\lambda \right)\right|\\ \left|B(y_{\infty }\left(a\right),y_{\infty }\left(b\right))-B_m(y_m\left(a\right),y_m\left(b\right))\right|\end{array}\right]\le \hfill \\ \hfill \hspace{1em}\le \left[\begin{array}{c}{\int }_a^b\left[K_1\left|x_{\infty }\left(s,z,\gamma ,\lambda \right)-x_m\left(s,z,\gamma ,\lambda \right)\right|+K_2\left|y_{\infty }\left(s,z,\gamma ,\lambda \right)-y_m\left(·,z,\gamma ,\lambda \right)\right|\right]ds\\ {\int }_a^b\left[K_3\left|x_{\infty }\left(s,z,\gamma ,\lambda \right)-x_m\left(s,z,\gamma ,\lambda \right)\right|+K_4\left|y_{\infty }\left(s,z,\gamma ,\lambda \right)-y_m\left(s,z,\gamma ,\lambda \right)\right|\right]ds\\ K_5\left|y_{\infty }(a,z,\gamma ,\lambda )-y_m(a,z,\gamma ,\lambda )\right|+K_6\left|y_{\infty }(b,z,\gamma ,\lambda )-y_m(b,z,\gamma ,\lambda )\right|\end{array}\right]\end{array}$$

(64)

and taking into account that

$${\int }_a^b\begin{array}{cccc}\hfill {\alpha }_1\left(t\right)dt& ={\displaystyle \frac{{(b-a)}^2}{3}},\hfill & \hfill {\alpha }_1\left(t\right)& \le {\displaystyle \frac{b-a}{2}},\hfill \end{array}$$

we get from (64) just (61)–(63). □

Based on both exact and approximate determining systems (52)–(54) and (58)–(60) let us introduce the mappings $H:D_a^x\times D_a^y\times D_b^y\to {\mathbb{R}}^{P+2q}$ and $H_m:D_a^x\times D_a^y\times D_b^y\to {\mathbb{R}}^{P+2q}$ by setting

$$H(z,\gamma ,\lambda ):=\left[\begin{array}{c}{\int }_a^b{f}_1(s,x_{\infty }\left(s,z,\gamma ,\lambda \right),y_{\infty }\left(s,z,\gamma ,\lambda \right))ds\\ \lambda -\gamma -{\int }_a^b{f}_2(s,x_{\infty }\left(s,z,\gamma ,\lambda \right),y_{\infty }\left(s,z,\gamma ,\lambda \right))ds\\ B(y_{\infty }\left(a,\gamma ,\lambda \right),y_{\infty }\left(b,\gamma ,\lambda \right))-d\end{array}\right],$$

(65)

$$H_m(z,\gamma ,\lambda ):=\left[\begin{array}{c}{\int }_a^b{f}_1(s,x_m\left(s,z,\gamma ,\lambda \right),y_m\left(s,z,\gamma ,\lambda \right))ds\\ \lambda -\gamma -{\int }_a^b{f}_2(s,x_m\left(s,z,\gamma ,\lambda \right),y_m\left(s,z,\gamma ,\lambda \right))ds\\ B(y_m\left(a,\gamma ,\lambda \right),y_m\left(b,\gamma ,\lambda \right))-d\end{array}\right],$$

(66)

where $\left(z,\gamma ,\lambda \right)\in D_a^x\times D_a^y\times D_b^y.$

We see from Theorem 2 that the critical points of the vector field H of the form (65) determine solutions of the non-linear problem (1)–(3). The next statement establishes a similar result based upon properties of vector field $H_m$ explicity known from (66).

Theorem 4. 

Let the assumptions of Theorem 1 hold. Moreover, one can specify an $m\ge 1$ and a set

$$\Omega :=D_1\times D_2\times D_3\subset {\mathbb{R}}^{p+2q},$$

where $D_1\subset D_a^x,D_2\subset D_a^y,D_3\subset D_b^y$ are certain bounded open sets such that the mapping $H_m$ satisfies the relations

$$\begin{array}{c}\left|{\int }_a^b{f}_1(s,x_m\left(s,z,\gamma ,\lambda \right),y_m\left(s,z,\gamma ,\lambda \right))ds\right|{⊳}_{\partial \Omega }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{27}}{(b-a)}^2{K}_1{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p+\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{10}{27}}{(b-a)}^2{K}_2{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q},\end{array}$$

(67a)

$$\begin{array}{c}\left|{\int }_a^b{f}_2(s,x_m\left(s,z,\gamma ,\lambda \right),y_m\left(s,z,\gamma ,\lambda \right))ds\right|{⊳}_{\partial \Omega }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\le {\displaystyle \frac{10}{27}}{(b-a)}^2{K}_3{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p+\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{10}{27}}{(b-a)}^2{K}_4{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q},\end{array}$$

(67b)

and

$$\begin{array}{c}\left|B(x_m\left(a,z,\gamma ,\lambda \right),x_m\left(b,z,\gamma ,\lambda \right)))-d\right|{⊳}_{\partial \Omega }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\begin{array}{c}{\displaystyle \frac{5}{9}}(b-a)K_5{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_1^p+\\ +{\displaystyle \frac{5}{9}}(b-a)K_6{\left\{Q^m{(I_{p+q}-Q)}^{-1}\left[\begin{array}{c}{\delta }_{D_x\times D_y}\left(f_1\right)\\ {\delta }_{D_x\times D_y}\left(f_2\right)\end{array}\right]\right\}}_{p+1}^{p+q}\end{array}\end{array}$$

(67c)

on the boundary $\partial \Omega$ of the set Ω. If, in addition

$$deg\left(H_m,\Omega ,0\right)\ne 0,$$

(68)

then there exists $(z^{*},{\gamma }^{*},{\lambda }^{*})\in D_1\times D_2\times D_3$ for which the function

$$\begin{array}{cccc}\hfill x^{*}(·)& :=x_{\infty }\left(·,z^{*},{\gamma }^{*},{\lambda }^{*}\right),\hfill & \hfill y^{*}(·)& :=y_{\infty }\left(·,z^{*},{\gamma }^{*},{\lambda }^{*}\right)\hfill \end{array}$$

(69)

is a solution of the non-linear boundary value problem (1)–(3).

In (67) the binary relation ${⊳}_{\partial \Gamma }$ is defined in [21] as a kind of strict inequality for vector functions and it means that, at every point on the boundary $\partial \Omega$, at least one of the components of the vector $\left|H_m\left(z,\eta \right)\right|$ is greater than the corresponding component of the vector at the right-hand side. The degree in (68) is the Brouwer degree because all the vectors fields are finite-dimensional. Likewise, all the terms in the right-hand side of (67) are computed explicitly e.g., by using computer algebra systems.

Proof. 

The proof can be carried out similarly as in Theorem 4 from [23]. □

5. Conclusions

The method is numerical-analytic in the sense that its realization consists of two stages. First we give an explicit construction of certain parametrized approximations in analytic form, then a system of non-linear algebraic equations is obtained for the introduced parameters, which can be solved numerically. The values of the unknown solution at the two extreme points of the given interval are considered as vector parameters whose dimension is the same as the dimension of the given differential equation. The original problem can be reduced to two auxiliary ones, with simple separable boundary conditions. To study these problems, we introduce two different types of successive approximations in analytic form. It can be noticed that in order to solve the given mixed boundary value problem, it was necessary to introduce two parametrized sequence of functions $x_m(z,\eta ,\lambda )$, $y_m(z,\eta ,\lambda )$ in different ways, and to prove their uniform convergence. Theorem 3 proves that our method determines all possible approximate solutions in the given domain. Theorem 4 gives a new constructive answer for the existence of an exact solution based on a certain approximation. In the example, we determine two distinct solutions. The dimension of the determining algebraic system of equations is $p+2q$, where p is the number of periodic and q is the number of non-periodic components.

The theoretical basis for robustness, as stated in Remark 1, is that, in our approach, an infinite-dimensional original boundary value problem (1)–(3) is reduced to a finite dimensional system of $p+2q$ algebraic or transcendental equations. The method thus consists of two parts, namely, the analytic part, when the integral Equation (33) are dealt with by using the method of successive approximations (27), (28) and the numerical one, which consists in finding values of the $p+2q$ unknown parameters from Equations (52)–(54) (in practice, from systems (58)–(60)).

To solve nonlinear systems of Equations (58)–(60), efficient methods available in symbolic computation packages can be used. We have used Maple 14. The reliability of our approach is also facilitated by its constructiveness, because all the theoretical conditions in the theorems can be verified in practice. In the example, we have carried out this check in detail.

Our parameterization technique can be used with conditions of a general form, for example with integral restrictions. Method can be easily applied also to examine the solutions of differential equations with argument deviations. The determination of successive approximations can be complicated by integration. To eliminate this, the polynomial approximation proposed in our paper [24] can be used baseed on parameterized Lagrangian polynomials. We note that, in the example, we have already applied this.

6. Example

Let us apply the approach desribed above to the system of differential equations

$$\begin{array}{cc}\hfill {\displaystyle \frac{dx\left(t\right)}{dt}}& =f_1(t,x,y)=x^2-y^2+{\displaystyle \frac{1}{36}}{sin}^2\left(2\pi t\right)+{\displaystyle \frac{t^4}{4}}-{\displaystyle \frac{1}{36}}-{\displaystyle \frac{\pi }{3}}sin\left(2\pi t\right),t\in \left[0,1\right],\hfill \end{array}$$

(70)

$$\begin{array}{cc}\hfill {\displaystyle \frac{dy\left(t\right)}{dt}}& =f_2(t,x,y)=x^{2}y+t-{\displaystyle \frac{t^2}{72}}{cos}^2\left(2\pi t\right),\hfill \end{array}$$

(71)

considered under periodic and two-point non-linear boundary conditions

$$\begin{array}{c}x\left(a\right)=x\left(b\right),\\ y^2\left(a\right)+y^2\left(b\right)={\displaystyle \frac{1}{4}}.\end{array}$$

(72)

Following (23), (24), introduce the parameters $z,\gamma ,\lambda .$

Let us consider the following choice of subsets, where one looks for the values $x\left(a\right)=x\left(b\right)=z$ and $y\left(a\right)=\gamma ,y\left(b\right)=\lambda :$ $D_a^x=D_b^x\subset {\mathbb{R}}^p$ and $D_a^y\subset {\mathbb{R}}^q$, $D_b^y\subset {\mathbb{R}}^q$

$$\begin{array}{c}{D}_a^x=D_b^x=\{x:-0.3\le x\le 0.2\},\\ D_a^y=D_b^y=\{y:-0.6\le y\le 0.7\}.\end{array}$$

(73)

This choice of these sets is motivated by the fact that the zeroth approximate determining system (i.e., (58)–(60) with $m=0$) has roots lying in these sets (73), see the second row in Table 1. Recall that, in order to obtain it, only functions (29) and (30) are used, and no iteration is yet carried out. We see that this piecewise linear function provides quite reasonable approximate values of the parameters. In this case, according to (17), we have

$$\begin{array}{cccc}\hfill D_{a,b}^x& =D_a^x=D_b^x,\hfill & \hfill D_{a,b}^y& =D_a^y=D_b^y.\hfill \end{array}$$

(74)

For ${\rho }_x$ and ${\rho }_y$ involved in (20) and (22), we choose the vectors

$$\begin{array}{cccc}\hfill {\rho }_x& =0.3,\hfill & \hfill {\rho }_y& =0.2.\hfill \end{array}$$

(75)

Then, in view of (73)–(75), the sets (19), (21) take the form

$$\begin{array}{cccc}\hfill D_x& =\left\{\begin{array}{c}x:-0.6\le x\le 0.5\end{array}\right\},\hfill & \hfill D_y& =\left\{\begin{array}{c}y:-0.8\le y\le 0.9\end{array}\right\}.\hfill \end{array}$$

(76)

We can compute the Lipschitz constants in (4)–(6) for the domains (76)

$$\begin{array}{cccccccccccc}\hfill K_1& =1.2,\hfill & \hfill K_2& =1.8,\hfill & \hfill K_3& =1.1,\hfill & \hfill K_4& =0.36,\hfill & \hfill K_5& =1.4,\hfill & K_6& =1.4.\end{array}$$

(77)

Therefore direct computations give

$$\begin{array}{c}K=\left[\begin{array}{cc}1.2& 1.8\\ 1.1& 0.36\end{array}\right],Q={\displaystyle \frac{3(b-a)}{10}}\left[\begin{array}{cc}1.2& 1.8\\ 1.1& 0.36\end{array}\right]=\left[\begin{array}{cc}0.36& 0.54\\ 0.33& 0.108\end{array}\right],r\left(Q\right)=0.6745,\\ \begin{array}{cccc}\hfill {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_1\right)& =0.2925,\hfill & \hfill {\displaystyle \frac{b-a}{2}}{\delta }_{D_x\times D_y}\left(f_2\right)& =0.153,\hfill \end{array}\end{array}$$

and hence inequalities (20) and (22) hold.

Table 1. Values of parameters for approximations of the exact solution.

m	N	z	$\mathit{\gamma }$	$\mathit{\lambda }$
Exact		${\displaystyle \frac{1}{6}}=0.16666667$	0	0.5
0	N = 10	-	-	-
0	N = 6	0.2140434389	$-0.8919493467\times {10}^{-2}$	0.4999204363
1	N = 10	0.1837692491	$-0.1143143303\times {10}^{-3}$	0.4999999869
1	N = 6	0.1839377292	$-0.1197725596\times {10}^{-3}$	0.4999999857
4	N = 10	0.1623073768	$0.3114629697\times {10}^{-4}$	0.499999999
4	N = 6	0.1676901732	$-0.9951170742\times {10}^{-5}$	0.4999999999
6	N = 10	0.1620684595	$0.33438782\times {10}^{-4}$	0.4999999989
6	N = 6	0.1644399950	$0.1713976081\times {10}^{-4}$	0.4999999997
8	N = 10	0.1619499438	$0.3412551874\times {10}^{-4}$	0.4999999988
8	N = 6	0.1621419152	$0.3262488797\times {10}^{-4}$	0.4999999989

We thus see that all the conditions of Theorem 1 are fulfilled, and the sequences of functions (27) and (28) for this example are uniformly convergent.

In the case of the given non-linear boundary value problems it is more appropriate to use a scheme with polynomial interpolation [24], when instead of (27), (28) we use the sequence $\{x_{m+1}^{N+1}(t,z,\gamma ,\lambda ):m=0,1,2,\dots \}$ of vector polynomials of degree ($N+1$) and the sequence $\left\{y_{m+1}^{N+1}(t,z,\gamma ,\lambda ):m=0,1,2,\dots \right\}$ of vector polynomials of degree ($N+1$) on $\left[a,b\right]$

$$\begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{x}_{m+1}^{N+1}(t,z,\gamma ,\lambda ):=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=a_{m+1,0}(z,\gamma ,\lambda )+a_{m+1,1}(z,\gamma ,\lambda )t+a_{m+1,2}(z,\gamma ,\lambda )t^2+\cdots +a_{m+1,N+1}(z,\gamma ,\lambda )t^{N+1}=\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=z+{\int }_a^t\left[A_{m,0}(z,\gamma ,\lambda )+A_{m,1}(z,\gamma ,\lambda )t+A_{m,2}(z,\gamma ,\lambda )t^2+\cdots +A_{m,N}(z,\gamma ,\lambda )t^N\right]dt-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{t-a}{b-a}}{\int }_a^b\left[A_{m,0}(z,\gamma ,\lambda )+A_{m,1}(z,\gamma ,\lambda )t+A_{m,2}(z,\gamma ,\lambda )t^2+\cdots +A_{m,N}(z,\gamma ,\lambda )t^N\right]dt,\end{array}$$

(78)

where

$$A_{m,0}(z,\gamma ,\lambda )+A_{m,1}(z,\gamma ,\lambda )t+A_{m,2}(z,\gamma ,\lambda )t^2+\cdots +A_{m,N}(z,\gamma ,\lambda )t^N$$

is the Lagrange interpolation polynomial of degree N which corresponds to the term $f_1\left(t,x_m^{N+1}(t,z,\gamma ,\lambda ),y_m^{N+1}(t,z,\gamma ,\lambda )\right)$ in (70) over the Chebyshev nodes translated from $\left(-1,1\right)$ to the interval $\left(a,b\right)$. Similarly,

$$\begin{array}{c}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{y}_{m+1}^{N+1}(t,z,\gamma ,\lambda ):=\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=b_{m+1,0}(z,\gamma ,\lambda )+b_{m+1,1}(z,\gamma ,\lambda )t+b_{m+1,2}(z,\gamma ,\lambda )t^2+\cdots +b_{m+1,N+1}(z,\gamma ,\lambda )t^{N+1}=\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=z+{\int }_a^t\left[B_{m,0}(z,\gamma ,\lambda )+B_{m,1}(z,\gamma ,\lambda )t+B_{m,2}(z,\gamma ,\lambda )t^2+\cdots +B_{m,N}(z,\gamma ,\lambda )t^N\right]dt-\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\displaystyle \frac{t-a}{b-a}}\left[B_{m,0}(z,\gamma ,\lambda )+B{A}_{m,1}(z,\gamma ,\lambda )t+B_{m,2}(z,\gamma ,\lambda )t^2+\cdots +B_{m,N}(z,\gamma ,\lambda )t^N\right]dt+\\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{t-a}{b-a}}\left[\lambda -\gamma \right],t\in \left[a,b\right],m=0,1,2,\dots ,\end{array}$$

(79)

where

$$B_{m,0}(z,\gamma ,\lambda )+B_{m,1}(z,\gamma ,\lambda )t+B_{m,2}(z,\gamma ,\lambda )t^2+\cdots +B_{m,N}(z,\gamma ,\lambda )t^N$$

is the Lagrange interpolation Chebyshev polynomials of degree N on the Chebyshev nodes translated from $\left(-1,1\right)$ to the interval $\left(a,b\right)$, corresponding to the Nemytskii operator defined by the term $f_2\left(t,x_m^{N+1}(t,z,\gamma ,\lambda ),y_m^{N+1}(t,z,\gamma ,\lambda )\right)$ in (71). Note that the coefficients of the interpolation polynomials depend on the parameters z, $\gamma$, $\lambda .$

The approximate determining system (58)–(60) takes the following form

$$\begin{array}{cc}\hfill {\Delta }_{m,x}(z,\gamma ,\lambda )& ={\int }_a^b[A_{m,0}(z,\gamma ,\lambda )+A_{m,1}(z,\gamma ,\lambda )t+A_{m,2}(z,\gamma ,\lambda )t^2+\dots \hfill \\ & +A_{m,N}(z,\gamma ,\lambda )t^N]dt=0,\hfill \\ \hfill {\Delta }_{m,y}(z,\gamma ,\lambda )& =\lambda -\gamma -{\int }_a^b[B_{m,0}(z,\gamma ,\lambda )+B_{m,1}(z,\gamma ,\lambda )t+B_{m,2}(z,\gamma ,\lambda )t^2+\dots \hfill \\ & +B_{m,N}(z,\gamma ,\lambda )t^N]dt=0,\hfill \\ \hfill {\Lambda }_m(z,\gamma ,\lambda )& =B\left(y_{m+1}^{N+1}(a,z,\gamma ,\lambda ),y_{m+1}^{N+1}(b,z,\gamma ,\lambda )\right)-d=0.\hfill \end{array}$$

(80)

The justification of this polynomial approach can be found in [24].

6.1. Approximations for the Exact Solution

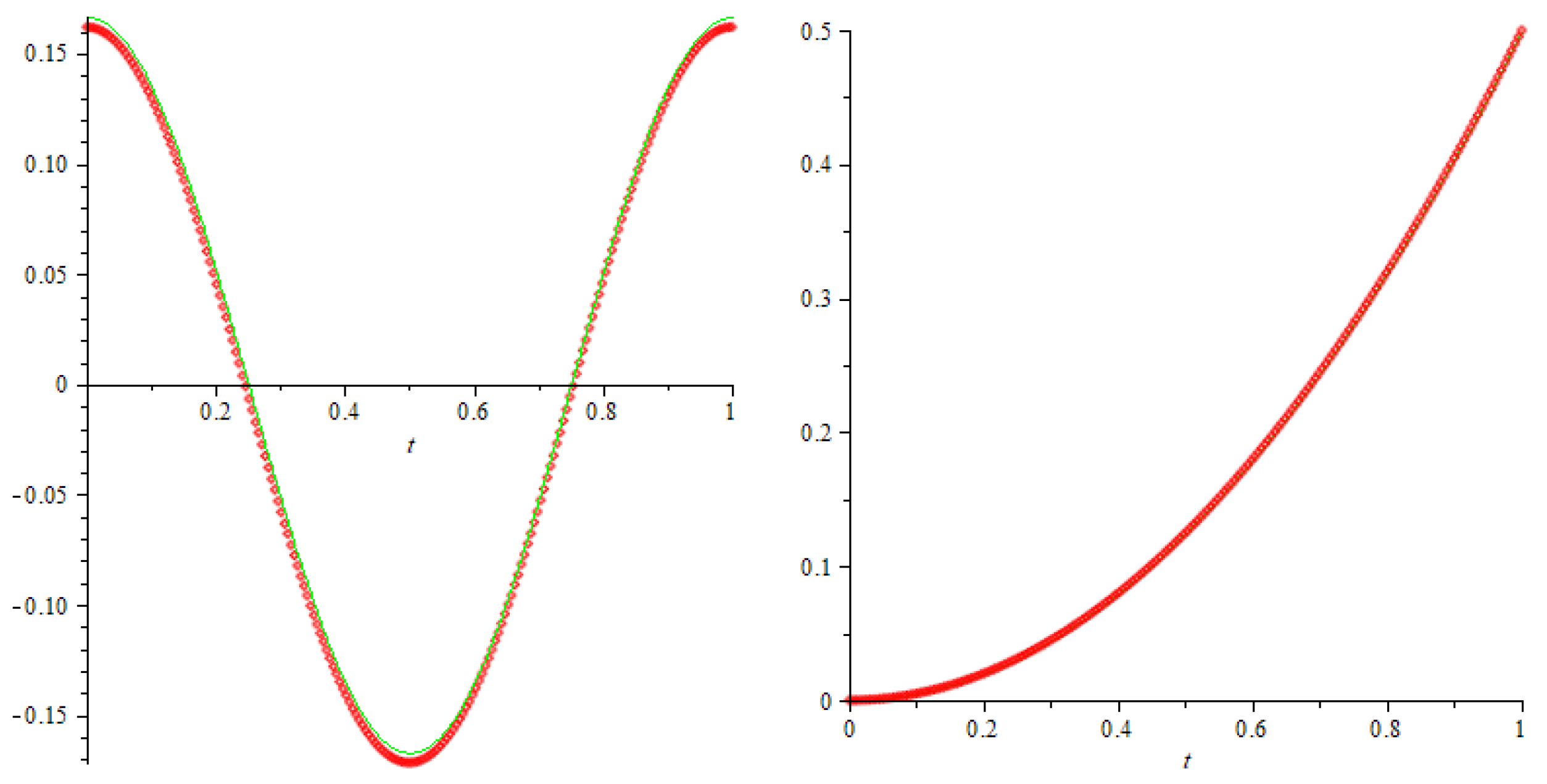
One can check that the pair of functions $x^{*}\left(t\right)={\displaystyle \frac{1}{6}}cos\left(2\pi t\right)$, $y^{*}\left(t\right)={\displaystyle \frac{t^2}{2}}$ is one of the solutions of the given boundary value problem. Using (78), (79) and applying Maple 14 for different values of m to implement the approximations $x_m(t,z,\gamma ,\lambda )$, $y_m(t,z,\gamma ,\lambda )$ and solving the approximate determining system (80), we find the values of introduced parameters with the degree of the approximating polynomials $N=10$ and $N=6.$ These values are presented in Table 1 for different m. The graphs of approximations and residuals are shown on Figure 1 and Figure 2.

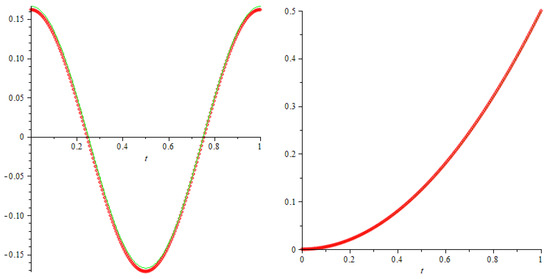
Figure 1. The graphs of the exact (solid line) and approximate solution (points) for $m=8,N=10$ for the x and y components.

Figure 2. The residual obtained as a result of substitution of the eighth approximation to exact solution for $N=10$ into the given differential Equations (70) and (71) for the x and y components.

6.2. Approximations for the Second Solution

Carrying out computations, we see that the approximate determining system (80) along with the solution given in Table 1, has another solution in set (73), which is presented in Table 2.

Table 2. Values of parameters for approximations of the exact solution.

m	N	z	$\mathit{\gamma }$	$\mathit{\lambda }$
0	N = 10	−0.2229737488	−0.4997757169	$-0.1497440580\times {10}^{-1}$
0	N = 6	−0.2231588675	−0.4997749377	$-0.1500038685\times {10}^{-1}$
1	N = 10	0.5140575206	−0.4984984084	$-0.3872127112\times {10}^{-1}$
1	N = 6	0.5140119167	−0.4984956534	$-0.3875672301\times {10}^{-1}$
3	N = 10	−0.1050783717	−0.4980623923	$-0.4397559982\times {10}^{-1}$
3	N = 6	−0.1052137197	−0.4980572003	$-0.4403436377\times {10}^{-1}$
5	N = 10	$-0.9303128843\times {10}^{-1}$	−0.4982341635	$-0.4198473952\times {10}^{-1}$
5	N = 6	$-0.9312630660\times {10}^{-1}$	−0.4982301679	$-0.4203212809\times {10}^{-1}$
7	N = 10	$-0.9261523108\times {10}^{-1}$	−0.4982446868	$-0.4185967128\times {10}^{-1}$
7	N = 6	$-0.9271142850\times {10}^{-1}$	−0.4982406880	$-0.4190724080\times {10}^{-1}$

With the help of the Maple program package, the second solution is obtained at the 9th iteration in the form of the 11th degree polynomials below

$$\begin{array}{cc}\hfill x_9\left(t\right)& =1.148257431t^{11}-5.316404582t^{10}+10.31079622t^9-17.33315601t^8\hfill \\ \hfill & +31.52751918t^7-31.14971134t^6+3.061277190t^5+10.47074659t^4\hfill \\ \hfill & +0.8178200919t^3-3.269716833t^2-0.2674279358t-0.09261226771,\hfill \\ \hfill y_9\left(t\right)& =7.680451214t^{11}-42.18446611t^{10}+94.98737130t^9-111.8199171t^8\hfill \\ \hfill & +73.13069674t^7-27.16587171t^6+6.726379104t^5-1.362951853t^4\hfill \\ \hfill & -0.01490299810t^3+0.4838387702t^2-0.004241974928t-0.4982447170.\hfill \end{array}$$

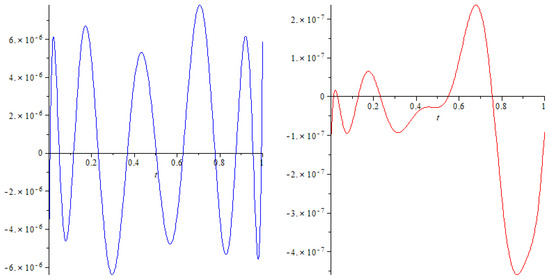
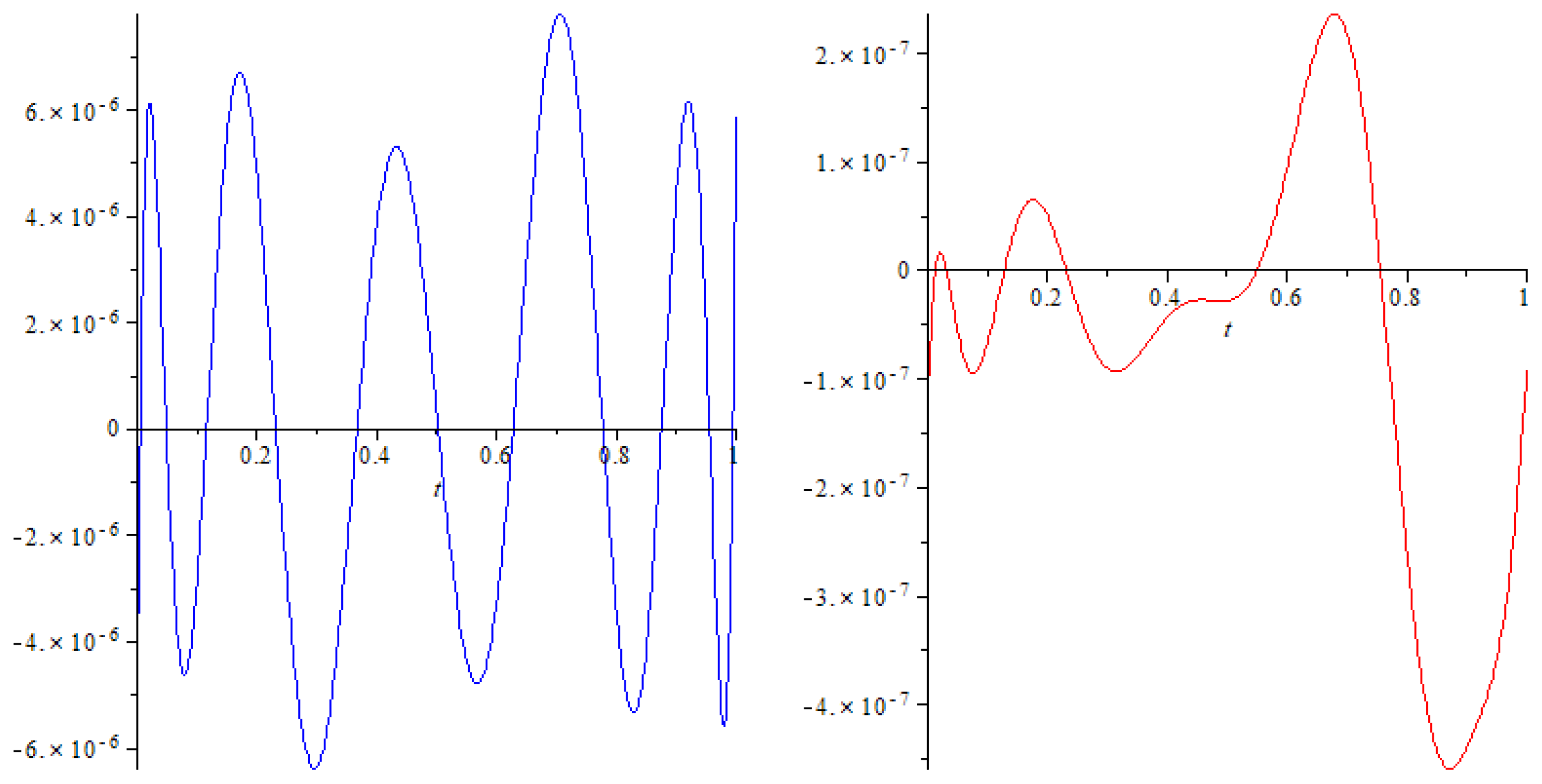
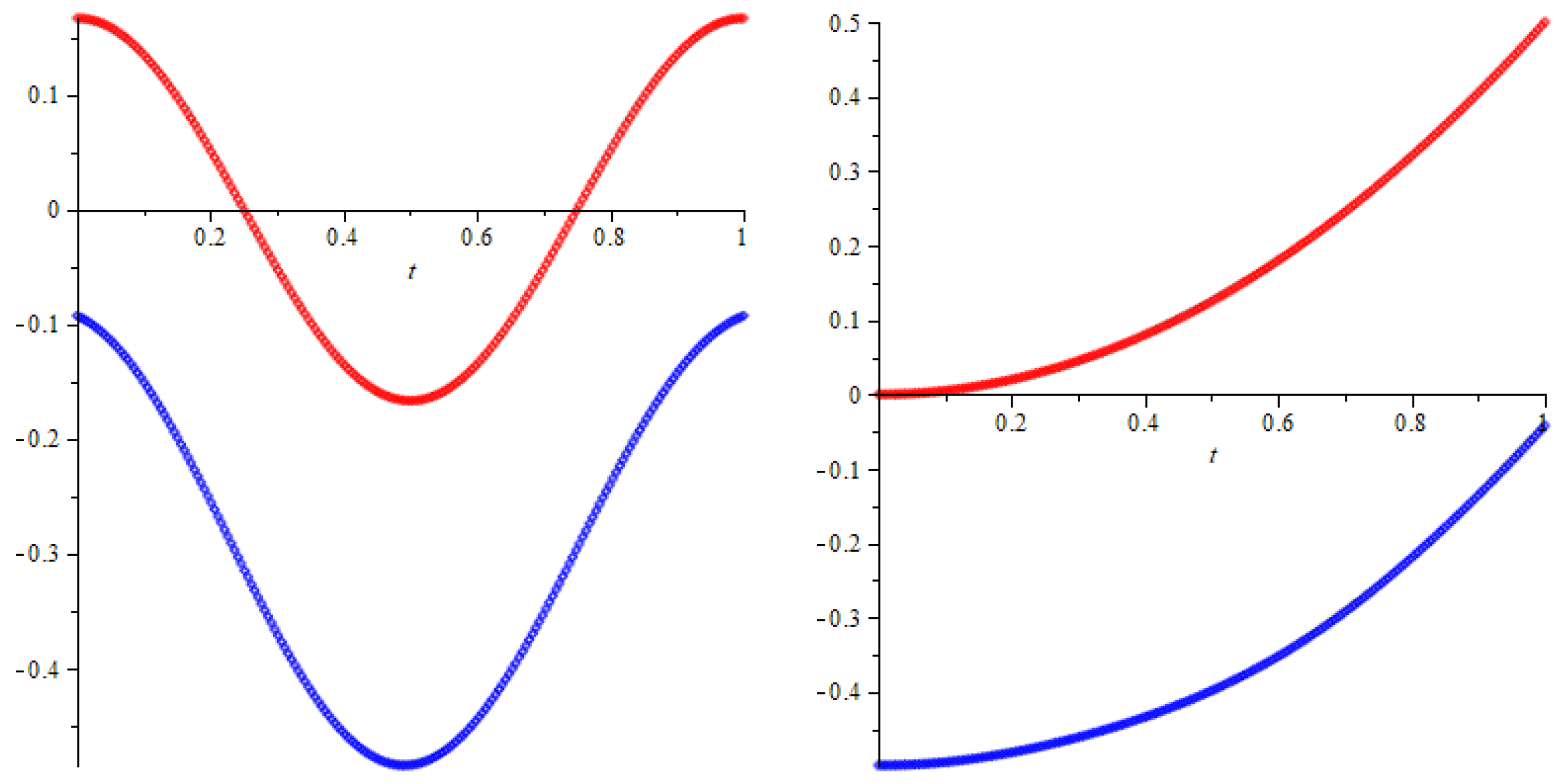
Figure 3 shows that the two solutions found look identical in appearance along the x and y coordinates, but they are shifted vertically. Figure 4 shows the residual.

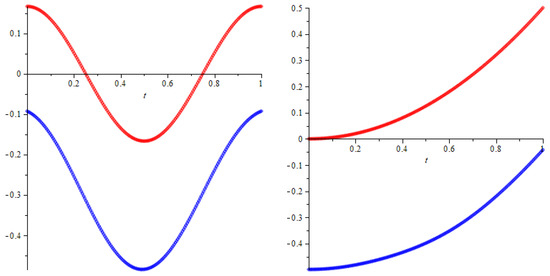
Figure 3. The graphs of the exact (red) and approximate second solutions (blue) for $m=9$, $N=10$ for the x and y components.

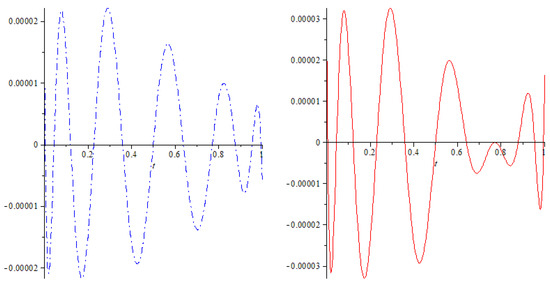
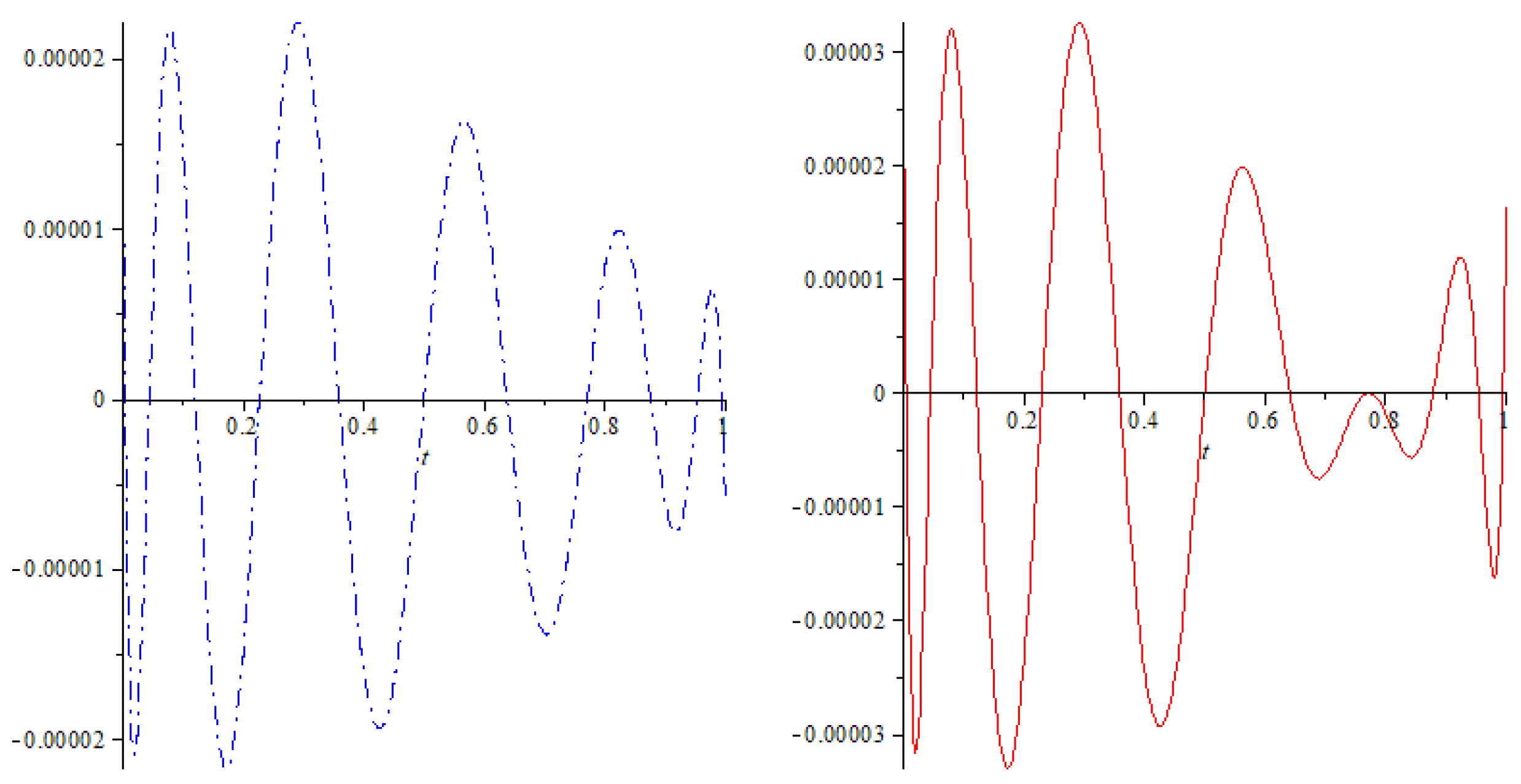
Figure 4. The residual of the ninth approximation for the second solution for $N=10$ for the x and y components.