Random Traveling Wave Equations for the Heisenberg Ferromagnetic Spin Chain Model and Their Optical Stochastic Solutions in a Ferromagnetic Materials

Abstract

In this paper, we investigate the stochastic Heisenberg ferromagnetic equation (SHFE) derived by a multiplicative Wiener process. We use a suitable transformation to change the SHF equation into another Heisenberg ferromagnetic equation with random variable coefficients (HFE-RVCs). We employ the mapping approach to obtain novel rational, trigonometric, elliptic and hyperbolic function solutions for HFE-RVCs. Following that, we can attain the solutions of the SHFE. For the first time in the Heisenberg ferromagnetic equation, we postulate that the solution to the wave equation is stochastic, whereas all previous investigations supposed that it was deterministic. Moreover, we give various visual representations to demonstrate the impact of the multiplicative Wiener process on the exact solutions to the stochastic Heisenberg ferromagnetic equation.

1. Introduction

The Heisenberg ferromagnetic equation, also known as the Heisenberg Hamiltonian, is a mathematical formulation that describes the dynamics of a ferromagnetic system. This equation was developed by the German physicist Werner Heisenberg in the 1920s and is a cornerstone of modern condensed matter physics. It is derived from the principles of quantum mechanics and provides a fundamental understanding of how the magnetic moments of atoms interact in a ferromagnet.

Moreover, the Heisenberg ferromagnetic equation describes the exchange interaction between neighboring magnetic moments in a material. The exchange interaction is a quantum mechanical phenomenon that arises due to the quantum mechanical nature of electrons. In a ferromagnetic material, neighboring atoms have aligned magnetic moments, and the Heisenberg equation describes how these moments influence each other. The equation involves the exchange integral, which quantifies the strength of the interaction, and the spin operators, which describe the orientation of the magnetic moments [1,2].

On the other hand, the effects of random fluctuations can be seen in the behavior of ferromagnetic materials at distinct temperatures. At low temperatures, the fluctuations are minimal, and the material tends to exhibit a strong magnetic response. As the temperature increases, however, the fluctuations become more pronounced, and the material’s magnetization may decrease due to the disruption caused by random changes in magnetic moment orientations. This is known as the Curie temperature, and above this point, the material transitions from a ferromagnetic to a paramagnetic state.

The stochastic Heisenberg ferromagnetic equation (SHFE) is taken into consideration as follows:

$$id\mathcal{G}+[{\gamma }_1{\mathcal{G}}_{x_1{x}_1}+{\gamma }_2{\mathcal{G}}_{x_2{x}_2}+{\gamma }_3{\mathcal{G}}_{x_1{x}_2}-{\gamma }_4{\left|\mathcal{G}\right|}^2\mathcal{G}]dt=i\sigma \mathcal{G}dW,$$

(1)

where $\mathcal{G}$ is a complex stochastic function of the variables $t$, $x_1$ and $x_2$; ${\gamma }_2$, ${\gamma }_2, {\gamma }_3$ and ${\gamma }_4$ are constants; $\sigma$ is the intensity of noise; and W is the standard Wiener process in one variable t.

Because of the relevance of the Heisenberg ferromagnetic equation (HFE) in the behavior of ferromagnetic materials, numerous researchers have acquired the exact solutions for this equation without stochastic terms by employing a variety of methods, for instance generalized Riccati mapping [3], Jacobi elliptic functions [4], the F-expansion method [5], modified exp-function expansion [6], auxiliary ordinary differential equation [7], sub-ODE [8] and Hirota bilinear equations [9,10]. The different solutions of the SHFE have been obtained by utilizing the mapping method, the $(G^{\prime }/G)$-expansion method, [11] and the Jacobi elliptic function method [12].

The objective of this study is to obtain exact solutions to the stochastic Heisenberg ferromagnetic equation (SHFE) (1). To obtain this, we use appropriate transformations to convert the SHFE to another HFE-RVC. After that, we use the mapping approach to obtain accurate answers for HFE-RVCs. Finally, we may obtain the stochastic solutions to the SHFE using the transformation applied. These obtained solutions are critical in understanding various difficult physical processes due to the significance of the Heisenberg ferromagnetic Equation (1) in the behavior of ferromagnetic materials. Ferromagnetic materials are commonly used in hard disk drives and magnetic tapes, where data are stored in the form of magnetic domains. Furthermore, we generated several earlier solutions, such as those given in [4]. In order to see the influence of stochastic terms, we introduce some figures by using MATLAB R2022b tools.

The remaining sections of this article are arranged as follows: In Section 2, we deduce the HFE-RVCs from the SHFE (1) and we find the exact solutions of HFE-RVCs by utilizing the mapping method. The solutions of the SHFE (1) are obtained in Section 3. In Section 4, we explain the results that we achieved. Finally, we introduce the article’s conclusion.

2. HFE-RVCs and Their Solutions

In this section, we derive the HFE-RVCs. By applying the transformation

$$\mathcal{G}(t,x_1,x_2)=\mathcal{Y}(t,x_1,x_2)exp[i\Theta (t,x_1,x_2)+\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t],$$

(2)

and the Itô derivatives, we obtain HFE-RVCs as follows

$$\begin{array}{c}i{\mathcal{Y}}_t-\mathcal{Y}{\Theta }_t+{\gamma }_1[{\mathcal{Y}}_{x_1{x}_1}+2i{\Theta }_{x_1}{\mathcal{Y}}_{x_1}+i{\Theta }_{x_1{x}_1}\mathcal{Y}-{\Theta }_{x_1}^2\mathcal{Y}]\hfill \\ +{\gamma }_2[{\mathcal{Y}}_{x_2{x}_2}+2i{\Theta }_{x_2}{\mathcal{Y}}_{x_2}+i{\Theta }_{x_2{x}_2}\mathcal{Y}-{\Theta }_{x_2}^2\mathcal{Y}]+{\gamma }_3[{\mathcal{Y}}_{x_1{x}_2}+i{\Theta }_{x_1{x}_2}\mathcal{Y}\hfill \\ +i{\Theta }_{x_1}{\mathcal{Y}}_{x_2}+i{\Theta }_{x_2}{\mathcal{Y}}_{x_1}-{\Theta }_{x_1}{\Theta }_{x_2}\mathcal{Y}]-f\left(t\right){\mathcal{Y}}^3=0,\hfill \end{array}$$

(3)

where $\mathcal{Y}$ is a stochastic real function and $f\left(t\right)={\gamma }_4{e}^{2\sigma W\left(t\right)-{\sigma }^{2}t}$.

Mapping Method

The mapping method reported in [13,14] is utilized here. To establish the solutions of the HFE-RVCs (3), we consider the solutions in specific forms:

$$\mathcal{Y}(t,x_1,x_2)=\sum _{k=0}^m{\theta }_k\left(t\right){\Omega }^k\left(\zeta \right),\zeta =k_1{x}_1+k_2{x}_2+{\int }_0^t\lambda \left(\tau \right)d\tau ,$$

(4)

and

$$\Theta (t,x_1,x_2)={\psi }_0\left(t\right)+x_1{\psi }_1\left(t\right)+x_2{\psi }_2\left(t\right).$$

(5)

where $\lambda , {\psi }_0, {\psi }_1$, ${\psi }_2, {\theta }_0$, ${\theta }_1$, ....., ${\theta }_{m-1}$ and ${\theta }_m\ne 0$ are functions of t and $\Omega$ achieves

$${\Omega }^{\prime }=\sqrt{{\alpha }_1{\Omega }^4+{\alpha }_2{\Omega }^2+{\alpha }_3},$$

(6)

with ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ being real constants. First, let us balance ${\mathcal{Y}}^{″}$ with ${\mathcal{Y}}^3$ in Equation (3) to obtain the value of m as

$$m+2=3m\Rightarrow m=1.$$

(7)

We rewrite Equation (4) as

$$\mathcal{Y}\left(\zeta \right)={\theta }_0+{\theta }_1\Omega \left(\zeta \right).$$

(8)

Using (6), we obtain

$${\Omega }^{″}={\alpha }_2\Omega +2{\alpha }_1{\Omega }^3.$$

(9)

Differentiating Equation (8) with regard to $t,x_1$ and $x_2$, we have

$$\begin{array}{ccc}\hfill {\mathcal{Y}}_t& =& {\stackrel{·}{\theta }}_0+{\stackrel{·}{\theta }}_1\Omega +{\theta }_1\lambda {\Omega }^{\prime },{\mathcal{Y}}_{x_1}=k_1{\theta }_1{\Omega }^{\prime },\hfill \\ \hfill {\mathcal{Y}}_{x_1{x}_1}& =& k_1^2{\theta }_1[{\alpha }_2\Omega +2{\alpha }_1{\Omega }^3],{\mathcal{Y}}_{x_2{x}_2}=k_2^2{\theta }_1[{\alpha }_2\Omega +2{\alpha }_1{\Omega }^3],\hfill \\ \hfill {\mathcal{Y}}_{x_1{x}_2}& =& k_1{k}_2{\theta }_1[{\alpha }_2\Omega +2{\alpha }_1{\Omega }^3],\hfill \\ \hfill {\mathcal{Y}}^3& =& {\theta }_1^3{\Omega }^3+3{\theta }_0{\theta }_1^2{\Omega }^2+3{\theta }_0^2{\theta }_1\Omega +{\theta }_0^3,\hfill \end{array}$$

(10)

and

$${\Theta }_t={\stackrel{·}{\psi }}_0+x_1{\stackrel{·}{\psi }}_1+x_2{\stackrel{·}{\psi }}_2,{\Theta }_{x_1}={\psi }_1,{\Theta }_{x_2}={\psi }_2,{\Theta }_{x_1{x}_1}={\Theta }_{x_2{x}_2}=0.$$

(11)

We insert Equations (9)–(11) into Equation (3). Then, putting each coefficient of ${\Omega }^k$ to zero, we attain

$${\Omega }^0:{\stackrel{·}{\theta }}_0=0,$$

$${\Omega }^1:{\stackrel{·}{\theta }}_1=0,$$

$${\Omega }^{\prime }:\lambda {\theta }_1+2k_1{\gamma }_1{\psi }_1{\theta }_1+2k_2{\gamma }_2{\psi }_2{\theta }_1+{\gamma }_3{k}_1{\psi }_2{\theta }_1+{\gamma }_3{k}_2{\psi }_1{\theta }_1=0,$$

$$\begin{array}{ccc}\hfill x_1{\Omega }^0& :& {\theta }_0{\stackrel{·}{\psi }}_1=0,\hfill \\ \hfill x_2{\Omega }^0& :& {\theta }_0{\stackrel{·}{\psi }}_2=0,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill x_1{\Omega }^1& :& {\theta }_1{\stackrel{·}{\psi }}_1=0,\hfill \\ \hfill x_2{\Omega }^1& :& {\theta }_1{\stackrel{·}{\psi }}_2=0,\hfill \end{array}$$

$${\Omega }^0:{\theta }_0{\stackrel{·}{\psi }}_0+{\gamma }_1{\psi }_1^2{\theta }_0+{\gamma }_2{\psi }_2^2{\theta }_0+{\gamma }_3{\psi }_1{\psi }_2{\theta }_0+f{\theta }_0^3=0,$$

$$\begin{array}{cc}\hfill {\Omega }^1:& {\theta }_1{\dot{\psi }}_0-{\gamma }_1{k}_1^2{\alpha }_2{\theta }_1-{\gamma }_2{k}_2^2{\alpha }_2{\theta }_1-{\gamma }_3{k}_1{k}_2{\alpha }_2{\theta }_1\hfill \\ & +{\gamma }_1{\psi }_1^2{\theta }_1+{\gamma }_2{\psi }_2^2{\theta }_1+{\gamma }_3{\psi }_1{\psi }_2{\theta }_1+3f{\theta }_0^2{\theta }_1=0,\hfill \end{array}$$

$${\Omega }^2:3f{\theta }_0{\theta }_1^2=0,$$

and

$${\Omega }^3:2{\gamma }_1{k}_1^2{\alpha }_1{\theta }_1+2{\gamma }_2{k}_2^2{\alpha }_1{\theta }_1+2{\gamma }_3{k}_1{k}_2{\alpha }_1{\theta }_1-f{\theta }_1^3=0.$$

We solve the previous system to obtain

$${\theta }_0=0,{\theta }_1=a,{\psi }_1=b_1,{\psi }_2=b_2,{\gamma }_1{k}_1^2+{\gamma }_2{k}_2^2+{\gamma }_3{k}_1{k}_2={\displaystyle \frac{a^2}{2{\alpha }_1}}f,$$

and

$${\stackrel{·}{\psi }}_0={\displaystyle \frac{a^2{\alpha }_2}{2{\alpha }_1}}f-{\gamma }_1{b}_1^2-{\gamma }_2{b}_2^2-{\gamma }_3{b}_1{b}_2,\lambda =-2{\gamma }_1{k}_1{b}_1-2{\gamma }_2{k}_2{b}_2-{\gamma }_3{k}_1{b}_2-{\gamma }_3{k}_2{b}_1.$$

where $b_1,b_2$ and a are constants. If we choose $b_1=k_1$ and $b_2=k_2$, then we obtain

$${\theta }_0=0,{\theta }_1=a,{\psi }_1=k_1,{\psi }_2=k_2,{\gamma }_1{k}_1^2+{\gamma }_2{k}_2^2+{\gamma }_3{k}_1{k}_2={\displaystyle \frac{a^2}{2{\alpha }_1}}f,$$

(12)

and

$${\psi }_0={\displaystyle \frac{a^2({\alpha }_2-1)}{2{\alpha }_1}}{\int }_0^{t}f\left(\tau \right)d\tau ,\lambda \left(t\right)={\displaystyle \frac{-a^2}{{\alpha }_1}}f\left(t\right).$$

(13)

Hence, by using Equations (12) and (13), the solution of the HFE-RVCs (3) is

$$\mathcal{Y}(t,x_1,x_2)=a\Omega \left(\zeta \right),\zeta =k_1{x}_1+k_2{x}_2-{\displaystyle \frac{{\gamma }_4{a}^2}{{\alpha }_1}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau .$$

(14)

Many cases based on ${\alpha }_1,{\alpha }_2$ and ${\alpha }_3$ can be written as follows:

Case 1: If ${\alpha }_1={\acute{n}}^2,{\alpha }_2=-(1+{\acute{n}}^2)$ and ${\alpha }_3=1,$ then $\Omega \left(\zeta \right)=sn\left(\zeta \right).$ Consequently, the solution of the HFE-RVCs (1), using Equation (14), is

$$\mathcal{Y}(t,x_1,x_2)=a\left(sn(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{{\gamma }_4{a}^2}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(15)

When $\acute{n}\to 1,$ Equation (15) turns into

$$\mathcal{Y}(t,x_1,x_2)=a\left(tanh(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(16)

Case 2: If ${\alpha }_1=1,{\alpha }_2=2{\acute{n}}^2-1$ and ${\alpha }_3=-{\acute{n}}^2(1-{\acute{n}}^2),$ then $\Omega \left(\zeta \right)=ds\left(\zeta \right).$ Hence, the solution of the HFE-RVCs (1), using Equation (14), is

$$\mathcal{Y}(t,x_1,x_2)=a\left(ds(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(17)

If $\acute{n}\to 1,$ Equation (17) tends to

$$\mathcal{Y}(t,x_1,x_2)=a\left(\mathrm{csch}(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(18)

If $\acute{n}\to 0,$ Equation (17) turns into

$$\mathcal{Y}(t,x_1,x_2)=a\left(csc(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(19)

Case 3: When ${\alpha }_1=1,{\alpha }_2=2-{\acute{n}}^2$ and ${\alpha }_3=(1-{\acute{n}}^2),$ then $\Omega \left(\zeta \right)=cs\left(\zeta \right).$ Consequently, the solution of the HFE-RVCs (1) is

$$\mathcal{Y}(t,x_1,x_2)=a\left(cs(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(20)

If $\acute{n}\to 1,$ then Equation (20) tends to

$$\mathcal{Y}(t,x_1,x_2)=a\left(\mathrm{csch}(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(21)

When $\acute{n}\to 0,$ Equation (20) turns into

$$\mathcal{Y}(t,x_1,x_2)=a\left(cot(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(22)

Case 4: If ${\alpha }_1={\displaystyle \frac{{\acute{n}}^2}{4}},{\alpha }_2={\displaystyle \frac{({\acute{n}}^2-2)}{2}}$ and ${\alpha }_3={\displaystyle \frac{1}{4}},$ then $\Omega \left(\zeta \right)=nc\left(\zeta \right)+sc\left(\zeta \right).$ So, the HFE-RVCs (1) are

$$\begin{array}{ccc}\hfill \mathcal{Y}(t,x_1,x_2)& =& a\left(nc\right(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{4{\gamma }_4{a}^2}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +sc(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{4{\gamma }_4{a}^2}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )).\hfill \end{array}$$

(23)

If $\acute{n}\to 1,$ then Equation (23) becomes

$$\begin{array}{ccc}\hfill \mathcal{Y}(t,x_1,x_2)& =& a(cosh(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +sinh(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )).\hfill \end{array}$$

(24)

Case 5: If ${\alpha }_1=-{\acute{n}}^2,{\alpha }_2=2{\acute{n}}^2-1$ and ${\alpha }_3=1-{\acute{n}}^2,$ then $\Omega \left(\zeta \right)=cn\left(\zeta \right).$ Consequently, the solution of the HFE-RVCs (1) is

$$\mathcal{Y}(t,x_1,x_2)=a\left(cn(k_1{x}_1+k_2{x}_2+{\displaystyle \frac{a^2{\gamma }_4}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(25)

When $\acute{n}\to 1,$ Equation (25) changes to

$$\mathcal{Y}(t,x_1,x_2)=a\left(\mathrm{sech}(k_1{x}_1+k_2{x}_2+a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(26)

Case 6: If ${\alpha }_1=-1,{\alpha }_2=2-{\acute{n}}^2$ and ${\alpha }_3={\acute{n}}^2-1,$ then $\Omega \left(\zeta \right)=dn\left(\zeta \right).$ Therefore, the HFE-RVCs (1), utilizing Equation (14), have the solution

$$\mathcal{Y}(t,x_1,x_2)=a\left(dn(k_1{x}_1+k_2{x}_2+a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(27)

If $\acute{n}\to 1,$ then Equation (27) turns into Equation (26).

Case 7: If ${\alpha }_1=1,{\alpha }_2=-{\acute{n}}^2-1$ and ${\alpha }_3={\acute{n}}^2,$ then $\Omega \left(\zeta \right)=ns\left(\zeta \right)={\displaystyle \frac{1}{sn\left(\zeta \right)}}.$ Therefore, the solution of the HFE-RVCs (1) is

$$\mathcal{Y}(t,x_1,x_2)=a\left(ns(k_1{x}_1+k_2{x}_2-a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(28)

If $\acute{n}\to 1,$ then Equation (28) tends to

$$\mathcal{Y}(t,x_1,x_2)=a\left(coth(k_1{x}_1+k_2{x}_2-a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(29)

If $\acute{n}\to 0,$ then Equation (28) changes to

$$\mathcal{Y}(t,x_1,x_2)=a\left(csc(k_1{x}_1+k_2{x}_2-a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(30)

Case 8: If ${\alpha }_1=1-{\acute{n}}^2,{\alpha }_2=2{\acute{n}}^2-1$ and ${\alpha }_3=-{\acute{n}}^2,$ then $\Omega \left(\zeta \right)=nc\left(\zeta \right)={\displaystyle \frac{1}{cn\left(\zeta \right)}}.$ Hence, the solution of the HFE-RVCs (1) is

$$\mathcal{Y}(t,x_1,x_2)=a\left(nc(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{a^2{\gamma }_4}{1-{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(31)

When $\acute{n}\to 0,$ Equation (31) turns into

$$\mathcal{Y}(t,x_1,x_2)=a\left(sec(k_1{x}_1+k_2{x}_2-a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(32)

Case 9: If ${\alpha }_1=1-{\acute{n}}^2,{\alpha }_2=2-{\acute{n}}^2$ and ${\alpha }_3=1,$ then $\Omega \left(\zeta \right)=sc\left(\zeta \right)={\displaystyle \frac{sn\left(\zeta \right)}{cn\left(\zeta \right)}}.$ Consequently, the solution of the HFE-RVCs (1) is

$$\mathcal{Y}(t,x_1,x_2)=a\left(sc(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{a^2{\gamma }_4}{1-{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(33)

If $\acute{n}\to 0,$ Equation (28) tends to

$$\mathcal{Y}(t,x_1,x_2)=a\left(tan(k_1{x}_1+k_2{x}_2-a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right).$$

(34)

Case 10: If ${\alpha }_1={\displaystyle \frac{1}{4}},{\alpha }_2={\displaystyle \frac{1-2{\acute{n}}^2}{2}}$ and ${\alpha }_3={\displaystyle \frac{1}{4}},$ then $\Omega \left(\zeta \right)=ns\left(\zeta \right)+cs\left(\zeta \right).$ So, the solution of the HFE-RVCs (1) is

$$\begin{array}{ccc}\hfill \mathcal{Y}(t,x_1,x_2)& =& a\left(ns\right(k_1{x}_1+k_2{x}_2-4a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +cs(k_1{x}_1+k_2{x}_2-4a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )).\hfill \end{array}$$

(35)

With $\acute{n}\to 1,$ Equation (35) turns into

$$\begin{array}{ccc}\hfill \mathcal{Y}(t,x_1,x_2)& =& a\left(\mathrm{csch}\right(k_1{x}_1+k_2{x}_2-4a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +\coth (k_1{x}_1+k_2{x}_2-4a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )).\hfill \end{array}$$

(36)

With $\acute{n}\to 0,$ Equation (35) changes to

$$\begin{array}{ccc}\hfill \mathcal{Y}(t,x_1,x_2)& =& a(csc(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +cot(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )).\hfill \end{array}$$

(37)

Case 11: If ${\alpha }_1={\displaystyle \frac{1-{\acute{n}}^2}{4}},{\alpha }_2={\displaystyle \frac{(1-{\acute{\mathrm{n}}}^2)}{2}}$ and ${\alpha }_3={\displaystyle \frac{1-{\acute{\mathrm{n}}}^2}{4}},$ then $\Omega \left(\zeta \right)={\displaystyle \frac{cn\left(\zeta \right)}{1+sn\left(\zeta \right)}}.$ Thus, the solution of the HFE-RVCs (1), using Equation (14), is

$$\mathcal{Y}(t,x_1,x_2)=a\left({\displaystyle \frac{cn(k_1{x}_1+k_2{x}_2-\frac{4{\gamma }_4{a}^2}{1-{\acute{n}}^2}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )}{1+sn(k_1{x}_1+k_2{x}_2-\frac{4{\gamma }_4{a}^2}{1-{\acute{n}}^2}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )}}\right).$$

(38)

When $\acute{n}\to 0,$ Equation (38) turns into

$$\mathcal{Y}(t,x_1,x_2)=a\left({\displaystyle \frac{cos(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )}{1+sin(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )}}\right).$$

(39)

Case 12: When ${\alpha }_1=1,{\alpha }_2=0$ and ${\alpha }_3=0,$ $\Omega \left(\zeta \right)={\displaystyle \frac{c}{\zeta }}.$ Consequently, the solution of the HFE-RVCs (1), using Equation (14), is

$$\mathcal{Y}(t,x_1,x_2)=a\left({\displaystyle \frac{c}{k_1{x}_1+k_2{x}_2-a^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau }}\right).$$

(40)

3. Exact Solutions of Stochastic HFEs

Substituting Equations (15)–(40) into Equation (2), we have the solutions of the SHFE (1) as

$$\mathcal{G}(t,x_1,x_2)=\mathcal{Y}(t,x_1,x_2)exp[i\Theta (t,x_1,x_2)+\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t],$$

(41)

where

$$\Theta (t,x_1,x_2)=k_1{x}_1+k_2{x}_2+{\displaystyle \frac{a^2({\alpha }_2-1)}{2{\alpha }_1}}{\int }_0^{t}f\left(\tau \right)d\tau .$$

From the previous section, the SHFE (1) has the following families of solutions:

Family 1:

Optical elliptic solutions

$$\mathcal{G}(t,x_1,x_2)=a\left(sn(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{{\gamma }_4{a}^2}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(42)

$$\mathcal{G}(t,x_1,x_2)=a\left(ds(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(43)

$$\mathcal{G}(t,x_1,x_2)=a\left(cs(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(44)

$$\begin{array}{ccc}\hfill \mathcal{G}(t,x_1,x_2)& =& a\left(nc\right(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{4{\gamma }_4{a}^2}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +sc(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{4{\gamma }_4{a}^2}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau ))e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.\hfill \end{array}$$

(45)

$$\mathcal{G}(t,x_1,x_2)=a\left(cn(k_1{x}_1+k_2{x}_2+{\displaystyle \frac{a^2{\gamma }_4}{{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(46)

$$\mathcal{G}(t,x_1,x_2)=a\left(dn(k_1{x}_1+k_2{x}_2+a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(47)

$$\mathcal{G}(t,x_1,x_2)=a\left(ns(k_1{x}_1+k_2{x}_2-a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(48)

$$\mathcal{G}(t,x_1,x_2)=a\left(nc(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{a^2{\gamma }_4}{1-{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(49)

$$\mathcal{G}(t,x_1,x_2)=a\left(sc(k_1{x}_1+k_2{x}_2-{\displaystyle \frac{a^2{\gamma }_4}{1-{\acute{n}}^2}}{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(50)

$$\begin{array}{ccc}\hfill \mathcal{G}(t,x_1,x_2)& =& a\left(ns\right(k_1{x}_1+k_2{x}_2-4a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +cs(k_1{x}_1+k_2{x}_2-4a^2{\gamma }_4{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau ))e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.\hfill \end{array}$$

(51)

$$\mathcal{G}(t,x_1,x_2)=a\left({\displaystyle \frac{cn(k_1{x}_1+k_2{x}_2-\frac{4{\gamma }_4{a}^2}{1-{\acute{n}}^2}{\int }_0^t{e}^{\sigma W\left(\tau \right)-\frac{1}{2}{\sigma }^2\tau }d\tau )}{1+sn(k_1{x}_1+k_2{x}_2-\frac{4{\gamma }_4{a}^2}{1-{\acute{n}}^2}{\int }_0^t{e}^{\sigma W\left(\tau \right)-\frac{1}{2}{\sigma }^2\tau }d\tau )}}\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(52)

Family 2:

Optical hyperbolic solutions

$$\mathcal{G}(t,x_1,x_2)=a\left(tanh(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(53)

$$\mathcal{G}(t,x_1,x_2)=a\left(coth(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(54)

$$\mathcal{G}(t,x_1,x_2)=a\left(\mathrm{sech}(k_1{x}_1+k_2{x}_2+{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(55)

$$\mathcal{G}(t,x_1,x_2)=a\left(\mathrm{csch}(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(56)

$$\begin{array}{ccc}\hfill \mathcal{G}(t,x_1,x_2)& =& a(cosh(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +sinh(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau ))e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill \mathcal{G}(t,x_1,x_2)& =& a\left(\mathrm{csch}\right(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +\coth (k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau ))e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.\hfill \end{array}$$

(58)

Family 3:

Optical trigonometric solutions

$$\mathcal{G}(t,x_1,x_2)=a\left(csc(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(59)

$$\mathcal{G}(t,x_1,x_2)=a\left(cot(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(60)

$$\mathcal{G}(t,x_1,x_2)=a\left(tan(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(61)

$$\mathcal{G}(t,x_1,x_2)=a\left(csc(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(62)

$$\mathcal{G}(t,x_1,x_2)=a\left(sec(k_1{x}_1+k_2{x}_2-{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(63)

$$\begin{array}{ccc}\hfill \mathcal{G}(t,x_1,x_2)& =& a(csc(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau )\hfill \\ & & +cot(k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau ))e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.\hfill \end{array}$$

(64)

Family 4:

Optical rational solutions

$$\mathcal{G}(t,x_1,x_2)=a\left({\displaystyle \frac{c}{k_1{x}_1+k_2{x}_2-4{\gamma }_4{a}^2{\int }_0^t{e}^{2\sigma W\left(\tau \right)-{\sigma }^2\tau }d\tau }}\right)e^{[i\Theta +\sigma W\left(t\right)-{\displaystyle \frac{1}{2}}{\sigma }^{2}t]}.$$

(65)

Remark 1.

If we put $\sigma =0$ in Equations (42), (46), (47), (53) and (55), we have the same solutions as those stated in [4].

4. Discussion and Impact of Noise

4.1. Discussion

In this work, the exact solutions of the SHFE (1) were obtained. We employed mapping methods, which give many kinds of solutions including elliptic solutions (42)–(52), optical hyperbolic solutions (53)–(58), optical trigonometric solutions (59)–(64) and optical rational solutions (65). Optical solutions play a crucial role in different industries, including telecommunications, healthcare and entertainment. In the telecommunications industry, optical solutions are vital for transmitting data over long distances at high speeds. Fiber optic cables are used to transmit large amounts of information quickly and securely, making them crucial for maintaining smooth communication networks. With the increasing demand for faster internet speeds and greater bandwidth, optical solutions have become even more important to keep pace with the growing needs of consumers and businesses.

4.2. Impacts of the Wiener Process

We now look at the influence of the multiplicative Wiener process on the exact solutions of the SHFE (1). Several numerical simulations of different solutions with various amounts of noise are provided by using Matlab. Figure 1 and Figure 2 show the solutions $\mathcal{G}(t,x_{11},x_2)$ specified in Equations (42) and (55) for distinct values of $\sigma$ as follows:

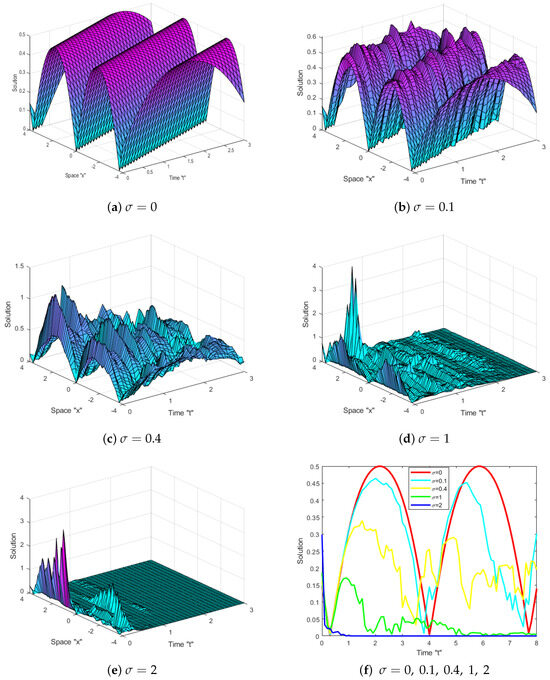
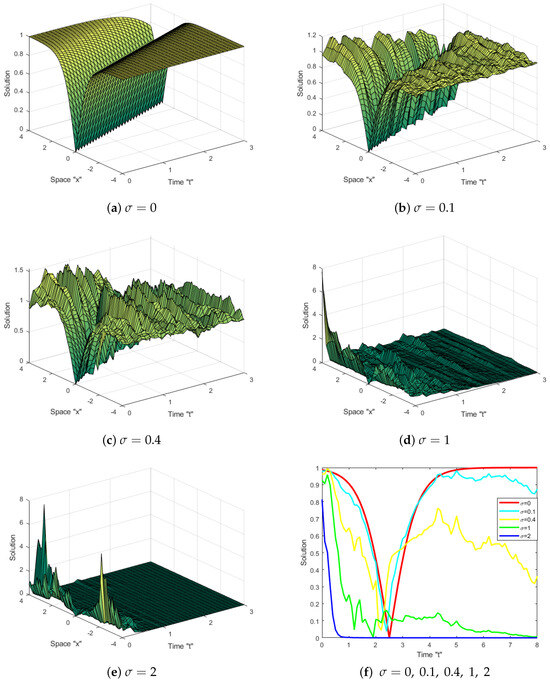
Figure 1 and Figure 2 display that when noise is disregarded (i.e., $\sigma =0$), a variety of solutions appear, such as optical periodic solutions, optical bright solutions, optical dark solutions and more. If the noise is injected at $\sigma =0.1,0.4,1$ and $2$, the surface flattens after some transit patterns. This result demonstrates how the multiplicative Wiener process impacts the solutions of the SHFE (1), stabilizing them at zero.

5. Conclusions

In this study, we looked at the stochastic Heisenberg ferromagnetic equation (SHFE) (1) perturbed by multiplicative noise in the Itô sense. We used suitable transformations to change the SHFE to another HFE-RVC (3). Using the mapping approach, we found novel stochastic exact solutions for HFE-RVCs in the type of elliptic, hyperbolic, trigonometric and rational functions. Following that, we obtained the solutions of the SHFE. Furthermore, we generated several earlier solutions, such as those given in [4]. Because of the significance of the Heisenberg ferromagnetic equation in the behavior of ferromagnetic materials, the obtained solutions are critical in comprehending various challenging physical processes. Finally, some visuals were given to explain how the stochastic Wiener process affects the stochastic precise solutions of the SHFE.