Abstract
The field of indices has been explored and advanced by various researchers for different purposes. One purpose is the optimization of indices in various problems. In this work, the general power-sum connectivity index is considered. The general power-sum connectivity index was investigated for k-generalized quasi-trees where optimal graphs were found. Further, in this work, we extend the idea of optimization to families of graphs, including uni-cyclic graphs, bi-cyclic graphs and trees. The optimization is carried out by means of operations named as Operation A, B, C and D. The first two operations increase the value of the general power-sum connectivity index, while the last two work opposite to Operations A and B. These operations are explained by means of diagrams, where one can easily obtain their working procedures.
Keywords:
general power-sum connectivity index; operations; optimization; uni-cyclic graphs; bi-cyclic graphs; trees MSC:
05XX; 05C05; 05C07; 05C09
1. Introduction
Many real-world problems can be neatly represented on a sheet of paper by means of structures consisting of sets of points (usually circles or dots) and the connection between these points can be represented using lines (or curves). The mathematical approach to structures having points and lines lead us to the concept of a graph. A graph G is a structure, containing vertices represented by the set , while the collection of edges called the edge set is represented by . Symbolically, a graph is represented by . The number of vertices and edges of G is the order and size, respectively. If represents the end vertices of edge e, then is an edge joining vertex q and vertex r, and e is incident to both q and r. Two or more edges are said to be parallel if these edges are between the same pair of vertices. An edge that emerges and enters the same vertex is called a loop. The degree of a vertex q in a graph G is the number of incident edges to q and is denoted by . Two vertices p and q in a graph G are said to be neighbors if these vertices are the end points of an edge. The set of all neighbors of vertex q in a graph G is called the neighborhood of q and is denoted by . If there is no confusion, the notation is use generally used, see [1]. A simple graph is a graph containing no loop or parallel edges, see [2]. In this work, the considered graphs are simple and finite, that is and are both finite.
A single numerical number that represents the structure of a chemical in graph-theoretical terms is known as a topological descriptor. Due to structure invariants, the topological index does not depend on graph labeling. If the topological descriptor correlates with a molecular property, then it is termed the topological index or molecular index, see [3]. In various cases, topological indices work in the measure of connection strength in chemical compounds. The first introduced topological index was the Wiener index, used for the investigation of the physico-chemical and thermodynamical properties of alkanes using molecular structures and shapes. This new approach and idea led the researchers to a new field, that is chemical graph theory in the field of theoretical chemistry, see [4]. Although topological indices are used in chemical graph theory, its applications are used in other fields also. In 1996, Mohar and Gutman initiated the use of indices to network the outside of chemical structures [5]. The role of indices for analyzing social networks was initiated by Rousseau and Otte [6]. In [7], the authors analyzed indices in an interconnection network.
The optimization of topological indices is a field of interest for researchers. Optimization is particularly related to the design of chemical compounds. Maranas and Raman developed a programming model for the optimization of combined topological indices that includes Randi’s, Wiener’s and Kier’s shape indices [8]. In [9], the authors optimized the molecular interconnectivity index for polymers. In [10], the author optimized topological indices for a problem related to chemical graph theory using a simplex algorithm. In [11], the authors optimized the Randi index and Wiener index for the maximum terrain problem. In [12], the authors provided upper and lower bounds for a forgotten topological index using graph size and irregularity. They categorized the graphs attaining new bounds of ; the new bounds are better than previously determined. In [13], the authors investigated sharp upper and lower bounds of the symmetric VDB topological index over . Applications to well-known topological indices were also determined. The authors also investigated extremal values of symmetric VDB indices. In [14], the authors gave upper and lower bounds for the class of topological indices in trees. The class contains the first variable Zagreb, Narumi–Katayama, modified Narumi–Katayama and Wiener indices. In [15], the authors obtained advanced inequalities for the family of topological indices restricted to uni-cyclic graphs and characterized the extremal uni-cyclic graphs. The considered family consisted of the first variable Zagreb, Narumi–Katayama and multiplicative second Zagreb indices. The authors investigated the upper and lower bounds for the stated indices. In [16], the authors considered the group of symmetries of regular polygons having a contribution in the theory of molecular vibrations. The authors considered the communication property of a dihedral group, associated with the group of symmetries, computed degree and distance-based topological properties of associated graphs using the computation of exact formulae for various indices given in [16]. In [17], the authors investigated a topology optimization scheme for designing waveguides with rotation and reflection symmetries. The authors constructed the scheme by developing a computational algorithm combining the Finite Element Method with group representation theory, see [18,19,20] and the references there in.
In this work, we optimized the general power-sum connectivity index for uni-cyclic graphs, bi-cyclic graphs and trees. We obtained optimal graphs in the the stated families of graphs. The general power-sum connectivity index for graph G is as follows:
2. Operations for Increasing General Power-Sum Connectivity Index
This section is devoted to the operations used for increasing the general power-sum connectivity index, as given in the following:
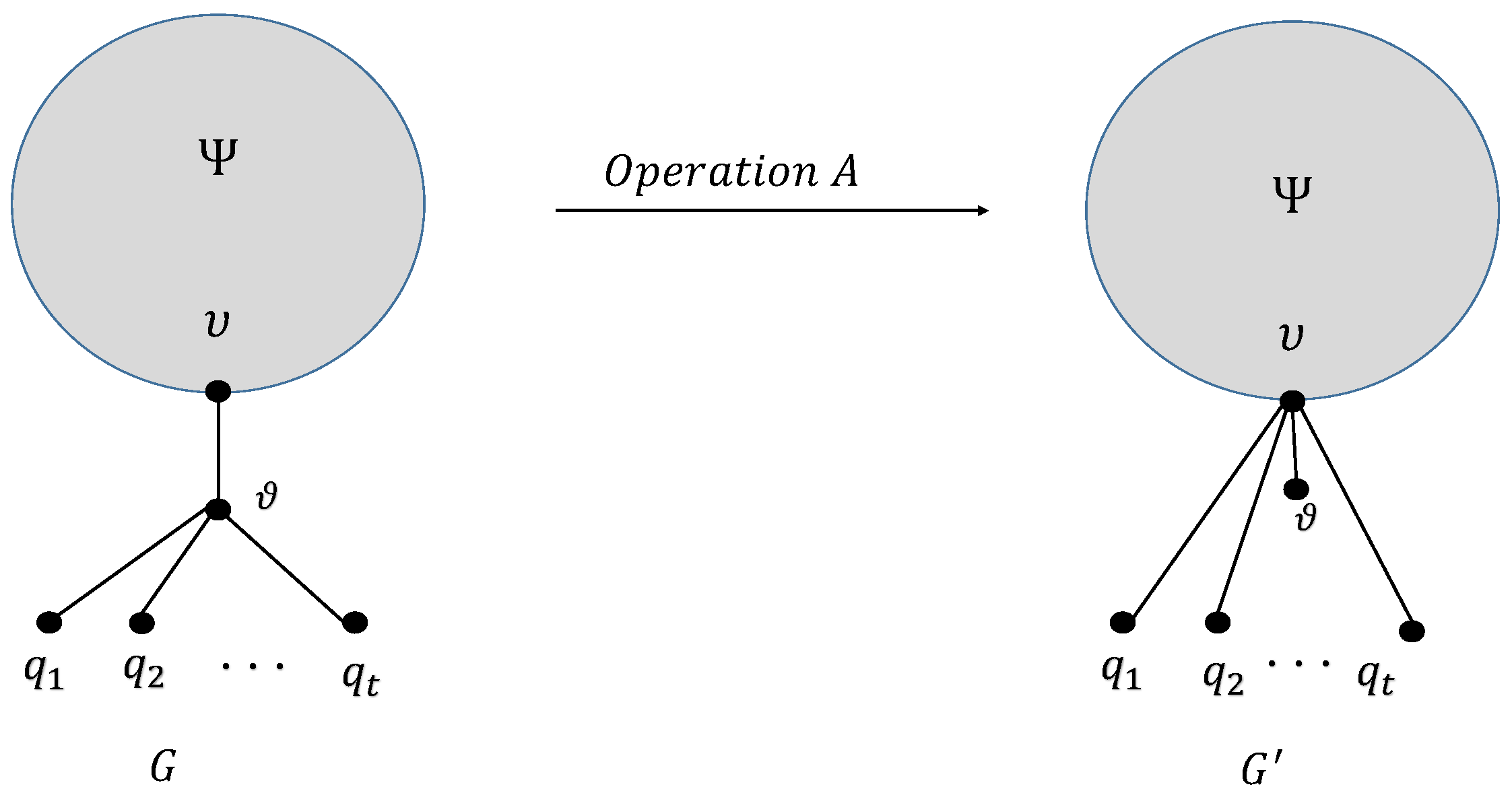
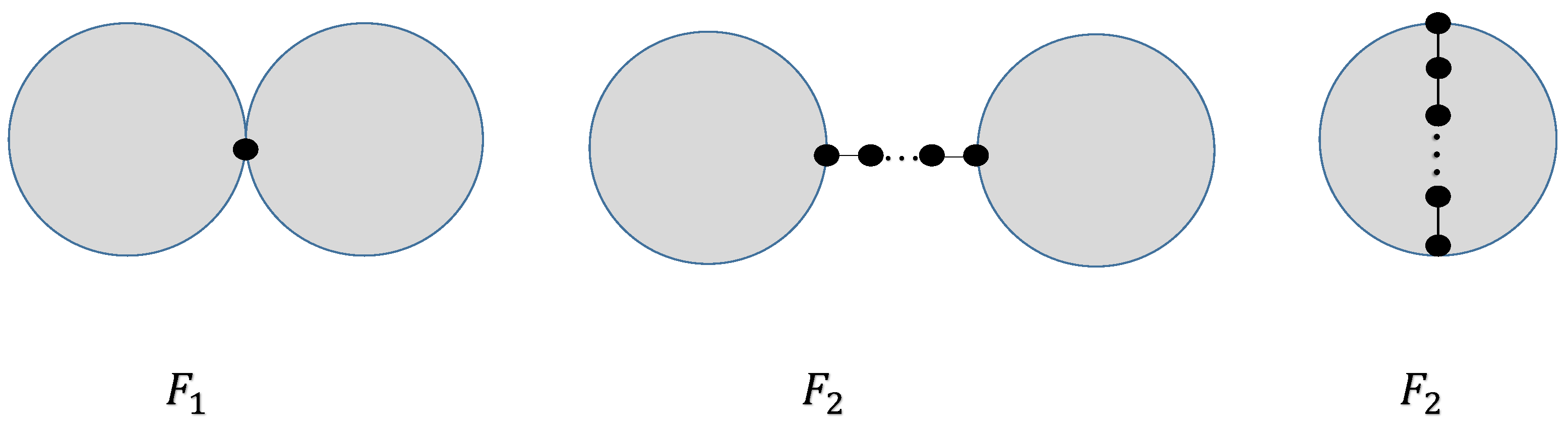
Operation A: Assume that where and . Here, are leaves and as given in Figure 1.

Figure 1.
Plot for Operation A.
In the whole proofs, we consider only the edges due to which the values of the desired index are affected; all the remaining edges are not considered because these edges have no effect in the difference.
Lemma 1.
Let G be a graph and be obtained from G by means of operation A; then,
Proof.
Suppose ; using the general power-sum connectivity index we have the following for :
Similarly, for G, we have the following:
The difference between (2) and (3) is given in the following:
The positive valve of the above last inequality can be carried out using a term by term comparison, that is,
as
From (5) and (6), we have the following:
□
Remark 1.
By means of operation A, every tree can be transform to a star, every uni-cyclic graph can be transformed into a uni-cyclic graph where all the non-cyclic edges are pendant edges and a bi-cyclic graph can be transformed into a bi-cyclic graph where all the non-cyclic edges are pendant edges.
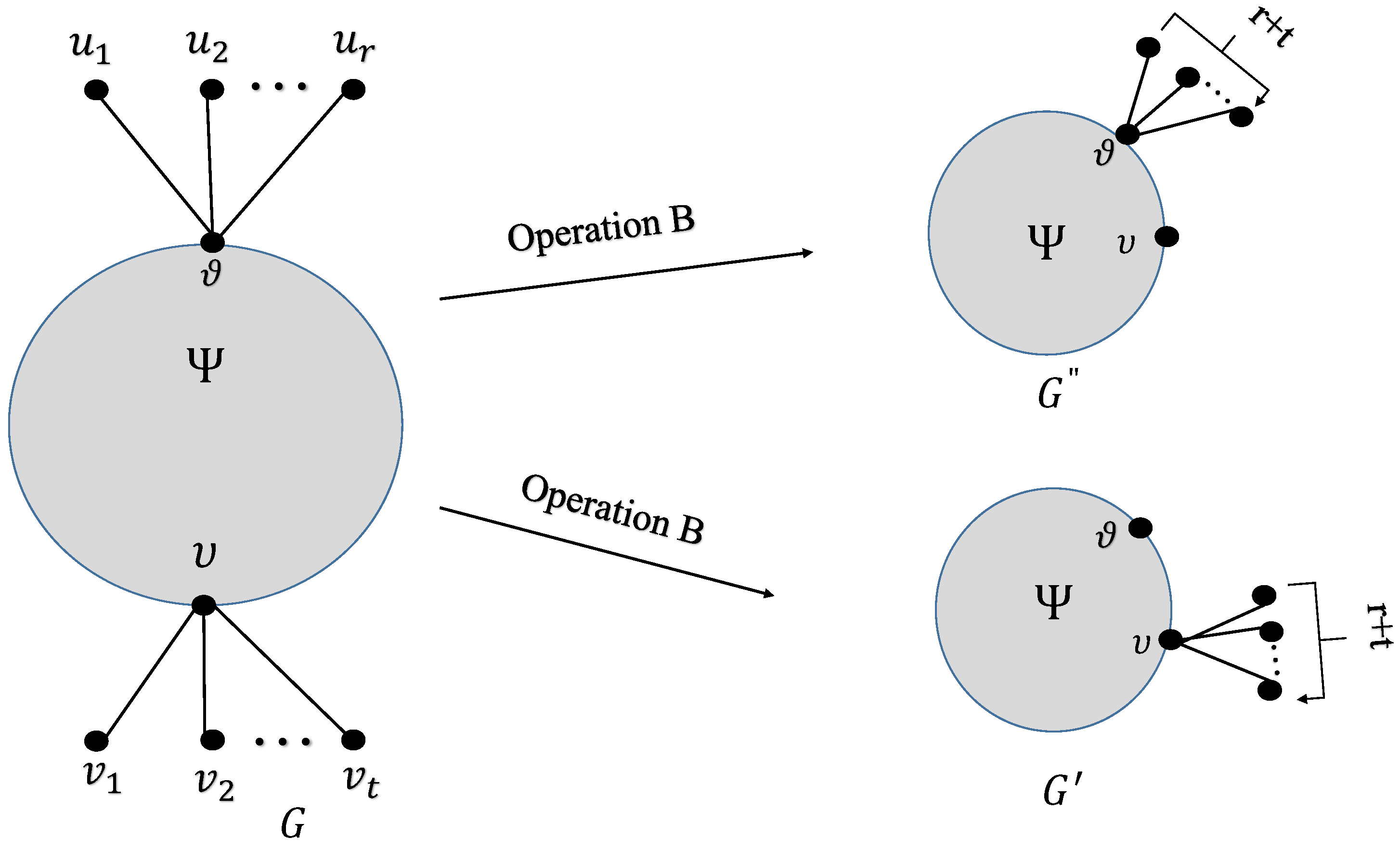
Operation B: Let G be a graph, be two vertices in G, leaves adjacent to be and leaves adjacent to vertex be . We obtain two graphs and such that and , as shown in Figure 2.
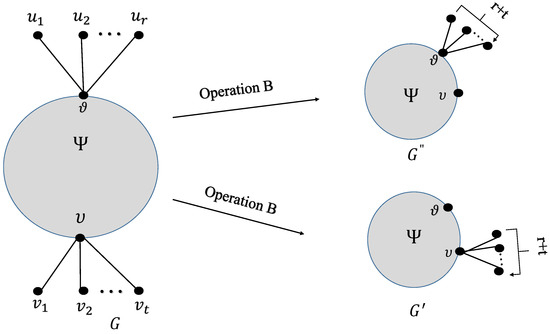
Figure 2.
Plot for Operation B.
Lemma 2.
Consider a graph G; let and be obtained from G by means of operation B; then, either or .
Proof.
Let ; for the graphs and we have to discuss two cases for which the following values of the general power-sum connectivity index are obtained.
Let and .
Case 1. If vertices and are not adjacent in G, using the general power-sum connectivity index we have the following values:
For , we have the following:
Similarly, for , we have the following:
Let and ; then, we have
The above difference if
When , we have ; for this, we proceed as follows:
Case 2. If the vertices and are adjacent in graph G then both and are neighbors, in this case, we have the following:
For , we have the following value:
For , we have the following value:
Consider the differences and . For , we have the following:
If the value of , then
If the condition in (17) holds, then
Hence, we have that if then , which completes the proof. □
Remark 2.
By repeated use of operation B, every uni-cyclic or bi-cyclic graph can be transformed into a uni-cyclic or bi-cyclic graph where all the pendant edges are attached to the same vertex.
2.1. Graphs Having Largest Value of
Definition 1.
The girth of a cycle means the length of the cycle.
Theorem 1.
[21] Consider a tree of order n denoted by T; if T is not , then .
Suppose that is a uni-cyclic graph which is obtained from having length k where edges having degree one are attached to the same vertex on ; then, by means of Lemmas 1 and 2 we have the following:
Theorem 2.
Consider a uni-cyclic graph G of girth k and order n. If G is other than , then we have .
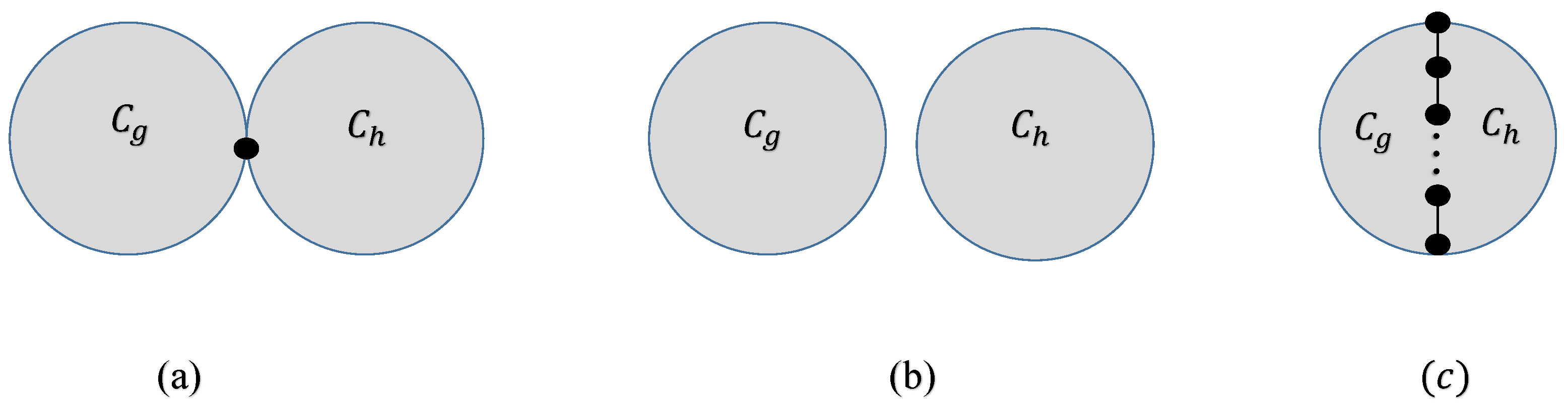
Let us suppose an is bi-cyclic of order n and size . Consider a set of simple and connected graphs denoted by . For every , there are two cycles in G denoted by and . We categorize having two cycles one of order g and the second of order h into three classes, as in the following:
- (1)
- is the collection containing , where the cycles and share only one common vertex.
- (2)
- is the collection containing , where the cycles and have no common vertex.
- (3)
- is the collection containing , where the cycles and have a common path of length l.
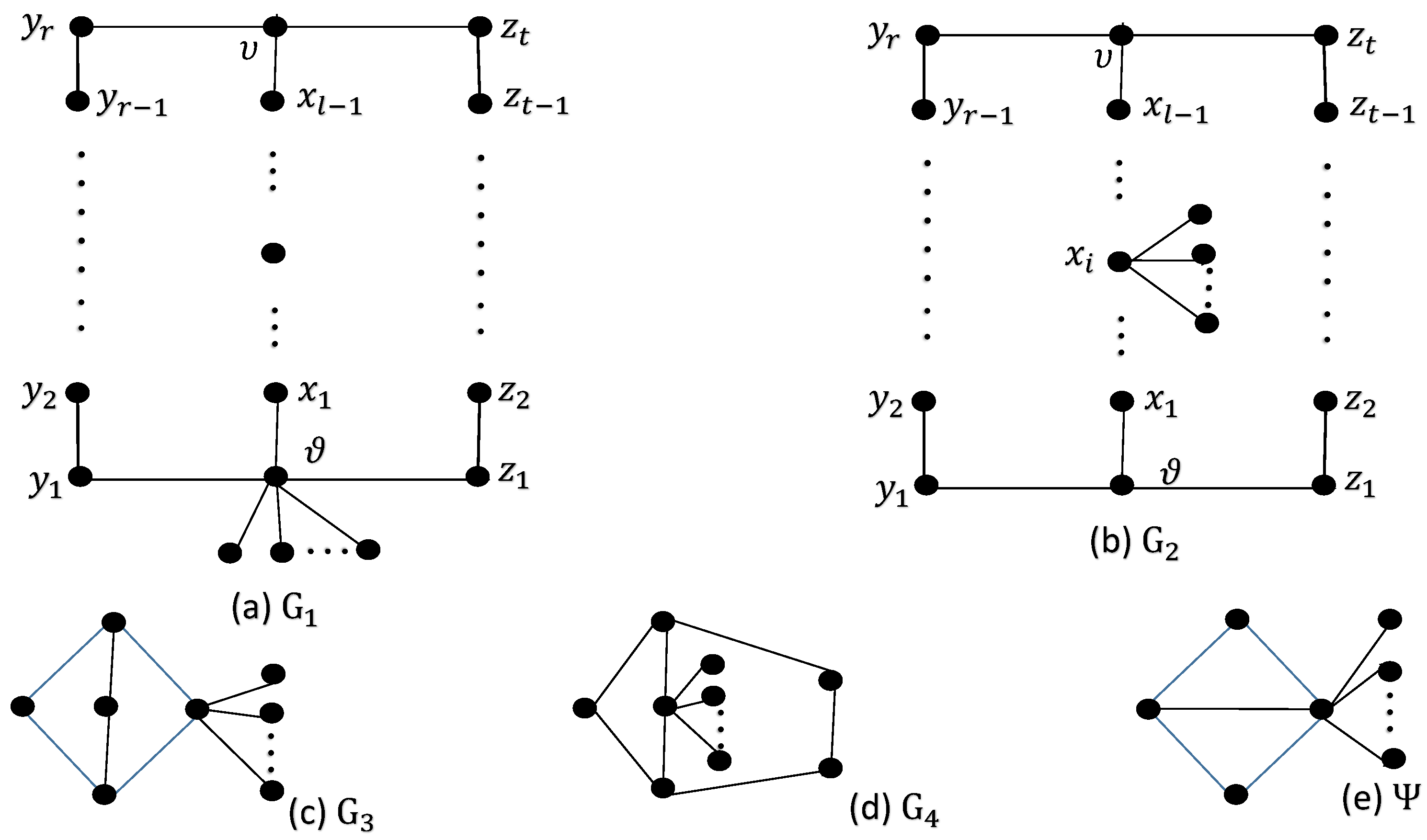
The induced sub-graphs of vertices on the cycles of (or , ) are shown in Figure 3a–c.
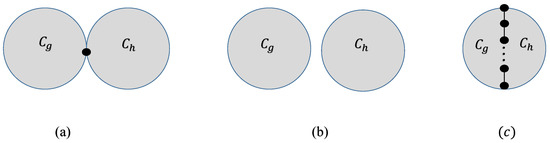
Figure 3.
Bi-cyclic graphs having (a) one common vertex, (b) no common vertex and (c) a common path of length l.
2.2. Largest General Power-Sum Connectivity Index in
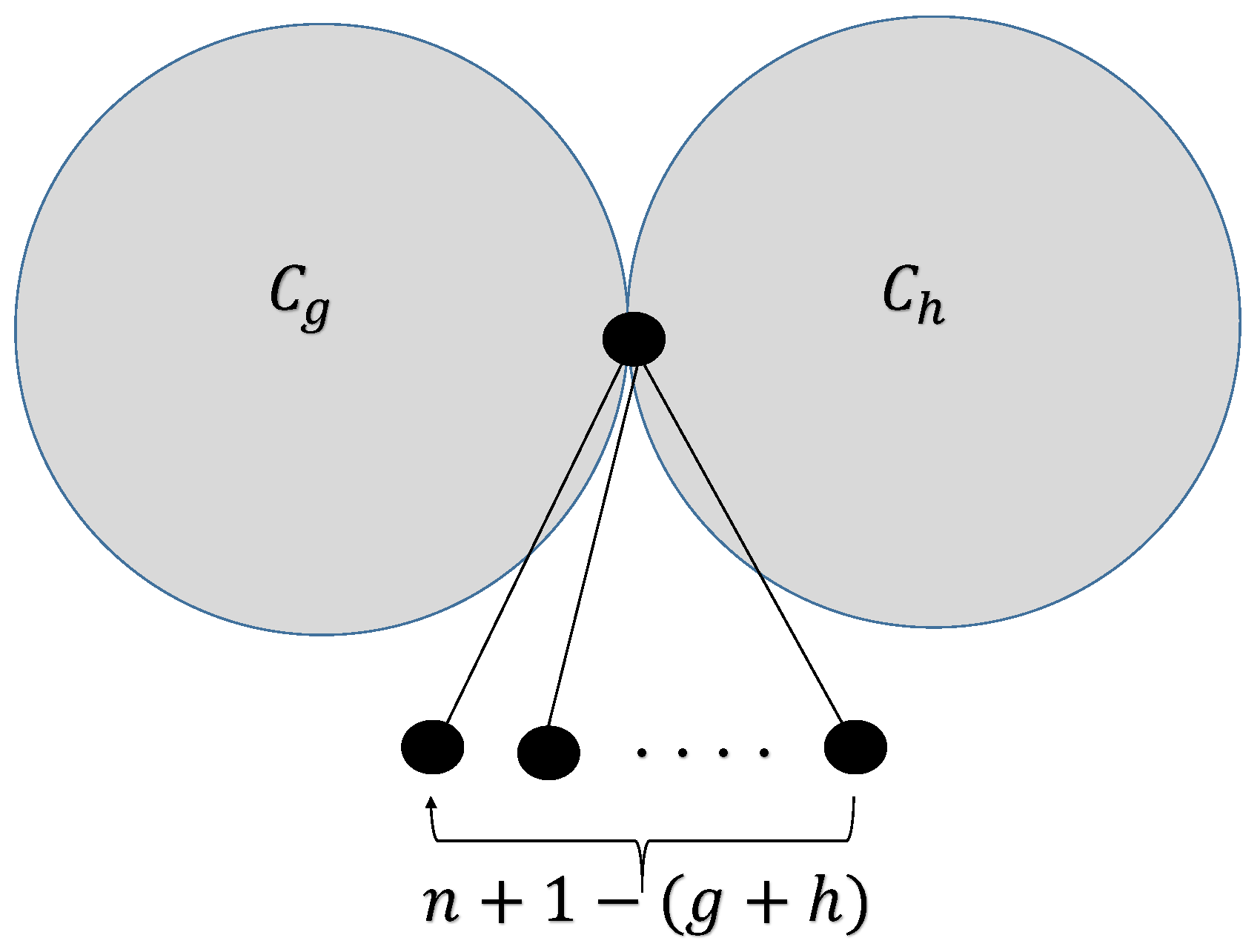
Let be a graph from in which pendant edges are connected to the vertex that is common in and as in Figure 4.
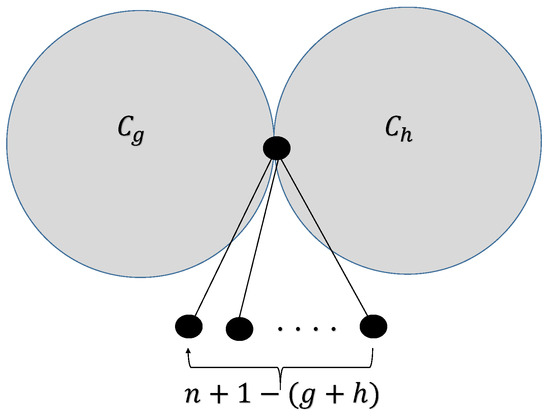
Figure 4.
Graph .
Theorem 3.
is the graph having the largest value of in .
Proof.
By means of operations A and B on G, we obtain where all the non-cyclic edges are attached to the same vertex v. Then, by means of Lemma 1 and Lemma 2, we have that the equality holds iff all the non-cyclic edges are attached to the same vertex in G. If , then u and v are not the same vertices, that is, and u is the common vertex of and .
Having no ambiguity, let us suppose that v is on the cycle . We have to discuss two cases:
Case I. If and are not adjacent, then
Similarly, for , we have the following:
Consider the difference as follows:
It is clear that the difference is greater than zero, while the equality holds iff .
Case II. If and are connected by an edge in , then we have the following:
Now, consider the following difference:
It is clear that the above last difference is greater than zero while the equality holds iff . □
For given and , using the above theorem, we have that is the graph which is unique having the largest value of in .
Lemma 3.
(i) If , then ;
(ii) If , then .
Proof.
(i) We know that
Replace g by ; we obtain
Consider the difference:
Clearly, the difference shows that .
For (ii), we have
Clearly, the difference shows that . □
Hence, from Theorem 3 and Lemma 3, the following result is obtained.
Theorem 4.
For every and , the unique graph of order n having the largest value of is in .
2.3. Largest General Power-Sum Connectivity Index in
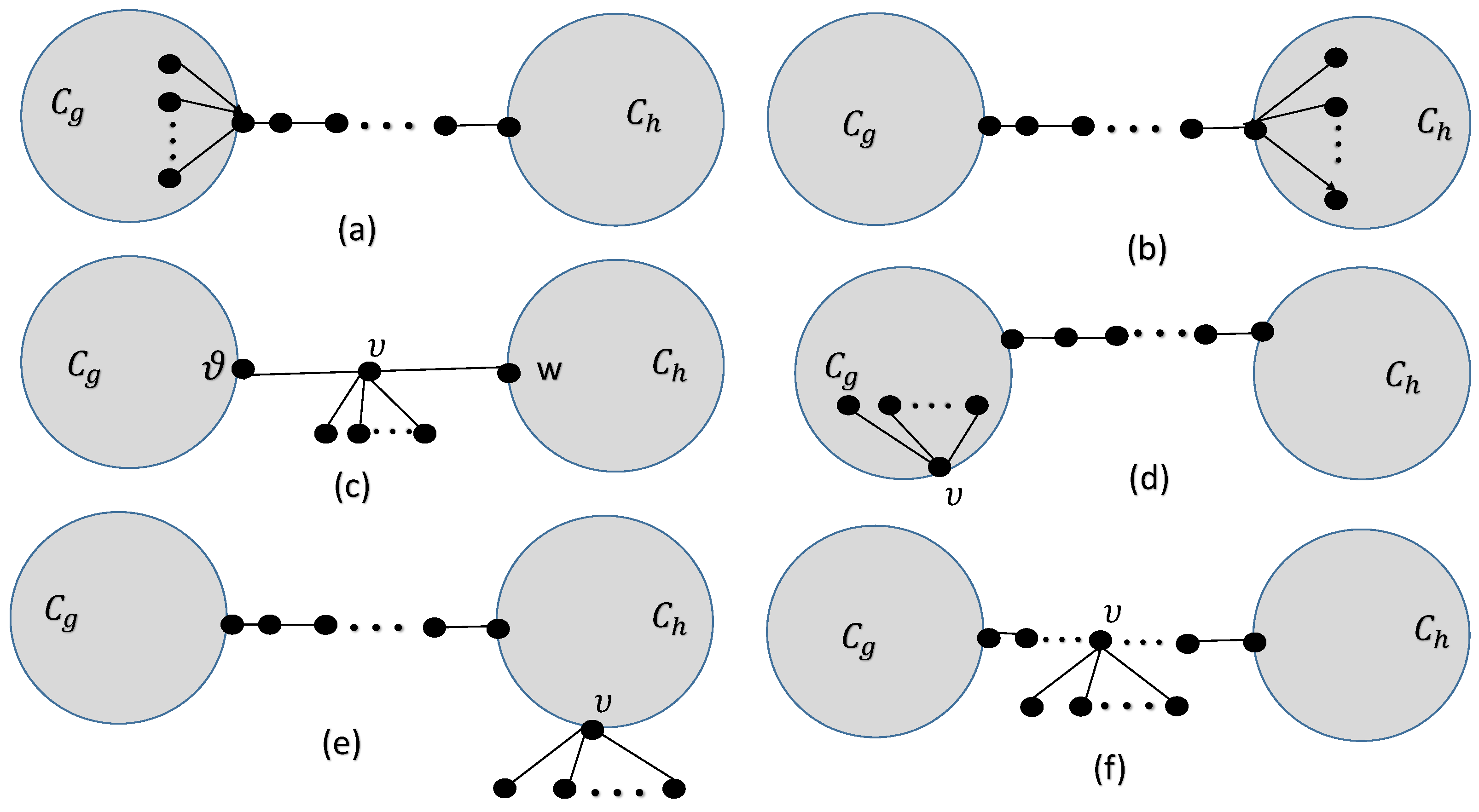
In this section, we have to find the bi-cyclic graphs having the largest value for the general power-sum connectivity index in . Suppose that is the graph having n vertices, edges, and two cycles and connected by a path having length r. The remaining edges are connected to the common vertex of the path and cycle , see Figure 5a. Similarly, the graph is in Figure 5b, while is the graph having n vertices, edges, and two cycles and connected by means of the path having length 2 and the remaining edges are connected to the vertex , see Figure 5c.
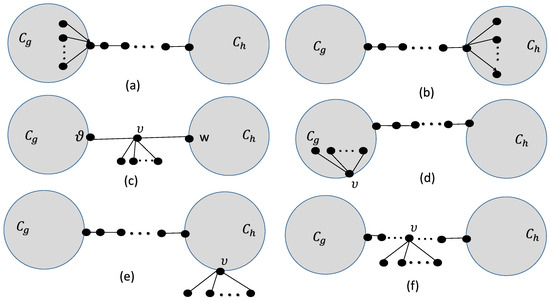
Figure 5.
(a) ; (b) ; (c) ; (d) is on the cycle and is not the common vertex of the path and cycle ; (e) is on the cycle and is not the common vertex of the path and cycle ; (f) is on the path.
Theorem 5.
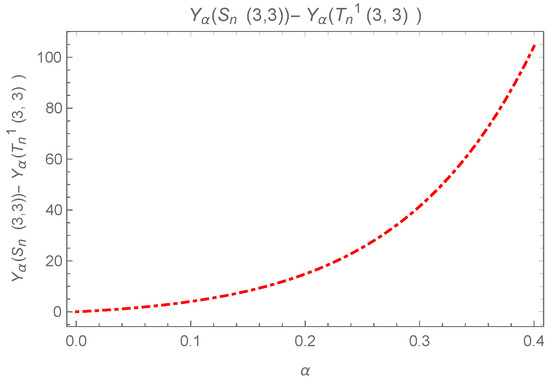
Let , and and be connected in G by means of a path having length r; then,
Proof.
Let be the path connecting and in G, the common vertex of and P be , and that of and P be . Using Operations A and B repeatedly on G, we obtain the graph as in Figure 5 where all the non-cyclic edges are pendant and attached to the same vertex v. By mean of Lemmas 1 and 2, we have that , while the equality is in the case iff all the non-cyclic pendant edges are attached to the same vertex in G. Further, we consider the following cases.
Case I. If is on the cycle such that and are not adjacent, as in Figure 5d, then we have the following:
Similarly, we have the following for :
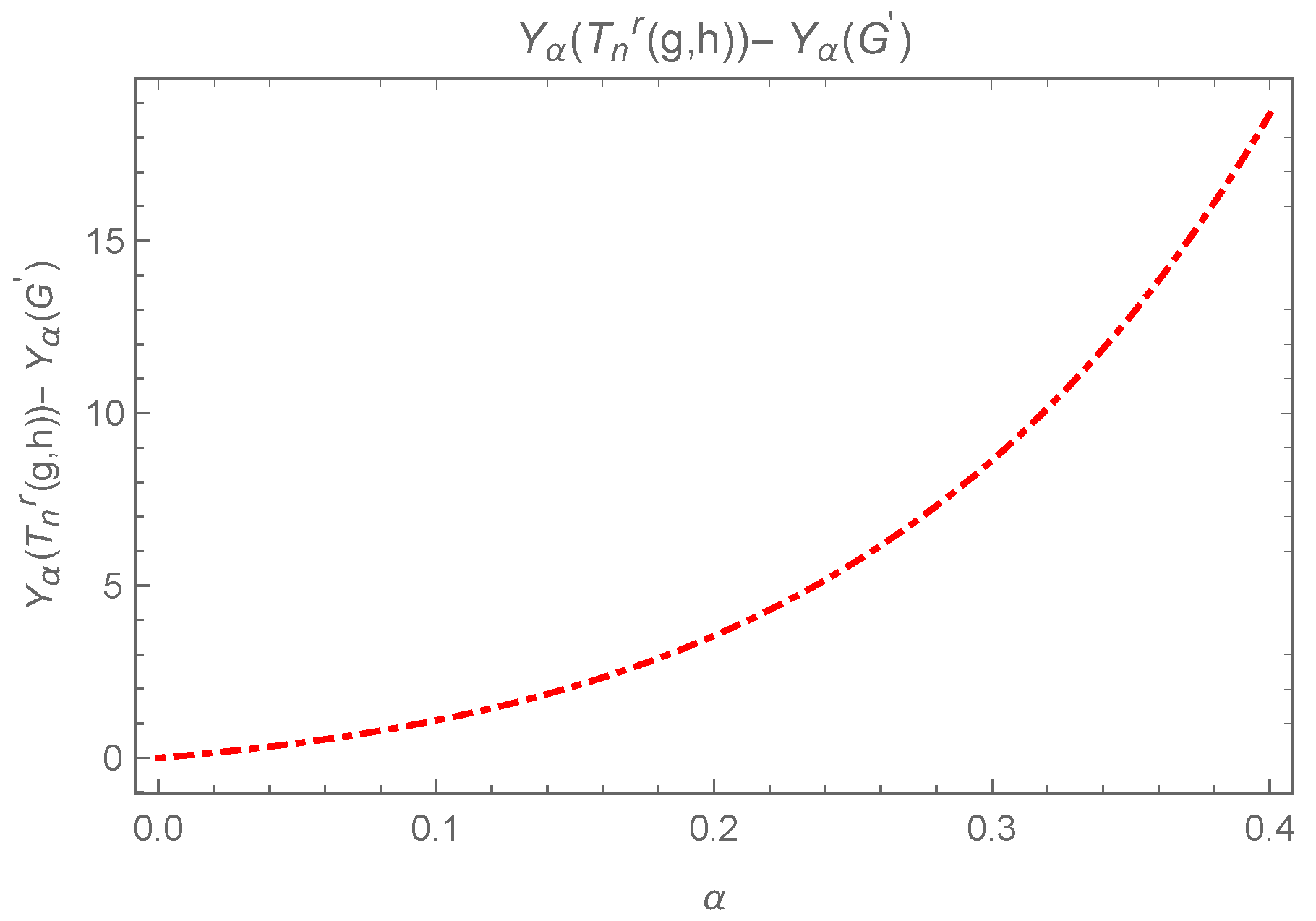
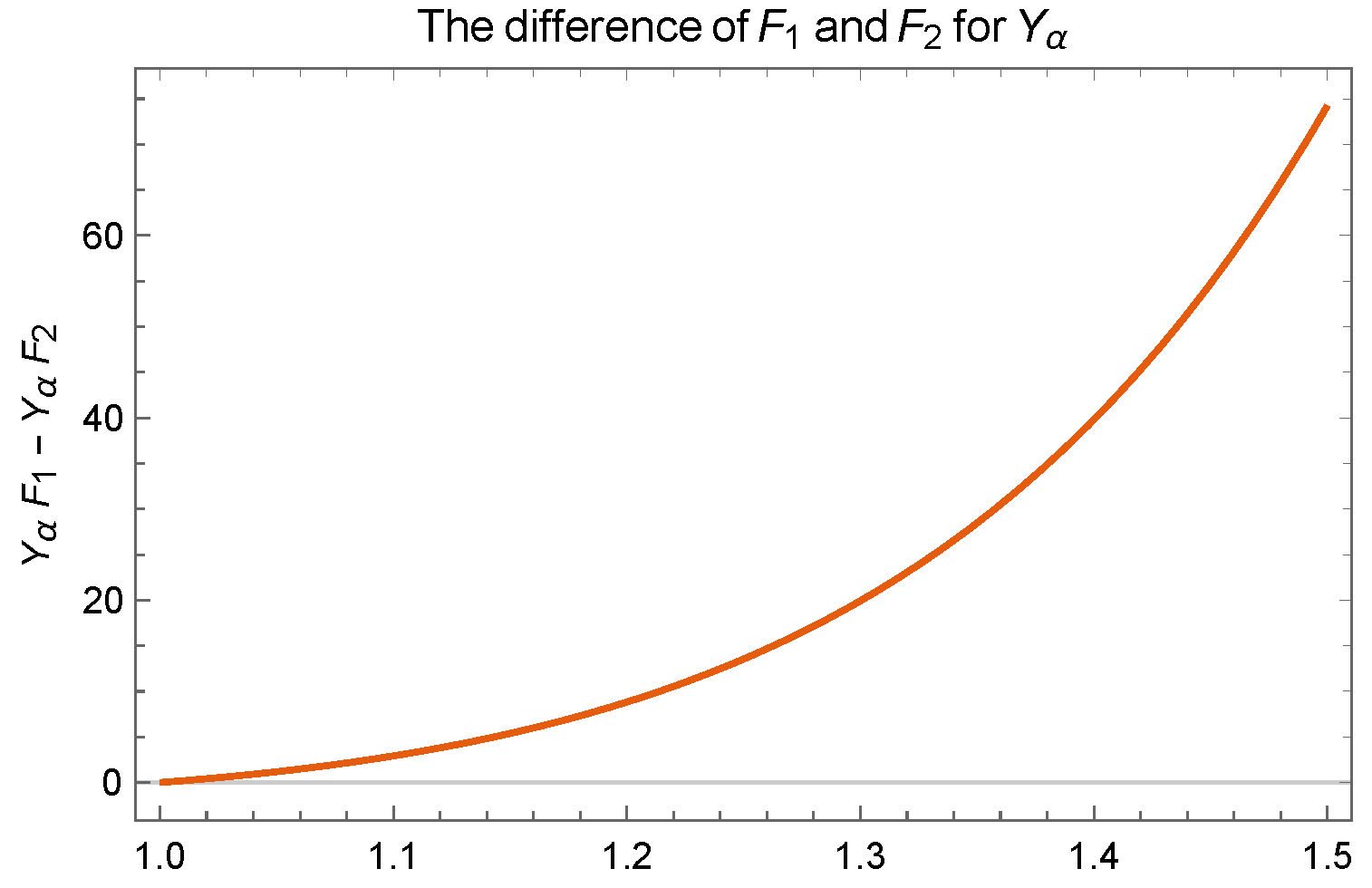
Consider the following difference:
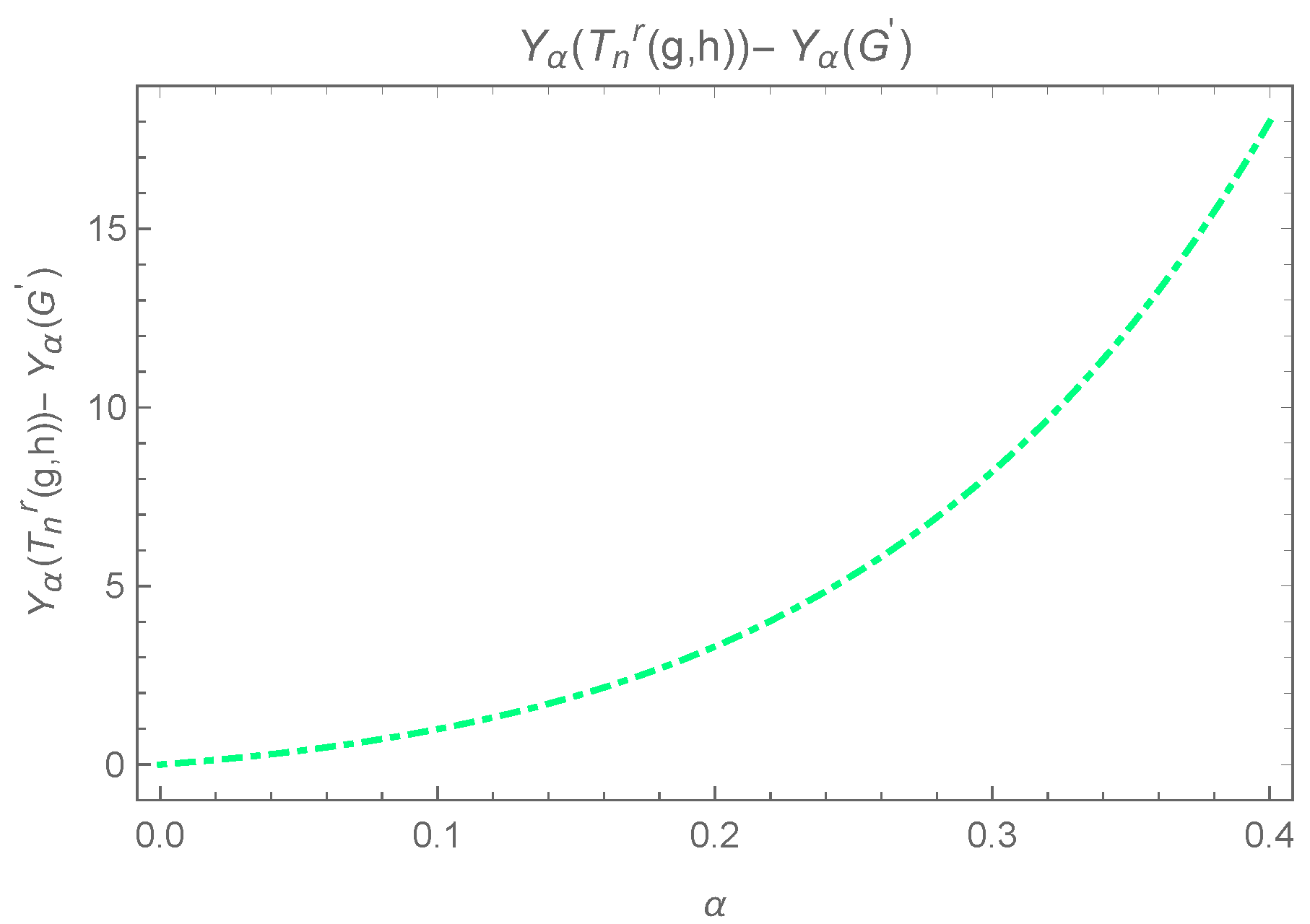
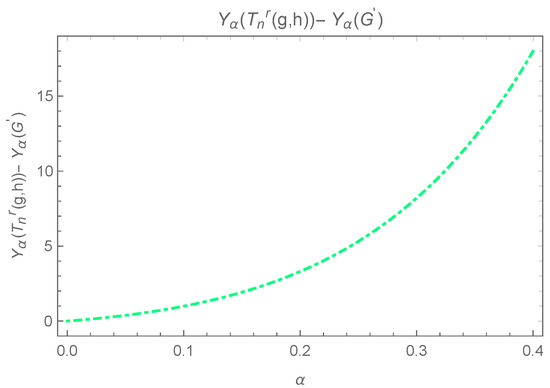
The above last difference , while the equality holds in the case iff . The inequality can be observed in Figure 6.

Figure 6.
Plot for , where and are not adjacent.
If and are adjacent in , then we have the following:
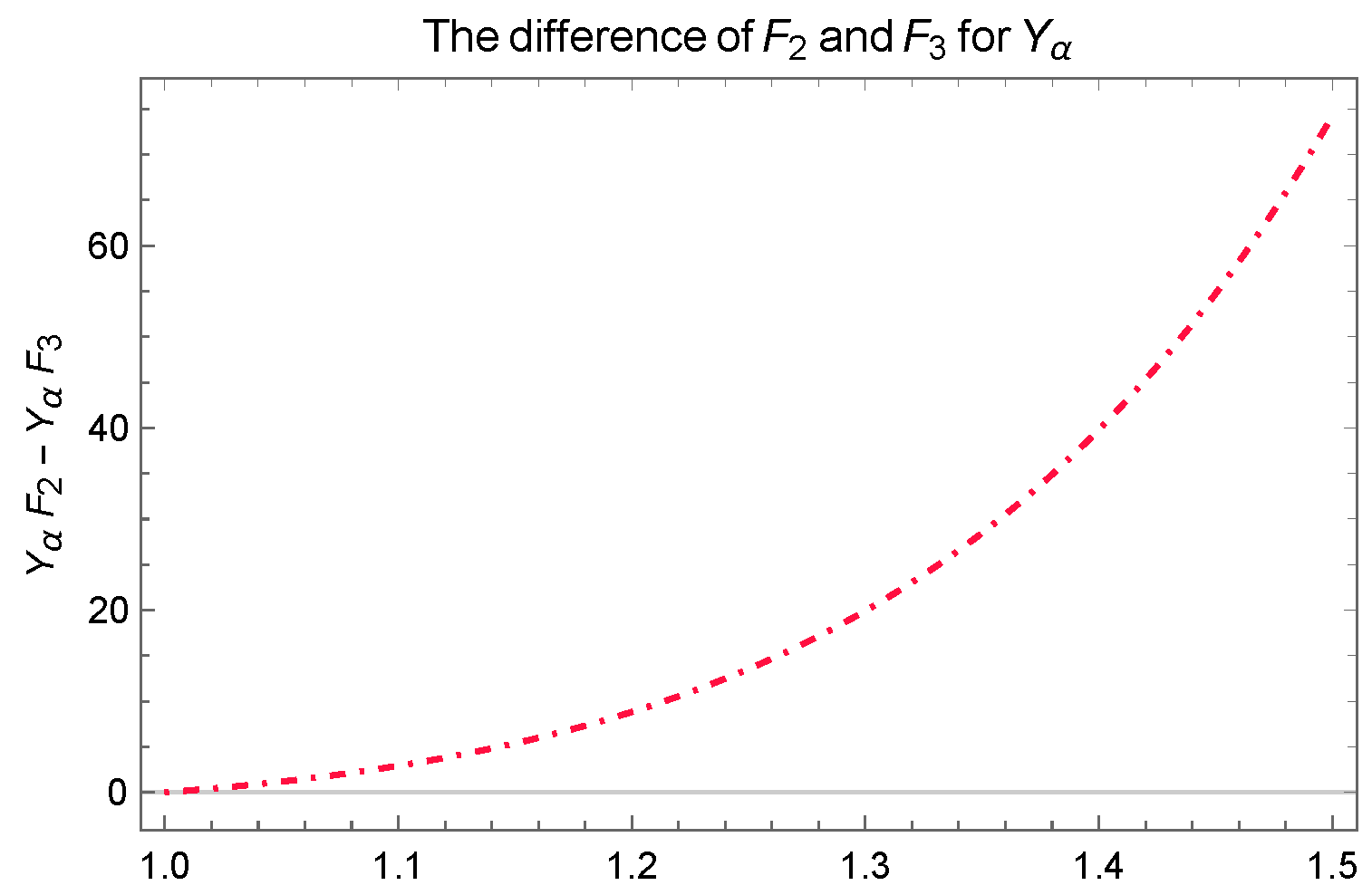
Consider the difference in the following:
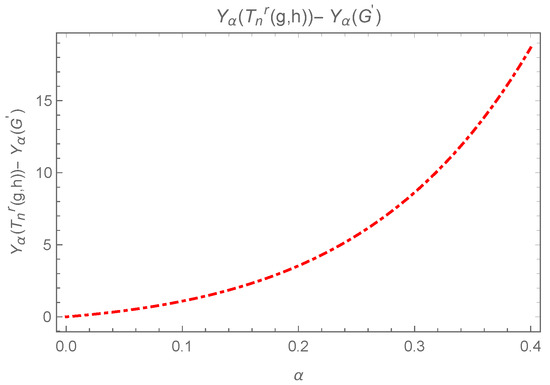
The above last difference , while equality is in the case iff . The difference can be observed in Figure 7.

Figure 7.
Plot for , where and v are adjacent.
Case II. If vertex lies on the cycle , the proof is similar to in Case I. The graph is given in Figure 5e.
Case III. If the vertex lies on the path P, which is shown in Figure 5f, if , then . We have the following:
If , then and we have the following:
Now, for , we have the following:
Consider the following difference:
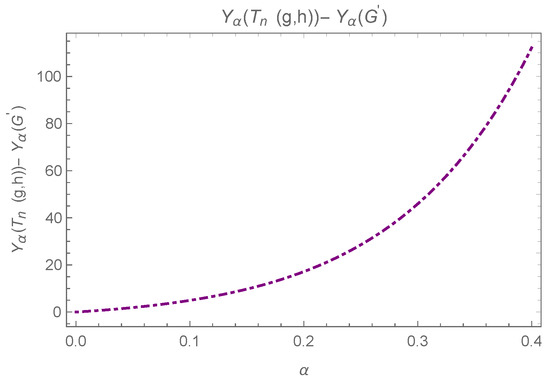
The difference can be observed in Figure 8.

Figure 8.
Plot for , where .
Now, if or , then we have the following value for :
Consider the difference in the following:
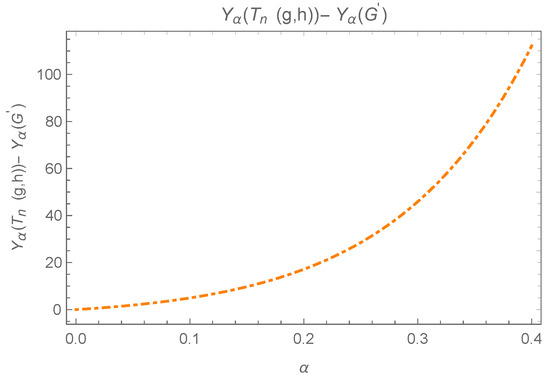
The above last difference can be observed in Figure 9.

Figure 9.
Plot for , where or .
From the figures, it is clear that all the differences are positive which shows the largest value of in the desired family of graphs. □
Lemma 4.
while the equality holds iff .
Proof.

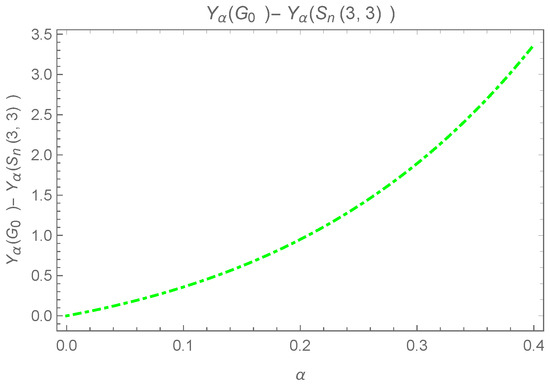
We have from the previous theorem
For , we have the following:
Consider the difference:
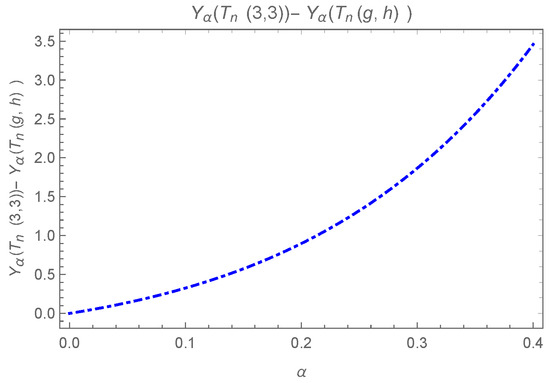
The above difference can be observed in Figure 10, while the equality holds iff which can be observed in Figure 11.

Figure 10.
Plot for .

Figure 11.
Plot for , where .
□
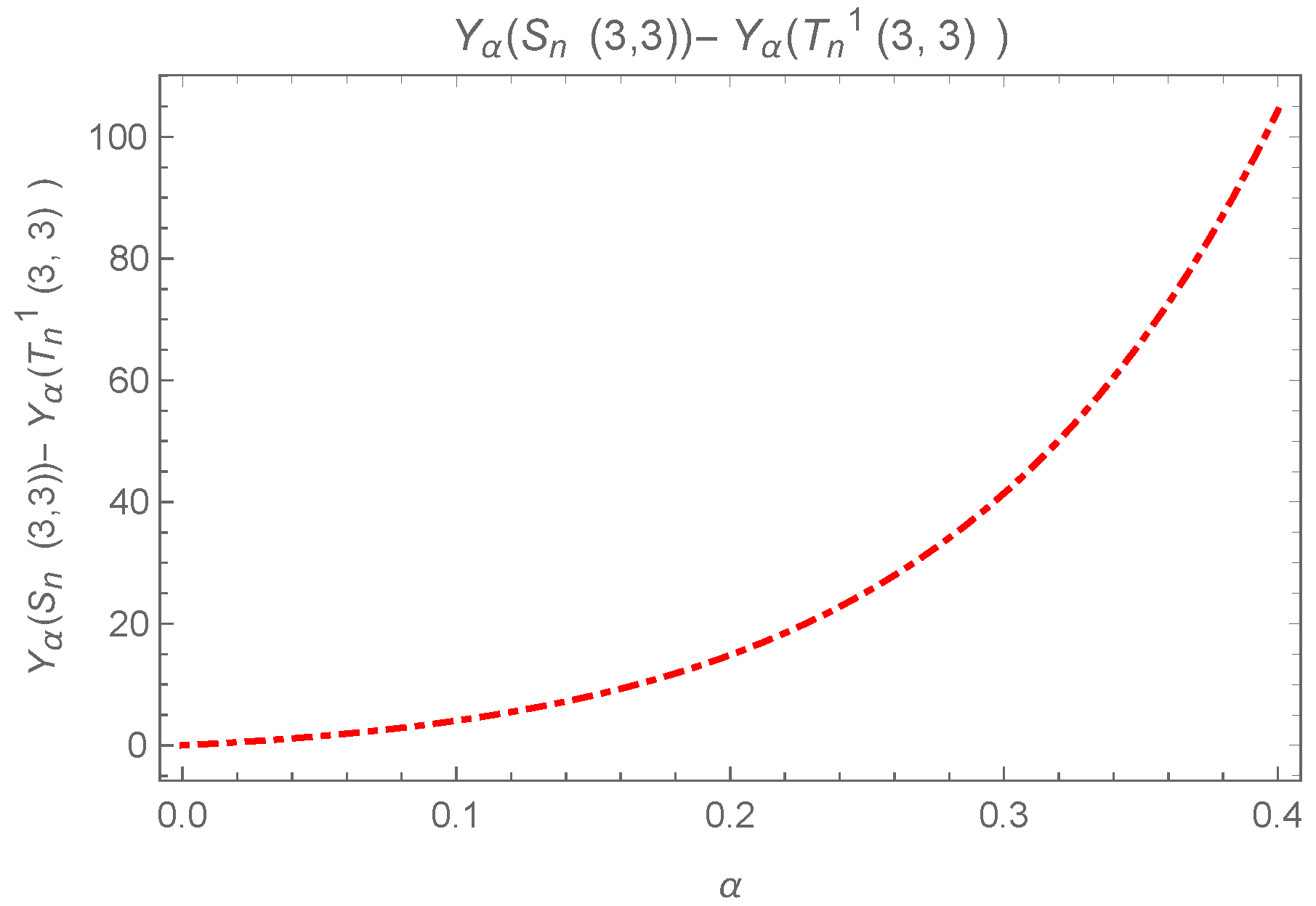
Lemma 5.
For , .
Proof.
We consider two cases:
If , then we have the following for :
As , we obtain the following:
Replace r by in (35); we obtain the following:
The difference between and is as follows:
The difference can be observed in Figure 12.

Figure 12.
Plot for where .
If , then we have the following:
Similarly,
Consider the difference , as in the following:
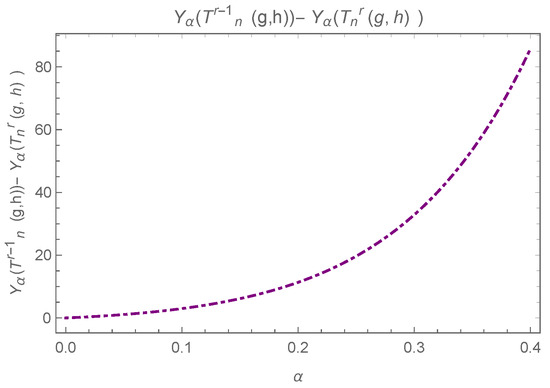
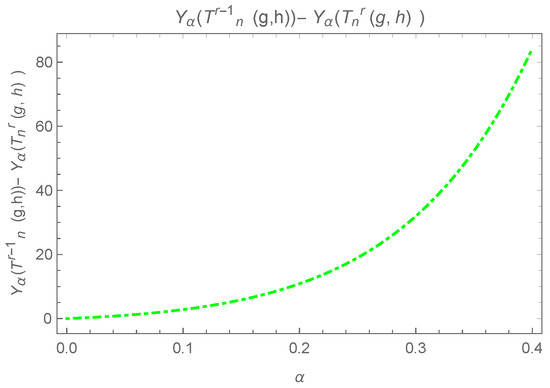
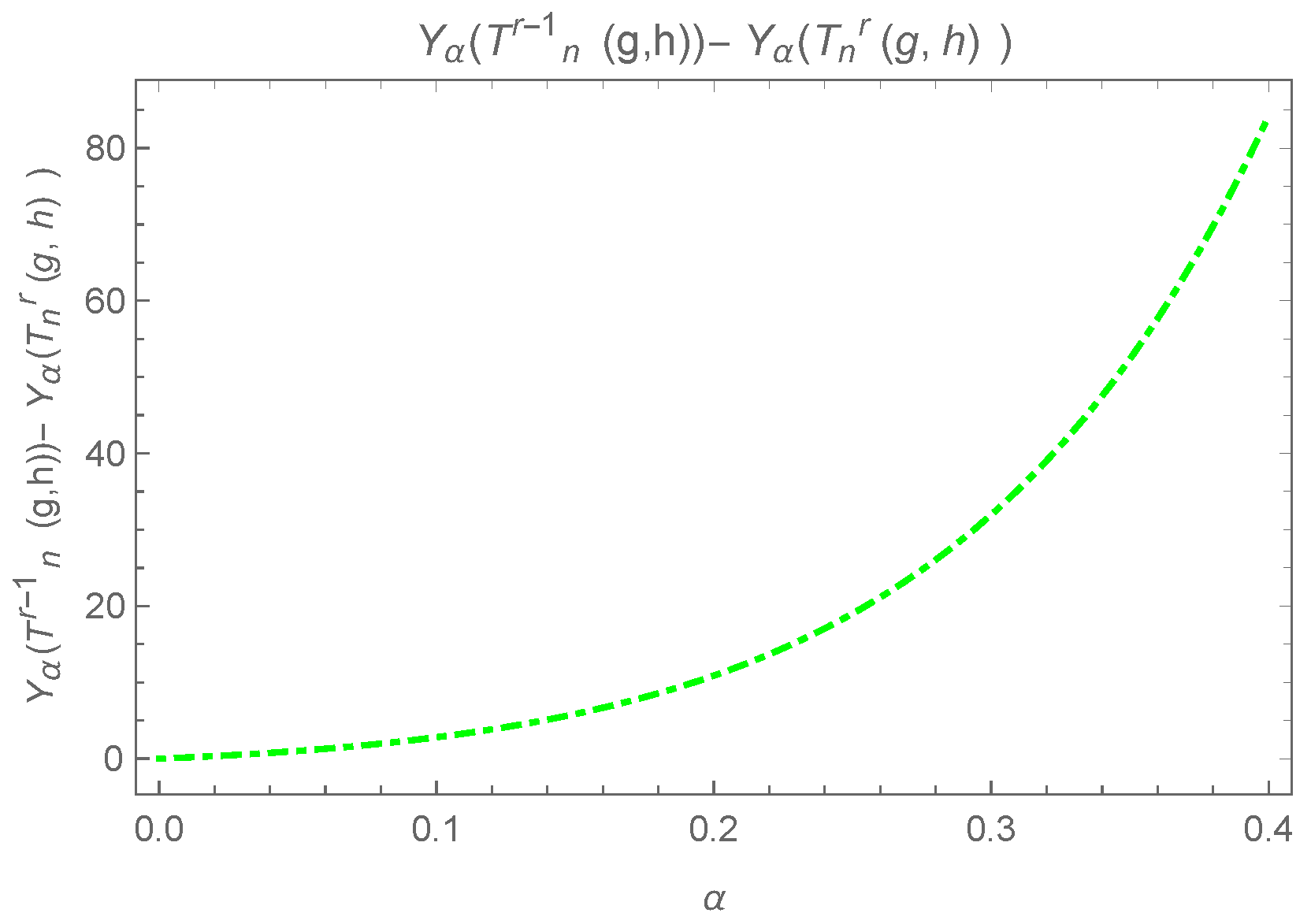
The above difference can be observed in Figure 13.
 □
□

Figure 13.
Plot for where .
Figure 13.
Plot for where .

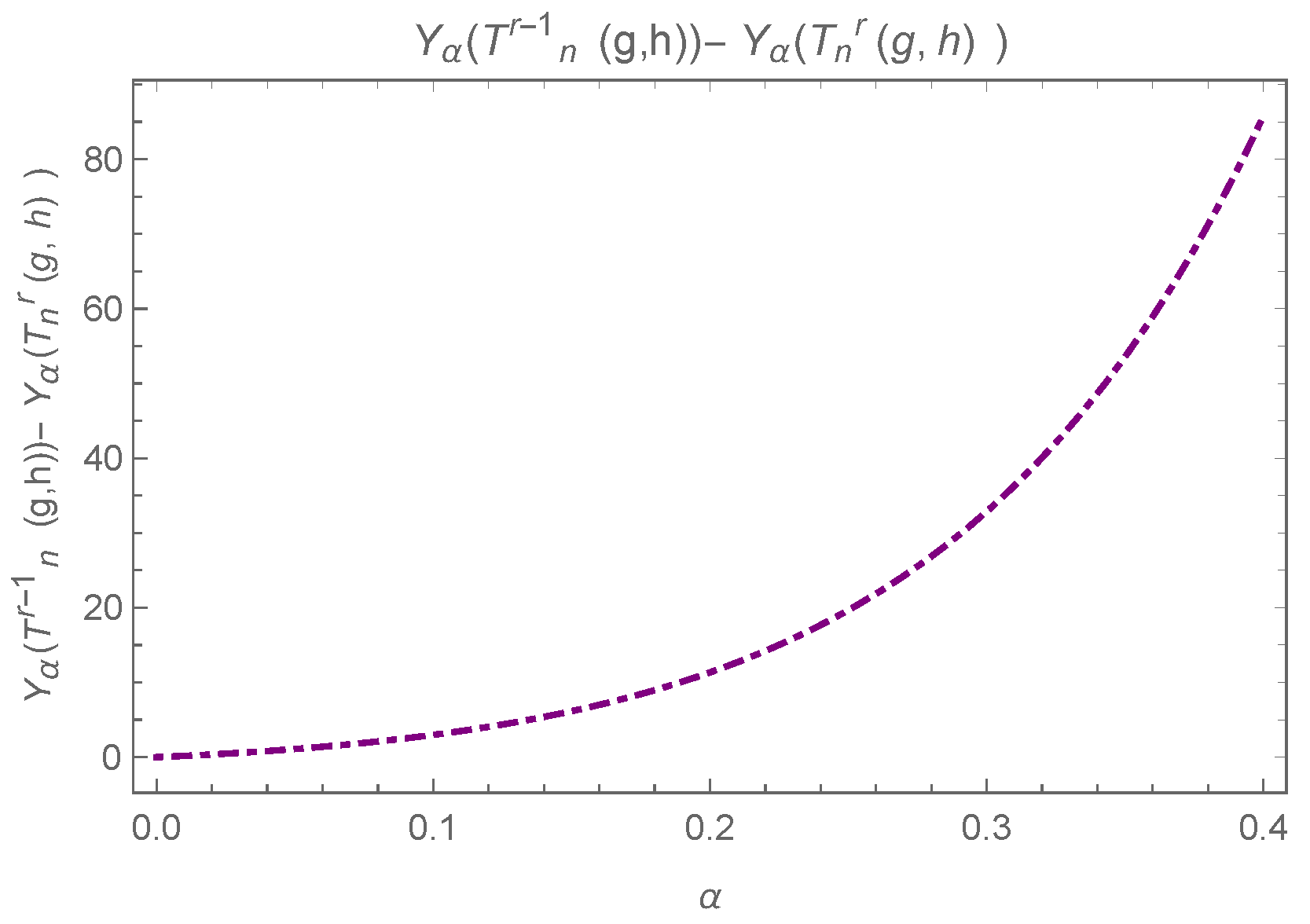
Lemma 6.
, while the equality holds iff .
Proof.
We know from the previous theorem that
Put in (36); we obtain the following:
Consider the difference:
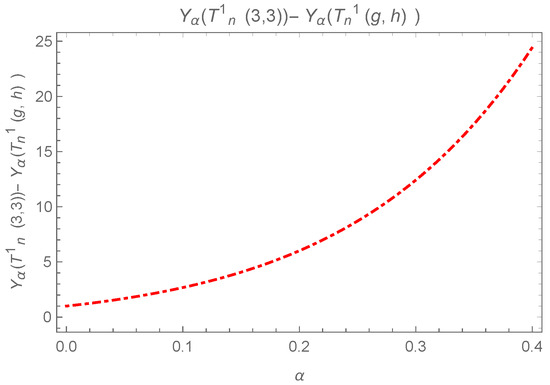
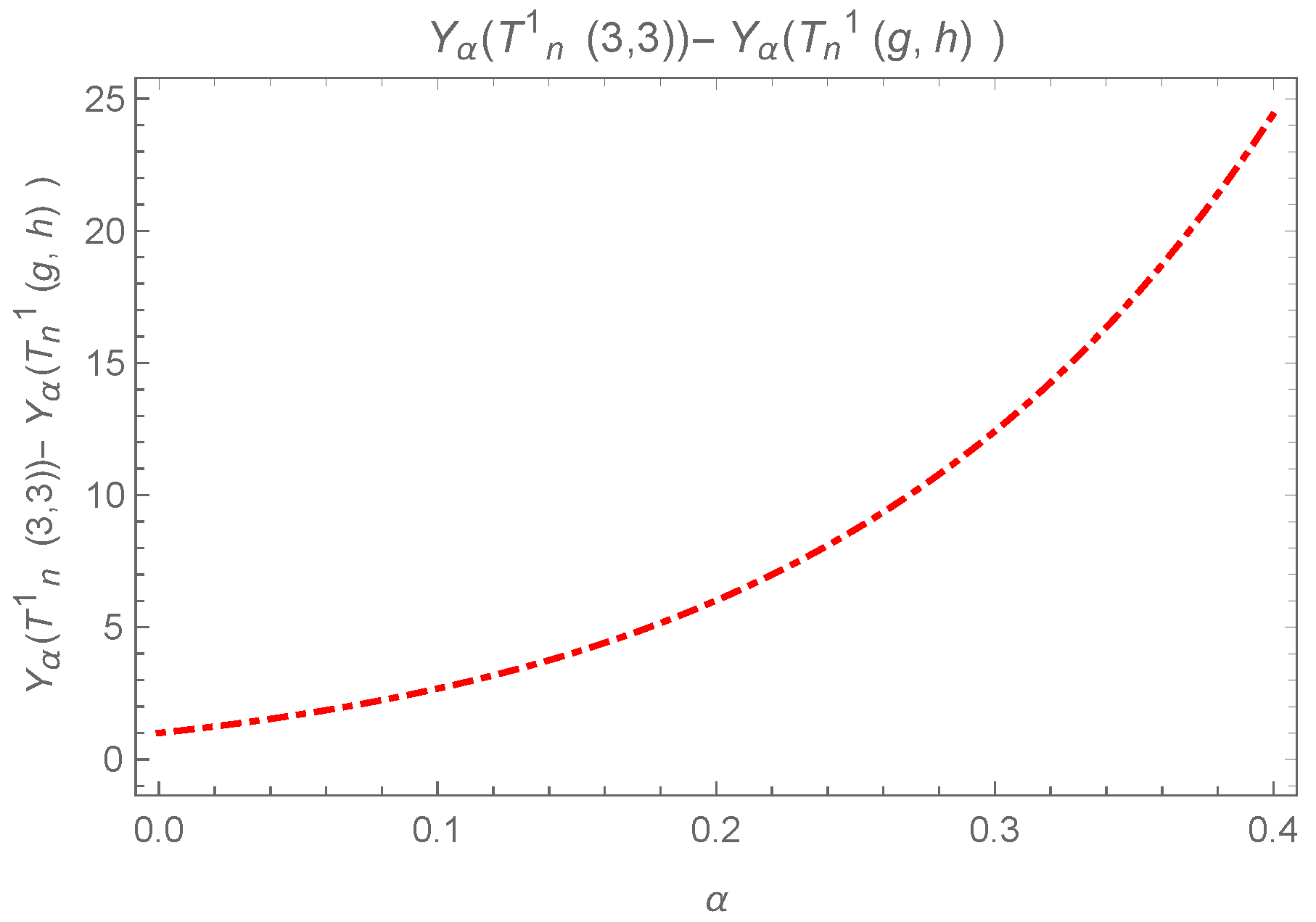
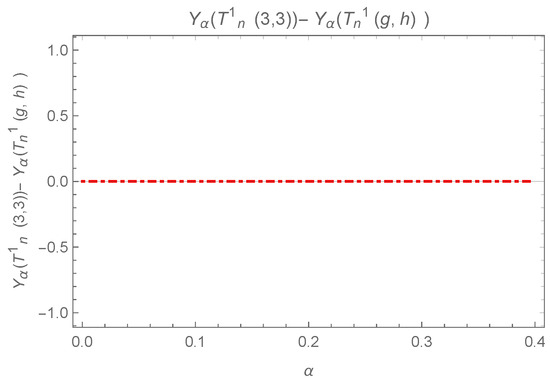
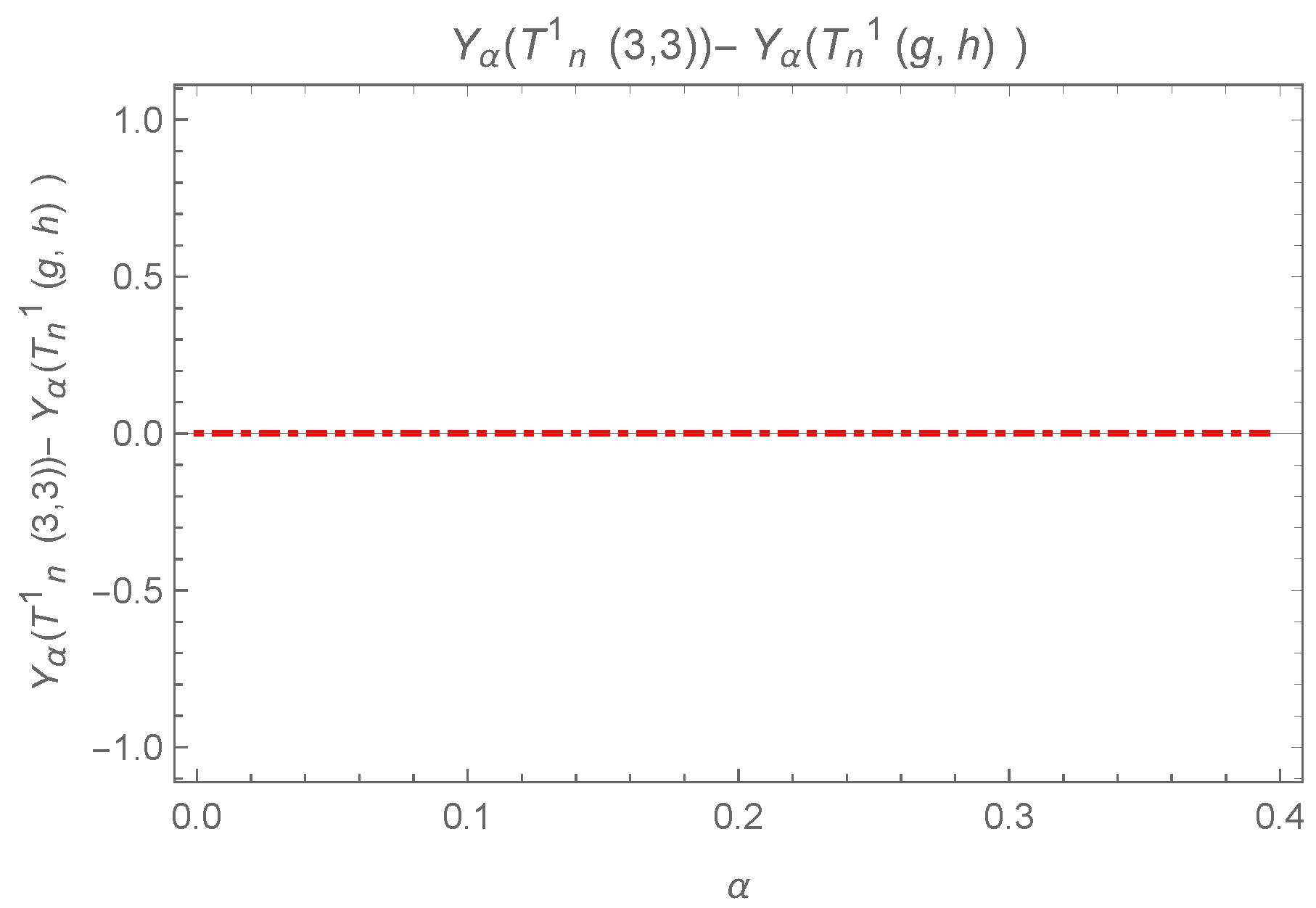
The difference can be observed in Figure 14 and Figure 15, where equality holds iff .
 □
□

Figure 14.
Plot for , where both g and h are not 3.
Figure 14.
Plot for , where both g and h are not 3.


Figure 15.
Plot for , where .
Figure 15.
Plot for , where .

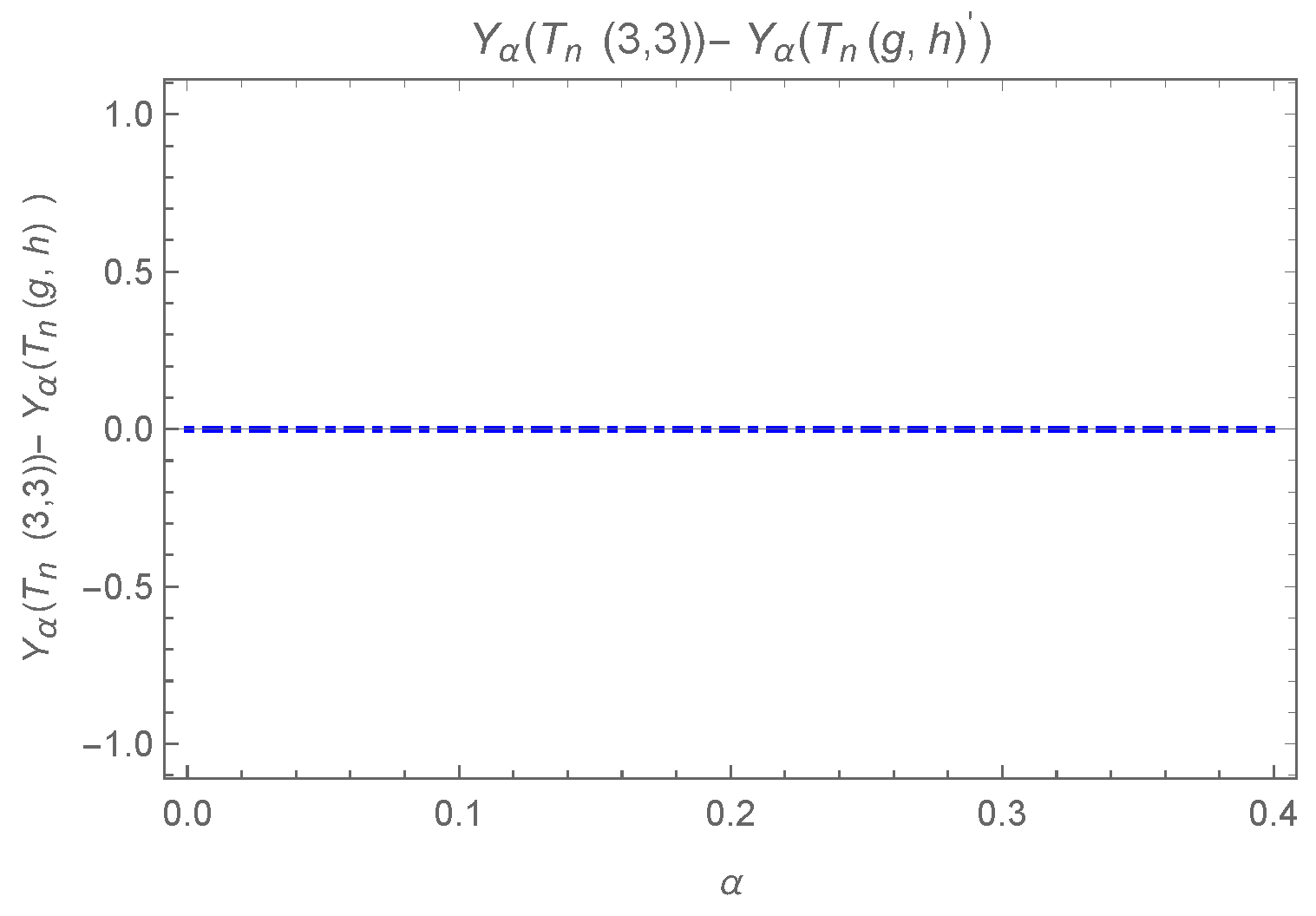
The value of the general power-sum connectivity index can be easily computed for and , and one can easily show that . Hence, we have the following theorem.
Theorem 6.
is the unique tree in having the largest general power-sum connectivity index for all and .
2.4. Largest General Power-Sum Connectivity Index in
represents a bi-cyclic graph; the cycles are and of length g and h, respectively. These two cycles are connected by means of a path of length l. Let be the graph which is obtained from Figure 3c by joining vertices to the vertex having degree 3, as given in Figure 16a.
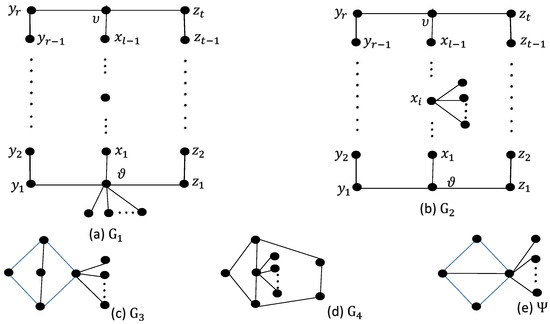
Figure 16.
The graphs (a) , (b) , (c) , (d) and (e) .
Theorem 7.
Consider the graph ; then, , while the equality holds iff .
Proof.
Using operations A and B repeatedly on the graph G, we obtain where all the non-cyclic pendant edges are attached to vertex , that is, is one of the graphs in Figure 16. By means of Lemmas 1 and 2, while the equality holds iff all the non-cyclic edges of degree one are attached to the same vertex in graph G.
Suppose that the common path of and is in as in Figure 16, and and are more paths from vertex to vertex from the cycles and ; , , , , and .
If there is an edge in the graph such that the degree of its vertices is two, we obtain graph where this edge is removed and attach a pendant edge to ; then, we have , since and . Hence, while the equality holds iff .
Similarly, if there are two edges in the graph where the degrees of their end vertices are both two, then we obtain by deleting these two edges and attach these edges to the vertex . Then, we have ; therefore, and . It is easy to compute that and . □
Finally we present the bi-cyclic graphs having the largest value of the general power-sum connectivity index.
Theorem 8.
Among all bi-cyclic graphs, Ψ is the unique graph having the largest general power-sum connectivity index.
3. Operations Which Decrease General Power-Sum Connectivity Index
This section is devoted to the operations used for decreasing the general power-sum connectivity index, as given in the following:
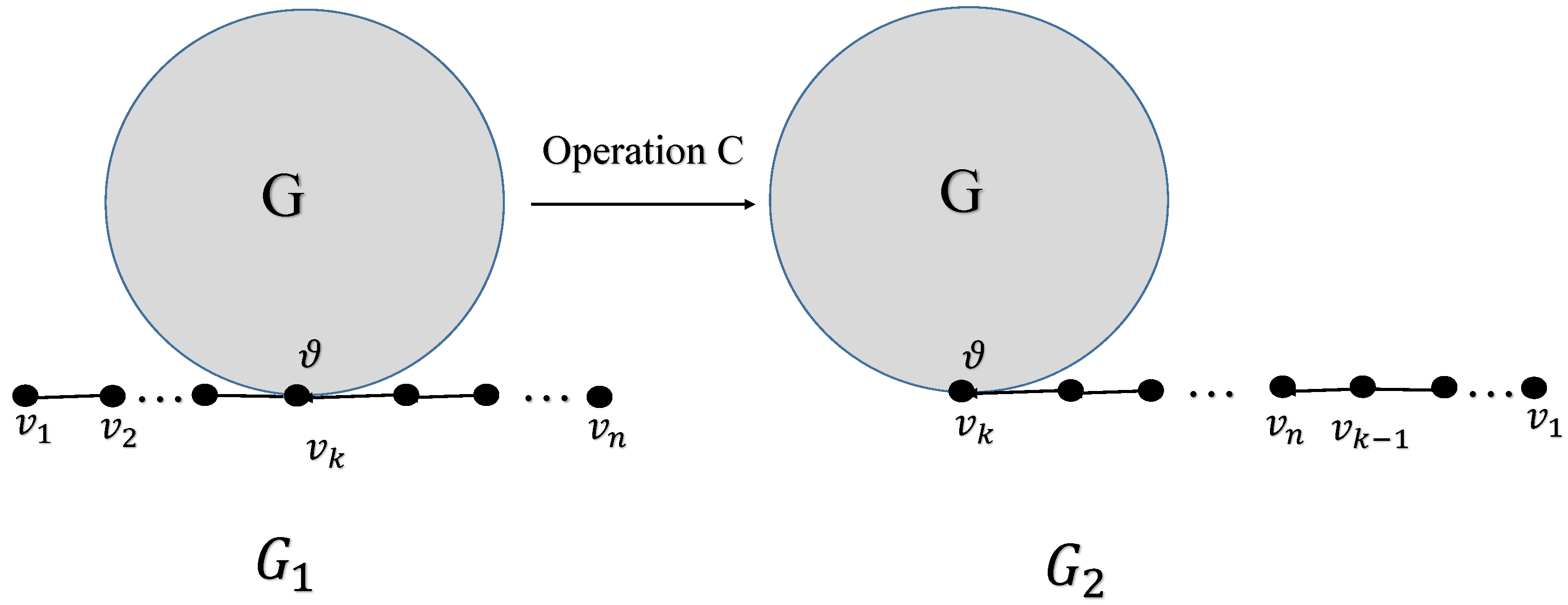
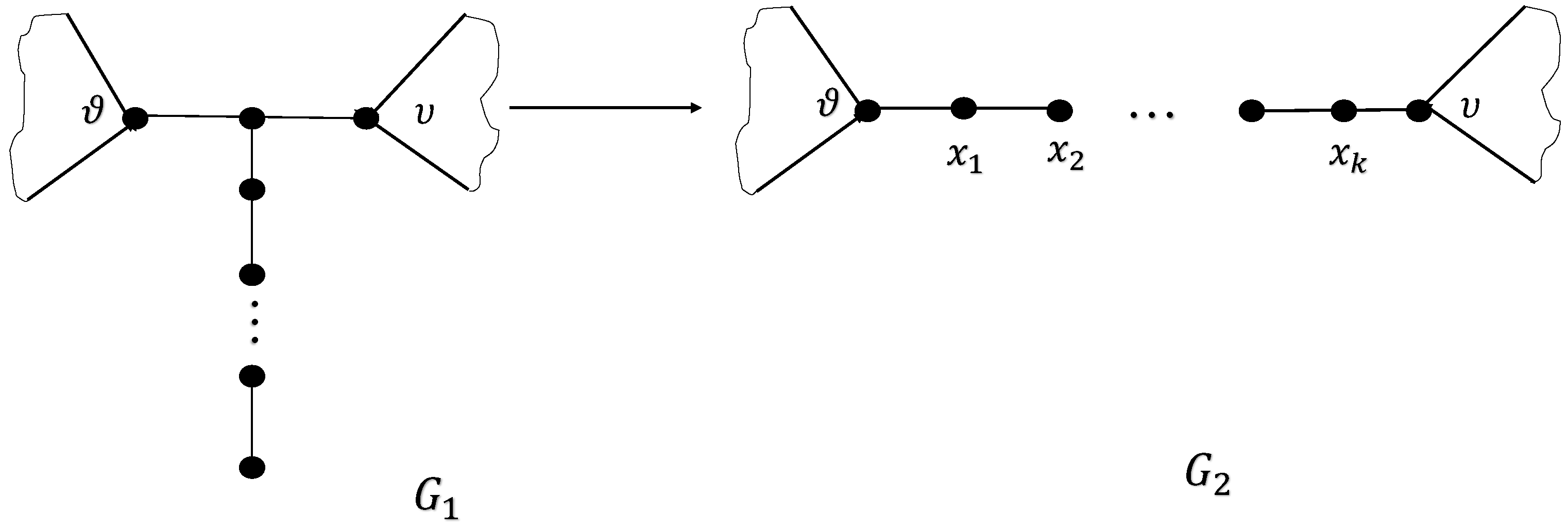
Operation C: Consider the graph G which is simple and not ; choose a vertex from . Let be the graph that is obtained by marking with of the simple path where . Let be obtained from graph by removing and adding as shown in Figure 19.
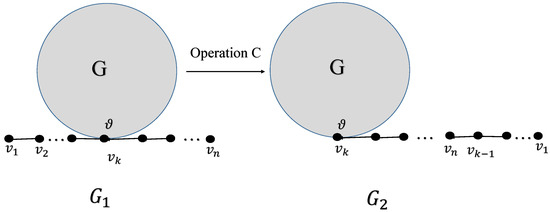
Figure 19.
Operation C.
Lemma 7.
Consider the graphs and as in Figure 19; then, .
Proof.
By means of the general power-sum connectivity index, we have
Similarly, for , we have the following:
We have to discuss the following cases:
CASE 1: If and .
In this case, we have the following:
Similarly, for , we have the following:
Consider the difference between and , as in the following:
The above last inequality can be carried out easily by making a comparison of the term-by-term process. Hence, in this case, we have .
CASE 2: If and .
In this case, we have the following:
Similarly, for , we have the following:
Consider the difference between and , as in the following:
The above last inequality can be easily observed by making a comparison term by term. Hence, in this case, we have .
CASE 3: If and .
In this case, we have the following:
Similarly, we have the following for :
Consider the difference between and , as in the following:
Making use of a term-by-term comparison, we obtain that the difference ; hence, .
CASE 4: If and .
Here, we have the following calculation for and :
Similarly, for , we have the following:
Consider the difference between and , as in the following:
The above last inequality can be clarified by making use of a term-by-term comparison for the first two terms, while for the last terms we have . Hence, we have that . This completes the required proof. □
Remark 3.
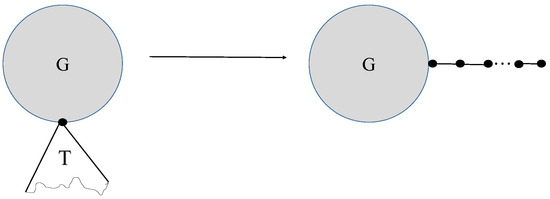
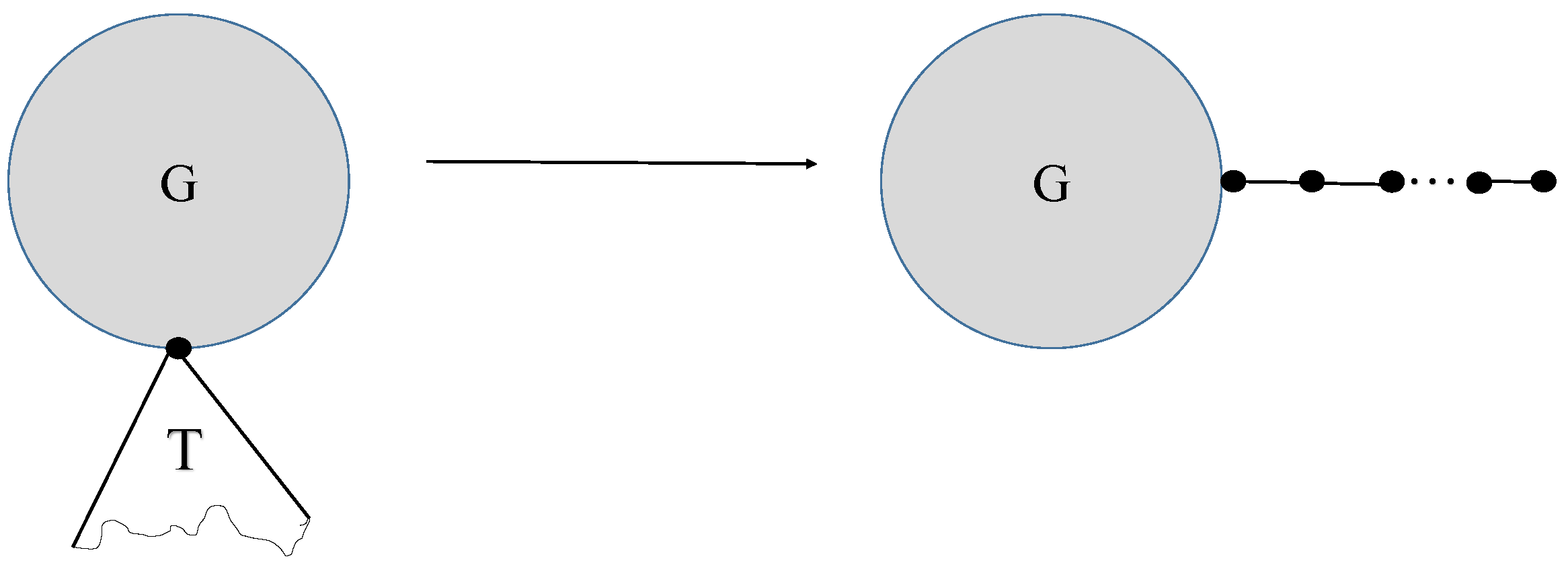
Using operation C continuously, any tree connected to a graph can be operated into a path as in Figure 20 and the general power-sum connectivity index decreases.

Figure 20.
Remark using Operation C.
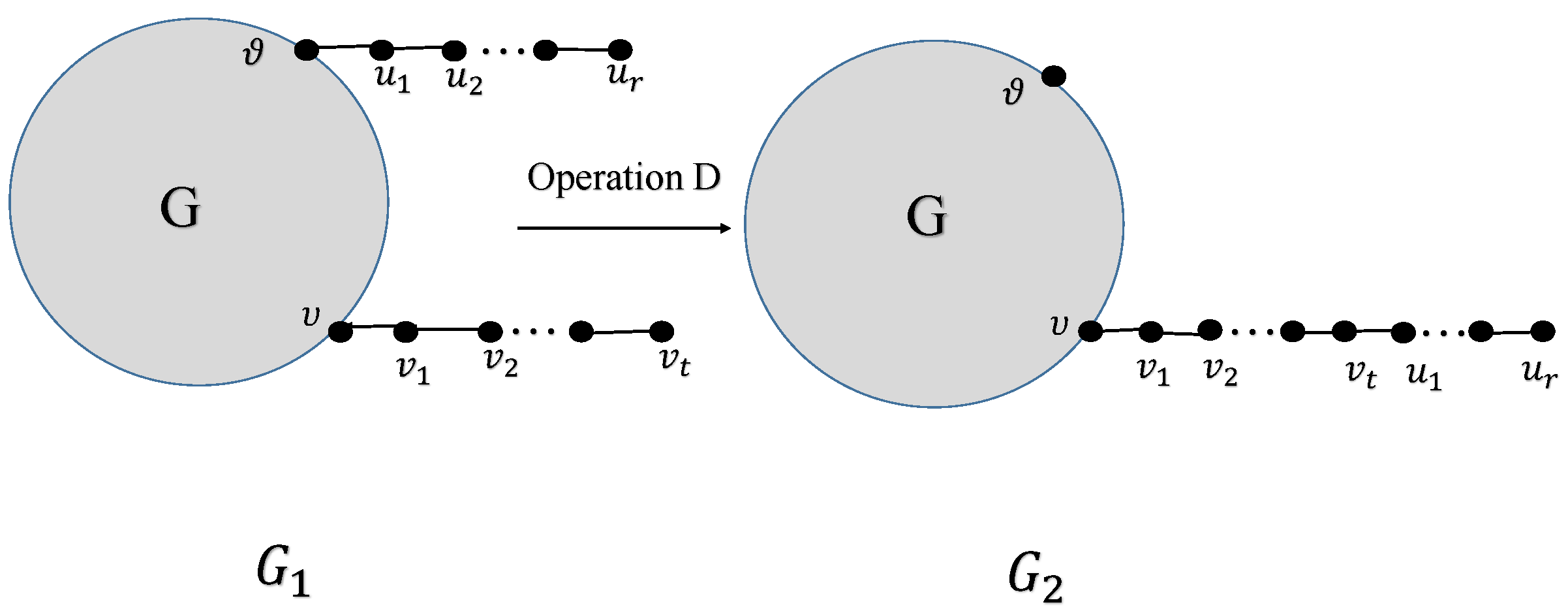
Operation D: Consider graph G and ; let be obtained from G by identifying with and with of the paths and , respectively. Let be obtained from by removing and adding as in Figure 21.
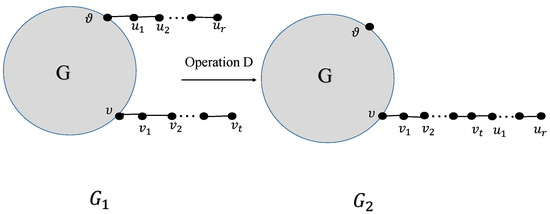
Figure 21.
Sketch for Operation D.
Lemma 8.
Suppose that and are the graphs in Figure 21 with , and ; then,
- (i)
- If , then ;
- (ii)
- If and , then .
Proof.
(i) Here, we have to note that and ; the following cases are considered:
Case 1. If and .
In this case, we have the following value for :
Similarly, for , we have the following:
Consider the difference between and , as in the following:
Hence, in this case, we have that .
Case 2. If and .
In this case, we have the following value for :
Similarly, for , we have the following:
Consider the difference between and , as in the following:
Hence, in this case, we have that .
Case 3. If and .
In this case, we have the following value of for :
Similarly, for , we have the following:
Consider the difference between and , as in the following:
Hence, in this case, we have .
Case 4. If and .
In this case, we have the following value of for :
Similarly, for , we have the following:
Consider the following difference:
In this case, we have that ; hence, .
(ii). If and , if and are adjacent vertices, then we have the following values for .
Similarly, for , we have the following:
Consider the difference between and , as in the following:
Hence, we have .
Similarly, if and are adjacent, then
Similarly, for , we have
Now, consider the difference as in the following:
Hence, we have that , which shows that . □
Remark 4.
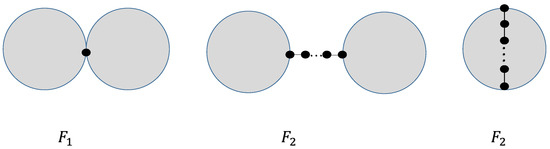
After continuous use of operation C , if we use operation D continuously, any tree can be operated on and changed to a path, any graph having one cycle can be changed to a graph having one cycle where the path is attached to the cycle and any graph having two cycles can be transformed into a graph having two cycles where the path is attached to one of the graphs in Figure 22 (Lemma 8(i)). More generally, the bi-cyclic graph can be transformed into a bi-cyclic graph where the path is attached to one of the vertices of degree 2 (Lemma 8(ii)), and the general power-sum connectivity index decreases.

Figure 22.
Sketch for , and .
Lemma 9.
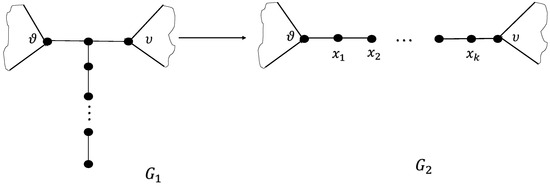
Let be the graph in Figure 23; if there is a path , where , attached to the vertex . Let be obtained from by deleting and adding ; then, .

Figure 23.
Sketch for Lemma 9.
Proof.
Here, we observe that the degree of and varies; if , then
Similarly, for , we have
Consider the difference between and , as in the following:
If , then we have for
Similarly, for , we have
Consider the difference between and , as in the following:
Hence, the difference in both the cases if and . This shows that . □
The Minimum General Power-Sum Connectivity Index in Trees, and Uni-Cyclic and Bi-Cyclic Graphs
This section is devoted to the minimum general power-sum connectivity index in trees, and uni-cyclic and bi-cyclic graphs; from Lemma 7, we have the following:
Theorem 9.
Suppose that T is any tree having order n; if T is not , then .
Suppose that is a uni-cyclic graph which is obtained by means of a path of length to cycle . Using Lemmas 7 and 8, we have the following:
Theorem 10.
Suppose that G is any uni-cyclic graph having girth k and order n; if G is not , then .
By means of Lemma 9, we have the following:
Theorem 11.
is the unique graph of order n having the smallest general power-sum connectivity index.
Consider the graphs , and as in Figure 22; from Lemmas 7 and 9, the bi-cyclic graph having the smallest general power-sum connectivity index is one of , and where
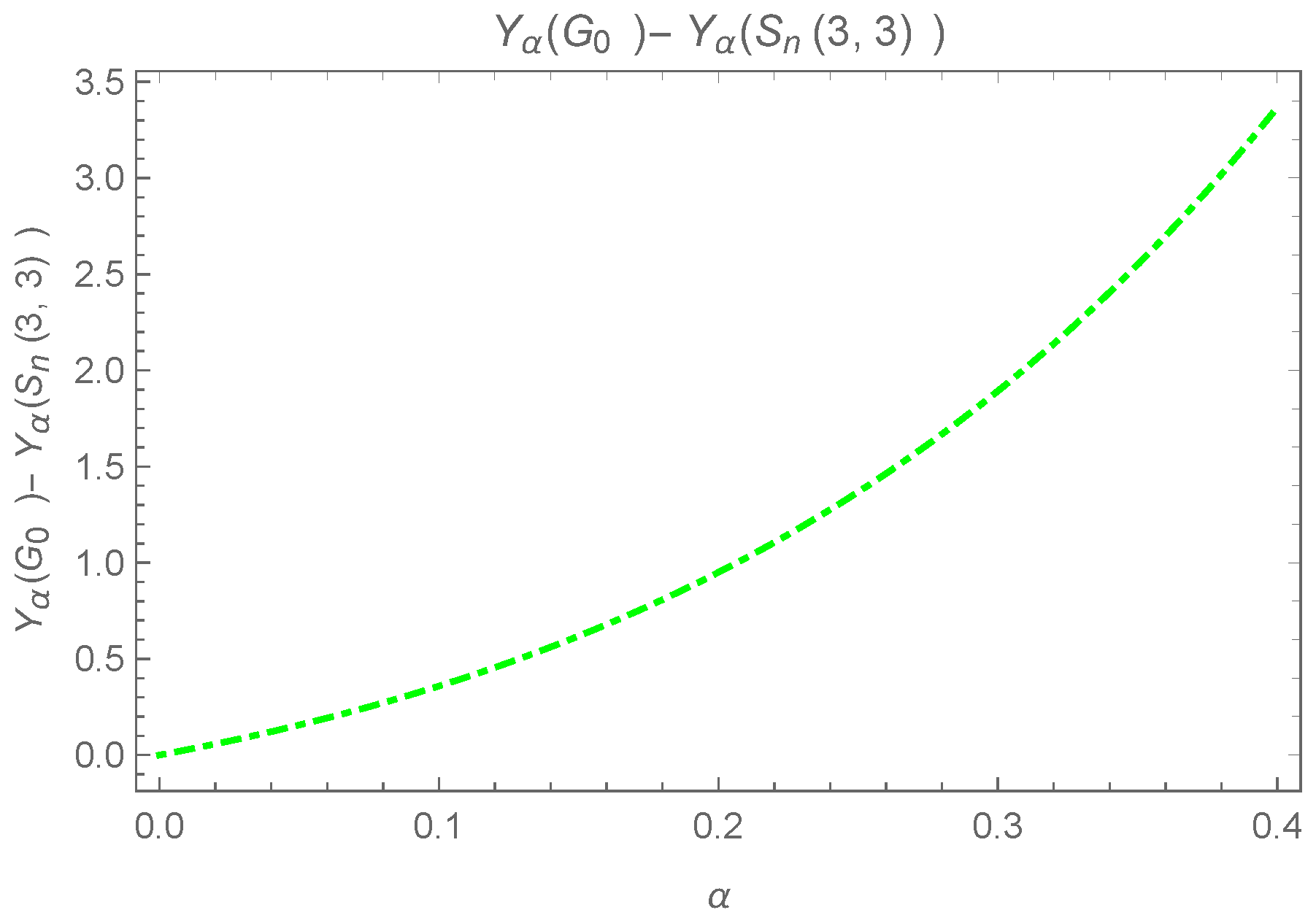
Consider the difference in the following:
The above last inequality can be observed in Figure 24.
The last inequality can be observed in Figure 25.
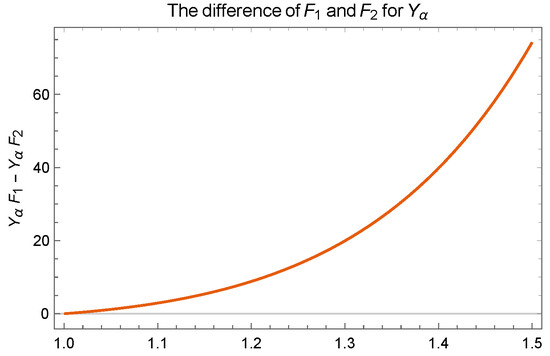
Figure 24.
Plot for .
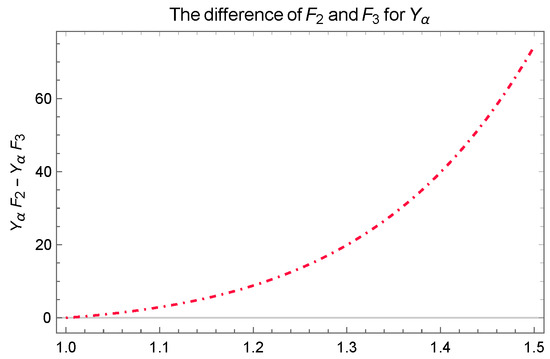
Figure 25.
Sketch for .
Hence, we have the following theorems:
Theorem 12.
Let G be the family of bi-cyclic graphs having order n; then, the largest general power-sum connectivity index is for the graph .
Theorem 13.
Let G be the family of bi-cyclic graphs having order n; then, the smallest general power-sum connectivity index is for the graph where the vertices of degree 3 are not adjacent, that is, .
4. Conclusions
In this article, the general power-sum connectivity index is consider for optimal values. Various operations were used for optimal graphs in the family of uni-cyclic graphs, bi-cyclic graphs and trees. The desired operations were very interesting and simple in use. The largest values of the desired index in the stated families are obtained by means of Operation A and Operation B, while Operation C and Operation D are used for the smallest values. For the comparison of results, various plots are provided for the greatest and smallest values of the general power-sum connectivity index.
Author Contributions
All the authors contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rosen, K.H. Discrete Mathematics and Its Applications; McGraw-Hill: New York, NY, USA, 2019. [Google Scholar]
- Balakrishnan, V.K. Schaum’s Outline of Theory and Problems of Graph Theory; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Mircea, V.D.; Gutman, I.; Jantschi, L. Molecular Topology; Nova Science Publishers: Huntington, NY, USA, 2001. [Google Scholar]
- Mahasinghe, A.C.; Erandi, K.K.W.H.; Perera, S.S.N. Optimizing Wiener and Randić Indices of Graphs. Adv. Oper. Res. 2020, 2020, 3139867. [Google Scholar] [CrossRef]
- Ivan, G.; Mohar, B. The quasi-Wiener and the Kirchhoff indices coincide. J. Chem. Inf. Comput. Sci. 1996, 36, 982–985. [Google Scholar]
- Evelien, O.; Rousseau, R. Social network analysis: A powerful strategy, also for the information sciences. J. Inf. Sci. 2002, 28, 441–453. [Google Scholar]
- Muhammad, I.; Hayat, S.; Mailk, M.Y.H. On topological indices of certain interconnection networks. Appl. Math. Comput. 2014, 244, 936–951. [Google Scholar]
- Kier, L.B. Indexes of molecular shape from chemical graphs. Med. Res. Rev. 1987, 7, 417–440. [Google Scholar] [CrossRef] [PubMed]
- Camarda, K.V.; Maranas, C.D. Optimization in polymer design using connectivity indices. Ind. Eng. Chem. Res. 1999, 38, 1884–1892. [Google Scholar] [CrossRef]
- Matamala, A.R.; Estrada, E. Generalised topological indices: Optimisation methodology and physico-chemical interpretation. Chem. Phys. Lett. 2005, 410, 343–347. [Google Scholar] [CrossRef]
- Preuß, M.; Dehmer, M.; Pickl, S.; Holzinger, A. On terrain coverage optimization by using a network approach for universal graph-based data mining and knowledge discovery. In Brain Informatics and Health, Proceedings of the International Conference, BIH 2014, Warsaw, Poland, 11–14 August 2014; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Che, Z.; Chen, Z. Lower and upper bounds of the forgotten topological index. MATCH Commun. Math. Comput. Chem. 2016, 76, 635–648. [Google Scholar]
- Juan, M.; Rada, J. Sharp upper and lower bounds of VDB topological indices of digraphs. Symmetry 2021, 13, 1903. [Google Scholar] [CrossRef]
- Martínez-Pérez, Á.; Rodríguez, J.M. New bounds for topological indices on trees through generalized methods. Symmetry 2020, 12, 1097. [Google Scholar] [CrossRef]
- Martínez-Pérez, Á.; Rodríguez, J.M. Upper and lower bounds for topological indices on unicyclic graphs. Topol. Its Appl. 2023, 339, 108591. [Google Scholar] [CrossRef]
- Wei, C.C.; Salman, M.; Ali, U.; Rehman, M.U.; Ahmad Khan, M.A.; Chaudary, M.H.; Ahmad, F. Some topological invariants of graphs associated with the group of symmetries. J. Chem. 2020, 2020, 6289518. [Google Scholar] [CrossRef]
- Chu, P.; Li, Y.; He, Z.; Li, E.; Ozgun, O.; Vandenbosch, G.A.; Zheng, X. A group theory based topology optimization scheme for the design of inhomogeneous waveguides with dihedral group symmetries. Eng. Anal. Bound. Elem. 2024, 166, 105845. [Google Scholar] [CrossRef]
- Öztürk Sözen, E.; Alsuraiheed, T.; Abdioğlu, C.; Ali, S. Computing Topological Descriptors of Prime Ideal Sum Graphs of Commutative Rings. Symmetry 2023, 15, 2133. [Google Scholar] [CrossRef]
- Balasubramanian, K. Topological indices, graph spectra, entropies, Laplacians, and matching polynomials of n-dimensional hypercubes. Symmetry 2023, 15, 557. [Google Scholar] [CrossRef]
- Kosaka, I.; Swan, C.C. A symmetry reduction method for continuum structural topology optimization. Comput. Struct. 1999, 70, 47–61. [Google Scholar] [CrossRef]
- Cheng, R.; Ali, G.; Rahmat, G.; Khan, M.Y.; Semanicova-Fenovcikova, A.; Liu, J.B. Investigation of General Power Sum-Connectivity Index for Some Classes of Extremal Graphs. Complexity 2021, 2021, 6623277. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).