Abstract
Differential evolution (DE) is one of the most promising black-box numerical optimization methods. However, DE algorithms suffer from the problem of control parameter settings. Various adaptation methods have been proposed, with success history-based adaptation being the most popular. However, hand-crafted designs are known to suffer from human perception bias. In this study, our aim is to design automatically a parameter adaptation method for DE with the use of the hyper-heuristic approach. In particular, we consider the adaptation of scaling factor F, which is the most sensitive parameter of DE algorithms. In order to propose a flexible approach, a Taylor series expansion is used to represent the dependence between the success rate of the algorithm during its run and the scaling factor value. Moreover, two Taylor series are used for the mean of the random distribution for sampling F and its standard deviation. Unlike most studies, the Student’s t distribution is applied, and the number of degrees of freedom is also tuned. As a tuning method, another DE algorithm is used. The experiments performed on a recently proposed L-NTADE algorithm and two benchmark sets, CEC 2017 and CEC 2022, show that there is a relatively simple adaptation technique with the scaling factor changing between 0.4 and 0.6, which enables us to achieve high performance in most scenarios. It is shown that the automatically designed heuristic can be efficiently approximated by two simple equations, without a loss of efficiency.
MSC:
90C26; 90C59; 68T20
1. Introduction
Single-objective numerical optimization methods for black-box problems represent a direction that is thoroughly studied in the evolutionary computation (EC) area. The reason for this is that evolutionary algorithms do not require any specific information about the target function except the possibility to calculate it, i.e., they are zero-order methods. First attempts to solve such problems with evolutionary algorithms were made with the classical Genetic Algorithm (GA), which searched the binary space [1]; however, later, more efficient approaches were proposed, including simulated binary crossover [2], as well as other nature-inspired methods, such as Particle Swarm Optimization [3]. However, in recent years, most of the researchers’ attention is toward the differential evolution (DE) algorithm [4].
The reasons for DE’s popularity are diverse and include simplicity in both understanding and realization and high performance across many domains and applications [5,6,7]. The high performance of DE is due to its implicit adaptation to the function landscape, which originates from the main idea—difference-based mutation. However, the performance of DE comes with a drawback: the few parameters of the algorithm, namely, the population size N, scaling factor F and crossover rate , should be carefully tuned, and most of the research on DE is focused on determining the best possible ways of tuning these parameters during the algorithm’s work [8].
This study focuses on finding a method for the automatic tuning of the most sensitive parameter, scaling factor F. Today, the most popular adaptation technique is success history-based adaptation (SHA), proposed 10 years ago in the SHADE algorithm [9]. However, despite the gradual improvements [10], there are possibilities to design even better adaptation methods. This paper is a follow-up work to a recent study [11], where success rate-based adaptation was proposed, and the surrogate-assisted search for Taylor series coefficients for F, and N was performed using the Efficient Global Optimization (EGO) algorithm [12]. Here, a similar hyper-heuristic approach is considered; however, instead of EGO, another differential evolution is applied on the upper level, and additional parameters are introduced to increase the flexibility of the approach. In particular, the scale parameter of Student’s t random distribution for sampling F values is also tuned, as well as the number of degrees of freedom. The experiments, performed with the L-NTADE algorithm [13] on two sets of test problems taken from the Congress on Evolutionary Computation (CEC) competition on numerical optimization 2017 [14] and CEC 2022 [15], demonstrated that the new approach enables us to find simpler and more efficient adaptation techniques.
The main contributions of this study can be outlined as follows:
- Setting the lower and upper border for the Taylor series when tuning the curve parameters for success rate-based scaling factor sampling improves flexibility and allows for finding a simpler dependence;
- The number of degrees of freedom, found by the proposed approach, places the Student’s distribution between the usually applied normal and Cauchy distributions;
- The DE algorithm applied instead of the EGO algorithm on the upper level is capable of finding efficient solutions, despite the problem complexity and dimension;
- The Friedman ranking procedure, used instead of the total standard score for heuristics comparison during a search, is a good alternative with comparable performance and does not require any baseline results;
- The designed heuristic for scaling factor adaptation is simple and can be efficiently applied to many other DE variants.
The rest of this paper is organized as follows. The next section describes the background studies; in the third section, the related works are discussed; in the fourth section, the proposed approach is described; the fifth section contains the experiments and results; and the sixth section contains the discussion, followed by the conclusion.
2. Background
2.1. Differential Evolution
The numerical optimization problem in a single-objective case consists of the search space , real-valued function f: and a set of bound constraints:
subject to , where is the vector of the lower boundaries, is the vector of the upper boundaries and D is the problem dimension. As bound constraints are easily satisfied, such problems are often called unconstrained. In this study, the black-box scenario is considered, which means that there is no information about the structure or properties of the function , so that it can be multimodal, non-convex, ill-conditioned, etc. The gradient is also not available.
Differential evolution starts by initializing a set of N D-dimensional vectors , randomly using uniform distribution within , .
After initialization, the main loop of the algorithm starts with the first operation called the difference-based mutation. There are many known mutation strategies, such as rand/1, rand/2, best/1 and current-to-rand/1, but the most popular is the current-to-pbest/1 strategy:
where F is the scaling factor parameter, is the newly generated mutant vector, and are the uniformly randomly chosen indexes of the vectors in the range and is chosen from the best of the individuals, , . Same as most evolutionary algorithms, DE relies on two variation operations: mutation and crossover. The crossover mixes the genetic information of the target vector and the newly generated mutant vector ; as a result, the trial vector is generated. The most popular scheme is the binomial crossover, which works as follows:
where is the crossover rate parameter, and is a random index in required to make sure that at least one solution is taken from the mutant vector. The trial vector is checked to be within the search boundaries; one of the popular methods to perform this is called the midpoint target:
After this step, the trial vector is evaluated using target function and compared to the target vector in the selection step:
At the end of the generation, some of the individuals may be replaced, and due to the selection step, the average fitness either increases or stays the same.
2.2. Parameter Adaptation in Differential Evolution
As mentioned in the Introduction, most of the works on DE are directed toward parameter adaptation and control methods [8]. The reason for this is that DE is highly sensitive to the F and settings, and one of the earliest studies that considered this problem was [16], where the authors proposed the jDE algorithm with the parameter values adapted as follows:
where and are the lower and upper boundaries for F, and and control the frequency of the F and changes, usually set to . If the trial vector is better, then the new parameter values are saved. The modifications of jDE have proven themselves to be highly competitive, for example, jDE100 [17] and j2020 [18] demonstrated high efficiency on bound-constrained test problems.
Despite the efficiency of jDE, nowadays, success history-based adaptation is one of the widely used methods [9], based on the originally proposed JADE algorithm [19]. Here, the working principle of SHA will be described.
Success history-based adaptation tunes both the scaling factor F and crossover rate . At the initialization step, a set of H memory cells and is created, each containing a constant value, such as 0.5. The values in the memory cells are used to sample the F and values to be used in the mutation and crossover as follows:
where is a Cauchy-distributed random value with location parameter m and scale parameter s; is a normally distributed random value with mean m and standard deviation s. In the SHADE algorithm, if the sampled , then it is generated again, and if , it is set to 1. The value is simply truncated to a interval. The index k of the memory cell to be used is generated randomly in . Note that the Cauchy distribution has “heavier tails”, i.e., it generates larger and smaller values more often compared to normal distribution—this gives more diverse F values.
During every selection step, if the newly generated trial vector is better than , then the F and values are stored in and , as well as the improvement value stored in . At the end of the generation, the new values updating the memory cells are calculated using the weighted Lehmer mean:
where . Two values are calculated, i.e., one using and another using . The memory cell with index h, iterated from 1 to H every generation, is updated as follows:
The SHA confirm and modify. Following highlights are same issue. method uses biased parameter adaptation, i.e., in the Lehmer mean in the nominator, the successful values are squared; thus, the mean is shifted toward larger values. In this study, the Lehmer mean was modified by introducing an additional parameter :
Increasing the parameter leads to more skewed means toward larger values. The standard setting in L-SHADE is , and it is shown that increasing this value and generating a larger F may lead to much better results in high-dimensional problems.
For the population size N, the third main parameter of DE, the following technique was proposed in the L-SHADE algorithm [20]:
where is the current number of target function evaluations, is the total available computational resource, and are the initial and final number of individuals and g is the generation number. This method called linear population size reduction (LPSR) has the main idea of spreading across the search space at the beginning and concentrating at the end of the search. LPSR allows for achieving significant improvements in performance, if the computational resource limit is known. In such a scenario, it makes sense to use a broader search at the beginning and more concentrated effort at the end. That is, if the computational resource is running out, it is better to converge to at least some good solution quickly with a small population rather than continuing a broad and slow search, hoping to get to the global optimum. Although the usage of LPSR may seem to contradict the global optimization setup, in a recent competition on global numerical optimization with unlimited resources [21], it was shown that algorithms with LPSR have some of the best performance characteristics.
In [22], it was shown that adding tournament or rank-based selection strategies to sample the indexes of individuals for further mutation may be beneficial. The exponential rank-based selection was implemented by selecting an individual depending on its fitness in a sorted array, with the ranks assigned as follows:
where is the parameter controlling the pressure, and i is the individual number. Larger ranks are assigned to better individuals, and a discrete distribution is used for selection.
The L-SHADE algorithm has become very popular among DE methods, and most of the prize-winning algorithms since 2014 are its variants and modifications, including jSO with specific adaptation rules [23], L-SHADE-RSP with selective pressure [24], DB-LSHADE with distance-based adaptation [25] and a recently proposed L-NTADE [13], which also relies on SHA and LPSR. There are other techniques, for example, the jDE algorithm [16] and its modifications, such as j100 [17] and j2020 [18], that have shown competitive results, but they are not as popular as SHADE. Nevertheless, in [11,26], it was shown that more efficient adaptation techniques can be proposed.
Other modifications of modern DE include the Gaussian–Cauchy mutation [27], modifications for binary search space [28], population regeneration in the case of premature convergence [29] and using an ensemble of mutation and crossover operators [30].
2.3. L-NTADE Algorithm
As a baseline approach, here the recently proposed L-NTADE algorithm [13] is considered. The main idea of L-NTADE is to diverge from the relatively general scheme of modern DE, where a single population is present, with an optional external archive of inferior solutions. Unlike these methods, L-NTADE uses two populations, one containing the best N individuals in found throughout the search and another containing the latest improved solutions in , . The mutation strategy used in L-NTADE is a modification of the current-to-pbest called r-new-to-ptop/n/t, with individuals taken from the top and newest populations as follows:
where and are random indexes, sampled with uniform distribution, and is sampled with rank-based selective pressure, with ranks assigned as , wherein is a parameter. More detailed research on the effects of selective pressure in DE is given in [22]. The index is chosen from the best solutions from the top population. Note that unlike current-to-pbest, the basic solution is not the same as in the first difference, i.e., index is different from i—in this sense, r-new-to-ptop/n/t is more similar to the rand/1 mutation.
The crossover step in L-NTADE is unchanged, i.e., the classical binomial crossover is applied, whereas the selection step is changed significantly:
where is iterated from 1 to N. The newly generated trial vector is compared not to the target vector but to the basic vector , which was chosen randomly. Moreover, a different individual with index is replaced as a result. This gives the effect of a continuous update of the newest individuals’ population. At the same time, to preserve the best solutions, the top population is updated in the following order. All the successful trial vectors are stored into a temporary population , and at the end of the generation, a joined set of and is formed, sorted by fitness, and the best N individuals are chosen to stay in . The population size control in L-NTADE is realized using the LPSR method, with both the newest and top population reducing the size in the same way.
2.4. Hyper-Heuristic Approach
The development of meta-heuristic approaches nowadays is mainly performed by researchers manually, i.e., new ideas are proposed, implemented and tested. However, the idea of automating this process has been discussed in the literature for several years. In particular, the so-called hyper-heuristic approach (HH) is considered [31], when some method, such as, for example, genetic programming (GP), is used to design new operators or even entire algorithms. There exist generative hyper-heuristics and selection hyper-heuristics, with the last used to configure a meta-heuristic algorithm. The generative hyper-heuristics are sometimes referred to as the automated design of algorithms (ADAs) or genetic improvement (GI) [32]. With modern computational capabilities, the HH approach opens possibilities of discovering new algorithmic ideas in an automated manner, thus significantly moving the whole field further. More details on the application of HH are given in the next section.
3. Related Work
Differential evolution is a highly competitive numerical optimizer, which has proven its efficiency across a variety of applications. Moreover, in the last 10 years, competitions on numerical optimization have been won by DE or its hybrids with other methods, such as CMA-ES (for example, the LSHADE-SPACMA performed well on the CEC 2017 benchmark) [33]. However, despite all these achievements, there is still room for further improvement. Success history adaptation, proposed in SHADE, is a method, which has proven its efficiency, delivering significant improvements.
One of the ways to propose new ideas for parameter adaptation is to use automated search methods. An attempt to create a new parameter adaptation technique with the hyper-heuristic approach was made in [26], where genetic programming for symbolic regression was used to create equations for adapting F and in DE. In particular, it was shown that it is possible to develop relatively simple and yet efficient methods, which are significantly different from success history-based adaptation.
The experiments with the L-NTADE algorithm, aimed at designing new adaptation techniques for an algorithm, whose general scheme is different from L-SHADE, were performed in [34]. In particular, it was found that the success rate, i.e., the number of improvements in the current generation divided by the population size (), is an important source of information for parameter adaptation. This value was included in the study where GP was used [26]; the connection was less obvious there. It is worth mentioning that the success rate is rarely used in evolutionary computation for parameter adaptation.
In an attempt to further explore the possible influence of and derive the important dependencies, in [11], the surrogate-assisted approach was proposed. In particular, a 10th-order Taylor series expansion was used to allow for a flexible tuning of the curve, which uses to determine the mean value for sampling F. It was shown that it is possible to find such curves and that the efficiency of DE can be greatly improved. However, this method had several disadvantages. First of all, as a higher-level optimizer, which searches for Taylor series coefficients, the surrogate-assisted method Efficient Global Optimization (EGO) was applied [12]. Although this is a well-performing method, which allowed for finding interesting solutions, it is not very suitable for this particular problem. The main reason is that the evaluation of a set of Taylor series parameters, determining the parameter adaptation technique, is a noisy function, i.e., it requires running an algorithm, which uses random values. The total standard score, used as the target function in [11], is not very suitable for Kriging approximation. Considering these drawbacks, a new approach was developed, which will be described in the next section.
4. Proposed Approach
4.1. Scaling Factor Sampling
The two main ideas of this study are to change the optimization tool, used on the upper level, and to replace the solution evaluation method. The hyper-heuristic approach may use any optimization tool, for example, genetic programming, to search for parameter adaptation techniques directly or EGO to tune the Taylor series parameters. In particular, in this study, the success rate parameter is used as a source of information for tuning the scaling factor parameter F. The success rate is calculated every generation as follows:
where is the number of successful replacements in the selection operation. The main idea of [11] was to use a Taylor series to approximate the dependence between and location parameter (mean F) for F sampling. The Taylor polynomials are used as function approximations using derivatives; however, as here the true dependence is unknown, the coefficients can be derived via computational experiments. The Taylor expansion is used due to the flexibility of the polynomials. The method consists of calculating the raw value and then normalizing it to a interval and scaling it. The first step is performed as follows:
where , are the coefficients to be found, and is a raw, non-normalized value. To perform the normalization, i.e., scale to the range, the minimum and maximum values are used:
where and are found by searching (via lattice search with step ) in , and is a scaled value. After this, an additional step is proposed in this study. To allow for a more flexible adaptation, the lower and upper boundaries for the fitted curve should also be tuned and not just set to . To perform this, the final value is calculated as follows:
where and are the lower and upper boundaries for . That is, if, say, and , then the curve, which depends on the success rate , will be in the range . This results in a pair of additional parameters added to those that should be optimized. The value is then used in Student’s t distribution instead of a Cauchy or normal one:
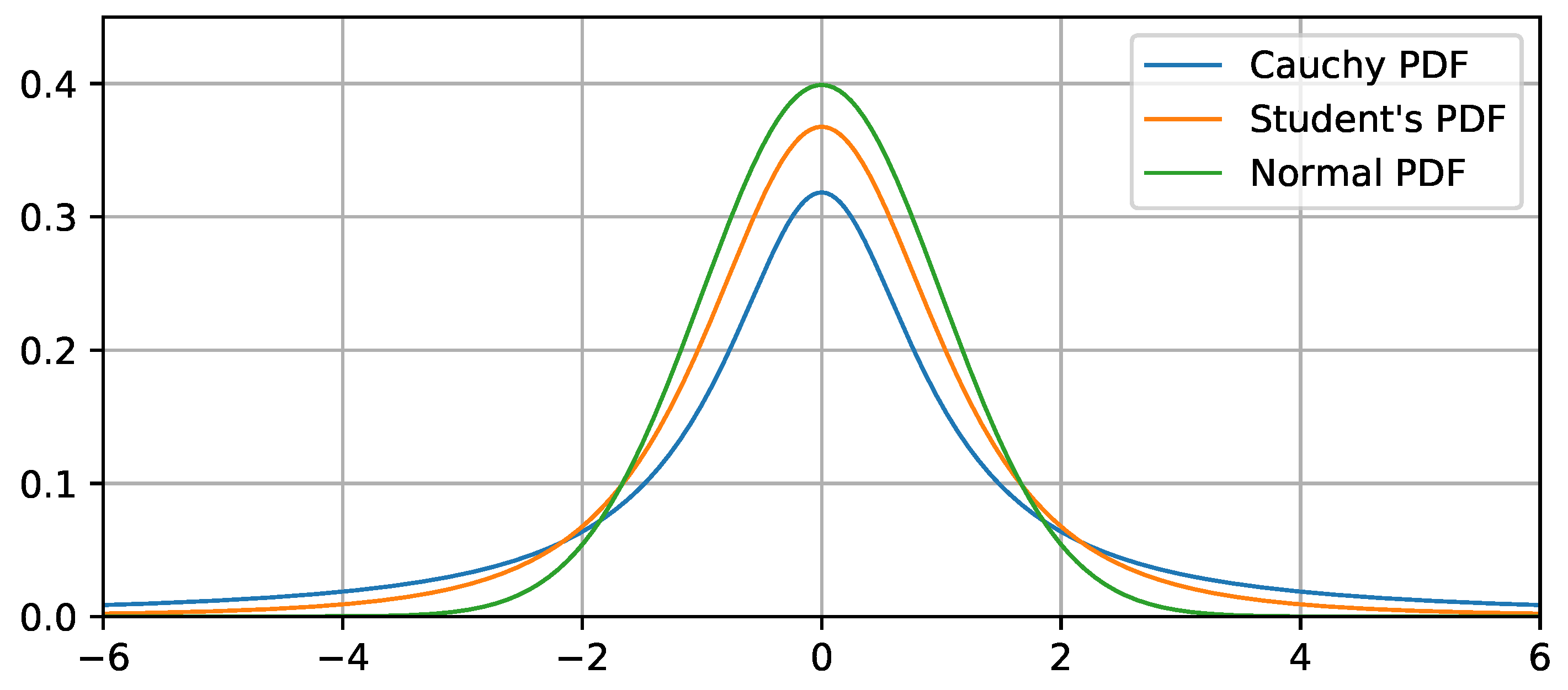
where is a Student’s t-distributed random value with a location parameter m, scale parameter s and number of degrees of freedom ; is another tuned parameter; and is a scale parameter (). The reason to use Student’s distribution is that it is a more general distribution, which is capable of becoming a Cauchy distribution when and a normal distribution when ( is enough in practice). When is small, the t distribution is heavy-tailed, i.e., more similar to Cauchy. Modern C++ libraries allow for setting to an arbitrary positive floating-point value, thus allowing us to tune the distribution arbitrarily. Also, note that sampling F is performed with the following rules: while , it is sampled again, and if , it is set to 1. Figure 1 shows the comparison of the normal, Cauchy and Student’s distribution.
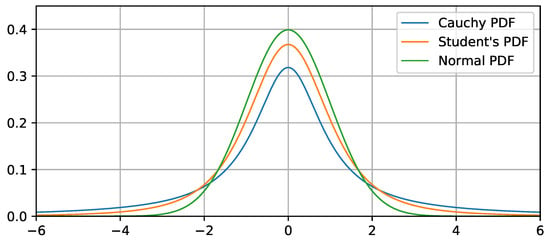
Figure 1.
Comparison of normal, Student’s () and Cauchy distributions.
To allow for even greater flexibility for the approach, the scale parameter is also tuned in the same way as . That is, another set of coefficients is used to determine the dependence of on the success rate . For clarity, we provide below the equations to calculate .
Equations (16)–(18) are the same as (12)–(14), but for a different parameter, and the resulting and values are used in (15). The search for and for normalization is performed in the same manner, i.e., with a lattice search with a step value of . It is important to tune the scale parameter, i.e., the width of the distribution, as it significantly influences the distribution of the sampled F values.
Thus, setting 12 parameters for a Taylor series curve plus two more for lower and upper boundaries gives a total of 14 values for . Another 14 are used to set and one more to tune the number of degrees of freedom . This gives a total of 29 numeric values, which should be set in order to determine the adaptation method in a 29-dimensional search space. The search for the optimal set of 29 parameters is described in Section 4.2, where each set of values corresponds to a specific adaptation heuristic, which is evaluated. The search itself is performed by another DE algorithm, L-SRDE.
4.2. Evaluating Designed Heuristics
The evaluation of the designed heuristic is an important step for determining its efficiency, and the evaluation method significantly influences the search for better heuristics. In [11], the idea was to apply statistical tests to evaluate the efficiency of an algorithm with a designed heuristic with a single numeric value. In particular, the baseline results were obtained, i.e., the L-NTADE algorithm was tested with success history parameter adaptation, and then the new results were compared to it. The comparison involved applying the Mann–Whitney statistical test to every function so that the best found target function values were compared. There are 51 independent runs in the CEC 2017 competition benchmark, so comparing two samples of 51 values allowed for using normal approximation (with tie-breaking) for the Mann–Whitney U statistics. That is, for every test function out of 30, the standard Z score was calculated. The total score was determined as follows:
where j is the function number. Such a metric gave an averaged evaluation of the adaptation technique, i.e., if two algorithms perform the same on the function, will be close to 0, but if the heuristic performed better, then , and corresponds to a statistical significance level of .
Although such an approach has shown that it is capable of finding efficient solutions, evaluating an adaptation technique across a variety of test functions with a single value creates a bottleneck, i.e., limits the amount of information that the upper-level optimizer receives from testing a newly designed heuristic. In order to overcome this, here, instead of Mann–Whitney tests and the EGO algorithm for optimization, the usage of Friedman ranking and another differential evolution algorithm for tuning coefficients c is proposed. The Friedman ranking is used in the Friedman statistical test to compare not a pair (like in the Mann–Whitney test) but a set of conditions, under which the experiments were performed.
One of the advantages of the classical DE algorithm is that it does not require exact fitness values to work. That is, the selection step only needs to determine if the newly generated individual is better than the target individual with index i. In other words, if there is a method to compare a pair (or rank a population) of solutions, then DE is able to work with this information. Hence, the idea is to use simplified DE to tune the coefficients of the heuristic , and . The main steps can be described as follows.
- Initialize the population of 29-dimensional vectors randomly, with N individuals.
- Pass the parameters c to the L-NTADE algorithm and run it for every set of coefficients.
- Collect a set of results, i.e., a tensor with dimensions .
- Rank the solutions using Friedman ranking; for this, perform independent ranking for every function and sum the ranks.
- Begin the main loop of DE and use ranks as fitness values; store N new solutions in the trial population .
- Evaluate new individuals in by running the L-NTADE algorithms with the corresponding tuning parameters.
- Join together the results of the current population and and apply Friedman ranking again to the tensor of size .
- If the rank of the trial individual with index i is better than the rank of the target individual, then perform the replacement.
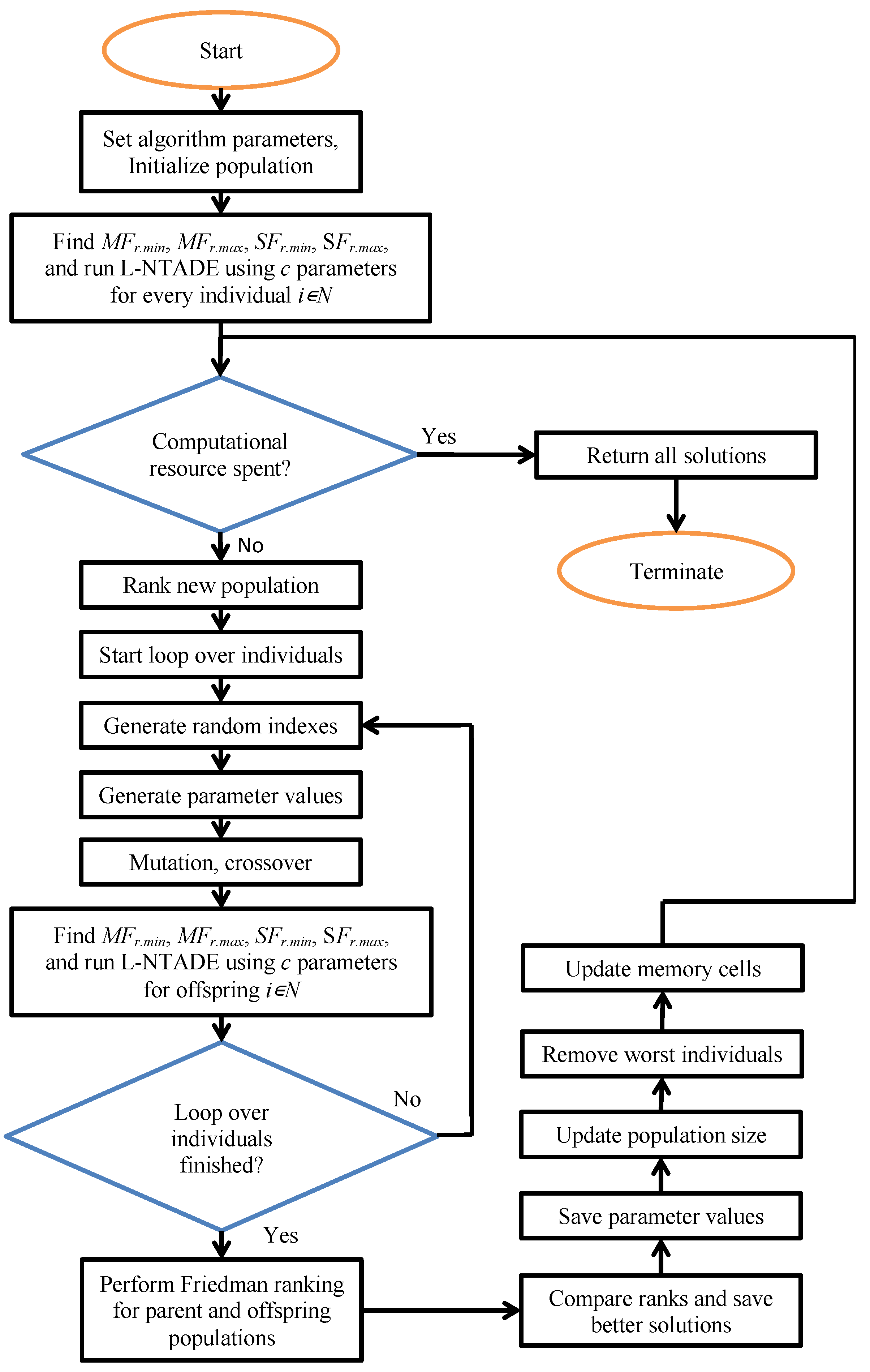
In this manner, the DE algorithm is applied without evaluating the fitness as a single value but rather ranking the best performing heuristics higher. A similar approach using Friedman ranking was used to evaluate the solutions of GP in [26]. That is, there is no single fitness value on the upper optimization level, while the lower level uses the target function value from the benchmark set as fitness. The flow chart of the proposed method is shown in Figure 2.
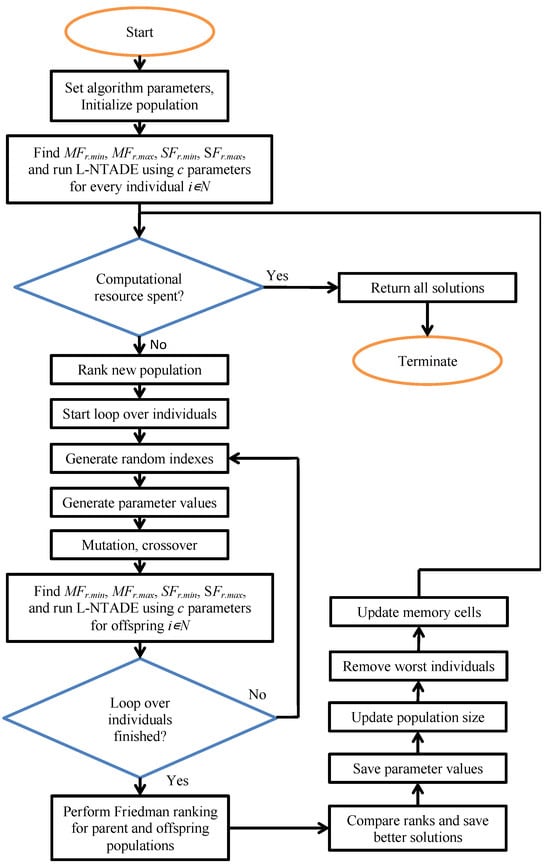
Figure 2.
Flow chart of the proposed approach.
The particular DE used on the upper level here was similar to the L-SHADE algorithm but with several important features for parameter tuning. First, the adaptation of was not performed, and was sampled with normal distribution with parameters and . The scaling factor was set as , i.e., it depended on the success rate as a 4th-order root. The mutation parameter , and the index in the current-to-pbest mutation strategy was sampled using exponential rank-based selective pressure with ranks assigned as . The archive set and the linear population size reduction were also used. This algorithm will be further referred to as L-SRDE (success rate-based DE with LPSR). The exact parameters of all the methods and results are given in the next section.
5. Experimental Setup and Results
5.1. Benchmark Functions and Parameters
The experiments in this study are divided into two phases. In the training phase, the coefficients c are searched by L-SRDE, and in the test phase, the performance of the found dependencies between the success rate and distribution parameters , and is evaluated on different benchmarks.
The two benchmarks used here are the Congress on Evolutionary Computation 2017 single-objective bound-constrained numerical optimization benchmark [14] and the CEC 2022 benchmark [15]. The former has 30 test functions, and according to the competition rules, there should be 51 independent runs made for every function. The dimensions are , 30, 50 and 100, and the available computational resource is limited by the evaluations. In the CEC 2022 benchmark, there are 12 test functions and 30 independent runs, the dimensions are and and the computational resource is bigger and set to and , respectively.
The CEC 2017 and CEC 2022 benchmarks have different evaluation metrics. In particular, in CEC 2017, the measure of algorithm efficiency is simply the best found function value, whereas in CEC 2022 the number of evaluations is also considered. If an algorithm was able to find the solution (with tolerance level ), then the number of evaluations it took on this run is recorded. The algorithms are then compared via the convergence speed and best found value at the same time [35].
In the training phase, the CEC 2017 benchmark is used as it has more diverse functions and a smaller resource, i.e., faster evaluation. The 30-dimensional problems are used, as in the case most of the test functions appear to be too simple for the available resource, and the difference between the parameter adaptation methods is small. The ranking of the solutions during the training phase was performed with the criteria from CEC 2022, i.e., both the convergence speed and best function value were considered.
The parameters for L-SRDE were described above, except for the initial population size, which was set to . The number of function evaluations given to L-SRDE was set to 1000, i.e., there were 1000 heuristics evaluated. The L-NTADE algorithm had the following settings: the initial size of both populations ; mutation strategy parameter ; memory size for SHA ; initial memory values , and ; adaptation bias for the scaling factor in the weighted Lehmer mean ; and selective pressure for the index . These settings were determined in [13] and later used in [11]. When sampling F was replaced by the heuristic, the tuning was still performed by SHA. The search range for c values was set as follows: , , , , , , and . Note that and are only named lower and upper for convenience, and in fact, it is possible that —this will result in flipping the curve.
The L-SRDE algorithm with Friedman ranking was implemented in Python 3.9, and L-NTADE was written in C++. L-NTADE ran on an OpenMPI-powered cluster of eight AMD Ryzen 3700 PRO processors using Ubuntu Linux 20.04. The python code automatically ran the L-NTADE algorithm and collected the results. The post-processing was also performed in Python 3.9.
5.2. Numerical Results
The training phase resulted in 1000 different heuristics evaluated, and each of them was saved independently. The eight best found heuristics and the corresponding curves are shown in Figure 3, and Table 1 contains the lower and upper c values and number of degrees of freedom , as well as the number at which the heuristic was found.
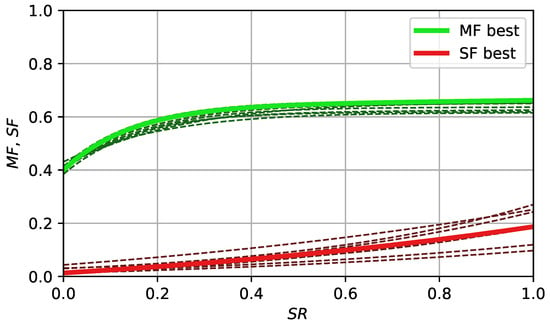
Figure 3.
Curves for parameter adaptation designed by EGO for Taylor series, best found function values used in ranking.

Table 1.
Parameters of eight best heuristics.
As can be seen from Figure 3, the best curves found by L-SRDE are relatively simple, i.e., they all start from around , and when , then it reaches . This is similar to some of the known recommendations about setting F, for example, in [36], quote, “A DE control parameter study by Gamperle et al. (2002) explored DE’s performance on two of the same test functions that Zaharie used and concluded that F < 0.4 was not useful. In Ali and Törn (2000), C–Si clusters were optimized with F never falling below F = 0.4”, end quote [37,38,39]. Thus, the heuristically found parameters are in line with the observations of DE behavior.
As for the spread parameter , its values are smaller than the mostly used . Moreover, there is a dependence between and the success rate : if the success rate is small, then is close to the 0.01–0.05 range, and it increases with an up to . The number of degrees of freedom in Student’s t-distribution is equal to 3, which places it in between the Cauchy distribution () and normal distribution (). The difference between the best eight heuristics is rather small.
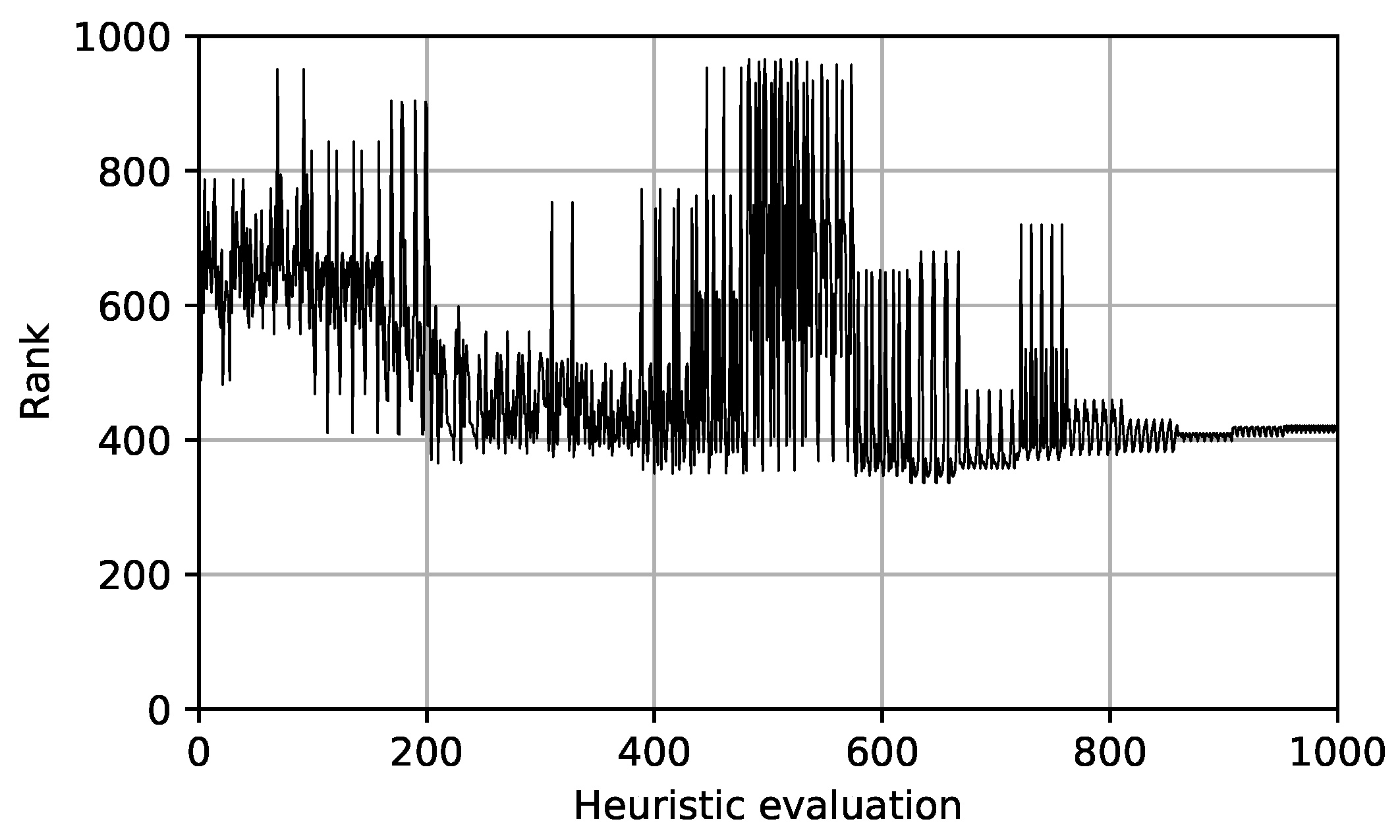
As each set of parameters was described by a vector of the results of the tested heuristic on a set of benchmark functions, it is not possible to plot a convergence curve, like for a classical single-objective optimization problem. However, it is possible to rank all the tested heuristics, and Figure 4 shows the ranks of 1000 evaluated heuristics, compared together with the Friedman ranking in the order in which they were evaluated.
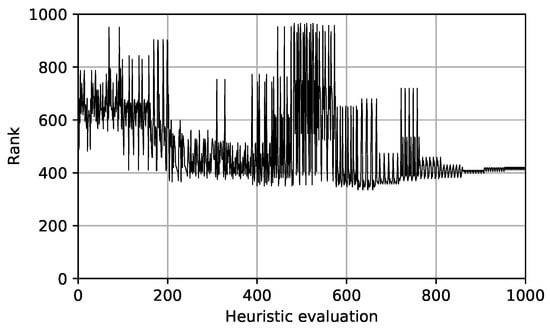
Figure 4.
Ranks of the evaluated heuristics.
From Figure 4, it can be seen that after 600 evaluations, some of the best heuristics were found, and the rest of the time the algorithm was trying to improve these solutions.
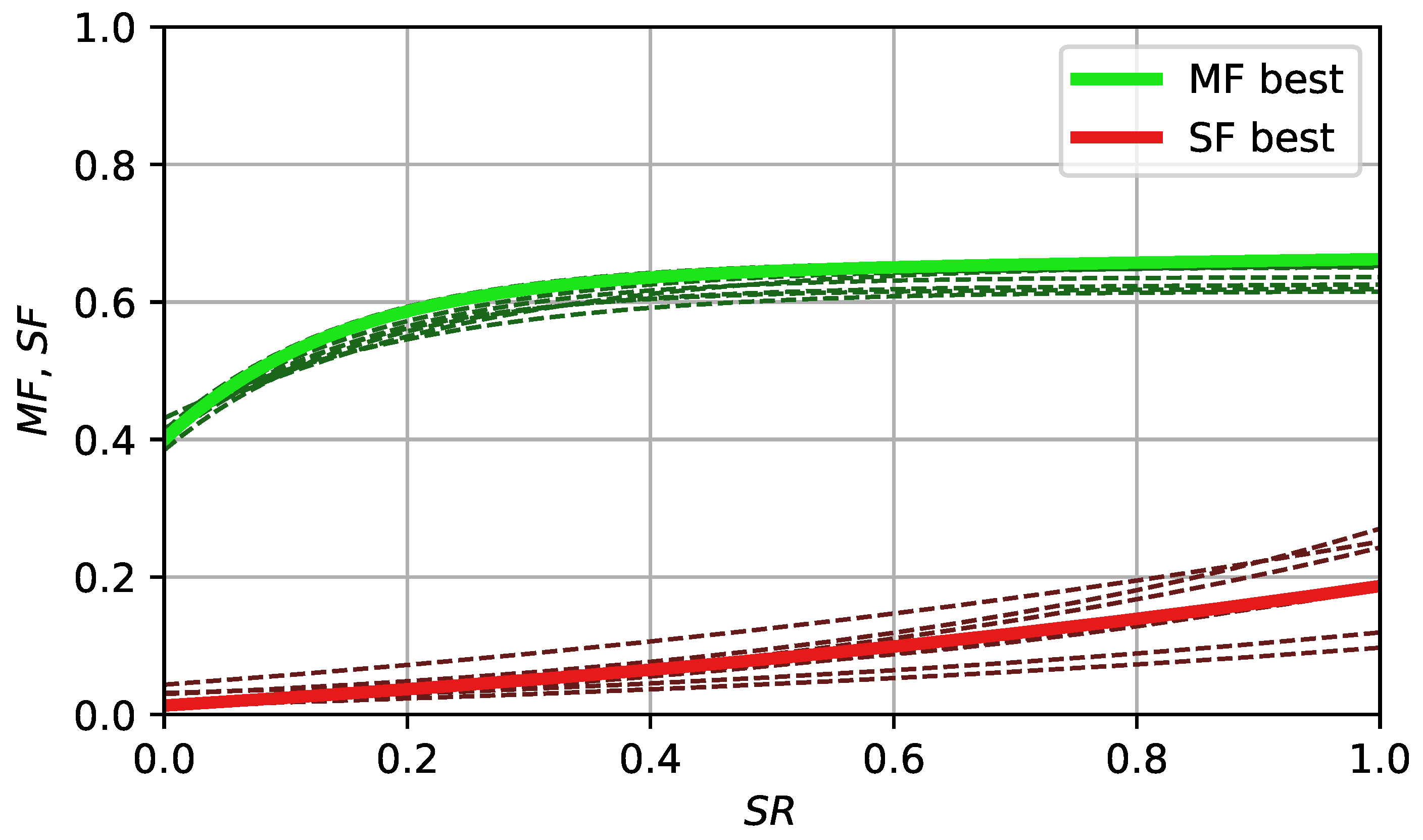
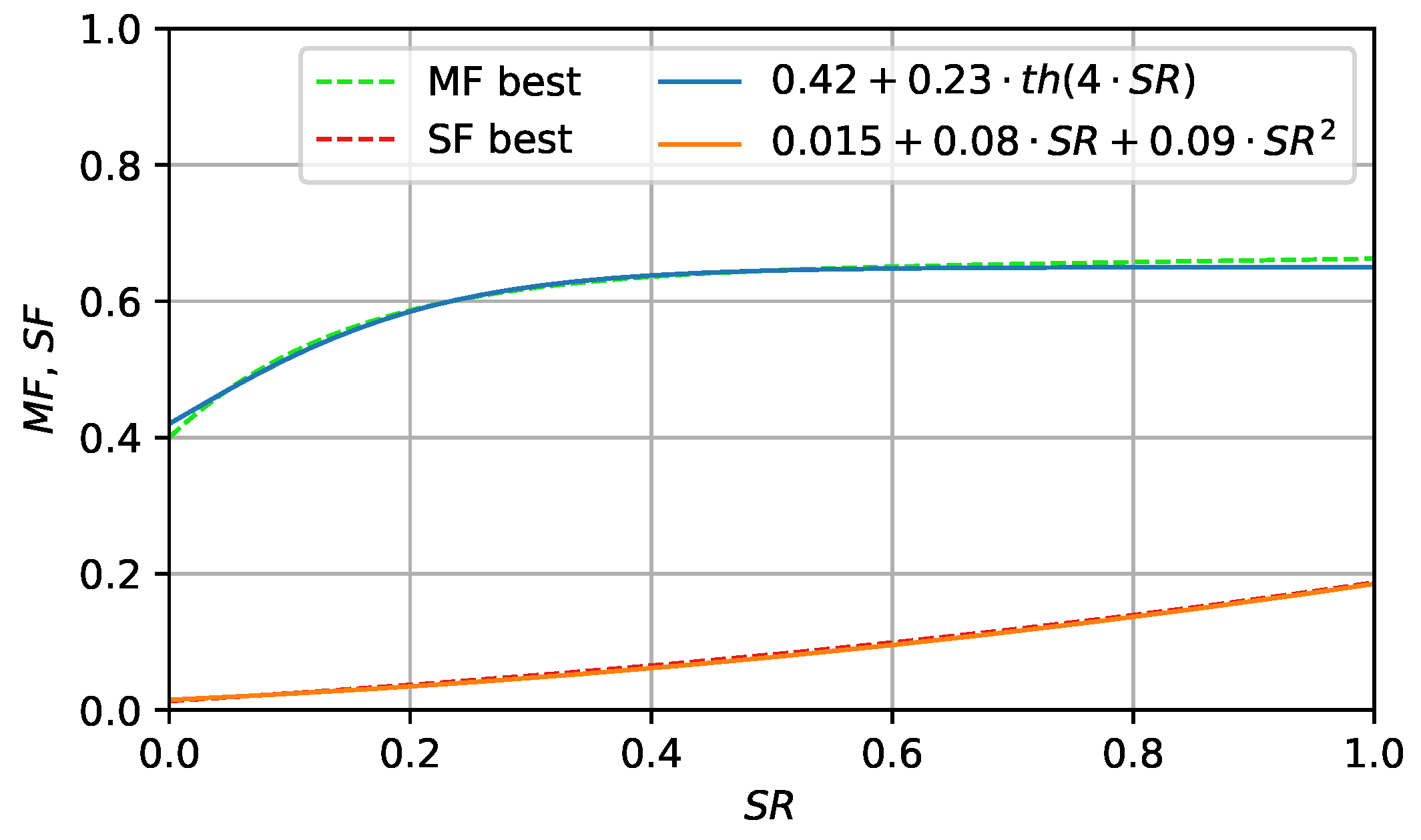
Introducing many hyperparameters into the algorithm may be inefficient, as tuning them is challenging. Such a large number was needed only to allow for significant flexibility of the search, as at the beginning of the experiment we had no knowledge on what the found curves should look like. As Figure 5 shows, the dependence appeared to be relatively simple (represented by two simple equations, which were hand-tuned), so there is no need to use 29 parameters after the learning process.
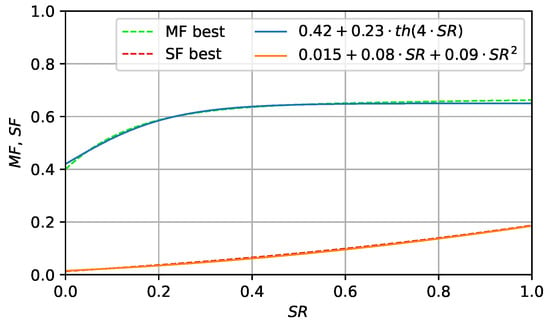
Figure 5.
Approximation of best found curves, applied in L-NTADE-AHF.
The values in Figure 5 are approximated by a hyperbolic tangent function, and the values are approximated with a quadratic function. A version of L-NTADE with these equations was additionally tested on both benchmarks (denoted as L-NTADE-AHF, L-NTADE with approximated heuristic F sampling, and the number of degrees of freedom was set to 3, in accordance with Table 1).
The best heuristic was tested on the whole CEC 2017 benchmark and compared to several alternative approaches. The results are shown in Table 2. For comparison, the Mann–Whitney statistical test was used, and each cell in the table contains the number of wins/ties/losses out of 30 test functions, as well as total standard score .

Table 2.
Mann–Whitney tests of L-NTADE with designed heuristic against alternative approaches, CEC 2017 benchmark, number of wins/ties/losses and total standard score.
As Table 2 demonstrates, the proposed heuristic, applied to L-NTADE, is capable of outperforming the alternative approaches in almost all cases. The L-NTADE-HHF (hyper-heuristic-based F sampling) is better than standard L-NTADE, and the gap in performance increases as the dimension grows. Compared to L-SHADE-RSP, the second best approach from the CEC 2018 competition, L-NTADE-HHF performs similar or better in the case and almost always better in the case. In , the only algorithm that outperformed L-NTADE-HHF is the EBOwithCMAR approach, but it fails in high-dimensional cases. Also, the comparison to the L-NTADEMF algorithm from [11] shows that the newly designed heuristics are more efficient. Table 3 contains the Friedman ranking of the same algorithms.

Table 3.
Friedman ranking of L-NTADE with designed heuristic against alternative approaches, CEC 2017 benchmark.
The comparison in Table 3 shows a similar picture: in the lower-dimensional case, the L-NTADE-HHF is comparable to other algorithms, but for and , the new algorithm is always better. As for the comparison between L-NTADE-HHF and L-NTADE-AHF with the approximation of the heuristic, the results of these methods are very similar.
Table 4 contains the comparison with the alternative approaches on the CEC 2022 benchmark using the Mann–Whitney tests, and Table 5 contains the Friedman ranking.

Table 4.
Mann–Whitney tests of L-NTADE-HHF against the competition top 3, and other approaches, CEC 2022, number of wins/ties/losses and total standard score.

Table 5.
Friedman ranking of L-NTADE with designed heuristic against alternative approaches, CEC 2022 benchmark.
For the CEC 2022 benchmark, the top 3 best methods were chosen for comparison, as well as some other algorithms.
Table 4 shows that L-NTADE-HHF is better than most state-of-the-art algorithms and is comparable to EA4eigN100, L-NTADEMF and L-NTADE (in the case). However, the comparison with the Friedman ranking has shown that EA4eigN100, the winner of the CEC 2022 competition, performs better in both the case and case, but L-NTADE-HHF is still second, considering the total ranking. These results show that the designed heuristic is applicable not only to CEC 2017, where the training was performed, but also CEC 2022, where different functions and different computational resources are used. Same as before, the results of L-NTADE-HHF and L-NTADE-AHF are very close, which means that the approximation is working well, and can be used in other algorithms.
The presented results demonstrate that the hyper-heuristic approach allowed for finding an efficient parameter adaptation technique, which was able to perform well not only on the set of functions, where the training was performed, i.e., 30-dimensional problems from CEC 2017, but also for different dimensions and a different benchmark, CEC 2022. The overall performance of L-NTADE-HHF is higher than most of the algorithms, and the designed heuristic can be efficiently approximated with relatively simple equations. In the next section, the obtained results and their meaning is discussed in more detail.
6. Discussion
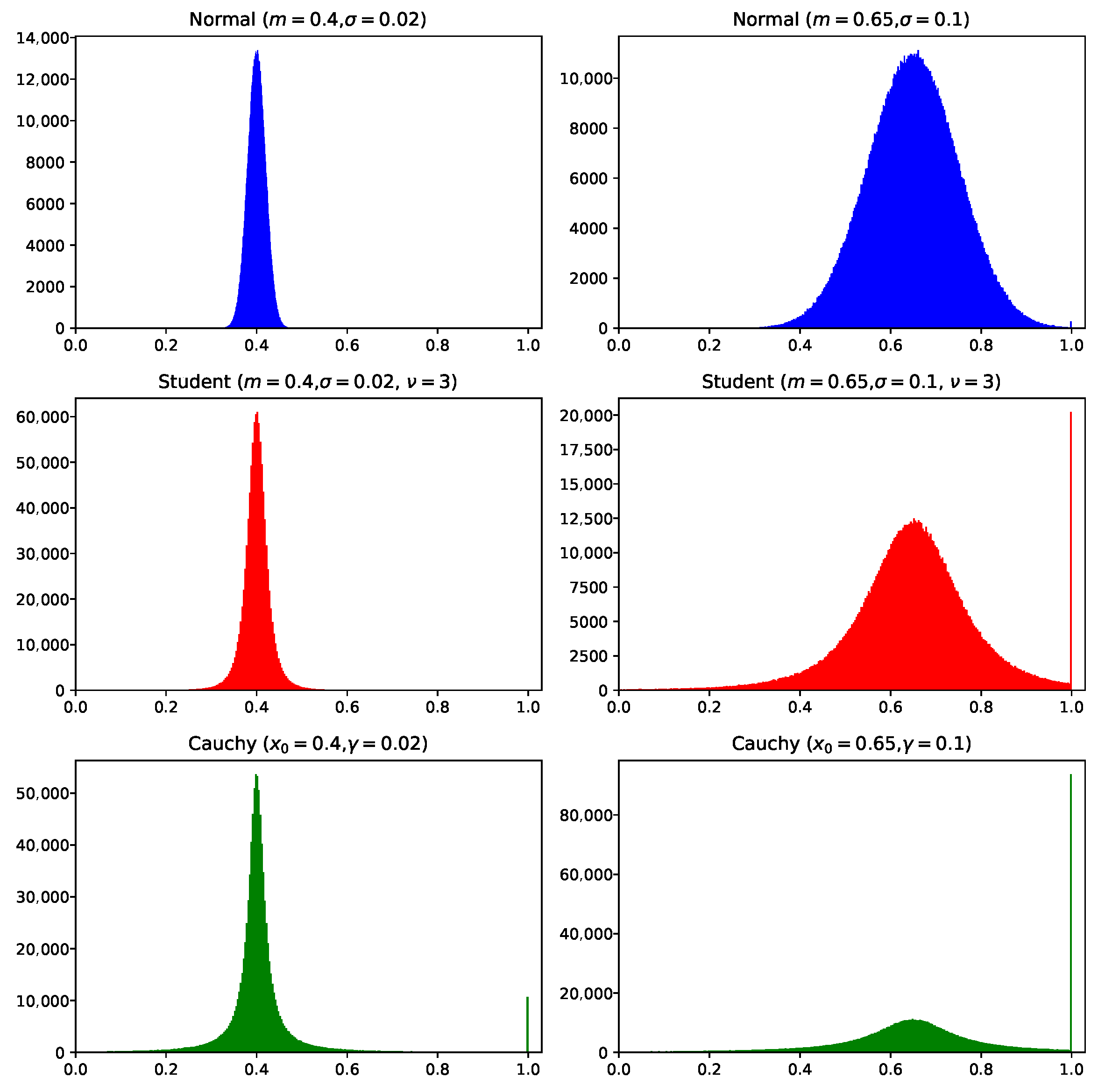
The heuristic for parameter adaptation based on the success rate, found by the L-SRDE algorithm, is relatively simple and straightforward. If the success rate is low, then F should be close to 0.4, and if the success rate is at least 20%, then F should be sampled with a mean of around 0.6. Also, for low success rates, the sampling should be performed with smaller variance, while an increased success rate requires larger variance. For a better understanding of the reasons of the high performance of such a simple method compared to success history adaptation with memory cells and weighted mean, it is worth considering the distributions that are used. For this purpose, in Figure 6, the histograms of six distributions are built, three for the case of a low ( and ) and three for a high ( and ). The sample size was points, and the same procedure as for generating F was used, i.e., while , it is sampled again, and if , it is set to 1.
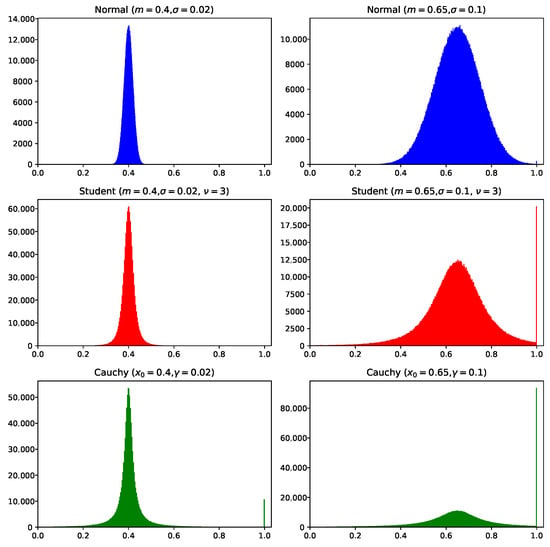
Figure 6.
Histograms of sampling F values with various distributions.
In Figure 6, in the case of small variance, all three distributions, i.e., normal, Student’s and Cauchy, are very compact, i.e., they generate F values close to . However, it can be seen that the Cauchy distribution has heavier tails, which results in a peak at —there is a certain percent of F values, which are larger than 1 and clipped back. Although Cauchy gives more diverse F values, it is not clear if a peak at is a useful thing. In the case when the is relatively high, the hyper-heuristic approach proposes increasing the variance. For example, with and , the normal distribution is much wider, but it still does not reach very often. The learned Student’s distribution with encounters clipping at but not as often as it happens with Cauchy distribution. At the same time, Student’s distribution is able to also generate small F values quite often.
Considering the above, it can be concluded that the hyper-heuristic approach was able to find such distribution parameters that the clipping does not happen very often, but the distribution is still wide enough. The fact that the variance changes with the success rate is new and has not been considered in most studies, where it was usually fixed to 0.1 as a small value. The hyper-heuristics have shown that smaller variances can be beneficial, especially if the algorithm is stuck. That is, if the success rate is high, a more wide search with arbitrary F values is allowed, but if the algorithm hits a local optimum, then smaller F values are better. The idea of depending on the success rate was discussed in [11]; the usage of a mutation strategy similar to current-to-pbest makes the algorithm go faster toward one of the best individuals (exploitation and faster convergence) when the is high and switch to exploration, when the second difference between individuals with indexes and is more important, if the success rate is low.
The proposed approach is a universal tool for tuning algorithms, designing new adaptation techniques and searching for dependencies between parameters based on extensive experiments. The only drawback is the computational effort required to use such a method. The usage of the Taylor series was dictated by the flexibility, but any other approximation method can be used. Further studies on DE and hyper-heuristics may include the following:
- Proposing more flexible methods to control the random distribution of F values and tuning them;
- Reducing the found heuristic to a set of simple rules and equations without many parameters of Taylor series;
- Applying the new heuristic to other DE-based algorithms and replacing the success history adaptation;
- Determining the dependence of the parameter on some of the values present in the DE algorithm.
7. Conclusions
In this study, the hyper-heuristic approach was used to generate new parameter adaptation methods for the scaling factor parameter in differential evolution. The training phase resulted in a relatively simple adaptation method, which relies on the success rate value. The comparison of the L-NTADE algorithm with the new heuristic has shown that it is able to outperform alternative approaches on two sets of benchmark problems, and the efficiency of the modification increases in higher dimensions. The hyper-heuristic approach described in this study can be applied to other evolutionary computation methods to search for parameter adaptation procedures. One of the drawbacks of this study is that here only symmetrical distributions were considered for sampling the scaling factor values, but it is possible that skewed distributions may give better results. The skewed distributions have not been used in differential evolution, to the best of our knowledge, and it can be a direction of further studies.
Author Contributions
Conceptualization, V.S. and E.S.; methodology, V.S., L.K. and E.S.; software, V.S.; validation, V.S., L.K. and E.S.; formal analysis, L.K.; investigation, V.S.; resources, E.S. and V.S.; data curation, E.S.; writing—original draft preparation, V.S.; writing—review and editing, V.S. and L.K.; visualization, V.S.; supervision, E.S. and L.K.; project administration, E.S.; funding acquisition, L.K. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Ministry of Science and Higher Education of the Russian Federation (Grant No. 075-15-2022-1121).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GA | Genetic Algorithms |
| GP | Genetic Programming |
| EC | Evolutionary Computation |
| DE | Differential Evolution |
| EGO | Efficient Global Optimization |
| CEC | Congress on Evolutionary Computation |
| SHADE | Success History Adaptive Differential Evolution |
| LPSR | Linear Population Size Reduction |
| LBC | Linear Bias Change |
| RSP | Rank-based Selective Pressure |
| HHF | Hyper-Heuristic Generation of Scaling Factor F |
| L-NTADE | Linear Population Size Reduction–Newest and Top Adaptive Differential Evolution |
References
- Eshelman, L.J.; Schaffer, J.D. Real-Coded Genetic Algorithms and Interval-Schemata. In Foundations of Genetic Algorithms; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Deb, K.; Agrawal, R.B. Simulated Binary Crossover for Continuous Search Space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Poli, R.; Kennedy, J.; Blackwell, T.M. Particle swarm optimization. Swarm Intell. 1995, 1, 33–57. [Google Scholar]
- Storn, R.; Price, K. Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Feoktistov, V. Differential Evolution in Search of Solutions; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Das, S.; Suganthan, P. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.; Suganthan, P. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Al-Dabbagh, R.D.; Neri, F.; Idris, N.; Baba, M.S.B. Algorithmic design issues in adaptive differential evolution schemes: Review and taxonomy. Swarm Evol. Comput. 2018, 43, 284–311. [Google Scholar]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; IEEE Press: Piscataway, NJ, USA, 2013; pp. 71–78. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. Step-by-step improvement of JADE and SHADE-based algorithms: Success or failure? Swarm Evol. Comput. 2018, 43, 88–108. [Google Scholar] [CrossRef]
- Stanovov, V.; Semenkin, E. Surrogate-Assisted Automatic Parameter Adaptation Design for Differential Evolution. Mathematics 2023, 11, 2937. [Google Scholar] [CrossRef]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient Global Optimization of Expensive Black-Box Functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. Dual-Population Adaptive Differential Evolution Algorithm L-NTADE. Mathematics 2022, 10, 4666. [Google Scholar] [CrossRef]
- Awad, N.; Ali, M.; Liang, J.; Qu, B.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Special Session and Competition on Single Objective Bound Constrained Real-Parameter Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Kumar, A.; Price, K.; Mohamed, A.K.; Suganthan, P.N. Problem Definitions and Evaluation Criteria for the CEC 2022 Special Session and Competition on Single Objective Bound Constrained Numerical Optimization; Technical Report; Nanyang Technological University: Singapore, 2021. [Google Scholar]
- Brest, J.; Greiner, S.; Boškovic, B.; Mernik, M.; Žumer, V. Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems. IEEE Trans. Evol. Comput. 2006, 10, 646–657. [Google Scholar] [CrossRef]
- Brest, J.; Maucec, M.; Bovsković, B. The 100-Digit Challenge: Algorithm jDE100. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 19–26. [Google Scholar]
- Brest, J.; Maucec, M.; Bosković, B. Differential Evolution Algorithm for Single Objective Bound-Constrained Optimization: Algorithm j2020. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Zhang, J.; Sanderson, A.C. JADE: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Comput. 2009, 13, 945–958. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the IEEE Congress on Evolutionary Computation, CEC, Beijing, China, 6–11 July 2014; pp. 1658–1665. [Google Scholar] [CrossRef]
- Price, K.V.; Awad, N.H.; Ali, M.Z.; Suganthan, P.N. The 2019 100-Digit Challenge on Real-Parameter, Single Objective Optimization: Analysis of Results; Technical Report; Nanyang Technological University: Singapore, 2019. [Google Scholar]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. Selective Pressure Strategy in differential evolution: Exploitation improvement in solving global optimization problems. Swarm Evol. Comput. 2019, 50, 100463. [Google Scholar]
- Brest, J.; Maučec, M.; Boškovic, B. Single objective real-parameter optimization algorithm jSO. In Proceedings of the IEEE Congress on Evolutionary Computation, Donostia, Spain, 5–8 June 2017; IEEE Press: Hoboken, NJ, USA, 2017; pp. 1311–1318. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. LSHADE Algorithm with Rank-Based Selective Pressure Strategy for Solving CEC 2017 Benchmark Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Viktorin, A.; Senkerik, R.; Pluhacek, M.; Kadavy, T.; Zamuda, A. Distance based parameter adaptation for Success-History based Differential Evolution. Swarm Evol. Comput. 2019, 50, 100462. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. The automatic design of parameter adaptation techniques for differential evolution with genetic programming. Knowl. Based Syst. 2022, 239, 108070. [Google Scholar] [CrossRef]
- Chen, X.; Shen, A. Self-adaptive differential evolution with Gaussian–Cauchy mutation for large-scale CHP economic dispatch problem. Neural Comput. Appl. 2022, 34, 11769–11787. [Google Scholar] [CrossRef]
- Santucci, V.; Baioletti, M.; Bari, G.D. An improved memetic algebraic differential evolution for solving the multidimensional two-way number partitioning problem. Expert Syst. Appl. 2021, 178, 114938. [Google Scholar]
- Yang, M.; Cai, Z.; Li, C.; Guan, J. An improved adaptive differential evolution algorithm with population adaptation. In Proceedings of the Annual Conference on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013. [Google Scholar]
- Yi, W.; Chen, Y.; Pei, Z.; Lu, J. Adaptive differential evolution with ensembling operators for continuous optimization problems. Swarm Evol. Comput. 2021, 69, 100994. [Google Scholar] [CrossRef]
- Burke, E.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Woodward, J. A Classification of Hyper-Heuristic Approaches: Revisited. In Handbook of Metaheuristics; Springer International Publishing: Cham, Switzerland, 2019; pp. 453–477. [Google Scholar] [CrossRef]
- Haraldsson, S.O.; Woodward, J. Automated design of algorithms and genetic improvement: Contrast and commonalities. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, Vancouver, BC, Canada, 12–16 July 2014. [Google Scholar]
- Mohamed, A.; Hadi, A.A.; Fattouh, A.; Jambi, K. LSHADE with semi-parameter adaptation hybrid with CMA-ES for solving CEC 2017 benchmark problems. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 145–152. [Google Scholar]
- Stanovov, V.; Semenkin, E. Genetic Programming for Automatic Design of Parameter Adaptation in Dual-Population Differential Evolution. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2023. [Google Scholar]
- Price, K.V.; Kumar, A.; Suganthan, P.N. Trial-based dominance for comparing both the speed and accuracy of stochastic optimizers with standard non-parametric tests. Swarm Evol. Comput. 2023, 78, 101287. [Google Scholar] [CrossRef]
- Price, K.; Storn, R.; Lampinen, J. Differential Evolution: A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Gamperle, R.; Muller, S.; Koumoutsakos, A. A Parameter Study for Differential Evolution. Adv. Intell. Syst. Fuzzy Syst. Evol. Comput. 2002, 10, 293–298. [Google Scholar]
- Zaharie, D. Critical values for the control parameters of differential evolution algorithms. Crit. Values Control Parameters Differ. Evol. Algorithmss 2002, 2, 62–67. [Google Scholar]
- Ali, M.; Törn, A. Optimization of Carbon and Silicon Cluster Geometry for Tersoff Potential using Differential Evolution. In Optimization in Computational Chemistry and Molecular Biology: Local and Global Approaches; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Kumar, A.; Misra, R.K.; Singh, D. Improving the local search capability of Effective Butterfly Optimizer using Covariance Matrix Adapted Retreat Phase. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 1835–1842. [Google Scholar]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. NL-SHADE-RSP Algorithm with Adaptive Archive and Selective Pressure for CEC 2021 Numerical Optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 809–816. [Google Scholar] [CrossRef]
- Stanovov, V.; Akhmedova, S.; Semenkin, E. NL-SHADE-LBC algorithm with linear parameter adaptation bias change for CEC 2022 Numerical Optimization. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022. [Google Scholar]
- Mohamed, A.W.; Hadi, A.A.; Agrawal, P.; Sallam, K.M.; Mohamed, A.K. Gaining-Sharing Knowledge Based Algorithm with Adaptive Parameters Hybrid with IMODE Algorithm for Solving CEC 2021 Benchmark Problems. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 841–848. [Google Scholar]
- Cuong, L.V.; Bao, N.N.; Binh, H.T.T. Technical Report: A Multi-Start Local Search Algorithm with L-SHADE for Single Objective Bound Constrained Optimization; Technical Report; SoICT, Hanoi University of Science and Technology: Hanoi, Vietnam, 2021. [Google Scholar]
- Biswas, S.; Saha, D.; De, S.; Cobb, A.D.; Das, S.; Jalaian, B. Improving Differential Evolution through Bayesian Hyperparameter Optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 832–840. [Google Scholar]
- Bujok, P.; Kolenovsky, P. Eigen Crossover in Cooperative Model of Evolutionary Algorithms Applied to CEC 2022 Single Objective Numerical Optimisation. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022. [Google Scholar]
- Biedrzycki, R.; Arabas, J.; Warchulski, E. A Version of NL-SHADE-RSP Algorithm with Midpoint for CEC 2022 Single Objective Bound Constrained Problems. In Proceedings of the 2022 IEEE Congress on Evolutionary Computation (CEC), Padua, Italy, 18–23 July 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).