Abstract
Differential cohomology is a topic that has been attracting considerable interest. Many interesting applications in mathematics and physics have been known, including the description of WZW terms, string structures, the study of conformal immersions, and classifications of Ramond–Ramond fields, to list a few. Additionally, it is an interesting application of the theory of infinity categories. In this paper, we give an expository account of differential cohomology and the classification of higher line bundles (also known as -banded gerbes) with a connection.We begin with how Čech cohomology is used to classify principal bundles and define their characteristic classes, introduce differential cohomology à la Cheeger and Simons, and introduce -banded gerbes with a connection.
Keywords:
Čech cohomology; non-abelian cohomology; characteristic classes; differential characters; differential cohomology; bundle gerbes; Deligne cohomology MSC:
primary 53C08; secondary 55R65; 14F03; 55N05
1. Introduction
Higher differential geometry is a study of differential geometry in the context of homotopy theory and higher category theory. It appears in many aspects of differential geometry, such as the theory of the higher analog of line bundles with a connection, considered as sheaves of ∞-groupoids, equivariant refinements, and the theory of orbifolds, and derived geometry (see, for example, [1,2,3]).
Differential cohomology and the theory of gerbes are topics that have been attracting interest. The idea of differential cohomology is that we can combine data from cohomology groups and differential forms in a homotopy theoretic way. The first construction of differential cohomology was due to Deligne [4] and Cheeger and Simons [5], and numerous applications have been found to date. A few examples include index theorems, the study of conformal immersions, topological quantum field theories, arithmetic Chow groups, and hyperbolic volumes. It is also an interesting application of the theory of infinity categories (see [5,6,7]). This theory, as generalized by Hopkins and Singer [8], explicitly constructs a differential cohomology theory for any generalized cohomology theory and brings in all of the objects in the category of spectra as topological data for differential extension.
-banded n-gerbes are higher analogs of principal -bundles. Just as line bundles represent, up to isomorphism, the degree-two integral cohomology group of the base space, one-gerbes (or simply gerbes) are geometric objects representing, up to isomorphism, the degree-three integral cohomology, and n-gerbes represent the degree integral cohomology. Endowed with a connection, we have the following pattern of classification:
and so on. It is thus clear that differential cohomology is the proper home for classifying gerbes with a connection and their higher-categorical generalizations.
Historically, gerbes were first conceived by Giraud [9] as sheaves of groupoids (cf. Grothendieck [10]) in the study of non-abelian cohomology. Perhaps the most popular model of gerbes in the literature would be bundle gerbes by Murray and Stevenson [11,12], which has an obvious advantage in that we can remain in the category of smooth manifold while handling it. There are numerous applications of gerbes with a connection, including the description of the Wess–Zumino–Witten terms, string structures, classifications of Ramond–Ramond fields, and topological insulators (see [13,14,15]). Of course, gerbes banded with other (possibly non-abelian) groups are of interest as well. We do not treat them in this paper, but interested readers should compare Schreiber and Waldorf [16].
The goal of this paper is to give a self-contained expository account of differential cohomology and gerbes and to guide readers to the literature at the forefront of this research. There are several well-written research papers and dissertations in this area from which one can learn about this topic. Nonetheless, there are not many monographs and expository articles for second- or third-year Ph.D. students trying to choose a topic for their dissertations. Perhaps Brylinski [17] is one of such a limited list of compilations. This paper pursues an exposition that is accessible to early-year Ph.D. students and takes the length of three standard 1 h talks. Indeed, this paper is based on the author’s notes for a minicourse at the 13th Korea Institute for Advanced Study (KIAS) Winter School on Differential Geometry, intended to accommodate non-experts in the audience.
This paper is organized as follows. In Section 2, we give a gentle introduction to the characteristic classes of complex line bundles and -gerbes. We begin with the principal G-bundles and Čech cohomology with coefficients in G, introduce relevant results from Dixmier and Douady [18], and then give various examples, each of which leads to the construction of a characteristic class. In Section 3, we introduce the differential cohomology group, as in Cheeger–Simons [5], and introduce a classification of complex line bundles with connection by the degree-two differential cohomology group. In Section 4, we introduce bundle gerbes and their Dixmier–Douady classes. After that, we explain what connections, curvings, and three-curvatures are. We then define the Deligne complex and introduce a classification of bundle gerbes with connection by the degree-three differential cohomology group. We also introduce the two-groupoid structure of the category of bundle gerbes with a connection.
2. Čech Cohomology and Characteristic Classes
In this section, we shall review the principal G-bundles and how Čech cohomology can be used to classify them and define their characteristic classes. A good reference for learning more about these topics is Brylinsky [17], which has a broader account.
Definition 1.
Let G be a Lie group. A principal G-bundle over a smooth manifold M is a smooth map and a right G-action on P satisfying:
- (1)
- π is G-invariant; that is, for all and .
- (2)
- On each fiber, G acts freely and transitively from the right.
- (3)
- P is locally trivial via G-equivariant trivialization; that is, at every , there exists an open subset and a diffeomorphism such that satisfying .
Conditions (1) and (2) mean that the G-orbits are fibers of . This is equivalent to saying , is a diffeomorphism; that is, P is a G-torsor.
Definition 2.
A bundle map of the principal G-bundles from to is a diffeomorphism that preserves the fiber and G-equivariant; that is, and .
The principal G-bundles over M with maps form a groupoid (a category whose morphisms are invertible), and it is denoted by . We will also use the notation to denote the groupoid of rank n complex vector bundles over M.
Example 1.
Let . Consider and take an associated fiber bundle with a fiber defined by with a diagonal G-action: . The bundle is a complex vector bundle over M of rank n. On the other hand, let . At each , consider the set of all bases of the vector space ; equivalently the set of all -linear maps . Then, the smooth map with and a right G-action on defined by is a principal G-bundle over M. It leads to the following equivalence of categories.
For this reason, in what follows, we do not distinguish a -, -, or -bundle from a complex line bundle.
Notation 1.
We shall use the notation to denote the n-fold intersection .
Definition 3.
Let G be an abelian group, M be a topological space, and be an open cover of M. The set inherits the operation from the group G and is termed the degree-p Čech cochain group. Together with the map , , the sequence of groups is the Čech cochain complex. (It is easy to verify that . Here, the hat means an omission.) The cohomology of this complex is the Čech cohomology of M defined on an open cover .
Now, if the group G in the definition above is not abelian, in general, the coboundary maps are not group homomorphisms, neither nor form a group, and, if we apply to a cocycle, we do not obtain . We shall see below what goes on starting from the lowest degree:
- : There is no problem. . This is a group under a pointwise group multiplication.
- : Neither nor form a group. On the set , we may impose an equivalence relation defined by the action of 0-cochainsSo, we may define as the pointed set with a distinguished element of the constant map . Notice where set is precisely the set of isomorphism classes of the principal G-bundles over M defined on the open cover U (see Remark below). For this reason, principal G-bundles are geometric models of a degree-one non-abelian cohomology of M with coefficients in a group G.
- : There is no reasonable way to make sense of .
Remark 1.
We shall closely look into how the set classifies the principal G-bundle over M up to isomorphism. Recall that each principal G-bundle is locally trivial and diffeomorphic to for some open . This means that if we are given a family of transition functions on every double overlap , that is, , we can rebuild the principal G-bundle. Since the transition functions satisfy
Equation (1) is called the cocycle condition of a principal G-bundle. So, if we have a principal bundle P over M, we have a family of transition functions satisfying condition (1) and vice versa (under a mild condition). Likewise, if we have a bundle map covering M, we have a family of functions on open sets in the cover satisfying that for all , and vice versa (under the same mild condition). Here, the mild condition is that the open cover has to be a good cover. A good cover (also known as Leray’s covering) is an open cover of M if all open sets and their intersections are contractible. Such a covering always exists (see [1] (Proposition A.1) and references therein). An open cover is a refinement of if such that for all . A refinement induces a map , and it satisfies . So, we can define the set as a direct limit over refinements of open cover; that is,
If the cover is good, the restriction map is an isomorphism. Therefore, we conclude that
If we remove the abelian assumption of groups, the long exact sequence induced by a short exact sequence of groups cannot go any further than the degree .
Proposition 1.
Let
be a short exact sequence of groups. We have the following long exact sequence of groups and pointed sets
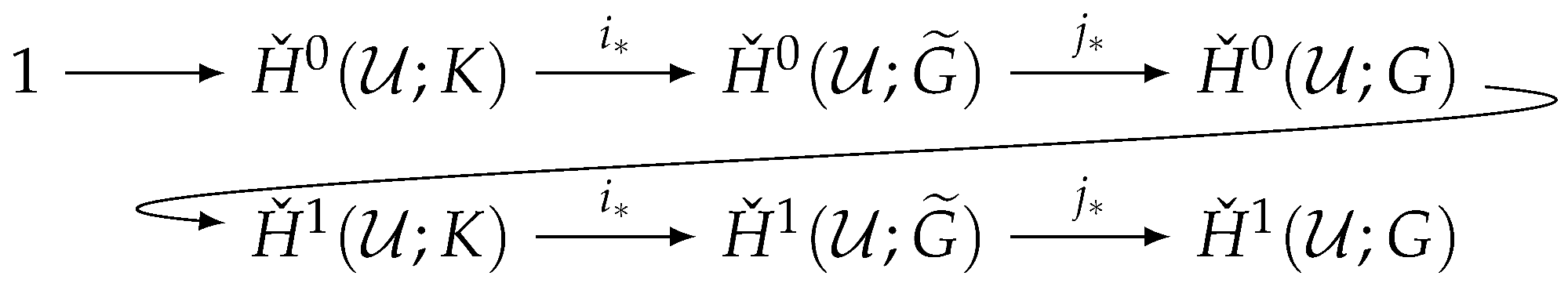
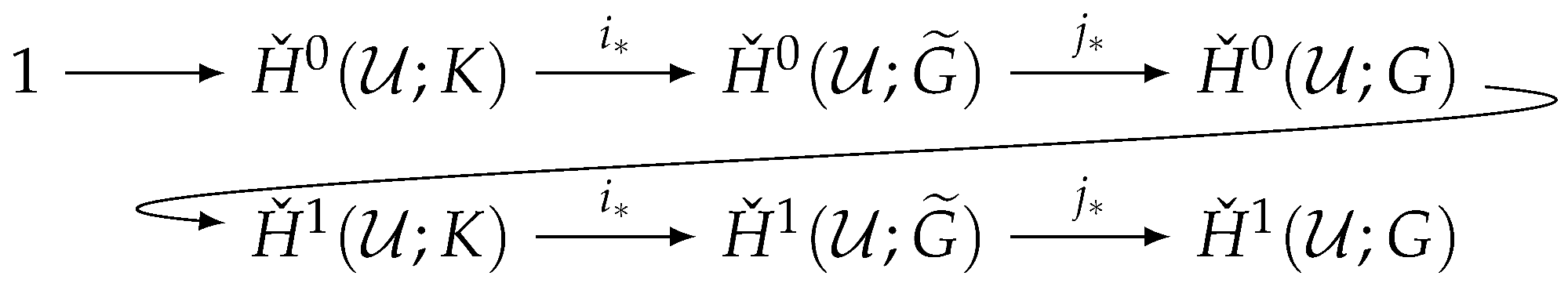
However, in the special case that the second term in the sequence is an abelian group whose image is in the center of the third, we can extend the long exact sequence just one term further. We have the following propositions.
Proposition 2.
If the group K in short exact sequence (3) is abelian and belongs to the center of , then the long exact sequence in Proposition 1 extends to :
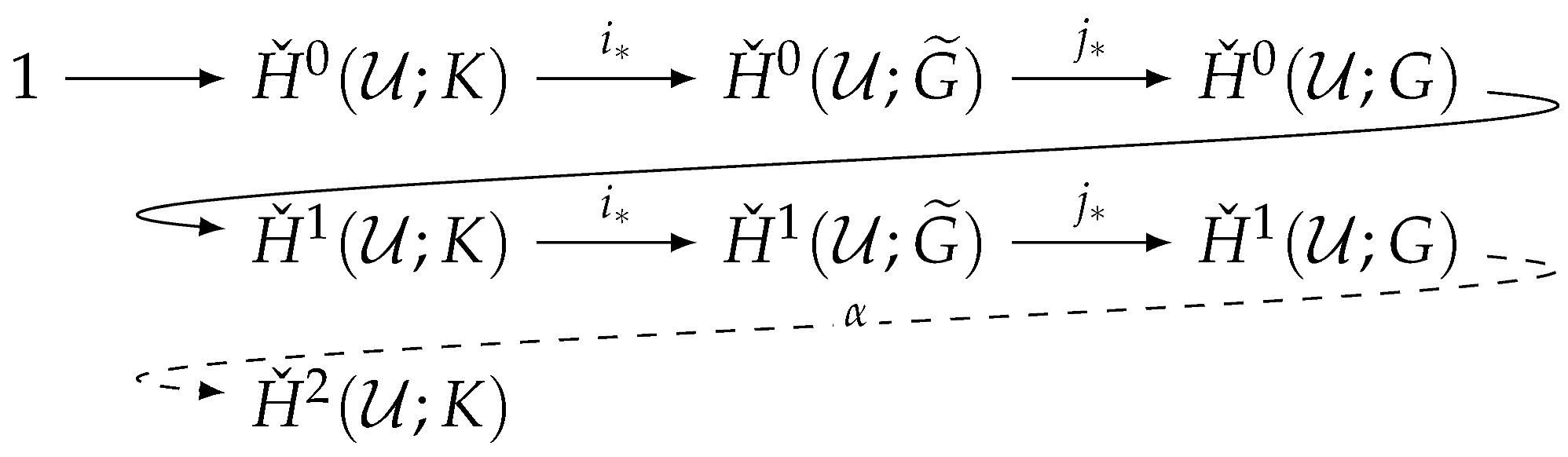
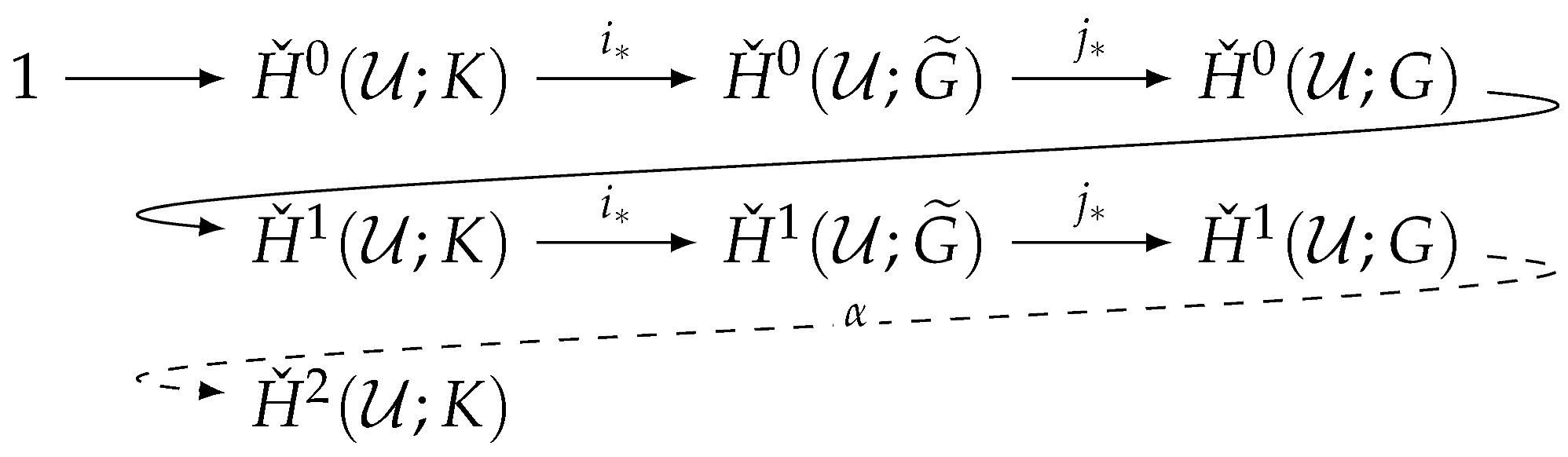
Proposition 3
(Dixmier–Douady [18]). If the sheaf is soft, then
is a bijection.
Proof.
See Dixmier–Douady [18] (Lemma 22, p. 278) or Brylinski [17] (Proposition 4.1.8, p. 162). □
In the above, is a sheaf such that is a group of smooth functions for each open . A sheaf is soft if is onto for every closed . Here, we can think of (since M is paracompact), where the direct limit is taken over all open neighborhoods of C.
Example 2.
(1) Consider a short exact sequence
The induced map is a correspondence , which is the first Stifel–Whitney class. So, if and only if P comes from an -bundle; that is, P is orientable. Equivalently, the obstruction for the transition maps of a Euclidean vector bundle to lift to is given by the first Stifel–Whitney class.
(2) Consider a short exact sequence
The induced map is a correspondence , which is the second Stifel–Whitney class. So, if and only if P comes from a -bundle. Equivalently, the obstruction for the transition maps of an oriented Euclidean vector bundle to lift to is given by the second Stifel–Whitney class. Here, one can think of as a double cover of , which is also a universal cover. For a construction of in terms of Clifford algebras, see [19] (Section 1.2).
Remark 2.
The Whitehead tower of is of particular interest. The Whitehead tower of a space X is a factorization of the point inclusion
such that each is -connected (that is, all homotopy groups vanish for ) and each map is a fibration, which is an isomorphism on all for . For the space , we have a Whitehead tower as follows:
Here, is a six-connected cover of
and is a seven-connected cover of
It is known that the obstruction to lift a -bundle to a -bundle is the first fractional Pontryagin class and to lift a -bundle to a -bundle is the second fractional Pontryagin class , and so on (see [20] for more details).
Example 3.
(3) Consider a short exact sequence
Note that is a soft sheaf (recall the Tietze extension theorem). The induced map is a correspondence , which is the first Chern class. Note that if group G is abelian, is a sheaf of locally constant functions in G, , and , then the degree-p singular cohomology with coefficients in G is the same. Since group is discrete, we can identify and for any degree p.
Proposition 4
(Dixmier–Douady [18]). Let be a complex separable Hilbert space. The sheaf is soft.
Proof.
See Dixmier–Douady [18] (Lemma 4, p. 252) or Brylinski [17] (Cor. 4.1.6, p. 162). □
Example 4.
(4) Consider a short exact sequence
Since is a soft sheaf, the induced map is a correspondence , which is the Dixmier–Douady class of a gerbe.
Definition 4.
A
characteristic class of a principal G-bundle P over M is an assignment
that is natural; that is, for
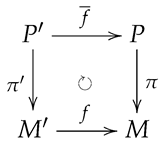 Here, A is an abelian group.
Here, A is an abelian group.

Since is representable by , by the Yoneda Lemma (see MacLane [21]), we have the following proposition.
Proposition 5.
An assignment
is one-to-one and onto.
Remark 3.
There is an alternative way to define characteristic classes using a “geometric datum”, that is, a connection on . This is the Chern–Weil theory. For example, given a line bundle with the connection , the first Chern class of is defined by a Chern–Weil form . Here, is the curvature two-form of the connection . The Chern–Weil theorem shows that the cohomology class of a Chern–Weil form does not depend on the choice of connection. So, is a topological invariant of a line bundle. A priori the class is a class in , but it can be shown that it is actually a class in . The realification of the first Chern class, Example 3 above, is equal to the first Chern class from the Chern–Weil theory. See Morita [22] (Chapter 5) to learn more about Chern–Weil theory of characteristic classes.
We have seen that, up to isomorphism, complex line bundles are classified by via the first Chern class (Example 3) and principal -bundles are classified by via the Dixmier–Douady class (Example 4). We can ask the following question: What classifies (higher) line bundles with a connection? For example, if we consider a groupoid whose objects are line bundles with the connection and whose morphisms are a bundle isomorphism preserving the connection, what classifies the isomorphism classes of ? This question leads us to “differential cohomology”. Up to isomorphism, line bundles with a connection are classified by the degree-two differential cohomology , gerbes with a connection are classified by , two-gerbes with a connection are classified by , and so on.
3. Cheeger–Simons Differential Characters
In this section, we introduce a differential extension of the singular cohomology theory on the site of smooth manifolds. Among various known models, we shall introduce the model by Cheeger and Simons [5] which is one of the historical landmarks. Interested readers are referred to the homotopy theoretic model by Hopkins and Singer [8], a spark complex model by Harvey, Lawson, and Zweck [23], and a novel construction using ∞-sheaves of spectra by Bunke, Nikolaus, and Völkl [24].
Notation 2.
We shall define some notations that will be used throughout this section. Let M be a smooth manifold and R be a commutative ring with unity:
- : smooth singular k-cochains in M with coefficients in R.
- : smooth singular k-cocycles in M with coefficients in R.
- : differential k-forms on M.
- is a -linear map , where is a pairing of a singular k-chain and a differential k-form.
- : closed differential k-forms with integral periods; that is, if and only if and .
- ∼ is the natural map .
A nonvanishing differential form does not take its values in a proper subring . Hence, we have the following:
Proposition 6.
The map
is one-to-one.
Definition 5
(Cheeger and Simons [5]). Let M be a smooth manifold. The group of differential characters of degree k consists of pairs , where and , satisfying that
where the group structure is the componentwise addition.
Remark 4.
The degree of the in the above definition is different from the one that appears in Cheeger and Simons [5], which defines the same group as degree . A consequence of adopting their convention would be a mismatch of degree in the group of differential characters and real cohomology, so the forgetful map (see below for a definition) would be . We stick to our convention for the sake of consistency with the literature from recent years.
The main goal of this section is to understand the following diagram, known as the differential cohomology hexagon diagram.
Proposition 7
(Cheeger and Simons [5]). The group of differential characters satisfies the following diagram; that is, all squares and triangles are commutative and the diagonal, upper, and lower sequences of the arrows are exact sequences.
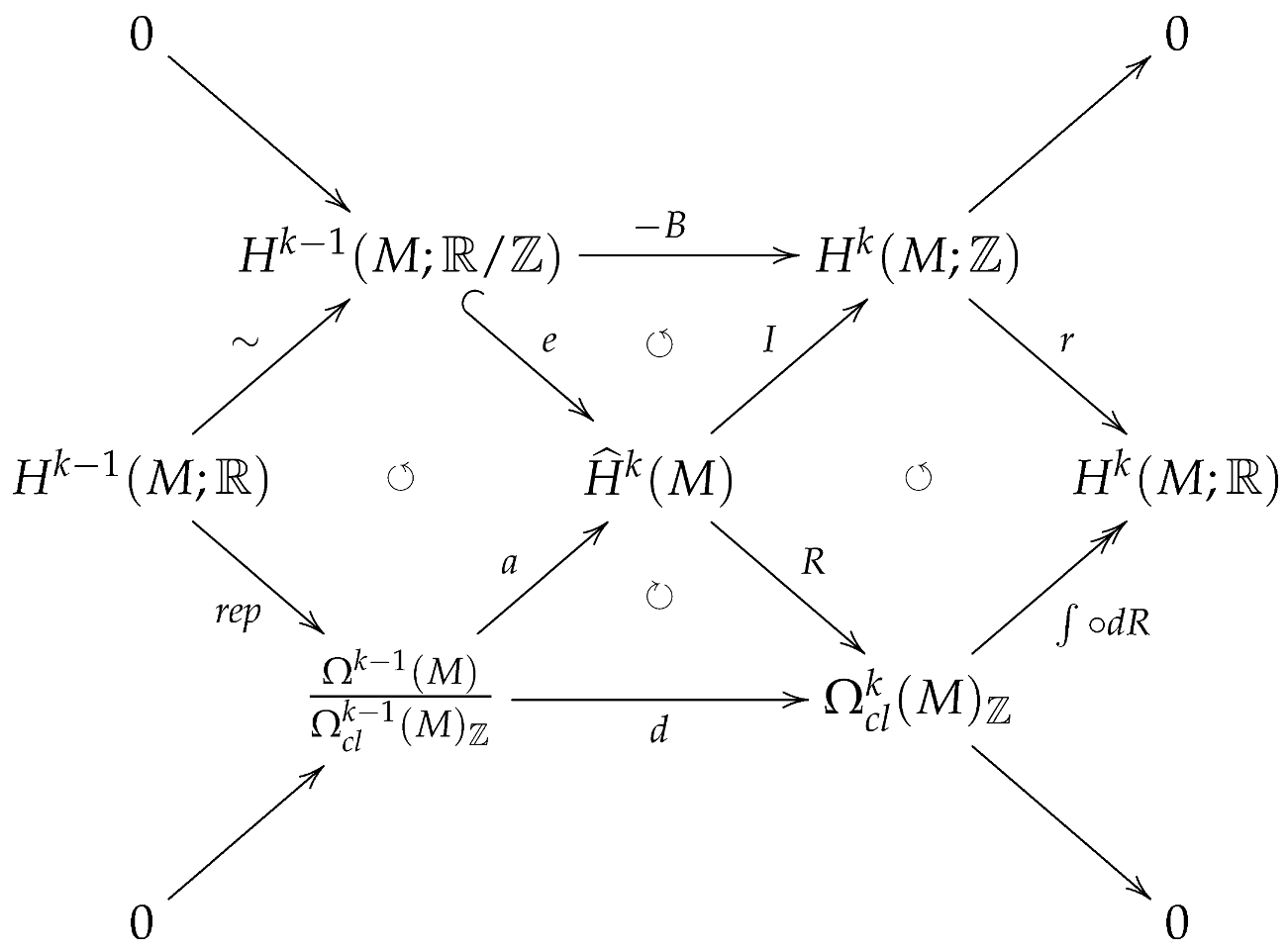

Proof.
We shall divide the proof into several parts and enumerate them.
(1) I and R maps: We begin with some algebra facts:
- A1.
- A subgroup of a free abelian group is free.
- A2.
- An abelian group G is divisible if, for any and any , there exists such that .
- A3.
- An abelian group G is divisible if and only if the group G is an injective object in the category of abelian groups; if and , there exists a map that satisfies .
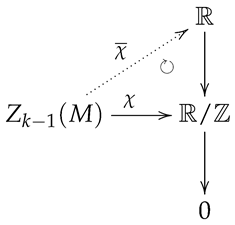
Take and consider . Since is a subgroup of a free abelian group , it is free (A1) and, hence, projective. We have the following commutative diagram:
 Now, since is divisible (A2), it is injective (A3). Hence, lifts to the map T satisfying the following commutative diagram:
Now, since is divisible (A2), it is injective (A3). Hence, lifts to the map T satisfying the following commutative diagram:
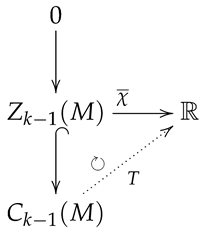 So, . It follows that . Here, the first equality is simply . Thus, there exists such that
Note that , so . Since a real differential form cannot take its value in a proper subring of , this means . It is readily seen that has an integral period. We define the maps I and R as follows:
Let us verify that these maps are well defined. Since the choice of lifts is not unique, we have to verify that the above definition does not depend on the choices we made. Suppose is another lift satisfying . Then, , so for some and . So, if and only if if and only if . Again, since the real differential form cannot take its value in a proper subring of , this means and .
So, . It follows that . Here, the first equality is simply . Thus, there exists such that
Note that , so . Since a real differential form cannot take its value in a proper subring of , this means . It is readily seen that has an integral period. We define the maps I and R as follows:
Let us verify that these maps are well defined. Since the choice of lifts is not unique, we have to verify that the above definition does not depend on the choices we made. Suppose is another lift satisfying . Then, , so for some and . So, if and only if if and only if . Again, since the real differential form cannot take its value in a proper subring of , this means and .


We show that R is surjective. Let be the realification map (which is from the universal coefficient theorem for cohomology; see [25] (Section 3.1)). Notice that, given , there exists a such that . Since has integral periods, is an integral cochain, and, since is closed, (Stokes’ theorem). Now, let for some . Then, for some . Define . So, R is surjective.
The map I is also surjective. Given any , as real cochains. By the de Rham theorem, there exists a such that for some . Define . So, the map I is surjective.
(2) The e map: We define the e map as follows:
The map e is well defined. If we take a different representative , the restriction of to vanishes. The map e is one-to-one: Let a proper subring. From the universal coefficient theorem, we have , since , from , for any . Since is exact if and only if is exact, is an injection.
(3) The a map: We define the a map as follows:
It is obvious that the a map is well defined, and the subgroup is the kernel of the map , .
(4) Diagonals are exact: First, . The inclusion ⊆ is clear. To see ⊇, take such that . Then, satisfying that , so T is a -valued cocycle, representing a class in , and .
Now, . Again, the inclusion ⊆ is clear. To see ⊇, take such that satisfying . By assumption, for some . From , we have for some , and for some . Then, vanishes when we restrict it to , and d also vanishes modulo . Thus, the preimage of I is .
(5) Squares commute: The map rep is defined as follows.
which does not depend on the choice of representatives since all exact forms are closed forms with integral periods. From this, it is clear that the square on the left is commutative. Notice that Equation (4) shows the commutativity of the square on the right.
(6) Triangles commute: Two triangle diagrams below commute.
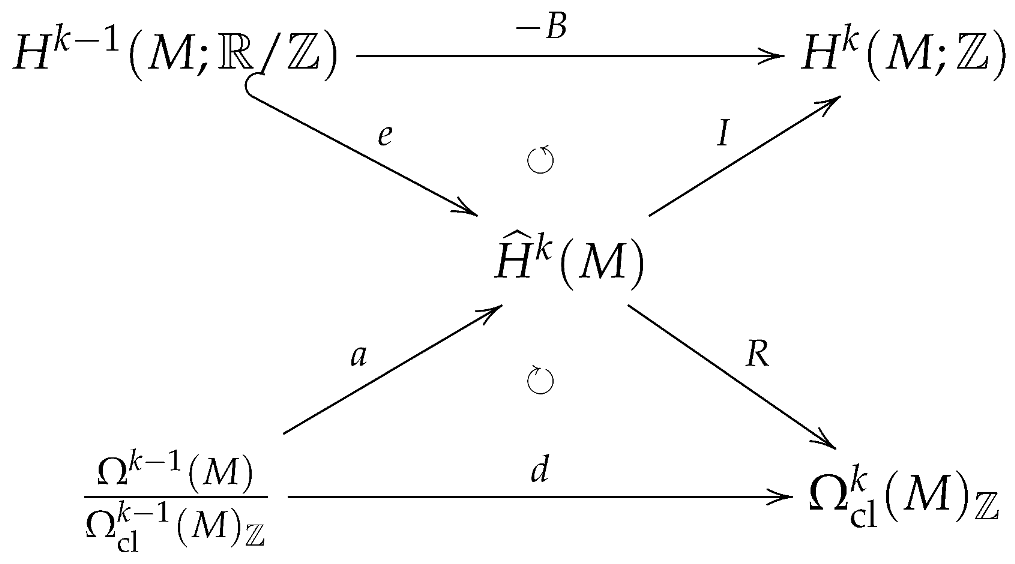 The commutativity of the lower triangle is obvious. Take a -valued cocycle x and consider . There exists such that satisfying for some , so .
The commutativity of the lower triangle is obvious. Take a -valued cocycle x and consider . There exists such that satisfying for some , so .

(7) Upper and lower sequences are exact: It is readily seen that the following are exact sequences.
□
Immediately from the definition, and . Moreover, note that if . When , we have the following proposition:
Proposition 8
(Cheeger and Simons [5]). The following assignment is a one-to-one correspondence:
where, for any loop γ in M, χ is defined by the holonomy of the loop γ; that is,
and, for any bounding γ,
which is extended to all by setting for any .
Given , as we have seen in the surjectivity of R, there exists such that . The class is the characteristic class that classifies P; that is, the first Chern class.
The above proposition addresses the question at the end of Section 2 at least for degree two. What is a higher analog of Proposition 8? How can one define a map? In the following section, we shall see that the isomorphism classes of gerbes with a connection are in one-to-one correspondence with , and, to establish the correspondence, one has to construct ; that is, a holonomy of gerbe.
Remark 5.
Although we do not go into detail, the differential cohomology group has a ring structure (see Cheeger and Simons [5] (p. 56, Theorem 1.11)).
In differential cohomology, the hexagon diagram plays an important role. One uses the hexagon diagram in Proposition 7 to compute differential cohomology groups. Furthermore, it is known that the hexagon diagram uniquely characterizes the differential cohomology. Phrased slightly differently, if there are two fitting into the middle of the hexagon diagram, then they are naturally isomorphic. This is a theorem of Simons and Sullivan [26] that has been generalized by Bunke and Schick [27] and Stimpson [28] to the uniqueness of the differential extension of all exotic cohomology theories under some mild assumptions.
4. -Banded Gerbes with Connection
Throughout this section, M is a smooth manifold. In Section 2, we have seen that elements of are represented by complex line bundles, and, in Section 3, differential cohomology classes in are represented by complex line bundles with a connection. What are the corresponding geometric objects representing and ? The answer is -gerbes with a connection.
Remark 6.
For a generalized cohomology theory and its differential extension , investigating geometric cocycles representing (differential) cohomology classes is a very interesting research topic that is not fully understood yet. For example, elements of even complex K-group are represented by vector bundles over M and odd complex K-group by Ω-vector bundles, but in other interesting generalized cohomology theories, such as elliptic cohomology and topological modular forms, it is largely unknown which geometric objects in the space M represent cohomology classes. Moreover, note that this question is closely related to the Stolz–Teichner program [29] wherein they have conjectured a hypothetical equivalence between the totality of supersymmetric field theories of degree n over M modulo concordance and the group . There are differential and twisted refinements of this conjecture as well (see, for example, Stoffel [30,31] and references therein).
Let us observe how a gerbe arises. Consider the short exact sequence of groups
In Example 4 above, we considered the map when . In the proposition below, we shall closely look at how this map is defined.
Proposition 9.
A principal G-bundle P over M lifts to a principal -bundle if and only if the cocycle representing is trivializable.
Proof.
We look at how the map is defined. Choose a good cover on M. Over each , consider the transition map of P. Since is a good cover, is contractible. Hence, there is a homotopy between the map and a constant map, which lifts by the homotopy-lifting property, since the map is a fibration. Let be a lift of . The cocycle condition , for some . It is an easy exercise to verify that is a degree-two Čech cocycle on and the class does not depend on the choice of lifting . So, the map is a correspondence , and, using the isomorphism (due to the softness of ), it is valued in . □
There are several models representing gerbes. The degree-two -valued Čech cocycle considered above as an obstruction to lifting a principal G-bundle to a -bundle is one model, and there are other ways to represent it as a stack. We refer the reader to Giraud [9], Brylinski [17], Behrend and Xu [32], and Moerdijk [33]. In this section, we will specialize in a model called a bundle gerbe by Murray [11], which is presumably the most widely used model in the literature.
Let be a surjective submersion. The p-fold fiber product of is
The projection of onto the copy of is . For example, let be an open cover of M. Then consider
The map is a surjective submersion, which is an open cover.
Remark 7.
Recall that a fiber product of is, in general, not a smooth manifold. If ϕ, π are submersions, then the fiber product is a smooth manifold. So, a surjective submersion is not only a generalization of an open cover; it also lets us stay within the category of smooth manifolds.
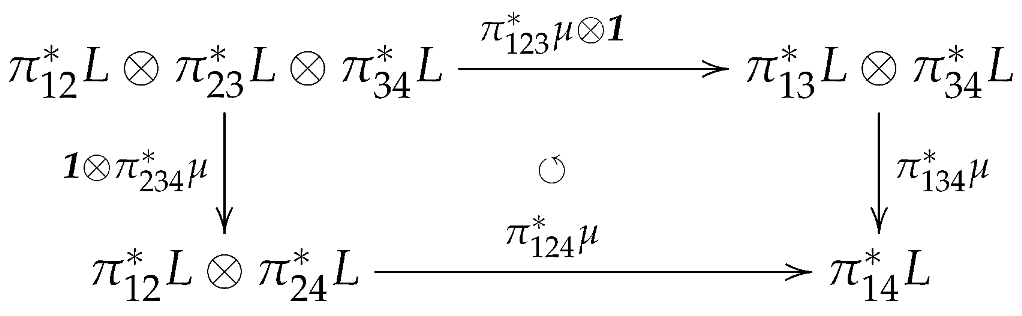
Definition 6
(Murray [11]). A bundle gerbe is a triple where:
- (1)
- is a surjective submersion.
- (2)
- .
- (3)
- is an -bundle isomorphism.
- (4)
- μ is associative over : that is,
Let us construct the Dixmier–Douady class, the characteristic class of a bundle gerbe. Let be a bundle gerbe over M. Take a good open cover (cf. Remark 1) of M. Then, local sections on each open set and on each double intersection can be defined. We consider the pullback of along .
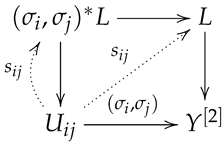 Take a section , or, equivalently, a map . Over triple intersections, we have
Here, the associativity of implies that is a degree-two Čech cocycle in M defined on .
Take a section , or, equivalently, a map . Over triple intersections, we have
Here, the associativity of implies that is a degree-two Čech cocycle in M defined on .

Definition 7.
Let be a bundle gerbe over M. The Dixmier–Douady class is the cohomology class .
It is not difficult to verify that does not depend on the choices we have made.
Let us recall connections and curvatures on a principal G-bundle. A connection on a principal G-bundle is a differential one-form on P valued in satisfying that:
- (1)
- where and for each .
- (2)
- .
The curvature of is a -valued two-form on P.
Now, we define the connection and curving of a bundle gerbe.
Definition 8.
A
connection
on is a connection on L compatible with μ; that is, is a connection preserving isomorphism.
So, a connection on has to be an -valued differential one-form on .
Definition 9.
A
curving
B of a bundle gerbe with a connection is a differential two-form on Y satisfying .
A connection and a curving on a bundle gerbe are called the connective structure. By a bundle gerbe with a connection, we mean a bundle gerbe with a connective structure.
To work with curvatures and curvings, we need the following proposition.
Proposition 10
(Murray [11]). Let be a surjective submersion. The following sequence is a long exact sequence
where
Proof.
See Murray [11] (Section 8). Compare Bott and Tu [34] (Proposition 8.5). □
Note that so there exists a unique such that . The differential form H is closed, so it represents a degree-three real cohomology class in M. Proposition 10 shows that the cohomology class of M does not depend on the choices involved.
Definition 10.
Let be a bundle gerbe with connection. The three-curvature (also known as the three-form flux or the Dixmier–Douady form) of is a real differential three-form on M satisfying that .
Remark 8.
In the literature, H is defined as a real-valued differential form in some places and -valued differential form in some other places. Recall that, in Definitions 8 and 9, connection forms and curving forms are -valued, as the Lie algebra of the Lie group is . If we consider the Lie group , its Lie algebra is (here ), and we consider differential forms valued in .
It turns out the three-curvature of a gerbe represents the corresponding de Rham cohomology class of the Dixmier–Douady class above.
Proposition 11
(Murray [11]). Let be a bundle gerbe with a connection. The de Rham cohomology class of its three-curvature form H is equal to the realification of its Dixmier–Douady class ; that is, , where r is the realification map considered in the proof of Proposition 7.
Proof.
See Murray [11] (Section 11). □
Example 5.
Consider the short exact sequence of groups
Let be a principal G-bundle. There is a natural map coming from the transitivity of the right G-action. Pull back the fibration to obtain a -bundle L over . Note that the fiber of is the coset in . So, the multiplication map is defined by the coset multiplication and is readily seen to be associative. So, is a bundle gerbe over M called the lifting bundle gerbe of the principal G-bundle . The Dixmier–Douady class is precisely the obstruction for the lifting of the G-valued cocycle to considered in Proposition 9.
Definition 11.
Let be a good cover of M. The Deligne complex is the double complex endowed with total differential on where the Čech differential is δ and the exterior derivative is d; that is,
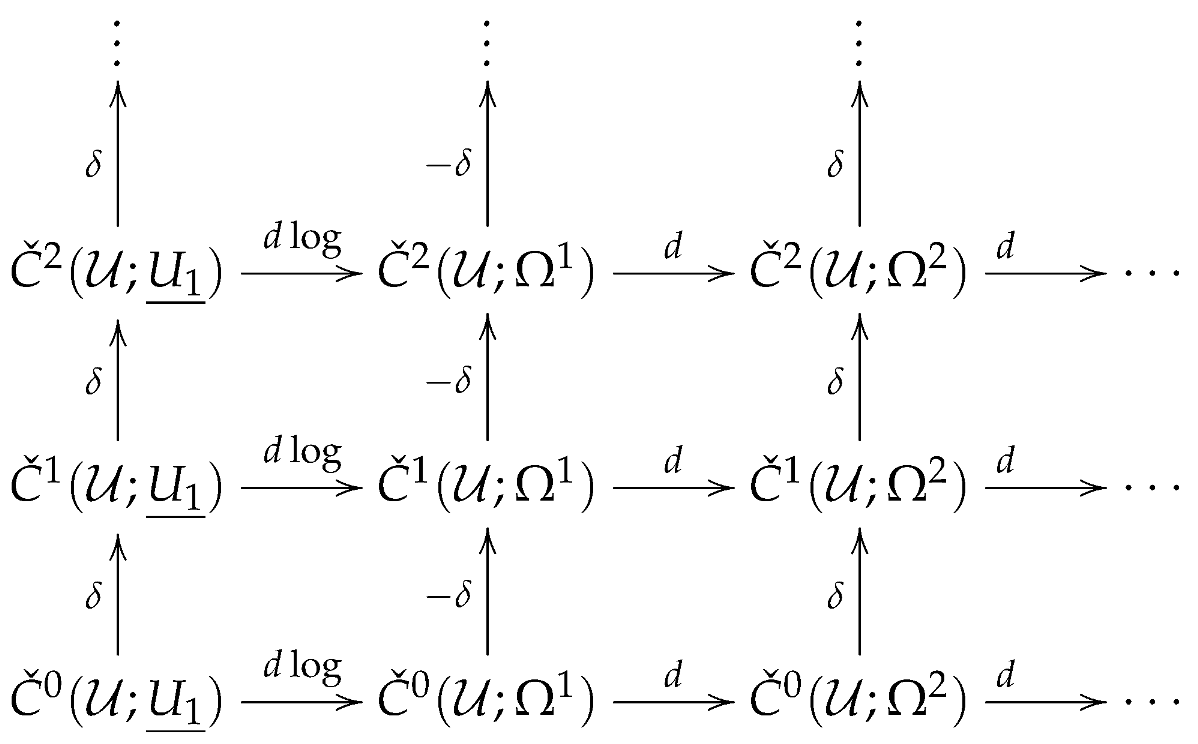 The cohomology of the total complex with the total degree n is the degree n Deligne cohomology group of M defined on .
The cohomology of the total complex with the total degree n is the degree n Deligne cohomology group of M defined on .
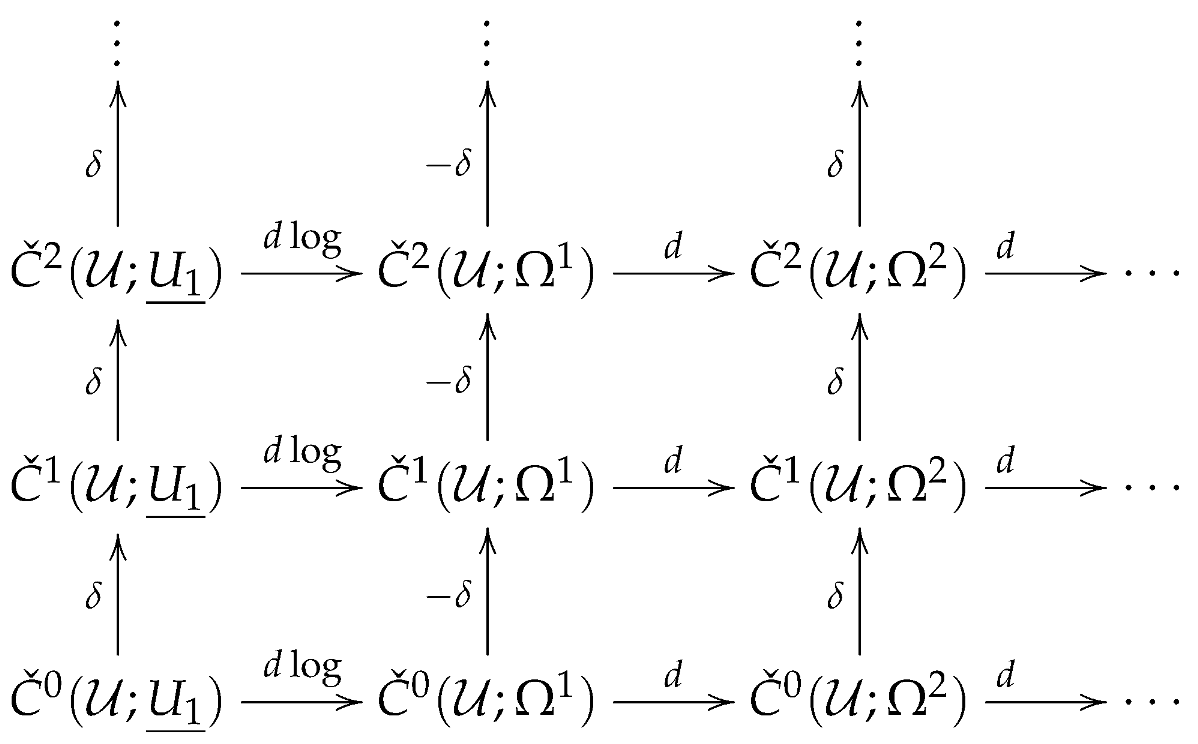
Proposition 12
(Murray [11]). A bundle gerbe with connection determines a total degree 2 cocycle in the Deligne complex.
Proof.
Recall notations in the paragraph between Definitions 6 and 7. In it, we have obtained a Čech 2-cocycle . Let us take and . It is readily seen that the triple satisfies and its cohomology class is independent of the choice of local sections . □
It is natural to ask if the isomorphic bundle gerbes with connection have Deligne-cohomologous cocycles in the Deligne complex. The answer is yes, but there is a subtlety in isomorphisms of bundle gerbes. One might guess that it is a -bundle isomorphism compatible with the bundle gerbe structure , but this is not a notion we want. We will then get non-isomorphic bundle gerbes having the same Dixmier–Douady class. Stevenson [35] and Murray and Stevenson [12] have found that the correct notion of bundle gerbe isomorphism is the “stable isomorphism”. We will introduce a version that Waldorf [36] came up with.
Definition 12
(Waldorf [36]). For , an isomorphism is a quadruple consists of the following.
- (1)
- A surjective submersion
- (2)
- such that .
- (3)
- An isomorphism of -bundles with connection over compatible with and .
Remark 9.
When , we recover the stable isomorphism of Murray and Stevenson [12].
Proposition 13
(Waldorf [36]). There is an equivalence of groupoids between the 1-groupoid of 1-morphisms of and the 1-groupoid of stable isomorphisms of .
Definition 13
(Waldorf [36]). A transformation , which is an isomorphism between isomorphisms from to (that is, a two-morphism), is an equivalence class of triples consisting of the following:
- (1)
- A surjective submersion .
- (2)
- An isomorphism over W compatible with and .
if there is a smooth manifold X with surjective submersions to W and such that the following diagram commutes
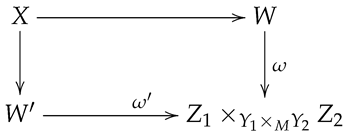 and and coincides if pulled back to X.
and and coincides if pulled back to X.

Proposition 14
(Stevenson [35]). The category consisting of bundle gerbes with the connection as objects, morphisms as defined in Definition 12, and two-morphisms as defined in Definition 13 is a two-groupoid (that is, a category whose morphisms are invertible and whose morphism between morphisms are invertible).
Now, we go back to our discussion on Deligne cohomology. Since the cover of M is good, we can define the Deligne cohomology group as a direct limit over refinements, which is isomorphic to the one defined on . We have the following result.
Proposition 15
(Murray and Stevenson [12]). Let . and are stably isomorphic if and only if they define the same Deligne cohomology class in .
Proof.
See Murray and Stevenson [12] (Theorem 4.1). □
Proposition 16
(Esnault [37]). Let M be a smooth manifold. The following correspondence is an isomorphism:
Proof.
See Brylinski [17] (Proposition 1.5.7) and references therein. □
Corollary 1.
Let M be a smooth manifold. The following are isomorphic as groups
5. Discussion
In this article, we have given an overview of differential cohomology and gerbes. We began with an introduction to characteristic classes and the classification of integral cohomology groups using geometric objects. We then saw differential cohomology and the classification of complex line bundles with connection. Finally, we have seen what a gerbe is and its two-groupoid structure, as well as how gerbes and their higher analogs correspond to cocycles in the Deligne complex.
There are numerous future directions for research based on what we have considered in this paper. We will give three possible directions. First, the G-equivariant differential cohomology has been considered by Redden [2] and Kübel and Thom [38] when the Lie group G is compact. Applications of these constructions have to be developed. Additionally, Redden and the author [39] have established that isomorphism classes of G-equivariant bundle gerbes with a connection are naturally isomorphic to the degree-three differential cohomology of the differential quotient stack. One can expect to establish analogous results for higher gerbes. As a different route, there is an interesting relationship between the arithmetic Chow group of a complex projective variety and its differential cohomology group [6]. One has to cast a light on this result to generalize it as a result over the Deligne–Mumford stacks. Finally, along the vein of the work of Freed and Moore [40] and Gawȩdzki [15], the theory of differential cohomology and gerbes should be further developed to investigate the topology of matters.
Funding
This research received no funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author thanks Sajjad Lakzian, Insong Choe, and Jaigyoung Choe for giving the motivation to write this paper and its earlier drafts. He also thanks the anonymous referees for helpful comments that improved the readability of the paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Fiorenza, D.; Schreiber, U.; Stasheff, J. Čech cocycles for differential characteristic classes: An ∞-Lie theoretic construction. Adv. Theor. Math. Phys. 2012, 16, 149–250. [Google Scholar]
- Redden, C. Differential Borel equivariant cohomology via connections. N. Y. J. Math. 2017, 23, 441–487. [Google Scholar]
- Behrend, K.; Liao, H.-Y.; Xu, P. Derived Differentiable Manifolds. arXiv 2021, arXiv:2006.01376. [Google Scholar] [CrossRef]
- Deligne, P. Théorie de Hodge. II. Inst. Hautes Études Sci. Publ. Math. 1971, 40, 5–57. [Google Scholar]
- Cheeger, J.; Simons, J. Differential Characters and Geometric Invariants; Springer: Berlin/Heidelberg, Germany, 1985; pp. 50–80. [Google Scholar] [CrossRef]
- Gillet, H.; Soulé, C. Arithmetic Chow Groups and Differential Characters; Springer: Berlin/Heidelberg, Germany, 1989; pp. 29–68. [Google Scholar]
- Neumann, W.D. Realizing Arithmetic Invariants of Hyperbolic 3-Manifolds; AMS: Providence, RI, USA, 2011; pp. 233–246. [Google Scholar] [CrossRef]
- Hopkins, M.J.; Singer, I.M. Quadratic functions in geometry, topology, and M-theory. J. Differ. Geom. 2005, 70, 329–452. [Google Scholar]
- Giraud, J. Cohomologie non Abélienne; Die Grundlehren der mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 1971; Volume Band 179, pp. ix+467. [Google Scholar]
- Grothendieck, A.; Raynaud, M. Revêtements Étales et Groupe Fondamental; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1971; Volume 224, pp. xxii+447. [Google Scholar]
- Murray, M.K. Bundle gerbes. J. Lond. Math. Soc. 1996, 54, 403–416. [Google Scholar] [CrossRef]
- Murray, M.K.; Stevenson, D. Bundle gerbes: Stable isomorphism and local theory. J. Lond. Math. Soc. 2000, 62, 925–937. [Google Scholar] [CrossRef]
- Berwick-Evans, D.; Pavlov, D. Smooth one-dimensional topological field theories are vector bundles with connection. Algebr. Geom. Topol. 2023, 23, 3707–3743. [Google Scholar] [CrossRef]
- Gawȩdzki, K.; Reis, N. WZW branes and gerbes. Rev. Math. Phys. 2002, 14, 1281–1334. [Google Scholar] [CrossRef]
- Gawȩdzki, K. Square root of gerbe holonomy and invariants of time-reversal-symmetric topological insulators. J. Geom. Phys. 2017, 120, 169–191. [Google Scholar] [CrossRef][Green Version]
- Schreiber, U.; Waldorf, K. Connections on non-abelian gerbes and their holonomy. Theory Appl. Categ. 2013, 28, 476–540. [Google Scholar]
- Brylinski, J.-L. Loop Spaces, Characteristic Classes and Geometric Quantization; Modern Birkhäuser Classics; Birkhäuser Boston, Inc.: Boston, MA, USA, 2008; pp. xvi+300, Reprint of the 1993 edition. [Google Scholar] [CrossRef]
- Dixmier, J.; Douady, A. Champs continus d’espaces hilbertiens et de C*-algèbres. Bull. Soc. Math. France 1963, 91, 227–284. [Google Scholar]
- Lawson, H.B., Jr.; Michelsohn, M.-L. Spin Geometry; Princeton Mathematical Series; Princeton University Press: Princeton, NJ, USA, 1989; Volume 38, pp. xii+427. [Google Scholar]
- Sati, H.; Schreiber, U.; Stasheff, J. Fivebrane structures. Rev. Math. Phys. 2009, 21, 1197–1240. [Google Scholar] [CrossRef]
- MacLane, S. Categories for the Working Mathematician; Graduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 1971; Volume 5, pp. ix+262. [Google Scholar]
- Morita, S. Geometry of Differential Forms; Translations of Mathematical Monographs; Translated from the Two-Volume Japanese Original (1997, 1998) by Teruko Nagase and Katsumi Nomizu—Iwanami Series in Modern Mathematics; American Mathematical Society: Providence, RI, USA, 2001; Volume 201, pp. xxiv+321. [Google Scholar] [CrossRef]
- Harvey, R.; Lawson, B.; Zweck, J. The de Rham-Federer theory of differential characters and character duality. Am. J. Math. 2003, 125, 791–847. [Google Scholar]
- Bunke, U.; Nikolaus, T.; Völkl, M. Differential cohomology theories as sheaves of spectra. J. Homotopy Relat. Struct. 2016, 11, 1–66. [Google Scholar] [CrossRef]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2002; pp. xii+544. [Google Scholar]
- Simons, J.; Sullivan, D. Axiomatic characterization of ordinary differential cohomology. J. Topol. 2008, 1, 45–56. [Google Scholar] [CrossRef]
- Bunke, U.; Schick, T. Uniqueness of smooth extensions of generalized cohomology theories. J. Topol. 2010, 3, 110–156. [Google Scholar] [CrossRef][Green Version]
- Stimpson, A.J. Axioms for Differential Cohomology. Ph.D. Thesis, State University of New York, Stony Brook, NY, USA, 2011; p. 55. [Google Scholar]
- Stolz, S.; Teichner, P. Supersymmetric Field Theories and Generalized Cohomology; American Mathematical Society: Providence, RI, USA, 2011; pp. 279–340. [Google Scholar] [CrossRef]
- Stoffel, A. Supersymmetric Field Theories and Orbifold Cohomology. Ph.D. Thesis, University of Notre Dame, Notre Dame, IN, USA, 2016; p. 137. [Google Scholar]
- Stoffel, A. Supersymmetric field theories from twisted vector bundles. Comm. Math. Phys. 2019, 367, 417–453. [Google Scholar] [CrossRef]
- Behrend, K.; Xu, P. Differentiable stacks and gerbes. J. Symplectic Geom. 2011, 9, 285–341. [Google Scholar] [CrossRef]
- Moerdijk, I. Introduction to the language of stacks and gerbes. arXiv 2002, arXiv:0212266. [Google Scholar] [CrossRef]
- Bott, R.; Tu, L.W. Differential Forms in Algebraic Topology; Graduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 1982; Volume 82, pp. xiv+331. [Google Scholar]
- Stevenson, D. The Geometry of Bundle Gerbes. Ph.D. Thesis, The University of Adelaide, Adelaide, Australia, 2000. [Google Scholar]
- Waldorf, K. More morphisms between bundle gerbes. Theory Appl. Categ. 2007, 18, 240–273. [Google Scholar]
- Esnault, H. Characteristic classes of flat bundles. Topology 1988, 27, 323–352. [Google Scholar] [CrossRef]
- Kübel, A.; Thom, A. Equivariant differential cohomology. Trans. Am. Math. Soc. 2018, 370, 8237–8283. [Google Scholar] [CrossRef]
- Park, B.; Redden, C. A classification of equivariant gerbe connections. Commun. Contemp. Math. 2019, 21, 1850001. [Google Scholar] [CrossRef]
- Freed, D.S.; Moore, G.W. Twisted equivariant matter. Ann. Henri Poincaré 2013, 14, 1927–2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).