New Results for the Investigation of the Asymptotic Behavior of Solutions of Nonlinear Perturbed Differential Equations

Abstract

This study focuses on investigating the oscillatory properties of a particular class of perturbed differential equations in the noncanonical case. Our research aims to establish more effective criteria for evaluating the absence of positive solutions to the equation under study and subsequently investigate its oscillatory behavior. We also perform a comparative analysis, contrasting the oscillation of the studied equation with another equation in the canonical case. To achieve this, we employ the Riccati technique along with other methods to obtain several sufficient criteria. Furthermore, we apply these new conditions to specific instances of the considered equation, assessing their performance. The significance of our work lies in its extension and broadening of the existing body of literature, contributing novel insights into this field of study.

1. Introduction

Natural and technological phenomena are usually described by differential equations (DEs): inevitable relationships that include continuous variables (as functions) and their rate of change in time (as derivatives). DEs appear in applied mathematics such as in classical mechanics where the motion of objects is described by speed and acceleration, which are the rates of the change in distance with respect to time. DEs are crucial for actually modeling technical, physical, ecological, biological, and epidemiological processes, such as celestial motion, bridge construction, interactions between neurons, relationships between species, disease spread within a population, etc., see for example [1,2,3,4,5,6].

Applications in the domains of biology, population, chemistry, medicine dynamics, social sciences, genetic engineering, economy, and others were made possible by science’s incredibly rapid development in the 20th century. With the aid of this type of mathematical modeling, all of these disciplines advanced, and new discoveries were made. Understanding these problems and phenomena—or at the very least knowing the features of the solutions to these equations—requires knowing the equation’s solution. However, it is possible that DEs employed to address real-world issues are not always directly solvable, i.e., do not have closed-form solutions. Only the simplest equations allow for clear, formulaic solutions. However, it is possible to determine some aspects of a solution to a specific DE without knowing their precise form. If there is not a self-contained formula for the solution, it could be numerically approximated by computers. In this situation, a recurrence relation—an equation that recursively defines a series—is required, in which each term in the sequence is defined as a function of the terms that came before it.

These numerous applications stimulated the study of the qualitative theory of DEs. The qualitative behaviors—stability, boundedness, periodicity and oscillatory, etc.—of the solutions of DEs give very important impressions and information when studying the various natural models.

In the first half of the 20th century, Fite [7] produced a ground-breaking paper that established the oscillation theory of DEs with divergent justifications. The basic principles of oscillation theory are to test the existence of oscillatory or nonoscillating solutions or to study the asymptotic behavior of nonoscillatory solutions. Oscillation theory generally follows one of two main streams. The first of them relies on the analysis of the zero distribution laws in order to establish the minimal distance between consecutive zeros. The second stream investigates the number of zeros in a given interval along with the relation between the oscillatory qualities and oscillatory processes in systems with different physical parameters. This interest is reflected in numerous studies, many of which are compiled in monographs [8,9,10,11,12,13,14].

In this study, using several techniques, we obtain new conditions that test the oscillatory properties of the solution of the perturbed DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·{\left(\frac{\mathrm{d}}{\mathrm{d}t}u\right)}^{\beta }\right)+F_1\left(t,u\right)=F_2\left(t,u,\frac{\mathrm{d}}{\mathrm{d}t}u\right),$$

(1)

where $t\in {\mathcal{I}}_0,$${\mathcal{I}}_i:=\left[t_i,\infty \right)$ and $\beta \ge 1$ is a ratio of odd natural numbers. In addition, we assume the following constraints:

H1. 

$a\in {\mathbf{C}}^1\left({\mathcal{I}}_0,{\mathbb{R}}^{+}\right)$, and $\eta \left(t_0\right)<\infty$, where

$$\eta \left(t\right):={\int }_t^{\infty }{a}^{-1/\beta }\left(v\right)\mathrm{d}v;$$

H2. 

$F_1\in \mathbf{C}\left({\mathcal{I}}_0\times \mathbb{R},\mathbb{R}\right)$, $F_2\in \mathbf{C}\left({\mathcal{I}}_0\times {\mathbb{R}}^2,\mathbb{R}\right),$ $u{F}_1\left(t,u\right)>0$ and $u{F}_2\left(t,u,y\right)>0$ for $u\ne 0$;

H3. 

There exist functions $\varphi ,$ $\phi \in \mathbf{C}\left({\mathcal{I}}_0,\mathbb{R}\right)$ and $h\in \mathbf{C}\left(\mathbb{R},\mathbb{R}\right)$ such that $\varphi \left(t\right)<\phi \left(t\right)$ for $t\in {\mathcal{I}}_0,$ $uh\left(u\right)>0$ for $u\ne 0,$ h is nondecreasing, $h\left(uy\right)\ge h\left(u\right)h\left(y\right)$, $F_1\left(t,u\right)\ge \phi \left(t\right)h\left(u\right)$ and $F_2\left(t,u,y\right)\le \varphi \left(t\right)h\left(u\right),$ for $u,y\in \mathbb{R}\backslash \left\{0\right\}$ and $t\in {\mathcal{I}}_0$.

For a solution of Equation (1), we denote a function $u\in {\mathbf{C}}^1\left({\mathcal{I}}_u\right)$ for $t_u\in {\mathcal{I}}_0$, which $a·{\left(u^{\prime }\right)}^{\beta }$$\in {\mathbf{C}}^1\left({\mathcal{I}}_u\right)$ and u satisfies (1) for $t\in {\mathcal{I}}_u$. We take into account these solutions u of Equation (1) such that $sup\left\{\left|u\left(t\right)\right|:t\ge T\right\}>0$ for $T\in {\mathcal{I}}_u$. A solution u of Equation (1) is said to be nonoscillatory if it is eventually positive or eventually negative; otherwise, it is said to be oscillatory.

In this paper, we obtain conditions that test the oscillation of solutions of perturbed DE Equation (1). Equations of this type have not received as much attention as other types of equations, such as half-linear equations or equations of the Emden–Fowler type. We use more than one approach to obtain the oscillation criteria. We couple the oscillation of DE Equation (1) with a canonical equation of the second-order. We further extend the approach used in [15] to obtain a new oscillation criterion for DE Equation (1). Furthermore, we use a generalized Riccati substitution to obtain sharper criteria. Finally, we present examples to support the theoretical results.

Relevant Literature Review

In the following, some of the previous works that are relevant to our study are reviewed.

In 1980, Grace and Lalli [16] investigated the oscillatory properties of the perturbed DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·\frac{\mathrm{d}}{\mathrm{d}t}u\right)+p·\frac{\mathrm{d}}{\mathrm{d}t}u+F_1\left(t,u\right)=F_2\left(t,u,\frac{\mathrm{d}}{\mathrm{d}t}u\right).$$

For a DE with alternating coefficients

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·\left[\psi \circ u\right]·\frac{\mathrm{d}}{\mathrm{d}t}u\right)+p·\frac{\mathrm{d}}{\mathrm{d}t}u+q·\left[F\circ u\right]=0,$$

(2)

Grace and Lalli [17] analyzed the convergence of its oscillatory solutions and developed some standards for the asymptotic behavior of this equation. Shortly before the previous works, Kartsatos [18] studied the oscillatory behavior of the n-order perturbed DE

$$\frac{{\mathrm{d}}^n}{\mathrm{d}{t}^n}u+F_1\left(t,u\right)=F_2\left(t,u\right).$$

Kirane and Rogovchenko [19] investigated the oscillatory properties of the DE Equation (2). To determine the oscillation criteria, they employed a method based on the average behavior of the integral of the coefficient q.

By using Riccati transformation, Jianchu and Xiaoping [20] created Philos-type standards that guarantee the oscillation of the perturbed DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·{\left(\frac{\mathrm{d}}{\mathrm{d}t}u\right)}^{\beta }\right)+p·{\left(\frac{\mathrm{d}}{\mathrm{d}t}u\right)}^{\beta }+F_1\left(t,u\right)=F_2\left(t,u,\frac{\mathrm{d}}{\mathrm{d}t}u\right).$$

Bohner and Saker [21] studied the oscillation of Equation (1) in the canonical and noncanonical case. They used Riccati substitution to constrain the coefficients to ensure that each solution of Equation (1) oscillates or approaches zero.

In 2005, Mustafa and Rogovchenko [22] discussed the oscillatory properties of solutions of

$$\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}u+F\left(t,u\right)=p\left(t\right)$$

under the constraint

$${\int }_{t_0}^{\infty }v\left|p\left(v\right)\right|\mathrm{d}v<\infty .$$

Recently, Moaaz et al. [23] studied the oscillatory properties of the damped DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·\frac{\mathrm{d}}{\mathrm{d}t}u\right)+p·\frac{\mathrm{d}}{\mathrm{d}t}u+q·\left[u\circ \tau \right]=0,$$

where p change their sign and q are nonnegative. They presented criteria of an iterative nature and that are characterized by having one condition. The iterative nature allows it to be used repeatedly even if it fails at first.

Despite the large number of recent works that discussed the oscillation of the solutions of DEs, this theory was and still is rich in interesting analytical issues and open problems.

In the noncanonical case $\eta \left(t_0\right)<\infty$, one of the interesting problems in studying the oscillation of DEs is obtaining a single criterion that guarantees the oscillation of all solutions. In 2017, Bohner et al. [24] presented one-condition criteria for the oscillation of neutral DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·{\left(\frac{\mathrm{d}}{\mathrm{d}t}\left(u+p·\left(u\circ \tau \right)\right)\right)}^{\beta }\right)+q·{\left(u\circ \sigma \right)}^{\beta }=0.$$

(3)

By iterative improvement of the monotonic properties, Bohner et al. [25] introduced sharp oscillation criteria for Equation (3).

In the neutral equations, one of the interesting issues is also obtaining sharp inequalities that link the solution to its associated function. The conventional inequality $u>\left(1-p\right)z$ is usually used when $\eta \left(t_0\right)=\infty$. On the other hand, for positive decreasing solutions, the inequality $u>z\left(1-p\left(\left(\eta \circ \tau \right)/\eta \right)\right)$ is used when $\eta \left(t_0\right)<\infty$, see [26]. Moaaz et al. [27] improved the last relationship and considered both cases $p<1$ and $p>1$. Nevertheless, the results in [27] were constrained by the condition $p\left(t\right)=p_0$ (a constant). Very recently, Bohner et al. [28] improved the relationship $u>z\left(1-p\left(\left(\eta \circ \tau \right)/\eta \right)\right)$ in both delay and advanced cases.

Third-order DEs have also not received the same attention as the equations of the even orders, and the study of the oscillation of these equations contains many open problems. Works [29,30,31] presented interesting results in the study of fluctuating solutions of third-order DEs.

On the other hand, for the higher-order equations, Onose [32] studied the oscillation of DE

$$\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}\left(a·\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}u\right)+F\left(\left(u\circ g\right),t\right)=0$$

and

$$\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}\left(a·\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}u\right)+q·F\left(u\circ g\right)=h,$$

under the restriction

$${\int }_T^{\infty }{a}^{-1}\left(\nu \right)\mathrm{d}\nu =\infty ,\mathrm{for}\mathrm{some}T>0.$$

The oscillatory characteristics of solutions for distinct classes of equations were discovered by utilizing a wide range of methodologies. Agarwal et al. [33] presented some oscillation results for the DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left[a_3^{-1}{\left(\frac{\mathrm{d}}{\mathrm{d}t}\left[a_2^{-1}{\left(\frac{\mathrm{d}}{\mathrm{d}t}\left[a_1^{-1}{\left(\frac{\mathrm{d}}{\mathrm{d}t}u\right)}^{{\alpha }_1}\right]\right)}^{{\alpha }_2}\right]\right)}^{{\alpha }_3}\right]\pm q·F\left(u\circ g\right)=0,$$

under the restrictions

$${\int }_{t_0}^{\infty }{a}_k^{1/{\alpha }_i}\left(\nu \right)\mathrm{d}\nu =\infty ,k=1,2,3.$$

Grace et al. [34] devised theorems that test the oscillation of the DE

$$\frac{{\mathrm{d}}^3}{\mathrm{d}{t}^3}\left(a·{\left(\frac{\mathrm{d}}{\mathrm{d}t}u\right)}^{\alpha }\right)+q·F\left(u\circ g\right)=0,$$

For the DE

$$\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}\left(a·{\left|\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}u\right|}^{\alpha -1}\frac{{\mathrm{d}}^2}{\mathrm{d}{t}^2}u\right)+q·{\left|u\right|}^{\beta -1}·u=0,$$

the oscillatory behavior of its solutions was tested by the results in [35,36]. In [37], Zhang et al. discussed the asymptotic properties of the solutions of the DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(a·{\left(\frac{{\mathrm{d}}^{n-1}}{\mathrm{d}{t}^{n-1}}u\right)}^{\alpha }\right)+q·\left(u^{\beta }\circ \sigma \right)=0,$$

(4)

where $\beta \le \alpha$.

2. Main Results

We start by defining some functions and notations that make it easier to present the results.

2.1. Notation and Preliminary Results

Lemma 1

([24]). Suppose that $H\left(s\right)=Ks-L{\left(s-M\right)}^{1+1/\beta }$, where $L>0$, K and M are constants. Then, at $s^{*}=M+{\left(\beta K/\left(\left(\beta +1\right)L\right)\right)}^{\beta }$, H reaches its maximum value on $\mathbb{R}$, and

$$\underset{s\in \mathbb{R}}{max}H\left(s\right)=H\left(s^{*}\right)=KM+\frac{{\beta }^{\beta }}{{\left(\beta +1\right)}^{\beta +1}}\frac{K^{\beta +1}}{L^{\beta }}.$$

Notation 1.

During the paper, we refer to the composition operation with the symbol $\left(\circ \right)$, so that $\left[f\circ g\right]\left(t\right):=f\left(g\left(t\right)\right)$. We denote the class of all eventually positive decreasing solutions of Equation (1) with the symbol ${\mathcal{P}}_s$.

Lemma 2.

Assume that

$$a^{1/\beta }·{\eta }^{\beta +1}·\left(\phi -\varphi \right)\ge \beta {\kappa }^{\beta },$$

(5)

for some $\kappa >0$. Then each nonoscillatory solution of Equation (1) is decreasing and converges to zero.

Proof. 

Assuming that Equation (1) has a nonoscillatory solution necessarily means that it has an eventually positive one, say u. Using assumption (H3), Equation (1) becomes

$$\begin{array}{ccc}\hfill {\left(a·{\left(u^{\prime }\right)}^{\beta }\right)}^{\prime }& =& F_2\left(t,u,u^{\prime }\right)-F_1\left(t,u\right)\hfill \\ & \le & -\left(\phi -\varphi \right)·\left[h\circ u\right].\hfill \end{array}$$

(6)

Then, $a·{\left(u^{\prime }\right)}^{\beta }$ is nonincreasing, and so $u^{\prime }$ is of one sign. Before proceeding to prove the required equation, we need to calculate the following integral:

$${\int }_{t_1}^{\infty }\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v,$$

for $t_1\in {\mathcal{I}}_0$. Based on assumption Equation (5), we conclude that

$$\begin{array}{ccc}\hfill {\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v& \ge & \beta {\kappa }^{\beta }{\int }_{t_1}^t\frac{1}{a^{1/\beta }\left(v\right){\eta }^{\beta +1}\left(v\right)}\mathrm{d}v\hfill \\ & =& {\kappa }^{\beta }\left(\frac{1}{{\eta }^{\beta }\left(t\right)}-\frac{1}{{\eta }^{\beta }\left(t_1\right)}\right).\hfill \end{array}$$

(7)

Since $\eta \to 0$ as $t\to \infty$, we find eventually that ${\eta }^{-\beta }\left(t\right)\ge \lambda {\eta }^{-\beta }\left(t\right)+{\eta }^{-\beta }\left(t_1\right)$ for all $\lambda \in \left(0,1\right)$.

Therefore,

$${\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v\ge {\kappa }^{\beta }\lambda \frac{1}{{\eta }^{\beta }\left(t\right)},$$

(8)

and so

$$\underset{t\to \infty }{lim}{\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v=\infty .$$

(9)

Suppose, conversely, that $u^{\prime }$ is positive. Then, $u\to c_0>0$ as $t\to \infty$, which leads to $u\left(t\right)\ge c_0$ for all $t\in {\mathcal{I}}_1$ for some $t_1\in {\mathcal{I}}_0$. It follows from Equation (6) that

$${\left(a·{\left(u^{\prime }\right)}^{\beta }\right)}^{\prime }\le -h\left(c_0\right)\left(\phi -\varphi \right).$$

After integrating this inequality, we obtain

$$a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }\ge h\left(c_0\right){\int }_{t_1}^{\infty }\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v.$$

(10)

Hence, taking ${lim}_{t\to \infty }$ and using Equation (9), we obtain that $a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }\to \infty$, which is a contradiction.

Now, we have that $u^{\prime }\left(t\right)<0$, and so $u\to c_1\ge 0$ as $t\to \infty$.

Suppose, conversely, that $c_1$ is positive. Then, $u\left(t\right)\ge c_1$ for all $t\in {\mathcal{I}}_1$ for some $t_1\in {\mathcal{I}}_0$.

Integrating Equation (6) from $t_1$ to t, we conclude that

$$\begin{array}{ccc}\hfill a\left(t\right){\left(u^{\prime }\left(t\right)\right)}^{\beta }& \le & a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }-{\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)h\left(u\left(v\right)\right)\mathrm{d}v\hfill \\ & \le & -h\left(c_1\right){\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v,\hfill \end{array}$$

which, with Equation (8), gives

$$u^{\prime }\le -\kappa {\left[\lambda h\left(c_1\right)\right]}^{1/\beta }\frac{1}{a^{1/\beta }·\eta }.$$

Then,

$$\begin{array}{ccc}\hfill u\left(t_1\right)& \ge & \kappa {\left[\lambda h\left(c_1\right)\right]}^{1/\beta }{\int }_{t_1}^t\frac{1}{a^{1/\beta }\left(v\right)\eta \left(v\right)}\mathrm{d}v\hfill \\ & =& \kappa {\left[\lambda h\left(c_1\right)\right]}^{1/\beta }log\frac{\eta \left(t_1\right)}{\eta \left(t\right)},\hfill \end{array}$$

which tends to ∞ as $t\to \infty$, which is a contradiction. Then, $c_1=0$. □

2.2. Oscillation Criteria

Using an approach that is an extension of the approach taken in Koplatadze et al. [15], we present through the next theorem, a new condition to ensure the oscillation of Equation (1).

Theorem 1.

Assume that Equation (5) holds for some $\kappa >0$, and

$$\underset{w\to 0}{lim}\frac{w^{\beta }}{h\left(w\right)}={\mu }_0<\infty .$$

(11)

If

$$\begin{array}{ccc}& & \underset{t\to \infty }{limsup}\left[{\eta }^{\beta }\left(t\right){\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v\right.\hfill \\ & & \left.+h\left(\frac{1}{\eta \left(t\right)}\right){\int }_t^{\infty }\left(\phi \left(v\right)-\varphi \left(v\right)\right){\eta }^{\beta }\left(v\right)h\left(\eta \left(v\right)\right)\mathrm{d}v\right]>\beta {\mu }_0,\hfill \end{array}$$

(12)

then DE Equation (1) is oscillatory.

Proof. 

Conversely, assuming that Equation (1) has a nonoscillatory solution necessarily means that it has an eventually positive one, say u. Assume that $u\left(t\right)>0$ for $t\ge t_1\in {\mathcal{I}}_0$. Since $a^{1/\beta }·u^{\prime }$ is decreasing, we obtain

$$-u\left(t\right)={\int }_t^{\infty }\frac{1}{a^{1/\beta }\left(v\right)}{a}^{1/\beta }\left(v\right)u^{\prime }\left(v\right)\mathrm{d}v\le a^{1/\beta }\left(t\right)u^{\prime }\left(t\right)\eta \left(t\right),$$

(13)

and so

$${\left(\frac{u}{\eta }\right)}^{\prime }=\frac{1}{{\eta }^2}\left(\eta ·u^{\prime }+a^{-1/\beta }·u\right)\ge 0.$$

From Equation (6), we have

$$\begin{array}{ccc}\hfill -\left(\phi -\varphi \right)·\left[h\circ u\right]& \ge & {\left(a·{\left(u^{\prime }\right)}^{\beta }\right)}^{\prime }\hfill \\ & =& \beta {\left(a^{1/\beta }·u^{\prime }\right)}^{\beta -1}{\left(a^{1/\beta }·u^{\prime }\right)}^{\prime }.\hfill \end{array}$$

(14)

It follows from Equation (13) that

$${\left(a^{1/\beta }·u^{\prime }\right)}^{\prime }\le -\frac{1}{\beta }\left(\phi -\varphi \right)·{\left(\frac{u}{\eta }\right)}^{1-\beta }·\left[h\circ u\right].$$

(15)

This inequality can be written in the form

$${\left(\eta ·a^{1/\beta }·u^{\prime }+u\right)}^{\prime }\le -\frac{1}{\beta }\eta ·\left(\phi -\varphi \right)·{\left(\frac{u}{\eta }\right)}^{1-\beta }·\left[h\circ u\right]\le 0.$$

(16)

Note that $\eta ·a^{1/\beta }·u^{\prime }+u$ is positive and decreasing. Then,

$$\eta \left(t\right)a^{1/\beta }\left(t\right)u^{\prime }\left(t\right)+u\left(t\right)\ge \frac{1}{\beta }{\int }_t^{\infty }\eta \left(v\right)\left(\phi \left(v\right)-\varphi \left(v\right)\right){\left(\frac{u\left(v\right)}{\eta \left(v\right)}\right)}^{1-\beta }h\left(u\left(v\right)\right)\mathrm{d}v.$$

(17)

Moreover, integration Equation (15) from $t_1$ to t gives

$$-a^{1/\beta }\left(t\right)u^{\prime }\left(t\right)\ge \frac{1}{\beta }{\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right){\left(\frac{u\left(v\right)}{\eta \left(v\right)}\right)}^{1-\beta }h\left(u\left(v\right)\right)\mathrm{d}v,$$

which, with Equation (17), gives

$$\begin{array}{ccc}\hfill \beta u\left(t\right)& \ge & \eta \left(t\right){\int }_{t_1}^t\left(\phi \left(\upsilon \right)-\varphi \left(\upsilon \right)\right)h\left(u\left(\upsilon \right)\right){\left(\frac{u\left(\upsilon \right)}{\eta \left(\upsilon \right)}\right)}^{1-\beta }\mathrm{d}v\hfill \\ & & +{\int }_t^{\infty }\eta \left(\upsilon \right)\left(\phi \left(\upsilon \right)-\varphi \left(\upsilon \right)\right)h\left(u\left(\upsilon \right)\right){\left(\frac{u\left(v\right)}{\eta \left(v\right)}\right)}^{1-\beta }\mathrm{d}v\hfill \end{array}$$

(18)

Using the facts that $u^{\prime }\left(t\right)<0$ and ${\left(u\left(t\right)/\eta \left(t\right)\right)}^{\prime }\ge 0$, we arrive at

$$\begin{array}{ccc}\hfill \beta \frac{u^{\beta }\left(t\right)}{h\left(u\left(t\right)\right)}& \ge & {\eta }^{\beta }\left(t\right){\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v\hfill \\ & & +h\left(\frac{1}{\eta \left(t\right)}\right){\int }_t^{\infty }\left(\phi \left(v\right)-\varphi \left(v\right)\right){\eta }^{\beta }\left(v\right)h\left(\eta \left(v\right)\right)\mathrm{d}v,\hfill \end{array}$$

This contradicts assumption Equation (12). □

It is easy to see that the oscillation criteria of the canonical DEs have been established using many methods and techniques, and these equations have received most attention in the past. Therefore, it is useful to compare the oscillation of the solutions of Equation (1) with another equation in the canonical case, as in the following theorem.

Theorem 2.

Assume that Equation (5) holds for some $\kappa >0$, and $h\left(w\right)=w^{\beta }$. If the DE

$${\left({\eta }^2·a^{1/\beta }·y^{\prime }\right)}^{\prime }+\frac{1}{\beta }{\eta }^{\beta +1}·\left(\phi -\varphi \right)·y=0$$

(19)

is oscillatory, then DE Equation (1) is oscillatory.

Proof. 

Conversely, assuming that Equation (1) has a nonoscillatory solution necessarily means that it has an eventually positive one, say u. Assume that $u\left(t\right)>0$ for $t\ge t_1\in {\mathcal{I}}_0$. Then, it follows from Lemma 2 that $u^{\prime }\left(t\right)<0$ for $t\ge t_1$. Proceeding as in the proof of Theorem 1, we arrive at Equation (16). Thus,

$${\left(\eta ·a^{1/\beta }·u^{\prime }+u\right)}^{\prime }+\frac{1}{\beta }{\eta }^{\beta }·\left(\phi -\varphi \right)·u\le 0,$$

which, with the fact that

$$\frac{\eta ·a^{1/\beta }·u^{\prime }+u}{a^{1/\beta }·{\eta }^2}={\left(\frac{u}{\eta }\right)}^{\prime },$$

gives

$${\left({\eta }^2·a^{1/\beta }·{\left(\frac{u}{\eta }\right)}^{\prime }\right)}^{\prime }+\frac{1}{\beta }{\eta }^{\beta }·\left(\phi -\varphi \right)·u\le 0.$$

(20)

Now, if we set $y=u/\eta >0$, then Equation (20) becomes

$${\left({\eta }^2·a^{1/\beta }·y^{\prime }\right)}^{\prime }+\frac{1}{\beta }{\eta }^{\beta +1}·\left(\phi -\varphi \right)·y\le 0.$$

Using Corollary 1 in [38], the associated Equation (19) also has a positive solution. This contradicts the hypotheses of the theorem. □

One of the well-known criteria that guarantee the oscillation of the solutions of DE

$${\left(r\left(t\right)y^{\prime }\left(t\right)\right)}^{\prime }+Q\left(t\right)y\left(t\right)=0,$$

in the canonical case, is

$$\underset{t\to \infty }{liminf}\left({\int }_{t_0}^t{r}^{-1}\left(v\right)\mathrm{d}v\right){\int }_t^{\infty }Q\left(\upsilon \right)\mathrm{d}\upsilon >\frac{1}{4},$$

see for example [39]. Using this criterion, we obtain the following corollary:

Corollary 1.

Assume that Equation (5) holds for some $\kappa >0$, and $h\left(w\right)=w^{\beta }$. If

$$\underset{t\to \infty }{liminf}\left({\int }_{t_0}^t\frac{1}{{\eta }^2\left(v\right)a^{1/\beta }\left(v\right)}\mathrm{d}v\right){\int }_t^{\infty }{\eta }^{\beta +1}\left(\upsilon \right)\left(\phi \left(\upsilon \right)-\varphi \left(\upsilon \right)\right)\mathrm{d}\upsilon >\frac{\beta }{4},$$

then DE Equation (1) is oscillatory.

The Riccati substitution technique is a popular method when studying the oscillation of DEs. In the following, using a generalized Riccati substitution, we establish another criterion for the oscillation of Equation (1).

Theorem 3.

Assume that Equations (5) and (11) hold for some $\kappa >0$. If

$$\underset{t\to \infty }{limsup}\frac{{\eta }^{\beta }\left(t\right)}{\rho \left(t\right)}{\int }_{t_0}^t\left(\frac{1}{{\mu }_0}\rho \left(\upsilon \right)\left(\phi \left(\upsilon \right)-\varphi \left(\upsilon \right)\right)-\frac{a\left(\upsilon \right){\left({\rho }^{\prime }\left(\upsilon \right)\right)}^{1+\beta }}{{\left(1+\beta \right)}^{1+\beta }{\rho }^{\beta }\left(\upsilon \right)}\right)\mathrm{d}\upsilon >1,$$

(21)

then DE Equation (1) is oscillatory.

Proof. 

Conversely, assuming that Equation (1) has a nonoscillatory solution necessarily means that it has an eventually positive one, say u. Assume that $u\left(t\right)>0$ for $t\ge t_1\in {\mathcal{I}}_0$.

Now, we define the function

$$\mathcal{R}:=\rho ·\left(a·{\left(\frac{u^{\prime }}{u}\right)}^{\beta }+\frac{1}{{\eta }^{\beta }}\right).$$

(22)

It follows from Equation (13) that $\mathcal{R}\ge 0$, for $t\in {\mathcal{I}}_1$. Then,

$${\mathcal{R}}^{\prime }=\frac{{\rho }^{\prime }}{\rho }·\mathcal{R}+\rho ·\left(\frac{{\left(a·{\left(u^{\prime }\right)}^{\beta }\right)}^{\prime }}{u^{\beta }}-\beta a·{\left(\frac{u^{\prime }}{u}\right)}^{\beta +1}+\frac{\beta }{a^{1/\beta }·{\eta }^{\beta +1}}\right),$$

which, with Equation (6), gives

$$\begin{array}{ccc}\hfill {\mathcal{R}}^{\prime }& \le & \frac{{\rho }^{\prime }}{\rho }·\mathcal{R}-\rho ·\left(\phi -\varphi \right)·\frac{\left[h\circ u\right]}{u^{\beta }}-\frac{\beta }{{\rho }^{1/\beta }·a^{1/\beta }}·{\left(\mathcal{R}-\frac{\rho }{{\eta }^{\beta }}\right)}^{1+1/\beta }\hfill \\ & & +\frac{\beta \rho }{a^{1/\beta }·{\eta }^{\beta +1}}.\hfill \end{array}$$

(23)

Using Equation (11) and the fact that $u\to 0$ as $t\to \infty$, there is $t_2\in {\mathcal{I}}_1$ such that $\left[h\circ u\right]/u^{\beta }\ge \frac{1}{{\mu }_0}$ for $t\in {\mathcal{I}}_2$. Thus, Equation (23) becomes

$${\mathcal{R}}^{\prime }\le \frac{{\rho }^{\prime }}{\rho }·\mathcal{R}-\frac{1}{{\mu }_0}\rho ·\left(\phi -\varphi \right)-\frac{\beta }{{\rho }^{1/\beta }·a^{1/\beta }}·{\left(\mathcal{R}-\frac{\rho }{{\eta }^{\beta }}\right)}^{1+1/\beta }+\frac{\beta \rho }{a^{1/\beta }·{\eta }^{\beta +1}}.$$

Using Lemma 1 with

$$A=\frac{{\rho }^{\prime }}{\rho },B=\frac{\beta }{{\rho }^{1/\beta }·a^{1/\beta }},C=\frac{\rho }{{\eta }^{\beta }},\mathrm{and}y=\mathcal{R},$$

we obtain

$$\begin{array}{ccc}\hfill {\mathcal{R}}^{\prime }& \le & -\frac{1}{{\mu }_0}\rho ·\left(\phi -\varphi \right)+\frac{{\rho }^{\prime }}{{\eta }^{\beta }}+\frac{1}{{\left(1+\beta \right)}^{1+\beta }}\frac{a·{\left({\rho }^{\prime }\right)}^{1+\beta }}{{\rho }^{\beta }}+\frac{\beta \rho }{a^{1/\beta }·{\eta }^{\beta +1}}\hfill \\ & =& -\frac{1}{{\mu }_0}\rho ·\left(\phi -\varphi \right)+{\left(\frac{\rho }{{\eta }^{\beta }}\right)}^{\prime }+\frac{1}{{\left(1+\beta \right)}^{1+\beta }}\frac{a·{\left({\rho }^{\prime }\right)}^{1+\beta }}{{\rho }^{\beta }}.\hfill \end{array}$$

(24)

Integrating Equation (24) from $t_2$ to t, we find

$$\begin{array}{ccc}& & \mathcal{R}\left(t_2\right)-\mathcal{R}\left(t\right)+\frac{\rho \left(t\right)}{{\eta }^{\beta }\left(t\right)}-\frac{\rho \left(t_2\right)}{{\eta }^{\beta }\left(t_2\right)}\hfill \\ & & \ge {\int }_{t_2}^t\left(\frac{1}{{\mu }_0}\rho \left(v\right)\left(\phi \left(v\right)-\varphi \left(v\right)\right)-\frac{a\left(v\right){\left({\rho }^{\prime }\left(v\right)\right)}^{1+\beta }}{{\left(1+\beta \right)}^{1+\beta }{\rho }^{\beta }\left(v\right)}\right)\mathrm{d}v.\hfill \end{array}$$

(25)

From Equations (13) and (24), we obtain

$$-\mathcal{R}+\frac{\rho }{{\eta }^{\beta }}=-\rho ·a·{\left(\frac{u^{\prime }}{u}\right)}^{\beta }\le \frac{\rho }{{\eta }^{\beta }},$$

which, with Equation (25), gives

$$\frac{{\eta }^{\beta }\left(t\right)}{\rho \left(t\right)}{\int }_{t_2}^t\left(\frac{1}{{\mu }_0}\rho \left(v\right)\left(\phi \left(v\right)-\varphi \left(v\right)\right)-\frac{a\left(v\right){\left({\rho }^{\prime }\left(v\right)\right)}^{1+\beta }}{{\left(1+\beta \right)}^{1+\beta }{\rho }^{\beta }\left(v\right)}\right)\mathrm{d}v\le 1$$

This contradicts assumption Equation (21). □

Lemma 3.

Assume that $h\left(w\right)=w^{\beta }$, and Equation (5) holds for some $\kappa >0$. If u is an eventually positive solution of Equation (1), then the functions $u/{\eta }^{\kappa }$ and $u/{\eta }^{1-{\kappa }^{\beta }}$ are decreasing and increasing, respectively.

Proof. 

Let u be an eventually positive solution of Equation (1). We find that integrating Equation (6) yields

$$\begin{array}{ccc}\hfill a\left(t\right){\left(u^{\prime }\left(t\right)\right)}^{\beta }& \le & a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }-{\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)u^{\beta }\left(v\right)\mathrm{d}v\hfill \\ & \le & a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }-u^{\beta }\left(t\right){\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right)\mathrm{d}v,\hfill \end{array}$$

and using Equation (7) implies that

$$a\left(t\right){\left(u^{\prime }\left(t\right)\right)}^{\beta }\le a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }-{\kappa }^{\beta }{u}^{\beta }\left(t\right)\left(\frac{1}{{\eta }^{\beta }\left(t\right)}-\frac{1}{{\eta }^{\beta }\left(t_1\right)}\right).$$

(26)

Since $u\to 0$ as $t\to \infty$, we have that

$$a\left(t_1\right){\left(u^{\prime }\left(t_1\right)\right)}^{\beta }+{\kappa }^{\beta }\frac{u^{\beta }\left(t\right)}{{\eta }^{\beta }\left(t_1\right)}\le 0,$$

eventually. Thus, Equation (10) reduces to

$$a^{1/\beta }{u}^{\prime }\le -\kappa \frac{u}{\eta },$$

(27)

which leads to

$${\left(\frac{u}{{\eta }^{\kappa }}\right)}^{\prime }=\frac{\eta u^{\prime }+\kappa a^{-1/\beta }u}{{\eta }^{\kappa +1}}\le 0.$$

(28)

Next, by integrating Equation (16) and using Equation (5), we obtain

$$\begin{array}{ccc}\hfill \eta \left(t\right)a^{1/\beta }\left(t\right)u^{\prime }\left(t\right)+u\left(t\right)& \ge & \frac{1}{\beta }{\int }_t^{\infty }{\eta }^{\beta }\left(v\right)\left(\phi \left(v\right)-\varphi \left(v\right)\right)u\left(v\right)\mathrm{d}v\hfill \\ & \ge & {\kappa }^{\beta }{\int }_t^{\infty }\frac{1}{a^{1/\beta }\left(v\right)}\frac{u\left(v\right)}{\eta \left(v\right)}\mathrm{d}v\hfill \\ & \ge & {\kappa }^{\beta }u\left(t\right).\hfill \end{array}$$

Thus, we obtain

$${\left(\frac{u}{{\eta }^{1-{\kappa }^{\beta }}}\right)}^{\prime }=\frac{\eta u^{\prime }+\left(1-{\kappa }^{\beta }\right)a^{-1/\beta }u}{{\eta }^{2-{\kappa }^{\beta }}}\ge 0.$$

(29)

The proof is now completed. □

Theorem 4.

Assume that $h\left(w\right)=w^{\beta }$, and Equation (5) holds for some $\kappa >0$. If $\kappa +{\kappa }^{\beta }>1$, then DE Equation (1) is oscillatory.

Proof. 

Conversely, assuming that Equation (1) has a nonoscillatory solution necessarily means that it has an eventually positive one, say u. Assume that $u\left(t\right)>0$ for $t\ge t_1\in {\mathcal{I}}_0$. Then, it follows from Lemma 2 that $u^{\prime }\left(t\right)<0$ for $t\ge t_1$. Proceeding as in the proof of Lemma 3, we obtain that Equations (28) and (29) hold. Thus, we have $\kappa +{\kappa }^{\beta }\le 1$, which is a contradiction. □

Using Lemma 3, we can improve Theorem 1.

Theorem 5.

Assume that $h\left(w\right)=w^{\beta }$, and Equation (5) holds for some $\kappa >0$. If

$$\begin{array}{ccc}& & \underset{t\to \infty }{limsup}\left[{\eta }^{1-\sqrt[\beta ]{\kappa }}\left(t\right){\int }_{t_0}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right){\eta }^{\beta +\sqrt[\beta ]{\kappa }-1}\left(v\right)\mathrm{d}v\right.\hfill \\ & & \left.+{\eta }^{{\kappa }^{\beta }-1}\left(t\right){\int }_t^{\infty }\left(\phi \left(v\right)-\varphi \left(v\right)\right){\eta }^{\beta -{\kappa }^{\beta }+1}\left(v\right)\mathrm{d}v\right]>\beta ,\hfill \end{array}$$

(30)

then DE Equation (1) is oscillatory.

Proof. 

Conversely, assuming that Equation (1) has a nonoscillatory solution necessarily means that it has an eventually positive one, say u. Assume that $u\left(t\right)>0$ for $t\ge t_1\in {\mathcal{I}}_0$.

Proceeding exactly as the proof of Theorem 1, we find that Equation (18) holds. From Lemma 3, we obtain that ${\left(u/{\eta }^{\kappa }\right)}^{\prime }\le 0$ and ${\left(u/{\eta }^{1-{\kappa }^{\beta }}\right)}^{\prime }\ge 0$. Then, Equation (18) becomes

$$\begin{array}{ccc}\hfill \beta & \ge & {\eta }^{1-\sqrt[\beta ]{\kappa }}\left(t\right){\int }_{t_1}^t\left(\phi \left(v\right)-\varphi \left(v\right)\right){\eta }^{\beta +\sqrt[\beta ]{\kappa }-1}\left(v\right)\mathrm{d}v\hfill \\ & & +{\eta }^{{\kappa }^{\beta }-1}\left(t\right){\int }_t^{\infty }\left(\phi \left(v\right)-\varphi \left(v\right)\right){\eta }^{\beta -{\kappa }^{\beta }+1}\left(v\right)\mathrm{d}v.\hfill \end{array}$$

This contradicts assumption Equation (30). □

2.3. Examples and Discussion

Example 1.

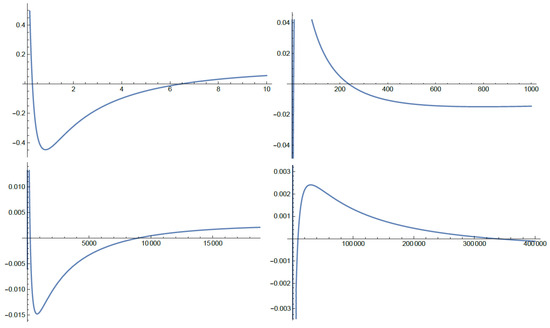
Consider the perturbed DE

$$\frac{\mathrm{d}}{\mathrm{d}t}\left(t^2·\frac{\mathrm{d}}{\mathrm{d}t}u\right)+b_{\phi }u\left(u^2+1\right)=b_{\varphi }u{\left({\left(\frac{\mathrm{d}}{\mathrm{d}t}u\right)}^2+1\right)}^{-1},$$

(31)

where $t>t_0$ and $b_{\phi }\ge b_{\varphi }>0$. We note that

$$F_1\left(t,w\right)=b_{\phi }w\left(w^2+1\right)\mathrm{and}{F}_2\left(t,w,v\right)=\frac{b_{\varphi }w}{\left(v^2+1\right)}.$$

By choosing $h\left(w\right)=w$, we obtain

$$\frac{F_1\left(t,w\right)}{h\left(w\right)}=b_{\phi }w\left(w^2+1\right)\ge b_{\phi }:=\phi \left(t\right),$$

and

$$\frac{F_2\left(t,w,v\right)}{h\left(w\right)}=\frac{b_{\varphi }}{\left(v^2+1\right)}\le b_{\varphi }:=\varphi \left(t\right).$$

It is easy to see that choosing $\kappa =\left(b_{\phi }-b_{\varphi }\right)$ satisfies condition Equation (5). Applying Theorem 1, DE Equation (31) is oscillatory if

$$b_{\phi }-b_{\varphi }>\frac{1}{2}.$$

whereas, by choosing $\rho \left(t\right)=1/t$, Theorem 3 leads us to the fact that DE (31) is oscillatory if

$$b_{\phi }-b_{\varphi }>\frac{1}{4}.$$

Figure 1 shows the numerical solution to Equation (31) when $b_{\phi }=2$ and $b_{\varphi }=1$.

Figure 1. The numerical solution of DE Equation (31) when $b_{\phi }=2$ and $b_{\varphi }=1$.

Remark 1.

Bohner and Saker [21] studied an equation similar to the studied equation and obtained criteria that guarantee that the equation is oscillating or converges to zero. As for our results, they guarantee that all solutions of the studied equation are oscillating, so our results are an improvement on the results they obtained.

Example 2.

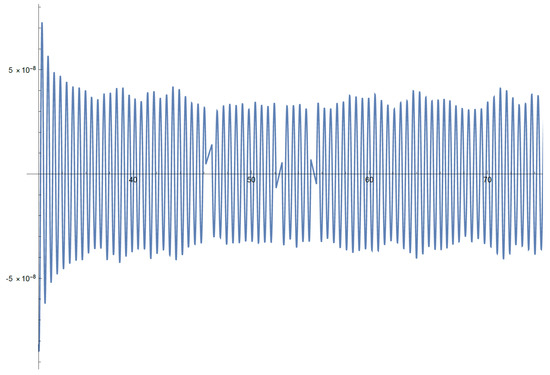
Consider the perturbed DE

$${\left({\mathrm{e}}^{\beta t}{\left(u^{\prime }\left(t\right)\right)}^{\beta }\right)}^{\prime }+{\mathrm{e}}^{\beta t+b_1}{u}^{\beta }\left(t\right)=\frac{{\mathrm{e}}^{\beta t+b_2}}{\left(u^2+1\right)}{u}^{\beta }\left(t\right).$$

(32)

where $b_1$ and $b_2$ are real numbers. We note that

$$a\left(t\right)={\mathrm{e}}^{\beta t},F_1\left(t,w\right)={\mathrm{e}}^{\beta t+b_1}{w}^{\beta },F_2\left(t,w,v\right)=\frac{{\mathrm{e}}^{\beta t+b_2}}{\left(w^2+1\right)}{w}^{\beta }\left(t\right)$$

By choosing $h\left(w\right)=w^{\beta }$, we obtain

$$\frac{F_1\left(t,w\right)}{h\left(w\right)}={\mathrm{e}}^{\beta t+b_1}:=\phi \left(t\right),$$

and

$$\frac{F_2\left(t,w,v^{\prime }\right)}{h\left(w\right)}=\frac{{\mathrm{e}}^{\beta t+b_2}}{\left(w^2+1\right)}\le {\mathrm{e}}^{\beta t+b_2}:=\varphi \left(t\right).$$

Theorem 3 leads us to the fact that DE Equation (32) is oscillatory if

$$b_1>ln\left[\frac{1}{4}\left(1+4{\mathrm{e}}^{b_2}\right)\right].$$

Figure 2 shows the numerical solution to Equation (32) when $b_1=5$ and $b_2=1$.

Figure 2. The numerical solution of DE Equation (32) when $b_1=5$ and $b_2=1$.

Remark 2.

Figure 1 and Figure 2 represent an approximate numerical solution to the solutions to Equations (31) and (32), respectively. As shown, we find that these numerical solutions have an infinite number of arbitrary zeros; that is, they are oscillatory solutions.The numerical solutions of the equations were obtained using Mathematica software.

3. Conclusions

In this paper, we investigated the oscillatory behavior of perturbed DEs in the noncanonical case. We used a technique based on pairing the studied equation with a canonical equation. We also extended Koplatadze’s results to the perturbed DEs. On the other hand, we used the Riccati approach to obtain more efficient criteria for oscillation. The new criteria were tested on specific cases of the studied equation to support and clarify the theoretical results.

It was clear from the results that the Recati technique presented more severe criteria and also did not adhere to the condition $h\left(w\right)=w^{\beta }$. However, this technique is not affected by the improvement of the monotonic properties of the solution, unlike Koplatadze’s technique. One interesting proposed issue is to extend our results to delay and neutral DEs.