Stability Results and Reckoning Fixed Point Approaches by a Faster Iterative Method with an Application

Abstract

In this manuscript, we investigate some convergence and stability results for reckoning fixed points using a faster iterative scheme in a Banach space. Also, weak and strong convergence are discussed for close contraction mappings in a Banach space and for Suzuki generalized nonexpansive mapping in a uniformly convex Banach space. Our method opens the door to many expansions in the problems of monotone variational inequalities, image restoration, convex optimization, and split convex feasibility. Moreover, some experimental examples were conducted to gauge the usefulness and efficiency of the technique compared with the iterative methods in the literature. Finally, the proposed approach is applied to solve the nonlinear Volterra integral equation with a delay.

1. Introduction

Many problems in mathematics and other fields of science may be modeled into an equation with a suitable operator. Therefore, it is self-evident that the existence of a solution to such issues is equivalent to finding the fixed points (FPs) of the aforementioned operators.

FP techniques are applied in many solid applications due to their ease and smoothness; these include optimization theory, approximation theory, fractional derivatives, dynamic theory, and game theory. This is the reason why researchers are attracted to this technique. Also, this technique plays a significant role not only in the above applications, but also in nonlinear analysis and many other engineering sciences. One of the important trends in FP methods is the study of the behavior and performance of algorithms that contribute greatly to real-world applications; see [1,2,3,4,5,6] for more details.

Throughout this paper, we assume that $\mathrm{\Omega }$ is a Banach space (BS); $\mathrm{\Theta }$ is a nonempty, closed, and convex subset (CCS) of an $\mathrm{\Omega }$; ${\mathbb{R}}^{+}=[0,\infty )$; and $\mathbb{N}$ is the set of natural numbers. Further, ⇀ and ⟶ stand for weak and strong convergence, respectively.

Suppose that $\lambda \left(\Im \right)$ refers to the class of all FPs of the operator $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$, which is described as an element $\theta \in \mathrm{\Theta }$ such that an equation $\theta =\Im \theta$ is true.

In [7], a new class of contractive mappings was introduced by Berinde as follows:

$$∥\Im \theta -\Im \vartheta ∥\le {\ell }_1∥\theta -\vartheta ∥+{\ell }_2∥\theta -\Im \theta ∥,\mathrm{for}\mathrm{all}\theta ,\vartheta \in \mathrm{\Theta },$$

(1)

where $0<{\ell }_1<1$, and ${\ell }_2\ge 0.$ The mapping ℑ is called an almost contraction mapping (ACM, for short).

The same author showed that the contractive condition (1) is more general than the contractive condition of Zamfirescu in [8].

In 2003, the ACM (1) was generalized by Imoru and Olantiwo [9] by replacing the constant ${\ell }_2$ with a strictly increasing continuous function $\varpi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ so that $\varpi \left(0\right)=0$ as follows:

$$∥\Im \theta -\Im \vartheta ∥\le {\ell }_1∥\theta -\vartheta ∥+\varpi \left(∥\theta -\Im \theta ∥\right),\mathrm{for}\mathrm{all}\theta ,\vartheta \in \mathrm{\Theta },$$

(2)

where $0<{\ell }_1<1$ and ℑ here is called a contractive-like mapping. Clearly, (2) generalizes the mapping classes taken into account by Berinde [7] and Osilike et al. [10].

Many authors tended to create many iterative methods for approximating FPs in terms of improving the performance and convergence behavior of algorithms for nonexpansive mappings. Over the past 20 years, a wide range of iterative techniques have been created and researched in order to approximate the FPs of various kinds of operators.

In the literature, the following are some common iterative techniques: Mann [11], Ishikawa [12], Noor [13], Argawal et al. [14], Abbas and Nazir [15], and HR [16,17].

Let $\left\{{\sigma }_j\right\}$ and $\left\{{\kappa }_j\right\}$ be sequences in $[0,1].$ Consider the following iterations:

$$\left\{\begin{array}{c}{\xi }_{\circ }\in \mathrm{\Theta },\hfill \\ {\rho }_j=(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j,\hfill \\ {\xi }_{j+1}=(1-{\kappa }_j){\xi }_i+{\gamma }_i\Im {\rho }_i,\hfill \end{array}\right.\forall j\ge 1.$$

(3)

$$\left\{\begin{array}{c}{\xi }_{\circ }\in \mathrm{\Theta },\hfill \\ {\rho }_j=(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j,\hfill \\ {\mathrm{{\rm Y}}}_j=(1-{\kappa }_j){\xi }_j+{\kappa }_j\Im {\rho }_j,\hfill \\ {\xi }_{j+1}=\Im {\mathrm{{\rm Y}}}_j,\hfill \end{array}\right.\forall j\ge 1.$$

(4)

$$\left\{\begin{array}{c}{\xi }_{\circ }\in \mathrm{\Theta },\hfill \\ {\rho }_j=(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j,\hfill \\ {\mathrm{{\rm Y}}}_j=\Im \left((1-{\kappa }_j){\xi }_j+{\kappa }_j{\rho }_j\right),\hfill \\ {\xi }_{j+1}=\Im {\mathrm{{\rm Y}}}_j,\hfill \end{array}\right.\forall j\ge 1.$$

(5)

$$\left\{\begin{array}{c}{\xi }_{\circ }\in \mathrm{\Theta },\hfill \\ {\rho }_j=(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j,\hfill \\ {\mathrm{{\rm Y}}}_j=\Im \left((1-{\kappa }_j){\xi }_j+{\kappa }_j{\xi }_j\right),\hfill \\ {\xi }_{j+1}=\Im {\mathrm{{\rm Y}}}_j,\hfill \end{array}\right.\forall j\ge 1.$$

(6)

The above procedures are known as the S algorithm [14], Picard-S algorithm [18], Thakur algorithm [19], and $K^{*}-$algorithm [20], respectively.

For contractive-like mappings, it is verified that technique (6) converges more quickly than both Karakaya et al. [21], (3)–(5) analytically and numerically.

On the other hand, nonlinear integral equations (NIEs) are used to describe mathematical models arising from mathematical physics, engineering, economics, biology, etc. [22]. In particular, spatial and temporal epidemic modeling challenges and boundary value problems lead to NIEs. Many academics have recently turned to iterative approaches to solve NIEs; for examples, see [23,24,25,26,27].

The choice of one iterative method over another is influenced by a few key elements, including speed, stability, and dependence. In recent years, academics have become increasingly interested in iterative algorithms with FPs that depend on data; for further information, see [28,29,30,31].

Inspired by the above work, in this paper, we develop a new faster iterative scheme as follows:

$$\left\{\begin{array}{c}{\xi }_{\circ }\in \mathrm{\Theta },\hfill \\ {\rho }_j=(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j,\hfill \\ {\mathrm{{\rm Y}}}_j=\Im \left((1-{\kappa }_j){\rho }_j+{\kappa }_j\Im {\rho }_j\right),\hfill \\ {\mathrm{\Lambda }}_j=\Im {\mathrm{{\rm Y}}}_j,\hfill \\ {\xi }_{j+1}=\Im \left((1-{\tau }_j){\mathrm{\Lambda }}_j+{\tau }_j\Im {\mathrm{\Lambda }}_j\right),\hfill \end{array}\right.\mathrm{for}\mathrm{all}j\in \mathbb{N},$$

(7)

where ${\sigma }_j,$ ${\kappa }_j$ and ${\tau }_j$ are sequences in $[0,1].$

The rest of the paper is arranged as follows: An analytical analysis of the performance and convergence rate of our approaches is presented in Section 3. We observed that the convergence rate is acceptable for ACMs in a BS. Also, Section 4 covers the weak and strong convergence of the suggested technique for SGNMs in the context of uniformly convex Banach spaces (UCBSs, for short). Moreover, in Section 5, we discuss the stability results of our iterative approach. In addition, some numerical examples are involved in Section 6 to study the efficacy and effectiveness of the proposed method. Ultimately, in Section 7, the solution to a nonlinear Volterra integral problem is presented using the method under consideration.

2. Preliminaries

This part is intended to give some definitions, propositions and lemmas that will assist the reader in understanding our manuscript and will be useful in the sequel.

Definition 1.

A mapping $\Im :\mathrm{\Omega }\to \mathrm{\Omega }$ is called a SGNM if

$$\frac{1}{2}∥\theta -\Im \theta ∥\le ∥\theta -\vartheta ∥\Rightarrow ∥\Im \theta -\Im \vartheta ∥\le ∥\theta -\vartheta ∥,forall\theta ,\vartheta \in \mathrm{\Omega }.$$

Definition 2.

A BS Ω is called a uniformly convex, if for each $ϵ\in (0,2],$ there exists $\delta >0$ such that for $\theta ,\vartheta \in \mathrm{\Omega }$ satisfying $∥\theta ∥\le 1$, $∥\vartheta ∥\le 1$ and $∥\theta -\vartheta ∥>ϵ,$ we have $∥\frac{\theta +\vartheta }{2}∥<1-\delta .$

Definition 3.

A BS Ω is called satisfy Opial’s condition, if for any sequence $\left\{{\theta }_j\right\}$ in Ω such that ${\theta }_j\rightharpoonup \theta \in \mathrm{\Omega },$ implies

$$\underset{j\to \infty }{lim\; sup}∥{\theta }_j-\theta ∥<\underset{j\to \infty }{lim\; sup}∥{\theta }_j-\vartheta ∥$$

for all $\vartheta \in \mathrm{\Omega },$ where $\theta \ne \vartheta$.

Definition 4.

Assume that $\left\{{\theta }_j\right\}$ is a bounded sequence in $\mathrm{\Omega }.$ For $\theta \in \mathrm{\Omega }$, we set

$$\nabla (\theta ,\left\{{\theta }_j\right\})=\underset{j\to \infty }{lim\; sup}∥{\theta }_j-\vartheta ∥.$$

The asymptotic radius and center of $\left\{{\theta }_j\right\}$ relative to Ω are described as

$$\nabla (\mathrm{\Omega },\left\{{\theta }_j\right\})=inf\{\nabla (\theta ,\left\{{\theta }_j\right\}):\theta \in \mathrm{\Omega }\}.$$

The asymptotic center of $\left\{{\theta }_j\right\}$ relative to Ω is defined by

$$Z(\mathrm{\Omega },\left\{{\theta }_j\right\})=\{\theta \in \mathrm{\Omega }:\nabla (\theta ,\left\{{\theta }_j\right\})=\nabla (\mathrm{\Omega },\left\{{\theta }_j\right\})\}.$$

Clearly, $Z(\mathrm{\Omega },\left\{{\theta }_j\right\})$ contains one single point in a UCBS.

Definition 5

([32]). Let $\left\{{\sigma }_j\right\}$ and {${\kappa }_j\}$ be nonnegative real sequences converge to σ and κ, respectively. If there exists $\zeta \in {\mathbb{R}}^{+}$ such that $\zeta ={lim}_{i\to \infty }\frac{∥{\sigma }_j-\sigma ∥}{∥{\kappa }_j-\kappa ∥}$, then, we have the following possibilities:

• If $\zeta =0,$ then $\left\{{\sigma }_j\right\}$ converges to σ faster than ${\kappa }_j$ does to $\kappa ;$
• If $\zeta \in (0,\infty ),$ then the two sequences have the same rate of convergence.

Definition 6

([33]). Let Ω be a BS. A mapping $\Im :\mathrm{\Omega }\to \mathrm{\Omega }$ is said to be satisfy Condition $I,$ if the inequality below holds

$$\Im \left(d\left(\vartheta ,\lambda \left(\Im \right)\right)\right)\le ∥\vartheta -\Im \vartheta ∥,$$

for all $\vartheta \in \mathrm{\Omega },$ where $d\left(\vartheta ,\lambda \left(\Im \right)\right)=inf\{∥\vartheta -\theta ∥:\theta \in \lambda \left(\Im \right)\}.$

Proposition 1

([34]). For a self-mapping $\Im :\mathrm{\Omega }\to \mathrm{\Omega },$ we have

$\left(1\right)$

ℑ is a SGNM if ℑ is nonexpansive.

$\left(2\right)$

If ℑ is a SGNM, then it is a quasi-nonexpansive mapping.

Lemma 1

([34]). Assume that Θ is any subset of a BS $\mathrm{\Omega },$ which verifies Opial’s condition. Let $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ be a SGNM. If $\left\{{\theta }_i\right\}\rightharpoonup \theta$ and ${lim}_{j\to \infty }∥\Im {\vartheta }_j-{\theta }_j∥=0,$ then $I-\Im$ is demiclosed at zero and $\Im \theta =\theta$.

Lemma 2

([34]). If $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ is a SGNM, and Θ is a weakly compact convex subset of a BS $\mathrm{\Omega },$ then, ℑ owns a FP.

Lemma 3

([32]). Let $\left\{{\psi }_i\right\}$ and $\left\{{\psi }_j^{*}\right\}$ be nonnegative real sequences such that

$${\psi }_{i+1}\le (1-{\varkappa }_j){\psi }_j+{\psi }_j^{*},{\varkappa }_j\in (0,1),foreachj\ge 1,$$

if ${\displaystyle \sum _{j=0}^{\infty }}{\varkappa }_j=\infty$ and ${lim}_{i\to \infty }\frac{{\psi }_j^{*}}{{\varkappa }_j}=0,$ then ${lim}_{j\to \infty }{\psi }_j=0.$

Lemma 4

([35]). Let $\left\{{\psi }_j\right\}$ and $\left\{{\psi }_j^{*}\right\}$ be nonnegative real sequences such that

$${\psi }_{j+1}\le (1-{\varkappa }_j){\psi }_j+{\varkappa }_j{\psi }_j^{*},{\varkappa }_j\in (0,1),foreachj\ge 1.$$

if ${\displaystyle \sum _{j=0}^{\infty }}{\varkappa }_j=\infty ,$ and ${\psi }_j^{*}\ge 0,$ then

$$\underset{j\to \infty }{lim\; sup}{\psi }_j\le \underset{j\to \infty }{lim\; sup}{\psi }_j^{*}.$$

Lemma 5

([36]). Let Ω be a UCBS and $\left\{{\varkappa }_j\right\}$ be a sequence such that $0<u\le {\varkappa }_j\le u^{*}<1,$ for all $j\ge 1.$ Assume that $\left\{{\theta }_j\right\}$ and $\left\{{\vartheta }_j\right\}$ are two sequences in Ω such that for some $\mu \ge 0,$

$$\underset{j\to \infty }{lim\; sup}\left\{{\vartheta }_j\right\}\le \mu ,\underset{j\to \infty }{lim\; sup}\left\{{\theta }_j\right\}\le \mu and\underset{i\to \infty }{lim\; sup}∥{\varkappa }_j{\theta }_j+(1-{\varkappa }_j){\vartheta }_j∥=\mu .$$

Then, ${lim}_{i\to \infty }∥{\theta }_j-{\vartheta }_j∥=0.$

3. Speed of Convergence

In this section, we discuss the speed of convergence of our iterative scheme under ACMs.

Theorem 1.

Assume that Θ is a nonempty CCS of a BS Ω and $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ is a mapping fulfills (1) with $\lambda \left(\Im \right)\ne \varnothing .$ If $\left\{{\xi }_j\right\}$ is the iterative sequence given by (7) with $\left\{{\sigma }_j\right\},\left\{{\kappa }_j\right\},\left\{{\tau }_j\right\}\in [0,1]$ and ${\displaystyle \sum _{j=0}^{\infty }}{\tau }_j=\infty$. Then, $\left\{{\xi }_j\right\}⟶\theta \in \lambda \left(\Im \right).$

Proof. 

Let $\theta \in \lambda \left(\Im \right)$; using (7), one has

$$\begin{array}{ccc}\hfill ∥{\rho }_j-\theta ∥& =& ∥(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j-\theta ∥\hfill \\ & =& ∥(1-{\sigma }_j)\left({\xi }_j-\theta \right)+{\sigma }_j\left(\Im {\xi }_j-\zeta \right)∥\hfill \\ & \le & (1-{\sigma }_j)∥{\xi }_j-\theta ∥+{\sigma }_j∥\Im {\xi }_j-\theta ∥\hfill \\ & \le & (1-{\sigma }_j)∥{\xi }_j-\zeta ∥+{\ell }_1{\sigma }_j∥{\xi }_j-\theta ∥\hfill \\ & =& \left(1-(1-{\ell }_1){\sigma }_j\right)∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(8)

From (7) and (8), one gets

$$\begin{array}{ccc}\hfill ∥{\mathrm{{\rm Y}}}_j-\theta ∥& =& ∥\Im \left((1-{\kappa }_j){\rho }_j+{\kappa }_j\Im {\rho }_j\right)-\theta ∥\hfill \\ & =& ∥\Im \theta -\Im \left((1-{\kappa }_j){\rho }_j+{\kappa }_j\Im {\rho }_j\right)∥\hfill \\ & \le & {\ell }_1∥\theta -\left((1-{\kappa }_j){\rho }_j+{\kappa }_j\Im {\rho }_j\right)∥+{\ell }_2∥\theta -\Im \theta ∥\hfill \\ & =& {\ell }_1∥(1-{\kappa }_j)\left({\rho }_j-\theta \right)+{\kappa }_j\left(\Im {\rho }_j-\theta \right)∥\hfill \\ & \le & {\ell }_1\left[(1-{\kappa }_j)∥{\rho }_j-\theta ∥+{\ell }_1{\kappa }_j∥{\rho }_j-\theta ∥\right]\hfill \\ & \le & {\ell }_1\left[1-(1-{\ell }_1){\kappa }_j\right]∥{\rho }_j-\zeta ∥\hfill \\ & \le & {\ell }_1\left(1-(1-{\ell }_1){\kappa }_j\right)\left(1-(1-{\ell }_1){\sigma }_j\right)∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(9)

Using (7) and (9), we have

$$\begin{array}{ccc}\hfill ∥{\mathrm{\Lambda }}_j-\theta ∥& =& ∥\Im {\mathrm{{\rm Y}}}_j-\theta ∥\le {\ell }_1∥{\mathrm{{\rm Y}}}_j-\theta ∥\hfill \\ & \le & {\ell }_1^2\left(1-(1-{\ell }_1){\kappa }_j\right)\left(1-(1-{\ell }_1){\sigma }_j\right)∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(10)

Utilizing (7) and (10), we can write

$$\begin{array}{ccc}\hfill ∥{\xi }_{j+1}-\theta ∥& =& ∥\Im \left((1-{\tau }_j){\mathrm{\Lambda }}_j+{\tau }_j\Im {\mathrm{\Lambda }}_j\right)-\theta ∥\hfill \\ & \le & {\ell }_1\left(1-(1-{\ell }_1){\tau }_j\right)∥{\mathrm{\Lambda }}_j-\theta ∥\hfill \\ & \le & {\ell }_1^3\left(1-(1-{\ell }_1){\tau }_j\right)\left(1-(1-{\ell }_1){\kappa }_j\right)\left(1-(1-{\ell }_1){\sigma }_j\right)∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(11)

As $\theta <1$ and $0\le {\kappa }_j,{\sigma }_j\le 1,$ for all $j\in \mathbb{N},$ then $\left(1-(1-{\ell }_1){\kappa }_j\right)\left(1-(1-{\ell }_1){\sigma }_j\right)<1.$

Hence, (11) takes the form

$$∥{\xi }_{j+1}-\theta ∥\le {\ell }_1^3\left(1-(1-{\ell }_1){\tau }_j\right)∥{\xi }_j-\theta ∥.$$

(12)

From (12), we deduce that

$$\begin{array}{ccc}\hfill ∥{\xi }_{j+1}-\theta ∥& \le & {\ell }_1^3\left(1-(1-{\ell }_1){\tau }_j\right)∥{\xi }_j-\theta ∥\hfill \\ & \le & {\ell }_1^3\left(1-(1-{\ell }_1){\tau }_{j-1}\right)∥{\xi }_{j-1}-\theta ∥\hfill \\ & & ⋮\hfill \\ & \le & {\ell }_1^3\left(1-(1-{\ell }_1){\tau }_0\right)∥{\xi }_0-\theta ∥.\hfill \end{array}$$

(13)

It follows from (13) that

$$∥{\xi }_{j+1}-\theta ∥\le {\ell }_1^{3(j+1)}∥{\xi }_0-\theta ∥\prod _{u=0}^j\left(1-(1-{\ell }_1){\tau }_u\right).$$

(14)

From the definition of $\theta$ and $\tau$, we have $\left(1-(1-\theta ){\gamma }_u\right)<1.$ Since $1-u\le e^{-u}$ for all $u\in [0,1],$ the inequality (14) can be written as

$$∥{\xi }_{j+1}-\theta ∥\le \frac{{\ell }_1^{3(j+1)}}{e^{(1-{\ell }_1){\displaystyle \sum _{u=0}^j}{\tau }_u}}∥{\xi }_0-\theta ∥.$$

(15)

Passing $j\to \infty$ in (15), we get $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥=0,$ i.e., $\left\{{\xi }_j\right\}⟶\theta \in \lambda \left(\Im \right).$

For uniqueness. Let $\theta ,{\theta }^{*}\in \lambda \left(\Im \right)$ such that $\theta \ne {\theta }^{*},$ then

$$\begin{array}{ccc}\hfill ∥\theta -{\theta }^{*}∥& =& ∥\Im \theta -\Im {\theta }^{*}∥\hfill \\ & \le & {\ell }_1∥\theta -{\theta }^{*}∥+{\ell }_2∥\theta -\Im \theta ∥\hfill \\ & =& {\ell }_1∥\theta -{\theta }^{*}∥\hfill \\ & <& ∥\theta -{\theta }^{*}∥,\hfill \end{array}$$

which is a contradiction; therefore, $\theta \ne {\theta }^{*}.$ □

According to Definition 5, the following theorem demonstrates that our method (7) converges faster than the iteration (6).

Theorem 2.

Assume that Θ is a nonempty CCS of a BS Ω and $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ is a mapping fulfills (1) with $\lambda \left(\Im \right)\ne \varnothing .$ If $\left\{{\xi }_j\right\}$ is the iterative sequence considered by (7) with $\left\{{\sigma }_j\right\},\left\{{\kappa }_j\right\},\left\{{\tau }_j\right\}\in [0,1]$ and $0<\tau \le {\tau }_j\le 1,$ for all $i\ge 1.$ Then, $\left\{{\theta }_j\right\}$ converges to θ faster than the procedure (6).

Proof. 

Using (14) and the assumption $0<\tau \le {\tau }_j\le 1$, one gets

$$\begin{array}{ccc}\hfill ∥{\xi }_{j+1}-\theta ∥& \le & {\ell }_1^{3(j+1)}∥{\xi }_0-\theta ∥\prod _{u=0}^j\left(1-(1-{\ell }_1){\tau }_u\right)\hfill \\ & =& {\ell }_1^{3(j+1)}∥{\xi }_0-\theta ∥{\left(1-(1-{\ell }_1)\tau \right)}^{j+1}.\hfill \end{array}$$

Obviously, the technique (6) ([20], Theorem 3.2) takes the form

$$∥m_{j+1}-\theta ∥\le {\ell }_1^{2(j+1)}∥m_0-\theta ∥\prod _{u=0}^j\left(1-(1-{\ell }_1){\tau }_u\right).$$

(16)

Since $0<\tau \le {\tau }_j\le 1,$ for some $\tau >0$ and all $j\ge 1,$ then (16) can be written as

$$\begin{array}{ccc}\hfill ∥m_{j+1}-\theta ∥& \le & {\ell }_1^{2(j+1)}∥m_0-\theta ∥\prod _{u=0}^j\left(1-(1-{\ell }_1){\tau }_u\right)\hfill \\ & =& {\ell }_1^{2(j+1)}∥m_0-\theta ∥{\left(1-(1-{\ell }_1)\tau \right)}^{j+1}.\hfill \end{array}$$

Set

$$\zeta ={\ell }_1^{3(j+1)}∥{\xi }_0-\theta ∥{\left(1-(1-{\ell }_1)\tau \right)}^{j+1},$$

and

$$\widehat{\zeta }={\ell }_1^{2(j+1)}∥m_0-\theta ∥{\left(1-(1-{\ell }_1)\tau \right)}^{j+1}.$$

Then

$${\Delta }_j=\frac{\zeta }{\widehat{\zeta }}=\frac{{\ell }_1^{3(j+1)}∥{\xi }_0-\theta ∥{\left(1-(1-{\ell }_1)\tau \right)}^{j+1}}{{\ell }_1^{2(j+1)}∥m_0-\theta ∥{\left(1-(1-{\ell }_1)\tau \right)}^{j+1}}={\ell }_1^{j+1}.$$

Letting $j\to \infty ,$ we get $\underset{j\to \infty }{lim}{\Delta }_j=0.$ Hence, $\left\{{\xi }_j\right\}$ converges faster than $\left\{m_j\right\}$ to $\theta .$ □

4. Convergence Results

In this section, we obtain some convergence results for our iteration scheme (7) using SGNMs in the setting of UCBSs. We begin with the following lemmas:

Lemma 6.

Assume that Θ is a nonempty CCS of a BS Ω and $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ is a SGNM with $\lambda \left(\Im \right)\ne \varnothing .$ Suppose that the sequence $\left\{{\xi }_j\right\}$ would be proposed by (7), then, $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥$ exists for each $\theta \in \lambda \left(\Im \right).$

Proof. 

For $\vartheta \in \mathrm{\Theta },$ assume that $\theta \in \lambda \left(\Im \right)$. From Proposition 1 $\left(2\right)$, one has

$$\frac{1}{2}∥\theta -\Im \theta ∥=0\le ∥\theta -\vartheta ∥\Rightarrow ∥\Im \theta -\Im \vartheta ∥\le ∥\theta -\vartheta ∥.$$

Utilizing (7), one gets

$$\begin{array}{ccc}\hfill ∥{\rho }_j-\theta ∥& =& ∥(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j-\theta ∥\hfill \\ & \le & (1-{\sigma }_j)∥{\xi }_j-\theta ∥+{\sigma }_j∥\Im {\xi }_j-\theta ∥\hfill \\ & \le & (1-{\sigma }_j)∥{\xi }_j-\theta ∥+{\sigma }_j∥{\xi }_j-\theta ∥\hfill \\ & =& ∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(17)

From (7) and (17), we can write

$$\begin{array}{ccc}\hfill ∥{\mathrm{{\rm Y}}}_j-\theta ∥& =& ∥\Im \left((1-{\kappa }_j){\rho }_j+{\kappa }_j\Im {\rho }_j\right)-\theta ∥\hfill \\ & \le & ∥(1-{\kappa }_j){\rho }_j+{\eta }_i\mathrm{\Xi }{\rho }_j-\theta ∥\hfill \\ & \le & (1-{\kappa }_j)∥{\rho }_j-\theta ∥+{\kappa }_j∥\mathrm{\Xi }{\rho }_j-\theta ∥\hfill \\ & \le & (1-{\kappa }_j)∥{\rho }_j-\theta ∥+{\kappa }_j∥{\rho }_j-\theta ∥\hfill \\ & =& ∥{\rho }_j-\theta ∥\hfill \\ & \le & ∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(18)

Analogously, by (7) and (18), we obtain that

$$\begin{array}{ccc}\hfill ∥{\mathrm{\Lambda }}_j-\theta ∥& =& ∥\Im {\mathrm{{\rm Y}}}_j-\theta ∥\hfill \\ & \le & ∥{\mathrm{{\rm Y}}}_j-\theta ∥\hfill \\ & \le & ∥{\xi }_j-\theta ∥.\hfill \end{array}$$

(19)

Finally, it follows from (7) and (19) that

$$\begin{array}{ccc}\hfill ∥{\xi }_{j+1}-\theta ∥& =& ∥\Im \left((1-{\tau }_j){\mathrm{\Lambda }}_j+{\tau }_j\Im {\mathrm{\Lambda }}_j\right)-\theta ∥\hfill \\ & \le & ∥(1-{\tau }_j)\left({\mathrm{\Lambda }}_j-\theta \right)+{\tau }_j\left(\Im {\mathrm{\Lambda }}_j-\theta \right)∥\hfill \\ & \le & (1-{\tau }_j)∥{\mathrm{\Lambda }}_j-\theta ∥+{\tau }_j∥{\mathrm{\Lambda }}_j-\theta ∥\hfill \\ & =& ∥{\mathrm{\Lambda }}_j-\theta ∥\hfill \\ & \le & ∥{\xi }_j-\theta ∥,\hfill \end{array}$$

which implies that $\left\{∥{\xi }_j-\theta ∥\right\}$ is bounded and nondecreasing sequence. Therefore $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥$ exists for each $\theta \in \lambda \left(\Im \right).$ □

Lemma 7.

Let Θ be a nonempty CCS of a UCBS Ω and $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ be a SGNM. If the sequence $\left\{{\xi }_j\right\}$ would be considered by (7), then $\lambda \left(\Im \right)\ne \varnothing$ if and only if $\left\{{\xi }_j\right\}$ is bounded and $\underset{j\to \infty }{lim}∥\Im {\xi }_j-{\xi }_j∥=0.$

Proof. 

Let $\lambda \left(\Im \right)\ne \varnothing$ and $\theta \in \lambda \left(\Im \right).$ Thank to Lemma 6, $\left\{{\xi }_j\right\}$ is bounded and $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥$ exists. Set

$$\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥=\omega .$$

(20)

From (20) in (17) and taking $\lim \sup ,$ one has

$$\underset{j\to \infty }{lim\; sup}∥{\rho }_j-\theta ∥\le \underset{j\to \infty }{lim\; sup}∥{\xi }_j-\theta ∥=\omega .$$

Based on Proposition 1 $\left(2\right),$ we get

$$\underset{j\to \infty }{lim\; sup}∥\Im {\xi }_j-\theta ∥\le \underset{j\to \infty }{lim\; sup}∥{\xi }_j-\theta ∥=\omega .$$

(21)

From (7) and (17)–(19), we have

$$\begin{array}{ccc}\hfill ∥{\xi }_{j+1}-\theta ∥& =& ∥\Im \left((1-{\tau }_j){\mathrm{\Lambda }}_j+{\tau }_j\Im {\mathrm{\Lambda }}_j\right)-\theta ∥\hfill \\ & \le & (1-{\tau }_j)∥{\mathrm{\Lambda }}_j-\theta ∥+{\tau }_j∥{\mathrm{\Lambda }}_j-\theta ∥\hfill \\ & =& ∥{\mathrm{\Lambda }}_j-\theta ∥\hfill \\ & =& ∥\Im {\mathrm{{\rm Y}}}_j-\theta ∥\hfill \\ & \le & ∥{\mathrm{{\rm Y}}}_j-\theta ∥\hfill \\ & =& ∥\Im \left((1-{\kappa }_j){\rho }_j+{\kappa }_j\Im {\rho }_j\right)-\theta ∥\hfill \\ & \le & (1-{\kappa }_j)∥{\rho }_j-\theta ∥+{\kappa }_j∥\Im {\rho }_j-\theta ∥\hfill \\ & \le & (1-{\kappa }_j)∥{\xi }_j-\theta ∥+{\kappa }_j∥{\rho }_j-\theta ∥\hfill \\ & =& ∥{\xi }_j-\theta ∥-{\kappa }_j∥{\xi }_j-\theta ∥+{\kappa }_j∥{\rho }_j-\theta ∥.\hfill \end{array}$$

Hence,

$$\frac{∥{\xi }_{j+1}-\theta ∥-∥{\xi }_j-\theta ∥}{{\kappa }_j}\le ∥{\rho }_j-\theta ∥-∥{\xi }_j-\theta ∥.$$

(22)

As ${\kappa }_j\in [0,1],$ from (22), we have

$$∥{\xi }_{j+1}-\theta ∥-∥{\xi }_j-\theta ∥\le \frac{∥{\xi }_{j+1}-\theta ∥-∥{\xi }_j-\theta ∥}{{\kappa }_j}\le ∥{\rho }_j-\theta ∥-∥{\xi }_j-\theta ∥,$$

which leads to $∥{\xi }_{j+1}-\theta ∥\le ∥{\rho }_j-\theta ∥.$ Applying (20), we get

$$\omega \le \underset{j\to \infty }{lim\; inf}∥{\rho }_j-\theta ∥.$$

(23)

Applying (21) and (23), we have

$$\begin{array}{ccc}\hfill \omega & =& \underset{j\to \infty }{lim}∥{\rho }_j-\theta ∥=\underset{i\to \infty }{lim}∥(1-{\sigma }_j){\xi }_j+{\sigma }_j\Im {\xi }_j-\theta ∥\hfill \\ & =& \underset{j\to \infty }{lim}∥(1-{\sigma }_j)\left({\xi }_j-\theta \right)+{\sigma }_j\left(\Im {\xi }_j-\theta \right)∥\hfill \\ & =& \underset{j\to \infty }{lim}∥{\sigma }_j\left(\Im {\xi }_j-\theta \right)+(1-{\sigma }_j)\left({\xi }_j-\theta \right)∥.\hfill \end{array}$$

(24)

It follows from (20), (21) and (24) and Lemma 5 that $\left\{{\xi }_j\right\}$ is bounded and $\underset{j\to \infty }{lim}∥\Im {\xi }_j-{\xi }_j∥=0.$

Otherwise, let $\left\{{\xi }_j\right\}$ is bounded and $\underset{j\to \infty }{lim}∥\Im {\xi }_j-{\xi }_j∥=0.$ Also, consider $\Im \theta \in Z(\mathrm{\Omega },\left\{{\xi }_j\right\})$; then, according to Definition 4, one has

$$\begin{array}{ccc}\hfill \nabla (\Im \theta ,\left\{{\xi }_j\right\})& =& \underset{j\to \infty }{lim\; sup}∥{\xi }_j-\Im \theta ∥\hfill \\ & \le & \underset{j\to \infty }{lim\; sup}\left(3∥\Im {\xi }_j-{\xi }_j∥+∥{\xi }_j-\theta ∥\right)\hfill \\ & =& \underset{j\to \infty }{lim\; sup}∥{\xi }_j-\theta ∥=\nabla \left(\theta ,\left\{{\xi }_j\right\}\right),\hfill \end{array}$$

which implies that $\theta \in Z(\mathrm{\Omega },\left\{{\xi }_j\right\}).$ As $\mathrm{\Omega }$ is uniformly convex and $Z\left(\mathrm{\Lambda },\left\{{\xi }_j\right\}\right)$ has exactly one point, then we have $\Im \theta =\theta .$ □

Theorem 3.

Let $\left\{{\xi }_j\right\}$ be a sequence iterated by (7) and let $\mathrm{\Omega },$ Θ and ℑ be defined as in Lemma 7. Then $\left\{{\xi }_j\right\}\rightharpoonup \theta \in \lambda \left(\Im \right)$ provided that Λ fulfills Opial’s condition and $\lambda \left(\Im \right)\ne \varnothing$.

Proof. 

Assume that $\theta \in \lambda \left(\Im \right)$; thanks to Lemma 6, $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥$ exists.

Next, we show that $\left\{{\xi }_j\right\}$ has a weak sequential limit in $\lambda \left(\Im \right).$ In this regard, consider $\left\{{\xi }_{j_a}\right\},\left\{{\xi }_{j_b}\right\}\subset \left\{{\xi }_j\right\}$ with $\left\{{\xi }_{j_a}\right\}\rightharpoonup \theta$ and $\left\{{\xi }_{j_b}\right\}\rightharpoonup {\theta }^{*}$ for all $\theta ,{\theta }^{*}\in \mathrm{\Theta }.$ From Lemma 7, one gets $\underset{j\to \infty }{lim}∥\Im {\xi }_j-{\xi }_j∥=0.$ Using Lemma 1 and since $I-\Im$ is demiclosed at 0, one has $\left(I-\Im \right)\theta =0,$ which implies that $\Im \theta =\theta .$ Similarly $\Im {\theta }^{*}={\theta }^{*}.$

Now, if $\theta \ne {\theta }^{*},$ then by Opial’s condition, we get

$$\begin{array}{ccc}\hfill \underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥& =& \underset{a\to \infty }{lim}∥{\xi }_{j_a}-\theta ∥<\underset{a\to \infty }{lim}∥{\xi }_{j_a}-{\theta }^{*}∥\hfill \\ & =& \underset{j\to \infty }{lim}∥{\xi }_j-{\theta }^{*}∥=\underset{b\to \infty }{lim}∥{\xi }_{j_b}-{\theta }^{*}∥\hfill \\ & <& \underset{b\to \infty }{lim}∥{\xi }_{j_b}-\theta ∥=\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥,\hfill \end{array}$$

which is a contradiction, hence $\theta ={\theta }^{*}$ and $\left\{{\xi }_j\right\}\rightharpoonup \theta \in \lambda \left(\Im \right).$ □

Theorem 4.

Let $\left\{{\xi }_j\right\}$ be a sequence iterated by (7). Also, let Θ be a nonempty CCS of a UCBS Ω and $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ be a SGNM. Then $\left\{{\xi }_j\right\}⟶\theta \in \lambda \left(\Im \right).$

Proof. 

Thank to Lemmas 2 and 7, $\lambda \left(\Im \right)\ne \varnothing$ and $\underset{j\to \infty }{lim}∥\Im {\xi }_j-{\xi }_j∥=0.$ Since $\mathrm{\Theta }$ is compact, then there exists a subsequence $\left\{{\xi }_{j_a}\right\}\subset$ $\left\{{\xi }_j\right\}$ so that ${\xi }_{j_a}\to \theta$ for any $\theta \in \mathrm{\Theta }.$ Clearly,

$$∥{\xi }_{j_a}-\Im \theta ∥\le 3∥{\xi }_{j_a}-\Im {\xi }_{j_a}∥+∥{\xi }_{j_a}-\theta ∥,\mathrm{for}\mathrm{all}j\in \mathbb{N}.$$

Letting $a\to \infty ,$ we get $\Im \theta =\theta ,$ i.e., $\theta \in \lambda \left(\Im \right).$ From Lemma 6, we conclude that $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥$ exists for each $\theta \in \lambda \left(\Im \right),$ hence $\left\{{\xi }_j\right\}⟶\theta .$ □

Theorem 5.

Let $\left\{{\xi }_j\right\}$ be a sequence iterated by (7) and let $\mathrm{\Omega },$ Θ and ℑ be defined as in Lemma 7. Then $\left\{{\xi }_j\right\}⟶\theta \in \lambda \left(\Im \right)$ if and only if $\underset{j\to \infty }{lim\; inf}d({\xi }_j,\lambda \left(\Im \right))=0,$ where $d\left(\theta ,\lambda \left(\Im \right)\right)=inf\{∥\theta -\vartheta ∥:\vartheta \in \lambda \left(\Im \right)\}.$

Proof. 

It is clear that the necessary condition is fulfilled. Consider $\underset{j\to \infty }{lim\; inf}d({\xi }_j,\lambda \left(\Im \right))=0,$ Using Lemma 6, one can see that $\underset{j\to \infty }{lim}∥{\xi }_j-\theta ∥$ exists for each $\theta \in \lambda \left(\Im \right),$ which leads to the finding that $\underset{j\to \infty }{lim\; inf}d({\xi }_j,\lambda \left(\Im \right))$ exists. Hence, $\underset{i\to \infty }{lim}d({\xi }_j,\lambda \left(\Im \right))=0.$

Now, we claim that $\left\{{\xi }_j\right\}$ is a Cauchy sequence in $\mathrm{\Theta }.$ Since $\underset{j\to \infty }{lim\; inf}d({\xi }_j,\lambda \left(\Im \right))=0,$ for every $ϵ>0$ there exists $j_0\in \mathbb{N}$ so that

$$d({\xi }_j,\lambda \left(\Im \right))\le \frac{ϵ}{2}\mathrm{and}d({\xi }_m,\lambda \left(\Im \right))\le \frac{ϵ}{2},\mathrm{for}\mathrm{each}j,m\ge j_0.$$

Therefore

$$\begin{array}{ccc}\hfill ∥{\xi }_j-{\xi }_m∥& \le & ∥{\xi }_j-\lambda \left(\Im \right)∥+∥\lambda \left(\Im \right)-{\xi }_m∥\hfill \\ & =& d({\xi }_j,\lambda \left(\Im \right))+d({\xi }_m,\lambda \left(\Im \right))\le \frac{ϵ}{2}+\frac{ϵ}{2}=ϵ.\hfill \end{array}$$

Thus $\left\{{\xi }_j\right\}$ is a Cauchy sequence in $\mathrm{\Theta }.$ The closeness of $\mathrm{\Theta }$ implies that there exists $\widehat{\theta }\in \mathrm{\Theta }$ such that $\underset{j\to \infty }{lim}{\xi }_j=\widehat{\theta }.$ As $\underset{i\to \infty }{lim}d({\xi }_j,\lambda \left(\Im \right))=0,$ then $\underset{i\to \infty }{lim}d(\widehat{\theta },\lambda \left(\Im \right))=0.$ Therefore, $\widehat{\theta }\in \lambda \left(\Im \right)$ and this completes the proof. □

5. Stability Analysis

This section demonstrates the stability of our iteration approach (7).

Theorem 6.

Let Θ be a nonempty CCS of a BS Ω, and let $\left\{{\xi }_j\right\}$ be a sequence iterated by (7) with $\left\{{\sigma }_j\right\},\left\{{\kappa }_j\right\},\left\{{\tau }_j\right\}\in [0,1]$ and ${\displaystyle \sum _{j=0}^{\infty }}{\tau }_j=\infty .$ If the mapping $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ satisfies (1), then the proposed algorithmm is $\Im -$stable.

Proof. 

Let $\left\{{\mathrm{{\rm Y}}}_j\right\}$ be an arbitrary sequence in $\mathrm{\Theta }$ and $\left\{{\xi }_j\right\}$ be a sequence proposed by (7) such that

$${\xi }_{j+1}=\hslash (\Im ,{\xi }_j),$$

with ${\xi }_j\to \zeta$ as $j\to \infty .$ Also, consider

$${\phi }_j=∥{\mathrm{{\rm Y}}}_{j+1}-\hslash (\Im ,{\mathrm{{\rm Y}}}_j)∥.$$

In order to show that ℑ is stable, it is sufficient to prove that

$$\underset{j\to \infty }{lim}{\phi }_j=0\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}\underset{j\to \infty }{lim}{\mathrm{{\rm Y}}}_j=\theta .$$

Now, let $\underset{j\to \infty }{lim}{\phi }_j=0$. Using (7) and (12), one has

$$\begin{array}{ccc}& & ∥{\mathrm{{\rm Y}}}_{j+1}-\theta ∥\hfill \\ & =& ∥{\mathrm{{\rm Y}}}_{j+1}-\hslash (\Im ,{\mathrm{{\rm Y}}}_j)+\hslash (\Im ,{\mathrm{{\rm Y}}}_j)-\theta ∥\hfill \\ & \le & ∥{\mathrm{{\rm Y}}}_{j+1}-\hslash (\Im ,{\mathrm{{\rm Y}}}_j)∥+∥\hslash (\Im ,{\mathrm{{\rm Y}}}_j)-\theta ∥\hfill \\ & =& {\phi }_j+∥\hslash (\Im ,{\mathrm{{\rm Y}}}_j)-\theta ∥\hfill \\ & =& {\phi }_j+∥\Im \left(\Im \left(\begin{array}{c}(1-{\tau }_j)\left[\Im \left(\begin{array}{c}(1-{\kappa }_j)\left[(1-{\sigma }_j){\mathrm{{\rm Y}}}_j+{\sigma }_j\Im {\mathrm{{\rm Y}}}_j\right]\\ +{\kappa }_j\Im \left[(1-{\sigma }_j){\mathrm{{\rm Y}}}_j+{\sigma }_j\Im {\mathrm{{\rm Y}}}_j\right]\end{array}\right)\right]\\ +{\tau }_j\Im \left[\Im \left(\begin{array}{c}(1-{\kappa }_j)\left[(1-{\sigma }_j){\mathrm{{\rm Y}}}_j+{\sigma }_j\Im {\mathrm{{\rm Y}}}_j\right]\\ +{\kappa }_j\Im \left[(1-{\sigma }_j){\mathrm{{\rm Y}}}_j+{\sigma }_j\Im {\mathrm{{\rm Y}}}_j\right]\end{array}\right)\right]\end{array}\right)\right)-\theta ∥\hfill \\ & =& {\ell }_1^3\left(1-(1-{\ell }_1){\tau }_j\right)∥{\mathrm{{\rm Y}}}_j-\theta ∥+{\phi }_j,\hfill \end{array}$$

for $j\in \mathbb{N}.$ Put

$${\psi }_j=∥{\mathrm{{\rm Y}}}_j-\theta ∥,e_j=(1-{\ell }_1){\tau }_j\in (0,1)\mathrm{and}{\psi }_j^{*}={\phi }_j.$$

Since $\underset{j\to \infty }{lim}{\phi }_j=0$, then $\underset{i\to \infty }{lim}\frac{{\psi }_j^{*}}{e_j}=\underset{i\to \infty }{lim}\frac{{\psi }_j}{e_j}=0.$ Therefore, all assumptions of Lemma 3 hold, consequently $\underset{j\to \infty }{lim}∥{\mathrm{{\rm Y}}}_j-\theta ∥=0,$ i.e., $\underset{j\to \infty }{lim}{\mathrm{{\rm Y}}}_j=\theta$.

Conversely, let $\underset{j\to \infty }{lim}{\mathrm{{\rm Y}}}_j=\theta ,$ then

$$\begin{array}{ccc}\hfill {\phi }_j& =& ∥{\mathrm{{\rm Y}}}_{j+1}-\hslash (\Im ,{\mathrm{{\rm Y}}}_j)∥\hfill \\ & =& ∥{\mathrm{{\rm Y}}}_{j+1}-\theta +\theta -\hslash (\Im ,{\mathrm{{\rm Y}}}_j)∥\hfill \\ & \le & ∥{\mathrm{{\rm Y}}}_{j+1}-\theta ∥+∥\theta -\hslash (\Im ,{\mathrm{{\rm Y}}}_j)∥\hfill \\ & \le & ∥{\mathrm{{\rm Y}}}_{j+1}-\theta ∥+{\ell }_1^3\left(1-(1-{\ell }_1){\tau }_j\right)∥{\mathrm{{\rm Y}}}_j-\theta ∥.\hfill \end{array}$$

Passing $j\to \infty$, we obtain $\underset{j\to \infty }{lim}{\phi }_j=0.$ This finishes the proof. □

To support Theorem 6, we investigate the following example:

Example 1.

Let $\mathrm{\Theta }=[0,1]$ and $\Im \xi =\frac{\xi }{4}.$ It is clear that, 0 is a FP of $\Im .$

First, we show that ℑ satisfies the condition (1). For this, take ${\ell }_1=\frac{1}{4}$ and for all ${\ell }_2\ge 0,$ we can write

$$\begin{array}{ccc}\hfill ∥\Im \xi -\Im \vartheta ∥-{\ell }_1∥\xi -\vartheta ∥-{\ell }_2∥\xi -\Im \xi ∥& =& \frac{1}{4}∥\xi -\vartheta ∥-\frac{1}{4}∥\xi -\vartheta ∥-{\ell }_2∥\xi -\frac{\xi }{4}∥\hfill \\ & =& -\frac{3{\ell }_2}{4}\xi \le 0,foreach\xi ,\vartheta \in [0,1].\hfill \end{array}$$

Next, we prove that the iterative (7) is $\Im -$stable. For this regard, take ${\sigma }_j={\kappa }_j={\tau }_j=\frac{1}{j+1}$ and ${\xi }_0\in [0,1],$ then

$$\begin{array}{ccc}\hfill {\rho }_j& =& \left(1-\frac{1}{j+1}\right){\xi }_j+\frac{1}{j+1}\left(\frac{{\xi }_i}{4}\right)=\left(1-\frac{3}{4(j+1)}\right){\xi }_i,\hfill \\ \hfill {\mathrm{{\rm Y}}}_j& =& \frac{1}{4}\left(\left(1-\frac{1}{j+1}\right){\rho }_j+\frac{1}{j+1}\left(\frac{{\rho }_j}{4}\right)\right)=\frac{1}{4}\left(1-\frac{3}{2(j+1)}+\frac{9}{{\left(4(j+1)\right)}^2}\right){\xi }_i,\hfill \\ \hfill {\mathrm{\Lambda }}_j& =& \frac{1}{4}{\mathrm{{\rm Y}}}_j=\frac{1}{16}\left(1-\frac{3}{2(j+1)}+\frac{9}{{\left(4(j+1)\right)}^2}\right){\xi }_i,\hfill \\ \hfill {\xi }_{j+1}& =& \frac{1}{4}\left(\left(1-\frac{1}{j+1}\right){\mathrm{\Lambda }}_j+\frac{1}{j+1}\left(\frac{{\mathrm{\Lambda }}_j}{4}\right)\right)=\frac{1}{4}\left(1-\frac{3}{4(j+1)}\right){\mathrm{\Lambda }}_j\hfill \\ & =& \frac{1}{64}\left(1-\frac{9}{4(j+1)}+\frac{27}{{\left(4(j+1)\right)}^2}-\frac{27}{{\left(4(j+1)\right)}^3}\right){\xi }_i\hfill \\ & =& \left(1-\left(\frac{63}{64}+\frac{9}{4(j+1)}-\frac{27}{{\left(4(j+1)\right)}^2}+\frac{27}{{\left(4(j+1)\right)}^3}\right)\right){\xi }_i.\hfill \end{array}$$

Set ${\mathrm{{\rm Y}}}_j=\frac{63}{64}+\frac{9}{4(j+1)}-\frac{27}{{\left(4(j+1)\right)}^2}+\frac{27}{{\left(4(j+1)\right)}^3}.$ Clearly, ${\mathrm{{\rm Y}}}_j\in (0,1)$ for all $j\in \mathbb{N},$ ${\displaystyle \sum _{i=0}^{\infty }}{\mathrm{{\rm Y}}}_j=0.$ Thank to Lemma 3, $\underset{j\to \infty }{lim}{\xi }_j=0.$ Consider ${\Re }_j=\frac{1}{j+2},$ we get

$$\begin{array}{ccc}\hfill {\phi }_j& =& ∥{\Re }_{j+1}-\hslash (\Im ,{\Re }_j)∥\hfill \\ & =& ∥\frac{1}{j+3}-\frac{1}{16}\left(\begin{array}{c}(1-\frac{1}{j+1})\left[\left(\begin{array}{c}(1-\frac{1}{j+1})\left[(1-\frac{1}{j+1}){\Re }_j+\frac{1}{j+1}\frac{{\Re }_j}{4}\right]\\ +\frac{1}{4(j+1)}\left[(1-\frac{1}{j+1}){\Re }_j+\frac{1}{j+1}\frac{{\Re }_j}{4}\right]\end{array}\right)\right]\\ +\frac{1}{4\left(i+1\right)}\left[\left(\begin{array}{c}(1-\frac{1}{j+1})\left[(1-\frac{1}{j+1}){\Re }_j+\frac{1}{j+1}\frac{{\Re }_j}{4}\right]\\ +\frac{1}{4(j+1)}\left[(1-\frac{1}{j+1}){\Re }_j+\frac{1}{j+1}\frac{{\Re }_j}{4}\right]\end{array}\right)\right]\end{array}\right)∥\hfill \\ & =& ∥\frac{1}{i+3}-\frac{1}{16}\left(\begin{array}{c}(1-\frac{1}{j+1})\left[\left(1-\frac{3}{2(j+1)}+\frac{9}{{\left(4(j+1)\right)}^2}\right){\Re }_j\right]\\ +\frac{1}{4\left(i+1\right)}\left[\left(1-\frac{3}{2(j+1)}+\frac{9}{{\left(4(j+1)\right)}^2}\right){\Re }_j\right]\end{array}\right)∥\hfill \\ & =& ∥\frac{1}{i+3}-\frac{1}{16}\left(1-\frac{9}{4(j+1)}+\frac{27}{{\left(4(j+1)\right)}^2}-\frac{27}{{\left(4(j+1)\right)}^3}\right){\Re }_j∥\hfill \\ & =& ∥\frac{1}{i+3}-\left(\frac{1}{16(j+2)}-\frac{9}{4(j+1)(j+2)}+\frac{27}{{\left(4(j+1)\right)}^2(j+2)}-\frac{27}{{\left(4(j+1)\right)}^3(j+2)}\right)∥,\hfill \end{array}$$

taking $i\to \infty ,$ we get $\underset{j\to \infty }{lim}{\phi }_j=0.$ This proves that the suggested method (7) is $\Im -$stable.

6. Numerical Experiments

The example that follows examines how well and quickly our method performs when compared to other algorithms, while also illuminating the analytical findings from Theorem 2.

Example 2.

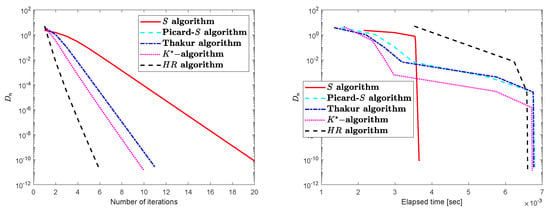
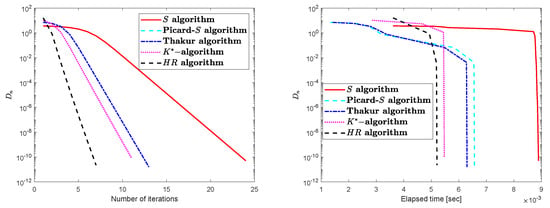
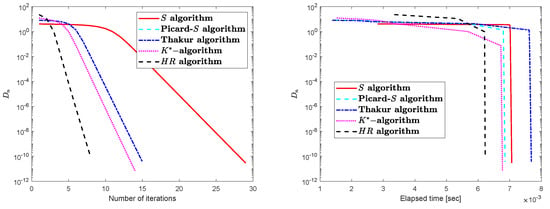
Let $\mathrm{\Omega }=(-\infty ,\infty )$, $\mathrm{\Theta }=[0,50]$, and $\Im :\mathrm{\Theta }\to \mathrm{\Theta }$ be a mapping described as

$$\Im \left(\xi \right)=\sqrt{{\xi }^2-9\xi +54}.$$

Obviously, 6 is a unique FP of $\Im .$ Consider ${\sigma }_j={\kappa }_j={\tau }_j=\frac{1}{5j+10},$ with distinct starting points. Then, we get Table 1, Table 2 and Table 3 and Figure 1, Figure 2 and Figure 3 for comparing the different iterative techniques.

Table 1. Example 2: ($HR-$algorithm) at ${\nu }_{\circ }=1$.

Iter (n)	S Algorithm	Picard-S Algorithm	Thakur Algorithm	${\mathit{K}}^{*}-$Algorithm	$\mathit{HR}-$Algorithm
1	8.70091704981746	7.16921920849454	7.16914772374443	6.36059443309194	6.00727524833131
2	7.16526232112099	6.10977177957558	6.10975923118057	6.01468466644452	6.00002780412529
3	6.39088232469395	6.00714403607375	6.00714316980988	6.00065450058063	6.00000018328059
4	6.10931564922512	6.00044721072023	6.00044715630748	6.00003168526056	6.00000000153606
5	6.02823416956883	6.00002793225376	6.00002792885454	6.00000161316022	6.00000000001474
6	6.00711636371271	6.00000174471605	6.00000174450373	6.00000008491151	6.00000000000015
7	6.00178220920879	6.00000010899371	6.00000010898045	6.00000000457683
8	6.00044563525887	6.00000000680959	6.00000000680876	6.00000000025113
9	6.00011139089900	6.00000000042547	6.00000000042542	6.00000000001397
10	6.00002784178933	6.00000000002659	6.00000000002658	6.00000000000079
11	6.00000695905778	6.00000000000166	6.00000000000166
12	6.00000173945939
13	6.00000043479852
14	6.00000010868515
15	6.00000002716811
16	6.00000000679132
17	6.00000000169767
18	6.00000000042438
19	6.00000000010609
20	6.00000000002652

Table 2. Example 2: $HR-$algorithm at ${\xi }_{\circ }=23$.

Iter (n)	S Algorithm	Picard-S Algorithm	Thakur Algorithm	${\mathit{K}}^{*}-$Algorithm	$\mathit{HR}-$Algorithm
1	19.3563152555029	15.9518056335603	15.9517798586745	12.5877267284391	6.85064626172682
2	15.9377280808459	10.1547429779848	10.1547063746371	7.21310921795745	6.00404110670722
3	12.8216267389821	6.83637415013381	6.83635232023217	6.07773436689889	6.00002666859578
4	10.1453665006161	6.07061076131832	6.07060799598213	6.00385998151440	6.00000022350839
5	8.09904894091384	6.00453182122915	6.00453163699128	6.00019677562843	6.00000000214472
6	6.83342864338475	6.00028356649349	6.00028355493982	6.00001035833149	6.00000000002245
7	6.26044908931579	6.00001771655983	6.00001771583789	6.00000055832830	6.00000000000025
8	6.07032543085564	6.00000110688254	6.00000110683744	6.00000003063582
9	6.01796113338512	6.00000006915944	6.00000006915662	6.00000000170455
10	6.00451434416413	6.00000000432139	6.00000000432122	6.00000000009591
11	6.00112994220417	6.00000000027003	6.00000000027002	6.00000000000545
12	6.00028253511929	6.00000000001687	6.00000000001687
13	6.00007062920329	6.00000000000105	6.00000000000105
14	6.00001765533615
15	6.00000441334114
16	6.00000110322227
17	6.00000027578013
18	6.00000006893931
19	6.00000001723354
20	6.00000000430809
21	6.00000000107696
22	6.00000000026923
23	6.00000000006730
24	6.00000000001683

Table 3. Example 2: $HR-$algorithm at ${\xi }_{\circ }=41$.

Iter (n)	S Algorithm	Picard-S Algorithm	Thakur Algorithm	${\mathit{K}}^{*}-$Algorithm	$\mathit{HR}-$Algorithm
1	36.9195393902310	32.9359459295575	32.9359410372494	28.6777050430159	18.0010100671820
2	32.9185209048623	25.1854713159820	25.1854637821918	19.1184050275537	6.99692674147933
3	28.9966652255498	17.9433658908193	17.9433563898048	11.5396125686070	6.00870649597241
4	25.1701649172411	11.6863804499820	11.6863697408416	7.09098245036886	6.00007316294814
5	21.4670877470757	7.49707008913586	7.49706191231517	6.07877285288080	6.00000070206652
6	17.9313757495734	6.15612940775542	6.15612775011077	6.00426075582864	6.00000000734890
7	14.6320375697776	6.01035659987680	6.01035647945727	6.00023000499555	6.00000000008173
8	11.6781275774842	6.00064966715110	6.00064965955411	6.00001262154899	6.00000000000095
9	9.23371552492475	6.00004060231534	6.00004060184040	6.00000070225384
10	7.49350575600870	6.00000253705577	6.00000253702609	6.00000003951159
11	6.53524954796329	6.00000015853311	6.00000015853125	6.00000000224357
12	6.15563769964487	6.00000000990656	6.00000000990645	6.00000000012838
13	6.04078294734902	6.00000000061907	6.00000000061906	6.00000000000739
14	6.01032406840519	6.00000000003869	6.00000000003869	6.00000000000043
15	6.00258903649963	6.00000000000242	6.00000000000242
16	6.00064771546926
17	6.00016194664418
18	6.00004048534517
19	6.00001012070523
20	6.00000253001219
21	6.00000063246434
22	6.00000015810715
23	6.00000003952473
24	6.00000000988071
25	6.00000000247007
26	6.00000000061749
27	6.00000000015437
28	6.00000000003859
29	6.00000000000965

Figure 1. The suggested algorithm ($HR-$algorithm) at ${\xi }_{\circ }=1$.

Figure 2. $HR-$algorithm at ${\xi }_{\circ }=23$.

Figure 3. $HR-$algorithm at ${\xi }_{\circ }=41$.

The example below illustrates how our technique (7) performs better than some of the best iterative algorithms in the prior literature in terms of convergence speed under specified circumstances.

Example 3.

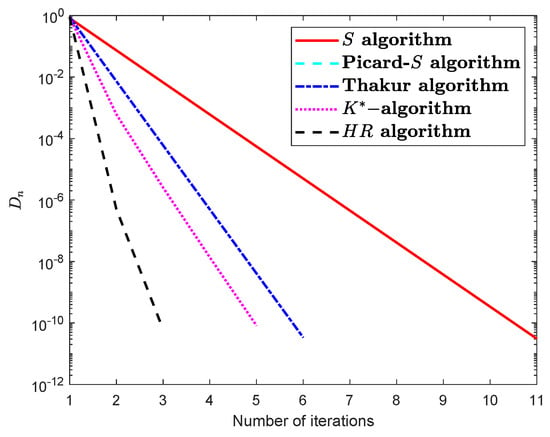
Define the mapping $\Im :[0,1]\to [0,1]$ by

$$\Im \left(\xi \right)=\left\{\begin{array}{cc}1-\xi ,& when0\le \xi <\frac{1}{14},\\ \frac{13+\xi }{14},& when\frac{1}{14}\le \xi \le 1.\end{array}\right.$$

First, we claim that the mapping ℑ is SGNM but not nonexpansive. Put $\xi =0.07$ and $\theta =\frac{1}{14},$ one has

$$\begin{array}{ccc}\hfill ∥\Im \xi -\Im \theta ∥& =& \left|\Im \xi -\Im \theta \right|=\left|1-\xi -\left(\frac{13+\xi }{14}\right)\right|\hfill \\ & =& \left|0.93-\frac{183}{196}\right|=\frac{9}{2450},\hfill \end{array}$$

and

$$∥\xi -\theta ∥=\left|\xi -\theta \right|=\frac{1}{700}.$$

Hence $∥\Im \xi -\Im \theta ∥=\frac{9}{2450}>\frac{1}{700}=∥\xi -\theta ∥.$ This proves that ℑ is not nonexpansive mapping.

After that, to prove the other part of what is required, we discuss the following cases:

(i) If $0\le \xi <\frac{1}{14},$ we have

$$\frac{1}{2}∥\xi -\Im \xi ∥=\frac{1}{2}\left|\xi -\left(1-\xi \right)\right|=\frac{1-2\xi }{2}\in \left(\frac{3}{7},\frac{1}{2}\right],$$

since $\frac{1}{2}∥\xi -\Im \xi ∥\le ∥\xi -\theta ∥,$ then we must write $\frac{1-2\xi }{2}\le \left|\xi -\theta \right|.$ Obviously, $\theta <\xi$ is impossible. So, $\theta >\xi .$ Hence, $\frac{1-2\xi }{2}\le \theta -\xi ,$ which implies that $\theta \ge \frac{1}{2}$, thus $\frac{1}{2}\le \theta <1.$ Now,

$$∥\Im \xi -\Im \theta ∥=\left|\frac{13+\theta }{14}-\left(1-\xi \right)\right|=\left|\frac{14\xi +\theta -1}{14}\right|<\frac{1}{14},$$

and

$$∥\xi -\theta ∥=\left|\frac{1}{14}-\frac{1}{2}\right|=\frac{3}{7}.$$

Therefore,

$$\frac{1}{2}∥\xi -\Im \xi ∥\le ∥\xi -\theta ∥\Rightarrow ∥\Im \xi -\Im \theta ∥<\frac{1}{14}<\frac{3}{7}=∥\xi -\theta ∥.$$

(ii) If $\frac{1}{14}\le \xi \le 1,$ we get

$$\frac{1}{2}∥\xi -\Im \xi ∥=\frac{1}{2}\left|\frac{13+\xi }{14}-\xi \right|=\frac{13-13\xi }{28}\in \left[0,\frac{169}{392}\right].$$

For $\frac{1}{2}∥\xi -\Im \xi ∥\le ∥\xi -\theta ∥,$ we obtain $\frac{13-13\xi }{28}\le \left|\xi -\theta \right|,$ which triggers the following positions:

$\left(p_1\right)$ If $\xi <\theta ,$ one can write

$$\frac{13-13\xi }{28}\le \theta -\xi ⟹\theta \ge \frac{13+15\xi }{28}⟹\theta \in \left[\frac{197}{392},1\right]\subset \left[\frac{1}{14},1\right].$$

Hence,

$$∥\Im \xi -\Im \theta ∥=\left|\frac{13+\xi }{14}-\frac{13+\theta }{14}\right|=\frac{1}{14}\left|\xi -\theta \right|\le \left|\xi -\theta \right|.$$

So, we have

$$\frac{1}{2}∥\xi -\Im \xi ∥\le ∥\xi -\theta ∥\Rightarrow ∥\Im \xi -\Im \theta ∥<∥\xi -\theta ∥.$$

$\left(p_2\right)$ If $\xi >\theta ,$ one has

$$\frac{13-13\xi }{28}\le \xi -\theta ⟹\theta \le \frac{41\xi -13}{28}⟹\theta \in \left[\frac{-141}{392},1\right].$$

Since $0\le \varpi \le 1$ and $\theta \le \frac{41\xi -13}{28},$ we have $\xi \ge \frac{13+28\theta }{41}\Rightarrow \xi \in [\frac{13}{41},1].$

Clearly, when $\frac{13}{41}\le \xi \le 1$ and $\frac{1}{14}\le \theta \le 1$ is similar to case $\left(p_1\right)$; so, we shall discuss when $\frac{13}{41}\le \nu \le 1$ and $0\le \varpi \le \frac{1}{14}.$ Consider

$$∥\Im \xi -\Im \theta ∥=\left|\frac{13+\xi }{14}-\left(1-\theta \right)\right|=\left|\frac{14\theta +\xi -1}{14}\right|<\frac{1}{14},$$

and

$$∥\xi -\theta ∥=\left|\xi -\theta \right|>\left|\frac{13}{41}-\frac{1}{14}\right|=\frac{141}{574}>\frac{1}{14},$$

which implies that

$$\frac{1}{2}∥\xi -\Im \xi ∥\le ∥\xi -\theta ∥\Rightarrow ∥\Im \xi -\Im \theta ∥<∥\xi -\theta ∥.$$

Based on the above cases, we conclude that ℑ is an SGNM.

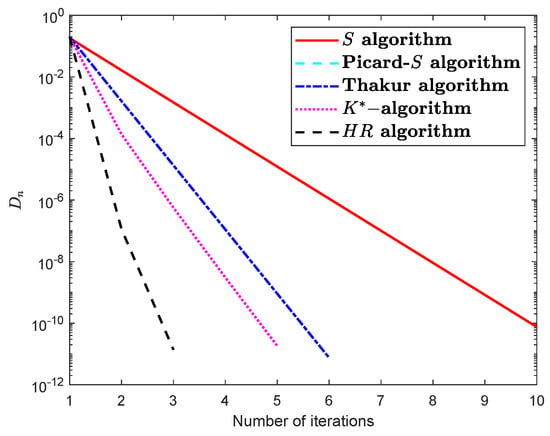
Finally, by employing various control circumstances ${\sigma }_j={\kappa }_j={\tau }_j=\frac{j}{j+1}$, we will describe the behavior of technique (7) and show how it is faster than the S, Tharkur, and $K^{*}-$iteration procedures; see Table 4 and Table 5 and Figure 4 and Figure 5.

Table 4. Example 3: Comparison of the suggested algorithm numerically ($HR-$algorithm) at ${\xi }_{\circ }=0.30$.

Iter (n)	S Algorithm	Picard-S Algorithm	Thakur Algorithm	${\mathit{K}}^{*}-$Algorithm	$\mathit{HR}-$Algorithm
1	0.918925619834711	0.992629601803156	0.992629601803156	0.999385287890171	0.999999491973463
2	0.992659381189810	0.999939333728841	0.999939333728841	0.999997438874483	0.999999999938058
3	0.999334187674034	0.999999499765345	0.999999499765345	0.999999986205653	0.999999999999984
4	0.999939559648030	0.999999995871843	0.999999995871843	0.999999999916912
5	0.999994510972627	0.999999999965918	0.999999999965918	0.999999999999467
6	0.999999501367829	0.999999999999719	0.999999999999719
7	0.999999954695558
8	0.999999995883263
9	0.999999999625887
10	0.999999999966000
11	0.999999999996910

Table 5. Example 3: Comparison of the suggested algorithm numerically ($HR-$algorithm) when ${\xi }_{\circ }=0.30$.

Iter (n)	S Algorithm	Picard-S Algorithm	Thakur Algorithm	${\mathit{K}}^{*}-$Algorithm	$\mathit{HR}-$Algorithm
1	0.981983471074380	0.998362133734035	0.998362133734035	0.999863397308927	0.999999887105214
2	0.998368751375513	0.999986518606409	0.999986518606409	0.999999430860996	0.999999999986235
3	0.999852041705341	0.999999888836743	0.999999888836743	0.999999996934589	0.999999999999996
4	0.999986568810673	0.999999999082632	0.999999999082632	0.999999999981536
5	0.999998780216139	0.999999999992426	0.999999999992426	0.999999999999881
6	0.999999889192851	0.999999999999938	0.999999999999938
7	0.999999989932346
8	0.999999999085170
9	0.999999999916864
10	0.999999999992444

Figure 4. Comparison of the suggested algorithm visually ($HR-$algorithm) at ${\xi }_{\circ }=0.30$.

Figure 5. Comparison of the suggested algorithm visually ($HR-$algorithm) when ${\xi }_{\circ }=0.80$.

7. Solving a Nonlinear Volterra Equation with Delay

In this section, we use the algorithm (7) that we developed to solve the following nonlinear Volterra equation with delay:

$$\xi \left(t\right)=\eta \left(t\right)+\daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\mathrm{\Phi }\left(t,\varsigma ,\xi \left(\varsigma \right),\xi (\varsigma -\mu ))\right)d\varsigma ,t\in J=[k,l].$$

(25)

with the condition

$$\xi \left(t\right)=\mathrm{\Xi }\left(t\right),t\in [k-\mu ,k],$$

(26)

where $k,l\in \mathbb{R},$ $\mathrm{\Xi }\in \left(C[k-\mu ,k],\mathbb{R}\right)$ and $\mu ,\daleth >0$. Clearly, the space $\beth =\left(\left(C[k,l],\mathbb{R}\right),{∥.∥}_{\infty }\right)$ is a BS, where the norm ${∥.∥}_{\infty }$ is described as ${∥\xi -\vartheta ∥}_{\infty }={max}_{t\in J}\left\{\left|\xi \left(t\right)-\vartheta \left(t\right)\right|\right\}$ and $\left(C[k,l],\mathbb{R}\right)$ is the space of all continuous functions defined on $[k,l].$

Now, we present the main theorem in this part.

Theorem 7.

Suppose that Θ is a nonempty CCS of a BS ℶ and $\left\{{\xi }_j\right\}$ is a sequence generated by (7) with $\left\{{\sigma }_j\right\},\left\{{\kappa }_j\right\},\left\{{\tau }_j\right\}\in [0,1].$ Let $\Im :\beth \to \beth$ be an operator described as

$$\Im \xi \left(t\right)=\eta \left(t\right)+\daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\mathrm{\Phi }\left(t,\varsigma ,\xi \left(\varsigma \right),\xi (\varsigma -\mu ))\right)d\varsigma ,t\in J,$$

with $\Im \xi \left(t\right)=\mathrm{\Xi }\left(t\right),$ $t\in [k-\mu ,k].$ Also, assume that the statements below are true:

$\left(s_i\right)$

the functions $\eta :J\to \mathbb{R},$ $\mathrm{\Pi }:J\times J\to \mathbb{R}$ and $\mathrm{\Phi }:J\times J\times \mathbb{R}\times \mathbb{R}\to \mathbb{R}$ are continuous;

$\left(s_{ii}\right)$

there exists a constant $A_{\mathrm{\Phi }}>0$ such that

$$\left|\mathrm{\Phi }\left(t,\varsigma ,{\xi }_1,{\xi }_2)\right)-\mathrm{\Phi }\left(t,\varsigma ,{\xi }_1^{*},{\xi }_2^{*})\right)\right|\le A_{\mathrm{\Phi }}\left(\left|{\xi }_1-{\xi }_1^{*}\right|+\left|{\xi }_2-{\xi }_2^{*}\right|\right),$$

for all ${\xi }_1,{\xi }_2,{\xi }_1^{*},{\xi }_2^{*}\in {\mathbb{R}}_{+}$ and $t,\varsigma \in J;$

$\left(s_{iii}\right)$

for each $t,\varsigma \in J,$ $2\daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )d\varsigma =\chi <1.$

Then the integral Equation (25) with (26) has a unique solution (US, for short) $\widehat{\xi }\in C[k,l].$ Further, if ℑ is a mapping fulfilling (1), then ${\xi }_j⟶\widehat{\xi }.$

Proof. 

First, we demonstrate that ℑ has a FP by applying the contraction principle. Recall that

$$\left|\Im \xi \left(t\right)-\Im {\xi }^{*}\left(t\right)\right|=0,\xi ,{\xi }^{*}\in \left(C[k-\mu ,k],\mathbb{R}\right),t\in [k-\mu ,k].$$

Next, for each $t\in J,$ we can write

$$\begin{array}{ccc}\hfill \left|\Im \xi \left(t\right)-\Im {\xi }^{*}\left(t\right)\right|& =& \left|\eta \left(t\right)+\daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\mathrm{\Phi }\left(t,\varsigma ,\xi \left(\varsigma \right),\xi (\varsigma -\mu )\right)d\varsigma \right.\hfill \\ & & -\left.\eta \left(t\right)+\daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\mathrm{\Phi }\left(t,\varsigma ,{\xi }^{*}\left(\varsigma \right),{\xi }^{*}(\varsigma -\mu )\right)d\varsigma \right|\hfill \\ & \le & \daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left|\mathrm{\Phi }\left(t,\varsigma ,\xi \left(\varsigma \right),\xi (\varsigma -\mu )\right)-\mathrm{\Phi }\left(t,\varsigma ,{\xi }^{*}\left(\varsigma \right),{\xi }^{*}(\varsigma -\mu )\right)\right|d\varsigma \hfill \\ & \le & \daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left[\left|\xi \left(\varsigma \right)-{\xi }^{*}\left(\varsigma \right)\right|+\left|\xi (\varsigma -\mu )-{\xi }^{*}(\varsigma -\mu )\right|\right]d\varsigma \hfill \\ & \le & \daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left[\underset{k-\mu \varsigma \le l}{max}\left|\xi \left(\varsigma \right)-{\xi }^{*}\left(\varsigma \right)\right|+\underset{k-\mu \varsigma \le l}{max}\left|\xi (\varsigma -\mu )-{\xi }^{*}(\varsigma -\mu )\right|\right]d\varsigma \hfill \\ & =& \daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left[{∥\xi -{\xi }^{*}∥}_{\infty }+{∥\xi -{\xi }^{*}∥}_{\infty }\right]d\varsigma \hfill \\ & =& 2\daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )∥\xi -{\xi }^{*}∥d\varsigma =\chi {∥\xi -{\xi }^{*}∥}_{\infty }.\hfill \end{array}$$

Since $\chi <1,$ we conclude that ℑ owns a unique FP and $\lambda \left(\Im \right)=\left\{\widehat{\xi }\right\}$ because it is a contraction. Hence, the problem (25) with (26) has a US $\widehat{\xi }\in C[k,l].$

Ultimately, we prove that ${\xi }_j⟶\widehat{\xi }.$ For each $\xi ,{\xi }^{*}\in \mathrm{\Theta },$ one has

$$\begin{array}{ccc}& & \left|\Im \xi \left(t\right)-\Im {\xi }^{*}\left(t\right)\right|\hfill \\ & \le & \left|\Im \xi \left(t\right)-\xi \left(t\right)\right|+\left|\xi \left(t\right)-\Im {\xi }^{*}\left(t\right)\right|\hfill \\ & \le & \left|\Im \xi \left(t\right)-\xi \left(t\right)\right|+\left|\eta \left(t\right)+\daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\mathrm{\Phi }\left(t,\varsigma ,\xi \left(\varsigma \right),\xi (\varsigma -\mu )\right)d\varsigma \right.\hfill \\ & & -\left.\eta \left(t\right)+\daleth \underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\mathrm{\Phi }\left(t,\varsigma ,{\xi }^{*}\left(\varsigma \right),{\xi }^{*}(\varsigma -\mu )\right)d\varsigma \right|\hfill \\ & \le & \left|\Im \xi \left(t\right)-\xi \left(t\right)\right|+\daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left[\left|\xi \left(\varsigma \right)-{\xi }^{*}\left(\varsigma \right)\right|+\left|\xi (\varsigma -\mu )-{\xi }^{*}(\varsigma -\mu )\right|\right]d\varsigma \hfill \\ & \le & \underset{k-\mu \varsigma \le l}{max}\left|\Im \xi \left(t\right)-\xi \left(t\right)\right|+\daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left[\underset{k-\mu \varsigma \le l}{max}\left|\xi \left(\varsigma \right)-{\xi }^{*}\left(\varsigma \right)\right|+\underset{k-\mu \varsigma \le l}{max}\left|\xi (\varsigma -\mu )-{\xi }^{*}(\varsigma -\mu )\right|\right]d\varsigma \hfill \\ & =& {∥\Im \xi -\xi ∥}_{\infty }+\daleth A_{\mathrm{\Phi }}\underset{k}{\overset{t}{\int }}\mathrm{\Pi }(t,\varsigma )\left[{∥\xi -{\xi }^{*}∥}_{\infty }+{∥\xi -{\xi }^{*}∥}_{\infty }\right]d\varsigma \hfill \\ & \le & {∥\Im \xi -\xi ∥}_{\infty }+\chi {∥\xi -{\xi }^{*}∥}_{\infty }.\hfill \end{array}$$

Hence,

$$∥\Im \xi -\Im {\xi }^{*}∥\le {∥\Im \xi -\xi ∥}_{\infty }+\chi {∥\xi -{\xi }^{*}∥}_{\infty }.$$

It is clear that the mapping ℑ fulfilling (1) with ${\ell }_1=\chi <1$ and ${\ell }_2=0.$ Therefore, all requirements of Theorem 1 are satisfied. Then, the sequence $\left\{{\xi }_j\right\}$ established by the iterative technique (7) converges strongly to the US of Equation (25) with (26). □

8. Conclusions and Open Problems

The effectiveness and success of iterative techniques are largely determined by two essential factors that are widely acknowledged. The two primary factors are the rate of convergence and the number of iterations; if convergence occurs more quickly with fewer repetitions, the method is successful in approximating the FPs. As a result, we have shown analytically and numerically in this work that, in terms of convergence speed, our method performs better than some of the most popular iterative algorithms, like the S algorithm [14], the Picard-S algorithm [18], the Thakur algorithm [19], and the $K^{*}-$algorithm [20]. Furthermore, comparison graphs of computations showed the frequency and speed of convergence and stability results. A solution to a fundamental problem served as an application that ultimately reinforced our methodology. Ultimately, we deem the following findings of this paper as potential contributions to future work:

• The variational inequality problem can be solved using our iteration (7) if we define the mapping ℑ in a Hilbert space $\mathrm{\Omega }$ endowed with an inner product space. This problem can be described as: find ${\wp }^{*}\in \mathrm{\Omega }$ such that

  $$⟨\Im {\wp }^{*},\wp -{\wp }^{*}⟩\ge 0\mathrm{for}\mathrm{all}\wp \in \mathrm{\Omega },$$

  where $\Im :\mathrm{\Omega }\to \mathrm{\Omega }$ is a nonlinear mapping. In several disciplines, including engineering mechanics, transportation, economics, and mathematical programming, variational inequalities are a crucial and indispensable modeling tool; see [37,38] for more details.
• Our methodology can be extended to include gradient and extra-gradient projection techniques, which are crucial for locating saddle points and resolving a variety of optimization-related issues; see [39].
• We can accelerate the convergence of the proposed algorithm by adding shrinking projections and CQ terms. These methods stimulate algorithms and improve their performance to obtain strong convergence; for more details, see [40,41,42,43].
• If we consider the mapping ℑ as an $\alpha -$inverse strongly monotone and if the inertial term is added to our algorithm, then we have the inertial proximal point algorithm. This algorithm is used in many applications, such as monotone variational inequalities, image restoration problems, convex optimization problems, and split convex feasibility problems [44,45]. For more accuracy, these problems can be expressed as mathematical models such as machine learning and the linear inverse problem.
• Second-order differential equations and fractional differential equations, which Green’s function can be used to transform into integral equations, can be solved using our approach. Therefore, it is simple to treat and resolve using the same method as in Section 7.