On Several Parameters of Super Line Graph ${\mathcal{L}}_2\left(G\right)$

Abstract

The super line graph of index r, denoted by ${\mathcal{L}}_r\left(G\right)$, is defined for any graph G with at least r edges. Its vertices are the sets of r edges of G, and two such sets are adjacent if an edge of one is adjacent to an edge of the other. In this paper, we give an explicit characterization for all graphs G with ${\mathcal{L}}_2\left(G\right)$ being a complete graph. We present lower bounds for the clique number and chromatic number of ${\mathcal{L}}_2\left(G\right)$ for several classes of graphs. In addition, bounds for the domination number of ${\mathcal{L}}_2\left(G\right)$ are established in terms of the domination number of the line graph $L\left(G\right)$ of a graph. A number of related problems on ${\mathcal{L}}_2\left(G\right)$ are proposed for a further study.

1. Introduction

The line graph $L\left(G\right)$ of a graph G is the graph with the edges of G as its vertices where two vertices of $L\left(G\right)$ are adjacent if and only if they share a common end vertex in G. There is a huge amount of literature devoted to the line graph and its various generalizations [1,2,3,4,5,6,7,8,9,10,11,12]. The super line graph of index r, denoted by ${\mathcal{L}}_r\left(G\right)$, is defined for any graph G with at least r edges. Its vertices are the sets of r edges of G, and two such sets are adjacent if an edge of one is adjacent to an edge of the other. As ${\mathcal{L}}_r\left(G\right)=L\left(G\right)$ for $r=1$, the super line graph is a kind of generalization of the notion of line graph. Index-r line graphs were first introduced by Bagga, Beineke, and Varma [13] in 1995. Some properties of ${\mathcal{L}}_2\left(G\right)$ were presented by Bagga, Beineke, and Varma [14] in 1999. In particular, they showed that ${\mathcal{L}}_2\left(G\right)$ is pancyclic for any connected graph G of size at least 2. A graph G of order n is path-comprehensive if every pair of vertices are joined by paths of all lengths in $\{2,3,\dots ,n-1\}$. In 2008, Li, Li, and Zhang [15] showed that if G has no isolated edges, then ${\mathcal{L}}_2\left(G\right)$ is path-comprehensive, and that if G has at most one isolated edge, then ${\mathcal{L}}_2\left(G\right)$ is vertex-pancyclic, answering a question posed by Bagga, Beineke, and Varma [14]. We refer to [16,17,18,19,20,21,22,23,24,25,26] for more results on super line graphs.

The symbols $K_n$, $C_n$, and $P_n$ represent the complete graph, cycle, and path of order n, respectively. The symbol $K_{m,n}$ denotes the complete bipartite graph with parts of size m and n. In addition, $K_{m,n}$ is called a star if $min\{m,n\}=1$. We use $K_{1,n-1}+e$ to denote the unicyclic graph graph of order n obtained from $K_{1,n-1}$ by adding an edge as shown in Figure 1, whereas $K_{1,n-1}^{\prime }$ denotes the tree obtained from $K_{1,n-1}+e$ by deleting an edge from its triangle, but distinct from $K_{1,n-1}$.

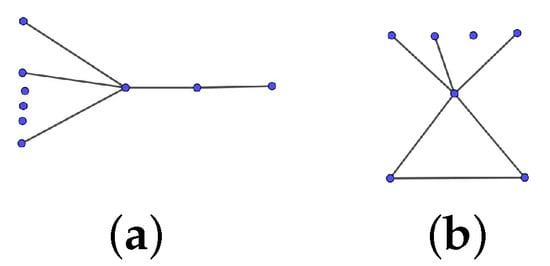
Figure 1. Graphs $K_{1,n-1}^{\prime }$ and $K_{1,n-1}+e$: (a) $K_{1,n-1}^{\prime }$; (b) $K_{1,n-1}+e$.

Let G be a graph. For a positive integer k, $kG$ denotes the graph consisting of k copies of G. The square of $G^2$ of G is the graph with $V\left(G^2\right)=V\left(G\right)$, in which two vertices u and v are adjacent if and only if $d_G(u,v)\le 2$, where $d_G(u,v)$ denotes the distance of u and v in G. The degree of a vertex v is denoted by $d_G\left(v\right)$. The maximum and the minimum degree of G are denoted by $\Delta \left(G\right)$ and $\delta \left(G\right)$, respectively. A vertex subset S of a graph G is a clique if $G\left[S\right]$ is a complete graph. The clique number of G, denoted by $\omega \left(G\right)$, is the maximum cardinality of a clique in G. A vertex subset S of a graph G is an independent set if $G\left[S\right]$ is an empty graph. The independence number of G, denoted by $\alpha \left(G\right)$, is the maximum cardinality of an independent set of G. An edge set M of G is called a matching if no two elements of M are adjacent in G. The matching number of G, denoted by ${\alpha }^{\prime }\left(G\right)$, is the maximum cardinality of a matching of G. Bagga, Beineke, and Varma [19] determined the independence number of ${\mathcal{L}}_r\left(G\right)$.

Theorem 1.

(Bagga, Beineke, and Varma [19]). If G is a graph of size at least r, then $\alpha \left({\mathcal{L}}_r\left(G\right)\right)=(\genfrac{}{}{0pt}{}{{\alpha }^{\prime }\left(G\right)}{r})$. Furthermore, if S is a maximum independent set of vertices in ${\mathcal{L}}_r\left(G\right)$, then either

(1) $S=(\genfrac{}{}{0pt}{}{X}{r})$ for some maximum matching of G, where $(\genfrac{}{}{0pt}{}{X}{r})=\{T:T\subseteq X$ with $\left|T\right|=r\}$, or

(2) S consists of $r+1$ disjoint stars $K_{1,r}$, or

(3) $r=3$ and the vertices in S are $K_{1,3}$ or $K_3$.

The line completion number $lc\left(G\right)$ of a graph G is the least index r for which ${\mathcal{L}}_r\left(G\right)$ is complete. This notion was investigated in [22,23,24,25,26]. For a graph G without an isolated vertex, $lc\left(G\right)=1$ means that $L\left(G\right)$ is complete. It is clear that $\omega \left(L\right(G\left)\right)=3$ if $\Delta \left(G\right)=2$ and G contains a triangle, and $\omega \left(L\right(G\left)\right)=\Delta \left(G\right)$ otherwise. In addition, $L\left(G\right)$ is complete if and only if G is a star or a triangle. Bagga, Beineke, and Varma [14] characterized all graphs with $lc\left(G\right)\le 2$, as we see in the next section.

In this paper, we give an explicit characterization for all graphs G with ${\mathcal{L}}_2\left(G\right)$ being a complete graph. We present lower bounds for the clique number and chromatic number of ${\mathcal{L}}_2\left(G\right)$ for several classes of graphs. In addition, bounds for the domination number of ${\mathcal{L}}_2\left(G\right)$ are established in terms of the domination number of the line graph $L\left(G\right)$ of a graph G. A number of related problems on ${\mathcal{L}}_2\left(G\right)$ are proposed for further study.

2. Clique

For convenience, $H\subseteq G$ means that H is a subgraph of G. More specifically, $H\subset G$ present the meaning that H is a proper subgraph of G. We start with an easy observation.

Lemma 1.

If $H\subseteq G$, then ${\mathcal{L}}_r\left(H\right)$ is an induced subgraph of ${\mathcal{L}}_r\left(G\right)$.

Theorem 2.

(Bagga, Beineke, and Varma [14]). For a graph G, ${\mathcal{L}}_2\left(G\right)$ is complete if and only if G does not contain $3K_2$ or $2K_{1,2}$ as a subgraph.

Next we give an explicit characterization for graphs whose super line graphs of index 2 are complete.

Theorem 3.

For a graph G of order n and size $m\ge 2$, ${\mathcal{L}}_2\left(G\right)$ is complete if and only if $G\subseteq K_5$ or G is a subgraph of $K_{1,n-1}+e$ for some n.

Proof. 

As both $3K_2$ and $2K_{1,2}$ have six vertices, $K_5$ does not contain $3K_2$ or $2K_{1,2}$ as a subgraph, and so neither does a subgraph of $K_5$. The same conclusion holds for $K_{1,n-1}+e$ for any n. By Lemma 1 and Theorem 2, ${\mathcal{L}}_2\left(G\right)$ is complete.

To prove the ’only if’ part, let G be a graph of order $n\ge 6$ and size $m\ge 2$ with no isolated vertex such that ${\mathcal{L}}_2\left(G\right)$ is complete. In view of Lemma 1, we may further assume that m is as large as possible, subject to the aforementioned property. It remains to show that $G\cong K_{1,n-1}+e$.

Claim 1.

G is connected.

Proof. 

Suppose G is disconnected. Since ${\mathcal{L}}_2\left(G\right)$ is a complete graph, by Theorem 2, $3K_2\cancel{\subseteq }G$, $2K_{1,2}\cancel{\subseteq }G$. It follows that G has exactly two components, one of which is isomorphic to $K_2$ and the other one is $K_{1,n-3}$. Thus $G\subseteq K_{1,n-1}+e$. However, this contradicts the assumption that m is as large as possible. □

Next we show that $\Delta \left(G\right)=n-1$. First of all, $\Delta \left(G\right)\ge 3$. Otherwise, $G\cong P_n$. Since $n\ge 6$, $2K_{1,2}\subseteq G$, a contradiction. Let v be a vertex of the maximum degree in G.

Claim 2.

$\Delta \left(G\right)\ge n-2$.

Proof. 

Suppose that there exist two vertices u and w that are not adjacent to v. If $d_G(u,w)\le 2$, then one can find a subgraph isomorphic to $2K_{1,2}$, contradicting our assumption. If $d_G(u,w)\ge 3$, then there exists a subgraph isomorphic to $3K_2$ with the edge set of form $\{u{u}^{\prime },w{w}^{\prime },v{v}^{\prime }\}$. □

Claim 3.

$\Delta \left(G\right)=n-1$.

Proof. 

By Claim 2, suppose that $\Delta \left(G\right)=n-2$, and let u be the unique vertex of G, which is not adjacent to v. Since $d_G\left(v\right)=n-2\ge 4$, $d_G\left(u\right)=1$; otherwise, one can find a subgraph of G isomorphic to $2K_2$. In addition, if any two neighbors of v are adjacent in G, either $3K_2\subseteq G$ or $2K_{1,2}\subseteq G$ occurs. Thus, $G\subset K_{1,n-1}+e$, a contradiction. □

Claim 4.

$G\cong K_{1,n-1}+e$.

Proof. 

By Claim 3, $\Delta \left(G\right)=n-1$. Since $L_2(K_{1,n-1}+e)$ is complete and by the maximality of m, $m\ge n$. If $m\ge n+1$, then by $n\ge 6$, either $3K_2\subseteq G$ or $2K_{1,2}\subseteq G$ occurs. This proves $G\subset K_{1,n-1}+e$.

The proof is completed. □

Theorem 4.

For any integer $n\ge 3$, $\omega \left({\mathcal{L}}_2\left(K_n\right)\right)\ge (\frac{5n}{2}-6)(n-1)$.

Proof. 

Label the vertices of $K_n$ as $1,2,\dots ,n$. Let $A_1=\{\{1i,ij\}:1\le i,j\le n,i\ne j\}$. Clearly, $|A_1|=(n-1)(n-2)$.

Claim 5.

$A_1$is a clique in${\mathcal{L}}_2\left(K_n\right)$.

Proof. 

Consider any two elements $\{1i,ij\}$ and $\{1a,ab\}$, where $1\le i,j\le n,i\ne j$, and $1\le a<b\le n$. It is enough to show that they are adjacent in ${\mathcal{L}}_2\left(K_n\right)$. If $i\ne a$, then the edges $1i$ and $1a$ are adjacent in G, implying that $\{1i,ij\}$ and $\{1a,ab\}$ are adjacent in ${\mathcal{L}}_2\left(K_n\right)$. If $i=a$, then $j\ne b$, implying that the edges $ij$ and $ab$ are adjacent in G, implying that $\{1i,ij\}$ and $\{1a,ab\}$ are adjacent in ${\mathcal{L}}_2\left(K_n\right)$. □

Let $A_2=\{\{12,3k\}:4\le k\le n\}\cup \{\{1i,2j\}:3\le i,j\le n,i\ne j\}$. One can see that $|A_2|=(n-1)(n-3)$.

Claim 6.

$A_2$is a clique in${\mathcal{L}}_2\left(K_n\right)$.

Proof. 

Observe that both $\left\{\right\{12,3k\}:4\le k\le n\}$ and $\left\{\right\{1i,2j\}:3\le i,j\le n,i\ne j\}$ are cliques of ${\mathcal{L}}_2\left(K_n\right)$. Moreover, $\{12,3k\}$ and $\{1i,2j\}$ are adjacent in ${\mathcal{L}}_2\left(K_n\right)$ for any $k\in \{4,\dots ,n\}$ and $i,j\in \{3,\dots ,n\}$. It follows that $A_2$ is a clique in ${\mathcal{L}}_2\left(K_n\right)$. □

Let $A_3=\{\{1i,1j\}:2\le i<j\le n\}$. It is easy to see that $A_3$ is a clique in ${\mathcal{L}}_2\left(K_n\right)$ with $|A_3|=\left(\genfrac{}{}{0pt}{}{n-1}{2}\right)$. Note that $A_1,A_2$, and $A_3$ are pairwise disjoint and $|A_1|+|A_2|+|A_3|=(\frac{5n}{2}-6)(n-1)$. Thus, the assertion of the theorem follows from the following claim.

Claim 7.

$A_1\cup A_2\cup A_3$is a clique in${\mathcal{L}}_2\left(K_n\right)$.

Proof. 

Take three vertices $u\in A_1$, $v\in A_2$, and $w\in A_3$ arbitrarily, where $u=\{1i,ij\}$ for $1\le i,j\le n,i\ne j\}$, $v=\{12,3k\}$ for $4\le k\le n$ or $v=\{1a,2b\}$ for some $3\le a,b\le n,a\ne b$, and $w=\{1s,1t\}\in A_3$ for some $2\le s<t\le n$.

First of all, w must be adjacent to u and v, because at least one of $1s$ and $1t$ is adjacent to $1i$, 12 and $1a$ in $K_n$.

It remains to show u and v are adjacent. Assume that $v=\{12,3k\}$ for $4\le k\le n$. If $i\ne 2$, then u and v are adjacent because $1i$ and 12 are adjacent in G. If $i=2$, then u and v are still adjacent because $1i$ and $ij$ are adjacent in G. Now we assume that $v=\{1a,2b\}$ for some $3\le a,b\le n,a\ne b$. One can show that u and v are adjacent by considering the cases when $i=a$ and $i\ne a$.

The proof is completed. □

At present, we did not know the exact value of $\omega \left({\mathcal{L}}_2\left(K_n\right)\right)$ for general n.

3. Chromatic Number

A mapping $f:V\left(G\right)\mapsto \{1,\dots ,k\}$ is a k-coloring of G if $f\left(u\right)\ne f\left(v\right)$ for any edge $uv\in E\left(G\right)$, where k is a positive integer. The chromatic number of G, denoted by $\chi \left(G\right)$, is the minimum integer k for which G has a k-coloring. Obviously, $\chi \left(G\right)\ge \omega \left(G\right)$ for any graph G. The well-known theorem of Vizing says that $\Delta \left(G\right)\le \chi \left(L\right(G\left)\right)\le \Delta \left(G\right)+1$ for a simple graph G. However, it is hard to determine $\omega \left({\mathcal{L}}_2\left(G\right)\right)$ and $\chi \left({\mathcal{L}}_2\left(G\right)\right)$ for a general graph G.

Theorem 5.

For a graph G of order n and size m without an isolated vertex,

$$\chi \left({\mathcal{L}}_2\left(G\right)\right)⩽\left(\genfrac{}{}{0pt}{}{m}{2}\right),$$

with equality if and only if either $G\subseteq K_5$ or $G\in \{K_{1,n-1},K_{1,n-1}^{\prime },K_{1,n-1}+e\}$.

Proof. 

Assume that G is a graph of order n and size m without an isolated vertex. Since the order of a graph is the trivial upper bound for its chromatic number and the order of ${\mathcal{L}}_2\left(G\right)$ is $\left(\genfrac{}{}{0pt}{}{m}{2}\right)$, the result follows trivially.

If $G\subseteq K_5$ or $G\subseteq K_{1,n-1}+e$, then by Theorem 3, ${\mathcal{L}}_2\left(G\right)$ is complete. Thus $\chi \left({\mathcal{L}}_2\left(G\right)\right)=\left(\genfrac{}{}{0pt}{}{m}{2}\right)$. For the converse, assume that $\chi \left({\mathcal{L}}_2\left(G\right)\right)=\left(\genfrac{}{}{0pt}{}{m}{2}\right)$. It follows that ${\mathcal{L}}_2\left(G\right)$ is complete. Again, by Theorem 3, $G\subseteq K_5$ or $G\subseteq K_{1,n-1}+e$, completing the proof. □

Corollary 1.

For a tree T of order n, $\chi \left({\mathcal{L}}_2\left(G\right)\right)⩽\left(\genfrac{}{}{0pt}{}{n-1}{2}\right)$ with equality if and only if $T\cong K_{1,n-1}$ or $T\cong K_{1,n-1}^{\prime }$.

Proof. 

It is immediate from Theorem 5. □

Corollary 2.

For a unicyclic graph G of order n, $\chi \left({\mathcal{L}}_2\left(G\right)\right)⩽\left(\genfrac{}{}{0pt}{}{n}{2}\right)$, with equality if and only if either $n\le 5$ or $G\cong K_{1,n-1}+e$.

Proof. 

Since G is a unicyclic graph G of order n, $m=n$, where m is the size of G. By Theorem 5, the result follows. □

All unicyclic graphs of order 5 are given in Figure 2.

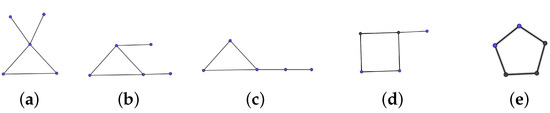
Figure 2. All unicyclic graphs of order 5, in which (a), (b) and (c) have the cycle length three, and (d) and (e) have the cycle length four and five, respectively.

Theorem 6.

For an odd integer $n\ge 3$,

$$\chi \left({\mathcal{L}}_2\left(P_n\right)\right)\le \frac{n-1}{2}+5.$$

(1)

Proof. 

First, label the edges of $P_n$ as $1,2,\dots ,n-1$ successively, as shown in Figure 3a. Since $n-1$ is even, the edges of $P_n$ can be divided into two maximum edge independent sets $\{1,3,5,\cdots ,n-2\}$ and $\{2,4,6,\cdots ,n-1\}$. Let $A_1=\{\{1,2k\}:1\le k\le \frac{n-1}{2}\}\backslash \{1,2\}$, let $A_i=\{\{i,2k\}:1\le k\le \frac{n-1}{2}\}\backslash \{\{i,i-1\},\{i,i+1\}\}$ for an integer $i\in \{3,5,\dots ,n-2\}$. Furthermore, let $B=\left\{\right\{i,j\}:$ both i and j are odd number between 1 and $n-2$}, $C=\left\{\right\{i,j\}:$ both i and j are even between 2 and $n-1$}, and $D=\left\{\right\{i,i+1\}:1\le i\le n-2\}$. A simple computation shows that ${\sum }_{j=1}^{\frac{n-1}{2}}|A_{2j-1}|+|B|+|C|+|D|=(\frac{n-1}{2}(\frac{n-1}{2}-2)+1)+2(\genfrac{}{}{0pt}{}{\frac{n-1}{2}}{2})+(n-2)=\frac{(n-1)(n-2)}{2}$. Observe that all $A_i$ for each i, B and C are independent sets in ${\mathcal{L}}_2\left(P_n\right)$, and the vertices in D can be properly colored in three additional colors. Thus

$$\chi \left({\mathcal{L}}_2\left(P_n\right)\right)\le \frac{n-1}{2}+2+3=\frac{n-1}{2}+5.$$

□

Figure 3. The labeling of edges of $P_n$ and ${\mathcal{L}}_2\left(P_n\right)\left[D\right]$: (a) $P_n$; (b) the subgraph induced by D.

By Theorem 5, ${\mathcal{L}}_2\left(P_5\right)\cong K_6$, and thus $\chi \left({\mathcal{L}}_2\left(P_5\right)\right)=6<7=\frac{5-1}{2}+5$. However, the bound in the above theorem can be attained by the following example.

Proposition 1.

$\chi \left({\mathcal{L}}_2\left(P_7\right)\right)=8.$

Proof. 

By the above theorem, $\chi \left({\mathcal{L}}_2\left(P_7\right)\right)\le \frac{7-1}{2}+5=8$. To show $\chi \left({\mathcal{L}}_2\left(P_7\right)\right)\ge \frac{7-1}{2}+5=8$, label the edges of $P_7$ as $1,2,\dots ,6$ successively, as illustrated in Figure 3. Let $A=\left\{\right\{i,j\}:1\le i<j\le 4\}$. ${\mathcal{L}}_2\left(P_7\right)\left[A\right]\cong K_6$. Let $v=\{2,5\}$. Since v is adjacent to all vertices of A in ${\mathcal{L}}_2\left(P_7\right)$, ${\mathcal{L}}_2\left(P_7\right)[A\cup \left\{v\right\}]\cong K_7$. Suppose $\chi \left({\mathcal{L}}_2\left(P_7\right)\right)=7$ and let c be a 7-coloring of ${\mathcal{L}}_2\left(P_7\right)$. We consider the two adjacent vertices $\{3,5\}$ and $\{3,6\}$ of ${\mathcal{L}}_2\left(P_7\right)$. One can check that $\{3,5\}$ is adjacent to all elements of $A\cup \left\{v\right\}$ except $\{1,3\}$. In addition, $\{3,5\}$ is adjacent to all elements of A except $\{1,3\}$ as well. It implies that $c\left(\right\{3,5\left\}\right)=c\left(\right\{3,6\left\}\right)$, contradicting that $c\left(\right\{3,5\left\}\right)\ne c\left(\right\{3,6\left\}\right)$. Thus $\chi \left({\mathcal{L}}_2\left(P_7\right)\right)>7$. This proves $\chi \left({\mathcal{L}}_2\left(P_7\right)\right)=8$. □

Theorem 7.

For an even integer $n\ge 4$,

$$\chi \left({\mathcal{L}}_2\left(C_n\right)\right)\le \left\{\begin{array}{cc}\frac{n}{2}+5,\hfill & if n\equiv 0\left(mod3\right)\hfill \\ \frac{n}{2}+6,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

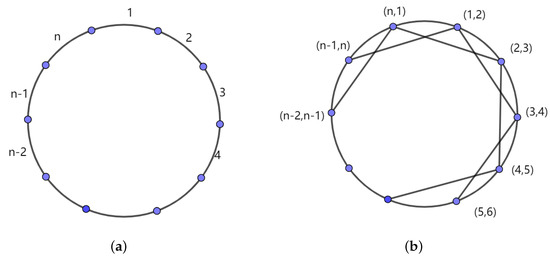
First, label the edges of $C_n$ as $1,2,\dots ,n$ successively in the clockwise order, as shown in Figure 4a. Since n is even, the edges of $C_n$ can be divided into two maximum matchings $\{1,3,5,\cdots ,n-1\}$ and $\{2,4,6,\cdots ,n\}$. By a similar way as in the proof of the previous theorem, let $A_1=\{\{1,2k\}:1\le k\le \frac{n}{2}\}\backslash \{\{1,2\},\{n,1\}\}$, let $A_i=\{\{i,2k\}:1\le k\le \frac{n}{2}\}\backslash \{\{i,i-1\},\{i,i+1\}\}$ for an integer $i\in \{3,5,\dots ,n-1\}$. Furthermore, let $B=\left\{\right\{i,j\}:$ both i and j are odd number between 1 and $n-1$}, $C=\left\{\right\{i,j\}:$ both i and j are even between 2 and n}, and $D=\left\{\right\{i,i+1\}:1\le i\le n-1\}\cup \{n,1\}$. A simple computation shows that ${\sum }_{j=1}^{\frac{n}{2}}|A_{2j-1}|+|B|+|C|+|D|=\frac{n}{2}(\frac{n}{2}-2)+2(\genfrac{}{}{0pt}{}{\frac{n}{2}}{2})+n=\frac{n(n-1)}{2}$. Observe that all $A_i$ for each i, B and C are independent sets in ${\mathcal{L}}_2\left(C_n\right)$. In addition, ${\mathcal{L}}_2\left(C_n\right)\left[D\right]\cong C_n^2$, where $C_n^2$ is as shown in Figure 4b. One can see that

$$\chi \left(C_n^2\right)=\left\{\begin{array}{cc}3,\hfill & \mathrm{if} n\equiv 0(\mathrm{mod} 3)\hfill \\ 4,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Figure 4. The labeling of edges of $C_n$ and ${\mathcal{L}}_2\left(C_n\right)\left[D\right]$: (a) $C_n$; (b) subgraph of ${\mathcal{L}}_2\left(C_n\right)$ induced by D.

Thus, combining above facts, we conclude that

$$\chi \left({\mathcal{L}}_2\left(C_n\right)\right)\le \left\{\begin{array}{cc}\frac{n}{2}+5,\hfill & \mathrm{if} n\equiv 0(\mathrm{mod} 3)\hfill \\ \frac{n}{2}+6,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

□

4. Domination

For a graph G, a subset $S\subseteq V\left(G\right)$ is called a dominating set if each vertex of $V\left(G\right)\setminus S$ is adjacent to some element of S in G. The domination number of G, denoted by $\gamma \left(G\right)$, is the minimum cardinality of a dominating set of G. A subset $S\subseteq V\left(G\right)$ is called a total dominating set of G if each vertex of G is adjacent to some element of S in G. The total domination number of G, denoted by ${\gamma }_t\left(G\right)$, is the minimum cardinality of a total dominating set of G. Obviously, for $\gamma \left(G\right)\le {\gamma }_t\left(G\right)$ for any graph G without an isolated vertex. Note that $\gamma \left(L\left(G\right)\right)\le {\alpha }^{\prime }\left(G\right)\le \frac{n}{2}$ for any connected graph G.

Theorem 8.

For a connected graph G of order $n\ge 3$,

$$\frac{1}{2}(\gamma \left(L\left(G\right)\right)-1)\le \gamma \left({\mathcal{L}}_2\left(G\right)\right)\le {\gamma }_t\left({\mathcal{L}}_2\left(G\right)\right)\le \gamma \left(L\left(G\right)\right).$$

Proof. 

First we show that ${\gamma }_t\left({\mathcal{L}}_2\left(G\right)\right)\le \gamma \left(L\left(G\right)\right)$. Let $\{e_1,e_2,\cdots ,e_k\}$ be a minimum dominating set of $L\left(G\right)$. For each $i\in \{1,\dots ,k\}$, we take an edge of G, say $f_i$, adjacent to $e_i$. It suffices to show that $\{\{e_i,f_i\}:i\in \{1,\dots ,k\}\}$ is a total dominating set of ${\mathcal{L}}_2\left(G\right)$. Consider a pair $\{e,f\}$ of edges. If $e\ne e_i$ for each i, then by e must be adjacent to some $e_j$. It follows that $\{e,f\}$ is adjacent to $\{e_j,f_j\}$ in ${\mathcal{L}}_2\left(G\right)$. If $e=e_j$ for some j, then by e is adjacent to $f_j$. Thus $\{e,f\}$ and $\{e_j,f_j\}$ are adjacent in ${\mathcal{L}}_2\left(G\right)$. This proves ${\gamma }_t\left({\mathcal{L}}_2\left(G\right)\right)\le \gamma \left(L\left(G\right)\right)$.

Let $\{\{e_i,f_i\}:1\le i\le k\}$ be a minimum dominating set of ${\mathcal{L}}_2\left(G\right)$. If ${\cup }_{i=1}^k\{e_i,f_i\}$ is a dominating set of $L\left(G\right)$, then $\gamma \left(L\left(G\right)\right)\le 2k=2{\mathcal{L}}_2\left(G\right)$, and hence

$$\gamma \left({\mathcal{L}}_2\left(G\right)\right)\ge \frac{1}{2}\gamma \left(L\left(G\right)\right).$$

Now assume that ${\cup }_{i=1}^k\{e_i,f_i\}$ is not a dominating set of $L\left(G\right)$. We choose a vertex, say e, which is not dominated by ${\cup }_{i=1}^k\{e_i,f_i\}$ in $L\left(G\right)$. We claim that e is the unique vertex of $L\left(G\right)$ with the aforementioned property. Let $f\in E\left(G\right)\setminus \left\{e\right\}$ be a vertex not dominated by ${\cup }_{i=1}^k\{e_i,f_i\}$ in $L\left(G\right)$. Since $\{e,f\}$ is dominated by $\{\{e_i,f_i\}:1\le i\le k\}$, one of e and f must be adjacent to some element of ${\cup }_{i=1}^k\{e_i,f_i\}$ in $L\left(G\right)$. This contradiction proves the claim. Thus $\left\{e\right\}\cup {\cup }_{i=1}^k\{e_i,f_i\}$ is a dominating set of $L\left(G\right)$. It follows that $\gamma \left(L\left(G\right)\right)\le 2k+1=2{\mathcal{L}}_2\left(G\right)+1$, and thus

$$\gamma \left({\mathcal{L}}_2\left(G\right)\right)\ge \frac{1}{2}(\gamma \left(L\left(G\right)\right)-1),$$

completing the proof. □

5. Discussion

Previously, the Hamiltonian property, line completion number of super line graphs was investigated. In this paper, we study several kind of parameters of ${\mathcal{L}}_2\left(G\right)$, such as clique number, chromatic number, and domination number. We do not know the exact value of $\omega \left({\mathcal{L}}_2\left(K_n\right)\right)$ yet. However, it is hard to decide these parameters of a general graph G, even though G is a complete graph, a cycle, or a path. Therefore, we provide some bounds for these parameters.

Since $G\subseteq K_n$ for any graph G of order n, $\chi \left({\mathcal{L}}_2\left(G\right)\right)\le \chi \left({\mathcal{L}}_2\left(K_n\right)\right)$. The following problem is worth being investigated.

Problem 1.

$\chi \left({\mathcal{L}}_2\left(K_n\right)\right)=?$

In view of Theorems 3.4 and 3.6, it is natural to seek the exact values for $P_n$ and $C_n$.

Problem 2.

$\chi \left({\mathcal{L}}_2\left(P_n\right)\right)=?$

Problem 3.

$\chi \left({\mathcal{L}}_2\left(C_n\right)\right)=?$

The following conjectures seem to be true.

Conjecture 1.

For any tree T of order n,$\chi \left({\mathcal{L}}_2\left(T\right)\right)⩾\chi \left({\mathcal{L}}_2\left(P_n\right)\right)$.

Conjecture 2.

For a unicyclic graph G of order n,$\chi \left({\mathcal{L}}_2\left(G\right)\right)⩾\chi \left({\mathcal{L}}_2\left(C_n\right)\right)$.

A more basic problem on ${\mathcal{L}}_2\left(G\right)$ is stated as follows.

Problem 4.

For a connected graph G of order n and size m, what are the exact bounds for the size $\left|E\right({\mathcal{L}}_2\left(G\right)\left)\right|$ of ${\mathcal{L}}_2\left(G\right)$?