Probabilistic Coarsening for Knowledge Graph Embeddings
Abstract
1. Introduction
- Coarsening reduces knowledge graph size whilst preserving the global structure, potentially revealing higher-order features.
- Training schemes that rely on stochastic gradient descent may learn embeddings that fall in local minima. Initializations learned on the coarse graph may be more resistant to this problem.
- Structurally equivalent entities are embedded jointly in coarse graphs, reducing training complexity.

2. Related Work
3. Proposed Strategy
- Probabilistic graph coarsening reduces the base graph to a smaller, coarsened graph and returns an entity mapping between the two graphs.
- Coarse graph embedding applies a predetermined embedding method on the coarse graph to obtain coarse embeddings.
- Reverse mapping and fine-tuning maps coarse embeddings back down to the base graph to obtain base embeddings. Base embeddings may be fine-tuned on the base graph.
3.1. Probabilistic Graph Coarsening
3.1.1. Collapsing First-Order Neighbours
3.1.2. Collapsing Second-Order Neighbours
| Algorithm 1: Coarse knowledge graph embeddings. |
| Input: base graph ; collapsing threshold ; random walk count Output: base embeddings
|
3.1.3. Neighbour Sampling
- Entities that meet the criteria for collapsing are likely to have smaller neighbourhoods.
- Entities that belong to smaller neighbourhoods have a higher chance of getting sampled as candidates for collapsing.
3.2. Coarse Graph Embedding
3.3. Reverse Mapping and Fine Tuning
4. Evaluation
4.1. Datasets
- MUTAG depicts the properties and interactions of molecules that may or may not be carcinogenic. We remove the labelling predicate isMutagenic from the dataset.
- AIFB reports the work performed at the AIFB research group and labels its members by affiliation. We remove predicates, employs, and affiliation.
- BGS captures geological data from the island of Great Britain and is used to predict the lithogenicity of rocks. As such, we remove the hasLithogenesis predicate.
- AM describes and categorises artefacts in the Amsterdam Museum. We remove the materials predicate as it correlates with artefact labels.
| Dataset | MUTAG | AIFB | BGS | AM |
|---|---|---|---|---|
| Triples | 74,227 | 29,043 | 916,199 | 5,988,321 |
| Entities | 23,644 | 8285 | 333,845 | 1,666,764 |
| Predicates | 23 | 45 | 103 | 133 |
| Labelled | 340 | 176 | 146 | 1000 |
| Classes | 2 | 4 | 2 | 11 |
4.2. Procedure
4.3. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Bordes, A.; Usunier, N.; Chopra, S.; Weston, J. Large-scale simple question answering with memory networks. arXiv 2015, arXiv:1506.02075. [Google Scholar]
- Das, R.; Dhuliawala, S.; Zaheer, M.; Vilnis, L.; Durugkar, I.; Krishnamurthy, A.; Smola, A.; McCallum, A. Go for a walk and arrive at the answer: Reasoning over paths in knowledge bases using reinforcement learning. arXiv 2017, arXiv:1711.05851. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van Den Berg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In European Semantic Web Conference; Springer: Cham, Switzerland, 2018; pp. 593–607. [Google Scholar]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. Adv. Neural Inf. Process. Syst. 2013, 26, 2787–2795. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. arXiv 2017, arXiv:1707.01476. [Google Scholar] [CrossRef]
- Bellini, V.; Schiavone, A.; Di Noia, T.; Ragone, A.; Di Sciascio, E. Knowledge-aware autoencoders for explainable recommender systems. In Proceedings of the 3rd Workshop on Deep Learning for Recommender Systems, Vancouver, BC, Canada, 6 October 2018. [Google Scholar]
- Ristoski, P.; Paulheim, H. Rdf2vec: Rdf graph embeddings for data mining. In International Semantic Web Conference; Springer: Cham, Switzerland, 2016; pp. 498–514. [Google Scholar]
- Nickel, M.; Tresp, V.; Kriegel, H.P. A three-way model for collective learning on multi-relational data. In Proceedings of the 28th International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011. [Google Scholar]
- Chen, H.; Perozzi, B.; Hu, Y.; Skiena, S. Harp: Hierarchical representation learning for networks. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 2127–2134. [Google Scholar]
- Liang, J.; Gurukar, S.; Parthasarathy, S. Mile: A multi-level framework for scalable graph embedding. arXiv 2018, arXiv:1802.09612. [Google Scholar] [CrossRef]
- Archdeacon, D. Topological graph theory. Surv. Congr. Numer. 1996, 115, 18. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. Line: Large-scale information network embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015. [Google Scholar]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed representations of words and phrases and their compositionality. Adv. Neural Inf. Process. Syst. 2013, 26, 3111–3119. [Google Scholar]
- Duvenaud, D.K.; Maclaurin, D.; Iparraguirre, J.; Bombarell, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional networks on graphs for learning molecular fingerprints. Adv. Neural Inf. Process. Syst. 2015, 28, 2224–2232. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef]
- Simonovsky, M.; Komodakis, N. Graphvae: Towards generation of small graphs using variational autoencoders. In International Conference on Artificial Neural Networks; Springer: Cham, Switzerland, 2018; pp. 412–422. [Google Scholar]
- Akyildiz, T.A.; Aljundi, A.A.; Kaya, K. Gosh: Embedding big graphs on small hardware. In Proceedings of the 49th International Conference on Parallel Processing (ICPP), Edmonton, AB, Canada, 17–20 August 2020; pp. 1–11. [Google Scholar]
- Karypis, G.; Kumar, V. Multilevelk-way partitioning scheme for irregular graphs. J. Parallel Distrib. Comput. 1998, 48, 96–129. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, L.; Jiang, X.; Ma, X.; Li, Y.; Zhang, H. KG2Vec: A node2vec-based vectorization model for knowledge graph. PLoS ONE 2021, 16, e0248552. [Google Scholar] [CrossRef]
- Fionda, V.; Pirró, G. Triple2Vec: Learning Triple Embeddings from Knowledge Graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020. [Google Scholar]
- Portisch, J.; Paulheim, H. Putting rdf2vec in order. In Proceedings of the International Semantic Web Conference (ISWC 2021): Posters and Demo, Virtual Conference, 24–28 October 2021. [Google Scholar]
- Busbridge, D.; Sherburn, D.; Cavallo, P.; Hammerla, N.Y. Relational graph attention networks. arXiv 2019, arXiv:1904.05811. [Google Scholar]
- Yasunaga, M.; Ren, H.; Bosselut, A.; Liang, P.; Leskovec, J. QA-GNN: Reasoning with Language Models and Knowledge Graphs for Question Answering. In 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 535–546. [Google Scholar]
- Alshahrani, M.; Thafar, M.A.; Essack, M. Application and evaluation of knowledge graph embeddings in biomedical data. PeerJ Comput. Sci. 2021, 7, e341. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Feng, J.; Chen, Z. Knowledge graph embedding by translating on hyperplanes. In Proceedings of the AAAI Conference on Artificial Intelligence, Portsmouth, NH, USA, 21–26 June 2014; Volume 28. [Google Scholar]
- Lin, Y.; Liu, Z.; Sun, M.; Liu, Y.; Zhu, X. Learning entity and relation embeddings for knowledge graph completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Ji, G.; He, S.; Xu, L.; Liu, K.; Zhao, J. Knowledge graph embedding via dynamic mapping matrix. In 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 1: Long Papers); Association for Computational Linguistics: Stroudsburg, PA, USA, 2015; pp. 687–696. [Google Scholar]
- Xiao, H.; Huang, M.; Hao, Y.; Zhu, X. TransA: An adaptive approach for knowledge graph embedding. arXiv 2015, arXiv:1509.05490. [Google Scholar]
- Nguyen, D.Q.; Sirts, K.; Qu, L.; Johnson, M. STransE: A novel embedding model of entities and relationships in knowledge bases. In 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies; Association for Computational Linguistics: Stroudsburg, PA, USA, 2016; pp. 460–466. [Google Scholar]
- Ebisu, T.; Ichise, R. Toruse: Knowledge graph embedding on a lie group. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. RotatE: Knowledge Graph Embedding by Relational Rotation in Complex Space. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Yang, B.; Yih, W.t.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and inference in knowledge bases. arXiv 2014, arXiv:1412.6575. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T. Holographic embeddings of knowledge graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Balazevic, I.; Allen, C.; Hospedales, T. TuckER: Tensor Factorization for Knowledge Graph Completion. In 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP); Association for Computational Linguistics: Stroudsburg, PA, USA, 2019; pp. 5185–5194. [Google Scholar]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Yu, P.S. A survey on knowledge graphs: Representation, acquisition and applications. arXiv 2020, arXiv:2002.00388. [Google Scholar] [CrossRef]
- Pietrasik, M.; Reformat, M. A Simple Method for Inducing Class Taxonomies in Knowledge Graphs. In European Semantic Web Conference; Springer: Cham, Switzerland, 2020; pp. 53–68. [Google Scholar]
- Hendrickson, B.; Leland, R.W. A Multi-Level Algorithm For Partitioning Graphs. SC 1995, 95, 1–14. [Google Scholar]
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1998, 20, 359–392. [Google Scholar] [CrossRef]
- Han, X.; Cao, S.; Xin, L.; Lin, Y.; Liu, Z.; Sun, M.; Li, J. OpenKE: An Open Toolkit for Knowledge Embedding. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Brussels, Belgium, 31 October–4 November 2018. [Google Scholar]
- Portisch, J.; Hladik, M.; Paulheim, H. RDF2Vec Light—A Lightweight Approach for Knowledge Graph Embeddings. In Proceedings of the International Semantic Web Conference, Posters and Demos, Virtual Conference, 1–6 November 2020. [Google Scholar]
- Portisch, J.; Paulheim, H. Walk this way! entity walks and property walks for rdf2vec. In The Semantic Web: ESWC 2022 Satellite Events: Hersonissos, Crete, Greece, 29 May–2 June 2022, Proceedings; Springer: Cham, Switerland, 2022; pp. 133–137. [Google Scholar]
- Cochez, M.; Ristoski, P.; Ponzetto, S.P.; Paulheim, H. Biased graph walks for RDF graph embeddings. In Proceedings of the 7th International Conference on Web Intelligence, Mining and Semantics, Amantea, Italy, 19–22 June 2017; pp. 1–12. [Google Scholar]
- Portisch, J.; Heist, N.; Paulheim, H. Knowledge graph embedding for data mining vs. knowledge graph embedding for link prediction–two sides of the same coin? Semant. Web 2022, 13, 399–422. [Google Scholar] [CrossRef]
- Bhatt, S.; Padhee, S.; Sheth, A.; Chen, K.; Shalin, V.; Doran, D.; Minnery, B. Knowledge graph enhanced community detection and characterization. In Proceedings of the twelfth ACM International Conference on Web Search and Data Mining, Melbourne, VIC, Australia, 11–15 February 2019; pp. 51–59. [Google Scholar]
- Shi, X.; Qian, Y.; Lu, H. Community Detection in Knowledge Graph Network with Matrix Factorization Learning. In Web and Big Data: APWeb-WAIM 2019 International Workshops, KGMA and DSEA, Chengdu, China, August 1–3, 2019, Revised Selected Papers 3; Springer: Cham, Switzerland, 2019; pp. 37–51. [Google Scholar]
- Paul, S.; Chen, Y. Consistent community detection in multi-relational data through restricted multi-layer stochastic blockmodel. Electron. J. Stat. 2016, 10, 3807–3870. [Google Scholar] [CrossRef]
- De Bacco, C.; Power, E.A.; Larremore, D.B.; Moore, C. Community detection, link prediction, and layer interdependence in multilayer networks. Phys. Rev. E 2017, 95, 042317. [Google Scholar] [CrossRef] [PubMed]
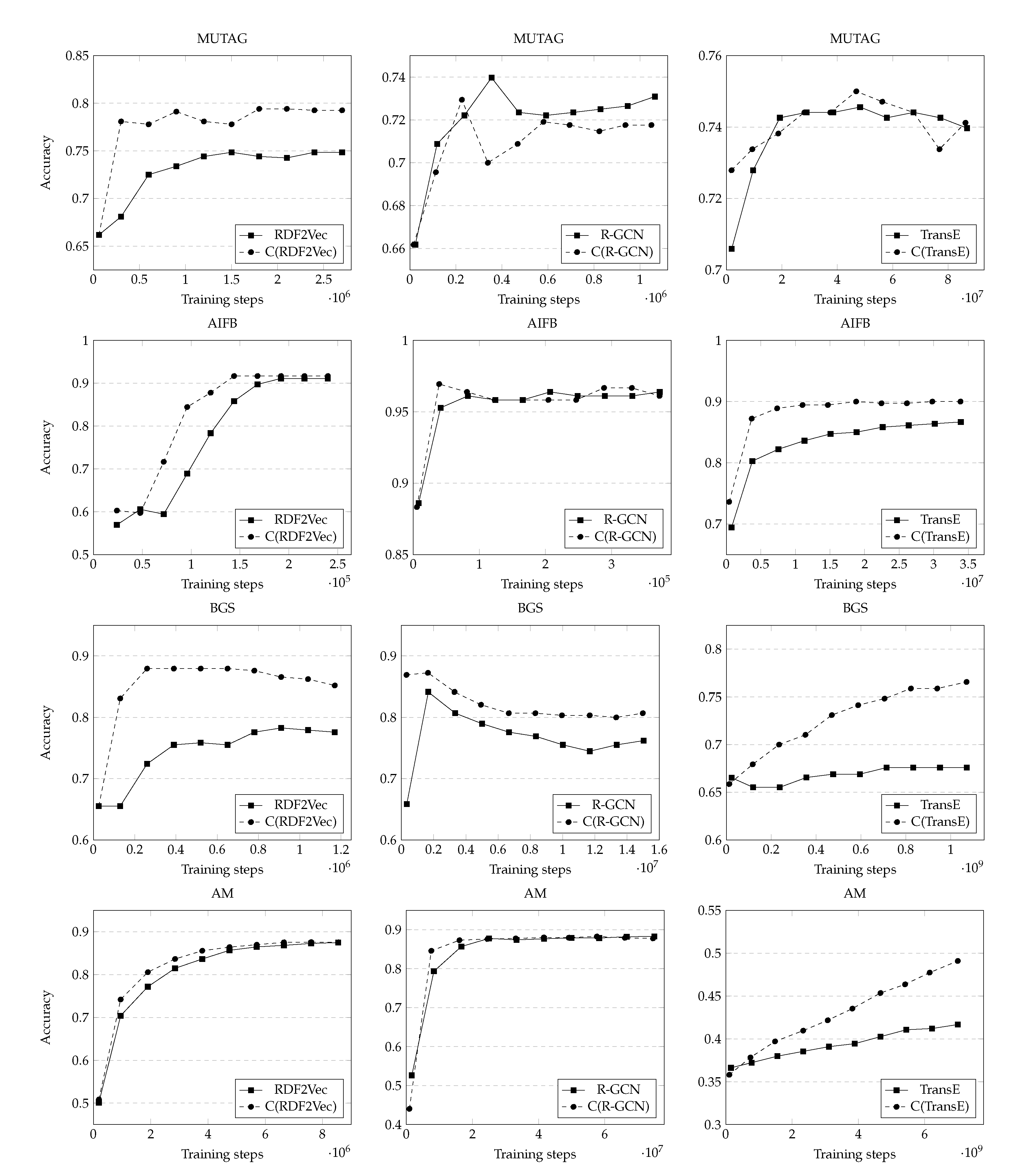
| Method | MUTAG | AIFB | BGS | AM |
|---|---|---|---|---|
| RDF2Vec | ||||
| C(RDF2Vec) | ||||
| Change | 6.1% * | 0.6% | 12.8% * | 0.2% |
| R-GCN | ||||
| C(R-GCN) | ||||
| Change | −1.4% | 1.7% * | 4.1% * | −0.1% |
| TransE | ||||
| C(TransE) | ||||
| Change | 0.3% | 3.8% * | 14.2% * | 17.7% * |
| Dataset | MUTAG | AIFB | BGS | AM |
|---|---|---|---|---|
| Triples | 52,179 | 20,134 | 501,722 | 4,080,981 |
| Change | −29.7% | −30.7% | −45.2% | −31.8% |
| Entities | 16,115 | 2801 | 78,335 | 944,759 |
| Change | −31.8% | −66.2% | −76.5% | −43.3% |
| Predicates | 23 | 43 | 97 | 129 |
| Change | 0% | −4.4% | −5.8% | −3.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietrasik, M.; Reformat, M.Z. Probabilistic Coarsening for Knowledge Graph Embeddings. Axioms 2023, 12, 275. https://doi.org/10.3390/axioms12030275
Pietrasik M, Reformat MZ. Probabilistic Coarsening for Knowledge Graph Embeddings. Axioms. 2023; 12(3):275. https://doi.org/10.3390/axioms12030275
Chicago/Turabian StylePietrasik, Marcin, and Marek Z. Reformat. 2023. "Probabilistic Coarsening for Knowledge Graph Embeddings" Axioms 12, no. 3: 275. https://doi.org/10.3390/axioms12030275
APA StylePietrasik, M., & Reformat, M. Z. (2023). Probabilistic Coarsening for Knowledge Graph Embeddings. Axioms, 12(3), 275. https://doi.org/10.3390/axioms12030275







